Crack Estimation of Beam Under the Moving Mass Using the Dynamic Characteristics Based on Two Contact Point Theory

Abstract

It is important to identify the presence of damage present in the structures like bridge which undergoes the excitation due to moving vehicles. In such type of problems, modal analysis and dynamic displacement response analysis are not sufficient to portray the crack presence. The presented work emphases on the analysis of acceleration response to investigate the crack presence. A mathematical model is developed by considering the two masses with fixed distance between them traversing on the Euler–Bernoulli beam having a crack. The acceleration response analysis can be effective to present the qualitative explanation of the fault present in the beam. A key features of the acceleration response of beam having a crack includes discontinuity at the crack location which vary with change in distance between the front and rear wheel and a greater response value compare to that for healthy in the last phase of travel from the time front wheel exits the beam. However, the effectiveness of the presentation of the crack through acceleration response depends upon the fixed distance between the front and rear wheel and the bridge length. The discontinuity will be higher for the higher ratio of distance between the front and rear wheel to the bridge length.

1 Introduction

An extensive literature is available on the problem of moving loads by considering the different loading, different boundary conditions, and different analytical as well as numerical techniques. However, only few studies are available in which the analysis is carried out on beam having fault and undergoes the moving mass excitation. Chondros et al. (1998) developed a theory to calculate the continuous vibrations of the cracked beam using fracture mechanics approach. This is presented for single-edge as well as for double-edge open crack. Considering a cracked beam as a one-dimensional continuum, a variational formulation was used to develop the differential equation and boundary conditions. The crack was modeled as the continuous flexibility using the displacement field only in the vicinity of the crack, and the stresses and the displacement field for the complete beam are modified by using the displacement field about the crack. The two independent theories, i.e., continuous cracked beam vibration theory and lumped cracked beam vibration theory are presented for vibration analysis of the cracked beam. An experimental data of aluminum beams with fatigue crack and steel beam with double-edge crack are presented which are compared well with that obtained by above method. The same method for finding out the mode shape of beam having crack has been used by many researchers to study the problem of damaged beam under the excitation of moving load. Wang and Lee (2012) suggested the reduction in stiffness of the beam due to the presence of crack with the development of a new sectional flexibility factor for the open single-edge crack. While, a crack modeled as a rotational spring has the sectional flexibility. The natural frequency and mode shapes are calculated by applying the continuity conditions and using the transfer matrix method. The suggested modified flexibility factor has the good agreement with the results of other literature for relative crack size less than 0.5. Lee and Singapore (1994) formulated the crack by placing a torsional spring at the crack location having an equivalent spring constant. A cracked beam is formed by joining the two separate segments of beam with a torsional spring at the crack location. The eigen-value of the cracked beam is found by formulating the separate vibrational mode functions for each segment which satisfy the boundary conditions. A beam with a crack at one side and subjected to the moving force on the other side is studied to analyze the dynamics response at the crack with a linear spring of very large stiffness. Lin and Chang (2006) carried out the vibration analysis of cracked cantilever beam, subjected to a single moving force, with respect to various parameters. Using the fracture mechanics method as referred by Chondros et al., compatibility conditions are formulated at the crack location, and transfer matrix was developed for establishing the relation in two segments of the beam. The mode shapes of the cracked beam are shown, and responses of the cantilever beam are obtained by convolution integral method. The response of free end is analyzed for the parameters like crack size, location, mode numbers and velocity ratio. The crack presence near the fixed end leads to the maximum displacement. Lin (2007) presented the method to determine the vibrational behavior of simply supported cracked beam subjected to the moving vehicle by using the modal expansion theory. The crack formulation is done to find the mode shapes of the each segment separated by crack. A vehicle with two axles is modeled as two concentrated moving loads separated by the fixed distance. The vehicle load is distributed on each axle from the center of gravity of the vehicle. Yang et al. (2008) studied an inhomogeneous Euler–Bernoulli beam having an open edge crack subjected to the moving force traversing in a longitudinal direction and axial compressive force to explore the free and forced vibration. A crack is modeled as a rotational spring having sectional flexibility and a beam is parted in the segments at the crack location. A relational matrix is formed using the compatibility requirements and boundary conditions at the end of beam segments and mode shapes can be found. The displacement of the beam with various boundary conditions is investigated analytically with respect to the velocity of the moving force. The major effect of the crack and compressive force can be observed on the frequency than it is on the displacement. The frequency of the damaged beam gets decreased and the deflection gets increased comparative to that for the healthy beam. The frequency and deflection are more sensitive to the applied compressive force than it is with the presence of crack and its location. Khorram et al. (2011) explored the response of the simply supported cracked beam subjected to the moving load for the crack of size 50% of the height. The variations in the response for various velocities and the displacement of beam at various locations due to the crack are compared with that for the healthy beam. Bakhtiari-Nejad and Mirzabeigy (2013) modeled the beam with breathing crack as a single-degree-of-freedom model with varying stiffness subjected to the moving force with constant velocity. The deflection of the beam is estimated by using the basic principle of strength of material and compared with that of the healthy beam found with modal expansion theory. The study also focused on effect of the location and size of crack with speed of the moving force. Mahmoud and Zaid (2002) discretized the beam into the number of elements, and the mass of each element is considered as lumped in the center of the element and assumed as connected by massless rod having flexural rigidity. A matrix is developed to form the relation which shows the status of the element at the locations immediately lies before and after the center of element through the inertia forces. This matrix gets modified with the presence of the crack. The modified recurrence equation for each element is developed and gets modified with the crack presence. The crack compliance is inserted in this equation which is found again using the fracture mechanics by considering the joining of two healthy beams at the crack location by torsional spring. The presence of crack leads to the increase in the deflection and also shifts the deflection peak to the right of beam. Ariaei et al. (2009) proposed a solution using discrete element method and finite element method. The variational method is used to extract the stiffness and mass matrix of the beam element. The dynamic response of the beam is evaluated for both the methods and comparison is made for the open and breathing crack. The methods are also evaluated with the results presented in the previous literature. The presence of crack leads to the increase in response with change in response pattern. A discontinuity appears in the response at the crack location which is very small to see with open eyes. Pala and Reis (2012) presented the inclusion of the centripetal, inertial and Coriolis forces remarkably affect the response of the system with increase in mass and speed of the moving mass. The crack is formulated by considering the two separate beam joined by torsional spring having spring constant. The fundamental vibration mode functions are found for the simply supported beam by satisfying the geometric boundary conditions at the end. The resulting equations form the relation between the two segments giving the transfer matrix, so that eigen-value and constants of each segment can be found. The response of the cracked beam is found by Duhamel integration over the domain of the beam. The study has shown the distinguished effect of considering these three forces, i.e., inertial, centripetal and Coriolis force on the response. The crack located in the middle leads to the higher deflection. The increase in crack size leads to the increase in deflection and shift of the peaks toward the right of beam. Zhong and Oyadiji used the Rayleigh method to obtain an approximate closed form solution for the simply supported beam having a crack under a roving mass. The effect of crack is introduced through the polynomial function to formulate the transverse response. The frequency of the cracked simply supported beam is observed to be reduced with increase in crack-depth and also as the roving mass traverse closer to the crack location (Zhong and Oyadiji 2007). Fernandez-Saez et al. found the Rayleigh method, natural frequency of the cracked simply supported beam. The same method of assuming the crack as a hinged torsional spring is used. A beam is not divided in two segments instead the traverse deflection response is assumed to be the addition of the response of undamaged beam and the polynomial function (Fernandez-Saez et al. 1999). Zhong et al. (2017) fixed a sensor consists of an artificial quasi-interferogram fringe pattern which is same as interferogram of 2D-OCVT system on the surface of beam structure for identification of crack presence. High-speed camera is used as a detector to capture the image sequences. The period density of the images observed to be changing with change in structural vibration. It is found that the frequency of the structure is changed as the roving auxiliary mass traversed over the structure. The method proved to be very effective for proving the information of spatial locations of crack.

The problem of damaged beam traversed by a vehicle with consideration of distributed weight over the front and rear wheel is discussed by very few researchers. Vaidya and Chatterjee (2017) used two contact point model of the vehicle traveling over the healthy beam to analyze the effect of the span between the front and rear wheel of the vehicle. Also the displacement response of the two contact point model compared with that of the single contact point model. The maximum displacement can be controlled by changing the distance between front and rear wheel especially in the case of heavy vehicles. Also in most of the research paper, the displacement response has been investigated while acceleration response should also be investigated. The dynamic response of the damaged beam contains a discontinuity at the crack location; however, it is not visible and can be seen only through magnification.

In the present work, simulated acceleration response in addition to the displacement response of damaged beam subjected to the single moving mass whose mass is distributed over the front and rear wheel. The model is equivalent to two mass moving with some fixed distance. The acceleration response contains a discontinuity at the location of crack with no change in the profile and trend of response curve. A two contact point model of vehicle is developed which includes the two moving masses with fixed distance traversing over the simply supported Euler–Bernoulli beam. The acceleration response presented has the discontinuity at the crack location with the additional feature of higher value of acceleration compare to the response value of healthy one in the last phase of travel. Therefore, the acceleration response presents the qualitative explanation about the presence of crack and its location.

2 Mathematical Modeling of a Damaged Beam

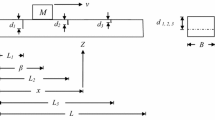
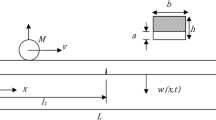
Here a simply supported beam with crack at mid-span is considered as shown in Fig. 1. Crack-depth is represented by the parameter a and a/h denotes the crack-depth ratio. l₁ denotes the location of crack from left end of the beam. The crack introduces a local flexibility which can be represented by a torsional spring (Chondros et al. 1998) as shown in Fig. 2.

Fig. 1

A simply supported beam with crack at mid-span

Fig. 2

Beam modeled with crack through a torsional spring

The crack divides the beam as two separate uniform segments connected by a torsional spring with local sectional flexibility at the crack location. This flexibility due to the crack is here termed as a parameter c, which can be found as (Chondros et al. 1998)

$$c = \frac{{\left( {1 - \vartheta^{2} } \right)}}{EI} 6\pi h\phi \left( \alpha \right)$$

(1)

where, $\alpha = a /h$ is the crack-depth ratio and $\vartheta$ is Poisson ratio

For a single-sided open crack, using fracture mechanics formulations, one can obtain

$$\begin{aligned} \phi \left( \alpha \right) & = 0.655563\alpha^{2} [0.9566 - 1.5944\alpha + 7.008\alpha^{2} - 15.21\alpha^{3} \\ & \quad + \,30.9534\alpha^{4} - 50.38657\alpha^{5} + 71.8488\alpha^{6} - 62.1624\alpha^{7} + 29.89486\alpha^{10} ] \\ \end{aligned}$$

(2)

For the cracked beam, deflection response for each segment of the beam can be written as

$$\begin{aligned} Y_{1} \left( x \right) & = C_{1} \sin \left( {\beta x} \right) + C_{2} \cos \left( {\beta x} \right) \\ & \quad + \,C_{3} \sinh \left( {\beta x} \right) + C_{4} \cosh \left( {\beta x} \right) \quad 0 < x < l_{1} \\ \end{aligned}$$

(3a)

$$\begin{aligned} Y_{2} \left( x \right) & = D_{1} \sin \left( {\beta \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta \left( {x - l_{1} } \right)} \right) \\ & \quad + \,D_{4} \cosh \left( {\beta \left( {x - l_{1} } \right)} \right) \quad l_{1} < x < L \\ \end{aligned}$$

(3b)

The applicable boundary conditions are

$$y|_{x = 0} = 0, \quad \frac{{\partial^{2} y}}{{\partial x^{2} }}|_{x = 0} = 0, \quad y|_{x = L} = 0 \;{\text{and}}\; \frac{{\partial^{2} y}}{{\partial x^{2} }}|_{x = L} = 0$$

(4)

which gives

$$\left[ {\begin{array}{*{20}l} {\sin \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill & {\cos \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill & {\sinh \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill & {\cosh \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill \\ { - \sin \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill & { - \,\cos \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill & {\sinh \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill & {\cosh \left( {\beta \left( {L - l_{1} } \right)} \right)} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \\ {D_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right]$$

(5)

denoting $y^{\prime} = \frac{\partial y}{\partial x}, y^{\prime \prime} = \frac{{\partial^{2} y}}{{\partial x^{2}}} \,{\text{and}}\,y^{\prime \prime \prime} = \frac{{\partial^{2} y}}{{\partial x^{2}}}$ and assuming the constant properties along the beam, the conditions at the crack location for both segments can be written as

$$y_{1} \left( {l_{1} ,t} \right) - y_{2} \left( {l_{1} ,t} \right) = 0$$

(6a)

$$y_{1}^{{\prime \prime }} \left( {l_{1} ,t} \right) - y_{2}^{{\prime \prime }} \left( {l_{1} ,t} \right) = 0$$

(6b)

$$y_{1}^{\prime \prime \prime} \left({l_{1},t} \right) - y_{2}^{\prime \prime \prime} \left({l_{1},t} \right) = 0$$

(6c)

$$y_{2}^{{\prime }} \left( {l_{1} ,t} \right)l_{1} - y_{1}^{{\prime }} \left( {l_{1} ,t} \right) = y_{2}^{{\prime \prime }} \left( {,t} \right)\left[ {\frac{{\left( {EIc} \right)}}{{l_{1} }}} \right]l_{1}$$

(6d)

where, (EIc/l₁) is the non-dimensional cracked section flexibility.

Equations (4, 6a–d) along with Eq. (3a) give

$$\left[ {\begin{array}{*{20}c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \\ {D_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {2a_{c} - Kb_{s} } \hfill & { - \,2b_{s} - Ka_{c} } \hfill & {Kb_{h} } \hfill & {K a_{h} } \hfill \\ {2b_{s} } \hfill & {2 a_{c} } \hfill & 0 \hfill & 0 \hfill \\ { - \,Kb_{s} } \hfill & { - \,K a_{c} } \hfill & {2a_{h} + Kb_{h} } \hfill & {2b_{hl} + Ka_{h} } \hfill \\ 0 \hfill & 0 \hfill & {2b_{h} } \hfill & {2a_{h} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ \end{array} } \right]$$

(7)

where $K = \beta EIc$

$$\begin{aligned} & a_{c} = \cos \left( {\beta l_{1} } \right)\quad a_{h} = \cosh \left( {\beta l_{1} } \right) \\ & b_{s} = \sin \left( {\beta l_{1} } \right)\quad b_{h} = \sinh \left( {\beta l_{1} } \right) \\ & a_{cl} = \cos \left( {\beta \left( {L - l_{1} } \right)} \right)\quad a_{hl} = \cosh \left( {\beta \left( {L - l_{1} } \right)} \right) \\ & b_{sl} = \sin \left( {\beta \left( {L - l_{1} } \right)} \right) \quad b_{hl} = \sinh \left( {\beta \left( {L - l_{1} } \right)} \right) \\ \end{aligned}$$

Now inserting Eq. (7) into Eq. (5) gives

$$\begin{aligned} & \left[ {\begin{array}{*{20}l} {b_{sl} } \hfill & {a_{cl} } \hfill & {b_{hl} } \hfill & {a_{hl} } \hfill \\ { - \,b_{sl} } \hfill & { - \,a_{cl} } \hfill & {b_{hl} } \hfill & {a_{hl} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {2a_{c} - Kb_{s} } \hfill & { - \,2b_{s} - Ka_{c} } \hfill & {Kb_{h} } \hfill & {K a_{h} } \hfill \\ {2b_{s} } \hfill & {2 a_{c} } \hfill & 0 \hfill & 0 \hfill \\ { - \,Kb_{s} } \hfill & { - \,K a_{c} } \hfill & {2a_{h} + Kb_{h} } \hfill & {2b_{hl} + Ka_{h} } \hfill \\ 0 \hfill & 0 \hfill & {2b_{h} } \hfill & {2a_{h} } \hfill \\ \end{array} } \right] \\ & \left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right] \\ \end{aligned}$$

(8)

This results in

$$\begin{aligned} & \left[ {\begin{array}{*{20}l} {b_{sl} N3 + 2b_{s} a_{cl} - Kb_{s} b_{hl} } \hfill & {b_{sl} N4 + 2 a_{c} a_{cl} - K a_{c} b_{hl} } \hfill & {Kb_{h} b_{sl} + N1} \hfill & {Ka_{h} b_{sl} + N2} \hfill \\ { - \,b_{sl} N3 - 2b_{s} a_{cl} - Kb_{s} b_{hl} } \hfill & { - \,b_{sl} N4 - 2 a_{c} a_{cl} - K a_{c} b_{hl} } \hfill & { - \,Kb_{h} b_{sl} + N1} \hfill & { - \,Ka_{h} b_{sl} + N2} \hfill \\ \end{array} } \right] \\ & \left[ {\begin{array}{*{20}c} {C_{1} } \\ 0 \\ {C_{3} } \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right] \\ \end{aligned}$$

(9)

where, the constants are

$$\begin{aligned} & N1 = \left( {2a_{h} + Kb_{h} } \right)b_{hl} + 2b_{h} a_{hl} \\ & N2 = b_{hl} \left( {2b_{hl} + Ka_{h} } \right) + 2a_{h} a_{hl} \\ & N3 = \left( {2a_{c} - Kb_{s} } \right) \\ & N4 = \left( { - 2b_{s} - Ka_{c} } \right) \\ \end{aligned}$$

For non-trivial solution of Eq. (9) to exit the coefficient determinant needs to be equal to zero which gives the required frequency equation as

$$\begin{aligned} & 2\cos \left( {l_{1} \beta } \right)\cosh \left( {l_{1} \beta } \right)\sin \left( {\left( {L - l_{1} } \right)\beta } \right)\sinh \left( {\left( {L - l_{1} } \right)\beta } \right) \\ & \quad + \,2\cos \left( {\left( {L - l_{1} } \right)\beta } \right)\cosh \left( {l_{1} \beta } \right)\sin \left( {l_{1} \beta } \right)\sinh \left( {\left( {L - l_{1} } \right)\beta } \right) \\ & \quad - \,K\cosh \left( {l_{1} \beta } \right)\sin \left( {\left( {L - l_{1} } \right)\beta } \right)\sin \left( {l_{1} \beta } \right)\sinh \left( {\left( {L - l_{1} } \right)\beta } \right) \\ & \quad + \,2\cos \left( {l_{1} \beta } \right)\cosh \left( {\left( {L - l_{1} } \right)\beta } \right)\sin \left( {\left( {L - l_{1} } \right)\beta } \right)\sinh \left( {l_{1} \beta } \right) \\ & \quad + \,2\cos \left( {\left( {L - l_{1} } \right)\beta } \right)\cosh \left( {\left( {L - l_{1} } \right)\beta } \right)\sin \left( {l_{1} \beta } \right)\sinh \left( {l_{1} \beta } \right) \\ & \quad - \,K\cosh \left( {\left( {L - l_{1} } \right)\beta } \right)\sin \left( {\left( {L - l_{1} } \right)\beta } \right)\sin \left( {l_{1} \beta } \right)\sinh \left( {l_{1} \beta } \right) \\ & \quad + \,K\cos \left( {l_{1} \beta } \right)\sin \left( {\left( {L - l_{1} } \right)\beta } \right)\sinh \left( {\left( {L - l_{1} } \right)\beta } \right)\sinh \left( {l_{1} \beta } \right) \\ & \quad + \,K\cos \left( {\left( {L - l_{1} } \right)\beta } \right)\sin \left( {l_{1} \beta } \right)\sinh \left( {\left( {L - l_{1} } \right)\beta } \right)\sinh \left( {l_{1} \beta } \right) = 0 \\ \end{aligned}$$

(10)

This determinant is solved to find the multiple values of $\beta$, i.e., non-dimensional natural frequency. Once this $\beta$ is obtained, it is inserted in Eq. (9) to find the value of the C₃ by assuming that C₁ = 1. Then we can find out the mode shape of the damaged beam.

3 Response Analysis of Damaged Beam Under Moving Vehicle

Figure 3a–e shows a two contact point model of the vehicle over the damaged beam during five phases of traversal. In dynamic response modeling for this case, the following assumptions are considered.

Fig. 3

Five phases of travel for two contact point model. a$0 < t \le d /v$, b$d /v < t \le l_{1} /v$, c$l_{1} /v < t \le \left( { l_{1} + d} \right) /v$, d$\left( {l_{1} + d} \right) /v < t \le L /v$, e$L /v < t \le \left( {L + d} \right) /v$

• (a) The beam is simply supported at both the ends.

• (b) Vehicle acts as a rigid mass and moves with a constant velocity, v.

• (c) Vehicle vibration is translational only. Rotational vibration is taken to be negligible and not considered.

• (d) At any time, only one vehicle traverses the bridge with zero initial conditions.

The governing differential equation of motion by considering the weight and inertia effects is written for the beam for these five different stages of travel of vehicle.

• For $t \le d /v$

  $$\begin{aligned} & EI\frac{{\partial^{4} y \left( {x, t} \right)}}{{\partial x^{4} }} + \rho A\frac{{\partial^{2} y \left( {x,t} \right)}}{{\partial t^{2} }} \\ & \quad = M_{1} g \cdot \delta \left( {x - vt} \right) - M_{1} \left[ {\frac{{\partial^{2} y}}{{\partial t^{2} }} + 2v\frac{\partial y}{\partial x}\frac{\partial y}{\partial t} + v^{2} \frac{{\partial^{2} y}}{{\partial x^{2} }}} \right] \cdot \delta \left( {x - vt} \right) \\ \end{aligned}$$

  (11)

• For $t > d /v\,{\text{and}}\,t \le l_{1} /v$;

• For $t > l_{1} /v\,{\text{and}}\,t \le \left( {l_{1} + d} \right) /v$;

• For $t > l_{1} + d /v\,{\text{and}}\,t \le L /v$

  $$\begin{aligned} & EI\frac{{\partial^{4} y \left( {x, t} \right)}}{{\partial x^{4} }} + \rho A\frac{{\partial^{2} y \left( {x,t} \right)}}{{\partial t^{2} }} \\ & \quad = M_{1} g \cdot \delta \left( {x - vt} \right) - M_{1} \left[ {\frac{{\partial^{2} y}}{{\partial t^{2} }} + 2v\frac{\partial y}{\partial x}\frac{\partial y}{\partial t} + v^{2} \frac{{\partial^{2} y}}{{\partial x^{2} }}} \right] \cdot \delta \left( {x - vt} \right) \\ & \quad + \,M_{2} g \cdot \delta \left[ {x - \left( {vt - d} \right)} \right] \\ & \quad - \,M_{2} \left[ {\frac{{\partial^{2} y}}{{\partial t^{2} }} + 2v\frac{\partial y}{\partial x}\frac{\partial y}{\partial t} + v^{2} \frac{{\partial^{2} y}}{{\partial x^{2} }}} \right] \cdot \delta \left[ {x - \left( {vt - d} \right)} \right] \\ \end{aligned}$$

  (12)

• For $t > L /v$ and $t \le \left( {L + d} \right) /v$

  $$\begin{aligned} & EI\frac{{\partial^{4} y \left( {x, t} \right)}}{{\partial x^{4} }} + \rho A\frac{{\partial^{2} y \left( {x,t} \right)}}{{\partial t^{2} }} \\ & \quad = M_{2} g \cdot \delta \left[ {x - \left( {vt - d} \right)} \right] \\ & \quad - \,M_{2} \left[ {\frac{{\partial^{2} y}}{{\partial t^{2} }} + 2v\frac{\partial y}{\partial x}\frac{\partial y}{\partial t} + v^{2} \frac{{\partial^{2} y}}{{\partial x^{2} }}} \right] \cdot \delta \left[ {x - \left( {vt - d} \right)} \right]. \\ \end{aligned}$$

  (13)

The mass $M_{1}$ is a front wheel mass and $M_{2}$ is the rear wheel mass. d is the fixed distance between the two base wheels. Using the series form solution as

$$y\left( {x,t} \right) = Y_{j} \left( x \right)\, q_{j} \left( t \right)$$

(14)

where, $q_{j} \left( t \right)$ are the modal coordinates and Y_j (x) are the mode shape spatial functions for simply supported beam. Now, substitution of Y_j (x) in Eq. (14) and multiplying each term of Eqs. (11–13) with $Y_{n} \left( x \right)$ and integrating over the domain (0, L) gives

• For $t \le d /v$

  $$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad = \frac{{2M_{1} g}}{mL}Y_{n} \left( x \right) - \frac{{2M_{1} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j} \left( x \right)Y_{n} \left( x \right)\ddot{q}_{j} \left( t \right) \\ & \quad - \frac{{4M_{1} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{'} \left( x \right) Y_{n} \left( x \right)\dot{q}_{j} \left( t \right) \\ & \quad - \frac{{2M_{1} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{''} \left( x \right)Y_{n} \left( x \right)q_{j} \left( t \right) \\ \end{aligned}$$

  (15)

• For $t > d /v\,{\text{and}}\,t \le l_{1} /v$;

• For $t > l_{1} /v\;{\text{and}}\,t \le \left( {l_{1} + d} \right) /v$;

• For $t > l_{1} + d /v\,{\text{and}}\,t \le L /v$

  $$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad = \frac{{2M_{1} g}}{mL}Y_{n} \left( x \right) - \frac{{2M_{1} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j} \left( x \right)Y_{n} \left( x \right)\ddot{q}_{j} \left( t \right) \\ & \quad - \frac{{4M_{1} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{'} \left( x \right)Y_{n} \left( x \right)\dot{q}_{j} \left( t \right) - \frac{{2M_{1} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{''} \left( x \right)Y_{n} \left( x \right)q_{j} \left( t \right) \\ & \quad + \frac{{2M_{2} g}}{mL}Y_{n} \left( {x - d} \right) - \frac{{2M_{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j} \left( {x - d} \right)Y_{n} \left( {x - d} \right)\ddot{q}_{j} \left( t \right) \\ & \quad - \frac{{4M_{2} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{'} \left( {x - d} \right)Y_{n} \left( {x - d} \right)\dot{q}_{j} \left( t \right) \\ & \quad - \frac{{2M_{2} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{''} \left( {x - d} \right)Y_{n} \left( {x - d} \right)q_{j} \left( t \right) \\ \end{aligned}$$

  (16)

• For $t > L /v$ and $t \le \left( {L + d} \right) /v$

  $$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) = \frac{{2M_{2} g}}{mL}Y_{n} \left( {x - d} \right) - \frac{{2M_{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j} \left( {x - d} \right)Y_{n} \left( {x - d} \right)\ddot{q}_{j} \left( t \right) \\ & \quad - \frac{{4M_{2} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{'} \left( {x - d} \right)Y_{n} \left( {x - d} \right)\dot{q}_{j} \left( t \right) \\ & \quad - \frac{{2M_{2} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } Y_{j}^{''} \left( {x - d} \right)Y_{n} \left( {x - d} \right)q_{j} \left( t \right) \\ \end{aligned}$$

  (17)

All these three Eqs. (15–17) can be detailed for total time of travel of vehicle, i.e., 0 < t < L/v by the following equation

$$\begin{aligned} & EI\mathop \sum \limits_{j = 1}^{\infty } \frac{{{\text{d}}^{4} Y_{j} \left( x \right)}}{{{\text{d}}x^{4} }} q_{j} \left( t \right) + \rho A\mathop \sum \limits_{j = 1}^{\infty } Y_{j} \left( x \right)\ddot{q}_{j} \left( t \right) \\ & \quad + \mathop \sum \limits_{k = 1}^{2} M_{k} \alpha_{k} \left\{ {\mathop \sum \limits_{j = 1}^{\infty } Y_{j} \left( x \right)\ddot{q}_{j} \left( t \right) + 2v\mathop \sum \limits_{j = 1}^{\infty } \frac{{{\text{d}}Y_{j} \left( x \right)}}{{{\text{d}}x}}\dot{q}_{j} \left( t \right) + v^{2} \mathop \sum \limits_{j = 1}^{\infty } \frac{{{\text{d}}^{2} Y_{j} \left( x \right)}}{{{\text{d}}x^{2} }}q_{j} \left( t \right)} \right\}\delta \left( {x + \overline{k - 1} d - vt} \right) \\ & \quad = \mathop \sum \limits_{k = 1}^{2} M_{k} \alpha_{k} g \delta \left( {x + \overline{k - 1} d - vt} \right). \\ \end{aligned}$$

(18)

Such that $\alpha_{k} = 1,\,{\text{when}}\, 0 < vt - \left( {k - 1} \right)d < L\,{\text{and}}\, \alpha_{k} = 0$ otherwise, which means that kth point is yet to enter the beam or it has already travelled past the beam. Now multiplying each term of Eq. (18) with $Y_{n} \left( x \right)$ and integrating over the domain (0, L), one obtains

$$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad + \frac{2}{mL} \mathop \sum \limits_{k = 1}^{2} \alpha_{k} M_{k} \mathop \sum \limits_{j = 1}^{\infty } Y_{j} \left( {vt - kd + d} \right)Y_{n} \left( {vt - kd + d} \right)\ddot{q}_{j} \left( t \right) \\ & \quad + \frac{4v}{mL}\mathop \sum \limits_{k = 1}^{2} \alpha_{k} M_{k} \mathop \sum \limits_{j = 1}^{\infty } \frac{{{\text{d}}Y_{j} \left( {vt - kd + d} \right)}}{{{\text{d}}x}}Y_{n} \left( {vt - kd + d} \right)\dot{q}_{j } \left( {\text{t}} \right) \\ & \quad + \frac{{2v^{2} }}{mL} \mathop \sum \limits_{k = 1}^{2} \alpha_{k} M_{k} \mathop \sum \limits_{j = 1}^{\infty } \frac{{{\text{d}}^{2} Y_{j} \left( {vt - kd + d} \right)}}{{{\text{d}}x^{2} }}Y_{n} \left( {vt - kd + d} \right)q_{j} \left( t \right) + \\ & \quad = \frac{2}{mL}\mathop \sum \limits_{k = 1}^{2} \alpha_{k} M_{k} gY_{n} \left( {vt - kd + d} \right). \\ \end{aligned}$$

(19)

Now, the dynamic response of the damaged beam can be found by inserting the mode shape derived in Eq. (3a) and (3b) for first and second segment of the beam in the above equations for the five phases of travel of vehicle as follows.

• For $t \le d/v$

• $$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad = \frac{{2M_{1} g}}{mL}\left[ {C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) + C_{4} \cosh \left( {\beta_{n} x} \right)} \right] \\ & \quad - \,\frac{{2M_{1} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \left[ {C_{1} \sin \left( {\beta_{j} x} \right) + C_{2} \cos \left( {\beta_{j} x} \right) + C_{3} \sinh \left( {\beta_{j} x} \right) + C_{4} \cosh \left( {\beta_{j} x} \right)} \right] \\ & \quad *\,\left[ {C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) + C_{4} \cosh \left( {\beta_{n} x} \right)} \right]*\ddot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{4M_{1} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} \left[ {C_{1} \cos \left( {\beta_{j} x} \right) - C_{2} \sin \left( {\beta_{j} x} \right) + C_{3} \cosh \left( {\beta_{j} x} \right) + C_{4} \sinh \left( {\beta_{j} x} \right)} \right] \\ & \quad *\,\left[ {C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) + C_{4} \cosh \left( {\beta_{n} x} \right)} \right] *\dot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{2M_{1} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j}^{2} *\left[ { - C_{1} \sin \left( {\beta_{j} x} \right) - C_{2} \cos \left( {\beta_{j} x} \right) + C_{3} \sinh \left( {\beta_{j} x} \right) + C_{4} \cosh \left( {\beta_{j} x} \right)} \right] \\ & \quad \left[ {C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) + C_{4} \cosh \left( {\beta_{n} x} \right)} \right] q_{j} \left( t \right) \\ \end{aligned}$$

  (20)

• For $t > d /v\,{\text{and}}\, t \le l_{1} /v$;

  $$\begin{aligned} & 4\omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad = \frac{{2M_{1} g}}{mL}\left[ {C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) + C_{4} \cosh \left( {\beta_{n} x} \right)} \right] \\ & \quad - \,\frac{{2M_{1} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \left[ {C_{1} \sin \left( {\beta_{j} x} \right) + C_{2} \cos \left( {\beta_{j} x} \right) + C_{3} \sinh \left( {\beta_{j} x} \right) + C_{4} \cosh \left( {\beta_{j} x} \right)} \right] \\ & \quad *\,\left[ {C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) + C_{4} \cosh \left( {\beta_{n} x} \right)} \right]\ddot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{4M_{1} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [C_{1} \cos \left( {\beta_{j} x} \right) - C_{2} \sin \left( {\beta_{j} x} \right) + C_{3} \cosh \left( {\beta_{j} x} \right) \\ & \quad \quad + \,C_{4} \sinh \left( {\beta_{j} x} \right)][C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{n} x} \right)]*\dot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{2M_{1} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j}^{2} [ - C_{1} \sin \left( {\beta_{j} x} \right) - C_{2} \cos \left( {\beta_{j} x} \right) + C_{3} \sinh \left( {\beta_{j} x} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{j} x} \right)][C_{1} \sin \left( {\beta_{n} x} \right) + C_{2} \cos \left( {\beta_{n} x} \right) + C_{3} \sinh \left( {\beta_{n} x} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{n} x} \right)]q_{j} \left( t \right) \\ & \quad + \,\frac{{2M_{2} g}}{mL}[C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)] \\ & \quad - \,\frac{{2M_{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } [C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)]*[C_{1} \sin \left( {\beta_{n} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{2} \cos \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{n} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{n} \left( {x - d} \right)} \right)]*\ddot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{4M_{2} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad + \,C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)]\,*\,[C_{1} \sin \left( {\beta_{n} \left( {x - d} \right)} \right) \\ & \quad \quad + C_{2} \cos \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{4} \cosh \left( {\beta_{n} \left( {x - d} \right)} \right)] \\ & \quad - \,\frac{{2M_{2} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)] \\ & \quad *\,[C_{1} \sin \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{n} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{n} \left( {x - d} \right)} \right)]q_{j} \left( t \right) \\ \end{aligned}$$

  (21)

• For $t > l_{1} /v\,{\text{and}}\,t \le \left( {l_{1} + d} \right) /v$

  $$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad = \frac{{2M_{1} g}}{mL}[D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right)] \\ & \quad - \,\frac{{2M_{1} }}{mL}\sum\limits_{j = 1}^{\infty } {[D_{1} \sin \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right)} \\ & \quad \quad + \,D_{4} \cosh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right)]*[D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) ]\ddot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{4M_{1} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [D_{1} \cos \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) - D_{2} \sin \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{3} \cosh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{4} \sinh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) ][D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) ]*\dot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{2M_{1} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j}^{2} [ - D_{1} \sin \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) - D_{2} \cos \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) \\ & \quad + \quad \,D_{4} \cosh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) ][D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) ]q_{j} \left( t \right) \\ & \quad + \,\frac{{2M_{2} g}}{mL}[C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)] \\ & \quad - \,\frac{{2M_{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } [C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)]*[C_{1} \sin \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{n} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{3} \sinh \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{4} \cosh \left( {\beta_{n} \left( {x - d} \right)} \right)]\ddot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{4M_{2} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)]*[C_{1} \sin \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{n} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{n} \left( {x - d} \right)} \right)] - \frac{{2M_{2} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j}^{2} [ - \,C_{1} \sin \left( {\beta_{j} \left( {x - d} \right)} \right) - C_{2} \cos \left( {\beta_{j} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{3} \sinh \left( {\beta_{j} \left( {x - d} \right)} \right) + C_{4} \cosh \left( {\beta_{j} \left( {x - d} \right)} \right)] \\ & \quad *\,[C_{1} \sin \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{2} \cos \left( {\beta_{n} \left( {x - d} \right)} \right) + C_{3} \sinh \left( {\beta_{n} \left( {x - d} \right)} \right) \\ & \quad \quad + \,C_{4} \cosh \left( {\beta_{n} \left( {x - d} \right)} \right)]q_{j} \left( t \right) \\ \end{aligned}$$

  (22)

• For $t > (l_{1} + d) /v\,{\text{and}}\,t \le L /v$

  $$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad = \frac{{2M_{1} g}}{mL}[D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) ] \\ & \quad - \,\frac{{2M_{1} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } [D_{1} \sin \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) ]*[D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad + \,D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) ] \\ & \quad *\,\ddot{q}_{j} \left( t \right) - \frac{{4M_{1} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [D_{1} \cos \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) - D_{2} \sin \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \cosh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{4} \sinh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) ]*[D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) ] \\ & \quad *\,\dot{q}_{j} \left( t \right) - \frac{{2M_{1} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j}^{2} [ - D_{1} \sin \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad - \,D_{2} \cos \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{j} \left( {x - l_{1} } \right)} \right)] \\ & \quad *\,[D_{1} \sin \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) + D_{3} \sinh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{4} \cosh \left( {\beta_{n} \left( {x - l_{1} } \right)} \right) ]q_{j} \left( t \right) \\ & \quad + \,\frac{{2M_{2} g}}{mL}[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad - \,\frac{{2M_{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } [D_{1} \sin \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad *\,[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) ]\ddot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{4M_{2} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [D_{1} \cos \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) - D_{2} \sin \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad + \,D_{3} \cosh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \sinh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad *\,[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) ]\dot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{2M_{2} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j}^{2} [ - D_{1} \sin \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) - D_{2} \cos \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad *\,[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)]q_{j} \left( t \right) \\ \end{aligned}$$

  (23)

• For $t \ge L/v$

  $$\begin{aligned} & \omega_{n}^{2} q_{n} \left( t \right) + \ddot{q}_{n} \left( t \right) \\ & \quad = \frac{{2M_{2} g}}{mL}[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad - \,\frac{{2M_{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } [D_{1} \sin \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad *\,[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) ]\ddot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{4M_{2} v}}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j} [D_{1} \cos \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) - D_{2} \sin \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \cosh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \sinh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad *\,[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) ]\dot{q}_{j} \left( t \right) \\ & \quad - \,\frac{{2M_{2} v^{2} }}{mL}\mathop \sum \limits_{j = 1}^{\infty } \beta_{j}^{2} [ - D_{1} \sin \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) - D_{2} \cos \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{j} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)] \\ & \quad *\,[D_{1} \sin \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{2} \cos \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) \\ & \quad \quad + \,D_{3} \sinh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right) + D_{4} \cosh \left( {\beta_{n} \left( {\left( {x - d} \right) - l_{1} } \right)} \right)]q_{j} \left( t \right) \\ \end{aligned}$$

  (24)

  These equations are solved by Fourth order Runge–Kutta numerical method.

4 Results and Discussion

A typical beam mass system with following parameters is considered for simulation.

$$L = 20\,{\text{m}},\,\rho A = 312\,{\text{kg/m}},\,E = 2.06 \times 10^{11} \,{\text{N/m}}^{2} \,{\text{and}}\,\rho = 7800\,{\text{kg/m}}^{3} .$$

The mid-span displacement responses are investigated by considering the moving mass to beam mass ratio as 0.2 in the range of velocity ratio [velocity of the moving mass to the critical velocity $\left( {\frac{{\omega_{n} L}}{n \pi }} \right)$] between 0.1 and 1 (critical velocity). The displacement responses of the beam show the combined effect of the first three modes of vibration. The crack-depth ratio (α) considered is 0.25, located at the center of the beam. The responses are normalized by dividing the dynamic deflection with static mid-span deflection $\left( {\frac{{WL^{3} }}{48 EI}} \right)$.

5 Deflection Response Analysis

The deflection response for healthy and damaged beam is compared for the velocity ratio [velocity of the moving mass to the critical velocity $\left( {\frac{{\omega_{n} L}}{n \pi }} \right)$] 0.1, 0.4, and 0.8. The distance between the wheels d is varied as 2 and 3 m. In Figs. 4, 5 and 6, x-axis represents the total time taken by the rear wheel to leave the right end of the beam. This time is increasing as the distance between the front and rear wheel is increasing. The normalized position of the moving mass is the distance travelled by rear wheel to the total length of beam.

Fig. 4

Mid-span deflection for healthy and damaged beam for velocity ratio = 0.2. ad = 3 m, bd = 2 m, cd = 0

Fig. 5

Mid-span deflection for healthy and damaged beam for velocity ratio 0.4. ad = 3 m, bd = 2 m, cd = 0

Fig. 6

Mid-span deflection for healthy and damaged beam for velocity ratio 0.8. ad = 3 m, bd = 2 m, cd = 0

Following observations can be noted from Figs. 4, 5 and 6

• (a) There is an increase in the deflection response with the presence of crack.

• (b) The deflection response of the cracked beam changes as function of velocity.

• (c) The difference in the peak value of the deflection for healthy and damaged is very small for lower velocity. At higher velocity, the presence of crack can be indicated by the rise in the deflection value.

• (d) At lower velocity, there is not any significant change in deflection response of cracked beam instead the displacement value suddenly gets jumped compared to that for healthy as soon as the front mass left the beam.

• (e) For lower velocity, the vehicle takes more time to travel the transition phase, when only the rear wheel is on the bridge. During this small part of time, the mass loading reduces to half and hence the difference seen between the two response.

6 Acceleration Response Analysis

The acceleration responses of the healthy and damaged beam are plotted to interpret the presence of the crack and its key features like its location and severity. The analysis is carried out with respect to the velocity of the moving mass, i.e., for velocity ratio 0.1, 0.2, 0.4, 0.6 and 0.8. The acceleration responses calculated by the fixed sensor approach at mid-span of the beam are shown in Figs. 7, 8, 9, 10 and 11. In fixed sensor approach, a sensor is considered to be attached at the center span of the beam. The displacement responses are obtained at the mid-span of beam by simulation.

Fig. 7

Acceleration response of the healthy and damaged beam, velocity ratio 0.1. ad = 0, bd = 1 m, cd = 2 m, dd = 3 m

Fig. 8

Acceleration response of the healthy and damaged beam, velocity ratio 0.2. ad = 0, bd = 1 m, cd = 2 m, dd = 3 m

Fig. 9

Acceleration response of the healthy and damaged beam, velocity ratio 0.4. ad = 0, bd = 1 m, cd = 2 m, dd = 3 m

Fig. 10

Acceleration response of the healthy and damaged beam, velocity ratio 0.6. ad = 0, bd = 1 m, cd = 2 m, dd = 3 m

Fig. 11

Acceleration response of the healthy and damaged beam, velocity ratio 0.8. ad = 0, bd = 1 m, cd = 2 m, dd = 3 m

The key points observed from the accelerations response are established as

• (a) At velocity ratio 0.1, the sudden distortion in the response of damaged beam remarkably represents the location of the crack.

• (b) For all the distance (d) between the wheels, the acceleration values are same as it is for healthy until the first wheel excites the crack location. After the wheel excites the crack location, change in acceleration values can be observed.

• (c) The fluctuations in the response are observed to take place at the crack location for a certain time period equivalent to the (d/v).

• (d) The same discontinuity in the response of the damaged beam can be observed when the front wheel leaves the beam.

• (e) At higher velocities, the acceleration response significantly changes after the excitation of crack location but the key features like discontinuity and the sudden change in acceleration at the end are not reflected in the graph.

So, the acceleration responses at the lower velocity ratios 0.1 and 0.2 can be helpful in finding the crack presence and its location. If the results of the moving sensor and fixed sensor are compared for identification of the crack, both approaches are helpful for this type of two contact point model. The visibility of discontinuity at crack location obtained by both approaches is sufficiently higher but only for lower velocities. Therefore, for crack identification, the vehicle can run over the bridge at the speeds corresponding to the velocity ratio 0.1 and 0.2.

A considerable increase in the value of the displacement response and acceleration response of damaged beam compared to that of healthy beam can be observed during the last phase of travel. This increase in the mid-span response during the last phase of vehicle travel cannot be ignored from the safety point of view.

7 Conclusion

A mathematical model has been developed for two contact point vehicle–bridge interaction in the present work. This model is more representative than single contact point model mostly adopted in the previous research works. The acceleration response illustrates the crack presence more effectively than the displacement response. A distortion at the crack location depends on the distance between the front and rear wheel. The distortion will be for more period as the distance between the front and rear wheel increases. A difference in the acceleration values also represents the presence of crack. These features are more distinguishable for lower velocity ratio than that for higher velocity ratio. The responses measured are useful in representing the information about crack.