1 Introduction

Nanotubes have a very broad range of electronic, thermal and structural properties that change depending on the different kinds of nanotube length, chirality or twist (Mongillo 2009). Since their discovery in 1991 by Iijima (1991), both single-wall carbon nanotubes (SWNTs) and multi-wall carbon nanotubes (MWNTs) have become an active area of research. Simply, carbon nanotubes (CNTs) are long, thin cylinders of carbon that are unique in their size, shape and remarkable physical properties. CNTs can be thought of as rolled up; closed graphite sheets (see Fig. 1).

Fig. 1
figure 1

Illustration of CNTs and cross section

Full size image

Being only a few times wider than atoms, CNTs offer exceptionally high material properties such as electrical and thermal conductivity, stiffness, toughness and remarkable strength (Wilson et al. 2002). Their properties and cylindrical shapes allow for their potential applications in such diverse fields as fibrous reinforcement, atomic label piping and nanostructures. Besides CNTs are structured to serve as a capstone design materials for new nanoelectronics and switching devices. For the sake of example, CNTs have been proposed as nanomachines. They make good nanotweezer tips for electron microscopy, and multi-wall nanotubes can be pulled in and out like pistons. Calculations have been made to understand their role as mechanical nanogears. Furthermore, CNTs with certain defects can act as transistors and CNTs can store hydrogen and may also be useful with lithium as batteries. They have unusual tensile strength and may make valuable building materials if manufactured cheaply in quantity, other potential applications of CNTs include: flat panel display screens, actuators, chemical sensors (Wilson et al. 2002). Behaviors of NEMS (Nanoelectromechanical systems) are usually described by two theoretical approaches such as molecular dynamics (MD) and continuum mechanics approach (CMA). MD is the most common method in examining CNT behavior. Liew et al. (2008) used MD based on a second-generation reactive empirical bond order (REBO) potential to simulate the flexural wave propagation in a single-walled carbon nanotube (SWCNT). Yakobson et al. (1996), Wu (2004), Cho et al. (2007), Zhang et al. (2009) and Tsai and Tu (2010) studied mechanical behavior of CNTs and single graphene layer and graphene flakes. Then continuum models have been proven to be important and efficient tools in the study of nanostructures (Narendar and Gopalakrishnan 2009).

Controlled experiments in nanoscale are difficult, and molecular dynamic simulations are computationally expensive and take excessive time to compute. To analyze small-scale structures by considering size effect, nonlocal theory is one of the theories which is the extension of the classical field theory for the application in nanoscale (Reddy 2007; Reddy and Pang 2008; Thai 2012; Shen and Zhang 2011). Nonlocal continuum modeling with nonlocal elasticity has been established and used as a reliable tool for the analyses of nanostructures (Peddieson et al. 2003; Wang and Liew 2007). Nevertheless, there is a need to upgrade the classical nonlocal continuum theories to account for the small-scale effects. Vibration analysis of CNTs is important for better understanding of mechanical responses of CNTs. In the literature, there have been a number of studies about vibration of CNTs (Wang et al. 2007; Wang 2009; Ansari and Gholami 2015; Demir et al. 2010; Yang et al. 2010; Murmu and Adhikari 2010; Ansari et al. 2011; Rafiei et al. 2012; Eltaher et al. 2012, 2013a, b; Nami and Janghorban 2015; Yan et al. 2013; Ansari et al. 2014; Chakraverty and Behera 2014; Ansari et al. 2013). Zhang et al. (2005) developed a double-elastic beam model based on Euler–Bernoulli beam theory for transverse vibrations of double-walled carbon nanotubes under compressive axial load to investigate the effects of the axial load on the natural frequencies of double-walled carbon nanotubes. Furthermore, Civalek and Akgöz (2010) studied free vibration of microtubules based on Euler–Bernoulli beam theory by differential quadrature method to show the effect of the behavior on the frequencies of microtubules. Besides, Civalek and Demir (2011) presented an approach for obtaining accurate bending moments and displacements in microtubules based on Euler–Bernoulli beam theory by differential quadrature method. Nonlocal constitutive equations used in all the studies (Wang et al. 2007; Wang 2009; Ansari and Gholami 2015; Demir et al. 2010; Yang et al. 2010; Murmu and Adhikari 2010; Ansari et al. 2011; Rafiei et al. 2012; Eltaher et al. 2012, 2013a, b; Nami and Janghorban 2015; Yan et al. 2013; Ansari et al. 2014; Chakraverty and Behera 2014; Ansari et al. 2013) are based on the hypothesis that the stress is a function of strains at all points in the continuum (Eringen 2002; Eringen 1983; Eringen 1976; Eringen 1972; Eringen and Edelen 1972). In the literature, finite element formulations are used and derived in some studies (Eltaher et al. 2013b; Phadikar and Pradhan 2010; Adhikari et al. 2013; Pradhan 2012). All these studies have focused on vibration analysis in terms of nonlocal, small-scale effects based on EBT or TBT by use of a great number of elements to converge analytical (also exact) solutions. Neither of them has constituted nor derived an exact element which provides exact solutions for the vibration problem of CNTs. Instead, they have employed too many elements to minimize error and also deviate from exact results. The present work aims to develop finite element method in such a way that it can be employed in the study of free vibration of CNTs based on both nonlocal EBT and TBT modeling with only one element per member. The size effect is taken into consideration using the Eringen’s nonlocal elasticity theory. Finite element method introduced widely in the 1960s, and formulations are based on cubic Hermitian functions (Cook et al. 2001). In this paper, by use of EBT and TBT governing equations, finite element formulations are derived. Applying the clamped end boundary conditions, the governing equation is solved to obtain exact dynamic shape functions by finite element method. The exact dynamic shape functions construct the bases for obtaining exact dynamic stiffness terms. Due to use of exact shape and dynamic stiffness terms, the proposed solution strictly satisfies equilibrium equations, not only at the element nodes but also within the element, which would not have been the case if Hermitian interpolation functions had been used. This is one of the benefits of the proposed element, and it only requires one element per member to obtain results and converges to exact solution with minimal computational effort. Explicit forms of both exact dynamic shape functions and exact dynamic stiffness terms are presented. Numerical results for free vibration of CNTs are also served up to demonstrate the benefits of the proposed solutions.

2 Equations of Nonlocal Beam Theories

2.1 Euler–Bernoulli Beam Theory

The governing equation for free vibration of carbon nanotubes based on Euler–Bernoulli beam theory (EBT) can be written as (Reddy and Pang 2008)

$$\frac{{\partial^{2} }}{{\partial x^{2} }}\left( { - EI\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \mu \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {m_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - m_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right] = m_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - m_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}$$
(1)

where \(\mu = e_{\text{o}}^{2} L_{{}}^{2}\) (nonlocal parameter), m 0 = ρA,  (mass inertia) \(m_{2} = \rho A\frac{{h^{2} }}{12},\) (mass inertia) ρ is the mass density and A is the cross-sectional area of the carbon nanotube.

e o is a material constant, L is the element length for carbon nanotube, and h is the depth of the carbon nanotube.

For free vibration, the solution can be written as

$$w\left( {x,t} \right) = W\left( x \right)e^{i\omega t}$$
(2)

where w(x, t) denotes the transverse displacements, depending on position and time, W is the mode shape, and ω is the frequency of natural vibration. Substitution of this expression into Eq. (1) yields

$$p\frac{{{\text{d}}^{4} W\left( x \right)}}{{{\text{d}}x^{4} }} + q\frac{{{\text{d}}^{2} W\left( x \right)}}{{{\text{d}}x^{2} }} - rW = 0$$
(3)

where \(p = EI - \mu m_{2} \omega^{2}\), q = m 2 ω 2 + μm 0 ω 2, r = m 0 ω 2

2.2 Timoshenko Beam Theory

The governing equations for the natural vibration of the Timoshenko beam theory (TBT) are (Reddy and Pang 2008)

$$\frac{d}{{{\text{d}}x}}\left( {GAK_{s} \left( {\Phi + \frac{{{\text{d}}W}}{{{\text{d}}x}}} \right)} \right) + \omega^{2} m_{0} \left[ {W - \mu \frac{{{\text{d}}^{2} W}}{{{\text{d}}x^{2} }}} \right] = 0$$
(4)
$$EI\frac{{{\text{d}}^{2}\Phi }}{{{\text{d}}x^{2} }} - GAK_{s} \left( {\Phi + \frac{{{\text{d}}W}}{{{\text{d}}x}}} \right) + \omega^{2} m_{2} \left[ {\Phi - \mu \frac{{{\text{d}}^{2}\Phi }}{{{\text{d}}x^{2} }}} \right] = 0$$
(5)

where W and \(\Phi\) are deflection and rotation that define the mode shapes. By eliminating \(\Phi\) from the two equations, Eq. (4) can be solved for \({\text{d}}\Phi /{\text{d}}x\)

$$\frac{{{\text{d}}\Phi }}{{{\text{d}}x}} = - \frac{{m_{0} \omega^{2} }}{{GAK_{s} }}W - \left( {1 - \frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right)\frac{{{\text{d}}^{2} W}}{{{\text{d}}x^{2} }}$$
(6)

By differentiating Eq. (5) once and substituting for \({\text{d}}\Phi /{\text{d}}x\) and \({\text{d}}^{3}\Phi /{\text{d}}x^{3}\) from Eq. (6), one can obtain

$$\begin{aligned} & \left( {EI - \mu m_{2} \omega^{2} } \right)\left( {1 - \frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right)\frac{{{\text{d}}^{4} {\text{W}}}}{{{\text{d}}x^{4} }} + \left( {GAK_{s} + \frac{{m_{0} \omega^{2} }}{{GAK_{s} }}\left( {EI - \mu m_{2} \omega^{2} } \right) + \left( {m_{2} \omega^{2} - GAK_{s} } \right)\left( {1 - \frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right)} \right) \\ & \frac{{{\text{d}}^{2} W}}{{{\text{d}}x^{2} }} + \frac{{m_{0} \omega^{2} }}{{GAK_{s} }}\left( {m_{2} \omega^{2} - GAK_{s} } \right)W = 0 \\ \end{aligned}$$
(7)

Equation (7) can be rewritten as same as the form given in Eq. (3).

Except that

$$p = \left( {EI - \mu m_{2} \omega^{2} } \right)\left( {1 - \frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right),$$
$$q = \left( {m_{0} \omega^{2} \left( {\Omega _{0} + \mu } \right) + m_{2} \omega^{2} \left( {1 - 2\frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right)} \right),$$
$$r = m_{0} \omega^{2} \left( {1 - \frac{{m_{2} \omega^{2} }}{{GAK_{s} }}} \right).$$

where G is shear modulus, K s is shear correction coefficient, \(\Omega _{0}\) is the shear deformation parameter, and A is the cross-sectional area of the carbon nanotube. From Eq. (3), it should be noted that the nonlocal parameter μ and shear deformation parameter \(\Omega _{0}\) have the effect of reducing the natural frequency. In the present study, clamped end type boundary conditions are considered for both EBT and TBT and are also given as w = 0, and dw/dx = 0.

3 Finite Element Analysis

The implementation of finite element analysis to the problem involves some steps explained briefly in this section. These steps are identical for both EBT and TBT.

Firstly, Eq. (3) can be rewritten as

$$\frac{{{\text{d}}^{4} y}}{{{\text{d}}x^{4} }} + A\frac{{{\text{d}}^{2} y}}{{{\text{d}}^{2} x}} - By = 0$$
(8)

For EBT;

$$A = \frac{{m_{2} \omega^{2} + \mu m_{0} \omega^{2} }}{{EI - \mu m_{2} \omega^{2} }}$$
(9)
$$B = \frac{{m_{0} \omega^{2} }}{{EI - \mu m_{2} \omega^{2} }}$$
(10)

For TBT;

$$A = \frac{{\left( {m_{0} \omega^{2} \left( {\Omega _{0} + \mu } \right) + m_{2} \omega^{2} \left( {1 - 2\frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right)} \right)}}{{\left( {EI - \mu m_{2} \omega^{2} } \right)\left( {1 - \frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right) }}$$
(11)
$$B = \frac{{m_{0} \omega^{2} \left( {1 - \frac{{m_{2} \omega^{2} }}{{GAK_{s} }}} \right)}}{{\left( {EI - \mu m_{2} \omega^{2} } \right)\left( {1 - \frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right) }}$$
(12)

By use of Eq. (8), elements should be formulated. As a result of this formulation, solution for dynamic shape functions and dynamic stiffness terms of the proposed element can be obtained.

The roots of the characteristic equation given in Eq. (8) are

$$D_{1} = - \beta i \quad D_{2} = \beta i$$
(13)
$$D_{3} = - \gamma \quad D_{4} = \gamma$$
(14)

where

$$\beta = \frac{{\sqrt {A + \sqrt {4B + A^{2} } } }}{\sqrt 2 }\quad \gamma = \frac{{\sqrt { - A + \sqrt {4B + A^{2} } } }}{\sqrt 2 }$$
(15)

provided that \(\sqrt {4B + A^{2} } > 0\). Then, the complementary solution for Eq. (8) is

$$y\left( x \right) = c_{1} {\text{Cos}} \left[ {\beta x} \right] + c_{2} \text{Cosh} \left[ {\gamma x} \right] + c_{3} \text{Sin} \left[ {\beta x} \right] + c_{4} \text{Sinh} \left[ {\gamma x} \right]$$
(16)

The constants c 1 − c 4 can be obtained after enforcing the following clamped end type boundary conditions:

$$y\left( 0 \right) = v_{1} , \quad \frac{{{\text{d}}y}}{{{\text{d}}x}}\left( 0 \right) = \theta_{1} ,\quad y\left( L \right) = v_{2} , \quad \frac{{{\text{d}}y}}{{{\text{d}}x}}\left( L \right) = \theta_{2}$$
(17)

Then,

$$\left\{ {\begin{array}{*{20}c} {v_{1} } \\ {\theta_{1} } \\ {v_{2} } \\ {\theta_{2} } \\ \end{array} } \right\} = \varvec{H }\left\{ {\begin{array}{*{20}c} {c_{1} } \\ {c_{2} } \\ {c_{3} } \\ {c_{4} } \\ \end{array} } \right\}$$
(18)

The matrix \(\varvec{H}\) can be constructed by substituting the boundary conditions into Eq. (16). Finally, Eq. (18) is solved for c 1 − c 4, and then, this result is substituted back into Eq. (16) to obtain the following:

$$y\left( x \right) = \left\lfloor {\begin{array}{*{20}c} {N_{1} } & {N_{2} } & {N_{3} } & {N_{4} } \\ \end{array} } \right\rfloor \left\{ {\begin{array}{*{20}c} {v_{1} } \\ {\theta _{1} } \\ {v_{2} } \\ {\theta _{2} } \\ \end{array} } \right\}$$
(19)

The functions N 1 − N 4 are the shape functions because they are directly derived from the solution of Eq. (8). In other words, Eq. (19) satisfies the governing equilibrium equation in Eq. (8). It is also verified that N 1 − N 4 converges to Hermitian (cubic) polynomials at the limit (i.e., μ and \(m_{0} \to 0\)). Explicit form of the shape functions is

$$N_{1} = \frac{{\left( {\begin{array}{*{20}c} {\beta {{\text{Cos}}} \left[ {\gamma x} \right] \left( { - \gamma + \beta \text{Sin} \left[ {L\beta } \right]\text{Sin} \left[ {L\gamma } \right]} \right) + } \\ {\beta \text{Cosh} \left[ {L\gamma } \right]\left( {\gamma {\text{Cos}} \left[ {\left( {L - x} \right)\beta } \right] + \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {\gamma x} \right] - \beta {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {\gamma x} \right]} \right) - } \\ {\gamma \left( {\beta {\text{Cos}} \left[ {\beta x} \right] + \text{Sinh} \left[ {L\gamma } \right]\left( {\gamma {\text{Sin}} \left[ {\left( {L - x} \right)\beta } \right] + \beta {\text{Cos}} \left[ {L\beta } \right]\text{Sinh} \left[ {\gamma x} \right]} \right)} \right)} \\ \end{array} } \right)}}{{2 \beta \gamma \left( { - 1 + {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right]) + \left( {\beta - \gamma } \right)\left( {\beta + \gamma } \right){\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]} \right)}}$$
(20)
$$N_{2} = \frac{{\left( {\begin{array}{*{20}c} { - \gamma {\text{Sin}} \left[ {\beta x} \right] + \beta \left( {{\text{Cos}} \left[ {\left( {L - x} \right)\beta } \right] - {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {\gamma x} \right]} \right)\text{Sinh} \left[ {L\gamma } \right] - } \\ {\left( {\beta + \gamma {\text{Sin}} \left[ {L\beta } \right] \text{Sinh} \left[ {L\gamma } \right]} \right)\text{Sinh} \left[ {\gamma x} \right] + } \\ {\text{Cosh} \left[ {L\gamma } \right]\left( {\gamma \text{Cosh} \left[ {\gamma x} \right]{\text{Sin}} \left[ {L\beta } \right] - \gamma {\text{Sin}} \left[ {\left( {L - x} \right)\beta } \right] + \beta {\text{Cos}} \left[ {L\beta } \right]\text{Sinh} \left[ {\gamma x} \right]} \right)} \\ \end{array} } \right)}}{{2 \beta \gamma \left( { - 1 + {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right]) + \left( {\beta - \gamma } \right)\left( {\beta + \gamma } \right){\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]} \right)}}$$
(21)
$$N_{3} = \frac{{\left( {\begin{array}{*{20}c} { - \gamma (\beta \left( {{\text{Cos}} \left[ {\left( {L - x} \right)\beta } \right] - {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {\gamma x} \right] + \text{Cosh} \left[ {L\gamma } \right]\left( { - {\text{Cos}} \left[ {\beta x} \right] + \text{Cosh} \left[ {\gamma x} \right]} \right)} \right) + } \\ {\gamma {\text{Sin}} \left[ {\beta x} \right]\text{Sinh} \left[ {L\gamma } \right]) + \beta \left( {\beta {\text{Sin}} \left[ {L\beta } \right] + \gamma \text{Sinh} \left[ {L\gamma } \right]} \right)\text{Sinh} \left[ {\gamma x} \right]} \\ \end{array} } \right)}}{{2 \beta \gamma \left( { - 1 + {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right]) + \left( {\beta - \gamma } \right)\left( {\beta + \gamma } \right){\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]} \right)}}$$
(22)
$$N_{4} = \frac{{\left( {\begin{array}{*{20}c} {\gamma {\text{Sin}} \left[ {\left( {L - x} \right)\beta } \right] + \gamma \text{Cosh} \left[ {L\gamma } \right]{\text{Sin}} \left[ {\beta x} \right] - \beta {\text{Cos}} \left[ {\beta x} \right]\text{Sinh} \left[ {L\gamma } \right] + } \\ {{\text{Cos}} \left[ {\gamma x} \right]\left( { - \gamma {\text{Sin}} \left[ {L\beta } \right] + \beta \text{Sinh} \left[ {L\gamma } \right]} \right) + \beta \left( {{\text{Cos}} \left[ {L \beta } \right] - \text{Cosh} \left[ {L\gamma } \right]} \right)\text{Sinh} \left[ {\gamma x} \right]} \\ \end{array} } \right)}}{{2 \beta \gamma \left( { - 1 + {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right]) + \left( {\beta - \gamma } \right)\left( {\beta + \gamma } \right){\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]} \right)}}$$
(23)

If these processes are continued by allowing γ and β also to approach zero in Eqs. (20), (21), (22), (23), one can obtain the cubic Hermitian polynomials as follows:

$$N_{1} = \frac{{\left( {L - x} \right)^{2} \left( {L + 2x} \right)}}{{L^{3} }}$$
(24)
$$N_{2} = \frac{{\left( {L - x} \right)^{2} x}}{{L^{2} }}$$
(25)
$$N_{3} = \frac{{\left( {3L - 2x} \right)x^{2} }}{{L^{3} }}$$
(26)
$$N_{4} = \frac{{x^{2} \left( { - L + x} \right)}}{{L^{2} }}$$
(27)

These expressions provide checks on the accuracy of the computations in that one can successively reduce Eqs. (20), (21), (22) and (23) to Eqs. (24), (25), (26), (27) by letting both A and B approach zero. This is a common theme for most derivations in this paper. Use of Hermitian polynomials leads to conventional stiffness terms in finite element. Herein the exact dynamic shape functions are compared with Hermitian polynomials in order to make clear the effect of nonlocal parameters in response. This is one of the advantages of Hermitian shape functions. One of the aims of this study is to show the relations such that at limiting cases of the parameters (such as \(m_{2} ,m_{0} ,\Omega _{0} ,G,A, K_{s}\) and \(\omega\)) when they approach to zero, the derived shape functions and dynamic stiffness terms converge to Hermitian shape functions and conventional stiffness terms, respectively.

For this reason, it is a guiding light to exemplify the variation of the shape function as a function of \(m_{2} ,m_{0} ,\Omega _{0} ,G,A,K_{s}\) and ω or nonlocal parameter \(\mu\) and to compare them with the corresponding Hermitian polynomials. This can be achieved by defining their interaction in the form of a three-dimensional surface graph. To serve this purpose, two new nondimensional variables, p and z, are introduced in such a way that z = AL 2 and p = BL 4. In Figs. 2 and 3, the surface plots of shape functions N 1 and N 2 are presented. These plots show the variation through a range of values for z at the values of p = 1 × 10−27, 10 × 10−27, 50 × 10−27 and 100 × 10−27. The horizontal axis denoted by ξ is the nondimensional axial coordinate which is x/L. The shapes for N3 and N4 are simply the antisymmetric mirror images of N1 and N2, respectively. It is observed from the figures that for small values of A (approximately characterized by 0 ≤ p ≤ 1 × 10−27), and the resulting shape is almost the same as Hermitian shape functions. Whereas, for large values of z (i.e., higher nonlocal effect), the shape functions deviate considerably from the Hermitian shape functions.

Fig. 2
figure 2

Surface plots of N 1

Full size image
Fig. 3
figure 3

Surface plots of N 2

Full size image

The convergence case can be also demonstrated in detail for N 1 by Table 1 and Fig. 4. For Table 1 and Fig. 4, as convergence parameters p and z (the appropriate combination of physical parameters given in Eqs. (9), (10) and (11), (12) for EBT and TBT, respectively) increase, the shape function diverges from Hermitian polynomials (Hermitian shape functions). In other words, if nonlocal effect increases (which is the case of larger z), N 1 diverges from Hermitian shape function (given in Eq. (24)). This is why error increases as p and z increase. The same results are also valid for other shape functions.

Table 1 Comparison of N 1 in terms of Hermitian polynomials and the convergence parameters
Full size table
Fig. 4
figure 4

Error of the Convergence of parameters for N 1

Full size image

Subsequently, dynamic stiffness matrix terms are obtained from the following equation:

$$K_{ij} = \mathop \int \limits_{0}^{L} \frac{{{\text{d}}^{2} N_{i} }}{{{\text{d}}x^{2} }}\frac{{{\text{d}}^{2} N_{j} }}{{{\text{d}}x^{2} }}{\text{d}}x - A\mathop \int \limits_{0}^{L} \frac{{{\text{d}}N_{i} }}{{{\text{d}}x}}\frac{{{\text{d}}N_{j} }}{{{\text{d}}x}}{\text{d}}x - B\mathop \int \limits_{o}^{L} N_{i} N_{j} {\text{d}}x .$$
(28)

in which the first integral yields material stiffness terms, the second integrals are related to element attributed to nonlocal effect and dynamic effects. The term N i represents ith shape function, and all of the above integrals are carried out over the element length L. It is interesting to note that the second and the third integrals have a destabilizing effect on the stiffness terms. This is also consistent with the fact that nonlocal effect reduces the stiffness (Wang et al. 2007; Wang 2009; Ansari and Gholami 2015; Demir et al. 2010; Yang et al. 2010; Murmu and Adhikari 2010; Ansari et al. 2011; Rafiei et al. 2012; Eltaher et al. 2012, 2013a, b; Nami and Janghorban 2015; Yan et al. 2013; Ansari et al. 2014; Chakraverty and Behera 2014; Ansari et al. 2013).

In the previous sections, the shape functions are derived separately. Now it is time to substitute them into the above equation to obtain dynamic stiffness terms. The dynamic stiffness terms are explicitly derived and obtained as follows:

$$k_{11} = - \frac{{ \beta \gamma \left( {\beta^{2} + \gamma^{2} } \right) \left( {\beta \text{Cosh} \left[ {L\gamma } \right]{\text{Sin}} \left[ {L \beta } \right] + \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]} \right)}}{{ - 2\beta \gamma + 2\beta \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right] + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]}}$$
(29)
$$k_{12} = \frac{{ \beta \gamma \left( { - \beta^{2} + \gamma^{2} + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Cos}} \left[ {L\beta } \right] \text{Cosh} \left[ {L\gamma } \right] - 2\beta \gamma {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]} \right) }}{{ - 2\beta \gamma + 2\beta \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right] + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]}}$$
(30)
$$k_{13} = \frac{{ \beta \gamma \left( {\beta^{2} + \gamma^{2} } \right) \left( {\beta {\text{Sin}} \left[ {L\beta } \right] + \gamma \text{Sinh} \left[ {L\gamma } \right]} \right)}}{{ - 2\beta \gamma + 2\beta \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right] + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]}}$$
(31)
$$k_{14} = \frac{{ \beta \gamma \left( {\beta^{2} + \gamma^{2} } \right) \left( { {\text{Cos}} \left[ {L\beta } \right] - \text{Cosh} \left[ {L\gamma } \right]} \right)}}{{ - 2\beta \gamma + 2\beta \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right] + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]}}$$
(32)
$$k_{22} = \frac{{ \left( {\beta^{2} + \gamma^{2} } \right) \left( { - \gamma \text{Cosh} \left[ {L\gamma } \right]{\text{Sin}} \left[ {L\beta } \right] + \beta {\text{Cos}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]} \right)}}{{ - 2\beta \gamma + 2\beta \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right] + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]}}$$
(33)
$$k_{23} = - \frac{{ \beta \gamma \left( {\beta^{2} + \gamma^{2} } \right) \left( {{\text{Cos}} \left[ {L\beta } \right] - \text{Cosh} \left[ {L\gamma } \right]} \right)}}{{ - 2\beta \gamma + 2\beta \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right] + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]}}$$
(34)
$$k_{24} = - \frac{{\left( {\beta^{2} + \gamma^{2} } \right) \left( { - {\text{Sin}} \left[ {L\beta } \right] + \beta \text{Sinh} \left[ {L\gamma } \right]} \right)}}{{ - 2\beta \gamma + 2\beta \gamma {\text{Cos}} \left[ {L\beta } \right]\text{Cosh} \left[ {L\gamma } \right] + \left( {\beta^{2} - \gamma^{2} } \right) {\text{Sin}} \left[ {L\beta } \right]\text{Sinh} \left[ {L\gamma } \right]}}$$
(35)
$$k_{33} = k_{11}$$
(36)
$$k_{34} = - k_{12}$$
(37)
$$k_{44} = k_{22}$$
(38)
$$\frac{{\beta = \sqrt {A + \sqrt {A^{2} + 4B} } }}{\sqrt 2 }\quad \frac{{\gamma = \sqrt { - A + \sqrt {A^{2} + 4B} } }}{\sqrt 2 }$$
(39)

Moreover, the derived stiffness terms are normalized with respect to their conventional stiffness terms and portrayed graphically in Fig. 5. It is noted from the figure that the diagonal terms decrease as p increases, and for some ranges of p and z, they can become negative.

Fig. 5
figure 5

Normalized stiffness terms

Full size image

3.1 Mass Matrix

Mass matrix is obtained by calculation of the third integral in Eq. (28). The 4 × 4 mass matrix m in terms of shape functions for a uniform segment with mass per unit length is found by computation of the following integral (Franklin 2001; Alemdar and Gülkan 1997).

$${\mathbf{m}} = B\int \varvec{N}^{\varvec{T}} \varvec{N}dx$$
(40)

When calculating the integral β, γ are being set to zero which is the case of use of Hermitian interpolation functions, the 4 × 4 matrix takes the following matrix form:

$${\mathbf{m}} = \frac{B}{420}\left[ {\begin{array}{*{20}c} {156} & {22L} & {54} & { - 13L} \\ {22L} & {4L^{2} } & {13L} & { - 3L^{2} } \\ {54} & {13L} & {156} & { - 22L} \\ { - 13L} & { - 3L^{2} } & { - 22L} & {4L^{2} } \\ \end{array} } \right]$$
(41)

3.2 Geometric Stiffness Matrix

Geometric stiffness matrix is obtained by calculation of the second integral in Eq. (28). Components of the geometric stiffness matrix can be obtained by computation of the following integral (Franklin 2001; Alemdar and Gülkan 1997).

$$\varvec{K}_{\varvec{G}} = A\int \frac{{{\text{d}}\varvec{N}^{T} }}{{{\text{d}}x}}\frac{{{\text{d}}\varvec{N}}}{{{\text{d}}x}}{\text{d}}x$$
(42)

The terms contained in Eq. (43) have also been obtained in closed form when β, \(\gamma\) are being set to zero which is the case of use of Hermitian interpolation functions.

The 4 × 4 matrix becomes

$$\varvec{K}_{\varvec{G}} = \frac{A}{30L}\left[ {\begin{array}{*{20}c} {36} & {3L} & { - 36} & {3L} \\ {3L} & {4L^{2} } & { - 3L} & { - L^{2} } \\ { - 36} & { - 3L} & {36} & { - 3L} \\ {3L} & { - L^{2} } & { - 3L} & {4L^{2} } \\ \end{array} } \right]$$
(43)

Equations (43) and  (41) are simply the outcomes of Eqs. (42) and (40), respectively, for p = z = 0. When only z = 0 is considered, the solution is for local Euler–Bernoulli beam theory.

3.3 Conventional Stiffness Matrix

When β, \(\gamma\) are being set to zero which is the case of use of Hermitian interpolation functions, the integral in Eq. (28) has been computed for each stiffness term. As a result, the following 4 × 4 consistent and conventional stiffness matrix is obtained.

$$\varvec{K} = \frac{EI}{{L^{3} }}\left[ {\begin{array}{*{20}c} {12} & {6L} & { - 12} & {6L} \\ {6L} & {4L^{2} } & { - 6L} & {2L^{2} } \\ { - 12} & { - 6L} & {12} & { - 6L} \\ {6L} & {2L^{2} } & { - 6L} & {4L^{2} } \\ \end{array} } \right]$$
(44)

4 Numerical Results

Numerical analysis related to free vibration of CNTs is presented in this section. Free vibration frequencies are calculated with the derived element. It should be noted that these frequencies are the values of ω which makes the determinant of stiffness matrix zero. These results are then compared to solutions obtained by analytical (Reddy and Pang 2008) and finite element method in which an eigenvalue analysis is carried out in such a way that \(\left( {\left( {K + K_{G} } \right) - \omega^{2} M} \right)\Phi = 0\) where K, K G and M are the assembled stiffness, geometric stiffness and mass matrices, respectively, and \(\Phi\) express the corresponding shapes of the vibrating system known as the eigenvectors (also called mode shapes). The resulting eigenvalue matrix dimension is 4 × 4 for clamped end type boundary conditions. This dimension is also the same for other types of boundary conditions. It should be noted that different boundary conditions yield different shape functions. In fact, this study has focused on clamped end type boundary condition. Here, the proposed solution requires more than one element per member so consistent mass matrices are used. The proposed element is added to a finite element library implemented in Mathematica (Wolfram 1988). The material and geometric values of CNT are given in Table 2. The analytical results of Reddy and Pang (2008) are compared with the present study results and given in Tables 3 and 4 for both EBT and TBT.

Table 2 Material and geometric properties of CNT (Reddy and Pang 2008)
Full size table
Table 3 Nondimensional natural frequencies clamped CNTs based on EBT when L = 1.5 × 10−9 m
Full size table
Table 4 Nondimensional natural frequencies clamped CNTs based on TBT when L = 1.5 × 10−9 m
Full size table

In Tables 3 and 4, deviation (%) in terms of error is considerably lower and is achieved by only one element. This situation proves that this study attains its aim.

Frequencies of 12 modes with various nonlocal parameters are plotted for clamped end CNT based on TBT and EBT in Figs. 6 and 7, respectively.

Fig. 6
figure 6

Variation of frequencies of clamped end CNT based on TBT

Full size image
Fig. 7
figure 7

Variation of frequencies of clamped end CNT based on EBT

Full size image

Figures 8 and 9 illustrate the effect of nonlocal parameter and L/h on the vibration characteristics for clamped CNTs.

Fig. 8
figure 8

Variation of frequencies for different L/h and nonlocal parameter based on TBT

Full size image
Fig. 9
figure 9

Variation of frequencies for different L/h and nonlocal parameter based on EBT

Full size image

As shown in both Figs. 8 and 9, as the nonlocal parameter increased, the frequencies decreased. No significant effect of slenderness ratio (L/h) on frequencies except for the third frequency based on TBT was observed. But this is not the case for the frequencies based on EBT. The effect of slenderness ratio is reduced by increasing the nonlocal parameter. This trend is compatible with experimental results. In Rudd and Broughton (1999), it was found that the fundamental frequency obtained by molecular simulation is always less than that obtained by the classical continuum elasticity theory. This tendency is also consistent with the findings in this study for the clamped CNTs.

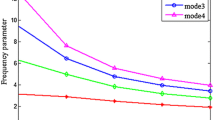
Figures 10 and 11 are presented to show the frequency response for different mode numbers and nonlocal parameters for both EBT and TBT separately.

Fig. 10
figure 10

Variation of frequencies for various mode numbers and nonlocal parameter based on EBT

Full size image
Fig. 11
figure 11

Variation of frequencies for various mode numbers and nonlocal parameter based on TBT

Full size image

As shown in both Figs. 10 and 11, as the nonlocal parameter and mode number increased, the frequencies decreased for both EBT and TBT. It should be noted that this decrease of frequency for the case of TBT is much more and quicker than that for the case of EBT. For instance, for the case e o = 10, at modes 21 and 22, the frequencies based on TBT approach zero quicker than those on EBT.

5 Discussion and Conclusions

Nonlocal theories of the Euler–Bernoulli and Timoshenko beam theories are furthered, and analytical solutions for clamped end boundary condition are derived for free vibration of CNTs.

By use of the derived finite element, this paper propounds a new approach for obtaining accurate frequencies of CNTs using both nonlocal theories: EBT and TBT. Dynamic shape functions and dynamic stiffness terms are explicitly derived and presented. The following observations and results are obtained from the figures and tables:

  • In general, the effect of nonlocal parameter, shear deformation parameter and mass inertia is to reduce the fundamental frequencies.

At the limiting cases of the physical parameters (i.e., \(\mu \to 0\), \(\Omega _{0} \to 0\) m 2 → 0, GAK s  → 0 and \(\omega \to 0\)), the derived shape functions and dynamic stiffness terms converge to the Hermitian shape functions and conventional stiffness terms, respectively.

  • If \(\frac{{m_{0} \omega^{2} }}{{EI - \mu m_{2} \omega^{2} }}\) for EBT and \(\frac{{m_{0} \omega^{2} \left( {1 - \frac{{m_{2} \omega^{2} }}{{GAK_{s} }}} \right)}}{{\left( {EI - \mu m_{2} \omega^{2} } \right)\left( {1 - \frac{{\mu m_{0} \omega^{2} }}{{GAK_{s} }}} \right) }}\) for TBT are described approximately by the interval \(0 \le p \le 1\times10^{ - 27}\), the resulting shape of shape functions is almost the same as the Hermitian shape. Conversely, the shape functions diverge remarkably from the Hermitian shape functions in case of higher nonlocal effect (for large values of z).

  • The effect of mode number is to decrease the fundamental frequencies in case of both EBT and TBT.

  • Numerical results prove that the nonlocal parameter yields an important contribution and has an effect on the vibration of CNTs.

  • Vibration analysis results are also in good agreement with CNTs nonlocal modeling based on both EBT and TBT.

  • The method may also be applicable for obtaining the bending and buckling solutions of CNTs using the nonlocal beam theory based on EBT and TBT.

  • This method leads to minimal computational effort with the advantage of using only one element which converges best to exact solution.

The present model is expected to be very efficient in the analysis and design of nanostructures under different boundary conditions with complex geometries and various load conditions. Further, the present work can be extended to higher order beam theories for accurate analysis of thick nanostructures.