1 Introduction

Weirs and gates are common and important structures usually used to control and measure flow in open channels. In waterways with alluvial beds where weirs are used, sediments deposit upstream of the weir, reduce its effective height over time, and ultimately deteriorate its performance. Compared to a single weir, a combined weir–gate structure may be used to measure flow discharge and, at the same time, avoid sediment deposition behind the structure.

As classical flow measuring devices, researchers have carried out extensive studies on flow over triangular sharp-crested weirs and through rectangular gates. Rajaratnam (1977), French (1986), Swamee (1992), Lozano et al. (2009), Habibzadeh et al. (2011), Belaud et al. (2012), and Khalili Shayan and Farhoudi (2013) were among researchers studying flow through gates (sluice gates). Among investigations conducted on weirs, studies by Swamee (1988), Bos (1989), Munson et al. (1994), Johnson (2000), Aydin et al. (2002), Martínez et al. (2005), Qu et al. (2009), Aydin et al. (2011), Chanson and Wang (2013), and Bautista-Capetillo et al. (2014) may be found in the literature.

Performance of a combined weir–gate structure has also been investigated by some researchers. Negm (1995) is among early researchers studying characteristics of a free combined flow over a rectangular weir with different side contractions and through a rectangular gate. El-Saiad et al. (1995) studied combined flow through high-discharge irrigation channels. They focused their investigations on a rectangular weir combined with a V-notch gate and a V-notch weir combined with a rectangular gate to present a flow estimation equation for both systems as:

$$\frac{{Q_{t} }}{{\sqrt {2g} d^{2.5} }} = - 5.119 + 1.475\left( {\frac{H + h}{d}} \right) - 2.531\left( {\frac{h}{b}} \right) + 0.367\left( {\frac{b}{{b_{1} }}} \right) + 1.2698$$
(1)

They also concluded that the combination of a V-notch weir and a rectangular gate performs better than the combination of a rectangular weir and a V-notch gate.

Negm et al. (1997) studied the effect of downstream submergence on flow discharge and derived a set of equations for free flow through a triangular weir over a contracting sluice gate and vice versa with specific restrictions. They concluded that the gate submergence ratio (tail water depth to the gate opening) affects upstream water height and flow discharge. They proposed the following equation for a triangular weir placed over a rectangular gate:

$$\frac{{Q_{t} }}{{\sqrt {2g} d^{2.5} }} = - 0.019 + 0.875\left( {\frac{H + h}{d}} \right) - 1.308\left( {\frac{h}{b}} \right) + 0.005\left( {\frac{b}{{b_{1} }}} \right) + 0.074\theta - 0.663\left( {\frac{{h_{\text{d}} }}{d}} \right)$$
(2)

The following constraints were considered in derivation of Eq. 2:

$$1 < \frac{b}{d} < 3,1 < \frac{y}{d} < 3,2.9 < \frac{(H + h)}{d} < 7.9\,{\text{and}}\,0.6 < \frac{b}{{b_{1} }} < 5.4.$$

Characteristics of combined flow through a triangular weir over a contracting rectangular gate were studied by Alhamid et al. (1997), too. He assumed that the combined weir–gate acts as a single gate and, therefore, derived a total discharge equation like that of a gate (a function of H1/2):

$$Q_{\text{t}} = \left[ {0.84 + \frac{{2.41\tan \left( {\frac{\theta }{2}} \right)^{0.498} \left( {\frac{h}{B}} \right)^{1.56} }}{{\left( {\frac{H}{y}} \right)^{1.76} \left( {\frac{d}{d + y}} \right)^{0.325} \left( {\frac{b}{B}} \right)^{0.522} }}} \right]^{4} \times A_{\text{g}} \sqrt {2gH}$$
(3)

The following constraints were considered in his study:

$$0.3 < \frac{y}{H} < 0.7,0.17 < \frac{b}{B} < 0.5,30 < \theta < 90,0.35 < \frac{d}{d + y} < 0.5\,{\text{and}}\,H > (d + y).$$

Negm (2000) simulated a combined rectangular weir and a rectangular gate model and developed a relationship for the flow. He generalized his model and presented an equation for both free and submerged flows. Negm et al. (2002) conducted similar experiments on different channel slopes and analyzed their model with different geometries for both mild and steep slopes and presented an equation for all models. Hayawi et al. studied the effect of hydraulic and geometric parameters on the discharge coefficient computed from an equation similar to the rectangular weir equation. They present the following equation for prediction of total discharge:

$$\frac{{Q_{\text{t}} }}{{g^{0.5} h^{2.5} }} = 0.0197\left( {\frac{y}{h}} \right)^{0.2195} \left( {\frac{b}{h}} \right)^{1.647} \left( {\frac{d}{h}} \right)^{0.543}$$
(4)

subject to the following constraints.

$$30 < \theta < 60,0.05 < y < 0.15$$

Altan-Sakaraya and Kokpinar (2013) conducted experiments to find a discharge–depth relationship for simultaneous flow through rectangular gates and over rectangular weirs.

In recent years, popularity of soft computing models has increased in various fields due to their capability for solving complex and nonlinear problems that might otherwise not have any tractable solution. Multilayer perceptron (MLP) artificial neural networks (ANN) and support vector machines (SVM) may be considered as two of the most popular soft computing models utilized in hydraulic applications. Baylar et al. (2009) used SVM to predict aeration performance of plunging overfall jets from weirs. Ozkan and Kaya (2010) used MLP and adaptive neuro-fuzzy inference system (ANFIS) models to predict air demand ratio in Venturi weirs. Bilhan et al. (2011) and Emiroghlu et al. (2011) used MLP, multiple linear and nonlinear regression models to predict discharge coefficient for a triangular labyrinth side weir in curved and straight channels, respectively. Juma et al. (2014) used MLP to determine discharge coefficient for a hollow semicircular crested weir. Mohammadpour et al. (2015) used SVM to predict water quality index in constructed wetlands. Balouchi et al. (2015) used ANN and M5P model tree to predict maximum scour depth at river confluences under live-bed conditions. Haghiabi et al. (2017) used MLP and SVM to predict head loss on a cascade weir. Their results show that SVM yields better results than MLP. Parsaie et al. (2017) evaluated ANFIS and MLP models for a cylindrical weir–gate similar to a broad crested weir and compared it with a sharp-crested weir. In their study, they showed that MLP is the superior model.

In the present study, four combined triangular weir and rectangular gate physical models with different gate dimensions, and a single weir physical model were constructed. Experiments were conducted for different discharges with extended measuring ranges for relevant parameters. Then, the effects of hydraulic and geometric parameters on discharge coefficient through these models were studied. MLP and support vector regression (SVR; as a certain type of SVM) models were constructed, trained, and tested to estimate discharge coefficients for a variety of combined weir–gate structures under different discharges. Results were compared with equations presented for flow through combined weir and gate structures in the literature.

2 Materials and Methods

Figure 1 shows the overall flowchart and methodology for this study. As shown, once dimensional analysis and experimental setup were completed, measurements were made and the effect of each non dimensional parameter on discharge coefficient was experimentally investigated. The collected data set was divided into training and validating subsets and fed to the soft computing models. Statistical indices were used to compare accuracy of the models for discharge coefficient prediction in combined weir–gate structures. Finally, results were compared and contrasted with equations presented in previous studies for similar structures.

Fig. 1
figure 1

Methodology flowchart for the current study

Full size image

2.1 Physical Model Setup and Dimensional Analyses

A 11-m-long, 0.25-m-wide, and 0.5-m-deep rectangular channel in Hydraulic Laboratory of Water Engineering Department at Shahid Chamran University was used for experimental tests. Water was pumped into an elevated tank and fed into the channel with a constant rate, measured by a standard 53° triangular weir and a digital gage with 0.1 mm accuracy.

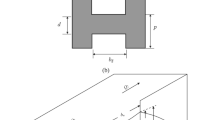
Four combined weir–gate structures and a single weir were all cut by a laser machine out of a 10-mm-thick Plexiglas sheet. All weirs were triangular ones with 60° top angles, and their top edges were beveled according to USBR standards. Figure 2 and Table 1 give variables and dimensions for the models. A total of 46 experiments were carried out with ranges of relevant dimensionless ratios as; \(0.96 < \frac{h}{b} < 3.62\), \(0.18 < \frac{h}{y} < 0.75\), \(2.12 < \frac{h}{d} < 12.16\), \(1 < \frac{b}{d} < 4\), \(4.6 < \frac{y}{d} < 21.4\), \(9.8 < \frac{(H + h)}{d} < 46.7\), and \(0.045 < \frac{d}{(d + y)} < 0.18\).

Fig. 2
figure 2

The physical model sketches and variables for combined weir–gate structures

Full size image
Table 1 Ranges of relevant variables for five models utilized in the study
Full size table

Performing a dimensional analysis, similar hydraulic characteristics of utilized weirs and gates were combined. For this purpose, it was inferred that the discharge through a combined structure depends upon geometric, kinematic, and dynamic variables:

$$\left\{ {Q_{t} ,g,h,\mu ,\theta ,\sigma ,\rho ,v,d,b,y,B} \right\}$$
(5)

where Qt is total discharge through the structure, g is gravitational acceleration, h is water head over the weir, µ is fluid dynamic viscosity, θ is the top angle of the triangular weir, σ is surface tension, ρ is flow density, v is fluid velocity, d is gate height, b is gate width, y is the distance between top of the gate and bottom of the weir, and B is channel width (all shown in Fig. 2). With a total of twelve independent parameters and three major quantities (length, mass, and time), nine dimensionless variables were derived based on Buckingham π theorem:

$$\frac{{Q_{t} }}{{b\sqrt {0.125g} (H - d)^{1.5} }} = f\left( {{\text{Re}},{\text{We}},{\text{Fr}},\theta ,\frac{h}{d},\frac{h}{y},\frac{h}{b},\frac{h}{B}} \right)$$
(6)

where Re, We, and Fr are Reynolds, Weber, and Froude numbers, respectively. In this study, water depth over the weir–gate was sufficiently high and surface tension (and Weber number) effects were neglected. Furthermore, the effect of viscosity (Reynolds number) was neglected due to dominance of a turbulent flow and relatively high discharges through the models. The term \(\frac{{Q_{\text{t}} }}{{b\sqrt {0.125g} (H - d)^{1.5} }}\) on Eq. 6 was considered as a representative for Froude number (Fr), and the number itself on the right-hand side of the equation was removed. θ was constant in all models, and therefore, it was concluded that the term \(\frac{{Q_{\text{t}} }}{{b\sqrt {0.125g} (H - d)^{1.5} }}\) (a dimensionless discharge, or discharge coefficient Cd) is a function of three dimensionless ratios only:

$$C_{\text{d}} = \frac{{Q_{\text{t}} }}{{b\sqrt {0.125g} (H - d)^{1.5} }} = f\left( {\frac{h}{d},\frac{h}{b},\frac{h}{y}} \right)$$
(7)

The conventional discharge equation for a triangular weir is a function of h2.5 and for a rectangular gate a function of H0.5 (Munson et al. 1994). Therefore, one may expect discharge through a combined triangular weir–rectangular gate structure (Qt) to be a function of a water head indicator somewhere between h and H, to a power between 0.5 and 2.5. Hence, for the combined structure authors proposed Eq. 7, where discharge is considered a function of (H − d)1.5.

2.2 Soft Computing Models

MLP and SVR soft computing models were constructed with three non dimensional parameters (\(\frac{h}{d},\frac{h}{b},\frac{h}{y}\)) as their inputs and the discharge coefficient as their output parameter. 70% of the data set was randomly selected from different experimental models and used to train the models, while the remaining 30% of the data set was used for models validation.

2.2.1 Multilayer Perceptron (MLP) Model

ANNs are based on the present understanding of biological nervous system, though much of the biological detail is neglected (Ozkan and Kaya 2010). They are generally used to predict an output vector based on known values in the input vector, especially where the relationships between the two are complex or nonlinear (Malekmohamadi et al. 2011). A typical configuration for an MLP model, a special class of ANNs, is shown in Fig. 3, where a set of data (x1; x2; …) is first fed into the network through the input layer. The data pass through one or more hidden layers and are finally outputted as predicted output, y (Bateni et al. 2007). The number of hidden layers determines complexity of the network, as a greater number of hidden layers increase the number of connections in the ANN.

Fig. 3
figure 3

A typical three-layer MLP neural network model

Full size image

In an MLP, neurons receive inputs from their upstream interconnections and generate outputs by their transformation with an appropriate nonlinear transfer function (Lee et al. 2007). In the case of sigmoid transfer function, for instance, the output yj from jth neuron in the layer is determined by:

$$y_{j} = f\left( {\sum {w_{ij} {\mkern 1mu} x_{i} } } \right) = \frac{1}{{1 + e^{{ - \left( {\sum {w_{ij} {\kern 1pt} x_{i} } } \right)}} }}$$
(8)

where wij is the weight of the connection joining jth neuron in the layer with ith neuron in the previous layer and xi is the value of ith neuron in the previous layer.

In an ANN training process, input and known output data are provided to the model simultaneously, and interconnection weights are adjusted to minimize the output error. Once the model is successfully trained, it is tested with a validation data set whereby the accuracy of model’s prediction is evaluated by comparing the model output with observed values.

In this study, a three-layer feed-forward back-propagation network with seven neurons in the hidden layer was used as the MLP model. Optimum number of neurons in the hidden layer (7 neurons) was determined through a trial and error process. Therefore, the final architecture of MLP configuration in this study was 3-7-1 (Homayoon et al. 2010; Keshavarzi et al. 2012). A hyperbolic tangent sigmoid function and a linear function were used as transfer functions in the second and the third layers, respectively, and Levenberg–Marquardt optimization method was used for the network training.

2.2.2 Support Vector Regression (SVR) Model

Vapnik (1995) introduced support vector machines (SVM) as a type of supervised machine learning technique belonging to a family of generalized linear classifiers. SVM is based on structural risk minimization (SRM) concept, as opposed to empirical risk minimization (ERM) approach, commonly employed within statistical learning methods. SRM minimizes an upper bound on the generalization error, as opposed to ERM which minimizes training data error. It is this difference that equips SVM with a greater potential to generalize. In addition, solutions offered by traditional ANN may tend to fall into a local optimal solution, whereas a global optimum solution is guaranteed in an SVM. SVM may be applied to both classification and regression problems (Jahangirzadeh et al. 2014). For further details on SVM methods, authors suggest Vapnik (1998) and Kecman (2001).

SVR finds a function that has at most a limited deviation from the actual target output vector for a given training data and has to be as flat as possible (Pal et al. 2011). SVR models depend on a kernel function and user defined parameters such as kernel specific parameter (γ), size of error insensitive zone (ε), and regularization cost parameter (C) which control model’s tolerance to error. Application of any SVR model involves optimization of cost parameter (C), kernel type, and kernel specific parameter (γ).

In nonlinear SVR, a kernel function simplifies the learning process by changing the representation of data in the input space to a linear representation in a higher-dimensional space, i.e., feature space (Hong et al. 2012). Several choices exist for a kernel function k, including linear, polynomial, and Gaussian radial basis functions. Gaussian function used in the current study is defined as (Hong et al. 2012):

$$k(x_{i} ,x) = \exp \left\{ { - \gamma \left| {x - x_{i} } \right|^{2} } \right\}$$
(9)

which is most commonly used to map samples into a higher-dimensional space to better handle nonlinear problems (Goyal and Ojha 2011). A large number of trials were carried out and statistical indices (highest correlation coefficient, smallest mean absolute error, MAE, and root mean-squared error, RMSE) were employed to find the optimum combination values for C and γ. In this study, γ = 1, C = 5, and ε = 0.1 were found to provide the best results. For further details on SVR, readers may refer to Vapnik (1995).

3 Results and Discussion

Effects of each dimensionless ratio in Eq. 7 on the total discharge and its coefficient were studied in four combined weir–gate and a weir-only (d = 0 mm) structures. Figure 4 depicts measured heads and discharges for all physical models. As expected, total discharge (Qt) increased with increasing head (h), however, at the same discharge, with increasing gate opening (d), water head over the weir decreased. In other words, as the gate opening increased, more discharge passed through it and less over the weir, causing a decrease in water elevation. The decrease in water head over the weir was greater at low discharges (Qt ≤ 0.01 m3/s). For instance, it decreased 23.4% from 0.128 m (for d = 0 mm) to 0.098 m (for d = 37.5 mm) at 0.0053 m3/s, but decreased 5.2% from 0.191 m (for d = 0 mm) to 0.181 m (for d = 37.5 mm) at 0.0135 m3/s. At low discharges, the gate (and its opening) may be considered as the main water head controller compared to the weir, while weir would mainly control water level at high discharges (Qt > 0.01 m3/s).

Fig. 4
figure 4

Variation of discharge versus h for all physical models

Full size image

As expected, discharge and its coefficient were directly proportional for all gate openings (Fig. 5). At the same discharge, however, discharge coefficient increased with increasing gate opening (d). For instance, at Qt = 0.008 m3/s, Cd increased from 0.55, to 0.59, 0.62 and 0.74 when d increased from 12.5, to 25, 37.5, and 50 mm, respectively (Fig. 5).

Fig. 5
figure 5

Variation of discharge versus its coefficient for all combined models

Full size image

Figure 6 depicts observed discharges for weir-only against the theoretical equation (\(Q_{\text{t}} = \frac{8}{15}C_{\text{d}} \tan \frac{\theta }{2}\sqrt {2g} h^{2.5}\)) for a triangular sharp-crested weir (Bos 1989). As shown, observed data agree very well with the theoretical discharges (R2 = 0.992), suggesting an overall data reliability.

Fig. 6
figure 6

Comparison between observed and theoretical discharges

Full size image

Figure 7 shows variations of discharge coefficient (Cd) against h/d for different gate openings (d). In general, Cd consistently increased with increasing h/d for all gate openings. However, this increase was sharp at high d’s and gentle at low ones. For instance, the slope of trend lines for d = 12.5 mm and d = 50 mm is 0.057 and 0.158, respectively. One may conclude that careful considerations should be given to water head measurements and Cd calculations, especially at high d values.

Fig. 7
figure 7

Variation of discharge coefficient (Cd) for combined weir–gate structure versus h/d for different gate openings

Full size image

Figures 8 and 9 show variations of discharge coefficient (Cd) for combined weir–gate structures versus h/y and h/b, respectively. In both figures, with constant d, as h/y or h/b increases, discharge coefficient increases. Any constant d (and the corresponding trend line) in these figures refers to a certain physical model, where not only d, but also b and y are constants, implying that the trend line reflects Cd variation as a function of h. As h is proportional to Qt, it may be concluded that total discharge is directly proportional to discharge coefficient (Cd) in any combined weir–gate structure.

Fig. 8
figure 8

Variation of discharge coefficient (Cd) for combined weir–gate structure versus h/y for different gate openings

Full size image
Fig. 9
figure 9

Variation of discharge coefficient (Cd) for combined weir–gate structure versus h/b for different gate openings

Full size image

3.1 Discharge Coefficient Prediction

In this study, capacity of MLP and SVR models to determine complex relationships was utilized to predict the discharge coefficient of a combined weir–gate structure. Figure 10 shows predicted versus observed coefficients for both MLP and SVR models. As shown, both models predict Cd more accurately when it is smaller (0.2 < Cd < 0.5) compared to larger (0.5 ≤ Cd < 1). However, R2 values of 0.966 and 0.967 for MLP and SVR models, respectively, show a very good agreement between predicted and observed Cd’s over the entire range. Ranges of errors for MLP and SVR models are (− 0.088 to 0.138) and (− 0.099 to 0.172), respectively.

Fig. 10
figure 10

Predicted versus observed discharge coefficients (Cd’s) for MLP and SVR models

Full size image

Figure 11 shows experimental data along with MLP and SVR results for training and validating data sets. As shown, data numbers 1–23 belong to the training, and 24–33 belong to validating data sets. In general, both models predict discharge coefficients well; however, MLP appears to demonstrate a better performance over SVR in the validation data set. A comprehensive accuracy analysis would evaluate performance of each model, quantitatively.

Fig. 11
figure 11

Comparison of observed data with MLP and SVR model results during training and validation

Full size image

Root mean-squared error (RMSE), mean absolute error (MAE), and R2 criteria were used to evaluate MLP and SVR model results more accurately. RMSE indicates the goodness of fit related to high-discharge coefficient values, whereas MAE measures a more balanced perspective of the goodness of fit at moderate discharge coefficients. They are defined as:

$${\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {(Y_{{i{\kern 1pt} {\kern 1pt} {\text{observed}}}} - Y_{{i{\kern 1pt} {\kern 1pt} {\text{estimated}}}} )^{2} } }$$
(10)
$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {Y_{{i{\kern 1pt} {\kern 1pt} {\text{observed}}}} - Y_{{i{\kern 1pt} {\kern 1pt} {\text{estimated}}}} } \right|}$$
(11)

where N is the number of data, and Yi is the discharge coefficient, in this study. RMSE, MAE, and R2 values for MLP and SVR models are shown in Table 2.

Table 2 Statistical indices for Cd’s estimated by MLP and SVR models
Full size table

As shown, RMSE, MAE, and R2 values are better for SVR model compared to MLP, in training data. However, for validation data set, these statistical indices are better for MLP model compared to SVR. For the total data set, on the other hand, the indices are very close in both models. Considering the fact that accuracy of validation data set is more important than training data set, it is concluded that MLP model may be used as an accurate and efficient model to predict discharge coefficient for a combined triangular weir–rectangular gate structure.

3.2 Comparing the Results with Existing Equations

As explained earlier, there are four main regression equations in the literature that predict discharge in a combined structure of triangular weir–rectangular gate (Eqs. 1: El-Saiad et al. 1995; 2: Negm et al. 1997; 3: Alhamid et al. 1997; and 4: Hayawi et al. 2008). It should be noted that the range of discharge (m3/s) for El-Saiad et al. (1995), Negm et al. (1997), Alhamid et al. (1997), and Hayawi et al.’s (2008) studies is (0.003, 0.015), (0.0019, 0.015), (0.007, 0.23), (0.000023, 0.000054) and (0.0015, 0.0135), respectively. A comparison of these equations with observed data in this study would be insightful (Fig. 12). As shown, El-Saiad et al. (1995) and Negm et al. (1997) equations match the observed data much better than Alhamid et al. (1997) and Hayawi et al.’s (2008) results, which are noticeably different. It was concluded that assuming the general form of a gate equation in Alhamid et al. (1997) and a weir equation in Hayawi et al. (2008) for the combined weir–gate structure shall be reconsidered before utilization.

Fig. 12
figure 12

Comparison of observed data with existing equations

Full size image

Figure 13 depicts the performance of MLP model in comparison to El-Saiad et al. (1995) and Negm et al.’s (1997) equations. As shown, MLP model predicts discharges much more accurately compared to both equations. Apparently, it was due to MLP being capable of determining complex relationships more flexibly than rigid regression equations. Additionally, small differences in scales and ranges of hydraulic parameters used in each study may have caused some differences, too.

Fig. 13
figure 13

Comparison of observed data, the equations, and MLP

Full size image

Table 3 shows RMSE, MAE, and R2 values for MLP model and Eqs. 1, 2, and 3. Considering these statistical indices, it was concluded that MLP model predicts total discharge (Qt) more accurately, followed by Negm et al. (1997), El-Saiad et al. (1995), and Alhamid et al. (1997) equations, respectively.

Table 3 Values of accuracy criteria for Qt estimated by MLP and existing regression equations
Full size table

4 Conclusions

In this study, experiments with extended measuring ranges for relevant parameters were conducted on combined triangular weir and rectangular gate structures under free flow conditions to estimate discharge coefficients (Cd) and compare them with those reported in the literature. Investigating effects of three dimensionless parameters (h/d, h/b, and h/y) on Cd showed that as the parameters increase, so does discharge (Qt) and its coefficient. At the same discharge, however, discharge coefficient increased with increasing gate opening (d). For instance, at Qt = 0.008 m3/s, Cd increased from 0.55, to 0.59, 0.62, and 0.74 when d increased from 12.5, to 25, 37.5, and 50 mm, respectively. Moreover, it was concluded that, at low discharges (Qt ≤ 0.1 m3/s), the gate and its opening are the main water head controllers, while water levels at high discharges (Qt > 0.1 m3/s) are mainly controlled by the weir.

Utilized soft computing models (MLP and SVR), both predicted Cd accurately (with R2 of 0.966 and 0.967, respectively). However, MLP was considered superior, due to better statistical indices of RMSE, MAE, and R2 (0.027, 0.022, and 0.984, respectively) in the validation data set compared to SVR (0.065, 0.042, and 0.948, respectively). Comparing results with existing equations showed that El-Saiad et al. (1995) and Negm et al.’s (1997) equations match the observed data much better than noticeably different Alhamid et al. (1997) and Hayawi et al.’s (2008) results. It was concluded that assuming the general form of a gate equation in Alhamid et al. (1997) and a weir equation in Hayawi et al. (2008) for the combined weir–gate structure shall be reconsidered before utilization in particular applications.