1 Introduction

Disputes are currently considered endemic in the construction industry. Over the past couple of decades, the construction industry has experienced an increase in disputes and difficulty in reaching reasonable and effective settlements (Barrie and Paulson 1992). As construction conflicts can cause large damages due to delays, cost overruns and decreasing productivity, developing new methodologies for resolving conflicts in construction projects is highly recommended.

Construction projects are usually long-term transactions with high complexities and large uncertainties, and it is almost impossible to resolve every detail at the beginning of the projects. As a result, situations often arise are not clearly addressed by contracts (Mitropoulos and Howell 2001).

In past decades, game theory has been successfully applied to many important issues in civil engineering (see the literature review provided by Niksokhan et al. 2009; Sadegh et al. 2010; Jafarzadegan et al. 2013; Ghodsi et al. 2016; Mahjour and Pourmand 2017 for more details). Applications of game theory in construction management have been relatively limited. Pena-Mora and Wang (1998) developed a system to facilitate collaborative negotiation in a large-scale civil engineering project, in which negotiators are motivated by both individual and group benefits. The negotiation mechanism is built based on a simple formal game. Ho (2001) utilized the game theory to analyze the information asymmetry problem during the procurement of a build–operation–transfer (BOT) project. Ho and Liu (2004) developed a game theoretic model for analyzing the behavioral dynamics of builders and owners in construction claims. Kassab et al. (2006) proposed a model for resolving contractual conflicts considering four different concepts of equilibrium. They used players’ preferences and a formal game theory to find an equilibrium status for opponents. Perng et al. (2006) established a conceptual model of competitive bidding in economically most advantageous tender projects to reflect the credibility of bidding situations using a bidding game. Shen et al. (2007) presented a new BOT concession model for identifying a concession period by using game theory. They presented an alternative method by which a group of concession period solutions is produced.

Aliahmadi et al. (2011) proposed a method for risk assessment of a tunnel project where there are three main parameters called taskmaster, adviser and contractor. Their model was built based on the interactive framework of a game theory where, in making a decision, each player considers other possible risks choices. They implemented three-person cooperative game theory combined with an interactive decision structural model of fuzzy analytical hierarchy process to perform a balance between actions and suitable cooperative strategy for each player. The results revealed that collaboration strategies give the highest outcome for the three players. Barough et al. (2012) discussed two types of probabilistic conflicts in construction projects and showed that the chicken and prisoners’ dilemma games are helpful for analyzing construction management problems.

Nasirzadeh et al. (2016) presented a cooperative-bargaining game model for quantitative risk allocation that accounts for both client and contractor costs. The behavior of contracting parties in the quantitative risk allocation process was modeled as the players’ behavior in a game. A bargaining process was then performed to share the benefit of a decrease in the contractor cost between the client and the contractor. Recently, Khanzadi et al. (2017) developed a model based on a discrete zero-sum two-person matrix game with gray numbers to study conflicts between contractor and employer in delayed design–bid–build projects. Based on different risk values, they determined suitable solutions for both parties.

When the game theory is applied to real-world problems such as decision making in managerial problems, it is difficult to exactly assess the payoffs. In such cases, it is reasonable to model the problems as games with fuzzy payoffs, in which payoffs are represented as fuzzy numbers. In this paper, we deal with a contractual conflict in a large construction project, in which we cannot exactly assess opponents’ payoffs. The fuzzy versions of two matrix games are proposed for resolving disputes in construction projects considering the fuzzy payoffs of owner and contractor.

The first model transforms the original matrix game into a family of its α-cut equivalents. A decomposition scheme is used to translate the original bilinear model into a set of α-parameterized linear optimization models. The second model introduces fuzzy goals for payoffs in order to incorporate ambiguity of player’s judgments. In this game, each player tries to maximize the degree of attainment of his fuzzy goal.

2 Case Study

The Persian Gulf and its coastal areas are the world’s largest source of crude oil. The largest offshore oilfield is also located in the Persian Gulf. Iran and Qatar have a giant gas field across the territorial median line (Fig. 1).

Fig. 1
figure 1

Geographical location of the South Pars gas field

Full size image

This gas field covers an area of 9700 km2, of which 3700 km2 belongs to Iran. The Iranian portion, which is called South Pars, is estimated to contain about 14 trillion cubic meters of gas reserves and about 18 billion barrels of gas condensates. This amounts to roughly 8 percent of the world’s gas reserves and approximately half of the Iran’s gas reserves. South Pars gas field development shall meet the Iran’s growing demands of natural gas.

Presently, the development of the gas field is conducted through large projects in 24 phases by an Iranian governmental company called Pars Oil and Gas Company (POGC). The underdevelopment phases of South Pars gas field mainly consist of offshore facilities, products transfer pipeline to onshore facilities, onshore facilities, gas transfer pipelines to the national gas distribution system and export facilities for exporting gas condensate, liquefied petroleum gas (LPG) and sulfur.

The conflict examined in this paper arose in a major oil industrial project in the South Pars Field, between the owner (POGC) and an international contractor company. (The name of the project and contractor has been omitted due to confidentiality.)

The total value of the project was estimated about $2 billion USD. The contractor was awarded the job by bringing the best proposal. The capital expenditure had a $1.9 billion GMP (guaranteed maximum price). The project has a restrictive time constraint, and the contractor started working on the site in 2006, after signing the contract.

Now that the project tends to be finished, contractor claims that project’s capital cost has increased due to additional works, which is not fully acceptable by the project’s owner. The contractor’s main argument is that the bid documents were not clear, and many addenda were issued during the bidding and construction period. The owner, on the other hand, while officially had rejected the contractor’s claim, evaluated the situation by its technical and financial consultants and decided to negotiate with contractor’s representative in project Joint Managerial Committee (JMC). The owner needs a speedy completion of construction so they do not want to extend the negotiation time. Owner options include full payment, partial payment and finally reject to reimburse. Consequently, the contractor can pressure the owner by stopping work, claim on lower demand, on upper demand or just not claim any reimbursement. During negotiations, it is assumed that both sides can estimate his and the opponent’s earned values.

To find an equilibrium solution to this conflict, we have to evaluate both sides’ options and related payoffs. Experts from the owner’s project management department and the contractor managerial boards were asked to fill in a special questionnaire. The questionnaire provides the fuzzy preferences in the range of 0 to 100. Owner’s options are represented by F for full payment, P for partial payments and R for rejection to reimburse. Consequently, contractor options are represented by N for not claiming any reimbursement, S for stop working on the project, 1 for lower level and 2 for a higher level of claim. Tables 1 and 2, respectively, show the estimated fuzzy payoffs for the owner (\(\tilde{a}_{ij}\)) and the contractor (\(\tilde{b}_{ij}\)), where i and j are the indices of the options of the owner and the contractor. The fuzzy payoffs are presented as triangular membership functions.

Table 1 The fuzzy payoffs of the owner (\(\tilde{a}_{ij}\))
Full size table
Table 2 The fuzzy payoffs of the contractor (\(\tilde{b}_{ij}\))
Full size table

In the next section, the concepts of fuzzy sets and fuzzy matrix games are described, and two fuzzy games are presented.

3 Fuzzy Matrix Games

A nonzero-sum game can be used for resolving conflicts between contractor and owner in a construction project. Communication is pointless in zero-sum games because there is no possibility of mutual gain from cooperating. In nonzero-sum games, on the other hand, the ability to communicate and the effectiveness of communication can affect the outcome. For games in which the players have both common and conflicting interests (in other words, in most nonzero-sum games, whether cooperative or noncooperative), a solution is much harder to define and make persuasive.

Although solutions to nonzero-sum games have been defined in a number of different ways, they sometimes seem inequitable or are not enforceable. One well-known cooperative solution to two-person variable-sum games was proposed by Nash (1950, 1951). Given a game with a set of possible payoffs and associated options for each player, Nash showed that there is a unique equilibrium (UE) that satisfies all conditions defined for a solution to the game.

Since Zadeh (1965) introduced the concept of a fuzzy set, it has been employed in numerous areas. A fuzzy set ã is defined by a membership function mapping the elements of a universe U to the unit interval [0, 1]:

$$\tilde{\alpha }:U \to \left[ {0,1} \right].$$
(1)

A fuzzy number is a fuzzy set ã on the set of real numbers such that:

  1. 1.

    There exists a unique real number x such that \(\tilde{a}\left( x \right) = 1\),

  2. 2.

    \(\mathop {\tilde{a}}\nolimits_{\alpha }\) must be a closed interval for every \(\alpha \in \left( {0,1} \right]\),

  3. 3.

    The support of \(\tilde{a}\) must be bounded, where \(\mathop {\tilde{a}}\nolimits_{\alpha } = \left\{ {x|A(x) \ge \alpha } \right\}\) is the α-cut of \(\tilde{a}\).

This paper considers a bimatrix game with fuzzy payoffs. In the crisp form of bimatrix games, the payoffs of players I and II are demonstrated as \(U_{1} (i,j) = a_{ij}\) and \(U_{2} (i,j) = b_{ij}\), when player I chooses a pure strategy \(i \in I\) and player II chooses a pure strategy \(j \in J\). Then a nonzero-sum two-person game in normal crisp is represented as a pair of m × n payoff matrices:

$$A = \left| {\begin{array}{*{20}c} {\mathop a\nolimits_{11} } & \ldots & {\mathop a\nolimits_{1n} } \\ \vdots & \ddots & \vdots \\ {\mathop a\nolimits_{m1} } & \ldots & {\mathop a\nolimits_{mn} } \\ \end{array} } \right|\quad B = \left| {\begin{array}{*{20}c} {\mathop b\nolimits_{11} } & \ldots & {\mathop b\nolimits_{1n} } \\ \vdots & \ddots & \vdots \\ {\mathop b\nolimits_{m1} } & \ldots & {\mathop b\nolimits_{mn} } \\ \end{array} } \right|$$
(2)

The game is defined by (A, B) and is also referred to as a bimatrix game. In this crisp game, when players do not have any dominant strategy, they have to choose a mixed strategy. Mixed strategies of players I and II are represented by probability distributions to pure strategies of them, i.e., \(x^{T} = (x_{1} , \ldots ,x_{m} ) \in X\) where \(0 < x_{i} < 1\) and \(\sum x_{i} = 1\) is a mixed strategy of player I. Expected payoffs of players I and II when player I chooses a mixed strategy \(x \in X\) and player II chooses a mixed strategy \(y \in Y\) are:

$$\begin{aligned} & \mathop E\nolimits_{1} (x,y) = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\mathop a\nolimits_{ij} \mathop x\nolimits_{ij} y_{j} = } } \mathop x\nolimits^{T} Ay \\ & \mathop E\nolimits_{2} (x,y) = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {b_{ij} \mathop x\nolimits_{ij} y_{j} = } } \mathop x\nolimits^{T} By \\ \end{aligned}$$
(3)

For a fuzzy bimatrix game \(\left( {\tilde{A},\tilde{B}} \right)\), a Nash equilibrium solution is a pair of strategies, namely m-dimensional column vector \(x^{*}\) and n-dimensional column vector \(y^{*}\), if for any other mixed strategies x and y:

$$\begin{aligned} & x^{*T} \tilde{A}y^{*} \ge x^{T} \tilde{A}y^{*} \\ & x^{*T} \tilde{B}y^{*} \ge x^{*T} \tilde{B}y \\ \end{aligned}$$
(4)

where \(\tilde{A}\) and \(\tilde{B}\) are the fuzzy payoff matrices of players I and II, respectively.

In this paper, we assume that fuzzy payoffs \(\mathop {\tilde{a}}\nolimits_{ij}\) and \(\mathop {\tilde{b}}\nolimits_{ij}\) are L–R type fuzzy numbers. L–R type fuzzy number M is defined by shape functions L(x) and R(x), mean value m, and parameters α and β that define the length of the base in the triangular fuzzy set M to the left and right of the mean value, using the simplified notation below (Zimmermann 2001):

$$M = \left( {m,\alpha ,\beta } \right)_{LR}$$
(5)

Shape functions \(L(x)\) and \(R(x)\) satisfy the following conditions:

  1. 1.

    L(x) = L(− x), R(x) = R(− x);

  2. 2.

    L(0) = 1, R(0) = 1;

  3. 3.

    both L and R are not increasing functions.

Then, L–R fuzzy number M is defined by L and R such as:

$$\mu_{M} (x) = \left\{ \begin{aligned} L\;\left( {\frac{m - x}{\alpha }} \right)\quad x \le m,\alpha \ge 0 \hfill \\ R\;\left( {\frac{m - x}{\beta }} \right)\quad x \ge m,\beta \ge 0 \hfill \\ \end{aligned} \right.$$
(6)

\(\mathop {\tilde{a}}\nolimits_{ij}\) and \(\mathop {\tilde{b}}\nolimits_{ij}\) can be presented as \(\mathop {\left( {\mathop a\nolimits_{ij} ,\mathop {a^{{\prime }} }\nolimits_{ij} ,\mathop {{}^\backprime a}\nolimits_{ij} } \right)}\nolimits_{{L_{ij} R_{ij} }}\) and \(\mathop {\left( {\mathop b\nolimits_{ij} ,\mathop {b^{{\prime }} }\nolimits_{ij} ,\mathop {{}^\backprime b}\nolimits_{ij} } \right)}\nolimits_{{L_{ij} R_{ij} }}\), while \(\mathop a\nolimits_{ij}\), \(a_{ij}^{{\prime }}\), \(\mathop {{}^\backprime a}\nolimits_{ij}\), \(\mathop b\nolimits_{ij}\), \(b_{ij}^{{\prime }}\) and \(\mathop {{}^\backprime b}\nolimits_{ij}\) are finite numbers.

In this paper, two different bimatrix games with fuzzy payoffs are utilized to resolve the existing conflict between the owner and the contractor in our case study. The first approach translates the original fuzzy game into a family of its α-cut equivalents, and a decomposition scheme is used to translate the original bilinear model into a set of α-parameterized linear optimization models. The second model considers fuzzy goals for players and assumes that players try to maximize the degree of attainment of their fuzzy goals. Details of the fuzzy games are presented in the following sections.

3.1 Model 1: A α-Cut-Based Fuzzy Bimatrix Game

A point \((x^{*} ,y^{*} ) \in X \times Y\) is a fuzzy Nash equilibrium strategy if and only if \(x^{*}\) is an optimal solution to the following fuzzy linear programming problem with parameter \(y^{*}\):

$$\begin{aligned} & \max_{x} \;\;x\tilde{A}y^{*} \\ & {\text{St}}:\;x \in X \\ \end{aligned}$$
(7)

and \(y^{*}\) is an optimal solution for the following fuzzy linear programming problem with parameter \(x^{*}\):

$$\begin{aligned} & \max_{y} \;\;x^{*} \tilde{B}y \\ & {\text{St}}:\;y \in Y \\ \end{aligned}$$
(8)

In this model, fuzzy Nash equilibrium strategies are evaluated by simultaneously solving both optimization problems (7) and (8). Therefore, the following fuzzy bilinear programming problem should be solved:

$$\begin{aligned} & \max_{x,y} \;\;x\tilde{A}y^{*} + x^{*} \tilde{B}y \\ & {\text{St}}:\;x \in X \\ & \quad \;y \in Y \\ \end{aligned}$$
(9)

The fuzzy bilinear optimization problem (8) cannot be solved using the conventional optimization methods. So we have to solve the equivalent following bilinear fuzzy optimization problem (Basar and Olsder 1999):

$$\begin{aligned} & \max_{x,y,p,q} \;\;x\tilde{A}y + x\tilde{B}y - p - q \\ & {\text{St}}:\;\tilde{A}y \le pe^{m} \\ & \quad \;\tilde{B}^{T} x \le qe^{n} \\ & \quad \;\sum\limits_{i = 1}^{m} {x_{i} } = 1 \\ & \quad \;\sum\limits_{j = 1}^{n} {y_{j} = 1} \\ & \quad \;x_{i} \ge 0,\,i = 1, \ldots ,m \\ & \quad \;y_{j} \ge 0,\,j = 1, \ldots ,m \\ \end{aligned}$$
(10)

where \(e^{m}\) and \(e^{n}\) are m- and n-dimensional vectors whose elements are all ones. In this paper, the α-cut method is used to translate the fuzzy bilinear problem in a set of α-parameterized conventional bilinear problems (details of α-cut method can be found in Kerachian et al. 2010). The α-cut of a fuzzy number \(\tilde{a}\) can be represented by the interval \(\left[ {\mathop {\tilde{a}}\nolimits_{\alpha }^{L} ,\mathop {\tilde{a}}\nolimits_{\alpha }^{U} } \right]\). Similarly, we can represent the α-cut of a fuzzy matrix \(\tilde{A}_{m \times n}\) by \(\tilde{A}_{\alpha } = \left( {\mathop A\nolimits_{\alpha }^{L} ,\mathop A\nolimits_{\alpha }^{U} } \right)\). Therefore, the bilinear model (9) becomes:

$$\begin{aligned} & \max_{x,y,p,q} \;\;x\;\left[ {A_{\alpha }^{L} ,A_{\alpha }^{U} } \right]\;y + x\;\left[ {B_{\alpha }^{L} ,B_{\alpha }^{U} } \right]\;y - p - q \\ & {\text{St}}:\;\left[ {A_{\alpha }^{L} ,A_{\alpha }^{U} } \right]\;y \le pe^{m} \\ & \quad \;\,\left[ {B_{\alpha }^{L} ,B_{\alpha }^{U} } \right]^{T} x \le qe^{n} \\ & \,\quad \,\sum\limits_{i = 1}^{m} {x_{i} } = 1 \\ & \quad \;\sum\limits_{j = 1}^{n} {y_{j} } = 1 \\ & \quad \;x_{i} \ge 0,\,i = 1, \ldots ,m \\ & \quad \;y_{j} \ge 0,\,j = 1, \ldots ,m \\ \end{aligned}$$
(11)

Given values for \(\alpha \in \left[ {0,\;1} \right]\), equilibrium solutions \((x^{*} ,y^{*} )\) can be found by solving the problem (10) for each α. To solve the bilinear problem (9), for each value of α, the α-cut values of the fuzzy numbers can be used instead of the original fuzzy numbers \(\mathop {\tilde{a}}\nolimits_{ij}\) and \(\mathop {\tilde{b}}\nolimits_{ij}\), and the bilinear optimization model can be solved by using a decomposition algorithm suggested in Bazaraa and Shetty (1979). This algorithm decomposes the bilinear problem into two linear programming optimizations. In the first one, a variable is optimized through the first LP model, while the other variable is constant. Consequently, in the next step, the optimized variable is kept constant and the second one optimized by the second LP model. This procedure is repeated until changes in the variables become less than a predefined value.

In our case study, we use α-cut method considering the α values of \(0,0.2, \ldots ,0.8\) and 1. For example, Figs. 2 and 3, respectively, depict the owner and the contractor payoffs in a status in which the owner accepts to pay partially (status P) and the contractor threatens to stop working (status S).

Fig. 2
figure 2

The owner’s payoffs in PS status (\(\tilde{a}_{\text{PS}}\))

Full size image
Fig. 3
figure 3

Contractor’s payoffs in PS status (\(\tilde{b}_{\text{PS}}\))

Full size image

3.2 Model 2: A Fuzzy Bimatrix Game with Fuzzy Goals

In this model, fuzzy goals are considered for players and it is assumed that players try to maximize the degree of attainment of their fuzzy goals. It is assumed that player I specifies the finite value \(\underline{a}\) of the payoff for which the degree of satisfaction is 0 and the finite value \(\bar{a}\) of the payoff for which the degree of satisfaction is 1. Let first player fuzzy goal \(\mathop {\tilde{G}}\nolimits_{1}\) for the payoff p be fuzzy set on the set of real numbers R characterized by the membership function \(\mu_{{\tilde{G}_{1} }} :R \to \left[ {0,1} \right]\):

$$\mu_{{\tilde{G}_{1} }} (p) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad p \le \underline{a} } \hfill \\ {\frac{{p - \underline{a} }}{{\bar{a} - \underline{a} }}} \hfill & {{\text{if}}\quad \underline{a} < p \le \bar{a}} \hfill \\ 1 \hfill & {{\text{if}}\quad \bar{a} < p} \hfill \\ \end{array} } \right.$$
(12)

The fuzzy goal \(\mathop {\tilde{G}}\nolimits_{2}\) of player II is a similar fuzzy set characterized by the membership function \(\mu_{{\tilde{G}_{2} }}\). A membership function value of the fuzzy goal can be interpreted as a degree of attainment of the fuzzy goal. Then it is assumed that for any pair of payoffs, a player prefers the payoff having the larger degree of attainment of his fuzzy goal.

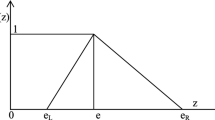
For any pair of mixed strategies \(\left( {x,y} \right)\), let the fuzzy expected payoff and the fuzzy goal of player I be, respectively, denoted by \(\tilde{E}_{1} \left( {x,y} \right)\) and \(\mathop {\tilde{G}}\nolimits_{1}\). As shown in Fig. 4, the degree of attainment of the fuzzy goal is defined as the maximum of the intersection of the fuzzy expected payoff \(\tilde{E}_{1} \left( {x,y} \right)\) and the fuzzy goal \(\mathop {\tilde{G}}\nolimits_{1}\).

Fig. 4
figure 4

Source: Adapted from (Nishizaki and Sakawa 2000)

Degree of attainment of fuzzy goal.

Full size image

It is assumed that the membership functions of the fuzzy goals and payoffs of both players have the following linear form (Nishizaki and Sakawa 2000):

$$\mu_{{\tilde{a}_{ij} }} (p) = h(p) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad p < a - a_{ij} } \hfill \\ {\frac{{p - a_{ij} + a^{\prime}_{ij} }}{{a^{\prime}_{ij}}}} \hfill & {{\text{if}}\quad a_{ij} - a^{\prime}_{ij} \le p < a_{ij} } \hfill \\ {\frac{{a_{ij} + {}^\backprime a_{ij} - p}}{{{}^\backprime a_{ij} }}} \hfill & {{\text{if}}\quad a_{ij} \le p \le a_{ij} + {}^\backprime a_{ij} } \hfill \\ 0 \hfill & {{\text{if}}\quad a_{ij} + {}^\backprime a_{ij} < p} \hfill \\ \end{array} } \right.$$
(13)

Therefore, for a pair of strategies x and y of players I and II, player I’s degree of attainment of fuzzy goal (\(d_{1} (x,y)\)) can be represented by (Nishizaki and Sakawa 2000):

$$d_{1} (x,y) = \frac{{x^{T} (A + {}^\backprime A)y - \underline{a} }}{{\bar{a} - \underline{a} + x^{T} {}^\backprime Ay}}.$$
(14)

Player II’s degree of attainment can also be presented in a similar way. Therefore, equilibrium with respect to the degree of attainment of the fuzzy goal and necessary conditions of Kuhn and Tucker is optimal solutions \(x^{*}\) and \(y^{*}\) to the following mathematical programming problems (Nishizaki and Sakawa 2000):

$$\begin{aligned} & \max_{x,y,\varphi ,\rho } \quad \bar{a}x^{T} (A + {}^\backprime A)y + \bar{b}x^{T} (B + {}^\backprime B)y - \underline{a} x^{T} Ay - \underline{b} x^{T} By \\ & \quad \quad \quad \quad \quad - \left( {\bar{a} - \underline{a} + x^{T} {}^\backprime Ay} \right)^{2} \varphi - \left( {\bar{b} - \underline{b} + x^{T} {}^\backprime By} \right)^{2} \rho \\ & {\text{s}} . {\text{t}}:\quad \left( {\bar{a} - \underline{a} + x^{T} {}^\backprime Ay} \right)Ay + \left( {\bar{a} - x^{T} Ay} \right){}^\backprime Ay - \left( {\bar{a} - \underline{a} + x^{T} {}^\backprime Ay} \right)^{2} \varphi e^{m} \le 0^{m} , \\ & \quad \quad \;\left( {\bar{b} - \underline{b} + x^{T} {}^\backprime By} \right)B^{T} x + \left( {\bar{b} - x^{T} By} \right){}^\backprime B^{T} x - \left( {\bar{b} - \underline{b} + x^{T} {}^\backprime By} \right)^{2} \rho e^{m} \le 0^{m} , \\ & e^{mT} x - 1 = 0, \quad x \ge 0^{m} \\ & e^{nT} y - 1 = 0, \quad y \ge 0^{m} \\ \end{aligned}$$
(15)

In the next section, the fuzzy games are applied to the case study, and the results are presented.

4 Results and Discussion

To find an equilibrium solution using the α-cut-based bilinear programming (Model 1), we implement the bilinear model (9) by finding both upper and lower values of \(\mathop {\tilde{a}}\nolimits_{ij}\) and \(\mathop {\tilde{b}}\nolimits_{ij}\) for \(\alpha = 0,0.2, \ldots ,0.8\) and 1. Then, the problem is decomposed into a dual linear programming (LP). In the first LP model, vector x is optimized, while vector y is constant. Consequently, in the next step, optimized vector x is kept constant, and y is optimized by the second LP model. This procedure is repeated until changes in vectors x and y become less than a predefined value, which is considered to be equal to 0.001. For each value of α, the equilibrium mixed strategies \((x^{ * } ,y^{ * } )\) and payoffs (\(E_{1}\) and \(E_{2}\)) can be calculated. For example, the values for \(\alpha = 1\) are as follows:

$$\begin{aligned} & x^{ * } = (0.0308,0.0,0.9692) \\ & y^{ * } = (0.0,0.0,0.3333,0.6667) \\ & E_{1} = 67.6667 \\ & E_{2} = 66.4077 \\ \end{aligned}$$

The opponents’ expected payoffs in an equilibrium status for each α value are represented in Fig. 5.

Fig. 5
figure 5

The membership functions of the expected payoffs of the opponents obtained using the Model 2

Full size image

To test the robustness of an equilibrium status, by changing in the opponents’ priority and then re-executing the analysis, one can observe how equilibrium varies from those obtained previously. In our case study, the owner was under time pressure, and he was ready to compromise his benefit to meet the existing deadline for project completion. Despite his apparent refusal to pay the contractor in full, his preference to save time was clear in his payoffs and consequently in the results. To do a sensitivity analysis, decision makers from the owner’s project management department were asked to disregard the project completion time in their assessment of statuses. The owner’s new payoffs are presented in Table 3. Figure 6 presents the membership function of opponents expected payoffs based on the revised payoffs for different statuses.

Table 3 The reassessed owner’s fuzzy payoffs
Full size table
Fig. 6
figure 6

The expected payoffs of the opponents obtained using the Model 2, considering the revised payoffs of the owner

Full size image

By revising the payoffs by the owner, he can put more pressure on the contractor as the length of the negotiation period is not important for him. The new values of \(x^{*}\) and \(y^{*}\) indicate that the possibility of the contractor stopping the work will increase when the owner neglects the time value in the negotiation process. Moreover, \(y_{4}\) for \(\alpha = 1\) in the first analysis was 0.6667, while in the second one it was 0.9381. So we can conclude that the contractor’s inclination to become noncooperative by stopping the work will increase. The results of the analysis for \(\alpha = 1\) are as follows:

$$\begin{aligned} & x^{ * } = (0.0,0.0417,0.9583) \\ & y^{ * } = (0.0,0.0,0.0619,0.9381) \\ & E_{1} = 62.1968 \\ & E_{2} = 66.4792 \\ \end{aligned}$$

To find an equilibrium solution using the second model, we have to consider all functions \(\mu_{{\tilde{G}_{1} }} (p)\), \(\mu_{{\tilde{G}2}} (p)\), \(\mu_{{\tilde{a}_{ij} }} (p)\) and \(\mu_{{\tilde{b}_{ij} }} (p)\). It is assumed that \(\underline{a}\) and \(\bar{a}\), similarly, \(\underline{b}\) and \(\bar{b}\) can be set by each player. Let us assume \(\underline{a} = 60\) and \(\bar{a} = 95\), and then \(\mu_{{\tilde{G}_{1} }} (p)\) according to Eq. 12 is as follows:

$$\mu_{{\tilde{G}_{1} }} (p) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad p \le 60} \hfill \\ {\frac{p - 60}{95 - 60}} \hfill & {{\text{if}}\quad 60 < p \le 95} \hfill \\ 1 \hfill & {{\text{if}}\quad 95 < p} \hfill \\ \end{array} } \right.$$
(16)

A similar function is considered for \(\mu_{{\tilde{G}2}} (p)\). The membership functions \(\mu_{{\tilde{a}_{ij} }} (p)\) and \(\mu_{{\tilde{b}_{ij} }} (p)\) are also evaluated using the fuzzy payoffs, presented in Table 1. For instance, \(\mu_{{\tilde{a}_{ps} }} (p)\) has been estimated using Eq. 13 as follows:

$$\mu_{{\tilde{a}_{PS} }} (p) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad p < 56} \hfill \\ {\frac{p - 56}{6}} \hfill & {{\text{if}}\quad 56 \le p < 62} \hfill \\ {\frac{72 - p}{6}} \hfill & {{\text{if}}\quad 62 \le p \le 72} \hfill \\ 0 \hfill & {{\text{if}}\quad 72 < p} \hfill \\ \end{array} } \right.$$
(17)

Then, we use optimization model (15) in order to find an equilibrium solution in which both sides gain their maximum satisfaction. To solve optimization model (15), we use the genetic algorithm toolbox in Matlab. The optimal values for decision variables for a population size of 65 and a generation number equal to 150 are as follows:

$$\underline{a} = 60,\;\bar{a} = 95,\;\underline{b} = 50,\;\bar{b} = 90$$

The equilibrium mixed strategy and degrees of satisfaction are also obtained as follows:

$$\begin{aligned} & x^{ * } = (0.1463,0.0034,0.8503) \\ & y^{ * } = (0.1299,0.5431,0.2111,0.2111) \\ & d_{{_{1} }}^{ * } \left( {x,y)} \right. = 0.6757 \\ & d_{2}^{ * } \left( {x,y)} \right. = 0.5273 \\ \end{aligned}$$

A sensitivity analysis is performed to test the robustness of the equilibrium status against changes in preferences. By changing the preferences of opponents and then re-executing the analysis, one can observe how equilibrium status varies from those obtained previously. In the first model, the owner was under a deadline constraint for completion of the project, and he was ready to compromise. Despite his apparent refusal to pay the contractor in full, his preference to save time was clear. In the sensitivity analysis, decision maker from the owner’s project management department is asked to disregard the time value in their assessment of statuses.

The new payoff, which reflects changes in the owner’s attitude from being a good team player to a noncooperative individual, causes an increase in the owner’s degree of satisfaction and decreases the contractor’s satisfaction level. As it was expected, the new values of \(x^{*}\) and \(y^{*}\) indicate that the possibility of choosing to pay nothing by the owner will be increased when the owner neglects time value in the negotiation process. Moreover, in the first analysis, the contractor is more likely to choose \(y_{2}\) as it has a maximum possibility (0.5431), while in the second analysis, \(y_{3}\) has the maximum value (0.5032). So we can conclude that the contractor’s inclination to compromise will be increased when the duration of the negotiation process is not considered in providing the payoffs by the owner. The equilibrium mixed strategy and degree of opponents’ satisfaction in the second analysis are as follows:

$$\begin{aligned} & x^{ * } = (0.0675,0.0344,0.8981) \\ & y^{ * } = (0.1209,0.2375,0.5032,0.1384) \\ & d_{{_{1} }}^{ * } \left( {x,y)} \right. = 0.6876 \\ & d_{{_{2} }}^{ * } \left( {x,y)} \right. = 0.5096 \\ \end{aligned}$$

5 Summary and Conclusion

In this paper, we dealt with a contractual conflict in a large construction project. As it is usually difficult to exactly assess the payoffs of owners and contractors in contractual conflicts, the payoffs were assumed to be fuzzy numbers. The fuzzy versions of two matrix games were also proposed for resolving the conflict considering the fuzzy payoffs of the owner and contractor. The first fuzzy game transforms the original matrix game into a family of its α-cut equivalents. A decomposition scheme was used to translate the original bilinear model into a set of α-parameterized linear optimization models. In the second fuzzy game, a fuzzy goal was considered for each player, and the player tries to maximize the degree of attainment of his fuzzy goal.

To evaluate the applicability and efficiency of the fuzzy games, they were applied to a large oil project in the Persian Gulf. The fuzzy games provided the optimal mixed strategies for the negotiation of the owner and contractor. The expected values of the payoffs were also calculated based on the optimal strategies. It is also shown that the optimal strategies directly depend on the payoff matrices and the proposed games can be effectively utilized for incorporating the existing uncertainties in the payoff matrices. The fuzzy games can be applied to more complicated contractual or constructional conflicts.