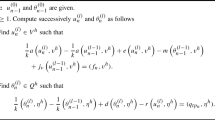Optimal Convergence of Thermoelastic Contact Problem Involving Nonlinear Hencky-Type Materials with Friction Conditions

Abstract

We study the linear finite element approximation of thermoelastic frictional contact problem. The unilateral contact condition is weakly imposed by the penalty method. Our analysis yields error estimates that are contingent upon the penalty parameter $\varepsilon$ and the mesh size h. Furthermore, provided the solution maintains regularity, we establish a convergence result.

1 Introduction

Contact-related challenges pervade various domains within mechanics, physics, and engineering applications. Instances within the automotive sector include the interaction between brake pads and rotors, as well as that between pistons and cylinders. The thermal aspects of contact processes have significant implications, exerting an influence on both the composition and rigidity of surfaces in contact, as well as triggering thermal stresses within the interacting bodies, see Shillor et al. (2004) for more details. Reciprocally, the prevailing temperature can impact the elastic material response. Numerous studies in the literature, illustrated for instance by Chouly et al. (2014); Benkhira et al. (2019a, 2019b); Benaissa et al. (2016); khalfi et al. (2023); Faiz et al. (2024, 2023) and the references therein (Benaissa et al. 2015), have delved into diverse thermo-mechanical frictional problems. In these works, not only were rigorous mathematical models of contact incorporating thermal effects established, but their unique weak solvability was also demonstrated through the application of variational and hemi-variational inequalities. Furthermore, other contributions in the literature have explored different aspects related to mechanical contact phenomena.

In recent literature, there has been an emergence of a new theoretical framework for modeling frictionless contact in thermoelastic materials, as discussed in Liu et al. (2021). This model introduces two sets of unilateral constraints: one governing normal displacement through the Signorini condition on a specified boundary portion, and the other imposing a unilateral restriction on temperature within a defined domain. Unlike the model presented in Liu et al. (2021), our study focuses on numerically investigating a frictionless contact scenario involving a thermoelastic body and a thermally conductive foundation. Notably, the determination of the heat exchange coefficient in this scenario relies on a function of the contact pressure, as detailed in Ramaniraka (1997). The novelty of our work lies in the numerical methodology employed, which employs two distinct contact algorithms based on penalty and augmented Lagrangian approaches. These algorithms are extensively discussed and effectively applied to simulate the considered system. Our research aims to explore the implications of incorporating a temperature field in the contact process between a thermoelastic body and a rigid foundation. Specifically, we consider a model describing a static frictional contact problem between a thermoelastic body and a thermally conductive foundation, assuming small deformations. The constitutive law governing material behavior incorporates Hencky’s nonlinear law and considers the interplay between mechanical and thermal properties.

The paper’s organization is as follows: In Sect. 2, we introduce relevant notations and preliminaries, and present a model depicting the process of frictional contact between a thermoelastic body and a rigid foundation. Section 3 focuses on deriving the penalized weak formulation of the model for both frictionless and Tresca’s friction scenarios. This section also addresses issues of existence and uniqueness, and discusses the finite element approximation of the penalized weak problems in detail. In Sect. 4, we establish error estimates for the numerical approximation, considering the dependence on both the penalty parameter $\varepsilon$ and the mesh size h. Moreover, provided specific regularity assumptions for the solution of contact problems and stipulated requirements on parameters $\varepsilon$ and h, we offer results regarding the convergence rate of the finite element approximation of the penalized solution.

2 Physical Statement of Problem $({\mathcal {P}})$

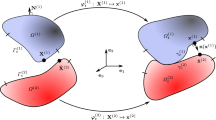
Problem $(\mathcal{ P})$ : we consider a thermoelastic body whose material particles occupy a polygonal or polyhedral domain $\Omega$ of $\mathbb {R}^d\,(d=2,3)$. The body’s equilibrium equations are characterized by

$$\begin{aligned}&\sigma ={\mathcal {A}}\varepsilon (u)-{\mathcal {M}}\theta \quad \text { in } \quad \Omega , \end{aligned}$$

(2.1)

$$\begin{aligned}&q_T= -{\mathcal {K}}\nabla \theta \quad \text { in }\quad \Omega , \end{aligned}$$

(2.2)

$$\begin{aligned}&Div\,\sigma +f_0 = 0 \quad \text { in }\quad \Omega , \end{aligned}$$

(2.3)

$$\begin{aligned}&div\,q_T -q_0 = 0 \quad \text { in }\quad \Omega . \end{aligned}$$

(2.4)

Here u is the displacement field, and $\theta$ is the temperature field. The symbols $\sigma$ and $q_T$ stand for the stress tensor and the heat flux vector field, respectively. The operator ${\mathcal {A}}:\Omega \times \mathbb {S}^d\rightarrow \mathbb {S}^d$ is the nonlinear elasticity operator that describes the behavior of Hencky’s materials, given by (see Han (2005); Haslinger and Mäkinen (1992); Chouly et al. (2014); Benkhira et al. (2019a, 2019b) for more details)

$$\begin{aligned} {\mathcal {A}}\varepsilon (u)=k_0\, tr(\varepsilon (u))\, I+2g(\Vert \bar{\varepsilon }(u)\Vert ^2)\, \bar{\varepsilon }(u) ~~\text { in } \Omega , \end{aligned}$$

(2.5)

where $k_0 > 0$ is a material coefficient, I is the second-order identity tensor, $tr(\varepsilon ) =\varepsilon _{ii}$ denotes the trace of $\varepsilon$, and $\overline{\varepsilon }$ represents its deviatoric part defined as follows

$$\begin{aligned} \overline{\varepsilon }=\varepsilon -\frac{1}{d}tr(\varepsilon )I. \end{aligned}$$

The operators ${\mathcal {M}} = ({\mathcal {M}}_{ij})$ and ${\mathcal {K}}= ({\mathcal {K}}_{ij})$ describe respectively, magentathe purely elastic, the thermal expansion and thermal conductivity properties of the material. The linearized strain $\varepsilon (u)$ is given by $\varepsilon (u)=\frac{1}{2}(\nabla u + (\nabla u)^T)$, where $(\nabla u)^T$ is the transpose of $(\nabla u)$. We recall that Div and div denote the divergence operator for tensors and vector valued functions. The densities $f_0 \in L^2(\Omega )^d$ and $q_0\in L^2(\Omega )$ represent the body force and the volume of heat source on the body, respectively.

We assume that the boundary $\Gamma =\partial \Omega$ of $\Omega$ is smooth and made of three mutually disjoined parts $\Gamma _1$, $\Gamma _2$, $\Gamma _3$. On part $\Gamma _1$, we assume that the body is clamped and a given temperature is described, we choose it equal to zero. On part $\Gamma _2$, we prescribe a surface forces and a heat flux of densities $q_2\in L^2(\Gamma _2)$ and $f_2 \in L^2(\Gamma _2)^d$, respectively. Finally, on $\Gamma _3$, the contact is unilateral, resulting in Signorini boundary conditions for mechanical effects, and thermal conditions dictate zero heat flux at points without contact and a prescribed temperature at points with contact for thermal effects. The boundary conditions on $\Gamma _1$ and $\Gamma _2$ are then specified as follows

$$\begin{aligned}&u=0 \text { on } \Gamma _1,\quad \theta =0 ~~\text { on }~~ \Gamma _1\cup \Gamma _2, \end{aligned}$$

(2.6)

$$\begin{aligned}&\sigma \nu = f_2 \text { on } \Gamma _2 ,\quad q_{T}\cdot \nu =q_2 \text { on } \Gamma _2, \end{aligned}$$

(2.7)

where the vector $\nu$ is the unit outward normal on $\Gamma$. We adopt the following decomposition: if v is a given vector field on $\Gamma _3$, we split it into its normal component $v_\nu$ and its tangential component $v_\tau$ by

$$\begin{aligned} v_\nu =v\cdot \nu ,\quad v_\tau =v-v_\nu \nu . \end{aligned}$$

Similarly, if $\sigma$ is a given tensor field on $\Gamma$, its normal and tangential components on $\Gamma$ are defined by

$$\begin{aligned} \sigma _\nu =(\sigma \nu )\cdot \nu ,\quad \sigma _\tau =\sigma \nu -\sigma _\nu \nu . \end{aligned}$$

According to this notation, $u_\nu$ and $u_\tau$ are the normal and tangential components of the displacement vector u, and $\sigma _\nu$ and $\sigma _\tau$ are the normal and tangential components of the stress tensor $\sigma$. Furthermore, to describe the unilateral contact on part $\Gamma _3$, we consider the following nonlinear boundary conditions

$$\begin{aligned}&u_{\nu }\le g ,~~ \sigma _{\nu }\le 0,~~ (u_{\nu }-g)\sigma _{\nu }=0 ~\text { on }~ \Gamma _3, \end{aligned}$$

(2.8)

$$\begin{aligned}&\left. \begin{array}{l} \Vert \sigma _{\tau }\Vert \le S, \\ \Vert \sigma _{\tau }\Vert < S \,\Rightarrow \, u_{\tau }=0, \\ \Vert \sigma _{\tau }\Vert = - S\, \dfrac{u_{\tau }}{\Vert u_{\tau }\Vert } \,\Rightarrow \, \exists \, \lambda \in \mathbb {R}^+;~~ \sigma _{\tau }= - \lambda \, u_{\tau } \end{array} \right\} \quad \text { on }~~ \Gamma _3, \end{aligned}$$

(2.9)

$$\begin{aligned}&~~~ q_T\cdot \nu =k_T(u_{\nu }-g)\, \varphi _L(\theta -\theta _F) \quad \text {on }\Gamma _{3}. \end{aligned}$$

(2.10)

In conditions (2.8), the function g denotes the maximum penetration between the body and the foundation. These equations (2.8) correspond to the classical Signorini conditions. The relations (2.9) describe the Tresca-type friction law, where $S \in L^2(\Gamma _{3})$ is a given nonnegative function. Equation (2.10) specifies the heat flux condition, with $\theta _F$ representing the foundation’s temperature and $k_T$ denoting the heat exchange function between the foundation and the body [see Duvaut (1981)]. Additionally, $\varphi _{L}$ is a truncation function defined for a large constant $L>0$ as follows

$$\varphi _{L} (s) = \left\{ {\begin{array}{*{20}l} { - L} \hfill & {{\text{if}}\,\,s < - L,} \hfill \\ s \hfill & {{\text{if}}\,\, - L \le s \le L,} \hfill \\ L \hfill & {{\text{if}}\,\,s < L.} \hfill \\ \end{array} } \right.$$

Our aim is a finite element analysis of Problem $({\mathcal {P}})$, given by (2.1)–(2.10), using penalty method. Todo that, consider $H^{m}(\Omega )$ where $m\ge 0$, and let $L^{2}(\Omega )$ denote the conventional Sobolev space $H^{0}(\Omega )$ equipped with its customary norms $\Vert \cdot \Vert _{m,\Omega }$. Our initial step involves introducing the subsequent

$$\begin{aligned}{} H&= L^{2}(\Omega )^{d} ,~ H_{1}=H^{1}(\Omega )^{d} ,~ {\mathcal {H}}=\lbrace \tau = (\tau _{ij})\in H: \tau _{ij}= \tau _{ji}\rbrace ,\,\\{} {\mathcal {H}}_{1}&= \lbrace \sigma \in {{\mathcal {H}}}: \sigma _{ij,j} \in {H}\rbrace . \end{aligned}$$

These are real Hilbert subspaces for the Euclidean associated norms to the following inner products

$$\begin{aligned} (u,v)_{H}= & {} \int _{\Omega }u_{i}v_{i} \,dx ,~~ (u,v)_{H_{1}}= (u,v)_{H}+ (\varepsilon (u), \varepsilon (v))_{{\mathcal {H}}},\\ (\sigma ,\tau )_{{\mathcal {H}}}= & {} \int _{\Omega }\sigma _{ij}\tau _{ij}\,dx ,~~ (\sigma ,\tau )_{{\mathcal {H}}_{1}}= (\sigma ,\tau )_{{\mathcal {H}}}+ (Div \sigma , Div \tau )_{{\mathcal {H}}}. \end{aligned}$$

According to the mechanical part of a condition (2.6), we consider the subspace

$$\begin{aligned} V:= \left\{ v \in \left( H^1(\Omega )\right) ^d: v=0 \text { on } \Gamma _1 \right\} , \end{aligned}$$

and the set K of admissible displacements satisfying the non-interpenetration condition, i.e.,

$$\begin{aligned} K:=\{v \in V: v_\nu \le g \text { on } \Gamma _3\}. \end{aligned}$$

Since $meas(\Gamma _1)>0$, the following Korn’s inequality holds, i.e.,

$$\begin{aligned} \Vert \varepsilon (v)\Vert _{\mathcal {H}}\ge c_k\, \Vert v\Vert _{H_1},\quad \forall \, v\in V, \end{aligned}$$

(2.11)

for a constant $c_k>0$ that depends only on $\Omega$ and $\Gamma _1$. Over the subspace V, let us consider the inner product and its associated Euclidean, defined as below

$$\begin{aligned} (u,v)_V= (\varepsilon (u),\varepsilon (v))_{\mathcal {H}},\quad \Vert u\Vert _V=(u,u)_V^{\frac{1}{2}}, \end{aligned}$$

(2.12)

Thus $(V,\Vert \cdot \Vert _{V})$ is a real Hilbert space. Moreover, by Sobolev trace theorem, relations (2.11) and (2.12), there exists a constant $c_0>0$ which depends only on $\Omega$, $\Gamma _1$ and $\Gamma _3$ such that

$$\begin{aligned} \Vert v\Vert _{L^{2}(\Gamma )^{d}}\le c_0\Vert v\Vert _V,\quad \forall \, v \in V. \end{aligned}$$

(2.13)

Now, according to the thermal part of a condition (2.6), we introduce the subspace

$$\begin{aligned} Q=\{ \xi \in H^{1}(\Omega )\,|\,\xi =0 \text { on }\Gamma _1\cup \Gamma _2\}. \end{aligned}$$

The spaces $(Q,\Vert \cdot \Vert _Q)$ is a real Hilbert space for the associated norm of the following scalar product

$$\begin{aligned} (\xi ,\psi )_Q=(\nabla \xi ,\nabla \psi )_{L^2(\Omega )}. \end{aligned}$$

It is worth noting that, given $meas(\Gamma _1)>0$, the Friedrichs-Poincaré inequality is applicable, implying the existence of a constant $c_F>0$ dependent solely on $\Omega$ and $\Gamma _a$, as follows

$$\begin{aligned} \Vert \xi \Vert _{Q}\ge c_F\, \Vert \xi \Vert _{H^1(\Omega )},\quad \forall \, \psi \in Q. \end{aligned}$$

(2.14)

Moreover, by Sobolev trace theorem, there exists $c_1>0$, depending only on $\Omega$, $\Gamma _1$ and $\Gamma _3$, such that

$$\begin{aligned} \Vert \xi \Vert _{L^{2}(\Gamma _3)}\le c_1\Vert \xi \Vert _Q,\quad \forall \, \xi \in Q. \end{aligned}$$

(2.15)

Also there exists a constant $c_T>0$, depending only on $\Omega$, $\Gamma _1$, $\Gamma _2$ and $\Gamma _3$, such that

$$\begin{aligned} \Vert \nabla \xi \Vert _{H}\le c_T\Vert \xi \Vert _{H^{1}(\Omega )},\quad \forall \, \xi \in Q. \end{aligned}$$

For any real Banach space $(X,\Vert \cdot \Vert )$, we denote by $\langle \cdot ,\cdot \rangle$ the duality pairing between X and its dual $X'$. Next, in the study of Problem $({\mathcal {P}})$, we need the following hypotheses.

$({\mathcal {H}}_1)$:

The function g is continuously differentiable in $[0,\infty )$ and satisfies

$$\begin{aligned} 0&< g_0 \le g(t) \le \frac{1}{2} \,d\,k_0, \end{aligned}$$

(2.16)

$$\begin{aligned} 0&< \alpha _1 \le g(t)+2g'(t)t\, \le \alpha _2, \end{aligned}$$

(2.17)

where $g_0$, $\alpha _1$ and $\alpha _2$ are a given positive constants.

$({\mathcal {H}}_2)$:

The thermal conductivity tensor ${\mathcal {K}} = (k_{ij}) : \Omega \times {\mathbb {R}}^d \rightarrow {\mathbb {R}}^d$ satisfies the standard properties:

$$\begin{aligned} k_{ij} = k_{ji} \in L^\infty (\Omega ), \end{aligned}$$

and there exists a nonnegative constant $m_{{\mathcal {K}}}$ such that

$$\begin{aligned} k_{ij}(x) \zeta _i \zeta _j \ge m_{{\mathcal {K}}} \Vert \zeta \Vert ^2, \quad \forall \zeta = (\zeta _i) \in {\mathbb {R}}^{d} \text { a.e. } x \in \Omega . \end{aligned}$$

Let $M_{\mathcal {F}} = \sup \nolimits _{i,j} \Vert k_{ij}\Vert _{L^\infty (\Omega )}$ denote the norm of ${\mathcal {K}}$.

$({\mathcal {H}}_3)$:

The tensor ${\mathcal {M}}=(m_{ij}):\Omega \times \mathbb {S}^{d}\rightarrow \mathbb {R}^{d}$ satisfies the properties

$$\begin{aligned} m_{ij}=m_{ji}\in L^{\infty }(\Omega ). \end{aligned}$$

Let $\Vert {\mathcal {M}}\Vert =\sup \nolimits _{i,j}\Vert m_{ij}\Vert _{L^\infty (\Omega )}$ be the norm of the thermal expansion tensor ${\mathcal {M}}$.

$({\mathcal {H}}_4)$:

The thermal conductance function $\psi = k_T:\Gamma _3 \times \mathbb {R} \rightarrow \mathbb {R}_+$, satisfy the properties

• (a) there exists $M_{\varphi }>0$ such that   $|k_T(x,u)|\le M_{\varphi } \,\text { for all }\, u\in \mathbb {R}$, a.e. $x\in \Gamma _3$,

• (b) the mapping $x\mapsto \psi (x,u)$ is measurable on $\Gamma _3$ for all $u\in \mathbb {R}$,

• (c) there exists $L_{\varphi }>0$ such that, for all $u_1$, $u_2 \in \mathbb {R}$, one has

  $$\begin{aligned} |\psi (x,u_1)-\psi (x,u_2)|\le L_{\varphi }|u_1-u_2| \,\text { a.e. }\, x\in \Gamma _3. \end{aligned}$$

$({\mathcal {H}}_5)$:

The body forces, traction and heat source densities satisfy the following properties

$$\begin{aligned} f_{0}\in L^{2}(\Omega )^{d},\, f_{2}\in L^{2}(\Gamma _{2})^{d},\, q_{0}\in L^{2}(\Omega ),\, q_2\in L^2(\Gamma _2). \end{aligned}$$

$({\mathcal {H}}_6)$:

The friction bound, the gap function and the foundation’s temperature satisfy

$$\begin{aligned} S\ge 0 \text { a.e. } x\in \Gamma _3 ,\;\; S\in L^{2}(\Gamma _{3}),\\ g\ge 0 \text { a.e. } x\in \Gamma _3 ,\;\; g \in L^{2}(\Gamma _3),\\ \theta _F \in L^2(\Gamma _3). \end{aligned}$$

In the other hand, to write the weak formulation, we define the following operators

$$\begin{aligned} \left\langle {\mathcal {A}}u,v\right\rangle _V&=\int _\Omega {\mathcal {A}} \varepsilon (u)\varepsilon (v)\,dx,\quad \forall \, u,\,v \in V, \end{aligned}$$

(2.18)

$$\begin{aligned} \left\langle {\mathcal {P}} \theta ,v\right\rangle _V&=\int _\Omega {\mathcal {P}}\theta \,\varepsilon (v)\,dx,\quad \forall \, \theta \in Q,\,\forall \, v\in V, \end{aligned}$$

(2.19)

$$\begin{aligned} \left\langle K \theta ,\eta \right\rangle _Q&=\int _\Omega {\mathcal {K}}\nabla \theta \,\nabla \eta \,dx,\quad \forall \, \theta ,\,\eta \in Q. \end{aligned}$$

(2.20)

Next, we consider the elements $f\in V'$ and $q \in Q'$ given by

$$\begin{aligned} \left\langle f,v\right\rangle _V&= \int _\Omega f_0\cdot v\,dx+\int _{\Gamma _2} f_2\cdot v\,da,\quad \forall \, v \in V, \end{aligned}$$

(2.21)

$$\begin{aligned} \left\langle q,\eta \right\rangle _Q&= \int _\Omega q_0\,\eta \,dx - \int _{\Gamma _2} q_2\eta \,da,\quad \forall \, \eta \in Q. \end{aligned}$$

(2.22)

3 Existence and Uniqueness Results

3.1 Penalty Formulation of the Frictionless Problem

Consider $(P')$ as the frictionless counterpart of Problem (P), derived by substituting (2.9) with the following condition

$$\begin{aligned} \sigma _{\tau }(u,\theta )=0. \end{aligned}$$

(3.1)

Subsequently, the weak formulation of the frictionless unilateral problem defined by (2.1)–(2.10) is as follows

Problem $({{\mathcal {P}}}{{\mathcal {V}}})$. Find a displacement field $u\in K$ and a temperature field $\theta \in Q$ such that

$$\begin{aligned}&({\mathcal {A}}\varepsilon (u) , \varepsilon (v)-\varepsilon (u))_{{\mathcal {H}}}-({\mathcal {M}}\theta , \varepsilon (v)-\varepsilon (u))_{{\mathcal {H}}}\\ &\quad \ge (f,v-u)_{V},\quad \forall \,v\in K, \end{aligned}$$

(3.2)

$$\begin{aligned} ({\mathcal {K}}\nabla \theta , \nabla \xi )_{{L^{2}(\Omega )}}+\ell (u,\theta ,\xi ) = (q,\xi )_Q,\quad \forall \,\xi \in Q, \end{aligned}$$

(3.3)

where the functional $\ell : V\times Q\times Q\rightarrow {\mathbb {R}}$ defined as follows

$$\begin{aligned} \ell (u,\theta ,\xi ) = \int _{\Gamma _3} k_T(u_{\nu }-g)\, \varphi _L(\theta -\theta _F)\,\xi \,da. \end{aligned}$$

The existence of a unique solution to Problem $({{\mathcal {P}}}{{\mathcal {V}}})$ relies on elliptic variational inequalities and fixed point arguments, as discussed in, for instance, Duvaut (1981). We then examine the product space $X = V \times Q$, which forms a Hilbert space with the corresponding norm defined by the inner product below

$$\begin{aligned} \left( x,y \right) _{X} = \left( u,v \right) _{V} +\left( \theta ,\xi \right) _{Q},\quad \forall \, x=(u,\theta ),\, y=(v,\xi ) \in X. \end{aligned}$$

(3.4)

We introduce the operator $B: X \rightarrow X$, defined as follows

$$\begin{aligned}{} & {} \left( Bx,y \right) _{X}=({\mathcal {A}}\varepsilon (u), \varepsilon (v))_{{\mathcal {H}}}-({\mathcal {M}}\theta , \varepsilon (v))_{{\mathcal {H}}}\nonumber \\{} & {} \quad +({\mathcal {K}}\nabla \theta , \nabla \xi )_{{L^{2}(\Omega )}} \end{aligned}$$

(3.5)

We also introduce the functional $j: X\rightarrow {\mathbb {R}}$ and the element $f^{e} \in X$ given by

$$\begin{aligned}&j(x,y )=\ell \left( u,\theta ,\xi \right) , \end{aligned}$$

(3.6)

$$\begin{aligned}&f^{e} =\left( f,q \right) \in X. \end{aligned}$$

(3.7)

Let $U = K\times Q$ be non-empty closed convex of X. Then, we get the following equivalent problem Problem $({{\mathcal {P}}}{{\mathcal {V}}})$. Find $x=(u,\theta )\in U$ such that

$$\begin{aligned}{} & {} \left( Bx,y-x \right) _{X} + j\left( x,y \right) - j\left( x,x \right) \ge \left( f^{e}, y-x\right) _{X},\nonumber \\{} & {} \quad \forall \, y=(v,\xi )\in U. \end{aligned}$$

(3.8)

Lemma 3.1

The operator B is strongly monotone and Lipschitz continuous.

Proof

To establish this, we need to ensure that the nonlinear elasticity operator ${\mathcal {A}}$, as defined in (2.5), is both strongly monotone and Lipschitz continuous. By performing algebraic manipulations akin to those in references (Benkhira et al. 2019a, b), we obtain:

$$\begin{aligned}{} & {} ({\mathcal {A}}\varepsilon (u)-{\mathcal {A}}\varepsilon (v), \varepsilon (u)-\varepsilon (v))_{{\mathcal {H}}} \ge m_{{\mathcal {A}}} \Vert u-v \Vert ^{2}_{V},~\nonumber \\{} & {} \quad \forall \, u,\, v \in V ~\text { with }~ m_{{\mathcal {A}}}=2\alpha _{1}, \end{aligned}$$

(3.9)

$$\begin{aligned}{} & {} \Vert {\mathcal {A}}\varepsilon (u)-{\mathcal {A}}\varepsilon (v) \Vert _{{\mathcal {H}}} \le M_{{\mathcal {A}}} \Vert u-v \Vert _{V},~\nonumber \\{} & {} \quad \forall \, u,\, v \in V~\text { with }~ M_{{\mathcal {A}}}=2d^{2}k_{0}. \end{aligned}$$

(3.10)

With (3.9)–(3.10) in mind, and employing similar algebraic manipulations as in Benkhira et al. (2019a, 2019b), we can readily establish the existence of positive constants $m_{B}$ and $M_{B}$, depending solely on ${\mathcal {A}}$, ${\mathcal {M}}$, ${\mathcal {K}}$, and $\Omega$, such that:

$$\begin{aligned}{} & {} (Bx-By, x-y)_{X}\ge m_{B} \Vert x-y \Vert ^{2}_{X},\quad \forall x,\, y \in X, \end{aligned}$$

(3.11)

$$\begin{aligned}{} & {} \Vert Bx-By \Vert _{X}\le M_{B} \Vert x-y \Vert _{X},\quad \forall x,\, y \in X. \end{aligned}$$

(3.12)

Therefore, we conclude the proof of the Lemma 3.1. $\square$

Let’s define the notation $[\,\cdot \,]^{+}$ to represent the positive part of each scalar $a\in {\mathbb {R}}$ as follows:

$$\begin{aligned}{}[a]^{+} ={\left\{ \begin{array}{ll} a&{}\quad \text { if } \;\; a\ge 0, \\ 0&{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

Throughout the remainder of this document, we will frequently utilize the following common properties:

$$\begin{aligned} a\le [a]^{+},\;\; a\cdot [a]^{+}={[a]^{+}}^2,\quad \forall a \in {\mathbb {R}}. \end{aligned}$$

(3.13)

The monotonicity property can be derived from the aforementioned properties, as detailed in Chouly and Hild (2013a); Chouly et al. (2014); Chouly and Hild (2013b).

$$\begin{aligned} \big ([a]^{+}-[b]^{+}\big )\,(a-b)\ge \big ([a]^{+} - [b]^{+}\big )^{2}. \end{aligned}$$

(3.14)

The variational inequality (3.8) poses challenges for solution using various methods, particularly due to the constraint subspace K which is not conducive for computations. Therefore, alternative techniques are needed, and one of the classical and widely used methods to address this inequality constraint is the penalty method. The penalty technique is a well-established approach for numerically handling constrained problems (see, for example, Li (1998); Kikuchi and Oden (1988)). Unlike the Lagrange multiplier technique, the penalty method does not require the introduction of a new variable. Furthermore, it is more readily implementable in many numerical algorithms. However, it’s important to note that this method still represents an approximation, as the solution of the penalized problem is expected to converge to the solution of the original problem only as the penalty parameter tends to zero.

Problem $({{\mathcal {P}}}{{\mathcal {V}}}_{\varepsilon })$. Find a displacement field $u_{\varepsilon }\in V$ and a temperature field $\theta _{\varepsilon }\in Q$ such that

$$\begin{aligned}{} & {} \left( Bx_{\varepsilon },y \right) _{X} + j\left( x_{\varepsilon },y \right) +\dfrac{1}{\varepsilon } \int _{\Gamma _{3}} [u_{\varepsilon ,\nu } ]^{+} v_{\nu }\,da \nonumber \\{} & {} \quad = \left( f^{e}, y\right) _{X},~~\forall \, y=(v,\xi )\in X=V\times Q. \end{aligned}$$

(3.15)

Note that this formulation is obtained by taking

$$\begin{aligned} \sigma _{\nu }(u_{\epsilon },\theta _{\varepsilon }) = \dfrac{1}{\varepsilon } \,[u_{\varepsilon ,\nu } ]^{+} ~\text { where }~ u_{\varepsilon ,\nu }=u_{\varepsilon }\cdot \nu . \end{aligned}$$

We have the following theorem, the proof of which can be found in (Bourichi et al. 2016, Theorem 3.1):

Theorem 3.2

Problem $(PV_{\epsilon })$ has a unique solution $x_{\epsilon }=(u_{\epsilon },\theta _{\epsilon }) \in X=V\times Q$.

3.2 Penalty Formulation of Tresca’s Friction Problem

Initially, employing conventional methods rooted in Green’s formula, we establish that when $(u, \sigma ,\theta , q)$ denote regular functions satisfying (2.1)-(2.10), the weak formulation of the Tresca’s friction problem can be articulated as follows.

Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}})$. Find $(u, \theta )\in V\times Q$ such that

$$\begin{aligned}&({\mathcal {A}}\varepsilon (u) , \varepsilon (v)-\varepsilon (u))_{{\mathcal {H}}} - ({\mathcal {M}}\theta , \varepsilon (v)-\varepsilon (u))_{{\mathcal {H}}}\nonumber \\&\quad + j_S(v)-j_S(u)\ge (f,v-u)_{V},~ \forall \,v\in V, \end{aligned}$$

(3.16)

$$\begin{aligned}&({\mathcal {K}}\nabla \theta , \nabla \xi )_{{L^{2}(\Omega )}}+\ell \left( u,\theta ,\xi \right) =(q,\xi )_Q,~ \forall \,\xi \in W, \end{aligned}$$

(3.17)

where the functionals $j_S$ and $\ell$ are defined as following

$$\begin{aligned} j_S= & {} \int _{\Gamma _3} S\Vert u_\tau \Vert \,ds,\\ \ell \left( u,\theta ,\xi \right)= & {} \int _{\Gamma _3}k_T(u_{\nu }-g)\varphi _L(\theta -\theta _F)\,\xi \,da. \end{aligned}$$

The following theorem can be found in Duvaut (1981).

Theorem 3.3

With assumptions $({\mathcal {H}}_1)$–$({\mathcal {H}}_6)$, Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}})$ possesses at least one solution. Furthermore, if the function k is given for some $\alpha \in \mathbb {R}$, by

$$\begin{aligned} k(\xi )=\alpha \,k_{0}(\xi ), \end{aligned}$$

(3.18)

Then, there exists $\alpha _1>0$ such that if

$$\begin{aligned} 0\le \alpha \le \alpha _1, \end{aligned}$$

(3.19)

the solution of Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}})$, is unique.

Lemma 3.4

The couple $x=(u,\theta ) \in X$ is a solution to Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}})$ if and only if

$$\begin{aligned}{} & {} (Bx,y-x)_{X} + j(x,y) - j(x,x) +\int _{\Gamma _3} S\big (\Vert v_\tau \Vert -\Vert u_\tau \Vert \big )ds \nonumber \\{} & {} \quad \ge (f^{e}, y-x)_{X},~ \forall \, y=(v,\xi )\in U. \end{aligned}$$

(3.20)

By employing the penalty method on Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$, we derive the subsequent penalized weak formulation.

Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$. Find a displacement field $u_{\varepsilon }\in V$ and a temperature field $\theta _{\varepsilon }\in Q$ such that

$$\begin{aligned}{} & {} (Bx_{\varepsilon },y)_{X} + j(x_{\varepsilon },y) + \dfrac{1}{\varepsilon } \int _{\Gamma _{3}} [u_{\varepsilon ,\nu } ]^{+} v_{\nu } da \nonumber \\{} & {} \quad + \frac{1}{\varepsilon }\int _{\Gamma _{3}}[u_{\varepsilon ,\tau }]_{\varepsilon g}v_{\tau }da = ( f^{e}, y)_{X},\quad \forall \, y=(v,\xi ) \in X, \end{aligned}$$

(3.21)

where the notation $[\,\cdot \,]_{\alpha }$ ($\alpha \in {\mathbb {R}}^{+}$) stands for the truncation of a scalar $x \in {\mathbb {R}}$, i.e.;

$$\begin{aligned}{}[x]_{\alpha } = {\left\{ \begin{array}{ll} x&{}\quad \text {if}\;\; \Vert x \Vert \le \alpha , \\ \alpha \frac{x}{\Vert x \Vert }&{}\quad \text { otherwise}. \end{array}\right. } \end{aligned}$$

The following theorem can be found in (Chouly and Hild 2013b, Theorem 4.1) and (Bourichi et al. 2016, Theorem 3.1).

Theorem 3.5

Under the assumptions $({\mathcal {H}}_1)$–$({\mathcal {H}}_6)$, $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$ has a unique solution.

3.3 Approximation of the Penalty Weak Formulations

For a given discretization parameter $h > 0$, we denote by ${\mathcal {T}}^{h}$ a coherent set of triangular finite element partitions of the closed domain $\overline{\Omega }$, which are compatible with the boundary partitions $\Gamma = \Gamma _{1} \cup \Gamma _{2} \cup \Gamma _{3}$. We contemplate two finite-dimensional subspaces $V^{h} \subset V$ and $Q^{h}\subset Q$, which approximate the spaces V and Q, respectively, as follows

$$\begin{aligned} V^{h}&= \left\{ v^{h} \in C(\overline{\Omega })^{d} :~ v^{h}_{\mid T} \in {\mathbb {P}}_{1}(T)^{d}, ~\forall \, T \in {\mathcal {T}}^{h}\right. \\&\quad \left. \text { and }~ v^{h}= 0 ~\text { on }~ \Gamma _{1} \right\} , \\ Q^{h}&= \left\{ \xi ^{h} \in C(\overline{\Omega }) :~ \xi ^{h}_{\mid T} \in {\mathbb {P}}_{1}(T), ~\forall \, T \in {\mathcal {T}}^{h}\right. \\&\quad \left. \,\text { and }~ \xi ^{h}= 0 ~\text { on }~ \Gamma _{1}\cup \Gamma _{2}\right\} \end{aligned}$$

where ${\mathbb {P}}_{1}(T)$ represents the space of polynomial functions with a global degree less than or equal to 1 within an arbitrary element $T\in {\mathcal {T}}^{h}$. Additionally, we examine the space ${\mathcal {X}}^{h}(\Gamma _{3})$ comprising the normal traces on $\Gamma _{3}$ for discrete functions in $V^{h}$, namely

$$\begin{aligned}{} & {} {\mathcal {X}}^{h}(\Gamma _{3}) = \left\{ \mu _{h} \in C(\overline{\Gamma _{3}}):~ \exists \, v^{h} \in V^{h},\right. \\{} & {} \quad \left. \forall T \in {\mathcal {T}}^{h};~ v^{h} \cdot \nu = \mu _{h} \right\} . \end{aligned}$$

The following lemmas outline pertinent properties of the $L^{2}(\Gamma _{3})$-projection operator ${\mathcal {P}}^{h}: L^{2}(\Gamma _{3})\rightarrow {\mathcal {X}}^{h}(\Gamma _{3})$, with further details available in Bernardi et al. (1994), Bramble et al. (2001), Bramble and Xu (1991).

Lemma 3.6

Suppose the mesh linked with ${\mathcal {X}}^{h}(\Gamma _{3})$ exhibits local quasi-uniformity, indicating that the ratio of the diameter of a simplex to the diameter of the largest ball enclosed within the simplex remains bounded irrespective of h for all simplices across all triangulations, as elaborated in Bramble et al. (2001). Under these conditions, for any $r \in [0,1]$ and every $v \in H^{r}(\Gamma _{3})$, the subsequent stability and interpolation estimates apply

$$\begin{aligned} \Vert {\mathcal {P}}^{h}(v) \Vert _{r,\Gamma _{3}}\le & {} c, \Vert v \Vert _{r,\Gamma _{3}}, \end{aligned}$$

(3.22)

$$\begin{aligned} \Vert v - {\mathcal {P}}^{h}(v) \Vert _{0,\Gamma _{3}}\le & {} ch^{r}, \Vert v \Vert _{r,\Gamma _{3}}, \end{aligned}$$

(3.23)

where the constant $c > 0$ in the two inequalities remains independent of v and the discretization size h.

Lemma 3.7

Suppose the mesh on $\Gamma _{3}$ is quasi-uniform. Then, there exists an extension operator ${\mathcal {R}}^{h}: {\mathcal {X}}^{h}(\Gamma _{3}) \rightarrow V^{h}(\Gamma _{3})$ and a constant $c >0$, independent of v and h, satisfying:

$$\begin{aligned}{} & {} {\mathcal {R}}^{h}(\mu _{h}){\mid \Gamma {3}} = \mu _{h}, \end{aligned}$$

(3.24)

$$\begin{aligned}{} & {} \Vert {\mathcal {R}}^{h}(\mu _{h}) \Vert _{1,\Omega } \le c, \Vert \mu _{h} \Vert _{\frac{1}{2},\Gamma _{3}},\quad \forall , \mu _{h} \in {\mathcal {X}}^{h}(\Gamma _{3}) . \end{aligned}$$

(3.25)

Subsequently, consider $\textbf{P}^{h}$ and $\textbf{R}^{h}$ as the vector representations of the operators ${\mathcal {P}}^{h}$ and ${\mathcal {R}}^{h}$, respectively, which are defined as follows

$$\begin{aligned}&\textbf{P}^{h}(\textbf{w}) := ({\mathcal {P}}^{h} (w_{i}))_{1\le i \le d},\quad \forall \,\, \textbf{w} : = (w_{i})_{1\le i \le d} \in L^{2}(\Gamma _{3}), \end{aligned}$$

(3.26)

$$\begin{aligned}&\textbf{R}^{h}(\textbf{w}):= ({\mathcal {R}}^{h} (w_{i}))_{1\le i \le d },\quad \forall \,\, \textbf{w} : = (w_{i})_{1\le i \le d} \in {\mathcal {X}}^{h}(\Gamma _{3}). \end{aligned}$$

(3.27)

It’s worth noting that $\textbf{P}^{h}$ and $\textbf{R}^{h}$ adhere to the stability and interpolation properties stated earlier in equations (3.22) through (3.25).

Remark 3.8

Consider a sequence of triangulations ${\mathcal {T}}=({\mathcal {T}}^{h})_{h>0}$. We define it as quasi-uniform if the ratio $h_{\tau }/\rho _{\tau }$, where $h_{\tau }$ denotes the diameter of an element $\tau \in {\mathcal {T}}^{h}$ and $\rho _{\tau }$ represents the diameter of its inscribed circle, is bounded by a constant $\hat{\sigma }$ independent of both $\tau$ and h. Furthermore, there exists a constant $c > 0$ that is invariant with respect to h and satisfies the following condition:

$$\begin{aligned} h_{\tau } \ge ch,~~\forall \, \tau \in {\mathcal {T}}^{h}. \end{aligned}$$

It’s important to highlight that the quasi-uniformity of the mesh on $\Gamma _{3}$ (the mesh associated with ${\mathcal {X}}^{h}(\Gamma _{3})$) implies its local quasi-uniformity.

3.3.1 Approximation of the Frictionless Problem

The finite element discretization $({{\mathcal {P}}}{{\mathcal {V}}}^{h}_{\varepsilon })$ of the penalized problem $({{\mathcal {P}}}{{\mathcal {V}}}_{\varepsilon })$ is outlined as follows.

Problem $({{\mathcal {P}}}{{\mathcal {V}}}^{h}_{\varepsilon })$. Find a displacement field $u^{h}_{\varepsilon }\in V^{h}$ and a temperature field $\theta ^{h}_{\varepsilon }\in Q^{h}$ such that

$$\begin{aligned}{} & {} (Bx^{h}_{\varepsilon },y^{h})_{X} + j(x^{h}_{\varepsilon },y^{h}) + \dfrac{1}{\varepsilon } \int _{\Gamma _{3}} [u^{h}_{\varepsilon ,\nu } ]^{+} v^{h}_{\nu }\,da \nonumber \\{} & {} \quad = (f^{e}, y^{h})_{X},~~ \forall \, y^{h}=(v^{h},\xi ^{h})\in X^{h}=V^{h}\times Q^{h}. \end{aligned}$$

(3.28)

Proof

By applying Theorem 3.2, replacing V and Q with $V^{h}$ and $Q^{h}$ respectively, we deduce that Problem $({{\mathcal {P}}}{{\mathcal {V}}}^{h}_{\varepsilon })$ has a unique solution $(u^{h}_{\varepsilon } ,\theta ^{h}_{\varepsilon })\in X^{h}=V^{h}\times Q^{h}$. $\square$

3.3.2 Approximation of the Tresca’s Friction Problem

The numerical approximation $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}^{h}_{\varepsilon })$ for the penalized problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$, is described as follows.

Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}^{h}_{\varepsilon })$. Find $u^{h}_{\varepsilon }\in V^{h}$ and $\theta ^{h}_{\varepsilon }\in Q^{h}$ such that

$$\begin{aligned} &(Bx^{h}_{\varepsilon },y^{h})_{X} + j(x^{h}_{\varepsilon },y^{h}) + \dfrac{1}{\varepsilon } \int _{\Gamma _{3}} [u^{h}_{\varepsilon ,\nu } ]^{+} v^{h}_{\nu } da \\&\quad + \frac{1}{\varepsilon }\int _{\Gamma _{3}}[u^{h}_{\varepsilon ,\tau }]_{\varepsilon g}v^{h}_{\tau }da = (f^{e} , y^{h})_{X}, \\&\qquad \hbox { for all}\ y^{h}=(v^{h} ,\xi ^{h})\in X^{h}=V^{h}\times Q^{h}. \end{aligned}$$

(3.29)

Remark 3.9

The uniqueness of the solution to problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}^{h}_{\varepsilon })$ can be established using similar reasoning as in (Chouly and Hild 2013b, Theorem 4.1) and (Bourichi et al. 2016, Theorem 3.1), with the respective spaces $V^{h}$ and $Q^{h}$ replacing V and Q.

The penalized problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$ is consistent with the finite element penalized problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}^{h}_{\varepsilon })$ in such a way that the solution $x_{\varepsilon }=(u_{\varepsilon }, \theta _{\varepsilon })$ of problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$ satisfies equation (3.29) for all test functions $y^{h}=(v^{h} ,\xi ^{h})\in X^{h}=V^{h}\times Q^{h}\subset X=V\times Q$. This implies that

$$\begin{aligned}{} & {} (Bx_{\varepsilon },y^{h})_{X} + j(x_{\varepsilon },y^{h}) + \dfrac{1}{\varepsilon } \int _{\Gamma _{3}} [u_{\varepsilon ,\nu } ]^{+} v^{h}_{\nu }da \nonumber \\{} & {} \quad + \frac{1}{\varepsilon }\int _{\Gamma _{3}}[u_{\varepsilon ,\tau }]_{\varepsilon g}v^{h}_{\tau }da = (f^{e}, y^{h})_{X}. \end{aligned}$$

(3.30)

We revisit the fundamental characteristics of projections as follows

$$\begin{aligned}{} & {} \big ([x]_{\alpha }-[y]_{\alpha }\big )\cdot (x-y) \ge 0 ~ \nonumber \\{} & {} \quad \text { and }~~\big \vert [x]_{\alpha }-[y]_{\alpha } \big \vert \le \vert x-y \vert ,\quad \forall \, x,\, y \in {\mathbb {R}}^{d-1}, \end{aligned}$$

(3.31)

expressed for any v and w belonging to V, we can represent this as

$$\begin{aligned}{} & {} \big ([v_{\tau }]_{\epsilon g}-[w_{\tau }]_{\epsilon g}\big )\cdot (v_{\tau }-w_{\tau }) \ge 0 ~\nonumber \\{} & {} \quad \text { and }~~ \big \vert [v_{\tau }]_{\epsilon g}-[w_{\tau }]_{\epsilon g}\big \vert \le \vert v_{\tau } - w_{\tau } \vert ~~\text { on }~~ \Gamma _{3}. \end{aligned}$$

(3.32)

4 Approximation and a Priori Estimate Results

4.1 A Priori Estimate of the Frictionless Problem

Lemma 4.1

Let $x=(u, \theta )\in [H^{\frac{3}{2}+r}(\Omega )]^{d} \times H^{\frac{3}{2}+r}(\Omega )$ with $r\in (0,\frac{1}{2}]$, respectively, $x^{h}_{\varepsilon }=(u^{h}_{\varepsilon }, \theta ^{h}_{\varepsilon })$ and $x_{\varepsilon }=(u_{\varepsilon }, \theta _{\varepsilon })$ be solutions of the problems $({{\mathcal {P}}}{{\mathcal {V}}})$, $({{\mathcal {P}}}{{\mathcal {V}}}^{h}_{\varepsilon })$ and $({{\mathcal {P}}}{{\mathcal {V}}}_{\varepsilon })$. Then, we have

$$\begin{aligned} &\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{-r , \Gamma _{3}} \\&\quad \le C\, \left[ h^{r}\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{0 , \Gamma _{3}} \right. \\&\left. \qquad +h^{r-\frac{1}{2}} \left( \Vert u-u^{h}_{\varepsilon } \Vert _{1,\Omega }+\Vert \theta -\theta ^{h}_{\varepsilon } \Vert _{1,\Omega } \right) \right] \end{aligned}$$

(4.1)

and

$$\begin{aligned}&\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u_{\varepsilon ,\nu } ]^{+} \right\| _{-r , \Gamma _{3}} \\&\quad \le C\, \left[ \varepsilon ^{r}\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u_{\varepsilon ,\nu } ]^{+} \right\| _{0 , \Gamma _{3}} \right. \\&\left. \quad +\varepsilon ^{r-\frac{1}{2}} \left( \Vert u-u_{\varepsilon } \Vert _{1,\Omega }+\Vert \theta -\theta _{\varepsilon } \Vert _{1,\Omega } \right) \right] , \end{aligned}$$

(4.2)

where the non-negative constant C is independent of $\varepsilon$, u , $u^{h}_{\varepsilon }$ and h.

Proof

First, we have [see Chouly and Hild (2013b) for more details]

$$\begin{aligned}{} & {} \left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{-r, \Gamma _{3}}\\{} & {} \quad =\sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+}, v\right\rangle _{\Gamma _{3}}}{\Vert v \Vert _{r, \Gamma _{3}}}. \end{aligned}$$

Hence, by using the relations (3.22)–(3.25), we get that

$$\begin{aligned}&\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{-r , \Gamma _{3}} \\&\quad \le \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta )+\dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+},v-{\mathcal {P}}^{h}v\right\rangle _{\Gamma _{3}}}{\Vert v \Vert _{r , \Gamma _{3}}} \\&\qquad +\sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} ,{\mathcal {P}}^{h}v\right\rangle _{\Gamma _{3}}}{\Vert v \Vert _{r , \Gamma _{3}}} \\&\quad \le \left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{0 , \Gamma _{3}}\,\,\,\, \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\Vert v-{\mathcal {P}}^{h}v \Vert _{0,\Gamma _{3}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}} \\&\qquad + C \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} ,{\mathcal {P}}^{h}v\right\rangle _{\Gamma _{3}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}} \\&\quad \le Ch^{r}\, \left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{0 , \Gamma _{3}} \\&\qquad + \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} ,{\mathcal {P}}^{h}v\right\rangle _{\Gamma _{3}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}}. \end{aligned}$$

Furthermore, we know that for all $v\in V$, we have

$$\begin{aligned}&({\mathcal {A}}\varepsilon (u) , \varepsilon (v))_{{\mathcal {H}}}-({\mathcal {M}}\theta , \varepsilon (v))_{{\mathcal {H}}} = (f,v)_{V} +\langle \sigma _{\nu }(u,\theta ),v_{\nu }\rangle _{\Gamma _{3}}, \\&({\mathcal {A}}\varepsilon (u_{\varepsilon }) , \varepsilon (v))_{{\mathcal {H}}}-({\mathcal {M}}\theta _{\varepsilon } , \varepsilon (v))_{{\mathcal {H}}} = (f,v)_{V} +\left\langle -\dfrac{1}{\varepsilon } [u_{\varepsilon ,\nu } ]^{+},v_{\nu }\right\rangle _{\Gamma _{3}}. \end{aligned}$$

Then, we find that

$$\begin{aligned}{} & {} \left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u_{\varepsilon ,\nu } ]^{+},v_{\nu }\right\rangle _{\Gamma _{3}} = ({\mathcal {A}}\varepsilon (u - u _{\varepsilon }), \varepsilon (v))_{{\mathcal {H}}}\nonumber \\{} & {} \quad +({\mathcal {M}}(\theta _{\varepsilon } - \theta ), \varepsilon (v))_{{\mathcal {H}}},~~\forall v\in V. \end{aligned}$$

(4.3)

Similarly, by using $V^{h}$ instead of V, we deduce that

$$\begin{aligned}{} & {} \left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+},v^{h}_{\nu }\right\rangle _{\Gamma _{3}} = ({\mathcal {A}}\varepsilon (u - u^{h}_{\varepsilon }), \varepsilon (v^{h}))_{{\mathcal {H}}}\\{} & {} \quad + ({\mathcal {M}}(\theta ^{h}_{\varepsilon } - \theta ), \varepsilon (v^{h}))_{{\mathcal {H}}}. \end{aligned}$$

On another side, the continuity of $(u,v)\mapsto ({\mathcal {A}}\varepsilon (u ) , \varepsilon (v))$ and $(\theta ,v)\mapsto ({\mathcal {M}}\theta ,\varepsilon (v))$ lead to

$$\begin{aligned}&\sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} ,{\mathcal {P}}^{h}v\right\rangle _{\Gamma _{3}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}}\\&\quad \le \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} ,{\mathcal {R}}^{h}\big ({\mathcal {P}}^{h}v\big )_{\mid \Gamma _{3}} \cdot \,\nu \right\rangle _{\Gamma _{3}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}}\\ {}&\quad \le \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\big ({\mathcal {A}}\varepsilon (u - u^{h}_{\varepsilon }) , \varepsilon {\mathcal {R}}^{h}\big ({\mathcal {P}}^{h}v\big )\big )_{{\mathcal {H}}} +\big ({\mathcal {M}}(\theta ^{h}_{\varepsilon } - \theta ) , \varepsilon {\mathcal {R}}^{h}\big ({\mathcal {P}}^{h}v\big )\big )_{{\mathcal {H}}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}}\\&\quad \le C\, \big (\Vert u - u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta - \theta ^{h}_{\varepsilon } \Vert _{1,\Omega }\big )\, \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\Vert {\mathcal {R}}^{h}({\mathcal {P}}^{h}v)\Vert _{1,\Omega }}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}} \\ {}&\quad \le C\, \big (\Vert u - u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta - \theta ^{h}_{\varepsilon } \Vert _{1,\Omega }\big )\, \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\Vert {\mathcal {R}}^{h}({\mathcal {P}}^{h}v)\Vert _{\frac{1}{2},\Gamma _{3}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r , \Gamma _{3}}} . \end{aligned}$$

Using next the following inverse inequality

$$\begin{aligned} \Vert {\mathcal {P}}^{h}v \Vert _{\frac{1}{2}, \Gamma _{3}} \le Ch^{r-\frac{1}{2}}\Vert {\mathcal {P}}^{h}v \Vert _{r, \Gamma _{3}} \end{aligned}$$

to find

$$\begin{aligned}{} & {} \sup _{v\in H^{r}(\Gamma _{3})} \dfrac{\left\langle \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+},{\mathcal {P}}^{h}v\right\rangle _{\Gamma _{3}}}{\Vert {\mathcal {P}}^{h}v \Vert _{r,\Gamma _{3}}}\nonumber \\{} & {} \quad \le Ch^{r-\frac{1}{2}}\,\big (\Vert u - u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta - \theta ^{h}_{\varepsilon } \Vert _{1,\Omega } \big ). \end{aligned}$$

Finally, we the following estimate

$$\begin{aligned}&\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{-r , \Gamma _{3}}\\&\quad \le C\,\Big [ h^{r-\frac{1}{2}}( \Vert u - u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta - \theta ^{h}_{\varepsilon } \Vert _{1,\Omega }) \\&\qquad + h^{r}\,\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{0 , \Gamma _{3}} \Big ]. \end{aligned}$$

We now introduce $V^{\varepsilon }$ a fictitious finite element space, defined identically as $V^{h}$ and with the choice of mesh size $h = \varepsilon$. We note ${\mathcal {P}}^{\varepsilon }: L^{2}(\Gamma _{3})\rightarrow {\mathcal {X}}^{\varepsilon }(\Gamma _{3})$ the $L^{2}(\Gamma _{3})$-projection operator onto ${\mathcal {X}}^{\varepsilon }(\Gamma _{3})$. Therefore, we can write

$$\begin{aligned}&\left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{-r , \Gamma _{3}}\\&\quad \le C\,\Big [ \varepsilon ^{r-\frac{1}{2}}( \Vert u - u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta - \theta ^{h}_{\varepsilon } \Vert _{1,\Omega })\\&\qquad + \varepsilon ^{r} \left\| \sigma _{\nu }(u,\theta ) + \dfrac{1}{\varepsilon } [u^{h}_{\varepsilon ,\nu } ]^{+} \right\| _{0 , \Gamma _{3}} \Big ], \end{aligned}$$

which is the desired result (4.2). $\square$

Theorem 4.2

Suppose $\Omega \subset {\mathbb {R}}^{d}$ is a bounded polygonal domain. Let $x=(u,\theta )$ and $x_{\varepsilon }=(u_{\varepsilon },\theta _{\varepsilon })$ denote the solutions of Problems $({\mathcal {P}})$ and $({{\mathcal {P}}}{{\mathcal {V}}} _{\varepsilon })$, respectively. Assuming that $(u,\theta )\in [H^{\frac{3}{2}+ r}(\Omega )]^d\times H^{\frac{3}{2}+r}(\Omega )$ (where $r\in (0,1/2]$), the subsequent prior estimate holds

$$\begin{aligned}{} & {} \Vert u - u_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta -\theta _{\varepsilon } \Vert _{1,\Omega } + \varepsilon ^{\frac{1}{2}} \left\| \sigma _{\nu }(u,\theta ) +\frac{1}{\varepsilon }[u_{\varepsilon ,\nu }]^{+}\right\| _{0,\Gamma _{3}}\nonumber \\{} & {} \quad \le C\, \varepsilon ^{\frac{1}{2}+r} \big (\Vert u \Vert _{\frac{3}{2} + r,\Omega } + \Vert \theta \Vert _{\frac{3}{2}+ r,\Omega }\big ) \end{aligned}$$

(4.4)

for a constant $C > 0$ which is independent of a parameter $\varepsilon$ and of a solution x of Problem $({\mathcal {P}})$.

Proof

By taking test functions $v \in (H^1(\Omega )^{d})$ and $\psi \in H^1(\Omega )$ and multiplying Eq. (2.1) and (2.2) by them, we subsequently employ Green’s formula and incorporate the boundary conditions (2.6), (2.7), and (2.10) to derive

$$\begin{aligned}{} & {} (Bx,y)_{X} +\ell (u,\theta ,\psi )+ \int _{\Gamma _{3}}\sigma _{\nu }(u,\theta )\,v_{\nu }\,da\nonumber \\{} & {} \quad =(f^{e},y)_{X},\quad \forall y=(v,\psi ) \in X. \end{aligned}$$

(4.5)

It’s worth mentioning that the Eq. (4.5) can be interpreted meaningfully if its integral term is viewed as a duality pairing between $H_{\Gamma _3}=H^{1/2}(\Gamma _3)$ and its dual space $H_{\Gamma _3}^*=H^{-1/2}(\Gamma _3)$. Hence, assuming $u\in [H^{\frac{3}{2}+r}(\Omega )]^d$ and $\psi \in H^{\frac{3}{2}+r}(\Omega )$ provides justification for this relationship by ensuring

$$\begin{aligned} \sigma _{\nu }\in H^{r}(\Gamma _3). \end{aligned}$$

Considering the ellipticity relation (3.11) of the operator A, along with the relations (3.15) and (4.5), we infer that

$$\begin{aligned} m_{B} \Vert x-x_{\varepsilon } \Vert _{X}^{2}&\le (Bx- Bx_{\varepsilon }, x- x_{\varepsilon })_{X} \\&\le (Bx, x- x_{\varepsilon })_{X} - (Bx_{\varepsilon }, x- x_{\varepsilon })_{X} \\&\le \int _{\Gamma _{3}}\big (\sigma _{\nu }(u,\theta )+\frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+}\big )(u_{\nu }-u_{\varepsilon ,\nu })\,da\\&~~~ + \ell (u_{\varepsilon },\theta _{\varepsilon },\theta -\theta _{\varepsilon })-\ell (u,\theta ,\theta -\theta _{\varepsilon })\\&\le \int _{\Gamma _{3}}\sigma _{\nu }(u,\theta )\,u_{\nu }\, da + \int _{\Gamma _{3}} \frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+}\,u_{\nu }\, da + {\mathcal {T}}\\ {}&~~~ - \int _{\Gamma _{3}} \sigma _{\nu }(u,\theta )\,u_{\varepsilon ,\nu }\,da - \int _{\Gamma _{3}} \frac{1}{\epsilon } [u_{\varepsilon ,\nu }]^{+}\, u_{\varepsilon ,\nu }\, da, \end{aligned}$$

(4.6)

where

$$\begin{aligned} {\mathcal {T}}= \ell (u_{\varepsilon },\theta _{\varepsilon },\theta -\theta _{\varepsilon })-\ell (u,\theta ,\theta -\theta _{\varepsilon }). \end{aligned}$$

Due to the contact conditions (2.8) on $\Gamma _{3}$, we observe that

$$\begin{aligned}&\int _{\Gamma _{3}} \sigma _{\nu }(u,\theta )\, u_{\nu }\, da = 0, \end{aligned}$$

(4.7)

$$\begin{aligned}&\int _{\Gamma _{3}} \frac{1}{\epsilon } [u_{\varepsilon ,\nu }]^{+}\, u_{\nu }\, da \le 0. \end{aligned}$$

(4.8)

Additionally, recalling the beneficial property (3.13), the identical condition (2.8) results in

$$\begin{aligned}&- \int _{\Gamma _{3}} \sigma _{\nu } (u,\theta )\, u_{\varepsilon ,\nu }\, da \le - \int _{\Gamma _{3}} \sigma _{\nu }(u,\theta )\, [u_{\varepsilon ,\nu }]^{+}\,da, \end{aligned}$$

(4.9)

$$\begin{aligned}&- \int _{\Gamma _{3}} \frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+}\, u_{\varepsilon ,\nu }\, da = - \int _{\Gamma _{3}} \frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+}\,[u_{\varepsilon ,\nu }]^{+}\, da. \end{aligned}$$

(4.10)

Then, using the relations (4.7)–(4.10) and the well-known Young inequality, (4.6) becomes

$$\begin{aligned}&m_{B} \Vert x-x_{\varepsilon } \Vert _{X}^{2} \\&\quad \le - \int _{\Gamma _{3}} \left( \sigma _{\nu }(u,\theta )+ \frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+}\right) [u_{\varepsilon ,\nu }]^{+}\,da +{\mathcal {T}} \\&\quad \le - \varepsilon \int _{\Gamma _{3}} \left( \sigma _{\nu }(u,\theta )+ \frac{1}{\varepsilon } [u_{\varepsilon , \nu }]^{+}\right) \,\\&\quad \left( \sigma _{\nu }(u,\theta ) - \sigma _{\nu }(u,\theta ) +\frac{1}{\varepsilon }[u_{\varepsilon , \nu }]^{+}\right) \, da+{\mathcal {T}} \\&\quad \le - \varepsilon \, \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+}\,\right\| ^{2}_{0,\Gamma _{3}} \\&\qquad + \varepsilon \int _{\Gamma _{3}} \left( \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+} \right) \, \sigma _{\nu }(u,\theta )\,da + {\mathcal {T}} \\&\quad \le - \varepsilon \, \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon } [u_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} + \varepsilon ^{\delta } \left\| \sigma _{\nu }(u,\theta ) \right. \\&\left. \qquad + \frac{1}{\varepsilon } [u_{\varepsilon , \nu }]^{+} \right\| _{- r,\Gamma _{3}}\varepsilon ^{1-\delta } \left\| \sigma _{\nu }(u,\theta ) \right\| _{r,\Gamma _{3}} + {\mathcal {T}} \\&\quad \le - \varepsilon \left\| \sigma _{\nu }(u,\theta ) \right. \\&\left. \qquad + \frac{1}{\varepsilon } [u_{\varepsilon , \nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} + \frac{\varepsilon ^{2\delta }}{2\beta }\, \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon } [u_{\varepsilon , \nu }]^{+} \right\| ^{2}_{-r,\Gamma _{3}} \\&\qquad + \frac{\beta \varepsilon ^{2-2\delta }}{2}\, \left\| \sigma _{\nu }(u,\theta ) \right\| ^{2}_{r,\Gamma _{3}}+ {\mathcal {T}}, \end{aligned}$$

(4.11)

where $\delta \in [0,1]$ and $\beta > 0$. Considering the two estimates (4.1)–(4.2), we can infer that

$$\begin{aligned}&m_{B} \Vert x-x_{\varepsilon } \Vert _{X}^{2} \\&\quad \le - \varepsilon \, \left( 1-C\,\frac{\varepsilon ^{2(\delta +r) -1}}{\beta }\right) \, \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon } [u_{\varepsilon , \nu }]^{+}\right\| ^{2}_{0,\Gamma _{3}} \\&\qquad + C\, \frac{\varepsilon ^{2(\delta +r) -1 }}{\beta }\, \left[ \Vert u-u_{\varepsilon }\Vert ^{2}_{1,\Omega } + \Vert \theta - \theta _{\varepsilon }\Vert ^{2}_{1,\Omega } \right] \\&\qquad + \frac{\beta \varepsilon ^{2(1-\delta )}}{2}\, \left\| \sigma _{\nu }(u,\theta ) \right\| ^{2}_{r,\Gamma _{3}} + {\mathcal {T}}. \end{aligned}$$

(4.12)

On the other hand, we have

$$\begin{aligned} {\mathcal {T}}&= \int _{\Gamma _3}k_T(u_{\varepsilon ,\nu }-g)\,\varphi _L(\theta _{\varepsilon }-\theta _F) (\theta -\theta _{\varepsilon })\,da\\&\quad -\int _{\Gamma _3}k_T(u_{\nu }-g)\,\varphi _L(\theta -\theta _F) (\theta -\theta _{\varepsilon })\,da \\&= \int _{\Gamma _3}k_T(u_{\varepsilon ,\nu }-g)\big (\varphi _L(\theta _{\varepsilon }-\theta _F) -\varphi _L(\theta -\theta _F)\big )(\theta -\theta _{\varepsilon })\,da \\&\quad +\int _{\Gamma _3} \big (k_T(u_{\varepsilon ,\nu }-g)-k_T(u_{\nu }-g)\big )\, \varphi _L(\theta -\theta _F)(\theta -\theta _{\varepsilon })\,da. \end{aligned}$$

Then, we deduce for some non-negative constant $C>L_{\varphi } L$ that

$$\begin{aligned} \vert {\mathcal {T}} \vert&\le M_{\varphi } \Vert \theta -\theta _{\varepsilon }\Vert ^{2}_{0,\Gamma _{3}} +L_{\varphi } L\, \Vert u_{\varepsilon ,\nu }-u_{\nu }\Vert _{0,\Gamma _{3}} \, \Vert \theta -\theta _{\varepsilon }\Vert _{0,\Gamma _{3}}\\&\le \left( M_{\varphi } + \dfrac{L_{\varphi }\, L}{4\alpha }\right) \, \Vert \theta -\theta _{\varepsilon }\Vert ^{2}_{0,\Gamma _{3}} +\alpha L_{\varphi } L\, \Vert u_{\varepsilon ,\nu }-u_{\nu }\Vert ^{2}_{0,\Gamma _{3}} \\&\le \left( M_{\varphi } + \dfrac{C}{4\alpha }\right) \, \Vert \theta -\theta _{\varepsilon }\Vert ^{2}_{1,\Omega } + C\,\alpha \, \Vert u_{\varepsilon }-u\Vert ^{2}_{1,\Omega }. \end{aligned}$$

(4.13)

We next use the two estimates (4.13) and (4.12) to deduce

$$\begin{aligned}&\left( m_{B} - C\,\,\frac{\varepsilon ^{2(\delta +r) -1}}{\beta } - C\, \alpha \right) \, \Vert u-u_{\varepsilon } \Vert _{1,\Omega }^{2} \\&\qquad + \left( m_{B} - C\,\,\frac{\varepsilon ^{2(\delta +r) -1}}{\beta } - M_{\varphi } -\dfrac{C}{4 \alpha }\right) \, \Vert \theta -\theta _{\varepsilon } \Vert _{1,\Omega }^{2} \\&\qquad + \varepsilon \left( 1-C\,\,\frac{\varepsilon ^{2(\delta +r) -1}}{\beta }\right) \, \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon } [u_{\varepsilon , \nu }]^{+}\right\| ^{2}_{0,\Gamma _{3}} \\&\quad \le \beta \,\, \frac{ \varepsilon ^{2(1-\delta )}}{2} \,\, \left\| \sigma _{\nu }(u,\theta ) \right\| ^{2}_{r,\Gamma _{3}}. \end{aligned}$$

(4.14)

We then choose $\delta = \frac{1}{2} - r$ (which give $2(\delta +r)-1= 0$), and

$$\begin{aligned}&\beta = C\, \left( 1+\dfrac{1}{m_{B}}+\dfrac{1}{m_{B}+M_{\varphi }}\right) , \\&\alpha = \dfrac{1}{C}\, \left( m_{B}-\frac{C}{\beta }\right) + \dfrac{C}{2\left( m_{B}+M_{\varphi } -\frac{C}{\beta }\right) }. \end{aligned}$$

This choice of $\delta$, $\alpha$ and $\beta$ was made in order to guarantee that

$$\begin{aligned}&m_{B} - C\,\, \frac{\varepsilon ^{2(\delta +r) -1}}{\beta } - C\,\alpha> 0, \\&m_{B} - C\,\, \frac{\varepsilon ^{2(\delta +r) -1}}{\beta } - M_{\varphi } -\dfrac{C}{4 \alpha }>0, \\&1- C\,\, \frac{\varepsilon ^{2(\delta +r) -1}}{\beta }>0. \end{aligned}$$

Thus, the desired bound (4.4) follows from the estimate

$$\begin{aligned} \big \Vert \sigma _{\nu }(u,\theta )\big \Vert _{r, \Gamma _{3}} \le C\,\big (\Vert u \Vert _{\frac{3}{2}+r,\Omega } + \Vert \theta \Vert _{\frac{3}{2}+r,\Omega }\big ). \end{aligned}$$

$\square$

4.2 A Priori Estimate of of Tresca’s Friction Problem

Theorem 4.3

Suppose $x=(u,\theta )$ and $x_{\varepsilon }=(u_{\varepsilon },\theta _{\varepsilon })$ represent the solutions of Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}})$ and Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$, respectively. If we assume the regularities $u\in (H^{\frac{3}{2}+ r}(\Omega ))^d$ and $\theta \in H^{\frac{3}{2}+ r}(\Omega )$ with $0<r\le 1/2$, then the following a priori estimate holds

$$\begin{aligned}&\Vert u - u_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta -\theta _{\varepsilon } \Vert _{1,\Omega } + \varepsilon ^{\frac{1}{2}}\,\left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon }[u_{\varepsilon ,\nu }]^{+}\right\| _{0,\Gamma _{3}} \\&\quad +\varepsilon ^{\frac{1}{2}}\, \left\| \sigma _{\tau }(u,\theta ) + \frac{1}{\varepsilon }[u_{\varepsilon ,\tau }]_{\varepsilon g} \right\| _{0,\Gamma _{3}} \\&\quad \le C\, \varepsilon ^{\frac{1}{2}+r}\, \left( \Vert u \Vert _{\frac{3}{2} + r ,\Omega } + \Vert \theta \Vert _{\frac{3}{2} + r ,\Omega }\Vert \right) , \end{aligned}$$

(4.15)

where $C > 0$ does not depend on a penalized parameter $\varepsilon$, nor on $x=(u,\theta )$ solution of Problem $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}})$.

Proof

It’s notable to observe that the friction conditions (2.9) and the definition of $[\cdot ]_{\varepsilon ,g}$ entail

$$\begin{aligned}&\int _{\Gamma _{3}} \left( \sigma _{\tau }(u,\theta ) +\frac{1}{\epsilon }\,[u_{\varepsilon , \tau }]_{\varepsilon g} \right) \, (u_{\tau } - u_{\varepsilon , \tau } ) \,da \\&\quad \le - \int _{\Gamma _{3}} \left( \sigma _{\tau }(u,\theta ) +\frac{1}{\epsilon }[u_{\varepsilon , \tau }]_{\varepsilon g} \right) \, u_{\varepsilon , \tau } \,da \\&\quad \le - \int _{\Gamma _{3}} \left( \sigma _{\tau }(u,\theta ) +\frac{1}{\varepsilon }[u_{\varepsilon , \tau }]_{\varepsilon g} \right) \, [u_{\varepsilon , \tau }]_{\varepsilon g}\, da. \end{aligned}$$

The estimate (4.2) obtained in Lemma 4.1 still holds, by replacing $\Vert \sigma _{\nu }(u,\theta ) +\frac{1}{\varepsilon }[u_{\varepsilon , \nu }]^{+} \Vert _{s,\Gamma _{3}}$ by

$$\begin{aligned} \left\| \sigma _{\nu }(u,\theta ) +\frac{1}{\varepsilon }[u_{\varepsilon ,\nu }]^{+} \right\| _{s,\Gamma _{3}} + \left\| \sigma _{\tau }(u,\theta ) +\frac{1}{\varepsilon }[u_{\varepsilon , \tau }]_{\varepsilon g} \right\| _{s,\Gamma _{3}}, \end{aligned}$$

for $s=-r$ or $s=0$, see (Chouly and Hild 2013b, Theorem 4.1). Subsequently, employing similar methodologies as presented in (Chouly and Hild 2013b, Theorem 4.1), we can derive the estimate (4.15), thereby establishing Theorem 4.2. $\square$

4.3 A Priori Estimate of the Approximation Frictionless Problem

Theorem 4.4

Consider $x^{h}_{\varepsilon }=(u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon })$ and $x_{\varepsilon }=(u_{\varepsilon },\theta _{\varepsilon })$ as the solutions of problems $({{\mathcal {P}}}{{\mathcal {V}}}^h_{\varepsilon })$ and $({{\mathcal {P}}}{{\mathcal {V}}}_{\varepsilon })$, respectively. Then, for any $\varepsilon >0$ and any $h >0$, the subsequent a priori error estimate is valid

$$\begin{aligned}&\Vert u_{\varepsilon } - u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta _{\varepsilon }-\theta ^{h}_{\varepsilon } \Vert _{1,\Omega } + (\varepsilon ^{\frac{1}{2}} + C h^{\frac{1}{2}})\, \left\| \frac{1}{\varepsilon }[u_{\varepsilon , \nu }]^{+} \right. \\&\left. \qquad - \frac{1}{\varepsilon } [u^{h}_{\varepsilon , \nu }]^{+} \right\| _{0,\Gamma _{3}} \\&\quad \le C \left\{ \left\| u - u_{\varepsilon } \right\| _{1, \Omega } + \left\| u - v^{h} \right\| _{1, \Omega } + \left\| \theta - \theta _{\varepsilon }\right\| _{1,\Omega } \right. \\&\left. \qquad + \Vert \theta - \xi ^{h} \Vert _{1,\Omega } \right\} ,~~ \forall \, y^{h}=(v^{h},\xi ^{h})\in X^{h}, \end{aligned}$$

(4.16)

where $C>0$ is independent of the constrained solution $x=(u,\theta )$ and the parameters h and $\varepsilon$.

Proof

Taking $y^{h} - x^{h}_{\epsilon }$ as test function in Problem $({{\mathcal {P}}}{{\mathcal {V}}}^h_{\epsilon })$, we obtain

$$\begin{aligned}&( Bx^{h}_{\varepsilon },y^{h} - x^{h}_{\varepsilon })_{X} + \ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) \\&\quad + \frac{1}{\varepsilon }\int _{\Gamma _{3}}[u^{h}_{\varepsilon , \nu }]^{+} ( v^{h}_{n}- u^{h}_{\varepsilon , \nu })\,da = (f^{e},y^{h} - x^{h}_{\varepsilon })_{X},\\&\qquad \forall \, y^{h}=(v^{h},\xi ^{h}) \in X^{h}. \end{aligned}$$

(4.17)

The penalized problem $({{\mathcal {P}}}{{\mathcal {V}}}_{\varepsilon })$ aligns with the finite element problem $({{\mathcal {P}}}{{\mathcal {V}}}^h_{\epsilon })$ in such a way that the solution $x_{\varepsilon }= (u_{\varepsilon },\theta _{\varepsilon })$ of Problem $({{\mathcal {P}}}{{\mathcal {V}}}_{\varepsilon })$ also satisfies, for every $y^{h} = (v^h,\xi ^h) \in X^{h}$, the equation

$$\begin{aligned}{} & {} ( Bx_{\varepsilon },y^{h})_{X} +\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h})\nonumber \\{} & {} \quad + \frac{1}{\varepsilon }\int _{\Gamma _{3}}[u_{\varepsilon ,\nu }]^{+} v^{h}_{\nu }\, da = (f^{e},y^{h})_{X}. \end{aligned}$$

(4.18)

We take the test function $x^h_{\varepsilon }= (u^h_{\varepsilon },\theta ^h_{\varepsilon }) \in X^{h}$ in equation (4.18) to deduce

$$\begin{aligned}&(Bx_{\varepsilon },y^{h} - x^{h}_{\varepsilon })_{X} +\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) \\&\quad + \frac{1}{\varepsilon }\int _{\Gamma _{3}}[u_{\varepsilon , \nu }]^{+} ( v^{h}_{n}- u^{h}_{\varepsilon , \nu })\,da = (f^{e},y^{h} - x^{h}_{\varepsilon })_{X},\\&\quad \forall \, y^{h}=(v^{h},\xi ^{h}) \in X^{h}. \end{aligned}$$

(4.19)

Given that the operator B exhibits strong monotonicity and Lipschitz continuity (see (3.11)–(3.12)), we have

$$\begin{aligned}&m_{B} \, \Vert x_{\varepsilon } - x^{h}_{\varepsilon } \Vert _{X}^{2} \le ( Bx_{\varepsilon } - Bx^{h}_{\varepsilon }, x_{\varepsilon } - x^{h}_{\varepsilon })_{X} \\&\quad \le (Bx_{\varepsilon } - Bx^{h}_{\varepsilon }, x_{\varepsilon } - y^{h})_{X} + ( Bx_{\varepsilon } - Bx^{h}_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X} \\&\quad \le M_{B}\, \Vert x_{\varepsilon } - x^{h}_{\varepsilon } \Vert _{X} \Vert x_{\varepsilon } - y^{h} \Vert _{X} \\&\qquad + (Bx_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X} - ( Bx^{h}_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X},\\&\qquad \quad \forall \, y^{h}=(v^{h},\xi ^{h}) \in X^{h}. \end{aligned}$$

(4.20)

Employing Young’s inequality and the triangle inequality, the preceding estimate (4.20) is transformed into

$$\begin{aligned}&m_{B} \Vert x_{\varepsilon } - x^{h}_{\varepsilon } \Vert _{X}^{2} \le \frac{1}{2 \alpha }\, \Vert x_{\varepsilon } - x^{h}_{\varepsilon }\Vert ^{2}_{X} + \dfrac{\alpha M_{B}^{2}}{2}\, \Vert x_{\varepsilon } - y^{h} \Vert ^{2}_{X} \\&\qquad + ( Bx_{\varepsilon } , y^{h} - x^{h}_{\varepsilon })_{X} - ( Bx^{h}_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X} \\&\quad \le \frac{1}{2 \alpha }\, \Vert x_{\varepsilon } - x^{h}_{\varepsilon } \Vert ^{2}_{X} + \alpha M_{B}^{2}\, \big (\Vert x_{\varepsilon } - x \Vert ^{2}_{X} + \Vert x - y^{h} \Vert ^{2}_{X} \big ) \\&\qquad + (Bx_{\varepsilon } , y^{h} - x^{h}_{\varepsilon })_{X} - ( Bx^{h}_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X},~~\forall \, y^{h}\\&\quad =(v^{h},\xi ^{h}) \in X^{h}. \end{aligned}$$

(4.21)

To assess the last two terms of the previous inequality, we utilize equations (4.17) and (4.19) to derive

$$\begin{aligned}&( Bx_{\varepsilon } , y^{h} - x^{h}_{\varepsilon })_{X} - ( Bx^{h}_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X} \\ {}&= \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+}\right) (v^{h}_{\nu }- u^{h}_{\varepsilon ,\nu })\, da \\ {}&\quad +\ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon })-\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) \\ {}&= \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\,[u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) (u^{h}_{\varepsilon , \nu } - u_{\varepsilon ,\nu })\, da \\ {}&\quad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\,[u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) (u_{\varepsilon , \nu }- v^{h}_{\nu })\,da\\ {}&\quad +\ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon })-\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }). \end{aligned}$$

(4.22)

We estimate the first term of (4.22) by

$$\begin{aligned}&\int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\,[u^{h}_{\varepsilon ,\nu }]^{+}\right) (u^{h}_{\varepsilon ,\nu } - u_{\varepsilon ,\nu })\, da \\ {}&\quad = - \varepsilon \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) \left( \frac{1}{\varepsilon }u_{\varepsilon ,\nu } -\frac{1}{\varepsilon } u^{h}_{\varepsilon ,\nu }\right) \, da \\ {}&\quad \le - \varepsilon \, \left\| \frac{1}{\varepsilon }\,[u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon } \,[u^{h}_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}}. \end{aligned}$$

(4.23)

For the second term of (4.22), we (3.26), (3.27) and Cauchy–Schwartz inequality to obtain

$$\begin{aligned}&\int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\,[u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) (u_{\varepsilon ,\nu } - v^{h}_{\nu })\, da \\&\quad = \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+}\right) \left( ( u_{\varepsilon } - v^{h})\cdot \nu - \textbf{P}^{h}(u_{\varepsilon } - v^{h})\cdot \nu \right) \,da \\&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+}\right) \, \textbf{P}^{h}(u_{\varepsilon } - v^{h})\cdot \nu \, da \\&\quad \le \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} \left\| _{0,\Gamma _{3}} \right\| (u_{\varepsilon } - v^{h})\cdot \nu \right. \\&\qquad \left. - \textbf{P}^{h}(u_{\varepsilon } - v^{h})\cdot \nu \right\| _{0,\Gamma _{3}} \\&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\,[u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\,[u^{h}_{\varepsilon ,\nu }]^{+}\right) \\&\quad \textbf{R}^{h}(\textbf{P}^{h}(u_{\varepsilon } - v^{h})\cdot \nu ) \,da. \end{aligned}$$

(4.24)

Through the utilization of interpolation (3.23), in conjunction with the continuity of the trace operator and Young’s inequality, we obtain

$$\begin{aligned}&\left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| _{0,\Gamma _{3}} \left\| (u_{\varepsilon } - v^{h})\cdot \nu - \textbf{P}^{h}( u_{\epsilon } - v^{h})\cdot \nu \right\| _{0,\Gamma _{3}} \\&\quad \le c h^{\frac{1}{2}}\, \left\| \frac{1}{\varepsilon }\,[u_{\epsilon , \nu }]^{+} - \frac{1}{\varepsilon }\,[u^{h}_{\varepsilon , \nu }]^{+} \right\| _{0,\Gamma _{3}} \left\| u_{\varepsilon } - v^{h} \right\| _{\frac{1}{2},\Gamma _{3}} \\&\quad \le ch\, \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} + c\, \left\| u_{\varepsilon } - v^{h} \right\| ^{2}_{1,\Omega } \\&\quad \le Ch\, \left\| \frac{1}{\varepsilon }\,[u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} \\&\qquad + C\, \left( \Vert u_{\varepsilon } - u \Vert ^{2}_{1,\Omega } + \Vert u - v^{h} \Vert ^{2}_{1,\Omega }\right) . \end{aligned}$$

(4.25)

Using condition (4.18) and stability properties in (3.22) and (3.25), and choosing

$$\begin{aligned} y^{*}&= \left( \textbf{R}^{h}(\textbf{P}^{h}( u_{\epsilon } - v^{h})), \theta _{\epsilon } - \xi ^{h}\right) , \\ {\mathcal {K}}&=\ell (u_{\varepsilon },\theta _{\varepsilon },\theta _{\epsilon }- \xi ^{h})-\ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\theta _{\epsilon } - \xi ^{h}), \end{aligned}$$

we can deduce from Problem $({{\mathcal {P}}}{{\mathcal {V}}}^h_{\varepsilon })$ that

$$\begin{aligned}&\int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\,[u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+}\right) \, \textbf{R}^{h}\left( \textbf{P}^{h}(u_{\varepsilon } - v^{h})\cdot \nu \right) \,da \\&\quad \le (Bx_{\varepsilon } - Bx^{h}_{\varepsilon },y^{*})_{X} +\ell (u_{\varepsilon },\theta _{\varepsilon },\theta _{\epsilon } - \xi ^{h})-\ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\theta _{\epsilon } - \xi ^{h}) \\&\quad \le M_{B}\, \Vert x_{\varepsilon }-x^{h}_{\varepsilon }\Vert _{X}\, \Vert y^{*} \Vert _{X} +{\mathcal {K}} \\&\quad \le M_{B}\, \Vert x_{\varepsilon }-x^{h}_{\varepsilon }\Vert _{X} \, \big \{ \Vert \textbf{R}^{h}(\textbf{P}^{h}( u_{\varepsilon } - v^{h})) \big \Vert _{1 , \Omega } \\&\qquad + \big \Vert \theta _{\varepsilon } - \xi ^{h} \big \Vert _{1 , \Omega } \big \} +{\mathcal {K}} \\&\quad \le C M_{B}\, \Vert x_{\varepsilon }-x^{h}_{\varepsilon }\Vert _{X} \, \big \{ \Vert \textbf{P}^{h}( u_{\varepsilon } - v^{h})\Vert _{\frac{1}{2} , \Gamma _3 } + \Vert \theta _{\varepsilon } - \xi ^{h}\Vert _{1,\Omega } \big \} +{\mathcal {K}} \\&\quad \le C M_{B} \Vert x_{\varepsilon }-x^{h}_{\varepsilon } \Vert _{X} \,\big \{ \Vert u_{\varepsilon } - u \Vert _{1,\Omega } \\&\qquad +\Vert u - v^{h} \Vert _{1,\Omega } +\Vert \theta _{\varepsilon } - \theta \Vert _{1,\Omega } + \Vert \theta - \xi ^{h} \Vert _{1 , \Omega }\big \} +{\mathcal {K}} \\&\quad \le \frac{1}{\alpha } \Vert x_{\varepsilon } - x^{h}_{\varepsilon } \Vert ^{2}_{X} \\ {}&~~~ + \dfrac{\alpha \, (C M_{B})^{2}}{2}\, \big \{ \Vert u_{\varepsilon } - u \Vert ^{2}_{1, \Omega } + \Vert u - v^{h} \Vert ^{2}_{1, \Omega } \\&\qquad + \Vert \theta _{\varepsilon } - \theta \Vert ^{2}_{1 , \Omega } + \Vert \theta - \xi ^{h} \Vert ^{2}_{1 , \Omega } \big \} +{\mathcal {K}}, \end{aligned}$$

(4.26)

where the term ${\mathcal {K}}$ is as follows

$$\begin{aligned} {\mathcal {K}}&= \int _{\Gamma _3} k_T(u_{\varepsilon ,\nu }-g)\,\varphi _L(\theta _{\varepsilon }-\theta _F)(\theta _{\varepsilon } -\xi ^{h})\,da\\ {}&\quad - \int _{\Gamma _3} k_T(u^{h}_{\varepsilon ,\nu }-g)\, \varphi _L(\theta ^{h}_{\varepsilon }-\theta _F)(\theta _{\varepsilon } -\xi ^{h})\,da\\ {}&= \int _{\Gamma _3} k_T(u_{\varepsilon ,\nu }-g)\, \big (\varphi _L(\theta _{\varepsilon }-\theta _F)-\varphi _L(\theta ^{h}_{\varepsilon }-\theta _F)\big )\,(\theta _{\varepsilon } -\xi ^{h})\,da\\ {}&\quad +\int _{\Gamma _3}\, \big (k_T(u_{\varepsilon ,\nu }-g)-k_T(u^{h}_{\varepsilon ,\nu }-g)\big )\, \varphi _L(\theta ^{h}_{\varepsilon }-\theta _F)\,(\theta _{\varepsilon } -\xi ^{h})\,da. \end{aligned}$$

Then, we finally find

$$\begin{aligned}&\vert {\mathcal {K}} \vert \\&\quad \le M_{\varphi } \Vert \theta _{\varepsilon } - \theta ^{h}_{\varepsilon }\Vert _{0,\Gamma _{3}}\, \Vert \theta _{\varepsilon } -\xi ^{h}\Vert _{0,\Gamma _{3}} \\&\qquad + L_{\varphi } L\, \Vert u_{\varepsilon ,\nu }-u^{h}_{\varepsilon ,\nu }\Vert _{0,\Gamma _{3}} \, \Vert \theta _{\varepsilon } -\xi ^{h}\Vert _{0,\Gamma _{3}}\\&\quad \le \frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon }-\theta ^{h}_{\varepsilon }\Vert ^{2}_{0,\Gamma _{3}} + \left( \alpha M_{\varphi } + \dfrac{L_{\varphi } L}{4\alpha }\right) \, \Vert \theta _{\varepsilon } -\xi ^{h}\Vert ^{2}_{0,\Gamma _{3}} \\&\qquad + \alpha L_{\varphi } L\, \Vert u_{\varepsilon ,\nu }-u^{h}_{\varepsilon ,\nu }\Vert ^{2}_{0,\Gamma _{3}}\\&\quad \le \frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon }- \theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } \\&\qquad + \big ( \alpha M_{\varphi } + \dfrac{C}{4\alpha }\big )\, \Vert \theta _{\varepsilon } -\xi ^{h}\Vert ^{2}_{1,\Omega } + \alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }\\&\quad \le \frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon }- \theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } + \left( \alpha M_{\varphi } + \dfrac{C}{4\alpha }\right) \left( \Vert \theta _{\varepsilon } -\theta \Vert ^{2}_{1,\Omega }\right. \\&\left. \qquad +\Vert \theta -\xi ^{h}\Vert ^{2}_{1,\Omega } \right) +\alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }. \end{aligned}$$

(4.27)

We now combine (4.25), (4.26) and (4.27) to rewrite the estimate (4.24) as follows

$$\begin{aligned}&\int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+}\right) (u_{\varepsilon , \nu } - v^{h}_{\nu })\, da\\ {}&\quad \le \frac{1}{\alpha }\, \Vert x_{\varepsilon }-x_{\varepsilon }^{h} \Vert ^{2}_{X} + c h\, \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}}\\&\qquad + C\, \left( 1 +\dfrac{\alpha M_{B}^{2}}{2}\right) \left( \Vert u_{\varepsilon } - u \Vert ^{2}_{1, \Omega } + \Vert u - v^{h} \Vert ^{2}_{1, \Omega } \right) \\&\qquad + \left( \alpha M_{\varphi } + \dfrac{C}{4\alpha }+\dfrac{\alpha C M_{B}^2}{2}\right) \, \left( \Vert \theta _{\varepsilon } - \theta \Vert ^{2}_{1, \Omega } + \Vert \theta - \xi ^{h} \Vert ^{2}_{1, \Omega } \right) \\&\qquad +\alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } +\frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon }- \theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }. \end{aligned}$$

(4.28)

For the third term of (4.22), wee know that

$$\begin{aligned}&\ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) -\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon })\\ {}&\quad = \int _{\Gamma _3}k_T(u^{h}_{\varepsilon ,\nu }-g) \varphi _L(\theta ^{h}_{\varepsilon }-\theta _F)(\xi ^{h}-\theta ^{h}_{\varepsilon } )\,da \\&\qquad - \int _{\Gamma _3}k_T(u_{\varepsilon ,\nu }-g)\varphi _L(\theta _{\varepsilon }-\theta _F)(\xi ^{h}-\theta ^{h}_{\varepsilon } )\,da \\&\quad =\int _{\Gamma _3}k_T(u^{h}_{\varepsilon ,\nu }-g)\big (\varphi _L(\theta ^{h}_{\varepsilon }-\theta _F) -\varphi _L(\theta _{\varepsilon }-\theta _F)\big )(\xi ^{h}-\theta ^{h}_{\varepsilon })\,da \\&\qquad +\int _{\Gamma _3}\big (k_T(u^{h}_{\varepsilon ,\nu }-g)-k_T(u_{\varepsilon ,\nu }-g)\big ) \varphi _L(\theta _{\varepsilon }-\theta _F)(\xi ^{h}-\theta ^{h}_{\varepsilon })\,da. \end{aligned}$$

Then, the following majoration inequality holds.

$$\begin{aligned}&\big \vert \ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon })-\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) \big \vert \\&\quad \le M_{\varphi } \Vert \theta ^{h}_{\varepsilon }-\theta _{\varepsilon }\Vert _{0,\Gamma _{3}}\, \Vert \xi ^{h}-\theta ^{h}_{\varepsilon } \Vert _{0,\Gamma _{3}}\\&\qquad +L_{\varphi } L\, \Vert u^{h}_{\varepsilon ,\nu }- u_{\varepsilon ,\nu }\Vert _{0,\Gamma _{3}} \, \Vert \xi ^{h} - \theta ^{h}_{\varepsilon } \Vert _{0,\Gamma _{3}} \\&\quad \le \frac{M_{\varphi }}{4\alpha }\, \Vert \theta ^{h}_{\varepsilon }-\theta _{\varepsilon }\Vert ^{2}_{0,\Gamma _{3}} + \left( \alpha M_{\varphi } + \dfrac{L_{\varphi }L}{4\alpha }\right) \,\\&\Vert \theta ^{h}_{\varepsilon } -\xi ^{h}\Vert ^{2}_{0,\Gamma _{3}} +\alpha L_{\varphi } L\, \Vert u_{\varepsilon ,\nu }-u^{h}_{\varepsilon ,\nu }\Vert ^{2}_{0,\Gamma _{3}}\\&\quad \le \frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon }- \theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } \\&\qquad + \left( \alpha M_{\varphi } + \dfrac{C}{4\alpha }\right) \, \Vert \theta ^{h}_{\varepsilon } -\xi ^{h}\Vert ^{2}_{1,\Omega } + \alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }\\&\quad \le \frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon } -\theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } + \left( \alpha M_{\varphi } + \dfrac{C}{4\alpha }\right) \\&\left( \Vert \theta _{\varepsilon } -\theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } +\Vert \theta _{\varepsilon } -\theta \Vert ^{2}_{1,\Omega }+\Vert \theta -\xi ^{h}\Vert ^{2}_{1,\Omega } \right) \\&\qquad +\alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }. \end{aligned}$$

(4.29)

Next, we combine (4.23), (4.28) and (4.29) to reformulate the estimate (4.22), we express it in the following manner

$$\begin{aligned}&(Bx_{\varepsilon } , y^{h} - x^{h}_{\varepsilon })_{X} - (Bx^{h}_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X}\\ {}&\quad \le \frac{1}{\alpha } \, \Vert x_{\varepsilon }-x_{\varepsilon }^{h} \Vert ^{2}_{X} + (C h - \varepsilon )\, \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} \\&\qquad + C \left[ 1 +\dfrac{\alpha M_{B}^{2}}{2}\right] \, \big (\Vert u_{\varepsilon } - u \Vert ^{2}_{1,\Omega } + \Vert u - v^{h} \Vert ^{2}_{1,\Omega } \big )\\&\qquad + \left[ 2\alpha M_{\varphi } + \dfrac{C}{2\alpha }+\dfrac{ \alpha C M_{B}^2}{2}\right] \, \left( \Vert \theta _{\varepsilon } - \theta \Vert ^{2}_{1, \Omega } + \Vert \theta - \xi ^{h} \Vert ^{2}_{1, \Omega } \right) \\&\qquad +2\alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }+\left[ \frac{M_{\varphi }}{2\alpha }+\alpha M_{\varphi } + \dfrac{C}{4\alpha }\right] \,\Vert \theta _{\varepsilon }- \theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }. \end{aligned}$$

(4.30)

Recalling $\Vert \cdot \Vert _{X}^{2} = \Vert \cdot \Vert ^{2} _{V}+\Vert \cdot \Vert ^{2} _{Q}$, $\Vert \cdot \Vert _{H_{1}}\underset{V}{\approx }\ \Vert \cdot \Vert _{V}$ and $\Vert \cdot \Vert _{Q} = \Vert \cdot \Vert _{1,\Omega }$, we use the inequality (4.30) to rewrite the estimate (4.21) as follows

$$\begin{aligned}&\left[ \,m_{B} - \frac{3}{2\alpha }-2\alpha C\, \right] \, \Vert u_{\varepsilon }-u^{h}_{\varepsilon } \Vert ^{2}_{1,\Omega } \\&\qquad + \left[ \,m_{B} - \frac{3}{2\alpha }-\dfrac{M_{\varphi }}{2\alpha } -\alpha M_{\varphi }-\dfrac{C}{4\alpha }\,\right] \, \Vert \theta _{\varepsilon }-\theta ^{h}_{\varepsilon } \Vert ^{2}_{1,\Omega }\\&\qquad +\varepsilon \,\left\| \frac{1}{\varepsilon }[u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon } [u^{h}_{\varepsilon , \nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} \\&\quad \le Ch\, \left\| \frac{1}{\varepsilon }[u_{\varepsilon , \nu }]^{+} -\frac{1}{\varepsilon } [u^{h}_{\varepsilon , \nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} \\&\qquad + C \left[ \,1+\dfrac{3 \alpha M_{B}^{2}}{2}\,\right] \, \left( \Vert u_{\varepsilon } - u \Vert ^{2}_{1,\Omega } + \Vert u - v^{h} \Vert ^{2}_{1,\Omega } \right) \\&\qquad + \left[ \,2\alpha M_{\varphi }+\dfrac{C}{2\alpha }+\dfrac{3C \alpha M_{B}^{2}}{2} \,\right] \, \left( \Vert \theta _{\varepsilon } - \theta \Vert ^{2}_{1,\Omega } + \Vert \theta - \xi ^{h} \Vert ^{2}_{1,\Omega } \right) . \end{aligned}$$

(4.31)

Under appropriate mathematical condition on $\alpha >0$ involving $m_B$, $M_{\varphi }$ and C, the terms $m_{B} - \frac{3}{2\alpha }-2\alpha C$ and $m_{B} - \frac{3}{2\alpha }-\frac{M_{\varphi }}{2\alpha } -\alpha M_{\varphi }-\frac{C}{4\alpha }$ are non-negative. So, (4.31) implies the desired estimation (4.16). $\square$

Theorem 4.5

Given the conditions stated in Theorem 4.4, if $x=(u,\theta )$ represents the solution of Problem (3.8) such that

$$\begin{aligned} u \in H^{\frac{3}{2}+r}(\Omega )^{d},~~~ \theta \in H^{\frac{3}{2}+r}(\Omega ) ~~\text { with }~~ 0 < r \le 2, \end{aligned}$$

then the ensuing estimate holds true

$$\begin{aligned}&\left\| u-u^{h}_{\varepsilon } \right\| _{1,\Omega } + \left\| \theta -\theta ^{h}_{\varepsilon } \right\| _{1,\Omega } + (\varepsilon ^{\frac{1}{2}} - Ch^{\frac{1}{2}})\, \left\| \sigma _{\nu }(u,\theta ) \right. \\&\left. \qquad + \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| _{0,\Gamma _{3}} \\&\quad \le C\, \left( h^{\frac{1}{2}+r} + \varepsilon ^{\frac{1}{2}+r}\right) \, \left( \Vert u \Vert _{\frac{3}{2}+r, \Omega } + \Vert \theta \Vert _{\frac{3}{2}+r, \Omega }\right) \end{aligned}$$

(4.32)

where $C >0$ is independent of $x=(u,\theta ), \varepsilon$ and h.

Proof

Given that $x^{h}=(u^{h},\theta ^{h}) \in X^{h}$, we select

$$\begin{aligned} x^{h}=(u^{h},\theta ^{h})= ({\mathcal {I}}^{1}_{h}(u),{\mathcal {I}}^{1}_{h}(\theta )), \end{aligned}$$

where ${\mathcal {I}}^{1}_{h}$ denotes Lagrange’s interpolation operator associated with $X^{h}= V^{h}\times Q^{h}$. The conventional Lagrange interpolation approximations in the $H^{1}(\Omega )$ norm are provided for $r\in (-\frac{1}{2}, \frac{1}{2}]$ as detailed in prior works (see khalfi et al. (2023); Bourichi et al. (2016); Dione (2019); Ern and Guermond (2004))

$$\begin{aligned}&\big \Vert u - {\mathcal {I}}^{1}_{h}(u) \big \Vert _{1,\Omega } \le ch^{\frac{1}{2}+r} \Vert u \Vert _{\frac{3}{2}+r,\Omega }, \\ {}&\big \Vert \theta - {\mathcal {I}}^{1}_{h}(\theta ) \big \Vert _{1,\Omega } \le ch^{\frac{1}{2}+r} \Vert \theta \Vert _{\frac{3}{2}+r,\Omega }. \end{aligned}$$

(4.33)

We opt for penalty and mesh parameters to ensure $\varepsilon > h$. Subsequently, utilizing the triangle inequality, Theorem 4.5 is derived from Theorems 4.4, 4.2, and the interpolation estimate (4.33). $\square$

Remark 4.6

Ultimately, to establish a convergence rate for the approximation (4.32), we may select $\varepsilon (h):= ch^{\gamma }$, where c and $\gamma$ are fixed positive constants; hence, the penalty parameter $\varepsilon$ becomes a function of the mesh size h. Consequently, we obtain

• 1. When $\varepsilon$ scales in accordance with h, meaning $\varepsilon (h):= (C+1)^{2}h$, we derive the following a priori estimate from Theorem 4.4:

  $$\begin{aligned}{} & {} \Vert u-u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta -\theta ^{h}_{\varepsilon } \Vert _{1,\Omega } + h^{\frac{1}{2}} \left\| \sigma _{\nu }(u,\theta ) \right. \\{} & {} \left. \quad + \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} \right\| _{0,\Gamma _{3}} \le C h^{\frac{1}{2}+r} \left( \Vert u \Vert _{\frac{3}{2}+r, \Omega } + \Vert \theta \Vert _{\frac{3}{2}+r, \Omega }\right) . \end{aligned}$$

• 2. When $\varepsilon (h):= C^{2}h^{\gamma }$ with $0<\gamma <1$, Theorem 4.4 gives us the following a priori estimate:

  $$\begin{aligned}&\Vert u-u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta -\theta ^{h}_{\varepsilon } \Vert _{1,\Omega } \\&\qquad + Ch^{\frac{\gamma }{2}} \left( 1-h^{\frac{1-\gamma }{2}}\right) \, \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon } [u^{h}_{\varepsilon , \nu }]^{+} \right\| _{0,\Gamma _{3}} \\&\quad \le C h^{\gamma (\frac{1}{2}+r)} \left( \Vert u \Vert _{\frac{3}{2}+r, \Omega } + \Vert \theta \Vert _{\frac{3}{2}+r, \Omega }\right) . \end{aligned}$$

4.4 A Priori Estimate of the Approximation Tresca’s Friction Problem

Theorem 4.7

Let $x_{\epsilon }=(u_{\epsilon },\theta _{\epsilon })$ and $x^{h}_{\varepsilon }=(u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon })$ solutions of problems $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}_{\varepsilon })$ and $(\overline{{{\mathcal {P}}}{{\mathcal {V}}}}^h_{\varepsilon })$, respectively. Subsequently, for any $\varepsilon >0$ and $h >0$, the ensuing a priori estimate is obtained

$$\begin{aligned}&\Vert u_{\varepsilon }-u^{h}_{\varepsilon } \Vert _{1,\Omega } + \Vert \theta _{\varepsilon }-\theta ^{h}_{\varepsilon } \Vert _{1,\Omega }\\&\qquad + \big (\varepsilon ^{\frac{1}{2}}-C h^{\frac{1}{2}}\big ) \left[ \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+}\right. \right. \\&\left. \left. \qquad + \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} \right\| _{0,\Gamma _{3}} + \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} -\frac{1}{\varepsilon } [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| _{0,\Gamma _{3}} \,\right] \\&\quad \le C\, \left( \left\| u_{\varepsilon } - u \right\| _{1, \Omega } + \Vert u - v^{h} \Vert _{1, \Omega } \right. \\&\left. \qquad + \Vert \theta _{\varepsilon } - \theta \Vert _{1,\Omega } + \Vert \theta - \xi ^{h} \Vert _{1,\Omega }\right) ,\quad \forall \, y^{h}=(v^{h},\xi ^{h})\in X^{h}, \end{aligned}$$

(4.34)

where a constant $C >0$ remains independent of $x=(u,\theta ), \varepsilon$ and h.

Proof

The proof technique employed here resembles that of Theorem 4.4. Initially, as utilized in establishing (4.21), we have

$$\begin{aligned} m_{B} \left\| {x_{\varepsilon } - x_{\varepsilon }^{h} } \right\|_{X}^{2} \\ & \le \frac{1}{{2\alpha }}\left\| {x_{\varepsilon } - x_{\varepsilon }^{h} } \right\|_{X}^{2} + \frac{{\alpha M_{B}^{2} }}{2}\left\| {x_{\varepsilon } - y^{h} } \right\|_{X}^{2} \\ \quad + \,(Bx_{\varepsilon } ,y^{h} - x_{\varepsilon }^{h} )_{X} - (Bx_{\varepsilon }^{h} ,y^{h} - x_{\varepsilon }^{h} )_{X} \\ & \le \frac{1}{{2\alpha }}\left\| {x_{\varepsilon } - x_{\varepsilon }^{h} } \right\|_{X}^{2} + \alpha M_{B}^{2} {\mkern 1mu} \left( {\left\| {x_{\varepsilon } - x} \right\| + \left\| {x - y^{h} } \right\|_{X}^{2} } \right)_{X}^{2} \\ \quad + \,\left( {Bx_{\varepsilon } ,y^{h} - x_{\varepsilon }^{h} } \right)_{X} - \left( {Bx_{\varepsilon }^{h} ,y^{h} - x_{\varepsilon }^{h} } \right)_{X} ,\forall {\mkern 1mu} y^{h} \\ & = (v^{h} ,\xi ^{h} ) \in X^{h} . \\ \end{aligned}$$

(4.35)

Recalling (3.29) and (3.30), where the terms $u_{\varepsilon , \nu }$ and $u_{\varepsilon ,\tau }$ are introduced, we derive

$$\begin{aligned}&(Bx_{\varepsilon } , y^{h} - x^{h}_{\varepsilon })_{X} - (Bx^{h}_{\varepsilon }, y^{h} - x^{h}_{\varepsilon })_{X} \\&\quad = \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\,[u^{h}_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\ [u_{\varepsilon , \nu }]^{+}\right) (v^{h}_{\nu }- u^{h}_{\varepsilon , \nu })\, da \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\,[u^{h}_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g}\right) (v^{h}_{\tau }- u^{h}_{\varepsilon , \tau })\, da \\ {}&\qquad +\ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) -\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) \\ {}&\quad = \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+}\right) (u^{h}_{\varepsilon , \nu } - u_{\varepsilon , \nu })\, da \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} \right) (u_{\varepsilon , \nu }- v^{h}_{\nu })\, da \\&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right) (u^{h}_{\varepsilon ,\tau }- u_{\varepsilon , \tau })\, da \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right) (u_{\varepsilon ,\tau }- v^{h}_{\tau })\, da \\ {}&\qquad + \ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon })-\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }) \\&\quad = S_1 + S_2 + S_3 + S_4 +S_5, \end{aligned}$$

(4.36)

where the quantities $S_1$, $S_2$, $S_3$ , $S_4$ and $S_5$ are defined as follows.

$$\begin{aligned} S_{1}&= \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) (u^{h}_{\varepsilon ,\nu }- u_{\varepsilon ,\nu })\, da, \end{aligned}$$

(4.37)

$$\begin{aligned} S_{2}&= \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) (u_{\varepsilon ,\nu }- v^{h}_{\nu })\, da, \end{aligned}$$

(4.38)

$$\begin{aligned} S_{3}&= \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g}\right) (u^{h}_{\varepsilon ,\tau }- u_{\varepsilon , \tau }) \,da, \end{aligned}$$

(4.39)

$$\begin{aligned} S_{4}&= \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\,[u^{h}_{\varepsilon , \tau }]_{\varepsilon g}\right) (u_{\varepsilon ,\tau }- v^{h}_{\tau }) \,da, \end{aligned}$$

(4.40)

$$\begin{aligned} S_{5}&= \ell (u^{h}_{\varepsilon },\theta ^{h}_{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon })-\ell (u_{\varepsilon },\theta _{\varepsilon },\xi ^{h} -\theta ^{h}_{\varepsilon }). \end{aligned}$$

(4.41)

We already have estimated the term $S_{1}$ in (4.23), and we get

$$\begin{aligned} S_{1} \le - \varepsilon \, \Big \Vert \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+} \Big \Vert ^{2}_{0,\Gamma _{3}}. \end{aligned}$$

(4.42)

Using the properties (3.31)–(3.32), we estimate the term $S_{3}$ as follows

$$\begin{aligned} S_{3}&= -\varepsilon \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right) \left( \frac{1}{\varepsilon }\, u_{\varepsilon , \tau } - \frac{1}{\varepsilon }\,u^{h}_{\varepsilon ,\tau }\right) \, da \\ {}&\le - \varepsilon \, \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| ^{2}_{0,\Gamma _{3}}. \end{aligned}$$

(4.43)

For the remaining terms $S_{2}$ and $S_{4}$, we use (3.24)–(3.27) and Cauchy-Schwartz inequality to get

$$\begin{aligned}&S_{2} + S_{4} \\&\quad = \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) \left( (u_{\varepsilon } - v^{h})\cdot \nu - \textbf{P}^{h}( u_{\varepsilon } - v^{h})\cdot \nu \right) \, da \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) \, \textbf{P}^{h}(u_{\varepsilon } - v^{h})\cdot \nu \, da \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g}\right) \left( (u_{\varepsilon } - v^{h})_{\tau } - \textbf{P}^{h}( u_{\varepsilon } - v^{h})_{\tau }\right) \,da \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g}\right) \, \textbf{P}^{h}( u_{\varepsilon } - v^{h})_{\tau } \, da. \end{aligned}$$

Hence, we conclude that

$$\begin{aligned}&S_{2} + S_{4} \le \, \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+}\right\| _{0,\Gamma _{3}} \Vert (u_{\varepsilon } - v^{h}) \\&\quad - \textbf{P}^{h}( u_{\varepsilon } - v^{h})\cdot \nu \Vert _{0,\Gamma _{3}} \\&\quad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \nu }]^{+}\right) \, \textbf{R}^{h}(\textbf{P}^{h}( u_{\varepsilon } - v^{h}))\cdot \nu \, da \\&\quad + \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| _{0,\Gamma _{3}} \left\| \left( (u_{\varepsilon } - v^{h}) - \textbf{P}^{h}( u_{\varepsilon } - v^{h})\right) _{\tau } \right\| _{0,\Gamma _{3}} \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g}\right) \, \textbf{R}^{h}(\textbf{P}^{h}( u_{\varepsilon } - v^{h}))_{\tau } \, da. \end{aligned}$$

(4.44)

Moreover, by the same arguments as those used in the estimation (4.25)–(4.26)–(4.27), we obtain

$$\begin{aligned}&\left\| \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| _{0,\Gamma _{3}} \left\| ((u_{\varepsilon } - v^{h}) \right. \\&\left. \qquad - \textbf{P}^{h} ( u_{\varepsilon } - v^{h}))\cdot \nu \right\| _{0,\Gamma _{3}} \\&\qquad + \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| _{0,\Gamma _{3}} \left\| ((u_{\varepsilon } - v^{h}) \right. \\&\left. \qquad - \textbf{P}^{h}( u_{\varepsilon } - v^{h}))_{\tau } \right\| _{0,\Gamma _{3}} \\&\quad \le C h\, \left\{ \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}}\right. \\&\left. \qquad + \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| ^{2}_{0,\Gamma _{3}} \right\} \\&\qquad + C \left\{ \Vert u_{\varepsilon } - u \Vert ^{2}_{1,\Omega } + \Vert u - v^{h} \Vert ^{2}_{1,\Omega } \right\} \end{aligned}$$

(4.45)

and

$$\begin{aligned}&\int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+}\right) \, \textbf{R}^{h}(\textbf{P}^{h}( u_{\varepsilon } - v^{h}))\cdot \nu \, da \\ {}&\qquad + \int _{\Gamma _{3}} \left( \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\epsilon g} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g}\right) \,\textbf{R}^{h}(\textbf{P}^{h}( u_{\varepsilon } - v^{h}))_{\tau } \, da \\ {}&\quad \le \frac{1}{\alpha }\, \Vert x_{\varepsilon }-x_{\varepsilon }^{h} \Vert ^{2}_{X} + \dfrac{\alpha \,C M_{B}^{2}}{2}\,\left( \Vert u_{\varepsilon } - u \Vert ^{2}_{1, \Omega } + \Vert u - v^{h} \Vert ^{2}_{1, \Omega } \right) \\ {}&\qquad + \left( \alpha M_{\varphi } + \dfrac{C}{4\alpha }+\dfrac{ \alpha CM_{B}^2}{2}\right) \, \left( \Vert \theta _{\varepsilon } - \theta \Vert ^{2}_{1, \Omega } + \Vert \theta - \xi ^{h} \Vert ^{2}_{1, \Omega } \right) \\ {}&\qquad +\alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } +\frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon }- \theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }. \end{aligned}$$

(4.46)

Thus, the sum $S_{2} + S_{4}$ can be estimated as follows

$$\begin{aligned}&S_{2} + S_{4} \\ {}&\quad \le C h \left\{ \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} + \left\| \frac{1}{\varepsilon }\,[u_{\varepsilon , \tau }]_{\varepsilon g} - \frac{1}{\varepsilon } [u^{h}_{\varepsilon , \tau }]_{\varepsilon g}\right\| ^{2}_{0,\Gamma _{3}}\right\} \\ {}&\qquad +\frac{1}{\alpha }\, \Vert x_{\varepsilon }-x_{\varepsilon }^{h} \Vert ^{2}_{X} + C\left( 1+\dfrac{\alpha M_{B}^{2}}{2}\right) \, \left( \Vert u_{\varepsilon } - u \Vert ^{2}_{1, \Omega } + \Vert u - v^{h} \Vert ^{2}_{1, \Omega } \right) \\ {}&\qquad + \left( \alpha M_{\varphi } + \dfrac{C}{4\alpha }+\dfrac{ \alpha C M_{B}^2}{2}\right) \, \left( \Vert \theta _{\varepsilon } - \theta \Vert ^{2}_{1, \Omega } + \Vert \theta - \xi ^{h} \Vert ^{2}_{1, \Omega } \right) \\ {}&\qquad +\alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }+\frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon }- \theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega }. \end{aligned}$$

(4.47)

Finally, we already have estimated the term $S_{5}$ in (4.29), as following

$$\begin{aligned} S_{5}&\le \frac{M_{\varphi }}{4\alpha }\, \Vert \theta _{\varepsilon } -\theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } +\alpha C\, \Vert u_{\varepsilon }-u^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } \\ {}&\quad + \left( \alpha M_{\varphi } + \dfrac{C}{4\alpha }\right) \, \left( \Vert \theta _{\varepsilon } -\theta ^{h}_{\varepsilon }\Vert ^{2}_{1,\Omega } +\Vert \theta _{\varepsilon } -\theta \Vert ^{2}_{1,\Omega }+\Vert \theta -\xi ^{h}\Vert ^{2}_{1,\Omega } \right) . \end{aligned}$$

(4.48)

We combine (4.35) with the estimates (4.42), (4.43), (4.47) and (4.48) to get

$$\begin{aligned}&\left( m_{B} - \frac{3}{2\alpha }-2\alpha C\right) \, \Vert u_{\varepsilon }-u^{h}_{\varepsilon } \Vert ^{2}_{1,\Omega } \\&\qquad + \left( m_{B} - \frac{3}{2\alpha }-\dfrac{M_{\varphi }}{2\alpha } -\alpha M_{\varphi }-\dfrac{C}{4\alpha }\right) \, \Vert \theta _{\varepsilon }-\theta ^{h}_{\varepsilon } \Vert ^{2}_{1,\Omega } \\&\qquad + \varepsilon \, \left[ \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} + \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g}\right. \right. \\&\left. \left. \qquad - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| ^{2}_{0,\Gamma _{3}} \right] \\&\quad \le Ch\, \left[ \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon ,\nu }]^{+} - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| ^{2}_{0,\Gamma _{3}} + \left\| \frac{1}{\varepsilon }\, [u_{\varepsilon , \tau }]_{\varepsilon g}\right. \right. \\&\left. \left. \qquad - \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| ^{2}_{0,\Gamma _{3}} \right] \\&\qquad + C\,\left( 1+\dfrac{3 \alpha M_{B}^{2}}{2}\right) \,\left( \Vert u_{\varepsilon } - u \Vert ^{2}_{1,\Omega }+\Vert u - v^{h} \Vert ^{2}_{1,\Omega }\right) \\&\qquad + \left( 2\alpha M_{\varphi }+\dfrac{C}{2\alpha }+\dfrac{3C\, \alpha M_{B}^{2}}{2} \right) \, \left[ \Vert \theta _{\varepsilon } - \theta \Vert ^{2}_{1,\Omega } + \Vert \theta - \xi ^{h} \Vert ^{2}_{1,\Omega } \right] , \end{aligned}$$

(4.49)

where $C>L_{\varphi } L$ is independent of $x=(u,\theta ), \varepsilon$ and h. As we have noted for estimation (4.31), we recall that for appropriate condition on $\alpha$ we have

$$\begin{aligned} m_{B} - \frac{3}{2\alpha }-2\alpha C>0 \quad \text {and}\quad m_{B} - \frac{3}{2\alpha }-\dfrac{M_{\varphi }}{2\alpha } -\alpha M_{\varphi }-\dfrac{C}{4\alpha }>0, \end{aligned}$$

which let us conclude the desired estimation (4.34). $\square$

Theorem 4.8

Under hypotheses of Theorem 4.7, if the solution $x=(u,\theta )$ of Problem (3.20) is such that

$$\begin{aligned} u \in H^{\frac{3}{2}+r}(\Omega )^{d} ~\text { and }~ \theta \in H^{\frac{3}{2}+r}(\Omega ) ~\text { with }~ 0 < r \le 2, \end{aligned}$$

there exists $c >0$ independent of $x=(u,\theta )$, $\epsilon$ and h such that

$$\begin{aligned}&\left\| u-u^{h}_{\varepsilon } \right\| _{1,\Omega } + \left\| \theta -\theta ^{h}_{\varepsilon } \right\| _{1,\Omega } + (\varepsilon ^{\frac{1}{2}} - C h^{\frac{1}{2}})\\&\left[ \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| _{0,\Gamma _{3}} + \left\| \sigma _{\tau }(u,\varphi ) + \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| _{0,\Gamma _{3}} \right] \\&\quad \le C(h^{\frac{1}{2}+r} + \varepsilon ^{\frac{1}{2}+r})\, \left( \Vert u \Vert _{\frac{3}{2}+r, \Omega } + \Vert \theta \Vert _{\frac{3}{2}+r, \Omega }\right) . \end{aligned}$$

(4.50)

Remark 4.9

Similar to the frictionless scenario, to ascertain the convergence rate outlined in Theorem 4.8, we adjust the penalty parameter as a function of the mesh size. Therefore, if we consider, for instance, $\varepsilon (h):= \big (C+1\big )^{2} h$, signifying that the penalty parameter $\varepsilon$ aligns with the mesh size h, we obtain the ensuing a priori estimate

$$\begin{aligned}&\left\| u-u^{h}_{\varepsilon } \right\| _{1,\Omega } + \left\| \theta -\theta ^{h}_{\varepsilon } \right\| _{1,\Omega }\\&\qquad + h^{\frac{1}{2}} \left[ \left\| \sigma _{\nu }(u,\theta ) + \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon ,\nu }]^{+} \right\| _{0,\Gamma _{3}} \right. \\&\left. \qquad + \left\| \sigma _{\tau }(u,\theta ) + \frac{1}{\varepsilon }\, [u^{h}_{\varepsilon , \tau }]_{\varepsilon g} \right\| _{0,\Gamma _{3}} \right] \\&\quad \le C h^{\frac{1}{2}+r}\, \left( \Vert u \Vert _{\frac{3}{2}+r, \Omega } + \Vert \theta \Vert _{\frac{3}{2}+r, \Omega } \right) . \end{aligned}$$

5 Conclusions

A thermoelastic unilateral contact problem in $d=2,3$ dimensional domain $\Omega$ with and without Tresca’s friction law has been presented in this work. First, the variational formulations and their corresponding linear finite element approximations are provided. The unilateral contact condition is weakly imposed here using the penalty method. Finally, error estimates dependent on the penalty parameter $\varepsilon$ and the mesh size h were obtained. Furthermore, assuming the solution maintains regularity, a convergence result was established.