1 Introduction

Mathematical modelling has been instrumental for decades in reproducing and comprehending complicated events, as well as in forecasting future consequences, in many scientific disciplines. Mathematical models are employed in physics to forecast particle interactions and characterize particle behaviour. The study of thermodynamics, energy conversion, and heat transmission has all been covered through modelling in mechanical and thermal science (Ezzat and El-Bary 2016). Mathematical models are used in biology to analyse population and ecosystem behaviour, as well as the development and spread of diseases (Berryman 1992; Malthus 1798; Verhulst 1838). The importance of mathematical modelling grows as more and more newly discovered diseases emerge that pose a hazard to human health and have the potential to seriously disrupt human livelihoods.

The investigation of prey refuge within the context of predator–prey dynamics has gained significant attention in the fields of applied mathematics and ecology. In natural ecosystems, when prey populations perceive the presence of predators, they tend to exhibit proactive behaviour by seeking refuge. This adaptive response serves the purpose of evading predators and ultimately enhancing the survival prospects of the prey species. This phenomenon is commonly referred to as the shelter effect in scientific literature (Sih 1987; Kar 2005). Due to the prevalence of refuges in prey populations, including them in the system makes for a more accurate model. While refuges play an essential role in biological pest management, an increase in refuge size may cause population explosions due to an increase in prey density (biomass). Numerous scholarly investigations have been conducted on predator–prey systems featuring the presence of prey refuge. These refuges can take several forms, including constant refuge as explored in previous studies (Din 2016; Maji 2022), or linear refuge as examined in other research (Qi and Meng 2021; Chakraborty et al. 2021). These investigations have been conducted within the framework of the respective systems under study.

Fractional-order differential equations have recently gained prominence as a modelling tool for studying dynamical systems (Diethelm 2010; Hilfer 2000; Kilbas et al. 2006; Miller and Ross 1993; Petras 2011; Podlubny 1999; Sabatier et al. 2007; Stamova and Stamov 2016; Das 2007; Wei et al. 2010). The fractional order derivative is defined in multiple ways. The definitions most frequently employed are those proposed by Caputo, Grunwald–Letnikov, and Riemann–Liouville. The Caputo definition is extended, and the initial conditions in Caputo fractional differential equations are given in the identical form as in differential equations of integer order. Fractional-order biological models have been the subject of increasing amounts of research lately (Ahmed et al. 2007; Li et al. 2016; Vargas-De-Leon 2015). It is possible to represent a higher-order system using a lower-order model in fractional-order system modelling. When it comes to theories of control, the fractional order system is usually more effective than the integer order system (Premakumari et al. 2022; Sindhu et al. 2021; Iyiola et al. 2021; Akinyemi and Iyiola 2020). The fundamental reason is that non-integer order differential equations have intimate relationships with fractals and are naturally tied to memory systems, which are present in most biological systems. Stability investigations of fractional-order predator–prey systems are still in their early stages because of the lack of adequate theories to analyse the dynamics of these systems (Li et al. 2015). Recently, linearization and Lyapunov procedures have shown to be effective strategies. In order to determine whether or not a given equilibrium point in a system of non-integer order differential equations is stable, several researchers have recently turned to the Lyapunov direct technique.

This FODE solution’s existence and uniqueness may be confirmed by applying the currently available fractional calculus techniques. This makes it possible to determine the asymptotic stability, both local and global, of various steady-states using currently available methodologies. A steady-state’s change in stability condition can be assessed using the obtained stability condition, but it is still difficult to determine the precise local and global bifurcation by using FODE. Although the conditions for Hopf-bifurcation for models based on FODE have recently been shown in (Deshpande et al. 2017; Abdelouahab et al. 2012; Gonzalez-Oliver and Tang 2018), the stability of the limit cycle that results from Hopf-bifurcation has not yet been determined. Using an expanded numerical simulation approach to FODE (Diethelm and Ford 2002), we can explore this problem and get some basic understanding. To provide more insights into this matter, we will now investigate a prey-predator interaction model based on FODEs that has reaction kinetics that follow the Bazykin formalism (McGehee et al. 2008). Bazykin’s prey-predator scheme expands on the Rosenzweig–MacArthur system by include a density-dependent mortality pace within the predators. With respect to the framework’s parameter quantities, this traditional system exhibits an extensive range of dynamic behaviour.

In this study, we focus primarily on exploring the ways in which different parameters in the mathematical model used to simulate population expansion affect the proposed model’s complex dynamic behaviours. According to the existing literature, the impact of memory length, including latency and prey refuge, has not been explored in any previous investigation. The dynamics of the model are significantly altered by these parameters, allowing us to learn more about the dynamics of the memory. This is the first study of its kind, and it shows how novel and important the memory effect is in the Bazykin’s prey-predator model with delay that we propose, which also accounts for prey refuge and a density-dependent mortality pace for predators.

The following outline constitutes the framework of this paper: In Sect. 2, we discuss some introductory concerns and the mathematical formulation of the scheme. Existence, uniqueness, and boundedness of the model are proven in Sect. 3. All feasible equilibrium points are analysed for their stability in Sect. 4. Additionally, we discussed the bifurcation criterion and global stability of the scheme. In Sect. 5, numerical simulations are executed to back up the theoretical findings of the framework. In the final section, we draw some final conclusions.

2 Model Formulation

Prey-predator interactions in the traditional Rosenzweig–MacArthur model (Kot 2001) are described by the coupled nonlinear ordinary differential equations

$$\frac{du}{{dt^{\prime}}} = \rho u - au^{2} - \frac{{k_{1} uv}}{{k_{2} + bu}},$$
$$\frac{dv}{{dt^{\prime}}} = \frac{{ck_{1} uv}}{{k_{2} + bu}} - k_{3} v,$$
(1)

under the non-negative initial conditions \(u\left( 0 \right),\;v\left( 0 \right) \ge 0\).

Table 1 A description of the system’s parameters’ biological importance, (1–4)
Full size table

Bazykin (1974; Bazykin et al. 1998) makes modifications to model (1) to address intraspecific competition among the predators. In the presence of low population densities of both prey and predators, the incorporation of intraspecific rivalry within the predators may effectively mitigate the occurrence of excessive amplitude oscillations. After accounting for the prey refuge, delay, and density-dependent mortality rate in the rise of predators, the Bazykin’s model is obtained as follows.

$$\frac{du}{{dt^{\prime}}} = \rho u - au^{2} - \frac{{k_{1} \left( {1 - w} \right)uv\left( {t^{\prime} - \tau } \right)}}{{k_{2} + b\left( {1 - w} \right)u}},$$
$$\frac{dv}{{dt^{\prime}}} = \frac{{ck_{1} \left( {1 - w} \right)uv\left( {t^{\prime} - \tau } \right)}}{{k_{2} + b\left( {1 - w} \right)u}} - k_{3} v - k_{4} v^{2} .$$
(2)

where \(w\) is the prey refuge \(0 \le w < 1\) and \(k_{4} \,\) is the level of intraspecific rivalry within the predator population. This scheme is of interest to us since it displays a variety of oscillatory dynamics under different parametric circumstances.

Before moving on, we briefly discuss the nondimensionalized version of the model (2) obtained using the same modification of variables as in (McGehee et al. 2008). When we include the transformation \(t^{\prime} = \frac{t}{{k_{3} }}\), \(u = k_{2} x\) and \(v = ek_{2} y\) in (2), we obtain the non dimensionalized equations, which are

$$\frac{dx}{{dt}} = r_{0} x\left( {1 - \frac{x}{{K_{0} }}} \right) - K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}},$$
$$\frac{dy}{{dt}} = K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}} - y - K_{f} y^{2} ,$$
(3)

where \(r_{0} = \frac{\rho }{{k_{3} }},\;K_{0} = \frac{\rho }{{ak_{2} }},\;K_{f} = \frac{{ek_{2} k_{4} }}{{k_{3} }},\;K_{1} = \frac{{ek_{1} }}{{k_{3} }}\). We use \(t\) as dimensionless time without any loss of generality. We now generalize model (3) to any order with respect to the Caputo fractional derivative, then

$$D^{\alpha } x = r_{0} x\left( {1 - \frac{x}{{K_{0} }}} \right) - K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}},$$
$$D^{\alpha } y = K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}} - y - K_{f} y^{2} .$$
(4)

As a matter of notational convenience, we write the Caputo derivative as \(D^{\alpha }\) rather than \(_{{t_{0} }}^{C} D_{t}^{\alpha }\) with \(t_{0} = 0\). The above model assumes \(x\left( 0 \right)\), \(y\left( t \right) = \varphi \left( t \right) > 0\left( {t \in \left[ { - \tau ,0} \right]} \right)\) with \(\varphi \left( t \right)\) is a continuous function. All the parameters description of model (4) are provided in Table 1. Our focus will be on understanding how the time latency affects the model’s dynamics (4).

In order to establish the major conclusions of this subsection, which concern the stability and bifurcation of model (4), we begin by establishing several lemmas relating fractional derivatives.

2.1 Preliminaries

Definition 1

(Podlubny 1993). For every function \(f \in C^{n} \left( {[t_{0} ,\infty ),{\mathbf{R}}} \right)\), we have the following definition for its Caputo fractional derivative of order \(\alpha\):

$$_{{t_{0} }}^{C} D_{t}^{\alpha } f\left( t \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\int\limits_{{t_{0} }}^{t} {\frac{{f^{\left( n \right)} \left( \zeta \right)}}{{\left( {t - \zeta } \right)^{\alpha - n + 1} }}} d\zeta ,$$

where \(n\) is a positive integer such that \(n - 1 < \alpha \le n.\) Furthermore, when \(0 < \alpha \le 1,\) we have

$$_{{t_{0} }}^{C} D_{t}^{\alpha } f\left( t \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\int\limits_{{t_{0} }}^{t} {\frac{{f^{\prime}\left( \zeta \right)}}{{\left( {t - \zeta } \right)^{\alpha } }}} d\zeta .$$

Definition 2

(Podlubny 1993). Let \(\alpha > 0,\;n - 1 < \alpha \le n \in {\mathbb{N}}.\) Consider \(f^{\left( k \right)} \left( t \right),\;k = 0,\;1,...,\;n - 1\), are continuous functions on \([t_{0} ,\,\infty )\), \(f^{\left( n \right)} \left( t \right)\) exists with exponential order and \(_{{t_{0} }}^{C} D_{t}^{\alpha } f\left( t \right)\) is piecewise continuous on \([t_{0} ,\,\infty )\). Then.

\(L\left\{ {_{{t_{0} }}^{C} D_{t}^{\alpha } f\left( t \right)} \right\} = s^{\alpha } F\left( s \right) - \sum\limits_{k = 0}^{n - 1} {s^{\alpha - k - 1} f^{\left( k \right)} \left( {t_{0} } \right),}\) where \(F\left( s \right) = L\left\{ {f\left( t \right)} \right\}\).

Lemma 1

(Matignon 1996). We consider the autonomous nonlinear fractional order system:

$$\frac{{d^{\alpha } \vec{\varepsilon }\left( t \right)}}{{dt^{\alpha } }} = \vec{f}\left( {\vec{\varepsilon }\left( t \right)} \right);\;\vec{\varepsilon }\left( 0 \right) = \vec{\varepsilon }_{0} ;\;0 < \alpha < 1.$$

The equilibrium points of the above system are solutions to the equation \(\vec{f}\left( {\vec{\varepsilon }\left( t \right)} \right) = 0.\) An equilibrium point \(\vec{\varepsilon }^{*}\) is locally asymptotically stable if all characteristic roots \(\left( {\lambda_{j} } \right)\) of the Jacobian matrix \(J = \frac{{\partial \vec{f}}}{{\partial \vec{\varepsilon }}}\) evaluated at equilibrium \(\vec{\varepsilon }^{*}\) satisfy \(\left| {\arg \left( {\lambda_{j} } \right)} \right| > \frac{\alpha \pi }{2}\).

If use the notation \(s\left( \alpha \right) = \frac{\alpha \pi }{2} - \mathop {\min }\limits_{1 \le j \le n} \left\{ {\arg \left( {\lambda_{j} } \right)} \right\}\) then the trivial solution of the system is locally asymptotically stable if \(s\left( \alpha \right) < 0\) and unstable if \(s\left( \alpha \right) > 0.\)

3 Existence, Uniqueness and Boundedness

We investigate whether or not there is a unique solution to the initial value problem (4).

$$D^{\alpha } x = r_{0} x\left( {1 - \frac{x}{{K_{0} }}} \right) - K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}},$$
$$D^{\alpha } y = K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}} - y - K_{f} y^{2} ,\;t \in \left[ {t_{0} ,\;t_{0} + H} \right],$$
(5)
$$\left( {x\left( t \right),\;y\left( t \right)} \right) = \delta \left( t \right): = \left( {\delta_{1} \left( t \right),\;\delta_{2} \left( t \right)} \right),\;t \in \left[ {t_{0} - \tau ,\;t_{0} } \right],$$

where \(0 < \alpha \le 1,\;t_{0} \ge 0,\;\tau > 0,\;H > 0,\) and the initial value function \(\delta \left( t \right) \in C\left( {\left[ {t_{0} - \tau ,\;t_{0} } \right],\;{\mathbf{R}}^{2} } \right).\)

Let’s write

$$V\left( t \right) = \left( {x\left( t \right),\;y\left( t \right)} \right),\;\Omega \left( {V\left( t \right)} \right) = \left( {\Omega_{1} \left( {V\left( t \right)} \right),\;\Omega_{2} \left( {V\left( t \right)} \right)} \right),$$

in which

$$\Omega_{1} \left( {V\left( t \right)} \right) = r_{0} x\left( {1 - \frac{x}{{K_{0} }}} \right) - K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}},$$
$$\Omega_{2} \left( {V\left( t \right)} \right) = K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}} - y - K_{f} y^{2} .$$
(6)

For \(V = \left( {x,y} \right) \in {\mathbf{R}}^{2} ,\) consider the norm \(\left\| V \right\| = \left| x \right| + \left| y \right|.\) Let \(\eta = C\left( {\left[ {t_{0} - \tau ,\;t_{0} + H} \right],\;{\mathbf{R}}^{2} } \right)\) and let \(\left\| V \right\|_{\eta } = \max_{{t \in \left[ {t_{0} - \tau ,\,t_{0} + H} \right]}} \left\| {V\left( t \right)} \right\|\) be the norm for \(V\left( t \right) = \left( {x\left( t \right),\;y\left( t \right)} \right) \in \eta\).

Consider

$$P = \left\{ {V \in \eta :V\left( t \right) = \delta \left( t \right)\;{\text{for}}\;t \in \left[ {t_{0} - \tau ,\;t_{0} } \right],\;{\text{and}}\;\max_{{t \in \left[ {t_{0} ,\,t_{0} + H} \right]}} \left\| {V\left( t \right) - \delta \left( {t_{0} } \right)} \right\| \le Q} \right\}\;\left( {Q > 0} \right).$$

It is obvious that \(\left\| V \right\|_{\eta } \le M: = \max \left\{ {\max_{{t \in \left[ {t_{0} - \tau ,\,t_{0} } \right]}} \left\| {\delta \left( t \right)} \right\|,\;\left\| {\delta \left( {t_{0} } \right)} \right\| + Q} \right\}\) for every \(V\left( t \right) \in P\).

Therefore, for any \(V\left( t \right) = \left( {x\left( t \right),\,y\left( t \right)} \right),\;\overline{V}\left( t \right) = \left( {\overline{x}\left( t \right),\;\overline{y}\left( t \right)} \right) \in P,\;t \in \left[ {t_{0} ,\;t_{0} + H} \right]\), we have

$$\begin{aligned} \left\| {\Omega \left( {V\left( t \right)} \right) - \Omega \left( {\overline{V} \left( t \right)} \right)} \right\| & = \left| {\Omega_{1} \left( {V\left( t \right)} \right) - \Omega_{1} \left( {\overline{V} \left( t \right)} \right)} \right| + \left| {\Omega_{2} \left( {V\left( t \right)} \right) - \Omega_{2} \left( {\overline{V} \left( t \right)} \right)} \right| \\ & = \left| {r_{0} x\left( {1 - \frac{x}{{K_{0} }}} \right) - K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}} - r_{0} \overline{x}\left( {1 - \frac{{\overline{x}}}{{K_{0} }}} \right) + K_{1} \frac{{\left( {1 - w} \right)\overline{x}\overline{y}\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)\overline{x}}}} \right| \\ & \quad + \left| {K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}} - y - K_{f} y^{2} - K_{1} \frac{{\left( {1 - w} \right)\overline{x}\overline{y}\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)\overline{x}}} + \overline{y} + K_{f} \overline{y}^{2} } \right|, \\ & \le \left( {r_{0} + \frac{{r_{0} }}{{K_{0} }}2M} \right)\left| {x - \overline{x}} \right| + \left( {1 + 2K_{f} M} \right)\left| {y - \overline{y}} \right| + \frac{{2K_{1} M\left( {1 - w} \right)}}{{\left( {1 + b\left( {1 - w} \right)M} \right)}}\left| {y\left( {t - \tau } \right) - \overline{y}\left( {t - \tau } \right)} \right|, \\ & \le L\left( {\left\| {V\left( t \right) - \overline{V}\left( t \right)} \right\| + \left\| {V\left( {t - \tau } \right) - \overline{V}\left( {t - \tau } \right)} \right\|} \right) \\ \end{aligned}$$
(7)

where \(L: = \max \left\{ {r_{0} \left( {1 + \frac{2M}{{K_{0} }}} \right),\;\left( {1 + 2MK_{f} } \right),\;\frac{{2MK_{1} \left( {1 - w} \right)}}{{1 + b\left( {1 - w} \right)M}}} \right\}.\)

Likewise, with respect to any \(V\left( t \right) \in P,\;t \in \left[ {t_{0} ,\;t_{0} + H} \right]\), we have

$$\begin{aligned} \left\| {\Omega \left( {V\left( t \right)} \right)} \right\| = \left| {\Omega_{1} \left( {V\left( t \right)} \right)} \right| + \left| {\Omega_{2} \left( {V\left( t \right)} \right)} \right| & = \left| {r_{0} x\left( {1 - \frac{x}{{K_{0} }}} \right) - K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}}} \right| \\ & \quad + \left| {K_{1} \frac{{\left( {1 - w} \right)xy\left( {t - \tau } \right)}}{{1 + b\left( {1 - w} \right)x}} - y - K_{f} y^{2} } \right|, \\ & \le \left( {r_{0} + \frac{{r_{0} M}}{{K_{0} }} + \frac{{2MK_{1} \left( {1 - w} \right)}}{{1 + b\left( {1 - w} \right)M}}} \right)\left| x \right| + \left( {1 + MK_{f} } \right)\left| y \right|, \\ & \le L\left\| {V\left( t \right)} \right\|. \\ \end{aligned}$$
(8)

Then, by using the fractional integral operator on system (5), we get the following equivalent second-kind Volterra equation.

$$V\left( t \right) = \delta \left( {t_{0} } \right) + \frac{1}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} f\left( {X\left( \zeta \right)} \right)d\zeta ,\;t \in \left[ {t_{0} ,\;t_{0} + H} \right],}$$
$$V\left( t \right) = \delta \left( t \right) = \left( {\delta_{1} \left( t \right),\;\delta_{2} \left( t \right)} \right),\;t \in \left[ {t_{0} - \tau ,\;t_{0} } \right].$$

Set up the operator \(\gamma :\psi \to \psi ,\) so as to

$$\gamma V\left( t \right): = \delta \left( {t_{0} } \right) + \frac{1}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \Omega \left( {V\left( \zeta \right)} \right)d\zeta ,\;t \in \left[ {t_{0} ,\;t_{0} + H} \right],}$$
(9)
$$\gamma V\left( t \right): = \delta \left( t \right) = \left( {\delta_{1} \left( t \right),\;\delta_{2} \left( t \right)} \right),\;t \in \left[ {t_{0} - \tau ,\;t_{0} } \right].$$

Then, because \(\gamma\) has only one fixed point in \(P\), it follows that (5) can only have one solution.

By (7) and (9), with respect to any \(V\left( t \right) = \left( {x\left( t \right),\;y\left( t \right)} \right),\;\overline{V}\left( t \right) = \left( {\overline{x}\left( t \right),\;\overline{y}\left( t \right)} \right) \in P,\;t \in \left[ {t_{0} ,\;t_{0} + H} \right],\) we have

$$\begin{aligned} \left\| {\gamma V\left( t \right) - \gamma \overline{V}\left( t \right)} \right\| & \le \frac{1}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \left\| {\Omega \left( {V\left( \zeta \right)} \right) - \Omega \left( {\overline{V}\left( \zeta \right)} \right)} \right\|d\zeta ,} \\ & \le \frac{1}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \left( {\left\| {V\left( \zeta \right) - \overline{V}\left( \zeta \right)} \right\| + \left\| {V\left( {\zeta - \tau } \right) - \overline{V}\left( {\zeta - \tau } \right)} \right\|} \right)d\zeta ,} \\ & \le \frac{1}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \left( {\mathop {\max }\limits_{{\zeta \in \left[ {t_{0} ,\,t_{0} + H} \right]}} \left\| {V\left( \zeta \right) - \overline{V}\left( \zeta \right)} \right\| + \max \left\{ {\mathop {\max }\limits_{{\zeta \in \left[ {t_{0} - \tau ,\,t_{0} } \right]}} \left\| {V\left( \zeta \right) - \overline{V}\left( \zeta \right)} \right\|,\mathop {\max }\limits_{{\zeta \in \left[ {t_{0} ,\,t_{0} + H} \right]}} \left\| {V\left( \zeta \right) - \overline{V}\left( \zeta \right)} \right\|} \right\}} \right)d\zeta ,} \\ & \le \frac{2L}{{\Gamma \left( \alpha \right)}}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \left( {\mathop {\max }\limits_{{\zeta \in \left[ {t_{0} ,\,\,t_{0} + H} \right]}} \left\| {V\left( \zeta \right) - \overline{V}\left( \zeta \right)} \right\|} \right)d\zeta ,} \\ & \le \frac{{2LH^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}\left\| {V - \overline{V}} \right\|_{\eta } . \\ \end{aligned}$$

So, we have \(\left\| {\gamma V\left( . \right) - \gamma \overline{V}\left( . \right)} \right\|_{\eta } \le \frac{{2LH^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}\left\| {V - \overline{V}} \right\|_{\eta } ,\) this suggests that \(\gamma\) is a contraction operator if \(H < \left( {\frac{{\Gamma \left( {\alpha + 1} \right)}}{2L}} \right)^{1/\alpha } .\)

For any \(V\left( t \right) \in P,\;t \in \left[ {t_{0} ,\;t_{0} + H} \right],\) by (8) and (9), we have

$$\begin{aligned} \left\| {\gamma V\left( t \right) - \delta \left( {t_{0} } \right)} \right\| & \le \frac{1}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \left\| {\Omega \left( {V\left( \zeta \right)} \right)} \right\|d\zeta ,} \\ & \le \frac{1}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \left\| {V\left( \zeta \right)} \right\|d\zeta ,} \\ & \le \frac{L}{\Gamma \left( \alpha \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \zeta } \right)^{\alpha - 1} \mathop {\max }\limits_{{\zeta \in \left[ {t_{0} ,\,t_{0} + H} \right]}} \left\| {V\left( \zeta \right)} \right\|\,d\zeta } , \\ & \le \frac{{LH^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}\mathop {\max }\limits_{{\zeta \in \left[ {t_{0} ,\,t_{0} + H} \right]}} \left\| {V\left( \zeta \right)} \right\|, \\ & \le \frac{{LH^{\alpha } M}}{{\Gamma \left( {\alpha + 1} \right)}}. \\ \end{aligned}$$
(10)

If \(H \le \left( {\frac{{\Gamma \left( {\alpha + 1} \right)Q}}{LM}} \right)^{1/\alpha }\), it may be deduced using (10) as \(\mathop {\max }\limits_{{\zeta \in \left[ {t_{0} ,\,t_{0} + H} \right]}} \left\| {\gamma \left( {V\left( t \right) - \delta \left( {t_{0} } \right)} \right)} \right\| \le Q\), this suggests that \(\gamma \left( {V\left( t \right)} \right) \in P,\) for every \(V\left( t \right) \in P.\)

According to the Banach contraction principle, if \(H < \min \left\{ {\left( {\frac{{\Gamma \left( {\alpha + 1} \right)Q}}{LM}} \right)^{1/\alpha } ,\left( {\frac{{\Gamma \left( {\alpha + 1} \right)}}{2L}} \right)^{1/\alpha } } \right\}\), there is only one fixed point in \(P\) for \(\gamma\). It is possible to derive the following theorem from the discussion above.

Theorem 1

If \(H < \min \left\{ {\left( {\frac{{\Gamma \left( {\alpha + 1} \right)Q}}{LM}} \right)^{1/\alpha } ,\left( {\frac{{\Gamma \left( {\alpha + 1} \right)}}{2L}} \right)^{1/\alpha } } \right\}\) holds, then there occurs only one solution to the initial value problem (5).

4 Stability Analysis and Hopf Bifurcation

The intersections of systems (4) such that \(D^{\alpha } \,x = 0\) and \(D^{\alpha } \,y = 0\) constitute the equilibria. Therefore, there are three equilibrium points in system (4): trivial equilibrium \(E_{0} \left( {0,\,0} \right)\), axial equilibrium \(E_{1} \left( {x,\,0} \right)\) and interior equilibrium \(E^{*} \left( {x^{*} ,\,y^{*} } \right)\).

It is necessary to linearize the framework (4) about a suitable equilibrium point in order to use Lemma 1 to determine the stability of distinct equilibria. The system (4)’s variational matrix is given by

$$J = \left( {\begin{array}{*{20}c} {r_{0} - \frac{{2r_{0} x}}{{K_{0} }} - \frac{{K_{1} \left( {1 - w} \right)y}}{{\left( {1 + b\left( {1 - w} \right)x} \right)^{2} }}} & { - \frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}e^{ - \lambda \tau } } \\ {\frac{{K_{1} \left( {1 - w} \right)y}}{{\left( {1 + b\left( {1 - w} \right)x} \right)^{2} }}} & {\frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}e^{ - \lambda \tau } - \left( {1 + 2K_{f} y} \right)} \\ \end{array} } \right).$$
(11)

Theorem 2

Equilibrium point \(E_{0} = \left( {0,\,0} \right)\) is inherently not stable if \(r_{0} > 0.\)

Proof

The variational matrix (11) at the trivial equilibrium point \(E_{0} = \left( {0,0} \right)\) is \(J = \left( {\begin{array}{*{20}c} {r_{0} } & 0 \\ 0 & { - 1} \\ \end{array} } \right)\).

The latent values of the variational matrix are \(\lambda_{1} = r_{0} > 0\) and \(\lambda_{2} = - 1 < 0\). Thus \(s\left( \alpha \right) = \frac{\alpha \pi }{2} - \min \left\{ {\arg \left( {\lambda_{1} } \right),\;\arg \left( {\lambda_{2} } \right)} \right\} = \frac{\alpha \pi }{2} - \min \left\{ {0,\pi } \right\} = \frac{\alpha \pi }{2} > 0\) as \(0 < \alpha \le 1\). Hence, using lemma1, the trivial equilibrium point is never stable.

Theorem 3

The equilibrium point \(E_{1} = \left( {K_{0} ,\,0} \right)\) is locally asymptotically stable if \(b > K_{1} \;{\text{and}}\;w < 1\) (as all values of \(\tau > 0\)).

Proof

The community matrix at \(E_{1}\) is given by.

$$J\left( {E_{1} } \right) = \left( {\begin{array}{*{20}c} {r_{0} - \frac{{2r_{0} x}}{{K_{0} }}} & { - \frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}e^{ - \lambda \tau } } \\ 0 & {\frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}e^{ - \lambda \tau } - 1} \\ \end{array} } \right)$$
(12)
$${\text{The characteristic equation is}}\;\lambda^{2\alpha } + C_{1} \lambda^{\alpha } + C_{2} - e^{ - \lambda \tau } \left( {C_{3} \lambda^{\alpha } + C_{4} } \right) = 0,$$
(13)

where \(C_{1} = 1 - r_{0} + \frac{{2r_{0} x}}{{K_{0} }},\;C_{2} = \frac{{2r_{0} x}}{{K_{0} }} - r_{0} ,\;C_{3} = \frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}\) and

$$C_{4} = \frac{{2r_{0} K_{1} \left( {1 - w} \right)x^{2} }}{{K_{0} \left( {1 + b\left( {1 - w} \right)x} \right)}} - \frac{{r_{0} K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}.$$

When \(\tau = 0\),

$$\lambda^{2\alpha } + \left( {C_{1} - C_{3} } \right)\lambda^{\alpha } + \left( {C_{2} - C_{4} } \right) = 0.$$
(14)

Equation (14) makes it clear that for \(C_{1} - C_{3} > 0\) and \(C_{2} - C_{4} > 0\), if \(b > K_{1} \,{\text{and}}\,w < 1\).

It is assumed that the validity of the solution \(\lambda = i\varphi\) to Eq. (13) holds under the condition that if \(\tau > 0\),

$$\left( {i\varphi } \right)^{2\alpha } + C_{1} \left( {i\varphi } \right)^{\alpha } + C_{2} - e^{ - i\varphi \tau } \left( {C_{3} \left( {i\varphi } \right)^{\alpha } + C_{4} } \right) = 0,$$
$$- \varphi^{2\alpha } + iC_{1} \varphi^{\alpha } + C_{2} - \left( {\cos \varphi \tau - i\sin \varphi \tau } \right)\left( {iC_{3} \varphi^{\alpha } + C_{4} } \right) = 0.$$

The equations provided pertain to the process of separating the real and imaginary components,

$$C_{3} \varphi^{\alpha } \sin \varphi \tau + C_{4} \cos \varphi \tau = C_{2} - \varphi^{2\alpha } ,$$
(15)
$$- C_{3} \varphi^{\alpha } \cos \varphi \tau + C_{4} \sin \varphi \tau = C_{1} \varphi^{\alpha } .$$
(16)

Solving (15) and (16), we get

$$\varphi^{4\alpha } + \left( {C_{1}^{2} - 2C_{2} - C_{3}^{2} } \right)\varphi^{2\alpha } + \left( {C_{2}^{2} - C_{4}^{2} } \right) = 0.$$
(17)

The asymptotic stability of equilibrium is confirmed by Eq. (13) for the case when \(\tau > 0\), suggesting the existence of two real and negative roots. In contrast, the latent Eq. (13) has two completely imaginary roots \(\pm \,i\varphi_{0}\), and (17) has one positive root by \(\varphi_{0}\) if \(\left( {C_{{_{1} }}^{2} - 2C_{2} - C_{{_{3} }}^{2} } \right) > 0\;{\text{and}}\;\left( {C_{2} - C_{4} } \right) < 0\) i.e.,\(b > K_{1} \,\,{\text{and}}\,\,\,w < 1\). We can get an appropriate \(\varphi_{0}\) using (15) and (16), and the root of (13) has to fulfil

$$\varphi_{0}^{2\alpha } = \frac{1}{2}\left( {C_{3}^{2} + 2C_{2} - C_{1}^{2} } \right) + \frac{1}{2}\sqrt {\left( {C_{3}^{2} + 2C_{2} - C_{1}^{2} } \right) - 4\left( {C_{2}^{2} - C_{4}^{2} } \right)} < 0.$$

Theorem 4

The coexisting equilibrium point \(E^{*} = \left( {x^{*} ,\,\,y^{*} } \right)\) of the framework (4) is asymptotically stable and unstable for \(\tau > \tau^{*}\). When \(\tau = \tau^{*}\), the characteristic Eq. (17) possesses two roots that are completely imaginary \(\pm \,i\xi_{0}^{\alpha }\) with.

\(\xi_{0}^{2\alpha } = \frac{1}{2}\left( {P_{3}^{2} + 2P_{2} - P_{1}^{2} } \right) + \frac{1}{2}\sqrt {\left( {P_{3}^{2} + 2P_{2} - P_{1}^{2} } \right)^{2} - 4\left( {P_{2}^{2} - P_{4}^{2} } \right)} < 0\) and \(\tau^{*} = \frac{1}{{\xi_{0} }}\arccos \left[ {\frac{{\left( {P_{4} + P_{1} P_{3} } \right)\xi_{0}^{2\alpha } - P_{2} P_{4} }}{{P_{4}^{2} + P_{3}^{2} \xi_{0}^{2\alpha } }}} \right] + \frac{2j\alpha \pi }{{\xi_{0}^{\alpha } }}.\)

Proof

The Jacobian matrix of model (4) may be derived at the positive equilibrium point \(E^{*}\) as.

$$J\left( {E^{*} } \right) = \left( {\begin{array}{*{20}c} { - \frac{{r_{0} x}}{{K_{0} }} + \frac{{bK_{1} \left( {1 - w} \right)^{2} xy}}{{\left( {1 + b\left( {1 - w} \right)x} \right)^{2} }}} & { - \frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}e^{ - \lambda \tau } } \\ {\frac{{K_{1} \left( {1 - w} \right)y}}{{\left( {1 + b\left( {1 - w} \right)x} \right)^{2} }}} & {\frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}e^{ - \lambda \tau } - \left( {1 + 2K_{f} y} \right)} \\ \end{array} } \right).$$

The characteristic equation is given by

$$\lambda^{2\alpha } + P_{1} \lambda^{\alpha } + P_{2} + e^{ - \lambda \tau } \left( {P_{3} \lambda^{\alpha } + P_{4} } \right) = 0.$$
(18)

where \(P_{1} = \frac{{r_{0} x}}{{K_{0} }} - \frac{{bK_{1} \left( {1 - w} \right)^{2} xy}}{{\left( {1 + b\left( {1 - w} \right)x} \right)^{2} }} + \left( {1 + 2K_{f} y} \right)\), \(P_{2} = \left( {\frac{{r_{0} x}}{{K_{0} }} - \frac{{bK_{1} \left( {1 - w} \right)^{2} xy}}{{\left( {1 + b\left( {1 - w} \right)x} \right)^{2} }}} \right)\left( {1 + 2K_{f} y} \right)\), \(P_{3} = - \frac{{K_{1} \left( {1 - w} \right)x}}{{1 + b\left( {1 - w} \right)x}}\), \(P_{4} = \frac{{K_{{_{1} }}^{2} \left( {1 - w} \right)^{2} xy}}{{\left( {1 + b\left( {1 - w} \right)x} \right)^{2} }} - \frac{{r_{0} K_{1} \left( {1 - w} \right)x^{2} }}{{K_{0} \left( {1 + b\left( {1 - w} \right)x} \right)}}\).

When \(\tau = 0\), then (18) becomes

$$\lambda^{2\alpha } + \left( {P_{1} + P_{3} } \right)\lambda^{\alpha } + \left( {P_{2} + P_{4} } \right) = 0.$$
(19)

The above Eq. (19) has two negative real roots if \(\left( {P_{1} + P_{3} } \right) > 0\,\,{\text{and}}\,\,\left( {P_{2} + P_{4} } \right) > 0\,\) when \(x < \frac{{K_{0} K_{1} \left( {1 - w} \right)y}}{{r_{0} \left( {1 + b\left( {1 - w} \right)x} \right)}} < \frac{{\left( {1 + b\left( {1 - w} \right)x} \right)}}{{b\left( {1 - w} \right)}},\;K_{1} < b\;{\text{and}}\;w > 1\). Hence, the equilibrium \(E^{*}\) can be considered asymptotically stable under the condition \(\tau = 0\). When \(\tau > 0\), it is assumed that the solution to Eq. (18) \(\lambda = i\xi\) has to fulfil

$$- \xi^{2\alpha } + P_{2} + P_{1} i\xi^{\alpha } + \left( {\cos \xi \tau - i\sin \xi \tau } \right)\left( {P_{3} i\xi^{\alpha } + P_{4} } \right) = 0,$$
$$\xi^{2\alpha } - P_{2} = P_{3} \xi^{\alpha } \sin \xi \tau + P_{4} \cos \xi \tau + P_{1} i\xi^{\alpha } + i\left( {P_{3} \xi^{\alpha } \cos \xi \tau - P_{4} \sin \xi \tau } \right).$$

After performing the process of separating the real and imaginary components, we get the following results,

$$P_{3} \xi^{\alpha } \sin \xi \tau + P_{4} \cos \xi \tau = \xi^{2\alpha } - P_{2} ,$$
(20)
$$P_{3} \xi^{\alpha } \cos \xi \tau - P_{4} \sin \xi \tau = - P_{1} \xi^{\alpha } .$$
(21)

When we square and combine both equations, we obtain

$$\xi^{4\alpha } + \left( {P_{1}^{2} - 2P_{2} - P_{3}^{2} } \right)\xi^{2\alpha } + \left( {P_{2}^{2} - P_{4}^{2} } \right) = 0.$$
(22)

Simple computations allow us to quickly confirm that \(\left( {P_{1}^{2} - 2P_{2} - P_{3}^{2} } \right) > 0\) for \(K_{1} < b\) and that there is no positive real \(\xi\) fulfilling (22) if \(\left( {P_{2} - P_{4} } \right) > 0\). Hence, (18) has negative roots. But in the case when \(\left( {P_{2} - P_{4} } \right) < 0\), there is only one positive root in Eq. (22) denoted by \(\xi_{0}\), and the characteristic Eq. (18) has two completely imaginary roots \(\pm \,i\xi_{0}\). Let \(\lambda \left( \tau \right) = \vartheta \left( \tau \right) + i\xi \left( \tau \right)\) be the eigenvalue of (18) such that \(\vartheta \left( {\tau^{*} } \right) = 0\,\,{\text{and}}\,\,\,\xi \left( {\tau^{*} } \right) = \xi_{0}\). From (20) and (21), we have \(\tau^{*} = \frac{1}{{\xi_{0} }}\arccos \left[ {\frac{{\left( {P_{4} + P_{1} P_{3} } \right)\xi_{0}^{2\alpha } - P_{2} P_{4} }}{{P_{4}^{2} + P_{3}^{2} \xi_{0}^{2\alpha } }}} \right] + \frac{2j\alpha \pi }{{\xi_{0}^{\alpha } }},\)

and from (22)

$$\xi_{0}^{2\alpha } = \frac{1}{2}\left( {P_{3}^{2} + 2P_{2} - P_{1}^{2} } \right) + \frac{1}{2}\sqrt {\left( {P_{3}^{2} + 2P_{2} - P_{1}^{2} } \right)^{2} - 4\left( {P_{2}^{2} - P_{4}^{2} } \right)} < 0.$$
(23)

Thus, the coexisting equilibrium of framework (4) is locally asymptotically stable for \(0 < \alpha \le 1\) according to Lemma 1.

4.1 Global Stability Analysis

Here, we further develop the study to investigate the requirements for global stability (Deng et al. 2007; Li and Zhang 2011) for the delay differential scheme of non-integer order. After transforming the framework by linearization into a suitable structure, we next examine the global stability of the equilibrium points in (4).

Theorem 5

If all the roots of the latent equation \(\left| {\Delta \left( s \right)} \right| = 0\) possess non-positive real parts, then the coexisting equilibrium point \(\left( {x^{*} ,\,\,y^{*} } \right)\) of the scheme (4) is Lyapunov globally asymptotically stable.

Proof

We linearize the system (4) into the form.

$$D^{\alpha } \,x\left( t \right) = h_{1} x\left( t \right) + h_{2} y\left( {t - \tau } \right),$$
$$D^{\alpha } \,y\left( t \right) = g_{1} x\left( t \right) + g_{2} y\left( t \right) + g_{3} y\left( {t - \tau } \right).$$
(24)

where

$$h_{1} = - r_{0} - \frac{{2r_{0} x^{*} }}{{K_{0} }} - \frac{{K_{1} \left( {1 - w} \right)y^{*} }}{{1 + b\left( {1 - w} \right)x^{*} }} + \frac{{K_{1} b\left( {1 - w} \right)^{2} x^{*} y^{*} }}{{\left( {1 + b\left( {1 - w} \right)x^{*} } \right)^{2} }},\;h_{2} = - \frac{{K_{1} \left( {1 - w} \right)x^{*} }}{{1 + b\left( {1 - w} \right)x^{*} }},$$
$$g_{1} = \frac{{K_{1} \left( {1 - w} \right)y^{*} }}{{1 + b\left( {1 - w} \right)x^{*} }} - \frac{{K_{1} b\left( {1 - w} \right)^{2} x^{*} y^{*} }}{{\left( {1 + b\left( {1 - w} \right)x^{*} } \right)^{2} }},\;g_{2} = - \left( {1 + 2K_{f} y^{*} } \right),\;g_{3} = \frac{{K_{1} \left( {1 - w} \right)x^{*} }}{{1 + b\left( {1 - w} \right)x^{*} }}.$$

If the equilibrium point of the linear non-integer differential equation is not zero, we can move it to the origin. Put \(\overline{x}\left( t \right) = x\left( t \right) - x^{*} ,\,\overline{y}\,\left( t \right) = y\left( t \right) - y^{*}\), then the Eq. (24) becomes

$$D^{\alpha } \,\overline{x}\left( t \right) = h_{1} \overline{x}\left( t \right) + h_{2} \overline{y}\left( {t - \tau } \right),$$
$$D^{\alpha } \,\overline{y}\left( t \right) = g_{1} \overline{x}\left( t \right) + g_{2} \,\overline{y}\left( t \right) + g_{3} \,\overline{y}\left( {t - \tau } \right).$$
(25)

We apply the Laplace transform (Muth 1977) on either side of (25) to examine the stability of model (4). Finally, we have

$$s^{\alpha } X\left( s \right) - s^{\alpha - 1} \gamma_{1} \left( 0 \right) = h_{1} X\left( s \right) + h_{2} e^{ - s\tau } \left( {Y\left( s \right) + \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \gamma_{1} \left( t \right)dt} \right),$$
$$s^{\alpha } Y\left( s \right) - s^{\alpha - 1} \gamma_{2} \left( 0 \right) = g_{1} X\left( s \right) + g_{2} Y\left( s \right) + g_{3} e^{ - s\tau } \left( {Y\left( s \right) + \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \gamma_{2} \left( t \right)dt} \right),$$
$$\left( {s^{\alpha } - h_{1} } \right)X\left( s \right) - h_{2} e^{ - s\tau } Y\left( s \right) = s^{\alpha - 1} \gamma_{1} \left( 0 \right) + h_{2} e^{ - s\tau } \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \gamma_{1} \left( t \right)dt,$$
$$- g_{1} X\left( s \right) + \left( {s^{\alpha } - g_{2} - g_{3} e^{ - s\tau } } \right)Y\left( s \right) = s^{\alpha - 1} \gamma_{2} \left( 0 \right) + g_{3} e^{ - s\tau } \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \gamma_{2} \left( t \right)dt.$$
(26)

Here, it should be stated that the initial values \(\overline{x}\left( t \right) = \gamma_{1} \left( t \right)\) and \(\overline{y}\left( t \right) = \gamma_{2} \left( t \right)\) with \(t \in \left[ { - \tau ,\,0} \right].\) Also \(X\left( s \right)\) and \(Y\left( s \right)\) are Laplace transform of \(\overline{x}\left( t \right)\) and \(\overline{y}\left( t \right)\) with \(X\left( s \right) = L\left( {\overline{x}\left( t \right)} \right)\) and \(Y\left( s \right) = L\left( {\overline{y}\left( t \right)} \right)\). The system (26) can be rewritten as follows.

$$\Delta \left( s \right)\left( {\begin{array}{*{20}c} {X\left( s \right)} \\ {Y\left( s \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {z_{1} \left( s \right)} \\ {z_{2} \left( s \right)} \\ \end{array} } \right).$$
(27)

In which.

\(\Delta \left( s \right) = \left( {\begin{array}{*{20}c} {s^{\alpha } - h_{1} } & { - h_{2} e^{ - s\tau } } \\ { - g_{1} } & {s^{\alpha } - g_{2} - g_{3} e^{ - s\tau } } \\ \end{array} } \right)\) and

\(z_{1} \left( s \right) = s^{\alpha - 1} \gamma_{1} \left( 0 \right) + h_{2} e^{ - s\tau } \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \gamma_{1} \left( t \right)dt\), \(z_{2} \left( s \right) = s^{\alpha - 1} \gamma_{2} \left( 0 \right) + g_{3} e^{ - s\tau } \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \gamma_{2} \left( t \right)dt.\)

\(\Delta \left( s \right)\) gives as the model (4)’s latent matrix with its polynomial \(\left| {\Delta \left( s \right)} \right|\). The reliability of model (4) is therefore determined by the pattern of the latent polynomial’s distinctive roots. In which mean that if all of the roots of the latent equation are not positive, the previously mentioned non-integer order prey predator’s equilibrium is Lyapunov globally asymptotically stable (Li and Zhang 2011). The result of multiplying two sides of (27) with \(s\) is

$$\Delta \left( s \right)\left( {\begin{array}{*{20}c} {s\,X\left( s \right)} \\ {s\,Y\left( s \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {s\,z_{1} \left( s \right)} \\ {s\,z_{2} \left( s \right)} \\ \end{array} } \right).$$
(28)

Since every root of the transcendental equation \(\left| {\Delta \left( s \right)} \right| = 0\) must be on the open left complex plane, i.e., \({\text{Re}} \left( s \right) < 0\), then we consider (28) in \({\text{Re}} \left( s \right) \ge 0.\) Within this limited area, system (28) possess only solution \(\left( {s\,X\left( s \right),\,\,s\,Y\left( s \right)} \right)\), so that

$$\mathop {\lim }\limits_{{s \to 0,\,{\text{Re}} \left( s \right) \ge 0}} sX\left( s \right) = 0,\;\mathop {\lim }\limits_{{s \to 0,\,{\text{Re}} \left( s \right) \ge 0}} sY\left( s \right) = 0.$$

Considering the Laplace transform’s final-value theorem (Khan et al. 2021) and the assumption in which every root of the characteristic equation \(\left| {\Delta \left( s \right)} \right| = 0\), we get

\(\mathop {\lim }\limits_{t \to + \infty } \overline{x}\left( t \right) \equiv \mathop {\lim }\limits_{{s \to 0,\,{\text{Re}} \left( s \right) \ge 0}} sX\left( s \right) = 0,\) and

$$\mathop {\lim }\limits_{t \to + \infty } \overline{y}\left( t \right) \equiv \mathop {\lim }\limits_{{s \to 0,\,{\text{Re}} \left( s \right) \ge 0}} sY\left( s \right) = 0.$$

This indicates that the non-integer order prey-predator model’s zero solution is Lyapunov globally asymptotically stable.

5 Numerical Simulations

In this section, we give one example to show the feasibility and effectiveness of the results obtained in this paper. The Adams–Bashforth-Moulton predictor–corrector system serves as the foundation for all of the simulation findings. The generalised Adams–Bashforth-Moulton type corrector system is based on a crucial fractional differential equation, which is

$$D_{t}^{\alpha } \hbar \left( t \right) = g\left( {t,\hbar \left( t \right),\;\delta \left( {t - \tau } \right)} \right),$$

\(\hbar^{\left( l \right)} \left( 0 \right) = \hbar_{0}^{l} ,\;l = 0,\;1,\;2, \ldots ,\;n - 1,\) where \(n = \left\lceil \alpha \right\rceil .\)

The following expression is same as the Volterra integral equation

$$\hbar \left( t \right) = \sum\limits_{l = 0}^{n - 1} {\hbar_{0}^{\left( l \right)} \frac{{t^{l} }}{l!} + \frac{1}{\Gamma \left( \alpha \right)}\int_{0}^{t} {\left( {t - s} \right)^{\alpha - 1} g\left( {s,\hbar \left( s \right)} \right)ds.} }$$
(29)

Diethelm et al. (2002), employed to good effect the predictor–corrector model predicated on the Adams–Bashforth-Moulton algorithm to integrate Eq. (29). On employing this model to the non-integer order delayed scheme (4), and taking \(h = \frac{T}{N},\;t_{n} = nh,\;n = 0,\;1,\;2, \ldots ,N \in Z^{ + } ,\) the discretization of the fractional-order delayed model (4) can be easily achieved.

$$\begin{aligned} x_{n + 1} & = x_{0} + \frac{{h^{\alpha } }}{{\Gamma \left( {\alpha + 2} \right)}}\left[ {r_{r} x_{n + 1}^{p} \left( {1 - \frac{{x_{n + 1}^{p} }}{{K_{0} }}} \right) - \frac{{K_{1} \left( {1 - w} \right)x_{n + 1}^{p} y_{n + 1}^{p} }}{{1 + b\left( {1 - w} \right)x_{n + 1}^{p} }}} \right] \\ & \quad + \frac{{h^{\alpha } }}{{\Gamma \left( {\alpha + 2} \right)}}\sum\limits_{j = 1}^{n} {a_{j,n + 1} \left[ {r_{0} x_{j} \left( {1 - \frac{{x_{j} }}{{K_{0} }}} \right) - \frac{{K_{1} \left( {1 - w} \right)x_{j} y_{j} }}{{1 + b\left( {1 - w} \right)x_{j} }}} \right],} \\ \end{aligned}$$
$$\begin{aligned} y_{n + 1} & = y_{0} + \frac{{h^{\alpha } }}{{\Gamma \left( {\alpha + 2} \right)}}\left[ {\frac{{K_{1} \left( {1 - w} \right)x_{n + 1}^{p} y_{n + 1}^{p} }}{{1 + b\left( {1 - w} \right)x_{n + 1}^{p} }} - y_{n + 1}^{p} - K_{f} \left( {y_{n + 1}^{p} } \right)^{2} } \right] \\ & \quad + \frac{{h^{\alpha } }}{{\Gamma \left( {\alpha + 2} \right)}}\sum\limits_{j = 1}^{n} {a_{j,n + 1} \left[ {\frac{{K_{1} \left( {1 - w} \right)x_{j} y_{j} }}{{1 + b\left( {1 - w} \right)\,x_{j} }} - y_{j} - K_{f} y_{j}^{2} } \right],} \\ \end{aligned}$$

where

$$x_{n + 1}^{p} = x_{0} + \frac{1}{\Gamma \left( \alpha \right)}\sum\limits_{j = 0}^{n} {c_{j,n + 1} \left[ {r_{0} x_{j} \left( {1 - \frac{{x_{j} }}{{K_{0} }}} \right) - \frac{{K_{1} \left( {1 - w} \right)x_{j} y_{j} }}{{1 + b\left( {1 - w} \right)x_{j} }}} \right],}$$
$$y_{n + 1}^{p} = y_{0} + \frac{1}{\Gamma \left( \alpha \right)}\sum\limits_{j = 0}^{n} {c_{j,n + 1} \left[ {\frac{{K_{1} \left( {1 - w} \right)x_{j} y_{j} }}{{1 + b\,\left( {1 - w} \right)x_{j} }} - y_{j} - K_{f} y_{j}^{2} } \right],}$$
$$a_{j,n + 1} = \begin{array}{*{20}l} {n^{\alpha - 1} - \left( {n - \alpha } \right)\left( {n + 1} \right),} \hfill & {j = 0,} \hfill \\ {\left( {n - j - 2} \right)^{\alpha + 1} + \left( {n - j} \right)^{\alpha + 1} - 2\left( {n - j + 1} \right)^{\alpha + 1} ,} \hfill & {1 \le j \le n} \hfill \\ {1.} \hfill & {j = n + 1} \hfill \\ \end{array}$$
$$c_{j,n + 1} = \frac{{h^{\alpha } }}{\alpha }\left[ {\left( {n - j + 1} \right)^{\alpha } - \left( {n - j} \right)^{\alpha } } \right],\;0 \le j \le n.$$

Since there is currently no data available that is relevant to our proposed model, we have to make the following hypothetical choices for the parameter values:

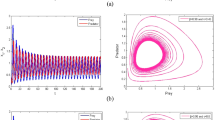
Using three distinct values of \(\tau = 0.2,\,0.4,\) and 0.6, we have now drawn the phase portraits of the system (4) about \(E_{2}\) for \(\alpha = 0.95\) as shown in Fig. 1. According to those figures, when \(\tau\) passes \(\tau^{*} = 0.35\), the behaviour of system (4) shifts from stable to unstable. At nontrivial equilibrium point \(E_{2}\), an unstable source is seen when \(\tau = 0.4 > \tau^{*}\). As \(E_{2}\) acts as a sink at \(\tau = 0.2 < \tau^{*}\), it becomes stable, as determined by Theorem 4.

Fig. 1
figure 1

Behavior of the model (4) with different time delays with the parameter values \(r_{0} = 0.9,\;K_{0} = 21,\;K_{1} = 0.791,\;w = 0.422,\;b = 0.002,{\kern 1pt} \;K_{f} = 0.004\), that displays periodic outbreak due to Hopf bifurcation

Full size image

The derivative of fractional order, as seen in Fig. 2, suppresses the oscillatory motion. The results show that the system is unstable for \(\alpha = 0.98\,\) and \(\alpha = 1\), but stable for \(\alpha = 0.85\). Our findings lead us to the conclusion that the dynamics of the system under consideration is significantly affected by the derivative’s fractional order.

Fig. 2
figure 2

The model (4) exhibiting distinct fractional order (\(0 < \alpha \le 1\)) while maintaining the same set of parameters as seen in Fig. 1. The fractional order derivative damps the oscillation behavior

Full size image

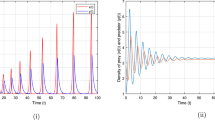
At last, we shall display how each population density is impacted by prey refuge, or more specifically, how the prey refuge rate, \(w\), affects it. As the quantity of refuge increases for fixed delays and fractional orders, Fig. 3 shows that it can cause population breakouts by raising prey density using the parameter values shown in Fig. 1 and for varying values of \(w\).

Fig. 3
figure 3

The system (4)’s phase portrait and time series with various refuge (\(w\)) values, using the other variables set to the same values as in Fig. 1 and \(\tau = 0.2,\;\alpha = 0.98\)

Full size image

In contrast to the predator population, which initially grows and then drops in density with prey refuge rate \(w\), the prey population density increases with prey refuge rate \(w\). When they have places to hide, such long grass, they can fend off predators like cats and owls, which helps to maintain a greater population biomass in rats. Prey refuge and fractional order have an impact on each population density, as demonstrated by our numerical research.

6 Conclusions

This work presents a new and detailed model based on the Caputo fractional order derivative that incorporates latency, prey refuge, and predator death rate dependence in order to simulate the dynamics of Bazykin’s prey-predator model. Incorporating a refuge into system (4) provides a more realistic model, since many prey populations contain some form of refuge. A refuge can be important for the biological control of pest, however, increasing the amount of refuge can increase prey density (biomass) and lead to population outbreaks. The work is significant because it takes into account three practical factors at once that haven’t been taken into account concurrently in other works: fractional order, refuge effect, and time delay. We analyse the uniqueness and boundedness of the changing behaviour of the framework (4). In addition, comprehensive local stability tests and the stability of equilibrium points have been computed to provide a better understanding of the stability of the system under various circumstances. The need for an interior equilibrium point to be globally asymptotically stable has also been determined. The system’s dynamic analysis (4) leads to the following deductions:

Hopf bifurcation occurs in the model when the time-delay crosses the critical value \(\tau^{*}\). A few numerical simulations have confirmed the theoretical predictions. Asymptotically, the interior equilibrium is stable at \(\tau = 0\). For \(\tau = \tau^{*}\), the stability holds. When \(\tau > \tau^{*}\), the instability in that model continues. The incorporation of memory, denoted by fractional derivatives and time delay, enhances the model’s dynamics. In order to preserve the ecological balance and allow biological species to cohabit sustainably, non-integer order and time-delay systems are essential.

The investigation of the fractional-order derivative’s impact on the system is the primary goal of our study. Based on our observations, the stability can be altered by fractional-order derivative. When \(\alpha = 1\) is used in an integer-order system with \(w = 0.422\), the system is unstable, but when \(\alpha\) is decreased, stability is achieved. Therefore, the dynamics of the system are profoundly affected by the non-integer order derivative. Thus, we infer that the model’s solutions are stable for the non-integer order derivative but unstable for the integer-order one system.

In this work, we are particularly interested in the impact of the fractional-order derivative on the system. We found that the stability may be altered by using a fractional-order derivative. When \(\alpha = 1\) with \(w = 0.422\) are applied to an integer-order system, the system is unstable, but when \(\alpha\) is decreased, stability is restored. Therefore, the non-integer order derivative has a significant impact on the system’s behaviour. Thus, we infer that the model’s solutions are stable for non-integer order derivative but unstable for the integer-order one system.

Our numerical simulations also demonstrate the impact of fractional order and prey refuge on population size. The coexistence equilibrium point of system (4) may be manipulated to the desired condition by adjusting the prey refuge rate \(w\). So, it’s good for both the prey population and the predator population if the refuge rate for prey is raised appropriately. From an ecological perspective, a higher density of predators is the result of a reduced value of the prey refuge rate, as more prey may be taken by the predator population. Since we assume that the predator population is entirely reliant on the prey population in our model, we find that when the refuge rate \(w\) for prey increases, the density of the predator population drops as a result of a shortage of food supplies. When prey refuge rates rise to a significant level, predator populations eventually become extinct. The study of fractional order systems numerically has made great strides. Numerical research employs a wide variety of techniques, including the Homotopy perturbation method, the Taylor basis approximations approach, the Adomian decomposition method, Diethelma’s method (Diethelm et al. 2002), etc. We want to perform more analysis of this work in the future using a variety of numerical methods in an effort to improve our findings.