1 Introduction

Nonlinear dynamics established in numerous species that associate across different period frames is an emerging field of exploration in light of its enormous significance on the long-term existence of many species. Mathematical modelling is an efficient technique for investigating to project the continuous existence of distinct species based on the known ecological relations between the individuals of the species at different trophic levels. To gain a greater insight into the changing aspects of the prey-predator scheme, a lot of research have been initiated [1,2,3,4]. In an effort to improve the traditional Lotka-Volterra scheme, investigators have recently included various types of biological factors, such as Allee effects, sickness, a predator’s alternate food source, and fear mechanisms. This has resulted in rich dynamics of the system. Although direct killing has a negligible impact on prey population changing aspects, it is envisaged that predators would have an impact on the prey population [5,6,7].

Recent research, however, asserts that in addition to directly killing prey, predators also instill fear in their victims, which has a considerable negative influence on the prey population’s rate of reproduction [8,9,10,11,12,13]. When the behaviour and physiology of some prey species are altered by predator fear, it is more severe in comparison to simple killing [5]. Wang et al. developed a predator–prey scheme in [9] that involved the dread effect and highlighted how stabilising the system could be accomplished by increasing the cost of fear. However, the focus of all of this study has been on how fear influences the prey population’s pace of reproduction. However, other studies revealed that the existence of predators affected both the prey population’s birth and mortality rates [14, 15]. Recently, Mukherjee [16] has concentrated on this problem in his study. By adding intraspecific competition for the predator and accounting for the cost of anxiety on the death amount of the prey population, he improved the scheme of Wang et al. [9]. He found that the system oscillates when intraspecific value rivalry is low and the degree of dread is low (on both reproduction and the mortality amount of the prey population), but that the system can be stabilised when intraspecific value competition is high.

The pace of change of the present state relies not only on the current state but also on the state of a particular instant or period of time in the past, owing to the complexity and variety of biological systems. Researchers have proposed differential equations with time delay to describe and investigate the time-delay system. This attribute of the systems is known as time delay. In particular, a great deal of research has been done on the dynamics of predator–prey (PP) systems with delays. Numerous scholars have examined the effects of previous states of biological systems on current and future conditions. Incorporating time delay into biological models to reflect resource regeneration time, maturation time, response time, capture time, feeding time, and gestation period has been studied by a number of researchers [17,18,19]. Biological systems with temporal delays, on the other hand, exhibit more intricate and varied dynamic behaviours. Delays may lead to instability, periodic solutions (Hopf bifurcation), chaos, and a variety of oscillations [20, 21]. However, the majority of such models have either been utilised to research integer-order equations including delays or have not.

Apart from the standard derivative, fractional calculus has gained significant attention in recent years due to its significant memory effect. The derivative of fractional order for every function is dependent upon both its present and its past states. The exploration of incorporating integer-order models into fractional-order derivatives has emerged as a prominent subject within the field of dynamical systems. Because fractional-order derivatives include nonlocal and weakly singular kernels, qualitative investigations of fractional-order systems are much more complex than those of integer-order systems. In the context of biological modelling, it has been shown that fractional-order derivatives provide a more accurate representation compared to integer-order derivatives, mostly owing to the incorporation of memory effects. Hence this mathematical tool could be inferred ‘far’ from ‘realism’. But there are various physical phenomena have ‘intrinsic’ fractional order interpretation and so fractional order calculus is useful in order to explain these phenomena. Fractional order differential equations accumulate the entire information of the function due to its long memory process. Fractional calculus has been employed to formulate problems in a wide range of disciplines, including finance, biology, medicine, economics, and engineering [22,23,24,25]. There are various types to describe the fractional-order derivative; the one most frequently used is the Caputo-type derivative [26]. The non-integer order system has been the area of numerous investigates in recent years [27,28,29,30, 40, 41]. A fractional-order system’s response to harvesting was studied by Javidi and Nyamoradi [20]. Also, there are very few models [45,46,47,48,49] have been studied where toxic environment is discussed in fractional order framework. However, no comparable work has been made in non-integer order systems, where the dread of the predator causes a predator density-dependent death rate [42,43,44]. Therefore, in this study, we incorporate the non-integer order and the delay components in the reaction kinetics model that adheres to the Bazykin’s formalism [31]. The Rosenzweig–MacArthur system is enhanced by Bazykin’s prey-predator scheme, which also involves a density-dependent mortality pace for the predators. Our current study’s main objective is to look at the cost of dread and the effect of populace growth depending on memory length on complex dynamic behaviour. We also provide detailed simulation findings for the purpose of identifying the influence of fear and memory length on the movement of local and global bifurcation limit values.

The article is organised as follows. In Sect. 2, the model’s mathematical formulation and a few preliminary issues are covered. In Sect. 3, the model’s existence, uniqueness and boundedness are obtainable. In Sect. 4, stability analysis of all possible equilibrium points is studied. The model’s bifurcation criteria and global stability were also covered. Numerical simulations are run in Sect. 5 to substantiate the model’s theoretical findings. In Sect. 6, conclusions are provided.

2 Model’s Mathematical Formulation

The relationship between prey and predator is regulated using a set of coupled nonlinear ordinary differential equations in the traditional Rosenzweig–MacArthur scheme [32]:

$$ \begin{gathered} \frac{dg}{{dt^{\prime } }} = \rho g - ag^{2} - \frac{{l_{1} \,g\,h}}{{l_{2} + b\,g}}, \hfill \\ \frac{dh}{{dt^{\prime } }} = \frac{{c\,l_{1} \,g\,h}}{{l_{2} + b\,g}} - l_{3} \,h\,, \hfill \\ \end{gathered} $$
(1)

with \(g\left( 0 \right),\,h\left( 0 \right) \ge 0\) being non-negative. The population amounts of prey and predators at an instant of time \(t^{\prime }\) are denoted by \(g\left( {t^{\prime } } \right)\) and \(h\left( {t^{\prime } } \right)\) correspondingly. The system (1)’s parameters are all positive quantities. The specific amount of increase and level of intraspecific rivalry within the prey population are \(\rho\) and \(a\) correspondingly. It is expected that the increasing prey population will adhere to the logistic law of increasing and exist in the nonappearance of a predator population. \(l_{1}\) denotes the level at which predators attack individual prey, \(l_{2}\) is the one-half of saturation amount and \(b\) is a deformation parameter for the saturating functional response [31]. It uses an equivalent parameterization for the saturating functional response as that given in [31]. The conversion rate and the predator’s intrinsic mortality rate are \(c\) and \(l_{3}\) respectively.

Bazykin [33, 34] modifies the model (1) to account for competition within species among predators. Although minimal population densities were maintained in each of the prey and predator populations, the existence of intra-specific rivalry within the predators may avoid excessive amplitude fluctuation. The Bazykin’s model, which incorporates the fear factor \(f\left( {k,h} \right) = \frac{1}{1 + kh},\,\) and \(l_{4}\) density dependent mortality amount in predator growth, is provided by

$$ \begin{gathered} \frac{dg}{{dt^{\prime } }} = \frac{\rho g}{{1 + kh}} - ag^{2} - \frac{{l_{1} \,g\,h}}{{l_{2} + b\,g}} \equiv f_{1} \left( {g,\,h} \right), \hfill \\ \frac{dh}{{dt^{\prime } }} = \frac{{c\,l_{1} \,g\,h}}{{l_{2} + b\,g}} - l_{3} \,h\, - l_{4} \,h^{2} \equiv f_{2} \left( {g,\,h} \right). \hfill \\ \end{gathered} $$
(2)

The model (2) is now extended to a Caputo fractional order derivative with delay, and it then transforms into

$$ \begin{gathered}_{{t_{0} }}^{C} D_{t}^{\beta } \,g = \frac{\rho g}{{1 + kh}} - ag^{2} - \frac{{l_{1} \,g\,h\left( {t - \tau } \right)}}{{l_{2} + b\,g}}, \hfill \\_{{t_{0} }}^{C} D_{t}^{\beta } \,h = \frac{{c\,l_{1} \,g\,h\left( {t - \tau } \right)}}{{l_{2} + b\,g}} - l_{3} \,h\, - l_{4} \,h^{2} , \hfill \\ \end{gathered} $$
(3)

We briefly explore the non-dimensionalized formulation of the non-integer differential equation system before continuing, employing the same parameters transformation as \(t^{\prime } = l_{3} t,\,g = l_{2} x_{1} ,\,h = cl_{2} x_{2}\) in (3) we find

$$ \begin{gathered} D^{\beta } \,x_{1} = r_{0} x_{1} \left( {\frac{1}{{1 + Kx_{2} }} - \frac{{x_{1} }}{{K_{0} }}} \right) - \frac{{K_{1} \,x_{1} \,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} }}, \hfill \\ D^{\beta } x_{2} = \frac{{K_{1} \,x_{1} \,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} }} - x_{2} \, - K_{f} x_{2}^{2} , \hfill \\ \end{gathered} $$
(4)

where \(r_{0} = \rho /l_{3} ,\,K_{0} = \rho /al_{2} ,\,K_{1} = l_{1} c/l_{3} ,\,K_{f} = cl_{2} l_{4} /l_{3}\). Without any loss of generality, we refer to \(t\) as dimensionless time. We substitute \(D^{\beta }\) as a Caputo derivative for \(_{{t_{0} }}^{C} D_{t}^{\beta }\) with \(t_{0} = 0\) in mathematical notation to make it easier to read. The scheme (4) with initial settings \(x_{1} \left( 0 \right)\) and \(x_{2} \left( t \right) = \varphi \left( t \right) > 0\left( {t \in \left[ { - \tau ,\,0} \right]} \right),\) where \(\varphi \left( t \right)\) is a smooth function. We will explore the influence of the time delay on the changing aspects of the scheme (4).

Before moving on to the stability and bifurcation findings from the scheme (4), we begin with certain lemmas associated to non-integer derivatives that will be beneficial in proving the essential conclusions of this subsection.

2.1 Preliminaries

Definition 1

([35]). The Caputo fractional derivative with order \(\beta > 0\) of a function \(f \in C^{n} \left( {[t_{0} ,\,\infty + ),\,{\mathbb{R}}} \right)\) is defined as:

\(_{{t_{0} }}^{C} D_{t}^{\beta } f\left( t \right) = \frac{1}{{\Gamma \left( {n - \beta } \right)}}\int\limits_{{t_{0} }}^{t} {\frac{{f^{\left( n \right)} \left( \nu \right)}}{{\left( {t - \nu } \right)^{\beta - n + 1} }}} \,d\nu ,\) where \(n \in {\mathbb{Z}}_{ + }\) such that \(n - 1 < \beta < n.\)

In particular, for \(0 < \beta \le 1:\)\(_{{t_{0} }}^{C} D_{t}^{\beta } f\left( t \right) = \frac{1}{{\Gamma \left( {1 - \beta } \right)}}\int\limits_{{t_{0} }}^{t} {\frac{{f^{\prime } \,\left( \nu \right)}}{{\left( {t - \nu } \right)^{\beta } }}} \,d\nu .\)

Definition 2

([35]). Let \(\beta > 0,\,\)\(\,n - 1 < \beta < n \in {\mathbb{N}}.\) Assume \(f^{k} \left( t \right),\,\,k = 0,\,1\,,\,...,\,\,n - 1\) are continuous functions on \([t_{0} ,\,\infty ),\)\(f^{n} \left( t \right)\) occurs with exponential order and \(_{{t_{0} }}^{C} D_{t}^{\beta } f\left( t \right)\) is piecewise continuous on \([t_{0} ,\,\infty ).\) Then.

\(L\left\{ {_{{t_{0} }}^{C} D_{t}^{\beta } f\left( t \right)} \right\} = s^{\beta } F\left( s \right) - \sum\limits_{k = 0}^{n - 1} {s^{\beta - k - 1} f^{\left( k \right)} \left( {t_{0} } \right),}\) and \(F\left( s \right) = L\left\{ {f\left( t \right)} \right\}.\)

Lemma 1

([36]). Consider the following \(n -\) dimensional fractional order system with delay: Let \(_{{t_{0} }}^{C} D_{t}^{\beta } x\left( t \right) = f_{i} \left( {x_{1} \left( t \right),...,\,x_{n} \left( t \right);\,\tau } \right)\,\,,\,\,i = 1,2,...,n,\) where \(0 < \beta < 1\) and the time delay \(\tau \ge 0\). The above system undergoes a Hopf bifurcation at the equilibrium \(x^{*} = \left( {x_{1}^{*} ,...,x_{n}^{*} } \right)\) when \(\tau = \tau^{*}\) if the following conditions are satisfied:

  1. i.

    All the eigenvalues \(\lambda_{i} \,\left( {i = 1\,,\,...\,,\,n} \right)\) of the coefficient matrix \(A\) of the linearised system of above with \(\tau = 0\) satisfy \(\left| {\arg \left( {\lambda_{i} } \right)} \right| > \frac{\beta \pi }{2}\).

  2. ii.

    The characteristic equation of the linearised system of above has a pair of purely imaginary roots \(\pm \,i\omega_{0}\) when \(\tau = \tau^{*}\).

  3. iii.

    (iii) \({\text{Re}} \left[ {\frac{ds\left( \tau \right)}{{d\tau }}} \right]_{{\left( {\tau = \tau^{*} \,,\,\omega = \omega_{0} } \right)}} \ne 0,\) where \({\text{Re}} \,[.]\) denotes the real part of the complex number.

3 Existence, Uniqueness and Boundedness

We investigate if a solution to the initial value scheme (4) exists and is unique.

$$ \begin{gathered} D^{\beta } \,x_{1} \left( t \right) = r_{0} x_{1} \left( t \right)\left( {\frac{1}{{1 + K\,x_{2} \left( t \right)}} - \frac{{x_{1} \left( t \right)}}{{K_{0} }}} \right) - \frac{{K_{1} \,x_{1} \left( t \right)\,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} \left( t \right)}}, \hfill \\ D^{\beta } x_{2} \left( t \right) = \frac{{K_{1} \,x_{1} \left( t \right)\,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} \left( t \right)}} - x_{2} \left( t \right)\, - K_{f} \,x_{2}^{2} \left( t \right),\,t \in \left[ {t_{0} ,\,t_{0} + E} \right], \hfill \\ \left( {x_{1} \left( t \right),\,x_{2} \left( t \right)} \right) = \mu \left( t \right): = \left( {\mu_{1} \left( t \right),\,\mu_{2} \left( t \right)} \right),\,\,t \in \left[ {t_{0} - \tau ,\,t_{0} } \right], \hfill \\ \end{gathered} $$
(5)

where \(0 < \beta \le 1,\,t_{0} \ge 0,\,\tau > 0,\,E > 0,\) and the initial value function \(\mu \left( t \right) \in C\left( {\left[ {t_{0} - \tau ,\,t_{0} } \right],\,{\mathbb{R}}^{2} } \right).\)

Let.

\(\Omega \left( t \right) = \left( {x_{1} \left( t \right),\,x_{2} \left( t \right)} \right),\,\,q\left( {\Omega \left( t \right)} \right) = \left( {q_{1} \left( {\Omega \left( t \right)} \right),q_{2} \left( {\Omega \left( t \right)} \right)} \right)\),

where

$$ \begin{gathered} q_{1} \left( {\Omega \left( t \right)} \right) = r_{0} x_{1} \left( t \right)\left( {\frac{1}{{1 + K\,x_{2} \left( t \right)}} - \frac{{x_{1} \left( t \right)}}{{K_{0} }}} \right) - \frac{{K_{1} \,x_{1} \left( t \right)\,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} \left( t \right)}} \hfill \\ q_{2} \left( {\Omega \left( t \right)} \right) = \frac{{K_{1} \,x_{1} \left( t \right)\,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} \left( t \right)}} - x_{2} \left( t \right)\, - K_{f} \,x_{2}^{2} \left( t \right), \hfill \\ \end{gathered} $$
(6)

For \(\Omega = \left( {x_{1} ,\,x_{2} } \right) \in {\mathbb{R}}^{2} ,\,\) take the norm \(\left\| \Omega \right\| = \left| {x_{1} } \right| + \left| {x_{2} } \right|.\) Take \(\sigma = C\left( {\left[ {t_{0} - \tau ,\,t_{0} + E} \right],\,{\mathbb{R}}^{2} } \right),\) and define the norm \(\left\| \Omega \right\|_{\sigma } = \max_{{t \in \left[ {t_{0} - \tau ,\,t_{0} + E} \right]}} \left\| {\Omega \left( t \right)} \right\|\) for \(\Omega \left( t \right) = \left( {x_{1} \left( t \right),\,x_{2} \left( t \right)} \right) \in \sigma\).

Set

$$\begin{aligned} U &= \left\{ X \in \sigma :\Omega \left( t \right)\vphantom{\max_{{t \in \left[ {t_{0} ,\,t_{0} + E}\right]}}} \right.\\ &= \left.\mu \left( t \right)\,{\text{for}}\,t \in \left[ {t_{0} - \tau ,\,t_{0} }\right]\,,\,{\text{and}}\,\max_{{t \in \left[ {t_{0} ,\,t_{0} + E}\right]}} \left\| {\Omega \left( t \right) - \mu \left( {t_{0} }\right)} \right\| \le R \right\}\left( {R > 0} \right).\end{aligned}$$

Clearly, for any \(\Omega \left( t \right) \in U\), we have \( \left\| \Omega \right\|_{\sigma } \le M: = \max \{ \max _{{t \in \left[ {t_{0} - \tau ,{\kern 1pt} t_{0} } \right]}} \left\| {\mu \left( t \right)} \right\|,\,\left\| {\mu \left( {t_{0} } \right)} \right\| + R\} . \)

Therefore, for any \(\Omega \left( t \right) = \left( {x_{1} \left( t \right),\,x_{2} \left( t \right)} \right),\,\overline{\Omega } = \left( {\overline{x}_{1} \left( t \right),\,\overline{x}_{2} \left( t \right)} \right) \in U,\,\,t \in \left[ {t_{0} ,\,t_{0} + E} \right]\), we have

$$ \begin{aligned} \left\| {q\left( {\Omega \left( t \right)} \right) - q\left( {\overline{\Omega }\left( t \right)} \right)} \right\| & = \left| {q_{1} \left( {\Omega \left( t \right)} \right) - q_{1} \left( {\overline{\Omega }\left( t \right)} \right)} \right| + \left| {q_{2} \left( {\Omega \left( t \right)} \right) - q_{2} \left( {\overline{\Omega }\left( t \right)} \right)} \right|, \\ & \le \left( {\frac{{r_{0} }}{{\left( {1 + KM} \right)}} + \frac{{2Mr_{0} }}{{K_{0} }}} \right)\left| {x_{1} \left( t \right) - \overline{x}_{1} \left( t \right)} \right| \\ & \quad + \left( {1 + 2MK_{f} + \frac{{r_{0} KM}}{{\left( {1 + KM} \right)^{2} }}} \right)\left| {\left( {x_{2} \left( t \right) - \overline{x}_{2} \left( t \right)} \right)} \right| \\ & \quad + \frac{{2K_{1} M}}{{\left( {1 + b\,M} \right)}}\left| {\left( {x_{2} \left( {t - \tau } \right) - \overline{x}_{2} \left( {t - \tau } \right)} \right)} \right|, \\ & \le L\left( {\left\| {\Omega \left( t \right) - \overline{\Omega }\left( t \right)} \right\| + \left\| {\Omega \left( {t - \tau } \right) - \overline{\Omega }\left( {t - \tau } \right)} \right\|} \right), \\ \end{aligned} $$
(7)

where \(L: = \max \left\{ {\left( {\frac{{r_{0} }}{{\left( {1 + KM} \right)}} + \frac{{2Mr_{0} }}{{K_{0} }}} \right),\,\,\left( {1 + 2MK_{f} + \frac{{r_{0} KM}}{{\left( {1 + KM} \right)^{2} }}} \right),\,\frac{{2K_{1} M}}{{\left( {1 + b\,M} \right)}}} \right\}\).

Similarly, for any \(\Omega \left( t \right) \in U,\,t \in \left[ {t_{0} ,\,t_{0} + E} \right]\), we have

$$ \begin{aligned} \left\| {q\left( {\Omega \left( t \right)} \right)} \right\| & = \left| {q_{1} \left( {\Omega \left( t \right)} \right)} \right| + \left| {q_{2} \left( {\Omega \left( t \right)} \right)} \right| \\ & = \left| {r_{0} x_{1} \left( t \right)\left( {\frac{1}{{1 + K\,x_{2} \left( t \right)}} - \frac{{x_{1} \left( t \right)}}{{K_{0} }}} \right) - \frac{{K_{1} \,x_{1} \left( t \right)\,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} \left( t \right)}}} \right| \\ & \quad + \left| {\frac{{K_{1} \,x_{1} \left( t \right)\,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} \left( t \right)}} - x_{2} \left( t \right)\, - K_{f} \,x_{2}^{2} \left( t \right)} \right|, \\ & \le \left( {\frac{{r_{0} }}{1 + KM} + \frac{{r_{0} M}}{{K_{0} }} + \frac{{2K_{1} \left| {x_{2} \left( {t - \tau } \right)} \right|}}{1 + bM}} \right)\left| {x_{1} \left( t \right)} \right| + \left( {1 + K_{f} M} \right)\left| {x_{2} \left( t \right)} \right|, \\ & \le \left( {\frac{{r_{0} }}{1 + KM} + \frac{{r_{0} M}}{{K_{0} }} + \frac{{2K_{1} M}}{1 + bM}} \right)\left| {x_{1} \left( t \right)} \right| + \left( {1 + K_{f} M} \right)\left| {x_{2} \left( t \right)} \right|, \le L\left\| {\Omega \left( t \right)} \right\| \\ \end{aligned} $$
(8)

Then, system (5) can be replaced into the corresponding Volterra equation of type two on applying the non-integer integral operator:

$$ \begin{gathered} \Omega \left( t \right) = \mu \left( {t_{0} } \right) + \frac{1}{\Gamma \left( \beta \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} q\left( {\Omega \left( \nu \right)} \right)\,d\nu ,\,\,t \in \left[ {t_{0} ,\,t_{0} + E} \right],} \hfill \\ \Omega \left( t \right) = \mu \left( t \right) = \left( {\mu_{1} \left( t \right),\,\mu_{2} \left( t \right)} \right),\,\,t \in \left[ {t_{0} - \tau ,\,t_{0} } \right]. \hfill \\ \end{gathered} $$

Define the operator \(\chi :U \to U,\) such that

$$ \begin{gathered} \chi \,\Omega \left( t \right): = \mu \left( {t_{0} } \right) + \frac{1}{\Gamma \left( \beta \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} q\left( {\Omega \left( \nu \right)} \right)\,d\nu ,\,\,t \in \left[ {t_{0} ,\,t_{0} + E} \right],} \hfill \\ \chi \,\Omega \left( t \right): = \mu \left( t \right) = \left( {\mu_{1} \left( t \right),\,\mu_{2} \left( t \right)} \right),\,\,t \in \left[ {t_{0} - \tau ,\,t_{0} } \right]. \hfill \\ \end{gathered} $$
(9)

Hence \(\chi\) possesses only a fixed point in \(U\) suggests that the scheme (5) has a unique solution.

From (7) and (9), if any \(\Omega \left( t \right) = \left( {x_{1} \left( t \right),\,x_{2} \left( t \right)} \right),\,\overline{\Omega }\left( t \right) = \left( {\overline{x}_{1} \left( t \right),\,\overline{x}_{2} \left( t \right)} \right) \in U,\,\,t \in \left[ {t_{0} ,\,t_{0} + E} \right],\) we have.

\(\begin{aligned}& \left\| {\chi \,\Omega \left( t \right) - \chi \,\overline{\Omega }\left( t \right)} \right\| \le \frac{1}{\Gamma \left( \beta \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} \left\| {q\left( {\Omega \left( \nu \right)} \right) - q\left( {\overline{\Omega }\left( \nu \right)} \right)} \right\|\,d\nu } , \\ & \quad \le \frac{1}{\Gamma \left( \beta \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} \left( {\left\| {\Omega \left( \nu \right) - \overline{\Omega }\left( \nu \right)} \right\| + \left\| {\Omega \left( {\nu - \tau } \right) - \overline{\Omega }\left( {\nu - \tau } \right)} \right\|} \right)\,d\nu } , \\ & \quad \le \frac{1}{\Gamma \left( \beta \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} \left( {\mathop {\max }\limits_{{\nu \in \left[ {t_{0} ,\,t_{0} + E} \right]}} \left\| {\Omega \left( \nu \right) - \overline{\Omega }\left( \nu \right)} \right\| + \max \left\{ \begin{gathered} \mathop {\max }\limits_{{\nu \in \left[ {t_{0} - \tau ,\,t_{0} } \right]}} \left\| {\Omega \left( \nu \right) - \overline{\Omega }\left( \nu \right)} \right\|, \hfill \\ \mathop {\max }\limits_{{\nu \in \left[ {t_{0} ,\,t_{0} + E} \right]}} \left\| {\Omega \left( \nu \right) - \overline{\Omega }\left( \nu \right)} \right\| \hfill \\ \end{gathered} \right\}} \right)\,d\nu } , \\ &\quad \le \frac{2L}{{\Gamma \left( \beta \right)}}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} \left( {\mathop {\max }\limits_{{\nu \in \left[ {t_{0} ,\,t_{0} + E} \right]}} \left\| {\Omega \left( \nu \right) - \overline{\Omega }\left( \nu \right)} \right\|} \right)\,d\nu } , \\ & \quad \le \frac{{2LE^{\beta } }}{{\Gamma \left( {\beta + 1} \right)}}\left\| {\Omega - \overline{\Omega }} \right\|_{\sigma } . \\ \end{aligned}\) Hence, we possess \(\left\| {\chi \,\Omega \left( . \right) - \chi \,\overline{\Omega }\left( . \right)} \right\|_{\sigma } \le \frac{{2LE^{\beta } }}{{\Gamma \left( {\beta + 1} \right)}}\left\| {\Omega - \overline{\Omega }} \right\|_{\sigma } ,\) indicating as \(\chi\) is a contraction operator when \(E < \left( {\frac{{\Gamma \left( {\beta + 1} \right)}}{2L}} \right)^{1/\beta } .\)

For any \(\Omega \left( t \right) \in U,\,\,t \in \left[ {t_{0} ,\,t_{0} + E} \right],\) by (8) and (9), we have

$$ \begin{aligned} \left\| {\chi \left( {\Omega \left( t \right) - \mu \left( {t_{0} } \right)} \right)} \right\| & \le \frac{1}{\Gamma \left( \beta \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} \left\| {q\left( {\Omega \left( \nu \right)} \right)} \right\|\,d\nu } , \\ & \le \frac{L}{\Gamma \left( \beta \right)}\int\limits_{{t_{0} }}^{t} {\left( {t - \nu } \right)^{\beta - 1} \left\| {\Omega \left( \nu \right)} \right\|\,d\nu } , \\ & \le \frac{{LE^{\beta } }}{{\Gamma \left( {\beta + 1} \right)}}\,\,\mathop {\max }\limits_{{\nu \in \left[ {t_{0} ,\,t_{0} + E} \right]}} \left\| {\Omega \left( \nu \right)} \right\|, \\ & \le \frac{{LE^{\beta } M}}{{\Gamma \left( {\beta + 1} \right)}}. \\ \end{aligned} $$
(10)

If \(E \le \left( {\frac{{\Gamma \left( {\beta + 1} \right)R}}{LM}} \right)^{1/\beta } ,\) hence it ensues from (10) that \( \mathop {\max }\limits_{{\nu \in \left[ {t_{0} ,\,t_{0} + E} \right]}} \,\left\| {\chi \left( {\Omega \left( t \right) - \mu \left( {t_{0} } \right)} \right)} \right\| \le R \), this indicates \(\chi \left( {\Omega \left( t \right)} \right) \in U,\) at all \(\Omega \left( t \right) \in U.\)

According to the Banach contraction rule, \(\chi\) possesses only a fixed point in \(U\) if \(E < \min \left\{ {\left( {\frac{{\Gamma \left( {\beta + 1} \right)R}}{LM}} \right)^{1/\beta } ,\left( {\frac{{\Gamma \left( {\beta + 1} \right)}}{2L}} \right)^{1/\beta } } \right\}\). The subsequent theorem can be drawn from the study stated above.

Theorem 1

If \(E < \min \left\{ {\left( {\frac{{\Gamma \left( {\beta + 1} \right)R}}{LM}} \right)^{1/\beta } ,\left( {\frac{{\Gamma \left( {\beta + 1} \right)}}{2L}} \right)^{1/\beta } } \right\}\), then the initial value problem (5) possesses a unique solution.

4 Stability Analysis and Hopf Bifurcation

The equilibria of scheme (4) are the points of intersections at which \(D^{\beta } \,x_{1} = 0\) and \(D^{\beta } \,x_{2} = 0\). Thus, scheme (4) has three equilibrium points namely, trivial equilibrium point \(E_{0} = \left( {0,\,0} \right)\), axial equilibrium point \(E_{1} = \left( {x_{1} ,\,0} \right)\) where \(x_{1} = K_{0}\) and interior equilibrium point \(E^{*} = \left( {x_{1}^{*} ,\,\,x_{2}^{*} } \right)\), where it is the positive solution of

$$ \begin{gathered} r_{0} x_{1} \left( {\frac{1}{{1 + Kx_{2} }} - \frac{{x_{1} }}{{K_{0} }}} \right) - \frac{{K_{1} \,x_{1} \,x_{2} }}{{1 + b\,x_{1} }} = 0, \hfill \\ \frac{{K_{1} \,x_{1} \,x_{2} \left( {t - \tau } \right)}}{{1 + b\,x_{1} }} - x_{2} \, - K_{f} x_{2}^{2} = 0. \hfill \\ \end{gathered} $$

It is important to note that the expression for \(x_{1}^{*}\) and \(x_{2}^{*}\) are therefore too complex to compute analytically, so we clearly derived these points numerically for the parameter values we were considering.

The scheme (4) must be linearized around the relevant equilibrium point before applying Lemma 1 to verify the stability of possible equilibria. The variational matrix [47] for the scheme (4) is provided by

$$ J = \left( {\begin{array}{l@{\qquad}l}{\frac{{r_{0} }}{{1 + Kx_{2} }} - \frac{{2r_{0} x_{1} }}{{K_{0} }} -\frac{{K_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }}} \hfill &{ - \frac{{r_{0} Kx_{1} }}{{\left( {1 + Kx_{2} } \right)^{2} }} -\frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{ - \lambda \tau } } \hfill \\{\frac{{K_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }}} \hfill & {\frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{ - \lambda \tau } - 1 -2K_{f} x_{2} } \hfill \\ \end{array} } \right),$$
(11)

At \(E_{0} ,\) the variational matrix is given by \(J\left( {E_{0} } \right) = \left( {\begin{array}{l@{\qquad}l} {r_{0} } & 0 \\ 0 & { - 1} \\ \end{array} } \right)\).

The characteristic equation of above matrix is \(\left( {\lambda^{\beta } - r_{0} } \right)\left( {\lambda^{\beta } + 1} \right) = 0\) and this possess a positive root \(\lambda^{\beta } = r_{0}\) for \(\beta \in \left( {0,1} \right]\). Hence the trivial equilibrium is unstable i.e., a saddle point.

Theorem 2

Suppose in Lemma 1, condition (i) holds for system (4) then the auxiliary equilibrium point \(E_{1} = \left( {x_{1} ,\,0} \right)\) is asymptotically stable for \(\tau = 0\) if \(b\left( {1 + r_{0} } \right) > K_{1}\) &\(\left( {1 + bK_{0} } \right) > K_{0} K_{1}\), then the auxiliary equilibrium point is asymptotically stable for \(\tau \in \left[ {0,\tau^{*} } \right)\) and system (4) undergoes a Hopf bifurcation at the auxiliary equilibrium while \(\tau = \tau^{*}\). Then the following transversality condition holds \({\text{Re}} \left. {\left[ {\frac{d\lambda }{{d\tau }}} \right]} \right|_{{\left( {\phi = \phi_{0} ,\,\tau = \tau^{*} } \right)}} \ne 0\) (condition (iii) of Lemma 1).

Proof

At \(E_{1}\), the variational matrix can be obtained.

$$ J\left( {E_{1} } \right) = \left( {\begin{array}{*{20}l} {r_{0} - \frac{{2r_{0} x_{1} }}{{K_{0} }}} \hfill & { - r_{0} Kx_{1} - \frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{{ - \lambda \tau }} } \hfill \\ 0 \hfill & {\frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{{ - \lambda \tau }} - 1} \hfill \\ \end{array} } \right) $$
(12)

The latent equation is \(\lambda^{2\beta } + T\lambda^{\beta } + D = 0\),

where \(T = - r_{0} + \frac{{2r_{0} x_{1} }}{{K_{0} }} - \frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{ - \lambda \tau } + 1\,,\,\,D = \frac{{r_{0} K_{1} x_{1} \left( {K_{0} - 2x_{1} } \right)}}{{K_{0} \left( {1 + bx_{1} } \right)}}e^{ - \lambda \tau } + \frac{{2r_{0} x_{1} }}{{K_{0} }} - r_{0}\).

$$ \begin{gathered} \lambda^{2\beta } + \left( { - r_{0} + \frac{{2r_{0} x_{1} }}{{K_{0} }} - \frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{ - \lambda \tau } + 1} \right)\lambda^{\beta } + \frac{{r_{0} K_{1} x_{1} \left( {K_{0} - 2x_{1} } \right)}}{{K_{0} \left( {1 + bx_{1} } \right)}}e^{ - \lambda \tau } + \frac{{2r_{0} x_{1} }}{{K_{0} }} - r_{0} = 0, \hfill \\ \lambda^{2\beta } + C_{1} \lambda^{\beta } + C_{2} - e^{ - \lambda \tau } \left( {C_{3} \lambda^{\beta } + C_{4} } \right) = 0 \hfill \\ \end{gathered} $$
(13)

where \(C_{1} = 1 - r_{0} + \frac{{2r_{0} x_{1} }}{{K_{0} }}\), \(C_{2} = \frac{{2r_{0} x_{1} }}{{K_{0} }} - r_{0}\), \(C_{3} = \frac{{K_{1} x_{1} }}{{1 + bx_{1} }}\), \(C_{4} = - \frac{{r_{0} K_{1} x_{1} \left( {K_{0} - 2x_{1} } \right)}}{{K_{0} \left( {1 + bx_{1} } \right)}}\).

When \(\tau = 0\),

$$ \lambda^{2\beta } + \left( {C_{1} - C_{3} } \right)\lambda^{\beta } + C_{2} - C_{4} = 0. $$
(14)

Equation (14) makes it clear that for \(C_{1} - C_{3} > 0\) i.e., \(b\left( {1 + r_{0} } \right) > K_{1}\) and \(C_{2} - C_{4} > 0\) i.e., \(\left( {1 + bK_{0} } \right) > K_{0} K_{1}\). Hence the auxiliary equilibrium point \(E_{1}\) is asymptotically stable for \(b\left( {1 + r_{0} } \right) > K_{1}\) and \(\left( {1 + bK_{0} } \right) > K_{0} K_{1}\) with \(\tau = 0\) satisfy \(\left| {\arg \left( {\lambda_{i} } \right)} \right| > \frac{\beta \pi }{2}\).

We assume that the solution \(\lambda = i\varphi\) to Eq. (13) must be true if \(\tau > 0\),

$$ \begin{gathered} \left( {i\varphi } \right)^{2\beta } + C_{1} \left( {i\varphi } \right)^{\beta } + C_{2} - e^{ - i\varphi \tau } \left( {C_{3} \left( {i\varphi } \right)^{\beta } + C_{4} } \right) = 0, \hfill \\ - \varphi^{2\beta } + iC_{1} \varphi^{\beta } + C_{2} - \left( {\cos \varphi \tau - i\sin \varphi \tau } \right)\left( {iC_{3} \varphi^{\beta } + C_{4} } \right) = 0. \hfill \\ \end{gathered} $$

We can obtain the following equations on separating the real and imaginary parts,

$$ C_{3} \varphi^{\beta } \sin \varphi \tau + C_{4} \cos \varphi \tau = C_{2} - \varphi^{2\beta } , $$
(15)
$$ - C_{3} \varphi^{\beta } \cos \varphi \tau + C_{4} \sin \varphi \tau = C_{1} \varphi^{\beta } . $$
(16)

Solving (15) and (16), we get

$$ \varphi^{4\beta } + \left( {C_{1}^{2} - 2C_{2} - C_{3}^{2} } \right)\varphi^{2\beta } + \left( {C_{2}^{2} - C_{4}^{2} } \right) = 0. $$
(17)

If \(\left( {C_{1}^{2} - 2C_{2} - C_{3}^{2} } \right) > 0\) and \(\left( {C_{2} - C_{4} } \right) > 0\) then there is no positive real \(\varphi\) satisfying (17). But, if \(C_{2} - C_{4} < 0\) i.e.,\(\left( {1 + bK_{0} } \right) < K_{0} K_{1}\) then (17) has one positive root by \(\varphi_{0}\), and the characteristic Eq. (13) with couple of roots are completely imaginary \(\pm \,i\varphi_{0}\). Assuming \(\lambda \left( \tau \right) = \vartheta \left( \tau \right) + i\phi \left( \tau \right)\) is the eigen value of (18) such that \(\vartheta \left( {\tau^{*} } \right) = 0\) and \(\,\xi \left( {\tau^{*} } \right) = \phi_{0}\). From (15) and (16), we have.

\(\tau^{*} = \frac{1}{{\phi_{0} }}\arccos \left[ {\frac{{C_{2} C_{4} - \left( {C_{4} + C_{1} C_{3} } \right)\phi_{0}^{2\beta } }}{{C_{4}^{2} + C_{3}^{2} \phi_{0}^{2\beta } }}} \right] + \frac{2j\beta \pi }{{\phi_{0}^{\beta } }},\) and from (17)

$$ \varphi_{0}^{2\beta } = \frac{1}{2}\left( {C_{3}^{2} + 2C_{2} - C_{1}^{2} } \right) + \frac{1}{2}\sqrt {\left( {C_{3}^{2} + 2C_{2} - C_{1}^{2} } \right) - 4\left( {C_{2}^{2} - C_{4}^{2} } \right)} < 0. $$

To complete the stability criterion of the delayed system we have to verify the following transversality condition. Let the characteristic Eq. (13) can be written as

$$ \gamma_{1} \left( \lambda \right) + \gamma_{2} \left( \lambda \right)e^{ - \lambda \tau } = 0. $$
(18)

Differentiating (18) with respect to \(\tau\),we get

$$ \begin{gathered} \left[ {\gamma_{1}^{\prime } \left( \lambda \right) + \gamma_{2}^{\prime } \left( \lambda \right)e^{ - \lambda \tau } - \tau \gamma_{2} \left( \lambda \right)e^{ - \lambda \tau } } \right]\frac{d\lambda }{{d\tau }} =\lambda \gamma_{2} \left( \lambda \right)e^{ - \lambda \tau } ,\hfill \\ {\text{from above we have}}\frac{d\lambda }{{d\tau }} =\frac{P\left( \lambda \right)}{{Q\left( \lambda \right)}} =\frac{{P\left( \lambda \right)\overline{Q\left( \lambda \right)}}}{{\left| {Q\left( \lambda \right)} \right|^{2} }}, \hfill \\\end{gathered} $$
(19)

where \(P\left( \lambda \right) = \lambda \gamma_{2}\left( \lambda \right)e^{ - \lambda \tau }\), \(Q\left( \lambda \right) = \gamma_{1}^{\prime } \left( \lambda \right) +\gamma_{2}^{\prime } \left( \lambda \right)e^{ - \lambda \tau } -\tau \gamma_{2} \left( \lambda \right)e^{ - \lambda \tau }\), \(P\left({i\phi_{0} } \right) = P_{1} +iP_{2}\) and \(Q\left({i\phi_{0} } \right) = Q_{1} +iQ_{2}\).

Taking the real part both sides from (19)

$$ {\text{Re}} \left. {\left[ {\frac{d\lambda }{{d\tau }}} \right]} \right|_{{\left( {\phi = \phi_{0} ,\,\tau = \tau^{*} } \right)}} = \frac{{P_{{_{1} }} Q_{1} + P_{2} Q_{2} }}{{Q_{1}^{2} + Q_{2}^{2} }}, $$
(20)

where \(P_{1} = \phi_{0} \left( {\gamma_{2}^{{\text{Im}}} \cos \phi_{0} \tau - \gamma_{2}^{{\text{Re}}} \sin \phi_{0} \tau } \right)\), \(P_{2} = \phi_{0} \left( { - \gamma_{2}^{{\text{Re}}} \cos \phi_{0} \tau - \gamma_{2}^{{\text{Im}}} \sin \phi_{0} \tau } \right)\), \(Q_{1} = \gamma_{1}^{{\prime {\text{Re}} }} - \gamma_{2}^{{\prime {\text{Re}} }} \cos \phi_{0} \tau + \tau \gamma_{2}^{{\text{Re}}} \cos \phi_{0} \tau + \tau \gamma_{2}^{{\text{Im}}} \sin \phi_{0} \tau\), \(Q_{2} = \gamma_{1}^{{\prime {\text{Im}} }} + \gamma_{2}^{{\prime {\text{Re}} }} \sin \phi_{0} \tau - \tau \gamma_{2}^{{\text{Re}}} \sin \phi_{0} \tau + \tau \gamma_{2}^{{\text{Im}}} \cos \phi_{0} \tau\).

From (20), if \(\frac{{P_{{_{1} }} Q_{1} + P_{2} Q_{2} }}{{Q_{1}^{2} + Q_{2}^{2} }} \ne 0\) then transversality condition holds. Hence the Lemma 1 is proved for auxiliary equilibrium point.

Theorem 3

Suppose in Lemma 1, condition (i) holds for system (4) then the coexistence equilibrium point \(E^{*} = \left( {x_{1}^{*} ,\,\,x_{2}^{*} } \right)\) is asymptotically stable for \(\tau = 0\) if \(r_{0} \left( {1 + bx_{1} } \right)^{2} > bK_{0} K_{1} x_{2}\), then the coexistence equilibrium point is asymptotically stable for \(\tau \in \left[ {0,\tau^{*} } \right)\) and system (4) undergoes a Hopf bifurcation at the coexistence equilibrium while \(\tau = \tau^{*}\). Then the following transversality condition holds \({\text{Re}} \left. {\left[ {\frac{d\lambda }{{d\tau }}} \right]} \right|_{{\left( {\xi = \xi_{0} ,\,\tau = \tau^{*} } \right)}} \ne 0\) (condition (iii) of Lemma 1).

Proof

The variational matrix of the scheme (4) at a positive equilibrium point \(E^{*}\) is given by.

$$ J\left( {E^{*} } \right) = \left( {\begin{array}{l@{\qquad}l} { - \frac{{r_{0} x_{1} }}{{K_{0} }} + \frac{{K_{1} bx_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }}} & { - \frac{{Kr_{0} x_{1} }}{{\left( {1 + Kx_{2} } \right)^{2} }} - \frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{ - \lambda \tau } } \\ {\frac{{K_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }}} & {\frac{{K_{1} x_{1} }}{{1 + bx_{1} }}\left( {e^{ - \lambda \tau } - 1} \right) - K_{f} x_{2} } \\ \end{array} } \right), $$

The characteristic equation is given by

$$ \begin{gathered} \lambda^{2\beta } - \left[ { - \frac{{r_{0} x_{1} }}{{K_{0} }} + \frac{{K_{1} bx_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }} + \frac{{K_{1} x_{1} }}{{1 + bx_{1} }}e^{ - \lambda \tau } - \frac{{K_{1} x_{1} }}{{1 + bx_{1} }} - K_{f} x_{2} } \right]\lambda^{\beta } \hfill \\ \,\,\,\,\,\,\, + \left[ \begin{gathered} \left( { - \frac{{r_{0} K_{1} x_{1}^{2} }}{{K_{0} \left( {1 + bx_{1} } \right)}} + \frac{{K_{1}^{2} x_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }}} \right)e^{ - \lambda \tau } + \frac{{r_{0} K_{1} x_{1}^{2} }}{{K_{0} \left( {1 + bx_{1} } \right)}} + \frac{{r_{0} K_{f} }}{{K_{0} }}x_{1} x_{2} - \frac{{bK_{1}^{2} }}{{\left( {1 + bx_{1} } \right)^{3} }}x_{1}^{2} x_{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{bK_{f} K_{1} }}{{\left( {1 + bx_{1} } \right)^{2} }}x_{1} x_{2}^{2} + \frac{{KK_{1} r_{0} }}{{\left( {1 + bx_{1} } \right)^{2} \left( {1 + Kx_{2} } \right)^{2} }}x_{1} x_{2} \hfill \\ \end{gathered} \right] = 0, \hfill \\ \lambda^{2\beta } + C_{1} \lambda^{\beta } + C_{2} + e^{ - \lambda \tau } \left( {C_{3} \lambda^{\beta } + C_{4} } \right) = 0, \hfill \\ \end{gathered} $$
(21)

where \(C_{1} = \left[ {\frac{{r_{0} x_{1} }}{{K_{0} }} - \frac{{K_{1} bx_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }} + \frac{{K_{1} x_{1} }}{{1 + bx_{1} }} + K_{f} x_{2} } \right],\) \(C_{2} = \frac{{r_{0} K_{1} x_{1}^{2} }}{{K_{0} \left( {1 + bx_{1} } \right)}} + \frac{{r_{0} K_{f} }}{{K_{0} }}x_{1} x_{2} - \frac{{bK_{f} K_{1} }}{{\left( {1 + bx_{1} } \right)^{2} }}x_{1} x_{2}^{2} + \frac{{KK_{1} r_{0} }}{{\left( {1 + bx_{1} } \right)^{2} \left( {1 + Kx_{2} } \right)^{2} }}x_{1} x_{2} ,\) \(C_{3} = - \frac{{K_{1} x_{1} }}{{1 + bx_{1} }}\,\,,\,\,C_{4} = \frac{{K_{1}^{2} x_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }} - \frac{{r_{0} K_{1} x_{1}^{2} }}{{K_{0} \left( {1 + bx_{1} } \right)}}\).

when \(\tau = 0\),

$$ \lambda^{2\beta } + \left( {C_{1} + C_{3} } \right)\lambda^{\beta } + \left( {C_{2} + C_{4} } \right) = 0. $$
(22)

where \(C_{1} + C_{3} = \frac{{r_{0} x_{1} }}{{K_{0} }} - \frac{{K_{1} bx_{1} x_{2} }}{{\left( {1 + bx_{1} } \right)^{2} }} + K_{f} x_{2}\), \(C_{2} + C_{4} = \frac{{r_{0} K_{f} }}{{K_{0} }}x_{1} x_{2} - \frac{{bK_{f} K_{1} }}{{\left( {1 + bx_{1} } \right)^{2} }}x_{1} x_{2}^{2} + \frac{{KK_{1} r_{0} }}{{\left( {1 + bx_{1} } \right)^{2} \left( {1 + Kx_{2} } \right)^{2} }}x_{1} x_{2} + \frac{{K_{1}^{2} }}{{\left( {1 + bx_{1} } \right)^{2} }}x_{1} x_{2}\).

\(\left( {C_{1} + C_{3} } \right) > 0\,\,{\text{and}}\,\left( {C_{2} + C_{4} } \right) > 0\,\) when \(r_{0} \left( {1 + bx_{1} } \right)^{2} > bK_{0} K_{1} x_{2}\), then there exists couple of roots which are real and nonpositive. Thus, for \(\tau = 0\) the equilibrium \(E^{*}\) is asymptotically stable. When \(\tau > 0\), we assume that the solution of Eq. (21) \(\lambda = i\xi\) must satisfy.

\(\begin{gathered} - \xi^{2\beta } + C_{2} + C_{1} i\xi^{\beta } + \left( {\cos \xi \tau - i\sin \xi \tau } \right)\left( {C_{3} i\xi^{\beta } + C_{4} } \right) = 0 \hfill \\ \xi^{2\beta } - C_{2} = C_{3} \xi^{\beta } \sin \xi \tau + C_{4} \cos \xi \tau + C_{1} i\xi^{\beta } + i\left( {C_{3} \xi^{\beta } \cos \xi \tau - C_{4} \sin \xi \tau } \right). \hfill \\ \end{gathered}\)

On separating real and imaginary components, we get the following:

$$ C_{3} \xi^{\beta } \sin \xi \tau + C_{4} \cos \xi \tau = \xi^{2\beta } - C_{2} , $$
(23)
$$ C_{3} \xi^{\beta } \cos \xi \tau - C_{4} \sin \xi \tau = - C_{1} \xi^{\beta } . $$
(24)

We can obtain the following equation on squaring and adding of Eqs. (23) and (24)

$$ \xi^{4\beta } + \left( {C_{1}^{2} - 2C_{2} - C_{3}^{2} } \right)\xi^{2\beta } + \left( {C_{2}^{2} - C_{4}^{2} } \right) = 0. $$
(25)

We can immediately establish that \(\left( {C_{1}^{2} - 2C_{2} - C_{3}^{2} } \right) > 0\) and if \(\left( {C_{2} - C_{4} } \right) > 0\) then there is no positive real \(\xi\) satisfying (25). As a result, (21)’s roots of are non-positive. On the other hand, if \(\left( {C_{2} - C_{4} } \right) < 0\) therefore (25) only has the one positive root denoted with \(\xi_{0}\), and the latent Eq. (21) has two completely imaginary roots \(\pm \,i\xi_{0}\). Assuming \(\lambda \left( \tau \right) = \vartheta \left( \tau \right) + i\xi \left( \tau \right)\) is the eigenvalue of (21) such that \(\vartheta \left( {\tau^{*} } \right) = 0\,\,{\text{and}}\,\,\,\xi \left( {\tau^{*} } \right) = \xi_{0}\). From (23) and (24), we have \(\tau^{*} = \frac{1}{{\xi_{0} }}\arccos \left[ {\frac{{\left( {C_{4} + C_{1} C_{3} } \right)\xi_{0}^{2\beta } - C_{2} C_{4} }}{{C_{4}^{2} + C_{3}^{2} \xi_{0}^{2\beta } }}} \right] + \frac{2j\beta \pi }{{\xi_{0}^{\beta } }},\) and from (25)

$$ \xi_{0}^{2\beta } = \frac{1}{2}\left( {C_{3}^{2} + 2C_{2} - C_{1}^{2} } \right) + \frac{1}{2}\sqrt {\left( {C_{3}^{2} + 2C_{2} - C_{1}^{2} } \right)^{2} - 4\left( {C_{2}^{2} - C_{4}^{2} } \right)} < 0. $$
(26)

To complete the stability criterion of the delayed system we have to verify the following transversality condition. Let the characteristic Eq. (21) can be written as \(\gamma_{1} \left( \lambda \right) + \gamma_{2} \left( \lambda \right)e^{ - \lambda \tau } = 0\).

Following the same procedure as in (Theorem 2), we obtain

$$ {\text{Re}} \left. {\left[ {\frac{d\lambda }{{d\tau }}} \right]} \right|_{{\left( {\xi = \xi_{0} ,\,\tau = \tau^{*} } \right)}} = \frac{{P_{{_{1} }} Q_{1} + P_{2} Q_{2} }}{{Q_{1}^{2} + Q_{2}^{2} }}, $$
(27)

where \(P_{1} = \xi_{0} \left( {\gamma_{2}^{{\text{Re}}} \sin \xi_{0} \tau - \gamma_{2}^{{\text{Im}}} \cos \xi_{0} \tau } \right)\), \(P_{2} = \xi_{0} \left( {\gamma_{2}^{{\text{Re}}} \cos \xi_{0} \tau + \gamma_{2}^{{\text{Im}}} \sin \xi_{0} \tau } \right)\), \(Q_{1} = \gamma_{1}^{{\prime {\text{Re}} }} + \gamma_{2}^{{\prime {\text{Re}} }} \cos \xi_{0} \tau - \tau \gamma_{2}^{{\text{Re}}} \cos \xi_{0} \tau - \tau \gamma_{2}^{{\text{Im}}} \sin \xi_{0} \tau\), \(Q_{2} = \gamma_{1}^{{\prime {\text{Im}} }} - \gamma_{2}^{{\prime {\text{Re}} }} \sin \xi_{0} \tau + \tau \gamma_{2}^{{\text{Re}}} \sin \xi_{0} \tau - \tau \gamma_{2}^{{\text{Im}}} \cos \xi_{0} \tau\). From (27), if \(\frac{{P_{{_{1} }} Q_{1} + P_{2} Q_{2} }}{{Q_{1}^{2} + Q_{2}^{2} }} \ne 0\) then the transversality condition holds.

Hence the Lemma 1 is proved for the coexistence equilibrium point.

5 Global Stability Analysis

Here, we expand on the investigation to examine the criteria for global stability [37, 38] for the non-integer order delay differential scheme. In order to investigate the global stability of the equilibrium points in scheme (4), we linearize the system into form

$$ \begin{gathered} D^{\beta } \,x_{1} \left( t \right) = m_{1} x_{1} \left( t \right) + m_{2} x_{2} \left( t \right) + m_{3} x_{2} \left( {t - \tau } \right), \hfill \\ D^{\beta } \,x_{2} \left( t \right) = n_{1} x_{1} \left( t \right) + n_{2} x_{2} \left( t \right) + n_{3} x_{2} \left( {t - \tau } \right), \hfill \\ \end{gathered} $$
(28)

where,

\(m_{1} = \frac{{r_{0} }}{{1 + K\,x_{2}^{*} }} - \frac{{2r_{0} x_{1}^{*} }}{{K_{0} }} - \frac{{K_{1} x_{2}^{*} }}{{1 + bx_{1}^{*} }} + \frac{{K_{1} b\,x_{1}^{*} x_{2}^{*} }}{{\left( {1 + bx_{1}^{*} } \right)^{2} }},\,\,m_{2} = - \frac{{r_{0} K\,x_{1}^{*} }}{{\left( {1 + K\,x_{2}^{*} } \right)^{2} }},\,\,m_{3} = - \frac{{K_{1} x_{1}^{*} }}{{1 + bx_{1}^{*} }}\), \(n_{1} = \frac{{K_{1} x_{2}^{*} }}{{1 + bx_{1}^{*} }} - \frac{{K_{1} b\,x_{1}^{*} x_{2}^{*} }}{{\left( {1 + bx_{1}^{*} } \right)^{2} }},\,n_{2} = - \left( {1 + 2K_{f} x_{2}^{*} } \right),\,n_{3} = \frac{{K_{1} x_{1}^{*} }}{{1 + bx_{1}^{*} }}\).

If the equilibrium point of the linear non-integer differential equation is not zero, we can move it to the origin. Put \(\overline{x}_{1} \left( t \right) = x_{1} \left( t \right) - x_{1}^{*} ,\,\,\overline{x}_{2} \left( t \right) = x_{2} \left( t \right) - x_{2}^{*}\), then the Eq. (28) becomes

$$ \begin{gathered} D^{\beta } \,\overline{x}_{1} \left( t \right) = m_{1} \overline{x}_{1} \left( t \right) + m_{2} \overline{x}_{2} \left( t \right) + m_{3} \overline{x}_{2} \left( {t - \tau } \right), \hfill \\ D^{\beta } \,\overline{x}_{2} \left( t \right) = n_{1} \overline{x}_{1} \left( t \right) + n_{2} \overline{x}_{2} \left( t \right) + n_{3} \overline{x}_{2} \left( {t - \tau } \right). \hfill \\ \end{gathered} $$
(29)

We apply the Laplace transform [39] on both sides of (29) to examine the stability of model (4). Finally, we have

$$ \begin{gathered} s^{\beta } \,X_{1} \left( s \right) - s^{\beta - 1} \varphi_{1} \left( 0 \right) = m_{1} X_{1} \left( s \right) + m_{2} X_{2} \left( s \right) + m_{3} e^{ - s\tau } \left( {X_{2} \left( s \right) + \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \varphi_{1} \left( t \right)\,dt} \right), \hfill \\ s^{\beta } \,X_{2} \left( s \right) - s^{\beta - 1} \varphi_{2} \left( 0 \right) = n_{1} X_{1} \left( s \right) + n_{2} X_{2} \left( s \right) + n_{3} e^{ - s\tau } \left( {X_{2} \left( s \right) + \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \varphi_{2} \left( t \right)\,dt} \right), \hfill \\ \left( {s^{\beta } \, - m_{1} } \right)X_{1} \left( s \right) - \left( {m_{2} + m_{3} e^{ - s\tau } } \right)X_{2} \left( s \right) = s^{\beta - 1} \varphi_{1} \left( 0 \right) + m_{3} e^{ - s\tau } \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \varphi_{1} \left( t \right)\,dt, \hfill \\ - n_{1} X_{1} \left( s \right) + \left( {s^{\beta } - n_{2} - n_{3} e^{ - s\tau } } \right)\,X_{2} \left( s \right) = s^{\beta - 1} \varphi_{2} \left( 0 \right) + n_{3} e^{ - s\tau } \int\limits_{ - \tau }^{0} {e^{ - s\tau } } \varphi_{2} \left( t \right)\,dt. \hfill \\ \end{gathered} $$
(30)

Here, it should be stated that the initial values \(\overline{x}_{1} \left( t \right) = \varphi_{1} \left( t \right)\) and \(\overline{x}_{2} \left( t \right) = \varphi_{2} \left( t \right)\) with \(t \in \left[ { - \tau ,\,0} \right].\) Also \(X_{1} \left( s \right)\) and \(X_{2} \left( s \right)\) are Laplace transform of \(\overline{x}_{1} \left( t \right)\) and \(\overline{x}_{2} \left( t \right)\) with \(X_{1} \left( s \right) = L\left( {\overline{x}_{1} \left( t \right)} \right)\) and \(X_{2} \left( s \right) = L\left( {\overline{x}_{2} \left( t \right)} \right)\). The system (30) can be rewritten as follows.

$$ \Delta \left( s \right)\left( {\begin{array}{*{20}c} {X_{1} \left( s \right)} \\ {X_{2} \left( s \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {p_{1} \left( s \right)} \\ {p_{2} \left( s \right)} \\ \end{array} } \right). $$
(31)

In which.

\(\Delta \left( s \right) = \left( {\begin{array}{*{20}c} {s^{\beta } \, - m_{1} } & { - m_{2} - m_{3} e^{ - s\tau } } \\ { - n_{1} } & {s^{\beta } - n_{2} - n_{3} e^{ - s\tau } } \\ \end{array} } \right)\) and.

\(p_{1} \left( s \right) = s^{\beta - 1} \varphi_{1} \left( 0 \right) + m_{3} e^{ - s\tau } \displaystyle\int\limits_{ - \tau }^{0} {e^{ - s\tau } } \varphi_{1} \left( t \right)\,dt\),

\(p_{2} \left( s \right) = s^{\beta - 1} \varphi_{2} \left( 0 \right) + n_{3} e^{ - s\tau } \displaystyle\int\limits_{ - \tau }^{0} {e^{ - s\tau } } \varphi_{2} \left( t \right)\,dt\).

\(\Delta \left( s \right)\) gives as the model (4)’s latent matrix with its polynomial \(\left| {\Delta \left( s \right)} \right|\). The distribution of the characteristic roots of the latent polynomial consequently establishes the stability of scheme (4). In which mean that if all of the roots of the latent equation are negative, the previously mentioned non-integer order prey predator’s equilibrium is Lyapunov globally asymptotically stable if the equilibrium exists [37]. The result of multiplying two sides of (31) with \(s\) is

$$ \Delta \left( s \right)\left( {\begin{array}{*{20}c} {s\,X_{1} \left( s \right)} \\ {s\,X_{2} \left( s \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {s\,p_{1} \left( s \right)} \\ {s\,p_{2} \left( s \right)} \\ \end{array} } \right). $$
(32)

Since every root of the transcendental equation \(\left| {\Delta \left( s \right)} \right| = 0\) must be on the open left complex plane, i.e., \({\text{Re}} \left( s \right) < 0\), then we consider (28) in \({\text{Re}} \left( s \right) \ge 0.\) Within this limited area, system (32) possess only solution \(\left( {s\,X_{1} \left( s \right),\,\,s\,X_{2} \left( s \right)} \right)\), so that

$$ \mathop {\lim }\limits_{{s \to 0,\,{\text{Re}} \left( s \right) \ge 0}} s\,X_{i} \left( s \right) = 0,\,\,i = 1,\,2. $$

Considering the Laplace transform’s final-value theorem [39]and the assumption in which every root of the characteristic equation \(\left| {\Delta \left( s \right)} \right| = 0\), we get.

\(\mathop {\lim }\limits_{t \to + \infty } \overline{x}_{1} \left( t \right) \equiv \mathop {\lim }\limits_{{s \to 0,\,{\text{Re}} \left( s \right) \ge 0}} s\,X_{1} \left( s \right) = 0,\,\) and

$$ \mathop {\lim }\limits_{t \to + \infty } \overline{x}_{2} \left( t \right) \equiv \mathop {\lim }\limits_{{s \to 0,\,{\text{Re}} \left( s \right) \ge 0}} s\,X_{2} \left( s \right) = 0. $$

This indicates that the non-integer order prey-predator model’s zero solution is Lyapunov globally asymptotically stable. As it turns out, we come to the following conclusion.

Theorem 4

If all the roots of the latent equation \(\left| {\Delta \left( s \right)} \right| = 0\) possess non positive real parts, then the positive equilibrium point \(\left( {x_{1}^{*} ,\,\,x_{2}^{*} } \right)\) of the scheme (4) is Lyapunov globally asymptotically stable.

6 Numerical Simulations

We provide some numerical simulation outcomes in this part to substantiate our analytical findings. Scheme (4) was solved using the two-step Adams–Bashforth–Moulton algorithm for the system of two FODE in order to achieve this. We concentrate on the effects of the parameter’s degree of dread \(K\), time delay \(\tau\), and fractional order \(\beta\) of scheme (4).

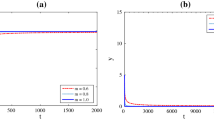
Employing the parameter values listed in the figure captions, the solution has been approximately estimated in each numerical run. According to the results of the analysis, it can be seen that when \(\tau < \tau^{*} = 0.315\), all paths of the non-integer order scheme (4) lead to the coexistence equilibrium point \(E^{*} \left( {0.6835,\,0.8375} \right)\), which is depicted in Fig. 1a; however, when \(\tau\) is raised to a level that exceed \(\tau^{*}\), the equilibrium becomes unstable and a stable limit cycle develops around the equilibrium point, as is depicted in Fig. 1b and c.

Fig. 1
figure 1

Behaviour of the scheme (4) for various values of delay parameter \(\tau = 0.3,\,0.45\,{\text{and}}\,0.8\) when \(r_{0} = 1.75,\,K = 0.113,\,\,K_{0} = 4.42\,,\,K_{1} = 1.64,b = 0.05,\) \(\alpha = 0.98,\,\,K_{f} = 0.100242,\) as shown in (a–c)

Full size image

Assuming that \(K = 0.08\) at this point, Fig. 2 indicates the solution to scheme (4) for various amounts of \(\beta\). We found that scheme (4) is not stable for the integer order scheme \(\beta = 1\) and \(\beta = 0.98\), whereas our suggested system is stable for \(\beta = 0.95\), coexistence equilibrium point \(E^{*} \left( {0.7627,\,0.8463} \right)\). The model exhibits an unstable behaviour once the influence of fear is extremely low for integer-order systems, however stability alters and turn into stable for fractional order-derivative systems. As a result, it is possible to draw the conclusion that the non-integer order derivative can stabilize the model.

Fig. 2
figure 2

Phase portrait of thescheme (4) using various amounts of \(\beta\) when \(r_{0} = 1.75,\,K_{0} = 4.42,\,K_{1} = 1.64,\)\(b = 0.05,\,\,\alpha = 0.98,\,K_{f} = 0.242,\,\,\tau = 0.6\)

Full size image

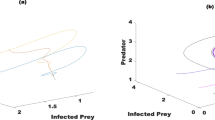
We’ve produced the diagram in Fig. 3 to analyse how fractional order derivative \(\beta\) affects each population because \(\beta\) is substantial to the changing aspects of the system. For various amounts of \(\beta\), this displays the phase plane of the prey predator as follows. If \(\beta = 0.91\) all trajectories get attracted to a stable equilibrium point, and if \(\beta = 0.98\), a stable limit cycle develops and is drawn to by all trajectories. The model’s oscillation behaviour has been observed to be dampened by the fractional derivative (see Figs. 3 and 4).

Fig. 3
figure 3

Phase portrait of fractional order scheme (4) for various amounts of fractional order effect \(\beta = 0.91,\,\,0.98\,,\,\,\tau = 0.8\) and remaining parameter values are same as Fig. 1

Full size image
Fig. 4
figure 4

Behaviors of the scheme (4) with different initial conditions and \(\beta = 0.8\,,\,\,\tau = 0.8 > \tau^{*}\), remaining parameter values are same as Fig. 1

Full size image

7 Conclusions

The coexistence of biological processes using fractional-order differential equations has been studied using numerous kinds of mathematical and analytical techniques. The nonlocal characteristic of a non-integer order system is dependent on the current state as well as all previous states. As a result, the order of differentiation \(\beta\) must be precisely converted from an integer-order model to a fractional order model because even a minor change in \(\beta\) can have a significant impact on the outcome. Certain processes that can’t be modelled by IDEs can be modelled using fractional order differential equations. FDEs are therefore mostly used in biological schemes because they are connected to memory-based schemes.

We developed a FODE-based delayed Bazykin’s scheme with the addition of the fear effect in order to analyse the effects of prey and predator population levels through time and precisely predict the increasing rates of each species at the moment in time. Our main goal is to look at how fear, time delay, and non-integer order derivatives affect the changing aspects of the system. Three equilibrium points exist in scheme (4), including the trivial equilibrium point \(E_{0}\),which is at all times a saddle point, the predator-free equilibrium \(E_{1}\), which is locally stable if \(b\left( {1 + r_{0} } \right) > K_{1}\) and \(\left( {1 + bK_{0} } \right) > K_{0} K_{1}\), and the interior equilibrium \(E^{*}\).

Investigations have been made into the requirements for both local and global stability of the interior equilibrium. Additionally, theoretical study reveals that non-integer order and time delay may have an impact on whether a Hopf bifurcation exists. Numerical simulations are used to substantiate all theoretical results in our work. It can be observed that the system exhibits several complex phenomena as the fractional-order derivative \(\beta\) is varied. We found that the integer-order system behaves in an unstable manner when the amount of fear is low, whereas the fractional-order derivative behaves in a stable manner. We can draw the conclusion that anon-integer order derivative can stabilise the system because of the memory effect. The next step in our research is to examine the impact of memory-based population growth on extinction probabilities for population models that include interactions with the Allee effect, as well as the behaviour in the population scheme(s), which will include the impact of predator-dependent functional response. Also, we aimed to study the optimal control of harvesting model in the influence of toxic substances under fractional order frame work in future.