1 Introduction

Diabetes mellitus also known as diabetes is a prominent public health issue. Diabetes continues to grow rapidly. According to the WHO report on diabetes (Organization 2016), around 422 million adults were diabetic in 2014, in contrast to 108 million in 1980. Diabetes mellitus is a problem of transformation of carbohydrate, fat, and protein transfiguration, induced either by reduction of insulin secretion or due to deficiency of response by tissues (Farman et al. 2019; Lombarte et al. 2013). Mainly diabetes is categorized into three categories, i.e., type 1, type 2, and gestational diabetes (Yang et al. 2015). Type 1 diabetes is usually due to poor antibodies of the patients which destroy β-cells in the islets of Langerhans of the pancreas due to which enough insulin is not produced by the pancreas (Yang et al. 2015). Around five to ten percent of total diabetic patients are facing discomfort from type 1 diabetes. Type 2 diabetes occurs when either sufficient insulin is not produced by β-cells or produced insulin is not used properly. Type 2 diabetes is the most common among diabetic patients. The common causes of occurrence being obesity and lack of physical exercise. Gestational diabetes is a temporary case of diabetes in pregnant women which occurs during the pregnancy period due to high blood glucose levels. This type of diabetes is observed in (around 2% to 4%) of the total pregnant women (Yang et al. 2015; Shabestari et al. 2018).

β-cells are the key element in glucose-insulin dynamics. Due to the physiological location of β-cells in the islets of Langerhans in the pancreas, it is not possible to monitor the mass of β-cells clinically (Brenner et al. 2017). To solve this problem, several mathematical models have been introduced by many researchers in the last few years (Ali et al. 2019). A composite mathematical model for the glucagon-glucose relationship of type 1 diabetes was designed by Farman et al. (2019). Bajaj et al. (1987) developed a three-dimensional mathematical model to incorporate β-cells. This model didn't consider the dependence of insulin on β-cells. The non-linear dependence of insulin on β-cells was observed by Topp et al. (2000). The response of genetic predisposition to the glucose-insulin dynamics was observed in Boutayeb et al. (2014). The consequence of growth hormone on glucose was modeled by Ali et al. (2019). A four-dimensional model was developed by Hernandez et al. (2001), to describe glucose, insulin, β-cells, and receptor dynamics. Stamper and Wang (2019) developed a combined multi-scale model to note the insulin secretion characteristics in various glucose protocols with varying degrees of β-cells loss. Mahata et al. (2017) discussed a model for glucose-insulin dynamics in both fuzzy and crisp cases. A three-dimensional model was discussed to observe the glucose-insulin dynamics of diabetic rats and healthy rats (Lombarte et al. 2013, 2018). Effects of leptin on glucose-insulin dynamics for type 1 diabetic patients were studied in Kadota et al. (2018). The impact of nanoparticles on insulin-based therapy was discussed in Jamwal et al. (2019). Ibrahim et al. (2019) developed an improved version of the minimal model to study the glucose-insulin regulatory system for healthy and type 2 diabetic patients. The consequences of physical exercises on insulin resistance, i.e., type 2 diabetes were discussed in Ho et al. (2016). The impact of non-esterified fatty acids, hepatic, and pancreatic lipids were discussed in Sweatman (2020). The study was carried out for a better understanding of the relationship between diet, obesity, and diabetes to lower the incidence of diabetes and its complications (Sweatman 2020). A study was carried out to observe glucose-insulin dynamics in healthy and corpulent mice (Brenner et al. 2017). A non-linear mathematical model was designed to fit the experimental data from pigs (Lopez-Zazueta et al. 2019). Loppini and Chiodo (2019) proposed a model to highlight the uncoupled and coupled behavior of β-cells in the percolated cluster architecture. The same network was applied within human islets along with structural and practical assortment. It tuned the parameters to describe the glucose discerning and adenosine triphosphate outcomes. This work also investigated the effects of practical assortment along with the presence of hubs in three principal dynamics regimes noticed within islets. The chaotic behavior of fractional-order predator–prey model was discussed in Kumar et al. (2020). Kumar et al. (2021a) developed a technique for fractional-order SEIR epidemic model. The nature of the predator–prey model in the presence of fractional derivative was studied by Kumar et al. (2021b).

Han et al. (2012) studied the connection between the atomic insulin-production system at the cell level and macroscopic glucose-insulin system at the body level incorporating β-cells. Camilo et al. (2018) discussed the effect of adiposity and family history of type 2 diabetes on insulin sensitivity and β-cells features. Insulin resistance and β-cells disorder glaring individually across communities and there was very little information available concerning the pathophysiology of type 2 diabetes for racially admixed teenagers (Camilo et al. 2018). Shabestari et al. (2018) developed a non-linear model for the glucose-insulin regulatory system based on the predator–prey model. In this model, numerical results validation with glucose-insulin data was ignored. Baskerville (2019) discussed the hypothesis to construct a non-linear model for better risk prediction. This study provided only the hypothesis but the validation of results using a mathematical model was absent. To verify the hypothesis given by Baskerville (2019), we propose a non-linear three-dimensional mathematical model to validate the glucose-insulin regulatory system. The dependence of plasma insulin and blood glucose on the mass of β-cells are studied by adjusting the value of parameters. The rest of the manuscript is organized as follows: Sect. 2 is associated with the proposed model and boundedness of the system. Section 3 demonstrates the existence and stability of the equilibria. The bifurcation analysis for the system is presented in Sect. 4. Section 5 presents the simulation results and discussion about glucose-insulin regulatory system. Finally, the conclusions are given in the last section.

2 A Mathematical Model for Glucose-Insulin and β-Cells Dynamics.

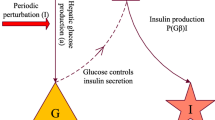
Numerous mathematical models have been developed to study the dynamics of diabetes mellitus. Bergman’s minimal model (Bergman and Cobelli 1980) is one of the well-known non-linear three-dimensional mathematical models for the study of diabetes mellitus. In literature, β-cells are considered a key factor in the modelling of diabetes (Shabestari et al. 2018; Topp et al. 2000; Turner et al. 1979). Topp et al. (2000) developed a three-dimensional mathematical model considering β-cells as one of the state variables. Turner et al. (1979) observed that β-cells play a central role in controlling both plasma glucose and insulin concentrations. A new mathematical model is proposed based on the physical relationship of the plasma glucose, insulin, and β-cells mass dynamics as shown in Fig. 1. It is noticed from Fig. 1 that β-cells work in a negative feedback loop. Due to a reduction in the number of β cells, plasma glucose level rises by liver till natural insulin level is achieved. The proposed model is based on the following assumptions:

  1. I.

    Plasma glucose is inversely proportional to β-cells (Turner et al. 1979).

  2. II.

    The secretion of plasma insulin is directly proportional to β- cells and is designed as a non-linear sigmoidal function of glucose (Topp et al. 2000).

Fig. 1
figure 1

The physical relationship between glucose, insulin and β-cells

Full size image

The proposed model is considered as the following equations:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}G}}{{{\text{d}}t}} = \frac{aN}{\beta } - cI + C_{1} } \hfill \\ {\frac{{{\text{d}}I}}{{{\text{d}}t}} = \frac{{d\beta G^{2} }}{{j + G^{2} }} - fI} \hfill \\ {\frac{{{\text{d}}\beta }}{{{\text{d}}t}} = \left( { - g + hG - iG^{2} } \right)\beta } \hfill \\ \end{array} } \right. $$
(1)

where \({\text{G}}\left( t \right)\) represents plasma glucose concentration, \(I\left( t \right)\) represents plasma insulin, β represents the mass of β-cells, a represents glucose production rate, c represents the rate of decrease in glucose-dependent on insulin, \(C_{1}\) represents the rate of increase in insulin in the lack of \(G\) and \(I\), \(N\) represents reduction rate in the number of β-cells, \(d\) represents insulin secretion rate, \(f\) represents insulin clearance rate, \(g\) represents the β-cells congenital death rate, \(h\) and \(i\) represent rate constants.

Lemma 2.1.

Li et al. (2012) If \(\dot{v}\left( t \right) \le p - qv\left( t \right)\) or \(\dot{v}\left( t \right) \ge p - qv\left( t \right) \) on the interval \( \left( {T_{1} , T_{2} } \right)\), where \(p, q > 0\) and \(T_{1} < T_{2}\), then.

$$ v\left( t \right) \le \frac{p}{q} + \left( {v\left( {T_{1} } \right) - \frac{p}{q}} \right)e^{{q\left( {T_{1} - t} \right)}} \;\;{\text{or}}\;\;v\left( t \right) \ge \frac{p}{q} + \left( {v\left( {T_{1} } \right) - \frac{p}{q}} \right)e^{{q\left( {T_{1} - t} \right)}} \;\;\;\;\forall \;t \in \left( {T_{1} ,T_{2} } \right). $$

Theorem 2.1.

Solutions of the system (1) are uniformly bounded if \(\beta \ge 1\).

Proof:

Suppose \(\eta = G + g I + d \beta\). Therefore, its derivative is given as

$$ \begin{aligned} \dot{\eta } = & \dot{G} + g \dot{I} + d\dot{\beta } \\ = & \frac{aN}{\beta } - cI + C_{1} + \frac{{gd\beta G^{2} }}{{\left( {j + G^{2} } \right)}} - fdI + d\left( { - g + hG - iG^{2} } \right)\beta \\ \le & \frac{aN}{\beta } + C_{1} + gd\beta + d\left( { - g + hG - iG^{2} } \right)\beta \\ \le & \frac{a N}{\beta } + C_{1} + hdG\beta \\ \le & a N + C_{1} + hdg\left( {\frac{\eta - G - g I}{d}} \right) \\ \le & \left( {a N + C_{1} } \right)\eta + hG\eta \\ \le & \left( {a N + \dot{C}_{1} } \right)\eta + h \eta^{2} \\ \Rightarrow & \dot{\eta } - \left( {a N + \dot{C}_{1} } \right)\eta \le h \eta^{2} \\ \end{aligned} $$

substituting \(- \eta^{ - 1} = v\), we have

$$ \dot{v} + \left( {a N + C_{1} } \right)v \le h $$
$$ \Rightarrow \dot{v} \le h - \left( {a N + C_{1} } \right)u $$

By lemma 2.1,\( v\left( t \right) \le \frac{h}{{\left( {a N + C_{1} } \right)}} + \left( {v\left( 0 \right) - \frac{h}{{\left( {a N + C_{1} } \right)}}} \right)e^{{ - \left( {a N + C_{1} } \right)t}} , \forall t \in \left( {0,\infty } \right)\).

As \(t \to \infty\), we have

$$ v\left( t \right) \le \frac{h}{{\left( {a N + C_{1} } \right)}}, \;\;\forall t \in \left( {0,\infty } \right) $$

i.e., the system (1) is bounded above by \(\frac{h}{{\left( {a N + C_{1} } \right)}}\), whenever \(\beta \ge 1\).

3 Existence and Stability of Equilibria

This section is devoted to finding the condition for the existence of equilibrium points for system (1). Stability analysis for system (1) is also accomplished. Routh-Hurwitz criterion is applied to calculate the stability of equilibrium points for system (1).

3.1 Existence of Equilibria

Different conditions for the existence of equilibria for the system (1) are evaluated in this subsection.

Theorem 3.1.

The number of equilibrium points for system (1) can be determined as follows:

  1. 1.

    If \(h^{2} < 4gi\) , then system (1) has no equilibrium point.

  2. 2.

    If \(h^{2} = 4gi\) and \(C_{1} f\left( {j + G_{1}^{2} } \right) + \sqrt {C_{1} f\left( {j + G_{1}^{2} } \right) + 4cdafG_{1}^{2} \left( {j + G_{1}^{2} } \right)} > 0,\) then the system (1) has one equilibrium point namely \(E_{1}^{*} \left( {G_{1} , I_{1} , \beta_{1} } \right), \) where \(G_{1} = \frac{h}{2 i}\) , \(I_{1} = \frac{{d \beta_{1} G_{1}^{2} }}{{f \left( {j + G_{1}^{2} } \right)}}, \) and \(\beta_{1} = \frac{{C_{1} f\left( {j + G_{1}^{2} } \right) + \sqrt {C_{1} f\left( {j + G_{1}^{2} } \right) + 4cdafG_{1}^{2} \left( {j + G_{1}^{2} } \right)} }}{{2 c d G_{1}^{2} }}.\)

  3. 3.

    If \(h^{2} > 4gi\) and \(C_{1} f\left( {j + G_{k}^{2} } \right) + \sqrt {C_{1} f\left( {j + G_{k}^{2} } \right) + 4cdafG_{k}^{2} \left( {j + G_{k}^{2} } \right)} > 0\) for \(k = 2,3,\) then the system (1) has two equilibrium point namely \(E_{2}^{*} \left( {G_{2} , I_{2} , \beta_{2} } \right) and E_{3}^{*} \left( {G_{3} , I_{3} , \beta_{3} } \right)\) , where \(G_{2} = \frac{{h + \sqrt {h^{2} - 4 g i} }}{2 i}\) , \(I_{2} = \frac{{d \beta_{2} G_{2}^{2} }}{{f \left( {j + G_{2}^{2} } \right)}}, \) and \(\beta_{2} = \frac{{C_{1} f\left( {j + G_{2}^{2} } \right) + \sqrt {C_{1} f\left( {j + G_{2}^{2} } \right) + 4cdafG_{2}^{2} \left( {j + G_{2}^{2} } \right)} }}{{2 c d G_{2}^{2} }}\) , \(G_{3} = \frac{{h - \sqrt {h^{2} - 4 g i} }}{2 i}\) , \(I_{3} = \frac{{d \beta_{3} G_{3}^{2} }}{{f \left( {j + G_{3}^{2} } \right)}} , \) and \(\beta_{3} = \frac{{C_{1} f\left( {j + G_{3}^{2} } \right) + \sqrt {C_{1} f\left( {j + G_{3}^{2} } \right) + 4cdafG_{3}^{2} \left( {j + G_{3}^{2} } \right)} }}{{2 c d G_{3}^{2} }}.\)

Proof:

Assume \(\beta \ne 0\) in the third part of Eq. (1), then we have

$$ g - hG\left( t \right) + iG\left( t \right)^{2} = 0\;\;{\text{or}}\;\; - g + hG\left( t \right) - iG\left( t \right)^{2} = 0 $$
(2)
$$ G_{k} = \frac{{h \pm \sqrt {h^{2} - 4gi} }}{2 i},\;\;{\text{for}}\;\;k = 2,3. $$
(3)

It is easy to observe that Eq. (3) has no real solution for \(G\left( t \right)\) when \(h^{2} - 4 g i < 0\) and hence, system (1) has no equilibrium point. Equation (3) has only one real solution for \(G\left( t \right)\), namely \(G_{1} = \frac{h}{2 i}\) when \(h^{2} - 4gi = 0\). In this case, system (1) has only one equilibrium point \(E_{1}^{*}\). Similarly, Eq. (3) has two real solutions for \(G\left( t \right){\text{ when }}h^{2} - 4 g i > 0\). As a result, system (1) has two equilibrium point namely \(E_{2}^{*}\) and \(E_{3}^{*}\).

3.2 Stability of Equilibria

The local stability of the system (1) is examined through the linearization process. After the linearization process, we have the following Jacobian matrix:

$$ J = \left[ {\begin{array}{*{20}l} 0 \hfill & { - c} \hfill & {\frac{ - a}{{\beta^{2} }}} \hfill \\ {\frac{{ - 2dG^{3} \beta }}{{\left( {j + G^{2} } \right)^{2} }} + \frac{2dG\beta }{{\left( {j + G^{2} } \right)}}} \hfill & { - f} \hfill & {\frac{{dG^{2} }}{{\left( {j + G^{2} } \right)}}} \hfill \\ {\left( {h - 2iG} \right)\beta } \hfill & 0 \hfill & { - g + hG - iG^{2} } \hfill \\ \end{array} } \right] $$
(4)

The characteristic equation for Jacobian matrix \(J\) is given as follows:

$$ {\Delta }\left( \lambda \right) = \lambda^{3} + a_{1} \lambda^{2} + a_{2} \lambda + a_{3} = 0 $$
(5)

We further apply the Routh-Hurwitz criterion to show the local stability of equilibria.

Theorem 3.2.

The equilibrium point \(E_{2}^{*}\) of the system (1) is locally stable if it satisfies the conditions: \(tr\left( J \right) < 0,\det \left( J \right) < 0,\) and \(( - tr\left( J \right)\left( {J_{11} + J_{22} + J_{33} + \det \left( J \right)} \right) > 0\) , where \(J_{11} , J_{22} , \) and \(J_{33}\) represent cofactor of \(j_{11} , j_{22}\) , and \(j_{33}\) , respectively.

Proof: By Eq. (5), the Hurwitz matrices are given as

$$ J_{1} = \left| {a_{1} } \right| = - tr\left( J \right) > 0\;\;{\text{i}}.{\text{e}}.,\;\;tr\left( J \right) < 0 $$
(6)
$$ J_{2} = \left| {\begin{array}{*{20}c} {a_{1} } & 1 \\ {a_{3} } & {a_{2} } \\ \end{array} } \right| = a_{1} a_{2} - a_{3} = - tr\left( J \right) * \left( {J_{11} + J_{22} + J_{33} + \det \left( J \right)} \right) > 0 $$
(7)
$$ J_{3} = \left| {\begin{array}{*{20}c} {a_{1} } & 1 & 0 \\ {a_{3} } & {a_{2} } & {a_{1} } \\ 0 & 0 & {a_{3} } \\ \end{array} } \right| = a_{3} \left( {a_{1} a_{2} - a_{3} } \right) = ( - {\text{det}}\left( J \right)\left( { - tr\left( J \right)\left( {J_{11} + J_{22} + J_{33} + \det \left( J \right)} \right)} \right) > 0 $$
(8)

from Eq. (6), (7), and (8), system (1) is locally stable if \(tr\left( J \right) < 0,\det \left( J \right) < 0\), and \(- tr\left( J \right)*\left( {J_{11} + J_{22} + J_{33} + \det \left( J \right)} \right) > 0\) by Hurwitz criterion.

4 Bifurcation Analysis of the Model

This section deals with the different types of bifurcation analysis for the system (1). The conditions for saddle-node, transcritical, and Hopf-bifurcation are investigated for distinct parameters.

4.1 Saddle-Node Bifurcation

In this subsection, different saddle-node bifurcation parameters for the system (1) are evaluated. It can be noticed from theorem 3.1 that the equilibrium points \(E_{2}^{*} \left( {G_{2} ,I_{2} ,\beta_{2} } \right)\) and \(E_{3}^{*} \left( {G_{3} ,I_{3} ,\beta_{3} } \right)\) of the system (1) are crashed and the system has a unique equilibrium point \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) at \(h^{2} = 4 g i\) and \(C_{1} \left( {j + \left( {G_{1} } \right)^{2} } \right) + \sqrt {\left( {C_{1} f\left( {j + \left( {G_{1} } \right)^{2} } \right)} \right)^{2} + 4cd\left( {G_{1} } \right)^{2} af\left( {j + \left( {G_{1} } \right)^{2} } \right)} > 0.\) Furthermore, one eigenvalue of the Jacobian matrix \(J\) at the equilibrium point \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) is zero. Therefore, there is a possibility of bifurcation at the point \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\). The value of bifurcation parameters \(h, g,i\) at \(h^{2} = 4gi\) are given by \(h^{*} = \sqrt {4gi}\), \({\text{g}}^{*} = \frac{{h^{2} }}{4 i}\), and \(i^{*} = \frac{{h^{2} }}{4 g}\), respectively.

Theorem 4.1.

The system (1) experiences saddle-node bifurcation at \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) corresponding to the bifurcation parameter \(h\) if \(h^{2} = 4gi\) and \(tr\left( J \right) < 0\) .

Proof:

The Jacobian matrix for the equilibrium point \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) is

$$ H_{1} = \left[ {\begin{array}{*{20}c} 0 & { - c} & {\frac{ - a}{{\beta^{2} }}} \\ {\frac{{ - 2d G^{3} \beta }}{{\left( {j + G^{2} } \right)^{2} }} + \frac{2 d G \beta }{{\left( {j + G^{2} } \right)}}} & { - f} & {\frac{{d G^{2} }}{{\left( {j + G^{2} } \right)}}} \\ {\left( {h - 2 i G} \right)\beta } & 0 & { - g + h G - i G^{2} } \\ \end{array} } \right] $$

The eigenvalues of the above matrix are given as follows:

$$ \lambda_{1} = 0,\;\lambda_{2} = \frac{{tr\left( J \right) + \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2},\;{\text{and}}\;\lambda_{3} = \frac{{tr\left( J \right) - \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2},\;{\text{where}}\;tr\left( J \right) = - f. $$

The saddle-node bifurcation occurs at the equilibrium point \(E_{1}^{*}\) if the Jacobian matrix \(H_{1}\) has an eigenvalue zero with multiplicity one (Pirayesh et al. 2016). Now, consider the value of \(h^{*}\) at which matrix \(H_{1}\) has a zero eigenvalue i.e., \({\text{det}}\left( {{\text{H}}_{1} } \right)_{{h = h^{*} }} = 0.\)

The right eigenvector corresponding to \(0\) eigenvalue is given as

$$ A = \left( {\begin{array}{*{20}c} {a_{1} } \\ {a_{2} } \\ {a_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {1 - \frac{{a f \left( {j + G_{1}^{2} } \right)^{2} }}{{2cdj G_{1} \beta_{1}^{3} }}} \\ {\frac{ - a}{{c \beta_{1}^{2} }}} \\ 1 \\ \end{array} } \right) $$

The left eigenvector corresponding to \(0\) eigenvalue is given as

$$ B = \left( {\begin{array}{*{20}c} {b_{1} } \\ {b_{2} } \\ {b_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right) $$

Let \(l = \left( {l^{\left( 1 \right)} ,{ }l^{\left( 2 \right)} , l^{\left( 3 \right)} } \right)^{T}\), where \(l^{\left( 1 \right)} = \frac{a N}{\beta } - c I + C_{1} , l^{\left( 2 \right)} = \frac{{d \beta G^{2} }}{{\left( {j + G^{2} } \right)}} - fI\), and \(l^{\left( 3 \right)} = \left( { - g + h G - i G^{2} } \right)\beta\).

Then, \(\frac{\partial l}{{\partial h}}|\left( {E_{1}^{*} ; h = h^{*} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ {G_{1} \beta_{1} } \\ \end{array} } \right)\).

After substituting the partial derivatives, we have

$$ \begin{aligned} D^{2} l\left( {\left[ {E_{1}^{*} ;h^{*} } \right]} \right)\left( {A,A} \right) = & \left( {\begin{array}{*{20}l} {\frac{{\partial^{2} l^{\left( 1 \right)} }}{{\partial G^{2} }}a_{1}^{2} + 2\frac{{\partial^{2} l^{\left( 1 \right)} }}{\partial G\partial I}a_{1} a_{2} + 2\frac{{\partial^{2} l^{\left( 1 \right)} }}{\partial G\partial \beta }a_{1} a_{3} + \frac{{\partial^{2} l^{\left( 1 \right)} }}{{\partial I^{2} }}a_{2}^{2} + 2\frac{{\partial^{2} l^{\left( 1 \right)} }}{\partial I\partial \beta }a_{2} a_{3} + \frac{{\partial^{2} l^{\left( 1 \right)} }}{{\partial \beta^{2} }}a_{3}^{2} } \hfill \\ {\frac{{\partial^{2} l^{\left( 2 \right)} }}{{\partial G^{2} }}a_{1}^{2} + 2\frac{{\partial^{2} l^{\left( 2 \right)} }}{\partial G\partial I}a_{1} a_{2} + 2\frac{{\partial^{2} l^{\left( 2 \right)} }}{\partial G\partial \beta }a_{1} a_{3} + \frac{{\partial^{2} l^{\left( 2 \right)} }}{{\partial I^{2} }}a_{2}^{2} + 2\frac{{\partial^{2} l^{\left( 2 \right)} }}{\partial I\partial \beta }a_{2} a_{3} + \frac{{\partial^{2} l^{\left( 2 \right)} }}{{\partial \beta^{2} }}a_{3}^{2} } \hfill \\ {\frac{{\partial^{2} l^{\left( 3 \right)} }}{{\partial G^{2} }}a_{1}^{2} + 2\frac{{\partial^{2} l^{\left( 3 \right)} }}{\partial G\partial I}a_{1} a_{2} + 2\frac{{\partial^{2} l^{\left( 3 \right)} }}{\partial G\partial \beta }a_{1} a_{3} + \frac{{\partial^{2} l^{\left( 3 \right)} }}{{\partial I^{2} }}a_{2}^{2} + 2\frac{{\partial^{2} l^{\left( 3 \right)} }}{\partial I\partial \beta }a_{2} a_{3} + \frac{{\partial^{2} l^{\left( 3 \right)} }}{{\partial \beta^{2} }}a_{3}^{2} } \hfill \\ \end{array} } \right) \\ = & \left( {\begin{array}{*{20}c} {\frac{2 a}{{\beta_{1}^{3} }}a_{3}^{2} } \\ {\frac{{2dj\left( {j - 3G_{1}^{2} } \right)\beta }}{{\left( {j + G_{1}^{2} } \right)^{3} }} a_{1}^{2} + 2 a_{1} a_{3} \frac{{2 d j G_{1} }}{{\left( {j + G_{1}^{2} } \right)^{2} }}} \\ {\left( { - 2 i \beta } \right)a_{1}^{2} + a_{1} a_{3} \left( {h - 2 i G_{1} } \right)} \\ \end{array} } \right) \\ \end{aligned} $$

The transversality conditions are

\(\alpha = B^{T} \left. {\frac{\partial l}{{\partial h}}} \right|\left( {E_{1}^{*} ;h = h^{*} } \right) = \left( {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ {G_{1} \beta_{1} } \\ \end{array} } \right) = G_{1} \beta_{1} \ne 0\), and

$$ \beta = B^{T} D^{2} l\left( {\left[ {E_{1}^{*} ;h = h^{*} } \right]} \right)\left( {A,A} \right) = \left( {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{2a}{{\beta_{1}^{3} }}a_{3}^{2} } \hfill \\ {\frac{{2dj\left( {j - 3G_{1}^{2} } \right)\beta_{1} }}{{\left( {j + G_{1}^{2} } \right)^{3} }}a_{1}^{2} + 2a_{1} a_{3} \frac{{2djG_{1} }}{{\left( {j + G_{1}^{2} } \right)^{2} }}} \hfill \\ {\left( { - 2i\beta_{1} } \right)a_{1}^{2} + a_{1} a_{3} \left( {h - 2iG_{1} } \right)} \hfill \\ \end{array} } \right) = - 2i\beta_{1} + \frac{{afi\left( {j + G_{1}^{2} } \right)^{2} }}{{\beta_{1}^{2} cdjG_{1} }} \ne 0 $$

Therefore, the system (1) undergoes saddle-node bifurcation at \((E_{1}^{*} ;h = h^{*}\)).

Theorem 4.2.

The system \(\left( 1 \right)\) experiences saddle-node bifurcation at \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) corresponding to the bifurcation parameter \(g\) if \(h^{2} = 4gi\) and \(tr\left( J \right) < 0\) .

Proof:

The Jacobian matrix for the equilibrium point \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) is.

$$ H_{2} = \left[ {\begin{array}{*{20}c} 0 & { - c} & {\frac{ - a}{{\beta^{2} }}} \\ {\frac{{ - 2d G^{3} \beta }}{{\left( {j + G^{2} } \right)^{2} }} + \frac{2 d G \beta }{{\left( {j + G^{2} } \right)}}} & { - f} & {\frac{{d G^{2} }}{{\left( {j + G^{2} } \right)}}} \\ {\left( {h - 2 i G} \right)\beta } & 0 & { - g + h G - i G^{2} } \\ \end{array} } \right] $$

The eigenvalues of the above matrix are given as follows:

$$ \lambda_{1} = 0,\;\lambda_{2} = \frac{{tr\left( J \right) + \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2},\;{\text{and}}\;\lambda_{3} = \frac{{tr\left( J \right) - \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2},\;{\text{where}}\;tr\left( J \right) = - f. $$

The saddle-node bifurcation occurs at the equilibrium point \(E_{1}^{*}\) if the Jacobian matrix \(H_{2}\) has an eigenvalue zero with multiplicity one (Pirayesh et al. 2016). Now, consider the value of \({\text{g}}^{*}\) at which matrix \(H_{2}\) has a zero eigenvalue i.e., \(\det \left( {H_{2} } \right)_{{g = g^{*} }} = 0.\)

The right eigenvector corresponding to zero eigenvalue is given as

$$ C = \left( {\begin{array}{*{20}c} {c_{1} } \\ {c_{2} } \\ {c_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {1 - \frac{{a f \left( {j + G_{1}^{2} } \right)^{2} }}{{2cdj G_{1} \beta_{1}^{3} }}} \\ {\frac{ - a}{{c \beta_{1}^{2} }}} \\ 1 \\ \end{array} } \right) $$

The left eigenvector corresponding to \(0\) eigenvalue is given as

$$ D = \left( {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ {d_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right) $$

Now, let \(m = \left( {m^{\left( 1 \right)} ,{ }m^{\left( 2 \right)} , m^{\left( 3 \right)} } \right)^{T}\), where \(m^{\left( 1 \right)} = \frac{a N}{\beta } - c I + C_{1} , m^{\left( 2 \right)} = \frac{{d \beta G^{2} }}{{\left( {j + G^{2} } \right)}} - fI\), and \(m^{\left( 3 \right)} = \left( { - g + h G - i G^{2} } \right)\beta .\)

Then, \( \frac{\partial m}{{\partial g}}|\left( {E_{1}^{*} ; g = g^{*} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ { - \beta_{1} } \\ \end{array} } \right)\).

After substituting the partial derivatives, we have

$$ \begin{aligned} D^{2} m\left( {\left[ {E_{1}^{*} ;g^{*} } \right]} \right)\left( {C,C} \right) = & \left( {\begin{array}{*{20}l} {\frac{{\partial^{2} m^{\left( 1 \right)} }}{{\partial G^{2} }}c_{1}^{2} + 2\frac{{\partial^{2} m^{\left( 1 \right)} }}{\partial G\partial I}c_{1} c_{2} + 2\frac{{\partial^{2} m^{\left( 1 \right)} }}{\partial G\partial \beta }c_{1} c_{3} + \frac{{\partial^{2} m^{\left( 1 \right)} }}{{\partial I^{2} }}c_{2}^{2} + 2\frac{{\partial^{2} m^{\left( 1 \right)} }}{\partial I\partial \beta }c_{2} c_{3} + \frac{{\partial^{2} m^{\left( 1 \right)} }}{{\partial \beta^{2} }}c_{3}^{2} } \hfill \\ {\frac{{\partial^{2} m^{\left( 2 \right)} }}{{\partial G^{2} }}c_{1}^{2} + 2\frac{{\partial^{2} m^{\left( 2 \right)} }}{\partial G\partial I}c_{1} c_{2} + 2\frac{{\partial^{2} m^{\left( 2 \right)} }}{\partial G\partial \beta }c_{1} c_{3} + \frac{{\partial^{2} m^{\left( 2 \right)} }}{{\partial I^{2} }}c_{2}^{2} + 2\frac{{\partial^{2} m^{\left( 2 \right)} }}{\partial I\partial \beta }c_{2} c_{3} + \frac{{\partial^{2} m^{\left( 2 \right)} }}{{\partial \beta^{2} }}c_{3}^{2} } \hfill \\ {\frac{{\partial^{2} m^{\left( 3 \right)} }}{{\partial G^{2} }}c_{1}^{2} + 2\frac{{\partial^{2} m^{\left( 3 \right)} }}{\partial G\partial I}c_{1} c_{2} + 2\frac{{\partial^{2} m^{\left( 3 \right)} }}{\partial G\partial \beta }c_{1} c_{3} + \frac{{\partial^{2} m^{\left( 3 \right)} }}{{\partial I^{2} }}c_{2}^{2} + 2\frac{{\partial^{2} m^{\left( 3 \right)} }}{\partial I\partial \beta }c_{2} c_{3} + \frac{{\partial^{2} m^{\left( 3 \right)} }}{{\partial \beta^{2} }}c_{3}^{2} } \hfill \\ \end{array} } \right) \\ = & \left( {\begin{array}{*{20}c} {\frac{2 a}{{\beta_{1}^{3} }}c_{3}^{2} } \\ {\frac{{2dj\left( {j - 3G_{1}^{2} } \right)\beta_{1} }}{{\left( {j + G_{1}^{2} } \right)^{3} }} c_{1}^{2} + 2 c_{1} c_{3} \frac{{2 d j G_{1} }}{{\left( {j + G_{1}^{2} } \right)^{2} }}} \\ {\left( { - 2 i \beta_{1} } \right)c_{1}^{2} + c_{1} c_{3} \left( {h - 2 i G_{1} } \right)} \\ \end{array} } \right) \\ \end{aligned} $$

The transversality conditions are

\(\alpha = D^{T} \left. {\frac{\partial m}{{\partial g}}} \right|\left( {E_{1}^{*} ;g = g^{*} } \right) = \left( {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ { - \beta_{1} } \\ \end{array} } \right) = - \beta_{1} \ne 0\) and

$$ \beta = D^{T} D^{2} m\left( {\left[ {E_{1}^{*} ;g = g^{*} } \right]} \right)\left( {C,C} \right) = \left( {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{2a}{{\beta_{1}^{a} }}c_{3}^{2} } \hfill \\ {\frac{{2dj\left( {j - 3G_{1}^{2} } \right)\beta_{1} }}{{\left( {j + G_{1}^{2} } \right)^{a} }}c_{1}^{2} + 2c_{1} c_{3} \frac{{2djG_{1} }}{{\left( {j + G_{1}^{2} } \right)^{2} }}} \hfill \\ {\left( { - 2i\beta_{1} } \right)c_{1}^{2} + c_{1} c_{3} \left( {h - 2iG_{1} } \right)} \hfill \\ \end{array} } \right) = - 2i\beta_{1} + \frac{{afi\left( {j + G_{1}^{2} } \right)^{2} }}{{\beta_{1}^{2} cdjG_{1} }} \ne 0 $$

Therefore, the system (1) experiences saddle-node bifurcation at \((E_{1}^{*} ;g = g^{*}\)).

Theorem 4.3.

The system \(\left( 1 \right)\) experiences saddle-node bifurcation at \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) corresponding to the bifurcation parameter \(i\) if \(h^{2} = 4 g i\) and \(tr\left( J \right) < 0\) .

Proof:

The Jacobian matrix for the equilibrium point \(E_{1}^{*} \left( {G_{1} ,I_{1} ,\beta_{1} } \right)\) is.

$$ H_{3} = \left[ {\begin{array}{*{20}c} 0 & { - c} & {\frac{ - a}{{\beta^{2} }}} \\ {\frac{{ - 2d G^{3} \beta }}{{\left( {j + G^{2} } \right)^{2} }} + \frac{2 d G \beta }{{\left( {j + G^{2} } \right)}}} & { - f} & {\frac{{d G^{2} }}{{\left( {j + G^{2} } \right)}}} \\ {\left( {h - 2 i G} \right)\beta } & 0 & { - g + h G - i G^{2} } \\ \end{array} } \right] $$

The eigenvalues of the above matrix are given as follows:

$$ \lambda_{1} = 0,\;\lambda_{2} = \frac{{tr\left( J \right)- \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2},\;{\text{and}}\;\lambda_{3} = \frac{{tr\left( J \right) - \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2},\;{\text{where}}\;tr\left( J \right) = - f. $$

The saddle-node bifurcation occurs at the equilibrium point \(E_{1}^{*}\) if the Jacobian matrix \(H_{3}\) has an eigenvalue zero with multiplicity one (Pirayesh et al. 2016). Now, consider the value of \({\text{i}}^{*}\) at which matrix \(H_{3}\) has a zero eigenvalue i.e., \({\text{det}}\left( {{\text{H}}_{3} } \right)_{{i = i^{*} }} = 0.\)

The right eigenvector corresponding to \(0\) eigenvalue is given as

$$ E = \left( {\begin{array}{*{20}c} {e_{1} } \\ {e_{2} } \\ {e_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {1 - \frac{{a f \left( {j + G_{1}^{2} } \right)^{2} }}{{2cdj G_{1} \beta_{1}^{3} }}} \\ {\frac{ - a}{{c \beta_{1}^{2} }}} \\ 1 \\ \end{array} } \right) $$

The left eigenvector corresponding to \(0\) eigenvalue is given as

$$ F = \left( {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ {f_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right) $$

Let \(n\) \(n = \left( {n^{\left( 1 \right)} ,n^{\left( 2 \right)} ,n^{\left( 3 \right)} } \right)^{T}\), where \(n^{\left( 1 \right)} = \frac{a N}{\beta } - c I + C_{1} , n^{\left( 2 \right)} = \frac{{d \beta G^{2} }}{{\left( {j + G^{2} } \right)}} - fI\), and \(n^{\left( 3 \right)} = \left( { - g + h G - i G^{2} } \right)\beta\).

Then, \(\frac{\partial n}{{\partial i}}|\left( {E_{1}^{*} ; i = i^{*} } \right) = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ { - 2G_{1} \beta_{1} } \\ \end{array} } \right)\).

After substituting the partial derivatives, we have

$$ \begin{aligned} D^{2} n\left( {\left[ {E_{1}^{*} ;i^{*} } \right]} \right)\left( {E,E} \right) = & \left( {\begin{array}{*{20}l} {\frac{{\partial^{2} n^{\left( 1 \right)} }}{{\partial G^{2} }}e_{1}^{2} + 2\frac{{\partial^{2} n^{\left( 1 \right)} }}{\partial G\partial I}e_{1} e_{2} + 2\frac{{\partial^{2} n^{\left( 1 \right)} }}{\partial G\partial \beta }e_{1} e_{3} + \frac{{\partial^{2} n^{\left( 1 \right)} }}{{\partial I^{2} }}e_{2}^{2} + 2\frac{{\partial^{2} n^{\left( 1 \right)} }}{\partial I\partial \beta }e_{2} e_{3} + \frac{{\partial^{2} n^{\left( 1 \right)} }}{{\partial \beta^{2} }}e_{3}^{2} } \hfill \\ {\frac{{\partial^{2} n^{\left( 2 \right)} }}{{\partial G^{2} }}e_{1}^{2} + 2\frac{{\partial^{2} n^{\left( 2 \right)} }}{\partial G\partial I}e_{1} e_{2} + 2\frac{{\partial^{2} n^{\left( 2 \right)} }}{\partial G\partial \beta }e_{1} e_{3} + \frac{{\partial^{2} n^{\left( 2 \right)} }}{{\partial I^{2} }}e_{2}^{2} + 2\frac{{\partial^{2} n^{\left( 2 \right)} }}{\partial I\partial \beta }e_{2} e_{3} + \frac{{\partial^{2} n^{\left( 2 \right)} }}{{\partial \beta^{2} }}e_{3}^{2} } \hfill \\ {\frac{{\partial^{2} n^{\left( 3 \right)} }}{{\partial G^{2} }}e_{1}^{2} + 2\frac{{\partial^{2} n^{\left( 3 \right)} }}{\partial G\partial I}e_{1} e_{2} + 2\frac{{\partial^{2} n^{\left( 3 \right)} }}{\partial G\partial \beta }e_{1} e_{3} + \frac{{\partial^{2} n^{\left( 3 \right)} }}{{\partial I^{2} }}e_{2}^{2} + 2\frac{{\partial^{2} n^{\left( 3 \right)} }}{\partial I\partial \beta }e_{2} e_{3} + \frac{{\partial^{2} n^{\left( 3 \right)} }}{{\partial \beta^{2} }}e_{3}^{2} } \hfill \\ \end{array} } \right) \\ = & \left( {\begin{array}{*{20}c} {\frac{2 a}{{\beta_{1}^{3} }}e_{3}^{2} } \\ {\frac{{2dj\left( {j - 3G_{1}^{2} } \right)\beta }}{{\left( {j + G_{1}^{2} } \right)^{3} }} e_{1}^{2} + 2 e_{1} e_{3} \frac{{2 d j G_{1} }}{{\left( {j + G_{1}^{2} } \right)^{2} }}} \\ {\left( { - 2 i \beta } \right)e_{1}^{2} + e_{1} e_{3} \left( {h - 2 i G_{1} } \right)} \\ \end{array} } \right) \\ \end{aligned} $$

The transversality conditions are

\(\alpha = F^{T} \left. {\frac{\partial n}{{\partial i}}} \right|\left( {E_{1}^{*} ;i = i^{*} } \right) = \left( {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ { - 2G_{1} \beta_{1} } \\ \end{array} } \right) = - 2G_{1} \beta_{1} \ne 0\) and

$$ \beta = F^{T} D^{2} n\left( {\left[ {E_{1}^{*} ;i = i^{*} } \right]} \right)\left( {E,E} \right) = \left( {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{2a}{{\beta_{1}^{3} }}e_{3}^{2} } \hfill \\ {\frac{{2dj\left( {j - 3G_{1}^{2} } \right)\beta_{1} }}{{\left( {j + G_{1}^{2} } \right)^{3} }}e_{1}^{2} + 2e_{1} e_{3} \frac{{2djG_{1} }}{{\left( {j + G_{1}^{2} } \right)^{2} }}} \hfill \\ {\left( { - 2i\beta_{1} } \right)e_{1}^{2} + e_{1} e_{3} \left( {h - 2iG_{1} } \right)} \hfill \\ \end{array} } \right) = 2i\beta_{1} + \frac{{afi\left( {j + G_{1}^{2} } \right)^{2} }}{{\beta_{1}^{2} cdjG_{1} }} \ne 0 $$

Therefore, the system (1) experiences saddle-node bifurcation at \((E_{1}^{*} ;i = i^{*}\)).

4.2 Hopf-Bifurcation

In this section, we derive the condition for Hopf-bifurcation for system (1). The Hopf-bifurcation is experienced corresponding to parameter \(f\), i.e., system (1) has a pair of imaginary roots if the relation \(\det \left( J \right) = tr\left( J \right)*\left( {J_{11} + J_{22} + J_{33} } \right)\) holds. The relation is proved in theorem 4.4. The more concise condition for the existence of Hopf-bifurcation is discussed in theorem 4.5.

Theorem 4.4.

The system (1) undergoes Hopf-bifurcation at \(E_{3}^{*} \left( {G_{3} , I_{3} , \beta_{3} } \right)\) corresponding to the bifurcation parameter \(f\) . If the parameters of system (1) satisfy the condition \(a_{3} = a_{1} a_{2}\) , then, the system (1) has a pair of imaginary eigenvalues given by.

$$ \lambda = \pm \omega i = \pm \sqrt {a_{2} } $$

In addition to the above condition, if system \(\left( 1 \right)\) satisfies the following condition, then system (1) experiences Hopf-bifurcation.

$$ \left\{ {\frac{d}{df}[Re\left( \lambda \right)|f = f^{*} ]} \right\} \ne 0 $$

Proof:

Let the characteristic Eq. (5) has a pair of imaginary eigenvalues \(\lambda = \pm \omega i(\omega > 0)\) at \(f = f^{*}\).

$$ - \omega^{3} i - a_{1} \omega^{2} + a_{2} \omega i + a_{3} = 0 $$
(9)
$$ i\left( { - \omega^{3} + a_{2} \omega } \right) + \left( {a_{3} - a_{1} \omega^{2} } \right) = 0 $$
(10)
$$ i.e.,\left\{ {\begin{array}{*{20}c} { - \omega^{3} + a_{2} \omega = 0} \\ {a_{3} - a_{1} \omega^{2} = 0} \\ \end{array} } \right. $$
(11)

From the first part of Eq. (11) and \(\omega > 0\), we have

$$ \omega^{2} = a_{2} $$
(12)

Moreover, from Eq. (12) and the second part of the Eq. (11), we have

$$ a_{3} = a_{1} a_{2} $$
(13)

Next, we compute the value of \(\frac{{{\text{d}}\lambda }}{{{\text{d}}f}}\), for the bifurcation parameter \(f\). Again, from the characteristic Eq. (5), we have

$$ \frac{{{\text{d}}\lambda }}{{{\text{d}}f}}\left( {3\lambda^{2} + 2a_{1} \lambda + a_{2} } \right) + \frac{{{\text{d}}a_{1} }}{{{\text{d}}f}}\lambda^{2} + \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}}\lambda + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}} = 0 $$

Since \(\lambda = \pm \omega i\) at \(f = f^{*}\). We have

$$ \frac{{{\text{d}}\lambda }}{{{\text{d}}f}}\left( { - 3\omega^{2} + 2a_{1} \omega i + a_{2} } \right) + \left( {\frac{{ - {\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}}\omega i + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right) = 0 $$
$$ \frac{{{\text{d}}\lambda }}{{{\text{d}}f}}\left[ {\left( { - 3\omega^{2} + a_{2} ) + (2a_{1} \omega i} \right)} \right] = - \left[ {\left( {\frac{{ - {\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right) + \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}}\omega i} \right] $$
$$ \frac{{{\text{d}}\lambda }}{{{\text{d}}f}} = - \frac{{\left[ {\left( {\frac{{ - {\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right) + \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}}\omega i} \right]}}{{\left[ {\left( { - 3\omega^{2} + a_{2} ) + (2a_{1} \omega i} \right)} \right]}}. $$

Also, we have

$$ {\text{sign}}\left\{ {\frac{{{\text{d}}\lambda }}{{{\text{d}}f}}\left[ {{\text{Re}} \lambda \left( f \right)} \right]} \right\} = {\text{sign}}\left\{ {{\text{Re}} \left( {\frac{{{\text{d}}\lambda }}{{{\text{d}}f}}} \right)} \right\} $$
(14)
$$ = - {\text{sign}}\frac{{2 a_{1} \omega \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}} + \left( {a_{2} - 3\omega^{2} } \right)\left( { - \frac{{{\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right)}}{{\left( {2 a_{1} \omega } \right)^{2} + \left( {a_{2} - 3\omega^{2} } \right)^{2} }} $$
(15)
$$ = - {\text{sign}}\left[ {2 a_{1} \omega \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}} + \left( {a_{2} - 3\omega^{2} } \right)\left( { - \frac{{{\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right)} \right] $$
(16)
$$ = - {\text{sign}}\left[ {2 a_{1} \omega \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}} + \left( { - 2a_{2} } \right)\left( { - \frac{{{\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right)} \right] $$
(17)

from Eqs. (13) and (17), we get

$$ {\text{sign}}\left\{ {\frac{{{\text{d}}\lambda }}{{{\text{d}}f}}\left[ {{\text{Re}} \lambda \left( f \right)} \right]} \right\} = - {\text{sign}}\left[ {2 a_{1} \omega \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}} + \left( {a_{2} - 3\omega^{2} } \right)\left( { - \frac{{{\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right)} \right] $$
(18)
$$ = - {\text{sign}}\left[ {2 a_{1} \omega \frac{{{\text{d}}a_{2} }}{{{\text{d}}f}} + \left( {a_{2} - 3\omega^{2} } \right)\left( { - \frac{{{\text{d}}a_{1} }}{{{\text{d}}f}}\omega^{2} + \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right)} \right] $$
(19)

Since \( a_{1} = - tr\left( J \right) = f, a_{2} = \left( {J_{11} + J_{22} + J_{33} } \right) = \frac{2 c d j G \beta }{{\left( {J + G^{2} } \right)^{2} }} + \frac{{a \left( {h - 2iG} \right)}}{\beta }\),\( a_{3} = \left( {h - 2iG} \right)\beta \left( {\frac{af}{{\beta^{2} }} + \frac{{cd G^{2} }}{{\left( {j + G^{2} } \right)}}} \right)\), therefore

$$ - {\text{sign}} \left[ {a_{1} \left( { \pm \sqrt {a_{2} } } \right)\frac{{{\text{d}}a_{2} }}{{{\text{d}}f}} + \left( {a_{2}^{2} \frac{{{\text{d}}a_{1} }}{{{\text{d}}f}} - a_{2} \frac{{{\text{d}}a_{3} }}{{{\text{d}}f}}} \right)} \right] = a_{2} \left( {\frac{2cdjG}{{\left( {j + G^{2} } \right)^{2} }}} \right) \ne 0 $$

Theorem 4.5.

If \(h^{2} > 4gi\) and \(C_{1} f(j + G_{k}^{2} ) + \sqrt {C_{1} f\left( {j + G_{k}^{2} } \right)^{2} + 4cd(G_{k}^{2} af\left( {j + G_{k}^{2} } \right)} > 0\) , i.e., the system (1) has two equilibrium points and \(p\left( 0 \right) > 0\) and \(p\left( {f^{1} } \right) < 0\) for some \(f^{1} > 0\) with \(p\left( f \right) = a_{3} - a_{1} a_{2}\) , then there exists \(f = f^{*} \in \left( {0, f^{1} } \right)\) at which the system undergoes Hopf-bifurcation.

Proof:

Substituting the value of \(a_{1} , a_{2} ,a_{3}\) in \(p\left( f \right)\), we have.

$$ p\left( f \right) = \left( {h - 2iG} \right)\beta \frac{{cdG^{2} }}{{\left( {j + G^{2} } \right)}} $$

If \(f = 0\), then \(p\left( 0 \right) = \left( {h - 2iG} \right)\beta \frac{{cdG^{2} }}{{\left( {j + G^{2} } \right)}} > 0\), and for some \(f = f^{1} , p\left( f \right) < 0\). Therefore, from the intermediate value theorem, there exists \(f = f^{*} \in \left( {0,f^{1} } \right)\).

4.3 Transcritical Bifurcation

In this subsection, we discuss the transcritical bifurcation behavior of the system (1).

Theorem 4.6.

The system (1) experiences no transcritical bifurcation corresponding to the parameter \(f\) .

Proof:

The Jacobian matrix for the equilibrium point \({\text{E}}_{3}^{*} \left( {{\text{G}}_{3} ,{\text{I}}_{3} ,{\upbeta }_{3} } \right)\) is.

$$ H_{4} = \left[ {\begin{array}{*{20}c} 0 & { - c} & {\frac{ - a}{{\beta^{2} }}} \\ {\frac{{ - 2d G^{3} \beta }}{{\left( {j + G^{2} } \right)^{2} }} + \frac{2 d G \beta }{{\left( {j + G^{2} } \right)}}} & { - f} & {\frac{{d G^{2} }}{{\left( {j + G^{2} } \right)}}} \\ {\left( {h - 2 i G} \right)\beta } & 0 & 0 \\ \end{array} } \right] $$

Consider the value of \(f_{1}^{*}\) at which matrix \(H_{4}\) has a zero eigenvalue at \(f = f_{1}^{*}\), i.e., \(\det \left( {H_{4} } \right)_{{f = f_{1}^{*} }} = 0\). The eigenvalues of the above matrix are given as follows:

\({\uplambda }_{1} { } = 0\), \(\lambda_{2} = \frac{{tr\left( J \right) + \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2}\), and \(\lambda_{3} = \frac{{tr\left( J \right) - \sqrt {tr\left( J \right)^{2} - 4 \left( {J_{11} + J_{22} + J_{33} } \right)} }}{2}\), where \(tr\left( J \right) = - f\). The transcritical bifurcation occurs at the equilibrium point \(E_{3}^{*}\) if the Jacobian matrix \(H_{4}\) has an eigenvalue zero with multiplicity one (Pirayesh et al. 2016).

The right eigenvector corresponding to \(0\) eigenvalue is given as

$$ L = \left( {\begin{array}{*{20}c} {l_{1} } \\ {l_{2} } \\ {l_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{{d G_{3}^{2} \beta_{3}^{2} }}{{a\left( {j + G_{3}^{2} } \right)}}} \\ 1 \\ {\frac{{2djG_{3} }}{{\left( {h - 2iG_{3} } \right)\left( {j + G_{3}^{2} } \right)^{2} }}} \\ \end{array} } \right) $$

The left eigenvector corresponding to \(0\) eigenvalue is given as

$$ P = \left( {\begin{array}{*{20}c} {p_{1} } \\ {p_{2} } \\ {p_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - \left( {h - 2iG_{3} } \right)\beta_{3} } \\ 0 \\ 1 \\ \end{array} } \right) $$

Let \(q\) \(= \left( {q^{\left( 1 \right)} ,{ }q^{\left( 2 \right)} , q^{\left( 3 \right)} } \right)^{T}\), where \(q^{\left( 1 \right)} = \frac{a N}{\beta } - c I + C_{1} , q^{\left( 2 \right)} = \frac{{d \beta G^{2} }}{{\left( {j + G^{2} } \right)}} - fI\), and \(q^{\left( 3 \right)} = \left( { - g + h G - i G^{2} } \right)\beta\), and \(r = \left( {r^{\left( 1 \right)} , r^{\left( 2 \right)} , r^{\left( 3 \right)} } \right)^{T}\), where \(r^{\left( 1 \right)} = 0, r^{\left( 2 \right)} = - I,\) and \(r^{\left( 3 \right)} = 0.\)

Then, \(\frac{\partial q}{{\partial f}}|\left( {E_{3}^{*} ; f = f_{1}^{*} } \right) = \left( {\begin{array}{*{20}c} 0 \\ { - I_{3} } \\ 0 \\ \end{array} } \right)\).

After substituting the partial derivatives, we have

$$ \begin{aligned} Dr\left( {\left[ {E_{3}^{*} ; f_{1}^{*} } \right]} \right)L = & \left( {\begin{array}{*{20}c} {\frac{{\partial r^{\left( 1 \right)} }}{\partial G}l_{1} + \frac{{\partial r^{\left( 1 \right)} }}{\partial I}l_{2} + \frac{{\partial r^{\left( 1 \right)} }}{\partial \beta }l_{3} } \\ {\frac{{\partial r^{\left( 2 \right)} }}{\partial G}l_{1} + \frac{{\partial r^{\left( 2 \right)} }}{\partial I}l_{2} + \frac{{\partial r^{\left( 2 \right)} }}{\partial \beta }l_{3} } \\ {\frac{{\partial r^{\left( 3 \right)} }}{\partial G}l_{1} + \frac{{\partial r^{\left( 3 \right)} }}{\partial I}l_{2} + \frac{{\partial r^{\left( 3 \right)} }}{\partial \beta }l_{3} } \\ \end{array} } \right) \\ = & \left( {\begin{array}{*{20}c} 0 \\ { - l_{2} } \\ 0 \\ \end{array} } \right) \\ \end{aligned} $$
$$ \begin{aligned} D^{2} q\left( {\left[ {E_{1}^{*} ;h^{*} } \right]} \right)\left( {L,L} \right) = & \left( {\begin{array}{*{20}l} {\frac{{\partial^{2} q^{\left( 1 \right)} }}{{\partial G^{2} }}l_{1}^{2} + 2\frac{{\partial^{2} q^{\left( 1 \right)} }}{\partial G\partial I}l_{1} l_{2} + 2\frac{{\partial^{2} q^{\left( 1 \right)} }}{\partial G\partial \beta }l_{1} l_{3} + \frac{{\partial^{2} q^{\left( 1 \right)} }}{{\partial I^{2} }}l_{2}^{2} + 2\frac{{\partial^{2} q^{\left( 1 \right)} }}{\partial I\partial \beta }l_{2} l_{3} + \frac{{\partial^{2} q^{\left( 1 \right)} }}{{\partial \beta^{2} }}l_{3}^{2} } \hfill \\ {\frac{{\partial^{2} q^{\left( 2 \right)} }}{{\partial G^{2} }}l_{1}^{2} + 2\frac{{\partial^{2} q^{\left( 2 \right)} }}{\partial G\partial I}l_{1} l_{2} + 2\frac{{\partial^{2} q^{\left( 2 \right)} }}{\partial G\partial \beta }l_{1} l_{3} + \frac{{\partial^{2} q^{\left( 2 \right)} }}{{\partial I^{2} }}l_{2}^{2} + 2\frac{{\partial^{2} q^{\left( 2 \right)} }}{\partial I\partial \beta }l_{2} l_{3} + \frac{{\partial^{2} q^{\left( 2 \right)} }}{{\partial \beta^{2} }}l_{3}^{2} } \hfill \\ {\frac{{\partial^{2} q^{\left( 3 \right)} }}{{\partial G^{2} }}l_{1}^{2} + 2\frac{{\partial^{2} q^{\left( 3 \right)} }}{\partial G\partial I}l_{1} l_{2} + 2\frac{{\partial^{2} q^{\left( 3 \right)} }}{\partial G\partial \beta }l_{1} l_{3} + \frac{{\partial^{2} q^{\left( 3 \right)} }}{{\partial I^{2} }}l_{2}^{2} + 2\frac{{\partial^{2} q^{\left( 3 \right)} }}{\partial I\partial \beta }l_{2} l_{3} + \frac{{\partial^{2} q^{\left( 3 \right)} }}{{\partial \beta^{2} }}l_{3}^{2} } \hfill \\ \end{array} } \right) \\ = & \left( {\begin{array}{*{20}c} {\frac{2a}{{\beta_{1}^{3} }}l_{3}^{2} } \\ {\frac{{2dj\left( {j - 3G_{3}^{2} } \right)\beta_{3} }}{{\left( {j + G_{3}^{2} } \right)^{3} }} l_{1}^{2} + 2 l_{1} l_{3} \frac{{2 d j G_{3} }}{{\left( {j + G_{3}^{2} } \right)^{2} }}} \\ {\left( { - 2 i \beta_{3} } \right)l_{1}^{2} + l_{1} l_{3} \left( {h - 2 i G_{3} } \right)} \\ \end{array} } \right) \\ \end{aligned} $$

The transversality conditions are

$$ \alpha = P^{T} \left. {\frac{\partial q}{{\partial f}}} \right|\left( {E_{3}^{*} ;f_{1}^{*} } \right) = \left( {\begin{array}{*{20}c} { - \left( {h - 2iG_{3} } \right)\beta_{3} } & 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ { - I_{3} } \\ 0 \\ \end{array} } \right) = 0 $$
$$ \beta = P^{T} D^{2} q\left( {\left[ {E_{3}^{*} ; f = f_{1}^{*} } \right]} \right)\left( {L,L} \right) = \left( {\begin{array}{*{20}c} { - \left( {h - 2iG_{3} } \right)\beta_{3} } & 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{2a}{{\beta_{1}^{3} }}l_{3}^{2} } \\ {\frac{{2dj\left( {j - 3G_{3}^{2} } \right)\beta_{3} }}{{\left( {j + G_{3}^{2} } \right)^{3} }} l_{1}^{2} + 2 l_{1} l_{3} \frac{{2 d j G_{3} }}{{\left( {j + G_{3}^{2} } \right)^{2} }}} \\ {\left( { - 2 i \beta_{3} } \right)l_{1}^{2} + l_{1} l_{3} \left( {h - 2 i G_{3} } \right)} \\ \end{array} } \right) \ne 0 $$
$$ \gamma = P^{T} Dr\left( {\left[ {E_{3}^{*} ; f_{1}^{*} } \right]} \right)L = \begin{array}{*{20}c} { - \left( {h - 2iG_{3} } \right)\beta_{3} } & 0 & 1 \\ \end{array} )\left( {\begin{array}{*{20}c} 0 \\ { - l_{2} } \\ 0 \\ \end{array} } \right) = 0 $$

In this case, there is a chance of transcritical bifurcation as the first condition of Sotomayor's theorem (Pirayesh et al. 2016) is satisfied, but the second condition is not satisfied. Therefore, system (1) has no transcritical bifurcation for parameter \(f\).

5 Numerical Simulation and Discussion

The applicable experimental data are generally based on glucose concentrations for a small-time scale. Therefore, it is not possible to validate mathematical models with experimental data for a long period (Lenbury et al. 2001). In modern research techniques, a model is acknowledged as correct if it has similar dynamics as noted in real-life data. In the proposed model, it is anticipated that the model shows stable behavior for normal conditions whereas bifurcation is observed in the case of type 2 diabetes and hyperinsulinemia (Jafari et al. 2013; Letellier et al. 2013).

The numerical simulation for system (1) is examined for 3000 days. The parameter values are given in Table 1. Figures 2, 3, and 4 represent the dynamics for glucose, insulin, and \(\beta\)-cells in days, respectively. It is noticed from Figs. 2, 3, and 4 that the system (1) approaches the stable equilibrium point for a longer time duration. Figures 5, 6, and 7 show the relationship between insulin-glucose, \(\beta\)-cells and glucose, and insulin and \(\beta\)-cells, respectively. From Figs. 5, 6, 7, it is easily noticed that there is a direct relationship between \(\beta\)-cells and insulin whereas glucose and \(\beta\)-cells are inversely related. The dynamical behavior of system \(\left( 1 \right)\) is observed through the stability analysis of the system. Due to the biological significance of the variables, all the equilibrium points are taken to be positive. For the stability analysis, we consider the Jacobian matrix in equation \(\left( 4 \right)\). System \(\left( 1 \right)\) has two equilibrium points. The equilibrium points and their corresponding eigenvalues are given in Table 2. It is noticed from Table 2 that \(E_{1}\) is stable-node which is asymptotically stable and \(E_{2}\) is a saddle point. It is also observed in Figs. 2, 3, and 4. The simulation results are validated with the help of MATLAB code. Simulation results are in agreement with the theoretical results.

Table 1 Values of the parameters for non-diabetic patient
Full size table
Fig. 2
figure 2

Dynamical behavior of glucose

Full size image
Fig. 3
figure 3

Dynamical behavior of insulin

Full size image
Fig. 4
figure 4

Dynamical behavior of β-cells

Full size image
Fig. 5
figure 5

Dynamical relationship between glucose and β-cells

Full size image
Fig. 6
figure 6

Dynamical relationship between insulin and β-cells

Full size image
Fig. 7
figure 7

Dynamical relationship between insulin and glucose

Full size image
Table 2 Equilibrium points and eigenvalues for system (1)
Full size table

5.1 Bifurcation Analysis

In this section, we discuss the chaotic behavior of system \(\left( 1 \right)\) numerically. From the previous studies, it is observed that the chaotic behavior of a system represents the existence of some complications in system (Jafari et al. 2013; Letellier et al. 2013). Moreover, we present numerical examples of different types of bifurcations for system \(\left( 1 \right)\) corresponding to distinct parameters and their bifurcation diagrams. We further discuss the biological significance of bifurcation diagrams. Some common diseases associated with glucose-insulin dynamics are also discussed.

5.1.1 Saddle-Node Bifurcation

In this subsection, we discuss the numerical examples of saddle-node bifurcation corresponding to parameters \(g\), \(h\), \(i\). Deficiency of \(\beta\)-cells mass dynamics and increase in glucose concentration results in saddle-node bifurcation. Saddle-node bifurcation occurs for model \(\left( 1 \right)\) when the rate constants decline. The bifurcation diagram is shown in Figs. 8, 9, 10. As \(h\) declines to \(h^{*}\), the saddle and physiological points overlap, and saddle-node bifurcation is observed at \(h^{*}\). Bifurcation analyses are carried out using MATLAB.

Fig. 8
figure 8

Saddle-node bifurcation for parameter h at \(h^{*} = 0.00071165834\)

Full size image
Fig. 9
figure 9

Saddle-node bifurcation for parameter g at \(g^{*} = 0.0735\)

Full size image
Fig. 10
figure 10

Saddle-node bifurcation for parameter \(i\) at \(i^{*} = 3.343695506* 10^{ - 6}\)

Full size image

5.1.2 Hopf-Bifurcation

In this section, we confer the Hopf-bifurcation numerically for parameter \(f\). In this work, an increase in the level of insulin regardless of glucose concentration conclude to Hopf-bifurcation. Hopf-bifurcation occurs for system \(\left( 1 \right)\) when the insulin clearance rate decreases. The bifurcation diagram is shown in Fig. 11a. The Hopf-bifurcation point is shown as a red star symbol. It is also noticed that system \(\left( 1 \right)\) is stable before the bifurcation point and it is unstable after the bifurcation point. The first Lyapunov coefficient is shown in Fig. 11b. Since the first Lyapunov coefficient is positive, there exists an unstable limit cycle for the system \(\left( 1 \right)\) and the bifurcation is subcritical. Hopf-bifurcation is executed with the help of MATCONT software.

Fig. 11
figure 11

Example of Hopf-bifurcation for parameter \(f\) at \(f^{*} = 0.0244613129132617.\) a Bifurcation diagram for parameter \(f\) in matcont. b Lyapunov coefficient for parameter \(f\) in MATLAB window

Full size image

5.2 Type 2 Diabetes and Hyperinsulinemia

Type 2 diabetes (insulin-independent diabetes) occurs when the effect of insulin on plasma glucose is less. In type 2 diabetes, the body is unable to track the increase in glucose level and the mass of \(\beta\)-cells are decreased from the normal level (Yang et al. 2015). Type 2 diabetes is observed in the proposed model at the small value of parameter \(h\). Figure 8 represents the bifurcation diagram corresponding to the parameter \(h\). As the value of bifurcation parameter \(h\) decreases, the level of glucose starts increasing from the normal level whereas the body is not responsive to it. The most common disorder associated with glucose-insulin dynamics is hyperinsulinemia. If the level of insulin is higher than the required amount of insulin, i.e., if the \(\beta\)-cells of the pancreas produce higher insulin irrespective of glucose levels, hyperinsulinemia is experienced (Shanik et al. 2008; Weyer et al. 2001). In the present study, hyperinsulinemia is observed corresponding to parameter \(f\). Here the parameter \(f\) represents the insulin clearance rate. As the value of parameter \(f\) declines, \(\beta\)-cells produce a high level of insulin and the system behaves chaotically. The bifurcation diagram for parameter \(f\) is shown in Fig. 11. System \(\left( 1 \right) \) is stable for large values of parameter \(f\) whereas system shows limit cycle at small value of \(f\).

6 Conclusions

In this manuscript, a new three-dimensional model has been proposed to study the dynamics of the glucose-insulin regulatory system. The impact of \(\beta\)-cells on the glucose-insulin regulatory system and the boundedness of solutions of the proposed model have been examined. Conditions for the existence of distinct equilibrium points are carried out analytically and numerically. The stability analysis of two distinct equilibrium points is examined. The stable equilibrium point known as the physiological point is more realistic in comparison to the physiological point observed by Topp et al. (Topp et al. 2000). The dynamical behavior of the proposed model has been analyzed. It is concluded that there is a direct relationship between \(\beta\)-cells and insulin whereas glucose and \(\beta\)-cells are inversely related which is also observed in the literature. Different types of bifurcation have been discussed for distinct control parameters. From the results, it is concluded that the system \(\left( 1 \right)\) illustrates distinct behaviors in diverse conditions and is capable of demonstrating the relation between glucose, insulin, and \(\beta\)-cells in various disorders, for instance, type 2 diabetes and hyperinsulinemia. The results may help the physician in observing the behavior of type 2 and hyperinsulinemia for a longer period.