Nilpotent Singularities and Periodic Perturbation of a $GI\beta$ Model: A Pathway to Glucose Disorder

Abstract

Bifurcations and related dynamical behaviors of a glucose metabolism model are thoroughly studied in this paper. It is shown that the model undergoes transcritical, Hopf, degenerate Hopf, saddle-node, cusp, and zero-Hopf bifurcations, as well as Bogdanov–Takens bifurcations of codimensions 2 and 3. Considering the periodicity of hepatic glucose production and $\beta$ cells’ glucose tolerance range, four elementary periodic mechanisms are also analyzed. These mechanisms lead to more complex dynamics, including periodic solutions of different periods, quasiperiodic solutions, chaos through torus destruction, or cascade of period doublings. Sensitivity analysis is performed to isolate the high-effect factors and explore a few advanced treatment approaches. The described dynamics explain well several clinical observations, which could provide sound guidance in the therapeutic process.

1 Introduction

Diabetes, a chronic disease, affects $9\%$ of the adult population worldwide, with a prevalence predicted by the World Health Organization (WHO) to double by 2030 (García-Jiménez et al. 2016; Zhou et al. 2016). At present, chronic hyperglycemia is increasingly recognized as a risk factor for microvascular and neuronal complications, representing an enormous social and economic health burden (Tsilidis et al. 2015). Because of its globally high mortality and morbidity, extensive studies (Meta-Analyses of Glucose and Insulin-related traits Consortium (MAGIC) Investigators 2012; Lean et al. 2018; Zhao et al. 2018; Song et al. 2014; Huang et al. 2012; Li et al. 2006; Shi et al. 2017) have been committed to finding out its pathogenesis, prevention, and reversal.

A constructive attempt was made by Topp et al. (2000). They proposed a nonlinear dynamical model of plasma glucose concentrations, plasma insulin concentrations, and $\beta$ cell mass,

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{G}=a-(b+cI)G,\\ \dot{I}=\displaystyle { \frac{d\beta G^2}{e+G^2}}-fI,\\ \dot{\beta }=(-g+hG-g_1G^2)\beta , \end{array}\right. } \end{aligned}$$

(1.1)

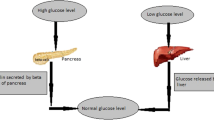
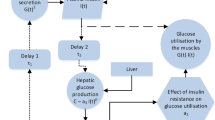
which is denoted as the $GI\beta$ model. Here, G, I, and $\beta$ represent the plasma glucose concentration (measured in mmol/l), the blood insulin concentration (measured in $\upmu$U/ml), and the $\beta$ cell mass (measured in mg), respectively. a denotes the hepatic glucose production, b is the rate of insulin-independent glucose utilization, c is the insulin sensitivity, d denotes the rate of insulin secretion, e determines the half-saturation constant, f denotes the rate of insulin clearance, g is the apoptosis rate of $\beta$ cell, h determines the $\beta$ cell’s glucose tolerance range, and $g_1$ presents the $\beta$ cell’s necrosis rate (Rathee 2017). The process of blood metabolism is shown in Fig. 1.

Fig. 1

Diagram of the $GI\beta$ model (1.1)

There have been several numerical results (Topp et al. 2000; De Gaetano et al. 2008; Ha et al. 2015) of the $GI\beta$ model. In Topp et al. (2000), the authors described three pathways in which such insufficient insulin concentrations and deficient insulin actions may develop regulated hyperglycemia, bifurcation, and dynamical hyperglycemia. Exact adaptation, a property of maintaining a constant set point for a regulated variable despite variation in model parameters was explored in De Gaetano et al. (2008). In Ha et al. (2015), the authors illustrated the consequence of bistability and other important aspects of glucose control, which underline the success of bariatric surgery and acute caloric restriction in rapidly reversing type 2 diabetes.

A fresh finding Chen et al. (2012) showed that an imminent bifurcation point can serve as a general early-warning signal before the disease occurs, especially for dysfunctional metabolic processes and regulations of cell proliferation, which enlightens us to investigate the bifurcations and related dynamic behaviors of model (1.1). Therefore, we theoretically study the global dynamic behaviors of model (1.1) in this paper. The analysis exhibits that the $GI\beta$ model has rich and complex dynamics such as Hopf and saddle-node bifurcations of codimension 1; cusp, zero-Hopf, and Bogdanov–Takens bifurcations of codimension 2; and even a Bogdanov–Takens bifurcation of codimension 3. The complexity of model (1.1) directly reflects the corresponding intricate process of glucose metabolism. Such a critical transition often occurs at the above various bifurcation points, at which the model shifts abruptly from one state to another. These sudden catastrophic shifts during gradual health deterioration imply various disease states, such as hypoglycemia, hyperglycemia, and diabetes.

However, growing evidence supports that blood glucose homeostasis is strongly regulated and controlled by internal or external periodically varying living environments. Experimental results have indicated that seasonal hyperthermia is significantly associated with increased risks of gestational diabetes mellitus (Booth et al. 2017). Besides, the circadian clock drives oscillations to regulate a diverse set of biological processes, including sleep, locomotor activity, blood pressure, body temperature, and blood hormone levels are found in all kingdoms of life (Depner et al. 2018; Dobin et al. 2013; Zhang et al. 2014; Ando et al. 2016; Morris et al. 2016). Clinical studies Ando et al. (2016), Morris et al. (2016) revealed that hepatic glucose production and glucose tolerance exhibit circadian rhythms in a pronounced 24-h cycle. Since the oscillating clock plays a critical role in generating these cyclic patterns, further studies are needed to elucidate how periodic factors influence a body’s glucose metabolism. Thus, exploring the dynamic behaviors of the $GI\beta$ model with four different periodicity mechanisms is one of our interests, doing so and would be clinically valuable. The perturbed terms are shown in Fig. 1.

In brief, the aims of this paper are twofold. First of all, for the lack of global dynamic analysis, we theoretically investigate the global dynamic behaviors of model (1.1). Moreover, we consider four more reasonable periodic mechanisms to explore the functional role of the circadian clock in global dynamics, including periodic solutions with different periods, quasiperiodic solutions, and chaotic solutions. We isolate the high-effect factors by comparing the sensitivity and correlation of the unperturbed model with those of the perturbed model. The periodically perturbed dynamics effectively fit the clinical data and appropriately explain the various phenomena of glucose level, oscillation, and disorder, which provide novel insights into practical pharmacology and medical treatment.

2 Bifurcations

Obviously, model (1.1) has three equilibria $E_0( \frac{a}{b}, 0, 0)$, $E_1(G_{1},I_{1},\beta _{1})$, $E_2(G_{2},I_{2},\beta _{2})$, where

$$\begin{aligned} \begin{aligned} G_{1,2}=\frac{h\pm \sqrt{h^2-4g_1g}}{2g_1}, I_{i}=\frac{a}{cG_{i}}-\frac{b}{c}, \beta _{i}=\frac{fI_{i}(e+G_{i}^2)}{dG_{i}^2}. \end{aligned} \end{aligned}$$

The Jacobian matrix of model (1.1) at any point $(G,I,\beta )$ is

$$\begin{aligned} J(G,I,\beta )= \left( \begin{matrix} -(b+cI)&{} \quad -cG&{} \quad 0\\ \displaystyle {\frac{2deG\beta }{(e+G^2)^2}}&{} \quad -f&{} \quad \displaystyle {\frac{dG^2}{e+G^2}}\\ (h-2g_1G)\beta &{} \quad 0&{} \quad hG-g_1G^2-g\\ \end{matrix} \right) . \end{aligned}$$

The characteristic equation at $E_i$ is

$$\begin{aligned} H(\lambda )_{i=1,2}=\lambda ^{3}+\delta (G_{i})\lambda ^{2}+\zeta (G_{i})\lambda +\theta (G_{i})=0, \end{aligned}$$

(2.1)

where

$$\begin{aligned} \begin{aligned} \delta (G_{i})&=f+\frac{a}{G_{i}},\\ \zeta (G_{i})&=\frac{af}{G_{i}}+\frac{2ef(a-bG_{i})}{G_{i}(e+G_{i}^2)},\\ \theta (G_{i})&=f(bG_{i}-a)(2g_1G_{i}-h).\\ \end{aligned} \end{aligned}$$

Theorem 1

For model (1.1), the trivial equilibrium $E_0( \frac{a}{b}, 0, 0)$ is

• a saddle-node of codimension 1, when $\displaystyle {\frac{hb}{a}-\frac{g_1b^2}{a^2}-g=0}$, $\displaystyle {\frac{2ag_1}{b}-h}\ne 0$,

• a semi-hyperbolic point of codimension 2, when $\displaystyle {\frac{hb}{a}\!-\!\frac{g_1b^2}{a^2}\!-\!g=\frac{2ag_1}{b}-h}=0$.

Proof

For $\displaystyle {\frac{hb}{a}-\frac{g_1b^2}{a^2}-g}=0$, the eigenvalues of Jacobian of model (1.1) at $E_{0}$ are $-b, 0, -f$. Define $T= (T_{ij})_{3\times 3}=({V}_{1}, {V}_{2}, {V}_{3})$, where ${V}_{1}, {V}_{2}, {V}_{3}$ are the corresponding eigenvectors of the Jacobian matrix. The transformation $\displaystyle {x=G-\frac{a}{b}}, y=I$ and $z=\beta$, brings $E_{0}$ to the origin. Let

$$\begin{aligned} \left( \begin{matrix} x\\ y\\ z\\ \end{matrix} \right) =T \left( \begin{matrix} u\\ v\\ w\\ \end{matrix} \right) , \end{aligned}$$

where

$$\begin{aligned} T= \left( \begin{matrix} 1&{} \quad 1&{} \quad 1\\ 0&{} \quad \displaystyle {-\frac{ b^2}{ac}}&{} \quad \displaystyle {\frac{b(f-b)}{ac}}\\ 0&{} \quad \displaystyle {\frac{-fb^2(a^2+eb^2)}{cda^3}}&{} \quad 0\\ \end{matrix} \right) . \end{aligned}$$

Model (1.1) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=-bu+\displaystyle {\sum _{i,j,k\in N}^{i+j+k=2}}{m}_{ijk}u^{i}v^{j}w^{k}+O(|u,v,w|^{3}),\\ \dot{v}=\displaystyle {\sum _{i,j,k\in N}^{i+j+k=2,3}}{l}_{ijk}u^{i}v^{j}w^{k}+O(|u,v,w|^{4}),\\ \dot{w}=-fw+ \displaystyle {\sum _{i,j,k\in N}^{i+j+k=2}}{n}_{ijk}u^{i}v^{j}w^{k}+O(|u,v,w|^{3}),\\ \end{array}\right. } \end{aligned}$$

(2.2)

where

$$\begin{aligned} l_{110}=l_{011}= l_{020}=h-\frac{2ag_1}{b},\ \ \ \ \ l_{030}=-g_1. \end{aligned}$$

Then, we compute the center manifold; for $v\sim 0$, there exists a center manifold

$$\begin{aligned} u=\frac{m_{020}}{b} v^{2}+O(v^{3}),w=\frac{n_{020}}{f} v^{2}+O(v^{3}). \end{aligned}$$

(2.3)

If $l_{020}=0$, model (2.2) reduced on the one dimension center manifold (2.3) is given by

$$\begin{aligned} \begin{aligned} \dot{v}&= \left( {l}_{030}+{l}_{110}\frac{{m}_{200}}{b}+{l}_{011}\frac{{n}_{200}}{f}\right) v^{3}+O(v^{4} ),\\&=-g_1v^{3}+O(v^{4}). \end{aligned} \end{aligned}$$

The coefficient of $v^{3}$ is defined and does not vanish. Hence, E is a semi-hyperbolic point of codimension 2.

If ${l}_{020}\ne 0,$ immediately we know that the model on the center manifold is topologically equivalent to

$$\begin{aligned} \dot{v}=\pm v^{2}+O(v^{3}). \end{aligned}$$

(2.4)

Therefore, it is a saddle-node of codimension 1. $\square$

In the following, we discuss the bifurcations of the nontrivial equilibrium.

Theorem 2

Model (1.1) undergoes a Hopf bifurcation at $E_{1}$, if $\delta (G_{1})\zeta (G_{1})=\theta (G_{1}).$

Proof

Consider $g_1$ as a bifurcation parameter. Substituting $\delta (G_{1})\zeta (G_{1})=\theta (G_{1})$ into Eq. (2.1) yields

$$\begin{aligned} (\lambda ^{2}+\zeta )(\lambda +\delta )=0. \end{aligned}$$

(2.5)

The three roots of Eq. (2.5) are

$$\begin{aligned} \lambda _{1,2}=\pm \sqrt{\zeta (G_{1}) }i,\lambda _{3}=\delta (G_{1}). \end{aligned}$$

We get

$$\begin{aligned} \frac{\partial \lambda _{1,2}}{\partial g_1}=\frac{2fg_1G_{1}(a-bG_{1})}{3\lambda ^2+2\delta \lambda +\zeta }, \end{aligned}$$

and for $\zeta >0$,

$$\begin{aligned} \begin{aligned} \left( {\text {Re}}\frac{\partial \lambda _{1,2}}{\partial g_1}\right) \mid _{\delta \zeta =\theta }&=\frac{bfg_1G_{1}}{\zeta ^2+\zeta \delta ^2}\ne 0,\\ \left( {\text {Im}}\frac{\partial \lambda _{1,2}}{\partial g_1}\right) \mid _{\delta \zeta =\theta }&=\frac{\sqrt{b}afg_1G_{1}}{\zeta ^2+\zeta \delta ^2}\ne 0.\\ \end{aligned} \end{aligned}$$

Similarly, if we take a as a bifurcation parameter, for $\zeta >0$, we get

$$\begin{aligned} \begin{aligned} \left( {\text {Re}}\frac{\partial \lambda _{1,2}}{\partial a}\right) \mid _{\delta \zeta =\theta }&=\frac{bf(bG_{1}-a)}{2(\zeta ^2+\zeta \delta ^2)}\ne 0,\\ \left( {\text {Im}}\frac{\partial \lambda _{1,2}}{\partial a}\right) \mid _{\delta \zeta =\theta }&=\frac{\sqrt{b}af(bG_{1}-a)}{2(\zeta ^2+\zeta \delta ^2)}\ne 0.\\ \end{aligned} \end{aligned}$$

Hence, model (1.1) undergoes Hopf bifurcation at $E_{1}$. $\square$

In the following, we prove that the model can undergo saddle-node bifurcation of codimension 1. Two nontrivial equilibria $E_{1}$ and $E_{2}$ collide at $\bar{E} (\bar{G}, \bar{I}, \bar{\beta } )$, where

$$\begin{aligned} \bar{G}=\frac{h}{2g_1},\ \ \bar{I}=\frac{2ag_1-bh}{ch},\ \ \bar{\beta }=\frac{4efg_1^2(2ag_1-bh)}{cdh}. \end{aligned}$$

Theorem 3

For model (1.1), the nontrivial equilibrium $\bar{E}( \bar{G}, \bar{I}, \bar{\beta })$ is a saddle-node of codimension 1, when $h^2-4g_1g=0$.

Proof

For $h^2-4g_1g=0$, the corresponding characteristic equation is $H(\lambda )=\lambda ^{3}+\delta (G_{i})\lambda ^{2}+\zeta (G_{i})\lambda ,$ with a zero-eigenvalue.

Using transformation $x=G-\bar{G}, y=I-\bar{I}$ and $z=\beta -\bar{\beta }$, model (1.1) can be written as

$$\begin{aligned} \left( \begin{array}{l} \dot{x}\\ \dot{y}\\ \dot{z}\\ \end{array} \right) =J(\bar{E}) \left( \begin{array}{l} x\\ y\\ z\\ \end{array} \right) + \left( \begin{array}{c} {a}_{110}xy \\ b_{200}y^2+b_{101}xz+b_{300}x^3+b_{201}x^2z\\ c_{200}z^2+c_{101}xz+c_{201}x^2z\\ \end{array} \right) +O(|x, y, z|)^{4},\nonumber \\ \end{aligned}$$

(2.6)

where

$$\begin{aligned} \begin{aligned} {a}_{110}&=-c, b_{101}=\frac{2ed\bar{G}}{(e+\bar{G}^2)^2}, b_{200}=\frac{ed\bar{\beta }(e-3\bar{G}^2)}{(e+\bar{G}^2)^3},c_{101}=h-2g_1\bar{G},\\ c_{201}&=-\frac{g_1}{3}, b_{300}=-\frac{2ed\bar{\beta }\bar{G}}{(e+\bar{G}^2)^3},b_{201}=\frac{ed(e-3\bar{G}^2)}{(e+\bar{G}^2)^3}, c_{200}=-g_1\bar{\beta }.\\ \end{aligned} \end{aligned}$$

Let $q_{0}\in \mathbb {R}^{3}$ be proper eigenvector for $Jq_{0}=0$ and $p_{0}\in \mathbb {R}^{3}$ be corresponding adjoint eigenvector for $J^{T}p_{0}=0$.

To achieve the necessary normalization $\langle p_{0},q_{0}\rangle = 1$, we can take

$$\begin{aligned} q_{0}= \left( \begin{matrix} \displaystyle {\frac{n}{s}}\\ \displaystyle {\frac{(b+c\bar{I})n}{cs\bar{G}}}\\ 1\\ \end{matrix} \right) , p_{0}= \left( \begin{matrix} 0\\ 0\\ 1\\ \end{matrix} \right) , \end{aligned}$$

where

$$\begin{aligned} n=\displaystyle {\frac{-d\bar{G}^2}{e+\bar{G}^2}},s =\displaystyle {f(b+c\bar{I})+\frac{2cde\bar{\beta }\bar{G}^2}{(e+\bar{G}^2)^2}}. \end{aligned}$$

By center manifold theorem, the restriction of model (2.6) to the center manifold takes the form

$$\begin{aligned} \dot{v}=\frac{1}{2}\langle p,B(q_{0},q_{0})\rangle v^2+O(v^{3}), \end{aligned}$$

where

$$\begin{aligned}B(q_{0},q_{0})=2\frac{n}{s} \left( \begin{matrix} a_{110}\displaystyle {\frac{n}{s}}\\ b_{200}\displaystyle {\frac{n}{s}+b_{101}}\\ c_{200}\displaystyle {\frac{n}{s}}\\ \end{matrix} \right) ,~ \langle p_{0},B(q_{0},q_{0})\rangle =-2g_1\bar{\beta }\frac{n^2}{s^2}\ne 0. \end{aligned}$$

Therefore, $\bar{E}$ is a non-degenerate saddle-node of codimension 1 and model (2.6) on the center manifold is topologically equivalent to model (2.4). $\square$

Next, we study zero-Hopf bifurcation of codimension 2, and Bogdanov–Takens bifurcation of codimension 2, 3. Here, we ignore the biological meaning to get the global bifurcations.

Theorem 4

For model (1.1), the nontrivial equilibrium $\bar{E}$ is

• a zero-Hopf bifurcation point of codimension 2, when $\delta (\bar{G})=\theta (\bar{G})=0, F(0)\ne 0$,

• a zero-Hopf bifurcation point of codimension at least 3, when $\delta (\bar{G})=\theta (\bar{G})=F(0)=0$,

where

$$\begin{aligned} F(0)=\frac{-mc\bar{G}}{[(b+c\bar{I})^2+\omega ^2+mc\bar{G}]}\left( \frac{1}{\bar{G}}-\frac{ed\bar{\beta } (e-3\bar{G}^2)}{(e+\bar{G}^2)^3}-\frac{g_1\bar{\beta }n(b+c\bar{I})}{cs\bar{G}}\right) . \end{aligned}$$

Proof

In the following, we theoretically consider the zero-Hopf bifurcation point. Choose a, c as bifurcation parameters and denote further by $\alpha = (a, c).$

For $\delta (\bar{G})=\theta (\bar{G})=0$, the corresponding characteristic equation of the coinciding equilibria is

$$\begin{aligned} H(\lambda )=\lambda ^{3}+\zeta (G_{i})\lambda =0, \end{aligned}$$

and its eigenvalues are 0 and $\pm \omega i$, where $\omega ^2= \displaystyle {\frac{af}{\bar{G}}+\frac{2ef(a-b\bar{G})}{\bar{G}(e+\bar{G}^2)}}.$

Let $q_{1}, p_1\in \mathbb {C}^{3}$ are corresponding eigenvector and adjoint eigenvector given by

$$\begin{aligned} Jq_{1} = i\omega ,\ \ \ \ J^{T}p_{1}=- i\omega , \end{aligned}$$

such that

$$\begin{aligned} \langle p_{0},q_{0}\rangle = 1,~\langle p_{1},q_{1}\rangle = 1,~\langle p_{0},q_{1}\rangle = 0,~\langle p_{1},q_{0}\rangle = 0. \end{aligned}$$

Here

$$\begin{aligned}{} & {} q_{1}= \left( \begin{matrix} 1\\ \displaystyle {\frac{-(i\omega +b+c\bar{I})}{c\bar{G}}}\\ 0\\ \end{matrix} \right) ,~ p_{1}\\{} & {} \quad =\displaystyle {\frac{-mc\bar{G}}{(b+c\bar{I})^2+\omega ^2+mc\bar{G}}} \left( \begin{matrix} -1\\ \displaystyle {\frac{-i\omega +b+c\bar{I}}{m}}\\ \displaystyle {\frac{n}{s}-\frac{n(b+c\bar{I})(b+c\bar{I}-i\omega )}{smc\bar{G}}}\\ \end{matrix} \right) , \end{aligned}$$

with $m=\displaystyle {\frac{2ed\bar{G}\bar{\beta }}{(e+{\bar{G}}^2)^2}}$.

Using the transformation

$$\begin{aligned} u =\langle p_{0}(\alpha ), x\rangle ,\\\ \ \ \ z =\langle p_{1}(\alpha ), x\rangle , \end{aligned}$$

with $x=uq_{0} + zq_{1} + \bar{z} \bar{q}_{1}$, the model (2.6) can be further put in the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=g(u,z,{\overline{z}},\alpha ),\\ \dot{z}=\lambda z+h(u,z,{\overline{z}},\alpha ),\\ \end{array}\right. } \end{aligned}$$

(2.7)

where $g(u,z,{\overline{z}},\alpha ) = \langle {p_0},F(u{q_0} + z{q_1} + {\overline{z}} \bar{q}_1,\alpha )\rangle ,$ $h(u,z,{\overline{z}},\alpha ) = \langle {p_1},F(u{q_0} + z{q_1} + {\overline{z}} \bar{q}_1,\alpha )\rangle .$

And these functions are smooth of their variables, which Taylor expansions in $u, z, \bar{z}$ start with quadratic terms

$$\begin{aligned} g(u,z,{\overline{z}},\alpha )= & {} \sum \limits _{i+ j + k\ge 2} {\frac{1}{{i!j!k!}}} {g_{ijk}}(\alpha ){u^i}{z^j}{{\overline{z}} ^k}, \\ h(u,z,{\overline{z}},\alpha )= & {} \sum \limits _{i+ j + k \ge 2} {\frac{1}{{i!j!k!}}} {h_{ijk}}(\alpha ){u^i}{z^j}{{\overline{z}} ^k}. \end{aligned}$$

By calculation, we obtain

$$\begin{aligned} \begin{aligned} {g}_{200}&=c_{200}\frac{n^2}{s^2}+c_{101}\frac{n}{s},~g_{020}=c_{200}, g_{002}=c_{200},~g_{101}=2c_{200}\frac{n}{s}+c_{101},\\ g_{110}&=2c_{200}\frac{n}{s}+c_{101},~ g_{011}=2c_{200},~h_{011} =2\left( \frac{(b+c\bar{I})}{\tilde{G}}+m_{1}\right) +2m_{2}i,\\ h_{020}&=\left( \frac{b+c\bar{I}}{\bar{G}}+m_{1}\right) +\left( \frac{\omega }{\bar{G}}+m_{2}\right) i,~ h_{002}=\left( \frac{b+c\bar{I}}{\bar{G}}+m_{1}\right) +\left( \frac{-\omega }{\bar{G}}+m_{2}\right) i,\\ h_{101}&=2m_{1}\frac{n}{s}+m_{3}+\left( \frac{-n\omega }{s\bar{G}}+\frac{2m_{2}n}{s}+m_{4}\right) i,~ h_{110}=2m_{1}\frac{n}{s}+m_{3}\\&\quad +\left( \frac{n\omega }{s\bar{G}}+\frac{2m_{2}n}{s}+m_{4}\right) i,\\ h_{200}&=\frac{-n^2(b+c\bar{I})}{s^2\bar{G}}+\left( m_{1}\frac{n}{s}+m_{3}\right) \frac{n}{s}+\left( m_{2}\frac{n}{s}+m_{4}\right) \frac{n}{s}i,\\ \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} m_{1}&=\frac{b_{200}(b+c\bar{I})}{m}+c_{200}\frac{nmc\bar{G}-n(b+c\bar{I})^2}{mcs\bar{G}},~m_{2}=\frac{\omega }{m}\left( -b_{200}+\frac{c_{200}n(b+c\bar{I})}{cs\bar{G}}\right) ,\\ m_{3}&=\frac{b_{101}(b+c\bar{I})}{m}+c_{101}\frac{nmc\bar{G}-n(b+c\bar{I})^2}{mcs\bar{G}},~ m_{4}=\frac{\omega }{m}\left( -b_{101}+\frac{c_{101}n(b+c\bar{I})}{cs\bar{G}}\right) . \end{aligned} \end{aligned}$$

Under the assumption $g_{200}\ne 0$ and $g_{011}\ne 0$, we introduce the changes

$$\begin{aligned} \begin{aligned} v =&u -\frac{1}{2}\frac{g_{020}}{2\omega i}z^2+\frac{1}{2}\frac{g_{002}}{2\omega i}\bar{z}^2-\frac{g_{110}}{\omega i}uz+\frac{g_{101}}{\omega i}u\bar{z},\\ w =&z+\frac{1}{2}\frac{h_{200}}{\omega i}u^2 -\frac{1}{2}\frac{h_{020}}{\omega i}bar{u}^2+\frac{1}{2}\frac{h_{002}}{3\omega i}\bar{z}^2+\frac{h_{101}}{2\omega i}u\bar{z}+\frac{h_{011}}{\omega i}z\bar{z},\\ \end{aligned} \end{aligned}$$

and a linear scaling of the variables and time

$$\begin{aligned} \begin{aligned} u&=v +\frac{1}{2} r_3 (\alpha ) v^2,\\ z&=w + K (\alpha ) vw,\\ \textrm{d}t&=(1 +r_1v + r_2 |w|^2)\textrm{d}\tau ,\\ \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} r_1&=\frac{{\text {Im}}g_{110}h_{200}}{g_{200}\omega },~K=\frac{r_2\omega i+H_{021}}{g_{011}},~r_3=2{\text {Re}}K-r_1\\&\quad -\frac{2g_{110}{\text {Im}}h_{011}+g_{020}{\text {Im}}h_{010}}{g_{011}\omega }, \end{aligned} \end{aligned}$$

with

$$\begin{aligned} H_{021}=\frac{i}{2\omega }\left( h_{011}h_{020}-\frac{1}{2}h_{101}g_{020}-2|h_{011}|^2-\frac{1}{3}{|h_{011}|^2}\right) . \end{aligned}$$

Then, model (2.7) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=\frac{1}{2}g_{200}u^2+g_{011}|z|^2+O(|| (u, z, \bar{z}) ||^4),\\ \dot{z}=i\omega z+D(0)uz+E(0)u^2z+O(|| (u, z, \bar{z}) ||^4),\\ \end{array}\right. } \end{aligned}$$

(2.8)

where

$$\begin{aligned} \begin{aligned} D(0)&=\displaystyle {2m_{1}\frac{n}{s}+m_{3}+\left( \frac{n\omega }{s\bar{G}}+\frac{4m_{2}n}{s}+3m_{4}\right) i},\\ F(0)&=\displaystyle {\frac{-mc\bar{G}}{[(b+c\bar{I})^2+\omega ^2+mc\bar{G}]} \left( \frac{1}{\bar{G}}-\frac{ed\bar{\beta }(e-3\bar{G}^2)}{(e+\bar{G}^2)^3}-\frac{g_1\bar{\beta }n(b+c\bar{I})}{cs\bar{G}}\right) }. \end{aligned} \end{aligned}$$

If $F(0)=0$, then $\bar{E}$ is a degenerate zero-Hopf bifurcation point of codimension at least 3.

Contrarily, if $F(0)\ne 0$, by linear scaling and time-reparametrization

$$\begin{aligned} u=\frac{g_{200}}{F_{0}}u_1,~ z=\frac{g_{200}^3}{g_{011}F^2(0)}v_1,~ t=\frac{F(0)}{g^2_{200}}\tau , \end{aligned}$$

model (2.8) is topologically equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u_1}=u_{1}^2\pm |u_1|^2+O(|| (u_{1}, v_{1}, \bar{v}_{1}) ||^4),\\ \dot{v_1}=\displaystyle {\frac{E(0)}{g^2_{200}}}i\omega u_1+ \displaystyle {\frac{D(0)}{g_{200}}}u_1v_1+u_1^2v_1+O(|| (u_{1}, v_{1}, \bar{v}_{1}) ||^4).\\ \end{array}\right. } \end{aligned}$$

(2.9)

Hence, $\bar{E}$ is a non-degenerate zero-Hopf bifurcation point of codimension 2. $\square$

Theorem 5

Suppose $\delta (\bar{G})=\theta (\bar{G})=0$ and $\bar{M}_{11}\ne 0$, then $\bar{E}$ is a Bogdanov–Takens point of codimension 2, and model (1.1) localized at $\bar{E}$ is topologically equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=v,\\ \dot{v}=u^2+ sign(\bar{M}_{11}) uv+O(|u,v|^{3}),\\ \end{array}\right. } \end{aligned}$$

(2.10)

where

$$\begin{aligned} \bar{M}_{11}=\frac{g_1f(e+\bar{G}^2)}{d\bar{G}^2}+\frac{cf[2(b+c\bar{I})-1]}{b+c\bar{I}}+\frac{(e-3\bar{G}^2)(2\bar{I}+d\bar{\beta }\bar{G})}{4e\bar{G}\bar{I}^2(e+\bar{G}^2)}. \end{aligned}$$

Proof

For $\delta (\bar{G})=\theta (\bar{G})=0$, the corresponding characteristic equation of the coinciding equilibria $\bar{E}$ is

$$\begin{aligned} H(\lambda )=\lambda ^{3}+\zeta (\bar{G}_{i})\lambda =0. \end{aligned}$$

The generalized eigenvectors of $\lambda _{1,2}=0$ and the eigenvector of $\lambda _{3}=-f-b-c\bar{I}$ are

$$\begin{aligned} V_{1}= \left( \begin{matrix} -f\\ \displaystyle {\frac{-2ef\bar{I}}{\bar{G}(e+\bar{G}^2)}}\\ 0\\ \end{matrix} \right) ,~ V_{2}= \left( \begin{matrix} \displaystyle {\frac{f(1-b-c\bar{I})}{(b+c\bar{I})}}\\ \displaystyle {\frac{2ef\bar{I}}{\bar{G}(e+\bar{G}^2)}}\\ \displaystyle {\frac{-(e+\bar{G^2})(f+b+c\bar{I})}{d\bar{G^2}(b+c\bar{I})}}\\ \end{matrix} \right) ,~ V_{3}= \left( \begin{matrix} b+c\bar{I}\\ \displaystyle {\frac{-2ef\bar{I}}{\bar{G}(e+\bar{G}^2)}}\\ 0\\ \end{matrix} \right) . \end{aligned}$$

Let $\bar{T}=(V_1, V_2, V_3)^{T}$, under the non-singular linear translation

$$\begin{aligned} \left( \begin{matrix} x\\ y\\ z\\ \end{matrix} \right) =\bar{T} \left( \begin{matrix} u\\ v\\ w\\ \end{matrix} \right) , \end{aligned}$$

model (1.1) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=-v+L_{20}u^2+L_{11}uv+L_{02}v^2+O(|u,v,w|^{3}),\\ \dot{v}=M_{20}u^2+M_{11}uv+M_{02}v^2+O(|u,v,w|^{3}),\\ \dot{w}=-(f+b+c\bar{I})w+O(|u,v,w|^{2}),\\ \end{array}\right. } \end{aligned}$$

(2.11)

where

$$\begin{aligned} \begin{aligned} L_{20}&= a_{110}\frac{f}{M}+b_{200}\frac{Nf^2}{Mm^2}+c_{200}\frac{n(MN-f)f^2}{m^2M^2},\\ L_{21}&=\frac{Nf^2}{Mm^2} \left[ 3b_{300}\frac{f(N-1)}{mN}+b_{201}\frac{N}{M}+c_{201}\frac{(MN-f)}{N^2}\right] ,\\ L_{12}&=\frac{(N-1)^2f^2}{Mm^2N^2} \left[ 3b_{300}\frac{-f}{mN}+b_{201}\frac{M}{n}+c_{201}\frac{(MN-f)}{1-N}\right] ,\\ M_{02}&=c_{101}\frac{f(N-1)}{mN},\ \ \ M_{21}=c_{201}\frac{f^2M}{m^2nN}, \ \ \ M_{20}=c_{200}\frac{nNf^2}{Mm^2}, \\ M_{11}&=c_{200}\frac{2n(1-N)f^2}{Mm^2},\\ L_{11}&= \frac{cf(2N-1)}{N}+\frac{f}{m}\left[ \frac{b_{200}Mf(2-N)}{m}-\frac{b_{201}}{n}\right] \\&\quad +\frac{nf(MN-f)}{mNM^2}\left[ c_{201}\frac{M}{n}+c_{200}\frac{f(N-2)}{m}\right] ,\\ \end{aligned} \end{aligned}$$

with $M=f+b+c\bar{I},~ N=b+c\bar{I},~ m=\displaystyle {\frac{2ef\bar{I}}{\bar{G}(e+G^2)}}.$ The other coefficients of quadratic terms of model (2.11) are omitted here.

According to the center manifold theorem, for $\varepsilon _{1}, \varepsilon _{2}$ sufficiently small, there exists a center manifold for model (2.11), which can be locally represented as follows

$$\begin{aligned} W^{c}= \left\{ (u, v, w) | w=H(u, v), |u|<\varepsilon _{1}, |v|<\varepsilon _{2}, H(0, 0)=0, DH(0, 0)=0 \right\} . \end{aligned}$$

Then, model (2.11) restricted to the center manifold is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=-v+L_{20}u^2+L_{11}uv+L_{02}v^2+O(|u,v,w|^{3}),\\ \dot{v}=M_{20}u^2+M_{11}uv+M_{02}v^2+O(|u,v,w|^{3}).\\ \end{array}\right. } \end{aligned}$$

(2.12)

Using the near-identify transformation

$$\begin{aligned} {\left\{ \begin{array}{ll} u=X, \\ v=-Y+L_{20}X^2+M_{02}XY+O(|X, Y|^{3}), \end{array}\right. } \end{aligned}$$

and rewriting X, Y into u, v, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=v,\\ \dot{v}=\bar{M}_{20}u^2+\bar{M}_{11}uv+O(|u, v|^{3}), \end{array}\right. } \end{aligned}$$

(2.13)

where $\bar{M}_{20}=-M_{20},~\bar{M}_{11}=-M_{02}-L_{11}$.

By calculation, we get

$$\begin{aligned} \begin{aligned} \bar{M}_{20}&=-\frac{f(b+c\bar{I})\bar{G}^2(e+\bar{G}^2)^2}{4g_1(f+b+c\bar{I})\bar{I}e^2}\ne 0,\\ \bar{M}_{11}&=\frac{g_1f(e+\bar{G}^2)}{d\bar{G}^2}+\frac{cf[2(b+c\bar{I})-1]}{b+c\bar{I}}+\frac{(e-3\bar{G}^2)(2\bar{I}+d\bar{\beta }\bar{G})}{4e\bar{G}\bar{I}^2(e+\bar{G}^2)}. \end{aligned} \end{aligned}$$

Under the above assumptions, making a change of coordinates and time to preserve the orientation by time

$$\begin{aligned} u\rightarrow {|\frac{\bar{M}_{20}}{\bar{M}_{11}^2}}|u,v \rightarrow {|\frac{\bar{M}_{20}^2}{\bar{M}_{11}^3}|v},t \rightarrow {|\frac{\bar{M}_{11}}{\bar{M}_{20}}|t}, \end{aligned}$$

model (1.1) is topologically equivalent to the normal form (2.10). $\square$

Theorem 6

Suppose that $\zeta (\bar{G})=\theta (\bar{G})=\bar{M}_{11}=0$ and $\bar{M}_{31}\ne 0$, then $\bar{E}$ is a codimension 3 degenerate Bogdanov–Takens singularity, and the model (1.1) localized at $\bar{E}$ is topologically equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=v,\\ \dot{v}=u^2+u^3v+O(|u, v|^4)v. \end{array}\right. } \end{aligned}$$

(2.14)

where $\bar{M}_{31}=-(2L_{12}M_{20}+L_{21}M_{11}+L_{11}M_{21})$.

Proof

The proof is long but standard, which can be divided into seven steps.

Step 1:

Expand the model (2.6) up to order 4, and diagonalize the linear part with transformation $\bar{T}$.

Step 2:

Calculate the center manifold $Z=H(u, v)$ up to $O(|u, v|^4)$ and reduce the model on the center manifold, then model is restricted on

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=-v+L_{20}u^2+L_{02}v^2+L_{11}u_1v_1+L_{30}u^3+L_{03}v^3+L_{21}u^2v+L_{12}v^2u+ O(|u, v|^4),\\ \dot{v}=M_{02}v^2 +M_{02}v^2+M_{03}v^3+M_{21}u^2v+ O(|u, v|^4).\\ \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.15)

Step 3:

Reduction to a nonlinear oscillator.

We make a near-identity transformation

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1=u,\\ v_1=-v+L_{20}u^2+L_{02}v^2+L_{11}u_1v_1+L_{30}u^3+L_{03}v^3+L_{21}u^2v+L_{12}v^2u+ O(|u, v|^4), \end{array}\right. } \end{aligned}$$

which brings model (2.15) into

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u_1}=v_1,\\ \dot{v_1}=\displaystyle {\sum _{i=2,3,4}}\bar{M}_{i0}u_1^{i}+\displaystyle {\sum _{i,j\in N}^{i+j=2,3,4}}\bar{M}_{ij}u_1^{i}v_1^{j}+O(|u_1, v_1|^{5}), \end{array}\right. } \end{aligned}$$

(2.16)

where $\bar{M}_{20}=-M_{20}$ and $\bar{M}_{31}=-2L_{12}M_{20}-L_{21}M_{11}-L_{11}M_{21}.$ The other coefficients of quadratic terms of model (2.16) are omitted here.

Step 4:

Eliminating non-resonant terms in model (2.16).

Under a series of near-identity transformations $(i=2, 3, 4)$,

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{i-1}=u_i+u_{i-1}^i,\\ v_{i-1}=v_i, \end{array}\right. } \end{aligned}$$

model (2.16) is transformed to

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u_4}=v_4,\\ \dot{v_4}=\bar{M}_{20}u_4^2+\bar{M}_{30}u_4^3+\bar{M}_{40}u_4^4+\bar{M}_{21}u_4^2v_4+\bar{M}_{31}u_4^3v_4+O(|u_4, v_4|^{5}). \end{array}\right. } \end{aligned}$$

(2.17)

Step 5:

Removing $u_4^2v_4$ terms from model (2.17).

Note that $\bar{M}_{20}\ne 0$, let $r=\displaystyle {\frac{\bar{M}_{21}}{\bar{M}_{20}}}$, then $\bar{M}_{20}u_4^2+\bar{M}_{21}u_4^2v_4=\bar{M}_{20}u_4^2(1+rv_4)$. We consider a change of variables $u_4=u_5$ and $v_4 = v_4(v_5) = v_5 + O(v_5^2)$ such that

$$\begin{aligned} v_5\textrm{d}v_5=\frac{v_4}{1+rv_4}\textrm{d}v_4. \end{aligned}$$

(2.18)

That is

$$\begin{aligned} v_5^2=\frac{2}{r}\left[ v_4-\frac{1}{r}ln(1+rv_4)\right] =v_4^2-\frac{2r}{3}v_4^3+\frac{r^2}{2}v_4^4+O(v_4^5). \end{aligned}$$

Or, equivalently

$$\begin{aligned} v_5=v_4-\frac{r}{3}v_4^2-\frac{7r^2}{36}v_4^3+ O(v_4^4), v_4=v_4(v_5)=v_5+\frac{r}{3}v_5^2+\frac{r^2}{36}v_5^3+ O(v_5^4).\nonumber \\ \end{aligned}$$

(2.19)

We change model (2.17) to the form

$$\begin{aligned} v_4\textrm{d}v_4=[Q(u_4,v_4)+ O(|u_4, v_4|^5)]\textrm{d}u_4, \end{aligned}$$

(2.20)

where $Q(u_4,v_4)=\bar{M}_{20}u_4^2+\bar{M}_{30}u_4^3+\bar{M}_{40}u_4^4+\bar{M}_{21}u_4^2v_4+\bar{M}_{31}u_4^3v_4$.

Now we divide both sides of (2.20) by $1 + rv_4$, and using (2.18) we find

$$\begin{aligned} v_5\textrm{d}v_5=\left\{ \frac{[Q(u_5,v_4(v_5))-\bar{M}_{20}u_5^2[1 + rv_4(v_5)]+ O(|u_5, v_4(v_5)|^5)}{1 + rv_4(v_5)}+\bar{M}_{20}u_5^2\right\} \textrm{d}u_5, \end{aligned}$$

then using the second equality of (2.19) we obtain

$$\begin{aligned} v_5\textrm{d}v_5=[\bar{M}_{20}u_5^2+ O(|u_5|^3)+\bar{M}_{31}u_5^3v_5+O(|u_5, v_5|^4)v_5]\textrm{d}u_5, \end{aligned}$$

which is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u_5}=v_5,\\ \dot{v_5}=\bar{M}_{20}u_5^2+ O(|u_5|^3)+\bar{M}_{31}u_5^3v_5+O(|u_5, v_5|^4)v_5. \end{array}\right. } \end{aligned}$$

(2.21)

Step 6:

Changing $\bar{M}_{20}$ and $\bar{M}_{31}$ to be 1 in (2.21).

Under the assumption that $\bar{M}_{20}\bar{M}_{31}\ne 0$, we make the following changes of variables and time,

$$\begin{aligned} u_5=\bar{M}_{20}^{\frac{1}{5}}\bar{M}_{31}^{-\frac{2}{5}}u_6,\ \ \ v_5=\bar{M}_{20}^{\frac{4}{5}}\bar{M}_{31}^{-\frac{3}{5}}v_6,\ \ \ t=\bar{M}_{20}^{-\frac{3}{5}}\bar{M}_{31}^{\frac{1}{5}}\tau , \end{aligned}$$

then model (2.21) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u_6}=v_6,\\ \dot{v_6}=u_6^2+ O(|u_6|^3)+u_6^3v_6+O(|u_6, v_6|^4)v_6. \end{array}\right. } \end{aligned}$$

(2.22)

Step 7:

Eliminating the term $O(|u_6|^3)$ in model (2.22).

Let $\phi (u_6)=u_6^2+O(u_6^3)$ and $\psi (u_6)=\int _{0}^{u_6}\phi (u_6)\textrm{d}u_6$. By a change of coordinates and time

$$\begin{aligned} u_6=(3\psi (u_6))^{\frac{1}{3}},\ \ \ v_6=v_6,\ \ \ \tau =(3\psi (u_6))^{-\frac{2}{3}}\phi (u_6)\tau , \end{aligned}$$

and rewriting $u_6, v_6$ into u, v, we get that

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{u}=v,\\ \dot{v}=u^2+u^3v+O(|u, v|^4)v. \end{array}\right. } \end{aligned}$$

Hence, $\bar{E}$ is a codimension 3 degenerate Bogdanov–Takens singularity. $\square$

Some bifurcation diagrams and bifurcation curves are shown in Fig. 2. Point H(LP, BT, ZH, GH, CP, BP) represents Hopf (fold, Bogdanov–Takens, zero-Hopf, degenerated Hopf, cusp, transcritical) bifurcation point. In Fig. 2a, the equilibrium is stable (unstable) on the solid (dashed) line. In Fig. 2c–f, purple (blue) curve is subcritical (supercritical) Hopf bifurcation curve; red curve is fold bifurcation curve; green curve represents Hopf bifurcation curve.

Fig. 2

a Bifurcation diagram with $a=16.5,~b=2,~c=1,~d=4,~e=3.6,~f=1,~g=27.4,~h=40,~g_1=1$. b Three families of periodic solutions corresponding to (a). c and d Fold bifurcation curve and Hopf bifurcation curve with $a=6.13,~b=5.9,~c=1,~d=4,~e=0.1,~f=1,~g=0.99,~h=1.83,~g_1=0.72$. e Fold-Hopf bifurcation curve with $a=0.34,~b=4,~c=2,~d=2,~e=100,~f=1,~g=7,~h=35.34,~g_1=39.93$. f Bogdanov–Takens bifurcation curve with $a=26.74,~b=4,~c=2,~d=2,~e=100, ~f=1,~g=7,~h=8.24,~g_1=1$

3 Dynamics of Perturbed Model

3.1 Method of Investigation

Maintaining blood glucose homeostasis is achieved by an intricate balance and affected by insomnia (Stein et al. 2018), obesity (Brenachot et al. 2017), smoking (Aulinas et al. 2016), diet (Micha et al. 2017), temperature (Booth et al. 2017), and time difference (Depner et al. 2018). The internal circadian oscillator regulates the physiological parameters and periodic external environment, which exhibit obvious circadian rhythmicity (Depner et al. 2018; Dobin et al. 2013; Zhang et al. 2014; Ando et al. 2016; Morris et al. 2016). Here, due to hepatic glucose production and $\beta$ cell’s glucose tolerance play key roles in glucose metabolism, we consider $GI\beta$ model (1.1) with four different periodicity mechanisms. That is,

$$\begin{aligned} \begin{aligned} \text {mechanism 1:}~a&=a_0(1+\varepsilon \sin 2\pi \omega t), \\ \text {mechanism 2:}~h&=h_0(1+\varepsilon \sin 2\pi \omega t),\\ \text {mechanism 3:}~a&=a_0(1+\varepsilon _{1}\sin 2\pi \omega t)\ \text{ and } \ h=h_0(1+\varepsilon _{2}\sin 2\pi \omega t),\\ \text {mechanism 4:}~a&=a_0(1+\varepsilon _{1}\sin 2\pi \omega t)\ \text{ and }\ h=h_0(1+\varepsilon _{2}\cos 2\pi \omega t). \end{aligned} \end{aligned}$$

(3.1)

Here, $\varepsilon$ is the degree of the periodicity. $a_0$, $h_0$ are the average value of a, h.

The bifurcations of the periodically perturbed model are obtained by Poincaré map via a continuous technique. The periodical perturbation can be done by adding a nonlinear oscillator with the desired periodic as the solution components. For model (1.1), the perturbed period is 1 day. Here, we take such an oscillator,

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{v}= v+2\pi w-v(v^2+w^2),\\ \dot{w}= -2\pi v+w-w(v^2+w^2), \end{array}\right. } \end{aligned}$$

(3.2)

with an asymptotically stable periodic solution $v=\sin 2\pi t,~w=\cos 2\pi t.$ In the periodicity mechanisms (3.1), model (1.1) can be transformed into four autonomous five-dimensional models. Taking the second mechanism of (3.1) as an example, the higher dimensional autonomous model is

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{G}= a-(b+cI)G,\\ \dot{I}= \displaystyle {\frac{d\beta G^2}{e+G^2}}-fI,\\ \dot{\beta }=(-g+h_0(1+\varepsilon v)G-g_1G^2)\beta ,\\ \dot{v}=v+2\pi w-v(v^2+w^2),\\ \dot{w}=-2\pi v+w-w(v^2+w^2). \end{array}\right. } \end{aligned}$$

(3.3)

The equilibrium $(x_{a},~y_{a},~z_{a})$ of model (1.1) corresponds the periodic solution $(x_{a},~y_{a},~z_{a},~\sin 2\pi t,~\cos 2\pi t)$ of the perturbed model (3.3). When $\varepsilon \ne 0$, we can calculate the bifurcation diagrams of model (3.3) by using the Poincaré map $\mathscr {P}$. For model (1.1), the first return map is

$$\begin{aligned} \begin{aligned} \mathscr {P}: (y_1(0),~y_2(0),~y_3(0),~v(0),~w(0)) \mapsto (y_1(1),~y_2(1),~y_3(1),~v(1),~w(1)). \end{aligned}\nonumber \\ \end{aligned}$$

(3.4)

The phase portrait of the Poincaré map $\mathscr {P}$ is composed of fixed points, regular and irregular invariant sets, and all other orbits. The k-period fixed points, regular and irregular invariant sets correspond to subharmonical periodic solutions with period k, quasiperiodic solutions, and chaotic solutions, respectively. In the bifurcation diagrams presented below, we use the following notation $h^{(k)}$, $t^{(k)}$, and $f^{(k)}$ to denote Hopf (Neimark–Sacker) bifurcation curve, tangent (fold) bifurcation curve, and flip (period doubling) bifurcation curve. In addition, A or $A_i,$ B or $B_i,$ C or $C_i,$ D or $D_i, (i\in \mathbb {N})$, represent 1:1 resonance, 1:2 resonance, 1:3 resonance, 1:4 resonance. See detailed descriptions in Ren and Li (2016).

3.2 Bifurcations of Perturbed Model with Periodic Mechanism 1 and 2.

According to Theorem 2, we classify the unperturbed model (1.1) into four cases, resorting to the types of Hopf bifurcations. In this subsection, we shall explore and present bifurcation diagrams of the Poincar’e map for the perturbed model with periodic mechanism 1 and mechanism 2.

Case 1 The unperturbed model (1.1) undergoes two supercritical Hopf bifurcations when a is varied. It undergoes two supercritical Hopf bifurcations if h is varied.

Taking $a_{0} = 16.51,~b = 2,~c = 1,~d = 4,~e = 3.559,~f = 1,~g = 27.425,~h_0 = 40,~g_1 = 1$, the unperturbed model (1.1) undergoes two supercritical Hopf bifurcations at $a^1_{H}=5.34$ and $a_{H}^2=1.66$ when $a_{0}$ is varied. It undergoes two supercritical Hopf bifurcations at $h_{H}^1=11.878$ and $h_{H}^2=15.01$ when $h_{0}$ is varied. For these values, the unperturbed model oscillates on a stable limit cycle. The asymptotic period of the cycle (evaluated numerically) is 1.497 (3.609) when $a_{0}$ approaches $a_{H}^1$ ($a_{H}^2$). It is 1.51 (2.809) while $h_{0}$ approaching $h_{H}^1$ ($h_{H}^2$). The bifurcation diagrams of the perturbed model on the $(\varepsilon ,a_{0})$ and $(\varepsilon ,h_{0})$ planes are given in Fig. 3a and c. Figure 3b and d is the partial enlargement drawings of Fig. 3a and c.

In Fig. 3a, the points $H_{1}$ and $H_{2}$ on the $a_{0}$-axis correspond to two supercritical Hopf bifurcations of the model (1.1). These points are the initial points of period-one torus curves $h_{1}^{(1)}$ and $h_{2}^{(1)}$. $h_{1}^{(1)}$ ($h_{2}^{(1)}$) passes through a 1:3 resonance $C_{1}$ ($C_{3}$) and terminates at a 1:2 resonance $B_{1}$ ($B_{3}$). Besides, the period-one flip bifurcation $f^{(1)}$ also passes through $B_{1}$ and $B_{2}$. At the point T on $a_{0}$-axis, the period of the stable limit cycle of model (1.1) is two. From T, two branches of tangent curves $t_{1}^{(2)}$ and $t_{2}^{(2)}$ originate; and $t_{2}^{(2)}$ intersects with $f^{(1)}$. A period-two torus bifurcation curve $h^{(2)}$ starts at a point of $t_{1}^{(2)}$ and terminates at a 1:2 resonance $B_{2}$. There are a 1:3 resonance $C_{2}$ and a 1:4 resonance D on it. There are flip curves $f^{(2)}$, $f^{(4)}$ in Fig. 3b.

Fig. 3

Bifurcation diagrams of the perturbed model with $a_{0} = 16.51,~b = 2,~c = 1,~d = 4,~e = 3.559,~f = 1,~g = 27.425,~h_0 = 40,~g_1 = 1.$ b, d is the partial enlargement drawings of (a) and (c)

The curve $h_{1}^{(1)}$ is formed by the continuation of a Neimark–Sacker bifurcation of Poincaré map $\mathscr {P}$. When the curve $h_{1}^{(1)}$ is crossed to below (i.e., from region 1 to 2 in Fig. 3b), a stable point of the Poincaré map $\mathscr {P}$ loses its stability and a stable closed invariant curve appears. Besides, this invariant curve in region 2 can be destroyed via a homoclinic structure near point $B_1$, giving rise to chaotic solutions. The perturbed stable limit cycle bifurcates a stable torus. And this fixed point becomes stable again while crossing the curve $h_{2}^{(1)}$ to the below and an unstable closed invariant curve appears. If $f^{(1)}$ is crossed to the right, the unstable point becomes a saddle in the region which is bounded by $f^{(1)}$ and $\varepsilon =1$.

Case 2 The unperturbed model (1.1) undergoes one subcritical Hopf bifurcation when a is varied. It undergoes two subcritical Hopf bifurcations if h is varied.

Taking $a_{0}=3, b=6.788, c=1.371, d=4, e=0.1697, f=450.3, g=1.948, h_{0}=2.459, g_1=0.72$, model (1.1) undergoes one subcritical Hopf bifurcation at $a_{H}=0.999$ when $a_{0}$ is varied. It undergoes two subcritical Hopf bifurcations at $h_{H}^1=3.158$ and $h_{H}^2=2.459$ when $h_{0}$ is varied. For these values, the unperturbed model has unstable limit cycles; the asymptotic period of the cycle (evaluated numerically) is 2.093 when $a_{0}$ approaches $a_{H}$. It is 2.093 (0.897) while $h_{0}$ approaching $h_{H}^1$ ( $h_{H}^2$). The bifurcation diagrams of the perturbed model on the $(\varepsilon ,a_{0})$ and the $(\varepsilon ,h_{0})$ planes are given in Fig. 4a and b. Figure 4c and d is the partial enlargement drawings of Fig. 4b.

In Fig. 4a, the point H on the $a_{0}$-axis represents the subcritical Hopf bifurcation of the unperturbed model and is the origin of the period-one torus bifurcations curve $h^{(1)}$. This torus curve terminates at $B_{1}$, a codimension-two bifurcation point called 1:2 resonance, where the multipliers equal to -1. Curve $f^{(1)}$ passes through B and a period-two torus bifurcation $h^{(2)}$ also starts from B. $t^{(2)}_1$ and $t^{(2)}_2$ are two fold bifurcations with period two.

The unstable period-one fixed point becomes stable while crossing $h^{(1)}$ from region 1 to region 2, and an unstable closed invariant curve appears. After that, the attracting point loses stability across $f^{(1)}$ to region 4 bounded by $f^{(1)}$, $h^{(2)}$ and $\varepsilon =1$.

Two pairs of period-two points appear while crossing $t^{(2)}_1$. The two saddles only exist in the region bounded by $t^{(2)}_1$ and $\varepsilon =1$. These two unstable points become unstable when crossing $h^{(2)}$ to region 3, and disappear when crossing $f^{(1)}$ from region 3 to 1 or from 4 to 2.

Fig. 4

Bifurcation diagrams of the perturbed model with $a_{0}=3, b=6.788, c=1.371, d=4, e=0.1697, f=450.3, g=1.948, h_{0}=2.459, g_1=0.72$. c, d are the partial enlargement drawings of b

In Fig. 4b, the points $H_{1}$ and $H_{2}$ on the $h_{0}$-axis correspond to two subcritical Hopf bifurcations of the unperturbed model (1.1), and are the roots of the period-one tours bifurcation curves $h_{1}^{(1)}$ and $h_{2}^{(1)}$. The curve $h_{2}^{(1)}$ terminates at $B_{1}$, a 1:2 resonance. A period-one flip curve $f_{1}^{(1)}$ passes through $B_{1}$ and $B_{2}$. Another period-one tours bifurcation $h_{1}^{(1)}$ curve passes through C (a 1:3 resonance), D (a 1:4 resonance) and terminates at $B_{2}$. In Fig. 4d, at $T_1$ and $T_{2}$, the period of limit cycles is 1 and 2, respectively. They are the roots of the period-one fold bifurcation $t^{(1)}$ and two period-two fold bifurcations $t_1^{(2)}$, $t_2^{(2)}$. There also exists a period-two flip bifurcation $f^{(2)}$.

Two unstable period-one fixed points collide on $t^{(1)}$ then disappear while crossing $t^{(1)}$ to the below. One point changes its stability, and an unstable closed invariant curve appears while crossing $h_{2}^{(1)}$ to the above. Then, it becomes unstable once again while crossing $h_{1}^{(1)}$, and a stable closed invariant curve appears. Besides, it becomes unstable inside the region bounded by $f^{(1)}$ and $\varepsilon =1$.

Two pairs of period-two fixed points (two saddles, two non-saddles) appear when $t_1^{(2)}$ or $t_2^{(2)}$ is crossed to the right. The two saddles disappear through the part of $f^{(1)}$ between $t_1^{(2)}$ and $t_2^{(2)}$. The other two points become unstable in the region bounded by $f^{(2)}$ and $\varepsilon =1$ and then disappear through the part of $f^{(1)}$ on the right of the intersections of $t_1^{(2)}$ with $f^{(1)}$, i.e., from region 1 to region 2 in Fig. 4d. Besides, while crossing $f^{(1)}$ (on the above of the intersection of $t^{(2)}_3$ with $f^{(1)}$) to the right, two unstable points appear and then disappear above $t^{(2)}_3$.

Case 3 The unperturbed model (1.1) undergoes one supercritical Hopf bifurcation when a or h is varied.

Taking $a_{0}=60, b=2, c=1, d=5, e=10, r=20, g=0.6, h_{0}= 0.177, g_1=2.14\times 10^{-3}$, the unperturbed model (1.1) undergoes one supercritical Hopf bifurcation at $a_{H}=60$ when $a_{0}$ is varied; it undergoes a supercritical Hopf bifurcation at $h_{H}=0.1754$ when $h_{0}$ is varied. For these values, the unperturbed model (1.1) oscillates on a stable limit cycle; the asymptotic period of the cycle (evaluated numerically) is 1.612 when $a_{0}$ approaches $a_{H}$. It is 1.621 when $h_{0}$ approaches $h_{H}$. The bifurcation diagrams of the perturbed model on the $(\varepsilon ,a_{0})$ and the $(\varepsilon ,h_{0})$ planes are given in Fig. 5a and b.

Fig. 5

Bifurcation diagrams of the perturbed model with $a_{0}=60, b=2, c=1, d=5, e=10, f=20, g=0.6, h_{0}= 0.177, g_1=2.14\times 10^{-3}$

In Fig. 5a, the point H on the $a_{0}$-axis corresponds to a supercritical Hopf bifurcation of the unperturbed model (1.1). It is the initial point of period-one torus curve $h_{1}$. At T, the period of the unstable cycle is 2. Two branches of period-two tangent bifurcation curve, $t^{(2)}_2$ and $t^{(2)}_ 3$, originate from T. A period-two torus bifurcation curve $h^{(2)}$ originates from A, a 1:1 resonance. While crossing $h^{(1)}$ to the above, the unstable period-one fixed point changes its stability, and an unstable closed invariant curve appears. It becomes a saddle while crossing the region $f^{(1)}$ and $\varepsilon =1$.

Two pairs of period-two fixed points (two saddle points, two attracting points) appear while crossing $t^{(2)}_1$ to the above. The two saddles only exist in the region bounded by $f^{(1)}$ and $\varepsilon =1$. The two attracting points become unstable and disappear through $t^{(2)}_2$. Two pairs of period-two points (two saddles, two non-saddles) appear when $t^{(2)}_2$ or $t^{(2)}_3$ is crossed to the right. The two saddles only exist in the region which is bounded by $t^{(2)}_2$, $t^{(2)}_3$, and $f^{(1)}$. The other two non-saddles are stable above $h^{(2)}$ and disappear through the part of $f^{(1)}$ on the right of the intersections with $t^{(2)}_3$.

In Fig. 5b, the point H on the $h_{0}$-axis corresponds to the supercritical Hopf bifurcation of the unperturbed model (1.1), and it is the root of curve $h^{(1)}$, which terminates at B, a 1:2 resonance. A period-one flip bifurcation curve $f^{(1)}$ passes through B. $T_1$ corresponds to the tangent bifurcation in the unperturbed model (1.1), and is the root of $t^{(1)}$. A branch of period-two tangent bifurcation curve, $t_1^{(2)}$ and $t_2^{(2)}$, originates from $T_2$. In addition, there is a period-two fold bifurcation curve $t_3^{(2)}$ originating from the point O on $f^{(1)}$. $F_1$ is the intersection of $f^{(1)}$ and $\varepsilon =1$.

The unstable period-one point becomes stable while crossing $h^{(1)}$ to the above. It becomes an unstable saddle while crossing the region bounded by the curve $f^{(1)}$ and $\varepsilon =1$. The saddle point and the non-saddle point collide on $t^{(1)}$ and then disappear on the below of $t^{(1)}$.

Two pairs of unstable period-two fixed points (two saddles, two unstable points) appear when $t_2^{(2)}$ is crossed to the above, and $t_1^{(2)}$ is crossed to the below. The two saddle points disappear through $f^{(1)}$ between $t_2^{(2)}$ and $t_1^{(2)}$ to the right. The two unstable points become attractive in the region surrounded by $f^{(2)}$ and $\varepsilon =1$ and then disappear through $f^{(1)}$ from region 2 to 1 and region 3 to 4. While crossing $OF_1$ (the part of $f^{(1)}$) to the above, two attractive points appear. And these points disappear above $t_3^{(2)}$.

Case 4 The unperturbed model (1.1) does not undergo Hopf bifurcation when a is varied. It undergoes one supercritical Hopf bifurcation if h is varied.

Taking $a_{0}= 58.81, b=51.61, c=1, d=5, e=10, f=20, g=0.6, h=7.27\times 10^{-2}, g_1=2.15\times 10^{-3}$, the unperturbed model (1.1) does not undergo Hopf bifurcations when a is varied; it undergoes a supercritical Hopf bifurcation at $h_{H}=0.167$ when $h_{0}$ is varied. For these values, model (1.1) oscillates on a stable limit cycle. While $h_{0}$ approaching $h_{H}$, the asymptotic period of the cycle (evaluated numerically) is 0.39. The bifurcation diagrams of the perturbed model on the $(\varepsilon , a_{0})$ and the $(\varepsilon , h_{0})$ planes are given in Fig. 6a and c. Figure 6a and d is the partial enlargement drawings of Fig. 6a and c.

Fig. 6

Bifurcation diagrams of the perturbed model with $a_{0}= 58.81, b=51.61, c=1, d=5, e=10, f=20, g=0.6, h=7.27\times 10^{-2}, g_1=2.15\times 10^{-3}$. b and d are the partial enlargement drawings of a and c

In Fig. 6a, a closed period-one flip bifurcation curve $f^{(1)}$ passes through two 1:2 resonances $B_1$ and $B_2$. And a torus bifurcation curve with period one $h^{(1)}$ originates from $B_2$ and terminates at a 1:1 resonance A. There are a 1:3 resonance C and a 1:4 resonance D on $h^{(1)}$. A tangent bifurcation with period-one curve $t^{(1)}$ passes through A. $h^{(2)}$, a period-two torus bifurcation curve, is connected by $B_1$ and $B_2$.

Two period-one fixed points collide on $t^{(1)}$ and then disappear while crossing $t^{(1)}$ to the above. One of the two fixed points is a saddle point. The other point loses its stability while crossing to the below of $h^{(1)}$. Two pairs of period-two points (two saddles, two non-saddles) appear when $t^{(2)}$ is crossed to the below. The two saddles exist in the closed region bounded by $f^{(1)}$. The other two points are unstable below $h^{(2)}$, lose stability above $h^{(2)}$, and then disappear through $f^{(1)}$.

In Fig. 6c, the point $T_1$ ($T_2$) on the $h_0$-axis corresponds to a fold bifurcation of model (1.1), and it is a root of the curve $t_1^{(1)}$ $(t_2^{(1)})$. The point H corresponds to a supercritical Hopf bifurcation of the unperturbed model and is a root of the curve $h^{(1)}$. A flip bifurcation curve $f_1^{(1)}$ passes through B. A fold bifurcation with period two $t_1^{(2)}$ starts at point O. $f^{(2)}$ is a period-two flip bifurcation in the region, which is bounded by $f_1^{(2)}$.

Two period-one fixed points collide on $t_1^{(1)}$ and then disappear while crossing $t_1^{(1)}$ to the below. One of the two fixed points is a saddle. The other point loses its stability when crossing $h^{(1)}$ to the above, and a stable closed invariant curve appears. It becomes a saddle point when $f_1^{(1)}$ is crossed to the inside. Besides, two pairs of period-two fixed points (two saddles and two non-saddles) appear when $t^{(2)}$ is crossed to the below. The two saddles exist in the closed region bounded by $f_2^{(1)}$ and $t^{(2)}$. The other two stable points become unstable while crossing $f^{(2)}$ to the inside, and then disappear while crossing the part of $f_1^{(1)}$ (above the point O) to the outside.

3.3 Bifurcations of Perturbed Model with Periodic with Periodic Mechanism 3 and 4

In this subsection, we consider the last two mechanisms of (3.1), which have periodic and non-synchronous perturbations. To thoroughly analyze bifurcation diagrams, we will not restrict the range of $\varepsilon _1$ and $\varepsilon _2$. For each periodic mechanism, we examine two cases corresponding to those of the unperturbed model (1.1) (with stable or unstable limit cycle).

The corresponding perturbed model with periodic mechanism 3 is

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{G}= a_0(1+\varepsilon _{1} v)-(b+cI)G,\\ \dot{I}= \displaystyle {\frac{d\beta G^2}{e+G^2}}-fI,\\ \dot{\beta }=(-g+h_{0}(1+\varepsilon _{2}v)G-g_1G^2)\beta ,\\ \dot{v}=v+2\pi w-v(v^2+w^2),\\ \dot{w}=-2\pi v+w-w(v^2+w^2). \end{array}\right. } \end{aligned}$$

(3.5)

In Fig. 7, these parameters are identical to those for case 2. For these values, the model has unstable limit cycles. For the perturbed model (3.5), an unstable period-one solution exists in region 1 and then becomes a saddle while crossing from region 1 to the region bounded by closed $f^{(1)}$. In addition, while crossing from region 3 to region 2, two pairs of period-two solutions appear and then disappear on the $t^{(2)}$. The two saddles only exist in the region bounded by closed $f^{(1)}$, and the other two points become stable while crossing the closed curve $f^{(2)}$ and disappear while crossing $f^{(1)}$ to the outside.

Taking $a_{0}= 1, b=5.9, c=1, d=4, e=0.1, r=1, g=1.152, h=1.83, g_1=0.72$, the bifurcation diagram on the $(\varepsilon _1, \varepsilon _2)$ plane is illustrated in Fig. 8. For these values, the unperturbed model (3.5) oscillates on a stable limit cycle. Three nontrivial periodic solutions exist in the region bounded by the closed curve $t^{(1)}$. Two nontrivial period-one solutions disappear while crossing the $t^{(1)}$ to the outside. Besides, while crossing the curve $h_1^{(1)}$ or $h_2^{(1)}$, the third fixed point changes its stability.

Fig. 7

Bifurcation diagrams of the perturbed model of (3.5) with $a=59.278, b=51.611, c=1, d=5, e=10, f=20, g=0.6, h= 7.32\times 10^{-2}, g_1=2.14\times 10^{-3}.$ b is the partial enlargement drawings of a

Fig. 8

Bifurcation diagrams of the perturbed model of (3.5) with $a_{0}= 1, b=5.9, c=1, d=4, e=0.1, f=1, g=1.152, h=1.83, g_1=0.72$

Fig. 9

Bifurcation diagrams of the perturbed model (3.6) with $a_{0}=3, b=6.788, c=1.371, d=4, e=0.1697, f=450.3, g=1.948, h_{0}=2.459, g_1=0.72$

Fig. 10

Bifurcation diagrams of the perturbed model (3.6) with $a_{0}= 5.05, b=2, c=1, d=4, e=3.559, f=1, g=27.425, h_{0}=40, g_1=1$. b is the partial enlargement drawings of a

The corresponding perturbed model with periodic mechanism 4 is

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{G}= a_0(1+\varepsilon _{1} v)-(b+cI)G,\\ \dot{I}= \displaystyle {\frac{d\beta G^2}{e+G^2}}-fI,\\ \dot{\beta }=(-g+h_{0}(1+\varepsilon _{2}w)G-g_1G^2)\beta ,\\ \dot{v}=v+2\pi w-v(v^2+w^2),\\ \dot{w}=-2\pi v+w-w(v^2+w^2). \end{array}\right. } \end{aligned}$$

(3.6)

In Fig. 9, these parameters are identical to those for case 2. For these values, the perturbed model (3.6) has unstable limit cycles. There exist two nontrivial period-one solutions between $t_1^{(1)}$ and $t_1^{(2)}$, one of which is stable. When $f^{(1)}$ is crossed into the region bounded by $f^{(1)}$ and $\varepsilon _1=1$, the stable point becomes a saddle, and a pair of stable period-two solutions appear. When $t^{(2)}$ is crossed to the above, two pairs of period-two solutions (two saddles, two stable points) appear. The saddle points only exist in the region bounded by $t^{(2)}$ and $f^{(1)}$. The other two stable points lose their stabilities through the part of $f^{(2)}$ (on the right of the intersections of $f^{(2)}$ and $t^{(2)}$), and then disappear through $f^{(1)}$.

Taking $a_{0}= 5.05, b=2, c=1, d=4, e=3.559, f=1, g=27.425, h_{0}=40, g_1=1$, the bifurcation diagram on the $(\varepsilon _1, \varepsilon _2)$ plane is illustrated in Fig. 10. For these values, the unforced model (3.6) oscillates on a stable limit cycle. The unstable period-one fixed point becomes stable crossing $h_1^{(1)}$ to the below, and an unstable closed invariant curve appears. After that, the attracting point loses its stability across $h_2^{(1)}$ to the below, and a stable closed invariant curve appears. Two pairs of period-two points (two saddles, two stable points) appear while crossing to the outside of the closed curve $t^{(2)}$. The two saddle points disappear through the part of $f^{(1)}$. The other two stable points change their stability while crossing $h^{(2)}$ to the above and then disappear while crossing $f^{(1)}$.

Fig. 11

Time series of model (3.3) with a $h=15,\varepsilon =0.4$, b $h=15.54,\varepsilon =0.01$, c $h=15.4,\varepsilon =0.17$

Fig. 12

Phase portraits (left) and corresponding Poincaré map portraits (right) of different solutions of model (3.3). a and b Quasiperiodic solution, c and d chaotic solution through torus destruction

Fig. 13

Bifurcation diagrams in (h, G) plane of model (3.3) with $\varepsilon = 0.4$ under initial value (4, 3, 1.5).

Fig. 14

Phase portraits (left) and corresponding Poincaré map portraits (right) of different solutions of model (3.3). a and b Periodic solution with period two, c and d periodic solution with period four

Fig. 15

Phase portraits (left) and corresponding Poincaré map portraits (right) of chaos with different topologies of model (3.3). d and e The largest Lyapunov exponents corresponding to (a) and (c)

3.4 Solutions and Chaos

In this subsection, we take case 1 of mechanism 1 as an example to demonstrate the more complex dynamics.

Periodic mechanism leads to multiple attractors. Indeed, the model without perturbation $( \varepsilon = 0 )$ only has attractors like attracting equilibria and limit cycles. Under the periodic perturbation $( \varepsilon \ne 0 )$, the model has multiple attractors. For instance, the stable cycle of period four (for $h=15,\varepsilon =0.4$) coexists with the quasiperiodic solution (for $h=15.54,\varepsilon =0.01$) and then with the chaotic solution (for $h=15.4,\varepsilon =0.17$) (see Fig. 11). Besides, homoclinic structures near strong resonances can destroy the closed invariant curves of a quasiperiodic solution (for $h= 15.54, \varepsilon = 0.01$), leading to the appearance of a chaotic solution (for $h= 15, \varepsilon = 0.04$), as in Fig. 12.

Moreover, periodicity gives rise to stable cycles of different periods. The corresponding two-dimensional bifurcation diagram in the (h, G) space is plotted in Fig. 13 for $\varepsilon = 0.4$. Phase portraits and corresponding Poincaré map portraits of the period-two solution (for $h= 29.4, \varepsilon = 0.4$) and the period-four solution (for $h= 26.27, \varepsilon = 0.4$ ) are shown in Fig. 14. We also present two chaos (for $h_1=26, h_2=18, \varepsilon = 0.4$) with different topologies which correspond to different periods in Fig. 15. These chaotic solutions are further corroborated by calculating the positive value of the maximum Lyapunov exponent. The spectrums of the Largest Lyapunov exponents are presented in Fig. 15e, f.

Furthermore, even a tiny change of periodicity can lead to bifurcation and a new periodic solution. There exists a stable cycle with period one near the curve $h_1^{(1)}$. If $\varepsilon$ is slowly increased with $h_0$ is fixed, the stable cycle varies smoothly and loses stability through $f_1^{(1)}$. After $f_1^{(1)}$ is crossed to the right, the model oscillates on another attractor, i.e., a stable cycle of period two. On the other hand, if $\varepsilon$ is fixed with $h_0$ is increased, a new period-one solution occurs when $h_2^{(1)}$ is crossed (Fig. 3c).

Table 1 Standard parameter values

4 Application and Discussion

In this paper, we thoroughly explore the bifurcations and the related dynamics of the $GI\beta$ model. The model (1.1) undergoes Hopf, degenerated Hopf, saddle-node, transcritical bifurcations of codimension 1; cusp, zero-Hopf, Bogdanov–Takens bifurcations of codimension 2; and a Bogdanov–Takens bifurcation of codimension 3. Moreover, considering that blood glucose homeostasis is strongly regulated and controlled by internal or external periodically varying environments, we also further investigate the dynamics of the periodic perturbed $GI\beta$ model with synchronous and/or non-synchronous variations of a and h. The periodicity results in multiple attractors, including stable and unstable cycles of different periods, quasiperiodic solutions, and chaos. The glycemic metabolic system shifts abruptly from one state to another at various bifurcation points rather than switched points, such as euglycemia/ hypoglycemia, euglycemia/ hyperglycemia, and hyperglycemia/diabetes. Thus, regulations and therapeutic measures near the various bifurcation curves and the conversion region would be clinically meaningful. It should be mentioned that high codimensional bifurcation (Zhu et al. 2003; Shan et al. 2016; Ren and Yu 2016) and the periodic perturbation (Ren and Yuan 2017; Tao et al. 2018; Li et al. 2018) are important issues in dynamical system theory. Our works can be seen as supplements to these issues, especially for codimension 3 bifurcation and non-synchronous periodic perturbation.

Fig. 16

Sensitivity indices (SI) for G, I, and $\beta$ with the standard parameters set in Table 1. a–c Unperturbed SI for G, I, $\beta$. d–f Perturbed SI for G, I, $\beta$

Fig. 17

The correlation values ($r_{NJ}$) between the dynamic sensitivities for all parameters with the standard set in Table 1. a–c Unperturbed $r_{NJ}$ for G, I, $\beta$. d–f Perturbed $r_{NJ}$ for G, I, $\beta$

Fig. 18

Chaotic evolution of the proposed model shows the effect of a tiny difference in the initial conditions. The initial conditions are $I_0 = 0.1$ and $I'_0 = 0.2$. ($G_0=G'_0=5, \beta _0=\beta '_0=1.5$ ). The parameter values are $a_0 = 16.51, b = 2, c = 1, d = 4, e = 3.559, f = 1, g = 27.425, h = 15.5, g_1 = 1, \varepsilon =0.4$

A local sensitivity analysis is performed for the standard set of parameters given in Table 1. Parametric sensitivity analysis investigates the effects of parameter changes on the model output, in this case, the glucose concentration, the insulin concentration, and $\beta$ cell mass. In this study, we use relative sensitivity indices at a range of parameter values ($10\%$ of the baseline values) computed by multiplying the partial derivative (the absolute sensitivity function) by the nominal value of the input and dividing by the output value. The relative sensitivity index ($SI(U_i, P_j)$) of the model output $U_i$ (G, I, $\beta$) to variations in the parameters $P_j$ ($a, b, c, d, e, f, g, h, g_1$) is given by,

$$\begin{aligned} SI(U_i, P_j)=\frac{1}{K}\sum _{k=1}^{K}\frac{P_j+\varDelta P_j}{U_{i_{k}}(P_j+\varDelta P_j)}\frac{[U_{i_{k}}(P_j+\varDelta P_j)-U_{i_{k}}(P_j)]}{\varDelta P_j}, \end{aligned}$$

where k is the time step grid, $1\le k\le K$. From Fig. 16, for the unperturbed model, sensitivity analysis (SA) shows that the sensitivities for a (hepatic glucose production), b (insulin-independent glucose utilization), and h (glucose tolerance) to glucose metabolism are more significant than other physiological parameters. While under the periodic perturbation ($\varepsilon _1=0.2$), SI(G, h), and SI(I, c), respectively, change from 1.512 and $-0.53$ to almost equal to 0, but both SI(I, a) and $SI(\beta , a)$ show trends of sharp growth. SA not only provides a way to reduce the complexity of glucose metabolism and identifies the potential high-impact factors but also reveals that a small perturbation may hide some high-impact factors.

Meanwhile, the correlation between parameters, which is in order to explain parameter inter-dependency, is studied by computing the correlation between the dynamic sensitivities as described in Sriram et al. (2012). The correlation matrix is generically defined by the term as

$$\begin{aligned} r_{\hat{i}\hat{j}}=\frac{\sum \limits _{1}^{\hat{m}}(SI_{\hat{i}}-\overline{SI}_{\hat{i}})(SI_{\hat{j}}-\overline{SI}_{\hat{j}})}{\sqrt{(\sum \limits _{1}^{_{\hat{m}}}(SI_{\hat{i}}-\overline{SI}_{\hat{i}})^2)(\sum \limits _{1}^{_{\hat{m}}}(SI_{\hat{j}}-\overline{SI}_{\hat{j}}^2)}}, \end{aligned}$$

where ${\hat{m}}$ is the time grid step, $1\le {\hat{i}},{\hat{j}}\le 9$, ${\hat{i}},{\hat{j}} \in {\mathbb {N}^+}.$ The correlation values between the dynamic sensitivities of all parameters for G, I, and $\beta$ in perturbed and unperturbed cases are shown in Fig. 17 with the diagonal being self-correlated. The levels of correlation are differently shaded, as shown on the horizontal bar on the right that ranges from highly correlated $(+1)$ to anti-correlated $(-1)$. We find that periodic perturbation can change correlation by comparing the perturbed correlation matrix and the unperturbed one. For example, the insulin’s correlation values between the sensitivities of the parameter a and other parameters vary to different degrees under the perturbation. When specific parameters are difficult to regulate during the therapeutic process, doctors can resort to the correlation results to explore a new treatment approach by adjusting the relevant parameters.

Fig. 19

Glucose levels in subjects with standard glucose tolerance (blue line, $\varepsilon _1=0.4$), impaired glucose tolerance (green line, $\varepsilon _2=0.405$), and type 2 diabetes (red line, $\varepsilon _3=0.42$) with $a = 16.51, b = 2, c = 1, d = 4, e = 3.559, f = 1, g = 27.425, h_0 = 26.4, g_1 = 1$

Fig. 20

Time series of a period-two solution with $a = 16.51, b = 2, c = 1, d = 4, e = 3.559, f = 1, g = 27.425, h_0 = 40, g_1 = 1, \varepsilon =0.2$

Fig. 21

Diabetic clinical data and fitted time series with $a=16.5, b=2, c=1, d=4, e=4, f=1, g=27.4, h=16.5, g_1=1, \varepsilon =0.6$

Fig. 22

Standard clinical data and fitted time series with $a=18, b=2, c=1, d=6, e=3.56, f=1, g=27.4, h=11, g_1=1, \varepsilon =0.61$

Apart from the theoretical meaning, the perturbed results can appropriately explain some experimental phenomena and effectively fit clinical data.

In Markus et al. (1985), experimental evidence of quasiperiodic and chaotic oscillations is observed by monitoring the fluorescence in glycolyzing bakers yeast under sinusoidal glucose input. Such chaotic biorhythms which have irregular periods or no period completely were also found in this paper (see Figs. 13, 15, 12). Under some parameters, periodic perturbation may destruct the homeostasis of glucose metabolism, leading to glucose disorder. And this glycemic instability may confer additional risk on endothelial function and oxidative stress, two key players in favoring cardiovascular complications in diabetes (Ceriello et al. 2008). Besides, in chaotic dynamics, a minor variation in initial conditions may cause significantly different dynamic behavior. Even a slight fluctuation in the insulin concentration may result in unpredictable outcomes over time. Tiny changes of the initial insulin concentration lead to different glucose time series, which can be observed in Fig. 18. Therefore, such patients who use an integration of scheduled nutrition and exercise and timetabled insulin administration need to consider the effect of apparent irregular alterations. The administration of insulin through an appropriate program is necessary and worthwhile in some therapeutic processes.

In Mari et al. (2008), Mari et al. studied the response of acute insulin release in diabetic subjects by examining the relationships between fasting plasma glucose and the secretory responses. To elucidate this response, they measured the plasma glucose after the glucose test for three types of people: standard glucose tolerance, impaired glucose tolerance, and Type 2 diabetes. The plasma glucose of three subjects is presented in Figure 1 in Mari et al. (2008). In this paper, we choose three amplitudes of perturbation ($\varepsilon _1=0.4, \varepsilon _2=0.405, \varepsilon _3=0.42$) on the glucose tolerance h, which adequately represents the three groups above, to see the fluctuation trend of plasma glucose. The glucose levels are presented in Fig. 19. Comparing the result of Mari et al. (2008), the numerical fluctuation trends are generally in agreement with the experimental data.

In Ceriello et al. (2008), Ceriello et al. proposed that the oscillating glucose, over 1 day, has more harmful effects on endothelial function than stable constant high glucose. When they investigated whether vitamin C can counterbalance the effect of oscillating glucose, they presented the glucose levels of diabetic patients with or without vitamin C infusion in Figure 4A in Ceriello et al. (2008). In the first period, glucose levels peaked and bottomed two times, returning to the original story in the next period. For the observed oscillations, we can draw an analogy with the bifurcation results of the periodically perturbed model (3.3). A stable period-two solution generated by the Neimark–Sacker bifurcation in the periodically perturbed model results in the phenomena above. To be precise, we show the time series of a period-two solution in Fig. 20.

To gain further clinically practical dynamics, we fit the diabetic and normal glucose concentration data with the perturbed and unperturbed time series in Figs. 21 and 22. The clinical data is recorded using a capillary fingertip blood sample by a portable glucose monitor from a volunteer with Type 2 diabetes and a regular volunteer for 400 h. The data is sampled approximately every 3 h during the hospital stay. It is shown that clinical data has prominent diurnal variation rhythms, which peak at noon and then decrease to the lower level. Besides, mixed values of glucose peaks occur after the three meals. Though circadian rhythm is also presented by the Hopf bifurcation of model (1.1), this single rhythm neglects the postprandial floating upward tendencies in the daytime. The agreement of the perturbed model is much better than that of the unperturbed one since it appropriately describes the postprandial glucose fluctuations three times a day.

Further factors could be added to the model by considering nonlocal delay and stochastic process of the metabolism. It may be more clinically useful for the variables to have a stabilization control algorithm and the parameters to have delay dependence and/or age dependence, as in Liu et al. (2020), Zhang et al. (2016), Wang et al. (2018), Chakraborty et al. (2009). Thus, it would be intriguing to see how perturbation affects such glucose metabolism.