Abstract
We deal with complete linear Weingarten hypersurfaces immersed into locally symmetric Riemannian manifolds whose sectional curvature obeys certain standard constraints. Under an assumption that such a hypersurface satisfies a suitable Okumura type inequality, we apply a version of the Omori–Yau maximum principle to prove that it must be either totally umbilical or isometric to an isoparametric hypersurface having two distinct principal curvatures. When the ambient space is Einstein, we also use a technique recently developed by Alías and Meléndez (Mediterr J Math 17(2): 61, 2020 [6]) to establish a sharp integral inequality for compact linear Weingarten hypersurfaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of geometric properties of hypersurfaces immersed into Riemannian manifolds, under certain curvature constraints, constitutes an important topic of Differential Geometry. In this field, Brasil Jr., Colares and Palmas [9] used the Omori–Yau maximum principle to characterize complete hypersurfaces with constant normalized scalar curvature in the unit Euclidean sphere \({\mathbb {S}}^{n+1}\). In [3], Alías and García-Martínez used a weak Omori–Yau maximum principle due to Pigola, Rigoli and Setti [20] to study the behavior of the normalized scalar curvature R of a complete hypersurface with constant mean curvature immersed into a space form \({\mathbb {Q}}_c^{n+1}\) of constant sectional curvature c, deriving a sharp estimate for the infimum of R. Afterwards, the same authors jointly with Rigoli [4] obtained another suitable weak maximum principle for complete hypersurfaces with constant scalar curvature in \({\mathbb {Q}}_c^{n+1}\), and gave some applications of it in order to estimate the norm of the traceless part of its second fundamental form and, in particular, they improved the result of [9].
In [16], Li, Suh and Wei obtained characterization results concerning compact (without boundary) linear Weingarten hypersurfaces immersed into \({\mathbb {S}}^{n+1}\) (that is, compact hypersurfaces of \({\mathbb {S}}^{n+1}\) whose mean and normalized scalar curvatures are linearly related). Later on, the second author jointly with Aquino and Velásquez [7, 8] established another characterization results related to complete linear Weingarten hypersurfaces immersed into \({\mathbb {Q}}_c^{n+1}\), under appropriate constraints on the norm of the traceless part of the second fundamental form. Next, the second author jointly with Alías, Meléndez and dos Santos [1] extended these results to the context of complete linear Weingarten hypersurfaces immersed into locally symmetric Riemannian manifolds obeying certain standard curvature conditions (in particular, in Riemannian spaces with constant sectional curvature). We recall that a Riemannian manifold is said to be locally symmetric if all covariant derivative components of its curvature tensor vanish identically. Under appropriate constrains on the scalar curvature function, they proved that such a hypersurface must be either totally umbilical or isometric to an isoparametric hypersurface with two distinct principal curvatures, one of them being simple.
More recently, the first and second authors [14] obtained a sharp estimate on the norm of the traceless second fundamental form of complete hypersurfaces with constant scalar curvature immersed into a locally symmetric Riemannian manifold obeying the same curvature constraints as assumed in [1]. When the equality holds, they proved that these hypersurfaces must be isoparametric with two distinct principal curvatures. Their approach involved a suitable Okumura type inequality which was introduced by Meléndez in [17], corresponding to a weaker hypothesis when compared with the assumption that these hypersurfaces have a priori at most two distinct principal curvatures. We point out that the same authors [12] had already used this Okumura type inequality to prove a sharp estimate on the scalar curvature of stochastically complete hypersurfaces with constant mean curvature immersed into a locally symmetric Riemannian manifold (see also [15] for other characterization results concerning complete hypersurfaces immersed into such an ambient space and having two distinct principal curvatures). Meanwhile, Alías and Meléndez [6] studied the rigidity of closed hypersurfaces with constant scalar curvature isometrically immersed into the unit Euclidean sphere \({\mathbb {S}}^{n+1}\). In particular, they established a sharp integral inequality for the behavior of the norm of the traceless second fundamental form, with the equality characterizing the totally umbilical hypersurfaces and certain Clifford tori.
Motivated by these works, here we deal with complete linear Weingarten hypersurfaces immersed into a locally symmetric Riemannian manifold, which is supposed to obey standard curvature constraints already considered in [1, 12, 14, 15]. Assuming that such a hypersurface satisfies the Okumura type inequality introduced in [17], we apply a version of the Omori–Yau maximum principle to prove that it must be either totally umbilical or isometric to an isoparametric hypersurface having two distinct principal curvatures (see Theorem 4.1). When the ambient space is Einstein, we use the ideas and techniques recently developed by Alías and Meléndez in [6] to establish a sharp integral inequality for compact linear Weingarten hypersurfaces (see Theorem 5.1).
2 Preliminaries
Let us denote by \(\Sigma ^n\) an orientable and connected hypersurface isometrically immersed into an arbitrary \((n \,{+}\, 1)\)-dimensional Riemannian manifold \({\overline{M}}{}^{n + 1}\). Let \(\{e_1, \ldots , e_{n + 1}\}\) be a local orthonormal frame on \({\overline{M}}{}^{n + 1}\) with dual coframe \(\{\omega _1, \ldots , \omega _{n + 1}\}\) such that at each point of \(\Sigma ^n\), \(e_1, \ldots , e_n\) are tangent to \(\Sigma ^n\) and \(e_{n + 1}\) is normal to \(\Sigma ^n\). We will use the following convention for the indices:
Restricting all the tensors to \(\Sigma ^n\), we see that \(\omega _{n + 1} = 0\) on \(\Sigma ^n\). Hence, \(0 = d\omega _{n + 1} = -\sum _{i}\omega _{n + 1 i} \wedge \omega _i\) and as it is well known we get
This gives the second fundamental form of \(\Sigma ^n\), \(A=\sum _{i, j}h_{ij}\omega _i{\otimes }\omega _{j}e_{n + 1}\), and its squared norm, \(|A|^2=\sum _{i,j}h_{ij}^2\). Furthermore, the mean curvature H of \(\Sigma ^n\) is defined by \(H=\frac{1}{n}\,\mathrm{tr}(A)=\frac{1}{n}\sum _{i}h_{ii}\).
Denoting by \({\overline{R}}_{ABCD}, {\overline{R}}_{AC}\) and \({\overline{R}}\), respectively, the Riemannian curvature tensor, the Ricci tensor and the scalar curvature function of the Riemannian manifold \({\overline{M}}{}^{n + 1}\), we have
It follows from the Gauss equation that the normalized scalar curvature R of \(\Sigma ^{n}\) is given by
The traceless second fundamental form is given (in local coordinates) by \(\Phi _{ij}=h_{ij}-H\delta _{ij}\), which corresponds to the symmetric tensor
Thus, we have \(|\Phi |^2 = \sum _{i,j}\Phi _{ij}^{2}\) is the squared norm of \(\Phi \). Moreover, from (2.1) we obtain
The Cheng–Yau operator [10], here denoted by L, is defined as being the second order linear differential operator \(L :C^{\infty }(\Sigma ) \rightarrow C^{\infty }(\Sigma )\) given by
where \(P :{\mathfrak {X}}(\Sigma ) \rightarrow {\mathfrak {X}}(\Sigma )\) is the first Newton transformation of \(\Sigma ^n\), which is defined as the operator \(P = nHI - A\), where I is the identity in the algebra of smooth vector fields on \(\Sigma ^n\), and \(\mathrm{hess}\,u :{\mathfrak {X}}(\Sigma ) \rightarrow {\mathfrak {X}}(\Sigma )\) denotes the self-adjoint linear operator metrically equivalent to the Hessian of u, \(\mathrm{Hess}\, u\), which are given by
respectively, for all \(X, Y \in {\mathfrak {X}}(\Sigma )\). It is not difficult to see that P is a self-adjoint operator which commutes with the second fundamental form A and satisfies \(\mathrm{tr}(P) = n(n - 1)H\).
3 Setup and key lemmas
In what follows, we assume \({\overline{M}}{}^{n+1}\) to be a locally symmetric Riemannian manifold, which means that all covariant derivative components \({\overline{R}}_{ABCD;E}\) of its curvature tensor vanish identically.
Let \(\Sigma ^n\) be a hypersurface immersed into \({\overline{M}}{}^{n + 1}\) and let \({\overline{K}}\) be the sectional curvature of \({\overline{M}}{}^{n + 1}\). Following the ideas of Nishikawa [18], Choi et al. [11, 21], Gomes et al. [15], and Alías et al. [1], among others, we will assume in our main result that there exist constants \(c_1\) and \(c_2\) such that the following relations hold:
and
for all \(i, j = 1, \ldots , n\).
Moreover, we say that a hypersurface \(\Sigma ^n\) is linear Weingarten when its normalized scalar curvature and mean curvature are linearly related. That said, we are going to consider \(\Sigma ^n\), a linear Weingarten hypersurface immersed into \({\overline{M}}{}^{n+1}\).
It is worth to point out that the Riemannian space forms \({\mathbb {Q}}^{n + 1}_c\) of constant sectional curvature \(c \in \{0, 1, -1\}\) satisfy conditions (3.1) and (3.2) for \(\frac{c_1}{n} = c_2 = c\). Just to mention other spaces having these properties, a standard computation proves that the Riemannian products \({\mathbb {R}}^{n - k}{\times }{\mathbb {S}}^{k + 1}\) and \({\mathbb {R}}^{n - k}{\times }{\mathbb {H}}^{k + 1}\) are locally symmetric Riemannian manifolds which also satisfy the above conditions for a wide class of hypersurfaces (for more details, see [1, Remark 3.1]).
We also observe that, in the case where \({\overline{M}}{}^{n+1}\) satisfies condition (3.1), its scalar curvature \({\overline{R}}\) is such that
Since the scalar curvature of a locally symmetric Riemannian manifold is constant, from (3.3) we see that \(\sum _{i,j}{\overline{R}}_{ijij}\) is a constant naturally attached to \({\overline{M}}{}^{n+1}\). In this context, for the sake of simplicity, we will consider the constant  and, assume that \({\overline{M}}{}^{n+1}\) also satisfies condition (3.2), we denote \(c_0:=2c_2-\dfrac{c_1}{n}\) for convenience.
and, assume that \({\overline{M}}{}^{n+1}\) also satisfies condition (3.2), we denote \(c_0:=2c_2-\dfrac{c_1}{n}\) for convenience.
Our first key lemma is an Okumura type result due to Meléndez [17] which is closely related to the total umbilicity tensor (for more details, see [17, Lemma 2.2]; see also [19]).
Lemma 3.1
Let \(\kappa _1, \ldots , \kappa _n\), \(n \hbox {\,\,\char 062\,\,}3\), be real numbers such that \(\sum _{i}\kappa _i = 0\) and \(\sum _{i}\kappa _{i}^{2} = \beta ^2\), where \(\beta \hbox {\,\,\char 062\,\,}0\). Then, the equation
holds if and only if p of the numbers \(\kappa _i\) are nonnegative (resp. nonpositive) and equal, and the rest \(n - p\) of the numbers \(\kappa _i\) are nonpositive (resp. nonnegative) and equal.
Next, we recall our second auxiliary result, which corresponds to [1, Lemma 3.2].
Lemma 3.2
Let \(\Sigma ^n\) be a linear Weingarten hypersurface immersed into a locally symmetric Riemannian manifold \({\overline{M}}{}^{n+1}\) satisfying curvature conditions (3.1) and (3.2), with \(R = aH + b\). Suppose that

then
Moreover, if inequality (3.4) is strict and equality in (3.5) holds on \(\Sigma ^n\), then H is constant on \(\Sigma ^n\).
For our purposes, it will be crucial to consider the following Cheng–Yau modified operator
So, for any \(u\in C^2(\Sigma ^n)\), from (2.3) we have that
with
Besides that, since \(R=aH+b\), equation (2.2) becomes

In our last key lemma, we collect some analytic properties of Cheng–Yau’s modified operator, namely: sufficient conditions for the ellipticity property of \({\mathscr {L}}\) and the validity of a generalized version of the Omori–Yau maximum principle on \(\Sigma ^n\), i.e., for any function \(u \in C^2(\Sigma ^n)\) with \(u^* = \sup u < +\infty \), there exists a sequence of points \(\{p_{j}\} \subset \Sigma ^n\) satisfying
for every \(j \in {\mathbb {N}}\). For the proof of these properties see Lemma 3.4, the beginning of the proof of Lemma 3.6, and Proposition 4.2 in [1].
Lemma 3.3
Let \(\Sigma ^n\) be a complete linear Weingarten hypersurface immersed into a locally symmetric Riemannian manifold \({\overline{M}}{}^{n+1}\) satisfying curvature conditions (3.1) and (3.2), with \(R=aH+b\) satisfying  (resp.
(resp.  ). In the case where
). In the case where  , assume in addition that the mean curvature function H does not change sign on \(\Sigma ^n\). Then:
, assume in addition that the mean curvature function H does not change sign on \(\Sigma ^n\). Then:
-
(i)
If we choose a local orthonormal frame \(\{e_1,\dots , e_n\}\) on \(\Sigma ^n\) such that \(h_{ij}=\lambda _i\delta _{ij}\), the formula
$$\begin{aligned} \begin{aligned} \!\!\!\!\!{\mathscr {L}}(nH)&= |\nabla A|^2 - n^2|\nabla H|^2 + nH\mathrm{tr}(A^3) - |A|^4 \\&\qquad + \sum _{i}{\overline{R}}_{(n + 1)i(n + 1)i}(nH\lambda _i - |A|^2) + \sum _{i, j}\,(\lambda _i - \lambda _{j})^2{\overline{R}}_{ijij} \end{aligned} \end{aligned}$$(3.9)holds on \(\Sigma ^n\), where \(\lambda _1, \ldots , \lambda _n\) denote the principal curvatures of \(\Sigma ^n\).
-
(ii)
The operator \({\mathscr {L}}\) is an elliptic (resp. semi-elliptic) operator or, equivalently, \({\mathscr {P}}\) is positive definite (resp. semi-definite), for an appropriate choice of the orientation of \(\Sigma ^n\).
-
(iii)
If \(\sup _{\Sigma }|\Phi | < +\infty \), then the Omori–Yau maximum principle holds on \(\Sigma ^n\) for the operator \({\mathscr {L}}\).
4 Rigidity of complete linear Weingarten hypersurfaces
In the setup of the previous section, we have the following rigidity result:
Theorem 4.1
Let \(\Sigma ^n\) be a complete linear Weingarten hypersurface immersed into a locally symmetric Riemannian manifold \({\overline{M}}{}^{n+1}\) satisfying curvature conditions (3.1) and (3.2), with \(R=aH+b\) such that \(a\hbox {\,\,\char 062\,\,}0\) and  . If its total umbilicity tensor \(\Phi \) satisfies
. If its total umbilicity tensor \(\Phi \) satisfies
for some \(1\hbox {\,\,\char 054\,\,}p\hbox {\,\,\char 054\,\,}\frac{n-\sqrt{n}}{2}\), then
-
(i)
either \(\sup |\Phi | = 0\) and \(\Sigma ^n\) is a totally umbilical hypersurface, or
-
(ii)
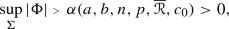
where
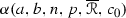 is a positive constant depending only on a, b, n, p,
is a positive constant depending only on a, b, n, p,  and \(c_0\). Moreover, if the equality
and \(c_0\). Moreover, if the equality 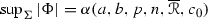 holds and this supremum is attained at some point of \(\Sigma ^n\), then \(\Sigma ^n\) is an isoparametric hypersurface with two distinct principal curvatures of multiplicities p and \(n - p\).
holds and this supremum is attained at some point of \(\Sigma ^n\), then \(\Sigma ^n\) is an isoparametric hypersurface with two distinct principal curvatures of multiplicities p and \(n - p\).
Proof
Initially we must obtain a suitable lower bound for the operator \({\mathscr {L}}\) acting on the squared norm of the total umbilicity tensor \(\Phi \) of \(\Sigma ^n\). Since  is constant, we get from (3.8) that
is constant, we get from (3.8) that
By Lemma 3.3 (ii), we have that the operator \({\mathscr {P}}\) is positive definite. In particular, from (4.2) we obtain
Without loss of generality we can choose the orientation of \(\Sigma ^n\) so that \(H > 0\), occurring the strict inequality because of  . From this, we claim that \(H-{a}/{2}>0\). Indeed, it is enough to see that we can rewrite equation (3.8) as
. From this, we claim that \(H-{a}/{2}>0\). Indeed, it is enough to see that we can rewrite equation (3.8) as

So, formula (3.9) and inequality (4.3) jointly with Lemma 3.2 give
The curvature constraints (3.1) and (3.2) yield
and
Thus, plugging (4.5) and (4.6) into (4.4), we obtain
On the other hand, it is not difficult to see that
Putting (4.8) into (4.7) we find
Now, taking into account the Okumura type inequality (4.1), from (4.9) we get
Since \(H-{a}/{2} > 0\), we observe that equation (3.8) implies that the mean curvature can be written as

Thus, substituting (4.11) into (4.10) we get

After some straightforward computations, inequality (4.12) gives us the next one

So, inequality (4.13) lead us to the following estimate:

where the function  is given by
is given by
Now, we are going to finish the proof by applying the Omori–Yau maximum principle to the operator \({\mathscr {L}}\) acting on the function \(|\Phi |^2\). We note that if \(\sup _{\Sigma }|\Phi | = +\infty \), then claim (ii) of Theorem 4.1 trivially holds and there is nothing to prove. Otherwise, if \(\sup _{\Sigma }|\Phi | < +\infty \), item (iii) of Lemma 3.3 says that there exists a sequence of points \(\{p_{j}\}\) in \(\Sigma ^n\) such that
Hence, estimate (4.14) implies that

and, taking the limit as \(j \rightarrow +\infty \), we infer

It follows that either \(\sup _{\Sigma }|\Phi | = 0\), which means that \(|\Phi | \equiv 0\) and the hypersurface is totally umbilical, or \(\sup _{\Sigma }|\Phi | > 0\) and then  . In the latter case, since
. In the latter case, since  , we have that
, we have that

Moreover, since \(1\hbox {\,\,\char 054\,\,}p\hbox {\,\,\char 054\,\,}\frac{n-\sqrt{n}}{2}\), we can reason as in [13, Remark 3.3] to conclude that the function  is strictly decreasing for \(x \hbox {\,\,\char 062\,\,}0\).
is strictly decreasing for \(x \hbox {\,\,\char 062\,\,}0\).
Hence, we guarantee existence of a unique positive real number \(pg{\alpha (a,b,n,p,\overline{{\mathscr {R}}},c_0) >0}\), depending only on  and \(c_0\), such that
and \(c_0\), such that  . Therefore, we must have
. Therefore, we must have

concluding the proof of the first part of Theorem 4.1.
Finally, let us assume that equality  holds. In particular, we get
holds. In particular, we get

on \(\Sigma ^n\) and then (4.14) assures that \(|\Phi |^2\) is a \({\mathscr {L}}\)-subharmonic function on \(\Sigma ^n\), that is,
Furthermore, since  , item (ii) of Lemma 3.3 asserts that the operator \({\mathscr {L}}\) is elliptic. Thus, since \(\Sigma ^n\) is complete and taking into account that we are assuming the existence of a point \(p\in \Sigma ^n\) such that
, item (ii) of Lemma 3.3 asserts that the operator \({\mathscr {L}}\) is elliptic. Thus, since \(\Sigma ^n\) is complete and taking into account that we are assuming the existence of a point \(p\in \Sigma ^n\) such that  , from (4.16) we can apply Hopf’s strong maximum principle for the elliptic operator \({\mathscr {L}}\) acting on the function \(|\Phi |^2\) to conclude that it must be constant, that is,
, from (4.16) we can apply Hopf’s strong maximum principle for the elliptic operator \({\mathscr {L}}\) acting on the function \(|\Phi |^2\) to conclude that it must be constant, that is,  . Hence, the equality in (4.14) holds, namely,
. Hence, the equality in (4.14) holds, namely,

Consequently, all the inequalities along the proof of (4.14) must be, in fact, equalities. In particular, we obtain that equation (4.3) must be an equality, which jointly with the positiveness of the operator \({\mathscr {P}}\) imply that the mean curvature H is constant. Moreover, also equality in (4.4) holds, that is,
Therefore, the principal curvatures of \(\Sigma ^n\) must be constant and \(\Sigma ^n\) is an isoparametric hypersurface. Besides, Eq. (4.10) is equality too, which implies by Lemma 3.1 that \(\Sigma ^n\) has exactly two distinct constant principal curvatures, with multiplicities p and \(n - p\). \(\square \)
Remark 4.2
When \({\overline{M}}{}^{n + 1} = {\mathbb {Q}}_c^{n + 1}\) is a Riemannian space form of constant sectional curvature c, the constants  and \(c_0\) in Theorem 4.1 just agree with c. For this reason, Theorem 4.1 can be regarded as a natural generalization of [13, Theorem 1].
and \(c_0\) in Theorem 4.1 just agree with c. For this reason, Theorem 4.1 can be regarded as a natural generalization of [13, Theorem 1].
5 A sharp integral inequality
In this last section, we will establish a sharp integral inequality concerning compact (without boundary) linear Weingarten hypersurface immersed into a locally symmetric Einstein manifold. This will be done by applying the ideas and techniques introduced by Alías and Meléndez in reference [6] for the case of hypersurfaces with constant scalar curvature in the Euclidean sphere.
We observe that the operator \({\mathscr {L}}\) defined in (3.6) is a divergence-type operator when the ambient space is an Einstein manifold. Indeed, choosing a local orthonormal frame \(\{e_{1},\ldots ,e_{n}\}\) on \(\Sigma ^{n}\) and using the standard notation \(\langle {\cdot },{\cdot }\rangle \) for the (induced) metric of \(\Sigma ^{n}\), from (2.3) we get
Thus, from (5.1) with a straightforward computation we have
where
Hence, from [5, Lemma 25] (see also [2, Lemma 3.1]) we have
where \(\overline{\mathrm{Ric}}\) stands for the Ricci tensor of \({\overline{M}}{}^{n+1}\) and N denotes the orientation of \(\Sigma ^{n}\). Assuming that the ambient space \({\overline{M}}{}^{n+1}\) is an Einstein manifold, from (5.3) we get
Consequently, from (5.2) we conclude that
So, returning to the operator \({\mathscr {L}}\), we get
where \({\mathscr {P}}\) is defined in (3.7).
Finally, we are able to establish the following sharp integral inequality.
Theorem 5.1
Let \(\Sigma ^n\) be a compact linear Weingarten hypersurface immersed into a locally symmetric Riemannian manifold \({\overline{M}}{}^{n+1}\) satisfying curvature conditions (3.1) and (3.2), with \(R=aH+b\) such that  . In the case where
. In the case where  , suppose that \(a>0\). If its totally umbilical tensor \(\Phi \) satisfies (4.1), for some \(1\hbox {\,\,\char 054\,\,}p\hbox {\,\,\char 054\,\,}\frac{n-\sqrt{n}}{2}\), then
, suppose that \(a>0\). If its totally umbilical tensor \(\Phi \) satisfies (4.1), for some \(1\hbox {\,\,\char 054\,\,}p\hbox {\,\,\char 054\,\,}\frac{n-\sqrt{n}}{2}\), then

for every \(q\hbox {\,\,\char 062\,\,}2\), where the real function  is defined in (4.15). Moreover, assuming
is defined in (4.15). Moreover, assuming  , the equality in (5.5) holds if and only if
, the equality in (5.5) holds if and only if
-
(i)
either \(\Sigma ^n\) is a totally umbilical hypersurface, or
-
(ii)
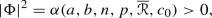
where
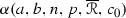 is a positive constant depending only on
is a positive constant depending only on 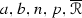 and \(c_0\), and \(\Sigma ^n\) is an isoparametric hypersurface with two distinct principal curvatures of multiplicities p and \(n - p\).
and \(c_0\), and \(\Sigma ^n\) is an isoparametric hypersurface with two distinct principal curvatures of multiplicities p and \(n - p\).
Proof
Taking \(u=|\Phi |^2\), we can rewrite inequality (4.14) as follows:

Since \(u\hbox {\,\,\char 062\,\,}0\) and \(a>0\) when  , we obtain
, we obtain

for every real number q. Besides that, the compactness of \(\Sigma ^n\) guarantees that we can integrate both sides of the previous equation getting

But, from (5.4) we deduce that
for every smooth function \(f\in C^1({\mathbb {R}})\). So, integrating both sides and using Stoke’s Theorem, we arrive at
for every smooth function f. In our case, we choose

With this choice, we get

for all real numbers \(q\hbox {\,\,\char 062\,\,}2\) and \(t\hbox {\,\,\char 062\,\,}0\). Putting (5.7) and (5.8) into (5.6), we obtain
since \({\mathscr {P}}\) is positive semi-defined by item (ii) of Lemma 3.3. Therefore,

proving inequality (5.5).
For the second part of Theorem 5.1, assuming that the equality in (5.10) holds, from (5.9) we obtain
Consequently, we get from (5.8) that

with equality if and only if \(u=0\) and \(q\hbox {\,\,\char 062\,\,}2\). Moreover, since  , we know from item (ii) of Lemma 3.3 that
, we know from item (ii) of Lemma 3.3 that
with equality if and only if \(\nabla u=0\). Thus, from (5.11) we have
Hence, the function \(u=|\Phi |^2\) must be constant, either \(u=0\) or \(\nabla u=0\). In the case that \(|\Phi |^2=0\), \(\Sigma ^n\) must be totally umbilical. Otherwise, \(|\Phi |^2\) is a positive constant and the equality in (5.5) implies  . Therefore, we can reason as in the last part of the proof of Theorem 4.1 to conclude that \(\Sigma ^n\) is an isoparametric hypersurface with two distinct principal curvatures of multiplicities p and \(n - p\).\(\square \)
. Therefore, we can reason as in the last part of the proof of Theorem 4.1 to conclude that \(\Sigma ^n\) is an isoparametric hypersurface with two distinct principal curvatures of multiplicities p and \(n - p\).\(\square \)
Remark 5.2
With the same argumentation made in Remark 4.2, we conclude that Theorem 5.1 corresponds to an extension of [6, Theorem 4.1].
References
Alías, L.J., de Lima, H.F., Meléndez, J., dos Santos, F.R.: Rigidity of linear Weingarten hypersurfaces in locally symmetric manifolds. Math. Nachr. 289(11–12), 1309–1324 (2016)
Alías, L.J., de Lira, J.H.S., Malacarne, J.M.: Constant higher-order mean curvature hypersurfaces in Riemannian spaces. J. Inst. Math. Jussieu 5(4), 527–562 (2006)
Alías, L.J., García-Martínez, S.C.: On the scalar curvature of constant mean curvature hypersurfaces in space forms. J. Math. Anal. Appl. 363(2), 579–587 (2010)
Alías, L.J., García-Martínez, S.C., Rigoli, M.: A maximum principle for hypersurfaces with constant scalar curvature and applications. Ann. Glob. Anal. Geom. 41(3), 307–320 (2012)
Alías, L.J., Impera, D., Rigoli, M.: Hypersurfaces of constant higher order mean curvature in warped products. Trans. Amer. Math. Soc. 365(2), 591–621 (2013)
Alías, L.J., Meléndez, J.: Integral inequalities for compact hypersurfaces with constant scalar curvature in the Euclidean sphere. Mediterr. J. Math. 17(2), Art. No. 61 (2020)
Aquino, C.P., de Lima, H.F., Velásquez, M.A.L.: A new characterization of complete linear Weingarten hypersurfaces in real space forms. Pacific J. Math. 261(1), 33–43 (2013)
Aquino, C.P., de Lima, H.F., Velásquez, M.A.L.: Generalized maximum principles and the characterization of linear Weingarten hypersurfaces in space forms. Michigan Math. J. 63(1), 27–40 (2014)
Brasil Jr., A., Colares, A.G., Palmas, O.: Complete hypersurfaces with constant scalar curvature in spheres. Monatsh. Math. 161(4), 369–380 (2010)
Cheng, S.Y., Yau, S.T.: Hypersurfaces with constant scalar curvature. Math. Ann. 255(3), 195–204 (1977)
Choi, S.M., Lyu, S.M., Suh, Y.J.: Complete space-like hypersurfaces in a Lorentz manifolds. Math. J. Toyama Univ. 22, 53–76 (1999)
de Lima, E.L., de Lima, H.F.: A sharp scalar curvature estimate for CMC hypersurfaces satisfying an Okumura type inequality. Ann. Math. Québec 42(2), 255–265 (2018)
de Lima, E.L., de Lima, H.F.: Complete Weingarten hypersurfaces satisfying an Okumura type inequality. J. Aust. Math. Soc. 109(1), 81–92 (2020)
de Lima, E.L., de Lima, H.F.: A gap theorem for constant scalar curvature hypersurfaces. Collect. Math. 10, 11–15 (2020). https://doi.org/10.1007/s13348-020-00304-3
Gomes, J.N., de Lima, H.F., dos Santos, F.R., Velásquez, M.A.L.: Complete hypersurfaces with two distinct principal curvatures in a locally symmetric Riemannian manifold. Nonlinear Anal. 133, 15–27 (2016)
Li, H., Suh, Y.J., Wei, G.: Linear Weingarten hypersurfaces in a unit sphere. Bull. Korean Math. Soc. 46(2), 321–329 (2009)
Meléndez, J.: Rigidity theorems for hypersurfaces with constant mean curvature. Bull. Brazilian Math. Soc. 45(3), 385–404 (2014)
Nishikawa, S.: On maximal spacelike hypersurfaces in a Lorentzian manifold. Nagoya Math. J. 95, 117–124 (1984)
Okumura, M.: Hypersurfaces and a pinching problem on the second fundamental tensor. Amer. J. Math. 96, 207–213 (1974)
Pigola, S., Rigoli, M., Setti, A.G.: Maximum Principles on Riemannian Manifolds and Applications, vol. 174, p. 822. American Mathematical Society, Providence (2005)
Suh, T.J., Choi, S.M., Yang, H.Y.: On space-like hypersurfaces with constant mean curvature in a Lorentz manifold. Houston J. Math. 28(1), 47–70 (2002)
Acknowledgements
The authors would like to thank the referee for his/her valuable suggestions which improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The second author is partially supported by CNPq, Brazil, Grant 301970/2019-0. The third author is partially supported by CAPES, Brazil.
Rights and permissions
About this article
Cite this article
de Lima, E.L., de Lima, H.F. & Rocha, L.S. Revisiting linear Weingarten hypersurfaces immersed into a locally symmetric Riemannian manifold. European Journal of Mathematics 8, 388–402 (2022). https://doi.org/10.1007/s40879-021-00467-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-021-00467-8
Keywords
- Locally symmetric Riemannian manifolds
- Riemannian space forms
- Linear Weingarten hypersurfaces
- Okumura type inequality



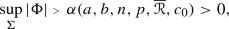
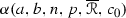 is a positive constant depending only on a, b, n, p,
is a positive constant depending only on a, b, n, p,  and
and 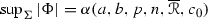 holds and this supremum is attained at some point of
holds and this supremum is attained at some point of 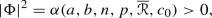
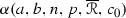 is a positive constant depending only on
is a positive constant depending only on 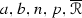 and
and