Abstract
After recalling basic definitions and constructions for a finite group G action on a k-linear category we give a concise proof of the following theorem of Elagin: if \(\mathscr {C}= \langle \mathscr {A}, \mathscr {B}\rangle \) is a semiorthogonal decomposition of a triangulated category which is preserved by the action of G, and \(\mathscr {C}^G\) is triangulated, then there is a semiorthogonal decomposition \(\mathscr {C}^G = \langle \mathscr {A}^G, \mathscr {B}^G \rangle \). We also prove that any G-action on \(\mathscr {C}\) is weakly equivalent to a strict G-action which is the analog of the Coherence theorem for monoidal categories.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The setting of finite groups acting on categories is a well-studied ground, see e.g. [2,3,4,5, 9] and references therein. A useful way to define the action is to require for every \(g \in G\) an autoequivalence \(\rho _g:\mathscr {C}\rightarrow \mathscr {C}\) together with a choice of isomorphisms \(\rho _g \rho _h \simeq \rho _{gh}\) satisfying a cocycle condition, see 2.1. One would then study the category of equivariant objects  , see 2.4.
, see 2.4.
1.2 The main goal of this paper is to give a direct proof of Elagin’s theorem [3, 4] stating that if \(\mathscr {C}= \langle \mathscr {A}, \mathscr {B}\rangle \) is a semi-orthogonal decomposition of triangulated categories and G is a finite group acting on \(\mathscr {C}\) by triangulated autoequivalences in such a way that the category of equivariant objects \(\mathscr {C}^G\) is triangulated and preserving \(\mathscr {A}\) and \(\mathscr {B}\), then there is a semi-orthogonal decomposition  , see Theorem 6.2.
, see Theorem 6.2.
1.3 In our proof we construct the functors  and
and  adjoint to the inclusion functors. The key step in the proof is to show that if \( \Phi :\mathscr {A}\rightarrow \mathscr {C}\) is a G-equivariant functor which admits a left or right adjoint functor \(\Psi \), then \(\Psi \) is automatically equivariant: see Proposition 3.9.
adjoint to the inclusion functors. The key step in the proof is to show that if \( \Phi :\mathscr {A}\rightarrow \mathscr {C}\) is a G-equivariant functor which admits a left or right adjoint functor \(\Psi \), then \(\Psi \) is automatically equivariant: see Proposition 3.9.
1.4 We also prove that every G-action is G-weakly equivalent to a strict G-action, that is to an action satisfying \(\rho _g \rho _h = \rho _{gh}\), see Theorem 5.4. This is analogous to the Coherence Theorem for monoidal categories: every monoidal category is equivalent to a strict monoidal category, see e.g. [7, 1.2.15].
1.5 In order to formulate and prove these facts we need to develop the language of G-functors, G-natural transformations and so on. Perhaps relevant definitions and constructions are well known to experts but we include these for completeness as we could not find the reference that fits our purpose.
1.6 All categories, functors, etc are k-linear where  . Groups acting on categories are finite and we denote by \(1 \in G\) the neutral element of the group.
. Groups acting on categories are finite and we denote by \(1 \in G\) the neutral element of the group.
We use the symbol “

” to denote vertical composition of natural transformations of functors, the other types of compositions are denoted by concatenation.
2 G-categories and equivariant objects
2.1 2.1 Definition
By a G -action on \(\mathscr {C}\) we mean the following data [4, Definition 3.1]:
-
For each element \(g \in G\) an autoequivalence \(\rho _g:\mathscr {C}\rightarrow \mathscr {C}\).
-
For each pair \(g,h \in G\) an isomorphism of functors
$$\begin{aligned} \phi _{g,h}:\rho _g \rho _h \cong \rho _{g h}. \end{aligned}$$
The data must satisfy the following associativity axiom: for all \(g,h,k \in G\) the diagram of functors \(\mathscr {C}\rightarrow \mathscr {C}\) is commutative:

2.2 It follows from the definition that there is an isomorphism of functors
obtained by post-composing \(\phi _{1,1}:\rho _1 \rho _1 \rightarrow \rho _1\) with  . That is we have
. That is we have
Furthermore one can show that \(\phi _1\) satisfies [5, 2.1.1 (e)]:
so that the definition 2.1 coincides with that of [5, 2.1].
On the other hand if one asks for \(\phi _1\) to be the identity transformation, one gets a slightly stronger definition of a G-descent datum of [8, Definition 1.1].
2.3 Using the language of monoidal functors [7, Definition 1.2.10], one can give a very concise definition of a group acting on a category. For that consider G as a monoidal category: G is discrete as a category and its monoidal structure is defined by

Now a G-action on \(\mathscr {C}\) amounts to the same thing as an action of monoidal category G on \(\mathscr {C}\) [7, Example 1.2.12], i.e. a weak monoidal functor

where on the right is the category of functors \(\mathscr {C}\rightarrow \mathscr {C}\) with monoidal structure given by composing functors.
2.2 2.4 Definition
One defines the category of G equivariant objects \(\mathscr {C}^G\) [4, 5] as follows: objects of \(\mathscr {C}^G\) are linearized objects, i.e. objects \(c \in \mathscr {C}\) equipped with isomorphisms
satisfying the condition that the following diagrams are commutative:

Morphisms of equivariant objects consist of those morphisms of the underlying objects in \(\mathscr {C}\) which commute with all \(\theta _g\), \(g \in G\).
3 G-functors and G-natural transformations
3.1 3.1 Definition
Given two categories \(\mathscr {C},\mathscr {D}\) with G-actions and a functor  , \(\Phi \) is called a right lax G-functor if there are given natural transformations
, \(\Phi \) is called a right lax G-functor if there are given natural transformations

such that the two natural transformations  coincide:
coincide:

This commutative diagram is called the pentagon axiom. Similarly \({\Phi }\) is called a left lax G-functor if there are given natural transformations

satisfying the dual pentagon axiom. A right (or left) lax G-functor \({\Phi }\) is called a weak G-functor if all \(\delta _g\) are isomorphisms.
The following lemma is a useful criterion for a weak G-functor.
3.2 3.2 Lemma
Let \({\Phi }\) be a right (or left) lax G-functor. The following conditions are equivalent:
-
(i)
The natural transformation
 is an isomorphism.
is an isomorphism. -
(ii)
\({\Phi }\) satisfies the identity element axiom:

-
(iii)
\({\Phi }\) is a weak G-functor.
Proof
Implications (iii) \(\Rightarrow \) (i), (ii) \(\Rightarrow \) (i) are obvious. Let us prove that (i) \(\Rightarrow \) (iii). Consider the case of the right lax G-functor. Applying the pentagon axiom to the pair  gives
gives

Since the natural transformation on the right-hand side is an isomorphism (note that \(\delta _1\) is an isomorphism by the identity element axiom) and \(\rho _{g},\rho _{g^{-1}}\) are equivalences, it follows that \(\delta _{g^{-1}}\) is left invertible and \(\delta _g\) is right invertible. Thus we see that all \(\delta _g\) are isomorphisms.
Now we prove (i) \(\Rightarrow \) (ii). Consider the natural transformation

We are given that \(\varepsilon \) is an isomorphism and we need to prove that \(\varepsilon \) is in fact an identity.
We use Lemma 3.3 applied to the trivial group  and the composition
and the composition
which gives a lax G-functor \((\mathscr {C}, \mathrm{id}) \xrightarrow {({\Phi }, \varepsilon )} (\mathscr {D}, \mathrm{id})\). The pentagon axiom for this functor yields

and we deduce that \(\varepsilon = \mathrm{id}\). \(\square \)
3.3 3.3 Lemma
If \(({\Phi }, \delta ^{\Phi }):\mathscr {C}\rightarrow \mathscr {D}\), \(({\Psi }, \delta ^{\Psi }):\mathscr {D}\rightarrow \mathscr {E}\) are right/left/weak G-functors, then their composition  is a right/left/weak G-functor.
is a right/left/weak G-functor.
For the proof one needs to check that the composition satisfies the pentagon and/or the identity element axioms; this is a straightforward check.
3.4 3.4 Lemma
A weak G-functor  induces a functor on the categories of equivariant objects
induces a functor on the categories of equivariant objects  such that the following diagram is commutative:
such that the following diagram is commutative:

Proof
For \((c, \theta ) \in \mathscr {C}^G\) we define linearization on \({\Phi }(c)\) as a composition of isomorphisms

of  with \(\delta _g\). It is now a standard check that \({\Phi }(c)\) becomes an equivariant object and that \({\Phi }^G\) is a functor. \(\square \)
with \(\delta _g\). It is now a standard check that \({\Phi }(c)\) becomes an equivariant object and that \({\Phi }^G\) is a functor. \(\square \)
3.5 3.5 Definition
A natural transformation between two weak G-functors  is called a G-natural transformation if for every \(g \in G\) the following diagram commutes:
is called a G-natural transformation if for every \(g \in G\) the following diagram commutes:

3.6 3.6 Lemma
A G-natural transformation \(\mu \) between two weak G-functors \({\Phi }_1, {\Phi }_2:\mathscr {C} \rightarrow \mathscr {D}\) induces a natural transformation  .
.
Proof
To prove that \(\mu \) descends to a natural transformation  we check that for every \((c, \theta ) \in \mathscr {C}^G\) the morphism \(\mu :{\Phi }_1(c) \rightarrow {\Phi }_2(c)\) commutes with linearizations:
we check that for every \((c, \theta ) \in \mathscr {C}^G\) the morphism \(\mu :{\Phi }_1(c) \rightarrow {\Phi }_2(c)\) commutes with linearizations:

The transformation \(\mu ^G\) is natural since the original transformation \(\mu \) is natural and the forgetful functor  is faithful. \(\square \)
is faithful. \(\square \)
3.7 3.7 Definition
Two weak G-functors  ,
,  are called G-adjoint if they are adjoint and the unit
are called G-adjoint if they are adjoint and the unit  and counit
and counit  of the adjunction are G-natural transformations.
of the adjunction are G-natural transformations.
3.8 3.8 Lemma
A G-adjoint pair of functors \({\Phi },{\Psi }\) induces an adjoint pair  between the categories of equivariant objects.
between the categories of equivariant objects.
Proof
From 3.6 it follows that we have natural transformations  ,
,  . The condition for \({\Psi }\) and \({\Phi }\) to be adjoint is that two compositions
. The condition for \({\Psi }\) and \({\Phi }\) to be adjoint is that two compositions

and

are identities. Since the forgetful functor  is faithful, the same holds for
is faithful, the same holds for  . \(\square \)
. \(\square \)
3.9 3.9 Proposition
A left or right adjoint \({\Psi }\) to a weak G-functor \({\Phi }\) can be made into a weak G-functor in such a way that \({\Psi }\) and \({\Phi }\) become G-adjoint.
Proof
Let \({\Psi }\) be the left adjoint to  . We construct the structure of a left lax G-functor on \({\Psi }\) using the structure of a right lax G-functor on \({\Phi }\).
. We construct the structure of a left lax G-functor on \({\Psi }\) using the structure of a right lax G-functor on \({\Phi }\).
Let  and
and  be the unit and the counit of the adjunction. Given a right lax G-structure
be the unit and the counit of the adjunction. Given a right lax G-structure  on \({\Phi }\), we define the left lax G-structure
on \({\Phi }\), we define the left lax G-structure  on \({\Psi }\) as a mate of \(\delta _g\) with respect to the adjunction [6, Proposition 2.1], [7, pp. 185–186], i.e.
on \({\Psi }\) as a mate of \(\delta _g\) with respect to the adjunction [6, Proposition 2.1], [7, pp. 185–186], i.e.

The pentagon axiom can be expressed as an equality of certain compositions in the double category of [6, p. 86], hence is preserved under taking mates by [6, Proposition 2.2]. Checking the identity axiom for \(\delta _1'\) is straightforward.
Now by 3.2, \({\Psi }\) becomes a weak G-functor. The proof for right adjoints is analogous.
We now need to prove that the unit and counit transformations \(\varepsilon ,\eta \) are G-natural. We do the proof for the unit \(\varepsilon \). We need to check that the following diagram commutes:

Here \(\delta _{{\Phi }{\Psi }}\) is defined using 3.3. Unraveling the definitions we are left with checking the diagram (where we use simplified notation for the natural transformations to denote the obvious compositions)

which is easily seen to commute. \(\square \)
3.10 3.10 Corollary
Let  be a weak G-functor. Then the following conditions are equivalent:
be a weak G-functor. Then the following conditions are equivalent:
-
(a)
\({\Phi }\) is an equivalence of categories
-
(b)
There exists a weak G-functor
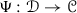 and G-natural isomorphisms
and G-natural isomorphisms  ,
,  .
.
In this case we will call \({\Phi }\) a weak G-equivalence.
Proof
We only need to prove (a) \(\Rightarrow \) (b) as the opposite implication is trivial. Let  be the quasi-inverse functor to \({\Phi }\). In particular \({\Psi }\) and \({\Phi }\) are adjoint (both ways) so that by 3.9 \({\Psi }\) has a structure of a weak G-functor with compositions G-isomorphic to identity functors. \(\square \)
be the quasi-inverse functor to \({\Phi }\). In particular \({\Psi }\) and \({\Phi }\) are adjoint (both ways) so that by 3.9 \({\Psi }\) has a structure of a weak G-functor with compositions G-isomorphic to identity functors. \(\square \)
4 Example: G-actions on the category of vector spaces
4.1 In this section we review a well-known example of how equivalence classes of G-actions on the category of k-vector spaces correspond bijectively to cohomology classes \(H^2(G, k^*)\).
4.2 Let \(\mathscr {C}= \mathrm{Vect}_k\) be the category of k-vector spaces, and let \(\rho \) be the G-action on \(\mathrm{Vect}_k\). As every autoequivalence of \(\mathscr {C}\) is isomorphic to the identity functor, let us assume \(\rho _g = \mathrm{id}\) for every \(g \in G\). In this setup the data of the G-action \(\rho \) defined in 2.1 is equivalent to specifying a cocycle \(\phi \in Z^2(G,k^*)\).
4.3 Consider two G-actions on \(\mathrm{Vect}_k\) given by cocycles  . For the G-actions to be equivalent there needs to exist a weak G-functor
. For the G-actions to be equivalent there needs to exist a weak G-functor

which is an equivalence of categories. Then the pentagon axiom 3.1 requires existence of an element \(\delta = (\delta _g)_{g \in G} \in Z^1(G,k^*)\) such that  for all g, h. Thus G-categories \((\mathrm{Vect}_k, \phi )\) and \((\mathrm{Vect}_k, \phi ')\) are equivalent if and only if
for all g, h. Thus G-categories \((\mathrm{Vect}_k, \phi )\) and \((\mathrm{Vect}_k, \phi ')\) are equivalent if and only if  .
.
4.4 The category of equivariant objects \((\mathrm{Vect}_k, \phi )^G\) is the category of \(\phi \)-twisted G-representations with objects given by vector spaces V together with isomorphism \(\theta _g:V \rightarrow V\) satisfying \(\theta _{gh} = \) and G-equivariant morphisms. In particular, if \(\phi \) is the trivial cocycle, so that G-action on \(\mathrm{Vect}_k\) is trivial, \(\mathrm{Vect}_k^G\) is the category of G-representations.
5 Strictifying G-actions
5.1 Let \({\Omega }(G)\) denote the category with one object for every element \(g \in G\) with  for \(g \ne h\).
for \(g \ne h\).
5.2 Let \(\mathscr {C}\) be a category with a G-action. Consider the category of weak G-functors and G-natural transformations from \({\Omega }(G)\) to \(\mathscr {C}\)

We endow \(\mathscr {C}'\) with the strict G-action induced by the G-action on \({\Omega }(G)\).
5.3 Explicitly the objects of \(\mathscr {C}'\) consist of families  together with isomorphisms
together with isomorphisms  satisfying the cocycle condition that two ways of getting an isomorphism
satisfying the cocycle condition that two ways of getting an isomorphism  coincide. The morphisms from \((c_g)_{g \in G}\) to \((d_g)_{g \in G}\) are morphisms
coincide. The morphisms from \((c_g)_{g \in G}\) to \((d_g)_{g \in G}\) are morphisms  satisfying the condition that the two natural ways of forming a morphism
satisfying the condition that the two natural ways of forming a morphism  coincide.
coincide.
5.1 5.4 Theorem
The functor  sending \((c_g)_{g \in G}\) to \(c_1\) is a weak G-equivalence. Hence, every G-action is weakly equivalent to a strict G-action.
sending \((c_g)_{g \in G}\) to \(c_1\) is a weak G-equivalence. Hence, every G-action is weakly equivalent to a strict G-action.
Proof
We need to check that \({\Phi }\) has a structure of a weak G-functor and that \({\Phi }\) is fully faithful and essentially surjective.
The structure of a weak G-functor on \({\Phi }\) is in fact simply given by the structure maps \(\delta _{h,g}\). That is we have functorial isomorphisms

and the pentagon axiom follows from the cocycle condition on \(\delta \).
To check that \({\Phi }\) is essentially surjective, one checks that for any \(c \in \mathscr {C}\) the family \((\rho _g(c))\) has a structure of an object from \(\mathscr {C}\). Furthermore, one can see that any object \((c_g)_{g \in G}\) is isomorphic to \((\rho _g(c_1))_{g \in G}\).
Thus to check that \({\Phi }\) is fully faithful, we may take two objects  and \((d_g)_{g \in G} = (\rho _g(d_1))\) and a morphism
and \((d_g)_{g \in G} = (\rho _g(d_1))\) and a morphism  between them. It is then easy to see that
between them. It is then easy to see that  and that conversely for any
and that conversely for any  , the collection \(\rho _g(f_1)\) defines a morphism between c and d. \(\square \)
, the collection \(\rho _g(f_1)\) defines a morphism between c and d. \(\square \)
6 Elagin’s theorem
6.1 If \(\mathscr {C}\) is a triangulated category and G acts by triangulated autoequivalences, then \(\mathscr {C}^G\) is endowed with a shift functor and a set of distinguished triangles: these are the triangles that are distinguished after applying the forgetful functor  . Furthermore under some mild technical assumptions this gives \(\mathscr {C}^G\) the structure of a triangulated category [4, Theorem 6.9], for instance existence of a dg-enhancement of \(\mathscr {C}\) is a sufficient condition for \(\mathscr {C}^G\) to be triangulated [4, Corollary 6.10].
. Furthermore under some mild technical assumptions this gives \(\mathscr {C}^G\) the structure of a triangulated category [4, Theorem 6.9], for instance existence of a dg-enhancement of \(\mathscr {C}\) is a sufficient condition for \(\mathscr {C}^G\) to be triangulated [4, Corollary 6.10].
6.1 6.2 Theorem
Let \(\mathscr {C}= \langle \mathscr {A}, \mathscr {B}\rangle \) be a semi-orthogonal decomposition of triangulated categories. Let G act on \(\mathscr {C}\) by triangulated autoequivalences which preserve \(\mathscr {A}\) and \(\mathscr {B}\). Assume that the equivariant category \(\mathscr {C}^G\) is triangulated with respect to triangles coming from \(\mathscr {C}\). Then  are triangulated and there is a semi-orthogonal decomposition
are triangulated and there is a semi-orthogonal decomposition

Proof
The existence of an adjoint pair between \(\mathscr {C}\) and \(\mathscr {C}^G\) [4, Lemma 3.7] implies that  and
and  . In particular, \(\mathscr {A}^G\) and \(\mathscr {B}^G\) are triangulated subcategories of
. In particular, \(\mathscr {A}^G\) and \(\mathscr {B}^G\) are triangulated subcategories of  .
.
Now in order to establish the semi-orthogonal decomposition  it suffices to show that the embedding
it suffices to show that the embedding  has a left adjoint [1, 1.5]. This holds true by 3.9, 3.8: the functor \(i:\mathscr {A}\rightarrow \mathscr {C}\) is (strictly) G-equivariant, hence its left adjoint \(p:\mathscr {C}\rightarrow \mathscr {A}\) induces an adjoint \(p^G\) to the embedding
has a left adjoint [1, 1.5]. This holds true by 3.9, 3.8: the functor \(i:\mathscr {A}\rightarrow \mathscr {C}\) is (strictly) G-equivariant, hence its left adjoint \(p:\mathscr {C}\rightarrow \mathscr {A}\) induces an adjoint \(p^G\) to the embedding  . \(\square \)
. \(\square \)
References
Bondal, A.I., Kapranov, M.M.: Representable functors, Serre functors, and mutations. Math. USSR Izv. 35(3), 519–541 (1990)
Deligne, P.: Action du groupe des tresses sur une catégorie. Invent. Math. 128(1), 159–175 (1997)
Elagin, A.D.: Descent theory for semiorthogonal decompositions. Sb. Math. 203(5–6), 645–676 (2012)
Elagin, A.: On equivariant triangulated categories (2014). arXiv:1403.7027
Ganter, N., Kapranov, M.: Symmetric and exterior powers of categories. Transform. Groups 19(1), 57–103 (2014)
Kelly, G.M., Street, R.: Review of the elements of \(2\)-categories. In: Dold, A., Eckmann, B. (eds.) Category Seminar. Lecture Notes in Mathematics, vol. 420, pp. 75–103. Springer, Berlin (1974)
Leinster, T.: Higher Operads, Higher Categories, vol. 298. Cambridge University Press, Cambridge (2004)
Niwa, M.: Theory of \(G\)-categories. Mem. Fac. Ed. Shiga Univ. Nat. Sci. Ped. Sci. 40 (1990), 1–24 (1991) (in Japanese)
Sosna, P.: Linearisations of triangulated categories with respect to finite group actions. Math. Res. Lett. 19(5), 1007–1020 (2012)
Acknowledgements
We thank Alexey Elagin, Sergey Galkin, Nick Gurski, Tom Leinster and François Petit for useful conversations and e-mail communications. We thank the referee for the suggestions on improving the exposition.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shinder, E. Group actions on categories and Elagin’s theorem revisited. European Journal of Mathematics 4, 413–422 (2018). https://doi.org/10.1007/s40879-017-0150-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-017-0150-8



 is an isomorphism.
is an isomorphism.
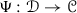 and G-natural isomorphisms
and G-natural isomorphisms  ,
,  .
.