Automated phase-type distribution fitting via expectation maximization

Abstract

In numerous practical domains such as reliability and performance engineering, finance, healthcare, and supply chain management, a common challenge revolves around accurately modeling intricate time-based data and event duration. The inherent complexities of real-world systems often make it challenging to use conventional statistical distributions. The phase-type (PH) distributions emerge as a remarkably adaptable class of distributions suited for modeling scenarios like failure or response times. These distributions are helpful in analytical and simulation-driven system evaluation approaches and are frequently used to fit empirical datasets. This paper introduces a strategy that leverages user-friendly tools, graphical adjustment features, and integration with existing tools to streamline the process of fitting PH distributions to empirical data. The simplicity of this procedure empowers domain experts to more accurately model complex systems, resulting in enhanced decision-making, more efficient resource allocation, improved reliability assessments, and optimized system performance across an extensive spectrum of practical domains where the analysis of time-based data remains pivotal. Furthermore, this study presents a method for the automated determination of parameters within a fitted Hyper-Erlang distribution. This method utilizes the Bayesian Information Criterion (BIC) within a Bayesian optimization framework integrated into an Expectation-Maximization (EM) algorithm. Consequently, it enables deriving a given dataset’s probability density function (PDF) through a combination of Hyper-Erlang distributions. Subsequently, the PDF serves as a tool for assessing system performance.

1 Introduction

Model-based benchmarking, an essential engineering field used to estimate attributes such as system reliability, security, and performance, often employs Markov Chains for the probabilistic description of state-based stochastic models. While mathematically manageable, Markov Chains still necessitate efficient numerical methods to compute large-scale systems’ stationary and transient metrics. When these models become non-Markovian, classical analytical approaches may prove unfeasible due to including non-exponential distributions.

There are three principal methodologies when evaluating performance: analytical modeling, simulation, and measurement. Analytical modeling uses equations to predict and analyze how computational systems behave. These equations are based on understanding and estimating system behavior within a finite period and can be enhanced using phase-type (PH) distributions. PH distributions are helpful for approximating non-exponential stochastic models, which are essential for performance and reliability engineering, and they densely populate the non-negative probability distribution space [1], which is crucial for generating approximate Markov models. As a result, there has been an increase in research focusing on stochastic models using both Markovian and non-Markovian methods. The maximum likelihood principle has shown promise in adjusting PH distributions, highlighting the importance of exploring methods for parameter approximation in contemporary research domains [2, 3].

The expectation–maximization (EM) method is pivotal in statistical analysis and machine learning applications, significantly facilitating the maximum likelihood estimation (MLE) in the presence of latent variables. This technique offers a direct approach to MLE, known for its precision and adaptability. However, it faces challenges when dealing with censored data that require tailored solutions for distributions that diverge from the exponential model. In this context, the phase-type (PH) distributions have emerged as a compelling tool, championing the creation of robust probabilistic models adept at capturing the nuances of lifetime systems.

Hyper-Erlang distributions, a class of PH distributions, provide a significant context for EM application. These distributions can model a wide range of behaviors in stochastic systems [4]. Applying the EM algorithm to hyper-Erlang distributions allows for estimating phase numbers, phase-associated distributions, and phase transition probabilities. This process, beginning with initial parameter assumptions, iteratively updates them until convergence.

This work proposes an iterative algorithm to fit the empirical distribution using PH distributions. Utilizing the established expectation–maximization algorithm, it provides the hyper-Erlang phase-type parameters. After determining the parameters of the fitted distributions, we define a function representing the fitted distribution. We then use this function to study the system’s performance and reliability and simulate other potential scenarios without additional data collection or modeling requirements. The main aims of this paper are: (1) proposing a methodology to automatically find the parameters of a hyper-Erlang distribution that accurately describes a system’s distribution; (2) Integrating the Bayesian Information Criterion (BIC) into the expectation–maximization (EM) algorithm for precisely determining the distribution parameters; (3) showing the algorithm’s usefulness and versatility by testing it on various datasets by applying the methodology; (4) derivating functions such as the dataset’s probability density and reliability functions.

This paper is structured as follows: Sect. 2 presents the knowledge required to obtain such functions. Section 3 offers a list of related works. Section 6 briefly describes the algorithm for fitting reliability using PH distributions. Section 5 introduces PhaseFitPro, a tool implemented to support the proposed fitting process. In Sects. 6.1 and 6.2, we apply the proposed methodology to an experiment for performance metrics. Finally, Sect. 7 presents final considerations and potential future research directions.

2 Background

This section presents the fundamental concepts necessary for developing the present text. One of the essential concepts in developing PH theory is the matrix analytical methods developed by Neuts, in particular, Refs. [5, 6]. These papers introduced the necessary mathematical tools to support the theory of PH distributions.

2.1 Exponential distributions

The exponential distribution, often used to model the time between events, provides insight into understanding the intervals or waiting times for specific occurrences. A defining characteristic of the exponential distribution is its memorylessness; past events or waiting times do not influence future outcomes [7]. Essentially, each instance is a fresh start, uninfluenced by prior results. Suppose X represents a continuous random variable with a single phase with parameter $\lambda$. The following formulas are widely known:

$$\begin{aligned}{} & {} f_X = \frac{dF(x)}{dx}= \lambda e^{-\lambda x}, \ \forall x>0, F(x)=1-e^{-\lambda x}, \nonumber \\ {}{} & {} E[X]=\frac{1}{\lambda }, \textrm{and} \ \sigma _{X}^2=\frac{1}{\lambda ^2}. \end{aligned}$$

(1)

However, the exponential distribution could better represent the studied distribution in many practical situations. However, the combination of n exponential phases has excellent flexibility and adjustment power. Fortunately, the computational advances that have occurred in recent decades have made it possible to create algorithms that determine the combination of exponential distributions that best represent the pdf of a dataset. Deciding on the infinitesimal matrix of the underlying Markov chain is possible. Thus, we can determine the probability density function (PDF) and the cumulative distribution function (CDF) of more general distributions.

2.2 Hyper-Erlang distributions

Suppose we are analyzing a system that is a succession of exponential phases with a parameter $\lambda$. In other words, consider a system with n exponential phases at the same rate. Such distributions are called hyper-Erlang distributions. We have $E(X) = \frac{n}{\lambda }$, $\sigma _{X}^2 = \frac{r}{\lambda ^2}$ and the squared coefficient of variation $C_T ^ 2 = \frac{1}{n}$. The density function and its respective cumulative probability function are given by

$$\begin{aligned} f_X(x)= & {} \frac{\lambda (\lambda x)^{n-1}e^{-\lambda x}}{(n-1)!}, \ \forall x>0, \nonumber \\ F_X(x)= & {} 1-e^{-\lambda x} \sum _0^{n-1}\frac{(\lambda x)^i}{i!}, x\ge 0, \ n=1,2, \ldots \end{aligned}$$

(2)

The distribution representing the mixture of n-distributions is given by

$$\begin{aligned} f_T (x)=\sum _{i=1}^n \alpha _i f_{X_i}. \end{aligned}$$

(3)

The results presented in [8] showed that the fitting processes defined by mixing Erlang-type distributions are as robust as those described by general PH’s or acyclic PHs. Furthermore, they show that distributions with many states can be fitted efficiently. The fitting algorithm is relatively stable due to the spatial structure of the density function, which produces a fast and reliable likelihood maximization method. In this work, Erlang-mixing structures will be used to model the frequency distributions of the experiments. These generated functions will be used for data-driven reliability analysis.

2.3 Continuous-time Markov chains

An absorbing state Markov chain is a stochastic process characterized by a set of states in which one or more states are absorbing, and the others are transient. If the chain starts transient, it will eventually reach an absorbing state and remain in it forever. The matrix Q is square $n \times n$ that describes the transition rates from one state to another. The vector $d_1$ is a vector $n \times 1$ that contains the transition probabilities to the absorbing state [9,10,11].

Note that when the Markov chain reaches an absorbing state, it stays in that state forever. The matrix $M = (-Q)^{-1}$ is the fundamental matrix (also known as the momentum matrix) of a continuous-time Markov chain with an absorbing state, and each element $(-Q)^{- 1}(i,j)$ gives us the average time required for the state j to be absorbed given the initial state i. The transition probability matrix satisfies the Kolmogorov equation: $\frac{dP(t)}{dt} = QP(t)$. Thus, $P(t) = ce^{Qt}$. Using the Taylor series of the exponential function, we write

$$\begin{aligned} P(t)=e^{Qt}=\sum _{i=0}^{\infty }\frac{(Qt)^i}{i!} \ and, \ \frac{dP(t)}{dt} = Qe^{Qt}. \end{aligned}$$

(4)

Using the initial probability vector $\pi (0),$ will set the state 1 as the initial state (at time $t = 0$) so that after time t, the process will still occupy one of the states $1, 2, \ldots , n$, with probability $\pi (0) \cdot M \cdot 1$, where 1 is a column vector of $1's$. Thus, the absorption time distribution function will be given by $F(t)=1-\pi (0) \cdot e^{Qt}\cdot 1$. Furthermore, the probability density is defined by $f(t)=\pi (0) \cdot e^{Qt} \cdot q$ where, $q=-d_1$, and $e^{Qt}$ is an exponential matrix. Let S be a set of states, a continuous-time stochastic process ${X}_{t \ge 0}^{\infty }(t)$ is a Markov process with a state described in $\frac{d P (t)}{dt} \, = \, P (t) \cdot Q, \hspace{0.5 cm} \Pi (0) \cdot 1 \, = \, 1$. With the solution of this system, we obtain $P (t) \, = \, P (0) \; e^{Qt}$, where P(0) vector is the initial probability vector, and Q infinitesimal generator. From that,

$$\begin{aligned} \sum _{\forall j, j \ne i} q_{ij} \, + \, q_{ii} \, = \, 0, \ and \ q_{ii}= - \, \sum _{\forall j, j \ne i} q_{ij}, \end{aligned}$$

(5)

knowing that a state i is an absorbing state if $q_{ii} = 0$. The choice of the continuous-time Markov chain over other modeling techniques was motivated by the fact that it allows the development of analytical models to assess component availability, following the principles presented in Refs. [12,13,14].

2.4 Fitting method

An expectation–maximization algorithm (EM) is an approach that performs the maximum likelihood estimation in the presence of latent variables. It does this by estimating the values for the latent variables and optimizing the model until convergence. It is a practical and commonly used approach to estimating densities with missing data. The popularity of the EM algorithm stems from the fact that it can be simple to implement and that the global maximum can be found reliably through stable and increasing steps.

The fitting of PH’s typically requires defining parameters such as the number of phases and clusters [15]. However, considering the application of this analysis technique in a production environment, it is crucial to devise a way to automate this parameter determination process, thereby ensuring both accurate and reliable models. Given this scenario, adopting Bayesian optimization tools emerges as a viable and effective strategy to address this challenge [16]. For hyper-Erlang distributions, the EM algorithm can be used to estimate phase number and phase-type distributions, as well as phase transition probabilities. The algorithm starts with initial guesses for these parameters and then iteratively updates them until convergence. The EM algorithm for hyper-Erlang distributions is implemented using the Baum–Welch algorithm, a particular case of the EM algorithm for hidden Markov models.

3 Related works

This section reviews research on estimating probability density functions (PDFs) and cumulative distribution functions (CDFs) for performance metrics. We also highlight this article’s contributions compared to the cited works.

3.1 Fitting methods for phase types

The tutorial in Ref. [17] offers a comprehensive guide to PH-fitting techniques. It introduces the PH-fitting algorithm, EM-based PH estimation, and standardization. In addition, it presents the phase-type software reliability model (PH-SRM) and its parameter estimation using the PH estimation algorithm. However, the authors acknowledge that this method can be computationally intensive in some scenarios.

In Ref. [18], a generic mathematical model is proposed for open queue systems, providing closed-form equations for estimating system response times. This work stands out for its parameterization without assuming specific arrival distributions. PHDs enhance flexibility and practicality in Time-To-Failure studies through continuous-time Markov chains (CTMC).

Barde et al. [19] use PHDs to approximate non-Markov models, enabling the analysis of complex systems under Markovian decay. The article includes numerical results and adjustments for transition probabilities in maintenance optimization Markov decision process models.

Zhang et al. [20] present an efficient algorithm for calculating the Fisher information matrix in fitting History Dependent Renewal Processes using PHs. This algorithm employs a smoothing technique in a continuous-time stochastic process (CTMC) to compute crucial second derivatives of the log-likelihood function (LLF). A computational algorithm is developed to expedite the Fisher information matrix calculation and compute LLF’s first and second derivatives for samples and probability density functions.

Bladt and Rojas-Nandayapa [21] tackle statistical inference for univariate and independent heavy tailed data. They propose fitting methods for these data using exponential mixture (EM) and phase-type distributions (NPH) scale mixture class distributions. This work introduces a new class of heavy tailed distributions and an EM algorithm for maximum likelihood parameter estimation. The authors consider various data types, including histograms, censored data, and theoretical distributions, and provide numerical examples using simulated and reference reinsurance datasets.

Albrecher et al. [22] introduce scaling PH distributions with continuous scaling components. They develop an EM algorithm for maximum likelihood estimation, particularly useful with empirical data, including censored data. Unlike NPH distributions, closed-form formulas for mixed distributions can be evaluated using functional calculus tools, avoiding infinite series truncation. The article also investigates products between phase-type distributed random variables and independent, positive, continuous random variables, establishing their asymptotic properties. Finally, an expectation–maximization algorithm is derived and implemented for statistical inference of these mixed distributions using real-world datasets, often exhibiting heavy tails and retaining phase-type distribution properties.

3.2 Reliability

Alkaff and Qomarudin [23] propose a straightforward method for functional reliability analysis of systems with general structures using the PH distribution. They present algorithms for system reliability modeling and analysis, efficiently generating system reliability functions for independent components and other reliability measures.

Wu et al. [24] extend PH distributions to cases with specific transition thresholds and time spent thresholds in selected states. They develop three models using aggregated stochastic processes theory and derive closed-form expressions for reliability indices, such as availability and lifetime distributions. Numerical examples illustrate the proposed formulas.

Wang et al. [25] introduce a new mathematical model for repairable systems with two types of exponentially distributed components and a repairer. They analyze this model using Markov process theory and the matrix analytical method, with an example of solar power generation.

He et al. [26] propose two random variable approximations using the ‘Erlangization’ technique, which is valuable for analyzing basic reliability structures. Li et al. [27] offer a PH-based method for time-dependent reliability analysis of deteriorating structures. They use PH adjustment techniques to generate a simple reliability expression, considering progressive and shock deterioration. Numerical examples demonstrate the method’s efficiency, with accuracy validated against Monte Carlo simulations.

Pereira et al. [12] present closed-form equations for evaluating system performance and capacity planning. They apply this methodology to assess how a web server in a fog node is affected by unexpected workloads, using Markov chains for analysis. Similarly, the article [25] provides an analytical approach for system description, claiming time savings in system modeling.

Zheng et al. [28] propose an approach for estimating the performance and reliability of a web service before deployment based on observed data. They use phase process expansion to create an expanded continuous-time homogeneous Markov chain for the web service, explicitly including failure and restart states. This approach enables performance and reliability calculations using the PH tuning method based on observations of service execution times. Experimental results from web services demonstrate the approach’s effectiveness.

Alkaff et al. [29] extend the state-space model and introduce a deceleration factor for available waiting systems with multistate components. These components follow matrix-based phase-type (PH) distributions. The resulting model represents the system lifetime distribution as a PH distribution, facilitating dynamic system reliability analysis. Comparisons with other methods from previous publications are included.

Finally, Balali et al. [30] review approaches to degradation-based reliability estimation models, focusing on their application in the Industrial Internet of Things (IIoT). They provide a roadmap for adopting IIoT-based reliability estimation models, explaining their application and advantages. The study underscores the importance of these models in monitoring system conditions over time.

3.3 Fitting tools

Efficient software tools for fitting phase-type distributions have been developed in recent years. Notable examples include HyperStar [2, 31] and BuTools [3, 32]. HyperStar is a modern tool tailored for fitting PH distributions to diverse datasets.

PH distributions are known for their versatility in approximating non-negative distributions, offering closed-form expressions for essential metrics and representation as Markov chains. While HyperStar is user-friendly and supports various export formats, it lacks streamlined distribution methods, and its source code remains proprietary, limiting community refinement.

BuTools—is a comprehensive suite designed for traffic modeling and queue analysis. It extensively supports PH distributions, including density function computations and moment matching. BuTools also covers Markov.

4 Automatic PH-fitting process

When applied to hyper-Erlang distributions, the EM algorithm can be streamlined using specific structural constraints [33]. Hyper-Erlang distributions can approximate any positive random variable distribution, with its parameters given as $(\pi , \lambda )$, and the Erlang branch orders represented as $r$. The algorithm for these phase-type distributions is outlined in references. A unique feature of the hyper-Erlang distribution is the ability to fully describe a continuous-time Markov process, generating a random variable $X_k$ through its initial state, sufficient for determining the selected Erlang branch. Outlined below are the EM algorithm steps tailored for the hyper-Erlang distribution:

1. Initialization: randomly define the initial values of the model parameters, $\Theta _0$. They help generate a preliminary estimate of the data’s probability distribution.

2. Likelihood Differentiation: determine the likelihood function for data using present model parameters, represented as

$$\begin{aligned} Q(\theta , \theta ^0)&= \sum _{i=1}^{n} \sum _{j=1}^{r} z_{ij} [ (r-1)\ln \lambda _j - \lambda _j x_i \\ {}&\quad + (r-1)\ln x_i - \ln (r-1)! ], \end{aligned}$$

where $z_{ij}$ signifies the posterior probability that data point $i$ belongs to cluster $j$, $x_i$ is sample $i$’s value, $r$ indicates the required events in the Erlang-r distribution, and $\lambda _j$ represents the event occurrence rate in cluster $j$.

3. Posterior probabilities calculation: determine the posterior probability distribution based on revised data and parameters. The posterior distribution for each Erlang-r cluster is expressed as

$$\begin{aligned} p(z_{ij}=1|x_i,\theta ) = \frac{\theta _j^r x_i^{r-1} e^{-\theta _j x_i}}{\sum _{l=1}^k \theta _l^r x_i^{r-1} e^{-\theta _l x_i}}, \end{aligned}$$

with $k$ representing the cluster count.

4. Optimal parameter determination: update the model parameters based on posterior probabilities. Differentiate the likelihood function for each parameter, equate the derivatives to zero, and deduce the parameters. The optimal value for every $\theta _i$ parameter within Erlang-r distributions is

$$\begin{aligned} \theta _j = \frac{r \sum _{i=1}^n z_{ij}}{\sum _{i=1}^n z_{ij} x_i}. \end{aligned}$$

5. Parameter update: use the revised parameters for recalculating the posterior probability distribution and iterate until the parameters reach a stable solution.

The EM algorithm’s core lies in its iterative nature. Each change in parameter estimates yields varied posterior probabilities, which, when recalculated in step 4, produce distinct parameter estimates. The algorithm involves two main actions: determining the posterior probability using current parameters and updating parameters based on the prevailing posterior probability. The process described above provides the vector $\pi$ and matrix Q described in this section with the following structures:

$$\begin{aligned} \pi = (\alpha _1,\alpha _2, \ldots , \alpha _{M-1},\alpha _M), \end{aligned}$$

$$Q = \begin{pmatrix} T_1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} T_2 &{} 0 &{} 0 &{} 0 \\ &{} &{} \ddots &{} &{} \\ 0 &{} 0 &{} 0 &{} T_{M-1} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} T_M \\ \end{pmatrix},$$

where each

$$T_i = \begin{pmatrix} -\lambda _i &{} \lambda _i &{} 0 &{} 0 &{} 0 \\ 0 &{} -\lambda _i &{} \lambda _i &{} 0 &{} 0 \\ &{} &{} \ddots &{} &{} \\ 0 &{} 0 &{} 0 &{} -\lambda _i &{} \lambda _i \\ 0 &{} 0 &{} 0 &{} 0 &{} \lambda _i\\ \end{pmatrix}.$$

Bayesian optimization requires the definition of value ranges to be tested and a metric to be optimized. After a predetermined number of iterations with random values, Bayesian optimization employs a surrogate model that estimates the objective function of the chosen metric. Each point on this function represents the probability of achieving a particular score for the evaluation metric, given a specific hyperparameter. This sequential search technique, anchored on the principles of Bayes’ theorem, guides the search for optimal points in an objective function by estimating the posterior probability distribution of the model parameters based on the data and a prior distribution. When dealing with a complex and multivariate parameter space, like in calibrating phase types (PH) with the expectation–maximization (EM) algorithm, Bayesian optimization proves particularly efficient [34].

In the context of the EM algorithm based on hyper-Erlangs for determining the number of clusters and phases, Bayesian optimization will be employed to explore the parameter space intelligently. First, the prior distribution of the hyperparameters will be defined, considering the boundaries and characteristics of each parameter. Then, based on previous iterations and the objective function (BIC obtained from log-likelihood), Bayesian optimization will suggest a new set of parameters to be tested. This process will continue until the optimal number of clusters and phases are found, thus allowing effective automation of PH fitting. The step-by-step process of this automated hyperparameter optimization is presented in the Algorithm 1.

Algorithm 1

Automated Hyperparameter Search Algorithm

The illustrated algorithm provides a general approach to automated hyperparameter optimization in the context of an expectation–maximization (EM) algorithm based on hyper-Erlangs. The goal is to determine the optimal number of clusters and phases, two critical hyperparameters in this context.

The algorithm begins by initializing placeholders for the best hyperparameters. The objective function, to be minimized, calculates the Bayesian Information Criterion (BIC), which is a statistical measure of model validity considering both the log-likelihood of observed data given the current model parameters and the number of parameters utilized in the model. The BIC is designed to penalize model complexity, thereby helping to prevent overfitting.

Hyperparameter values are searched within a specified range using a specific algorithm that selects a new set of hyperparameters to evaluate at each iteration, aiming to minimize the objective function. The algorithm iteratively refines its hyperparameter selections based on the results of previous evaluations, guided by the objective of locating the global minimum of the objective function in the hyperparameter space.

Once the algorithm has concluded its search-either by exhausting the number of permitted evaluations or meeting a specific stopping criterion—it retrieves the best hyperparameters corresponding to the minimum value of the BIC obtained. These hyperparameters, representing the optimal number of clusters and phases, are then returned by the algorithm.

Hyper-Erlangs were selected for this study due to their flexibility and deference to an analytical expression for the probability density function (PDF), the CDF, and the derived functions utilized in reliability analysis. The generation of these functions depends on Calculus techniques, thus necessitating the functions to be integrable and preferably simple—meaning, a smaller number of parameters derived from the fitting process is desirable. To yield such functions, the BIC was selected as the stopping criterion for Bayesian optimization. This criterion imposes a penalty on models with a more significant number of parameters, thus encouraging simpler models.

As outlined by Bladt [35], observing the negative log-likelihood when choosing fitted dimensions and structures is advisable. While the authors concede that larger matrices often result in better likelihoods, they also note that it is common for this likelihood increase to plateau in practical scenarios. One can proceed to model selection regarding regression coefficients after determining dimension and structure. These coefficients align with the conventional system, allowing the use of AIC or BIC criteria for Comparison and selection among various proposed models.

This study’s approach focuses on achieving the fitting via log-likelihood. In addition, the Bayesian optimization process, with its objective function defined as $BIC = -2 \times \text {log-likelihood} + \text {num-params} \times \text {np.log}(n)$, where $num-params = num-clusters \times (phases + 1)$ and $n =$ length of data. This method has shown effectiveness, yielding promising results in automating selecting the number of phases and clusters for fitting PH distributions.

Having obtained the parameters from the abovementioned process, we construct the probability density functions (PDFs) with mixture distributions. Following this, the reliability evaluation methodology is carried out in a series of steps:

• The first step involves collecting data associated with the system’s behavior over time. These data should include information about the various states of the system, along with the time required for transitions between these states.

• Using the collected data, we estimate the parameters of a phase-type (PH) distribution. This estimation process utilizes the expectation–maximization (EM) algorithm, and Bayesian optimization is employed to ascertain the optimal number of clusters and phases.

• Once the PH distribution has been fitted, it is then used to model the system’s behavior. This provides us with the ability to predict the state of the system at a given point in time. It also allows for calculating various reliability metrics, such as the probability density function (PDF), its complementary function, and other metrics crucial for dependability analysis.

Through this process, we develop a model of the system’s behavior and gain the capacity to predict its future state and assess its reliability using various established metrics. While the flexibility of hyper-Erlang distributions is a significant advantage, it is crucial to emphasize that fitting through this mixture of distributions only sometimes guarantees accuracy in real-world systems. Additional data treatment steps may be necessary depending on the collected data’s peculiarities. Therefore, the direct application of the proposed methodology without careful preliminary analysis of the data can lead to inaccurate or misleading results. It is, then, essential to comprehensively validate the model assumptions and precisely fit the data in question. This involves pre-processing stages, such as data cleaning, handling missing values, and normalization. It is also crucial to conduct exploratory data analysis identifying trends, patterns, variable relationships, and outliers. These steps ensure the reliability and robustness of the results obtained by applying the proposed methodology.

Fig. 1

Alpha version of AutoFitting tool

5 EMA Tool

This section introduces the EMA (Expectation-Maximization Algorithm) Tool to automate the fitting process. We aim to provide a user-friendly interface for those seeking a hassle-free automatic fitting experience and a more detailed one for enthusiasts/experts who prefer a finer control via manual fitting (Fig. 1). This balance between simplicity and functionality not only broadens our tool’s accessibility to a broader range of users but also ensures that every user can achieve their desired outcomes tailored to their specific needs. The alpha version of EMA was added to Mercury1 Tool (version 5.2 onwards).

6 Case studies

This section introduces two distinct case studies. The first case study aims to showcase the algorithm’s versatility by applying automated fitting using the hyper-Erlang distribution to a variety of datasets. This evaluates its ability to manage intricate scenarios and sets the stage for validation in computational analyses across diverse contexts. The second case study delves into characterizing the Time-To-Failure (TTF) and Time To Restore (TTR) distributions within a fog computing environment. This highlights the utility of automated fitting with the hyper-Erlang distribution in reliability analysis.

6.1 Case study 1: automatic fitting in different scenarios

In this section, we conduct a case study applying automated hyper-Erlang distribution fitting to diverse datasets, assessing its ability to handle complexity and paving the way for validation in various computational analysis scenarios.

The method described in Sect. 4 has been applied to several datasets. These datasets are detailed in tables 7.13, 7.20, 7.41, 7.42, 24.14, and 24.23, as referenced in Refs. [10, 11]. These cited works are foundational in the realm of computational system evaluations. They offer an extensive dataset that captures a wide range of dynamics essential for analyzing and modeling such systems. For our study, we employed an automated fitting technique on these datasets and conducted an analysis using the hyper-Erlang distribution. This section provides further details on the parameters chosen and the outcomes of the fitting for each scenario.

Consider the dataset in Fig. 2, comprising 80 measures. These data have a coefficient of variation (CoV) of 0.541 and an interquartile range (IQR) of 184.5. It is evident from the observation that the data are divided into two distinct groups. By employing automated fitting with the hyper-Erlang distribution, we have identified 30 phases and two clusters. The fitting proved more efficient for the first data group in the histogram.

The sample size depicted in Fig. 3 is 60. By analyzing the sample histogram, a quick observation allows us to hypothesize that the sample comprises two or three clusters. On the other hand, the fitting procedure determined the presence of 2 clusters and 13 phases on each. This configuration suggests a level of complexity lower than what was previously observed. This can be attributed to the data being more densely grouped, forming cohesive clusters.

Fig. 2

Algorithm applied in table 7.13, obtained parameters (0.1016, 0.2873), and initial probability vector (0.3756, 0.6243)

Fig. 3

Algorithm applied in table 7.20, obtained parameters (0.0147, 0.1317), and initial probability vector (0.8333, 0.1666)

Fig. 4

Algorithm applied in table 7.41, obtained parameters (0.0942, 0.3469), and initial probability vector (0.9333, 0.0666)

In the fitting displayed in Fig. 4, the algorithm successfully detected the two portions into which the distribution divides, yielding a result of 2 clusters. However, there was a substantial increase in the number of phases, totaling 31. This suggests that the algorithm encountered challenges in converging due to the inherent complexity of the data distribution. To deepen the analysis, we examined the empirical moments $(312.9055, 104366.9098, 36132253.8337)$ and contrasted them with the moments of the adjusted distribution $(312.9055, 6080.9833, 180569.4677)$. A more pronounced discrepancy between the second and third moments becomes evident through this comparison.

Fig. 5

Algorithm applied in table 7.42, obtained parameters (0.0192, 0.0856, 0.7384), and initial probability vector (0.5411, 0.3588, 0.09999)

Due to the more dispersed nature of the data, the poorest result was recorded in the dataset referenced in Fig. 5. However, it is noteworthy that the peak present in the PDF was detected. There was a need for 3 clusters, each comprising 11 phases. This configuration was influenced by the frequency distribution having three distinct concentration regions.

Fig. 6

Algorithm applied in table 24.14, obtained parameters (0.1410, 0.2847, 0.5792), and initial probability vector (0.2589, 0.4915, 0.2495)

The histogram in Fig. 6 displays multimodal data with a CoV of 0.51. Datasets of this nature pose significant challenges when attempting fitting using traditional distributions. However, with the algorithm discussed in this text, 3 clusters were required, each consisting of 49 phases. Notably, the number of phases has considerably increased compared to the other cases presented, underscoring the high complexity of the system under consideration.

Fig. 7

Algorithm applied in table 24.23, obtained parameters (0.2677, 0.2677, 0.2677, 0.5374, 2.7045), and initial probability vector (7.9441exp($-09$), 0.0636, 0.2434, 0.6439, 0.0490)

Lastly, using another multimodal dataset, the automated fitting using the hyper-Erlang distribution yielded a phase-type distribution (PH) with 4 clusters, each comprising 53 phases. The fitting algorithm detected the first two groupings of data, as illustrated in Fig. 7. However, a good fit is achieved at the expense of high dimensionality. Such scenarios illuminate the need for refinements in future iterations of the algorithm.

Building upon the methodologies highlighted, the next section will apply this approach to a real-world scenario. The plan is to integrate the fitting algorithm into experiments previously discussed in various works. Through this, we aim to validate its performance across different systems and datasets. This implementation will bolster the algorithm’s credibility and highlight its scalability in the dynamic landscape of computational analysis. The second case study characterizes TTF and TTR distributions in a fault-injected fog computing environment. It demonstrates automated fitting with hyper-Erlang distributions for reliability analysis in complex real-world systems.

6.2 Case study 2: the fog computing environment

In this study, we seek to characterize the Time-to-Failure (TTF) and Time to Repair (TTR) distributions within a fog computing environment, where the observed times were expedited through a fault injector. Comprehensive insights on this approach are provided in Refs. [36, 37].

The system was exercised by injecting faults in the system infrastructure and monitoring its availability during an observational period. After the experimental phase, the TTFs and TTRs were obtained. Then, the maximum likelihood estimation algorithm was executed to fit an Erlang-r distribution. Once the Erlang-r distribution was fitted, the distribution function was determined.

After fitting, the PDF and CDF of the fitted distribution functions are determined using Eq. (2). With these functions in hand, the system’s reliability study begins, for instance, using the CDF F(t) to find the reliability, with relation $F(t) + R(t) = 1$. The average time to absorption state is $MTTA = \int _{0}^{\infty } R(t) dt$.

Fig. 8

Fitted PDF and CDF

However, despite the inherent flexibility of this approach, it is crucial to emphasize that employing hyper-Erlang distributions for fitting systems derived from real-world scenarios often necessitates the use of a significant number of phases and clusters. Such a trait might lead to less than optimal fitting results or yield intricate integration functions, jeopardizing the calculation procedure for reliability metrics outlined in this study. Therefore, thoroughly validating underlying assumptions and adjusting the model to the data becomes pivotal. Succinctly put, constructing an automated reliability evaluator based on hyper-Erlang distributions would encompass the following stages:

• 1. Collect data on system behavior over a period, capturing state transitions and the durations of each state.

• 2. Employ the gathered data to determine PH distribution parameters through the EM algorithm.

• 3. Utilize the deduced PH function to establish analytical functions for reliability metrics.

• 4. Derive other reliability metrics and generate their respective graphical representations.

• 5. Periodically refine the model with fresh data to improve its predictive accuracy.

The following section explores the automated fitting process for a fault injector infrastructure within a fog computing environment. Metrics and initial functions are detailed, with specific functions omitted if deemed overly extensive.

6.2.1 Enhanced system modeling and analysis

In the dynamic landscape of modern computing, cloud infrastructures have secured a cornerstone position, offering scalable and proficient solutions to address a diverse range of computational demands. As elucidated in Sect. 6, these infrastructures play a foundational role in various applications, accentuating the need for comprehensive reliability assessments. Simultaneously, there is a shift toward more intuitive models. While the traditional analytical model, defined by its mathematical blueprint of systems and reliance on deductive processes, is esteemed for characterizing systems through structured expressions [38, 39], it grapples with the challenge of authentically mirroring prevailing effects and interactions. This lacuna paves the way for functions that imbue flexibility, often eluding conventional modeling.

The significance of automated fitting becomes palpable when transitioning to the framework delineated in Sect. 4. Championing a data-driven methodology, it equips stakeholders to sculpt the stochastic behavior of systems grounded in empirical observations. Such a paradigm underscores the aptness of phase-type distributions, adept at echoing the subtleties inherent to complex, tangible systems like the discussed cloud infrastructure.

Utilizing this approach on the collected data, a phase-type distribution with 3 clusters, each having 10 phases, was determined. The parameters $(0.00338, 0.012433, 0.046129)$ represent the hyper-Erlang distribution parameters and the initial state probabilities. This is further complemented by the initial probability vector $(0.39, 0.45, 0.16)$. This means that the PH is characterized by a mixture of these specific functions 6, showcasing the inherent variability and stochastic nature of the underlying system’s performance and behavior:

$$\begin{aligned} f_{T1}(t)= & {} \frac{0.00338(0.00338 t)^{9}e^{-0.00338 t}}{9!}, \nonumber \\ f_{T2}(t)= & {} \frac{0.012433(0.012433 t)^{9}e^{-0.012433 t}}{9!}, \nonumber \\ f_{T3}(t)= & {} \frac{0.046129(0.046129 t)^{9}e^{-0.046129 t}}{9!}. \end{aligned}$$

(6)

Through these equations, the analytical PDF can be ascertained, as referenced in Eq. (7). The corresponding cumulative distribution function (CDF) is given by $F(t) = P(t) = \int _0^{t} f(x)dx$. However, due to the extensive nature of the formula, it will be omitted here. The graphical representations of these functions are showcased in Fig. 8:

$$\begin{aligned} f(t)= & {} 1.90732exp(-20)t^9e^{-0.0461298t}\nonumber \\{} & {} + 1.10205exp(-25)t^9e^{-0.01243t} \nonumber \\{} & {} + 2.10596exp(-31)t^9e^{-0.00338t}. \end{aligned}$$

(7)

In the endeavor to assure the quality of the fitting process, the distribution obtained from the automated fitting was compared against every distribution within the distfit library—a comprehensive repository for goodness-of-fit functions.¹ Among the contenders, the log-Laplace distribution surfaced as the superior fit, with a Residual Sum of Squares (RSS) registering at $6.0 \times 10^{-7}$. Notably, the algorithm proposed in this investigation outperformed with an RSS score of $2.39 \times 10^{-7}$. Such a result endorses the algorithm’s efficacy and resonates with the graphical evidence, as seen in Fig. 9.

Fig. 9

Comparison between the algorithm and the goodness of fit

In the context of the infrastructure under examination, there is a pronounced pivot towards a data-driven approach, steering clear of traditional modeling paradigms. Given the intricate nature of contemporary systems, especially within cloud and fog computing environments, there is an imperative to adopt frameworks that minimize abstraction. The crux of this strategy is to derive models directly from empirical data, positioning such data as the cornerstone of the analysis.

Leveraging the automated fitting method, this study emphasizes the derivation of PH distributions with constrained phases. This constraint ensures the resulting functions remain integrable, a crucial consideration for practical application. Fundamentally, all metrics related to reliability modeling are sculpted from the pdf derived from the fitting of the collected data. This approach negates the necessity to engage with more conventional or external models, underlining the self-sufficiency and pertinence of the proposed methodology.

In the system under consideration, the Time-to-Failure, $T$, represents a continuous random variable, signifying the elapsed time from when the unit is first operationalized to its inaugural failure. The pdf will be determined by leveraging the parameters from the automated fitting process. Subsequently, various quantitative reliability measures: the reliability function $R(t)$, the hazard rate function $h(t)$, and the Mean Residual Life (MRL).

For any given time $t > 0$, the reliability function (Fig. 10) is mathematically described as $R(t) = 1 - F(t) = \int _t^{\infty } f(x)dx$. Furthermore, the approximate MTTF value is, $MTTF = \int _{0}^{\infty }R(t)dt \approx 1544.26$h.

Fig. 10

Obtained reliability function

The hazard function provides a measure of the instantaneous failure rate of a system unit. Mathematically, it is captured by $h(t) = \frac{f(t)}{R(t)}$. An insightful examination of the graphical representation, derived from the fitted function and showcased in Fig. 11 reveals distinct behavioral phases. Notably, there is a discernible decrease in the failure rate between 1000 and 1500 h. However, after this interval, the rate escalates dramatically. This observation underscores the variable nature of system reliability over time, highlighting critical periods of heightened vulnerability.

Fig. 11

Obtained hazard function

As we further examine the reliability of cloud and fog computing infrastructures, the Mean Residual Life (MRL) stands out as a significant metric. Illustrated in Fig. 12, the MRL at a particular time $t$ conveys an expectation—it outlines the projected remaining lifetime of a unit that has persisted beyond the interval $(0, t]$. This metric is rooted in the formula $\text {MRL}(t) = \frac{1}{R(t)} \int _t^{\infty } R(x) \, dx$. Importantly, at the outset, the MRL matches the Mean Time To Failure, represented as $\text {MRL}(0) = \text {MTTF}$. From the data, a discernible trend is an increase in the MRL between 1000 and 1500 h, swiftly followed by a marked decrease. This shift offers insights into the system’s reliability patterns, signaling enhanced resilience or susceptibility phases.

Fig. 12

Obtained MRL function

Fig. 13

Fitted time to repair

In examining system reliability, both Time-To-Failure (TTF) and repair time, Time-To-Repair (TTR) were analyzed using the same methodology. By converting U and D values into TTFs and TTRs, approximately 60 sample points were generated.

It utilizes the fitting process on the repair time, resulting in a frequency distribution highlighting two distinct clusters, each encompassing 12 phases. The characterization of these clusters is defined by the parameters $(1.47720, 3.35437)$. The initial probability vector $(0.48, 0.52)$ supports and enhances these parameters. In alignment with the TTF (Time-To-Failure) methodology, the function epitomizing maintainability is inferred by the mixture of distributions with the parameters ascertained from the TTR (Time-To-Repair) fitting process:

$$\begin{aligned} f_{R1}(t)= & {} \frac{1.47720(1.47720 t)^{11}e^{-1.47720 t}}{11!},\nonumber \\ f_{R2}(t)= & {} \frac{3.35437(3.35437 t)^{11}e^{-3.35437 t}}{11!}.\nonumber \\ \end{aligned}$$

(8)

The derived pdf is presented in Eq. (9), and its corresponding graphical representation can be observed in Fig. 13:

$$\begin{aligned} f_R(t)= & {} 0.02648t^{11}e^{-3.35460t} \nonumber \\{} & {} + 1.30226exp(-6)t^{11}e^{-1.47845t} \nonumber \\{} & {} + 1.94651exp(-9)t^{11}e^{-1.31540t}. \end{aligned}$$

(9)

Following the methodology outlined, the cumulative function is determined as $F_R(t) = M(t) = \int _0^t f_R(x)dx$, where $f_R(x)$ is the PDF of the repair time, represents function maintainability. This interpretation of maintainability provides insights into how quickly and efficiently a system is restored after a failure by representing the probability that a system is repaired by time $t$.

Fig. 14

Maintainability graph

Fig. 15

Different types of estimated scenarios with reliability function

We apply the same concepts to system repair times to determine maintainability and the respective repair rate. Equations will be omitted, but graphs can be seen in Fig. 14. The MTTR of the system can be obtained by the following integral MTTR = $\int _{0}^{\infty }t \cdot M(t)dt \approx 5.73$ h. Using the values obtained for the MTTF and MTTR, it is possible to determine the system’s availability through the formula $A = \frac{MTTF}{MTTF+MTTR} \approx \displaystyle 0.996296866948173$.

In exploring cloud and fog computing infrastructures discussed throughout this section, reliability, and maintainability have been articulated through mathematical functions, bypassing traditional models. The hazard function, MRL, and concepts surrounding Time-to-Failure (TTF) and Time to Repair (TTR) were delved into, laying down a robust framework for grasping system dependability via functions. The insights derived from these metrics present tangible perspectives on system behavior, especially during stress periods or specific operational conditions.

Employing the fitting process for failure and repair times has brought valuable insights. This approach illuminated patterns within the data and fostered a comprehensive comprehension of the system’s reliability dynamics. The functions derived, especially the one denoting maintainability, offer a detailed perspective into system resilience following a failure.

6.2.2 Scenarios evaluation

decision-making and service pricing are often anchored in business operations by diverse modeling and process evaluation techniques. This study aims to model the incorporation of additional servers to scrutinize shifts in system reliability using the functions obtained in the previous section. Previous sections validated the modeling process with functions, and this section delves into scenarios where replicas of the modeled system are examined under various configurations: serial, parallel, a combination of serial and parallel, and k-out-n.

Utilizing the functions secured in Sect. 6.2.1, various scenarios can be modeled under the assumption that a component’s failure remains independent and does not influence the failure rates of its counterparts. Starting with a series connection of $n$ components, the system reliability, denoted as $R_S$, equates to the product of the reliabilities of the individual components, expressed as $R_S = \prod _{i = 1}^{ n } R_i$. Conversely, when considering these $n$ components in a parallel configuration, the system reliability, $R_P$, is deduced from $R_P = 1- \prod _{i = 1}^{n}(1-R_i)$. For further exploration, let us examine a hybrid setup: two components connected in series with a third in parallel; see Fig. 15.

Drawing from the functions deduced in the context of the fitted phase-type distribution, all the assumptions and subsequent analyses are grounded in a data-driven process. Notably, the modeling is not confined to a specific number of components; by integrating more components into the scenarios, analysts can delve deeper into the system’s intricacies. This enriched perspective can empower them to pinpoint the optimal cost–benefit ratio for the system in focus. The upcoming figure elucidates varied configurations employing five components, offering a detailed lens into the system’s potential behavior and outcomes.

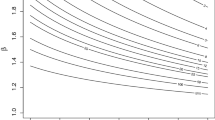
Constructing a k-out-of-n configuration necessitates a minimum number ($k$) of functioning components out of the total parallel components ($n$) for the system to operate efficiently. The k-out-of-n design can be visualized as an extended version of parallel systems. Specifically, as the value of $k$ inches closer to $n$, the overarching behavior of the system gravitates towards mirroring that of a serial setup. The reliability formula for a k-out-of-n structure is expressed as $R_{kon}(k,n,R)=\sum _{r=k}^{n} \left( {\begin{array}{c}n\\ r\end{array}}\right) R ^ r( 1-R)^{n-r}$.

Building upon this foundation and under the assumption that all components are homogeneous, possessing a reliability function as depicted in Fig. 10, and setting $n=6$, the potential scenarios can be viewed in Fig. 16.

Fig. 16

Different scenarios

This section is dedicated to scenario evaluation, dissecting various configurations and their implications on operational integrity. From simple serial and parallel configurations to the more intricate k-out-of-n setups, the discourse shows the nuanced dynamics of system interplay and the impact of each component on overall reliability. The data-driven approach, rooted in previously obtained functions, has been pivotal in these analyses. This methodology empowers analysts with detailed insights and offers a robust framework for determining the optimal cost–benefit ratio for the system under study.

7 Conclusion

Recent technological advancements have made analyzing stochastic models with non-exponential time distributions increasingly efficient. PH distributions have risen to the forefront in this scenario, buoyed by their adaptability and extensive generalization capacity. This work unveiled a strategic approach to deduce an analytical function that mirrors a given dataset endowed with parameters and an algorithm proficient in estimating the necessary number of phases for system automation and fine-tuning.

Traditionally, systems valuation exercises have leaned on numerical methodologies or simulations to ascertain the Mean Time To Failure (MTTF). Such methods, though effective, are typically more time-consuming. The technique introduced in this paper curtails this time drastically, paving the way for a more streamlined and automated system analysis. The horizon ahead is teeming with potential. The ambition is to broaden the scope of research in this domain, introducing a more comprehensive array of availability metrics such as failure rate, repair rate, and mean time between failures.

Throughout this investigative journey, there were instances where the infinitesimal generator matrix manifested in extremely high orders. In addition, there were cases where the algorithm’s stopping criterion for ascertaining the phase number faltered. Such observations highlight the pressing need for in-depth research to fathom the boundaries of this methodology and to navigate a course for its seamless adoption across varied scenarios.

What stands out in this exploration is a palpable tilt towards function-based simulations and methodologies anchored in the Monte Carlo Markov chain—a promising avenue for future endeavors. Even though the deduced function primarily aligns with the dataset under scrutiny in this study, the broader vision is to extend its applicability. Moreover, the aspiration to incorporate control theory more intensely in subsequent investigations is on the horizon.