On Perfect Balanced Rainbow-Free Colorings and Complete Colorings of Projective Spaces

Abstract

This paper is motivated by the problem of determining the related chromatic numbers of some hypergraphs. A hypergraph $\Pi _{q}(n,k)$ is defined from a projective space PG$(n-1,q)$, where the vertices are points and the hyperedges are $(k-1)$-dimensional subspaces. For the perfect balanced rainbow-free colorings, we show that ${\overline{\chi }}_{p}(\Pi _{q}(n,k))=\frac{q^n-1}{l(q-1)}$, where $k\ge \lceil \frac{n+1}{2}\rceil$ and l is the smallest nontrivial factor of $\frac{q^n-1}{q-1}$. For the complete colorings, we prove that there is no complete coloring for $\Pi _{q}(n,k)$ with $2\le k<n$. We also provide some results on the related chromatic numbers of subhypergraphs of $\Pi _{q}(n,k)$.

1 Introduction

The coloring of a hypergraph is an important content in graph theory, which is related to general graphs, designs, optimization problems and so on [10, 15, 22]. In recent years, hypergraphs from projective spaces have been attracted much attentions [2,3,4,5, 13]. In this paper, we study the problems of balanced rainbow-free colorings and complete colorings of hypergraphs arising from projective spaces.

A hypergraph ${\mathcal {H}}$ is a pair (V, E), where V is the vertex set, E is the set of subsets (called hyperedges) of V. A hypergraph ${\mathcal {H}}$ is k-uniform if each hyperedge of ${\mathcal {H}}$ contains k vertices. A degree of a vertex p, denoted by $d_{p}$, is the number of hyperedges containing p. A hypergraph ${\mathcal {H}}$ is called r-regular if the degree of each vertex of V is r. For an integer c, a c-coloring of ${\mathcal {H}}$ is a surjective mapping from V to a set of c colors, that is $\tau :V\rightarrow [c]$, where $[c]=\{0,1,\dots ,c-1\}$. The inverse images of the colors are called the color classes, that is $C_{i}=\{p\in V: \tau (p)=i\}$ for $i\in [c]$.

Given a c-coloring of ${\mathcal {H}}$, a hyperedge of ${\mathcal {H}}$ is called rainbow if there are no vertices with the same color. A c-coloring of ${\mathcal {H}}$ is called rainbow-free if it contains no rainbow hyperedge, and it is called rainbow if its hyperedges are all rainbow. A balanced coloring of ${\mathcal {H}}$ is a coloring in which the cardinality of all color classes differs at most in one, and the balanced upper chromatic number of ${\mathcal {H}}$, denoted by ${\overline{\chi }}_{b}({\mathcal {H}})$, is the largest integer c for which there is a balanced rainbow-free c-coloring of ${\mathcal {H}}$. A c-coloring of a k-uniform hypergraph ${\mathcal {H}}$ is said to be complete if each hyperedge of ${\mathcal {H}}$ is rainbow and each k-element subset of [c] appears as the color set of some hyperedges. The maximum possible number of colors in a complete coloring of ${\mathcal {H}}$ is denoted by ${\overline{\chi }}_{c}({\mathcal {H}})$.

The rainbow-free coloring of a hypergraph was proposed by Voloshin [20] in 1995, and has been extensively studied in several papers, such as [8, 11, 12, 16, 21]. On the other hand, the complete coloring of a k-uniform hypergraph was first introduced by Dȩski, Lonc and Rza̧ażwski [6] in 2017, and has been carried out further research by Edwards and Rzazewski [7] in 2020.

A projective space can be considered as a hypergraph, where the vertices are points and the hyperedges are subspaces. In particular, PG$(n-1, q)$ is an $(n-1)$-dimensional projective space, whose $(k-1)$-dimensional subspaces for $1\le k\le n$ are the k-dimensional subspaces of the n-dimensional vector space $V_n$ over a finite field of q elements. It is well known that the $(n-1)$-dimensional projective space of order q exists if q is a prime power and it is isomorphism to PG$(n-1,q)$ when $n\ge 4$. For convenience, we call the hypergraph arising from a projective space projective hypergraph and use $\Pi _{q}(n, k)$ to denote the projective hypergraph from PG$(n-1,q)$, i.e., using the dimension of the corresponding vector space. Specially, we use $\Pi _{q}$ to denote the projective hypergraph from projective plane PG(2, q).

In 2015, Araujo-Pardo et al. [1] initially considered the balanced rainbow-free c-colorings of projective spaces. And the balanced upper chromatic number of projective planes is further refined by Blázsik et al. [4] in 2021. The following are some results related to projective spaces.

Result 1.1

[1] For projective hypergraph $\Pi _{q}$, there is

$$\begin{aligned} {\overline{\chi }}_{b}(\Pi _{q})=\lfloor \frac{q^2+q+1}{3}\rfloor . \end{aligned}$$

Result 1.2

[1] For projective hypergraphs $\Pi _{q}(n,k)$ with $n\ge 4$, there is

$$\begin{aligned} {\overline{\chi }}_{b}(\Pi _{q}(n,n-1))\ge \frac{q^{n}-1}{q-1}-q^{\frac{n}{2}}-1. \end{aligned}$$

In particular, when $n=4$, there is

$$\begin{aligned} {\overline{\chi }}_{b}(\Pi _{q}(4,3))=q^{3}+q; \end{aligned}$$

If $q\equiv 1~ (\textrm{mod}~3)$, there is

$$\begin{aligned} \frac{q^2+q+1}{3}\le {\overline{\chi }}_{b}(\Pi _{q}(4,2))\le \frac{q^2+1}{2}. \end{aligned}$$

In this paper, we investigate the balanced rainbow-free colorings and the complete colorings of projective hypergraphs. In Sect. 2, we recall some notations of projective spaces and define the cyclic projective hypergraphs.

In Sect. 3, we consider the balanced rainbow-free colorings of projective hypergraphs with the same size of color classes, which we call perfect balanced rainbow-free colorings, and the perfect balanced upper chromatic number is denoted by ${\overline{\chi }}_{p}({\mathcal {H}})$. We first show that

$$\begin{aligned} {\overline{\chi }}_{p}(\Pi _{q}(n,k))=\frac{q^{n}-1}{l(q-1)} \end{aligned}$$

where $k\ge \lceil \frac{n+1}{2}\rceil$ and l is the smallest nontrivial factor of $\frac{q^{n}-1}{q-1}$. Then we define a subhypergraph of $\Pi _{q}(n,k)$, denoted by $\Lambda _{q}(n,k)$, and give a range of ${\overline{\chi }}_{p}(\Lambda _{q}(n,k))$ for odd prime n and $k=\frac{n+1}{2}$. Furthermore, we determine the exact value

$$\begin{aligned} {\overline{\chi }}_{p}(\Lambda _{q}(3,2))=\frac{q^{2}+q}{3} \end{aligned}$$

for $q\equiv 0,2~($mod 3).

In Sect. 4, we consider the complete colorings of projective hypergraphs. We first prove that there is no complete coloring for $\Pi _{q}(n,k)$ with $2\le k<n$. Besides, We define another subhypergraph of $\Pi _{q}(n,k)$, denoted by $\Omega _{q}(n,k)$, and provide some results of ${\overline{\chi }}_{c}(\Omega _{q}(n,k))$ and ${\overline{\chi }}_{c}(\Lambda _{q}(n,k))$.

2 Preliminaries

In this section, we recall some notations in finite projective spaces and introduce the definition of cyclic projective hypergraph. For a set A, define $A^{*}=A\backslash \{0\}$.

Let $F_{q}$ be a finite field of order q, where q is a prime power. Let $V_{n}$ be an n-dimensional vector space over $F_{q}$. The number of k-dimensional subspaces in $V_{n}$ is given by Gaussian coefficient

$$\begin{aligned} \begin{bmatrix} n \\ k \end{bmatrix}_{q} =\prod \limits _{i=1}^{k}\frac{q^{n-k+i}-1}{q^{i}-1}, \end{aligned}$$

see e.g. [9]. In particular, $\big [\begin{array}{c} a\\ b \end{array}\big ]_{q}=0$ unless $0\le b\le a$. So, the number of k-dimensional subspaces of $V_n$ containing a given t-dimensional subspace in $V_n$ is

$$\begin{aligned} \begin{bmatrix} n-t \\ k-t \end{bmatrix}_{q} \end{aligned}$$

where $0\le t\le k\le n$. In what follows, we will also use the notation

$$\begin{aligned} \theta _{n}= \begin{bmatrix} n \\ 1 \end{bmatrix}_{q} =\frac{q^{n}-1}{q-1}=q^{n-1}+q^{n-2}+\cdots +q+1 \end{aligned}$$

to denote the number of vertices in the projective hypergraph $\Pi _{q}(n,k)$ defined from PG$(n-1,q)$. Furthermore, we can obtain the regularity and uniformity of $\Pi _{q}(n,k)$.

Theorem 2.1

$\Pi _{q}(n,k)$ has the following basic parameters:

• (1) There are $\theta _{n}$ vertices and $\big [\begin{array}{c} n\\ k \end{array}\big ]_{q}$ hyperedges.

• (2) It is regular and uniform with parameters $\big [\begin{array}{c} n-1\\ k-1 \end{array}\big ]_{q}$ and $\theta _{k}$ respectively.

For the need of later research, we give a specific description of $\Pi _{q}(n,k)$. Throughout the paper, we always let $K=F_{q}$ and $F=F_{q^{n}}$, an n degree extension field of $F_{q}$, then F is an n-dimensional vector space over K. Let $\alpha$ be a primitive element of F, then $K^{*}=\{1,\alpha ^{\theta _{n}},\alpha ^{2\theta _{n}},\dots ,\alpha ^{(q-2)\theta _{n}}\}$. Further, we have $\Pi _{q}(n,k)=(V,E)$ where

$$\begin{aligned} V= & {} \{\langle \alpha ^{i}\rangle =\{a\alpha ^{i}: a\in K\}: ~ i=0,1,\dots ,\theta _{n}-1\};\\ E= & {} \{\langle \alpha ^{i_{1}},\alpha ^{i_{2}},\dots ,\alpha ^{i_{k}}\rangle =\{a_{1}\alpha ^{i_{1}}+a_{2}\alpha ^{i_{2}}+\dots +a_{k}\alpha ^{i_{k}}~:~a_{j}\in K,j=1,2,\dots ,k,\\{} & {} \quad \alpha ^{i_{1}},\alpha ^{i_{2}},\dots ,\alpha ^{i_{k}} \text { are linear independence over }K\}. \end{aligned}$$

In 2015, Araujo-Pardo et al. [1] introduced the concept of cyclic projective plane. Theoretically, the class of cyclic projective planes is wider than the class of Desarguesian planes, but each known finite cyclic plane is isomorphic to PG(2, q) for a suitable q. We generalize it to projective hypergraph.

Let G be a finite additive group with v elements. A subset $D=\{d_{0},d_{1},\dots ,d_{k-1}\}$ of G is called a $(v,k,\lambda )$-difference set [17] if for every $g\in G,g\ne 0$, there exist exactly $\lambda$ pairs of distinct elements $d_{i},d_{j}\in D$ such that $g=d_{i}-d_{j}$.

Let q be a prime power, $v=q^{2}+q+1$. If the group $Z_{v}=Z/vZ$ contains a difference set $D=\{d_{0},d_{1},\dots ,d_{q}\}$, then there exists a cyclic projective plane of order q, the points are the elements of $Z_{v}$ and the hyperedges are $D+i=\{d_{0}+i,d_{1}+i,\dots ,d_{q}+i\}$, $i=0,1,\dots ,v-1$.

Now, we define a cyclic hypergraph ${\mathcal {H}}$. If the set of vertices in a hyperedge of ${\mathcal {H}}$ forms a difference set, and other hyperedges can be obtained by the modulo addition of the hyperedge, then we call any hypergraph isomorphic to ${\mathcal {H}}$ a cyclic hypergraph. Further, a projective hypergraph is called a cyclic projective hypergraph if it is cyclic.

Lemma 2.2

(Singer’s Theorem [18]) Suppose q is a prime power, $n\ge 3$ an integer. Then there exists a $(v, k,\lambda )$-difference set with the parameters

$$\begin{aligned} v=\theta _{n}, k=\theta _{n-1},\lambda =\theta _{n-2}. \end{aligned}$$

Corollary 2.3

$\Pi _{q}(n,n-1)$ is a cyclic projective hypergraph with $n\ge 3$.

3 Perfect Balanced Rainbow-Free Colorings of Projective Hypergraphs

In [1], Araujo-Pardo, Kiss and Montejano studied the balanced upper chromatic number of cyclic projective planes and projective spaces. We spread their ideas and further restrict the balanced condition. When the color classes of a rainbow-free coloring have the same size, we call the coloring perfect balanced, and use ${\overline{\chi }}_{p}({\mathcal {H}})$ to denote the perfect balanced upper chromatic number of a hypergraph ${\mathcal {H}}$. In this section, we will discuss the perfect balanced rainbow-free colorings of the projective hypergraph $\Pi _{q}(n,k)$ and a subhypergraph of $\Pi _{q}(n,k)$.

According to the method given in the proof of Theorem 2.3 in [1], we can have the following theorem.

Theorem 3.1

Suppose ${\mathcal {H}}$ is a cyclic hypergraph with v vertices, and l is the minimum nontrivial factor of v, then ${\overline{\chi }}_{p}({\mathcal {H}})=\frac{v}{l}$.

Proof

For the cyclic hypergraph ${\mathcal {H}}$, we define the color classes as follows:

$$\begin{aligned} C_{i}=\{i,i+\frac{v}{l},\dots ,i+\frac{(l-1)v}{l}\},~ 0\le i\le \frac{v}{l}-1. \end{aligned}$$

From the definition of a cyclic hypergraph, each hyperedge of ${\mathcal {H}}$ contains a pair of vertices with the difference $\frac{v}{l}$, i.e., each hyperedge of ${\mathcal {H}}$ contains a pair of vertices of the form $\{i,i+\frac{v}{l}\}$. So the coloring is rainbow-free. $\square$

From Corollary 2.3, we have the following result.

Corollary 3.2

Suppose q is a prime power and $n\ge 3$. Then ${\overline{\chi }}_{p}(\Pi _{q}(n,n-1))=\frac{\theta _{n}}{l}$, where l is the minimum nontrivial factor of $\theta _{n}$.

For projective planes, the result of perfect balanced rainbow-free coloring is obvious. Next, we consider higher dimensional projective hypergraphs. Take $N=\{x^{q}-x:~x\in F\}$, then N is an additive subgroup of F, $|N|=q^{n-1}$, and N is an $(n-1)$-dimensional subspace of F from [14].

Lemma 3.3

[14] For any $a,b\in F^{*}$, aN is an $(n-1)$-dimensional subspace of F, $aN=bN$ if and only if $ab^{-1}\in K^{*}$, where $F^{*}, K^{*}$ are the multiplicative groups of F, K respectively, and $\{aN: a\in F^{*}\}$ is the set of all $(n-1)$-dimensional subspaces of F. Moreover, for any $(n-t)$-dimensional subspace T of F, there are t linearly independent elements $a_{1}^{-1},a_{2}^{-1},\dots ,a_{t}^{-1}$ over K such that $T=a_{1}N\cap a_{2}N\cap \dots \cap a_{t}N$.

Theorem 3.4

Suppose q is a prime power, $n\ge 3$, l is the smallest nontrivial factor of $\theta _{n}$. Then ${\overline{\chi }}_{p}(\Pi _{q}(n,k))=\frac{\theta _{n}}{l}$, where $k\ge \lceil \frac{n+1}{2}\rceil$.

Proof

For $\Pi _{q}(n,k)$, we define the color classes as follows:

$$\begin{aligned} C_{i}=\{\langle \alpha ^{i}\rangle ,\langle \alpha ^{i+\frac{\theta _{n}}{l}}\rangle ,\dots ,\langle \alpha ^{i+(l-1)\frac{\theta _{n}}{l}}\rangle \}, 0\le i\le \frac{\theta _{n}}{l}-1, \end{aligned}$$

where $\alpha$ is a primitive element of F. Then the coloring is a perfect balanced coloring, and it is shown below that it is also a rainbow-free coloring.

For $t\le \lfloor \frac{n-1}{2}\rfloor$ and any $(n-t)$-dimensional subspace T of F, there are t linearly independent elements $a_{1}^{-1},a_{2}^{-1},\dots ,a_{t}^{-1}\in K$ such that $T=a_{1}N\cap a_{2}N\cap \dots \cap a_{t}N$ by Lemma 3.3. Let $a=\alpha ^{\frac{\theta _n}{l}}$, there is $dim(aT\cap T)=dim(aT)+dim(T)-dim(aT+T)\ge n-2t\ge 1$. So $aT^{*}\cap T^{*}\ne \emptyset$, i.e., there exist $u,v\in T^{*}$ such that $au=v$. Further, u, v are linearly independent over K. Otherwise, there exists $c\in K^{*}$ such that $u=cv$, then $a=v(cv)^{-1}=c^{-1}\in K$, this contradicts with $a=\alpha ^{\frac{\theta _n}{l}}\notin K$. At this time, T is a hyperedge of $\Pi _{q}(n,n-t)$, the vertices $\langle u\rangle ,\langle v\rangle$ are different in T, but they are belong to the same color class. Thus, this coloring is rainbow-free. So for any $t\le \lfloor \frac{n-1}{2}\rfloor$, there is

$$\begin{aligned} {\overline{\chi }}_{p}(\Pi _{q}(n,n-t))=\frac{\theta _n}{l}. \end{aligned}$$

That is ${\overline{\chi }}_{p}(\Pi _{q}(n,k))=\frac{\theta _n}{l}$, where $k\ge \lceil \frac{n+1}{2}\rceil$. $\square$

In addition, any k-dimensional subspace is contained in some $(k+1)$-dimensional subspaces, we have ${\overline{\chi }}_{p}(\Pi _{q}(n,k))\le {\overline{\chi }}_{p}(\Pi _{q}(n,k+1))$.

In 2018, Thakkar and Dave [19] constructed a subhypergraph by removing a vertex from a projective plane and considered the edge independence number of the subhypergraph. In a similar way, we want to define a subhypergraph of $\Pi _{q}(n,k)$ and consider the coloring problem of the subhypergraph.

Given a vertex of $\Pi _{q}(n,k)$, let $\Lambda _{q}(n,k)$ be the subhypergraph obtained by removing the vertex and all the hyperedges through the vertex of $\Pi _{q}(n,k)$. Obviously, $\Lambda _{q}(n,k)$ is unique in the sense of isomorphism. According to the relevant combinatorial properties of vector spaces, we have the following results.

Theorem 3.5

$\Lambda _{q}(n,k)$ has the following basic parameters:

• (1) There are $\theta _{n}-1$ vertices and $q^{k}\big [\begin{array}{c} n-1\\ k \end{array}\big ]_{q}$ hyperedges.

• (2) It is regular and uniform with parameters $q^{k-1}\big [\begin{array}{c} n-2\\ k-1 \end{array}\big ]_{q}$ and $\theta _{k}$ respectively.

Take the vertex $\langle 1\rangle \in \Pi _{q}(n,k)$, we consider the corresponding subhypergraph $\Lambda _{q}(n,k)$. Note that $\langle 1\rangle =K$, we can set

$$\begin{aligned} V(\Lambda _{q}(n,k))= & {} \{\langle \alpha ^{i}\rangle =\{a\alpha ^{i}: a\in K\}: i=1,2,\dots ,\theta _{n}-1\}; \\ E(\Lambda _{q}(n,k))= & {} \{\langle \alpha ^{i_{1}},\alpha ^{i_{2}},\dots ,\alpha ^{i_{k}}\rangle =\{a_{1}\alpha ^{i_{1}}+a_{2}\alpha ^{i_{2}}+\dots +a_{k}\alpha ^{i_{k}}: a_{j}\in K,\\{} & {} \ j=1,2,\dots ,k,\text { and }1,\alpha ^{i_{1}},\alpha ^{i_{2}},\dots ,\alpha ^{i_{k}}\text { are linearly independent over }K\}. \end{aligned}$$

When $n=3,k=2$, denote it by $\Lambda _{q}$ for short.

Lemma 3.6

Suppose q is a prime power and n is an odd prime. If $(n,q-1)=1$, then $\langle x\rangle =\langle x^{q}\rangle$ if and only if $x\in K$.

Proof

Because $\langle x\rangle =\langle x^{q}\rangle$ if and only if there exists $k\in K$ such that $x^{q}=kx$. Both sides at the same time action q power, $q^{2}$ power, $\dots$, $q^{n-1}$ power, then we have $x^{q^{2}}=kx^{q}, x^{q^{3}}=kx^{q^{2}},\dots ,x^{q^{n}}=kx^{q^{n-1}}$, so $x=k^{n}x$, that is $k^{n}=1$. Since $(n,q-1)=1$, we have $k^{n}=1$ if and only if $k=1$. So $\langle x\rangle =\langle x^{q}\rangle$ if and only if $x^{q}=x$, that is $x\in K$. $\square$

Theorem 3.7

Suppose q is a prime power. If $q\equiv 0,2~ (\textrm{mod}~3)$, then ${\overline{\chi }}_{p}(\Lambda _{q})=\frac{q^{2}+q}{3}$.

Proof

Construct an automorphism of F:

$$\begin{aligned}{} & {} \sigma : F \rightarrow F\\{} & {} \quad x\mapsto x^{q}, x\in F. \end{aligned}$$

Then $\langle \sigma \rangle$ is a cyclic group of order 3. The group $\langle \sigma \rangle$ acts on the vertex set $V(\Lambda _{q})$, then $\overline{\langle x\rangle }=\{\langle x\rangle ,\langle x^{q}\rangle ,\langle x^{q^{2}}\rangle \}$, $x\in F\backslash K$ are all orbits with length 3 from Lemma 3.6. By taking vertices in the same orbit as a color class, we can get $\frac{q^{2}+q}{3}$ color classes. The following shows that the coloring is rainbow-free.

Take any $\langle x,y\rangle \in E(\Lambda _{q})$, if $z\in \langle x,y\rangle$, then $\langle z\rangle \subseteq \langle x,y\rangle$. So we only need to verify that there exists an element $z\in \langle x,y\rangle$ with $z^{q}\in \langle x,y\rangle$. From $\langle x,y\rangle \in E(\Lambda _{q})$, we have $x\ne y,x\ne x^{q},y\ne y^{q}$, and $x,y,x^{q},y^{q}$ must be linear dependence over K because $x,y,x^{q},y^{q}\in F$. So there exist $a,b,c,d\in K$ such that $ax^{q}+by^{q}=cx+dy$, where a and b are not all 0. Let $z=ax+by\in \langle x,y\rangle$, then the vertices $\langle z\rangle$ and $\langle z^{q}\rangle$ in $\langle x,y\rangle$ have the same color. Therefore,

$$\begin{aligned}{\overline{\chi }}_{p}(\Lambda _{q})\ge \frac{q^{2}+q}{3}.\end{aligned}$$

On the other hand, when $q\equiv 0,2~($mod 3), the smallest nontrivial factor of $q^{2}+q$ is 2. Suppose there is a perfect balanced rainbow-free coloring with the color class of size 2, then there are $\frac{q^{2}+q}{2}$ color classes. Each color class contains a 2-subset of vertices, so there are at most $\frac{q^{2}+q}{2}$ hyperedges which are rainbow. We have $\frac{q^{2}+q}{2}\ge q^{2}$ because $\Pi _{q}$ has $q^{2}$ hyperedges and the coloring is rainbow-free. It yields $q\le 1$, this contradicts that q is a prime power. Hence, there is no perfect balanced rainbow-free coloring with the color class of size 2. Therefore

$$\begin{aligned}{\overline{\chi }}_{p}(\Lambda _{q})\le \frac{q^{2}+q}{3}.\end{aligned}$$

To sum up, the conclusion holds. $\square$

Below, let n be an odd prime. We will consider the perfect balanced rainbow-free coloring of $\Lambda _{q}(n,\frac{n+1}{2})$, and give the upper and lower bounds of ${\overline{\chi }}_{p}(\Lambda _{q}(n,\frac{n+1}{2}))$.

Theorem 3.8

Suppose q is prime power, n is an odd prime. If $(n,q-1)=1$, then

$$\begin{aligned}{\overline{\chi }}_{p}(\Lambda _{q}(n,\frac{n+1}{2}))\ge \frac{q^{n}-q}{n(q-1)}.\end{aligned}$$

Proof

Construct an automorphism of $F=F_{q^{n}}$:

$$\begin{aligned}{} & {} \sigma : F\rightarrow F\\{} & {} \quad x\mapsto x^{q}, x\in F. \end{aligned}$$

Then $\langle \sigma \rangle$ is a cyclic group of order n. The group $\langle \sigma \rangle$ acts on the vertex set $V(\Lambda _{q}(n,\frac{n+1}{2}))$, then $\overline{\langle x\rangle }=\{\langle x\rangle ,\langle x^{q}\rangle ,\dots ,\langle x^{q^{n-1}}\rangle \}$, $x\in F\backslash K$ are all orbits with length n by Lemma 3.6. By taking vertices in the same orbit as a color class, we can get $\frac{q^{n}-q}{n(q-1)}$ color classes. The following shows that the coloring is rainbow-free.

Take a hyperedge $\langle x_{1},x_{2},\dots ,x_{\frac{n+1}{2}}\rangle \in E(\Lambda _{q}(n,\frac{n+1}{2}))$, if $z\in \langle x_{1},x_{2},\dots ,x_{\frac{n+1}{2}}\rangle$, then $\langle z\rangle \subseteq \langle x_{1},x_{2},\dots ,x_{\frac{n+1}{2}}\rangle$. So we only need to verify that there exists an element $z\in \langle x_{1},x_{2},\dots ,$ $x_{\frac{n+1}{2}}\rangle$ with $z^{q^{i}}\in \langle x_{1},x_{2},\dots ,x_{\frac{n+1}{2}}\rangle$, $i=1,\dots ,n-2$ or $n-1$. From $\langle x_{1},x_{2},\dots ,x_{\frac{n+1}{2}}\rangle \in E(\Lambda _{q}(n,\frac{n+1}{2}))$, we have $x_{i}\ne x_{j},x_{i}\ne x_{i}^{q},i,j=1,2,\dots ,\frac{n+1}{2},i\ne j$, and $x_{i},x_{i}^{q},i=1,2,\dots ,\frac{n+1}{2}$ must be linear dependence over K because $x_{i},x_{i}^{q}\in F=F_{q^n}$. So there exist $a_{1},a_{2},\dots ,a_{\frac{n+1}{2}},b_{1},b_{2},\dots ,b_{\frac{n+1}{2}}\in K$ such that $\sum _{i=1}^{(n+1)/2} a_{i}x_{i}^{q}=\sum _{i=1}^{(n+1)/2} b_{i}x_{i}$, where $a_{i}$ and $b_{i}$ are not all 0. Let $z=\sum _{i=1}^{(n+1)/2} a_{i}x_{i}$, then $z^{q}\in \langle x_{1},x_{2},\dots ,x_{\frac{n+1}{2}}\rangle$. The vertices $\langle z\rangle$ and $\langle z^{q}\rangle$ in $\langle x_{1},x_{2},\dots ,x_{\frac{n+1}{2}}\rangle$ have the same color. Therefore

$$\begin{aligned} {\overline{\chi }}_{p}(\Lambda _{q}(n,\frac{n+1}{2}))\ge \frac{q^{n}-q}{n(q-1)}. \end{aligned}$$

$\square$

Theorem 3.9

Suppose q is a prime power. All perfect balanced rainbow-free colorings of $\Lambda _{q}(n,\frac{n+1}{2})$ satisfy that the size of the color classes is at least three, and

$$\begin{aligned}{\overline{\chi }}_{p}(\Lambda _{q}(n,\frac{n+1}{2}))\le \frac{q^{n}-q}{3(q-1)}.\end{aligned}$$

Proof

There are $\frac{q^{n}-q}{q-1}$ vertices and $q^{\frac{n+1}{2}}\big [\begin{array}{c} n-1 \\ \frac{n+1}{2} \end{array}\big ]_{q}$ hyperedges in $\Lambda _{q}(n,\frac{n+1}{2})$ from Theorem 3.5. Suppose that the perfect balanced rainbow-free coloring of $\Lambda _{q}(n,\frac{n+1}{2})$ has h color classes of size t, then $t\ge 2$. If $t=2$, we have $h=\frac{q^{n}-q}{2(q-1)}$.

Because any two vertices of $\Lambda _{q}(n,\frac{n+1}{2})$ are contained in exacly $\big [\begin{array}{c} n-2\\ \frac{n-3}{2} \end{array}\big ]_{q}-\big [\begin{array}{c} n-3\\ \frac{n-5}{2} \end{array}\big ]_{q}=q^{\frac{n-3}{2}}\cdot \big [\begin{array}{c} n-3\\ \frac{n-3}{2} \end{array}\big ]_{q}$ hyperedges, the h 2-subsets with the same colors cover up to $hq^{\frac{n-3}{2}}\cdot \big [\begin{array}{c} n-3\\ \frac{n-3}{2} \end{array}\big ]_{q}$ hyperedges, which is less than the number of hyperedges. So $t\ge 3$ and ${\overline{\chi }}_{p}(\Lambda _{q}(n,\frac{n+1}{2}))\le \frac{q^{n}-q}{3(q-1)}$. $\square$

4 Complete Colorings of Projective Hypergraphs

In [7], the complete c-colorings of k-uniform hypergraphs are studied. $\Pi _{q}(n,k)$ and $\Lambda _{q}(n,k)$ are uniform hypergraphs, we will consider their complete colorings in this section. In addition, we will define another subhypergraph of $\Pi _{q}(n,k)$ and discuss its complete colorings.

Theorem 4.1

Suppose q is a prime power. For any positive integer c, there is no complete c-coloring for the projective hypergraph $\Pi _{q}(n,k)$ with $2\le k<n$.

Proof

First, we discuss the rainbow coloring of $\Pi _{q}(n,k)$. When $2\le k<n$, any two vertices in $\Pi _{q}(n,k)$ are contained in some hyperedges, so any two vertices have different colors in a rainbow coloring of $\Pi _{q}(n,k)$. That is, there are $\theta _{n}$ color classes. Furthermore, if there exists a complete c-coloring of $\Pi _{q}(n,k)$, then ${c\atopwithdelims ()\theta _{k}}\le \big [\begin{array}{c} n\\ k \end{array}\big ]_{q}$, i.e., ${\theta _{n}\atopwithdelims ()\theta _{k}}\le \big [\begin{array}{c} n\\ k \end{array}\big ]_{q}$. This will result in $q=1$ or $n=k$, it is inconsistent with the conditions of the theorem. Therefore, there is no complete c-coloring for the projective hypergraph $\Pi _{q}(n,k)$ with $2\le k<n$. $\square$

Although $\Pi _{q}(n,k)$ does not have complete colorings with $2\le k<n$, its subhypergraphs maybe have complete colorings. Next, we consider two subhypergraphs of $\Pi _{q}(n,k)$.

4.1 $\Lambda _{q}(n,k)$

The subhypergraph $\Lambda _{q}(n,k)$ is defined in Sect. 3. We know that there are $\big [\begin{array}{c} n-1 \\ 2-1 \end{array}\big ]_{q}=\theta _{n-1}$ hyperedges through a fixed vertex $p_{0}$ in PG$(n-1,$ q). Let $L_{p_{0}}=\{l_{p_{0}}^{0},l_{p_{0}}^{1},\dots ,l_{p_{0}}^{\theta _{n-1}-1}\}$ be the set of hyperedges by removing $p_{0}$ from the $\theta _{n-1}$ hyperedges, then $|l_{p_{0}}^{i}|=q$, $i=0,1,\dots ,\theta _{n-1}-1$, and $L_{p_{0}}$ forms a partition of $V(\Lambda _{q}(n,k))$.

Lemma 4.2

Suppose q is a prime power. Then ${\overline{\chi }}_{c}(\Lambda _{q})=q+1$.

Proof

Given a vertex $p_{0}$, there are $q+1$ hyperedges through $p_{0}$ in $\Pi _{q}$ and $L_{p_{0}}$ forms a partition of $V(\Lambda _{q})$. Now, we give a coloring of $\Lambda _{q}$ by defining the color classes

$$\begin{aligned}C_{i}=l_{p_{0}}^{i}, i=0,1,\dots ,q.\end{aligned}$$

From the definition of $\Lambda _{q}$ and the combinatorial properties of projective planes, we know that the vertices in any hyperedge of $\Lambda _{q}$ have $q+1$ different colors and come from the $q+1$ different color classes. So $\Lambda _{q}$ has a complete $(q+1)$-coloring.

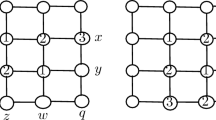
On the other hand, suppose $\Lambda _{q}$ has a complete c-coloring $\tau$ with $c\ge q+2$. For any hyperedge of $\Lambda _{q}$, it intersects each hyperedge of $L_{p_{0}}$ at a unique vertex. Choose a hyperedge l of $\Lambda _{q}$, the relationship between l and $l_{p_{0}}^{i}, i=0,1,\dots ,q$ can be shown below (Fig. 1).

Fig. 1

The relationship between l and $l_{p_{0}}^{i}$ in $\Lambda _{q}$

Let’s color the intersection $p_{1i}$ of l and $l_{p_{0}}^{i}$ with color i, $i=0,1,\dots ,q$. Because $c\ge q+2$, there is a vertex $p_{x}\notin l$ with color $q+1$. Without loss of generality, let $p_{x}\in l_{p_{0}}^{0}$. Because any two vertices from different hyperedges of $L_{p_{0}}$ appear in a unique hyperedge in $\Lambda _{q}$, then there is no $y\in l_{p_{0}}^{i}$ with color 0 or $q+1$, $i=1,2,\dots ,q$. At this time, there is no hyperedge in $E(\Lambda _{q})$ with two vertices coloring 0, $q+1$ respectively, which contradicts the definition of complete coloring. So $\Lambda _{q}$ has no complete c-coloring when $c\ge q+2$.

To sum up, $\Lambda _{q}$ has and only complete $(q+1)$-coloring. $\square$

Theorem 4.3

Suppose q is a prime power. Then there exists a complete coloring for $\Lambda _{q}(n,2)$ if and only if $n=3$.

Proof

By Lemma 4.2, there exists a complete $(q+1)$-coloring of $\Lambda _{q}(n,2)$ for $n=3$.

Now we consider the case of $n\ge 4$. If there exists a complete c-coloring of $\Lambda _{q}(n,2)$, then $c\ge \theta _{n-1}$ because any two vertices from different hyperedges of $L_{p_{0}}$ have a hyperedge connecting them in $\Lambda _{q}(n,2)$. From the definition of the complete c-coloring, we have

$$\begin{aligned}{\theta _{n-1}\atopwithdelims ()q+1}\le {c\atopwithdelims ()q+1}\le q^{2} \begin{bmatrix} n-1 \\ 2 \end{bmatrix}_{q}. \end{aligned}$$

This simplifies to

$$\begin{aligned} (q^{n-1}-2q+1)(q^{n-1}-3q+2)\cdots (q^{n-1}-q^{2}+q-1)\le q(q-1)^{q-1}q!. \end{aligned}$$

(1)

When $q=2$, we have $2^{n-1}-3\le 4$. So $n\le 3$.

When $q\ge 3$, on the one hand,

$$\begin{aligned} \begin{aligned}&(q^{n-1}-2q+1)(q^{n-1}-3q+2)\cdots (q^{n-1}-q^{2}+q-1)\\&~~~>(q^{n-1}-2q)(q^{n-1}-3q)\cdots (q^{n-1}-q^{2})\\&~~~=q^{q-1}(q^{n-2}-2)(q^{n-2}-3)\cdots (q^{n-2}-q)\\&~~~>q^{q}(q^{n-2}-q)^{q-2}(q^{n-3}-1)\\&~~~=q^{2q-2}(q^{n-3}-1)^{q-1}. \end{aligned} \end{aligned}$$

On the other hand,

$$\begin{aligned}q(q-1)^{q-1}q!<q^{q}q!=2q^{q}q(q-1)\cdots 3<2q^{2q-2}.\end{aligned}$$

When $n\ge 4$, there is $(q^{n-3}-1)^{q-1}>2$. So, the inequality (1) is true if and only if $n\le 3$.

Therefore, there is a complete coloring for $\Lambda _{q}(n,2)$ if and only if $n=3$. $\square$

Theorem 4.4

Suppose q is a prime power. If there exists a complete coloring for $\Lambda _{q}(n,k)$, then ${\overline{\chi }}_{c}(\Lambda _{q}(n,k))=\theta _{n-1}$.

Proof

We know that $L_{p_{0}}=\{l_{p_{0}}^{0},l_{p_{0}}^{1},\dots ,l_{p_{0}}^{\theta _{n-1}-1}\}$ forms a partition of $V(\Lambda _{q}(n,k))$. Similar to $\Lambda _{q}$, if there exists a complete coloring of $\Lambda _{q}(n,k)$, then the vertices from different $l_{p_{0}}^{i}$ must have different colors because there are some hyperedges containing two vertices from different $l_{p_{0}}^{i}$ in $\Lambda _{q}(n,k)$. On the other hand, the vertices from the same $l_{p_{0}}^{i}$ must have the same color. Otherwise, if there are two vertices from the same $l_{p_{0}}^{i}$ coloring different colors, we denote the colors by i and $\theta _{n-1}$. Since the hyperedges containing these two vertices in $\Lambda _{q}(n,k)$ correspond to the hyperedges containing the vertex $p_{0}$ in $\Pi _{q}(n,k)$, and the vertices from different $l_{p_{0}}^{i}$ have different colors, there is no hyperedge in $\Lambda _{q}(n,k)$ with two vertices coloring i and $\theta _{n-1}$. This contradicts the definition of complete coloring. Therefore, if there exists a complete coloring for $\Lambda _{q}(n,k)$, it is complete $\theta _{n-1}$-coloring. $\square$

From the above discussion, if there exists a complete coloring of $\Lambda _{q}(n,k)$, then the number of $\theta _k$-subsets of the colors is less than or equal to the number of hyperedges. So we have

$$\begin{aligned} {\theta _{n-1}\atopwithdelims ()\theta _{k}}\le q^{k} \begin{bmatrix} n-1 \\ k \end{bmatrix}_{q}. \end{aligned}$$

By plugging in the values of n, k, q, we can preliminarily determine whether $\Lambda _{q}(n,k)$ has a complete coloring. Obviously, ${\overline{\chi }}_{c}(\Lambda _q(n,n-1))=\theta _{n-1}$.

4.2 $\Omega _{q}(n,k)$

In this subsection, we define another subhypergraph of $\Pi _{q}(n,k)$ and study the problem of the complete colorings.

Let S be a hyperplane of $\Pi _{q}(n,k)$, then $|S|=\theta _{n-1}$. Let $p_{0}$ be a fixed vertex in S. We define a subhypergraph of $\Pi _{q}(n,k)$, denoted by $\Omega _{q}(n,k)=(V',E')$, where

$$\begin{aligned} V'= & {} V(\Pi _{q}(n,k))\backslash S;\\ E'= & {} \{l\backslash S: l\in E(\Pi _{q}(n,k)),~ p_{0}\notin l\}. \end{aligned}$$

When $n=3,k=2$, it is denoted by $\Omega _{q}$ for short. $\Omega _{q}(n,k)$ is unique in the isomorphic sense, because the subspaces of $\Pi _{q}(n,k)$ are transitive under the action of the general linear group GL(n, q) when $n\ge 3$.

Similar to Theorem 3.5, the basic properties of $\Omega _{q}(n,k)$ can be given.

Theorem 4.5

$\Omega _{q}(n,k)$ has the following basic parameters:

• (1) There are $q^{n-1}$ vertices and $q^{n-1}\big [\begin{array}{c} n-2\\ k-1 \end{array}\big ]_{q}$ hyperedges.

• (2) It is regular and uniform with parameters $\frac{q^{n-1}-q^{k-1}}{q^{k-1}-1}\big [\begin{array}{c} n-2\\ k-2 \end{array}\big ]_{q}$ and $q^{k-1}$ respectively.

We first consider the case of $k=2$. For $\Pi _{q}$, the hyperedges are the hyperplanes. Take a hyperedge l of $\Pi _{q}$, and denote by $l=\{p_{0},p_{1},\dots ,p_{q}\}$. For the vertex $p_i\in l$, define a set $L_{p_{i}}=\{m\backslash \{p_i\}: m$ is a hyperedge of $\Pi _{q}$, $p_i \in m$ and $m\ne l\}$, $i=0,1,\dots ,q$. Since there are $q+1$ hyperedges through $p_{i}$ in $\Pi _{q}$, thus $|L_{p_{i}}|=q$. We set $L_{p_{i}}=\{l_{p_{i}}^{j}: j=1,2,\dots ,q\}$, $i=0,1,\dots ,q$. From the properties of $\Pi _{q}$, $\Omega _{q}$ can be expressed as $(V',E')$, where $V'=V(\Pi _{q})\backslash l$ and $E'=\{l_{p_{i}}^{j}:l_{p_{i}}^{j}\in L_{p_{i}},i,j=1,2,\dots ,q\}$.

Lemma 4.6

Suppose q is a prime power. Then ${\overline{\chi }}_{c}(\Omega _{q})=q$.

Proof

By the definition of $\Omega _{q}$, $L_{p_{i}}$ forms exactly a partition of $V'$, $i=0,1,\dots ,q$. We give the color classes as

$$\begin{aligned} C_{j-1}=l_{p_{0}}^{j}, ~~l_{p_{0}}^{j}\in L_{p_{0}},~ j=1,2,\dots ,q. \end{aligned}$$

Then the vertices in any hyperedge of $\Omega _{q}$ have q different colors and come from the q different color classes. So $\Omega _{q}$ has a complete q-coloring.

When $c\ge q+1$, suppose $\Omega _{q}$ has a complete c-coloring $\tau$. Since $L_{p_{i}}$ forms a partition of $V'$ in $\Omega _{q}$, $1\le i\le q$, then each hyperedge in $L_{p_{i}}$ intersects any hyperedge in $L_{p_{0}}$ at a unique vertex. The relationship between $L_{p_{0}}$ and $L_{p_{1}}$ can be shown below (Fig. 2).

Fig. 2

The relationship between $L_{p_{0}}$ and $L_{p_{1}}$ in $\Omega _{q}$

Let’s color the intersection $p_{1j}$ of $l_{p_{1}}^{1}$ and $l_{p_{0}}^{j}$ with color $j-1$, $j=1,2,\dots ,q$. Because $c\ge q+1$, there is a vertex $p_{x}$ in $l_{p_{1}}^{2}\cup l_{p_{1}}^{3}\cup \dots \cup l_{p_{1}}^{q}$ with $\tau (p_{x})=q$. Without loss of generality, let $p_{x}\in l_{p_{0}}^{1}\cap l_{p_{1}}^{2}$.

Because any two vertices from different hyperedges in $L_{p_{0}}$ have a unique hyperedge of $\Omega _{q}$ containing them, there is $\tau (y)\ne 0$ or q for any $y\in l_{p_{0}}^{j}$, $j=2,3,\dots ,q$. At this time, there is no hyperedge in $E'$ with two vertices coloring 0 and q, which contradicts the definition of complete coloring. So $\Omega _{q}$ has no complete c-coloring when $c\ge q+1$.

To sum up, ${\overline{\chi }}_{c}(\Omega _{q})=q$. $\square$

Lemma 4.7

${\overline{\chi }}_{c}(\Omega _{2}(n,2))=2^{n-2}$.

Proof

There are $2^{n-1}-1$ hyperedges through a fixed vertex $p_{0}$ in $\Pi _{2}(n,2)$. Let S be a hyperplane of $\Pi _{2}(n,2)$. Delete the hyperedges in hyperplane S, then the remaining $2^{n-2}$ hyperedges through the vertex $p_{0}$ could form a partition of $V'$ by removing $p_{0}$, i.e., $L_{p_{0}}$ is the partition. Define the color classes

$$\begin{aligned}C_{j-1}=l_{p_{0}}^{j},~~l_{p_{0}}^{j}\in L_{p_{0}},~j=1,2,\dots ,2^{n-2}.\end{aligned}$$

Then two vertices in any hyperedge of $\Omega _{2}(n,2)$ have different colors. We know that $\Omega _{2}(n,2)$ is a 2-uniform hypergraph, any two vertices in $V'$ determine a unique hyperedge. That is, each 2-subset of the colors appears as a color set of a certain hyperedge. Thus, $\Omega _2(n,2)$ has a complete $2^{n-2}$-coloring.

On the other hand, suppose there exists a complete c-coloring with $c>2^{n-2}$. Because two vertices from different $l_{p_{0}}^{j}$ determine a unique hyperedge in $\Omega _{2}(n,2)$, the vertices in different $l_{p_{0}}^{j}$ have different colors. Suppose there is a vertex $p_{1j}$ coloring $j-1$ in $l_{p_{0}}^{j}$, $j=1,2,\dots ,2^{n-2}$. Because $c>2^{n-2}$, there exists a $l_{p_{0}}^{j}$ such that the other vertex of $l_{p_{0}}^{j}$ coloring $2^{n-2}$. Without loss of generality, let it be $l_{p_{0}}^{1}$. Similar to $\Omega _{q}$, because any two vertices from different hyperedges of $L_{p_{0}}$ determine a unique hyperedge in $\Omega _{2}(n,2)$, there is $\tau (y)\ne 0$ or $2^{n-2}$ for any $y\in l_{p_{0}}^{j}$, $j=2,3,\dots ,2^{n-2}$. The 2-subset $\{0,2^{n-2}\}$ of colors can not appear as a color set of a hyperedge in $\Omega _{2}(n,2)$. It conflicts the definition of complete c-coloring. So $c\le 2^{n-2}$. That is ${\overline{\chi }}_{c}(\Omega _{2}(n,2))=2^{n-2}$. $\square$

Lemma 4.8

For any positive integer c, there is no complete c-coloring for $\Omega _{3}(4,2)$.

Proof

There are 13 hyperedges through a fixed vertex $p_{0}$ in $\Pi _{3}(4,2)$. Let S be a hyperplane of $\Pi _{3}(4,2)$. We delete the hyperedges in hyperplane S, then the remaining 9 hyperedges through the vertex $p_{0}$ could form a partition of $V'$ by removing $p_{0}$, i.e., $L_{p_{0}}$ is the partition. Similar to Lemma 4.6, if $\Omega _{3}(4,2)$ has a complete c-coloring, the vertices from different hyperedges of $L_{p_{0}}$ must be have different colors and the vertices in the same hyperedge have the same color. So if $\Omega _{3}(4,2)$ has a complete c-coloring, there is a unique way to color, i.e. a hyperedge of $L_{p_{0}}$ as a color class, and $c=9$. Now we consider whether this coloring satisfies the conditions of a complete coloring.

Let $x^{4}+x^{3}+2$ be a primitive polynomial of $F_{3^4}$, and let $\alpha$ be a primitive element of $F_{3^4}$. Without loss of generality, we suppose the hyperplane $S=\langle 1,\alpha ,\alpha ^{2}\rangle$ and the vertex $p_{0}=\langle 1\rangle$, then

$$\begin{aligned} S=\{\langle 1\rangle ,\langle \alpha \rangle ,\langle \alpha ^{2}\rangle ,\langle \alpha ^{8}\rangle , \langle \alpha ^{16}\rangle ,\langle \alpha ^{18}\rangle ,\langle \alpha ^{23}\rangle ,\langle \alpha ^{25}\rangle ,\langle \alpha ^{28}\rangle , \langle \alpha ^{29}\rangle ,\langle \alpha ^{34}\rangle ,\langle \alpha ^{37}\rangle ,\langle \alpha ^{38}\rangle \}. \end{aligned}$$

$L_{p_{0}}$ forms a partition of $\Omega _{3}(4,2)$. For convenience, we use the index i to denote $\langle \alpha ^{i}\rangle$, and define the sets of color classes as follows:

$$\begin{aligned}\begin{array}{ccc} C_{0}=\{3,4,31\},~~ &{}C_{1}=\{5,11,19\},~ &{}C_{2}=\{6,14,35\},~\\ C_{3}=\{7,22,24\},~ &{}C_{4}=\{9,12,13\},~ &{}C_{5}=\{10,20,30\},\\ C_{6}=\{15,17,33\}, &{}C_{7}=\{21,26,32\}, &{}C_{8}=\{27,36,39\}.\\ \end{array} \end{aligned}$$

The hyperedges are listed below : 

$$\begin{aligned}{} & {} \begin{array}{ccccc} \{3,19,26\},~ &{}\{4,5,32\},~~ &{}\{6,12,20\},~ &{}\{7,15,36\},~ &{}\{9,30,35\},~\\ \{10,13,14\}, &{}\{11,21,31\}, &{}\{17,24,39\}, &{}\{22,27,33\}; \end{array}\\{} & {} \begin{array}{ccccc} \{3,30,39\},~ &{}\{4,20,27\},~ &{}\{5,6,33\},~~ &{}\{7,13,21\},~ &{}\{9,24,26\},~\\ \{10,31,36\}, &{}\{11,14,15\}, &{}\{12,22,32\}, &{}\{17,19,35\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,14,22\},~ &{}\{4,7,35\},~~ &{}\{5,9,36\},~~ &{}\{6,24,31\},~ &{}\{10,26,33\},\\ \{11,12,39\}, &{}\{13,19,27\}, &{}\{15,30,32\}, &{}\{17,20,21\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,12,15\},~ &{}\{4,13,17\},~ &{}\{5,10,24\},~ &{}\{6,26,36\},~ &{}\{7,19,20\},~\\ \{9,31,33\},~ &{}\{11,22,30\}, &{}\{14,32,39\}, &{}\{21,27,35\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,20,36\},~ &{}\{4,10,39\},~ &{}\{5,14,17\},~ &{}\{6,15,19\},~ &{}\{7,12,26\},~\\ \{9,21,22\},~ &{}\{11,33,35\}, &{}\{13,24,32\}, &{}\{27,30,31\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,13,33\},~ &{}\{4,9,15\},~~ &{}\{5,7,30\},~~ &{}\{6,21,39\},~ &{}\{10,19,22\},\\ \{11,20,24\}, &{}\{12,17,31\}, &{}\{14,26,27\}, &{}\{32,35,36\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,10,27\},~ &{}\{4,30,36\},~ &{}\{5,15,35\},~ &{}\{6,11,17\},~ &{}\{7,9,32\},~~\\ \{12,21,24\}, &{}\{13,22,26\}, &{}\{14,19,33\}, &{}\{20,31,39\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,5,21\},~~ &{}\{4,11,26\},~ &{}\{6,13,30\},~ &{}\{7,33,39\},~ &{}\{9,14,20\},~\\ \{10,12,35\}, &{}\{15,24,27\}, &{}\{17,22,36\}, &{}\{19,31,32\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,24,35\},~ &{}\{4,6,22\},~~ &{}\{5,12,27\},~ &{}\{7,14,31\},~ &{}\{9,19,39\},~\\ \{10,15,21\}, &{}\{11,13,36\}, &{}\{17,26,30\}, &{}\{20,32,33\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,6,7\},~~~ &{}\{4,14,24\},~ &{}\{5,13,39\},~ &{}\{9,11,27\},~ &{}\{10,17,32\},\\ \{12,19,36\}, &{}\{15,20,26\}, &{}\{21,30,33\}, &{}\{22,31,35\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,11,32\},~ &{}\{4,19,21\},~ &{}\{5,26,31\},~ &{}\{6,9,10\},~~ &{}\{7,17,27\},~\\ \{12,14,30\}, &{}\{13,20,35\}, &{}\{15,22,39\}, &{}\{24,33,36\};\\ \end{array}\\{} & {} \begin{array}{ccccc} \{3,9,17\},~~ &{}\{4,12,33\},~ &{}\{5,20,22\},~ &{}\{6,27,32\},~ &{}\{7,10,11\},~\\ \{13,15,31\}, &{}\{14,21,36\}, &{}\{19,24,30\}, &{}\{26,35,39\}.\\ \end{array} \end{aligned}$$

In this case, many 3-subsets of the colors, such as $\{0,1,2\}$, cannot appear as the color sets of the hyperedges. So there is no complete 9-coloring. And since $\Omega _{3}(4,2)$ is unique in the isomorphism sense, there is no complete coloring for $\Omega _{3}(4,2)$. $\square$

Lemma 4.9

Suppose $q\ge 3$ is a prime power. There is no complete c-coloring for $\Omega _{q}(n,2)$ with $n\ge 4$ and positive integer c.

Proof

Given a vertex $p_0$ and define the set $L_{p_{0}}$ as above. If $\Omega _{q}(n,2)$ has a complete c-coloring, the two vertices from different $l_{p_{0}}^j$ have different colors, so $c\ge q^{n-2}$ and

$$\begin{aligned}{c\atopwithdelims ()q}\le q^{n-1}\theta _{n-2}.\end{aligned}$$

Due to

$$\begin{aligned} {q^{n-2}\atopwithdelims ()q}=\frac{q^{n-2}(q^{n-2}-1)\cdots (q^{n-2}-q+1)}{q!}\le \frac{q^{n-1}(q^{n-2}-1)}{q-1} \end{aligned}$$

if and only if $n=3$ or $q=2$ or $(n,q)=(4,3)$. $\Omega _{3}(4,2)$ has no complete c-coloring by Lemma 4.8. So there is no complete c-coloring of $\Omega _{q}(n,2)$ when $n\ge 4$ and $q\ge 3$. $\square$

In summary, we have completely solved the problem of the complete colorings of $\Omega _{q}(n,2)$ and get the following theorem.

Theorem 4.10

There exists a complete coloring for $\Omega _{q}(n,2)$ if and only if $n=3$ or $q=2$.

Finally, for the case of $k>2$, similar to Lemma 4.6 and Theorem 4.4, we have the following theorem.

Theorem 4.11

Suppose q is a prime power. If there exists a complete coloring for $\Omega _{q}(n,k)$ with $k>2$, then ${\overline{\chi }}_{c}(\Omega _{q}(n,k))=q^{n-2}$.

Furthermore, if there exists a complete coloring for $\Omega _{q}(n,k)$, the number of $q^{k-1}$-subsets from the colors is less than or equal to the number of hyperedges, then we have

$$\begin{aligned} {q^{n-2}\atopwithdelims ()q^{k-1}}\le q^{n-1} \begin{bmatrix} n-2 \\ k-1 \end{bmatrix}_{q}. \end{aligned}$$

By plugging in the values of n, k, q, we can also preliminarily determine whether $\Omega _{q}(n,k)$ has complete coloring. Obviously, ${\overline{\chi }}_{c}(\Omega _{q}(n,n-1))=q^{n-2}$.

5 Conclusions

In this paper, we mainly study the perfect balanced rainbow-free colorings and the complete colorings of projective hypergraphs. We present the perfect balanced upper chromatic number of $\Pi _{q}(n,k)$ with $k\ge \lceil \frac{n+1}{2}\rceil$ and prove that $\Pi _{q}(n,k)$ has no complete coloring with $2\le k<n$. We define two subhypergraphs with strong properties of $\Pi _{q}(n,k)$, $\Lambda _{q}(n,k)$ and $\Omega _{q}(n,k)$. As a consequence, we show that ${\overline{\chi }}_{p}(\Lambda _{q}(3,2))=\frac{q^{2}+q}{3}$ for $q\equiv 0,2~($mod 3) and provide some results of ${\overline{\chi }}_{c}(\Lambda _{q}(n,k))$ and ${\overline{\chi }}_{c}(\Omega _{q}(n,k))$. In particular, we solve the problem of the complete colorings of $\Lambda _{q}(n,2)$ and $\Omega _{q}(n,2)$. For the higher dimensions, further research on the colorings of the projective hypergraphs $\Pi _{q}(n,k)$, $\Lambda _{q}(n,k)$ and $\Omega _{q}(n,k)$ is needed.