Betti Numbers of Edge Ideals of Grimaldi Graphs and Their Complements

Abstract

Let $n\ge 2$ be an integer. The Grimaldi graph G(n) is defined by taking the elements of the set $\{ 0, \ldots , n-1 \}$ as vertices. Two distinct vertices x and y are adjacent in G(n) if and only if $\gcd (x+y, n) =1$. In this paper, we examine the Betti numbers of the edge ideals of these graphs and their complements.

1 Introduction

Let $R = \Bbbk [x_1,\ldots , x_n]$ be the polynomial ring over an arbitrary field $\Bbbk$. It is well known that associated to any homogeneous ideal I of R there is a minimal graded free resolution

$$\begin{aligned} 0\rightarrow \bigoplus _{j} R(-j)^ {\beta _ {\ell ,j} (R/I)} \rightarrow \cdots \rightarrow \bigoplus _{j} R(-j)^ {\beta _{0,j}(R/I)} \rightarrow R/I \rightarrow 0, \end{aligned}$$

where $R(-j)$ denotes the free R-module obtained by shifting the degrees of R by j. The quantity $\beta _{i,j}(R/I)$, which is called the (i, j)th graded Betti number of R/I, is equal to the number of generators of degree j in the ith syzygy module. The graded Betti numbers are collected in the Betti table, in which the entry at column i and row j is $\beta _{i,i+j}(R/I)$. The regularity and the projective dimension are two important invariants associated with R/I that can be read off from the minimal free resolution. The regularity of R/I is defined by ${{\,\textrm{reg}\,}}(R/I)=\max \{j-i\mid \beta _{i,j}(R/I)\ne 0\}$ and the projective dimension of R/I is defined by ${{\,\textrm{pd}\,}}(R/I) = \max \{i\mid \beta _ {i,j} (R/I) \ne 0 \text { for some } j\}.$

1.1 Minimal Resolutions and the Edge Ideals

Let us now connect the above-mentioned notions with the ideals arising from graphs. In order to do this, let G be a finite simple graph with the vertex set $V(G)=\{x_1, \ldots , x_n\}$ and the edge set E(G). One may associate to the graph G a quadratic squarefree monomial ideal

$$\begin{aligned} I(G) = (x_i x_j \mid \{x_i, x_j\} \in E(G)) \subseteq R, \end{aligned}$$

which is called the edge ideal of G. One of the central problems in combinatorial commutative algebra is a description of the minimal resolutions of these ideals. The structure of the resulting resolutions is very poorly understood. This problem has been studied by many authors (e.g., [8, 10, 13,14,15]). In particular, Katzman [15] and Kimura [16] have provided some results on the nonvanishing of the graded Betti numbers. For the Ferrers graphs, Corso and Nagel [5] have proved that their edge ideals have linear resolutions, and furthermore they have given an explicit formula for the Betti numbers of such ideals. Recently, Fröberg [8] has described the Betti numbers of the edge ideals of fat forests. We refer the reader to [7, 10, 17, 20] for other problems and results on this area.

1.2 A Class of Graphs Due to Grimaldi

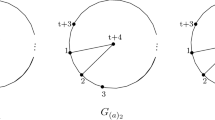
Let $n \ge 2$ be an integer. In 1990, Grimaldi [9] defined a graph G(n) based on the elements of $[n]=\{0,\ldots ,n-1\}$ and the notion of coprimeness, that is, a graph with a number-theoretical nature. The vertices of G(n) are the elements of [n] and distinct vertices x and y are defined to be adjacent if and only if $\gcd (x+y,n)=1$. This graph is called a Grimaldi graph. By letting $\varphi$ as the Euler’s phi function, it follows that when n is even, G(n) is a $\varphi (n)$-regular graph, whereas it is $(\varphi (n), \varphi (n)-1)$-biregular when n is odd. This means by [1] that G(n) is an almost regular graph. Also, when $n \ne 2$ is even, G(n) can be expressed as the union of $\varphi (n)/2$ Hamiltonian cycles, that is, cycles containing all the vertices of the graph. The odd case is not quite so easy, but the structure is clear and the results are similar to the even case. Grimaldi has given an explicit formula for the chromatic polynomial of G(p) and has investigated some properties of the graph $G(p^{ \alpha })$, where p is a prime and $\alpha \ge 2$ is an integer. Hoang et al. [13] have characterized Cohen–Macaulay and Gorenstein properties for a kind of circulant graphs and their complements. When n is even, these latter graphs coincide with Grimaldi graphs and their complements. The complement of G(n), denoted by $G'(n)$, is a graph whose vertex set is [n] in which two distinct vertices x and y are adjacent if and only if $\gcd (x+y,n)\ne 1$. In [2], we have characterized when these graphs are well-covered, Cohen–Macaulay, vertex-decomposable, or Gorenstein.

1.3 The Aim of this Paper

In this paper, we focus on finding the Betti numbers of the edge ideals of G(n)’s and $G'(n)$’s. The rest of the paper is organized as follows. In Sect. 2, we provide some basic notation and terminology about the Betti numbers of the Stanley–Reisner rings and the edge ideals of graphs. In Sect. 3, we give a useful technique to compute the Betti numbers of the edge ideal of $G(p^{\alpha } )$, where p is a prime. Finally, in Sect. 4, we give a formula for the Betti numbers of the edge ideal of $G'(n)$, when n is either even or a prime power.

2 Preliminaries

In this section, we introduce some basic notation which will be used in the sequel. We refer the reader to [18, 21] for detailed information about the combinatorial and algebraic backgrounds.

2.1 The Betti Numbers of the Stanley–Reisner Rings

A simplicial complex $\Delta$ with the vertex set $V(\Delta )= \{ v_1, \ldots , v_n\}$ is a collection of subsets of $V(\Delta )$ such that $F\in \Delta$ whenever $F\subseteq F'$ for some $F'\in \Delta$. The restriction of $\Delta$ to a subset S of $V(\Delta )$ is $\Delta [S] = \{F\in \Delta \mid F \subseteq S\}$. For a given field $\Bbbk$, we attach to $\Delta$ the Stanley–Reisner ideal $I_{\Delta }$ of $\Delta$ to be the squarefree monomial ideal

$$\begin{aligned} I_{\Delta } = (x_{j_1} \cdots x_{j_i} \mid j_1<\cdots < j_i \ \text { and } \{j_1,\ldots ,j_i\} \notin \Delta ) \end{aligned}$$

in $R =\Bbbk [x_1,\ldots ,x_n]$ and the Stanley–Reisner ring of $\Delta$ to be the quotient ring $\Bbbk [\Delta ] = R/I_{\Delta }$. This provides a bridge between combinatorics and commutative algebra (see [14]). We denote by $\widetilde{H}_j(\Delta ; \Bbbk )$ the reduced homology group of $\Delta$ with coefficients in $\Bbbk$. A very useful result about the graded Betti numbers of a Stanley–Reisner ring is the following so-called Hochster’s formula (c.f. [11, Theorem 8.1.1]):

$$\begin{aligned} \beta _{i,j}(\Bbbk [\Delta ]) =\sum _{\begin{array}{c} W \subseteq V(\Delta )\\ |W|=j \end{array}}\dim _{\Bbbk } \widetilde{H}_{j-i-1} (\Delta [W]; \Bbbk ). \end{aligned}$$

The dimension of a face $F\in \Delta$ is given by $\dim F = |F| - 1$. The dimension of $\Delta$, denoted by $\dim \Delta$, is the maximum dimension of all its faces. By letting $d-1=\dim \Delta$, the f-vector of $\Delta$ is the vector $(f_{-1}, f_0, \ldots , f_{d-1})$, where $f_{-1}=1$ and $f_i$ is the number of faces of dimension i. The reduced Euler characteristic of $\Delta$, denoted by $\widetilde{\chi }(\Delta )$, is defined to be $\widetilde{\chi }(\Delta ) = \sum _{i=-1}^{d-1}(-1)^i f_i(\Delta ).$ The h-vector of $\Delta$ is the vector $(h_0, \ldots , h_d)$, where

$$\begin{aligned} h_k =\sum _{i=0}^k (-1)^{k-i} \left( {\begin{array}{c}d-i\\ d-k\end{array}}\right) f_{i-1}, \quad 0\le k\le d. \end{aligned}$$

The Hilbert–Poincaré series of the R-module $\Bbbk [\Delta ]$ is $HP_{\Bbbk [\Delta ] }(t)= \sum _{i\ge 0} H_{\Bbbk [\Delta ]}(i) t^i$, where $H_{\Bbbk [ \Delta ]}$ is the Hilbert function of $\Bbbk [\Delta ]$. By [18, Corollary 1.5], this series can be expressed as follows:

$$\begin{aligned} HP_{\Bbbk [\Delta ]}(t)= \frac{h_0+h_1t + \cdots +h_dt^d}{(1-t)^d}. \end{aligned}$$

Let $\Gamma$ and $\Lambda$ be two simplicial complexes with the disjoint vertex sets $V(\Gamma )$ and $V(\Lambda )$, respectively. We define their join on the vertex set $V(\Gamma )\cup V(\Lambda )$ to be $\Gamma * \Lambda = \{ \sigma \cup \tau \mid \sigma \in \Gamma ,\ \tau \in \Lambda \}.$ By using the Künneth’s formula (c.f. [3, Proposition 3.2]), we can describe the reduced homology of the join of two simplicial complexes in terms of the reduced homologies of the factors for each i as follows:

$$\begin{aligned} \widetilde{H}_ {i}(\Gamma * \Lambda ; \Bbbk )\cong \bigoplus _{p+q=i-1} \widetilde{H}_p(\Gamma ;\Bbbk ) \otimes \widetilde{H} _q( \Lambda ; \Bbbk ). \end{aligned}$$

The following lemma gives us the Betti numbers of the Stanley–Reisner rings of simplicial complexes which are join of finitely many disjoint subcomplexes.

Lemma 2.1

([12], Lemma 1.2) Let $\Delta$ be a simplicial complex. If $\Delta =\Delta _1*\cdots *\Delta _m$, where the $\Delta _i$’s are disjoint subcomplexes of $\Delta$, then

$$\begin{aligned} \beta _ {i,j}(\Bbbk [ \Delta ]) = \sum _{\begin{array}{c} a_1+\cdots +a_m=i\\ b_1+ \cdots +b_m=j \end{array}} \left( \prod _{k=1}^m \beta _{a_k,b_k}(\Bbbk [\Delta _k])\right) . \end{aligned}$$

In particular, ${{\,\textrm{pd}\,}}(\Bbbk [ \Delta ]) = \sum _{k=1}^m {{\,\textrm{pd}\,}}(\Bbbk [\Delta _k])$ and ${{\,\textrm{reg}\,}}(\Bbbk [\Delta ]) = \sum _ {k=1}^m {{\,\textrm{reg}\,}}(\Bbbk [\Delta _k])$.

We now state and prove the following lemma for later use.

Lemma 2.2

Let $\Delta _1$ and $\Delta _2$ be two simplicial complexes. If $V(\Delta _1) \cap V(\Delta _2) = \emptyset$, then ${{\,\textrm{reg}\,}}( \Bbbk [ \Delta _1 \cup \Delta _2 ] ) = \max \{ {{\,\textrm{reg}\,}}(\Bbbk [\Delta _1]), {{\,\textrm{reg}\,}}(\Bbbk [\Delta _2])\}.$

Proof

Note that [11, Proposition 5.1.8] implies $I_{\Delta _1} \cap I_{\Delta _2} = I_ {\Delta _1 \cup \Delta _2}$ and $I_{\Delta _1} + I_{\Delta _2}= I_{ \Delta _1 \cap \Delta _2}$. Therefore, we obtain the following exact sequence:

$$\begin{aligned} 0\rightarrow R/I _{\Delta _1 \cup \Delta _2} \rightarrow R/I_{\Delta _1} \oplus R/I_{\Delta _2} \rightarrow R/I_{ \Delta _1 \cap \Delta _2} \rightarrow 0. \end{aligned}$$

Now, by [19, Proposition 18.6], ${{\,\textrm{reg}\,}}(\Bbbk [ \Delta _1 \cup \Delta _2]) = \max \{ {{\,\textrm{reg}\,}}(\Bbbk [\Delta _1]), {{\,\textrm{reg}\,}}( \Bbbk [ \Delta _2 ])\}$, as required. $\square$

Let $\Delta _1$ and $\Delta _2$ be two simplicial complexes with n and m vertices, respectively. It is known that if $I_{\Delta _1} \subseteq \Bbbk [ x_1, \ldots , x_n ]$ is the Stanley–Reisner ideal of $\Delta _1$ and $I_{\Delta _2} \subseteq \Bbbk [ y_1, \ldots , y_m ]$ is the Stanley–Reisner ideal of $\Delta _2$, then

is the Stanley–Reisner ideal of in $\Bbbk [x_1,\ldots ,x_n,y_1,\ldots ,y_m]$. In this direction, Whieldon [22] has determined the graded Betti numbers of the edge ring . We close this subsection by stating it.

Lemma 2.3

([22], Lemma 5.4) Let $\Delta _1$ and $\Delta _2$ be two simplicial complexes with n and m vertices, respectively. If $s \ge 2$ is an integer, then the following formulas hold true:

2.2 The Betti Numbers of the Edge Ideals of Graphs

In the sequel, by a graph we mean a finite undirected graph without loops or multiple edges. For a graph G, let V(G) denote the set of vertices of G and let E(G) denote the set of edges of G. A graph with just one vertex is referred to as trivial. All other graphs are nontrivial. A graph is called totally disconnected if it is either a null graph or it contains no edge. An edge $e \in E(G)$ connecting two vertices x and y will also be written as $\{x, y\}$. In this case, it is said that x and y are adjacent. For a subset S of V(G), we denote by G[S] the induced subgraph of G on the vertex set S and denote $G\backslash S$ by $G[V \backslash S]$. If $S = \{x\}$, we write $G\backslash x$ instead of $G\backslash \{x\}$. The neighborhood of x in G is the set $N_G(x)= \{y \in V(G) \mid \{x,y\} \in E(G)\},$ and the closed neighborhood of x is $N_G[x] = \{x\} \cup N_G(x)$.

A bipartite graph is one whose vertex set can be partitioned into two disjoint parts in such a way that the two end vertices for each edge lie in distinct parts. A complete bipartite graph is one in which each vertex is joined to every vertex that is not in the same partition. The complete bipartite graph with exactly two parts of size m and n, is denoted by $K_{m,n}$. A complete graph is a graph in which each pair of distinct vertices is joined by an edge. We denote the complete graph with n vertices by $K_n$.

To every graph G with the vertex set $V(G)=\{x_1,\ldots ,x_n\}$ and the edge set E(G) , one may associates the edge ideal I(G) of the polynomial ring $\Bbbk [V(G)] =\Bbbk [x_1,\ldots ,x_n]$. Let $\Delta (G)$ be the set of all independent sets of G. Then $\Delta (G)$ is a simplicial complex, which is called the independence complex of G. It is easy to see that $I_{ \Delta (G)} = I(G)$. Note that $\Delta (G[W]) = \Delta (G)[W]$ for any $W \subseteq V(G)$. Therefore, the Hochster’s formula is also applied to compute the Betti numbers of edge ideals. We write $\beta _{i,j} (G)$, ${{\,\textrm{pd}\,}}(G)$, and ${{\,\textrm{reg}\,}}(G)$ as shorthand for $\beta _{i,j} (\Bbbk [ \Delta (G)])$, ${{\,\textrm{pd}\,}}(\Bbbk [\Delta (G)])$, and ${{\,\textrm{reg}\,}}( \Bbbk [ \Delta (G)])$, respectively.

We close this section by recalling the following result which gives us the Betti numbers of the complete graph $K_n$ and the complete bipartite graph $K_{n,m}$.

Proposition 2.4

([14], Theorems 5.1.1 and 5.2.4) The following statements hold true:

• (1) The edge ring of $K_{n}$ has a 2-linear resolution and $\beta _{i,i+1}(K_n) = i\left( {\begin{array}{c}n\\ i+1\end{array}}\right) .$

• (2) The edge ring of $K_{n,m}$ has a 2-linear resolution and

  $$\begin{aligned} \beta _{i,i+1}(K_{n,m})= \sum \limits _{\begin{array}{c} s+t=i+1\\ s,t\ge 1 \end{array}} \left( {\begin{array}{c}n\\ s\end{array}}\right) \left( {\begin{array}{c}m\\ t\end{array}}\right) . \end{aligned}$$

3 The Betti Numbers of the $G(p^{\alpha })$’s

In this section, we find some invariants regarding the graphs $G(p^{\alpha } )$’s, where p is a prime. In particular, we find the Betti numbers of these graphs. The case $p=2$ is easy to handle, while the odd case is not quite so easy. For this latter case, we give a useful technique to compute the Betti numbers. Let us start with the following purely combinatorial lemma, which is useful for later use.

Lemma 3.1

Let $m, n, i, j, k \in {{\mathbb {N}}}$, $0 \le i \le n$, and $0 \le j \le m$. Then the following equalities hold true:

• (1) $\sum \limits _ {\begin{array}{c} i+j=k \\ i, j \ge 0 \end{array}} \left( {\begin{array}{c}n\\ i\end{array}}\right) \left( {\begin{array}{c}m\\ j\end{array}}\right) = \left( {\begin{array}{c}n+m\\ k\end{array}}\right)$.

• (2) $\sum \limits _{\begin{array}{c} i+j=k \\ i, j \ge 0 \end{array}} ij \left( {\begin{array}{c}n\\ i+1\end{array}}\right) \left( {\begin{array}{c}m\\ j+1\end{array}}\right) = (k+1) \left\{ \frac{kmn-m^2-n^2+m+n}{(m+n-1) (m+n)}\left( {\begin{array}{c}m+n\\ k+2\end{array}}\right) + \left( {\begin{array}{c}n\\ k+2\end{array}}\right) + \left( {\begin{array}{c}m\\ k+2\end{array}}\right) \right\} .$

Proof

(1): By the binomial expansion theorem we have the following equalities:

$$\begin{aligned} (1+x)^n(1+x)^m = \sum _{i=0}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) x^i \sum _{j=0}^m \left( {\begin{array}{c}m\\ j\end{array}}\right) x^j = \sum _{k=0}^ {n+m} \left( \sum _{\begin{array}{c} i+j=k \\ i,j\ge 0 \end{array}} \left( {\begin{array}{c}n\\ i\end{array}}\right) \left( {\begin{array}{c}m\\ j\end{array}}\right) \right) x^{k} \end{aligned}$$

and $(1+x)^{n+m} = \sum _{k=0}^{n+m} \left( {\begin{array}{c}n+m\\ k\end{array}}\right) x^{k}.$ It is noteworthy that the coefficients of the monomials of degree k of two above expressions are $\sum _{\begin{array}{c} i+j=k\\ i,j\ge 0 \end{array}} \left( {\begin{array}{c}n\\ i\end{array}}\right) \left( {\begin{array}{c}m\\ j\end{array}}\right)$ and $\left( {\begin{array}{c}n+m\\ k\end{array}}\right)$. Hence, they are equal, as required.

(2): Note that $\sum _{i=0}^{n} \left( {\begin{array}{c}n\\ i\end{array}}\right) x^{i} = (1+x)^n$, and thus, we obtain that

$$\begin{aligned} \sum _{i=1}^{n-1} i \left( {\begin{array}{c}n\\ i+1\end{array}}\right) x^{i+1}= & {} x^2\sum _{i=1}^ {n-1} i \left( {\begin{array}{c}n\\ i+1\end{array}}\right) x^{i-1} = x^2 \left( \sum _{i=0}^{n-1} \left( {\begin{array}{c}n\\ i+1\end{array}}\right) x^{i}\right) ' \\= & {} x^2 \left( \frac{1}{x} \sum _{i=0}^ {n-1} \left( {\begin{array}{c}n\\ i+1\end{array}}\right) x^{i+1} \right) ' = x^2 \left( \frac{1}{x} \sum _{i=1}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) x^{i}\right) '\\= & {} x^2 \left( \frac{(1+x)^n-1}{x} \right) ' = nx(1+x)^{n-1}-(1+x)^n+1. \end{aligned}$$

Therefore, $\sum _{i=1}^{n-1} i \left( {\begin{array}{c}n\\ i+1\end{array}}\right) x^{i+1} = nx (1+x)^ {n-1} -(1+ x)^ n+1.$ On the other hand,

$$\begin{aligned}{} & {} \left\{ \sum _{i=0}^{n-1} i \left( {\begin{array}{c}n\\ i+1\end{array}}\right) x^ {i +1}\right\} \left\{ \sum _{j=0}^{m-1} j\left( {\begin{array}{c}m\\ j+1\end{array}}\right) x^{j+1}\right\} \\{} & {} \quad = x^2 \sum _ {k =0}^ {m+n-2} \sum _{\begin{array}{c} i+j=k\\ i,j\ge 0 \end{array}} ij \left( {\begin{array}{c}n\\ i+1\end{array}}\right) \left( {\begin{array}{c}m\\ j+1\end{array}}\right) x^{k}. \end{aligned}$$

Hence, the coefficients of the monomials of degree $k+2$ ($0\le k\le m+n-2$) of the above expression are

$$\begin{aligned} \sum _{ \begin{array}{c} i+j =k\\ i,j\ge 0 \end{array}} ij \left( {\begin{array}{c}n\\ i+1\end{array}}\right) \left( {\begin{array}{c}m\\ j+1\end{array}}\right) . \end{aligned}$$

Moreover, the product of two polynomials $nx(1+x)^{n-1}-(1+x)^n+1$ and $mx(1+x)^{m-1}-(1+x)^m+1$ is

$$\begin{aligned}{} & {} nmx^2(1+x)^{n+m-2} - (n+m)x(1+x)^{n+m-1} + (1+x)^{n+m} + nx(1+x)^{n-1}\\{} & {} \hspace{1cm} -(1+x)^n + mx(1+x)^{m-1}-(1+x)^m +1. \end{aligned}$$

This implies that the coefficient of the monomials of degree $k+2$ $(0 \le k \le m+n-2)$ of the above polynomial is

$$\begin{aligned}{} & {} \left\{ nm\left( {\begin{array}{c}m+n-2\\ k\end{array}}\right) -(m+n)\left( {\begin{array}{c}m+n-1\\ k+1\end{array}}\right) + \left( {\begin{array}{c}n+m\\ k+2\end{array}}\right) \right\} \\{} & {} \quad \qquad + \left\{ n\left( {\begin{array}{c}n-1\\ k+1\end{array}}\right) -\left( {\begin{array}{c}n\\ k+2\end{array}}\right) \right\} + \left\{ m \left( {\begin{array}{c}m-1\\ k+1\end{array}}\right) - \left( {\begin{array}{c}m\\ k+2\end{array}}\right) \right\} \\{} & {} \qquad = (k+1) \left\{ \frac{kmn-m^2-n^2+m+n}{(m+n-1)(m+n)} \left( {\begin{array}{c}m+n\\ k+2\end{array}}\right) + \left( {\begin{array}{c}n\\ k+2\end{array}}\right) + \left( {\begin{array}{c}m\\ k+2\end{array}}\right) \right\} .\\ \end{aligned}$$

We now get the result by comparing the two coefficients above. $\square$

The following proposition deals with the graphs $G( 2^{\alpha } )$’s and gives us the projective dimension of these graphs.

Proposition 3.2

Let $\alpha$ be a positive integer. Then the edge ring of $G( 2^{\alpha } )$ has a 2-linear resolution. Moreover, we have

$$\begin{aligned} \beta _{i,i+1}(G(2^{\alpha })) = \left( {\begin{array}{c}2^{\alpha }\\ i+1\end{array}}\right) -2 \left( {\begin{array}{c}2^{\alpha -1}\\ i+1\end{array}}\right) . \end{aligned}$$

In particular, ${{\,\textrm{pd}\,}}( G(2^{\alpha }) ) = 2^{\alpha }-1.$

Proof

Let $A = \{0,2, \ldots , 2^{\alpha }-2\}$ and $B = \{1,3, \ldots , 2^{\alpha }-1 \}$. If either $x,y\in A$ or $x,y\in B$, then $x+y = 0 \pmod 2$, and thus, $\{x, y\} \notin E(G(2^{\alpha }))$. On the other hand, if $x\in A$ and $y\in B$, then $x+y = 1 \pmod 2$, and thus, $\{x, y\} \in E(G(2^{\alpha }))$. Therefore, A and B are the maximal independent sets of $G(2^{ \alpha })$, and furthermore, $G( 2^{\alpha } )$ is a complete bipartite graph with bipartition (A, B). By Proposition 2.4(2), we obtain that

$$\begin{aligned} \beta _ {i,i+1} (G (2^ {\alpha }) ) = \sum _ {\begin{array}{c} s+t=i+1 \\ s,t\ge 1 \end{array}} \left( {\begin{array}{c}2^ {\alpha -1}\\ s\end{array}}\right) \left( {\begin{array}{c}2^ {\alpha -1}\\ t\end{array}}\right) . \end{aligned}$$

This, together with Lemma 3.1(1), completes the proof. $\square$

We now continue the paper with the odd case.

Proposition 3.3

Let p be an odd prime. Then $\alpha (G(p))=2$, the edge ring of G(p) has a 2-linear resolution, and we have

$$\begin{aligned} \beta _{i,i+1}(G(p)) = {\left\{ \begin{array}{ll} \frac{p-1}{2} \left\{ \left( {\begin{array}{c}p\\ i+1\end{array}}\right) -\left( {\begin{array}{c}p-2\\ i+1\end{array}}\right) \right\} - \left( {\begin{array}{c}p-1\\ i+1\end{array}}\right) &{}\text { if }\ 1\le i\le p-3,\\ \frac{p^2-p-2}{2} &{}\text { if }\ i=p-2,\\ \frac{p-1}{2} &{}\text { if }\ i=p-1. \end{array}\right. } \end{aligned}$$

In particular, ${{\,\textrm{pd}\,}}(G(p))=p-1$.

Proof

Since p is a prime, it is easy to see that the vertex 0 is adjacent to all of the other vertices in G(p), and $\{x,y\}\notin E(G(p))$ for some $x,y\in [p]$ if and only if $x+y=p$. Thus, all of the maximal independent sets of G(p) are $\{0\}$ and $\{ i, p-i \}$ for all $1 \le i \le \frac{p-1}{2}$. Therefore, the independence complex of G(p) is a disjoint union of $\frac{p-1}{2}$ edges and one vertex. This means that the Hilbert series of $\Bbbk [\Delta (G(p) ]$ is

$$\begin{aligned} \frac{p-1}{2} \frac{1}{(1-t)^2} + \frac{1}{1-t} - \frac{p-1}{2} = \frac{ \frac{p-1}{2} (1-t) ^ {p-2} + (1-t) ^ {p-1} - \frac{p-1}{2} (1-t) ^{p}}{(1-t)^p}. \end{aligned}$$

This implies that $\beta _ {p-1,p} (G(p)) = \frac{p-1}{2}$, $\beta _ {p-2,p-1} (G(p)) = \frac{p^2-p-2}{2}$, and

$$\begin{aligned} \beta _ {i,i+1} (G(p)) = \frac{p-1}{2} \left\{ \left( {\begin{array}{c}p\\ i+1\end{array}}\right) - \left( {\begin{array}{c}p-2\\ i+1\end{array}}\right) \right\} - \left( {\begin{array}{c}p-1\\ i+1\end{array}}\right) \end{aligned}$$

for all $1\le i\le p-3$, as required. $\square$

The following lemma gives us a decomposition for a class of Grimaldi graphs involving the join of graphs. Let us recall that the join of two graphs G and H, denoted by $G*H$, is a graph formed from disjoint copies of G and H by connecting each vertex of G to each vertex of H.

Lemma 3.4

Let p be an odd prime and $\alpha > 1$ be an integer. Then we have

$$\begin{aligned} G( p^{ \alpha } ) = G[I_ 0] * G[I_{1}\cup I_{p-1}] * \cdots * G[I_{\frac{p-1}{2}}\cup I_{ \frac{p+1}{2}}], \end{aligned}$$

where $I_i = \{x \in [p^{\alpha }] \mid x=i \pmod p\}$ for every $0 \le i \le p-1$, $G[I_0]$ is a totally disconnected graph, and $G[ I_i \cup I_{p- i}]$ is an induced graph of $G(p^{\alpha })$ with the edge set

$$\begin{aligned} E(G[I_i \cup I_ {p-i}])= \{ \{x,y\} \mid x,y \in I_i\} \cup \{ \{x,y \} \mid x, y \in I_{ p-i} \}. \end{aligned}$$

Proof

In order to prove the lemma, it is enough to prove the following claims:

Claim 1: $G[I_0]$ is a totally disconnected graph.

Claim 2: $G[I_i]$ is a complete graph for $1\le i\le p-1$.

Claim 3: $\{x,y\} \notin E(G(p^{\alpha }))$ for $x\in I_{i}$ and $y\in I_{p-i}$ with $1\le i\le \frac{p-1}{2}$.

Claim 4: $\{x,y\} \in E(G(p^{\alpha }))$ for $x\in I_0$ and $y\in I_{i} \cup I_{ p-i}$ with $1\le i\le \frac{p-1}{2}$.

Claim 5: $\{x,y\} \in E(G(p^{\alpha }))$ for $x\in I_{i} \cup I_{p-i}$ and $y\in I_{j} \cup I_{p-j}$ with $1\le i\ne j\le \frac{p-1}{2}$.

Claim 1 is true since for every $x, y \in I_0$, $x+y=0 \pmod p$, and thus, x and y are not adjacent in $G(p^{\alpha })$. Claim 2 is true since for every $x, y \in I_i$ with $1\le i\le p-1$, $\gcd ( x+y, p^{ \alpha } )=1$, and thus, x is adjacent to y in $G(p^{\alpha })$. Claim 3 is true since by the assumption, $x+y=0 \pmod p$, and thus, x is not adjacent to y in $G(p^{\alpha })$. Claim 4 is true since by the assumption, $x+y = y \pmod p$, and thus, x is adjacent to y in $G(p^{\alpha })$. Claim 5 is true since by the assumption, $\gcd (x+y, p^ {\alpha }) = 1$, and thus, x is adjacent to y in $G (p^ {\alpha } )$. $\square$

Proposition 3.5

Let p be an odd prime and $\alpha > 1$ be an integer. Then $\alpha (G(p^{ \alpha })) = p^ {\alpha -1}$ and the f-vector of $\Delta ( G(p^ {\alpha }))$ is $(f_{-1},f_0,\ldots ,f_{p^{\alpha -1}-1})$, where $f_{-1}=1$, $f_0= p^{\alpha }$, $f_1 = \frac{ (p^{\alpha }-1) p^{ \alpha -1}}{2}$, and $f_i = \left( {\begin{array}{c}p^ {\alpha -1}\\ i+1\end{array}}\right)$ for all $2 \le i \le p^{ \alpha -1 } - 1$. In particular,

$$\begin{aligned} \widetilde{\chi }(\Delta (G(p^{\alpha })))=(p^{\alpha }-p^{\alpha -1})(1-\frac{p^{\alpha -1}}{2}). \end{aligned}$$

Proof

By Lemma 3.4, all of the maximal independent sets of $G(p^{\alpha })$ are $I_0$ and $I_{uv}=\{\{u,v\}\mid 0\le u<v\le p^{\alpha }-1, u+v=0\pmod p \}$. Thus, $\alpha (G(p^{\alpha })) = p^{\alpha -1}$. We also obtain that $f_i = \left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right)$ for all $2\le i\le p^{\alpha -1}-1$. Moreover, we claim that $f_1=\frac{(p^{\alpha }-1)p^{\alpha -1}}{2}$. Indeed, by the structure of the graph $G(p^{\alpha })$, for $x\in V(G(p^{\alpha }))$, we have

$$\begin{aligned} \deg (x)= {\left\{ \begin{array}{ll} p^{\alpha }-p^{\alpha -1} &{} \text { if }x\in I_0,\\ p^{\alpha }-p^{\alpha -1}-1 &{} \text { otherwise. } \end{array}\right. } \end{aligned}$$

Hence,

$$\begin{aligned} |E(G(p^{\alpha }))|= & {} \frac{1}{2}\sum _{x\in V(G(p^{\alpha }))} \deg (x) = \frac{1}{2} \left( \sum _{x\in I_0} \deg (x)+\sum _{x\in (I_1\cup \cdots \cup I_{p-1})}\deg (x)\right) \\= & {} \frac{1}{2}\left[ p^{\alpha -1}(p^{\alpha }-p^{\alpha -1}) + (p^{\alpha }-p^{\alpha -1})(p^{\alpha }-p^{\alpha -1}-1)\right] \\= & {} \frac{1}{2}\left[ (p^{\alpha }-p^{\alpha -1})(p^{\alpha }-1)\right] . \end{aligned}$$

This implies that $f_1 = \left( {\begin{array}{c}p^{\alpha }\\ 2\end{array}}\right) - |E(G(p^{\alpha }))| = \frac{(p^{\alpha }-1)p^{\alpha -1}}{2}.$ Now, these computations lead to

$$\begin{aligned} \widetilde{\chi }(\Delta (G(p^{\alpha })))= & {} \sum _ {i=-1} ^{p^{\alpha -1}-1} (-1)^i f_i = -1 + p^{\alpha } - \frac{(p^{\alpha }-1)p^{\alpha -1}}{2} \\{} & {} + \sum _{i=2}^{p^{\alpha -1}-1} (-1)^{i}\left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right) . \end{aligned}$$

We know that $\sum \limits _{i=0}^ {p^{\alpha -1}} (-1)^{i} \left( {\begin{array}{c}p^{\alpha -1}\\ i\end{array}}\right) = (1-1)^ {p^ {\alpha -1}} =0$, and so,

$$\begin{aligned} \sum \limits _ {i=2}^{p^{\alpha -1}-1} (-1)^ {i} \left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right) = - \sum \limits _{i=3}^{p^ {\alpha -1}} (-1)^ {i} \left( {\begin{array}{c}p^{\alpha -1}\\ i\end{array}}\right) = 1 - p^{\alpha -1} + \frac{(p^{ \alpha -1}-1) p^ {\alpha -1}}{2}. \end{aligned}$$

Hence, we conclude that

$$\begin{aligned} \widetilde{\chi }(\Delta (G(p^{\alpha })))= & {} p^{\alpha } -p^{\alpha -1} + \frac{(p^{\alpha -1}-1)p^{\alpha -1}}{2} - \frac{(p^{\alpha }-1)p^{\alpha -1}}{2} \\ {}= & {} (p^{\alpha }-p^{\alpha -1})(1-\frac{p^{\alpha -1}}{2}), \end{aligned}$$

as required. $\square$

Lemma 3.6

Let p be an odd prime and $\alpha > 1$ be an integer. Then ${{\,\textrm{reg}\,}}(G( p^{ \alpha } )) = 2$ and ${{\,\textrm{pd}\,}}(G(p^ {\alpha })) = p^{\alpha }-1$.

Proof

By considering $G=G(p^{\alpha })$ and applying Lemma 3.4, we have $\Delta (G) = \left<I_0\right> \cup \Delta _1 \cup \cdots \cup \Delta _{ \frac{p-1}{2}},$ where $\left<I_0\right>$ is the simplex over the set $I_0$ and each $\Delta _i$ denotes the independence complex of the induced subgraph of $G[I_{i} \cup I_{p-i}]$. Note that at this point, for every $1 \le i \le \frac{p-1}{2}$, $\dim \Delta _i=1$, and so, $\Delta _i$ is regarded as a complete bipartite graph. Hence, $G [I_i \cup I_{p-i}]$ is a disjoint union of two complete graphs. Thus, ${{\,\textrm{reg}\,}}(\Delta _i) = {{\,\textrm{reg}\,}}(G [I_i \cup I_{p-i}])=2$. Now, by Lemma 2.2, we obtain that ${{\,\textrm{reg}\,}}( \Delta (G) ) = \max \{ {{\,\textrm{reg}\,}}( \left<I_0\right>), {{\,\textrm{reg}\,}}(\Delta _1), \ldots , {{\,\textrm{reg}\,}}( \Delta _ { \frac{p-1}{2}} ) \}= 2,$ as required. $\square$

Theorem 3.7

Let p be an odd prime and $\alpha > 1$ be an integer. If $G=G(p^{\alpha })$ and $I_0 = \{x\in [p^{\alpha }]\mid x=0\pmod p\}$, then

$$\begin{aligned} \beta _{i,i+1}(G)= & {} {\left\{ \begin{array}{ll} \sum \limits _{t=0}^{p^{\alpha -1}-1} \left\{ \left( {\begin{array}{c}t+p^{\alpha }-p^{\alpha -1}\\ i\end{array}}\right) - \left( {\begin{array}{c}t\\ i\end{array}}\right) \right\} + \sum \limits _{k=0}^{i-1} \left( {\begin{array}{c}p^{\alpha -1}\\ k\end{array}}\right) \beta _{i-k,i-k+1}(G\backslash I_0) \text { if }\ i < p^{\alpha -1}, \\ \sum \limits _{t=0}^{p^{\alpha -1}-1} \left( {\begin{array}{c}t+p^{\alpha }-p^{\alpha -1}\\ i\end{array}}\right) + \sum \limits _ {k=0}^ {p^ {\alpha -1}} \left( {\begin{array}{c}p^{\alpha -1}\\ k\end{array}}\right) \beta _ {i-k,i-k+1} (G \backslash I_0) \text { if }\ i\ge p^{\alpha -1},\\ \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \beta _{i,i+2}(G)= & {} {\left\{ \begin{array}{ll} \sum \limits _{k=0}^{p^{\alpha -1}} \left( {\begin{array}{c}p^{\alpha -1}\\ k\end{array}}\right) \beta _{i-p ^{\alpha -1} +k, i-p^ {\alpha -1}+k+2} (G \backslash I_0) &{}\text { if }\ i\ge 2, \\ 0 &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

Proof

By Lemma 3.4, we have $G =G[I_0]* G[I_{1} \cup I_{p-1}] * \cdots * G [I_ {\frac{p-1}{2}} \cup I_{\frac{p+1}{2}}],$ where $G[I_0]$ is a totally disconnected graph and for every $1 \le i \le \frac{p-1}{2}$, $G[I_i \cup I_ {p -i}]$ is an induced subgraph of G with the edge set

$$\begin{aligned} E ( G[ I_i \cup I_ {p - i}]) = \{ \{ x,y \} \mid x, y \in I_i \} \cup \{ \{ x,y \} \mid x, y \in I_{p - i}\}. \end{aligned}$$

This implies that $G \backslash I_0 = G[ I_{1} \cup I_{p-1} ] * \cdots *G [I_ {\frac{p-1}{2}} \cup I_{\frac{p+1}{2}}].$ Also, for every $x\in I_0$, $N_ G (x) = I_1 \cup \cdots \cup I_{p-1}$, and so, $G\backslash N_G[x] = G [I_0 \backslash \{x\}]$ is a totally disconnected graph. Now, by [6, Lemma 3.1], we have $I(G):x = I(G \backslash N_G[x]) + (N_G(x))$ and $(I(G),x) = I(G\backslash x) + (x).$ Thus, we obtain that

$$\begin{aligned} \beta _{i,j}(R/(I(G):x)(-1))= & {} \beta _{i,j-1}(R/(I(G):x)) = \beta _{i,j-1}(\Bbbk [V(I_0)]/I(G\backslash N_G[x])) \\= & {} {\left\{ \begin{array}{ll} \left( {\begin{array}{c}p^{\alpha }-p^{\alpha -1}\\ i\end{array}}\right) &{}\text { if } j=i+1, \\ 0&{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

On the other hand, by applying the long exact sequence theorem to the short exact sequence $0 \longrightarrow R/ (I(G):x) (-1) \overset{\cdot x}{\longrightarrow } R/I(G) \longrightarrow R/(I(G),x) \rightarrow 0,$ we obtain the following long exact sequence:

$$\begin{aligned} \cdots \rightarrow {{\,\textrm{Tor}\,}}_i(R/(I(G):x)(-1);\Bbbk )_{j}\rightarrow & {} {{\,\textrm{Tor}\,}}_i(R/I(G);\Bbbk )_j \rightarrow {{\,\textrm{Tor}\,}}_i(R/(I(G),x);\Bbbk )_j \\\rightarrow & {} {{\,\textrm{Tor}\,}}_{i-1}(R/(I(G):x)(-1);\Bbbk )_{j} \rightarrow \cdots . \end{aligned}$$

This, together with the fact that for $j=i+1$ with $i\ge 0$, ${{\,\textrm{Tor}\,}}_{i+1} (R/(I(G),x); \Bbbk )_{i+1}=0$ and ${{\,\textrm{Tor}\,}}_ {i-1}(R/(I(G):x)(-1);\Bbbk )_{i+1} = 0,$ lead us to the following short exact sequence:

$$\begin{aligned} 0 \rightarrow {{\,\textrm{Tor}\,}}_i(R/(I(G):x) (-1);\Bbbk )_{i+1}\rightarrow & {} {{\,\textrm{Tor}\,}}_i(R/I(G);\Bbbk )_{i+ 1} \\\rightarrow & {} {{\,\textrm{Tor}\,}}_i(R/(I(G),x);\Bbbk )_{i+1} \rightarrow 0. \end{aligned}$$

By using the above observations, we have for every $i \ge 1$,

$$\begin{aligned} \beta _{i,i+1}(G)= & {} \beta _{i,i+1}(R/(I(G):x)(-1))+ \beta _ {i, i+1} (R/ (I(G), x) ) \\= & {} \left( {\begin{array}{c}p^{\alpha }-p^{\alpha -1}\\ i\end{array}}\right) +\beta _{i,i+1}(R/(I(G),x)). \end{aligned}$$

Also, by [4, Remark 2.1], the equality $\beta _ {i, i+1} (R/(I(G), x)) = \beta _ {i,i+1} (G \backslash x) + \beta _{i-1,i} (G \backslash x)$ holds true for every $i \ge 1$. This implies the following recurrence formula for computing the Betti numbers of the graph G, where $\beta _{0,1}(G\backslash x)=0$ and $\beta _{1,2}(G) = (p^{\alpha }-p^{\alpha -1}) + \beta _ {1,2} (G \backslash x)$, as follows:

$$\begin{aligned} \beta _{i,i+1}(G)= & {} \left( {\begin{array}{c}p^ {\alpha }-p^ {\alpha -1}\\ i\end{array}}\right) + \beta _ {i,i+1} (G \backslash x) + \beta _{i-1,i}(G \backslash x). \end{aligned}$$

As a result of applying this process consecutively by replacing G by $G \backslash x$, we obtain that $\beta _ {0,1} (G) = \beta _ {0,1} (G \backslash I_0)=0$ and

$$\begin{aligned} \beta _ {i,i+1}(G) = {\left\{ \begin{array}{ll} \sum \limits _{t=0}^{p^{\alpha -1}-1}\sum \limits _{k=0}^{i-1} \left( {\begin{array}{c}t\\ k\end{array}}\right) \left( {\begin{array}{c}p^{\alpha }-p^ {\alpha -1}\\ i-k\end{array}}\right) + \sum \limits _ {k=0}^{i-1} \left( {\begin{array}{c}p^ {\alpha -1}\\ k\end{array}}\right) \beta _{i-k, i-k+1} (G \backslash I_0) &{}\text { if } i < p^ {\alpha -1}, \\ \sum \limits _{t=0}^ {p^{\alpha -1}-1} \sum \limits _{k=0}^t \left( {\begin{array}{c}t\\ k\end{array}}\right) \left( {\begin{array}{c}p^ {\alpha } -p^ {\alpha -1}\\ i-k\end{array}}\right) + \sum \limits _{k=0}^ {p^{\alpha -1}} \left( {\begin{array}{c}p^{ \alpha -1}\\ k\end{array}}\right) \beta _{i-k,i-k+1} (G\backslash I_0) &{}\text { if } i\ge p^{ \alpha -1}.\\ \end{array}\right. } \end{aligned}$$

In order to simplify the formula, we apply Lemma 3.1(1) and obtain

$$\begin{aligned} \sum \limits _{k=0}^{i-1} \left( {\begin{array}{c}t\\ k\end{array}}\right) \left( {\begin{array}{c}p^ {\alpha } -p^ {\alpha -1}\\ i- k\end{array}}\right)= & {} \sum \limits _{\begin{array}{c} s+t=i\\ s,t\ge 0 \end{array}}\left( {\begin{array}{c}t\\ s\end{array}}\right) \left( {\begin{array}{c}p^ {\alpha }-p^{\alpha -1}\\ t\end{array}}\right) - \left( {\begin{array}{c}t\\ i\end{array}}\right) \\= & {} \left( {\begin{array}{c}t+p^ {\alpha } -p^{ \alpha -1 }\\ i\end{array}}\right) - \left( {\begin{array}{c}t\\ i\end{array}}\right) . \end{aligned}$$

Moreover, if $i\ge p^{\alpha -1}>t$, we have

$$\begin{aligned} \sum \limits _{k=0}^t \left( {\begin{array}{c}t\\ k\end{array}}\right) \left( {\begin{array}{c}p^{\alpha }-p^{\alpha -1}\\ i-k\end{array}}\right)= & {} \sum \limits _{k=0}^i \left( {\begin{array}{c}t\\ k\end{array}}\right) \left( {\begin{array}{c}p^{\alpha }-p^{\alpha -1}\\ i-k\end{array}}\right) = \sum \limits _{\begin{array}{c} s+t=i\\ s,t\ge 0 \end{array}}\left( {\begin{array}{c}t\\ s\end{array}}\right) \left( {\begin{array}{c}p^{\alpha } -p^{\alpha -1}\\ t\end{array}}\right) \\= & {} \left( {\begin{array}{c}t+p^ {\alpha }-p^ {\alpha -1}\\ i\end{array}}\right) . \end{aligned}$$

This implies that

$$\begin{aligned} \beta _{i,i+1}(G) = {\left\{ \begin{array}{ll} \sum \limits _{t=0}^{p^{\alpha -1}-1} \left\{ \left( {\begin{array}{c}t+p^{\alpha }-p^{\alpha -1}\\ i\end{array}}\right) - \left( {\begin{array}{c}t\\ i\end{array}}\right) \right\} + \sum \limits _{k=0}^{i-1} \left( {\begin{array}{c}p^{\alpha -1}\\ k\end{array}}\right) \beta _{i-k,i-k+1}(G\backslash I_0) &{}\text { if } i < p^{\alpha -1}, \\ \sum \limits _{t=0}^{p^{\alpha -1}-1} \left( {\begin{array}{c}t+p^{\alpha }-p^{\alpha -1}\\ i\end{array}}\right) + \sum \limits _{k=0}^ {p^ {\alpha -1}} \left( {\begin{array}{c}p^{\alpha -1}\\ k\end{array}}\right) \beta _ {i-k, i-k+1}(G \backslash I_0) &{}\text { if } i\ge p^{\alpha -1}.\\ \end{array}\right. } \end{aligned}$$

For the second formula, we have

$$\begin{aligned} \beta _ {i,i+2} (R/(I(G): x) (-1)) = \beta _ {i- 1,i+2} (R/(I(G):x)(-1)) = 0. \end{aligned}$$

This implies that ${{\,\textrm{Tor}\,}}_ i (R/I(G); \Bbbk )_ {i+2} \cong {{\,\textrm{Tor}\,}}_ i (R/(I(G),x); \Bbbk )_ {i+2}$, and so, by [4, Remark 2.1], $\beta _ {i, i + 2} (G) = \beta _{i,i+2}(R/(I(G),x)) = \beta _ {i-1, i+1}( G \backslash x) + \beta _ {i, i+2} (G \backslash x).$ As a result of applying this process consecutively by replacing G by $G \backslash x$, we obtain that

$$\begin{aligned} \beta _ {i,i+2} (G) = \sum _ {k=0}^ {p^ {\alpha -1}} \left( {\begin{array}{c}p^ { \alpha -1}\\ k\end{array}}\right) \beta _ {i-p^ {\alpha -1}+k, i-p^ {\alpha -1}+k+2}(G\backslash I_0), \end{aligned}$$

as required. $\square$

By keeping the notation of the previous theorem, its proof shows that $G \backslash I_0 = G[I_{1} \cup I_{p-1}] * \cdots *G[I_{\frac{p-1}{2}} \cup I_{ \frac{p+1}{2}}].$ Also, by Lemma 3.4, we have where for every $1 \le k \le \frac{p-1}{2}$, $\Delta _k = \Delta (G[I_k \cup I_{p-k}])$. Thus, in order to finding the Betti numbers of $G(p^{\alpha })$ by Lemma 2.3, we need to compute the Betti numbers of $G[I_k \cup I_{p-k}]$ for all $1\le k\le \frac{p-1}{2}$. To this end, we state and prove the following proposition.

Proposition 3.8

Let p be an odd prime and $\alpha > 1$ be an integer. If $G=G(p^{\alpha })$ and $I_i = \{x\in [p^{\alpha }]\mid x=i \pmod p\}$ for $0\le i\le p-1$, then

$$\begin{aligned} \beta _{i,j}(G[I_k\cup I_{p-k}]) = {\left\{ \begin{array}{ll} 2i\left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right) &{}\text { if }\ j=i+1, \\ (i+1)\left\{ \frac{(i-2) p^{\alpha -1}+2}{2(2p^{\alpha -1}-1)} \left( {\begin{array}{c}2p^ {\alpha -1}\\ i+2\end{array}}\right) + 2\left( {\begin{array}{c}p^{\alpha -1}\\ i+2\end{array}}\right) \right\} &{}\text { if }\ j=i+2, \\ 0 &{}\text { otherwise. } \end{array}\right. } \end{aligned}$$

Proof

By the proof of Lemma 3.6, for every $1\le k\le \frac{p-1}{2}$, the graph $G[I_k\cup I_{p-k}]$ is a disjoint union of two complete graphs. Thus, $\Delta (G[I_k\cup I_{p-k}]) = \Delta (G[I_k])* \Delta (G[I_{p-k}])$, where $\Delta (-)$ denotes the independence complex of −. Since ${{\,\textrm{reg}\,}}(G[I_k\cup I_{p-k}])=2$ and $\beta _{i,j}(G[I_k\cup I_{p-k}])=0$ for all $j>i+2$, by Lemma 2.1, we obtain that

$$\begin{aligned} \beta _{i,j}(G[I_k \cup I_{p-k}]) = {\left\{ \begin{array}{ll} \beta _{i,i+1}(G[I_k]) + \beta _{i,i+1}(G[I_{p-k}])&{}\text { if } j=i+1, \\ \sum \limits _{i_1+i_2=i} \beta _{i_1,i_1+1}(G[I_k]) \beta _{i_2, i_2+1}(G[I_{p-k} ])&{}\text { if } j=i+2, \\ 0 &{}\text { otherwise. } \end{array}\right. } \end{aligned}$$

Now, Proposition 2.4(1) implies that

$$\begin{aligned} \beta _{i,j}(G[I_k\cup I_{p-k}]) = {\left\{ \begin{array}{ll} 2i\left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right) &{}\text { if } j=i+1, \\ \sum \limits _{i_1+i_2=i} i_1 i_2 \left( {\begin{array}{c}p^{ \alpha -1} \\ i_1+1\end{array}}\right) \left( {\begin{array}{c}p^{ \alpha -1}\\ i_2+1\end{array}}\right) &{}\text { if } j=i+2, \\ 0 &{}\text { otherwise. } \end{array}\right. } \end{aligned}$$

Note that, by Lemma 3.1(2),

$$\begin{aligned} \sum \limits _{i_1+i_2=i} i_1 i_2 \left( {\begin{array}{c}p^{\alpha -1}\\ i_1+1\end{array}}\right) \left( {\begin{array}{c}p^{\alpha -1}\\ i_2+1\end{array}}\right) = (i+1) \left\{ \frac{(i-2) p^ {\alpha -1}+2}{2(2p^{\alpha -1}-1)} \left( {\begin{array}{c}2p^ {\alpha -1}\\ i+2\end{array}}\right) + 2 \left( {\begin{array}{c}p^ {\alpha -1}\\ i+2\end{array}}\right) \right\} , \end{aligned}$$

and thus,

$$\begin{aligned} \beta _{i,j}(G[I_k\cup I_{p-k}] )= {\left\{ \begin{array}{ll} 2i \left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right) &{}\text { if } j=i+1, \\ (i+1) \left\{ \frac{(i-2) p^{\alpha -1}+2}{2(2p^{\alpha -1}-1)} \left( {\begin{array}{c}2p^ {\alpha -1}\\ i+2\end{array}}\right) + 2\left( {\begin{array}{c}p^{\alpha -1}\\ i+2\end{array}}\right) \right\} &{}\text { if } j=i+2, \\ 0 &{}\text { otherwise, } \end{array}\right. } \end{aligned}$$

as required. $\square$

We conclude this section with the following example.

Example 3.9

Consider the graph $G=G(3^2)$ and let $I_0 = \{0,3,6\}$, $I_1 = \{1,4,7\}$, and $I_2 = \{2,5,8\}$. By applying Proposition 3.8 with $p=3$ and $\alpha =2$, we obtain the Betti table of $G\backslash I_0 = G[I_1 \cup I_2]$ as follows:

$$\begin{aligned} \begin{array}{rcccccc} &{} 0 &{} 1 &{} 2 &{} 3 &{} 4 \\ total: &{} 1 &{} 6 &{} 13&{} 12 &{}4\\ 0: &{} 1 &{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ 1: &{} \cdot &{} 6 &{} 4 &{} \cdot &{} \cdot \\ 2: &{} \cdot &{} \cdot &{} 9 &{} 12 &{} 4 \end{array} \end{aligned}$$

Now, by Theorem 3.7, we have

$$\begin{aligned} \beta _{i,i+1}(G) = {\left\{ \begin{array}{ll} 0 &{}\text { if } i=0, \\ 18 + \beta _{1,2}(G \backslash I_0)&{}\text { if } i=1, \\ 63 + \beta _ {2,3}(G \backslash I_0) + 3 \beta _{1,2}(G \backslash I_0) &{}\text { if } i=2, \\ \left( {\begin{array}{c}6\\ i\end{array}}\right) + \left( {\begin{array}{c}7\\ i\end{array}}\right) + \left( {\begin{array}{c}8\\ i\end{array}}\right) + \sum \limits _{k=0}^{3} \left( {\begin{array}{c}3\\ k\end{array}}\right) \beta _{i-k, i-k+1}(G \backslash I_0)&\text { if } i\ge 3, \end{array}\right. } \end{aligned}$$

and $\beta _ {i,i+2}(G) = \beta _{i-3,i-1}(G \backslash I_0) + 3 \beta _ {i-2,i} (G\backslash I_0)+3\beta _{i-1,i+1}(G\backslash I_0)+\beta _{i,i+2}(G \backslash I_0).$ Thus, we obtain the Betti table of G as follows:

$$\begin{aligned} \begin{array}{rccccccccc} &{} 0 &{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 &{} 7 &{} 8 \\ total: &{} 1&{} 24&{} 94&{} 180&{} 205&{} 144&{} 60&{} 13&{}1 \\ 0: &{} 1 &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ 1: &{} \cdot &{} 24 &{} 85 &{} 141 &{} 138 &{} 87 &{} 36 &{} 9 &{} 1 \\ 2: &{} \cdot &{} \cdot &{} 9 &{} 39 &{} 67 &{} 57 &{} 24 &{} 4 &{} \cdot \end{array} \end{aligned}$$

4 The Betti Numbers of the $G'(n)$’s

In this section, we focus on the $G'(n)$’s, the complements of the G(n)’s. Let us recall that $G'(n)$ is the graph whose vertex set is [n] in which two distinct vertices x and y are adjacent if and only if $\gcd (x+y,n)\ne 1$. It is obvious that $G'(p)$, p prime, contains one isolated vertex and disjoint edges. By [2, Lemma 4.1], if n is even, $G'(n)$ is well-covered. Because of this, we first consider the graph $G'(n)$ with even n.

Lemma 4.1

Let n be an even integer. Then $\alpha (G'(n)) = 2$ and the f-vector of $\Delta (G'(n))$ is $(1, n, \frac{n}{2} \varphi (n))$, where $\varphi$ is the Euler’s phi function.

Proof

By the proof of [2, Lemma 4.1], we obtain that $\alpha (G'(n))=2$ and the f-vector of $\Delta (G'(n))$ is $(f_{-1}, f_0, f_1)$, where $f_{-1}=1$, $f_0=n$, and $f_1= |E(G(n))| = \frac{n}{2}\varphi (n)$, as required. $\square$

Proposition 4.2

Let n be an even integer. Then the following statements hold true:

• (1) The Hilbert series of $R/I(G'(n))$ is $HP_{R/I(G'(n))}(t) = \frac{1+(n-2)t + (1-n+\frac{n}{2}\varphi (n))t^2}{(1-t)^2}.$

• (2) ${{\,\textrm{reg}\,}}(G'(n)) =2$ and ${{\,\textrm{pd}\,}}(G'(n)) = n-2$.

• (3) $\beta _{n-2, n} (G'(n)) = 1 - n + \frac{n}{2} \varphi (n)$ is the unique extremal Betti number, where $\varphi$ is the Euler’s phi function.

Proof

(1): By Lemma 4.1, the components of the h-vector of $\Delta (G'(n))$ are $h_0 = \left( {\begin{array}{c}2\\ 0\end{array}}\right) f_{-1} = 1$, $h_1=(-1)^ 1 \left( {\begin{array}{c}2-0\\ 1-0\end{array}}\right) f_{-1} + (-1)^ 0 \left( {\begin{array}{c}2-1\\ 1-1\end{array}}\right) f_0 = n-2,$ and

$$\begin{aligned} h_2 = (-1)^2 \left( {\begin{array}{c}2\\ 2\end{array}}\right) f_ {-1} + (-1)^1 \left( {\begin{array}{c}2-1\\ 2-1\end{array}}\right) f_0 + (-1)^0 \left( {\begin{array}{c}2-2\\ 2-2\end{array}}\right) f_1 = 1-n + \frac{n}{2} \varphi (n). \end{aligned}$$

This implies that the Hilbert–Poincaré series of $R/I(G'(n) )$ is

$$\begin{aligned} HP_{R/I(G'(n))}(t) = \frac{1 + (n-2)t + (1-n + \frac{n}{2}\varphi (n)) t^2}{(1-t)^2}, \end{aligned}$$

as required.

(2): By [2, Theorem B], the graph $G'(n)$ is Cohen–Macaulay with $\alpha (G'(n) ) = 2$, and also, by the Auslander–Buchsbaum formula, we have ${{\,\textrm{pd}\,}}(G'(n)) = n - \dim R/I(G'(n) ) = n - \alpha (G'(n)) = n-2.$ Moreover, since $1-n+\frac{n}{2} \varphi (n) \ne 0$, by part (1), we obtain that ${{\,\textrm{pd}\,}}( G'(n))+{{\,\textrm{reg}\,}}(G'(n))=n$, and thus, ${{\,\textrm{reg}\,}}(G'(n) ) = 2$. (3): It is followed from (1) and (2). $\square$

Next, we consider the Betti numbers of the graph $G'(p^{\alpha })$, p prime. We recall the structure of the graph $G'(p^{\alpha })$ as follows:

Lemma 4.3

([2], Lemma 4.2) Let p be an odd prime and $\alpha$ be a positive integer. Then the graph $G'( p^{\alpha })$ is a disjoint union of one complete graph $K_{ p^{\alpha -1}}$ and $\frac{p-1}{2}$ complete bipartite graphs $K_{p^{\alpha -1}, p^{\alpha -1}}$, that is,

$$\begin{aligned} G'(p^{\alpha }) \cong K_{p^{\alpha -1}} \cup \underbrace{K_{p^{\alpha -1}, p^{ \alpha -1}} \cup K_{p^{\alpha -1},p^{\alpha -1}} \cup \cdots \cup K_{p^ {\alpha -1 }, p^{ \alpha -1}}}_{\frac{p-1}{2}\ \text { times}}. \end{aligned}$$

Lemma 4.4

Let p be an odd prime and $\alpha$ be a positive integer. Then the following statements hold true:

• (1) $\alpha (G'(p^{\alpha })) = \frac{(p-1)p^{\alpha -1}}{2} +1$.

• (2) The f-vector of $\Delta (G'(p^{\alpha }))$ is $(1,p^{\alpha }, f_ {1}, \ldots , f_{\alpha (G'(p^{\alpha }))-1})$, where $f_1=\frac{1}{2}(p^{\alpha }-p^{\alpha -1})(p^{\alpha }-1)$ and

  $$\begin{aligned} f_i= & {} p^ {\alpha -1} \cdot \left[ \underset{ 0\le c_1,\ldots , c_{\frac{p-1}{2}}\le p^{\alpha -1}}{\underset{c_1+\cdots + c_{\frac{p-1}{2}}=i}{\sum }} \left\{ \prod _{j=1}^{\frac{p-1}{2}} \left( {\begin{array}{c}p^{\alpha -1}\\ c_j\end{array}}\right) \right\} 2^{|\{j\mid c_j>0\}|} \right] \\{} & {} + \underset{ 0\le c_1,\ldots , c_{\frac{p-1}{2}}\le p^{\alpha -1}}{\underset{c_1+\cdots + c_{\frac{p-1}{2}}=i}{\sum }} \left\{ \prod _{j=1}^{\frac{p-1}{2}} \left( {\begin{array}{c}p^{\alpha -1}\\ c_j\end{array}}\right) \right\} 2^{|\{j\mid c_j>0\}|} \end{aligned}$$

  $\text { for all } 2\le i \le \frac{(p-1)p^{\alpha -1}}{2}.$

Proof

By Lemma 4.3, the graph $G'(p^{\alpha })$ is well-covered and $\alpha (G'(p^{ \alpha })) = \frac{(p-1)p^ {\alpha -1}}{2} +1$. It is clear that $f_{-1}=1, f_0=p^{\alpha }$. Applying the proof of Proposition 3.5, $f_1= |E(G(p^{\alpha }))|=\frac{1}{2}(p^{\alpha }-p^{\alpha -1})(p^{\alpha }-1)$.

Based on the structure of the graph $G'(p^{\alpha })$, we now assume that

$$\begin{aligned} G'(p^{\alpha }) =K_{p^{\alpha -1}} \cup K_{p^{\alpha -1}, p^{ \alpha -1}}^{(1)} \cup K_{p^{\alpha -1},p^{\alpha -1}}^{(2)} \cup \cdots \cup K_{p^ {\alpha -1 }, p^{ \alpha -1}}^{(\frac{p-1}{2})}. \end{aligned}$$

Let $(U^{(j)}, V^{(j)})$ be the bipartition of $K_{p^ {\alpha -1 }, p^{ \alpha -1}}^{(j)}$ for $1\le j\le \frac{p-1}{2}$. Let $I_i$ be the set of independent sets of $K_{p^{\alpha -1}, p^{ \alpha -1}}^{(1)} \cup K_{p^{\alpha -1},p^{\alpha -1}}^{(2)} \cup \cdots \cup K_{p^ {\alpha -1 }, p^{ \alpha -1}}^{(\frac{p-1}{2})}$ with size i. We see that $f_i= p^{\alpha -1}\cdot |I_i| + |I_j|.$ We observe that each element of $I_i$ has the following form

$$\begin{aligned} X^{(1)} \cup \cdots \cup X^{(\frac{p-1}{2})}, \end{aligned}$$

where $0\le |X^{(j)}|\le p^{\alpha -1}$ and $|X^{(1)}| + \cdots + |X^{(\frac{p-1}{2})}|=i$ and either $X^{(j)}\subset U^{(j)}$ or $X^{(j)}\subset V^{(j)}$ if $|X^{(j)}|>0$ for all $1\le j \le \frac{p-1}{2}$. By virtue of this observation, we have

$$\begin{aligned} |I_i| = \underset{ 0\le c_1,\ldots , c_{\frac{p-1}{2}}\le p^{\alpha -1}}{\underset{c_1+\cdots + c_{\frac{p-1}{2}}=i}{\sum }} \left\{ \prod _{j=1}^{\frac{p-1}{2}} \left( {\begin{array}{c}p^{\alpha -1}\\ c_j\end{array}}\right) \right\} 2^{|\{j\mid c_j>0\}|}. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} f_i= & {} p^ {\alpha -1} \cdot \left[ \underset{ 0\le c_1,\ldots , c_{\frac{p-1}{2}}\le p^{\alpha -1}}{\underset{c_1+\cdots + c_{\frac{p-1}{2}}=i}{\sum }} \left\{ \prod _{j=1}^{\frac{p-1}{2}} \left( {\begin{array}{c}p^{\alpha -1}\\ c_j\end{array}}\right) \right\} 2^{|\{j\mid c_j>0\}|} \right] \\{} & {} + \underset{ 0\le c_1,\ldots , c_{\frac{p-1}{2}}\le p^{\alpha -1}}{\underset{c_1+\cdots + c_{\frac{p-1}{2}}=i}{\sum }} \left\{ \prod _{j=1}^{\frac{p-1}{2}} \left( {\begin{array}{c}p^{\alpha -1}\\ c_j\end{array}}\right) \right\} 2^{|\{j\mid c_j>0\}|} \end{aligned}$$

for every $1 \le i \le \frac{(p-1)p^{\alpha -1}}{2}$, as required. $\square$

Proposition 4.5

Let p be an odd prime. Then $\beta _{i,j}(G'(p)) = {\left\{ \begin{array}{ll} \left( {\begin{array}{c}\frac{p-1}{2}\\ i\end{array}}\right) &{}\text { if }\ j=2i, \\ 0 &{}\text { if }\ j\ne 2i. \end{array}\right. }$ In particular, ${{\,\textrm{pd}\,}}(G'(p)) = {{\,\textrm{reg}\,}}(G'(p))= \frac{p-1}{2}$.

Proof

Since the graph $G'(p)$ is a disjoint union of $\frac{p-1}{2}$ graphs $K_2$ and one graph $K_1$,

$$\begin{aligned} \Delta (G'(p)) = \Delta (K_1)* \Delta (K_2)* \cdots *\Delta (K_ 2). \end{aligned}$$

Now, by Lemma 2.1 and Proposition 2.4(1), we obtain that

$$\begin{aligned} \beta _{i,j} (G'(p))= & {} \sum _ {\begin{array}{c} a_1 + \cdots + a_{\frac{p-1}{2}} =i\\ b_1+\cdots +b_{\frac{p-1}{2}}=j \end{array}} \prod _{k=1}^{\frac{p-1}{2}} \beta _ {a_k,b_k} (K_2) = {\left\{ \begin{array}{ll} \left( {\begin{array}{c}\frac{p-1}{2}\\ i\end{array}}\right) &{}\text { if } j=2i, \\ 0 &{}\text { if } j\ne 2i. \end{array}\right. } \end{aligned}$$

Therefore, ${{\,\textrm{pd}\,}}(G'(p)) = {{\,\textrm{reg}\,}}(G'(p))= \frac{p-1}{2}$, as required. $\square$

Theorem 4.6

Let p be an odd prime and $\alpha > 1$ be an integer. Let i and j be positive integers. If $1\le j-i\le \frac{p+1}{2}$, then

$$\begin{aligned}{} & {} \beta _{i,j} (G'(p^{\alpha })) = \left( {\begin{array}{c}\frac{p-1}{2}\\ j-i\end{array}}\right) \sum \limits _{\begin{array}{c} u_1 + \cdots + u_{j-i} = i \\ u_1, \ldots , u_{j-i} \ge 1 \end{array}} \left[ \prod \limits _{k=1}^{j-i} \left\{ \left( {\begin{array}{c}2p^{\alpha -1}\\ u_{k}+1\end{array}}\right) -2 \left( {\begin{array}{c}p^{\alpha -1}\\ u_{k}+1\end{array}}\right) \right\} \right] \\{} & {} \hspace{1em} + \left( {\begin{array}{c}\frac{p-1}{2}\\ j-i-1\end{array}}\right) \sum \limits _{\begin{array}{c} u_0 + \cdots + u_{j-i-1} = i \\ u_0, \ldots , u_{j-i-1} \ge 1 \end{array}} u_0\left( {\begin{array}{c}p^{\alpha -1}\\ u_0+1\end{array}}\right) \left[ \prod \limits _{k=1}^{j-i-1} \left\{ \left( {\begin{array}{c}2p^{\alpha -1}\\ u_{k}+1\end{array}}\right) -2 \left( {\begin{array}{c}p^{\alpha -1}\\ u_{k}+1\end{array}}\right) \right\} \right] . \end{aligned}$$

In the case $j-i>\frac{p+1}{2}$, we have $\beta _{i,j} (G'(p^{\alpha }))=0$.

Proof

By Lemma 4.3, the graph $G'(p^{\alpha })$ is a disjoint union of one complete graph $K_{p^{\alpha -1}}$ and $\frac{p-1}{2}$ complete bipartite graphs $K_{p^{\alpha -1},p^{\alpha -1}}$. This implies that

$$\begin{aligned} \Delta (G'(p^{\alpha })) = \Delta (K_{p^{\alpha -1}}) *\Delta (K_{p^{\alpha -1}, p^{\alpha -1}}) * \cdots * \Delta (K_{p^{\alpha -1},p^{\alpha -1}}). \end{aligned}$$

Note that $\beta _{0,0} (K_{p^ {\alpha -1}}) = \beta _{0,0} (K_{p^{\alpha -1}, p^{\alpha -1}})=1$. Also, by Proposition 2.4, the edge rings of $K_{p^{\alpha -1}}$ and $K_{p^{\alpha -1}, p^{ \alpha - 1}}$ have 2-linear resolutions. Now, $\beta _ {u_0, u_0+1} (K_{ p^{ \alpha -1}}) = u_0 \left( {\begin{array}{c}p^{ \alpha -1}\\ u_0+1\end{array}}\right)$, together with Lemma 3.1(1), implies that

$$\begin{aligned} \beta _{u_k,u_k+1}(K_{p^{\alpha -1}, p^{ \alpha -1}})= & {} \sum _{\begin{array}{c} s+t = u_k+1 \\ s,t \ge 1 \end{array}} \left( {\begin{array}{c}p^{ \alpha -1 }\\ s\end{array}}\right) \left( {\begin{array}{c}p^ {\alpha -1}\\ t\end{array}}\right) = \left( {\begin{array}{c}2p^{\alpha -1}\\ u_k+1\end{array}}\right) - 2\left( {\begin{array}{c}p^ { \alpha -1}\\ u_k+1\end{array}}\right) . \end{aligned}$$

Therefore, by Lemma 2.1, we obtain that for every i and j,

$$\begin{aligned} \beta _{i,j} (G'(p^{\alpha })) =\sum _{\begin{array}{c} u_0+\cdots +u_{ \frac{p-1}{2}} =i\\ v_0+\cdots +v_{\frac{p-1}{2}}=j \end{array}} \beta _{u_0,v_0}(K_{p^{\alpha -1}}) \left\{ \prod _{k=1}^{\frac{p-1}{2}} \beta _{u_k,v_k} (K_{ p^{\alpha -1}, p^{\alpha -1}})\right\} , \end{aligned}$$

(1)

where $u_k, v_k\ge 0$ are integers.

First, suppose that $j-i=1$. By Eq. 1, we obtain that

$$\begin{aligned} \beta _{i,j}(G'(p^{\alpha }))= & {} \beta _{i,i+1}(K_{p^{\alpha -1}})+\frac{p-1}{2} \beta _{i,i+1}(K_{p^{\alpha -1}, p^{\alpha -1} }) \\= & {} i\left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right) + \frac{p-1}{2} \left\{ \left( {\begin{array}{c}2p^{\alpha -1}\\ i+1\end{array}}\right) - 2\left( {\begin{array}{c}p^{\alpha -1}\\ i+1\end{array}}\right) \right\} . \end{aligned}$$

Second, suppose that $j-i=\frac{p+1}{2}$. Therefore, there exists $0\le k\le \frac{p-1}{2}$ such that $u_k, v_k \ge 1$ and $v_k \ne u_k+1$. Thus, $\beta _ {u_k,v_k} (K_{p^{ \alpha -1}}) = 0$ and $\beta _ {u_k, v_k} (K_{p^ {\alpha -1}, p^{ \alpha -1}} ) = 0$. Now, by Eq. 1, we obtain that

$$\begin{aligned} \beta _ {i,j}(G'(p^{\alpha }))= & {} \sum \limits _{\begin{array}{c} u_0+\cdots + u_{ \frac{p-1}{2}} = i \\ u_0, \ldots , u_{ \frac{p-1}{2}} \ge 1 \end{array}} \beta _ {u_0, u_0+1} (K_{p^{\alpha -1}}) \left( \prod \limits _{\ell =1}^{\frac{p-1}{2}} \beta _{u_{\ell },u_{\ell }+1} (K_{p^{\alpha -1}, p^{\alpha -1} }) \right) \\= & {} \sum \limits _{\begin{array}{c} u_0+ \cdots + u_{\frac{p-1}{2}} = i \\ u_0, \ldots , u_{ \frac{p-1}{2}} \ge 1 \end{array}} u_0 \left( {\begin{array}{c}p^{\alpha -1}\\ u_0+1\end{array}}\right) \left[ \prod \limits _{\ell =1}^{\frac{p-1}{2}} \left\{ \left( {\begin{array}{c}2p^ {\alpha -1}\\ u_{\ell }+1\end{array}}\right) - 2\left( {\begin{array}{c}p^{\alpha -1}\\ u_{\ell }+1\end{array}}\right) \right\} \right] . \end{aligned}$$

Third, suppose that $1<j-i< \frac{p+1}{2}$. This implies that $j-i=\sum _{k=0}^ {\frac{p-1}{2}} (v_k-u_k) < \frac{p+1}{2}.$ Therefore, there exists $0\le k \le \frac{p-1}{2}$ such that $v_k-u_k<1$. Note that if $\beta _{i, j} (K_{p^ {\alpha - 1}})\ne 0$ then $i=j=0$ or $j=i+1\ge 2$. This is also true for $\beta _{i, j} (K_{p^ {\alpha - 1}, p^ {\alpha - 1}})\ne 0$. Hence, if $1<j-i< \frac{p+1}{2}$, it implies that

$$\begin{aligned}{} & {} \beta _{i,j}(G'(p^{\alpha })) = \sum _{\begin{array}{c} u_0+\cdots +u_{ \frac{p-1}{2}} =i\\ v_0+\cdots +v_{\frac{p-1}{2}}=j \end{array}} \beta _{u_0,v_0}(K_{p^{\alpha -1}}) \left\{ \prod _{k=1}^{\frac{p-1}{2}} \beta _{u_k,v_k} (K_{ p^{\alpha -1}, p^{\alpha -1}})\right\} \\{} & {} \hspace{1em}= \sum _{\begin{array}{c} u_0+\cdots +u_{ \frac{p-1}{2}} =i\\ v_0+\cdots +v_{\frac{p-1}{2}}=j \\ u_{\ell }=v_{\ell }=0 \text { or } v_{\ell }=u_{\ell }+1\ge 2\\ |\{0\le \ell \le \frac{p-1}{2}\mid v_{\ell }=u_{\ell }+1\ge 2\}|=j-i \end{array}} \beta _{u_0,v_0}(K_{p^{\alpha -1}}) \left\{ \prod _{k=1}^{\frac{p-1}{2}} \beta _{u_k,v_k} (K_{ p^{\alpha -1}, p^{\alpha -1}})\right\} . \end{aligned}$$

Hence, we obtain that

$$\begin{aligned} \beta _{i,j}(G'(p^{\alpha }))= & {} \sum _{\begin{array}{c} u_1+\cdots +u_{ \frac{p-1}{2}} =i\\ v_1+\cdots +v_{\frac{p-1}{2}}=j \\ u_0=v_0=0\\ u_{\ell }=v_{\ell }=0 \text { or } v_{\ell }=u_{\ell }+1\ge 2\\ |\{1\le \ell \le \frac{p-1}{2}\mid v_{\ell }=u_{\ell }+1\ge 2\}|=j-i \end{array}} \beta _{u_0,v_0}(K_{p^{\alpha -1}}) \left\{ \prod _{k=1}^{\frac{p-1}{2}} \beta _{u_k,v_k} (K_{ p^{\alpha -1}, p^{\alpha -1}})\right\} \\{} & {} \quad + \sum _{\begin{array}{c} u_0+\cdots +u_{ \frac{p-1}{2}} =i\\ v_0+\cdots +v_{\frac{p-1}{2}}=j \\ v_0=u_0+1\ge 2\\ u_{\ell }=v_{\ell }=0 \text { or } v_{\ell }=u_{\ell }+1\ge 2\\ |\{1\le \ell \le \frac{p-1}{2}\mid v_{\ell }=u_{\ell }+1\ge 2\}|=j-i-1 \end{array}} \beta _{u_0,v_0}(K_{p^{\alpha -1}}) \left\{ \prod _{k=1}^{\frac{p-1}{2}} \beta _{u_k,v_k} (K_{ p^{\alpha -1}, p^{\alpha -1}})\right\} . \end{aligned}$$

Since $\beta _{0,0}(K_{p^{\alpha -1}})=1$ and $\beta _{u_0,u_0+1}(K_{p^{\alpha -1}}) =u_0\left( {\begin{array}{c}p^{\alpha -1}\\ u_0+1\end{array}}\right)$, we obtain that

$$\begin{aligned} \beta _{i,j}(G'(p^{\alpha }))= & {} \sum _{\begin{array}{c} u_1+\cdots +u_{ \frac{p-1}{2}} =i\\ v_1+\cdots +v_{\frac{p-1}{2}}=j \\ u_{\ell }=v_{\ell }=0 \text { or } v_{\ell }=u_{\ell }+1\ge 2\\ |\{1\le \ell \le \frac{p-1}{2}\mid v_{\ell }=u_{\ell }+1\ge 2\}|=j-i \end{array}} \prod _{k=1}^{\frac{p-1}{2}} \beta _{u_k,v_k} (K_{ p^{\alpha -1}, p^{\alpha -1}}) \\{} & {} \quad + \sum _{\begin{array}{c} u_0+\cdots +u_{ \frac{p-1}{2}} =i\\ v_0+\cdots +v_{\frac{p-1}{2}}=j \\ v_0=u_0+1\ge 2\\ u_{\ell }=v_{\ell }=0 \text { or } v_{\ell }=u_{\ell }+1\ge 2\\ |\{1\le \ell \le \frac{p-1}{2}\mid v_{\ell }=u_{\ell }+1\ge 2\}|=j-i-1 \end{array}} u_0\left( {\begin{array}{c}p^{\alpha -1}\\ u_0+1\end{array}}\right) \left\{ \prod _{k=1}^{\frac{p-1}{2}} \beta _{u_k,v_k} (K_{ p^{\alpha -1}, p^{\alpha -1}})\right\} \\{} & {} = \left( {\begin{array}{c}\frac{p-1}{2}\\ j-i\end{array}}\right) \sum \limits _{\begin{array}{c} u_1 + \cdots + u_{j-i} = i \\ u_1, \ldots , u_{j-i} \ge 1 \end{array}} \left[ \prod \limits _{k=1}^{j-i} \left\{ \left( {\begin{array}{c}2p^{\alpha -1}\\ u_{k}+1\end{array}}\right) -2 \left( {\begin{array}{c}p^{\alpha -1}\\ u_{k}+1\end{array}}\right) \right\} \right] \\{} & {} \hspace{1em} + \left( {\begin{array}{c}\frac{p-1}{2}\\ j-i-1\end{array}}\right) \sum \limits _{\begin{array}{c} u_0 + \cdots + u_{j-i-1} = i \\ u_0, \ldots , u_{j-i-1} \ge 1 \end{array}} u_0\left( {\begin{array}{c}p^{\alpha -1}\\ u_0+1\end{array}}\right) \\{} & {} \hspace{1em}\left[ \prod \limits _{k=1}^{j-i-1} \left\{ \left( {\begin{array}{c}2p^{\alpha -1}\\ u_{k}+1\end{array}}\right) -2 \left( {\begin{array}{c}p^{\alpha -1}\\ u_{k}+1\end{array}}\right) \right\} \right] . \end{aligned}$$

Forth, suppose that $j-i>\frac{p+1}{2}$. Therefore, there exists $0\le k \le \frac{p-1}{2}$ such that $v_k>u_k+1$. This implies that $\beta _{u_k,v_k}(H)= 0$, where H is either the complete graph $K_{p^{\alpha -1}}$ or the complete bipartite graph $K_{p^{\alpha -1}, p^{\alpha -1}}$. Now, by Eq. 1, we obtain that $\beta _{i,j} (G'(p^{\alpha })) = 0$, and so, the proof is completed. $\square$

As an immediate corollary, we obtain that

Corollary 4.7

If p is an odd prime and $\alpha > 1$ is an integer, then ${{\,\textrm{reg}\,}}(G'(p^{\alpha })) = \frac{p+1}{2} \text { and } {{\,\textrm{pd}\,}}(G'(p^{\alpha })) = p^{\alpha } -\frac{p+1}{2}.$

We close this paper with the following example.

Example 4.8

Consider the graph $G=G'(3^2)$. By Theorem 4.6, we obtain

$$\begin{aligned} \beta _{i,i+1}(G)= & {} i\left( {\begin{array}{c}3\\ i+1\end{array}}\right) + \left\{ \left( {\begin{array}{c}6\\ i+1\end{array}}\right) - 2\left( {\begin{array}{c}3\\ i+1\end{array}}\right) \right\} \\= & {} (i-2)\left( {\begin{array}{c}3\\ i+1\end{array}}\right) + \left( {\begin{array}{c}6\\ i+1\end{array}}\right) . \end{aligned}$$

Moreover, $\beta _{i,i+2}(G) = \sum _{\begin{array}{c} i_0+i_1=i\\ i_0,i_1\ge 1 \end{array}} i_0\left( {\begin{array}{c}3\\ i_0+1\end{array}}\right) \left\{ \left( {\begin{array}{c}6\\ i_1+1\end{array}}\right) - 2\left( {\begin{array}{c}3\\ i_1+1\end{array}}\right) \right\} .$ Thus, we obtain the Betti table of G as follows:

$$\begin{aligned} \begin{array}{rccccccccc} &{} 0 &{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 &{} 7 \\ total: &{}1&{} 12&{} 47&{} 87&{} 87&{} 49&{} 15&{} 2 \\ 0: &{} 1 &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ 1: &{} \cdot &{} 12 &{} 20 &{} 15 &{} 6 &{} 1 &{} \cdot &{} \cdot \\ 2: &{} \cdot &{} \cdot &{} 27 &{} 72 &{} 81 &{} 48 &{} 15 &{} 2 \end{array} \end{aligned}$$