1 Introduction

Let \(G=(V(G), E(G))\) be a simple graph (without loops or multiple edges), \(V(G)=\{v_1, v_2, \ldots , v_n\}\), A(G) its (0, 1)-adjacency matrix with \(a_{ij}=1\) if \(v_i\) and \(v_j\) are adjacent and 0 otherwise. Since A(G) is symmetric, its eigenvalues are real and they can be indexed in a non-increasing order as \(\lambda _1(G)\ge \lambda _2(G)\ge \cdots \ge \lambda _n(G)\). We write \(\sigma (G)\) to denote the spectrum of G, i.e. the multiset of eigenvalues of G.

Threshold graphs are \(\{2K_2, P_4, C_4\}\)-free graphs. In the spectral graph theory, they feature as connected graphs with largest eigenvalue with respect to adjacency and signless Laplacian spectrum within the connected graphs of fixed order and size. They are also known as nested split graphs (in [21, 22]). Recently, spectral properties of threshold graphs with respect to adjacency, signless Laplacian and distance spectrum were studied in [2, 4, 8, 10]. Numerous applications of threshold graphs, ranging from computer science to psychology can be found in [20]. In addition, threshold graphs are related to a very important combinatorial object: Ferrers diagram, since their non-zero Laplacian eigenvalues are equal to the number of boxes in each column of the Ferrers diagram corresponding to the sequence of vertex degrees (see [3]).

Fig. 1
figure 1

A sketch of a threshold graph \({\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\)

Full size image

The structure of a threshold graph is illustrated in Fig. 1. The set of vertices consists of two subsets, U and V, with vertices in U forming an independent set and vertices in V forming a clique. In addition, both U and V are partitioned into h subsets, say \(U=\bigcup _{i=1}^h U_i\) and \(V=\bigcup _{i=1}^h V_i\). The cross edges are added according to the following rule: all vertices in \(U_k\), \(1\le k\le h\) are adjacent to all vertices in \(\bigcup _{i=k}^h V_i\). They are uniquely determined by the parameters, \(t_i, s_i, 1\le i\le h\), where \(|U_i|=t_i\) and \(|V_i|=s_i\). The respective graph is denoted by \({\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\).

The problem of finding graphs with large gap sets has recently attracted a great deal of attention. Kollár and Sarnak [18] studied gaps in the spectra of large finite cubic graphs. This topic was afterwards investigated in [1], where the large gap sets in the spectra of cubic and quartic graphs with the minimum spectral gap were identified for two infinite families of these types of graphs. (The spectral gap is the difference \(\lambda _1(G)- \lambda _2(G)\).) Also the applications of large graphs with gaps in their spectra come from different areas. In combinatorics and engineering “cubic expanders” are defined by gaps [15]. In [17] on microwave coplanar waveguide resonators gap at the bottom \(-3\) is of the interest. In chemistry, for the case of closed shells, the stability properties of carbon fullerene molecules are closely related to gap at 0 [12]. Our goal is to determine what gaps can be achieved by threshold graphs and to identify the corresponding graphs. In other words, we pursue this problem to the class of threshold graphs.

We show that for any positive real number \(R>\frac{1}{2}(-1+\sqrt{2})\), there exist infinitely many connected graphs with the gap interval that is of the length at least R. This result can be considered as a contribution to the theory of graph limit points due to Hoffman [14] who investigated the density of graphs’ eigenvalues on the real line. In particular, we show that the sequence of the least positive eigenvalues (resp. largest negative eigenvalues different from \(-1\)) of the sequence of threshold graphs of the form \(G_h={\textrm{NSG}}(t_1, \ldots , t_h; s_1, \ldots , s_h)\) converges. Here, \(G_{h+1}\) is obtained from \(G_h\) by adding \(t_{h+1}\), (resp. \(s_{h+1}\)) vertices in \(U_{h+1}\), (resp. \(V_{h+1}\)). We characterize the limit points for the threshold graphs of the form

$$\begin{aligned} {\textrm{NSG}}(\underbrace{t_1, \ldots ,t_{k-1}, t_k, \ldots , t_k}_h;\underbrace{s_1, \ldots , s_{k-1}, s_k, \ldots , s_k}_h), \end{aligned}$$

where the number of cells h tends to \(\infty \). We show that the corresponding limit point is the least positive (resp. largest negative \(\ne -1\)) solution of certain equation. Our results confirm those of [13] where it was shown that \(\frac{1}{2}(-1-\sqrt{2})\) and \(\frac{1}{2}(-1+\sqrt{2})\) are the limit points of the least positive (resp. largest negative) eigenvalue of the sequence of antiregular graphs \({\textrm{NSG}}(\underbrace{1, \ldots , 1}_h;\underbrace{1, \ldots , 1}_h)\), when \(h\rightarrow \infty \).

Recently in [5] an algorithm for constructing I-free threshold graphs, i.e. the threshold graphs without any eigenvalues in a given interval I was presented. The content of this paper can be considered as an alternative approach towards the same problem.

The structure of the paper is as follows. Preliminary results are reported in Sect. 2. Results on eigenvalue gaps of threshold graphs, both positive and negative, are the content of Sect. 3. Sequences of threshold graphs, corresponding sequences of least positive (resp. largest negative) eigenvalues along with their properties are subject of Sect. 4. A conclusion and possible extensions are presented in final Sect. 5.

2 Preliminaries

An explicit formula for calculating the characteristic polynomial of a threshold graph \(G={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\) was obtained in [10, 19]. It reads the following.

Lemma 2.1

( [10]) Let \(G={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\) and let \(\phi (x;G)\) be its characteristic polynomial. Then,

$$\begin{aligned} \phi (x;G)=x^{\sum _{i=1}^h t_i-h}(x+1)^{\sum _{i=1}^h s_i-h}\det N^h_G(x), \end{aligned}$$

where

$$\begin{aligned} N^h_G(x) =\left( \begin{array}{ccccccc} x+t_1 &{} x+1 &{} &{} &{} &{} \\ x &{} s_1 &{} x&{} &{}&{}\\ &{} x+1&{} t_2 &{} x+1 &{} &{} \\ &{}&{} &{} &{} &{} \\ &{}&{}\ddots &{}\ddots &{} \ddots &{}\\ &{} &{} &{}&{}&{} \\ &{} &{} &{}x+1&{}t_h&{} x+1\\ &{}&{}&{} &{}x &{} s_h \end{array} \right) _{2h} \end{aligned}$$

The eigenvalues of G different from 0 and \(-1\) (except the case when \(t_1=1\)) are the eigenvalues of the corresponding divisor matrix

$$\begin{aligned} D_h(G)=\left( \begin{array}{cccc|cccc} &{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_h\\ &{}&{}&{}&{}&{}s_2&{}\cdots &{}s_h\\ &{}&{}&{}&{}&{}&{}\ddots &{}\vdots \\ &{}&{}&{}&{}&{}&{}&{}s_h\\ \hline t_1&{}&{}&{}&{}s_1-1&{}s_2&{}\cdots &{}s_h\\ t_1&{}t_2&{}&{}&{}s_1&{}s_2-1&{}\cdots &{}s_h\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_h&{}s_1&{}s_2&{}\cdots &{}s_h-1 \end{array}\right) _{2h}, \end{aligned}$$

due to the equitable partition \({\mathcal {D}}(G): U_1\cup \cdots \cup U_h\cup V_1\cup \cdots \cup V_h\). If \(t_1=1\), then \(-1\) is a simple eigenvalue of \(D_h(G)\). The characteristic polynomial of \(D_h(G)\) up to the sign is equal to \(\det N^h_G(x)\).

For a threshold graph \(G={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\) the following gap interval was identified in [10].

Theorem 2.2

([10])

$$\begin{aligned} Let G&={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h),\\ N_h&=\dfrac{1}{\cos ^2(\frac{\pi }{2\,h+1})}\min _{2\le i\le 2\,h-1}a_ia_{i+1} \end{aligned}$$

and \(c_1=\dfrac{s_1}{4\cos ^2 (\frac{\pi }{2\,h+1})}\), where \((a_1,a_2,\ldots , a_{2\,h-1},a_{2\,h})=(t_1,s_1,\ldots , t_{h},s_h)\). Then,

  • if \(t_1=1\), then G does not have any eigenvalue in

    $$\begin{aligned} \left( \dfrac{1}{2}\left( -1-\sqrt{1+N_h}\right) ,\min \left\{ \dfrac{1}{2}(-1+\sqrt{1+N_h}), c_1\right\} \right) \end{aligned}$$

    except possibly \(-1\) and 0.

  • otherwise, G does not have any eigenvalue in \((l_h, r_h)\), where

    $$\begin{aligned} l_h=\max \left\{ \frac{1}{2}\left( -1-\sqrt{1+N_h}\right) ,\frac{1}{2}\left( -1+c_1-\sqrt{(-1+c_1)^2+4c_1t_1}\right) \right\} \end{aligned}$$

    and

    $$\begin{aligned}{} & {} r_h=\min \left\{ \frac{1}{2}(-1+\sqrt{1+N_h}), \dfrac{1}{2}\left( -1+c_1+\sqrt{(-1+c_1)^2+4c_1t_1}\right) \right\} ,\\{} & {} \quad {except~ possibly} -1~ {and}~ 0. \end{aligned}$$

As a consequence it has been proved that no threshold graph has eigenvalues in \((\frac{-1-\sqrt{2}}{2},\frac{-1+\sqrt{2}}{2})\). We point out that a similar problem in the context of signed graphs was considered in [9].

3 Gap Intervals in Threshold Graphs

In this section, we show that there exist infinitely many threshold graphs with prescribed gap interval of the form (0, R) or \((L, \frac{1}{2}(-1-\sqrt{2}))\). For the positive eigenvalue-free intervals, we first provide a refinement of the results of Theorem 2.2.

Theorem 3.1

Let \(G={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\) and let

$$\begin{aligned} N_h=\dfrac{1}{\cos ^2\big (\frac{\pi }{2h+1}\big )}\min _{1\le i\le 2h-1}a_ia_{i+1}, \end{aligned}$$

where \((a_1,a_2,\ldots , a_{2\,h-1},a_{2\,h})=(t_1,s_1,\ldots , t_{h},s_h)\). Then, G does not have any eigenvalue in \((0, \frac{1}{2}(-1+\sqrt{1+N_h}))\).

Proof

We first observe that \(\det N^h_G(x)\) equals to

$$\begin{aligned} \det \left( \begin{array}{ccccccc} t_1 &{} x+1 &{} &{} &{} &{} \\ x &{} s_1 &{} x&{} &{}&{}\\ &{} x+1&{} t_2 &{} x+1 &{} &{} \\ &{}&{} &{} &{} &{} \\ &{}&{}\ddots &{}\ddots &{} \ddots &{}\\ &{} &{} &{}&{}&{} \\ &{} &{} &{}x+1&{}t_h&{} x+1\\ &{}&{}&{} &{}x &{} s_h \end{array} \right) _{2h}+x\det \left( \begin{array}{cccccc} s_1 &{} x&{} &{}&{}\\ x+1&{} t_2 &{} x+1 &{} &{} \\ &{} &{} &{} &{} \\ &{}\ddots &{}\ddots &{} \ddots &{}\\ &{} &{}&{}&{} \\ &{} &{}x+1&{}t_h&{} x+1\\ &{}&{} &{}x &{} s_h \end{array} \right) _{2h-1}. \end{aligned}$$

By [7, Proposition 2.2], the previous two matrices are positive definite if \(x(x+1)<\frac{N_h}{4}\). If we assume that \(x>0\), then \(\det N^h_G(x)>0\) provided that \(x< \frac{1}{2}\left( -1+\sqrt{1+N_h}\right) \). This completes the proof. \(\square \)

Based on Theorem 3.1, we can construct a threshold graph with an arbitrary large positive gap interval.

Theorem 3.2

Let \(R>\frac{1}{2}(-1+\sqrt{2})\) be a positive real number and

$$\begin{aligned} M_h=\Big \lceil 4R(R+1)\cos ^2 \big (\frac{\pi }{2h+1}\big )\Big \rceil . \end{aligned}$$

Then, a threshold graph \({\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\) has gap interval (0, R), provided that \(t_1s_1, t_is_i, t_is_{i-1}\ge M_h\), for any \(2\le i\le h\).

Proof

Let \(G={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\). Then, following the notation of Theorem 2.2, G has gap interval (0, R) provided that

$$\begin{aligned} R&<\frac{1}{2}(-1+\sqrt{1+N_h}) \end{aligned}$$

holds, i.e.

$$\begin{aligned} 4R(R+1)&<N_h. \end{aligned}$$

The previous inequality is equivalent to

$$\begin{aligned} \min _{2\le i\le h}\{t_1s_1, t_is_i, t_is_{i-1}\}>4\cos ^2\big (\frac{\pi }{2h+1}\big )R(R+1). \end{aligned}$$

\(\square \)

Corollary 3.3

Let \(R>\frac{1}{2}(-1+\sqrt{2})\) be a real number, \(a_1=t_1\) positive integer and

$$\begin{aligned} a_i\ge \Big \lceil \dfrac{4R(R+1)\cos ^2 (\frac{\pi }{2h+1})}{a_{i-1}}\Big \rceil , \quad \text{ for } \quad 2\le i\le 2h. \end{aligned}$$

Then, a threshold graph \({\textrm{NSG}}(a_1, \ldots , a_{2\,h-1}; a_2, \ldots ,a_{2\,h})\) has gap interval (0, R).

The choice of \(a_{2h}\) in the above corollary is constrained by the condition \(a_{2h-1}a_{2h}>4R(R+1)\cos ^2 (\frac{\pi }{2h+1})\), which guarantees infinitely many possibilities. This fact yields our main result.

Theorem 3.4

For any real number \(R>\frac{1}{2}(-1+\sqrt{2})\), there exist infinitely many threshold graphs with gap interval (0, R).

Taking into account that \(\cos ^2 (\frac{\pi }{2h+1})\) is increasing function in h that approaches to 1 as h tends to infinity, the following corollary easily follows.

Corollary 3.5

Let \(R>\frac{1}{2}(-1+\sqrt{2})\), \(a_1=t_1\) positive integer and

$$\begin{aligned} s_1=\Big \lceil \dfrac{4R(R+1)}{t_1}\Big \rceil . \end{aligned}$$

Then, a threshold graph \(G={\textrm{NSG}}(\underbrace{t_1, \ldots ,t_1}_h;\underbrace{s_1, \ldots ,s_1}_h)\) has no eigenvalues in (0, R), for any \(h\ge 1\).

Example 3.1

Let \(R=4.8\), \(h=4\). Then,

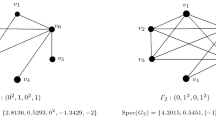
$$\begin{aligned} M_4=\Big \lceil 4\cdot 4.8\cdot 5.8\cos ^2 (\frac{\pi }{9})\Big \rceil =99. \end{aligned}$$

The threshold graph \(G={\textrm{NSG}}(99,99,99,99;1,1,1,1)\) has no eigenvalues in (0, 4.8) (\(\lambda _4(G)=4.824\)). Also the threshold graph \(G'={\textrm{NSG}}(11,11,11,11;9,9,9,9)\) satisfies the same property (\(\lambda _4(G)=4.85426\)). We stress out that the condition of Theorem 3.2 is not necessary. For example, the threshold \(G''={\textrm{NSG}}(8,11,11,11;9,9,9,9)\) has no eigenvalue in (0, 4.83611), even though \(\min _{2\le i\le 4} \{t_1s_1, t_is_i, t_{i}s_{i-1}\}=72<99\).

Remark 3.1

By the interlacing theorem (see [11, p.17]), if \(t_h'<t_h\), then

$$\begin{aligned} \lambda _h( {\textrm{NSG}}(t_1, \ldots ,t_h';s_1, \ldots ,s_h))\le \lambda _h( {\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)). \end{aligned}$$

Note that by [2], both graphs have exactly h positive eigenvalues, i.e. \(\lambda _h\) denotes the least positive eigenvalue in both graphs. This property can help in adjusting gap intervals. For example, \(\lambda _4({\textrm{NSG}}(99,99,99,95;1,1,1,1))=4.80237.\)

In the sequel, we focus on negative gap intervals.

Theorem 3.6

Let \(L<\frac{1}{2}(-1-\sqrt{2})\) be a real number, \(a_1=t_1\) a positive integer, and

$$\begin{aligned} a_i\ge \Big \lceil \dfrac{4L(L+1)\cos ^2 \big (\frac{\pi }{2h+1}\big )}{a_{i-1}}\Big \rceil , \quad {\text{ f }or} \quad 2\le i\le 2h. \end{aligned}$$

Then, a threshold graph \({\textrm{NSG}}(a_1, \ldots , a_{2\,h-1}; a_2, \ldots ,a_{2\,h})\) has gap interval \((L, \frac{1}{2}(-1-\sqrt{2}))\), provided that \(a_2\ge \lceil \frac{4L(L+1)\cos ^2{\big (\frac{\pi }{2h+1}}\big )}{L+t_1}\rceil \) for \(t_1\ne 1\).

Proof

We follow the notation and results of Theorem 2.2.

Let \(t_1=1\). Then, if \(L>\frac{1}{2}(-1-\sqrt{1+N_h})\), i.e. if

$$\begin{aligned} \min _{2\le i\le 2h-1}\{a_ia_{i+1}\}>4L(L+1)\cos ^2{\big (\frac{\pi }{2h+1}\big )}, \end{aligned}$$

then a threshold graph \({\textrm{NSG}}(a_1, \ldots , a_{2h-1}; a_2, \ldots ,a_{2h})\) has no eigenvalues in \((L, \frac{1}{2}(-1-\sqrt{2}))\).

Similarly, if \(t_1>1\), then \(L>\frac{1}{2}(-1+c_1-\sqrt{(-1+c_1)^2+4c_1t_1})\), i.e. \(L(L+1)<c_1(L+t_1)\) gives that \(a_2=s_1\ge \lceil \frac{4L(L+1)\cos ^2{\big (\frac{\pi }{2h+1}}\big )}{L+t_1}\rceil ,\) provided that \(L+t_1>0\). Together with \(L>\frac{1}{2}(-1-\sqrt{1+N_h})\), we obtain

$$\begin{aligned} a_{i}\ge \Big \lceil \frac{4L(L+1)\cos ^2{\big (\frac{\pi }{2h+1}}\big )}{a_{i-1}}\Big \rceil ,\quad { \text{ for }}\quad 3\le i\le 2h. \end{aligned}$$

\(\square \)

Remark 3.2

One of the requirements in the previous proof, due to non-negativity of \(L(L+1)\), is \(L+t_1>0\), which implies that \(L>-t_1\).

Example 3.2

Let \(L=-4.8\) and \(h=4.\) Then, \(\lceil 4\,L(L+1)\cos ^2 (\frac{\pi }{9})\rceil =65\) and the threshold graph \({\textrm{NSG}}(65,65,65,65;1,1,1,1)\) has the largest negative eigenvalue different from \(-1\) approximately equal to \(-4.80968\).

4 Sequences of Threshold Graphs

In this section, we consider the sequence of threshold graphs \((G_h)_{h\in {\mathbb {N}}}\), where \(G_h={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\) and \(G_{h+1}={\textrm{NSG}}(t_1, \ldots ,t_h, t_{h+1};s_1, \ldots ,s_h, s_{h+1})\). This sequence can be seen as a growing sequence, in the sense that \(G_h\) is an induced subgraph of \(G_{h+1}\). We denote by \(\tau (G)\) the smallest positive eigenvalue of G and by \(\theta (G)\) the largest negative eigenvalue different from \(-1\). We first deduce the following lemma.

Lemma 4.1

Let \(G={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\) and \(G'={\textrm{NSG}}(t_1, \ldots ,t_h, t_{h+1};s_1, \ldots ,s_h, s_{h+1})\). Then, \(\tau (G')\le \tau (G)\) and \(\theta (G)\le \theta (G')\).

Proof

By [19] any eigenvalue of G (resp. \(G'\)) different from \(0,-1\) is an eigenvalue of the divisor matrix \(D_h(G)\) (resp. \(D_{h+1}(G')\)) as well. Therefore, \(\tau (G)\) is an eigenvalue of \(D_h(G)\), while \(\tau (G')\) is eigenvalue of \(D_{h+1}(G')\). In addition \(D_h(G)\) and \(D_{h+1}(G')\) are symmetrizable. For

$$\begin{aligned} P_h(G)={\textrm{diag}}\left( \sqrt{t_1},\ldots , \sqrt{t_h},\sqrt{s_1},\ldots , \sqrt{s_h}\right) \end{aligned}$$

we obtain \(D^s_h(G)=P_h(G)D_h(G)(P_h(G))^{-1}\) with

$$\begin{aligned} D^s_h(G)=\left( \begin{array}{cccc|cccc} &{}&{}&{}&{}\sqrt{t_1s_1}&{}\sqrt{t_1s_2}&{}\cdots &{}\sqrt{t_1s_h}\\ &{}&{}&{}&{}&{}\sqrt{t_2s_2}&{}\cdots &{}\sqrt{t_2s_h}\\ &{}&{}&{}&{}&{}&{}\ddots &{}\vdots \\ &{}&{}&{}&{}&{}&{}&{}\sqrt{t_hs_h}\\ \hline \sqrt{t_1s_1}&{}&{}&{}&{}s_1-1&{}\sqrt{s_1s_2}&{}\cdots &{}\sqrt{s_1s_h}\\ \sqrt{t_1s_2}&{}\sqrt{t_2s_2}&{}&{}&{}\sqrt{s_1s_2}&{}s_2-1&{}\cdots &{}\sqrt{s_2s_h}\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ \sqrt{t_1s_h}&{}\sqrt{t_2s_h}&{}\cdots &{}\sqrt{t_hs_h}&{}\sqrt{s_1s_h}&{}\sqrt{s_2s_h}&{}\cdots &{}s_h-1 \end{array}\right) , \end{aligned}$$

and similarly for \(D^s_{h+1}(G')=P_{h+1}(G')D_{h+1}(G')(P_{h+1}(G'))^{-1}\). By deleting the last row and the last column in \(D^s_{h+1}(G')\), we obtain the matrix \(C^s_h(G')\) with zero \((h+1)\)-th row and column, while the remaining submatrix is equal to \(D^s_h(G)\). Its spectrum is comprised from 0 and simple eigenvalues of \(D^s_h(G)\). The statement of the lemma follows by the interlacing theorem ( [11]), taking into account that, if \(t_1\ne 1\) in both graphs remaining eigenvalues, other from those of \(D^s_h(G),D^s_{h+1}(G')\) are only 0 and \(-1\) with certain multiplicities. Case \(t_1=1\) is treated in a similar fashion.

Therefore, \(\tau (G')\le \tau (G)\) and \(\theta (G)\le \theta (G')\). \(\square \)

By the previous lemma, we easily deduce the monotonicity of \((\tau (G_h))_{h\in {\mathbb {N}}}\) and \((\theta (G_h))_{h\in {\mathbb {N}}}\) for threshold graphs built on same initial cells.

Theorem 4.2

Let \(\{t_h\}_{h\in {\mathbb {N}}}\), \(\{s_h\}_{h\in {\mathbb {N}}}\) be sequences of positive integers and \(G_h={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\). Then, the sequences \((\tau (G_h))_{h\in {\mathbb {N}}}\) and \((\theta (G_h))_{h\in {\mathbb {N}}}\) are convergent.

Proof

By Lemma 4.1, the sequence \((\tau (G_h))_{h\in {\mathbb {N}}}\) is non-increasing, and by [10, Corollary 5.5], it is bounded below by \(\frac{1}{2}(-1+\sqrt{2})\). Therefore, it is convergent. On the other hand \((\theta (G_h))_{h\in {\mathbb {N}}}\) is non-decreasing and bounded above by \(\frac{1}{2}(-1-\sqrt{2})\). \(\square \)

A natural question that arises in this context is about possible limit points. We show that they can be determined in some particular cases. For this purpose, we first provide a recurrence relation to compute the characteristic polynomial of threshold graphs. We point out that several approaches for the computation of the characteristic polynomial of a threshold graph have been already published (see for example [6, 10, 19]). However, the one presented in the sequel is an original contribution.

Theorem 4.3

Let \(G_h={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\). Then, its characteristic polynomial \(\phi (x,G_h)\) is equal to

$$\begin{aligned} \phi (x,G_h)=x^{\sum _{i=1}^h t_i-h}(x+1)^{\sum _{i=1}^h s_i-h} \Delta _h(x), \end{aligned}$$

where \(\Delta _h(x)=\det (D_h(G_h)-xI_{2h})\) satisfies the recurrence relation

$$\begin{aligned} \Delta _h(x)=\Big (\frac{s_{h-1}+s_h}{s_{h-1}}x(x+1)-t_hs_h\Big )\Delta _{h-1}-\frac{s_h}{s_{h-1}}x^2(1+x)^2\Delta _{h-2}(x) \end{aligned}$$
(4.1)

with the initial conditions

$$\begin{aligned} \Delta _0(x)= & {} 1, \end{aligned}$$
(4.2)
$$\begin{aligned} \Delta _1(x)= & {} \det \begin{pmatrix} -x&{}s_1\\ t_1&{}s_1-1-x \end{pmatrix}=x^2-(s_1-1)x-t_1s_1. \end{aligned}$$
(4.3)

Proof

By expanding the determinant of

$$\begin{aligned} D_h(G)-xI_{2h}=\left( \begin{array}{cccc|cccc} -x&{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_h\\ &{}-x&{}&{}&{}&{}s_2&{}\cdots &{}s_h\\ &{}&{}\ddots &{}&{}&{}&{}\ddots &{}\vdots \\ &{}&{}&{}-x&{}&{}&{}&{}s_h\\ \hline t_1&{}&{}&{}&{}s_1-1-x&{}s_2&{}\cdots &{}s_h\\ t_1&{}t_2&{}&{}&{}s_1&{}s_2-1-x&{}\cdots &{}s_h\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_h&{}s_1&{}s_2&{}\cdots &{}s_h-1-x \end{array}\right) _{2h} \end{aligned}$$

along the h-th row, we obtain

$$\begin{aligned} \Delta _h(x)=(-x)\det T_h(x) + (-1)^{3h}s_h\det S_h(x), \end{aligned}$$

where

$$\begin{aligned} T_h(x)=\left( \begin{array}{cccc|ccccc} -x&{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}&{}s_h\\ &{}-x&{}&{}&{}&{}s_2&{}\cdots &{}s_{h-1}&{}s_h\\ &{}&{}\ddots &{}&{}&{}&{}\ddots &{}\vdots &{}\vdots \\ &{}&{}&{}-x&{}&{}&{}&{}s_{h-1}&{}s_h\\ \hline t_1&{}&{}&{}&{}s_1-1-x&{}s_2&{}\cdots &{}s_{h-1}&{}s_h\\ t_1&{}t_2&{}&{}&{}s_1&{}s_2-1-x&{}\cdots &{}s_{h-1}&{}s_h\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}-1-x&{}s_h\\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}&{}s_h-1-x \end{array}\right) _{(2h-1)} \end{aligned}$$

while

$$\begin{aligned} S_h(x)=\left( \begin{array}{ccccc|cccc} -x&{}&{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}\\ &{}-x&{}&{}&{}&{}&{}s_2&{}\cdots &{}s_{h-1}\\ &{}&{}\ddots &{}&{}&{}&{}&{}\ddots &{}\vdots \\ &{}&{}&{}-x&{}0&{}&{}&{}&{}s_{h-1}\\ \hline t_1&{}&{}&{}&{}&{}s_1-1-x&{}s_2&{}\cdots &{}s_{h-1}\\ t_1&{}t_2&{}&{}&{}&{}s_1&{}s_2-1-x&{}\cdots &{}s_{h-1}\\ \vdots &{}&{}\ddots &{}&{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}-x\\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}t_h&{}s_1&{}s_2&{}\cdots &{}s_{h-1} \end{array}\right) _{(2h-1)}. \end{aligned}$$

Next in \(T_h(x)\), we perform the following operations:

  • \(C_{2h-1}\leftarrow C_{2h-1}+C_{2h-2}\) and we obtain

    $$\begin{aligned} \left( \begin{array}{cccc|ccccc} -x&{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ &{}-x&{}&{}&{}&{}s_2&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ &{}&{}\ddots &{}&{}&{}&{}\ddots &{}\vdots &{}\vdots \\ &{}&{}&{}-x&{}&{}&{}&{}s_{h-1}&{}s_{h-1}+s_h\\ \hline t_1&{}&{}&{}&{}s_1-1-x&{}s_2&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ t_1&{}t_2&{}&{}&{}s_1&{}s_2-1-x&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}-1-x&{}s_{h-1}+s_h-1-x\\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h-1-x \end{array}\right) _{(2h-1)}. \end{aligned}$$

  • \(R_{2h-1}\leftarrow R_{2h-1}-R_{2h-2}\) This leads to

    $$\begin{aligned} \left( \begin{array}{cccc|ccccc} -x&{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ &{}-x&{}&{}&{}&{}s_2&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ &{}&{}\ddots &{}&{}&{}&{}\ddots &{}\vdots &{}\vdots \\ &{}&{}&{}-x&{}&{}&{}&{}s_{h-1}&{}s_{h-1}+s_h\\ \hline t_1&{}&{}&{}&{}s_1-1-x&{}s_2&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ t_1&{}t_2&{}&{}&{}s_1&{}s_2-1-x&{}\cdots &{}s_{h-1}&{}s_{h-1}+s_h\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}-1-x&{}s_{h-1}+s_h-1-x\\ 0&{}0&{}\cdots &{}0&{}0&{}0&{}\cdots &{}1+x&{}0 \end{array}\right) _{(2h-1)}. \end{aligned}$$

  • \(C_{2h-1}\leftarrow C_{2h-1}-\frac{s_{h-1}+s_h}{s_{h-1}}C_{2h-2}\) The resulting matrix is:

    $$\begin{aligned} \left( \begin{array}{cccc|ccccc} -x&{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}&{}0\\ &{}-x&{}&{}&{}&{}s_2&{}\cdots &{}s_{h-1}&{}0\\ &{}&{}\ddots &{}&{}&{}&{}\ddots &{}\vdots &{}\vdots \\ &{}&{}&{}-x&{}&{}&{}&{}s_{h-1}&{}0\\ \hline t_1&{}&{}&{}&{}s_1-1-x&{}s_2&{}\cdots &{}s_{h-1}&{}0\\ t_1&{}t_2&{}&{}&{}s_1&{}s_2-1-x&{}\cdots &{}s_{h-1}&{}0\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}-1-x&{}\frac{s_h}{s_{h-1}}(x+1)\\ 0&{}0&{}\cdots &{}0&{}0&{}0&{}\cdots &{}x+1&{}-\frac{s_{h-1}+s_h}{s_{h-1}}(x+1) \end{array}\right) _{(2h-1)}. \end{aligned}$$

  • \(C_{2h-2}\leftarrow C_{2h-2}+\frac{s_{h-1}}{s_{h-1}+s_h}C_{2h-1}\) Finally, we obtain

    $$\begin{aligned} \left( \begin{array}{cccc|ccccc} -x&{}&{}&{}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}&{}0\\ &{}-x&{}&{}&{}&{}s_2&{}\cdots &{}s_{h-1}&{}0\\ &{}&{}\ddots &{}&{}&{}&{}\ddots &{}\vdots &{}\vdots \\ &{}&{}&{}-x&{}&{}&{}&{}s_{h-1}&{}0\\ \hline t_1&{}&{}&{}&{}s_1-1-x&{}s_2&{}\cdots &{}s_{h-1}&{}0\\ t_1&{}t_2&{}&{}&{}s_1&{}s_2-1-x&{}\cdots &{}s_{h-1}&{}0\\ \vdots &{}&{}\ddots &{}&{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ t_1&{}t_2&{}\cdots &{}t_{h-1}&{}s_1&{}s_2&{}\cdots &{}s_{h-1}-1-x+\frac{s_h}{s_{h-1}+s_h}(x+1)&{}\frac{s_h}{s_{h-1}}(x+1)\\ 0&{}0&{}\cdots &{}0&{}0&{}0&{}\cdots &{}0&{}-\frac{s_{h-1}+s_h}{s_{h-1}}(x+1) \end{array}\right) . \end{aligned}$$

By expanding the determinant of the last matrix along the last row and then by presenting the last column in the obtained submatrix as a sum of two, we get

$$\begin{aligned} \det T_h(x)=-\frac{s_{h-1}+s_h}{s_{h-1}}(x+1)\Delta _{h-1}+\frac{s_h}{s_{h-1}}x(1+x)^2\Delta _{h-2}. \end{aligned}$$

This leads to

$$\begin{aligned} \Delta _h(x)=\Big (\frac{s_{h-1}+s_h}{s_{h-1}}x(x+1)-t_hs_h\Big )\Delta _{h-1}-\frac{s_h}{s_{h-1}}x^2(1+x)^2\Delta _{h-2}(x), \end{aligned}$$

taking into account that \(\det S_h(x)=(-1)^{3h-1}t_h\Delta _{h-1}\), by expansion along the h-th column. \(\square \)

Remark 4.1

The initial conditions (4.2) and (4.3) correspond to the characteristic polynomials of the divisor matrices of the empty and the complete split graphs (with parameters \(t_1, s_1\)), respectively.

In case that the sequences \((s_h)_{h\in {\mathbb {N}}}\) and \((t_h)_{h\in {\mathbb {N}}}\) are convergent, i.e. \(s_h=s\), for \(h\ge N_1\) and \(t_h=t\), for \(h\ge N_2\), we are able to compute the limit points of the sequences \((\tau (G_h))_{h\in {\mathbb {N}}}\), and \((\theta (G_h))_{h\in {\mathbb {N}}}\).

Theorem 4.4

Let \(\{t_h\}_{h\in {\mathbb {N}}}\), \(\{s_h\}_{h\in {\mathbb {N}}}\) be the sequences of positive integers, such that \(t_h=t\) and \(s_h=s\), for \(h\ge h_0\). If \(G_h={\textrm{NSG}}(t_1, \ldots ,t_h;s_1, \ldots ,s_h)\), then \(\lim _{h\rightarrow \infty }\tau (G_h)=\tau \) and \(\lim _{h\rightarrow \infty }\theta (G_h)=\theta \) exist.

  • If the equation

    $$\begin{aligned} \Delta _0(x)\Big (2x(x+1)-ts+\sqrt{t^2s^2-4tsx(x+1)}\Big )-2\Delta _1(x)=0, \end{aligned}$$
    (4.4)

    has a positive solution (resp. a negative solution less than \(-1\)), then \(\tau \) (resp. \(\theta \)) is the largest positive (resp. the least negative less than \(-1\)) solution of the equation (4.4), where \(\Delta _0(x)\) and \(\Delta _1(x)\) are the characteristic polynomials of \(D_{h_0}(G_{h_0})\) and \(D_{h_{0}+1}(G_{h_{0}+1})\), respectively.

  • Otherwise, \(\tau =\frac{-1+\sqrt{1+ts}}{2}\) and \(\theta =\frac{-1-\sqrt{1+ts}}{2}\).

Proof

By (4.1), the sequence \(\Delta _h(x)=\det (D_{h+h_0}(G_{h+h_0})-xI)\) satisfies

$$\begin{aligned} \Delta _h(x)=\Big (2x(x+1)-ts\Big )\Delta _{h-1}-x^2(1+x)^2\Delta _{h-2}(x), \end{aligned}$$

for \(h>1\), with the initial conditions

$$\begin{aligned} \Delta _0(x)=\det (D_{h_0}(G_{h_0})-xI)\quad \text {and}\quad \Delta _1(x)=\det (D_{h_0+1}(G_{h_0+1})-xI). \end{aligned}$$

By solving this recurrence relation, we obtain that

$$\begin{aligned} \Delta _h(x)=c_1(x)\alpha (x)^h+c_2(x)\beta (x)^h, \end{aligned}$$
(4.5)

where

$$\begin{aligned}\alpha (x)&=\frac{1}{2}\Big (2x(x+1)-ts- \sqrt{\Big (2x(x+1)-ts\Big )^2-4x^2(1+x)^2}\Big ),\\ \beta (x)&=\frac{1}{2}\Big (2x(x+1)-ts+ \sqrt{\Big (2x(x+1)-ts\Big )^2-4x^2(1+x)^2}\Big ), \end{aligned}$$

i.e. they are the solutions of the equation

$$\begin{aligned} T^2-\Big (2x(x+1)-ts\Big )T+x^2(1+x)^2=0. \end{aligned}$$

The initial conditions for (4.5) are

$$\begin{aligned} c_1(x)+c_2(x)= & {} \Delta _0(x), \\ c_1(x)\alpha (x)+c_2(x)\beta (x)= & {} \Delta _1(x). \end{aligned}$$

We plug \(\tau (G_h)\) in (4.5), and afterwards, we divide by \(\big (\beta (\tau (G_h))\big )^h\). This leads to:

$$\begin{aligned} 0=c_1(\tau (G_h))\big (\frac{\alpha (\tau (G_h))}{\beta (\tau (G_h))}\big )^h+c_2(\tau (G_h)). \end{aligned}$$

We let h tend to \(\infty \).

  • If \(\lim _{h\rightarrow \infty }\alpha (\tau _h)<\lim _{h\rightarrow \infty }\beta (\tau _h)\), i.e. if \(\alpha (\tau )<\beta (\tau )\), then \(0=c_2(\tau )\), since \(\lim _{h\rightarrow \infty }\big (\frac{\alpha (\tau (G_h))}{\beta (\tau (G_h))}\big )^h=0\). Taking into account that

    $$\begin{aligned} c_2(x)=\frac{\Delta _1(x)-\Delta _0(x)\alpha (x)}{\beta (x)-\alpha (x)}, \end{aligned}$$

    it easily follows that \(\tau \) is the least positive solution of the equation

    $$\begin{aligned} \Delta _1(x)-\Delta _0(x)\alpha (x)=0. \end{aligned}$$

    Similarly, \(\theta \) is the largest negative solution less than \(-1\) of (4.4).

  • If the previous equation has no positive solution or the only negative solution is \(-1\), then \(\alpha (\tau )=\beta (\tau )\). This implies that \(t^2s^2-4ts\tau (\tau +1)=0\), i.e. \(\tau =\frac{-1+\sqrt{1+ts}}{2}.\) Similarly, \(\theta =\frac{-1-\sqrt{1+ts}}{2}.\)

\(\square \)

Example 4.1

Set \(G_h={\textrm{NSG}}(\underbrace{t, \ldots ,t}_h;\underbrace{s,\ldots ,s}_h).\) Then, \(\Delta _0(x)=1\), \(\Delta _1(x)=x^2-(s-1)x-ts,\) and (4.4) becomes:

$$\begin{aligned} \Big (2x(x+1)-ts+\sqrt{t^2s^2-4tsx(x+1)}\Big )-2(x^2-(s-1)x-ts)=0. \end{aligned}$$

Since the unique negative solution is \(x=-\frac{t(s+1)}{t+s}\), if \(t=1\), then \(\tau , \theta =\frac{-1\pm \sqrt{1+ts}}{2}\), because for \(t=1\), \(-\frac{t(s+1)}{t+s}=-1\). Otherwise, \(\tau =\frac{-1+\sqrt{1+ts}}{2}\) and \(\theta =-\frac{t(s+1)}{t+s}\).

Example 4.2

Set \(G_h={\textrm{NSG}}(\underbrace{12,12, \ldots ,12}_h;\underbrace{3,8,\ldots ,8}_h).\) Then, the limit points are the largest positive solution/negative solution of the equation

$$\begin{aligned}{} & {} (x^2-2x-36)\Big (2x(x+1)-96+\sqrt{96^2-4\cdot 96x(x+1)}\Big )\\{} & {} \qquad -2(x^4-9x^3-238x^2+60x+3456)=0, \end{aligned}$$

since \(\Delta _0(x)=x^2-2 x-36\), while \(\Delta _1(x)=x^4-9x^3-238x^2+60x+3456\), i.e. \(\lim _{h\rightarrow \infty }\tau (G_h)=3.6953\) and \(\lim _{h\rightarrow \infty }\theta (G_h)=-4.16646\).

Example 4.3

Numerical examples show that for

$$\begin{aligned} G_h={\textrm{NSG}}(1,2, \ldots ,h;1,2, \ldots ,h), \end{aligned}$$

\(\lim _{h\rightarrow \infty }\tau (G_h)=0.507\). Since the corresponding recurrence relation is not linear, we cannot apply the standard procedure for solving difference equations with constant coefficients.

5 Conclusion

We showed that for any positive real number R there exist infinitely many connected graphs whose eigenvalue gap is at least R. All of our examples of threshold graphs and all intervals are either contained in \((-\infty , \frac{1}{2}(-1-\sqrt{2}))\) or in \(( \frac{1}{2}(-1+\sqrt{2}),\infty )\). These constraints can be overcome by considering some graph operations on threshold graphs, such as corona, joins, and different types of NEPSes.

“Does any real number in the above mentioned intervals can be a limit point of certain sequence of eigenvalues of growing sequence of threshold graphs?” remains as an open problem for future considerations.