1 Introduction

In life science research, it is recognized that the current linear kinetic modeling paradigm of substance transport has to be shifted to more sophisticate but complete mathematical approaches to accurately capture the newly discovered nonlinear reality. For instance, research on new drug kinetics often involves specific binding interactions between ligands/substrates and proteins/enzymes, stimulated by various biological activities, such as immune response, gene expression, macromolecular assembly, and metabolism regulation [1, 2]. The binding is normally performed in two ways: noncooperative or cooperative. In noncooperative binding, initial binding does not affect subsequent bindings, and binding velocity usually follows Michaelis–Menten kinetics. In cooperative binding, initial binding of ligands/substrates significantly affects subsequent bindings. Conformational change of protein induced by the binding of one ligand/substrate molecular gives rise to the apparent change in affinity of the vacant sites to ligands/substrates. Cooperativity can also be positive or negative, determined by the change in binding affinity of ligands/substrates to proteins/enzymes. Cooperativity is positive if initial binding increases the binding affinity of subsequent ligands/substrates to proteins/enzymes and negative if initial binding decreases the binding affinity. Generally, the velocity of cooperativity is fitted by the Hill equation [3,4,5], namely,

$$\begin{aligned} \frac{V_{\max }C^{\alpha }(t)}{K_{D}^{\alpha }+C^{\alpha }(t)}, \end{aligned}$$
(1.1)

where C(t) is the concentration of ligands/substrates at time t, \(V_{\max }\) is the maximum velocity of cooperative binding, \(K_{D}\) is the concentration at which the velocity reaches half of \(V_{\max }\), and \(\alpha \) is the Hill coefficient. Additionally, positive or negative cooperativity is suggested by \(\alpha >1\) or \(\alpha <1\), respectively. As an effective modeling approach, Hill kinetics have been widely used in pharmacology to represent nonlinear and saturating drug elimination or drug effects induced by drug concentration [6, 7].

Because of the aforementioned widely use of Hill elimination kinetics in pharmacokinetic modeling, one-compartment pharmacokinetic model with a single sigmoidal elimination pathway has been proposed in many studies [8, 9]. Thus, the change of drug molecular concentration follows the differential equation:

$$\begin{aligned} \frac{dC(t)}{dt}=-\frac{V_{\max }C^{\alpha }(t)}{K_{D}^{\alpha }+C^{\alpha }(t)}. \end{aligned}$$
(1.2)

Analytical solutions of C(t) are required in pharmacology for many reasons, particularly for different drug administration routes as discussed in [10]. Specialists in clinical pharmacology appeal to the mathematical community to work on such drug models as they are important for drug development [11, 12]. Unlike linear drug models, where analytical solutions of C(t) using common algebraic functions are available, the solution C(t) of model (1.2) is difficult due to the presence of nonlinearity. Therefore, we have recourse to transcendent functions to represent the exact analytical solutions of drug concentration over time for such nonlinear pharmacokinetic models.

The use of transcendent functions to solve pharmacokinetic models is not uncommon. The Lambert W function is a typical example, which is defined as an implicit solution of W(s) satisfying

$$\begin{aligned} W(s)e^{W(s)}=s,\quad s\in \mathbb {R}. \end{aligned}$$
(1.3)

This function is known for having two real branches: a principal \(W_0(s)\) defined in the interval \(s\in [-e^{-1},\infty )\) and the other \(W_{-1}(s)\) defined in the interval \(s\in [-e^{-1},0)\) [13]. These two real branches are used for expressing the analytic solutions of C(t) for one-compartment pharmacokinetic model with Michaelis–Menten elimination alone for the case of intravenous bolus or constant infusion administrations [14]. In 2015, Wu and coauthors studied the analytical solution of C(t) for a one-compartment pharmacokinetic model with simultaneous first-order and Michaelis–Menten elimination in the case of intravenous bolus administration. In that paper, they proposed a transcendent X function satisfying

$$\begin{aligned} \left( X(s)\right) ^{p}\left( X(s)+1\right) ^{q}=s,\quad \text{ for } \text{ all }\, s\in \mathbb {R} \end{aligned}$$
(1.4)

to provide the analytical solution of drug concentration over time [10], where both p and q are positive parameters. The morphism classification of real branches for the newly developed X function has been investigated at the scope of real numbers [15].

In a recent study, we have investigated the pharmacokinetic Model (1.2) under single/multiple intravenous bolus administrations [16], where a new transcendent function, the H function, was proposed to express the model solution C(t). Given \(s\in \mathbb {R}\), H(s) is a multi-valued inverse solution of the following equation

$$\begin{aligned} \frac{1}{1-\alpha }H^{1-\alpha }(s)+H(s)=s, \end{aligned}$$
(1.5)

where \(\alpha \ne 1\) is the aforementioned Hill coefficient. The importance of the transcendent H function that we developed is evidenced by its application in studying several key pharmacokinetic parameters such as half-life, clearance, and drug exposure. This has enabled the delineation of the impact of nonlinear Hill elimination on drug disposition and the derivation of new quantitative estimates for real drugs [16]. These facts manifest the importance of the transcendent H function that we developed. However, the mathematical properties of this H function are marginal and deserve further exploration.

The objective of this study is to investigate the morphism of real branches of the transcendent H function, including their number, branch point, monotonicity, and convexity, and compare them to the real branches of the Lambert W function. This comparison will demonstrate how the Hill coefficient \(\alpha \) can lead to complex branches. Since the Hill coefficient \(\alpha \) describes the cooperativity of macromolecules and enzyme/protein/receptor binding interaction, its value may undergo small changes at every data-fitting process. Hence, we will investigate how slight variations in \(\alpha \) affect the stability of the real branches. This will provide a rationale for utilizing the H function for nonlinear pharmacokinetic models.

The paper is organized as follows: In Sect. 2, we introduce the definition of the transcendental H function and use it to derive the analytical solution C(t) of a one-compartment pharmacokinetic model with a single sigmoidal Hill elimination pathway under a single intravenous bolus dose administration. We also provide the relationship between the H and Lambert W functions. In Sect. 3, we present the morphism and stability of the real branches of the H function. In Sect. 4, we compare a set of numerical experiments of the aforementioned pharmacokinetic model using both the direct differential method as implemented in the ode45 solver in Matlab and our proposed algebraic H function. Finally, a brief discussion and conclusion concludes the article in Sect. 5.

2 Transcendent H Function in Pharmacokinetic Modeling

2.1 Introduction of H Function

One-compartment model of Michaelis–Menten elimination is very common in pharmacokinetic practice. If we assume a single intravenous bolus dose administration, it can be mathematically described as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{dC(t)}{dt}=-\frac{V_{\max }C(t)}{K_{m}+C(t)},t>t_{0},\\ \displaystyle C(t_{0}^{+})=D/V_{d}\triangleq C_{0} \end{array} \right. \end{aligned}$$
(2.1)

where C(t) represents the drug concentration at time t; \(V_{\max }\) is the maximum rate of the Michaelis–Menten elimination process in the unit of concentration/time; \(K_{m}\) is a constant in the unit of drug concentration, and the drug concentration at \(K_{m}\) means the elimination rate will be a half of \(V_{\max }\). Moreover, D is the dose at the initial time \(t_{0}\), and \(V_{d}\) is the volume of distribution. Thus, we define \(C_{0}\) the drug concentration immediately after the administration. It has to be reminded that all model parameters are positive to be pharmacologically meaningful.

For Model (2.1), we can integrate both sides of the differential equation from \(t_{0}\) to t and further rearrange it into the following algebraic equation

$$\begin{aligned} \ln \left( \frac{C(t)}{K_{m}}\right) +\frac{C(t)}{K_{m}}=\ln \frac{C_{0}}{K_{m}}+\frac{C_{0}}{K_{m}}-\frac{V_{\max }}{K_{m}}(t-t_{0}). \end{aligned}$$
(2.2)

After using variable substitution \(x=C(t)/K_{m}\) and taking exponentiation, Eq. (2.2) becomes

$$\begin{aligned} x\exp (x)=\frac{C_{0}}{K_{m}}\exp \left( \frac{C_{0}-V_{\max }(t-t_{0})}{K_{m}}\right) . \end{aligned}$$
(2.3)

Since the left term of Eq. (2.3) is the primitive of the Lambert W function, whereas its right term is independent with respect to x, the solution C(t) of Model (2.1) can be analytically expressed as

$$\begin{aligned} C(t)=K_{m}\times W_0\left( \frac{C_{0}}{K_{m}}\exp \left( \frac{C_{0}-V_{\max }(t-t_{0})}{K_{m}}\right) \right) , \quad t\ge t_{0}. \end{aligned}$$
(2.4)

Here, \(W_0\) is the principal real branch of the Lambert W function.

Let us consider the more general one compartment model of Hill elimination, which can be described for the case of intravenous bolus administration as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{dC(t)}{dt}=-\frac{V_{\max }C^{\alpha }(t)}{K^{\alpha }_{D}+C^{\alpha }(t)},\quad t>t_{0},\\ C(t_{0}^{+})=D/V_{d}\triangleq C_{0}, \end{array} \right. \end{aligned}$$
(2.5)

with \(\alpha \) the so-called Hill coefficient that usually represents the cooperative capacity between drug molecules and proteins/enzymes/receptors. Moreover, we set \(\alpha \ne 1\) to distinguish the Hill elimination from the Michaelis–Menten elimination. However, other parameters are kept the same meanings as those in Model (2.1).

By integrating, in Model (2.5), both sides of the differential equation from \(t_{0}\) to t, we can obtain the following algebraic equation:

$$\begin{aligned} \frac{1}{1-\alpha }\left( \frac{C(t)}{K_{D}}\right) ^{1-\alpha }+\frac{C(t)}{K_{D}} =\frac{1}{1-\alpha }\left( \frac{C_{0}}{K_{D}}\right) ^{1-\alpha }+\frac{C_{0}}{K_{D}}-\frac{V_{\max }}{K_{D}}(t-t_{0}). \end{aligned}$$
(2.6)

With the same variable substitution \(x=C(t)/K_{D}\) as that used for Model (2.1), we have

$$\begin{aligned} \frac{1}{1-\alpha }x^{1-\alpha }+x=\frac{1}{1-\alpha }\left( \frac{C_{0}}{K_{D}}\right) ^{1-\alpha } +\frac{C_{0}-V_{\max }(t-t_{0})}{K_{D}}. \end{aligned}$$
(2.7)

The right side of Eq. (2.7) is independent with respect to x. So, by introducing a transcendent H function as shown in Eq. (1.5), Model (2.5) has an analytical solution as

$$\begin{aligned} C(t)=K_{D}\times H_{0}\left( \frac{1}{1-\alpha }\left( \frac{C_{0}}{K_{D}}\right) ^{1-\alpha } +\frac{C_{0}}{K_{D}}-\frac{V_{\max }}{K_{D}}(t-t_{0}) \right) ,\quad t\ge t_{0}. \end{aligned}$$
(2.8)

Here, \(H_{0}\) is the principal real branch of the H function that we will characterize later.

Remark 2.1

We choose the simplest way to define the H function directly from Eq. (2.7) instead of using its exponential version as that used for the Lambert W function.

Remark 2.2

\(\alpha \) is positive in the pharmacokinetic Model (2.5); however, it can be mathematically any non-unity real number in the definition of H function.

2.2 Relationship Between Lambert W and H Functions

If \(\alpha =1\), Model (2.5) turns out to be Model (2.1), from which the transcendent Lambert W function can be deduced for expressing the analytical solution. Therefore, it is worth clarifying the relationship between H and Lambert W functions.

Now, we consider Model (2.5) where \(\alpha \ne 1\), we can rewrite Eq. (2.6) as

$$\begin{aligned} \frac{1}{1-\alpha }\left( \Bigl (\frac{C(t)}{K_{D}}\Bigl )^{1-\alpha }-\Bigl (\frac{C_{0}}{K_{D}}\Bigl )^{1-\alpha }\right) =\frac{C_{0}}{K_{D}}-\frac{C(t)}{K_{D}}-\frac{V_{\max }}{K_{D}}(t-t_{0}). \end{aligned}$$
(2.9)

Taking Taylor series expansion around \(\alpha =1\), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \Bigl (\frac{C(t)}{K_{D}}\Bigl )^{1-\alpha }&{}\displaystyle =1+\ln \Bigl (\frac{C(t)}{K_{D}}\Bigl )(1-\alpha )+o(1-\alpha ),\\ \displaystyle \Bigl (\frac{C_{0}}{K_{D}}\Bigl )^{1-\alpha }&{}\displaystyle =1+\ln \Bigl (\frac{C_{0}}{K_{D}}\Bigl )(1-\alpha )+o(1-\alpha ). \end{array}\right. } \end{aligned}$$

Thus,

$$\begin{aligned} \lim \limits _{\alpha \rightarrow 1}\frac{1}{1-\alpha }\left( \Bigl (\frac{C(t)}{K_{D}}\Bigl )^{1-\alpha }-\Bigl (\frac{C_{0}}{K_{D}}\Bigl )^{1-\alpha }\right) =\ln \frac{C(t)}{K_D}-\ln \frac{C_0}{K_D}. \end{aligned}$$

Finally, this yields

$$\begin{aligned} \ln \frac{C(t)}{K_D}-\ln \frac{C_0}{K_D} =\frac{C_0}{K_D}-\frac{C(t)}{K_D}-\frac{V_{\max }}{K_{D}}(t-t_{0}), \end{aligned}$$
(2.10)

which is exactly Eq. (2.2) if \(K_m=K_D\). If we raise natural exponential on both sides of Eq. (2.10) and rearrange the equation, we will have

$$\begin{aligned} \displaystyle \frac{C(t)}{K_D}\exp {\frac{C(t)}{K_D}}=\frac{C_0}{K_D} \exp {(\frac{C_0}{K_D}-\frac{V_{max}}{K_D}(t-t_0))}. \end{aligned}$$
(2.11)

If we check Eq.(1.3) that defines Lambert W function, we have

$$\begin{aligned} C(t)=K_D\times W_0\left( \frac{C_0}{K_D} \exp {(\frac{C_0-V_{max}(t-t_0)}{K_D})}\right) ,\quad t\ge t_0. \end{aligned}$$
(2.12)

This is the solution of pharmacokinetic Model (2.1) of Michaelis–Menten elimination, which can thus be approximated by the solution of pharmacokinetic model (2.5) of Hill elimination by letting \(\alpha \rightarrow 1\). Denoting \(C_H(t)\) for the former and \(C_M(t)\) for the latter, it means

$$\begin{aligned}\lim \limits _{\alpha \rightarrow 1} C_H(t)=C_M(t).\end{aligned}$$

The relationship between \(H_0\) and \(W_0\) functions can be summarized in the following theorem.

Theorem 2.1

Denote \(\displaystyle u=\frac{C_{0}}{K_{D}}\exp \left( \frac{C_{0}-V_{\max }(t-t_{0})}{K_{D}}\right) \), the principal real branches of Lambert W function is the limit of the principal real branches of H function as \(\alpha \rightarrow 1\), i.e.,

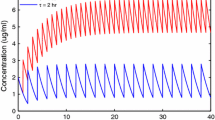
$$\begin{aligned} \lim \limits _{\alpha \rightarrow 1} H_{0}\left( \frac{1}{1-\alpha }\left( \frac{C_{0}}{K_{D}}\right) ^{1-\alpha } +\ln \left( \frac{uK_{D}}{C_{0}}\right) \right) =W_{0}(u). \end{aligned}$$
(2.13)

Several concentration-time courses of Model (2.1) and Model (2.5) are simulated and displayed in Fig. 1, which clearly shows that the curves of \(C_H(t)\) approximate to that of \(C_M(t)\) when \(\alpha \) tends to unity.

Fig. 1
figure 1

The concentration-time courses (\(C_M(t)\) and \(C_H(t)\)) of Model (2.1) and Model (2.5). \(\alpha :\) 0.2, 0.6, 1.0, 3.2, 7.2. \(D=4\,mg\), \(V_{\max }=1\,mg/L\), \(K_{D}=0.8\,mg/L\), \(V_{d}=1\,L\)

Full size image

3 Real Branches of H(s): Morphism and Stability

Lambert W function is known for the two distinct real branches with particular mathematical properties and scientific applications. Since H function can be considered as a generalized form of Lambert W function, it is worthwhile to investigate its real branches and make their classifications.

For this purpose, we separate \(\alpha \) into two scenarios: \(\alpha >1\) and \(\alpha <1\).

Since \(\alpha \) acts as a power in the definition of H function, it is reasonable to first discuss \(\alpha \in \mathbb {Q}\). After that, we may use the denseness of \(\mathbb {Q}\) in \(\mathbb {R}\) to generate the result for \(\alpha \in \mathbb {R}\backslash \mathbb {Q}\).

3.1 Real Branches of H(s) for \(\alpha \in \mathbb {Q}\)

For \(\alpha \in \mathbb {Q}\), we write \(\alpha =p/q\) for \(\alpha >0\) or \(\alpha =-p/q\) for \(\alpha <0\), where \(p, q\in \mathbb {Z}^+\) are mutually prime. Further, we will take into account three possible sets or cases based on even-odd properties of a pair (p, q), i.e., (o, o), (o, e) and (e, o), where “e" or “o" represents the class of even or odd numbers, respectively.

According to the inverse function theorem, the real branches of H(s) can be identified by its primitive function. For this, we define the corresponding primitive function \(f:\mathbb {R}\rightarrow \mathbb {R}\) as

$$\begin{aligned} f(x)=\frac{1}{1-\alpha }x^{1-\alpha }+x,\,\, \alpha \ne 1. \end{aligned}$$
(3.1)

We can observe that \(f(0)=0\) for \(\alpha <1\), which means H(s) passes through (0, 0); however, f is not well defined at \(x=0\) for \(\alpha >1\), and \(\lim \limits _{x \rightarrow 0-}f(x)=+\infty \) and \(\lim \limits _{x \rightarrow 0+}f(x)=-\infty \). Also, we note that, for a positive real number a, there are two real n-th roots \(\pm a^{\frac{1}{n}}\) if n is even; and there is only one positive real n-th root \(a^{\frac{1}{n}}\) if n is odd. Thus, \(f'(x)=\frac{1}{x^{\alpha }}+1=0\) leads to a stationary point as

$$\begin{aligned} x=-1,\,\, \text{ if }\,\, (p,q)\in (o,o)\quad \text{ or }\quad x^-=1,\,\, \text{ if }\,\, (p,q)\in (o,e). \end{aligned}$$
(3.2)

It conversely suggests a critical point as

$$\begin{aligned} (s^*,H^*)&=\left( \frac{\alpha }{1-\alpha },-1\right) \,\, \text{ if }\,\, (p,q)\in (o,o)\quad \text{ or }\quad (s^{-},H^{-})\nonumber \\&=\left( -\frac{\alpha }{1-\alpha },1\right) ,\,\, \text{ if }\,\, (p,q)\in (o,e) \end{aligned}$$
(3.3)

for determining the morphism of real branches of H(s). The notations with superscript "-" are related to the above mentioned negative root.

3.1.1 \(\alpha >1\)

In this case, we have \(p>q\) and

$$\begin{aligned} f'(x)=\frac{1}{\left( x^{p}\right) ^{\frac{1}{q}}}+1 ,\quad f''(x)=\frac{-p/q}{\left( x^{p+q}\right) ^{\frac{1}{q}}}. \end{aligned}$$
(3.4)

(i) \((p,q)\in (o,o)\). In this case, \(p+q\) is even and q is odd. From Eq. (3.4), \(x=0\) and \(x=-1\) are critical for the morphism of f(x). We have \(f'(x)>0\) for \(x\in (-\infty ,-1)\cup (0,\infty )\) and \(f'(x)<0\) for \(x\in (-1,0)\), whereas \(f''(x)<0\) for all \(x\in \mathbb {R}\setminus \{0\}\). Furthermore, the asymptotic properties \(\lim \limits _{x\rightarrow \pm \infty } f(x)=\pm \infty \) and \(\lim \limits _{x\rightarrow 0^{\pm }} f(x)=-\infty \) can be verified.

Consequently, we have three situations. For \(x\in (-\infty ,-1)\), f(x) is strictly increasing from \(-\infty \) to \(\frac{\alpha }{1-\alpha }=H^*\) and concave down; for \(x\in (-1,0)\), f(x) is strictly decreasing from \(H^*\) to \(-\infty \) and concave down; for \(x\in (0,\infty )\), f(x) is strictly increasing from \(-\infty \) to \(+\infty \) and concave down. Thus, it implies that, corresponding to a same value f(x), there exist three real values of x. Accordingly, by the inverse function theorem and convexity of the inverse function [17], there exist three real branches of H(s) in the real domain of s. Namely, \(H_0(s)\triangleq H(s)\in (0,\infty )\) for \(s\in (-\infty ,+\infty )\), which is strictly increasing and concave up; \(H_{-1}(s)\triangleq H(s)\in (H^*,0)\) for \(s\in (-\infty ,s^*)\), which is strictly decreasing and concave down; \(H_{-2}(s)\triangleq H(s)\in (-\infty ,H^*)\) for \(s\in (-\infty ,s^*)\), which is strictly decreasing and concave up. Following the naming convention as the Lambert W function, we call \(H_0(s)\) the principal real branch of the H function for its positiveness for \(s\in (-\infty ,+\infty )\). Without confusion, this rule will be applied in the current article.

(ii) \((p,q)\in (o,e)\). In this case, f(x) is well defined only for \(x>0\). Since a positive number could take two real q-th roots, one positive and one negative, we have: (a) if the positive root is considered, \(f'(x)>0\) and \(f''(x)<0\) for all \(x>0\), and \(\lim \limits _{x\rightarrow +\infty } f(x)=+\infty \) and \(\lim \limits _{x\rightarrow 0^+} f(x)=-\infty \). By the inverse function theorem and convexity of the inverse function [17], there is a principal real branch \(H_0(s)\in (0,\infty )\) for \(s\in \mathbb {R}\), which is strictly increasing and concave up; (b) if the negative root is taken, \(f'(x)<0\) for \(x\in (0,1)\), \(f'(x)>0\) for \(x\in (1,+\infty )\) and \(f'(1)=0\), whereas \(f''(x)>0\) for \(x>0\). Moreover, \(\lim \limits _{x\rightarrow 0^+} f(x)=\lim \limits _{x\rightarrow +\infty } f(x)=+\infty \). So, there are two possible real branches of H function, among which a decreasing and concave up \(H_{-1}^{-}(s)\in (0,H^{-})\) is defined for \(s\in (s^-,\infty )\), and an increasing and concave down \(H_{-2}^{-}(s)\in (H^{-},+\infty )\) is defined for \(s\in (s^{-},+\infty )\). It has to be reminded that the subscript ‘−’ is related to the negative root and \((s^-,H^-)\) is given in Eq. (3.3).

(iii) \((p,q)\in (e,o)\). In this case, f(x) is well defined for \(x\in \mathbb {R}\backslash \{0\}\). It is easy to check that \(f'(x)>0\) for \(x\in \mathbb {R}\backslash \{0\}\), and \(f''(x)>0\) for \(x<0\) while \(f''(x)<0\) for \(x>0\). Moreover, \(\lim \limits _{x\rightarrow +\infty } f(x)=\lim \limits _{x\rightarrow 0^-} f(x)=+\infty \), \(\lim \limits _{x\rightarrow -\infty } f(x)=\lim \limits _{x\rightarrow 0^+} f(x)=-\infty \). So, f(x) is monotonically increasing and upward concave for \(x<0\), while monotonically increasing but concave down for \(x>0\). Therefore, there are two real branches: an increasing and concave up \(H_0(s)\in (0,\infty )\) for \(s\in \mathbb {R}\) and an increasing and concave down \(H_{-1}(s)\in (-\infty ,0)\) for \(s\in \mathbb {R}\).

The results are summarized in the following theorem.

Theorem 3.1

If \(\alpha >1\), there are three classes of real branches of H(s) deduced from Eq. (1.5). Specifically, a principal real branch \(H_{0}(s)>0\) always exists and is well defined for \(s\in \mathbb {R}\), which is concave up and monotonically increasing w.r.t. s. Moreover,

  • If \((p,q)\in (o,o)\), there are two additional real branches \(H_{-1}(s)\in (H^*,0)\) and \(H_{-2}(s)\in (-\infty ,H^*)\), which are well defined for \(s\in (-\infty ,s^*)\) and joined at \((s^*,H^*)\);

  • if \((p,q)\in (o,e)\), there are two additional real branches \(H^-_{-1}(s)\in (0,H^-)\) and \(H^-_{-2}(s)\in (H^-,+\infty )\). which are well defined for \(s\in (s^-,+\infty )\) and joined at \((s^-,H^-)\);

  • If \((p,q)\in (e,o)\), there exists an additional real branch \(H_{-1}(s)<0\) defined for \(s\in (-\infty ,+\infty )\).

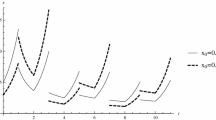
In Fig. 2, we provide several numerical examples that illustrate the morphism of real branches in the H function for \(\alpha >1\). Specifically, when \((p,q)\in (e,o)\), \(H_0(s)\) is symmetric to \(H_{-1}(s)\) about the origin.

Fig. 2
figure 2

The real branches of \(H(s,\alpha )\) for \(\alpha >1\). a \((p,q)=(9,7)\in (o,o)\); b \((p,q)=(9,6)\in (o,e)\); c \((p,q)=(8,7)\in (e,o)\)

Full size image

3.1.2 \(0<\alpha <1\)

In this case, \(f(0)=0\) and H(s) passes through (0, 0). As the discussion of classification is similar to that we performed for the case of \(\alpha >1\), we summarize the result in the following theorem and provide the detailed proof as supplemental material.

Theorem 3.2

If \(0<\alpha <1\), there are three classes of real branches of H(s) deduced from Eq. (1.5). Specifically, a principal real branch \(H_{0}(s)\ge 0\), which is concave up and monotonically increasing w.r.t. s, always exists and is well defined for \(s\ge 0\). Moreover,

  • If \((p,q)\in (o,o)\), there are two additional real branches \(H_{-1}(s)\in (H^*,0)\) and \(H_{-2}(s)\in (-\infty ,H^*)\), with the former well defined for \(s\in [0, s^*]\) and the latter for \(s\in (-\infty , s^*]\). \(H_0\), \(H_{-1}\) and \(H_{-2}\) are successively joined at (0, 0) and \((s^*,H^*)\);

  • If \((p,q)\in (o,e)\), there are two additional real branches \(H^-_{-1}(s)\in (0,H^-)\) and \(H^-_{-2}(s)\in (H^-,+\infty )\), with the former well defined for \(s\in [s^-, 0] \) and the latter for \(s\in [s^-, +\infty )\). \(H_0\), \(H^-_{-1}\) and \(H^-_{-2}\) are successively joined at (0, 0) and \((s^-,H^-)\);

  • If \((p,q)\in (e,o)\), there is a well-defined negative real branch \(H_{-1}(s)<0\) for \(s<0\), which is smoothly linked, at (0, 0), with the principal real branch \(H_0(s)\) situated in the first quadrant. If combined together, these two branches can be considered as one single real branch.

In Fig. 3, we provide several numerical examples that illustrate the morphism of real branches in the H function for \(0<\alpha <1\). Furthermore, when \((p,q)\in (e,o)\), the entire real branch is symmetric about the origin.

Fig. 3
figure 3

The real branches of H(s) for \(0<\alpha <1\). a \((p,q)=(5,7)\in (o,o)\); b \((p,q)=(1,2)\in (o,e)\); c \((p,q)=(2,3)\in (e,o)\)

Full size image

3.1.3 \(\alpha <0\)

In this case, \(f'(x)>0\) and \(f''(x)>0\) for \(x>0\). The principal real branch \(H_0(s)\) exists in the first quadrant, which is increasing, concave down and starts from (0, 0). We summarize the details in the following theorem and use several numerical examples to illustrate the morphism of real branches of H function in Fig. 4.

Theorem 3.3

If \(\alpha <0\), there are three classes of real branches of H(s) deduced from Eq. (1.5). Specifically, a principal real branch \(H_{0}(s)\ge 0\) always exists in the first quadrant, which is well defined for \(s\ge 0\), concave down and monotonically increasing w.r.t. s. Moreover,

  • if \((p,q)\in (o,o)\), \(H_0(s)\) can be smoothly extended to \((H^*,+\infty )\) for \(s\in (s^*,+\infty )\) and joined at \((s^*, H^*)\) by another real branch \(H_{-1}(s)\in (-\infty ,H^*)\) that is well defined for \(s\in (s^*,+\infty )\);

  • if \((p,q)\in (o,e)\), there are two additional real branches \(H^-_{-1}(s)\in (0,H^-)\) and \(H^-_{-2}(s)\in (H^-,+\infty )\). The former well defined for \(s\in [0, s^-] \) and the latter for \(s\in (-\infty , s^-]\). Moreover, \(H_0\), \(H^-_{-1}\) and \(H^-_{-2}\) are successively joined at (0, 0) and \((s^-,H^-)\);

  • if \((p,q)\in (e,o)\), there is a well-defined negative real branch \(H_{-1}(s)<0\) for \(s<0\), which is smoothly linked, at (0, 0), with the principal real branch \(H_0(s)\) situated in the first quadrant. If combined together, these two branches can be considered as one single real branch.

Fig. 4
figure 4

The real branches of \(H(s,\alpha )\) for \(\alpha <0\). a \((p,q)=(3,5)\in (o,o)\); b \((p,q)=(1,2)\in (o,e)\); c \((p,q)=(2,3)\in (e,o)\)

Full size image

Furthermore, if \((p,q)\in (e,o)\), the entire real branch of H is symmetric about the origin.

Before delving into the morphism of H(s) for \(\alpha \in \mathbb {R}\backslash \mathbb {Q}\), we must first examine the stability of H(s) with respect to \(\alpha \). For this purpose, we use \(H_{0}(s, \alpha )\) instead of \(H_{0}(s)\) in the next subsection.

3.2 Stability and Several Properties of the Principal Real Branch \(H_0(s,\alpha )\) with Respect to \(\alpha \in \mathbb {R}\)

Considering practical applications, the true value of \(\alpha \) is typically obtained through approximations or applied using rational numbers. Therefore, it is important to investigate how the small change of \(\alpha \) value used in the algebraic equation could impact on the solution of H function, which we refer to as the stability of real branches of H function. We begin by examining the morphism stability of the principal real branch \(H_0(s,\alpha )\) with respect to \(\alpha \in \mathbb {R}\).

In the previous section, we established that the principal real branch is well defined for \(s\in \mathbb {R}\) if \(\alpha >1\), and for \(s\in \mathbb {R}^+\) if \(\alpha <1\), when \(\alpha \) is rational. Our investigation in this section will focus on s belonging to these domains, denoted below as \(\mathcal {D}\).

Theorem 3.4

Consider the principal real branch \(H_0(s,\alpha )\) for \(\alpha \ne 1\), \(H_0(s,\alpha )\) is stable for \(s\in \mathcal {D}\). That is to say, given \(\alpha _0\ne 1\), we have

$$\begin{aligned}\lim _{\alpha \rightarrow \alpha _0}H_{0}(s,\alpha )=H_{0}(s,\alpha _0)\end{aligned}$$

for any \(s\in \mathcal {D}\).

Proof

We have proved that, given \(s\in \mathcal {D}\), \(H_{0}\) is well defined for \(\alpha \in \mathbb {Q}\) in Sect. 3.1. Hence, given \(s\in \mathcal {D}\), to prove the continuity of \(H_0\) w.r.t. \(\alpha \), either \(\alpha \in \mathbb {Q}\) or \(\alpha \in \mathbb {R}\backslash \mathbb {Q}\), we need to prove that, for any sequence \(\{\alpha _k\}_{k=1}^\infty \) satisfying \(\lim \limits _{k\rightarrow \infty }\alpha _k=\alpha \), \(H_0(s,\alpha _k)\) is a Cauchy sequence such that \(\lim \limits _{\alpha _k\rightarrow \alpha }H_0(s,\alpha _k)=H_0(s, \alpha )\) if \(\alpha \in \mathbb {Q}\), or we define \(H_0(s, \alpha )=\lim \limits _{\alpha _k\rightarrow \alpha }H_0(s,\alpha _k)\) if \(\alpha \in \mathbb {R}\backslash \mathbb {Q}\).

This can be seen by the definition of H in Eq. (1.5), i.e., for a given \(s\in \mathcal {D}\), we have

$$\begin{aligned} \frac{1}{1-\alpha _m}H_0^{1-\alpha _m}(s, \alpha _m)+H_0(s, \alpha _m)=\frac{1}{1-\alpha _n}H_0^{1-\alpha _n}(s, \alpha _n)+H_0(s, \alpha _n) \end{aligned}$$
(3.5)

for any \(m, n\in \mathbb {N}\).

In fact, Eq. (3.5) can be arranged as

$$\begin{aligned}&\frac{1}{1-\alpha _m}(H_0^{1-\alpha _m}(s, \alpha _m)-H_0^{1-\alpha _n}(s, \alpha _n))+(\frac{1}{1-\alpha _m}-\frac{1}{1-\alpha _n})H_0^{1-\alpha _n}(s, \alpha _n)\nonumber \\ {}&\qquad +(H_0(s, \alpha _m)-H_0(s, \alpha _n))=0 \end{aligned}$$
(3.6)

Based on the above equation, we conclude that \(\{H_0(s,\alpha _k)\}\) is a Cauchy sequence. Otherwise, \(\exists \epsilon >0\), for any \(N>0\), \(\exists m, n>N\), such that \(H_0(s,\alpha _m)-H_0(s,\alpha _n)>\epsilon \). However, this also induces that, no matter \(\alpha <1\) or \(\alpha >1\), the first term in the sum on the left side of Eq. (3.6) is always positive. As the second term in the sum tends to zero when \(m, n\rightarrow \infty \) since \(\lim \limits _{k\rightarrow \infty }\alpha _k=\alpha \). Then, we have the strict positivity of the left side of Eq. (3.6), which clearly contradicts the equality of Eq. (3.6).

In conclusion, \(\forall \epsilon >0\), \(\exists N>0\), we have \(|H_0(s,\alpha _m)-H_0(s,\alpha _n)|<\epsilon \) for \(m, n>N\), i.e., \(\{H_0(s,\alpha _k)\}\) is a Cauchy sequence for any \(\alpha _k\rightarrow \alpha \). Therefore, we have Theorem 3.4. \(\square \)

Moreover, we can summarize the derivative and stationary points of \(H_0(s,\alpha )\) with respect to \(\alpha \) in the following theorem.

Theorem 3.5

  1. (i)

    The principal real branch \(H_0(s,\alpha )\) is continuous and differentiable w.r.t. \(\alpha \ne 1\) for \(s\in \mathcal {D}\) with the derivative

    $$\begin{aligned} \frac{d}{d\alpha }H_0(s,\alpha )=\frac{H_0(s,\alpha )}{1+H_0^{\alpha }(s,\alpha )}\frac{1}{1-\alpha } \Big (\ln H_0(s,\alpha )-\frac{1}{1-\alpha }\Big ). \end{aligned}$$
    (3.7)
  2. (ii)

    There is a critical curve formed by the stationary points of \(H_0(s,\alpha )\) w.r.t. \(\alpha \) for \(s\in \mathcal {D}\). And these points, denoted as \((\alpha _S,H_{0S})\), are unique for each s and can be obtained by

    $$\begin{aligned} \frac{e}{1-\alpha _S}+e^{\frac{1}{1-\alpha _S}}=s\quad \text{ and }\quad H_{0S}=e^\frac{1}{1-\alpha _S}. \end{aligned}$$
    (3.8)
  3. (iii)

    Both \(\alpha _S\) and \(H_{0\,S}\) are increasing functions w.r.t. s. Moreover, \((\alpha _S,H_{0\,S})\in (-\infty , 1)\times (1,+\infty )\) for \(\alpha <1\), and \((\alpha _S,H_{0S})\in (1, +\infty )\times (0, 1)\) for \(\alpha >1\).

To facilitate the proof of Theorem 3.5, we need the following lemma.

Lemma 3.1

The function \(g(x)=ex+e^x\) is strictly increasing w.r.t. \(x\in \mathbb {R}\). While \(g(0)=1\), we have \(g(x)<1\) for \(x<0\) and \(g(x)>1\) for \(x>0\).

Proof

Since \(g'(x)=e+e^x>0\), the claims is evident. \(\square \)

Proof of Theorem 3.5

(i) By the definition of H from Eq.(1.5), \(H_0(s,\alpha )\) satisfies

$$\begin{aligned} \frac{1}{1-\alpha }H_0^{1-\alpha }(s,\alpha )+H_0(s,\alpha )=s. \end{aligned}$$
(3.9)

Taking derivatives w.r.t \(\alpha \) of both sides of Eq. (3.9) leads to

$$\begin{aligned}&\frac{1}{(1-\alpha )^2}H_0^{1-\alpha }(s,\alpha )+\frac{1}{1-\alpha }H_0^{1-\alpha }(s,\alpha )\Big [-\ln H_0(s,\alpha )+\frac{(1-\alpha )}{H_0(s,\alpha )}\frac{d}{d\alpha }H_0(s,\alpha )\Big ] \nonumber \\ {}&\qquad +\frac{d}{d\alpha }H_0(s,\alpha )=0, \end{aligned}$$
(3.10)

which yields

$$\begin{aligned} \frac{d}{d\alpha }H_0(s,\alpha )=\frac{H_0(s,\alpha )}{1+H_0^{\alpha }(s,\alpha )}\frac{1}{1-\alpha } \Big [\ln H_0(s,\alpha )-\frac{1}{1-\alpha }\Big ] \end{aligned}$$
(3.11)

(ii) Let us have \(\frac{d}{d\alpha }H_0(s,\alpha )=0\) and consider Eq. (3.9), a stationary point \(\alpha _S\) can be obtained by solving the following equation

$$\begin{aligned} \frac{e}{1-\alpha }+e^{\frac{1}{1-\alpha }}=s \end{aligned}$$
(3.12)

while

$$\begin{aligned} H_{0S}\triangleq H_{0}(s,\alpha _S)=e^{\frac{1}{1-\alpha _S}}. \end{aligned}$$
(3.13)

\(\square \)

(iii) From Lemma 3.1, there is a unique solution \(\alpha _S\) such that Eq. (3.12) holds, and we have \(\alpha _S>1\) for each \(s<1\) or \(\alpha _S<1\) for each \(s>1\). That is, there are two families of stationary points \(\alpha _S\), \(\alpha _S>1\) and \(\alpha _S<1\), which represent the case of \(\alpha >1\) and \(\alpha <1\), respectively. Moreover, from Eq. (3.12), we have

$$\begin{aligned}\frac{d\alpha }{ds}=\frac{(1-\alpha )^2}{e+e^{\tfrac{1}{1-\alpha }}}>0,\end{aligned}$$

which implies that \(\alpha _S\) are increasing functions w.r.t. s for both cases of \(s<1\) and \(s>1\). The increasing property of \(H_{0S}\) w.r.t. \(\alpha _S\) is obvious.

Fig. 5
figure 5

The critical curves of the principle real branch \(H_0\): a \(\alpha _S\) vs. s; b \(H_{0S}\) vs. \(\alpha _S\)

Full size image

To provide a clear idea, we present the relationship between s, \(\alpha _S\) and \(H_{0\,S}\) in Fig. 5. In Fig. 5a, we can see that \(\alpha _S\) monotonically increases with respect to s for both cases of \(\alpha >1\) and \(\alpha <1\), with the former being concave down and the latter concave up. In Fig. 5b, the properties of the critical curves \((\alpha _S, H_{0S})\) can be equally visualized.

The following theorem claims how the principal real branch \(H_0(s,\alpha )\) changes with the Hill coefficient \(\alpha \).

Theorem 3.6

For the principal real branch \(H_0(s,\alpha )\) defined in Eq. (1.5), we have the following scenarios:

  1. (1)

    If \(\alpha >1\), then

    1. (i)

      for \(s\ge 1\), \(H_0\) decreases w.r.t. \(\alpha \);

    2. (ii)

      for \(s<1\), \(H_0\) decreases first w.r.t. \(\alpha \) if \(\alpha <\alpha _S\) till \(H_{0S}\) at \(\alpha _S\), then increases w.r.t. \(\alpha \) if \(\alpha >\alpha _S\);

  2. (2)

    If \(\alpha <1\), then

    1. (i)

      for \(0<s\le 1\), \(H_0\) decreases w.r.t. \(\alpha \);

    2. (ii)

      for \(s>1\), \(H_0\) increases first w.r.t. \(\alpha \) if \(\alpha <\alpha _S\) till \(H_{0S}\) at \(\alpha _S\), then decreases w.r.t. \(\alpha \) if \(\alpha >\alpha _S\).

Proof

(1) Given \(\alpha >1\), \(H_0\) is an increasing function w.r.t. \(s\in \mathbb {R}\) as proved in Theorem 3.1.

Consider \(x=\frac{1}{1-\alpha }\) in Lemma 3.1, we have

$$\begin{aligned}\frac{1}{1-\alpha }\left( e^{\frac{1}{1-\alpha }}\right) ^{1-\alpha }+e^{\frac{1}{1-\alpha }} =\frac{1}{1-\alpha }e+e^{\frac{1}{1-\alpha }}<e^0=1,\end{aligned}$$

which conversely implies that, for all \(s\ge 1\), \(H_0(s,\alpha )>e^{\frac{1}{1-\alpha }}\). This inequality is equivalent to \(\ln H_0(s,\alpha )>\frac{1}{1-\alpha }\) that we can affirm \(\frac{dH_0}{d\alpha }(s,\alpha )<0\) by Eq. (3.7), which leads to (1)(i).

For each \(s<1\), by Lemma 3.1 and the definition of H, there is a unique \(\alpha _S\) and many \(\alpha \) such that

$$\begin{aligned} \frac{1}{1-\alpha _S}e+e^{\frac{1}{1-\alpha _S}}=s=\frac{1}{1-\alpha } H_0^{1-\alpha }+(H_0^{1-\alpha })^{\frac{1}{1-\alpha }}. \end{aligned}$$
(3.14)

If \(\alpha>\alpha _S>1\), which is equivalent to \(0>\frac{1}{1-\alpha }>\frac{1}{1-\alpha _S}\), we have \(H_0^{1-\alpha }>e\). This can be seen as if we assume \(H_0^{1-\alpha }<e\), then, \(\frac{1}{1-\alpha }H_0^{1-\alpha }>\frac{1}{1-\alpha _S}e\) and \(H_0>e^{\frac{1}{^{1-\alpha }}}>e^{\frac{1}{^{1-\alpha _S}}}\) which implies

$$\begin{aligned} \frac{1}{1-\alpha } H_0^{1-\alpha }+(H_0^{1-\alpha })^{\frac{1}{1-\alpha }}>\frac{1}{1-\alpha _S}e+e^{\frac{1}{1-\alpha _S}}. \end{aligned}$$

Thus, Eq. (3.14) implies that

$$\begin{aligned}H_0^{1-\alpha }>e\Leftrightarrow \ln H_0^{1-\alpha }>1 \Leftrightarrow \frac{dH_0}{d\alpha }(s,\alpha )>0.\end{aligned}$$

If \(1<\alpha <\alpha _S\), then, \(\frac{1}{1-\alpha }<\frac{1}{1-\alpha _S}<0\). Using the same reasoning as above, we have \(H_0^{1-\alpha }<e\), which gives \(\ln H_0^{1-\alpha }<1\). This implies \(\frac{dH_0}{d\alpha }(s,\alpha )<0\). Thus, we have (1)(ii).

(2) Given \(\alpha <1\), similarly, we can see \(H_0\) is well defined and increasing w.r.t. \(s>0\). Moreover, we have

$$\begin{aligned}\frac{1}{1-\alpha }\left( e^{\frac{1}{1-\alpha }}\right) ^{1-\alpha }+e^{\frac{1}{1-\alpha }}=\frac{1}{1-\alpha }e+e^{\frac{1}{1-\alpha }}>e^0=1.\end{aligned}$$

Then, for \(0<s\le 1\), there is no solution \(\alpha _S\) of stationary point. This implies \(H_0(s,\alpha )<e^{\frac{1}{1-\alpha }}\) or \(\ln H_0(s,\alpha )<\frac{1}{1-\alpha }\), which directly gives \(\frac{dH_0}{d\alpha }(s,\alpha )<0\) leading to (2)(i).

For \(s>1\), we can apply the same reasoning as used above based on Eq. (3.14).

If \(1>\alpha >\alpha _S\), we have \(\frac{1}{1-\alpha }>\frac{1}{1-\alpha _S}>0\), which leads to \(H_0^{1-\alpha }<e\) or \(\ln H_0^{1-\alpha }<1\) directly resulting \(\frac{dH_0}{d\alpha }(s,\alpha )<0\).

If \(\alpha<\alpha _S<1\), we have \(0<\frac{1}{1-\alpha }<\frac{1}{1-\alpha _S}\), which leads to \(H_0^{1-\alpha }>e\) or \(\ln H_0^{1-\alpha }>1\) directly resulting \(\frac{dH_0}{d\alpha }(s,\alpha )>0\). Then, we have (2)(ii). \(\square \)

Fig. 6
figure 6

Monotonicity of the principal real branch \(H_0\) vs. \(\alpha \) at particular values of s. a \(\alpha >1\); b \(\alpha <1\)

Full size image

Figure 6 shows the numerical relationship between \(H_0\) and \(\alpha \) at several s values. In the case of \(\alpha >1\) displayed in Fig. 6a, \(H_0\) decreases with \(\alpha \) at \(s=1.1\), but it is always greater than one. For \(s<1\), there is a critical curve where \(H_{0S}\) is less than one. As shown by the examples of \(s=-2,-1,0\), \(H_{0}\) decreases for \(\alpha <\alpha _S\) and increases for \(\alpha >\alpha _S\). Similarly, in the case of \(\alpha <1\) shown in Fig. 6b, \(H_0\) decreases with \(\alpha \) at \(s=0.8\), and it is always less than one. However, for \(s>1\), there is a critical curve where \(H_{0S}\) is greater than one. As illustrated by the examples of \(s=2,3,4\), \(H_0\) first increases for \(\alpha <\alpha _S\) to its maximum value \(H_{0S}\) at \(\alpha _S\), and then decreases for \(\alpha >\alpha _S\).

In Figs. 7, 8 and 9, we present several numerical simulations to demonstrate the stability of the principal real branch \(H_0\) with respect to \(\alpha \) for \(\alpha >1\), \(0<\alpha <1\), and \(\alpha <0\), respectively. As shown in the figures, the three types of principal real branch \(H_0(s)\) are stable in their corresponding cases. This indicates that even if the numerical approximations to \(\alpha \) vary between (o, o), (e, o), and (o, e), the domain, range, and morphism of the approximate principal real branches \(H_0\) remain stable with respect to \(H_0(s,\alpha )\).

However, shifting the type (p, q) among (o, o), (e, o), and (o, e) when approximating a true \(\alpha \) can lead to different domains, ranges, and morphisms for other real branches \(H_{j}(s)\) and \(H^-_{j}(s)\) \((j=-1,-2)\). This results in instability in their applications. When considering any \(\alpha \in \mathbb {R}\backslash \mathbb {Q}\), it is known that \(\alpha \) is the limit of a sequence \(\alpha _k\in \mathbb {Q}\), \(k=1,2,3,\ldots \). By shifting elements in the sequence alternatively among (o, o), (e, o), and (o, e), we will see the corresponding morphisms shift among other real branches \(H_{j}(s)\) and \(H^-_{j}(s)\) \((j=-1,-2)\), etc. Theoretically, this instability denies the existence of other real branches for \(\alpha \in \mathbb {R}\backslash \mathbb {Q}\).

Fig. 7
figure 7

Stability and instability of the real branches of H(s) for \(\alpha >1\)

Full size image
Fig. 8
figure 8

Stability and instability of the real branches of H(s) for \(0<\alpha <1\)

Full size image
Fig. 9
figure 9

Stability and instability of the real branches of H(s) for \(\alpha <0\)

Full size image

Therefore, we also have

Theorem 3.7

For any \(\alpha \in \mathbb {R}\backslash \mathbb {Q}\), there exists a unique principal real branch \(H_{0}(s)\in (0,+\infty )\) satisfying  Eq.(1.5), which is defined for \(s\in (-\infty ,+\infty )\) if \(\alpha >1\), or for \(s\in (0,+\infty )\) if \(\alpha <1\). Moreover, \(H_{0}(s)\) is strictly increasing and concave down within its domain of definition.

4 Numerical Computation of \(H_0(s,\alpha )\)

Although we have obtained a closed-form algebraic expression for the principal real branch \(H_0\) to represent the exact solution of the pharmacokinetic model with sigmoidal Hill elimination [16], it is worth comparing the accuracy of different algorithms in solving Model (2.5) using either the closed-form of \(H_0\) or other standard numerical techniques such as the ode45 solver for ODEs.

To compare the accuracy of different algorithms, we calculated and compared drug concentrations over time using Model (2.5). Specifically, \(C_H(t)\) is the concentration directly calculated from the \(H_0\) function we programmed in Matlab using the definition in Eq. (1.5). \(C_{Im}(t)\) is the concentration obtained from Eq.(2.6) using an implicit solver of algebraic equations in Matlab. \(C_{RK}(t)\) is the concentration calculated from ordinary differential equation in Model (2.5) using the ode45 solver in Matlab. The tolerance error was fixed at \(\varepsilon =10^{-3}\) for all three algorithms. For the algorithm of the \(H_0\) function, we used the information from the definitions and real branches characterized in Theorems 3.1-3.2-3.3. Then, we used the idea of dichotomy (i.e., binary search algorithm) to generate a self-programmed code.

As shown in Fig. 10, we observe that for both \(\alpha >1\) and \(\alpha <1\), \(C_H(t)\) almost coincides with \(C_{Im}(t)\), whereas \(C_{RK}(t)\) is significantly different from \(C_{Im}(t)\). Specifically, a large portion of \(C_{RK}(t)\) is below \(C_{Im}(t)\) for \(\alpha <1\), while it is above \(C_{Im}(t)\) for \(\alpha >1\). These results indicate a distortion of \(C_{RK}(t)\).

To quantify the distortion, we computed the absolute relative error between the results obtained using ode45 and our direct method of \(H_0\) function (which gives the same results as implicit):

$$\begin{aligned}\mathrm{Error(t)}=\Big |\frac{C_{RK}(t)-C_H(t)}{C_H(t)}\Big |.\end{aligned}$$

As shown in Fig. (10)e and f, the relative error can reach 300–800% for \(\alpha >1\). This phenomenon is still observed even when a higher tolerance of \(\varepsilon =10^{-7}\) is used (results not shown).

Fig. 10
figure 10

Numerical estimation of drug concentrations over time of Model (2.5) and the absolute relative error of ode45 compared to the direct method based on \(H_0\) function. From left to right: \(\alpha =0.2, 1.5, 2\). Upper panels: drug concentrations calculated using different algorithms; lower panels: the absolute relative error. \(C_{RK}(t)\): red dot lines; \(C_{H}(t)\): blue solid lines; \(C_{Im}(t)\): green solid lines. \(D=4\,mg\), \(V_{\max }=1\,mg/h/L\), \(K_{D}=0.15mM\), \(V_{d}=1\,L\), and the tolerance level is set to \(\varepsilon =10^{-3}\)

Full size image

5 Conclusion and Discussion

The main objective of this paper is to investigate the morphism and stability of the real branches of a newly discovered transcendent H function. This function arises from one-compartmental pharmacokinetic models with sigmoidal Hill elimination [16]. The idea for this investigation comes from the morphism of the well-known Lambert W function and our recent work on the X function, a generalized version of the Lambert W function that we discovered in the pharmacokinetic model of simultaneous linear and Michaelis–Menten elimination pathways [15]. The Lambert W function has two real branches, the principal branch \(W_0(s)\) defined for \(s\in [-1,+\infty )\) and the other branch \(W_{-1}(s)\) defined for \(s\in [-1,0)\), while the X function has a more complicated morphism of real branches [13, 15]. Additionally, there are a variety of applications that involve these real branches of the Lambert W function in real-world problems such as physics, physiology, epidemiology, pharmacokinetics, etc. [13, 14, 19, 20]. These applications highlight the potential and significance of such transcendent functions in solving nonlinear problems. We have proven that the transcendent H function is a natural extension of the Lambert W function. Furthermore, sigmoidal saturated Hill kinetics have wide recognition in biochemistry and pharmacology due to diverse biochemical activities [18]. Therefore, it is important to explore the mathematical properties of the H function and analyze its real branches, which will help us further our understanding of similar mathematical models, such as pharmacokinetic models with sigmoidal Hill elimination and first-order absorption.

Another concern of ours is the numerical stability of the H function. Unlike the Lambert W function, the morphism of the H function has multiple real branches, which are highly sensitive to the Hill coefficient \(\alpha \). In simulations and investigations in real-world science, only rational numbers can be used in numerical computations. Therefore, if \(\alpha \) is not a rational number, can its rational approximations provide a close approximation of the truth? This problem lies at the intersection of pure and applied mathematics.

To outline the morphism of the H function, we first considered \(\alpha \) as a rational number. The algebraic advantage of expressing \(\alpha \in \mathbb {Q}\) as a fraction with co-prime numerator p and denominator q shortens the process of determining the real branches and their mathematical properties. For all these morphisms, a common characteristic is the presence of the positive principal real branch \(H_0(s,\alpha )\), while they greatly differ in other real branches. If \(\alpha \) is an irrational number, this situation causes instability on other real branches, which continuously shift among three morphisms as \(\alpha \) is approached numerically by its rational approximates. Finally, the only stable real branch is proved to be the principal real branch \(H_0(s,\alpha )\), which is what we encounter in practical situations. For instance, as the Hill coefficient \(\alpha \) is a highly sensitive parameter for certain drugs’ pharmacology, its value is usually established through data fitting using approximations with several decimal digits, which raises concerns about the stability of these principal real branches \(H_0(s,\alpha )\). Our results have provided a positive answer!

We get also intrigued by the uncertainty associated with different numerical model solvers, particularly their robustness in terms of accuracy. Most models are described using differential equations, making ODE solvers straightforward to use and manipulate, but the conditions for their use are often challenging to analyze without expert knowledge. As pharmacokinetic models become increasingly complex, the choice of solvers becomes subjective. Our simulations confirm this. In fact, solvers based on the algebraic form, such as the implicit function solver, are the most robust. In our case, we have developed an algorithm to calculate the H function [16], which has been shown to be as efficient as the former. Furthermore, representing the model solution using the H function can provide a better understanding of the underlying mechanism. All of these highlight the progress made in closed-form solutions and their benefits for non-expert users. It is therefore an important consideration for mathematical developers.