The Stochastic Periodic Behavior of a Chemostat Model with Periodic Nutrient Input

Abstract

In this paper, we study the stochastic periodic behavior of a chemostat model with periodic nutrient input. We first prove the existence of global unique positive solution with any initial value for stochastic non-autonomous periodic chemostat system. After that, the sufficient conditions are established for the existence of nontrivial positive $T-$periodic solution. Moreover, we also analyze the conditions for extinction exponentially of microorganism, and we find that there exists a unique boundary periodic solution for stochastic chemostat model, which is globally attractive. At the same time, in the end of this paper, we also give some numerical simulations to illustrate our main conclusions.

1 Introduction

The chemostat is mainly used for continuous culture of microorganisms. The basic design and theory of continuous culture were originally described independently by [1, 2]. Chemostat consists of three parts, namely, nutrient vessel, culture vessel and collection vessel. In industry, chemostats can be used to simulate the decomposition of biological wastes, or evolve water with microorganisms, etc. In [3,4,5,6,7,8,9], many authors have analyzed various deterministic chemostat models and introduced many mathematical methods for analyzing chemostat models.

In chemostat, a single microbial growth model was first proposed by [1]. Moreover, in [3], Smith and Waltman described a deterministic chemostat model with Monod-type functional response function, as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} S'(t)=(S^0-S(t))D-\frac{mS(t)x(t)}{\delta (a+S(t))},\\ x'(t)=-Dx(t)+\frac{mS(t)x(t)}{a+S(t)}, \end{array}\right. \end{aligned}$$

(1.1)

where all parameters are positive constants, and S(t), x(t) stand for the concentrations of the nutrient and microorganism at time t respectively; $S^0$ represents the input concentration of the nutrient; D is the common washout rate; $\delta$ is a yield constant reflecting the conversion of nutrient to organism. $\frac{mS(t)}{a+S(t)}$ denotes the Monod growth functional response, where $m>0$ is called the maximal growth rate and $a>0$ is the Michaelis-Menten ( or half-saturation ) constant [1].

In model (1.1), if the nutrient supply is periodic, that is to say, we replace $S^0$ with $S^0+be(t)$, where e(t) denotes the fluctuation of nutrient input and it is a continuous and $T-$periodic function ($e(t+T)=e(t)$) with $be_*=b(\min _{t\in [0,T]}e(t))>-S^0$ and $\int _0^T e(t)\textrm{d}t=0$, which is to simulate seasons or day/night cycles in a chemostat environment; b is the amplitude of nutrient supply. Thus, we obtain a deterministic chemostat model with periodic nutrient input, as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} S'(t)=(S^0+be(t)-S(t))D-\frac{mS(t)x(t)}{\delta (a+S(t))},\\ x'(t)=-Dx(t)+\frac{mS(t)x(t)}{a+S(t)}. \end{array}\right. \end{aligned}$$

(1.2)

Model (1.2) is first established and studied by [10]. Furthermore, in [11, 12], a model of two species consuming a single, limited, periodically added resource is discussed, and coexistence of two species due to seasonal variation is indicated by numerical studies; in [13], the author considered a model of the competition of n species for a single essential periodically fluctuating nutrient. For two species systems the following very general result is proven: all solutions of a $T-$periodic, dissipative, competitive system are either $T-$periodic or approach a $T-$periodic solution.

However, the system (1.2) will inevitably be disturbed by some random environmental factors. In the process of continuous cultivation of microorganisms, even if the experimental conditions can be well controlled, we can not ignore the interference of external environment and human factors on the continuous cultivation of microorganisms. Therefore, it is of great practical significance to consider the stochastic chemostat model. In recent years, various stochastic chemostat models have been introduced and studied by many authors, see [14,15,16,17,18,19,20,21,22,23,24]. For example, in [14], Sun et.al studied a stochastic two-species Monod-type competition chemostat model which is subject to environment noises. Such noises are described by independent standard Brownian motions. In [15], the authors studied a stochastic differential equation (SDE) version of the chemostat model with white noise on the positive parameter m (maximal growth rate). In [16], a variant of the deterministic single-substrate chemostat model is studied, and modeled the influence of random fluctuations by setting up and analyzing a stochastic differential equation (SDE). In [17], the authors considered the problem of a single-species stochastic chemostat model in which the maximal growth rate is influenced by the white noise in environment. In [18], a stochastic chemostat model with an inhibitor is considered. In [19, 20], Sun and Zhang considered the asymptotic behavior of a stochastic delayed chemostat model with nutrient storage and nonmonotone uptake function respectively.

Generally, there are many ways to establish stochastic chemostat models by introducing stochastic environmental variation described by Brownian motion in deterministic chemostat model. In [25], Xu and Yuan replaced the washout rate D by $D+\alpha {\dot{B}}(t)$, where B(t) is Brownian motion and $\alpha \ge 0$ is the intensity of noise. In [17], they tackled the problem of stochastic with maximum growth rate m disturbed by noise. In [19], the authors assumed that stochastic perturbations are the white noise type which are directly proportional to S(t) and x(t). In general, the noise intensity is a positive constant in many the existing literatures, however, the stochastic chemostat model with periodic disturbance is seldom studied. Therefore, in this paper, we will consider a stochastic chemostat model with periodic nutrient input and periodic interference, meanwhile, we also consider the natural death of microorganism. We assume that stochastic perturbations are the white noise type which are directly proportional to S(t) and x(t) in system. Thus, the stochastic chemostat model with periodic nutrient input and periodic interference can be expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} \textrm{d}S(t)=[(S^0+be(t)-S(t))D-\frac{mS(t)x(t)}{\delta (a+S(t))}]\textrm{d}t+\sigma _1(t)S(t)\textrm{d}B_1(t),\\ \textrm{d}x(t)=[-D_1x(t)+\frac{mS(t)x(t)}{a+S(t)}]\textrm{d}t+\sigma _2(t)x(t)\textrm{d}B_2(t), \end{array}\right. \end{aligned}$$

(1.3)

where $D_1=D+\kappa$, $\kappa$ is the natural death rate of microorganism x, $B_i(t) (i=1,2)$ are mutually independent standard Brownian motion defined on a complete probability space ($\Omega , {\mathscr {F}}, {\mathbb {P}}$) with a filtration $\{{{\mathscr {F}}}_t\}_{t\ge 0}$ satisfying the usual conditions (i.e., it is increasing and right continuous while ${\mathscr {F}}_0$ contains all ${\mathbb {P}}$-null sets ), $\sigma _i(t)(i=1,2)$ denote the intensity of the white noise with $\sigma _i(t)>0 (i=1,2)$ for any $t>0$, and it is a continuous and $T-$periodic function with $\sigma _i(t+T)=\sigma _i(t) (i=1,2)$.

At present, some works have been discussed on stochastic periodic chemostat model, see [26,27,28], in [26], a stochastic chemostat model with periodic washout rate is proposed and the sufficient conditions are established for the existence of stochastic nontrivial positive periodic solution for the chemostat system. [27] addressed a stochastic chemostat model with periodic dilution rate and general class of response functions, derived the sufficient criteria for the existence of the stochastic nontrivial positive periodic solution. In [28], Zhao and Yuan formulated a single-species stochastic chemostat model with periodic coefficients due to seasonal fluctuation.

Thus, this paper is organized as follows. In Sect. 2, some preliminaries are given. In Sect. 3, we will prove the existence and uniqueness of global positive solutions of the system (1.3) for any initial value. In Sect. 4, we obtain the sufficient conditions for the existence of the stochastic nontrivial positive $T-$periodic solution. Sufficient conditions for the extinction of microorganism are given in Sect. 5. In Sect. 6, we find that there is a globally attractive boundary periodic solution for system (1.3). In Sects. 7 and 8, some numerical simulations and conclusions are given.

2 Preliminary

In this section, we will introduce some preliminaries and notations, which will be needed later.

First, we define some notations. If f(t) is an integrable function on $[0,\infty )$, then we define $\langle f\rangle _t=\frac{1}{t}\int _0^tf(s)\textrm{d}s$ for any $t>0$; if f(t) is a bounded function on $[0,\infty )$, we can define $f^*=\sup _{t\in [0,\infty )}f(t)$, $f_*=\inf _{t\in [0,\infty )}f(t)$.

Next, we will give some preliminaries about periodic Markov process (see [29] for details).

Definition 2.1

([29], Chapter 3) A stochastic process $X(t,\omega )$ with values in ${\mathbb {R}}^l$, defined for $t\ge 0$ on a probability space ($\Omega , {\mathscr {F}}, {\mathbb {P}}$), is called a Markov process if for all $A\in {\mathcal {B}}$ (where ${\mathcal {B}}$ is the Borel $\sigma -$algebra), $0\le s<t$,

$$\begin{aligned} {\mathbb {P}}\{X(t,\omega )\in A|{\mathcal {N}}_s\}={\mathbb {P}}\{X(t,\omega )\in A|X(s,\omega )\},\ \ a.s., \end{aligned}$$

where $\omega$ is a sample point in space $\Omega$, and ${\mathcal {N}}_s$ is the $\sigma -$algebra of events generated by all events of the form

$$\begin{aligned} \{X(u,\omega )\in A\}\ \ (u\le s, A\in {\mathcal {B}}). \end{aligned}$$

Remark 2.1

([29]) It can be proved that there exists a function P(s, x, t, A), defined for $0\le s\le t$, $x\in {\mathbb {R}}^l$, $A\in {\mathcal {B}}$, which is ${\mathcal {B}}-$measurable in x for every fixed s, t, A,  and which constitutes a measure as a function of the set A, satisfying the condition

$$\begin{aligned} {\mathbb {P}}\{X(t,\omega )\in A|X(s,\omega )\}=P\{s,X(s,\omega ),t,A\}\ \ a.s. \end{aligned}$$

One can also prove that for all x, except possibly those from a set B such that ${\mathbb {P}}\{X(s,\omega )\in B\}=0$, the Chapman-Kolmogorov equation holds:

$$\begin{aligned} P\{s,x,t,A\}=\int _{{\mathbb {R}}^l}P(s,x,u,dy)P(u,y,t,A). \end{aligned}$$

The function $P\{s,x,t,A\}$ is called the transition probability function of the Markov process.

Definition 2.2

([29]) A stochastic process $X(t)\ (-\infty<t<+\infty )$ is said to be periodic with period T if for every finite sequence of numbers $t_1,t_2,...,t_n$, the joint distribution of random variables $X(t_1+h),...,X(t_n+h)$ is independent of h, where $h=kT\ (k=\pm 1,\pm 2,...)$.

Remark 2.2

In [29], Khasminskii shows that a Markov process X(t) is $T-$periodic if only if its transition probability function is $T-$periodic and the function $P(0,X(0,\omega ),t,A):=P_0(t,A)={\mathbb {P}}\{X(t)\in A| X(0,\omega )\}$ satisfies the equation

$$\begin{aligned} P_0(s,A)=\int _{{\mathbb {R}}^l}P_0(s,dx)P(s,x,s+T,A)\equiv P_0(s+T,A), \end{aligned}$$

for every $A\in {\mathcal {B}}$. We consider the following equation

$$\begin{aligned} X(t)=X(t_0)+\int _{t_0}^tb(s,X(s))\textrm{d}s+\sum _{r=1}^k\int _{t_0}^t\sigma _r(s,X(s))dB_r(s), \end{aligned}$$

(2.1)

where the vector $b(s,x),\sigma _1(s,x),...,\sigma _k(s,x)(s\in [t_0,T],x\in {\mathbb {R}}^l)$ are continuous functions of (s, x), such that for some constant C the following conditions hold:

$$\begin{aligned} |b(s,x)-b(s,y)|+\sum _{r=1}^k|\sigma _r(s,x)-\sigma _r(s,y)|\le C|x-y|, \end{aligned}$$

(2.2)

and

$$\begin{aligned} |b(s,x)|+\sum _{r=1}^k|\sigma _r(s,x)|\le C(1+|x|), \end{aligned}$$

(2.3)

Let U be a given open set, and $E=I\times {\mathbb {R}}^l$. Let $C^2$ denote the family of functions on E which are twice continuously differentiable with respect to $x_1,x_2,...,x_l$ and continuously differentiable with respect to t.

Lemma 2.1

Suppose that the coefficient of (2.1) is $T-$periodic in t and satisfies the conditions (2.2) and (2.3) in every cylinder $I\times U$ and suppose further that there exists a function $V(t,x)\in C^2$ in E which is $T-$periodic in t, and satisfies the following conditions

$$\begin{aligned} \inf _{|x|>H}V(t,x)\rightarrow \infty \ \ \ \textrm{as}\ \ H\rightarrow \infty \end{aligned}$$

(2.4)

and

$$\begin{aligned} LV(t,x)\le -1\ \mathrm {outside\ some\ compact\ set}, \end{aligned}$$

(2.5)

where the operator L is given by

$$\begin{aligned} l=\frac{\partial }{\partial t}+\sum _{i=1}^lb_i(t,x)\frac{\partial }{\partial x_i}+\frac{1}{2}\sum _{i,j=1}^la_{ij}(t,x)\frac{\partial ^2}{\partial x_i\partial x_j}, \end{aligned}$$

where

$$\begin{aligned} a_{ij}=\sum _{r=1}^k\sigma _r^i(t,x)\sigma _r^j(t,x). \end{aligned}$$

Then there exists a solution of (2.1) which is a $T-$periodic Markov process.

Remark 2.3

The proof of Lemma 2.1 can be found in [29], Chapter 3, Page 80, and condition (2.5) is a weaker condition which replace the condition (3.52) of Theorems 3.7 and 3.8 in [29]. According to the proof of Lemma 2.1, we can see that the conditions (2.2) and (2.3) is only used to guarantee the existence and uniqueness of the solution of (2.1). Thus, it is crucial to prove the existence and uniqueness of the global positive solution of the stochastic chemostat model (1.3) for any given initial value, which is helpful to prove the existence of the nontrivial positive periodic solution of system (1.3). So in the next section, we will prove that the system (1.3) has a global unique positive solution for any given initial value.

3 Existence and Uniqueness of the Global Positive Solution for any Given Initial Value

In this section, we will use Lyapunov function method to prove that the solution of the stochastic chemostat model (1.3) is global, unique and positive for any given initial value.

Theorem 3.1

For any initial value $(S(0),x(0))\in {\mathbb {R}}^2_+$, system (1.3) has a unique positive solution (S(t), x(t)) on $t\ge 0$, and the solution will remain in ${\mathbb {R}}^2_+$ with probability one, namely, $(S(t), x(t)) \in {\mathbb {R}}^2_+$ for all $t\ge 0$ almost surely (a.s).

Proof

Since the coefficients of stochastic system (1.3) satisfy the local Lipschitz condition, then system (1.3) has a unique local solution (S(t), x(t)) on $t\in [0, \tau _\textrm{e})$, where $\tau _\textrm{e}$ is the explosion time [30]. To show this solution is global, we only need to show that $\tau _\textrm{e} = \infty$ a.s. To this end, let $k_0\ge 1$ be sufficiently large such that S(0) and x(0) all lie within the interval $[\frac{1}{k_0},k_0]$. For each integer $k\ge k_0$, define the stopping time

$$\begin{aligned} \tau _k=\inf \left\{ t\in [0,\tau _\textrm{e}):S(t)\notin \left( \frac{1}{k},k\right) \quad \textrm{or} \ \ \ x(t)\notin \left( \frac{1}{k},k\right) \right\} , \end{aligned}$$

where throughout this paper, we set $\inf \emptyset =\infty$ (as usual $\emptyset$ is the empty set). Clearly $\tau _k$ is increasing when $k\rightarrow \infty$. Set $\tau _\infty =\lim _{k\rightarrow \infty }\tau _k$, whence $\tau _\infty \le \tau _\textrm{e}$ a.s. If we can verify $\tau _\infty =\infty$ a.s., then $\tau _\textrm{e}=\infty$ and $(S(t), x(t)) \in {\mathbb {R}}^2_+$ a.s. for all $t\ge 0$. That is to say, to complete the proof we need to show that $\tau _\infty =\infty$ a.s. If this assertion is not true then there is a pair of constants $T>0$ and $\varepsilon \in (0,1)$ such that

$$\begin{aligned} {\mathbb {P}}\{\tau _\infty \le T\}>\varepsilon , \end{aligned}$$

there exists an integer $k_1\ge k_0$ such that for all $k\ge k_1$,

$$\begin{aligned} {\mathbb {P}}\{\tau _k\le T\}\ge \varepsilon . \end{aligned}$$

(3.1)

Define a $C^2-$function $V:{\mathbb {R}}^2_+\rightarrow {\mathbb {R}}_+$ by

$$\begin{aligned} V(S,x)=\delta \left( S+\mu -\mu \ln \frac{S}{\mu }\right) +x+1-\ln x, \end{aligned}$$

where $\mu$ is a positive constant to be determined later. The nonnegativity of this function can be obtained from

$$\begin{aligned} u+1-\ln u>0, \ \ u>0. \end{aligned}$$

Applying Itô formula to V(S, x), we have

$$\begin{aligned} \begin{array}{rl} \textrm{d}V(S,x)=LV(S,x)\textrm{d}t+\delta \sigma _1(t)(S-\mu )\textrm{d}B_1(t)+\sigma _2(t)(x-1)\textrm{d}B_2(t), \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rl} LV(S,x)&{}= \delta \left( 1-\frac{\mu }{S}\right) \big [(S^0+be(t)-S)D-\frac{mSx}{\delta (a+S)}\big ] +\left( 1-\frac{1}{x}\right) \left[ \frac{mSx}{a+S}-D_1x\right] \\ &{}\quad +\frac{1}{2}\delta \mu \sigma _1^2(t)+\frac{1}{2}\sigma _2^2(t)\\ &{}\le \delta DS^0+\delta bDe^*+\mu D\delta +D_1+\frac{1}{2}\delta \mu (\sigma _1^*)^2+\frac{1}{2}(\sigma _2^*)^2+\left( \frac{m\mu }{a}-D_1\right) x. \end{array} \end{aligned}$$

We can choose $\mu =\frac{aD_1}{m}$, such that $(\frac{m\mu }{a}-D_1)x=0$, then we can obtain

$$\begin{aligned} \begin{array}{rl} LV(S,x)\le \delta DS^0+\delta bDe^*+\mu D\delta +D_1+\frac{1}{2}\delta \mu (\sigma _1^*)^2+\frac{1}{2}(\sigma _2^*)^2:= M, \end{array} \end{aligned}$$

where M is a positive constant. Thus we have

$$\begin{aligned} \textrm{d}V(S,x)\le M\textrm{d}t+\delta \sigma _1(t)(S-\mu )\textrm{d}B_1(t)+\sigma _2(t)(x-1)\textrm{d}B_2(t). \end{aligned}$$

(3.2)

Integrating both sides of (3.2) from 0 to $\tau _k\wedge T$ and taking the expectations, we can obtain

$$\begin{aligned} {\mathbb {E}}V\left( S(\tau _k\wedge T),x(\tau _k\wedge T)\right) \le V\left( S(0),x(0)\right) +M{\mathbb {E}}(\tau _k\wedge T). \end{aligned}$$

Consequently

$$\begin{aligned} {\mathbb {E}}V\left( S(\tau _k\wedge T),x(\tau _k\wedge T)\right) \le V\left( S(0),x(0)\right) +MT. \end{aligned}$$

(3.3)

Set $\Omega _k=\{\tau _k\le T\}$ for $k\ge k_1$ and in view of (3.1), we get ${\mathbb {P}}(\Omega _k)\ge \varepsilon$. Notice that for every $\omega \in \Omega _k$, it exists that $S(\tau _k,\omega )$ or $x(\tau _k,\omega )$ equals either k or $\frac{1}{k}$. Thereby, $V\left( S(\tau _k,\omega ),x(\tau _k,\omega )\right)$ is no less than either

$$\begin{aligned} \min \{\delta \left( k+\mu -\mu \ln \frac{k}{\mu }\right) , (k+1-\ln k)\} \end{aligned}$$

or

$$\begin{aligned} \min \left\{ \delta \left( \frac{1}{k}+\mu +\mu \ln k\mu \right) ,\left( \frac{1}{k}+1+\ln k\right) \right\} . \end{aligned}$$

That is

$$\begin{aligned} \begin{array}{rl} V\left( S(\tau _k,\omega ),x(\tau _k,\omega )\right) &{}\ge \min \{\delta (k+\mu -\mu \ln \frac{k}{\mu }), (k+1-\ln k)\}\\ &{}\wedge \min \{\delta (\frac{1}{k}+\mu +\mu \ln k\mu ),(\frac{1}{k}+1+\ln k)\}\\ &{}:=H(k). \end{array} \end{aligned}$$

It follows from (3.3) that

$$\begin{aligned} \begin{array}{rl} V(S(0),x(0))+KT &{}\ge {\mathbb {E}}\left( I_{\Omega _k}(\omega )V\left( S(\tau _k,\omega ),x(\tau _k,\omega )\right) \right) \\ &{}\ge {\mathbb {P}}\left( \Omega _k(\omega )\right) \\ H(k)&{}\ge \varepsilon H(k), \end{array} \end{aligned}$$

where $I_{\Omega _k}$ represents the indicator function of $\Omega _k$. Letting $k\rightarrow \infty$, then

$$\begin{aligned} \infty >V\left( S(0),x(0)\right) +KT=\infty , \end{aligned}$$

which leads to the contradiction. Thus we must have $\tau _\infty =\infty$. Therefore, it implies S(t) and x(t) will not explode in a finite time with probability one. This completes the proof. $\square$

4 Existence of the Nontrivial Positive $T-$Periodic Solution

In Sect. 3, we have proved that there exists a global unique positive solution for system (1.3) for any given initial value. In this section, we will prove the existence and uniqueness of the positive periodic solution.

Theorem 4.1

Let $\lambda =\frac{mS^0}{a+S^0}-D_1-\langle R_0\rangle _T$, if there exists a positive constant $c_1$ satisfying

$$\begin{aligned} c_1>\frac{ma}{D(S^0)^2}, \end{aligned}$$

such that $\lambda >0$, then stochastic system (1.3) has a nontrivial positive $T-$periodic solution, where

$$\begin{aligned} R_0(t)=c_1Dbe(t)+\frac{c_1S^0}{2}\sigma _1^2(t)+\frac{1}{2}\sigma _2^2(t). \end{aligned}$$

Proof

From Theorem 3.1, we know that for any initial value $(S(0),x(0))\in {\mathbb {R}}^2_+$, stochastic periodic system (1.3) has a unique positive solution (S(t), x(t)) on $t\ge 0$, and the solution will remain in ${\mathbb {R}}^2_+$ with probability one. It is very easy to verify that the coefficients of system (1.3) satisfy the conditions of Lemma 2.1. According to Lemma 2.1, we need to find a $C^2-$function V(t, S, x) and a closed set $U\in {\mathbb {R}}^2_+$, such that the (2.4) and (2.5) hold. Define a $C^2-$function $V(t,S,x): [0,+\infty )\times {\mathbb {R}}^2_+\rightarrow {\mathbb {R}}$:

$$\begin{aligned} \begin{array}{rl} V(t,S,x)&{}=\frac{1}{\theta +1}(\delta S+x)^{\theta +1}+M[c_1(S-S^0-S^0\ln \frac{S}{S^0})\\ {} &{} -c_2(\delta S+x)-\ln x+\omega (t)]-\ln S\\ &{}:=V_1+MV_2+V_3, \end{array} \end{aligned}$$

where $V_1=\frac{1}{\theta +1}(\delta S+x)^{\theta +1},$ $V_2=c_1(S-S^0-S^0\ln \frac{S}{S^0})-c_2(\delta S+x)-\ln x+\omega (t),$ $V_3=-\ln S,$ $c_2=\frac{ma}{\delta D(a+S^0)^2},$ and $\theta \in (0,1)$ satisfies

$$\begin{aligned} D-\frac{\theta }{2}(\sigma _1^*)^2>0, \end{aligned}$$

and

$$\begin{aligned} D_1-\frac{\theta }{2}(\sigma _2^*)^2>0. \end{aligned}$$

Meanwhile $\omega (t)$ satisfies

$$\begin{aligned} {\dot{\omega }}(t)=\langle R_0\rangle _T-R_0(t) \end{aligned}$$

where

$$\begin{aligned} R_0(t)=c_1Dbe(t)+\frac{c_1S^0}{2}\sigma _1^2(t)+\frac{1}{2}\sigma _2^2(t). \end{aligned}$$

It is obvious that $\omega (t)$ is $T-$periodic, that’s because $R_0(t)$ is $T-$periodic. M is a positive constant big enough such that

$$\begin{aligned} f^*-M\lambda \le -2, \end{aligned}$$

where the function f will be determined later. By Itô formula, we have

$$\begin{aligned}{} & {} \begin{array}{rl} LV_1&{}=(\delta S+x)^\theta \left( \delta D(S^0+be(t)-S)-D_1x\right) \\ &{}\quad +\frac{\theta }{2}(\delta S+x)^{\theta -1}(\delta ^2\sigma _1^2(t)S^2+\sigma _2^2(t)x^2)\\ &{}\le (\delta DS^0+\delta Dbe^*)(\delta S+x)^\theta -\delta DS(\delta S+x)^\theta -D_1x(\delta S+x)^\theta \\ &{}\quad +\frac{\theta }{2}(\delta S+x)^{\theta -1}(\delta ^2S^2\sigma _1^2(t)+\sigma _2^2(t)x^2)\\ &{}\le 2^\theta (\delta DS^0+\delta Dbe^*)(\delta S)^\theta +2^\theta (\delta DS^0+\delta Dbe^*)x^\theta -D(\delta S)^{\theta +1}-D_1x^{\theta +1}\\ &{}\quad +\frac{\theta }{2}\sigma _1^2(t)(\delta S)^{\theta +1}+\frac{\theta }{2}\sigma _2^2(t)x^{\theta +1}\\ &{}\le 2^\theta \delta ^{\theta +1}D(S^0+be^*)S^\theta +2^\theta \delta D(S^0+be^*)x^\theta -\left( D\delta ^{\theta +1}-\frac{\theta }{2}(\sigma _1^*)^2\delta ^{\theta +1}\right) S^{\theta +1}\\ &{}\quad -\left( D_1-\frac{\theta }{2}(\sigma _2^*)^2\right) x^{\theta +1}, \end{array} \\{} & {} \begin{array}{rl} L(S-S^0-S^0\ln \frac{S}{S^0})&{}=\left( 1-\frac{S^0}{S}\right) [(S^0+be(t)-S)D-\frac{mSx}{\delta (a+S)}]+\frac{1}{2}S^0\sigma _1^2(t)\\ &{}=-\frac{D(S-S^0)^2}{S}+Dbe(t)\left( 1-\frac{S}{S^0}\right) -\frac{m(S-S^0)x}{\delta (a+S)}+\frac{1}{2}S^0\sigma _1^2(t)\\ &{}\le -\frac{D(S-S^0)^2}{S}+Dbe(t)+\frac{mS^0}{\delta a}x+\frac{1}{2}S^0\sigma _1^2(t), \end{array} \\{} & {} \begin{array}{rl} L(\delta S+x)=\delta D(S^0+be(t)-S)-D_1x, \end{array} \\{} & {} \begin{array}{rl} L(-\ln x)&{}=-\frac{1}{x}[-D_1x+\frac{mSx}{a+S}]+\frac{1}{2}\sigma _2^2(t)\\ &{}=D_1-\frac{mS}{a+S}+\frac{1}{2}\sigma _2^2(t). \end{array} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{array}{rl} LV_2&{}\le -\frac{c_1D(S-S^0)^2}{S}+c_1Dbe(t)+\frac{c_1mS^0}{\delta a}x+\frac{1}{2}c_1S^0\sigma _1^2(t)+c_2\delta D(S-S^0)-c_2\delta Dbe(t)\\ &{}\quad +c_2D_1x+D_1-\frac{mS}{a+S}+\frac{1}{2}\sigma _2^2(t)+{\dot{\omega }}(t)\\ &{}\le F(S)+\left( \frac{c_1mS^0}{\delta a}+c_2D_1\right) x-\left( \frac{mS^0}{a+S^0}-D_1-\langle R_0\rangle _T\right) , \end{array} \end{aligned}$$

where

$$\begin{aligned} F(S)=\frac{mS^0}{a+S^0}-\frac{mS}{a+S}+c_2\delta D(S-S^0)-\frac{c_1D(S-S^0)^2}{S}. \end{aligned}$$

By calculation, we can get

$$\begin{aligned} F'(S)=-\frac{ma}{(a+S)^2}+c_2\delta D-c_1D\left( 1-\frac{(S^0)^2}{S^2}\right) , \end{aligned}$$

and

$$\begin{aligned} F''(S)=\frac{2ma}{(a+S)^3}-2c_1D(S^0)^2\frac{1}{S^3}. \end{aligned}$$

It is obviously that

$$\begin{aligned} F'(S^0)=0,\ \ \ F''(S^0)\le \frac{1}{(S^0)^3}[2ma-2c_1D(S^0)^2]<0. \end{aligned}$$

Therefore, we have

$$\begin{aligned} F(S)\le F(S^0)=0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \begin{array}{rl} LV_2&\le -\lambda +\left( \frac{c_1mS^0}{\delta a}+c_2D_1\right) x, \end{array} \end{aligned}$$

where

$$\begin{aligned}{} & {} \lambda =\frac{mS^0}{a+S^0}-D_1-\langle R_0\rangle _T. \\{} & {} \begin{array}{rl} LV_3&{}=-\frac{D}{S}(S^0+be(t)-S)+\frac{mx}{\delta (a+S)}+\frac{1}{2}\sigma _1^2(t)\\ &{}=-\frac{DS^0}{S}+D-\frac{Db}{S}e(t)+\frac{mx}{\delta (a+S)}+\frac{1}{2}\sigma _1^2(t)\\ &{}\le -\frac{DS^0}{S}+D-\frac{Db}{S}e_*+\frac{mx}{\delta a}+\frac{1}{2}(\sigma _1^*)^2\\ &{}=-\frac{DS^0+Dbe_*}{S}+D+\frac{mx}{\delta a}+\frac{1}{2}(\sigma _1^*)^2, \end{array} \end{aligned}$$

Therefore, we can obtain

$$\begin{aligned} \begin{array}{rl} LV&{}=LV_1+MLV_2+LV_3\\ &{}\le 2^\theta \delta ^{\theta +1}D(S^0+be^*)S^\theta +2^\theta \delta D(S^0+be^*)x^\theta -(D\delta ^{\theta +1}-\frac{\theta }{2}(\sigma _1^*)^2\delta ^{\theta +1})S^{\theta +1}\\ &{}-(D_1-\frac{\theta }{2}(\sigma _2^*)^2)x^{\theta +1}-M\lambda +M\left( \frac{c_1mS^0}{\delta a}+c_2D_1\right) x-\frac{DS^0+Dbe_*}{S}+D+\frac{1}{2}(\sigma _1^*)^2+\frac{mx}{\delta a}\\ &{}=f(S)+g(x), \end{array} \end{aligned}$$

where

$$\begin{aligned} f(S)= & {} 2^\theta \delta ^{\theta +1}D(S^0+be^*)S^\theta -(D\delta ^{\theta +1}-\frac{\theta }{2}(\sigma _1^*)^2\delta ^{\theta +1})S^{\theta +1} \\{} & {} -\frac{DS^0+Dbe_*}{S}+D+\frac{1}{2}(\sigma _1^*)^2, \\ g(x)= & {} 2^\theta \delta D(S^0+be^*)x^\theta -(D_1-\frac{\theta }{2}(\sigma _2^*)^2)x^{\theta +1} \\{} & {} -M\lambda +M\left( \frac{c_1mS^0}{\delta a}+c_2D_1\right) x+\frac{mx}{\delta a}. \end{aligned}$$

It is noteworthy that g(x) has upper bounds $g^*$ when $S\rightarrow +\infty$ or $S\rightarrow 0^+$, and f(x) also has upper bounds $f^*$ when $x\rightarrow +\infty$ or $x\rightarrow 0^+$. Thus, we can observe that

$$\begin{aligned}{} & {} f(S)+g^*\rightarrow -\infty ,\ \ \ \textrm{as}\ S\rightarrow +\infty , \\{} & {} f^*+g(x)\rightarrow -\infty ,\ \ \ \textrm{as}\ x\rightarrow +\infty , \\{} & {} f(S)+g^*\rightarrow -\infty ,\ \ \ \textrm{as}\ S\rightarrow 0^+, \\{} & {} f^*+g(x)\rightarrow f^*-M\lambda \le -1,\ \ \ \textrm{as}\ x\rightarrow 0^+, \end{aligned}$$

This shows that we can take $\varepsilon$ small enough, and let $U=[\varepsilon ,\frac{1}{\varepsilon }]\times [\varepsilon ,\frac{1}{\varepsilon }]$. We can obtain that

$$\begin{aligned} LV\le -1,\ (S,x)\in {\mathbb {R}}^2_+\setminus U. \end{aligned}$$

This completes the proof. $\square$

Remark 4.1

From Theorem 4.1, we can see that the model (1.3) has a nontrivial $T-$periodic solution, that is to say, under the condition of Theorem 4.1, the microorganism x can survive in chemostat.

5 Extinction of Microorganism

In this section, we will study the conditions for the extinction of microorganism x. Before we give the main theorem, we first give the following two important lemmas, which is very helpful for the proof of the main theorem.

Lemma 5.1

Let (S(t), x(t)) be the solution of system (1.3) with any initial value $(S(0),x(0))\in {\mathbb {R}}^2_+$. Then we have

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{\delta S(t)+x(t)}{t}=0\ \ a.s. \end{aligned}$$

Moreover

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{S(t)}{t}=0, \ \ \lim _{t\rightarrow \infty }\frac{x(t)}{t}=0\ \ a.s. \end{aligned}$$

Proof

Let $u(t)=\delta S(t)+x(t)$. Define a $C^2-$function

$$\begin{aligned} W(u)=(1+u)^\alpha , \end{aligned}$$

where $\alpha$ is a positive constant to be determined later, and it satisfies $1<\alpha <\frac{2D}{(\sigma _1^*)^2\vee (\sigma _2^*)^2}+1$. Then, we have

$$\begin{aligned} \textrm{d}W(u)=LW(u)\textrm{d}t+\alpha (1+u)^{\alpha -1}(\delta \sigma _1(t) S\textrm{d}B_1(t)+\sigma _2(t)x\textrm{d}B_2(t)), \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rl} LW(u)&{}=\alpha (1+u)^{\alpha -1}[\delta D(S^0+be(t)-S)-D_1x]\\ {} &{} \quad +\frac{\alpha (\alpha -1)}{2}(1+u)^{\alpha -2}[\sigma _1^2(t)(\delta S)^2+\sigma _2^2(t)x^2]\\ &{}=\alpha (1+u)^{\alpha -2}\{(1+u)[\delta D(S^0+be(t)-S)-D_1x]\\ {} &{}\quad +\frac{\alpha -1}{2}[\sigma _1^2(t)(\delta S)^2+\sigma _2^2(t)x^2]\}\\ &{}\le \alpha (1+u)^{\alpha -2}\{(1+u)[\delta D(S^0+be^*)-Du]+\frac{\alpha -1}{2}[(\sigma _1^*)^2\vee (\sigma _2^*)^2]u^2\}\\ &{}=\alpha (1+u)^{\alpha -2}\{-[D-\frac{\alpha -1}{2}((\sigma _1^*)^2\vee (\sigma _2^*)^2)]u^2\\ &{}\quad +[\delta D(S^0+be^*)-D]u+\delta D(S^0+be^*)\}. \end{array} \end{aligned}$$

Since $1<\alpha <\frac{2D}{(\sigma _1^*)^2\vee (\sigma _2^*)^2}+1$, we get

$$\begin{aligned} D-\frac{\alpha -1}{2}((\sigma _1^*)^2\vee (\sigma _2^*)^2):=A>0, \end{aligned}$$

and

$$\begin{aligned} \delta D(S^0+be^*):=B. \end{aligned}$$

Then, we have

$$\begin{aligned} LW(u)\le \alpha (1+u)^{\alpha -2}\{-Au^2+(B-D)u+B\}, \end{aligned}$$

(5.1)

and

$$\begin{aligned} \begin{array}{rl} \textrm{d}W(u)&{}\le \alpha (1+u)^{\alpha -2}[-Au^2+(B-D)u+B]\textrm{d}t\\ &{}+\alpha (1+u)^{\alpha -1}[\delta \sigma _1(t) S\textrm{d}B_1(t)+\sigma _2(t)x\textrm{d}B_2(t)]. \end{array} \end{aligned}$$

(5.2)

For $0<k<\alpha A$, we have

$$\begin{aligned} \begin{array}{rl} \textrm{d}[e^{kt}W(u)]=L(e^{kt}W(u))\textrm{d}t+e^{kt}\alpha (1+u)^{\alpha -1}[\delta \sigma _1(t) S\textrm{d}B_1(t)+\sigma _2(t)x\textrm{d}B_2(t)], \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rl} L(e^{kt}W(u))&{}=ke^{kt}W(u)+e^{kt}LW(u)\\ &{}\le ke^{kt}(1+u)^\alpha +e^{kt}\alpha (1+u)^{\alpha -2}[-Au^2+(B-D)u+B]\\ &{}=e^{kt}(1+u)^{\alpha -2}\{k(1+u)^2+\alpha [-Au^2+(B-D)u+B]\}\\ &{}=e^{kt}(1+u)^{\alpha -2}\{-(\alpha A-k)u^2+[\alpha (B-D)+2k]u+B\alpha +k\}\\ &{}\le e^{kt}H, \end{array} \end{aligned}$$

where

$$\begin{aligned} H:=\sup _{u\in {\mathbb {R}}^2_+}(1+u)^{\alpha -2}\{-(\alpha A-k)u^2+[\alpha (B-D)+2k]u+B\alpha +k\}. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{array}{rl} {\mathbb {E}}[e^{kt}W(u(t))]&{}=W(u(0))+{\mathbb {E}}\int _0^tL(e^{ks}W(u(s)))\textrm{d}s\\ &{}\le (1+u(0))^\alpha +\frac{e^{kt}H}{k}-\frac{H}{k}. \end{array} \end{aligned}$$

Consequently,

$$\begin{aligned} \lim _{t\rightarrow \infty }\sup {\mathbb {E}}[(1+u(t))^\alpha ]\le \frac{H}{k}:=H_0, \ \ a.s., \end{aligned}$$

which together with the continuity of u(t) implies that there exists a constant $M>0$ such that

$$\begin{aligned} {\mathbb {E}}(1+u(t))^\alpha \le M,\ \ t\ge 0. \end{aligned}$$

(5.3)

Note that (5.2), for sufficiently small $\delta >0, k=1,2,...,$ we have

$$\begin{aligned} {\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha ]\le {\mathbb {E}}[(1+u(k\delta ))^\alpha ]+H_1+H_2\le M+H_1+H_2, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rl} H_1&{}={\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }|\int _{k\delta }^t\alpha (1+u(s))^{\alpha -2}(-Au^2(s)+(B-D)u(s)+B)\textrm{d}s|]\\ &{}\le C_1{\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }|\int _{k\delta }^t(1+u(s))^\alpha \textrm{d}s|]\\ &{}\le C_1{\mathbb {E}}[\int _{k\delta }^{(k+1)\delta }(1+u(s))^\alpha \textrm{d}s]\\ &{}\le C_1\delta {\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha ], \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{rl} H_2&{}={\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }|\int _{k\delta }^t \alpha (1+u(s))^{\alpha -1}(\sigma _1(s)\delta S(s)\textrm{d}B_1(s)+\sigma _2(s)x(s)\textrm{d}B_2(s))|]\\ &{}\le C_2{\mathbb {E}}[\int _{k\delta }^{(k+1)\delta }\alpha ^2(1+u(s))^{2(\alpha -1)} \left( (\sigma _1^*)^2\delta ^2S^2(s)+(\sigma _2^*)^2x^2(s)\right) \textrm{d}s]^{\frac{1}{2}}\\ &{}\le C_2\alpha [(\sigma _1^*)^2\vee (\sigma _2^*)^2]^{\frac{1}{2}}\delta ^{\frac{1}{2}}{\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^{2\alpha }]^{\frac{1}{2}}\\ &{}\le C_2\alpha [(\sigma _1^*)^2\vee (\sigma _2^*)^2]^{\frac{1}{2}}\delta ^{\frac{1}{2}}{\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^{\alpha }]. \end{array} \end{aligned}$$

where in the above inequality, we have used the Burkholder-Davis-Gundy inequality [30]. Thus, we have

$$\begin{aligned}{} & {} {\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha ]\le {\mathbb {E}}[(1+u(k\delta ))^\alpha ] \\{} & {} \quad +[C_1\delta +C_2\alpha ((\sigma _1^*)^2\vee (\sigma _2^*)^2)^{\frac{1}{2}}\delta ^{\frac{1}{2}}]{\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha ]. \end{aligned}$$

We can choose $\delta >0$ such that $C_1\delta +C_2\alpha [(\sigma _1^*)^2\vee (\sigma _2^*)^2]^{\frac{1}{2}}\delta ^{\frac{1}{2}}\le \frac{1}{2}$, then we have

$$\begin{aligned} {\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha ]\le 2{\mathbb {E}}[(1+u(k\delta ))^\alpha ]\le 2M. \end{aligned}$$

Let $\varepsilon >0$ be arbitrary. By Chebyshev’s inequality, we have

$$\begin{aligned} {\mathbb {P}}\{\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha >(k\delta )^{1+\varepsilon }\}\le \frac{{\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha ]}{(k\delta )^{1+\varepsilon }}\\ \le \frac{2M}{(k\delta )^{1+\varepsilon }}, \ k=1,2,... \end{aligned}$$

According to the Borel-Cantelli lemma [30], for almost all $\omega \in \Omega$, we can see that

$$\begin{aligned} \sup _{k\delta \le t\le (k+1)\delta }(1+u(t))^\alpha \le (k\delta )^{1+\varepsilon } \end{aligned}$$

(5.4)

holds for all but finitely many k. Hence, there exists a $k_0(\omega )$, for almost all $\omega \in \Omega$, when $k\ge k_0$, (5.4) holds. Therefore, for almost all $\omega \in \Omega$, if $k\ge k_0$ and $k\delta \le t\le (k+1)\delta$, we can obtain

$$\begin{aligned} \frac{\ln (1+u(t))^\alpha }{\ln t}\le \frac{(1+\varepsilon )\ln k\delta }{\ln k\delta }=1+\varepsilon . \end{aligned}$$

Thus,

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln (1+u(t))^\alpha }{\ln t}\le 1+\varepsilon \ \ a.s.. \end{aligned}$$

Letting $\varepsilon \rightarrow 0$, yields

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln (1+u(t))^\alpha }{\ln t}\le 1\ \ a.s.. \end{aligned}$$

For $1<\alpha <\frac{2D}{(\sigma _1^*)^2\vee (\sigma _2^*)^2}+1$, we have $D>\frac{\alpha -1}{2}[(\sigma _1^*)^2\vee (\sigma _2^*)^2]$, so

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln u(t)}{\ln t}\le \limsup _{t\rightarrow \infty }\frac{\ln (1+u(t))}{\ln t}\le \frac{1}{\alpha }\ \ a.s.. \end{aligned}$$

That is to say, for any small $0<\xi <1-\frac{1}{\alpha }$, there exists a constant $T=T(\omega )$ and a set $\Omega _\xi$ such that ${\mathbb {P}}(\Omega _\xi )\ge 1-\xi$ and for any $t\ge T$, $\omega \in \Omega _\xi$, we have

$$\begin{aligned} \ln u(t)\le \left( \frac{1}{\alpha }+\xi \right) \ln t \end{aligned}$$

and so

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{u(t)}{t}\le \limsup _{t\rightarrow \infty }\frac{t^{\frac{1}{\alpha }+\xi }}{t} =\limsup _{t\rightarrow \infty }t^{\frac{1}{\alpha }+\xi -1}=0, \end{aligned}$$

which together with the positive of the solution implies

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{u(t)}{t}=\lim _{t\rightarrow \infty }\frac{\delta S(t)+x(t)}{t}=0\ \ a.s. \end{aligned}$$

(5.5)

Together with the positive of the solution and (5.5), we have

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{S(t)}{t}=0,\ \ \lim _{t\rightarrow \infty }\frac{x(t)}{t}=0\ \ a.s.. \end{aligned}$$

This completes the proof. $\square$

Lemma 5.2

Assume $2D>(\sigma _1^*)^2\vee (\sigma _2^*)^2$. Let (S(t), x(t)) be the solution of system (1.3) with any initial value $(S(0),x(0))\in {\mathbb {R}}^2_+$, then

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{\int _0^t S(s)\textrm{d}B_1(s)}{t}=0,\ \ \lim _{t\rightarrow \infty }\frac{\int _0^t x(s)\textrm{d}B_2(s)}{t}=0. \end{aligned}$$

Proof

Let $M(t)=\int _0^t S(s)\textrm{d}B_1(s)$, $N(t)=\int _0^t x(s)\textrm{d}B_2(s)$ and $2<\alpha <\frac{2D}{(\sigma _1^*)^2\vee (\sigma _2^*)^2}+1$. By Burkholder-Davis-Gundy inequality [30] and (5.3), we have

$$\begin{aligned} \begin{array}{rl} {\mathbb {E}}[\sup _{0\le s\le t}|M(s)|^\alpha ]&{}\le C_\alpha {\mathbb {E}}[\int _0^t S^2(r)\textrm{d}r]^{\frac{\alpha }{2}}\\ &{}\le C_\alpha t^{\frac{\alpha }{2}}{\mathbb {E}}[\sup _{0\le r\le t}S^2(r)]^{\frac{\alpha }{2}}\\ &{}=\frac{C_\alpha }{\delta ^\alpha }t^{\frac{\alpha }{2}}{\mathbb {E}}[\sup _{0\le r\le t}\delta ^\alpha S^\alpha (r)]\\ &{}\le 2M\frac{C_\alpha }{\delta ^\alpha }t^{\frac{\alpha }{2}}. \end{array} \end{aligned}$$

Let $\varepsilon _M$ be an arbitrary positive constant, then according to Doob’s martingale inequality [30], we have

$$\begin{aligned} \begin{array}{rl} {\mathbb {P}}\{\omega :\sup _{k\delta \le t\le (k+1)\delta }|M(t)|^\alpha >(k\delta )^{1+\varepsilon _M+\frac{\alpha }{2}}\} &{}\le \frac{{\mathbb {E}}[\sup _{k\delta \le t\le (k+1)\delta }|M(t)|^\alpha ]}{(k\delta )^{1+\varepsilon _M+\frac{\alpha }{2}}}\\ &{}\le \frac{2M\frac{C_\alpha }{\delta ^\alpha }((k+1)\delta )^{\frac{\alpha }{2}}}{(k\delta )^{1+\varepsilon _M+\frac{\alpha }{2}}}\\ &{}\le \frac{2^{1+\frac{\alpha }{2}}M\frac{C_\alpha }{\delta ^\alpha }}{(k\delta )^{1+\varepsilon _M}}(k=1,2,...). \end{array} \end{aligned}$$

So by Borel-Cantelli lemma [30], for almost all $\omega \in \Omega$, we can obtain that

$$\begin{aligned} \sup _{k\delta \le t\le (k+1)\delta }|M(t)|^\alpha \le (k\delta )^{1+\varepsilon _M+\frac{\alpha }{2}} \end{aligned}$$

(5.6)

holds for all but finitely many k. Thus, there exists a positive $k_{M_0}(\omega )$, for almost all $\omega \in \Omega$, whenever $k\ge k_{M_0}$, (5.6) holds. Therefore, for almost all $\omega \in \Omega$, if $k\ge k_{M_0}$ and $k\delta \le t\le (k+1)\delta$, we have

$$\begin{aligned} \frac{\ln |M(t)|^\alpha }{\ln t}\le \frac{(1+\varepsilon _M+\frac{\alpha }{2})\ln (k\delta )}{\ln (k\delta )}=1+\varepsilon _M+\frac{\alpha }{2}. \end{aligned}$$

Therefore,

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln |M(t)|}{\ln t}\le \frac{1+\varepsilon _M+\frac{\alpha }{2}}{\alpha }. \end{aligned}$$

Letting $\varepsilon _M\rightarrow 0$, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\ln |M(t)|}{\ln t}\le \frac{1+\frac{\alpha }{2}}{\alpha }=\frac{1}{2}+\frac{1}{\alpha }. \end{aligned}$$

Then, for any small $0<\eta <\frac{1}{2}-\frac{1}{\alpha }$, there exist a constant ${\bar{T}}={\bar{T}}(\omega )>0$ and a set $\Omega _\eta$, such that ${\mathbb {P}}(\Omega _\eta )\ge 1-\eta$ and for $t\ge {\bar{T}}$, $\omega \in \Omega _\eta$, we have

$$\begin{aligned}\ln |M(t)|\le (\frac{1}{2}+\frac{1}{\alpha }+\eta )\ln t, \end{aligned}$$

and so

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{M(t)}{t}\le \limsup _{t\rightarrow \infty }\frac{t^{\frac{1}{2}+\frac{1}{\alpha }+\eta }}{t}=0. \end{aligned}$$

Together with $\liminf _{t\rightarrow \infty }\frac{|M(t)|}{t}\ge 0,$ then

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{|M(t)|}{t}=0\ \ a.s.. \end{aligned}$$

Therefore

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{M(t)}{t}=0\ \ a.s.. \end{aligned}$$

Similarly, we can obtain

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{N(t)}{t}=0\ \ a.s.. \end{aligned}$$

This finishes the proof. $\square$

Lemma 5.3

(The strong law of large number for local martingale [31]) Let $M=\{M_t\}_{t\ge 0}$ be a real-valued continuous local martingale vanishing at $t=0$. Then

$$\begin{aligned} \lim _{t\rightarrow \infty }\langle M,M\rangle _t=\infty \ \ a.s.\ \Rightarrow \lim _{t\rightarrow \infty }\frac{M_t}{\langle M,M\rangle _t}=0\ \ a.s. \end{aligned}$$

and also

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\langle M,M\rangle _t}{t}<\infty \ \ a.s.\ \Rightarrow \lim _{t\rightarrow \infty }\frac{M_t}{t}=0\ \ a.s. \end{aligned}$$

Theorem 5.1

Let (S(t), x(t)) be the solution of stochastic periodic system (1.3) with the initial value $(S(0),x(0))\in {\mathbb {R}}^2_+$. Assume the following conditions hold

$$\begin{aligned} 2D>(\sigma _1^*)^2\vee (\sigma _2^*)^2 \end{aligned}$$

and

$$\begin{aligned} R=\frac{m(S^0+b\langle e\rangle _T)}{aD_1}>1, \end{aligned}$$

then the microorganism x will be extinct with probability one, that is to say,

$$\begin{aligned} \lim _{t\rightarrow +\infty }x(t)=0\ \ a.s. \end{aligned}$$

Moreover, we have

$$\begin{aligned} S^0+be_*\le \lim _{t\rightarrow +\infty }\langle S\rangle _t=S^0+b\langle e\rangle _T\le S^0+be^*\ a.s.. \end{aligned}$$

Proof

From model (1.3), we have

$$\begin{aligned}{} & {} \begin{array}{rl} \frac{\delta (S(t)-S(0))}{t}&=\delta DS^0+\delta Db\langle e\rangle _t-\delta D\langle S\rangle _t-\frac{1}{t}\int _0^t\frac{mS(s)x(s)}{a+S(s)}\textrm{d}s+\frac{1}{t}\int _0^t\delta \sigma _1(s)S(s)\textrm{d}B_1(s), \end{array} \\{} & {} \begin{array}{rl} \frac{x(t)-x(0)}{t}&=\frac{1}{t}\int _0^t\frac{mS(s)x(s)}{a+S(s)}\textrm{d}s-D_1\langle x\rangle _t+\frac{1}{t}\int _0^t\sigma _2(s)x(s)\textrm{d}B_2(s). \end{array} \end{aligned}$$

Then

$$\begin{aligned} \begin{array}{rl} \frac{\delta (S(t)-S(0))}{t}+\frac{x(t)-x(0)}{t}&{}=\delta DS^0+\delta Db\langle e\rangle _t-\delta D\langle S\rangle _t-D_1\langle x\rangle _t\\ &{}+\frac{1}{t}\int _0^t\sigma _1(s)S(s)\textrm{d}B_1(s)+\frac{1}{t}\int _0^t\sigma _2(s)x(s)\textrm{d}B_2(s). \end{array} \end{aligned}$$

It is easy to obtain

$$\begin{aligned} \langle S\rangle _t=S^0+b\langle e\rangle _t-\frac{D_1}{\delta D}\langle x\rangle _t+Q(t), \end{aligned}$$

where

$$\begin{aligned} Q(t)= & {} \frac{1}{\delta D}\frac{1}{t}\int _0^t\sigma _1(s)S(s)\textrm{d}B_1(s)+\frac{1}{\delta D}\frac{1}{t}\int _0^t\sigma _2(s)x(s)\textrm{d}B_2(s) -\frac{1}{D}\frac{S(t)-S(0)}{t}\\{} & {} -\frac{1}{\delta D}\frac{x(t)-x(0)}{t}. \end{aligned}$$

According to Lemmas 5.1, 5.2 and 5.3, we know that

$$\begin{aligned} \lim _{t\rightarrow \infty }Q(t)=0\ \ a.s. \end{aligned}$$

(5.7)

From the second equation of system (1.3), we can obtain by Itô formula

$$\begin{aligned} \textrm{d}\ln x(t)=\left( \frac{mS}{a+S}-D_1-\frac{1}{2}\sigma _2^2(t)\right) \textrm{d}t+\sigma _2(t)\textrm{d}B_2(t). \end{aligned}$$

(5.8)

Integrating (5.8) from 0 to t and dividing t on both sides, we obtain

$$\begin{aligned} \begin{array}{rl} \frac{\ln x(t)-\ln x(0)}{t}&{}=\frac{1}{t}\int _0^t\frac{mS}{a+S}\textrm{d}s-D_1-\frac{1}{2}\frac{1}{t}\int _0^t\sigma _2^2(s)\textrm{d}s+\frac{1}{t}\int _0^t\sigma _2(s)\textrm{d}B_2(s)\\ &{}\le \frac{1}{t}\int _0^t\frac{mS}{a}\textrm{d}s-D_1+\frac{1}{t}\int _0^t\sigma _2(s)\textrm{d}B_2(s)\\ &{}=\frac{m}{a}\langle S\rangle _t-D_1+\frac{1}{t}\int _0^t\sigma _2(s)\textrm{d}B_2(s). \end{array} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{array}{rl} \frac{\ln x(t)}{t}&{}\le \frac{mS^0}{a}+\frac{mb\langle e\rangle _t}{a}-\frac{mD_1\langle x\rangle _t}{\delta aD}+\frac{mQ(t)}{a}-D_1+\frac{1}{t}\int _0^t\sigma _2(s)\textrm{d}B_2(s)+\frac{\ln x(0)}{t}\\ &{}\le \frac{mS^0}{a}+\frac{mb\langle e\rangle _t}{a}+\frac{mQ(t)}{a}-D_1+\frac{1}{t}\int _0^t\sigma _2(s)\textrm{d}B_2(s)+\frac{\ln x(0)}{t}. \end{array} \end{aligned}$$

(5.9)

Taking the limit superior of both sides of (5.9) and using Lemma 4.2 and (5.7), we can get

$$\begin{aligned} \begin{array}{rl} \limsup _{t\rightarrow \infty }\frac{\ln x(t)}{t}&{}\le \frac{mS^0}{a}+\frac{mb\langle e\rangle _t}{a}-D_1\\ &{}=D_1\left( \frac{m(S^0+b\langle e\rangle _T)}{aD_1}-1\right) \\ &{}:=D_1(R-1), \end{array} \end{aligned}$$

(5.10)

where $R=\frac{m(S^0+b\langle e\rangle _T)}{aD_1},$ obviously, when $R>1$, $\limsup _{t\rightarrow \infty }\frac{\ln x(t)}{t}<0$, that is to say, $\lim _{t\rightarrow \infty }x(t)=0\ \ a.s.$ Thus,

$$\begin{aligned} \lim _{t\rightarrow +\infty }\langle S\rangle _t=S^0+b\langle e\rangle _T. \end{aligned}$$

Naturally, we have

$$\begin{aligned} S^0+be_*\le \lim _{t\rightarrow +\infty }\langle S\rangle _t=S^0+b\langle e\rangle _T\le S^0+be^*. \end{aligned}$$

This completes the proof. $\square$

6 Existence and Global Attraction of the Boundary Periodic Solution

In this section, we will give the existence and global attraction of the boundary periodic solution of stochastic system (1.3). First, we give two Lemmas as follows.

Lemma 6.1

Consider the following stochastic differential equation

$$\begin{aligned} \textrm{d}Y(t)=D(S^0+be(t)-Y(t))\textrm{d}t+\sigma _1(t)Y(t)\textrm{d}B_1(t) \end{aligned}$$

(6.1)

with initial value $Y(0)=S(0)$, where e(t) and $\sigma _1(t)$ are $T-$periodic functions defined on $[0,\infty )$. Then (6.1) has a positive periodic solution $Y_p(t)$, which is globally attractive, i.e. attracts all other positive solutions of (6.1).

Proof

The proof is similar to Theorem 4.1, we need to find a $C^2-$function V(t, Y) as follows:

$$\begin{aligned} V(t,Y)=Y-1-\ln Y+\nu (t), \end{aligned}$$

where $\nu (t)$ is a $T-$periodic functions defined on $[0,\infty )$ and satisfies

$$\begin{aligned} {\dot{\nu }}(t)=\langle Dbe(t)+\frac{1}{2}\sigma _1^2(t)\rangle _T-Dbe(t)-\frac{1}{2}\sigma _1^2(t),\ \nu _1(0)=0. \end{aligned}$$

By Itô formula, we have

$$\begin{aligned} \begin{array}{rl} LV(t,Y)&{}=(1-\frac{1}{Y})[D(S^0+be(t)-Y)]+\frac{1}{2}\sigma _1^2(t)+{\dot{\nu }}(t)\\ &{}=DS^0+Dbe(t)-DY-\frac{DS^0}{Y}-\frac{Dbe(t)}{Y}+D+\frac{1}{2}\sigma _1^2(t)+{\dot{\nu }}(t)\\ &{}\le DS^0-DY-\frac{DS^0}{Y}+D+\langle Dbe(t)+\frac{1}{2}\sigma _1^2(t)\rangle _T\\ &{}:=\varphi (Y). \end{array} \end{aligned}$$

It is obvious that $\varphi (Y)\rightarrow -\infty$ when $Y\rightarrow 0^+$ or $Y\rightarrow +\infty$. Thus, we can take $\varepsilon >0$ small enough and let $U=[\varepsilon ,\frac{1}{\varepsilon }]$, and we have $LV(t,Y)<-1, Y\in {\mathbb {R}}{\setminus } U$. Then (6.1) has a positive $T-$periodic solution $Y_p(t)$. Next, we will prove that $Y_p(t)$ is globally attractive. Because $Y_p(t)$ is the solution of (6.1), then we can get

$$\begin{aligned} \textrm{d}(Y(t)-Y_p(t))=-D(Y(t)-Y_p(t))\textrm{d}t+\sigma _1(t)(Y(t)-Y_p(t))\textrm{d}B_1(t). \end{aligned}$$

Therefore,

$$\begin{aligned} Y(t)-Y_p(t)=(Y(0)-Y_p(0))\textrm{e}^{-\int _0^t(D+\frac{1}{2}\sigma _1^2(s))\textrm{d}s+{\tilde{M}}(t)}, \end{aligned}$$

where

$$\begin{aligned} {\tilde{M}}(t)=\int _0^t\sigma _1(s)\textrm{d}B_1(s) \end{aligned}$$

and ${\tilde{M}}(t)$ is a local martingale whose quadratic variation is

$$\begin{aligned} \langle {\tilde{M}}(t),{\tilde{M}}(t)\rangle =\int _0^t\sigma _1^2(s)\textrm{d}s\le (\sigma _1^*)^2t. \end{aligned}$$

According to the strong law of large number for local martingales (Lemma 5.3), we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }\frac{{\tilde{M}}(t)}{t}=0\ \ a.s. \end{aligned}$$

(6.2)

Thus,

$$\begin{aligned} \ln |Y(t)-Y_p(t)|=\ln |Y(0)-Y_p(0)|-\int _0^t(D+\frac{1}{2}\sigma _1^2(s))\textrm{d}s+{\tilde{M}}(t). \end{aligned}$$

(6.3)

Consequently,

$$\begin{aligned} \frac{\ln |Y(t)-Y_p(t)|}{t}=\frac{\ln |Y(0)-Y_p(0)|}{t}-\frac{1}{t}\int _0^t(D+\frac{1}{2}\sigma _1^2(s))\textrm{d}s+\frac{{\tilde{M}}(t)}{t}. \end{aligned}$$

(6.4)

Take limits in (6.4) and together with (6.3), we can get

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{\ln |Y(t)-Y_p(t)|}{t}=-\langle D+\frac{1}{2}\sigma _1^2(s)\rangle _T<0. \end{aligned}$$

This implies that $Y(t)-Y_p(t)\rightarrow 0\ a.s.,$ so the $T-$periodic solution $Y_p(t)$ is globally attractive. This completes the proof. $\square$

Lemma 6.2

Let Y(t) be the solution of (6.1) with the initial value $Y(0)\in {\mathbb {R}}_+$. If $2D>(\sigma _1^*)^2$, then

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{Y(t)}{t}=0,\ \ \ \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^t\sigma _1(s)Y(s)\textrm{d}B_1(s)=0. \end{aligned}$$

Moreover,

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s=S^0+b\langle e(t)\rangle _T, \end{aligned}$$

that is

$$\begin{aligned} S^0+be_*\le \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s\le S^0+be^*. \end{aligned}$$

Proof

Define a $C^2-$function $V(Y(t))=(1+Y(t))^\beta$, where $\beta$ is a positive constant and satisfies $1<\beta <\frac{2D}{(\sigma _1^*)^2}+1$. Thus, we have

$$\begin{aligned} \textrm{d}V(Y(t))=LV(Y(t))\textrm{d}Y(t)+\beta (1+Y(t))^{\beta -1}\sigma _1(t)Y(t)\textrm{d}B_1(t), \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rl} LV(Y(t))&{}=\beta (1+Y(t))^{\beta -1}D(S^0+be(t)-Y(t))+\frac{\beta (\beta -1)}{2}(1+Y(t))^{\beta -2}\sigma _1^2(t)Y^2(t)\\ &{}=\beta (1+Y(t))^{\beta -2}\left[ (1+Y(t))D(S^0+be(t)-Y(t))+\frac{\beta -1}{2}\sigma _1^2(t)Y^2(t)\right] \\ &{}\le \beta (1+Y(t))^{\beta -2}\left[ -\left( D-\frac{\beta -1}{2}(\sigma _1^*)^2\right) Y^2(t)\right. \\ &{}\quad \left. +(D(S^0+be^*)-D)Y(t)+D(S^0+be^*)\right] \\ &{}:=\beta (1+Y(t))^{\beta -2}[-{\hat{A}}Y^2(t)+({\hat{B}}-D)Y(t)+{\hat{B}}], \end{array} \end{aligned}$$

where

$$\begin{aligned} {\hat{A}}=D-\frac{\beta -1}{2}(\sigma _1^*)^2 \end{aligned}$$

and

$$\begin{aligned} {\hat{B}}=D(S^0+be^*). \end{aligned}$$

The following part of the proof is similar to Lemmas 5.1 and 5.2, so we omit it, and we can get

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{Y(t)}{t}=0,\ \ \ \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^t\sigma _1(s)Y(s)\textrm{d}B_1(s)=0. \end{aligned}$$

For (6.1), we have

$$\begin{aligned} \frac{Y(t)-Y(0)}{t}=DS^0+Db\langle e(t)\rangle _t-D\langle Y(t)\rangle _t+\frac{1}{t}\int _0^t\sigma _1(s)Y(s)\textrm{d}B_1(s). \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{array}{rl} 0&{}=\lim _{t\rightarrow \infty }\frac{Y(t)}{t}\\ &{}=\lim _{t\rightarrow \infty }\frac{Y(0)}{t}+DS^0+Db\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^te(s)\textrm{d}s\\ &{}-D\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s+\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^t\sigma _1(s)Y(s)\textrm{d}B_1(s)\\ &{}=DS^0+Db\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^te(s)\textrm{d}s-D\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s\\ &{}=DS^0+Db\langle e(t)\rangle _T-D\lim _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s. \end{array} \end{aligned}$$

Thus,

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s=S^0+b\langle e(t)\rangle _T. \end{aligned}$$

Obviously, we can obtain that

$$\begin{aligned} S^0+be_*\le \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s\le S^0+be^*. \end{aligned}$$

$\square$

Theorem 6.1

If $2D>(\sigma _1^*)^2$ and $\frac{m\eta }{a+\eta }-\langle D_1+\frac{1}{2}\sigma _2^2(t)\rangle _T<0$ hold, then $(Y_p(t),0)$ is the boundary periodic solution of system (1.3), which is globally attractive, where

$$\begin{aligned} \eta =S^0+be^*. \end{aligned}$$

Proof

From Theorem 3.1, we know that the solution of the stochastic chemostat model (1.3) is global, unique and positive. Then, we have

$$\begin{aligned} \begin{array}{rl} \textrm{d}S(t)&{}=\left[ (S^0+be(t)-S(t))D-\frac{m}{\delta }\frac{S(t)x(t)}{a+S(t)}\right] \textrm{d}t+\sigma _1(t)S(t)\textrm{d}B_1(t)\\ &{}\le (S^0+be(t)-S(t))D\textrm{d}t+\sigma _1(t)S(t)\textrm{d}B_1(t). \end{array} \end{aligned}$$

By the comparison theorem for stochastic differential equation, we have

$$\begin{aligned} S(t)\le Y(t),\ \ t\in [0,+\infty )\ a.s.. \end{aligned}$$

Thus,

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{1}{t}\int _0^tS(s)\textrm{d}s\le \limsup _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s\le S^0+be^*:=\eta . \end{aligned}$$

We note that $\phi (S(t))=\frac{mS(t)}{a+S(t)}$ is a concave function, so

$$\begin{aligned} \frac{1}{t}\int _0^t\phi (S(s))\textrm{d}s\le \phi \left( \frac{1}{t}\int _0^tS(s)\textrm{d}s\right) . \end{aligned}$$

Let $V(x(t))=\ln x(t)$, and using Itô formula, we can obtain

$$\begin{aligned} \ln x(t)-\ln x(0)=\int _0^t\frac{mS(s)}{a+S(s)}\textrm{d}s-\int _0^t(D_1+\frac{1}{2}\sigma _2^2(s))\textrm{d}s+\int _0^t\sigma _2(s)\textrm{d}B_2(s). \end{aligned}$$

That is to say

$$\begin{aligned} \begin{array}{rl} \frac{\ln x(t)}{t}=\frac{\ln x(0)}{t}+\frac{1}{t}\int _0^t\frac{mS(s)}{a+S(s)}\textrm{d}s-\frac{1}{t}\int _0^t(D_1+\frac{1}{2}\sigma _2^2(s))\textrm{d}s +\frac{1}{t}\int _0^t\sigma _2(s)\textrm{d}B_2(s). \end{array}\nonumber \\ \end{aligned}$$

(6.5)

Taking limits in (6.5), we have

$$\begin{aligned} \begin{array}{rl} \limsup _{t\rightarrow \infty }\frac{\ln x(t)}{t}&{}\le \limsup _{t\rightarrow \infty }\phi \left( \frac{1}{t}\int _0^tS(s)\textrm{d}s\right) -\langle D_1+\frac{1}{2}\sigma _2^2(t)\rangle _T\\ &{}\le \phi \left( \limsup _{t\rightarrow \infty }\frac{1}{t}\int _0^tY(s)\textrm{d}s\right) -\langle D_1+\frac{1}{2}\sigma _2^2(t)\rangle _T\\ &{}\le \frac{m\eta }{a+\eta }-\langle D_1+\frac{1}{2}\sigma _2^2(t)\rangle _T. \end{array} \end{aligned}$$

(6.6)

Thus, when $\frac{m\eta }{a+\eta }-\langle D_1+\frac{1}{2}\sigma _2^2(t)\rangle _T<0$, we have $\lim _{t\rightarrow \infty }x(t)=0\ a.s..$ That is to say, for any small $\tau >0$, there exists a positive constant $t_0$ and a set $\Omega _\tau \in \Omega$ such that ${\mathbb {P}}(\Omega _\tau )>1-\tau$ and $x(t)<\tau$ for any $t>t_0$ and $\omega \in \Omega _\tau$. From the first equation of system (1.3), we can get that for any $t>t_0$ and $\omega \in \Omega _\tau$

$$\begin{aligned} \begin{array}{rl} dS(t)&{}=\left[ D(S^0+be(t)-S(t))-\frac{mS(t)x(t)}{\delta (a+S(t))}\right] \textrm{d}t+\sigma _1(t)S(t)\textrm{d}B_1(t)\\ &{}\ge \left[ D(S^0+be(t)-S(t))-\frac{m\tau }{\delta }\right] \textrm{d}t+\sigma _1(t)S(t)\textrm{d}B_1(t) \end{array} \end{aligned}$$

(6.7)

Let ${\tilde{Y}}(t)$ be the solution of the equation

$$\begin{aligned} \textrm{d}{\tilde{Y}}(t)=\left[ D(S^0+be(t)-{\tilde{Y}}(t))-\frac{m\tau }{\delta }\right] \textrm{d}t+\sigma _1(t){\tilde{Y}}(t)\textrm{d}B_1(t) \end{aligned}$$

with initial value ${\tilde{Y}}(0)=S(0)$. According to the stochastic comparison theorem of stochastic differential equation, we can get that for almost all $\omega \in \Omega _\tau$ and $t>t_0$,

$$\begin{aligned} {\tilde{Y}}(t)\le S(t)\le Y(t). \end{aligned}$$

When $\tau \rightarrow 0$, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }|{\tilde{Y}}(t)-Y(t)|=0\ a.s., \end{aligned}$$

where Y(t) is the solution of (6.1) with initial value $Y(0)=S(0)$. Then we can get

$$\begin{aligned} \lim _{t\rightarrow \infty }|S(t)-Y(t)|=0\ a.s., \end{aligned}$$

According to the global attraction of $Y_p(t)$, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }|S(t)-Y_p(t)|=0\ a.s.. \end{aligned}$$

Therefore, the boundary periodic solution $(Y_p(t),0)$ of system (1.3) is globally attractive. $\square$

7 Numerical Simulations and Conclusions

In order to verify the correctness of the theoretical results obtained in this paper, we will give the numerical simulations of stochastic chemostat model (1.3) with periodic nutrient input and periodic interference and its corresponding deterministic chemostat model (1.2).

By the Milstein’s higher order method [33], we can get the discretized equations of model (1.3) as follows:

$$\begin{aligned} \left\{ \begin{array}{l} S_{i+1}=S_i+\left( (S^0+be(i\Delta t)-S_i)D-\frac{mS_ix_i}{\delta (a+S_i)}\right) \Delta t +S_i\left( \sigma _1(i\Delta t)\xi _i\sqrt{\Delta t}+\frac{\sigma ^2_1(i\Delta t)}{2}(\xi ^2_i-1)\Delta t\right) ,\\ x_{i+1}=x_i+\left( -D_1x_i+\frac{mS_ix_i}{a+S_i}\right) \Delta t +x_i\left( \sigma _2(i\Delta t)\eta _i\sqrt{\Delta t}+\frac{\sigma ^2_2(i\Delta t)}{2}(\eta ^2_i-1)\Delta t\right) . \end{array}\right. \end{aligned}$$

(7.1)

where $\xi _i, \eta _i (i=1,2,....)$ are independent ${\mathbb {N}}(0,1)-$distributed Gaussian random variables, and the periodicity of parameters $e(t),\sigma _1(t),\sigma _2(t)$ are represented by $\sin$ functions.

Example 7.1

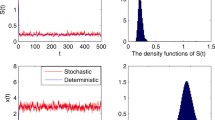
When the conditions of Theorem 4.1 is satisfied, in order to verify the existence of nontrivial positive periodic solution for system (1.3), we assume that the parameters of system (1.3) are taken as follows $S^0=5.0, D=1, a=2, b=1, m=3, D_1=1.2, \delta =0.5, \sigma _1(t)=0.2+0.1\sin 4t, \sigma _2(t)=0.2+0.1\sin 4t, e(t)=2\sin 4t$ and initial values are $S(0)=0.4, x(0)=0.1.$ By calculation, we find that $\frac{ma}{D(S^0)^2}=0.2400$, so we can let $c_1=0.25$. At this moment, $\lambda =\frac{mS^0}{a+S^0}-D_1-\langle R_0\rangle _T=0.8922>0$. According to Theorem 4.1, system (1.3) has a nontrivial positive $T-$periodic solution. The numerical simulations are given in Fig. 1. From Fig. 1a and b, we can find that the solution of the deterministic model (1.2) is periodic, and the solution of stochastic system (1.3) will oscillate around the solution of deterministic system (1.2), which means the microorganism x can survive in chemostat. The Fig. 1c is the two dimensional phase diagram of S(t) and x(t). From Fig. 1c, we can see easily that global dynamics of system (1.2) and (1.3). For given initial value, the solution of deterministic system (1.2) will trend to the periodic orbit after some time, and the solution of stochastic system (1.3) will fluctuate in a small neighborhood of the periodic orbit.

Fig. 1

Numerical simulations of the solution of system (1.2) and (1.3). a Sample paths of S(t); b Sample paths of x(t); c The phase diagram of S and x

Example 7.2

According to Theorem 5.1, in order to verify the extinction of microorganism, we assume that the parameters of system (1.3) are taken as follows $S^0=1.0, D=4, a=2, b=0.5, m=3, D_1=4.2, \delta =0.5, \sigma _1(t)=0.2+0.1\sin 4t, \sigma _2(t)=0.2+0.1\sin 4t, e(t)=2\sin 4t$ and initial values are $S(0)=0.4, x(0)=0.1.$ By calculation, we find that $2D=8>(\sigma _1^*)^2\vee (\sigma _2^*)^2=0.09$, and $R=\frac{m(S^0+b\langle e\rangle _T)}{aD_1}=0.3571<1$. Thus, from Theorem 5.1, we know that $\lim _{t\rightarrow +\infty }x(t)=0\ a.s.$, that is to say, the microorganism x will be extinct with probability one (see Fig. 2b). Meanwhile, we have $S^0+be_*=0\le \lim _{t\rightarrow +\infty }\langle S\rangle _t=S^0+b\langle e\rangle _T\le S^0+be^*=2\ a.s.,$ which means the solution S(t) of the deterministic model (1.2) is still periodic, and the solution S(t) of stochastic system (1.3) will oscillate around the solution S(t) of deterministic system (1.2), and the amplitude of periodic oscillation is between 0 and 2 almost surely (see Fig. 2a). The Fig. 2c is the two dimensional phase diagram of S(t) and x(t), from Fig. 2c, we can see more intuitively that the solution of stochastic system (1.3) and deterministic model (1.2) will eventually tend to S-axis.

Fig. 2

Numerical simulations of the solution of system (1.2) and (1.3). a Sample paths of S(t); b Sample paths of x(t); c The phase diagram of S and x

Example 7.3

According to Theorem 6.1, in order to verify the existence and global attractiveness of boundary periodic solution for system (1.3), we assume that the parameters of system (1.3) are taken as follows $S^0=3.0, D=2, a=2, b=1, m=3, D_1=2.5, \delta =0.5, \sigma _1(t)=0.2+0.1\sin 4t, \sigma _2(t)=0.2+0.1\sin 4t, e(t)=2\sin 4t$ and initial values are $S(0)=0.4, x(0)=0.1.$ By calculation, we find that $2D=4>(\sigma _1^*)^2=0.09$, and $\frac{m\eta }{a+\eta }-\langle D_1+\frac{1}{2}\sigma _2^2(t)\rangle _T=-0.3796<0$. Thus, from Theorem 6.1, we know that system (1.3) has a boundary periodic solution $(Y_p(t),0)$ (see Fig. 3). In order to verify that the boundary periodic solution $(Y_p(t),0)$ is globally attractive, we keep the system parameters unchanged and observe the numerical simulation of the model (1.2) and (1.3) by choosing different initial values. We chose two initial values, respectively, they are

$$\begin{aligned} S(0)=10, x(0)=1 \end{aligned}$$

and

$$\begin{aligned} S(0)=2, x(0)=2. \end{aligned}$$

Under the condition of two different initial values, we get two sample paths of S(t) and x(t) (see Fig. 4). From Fig. 4, we can see that although the sample paths of S(t) and x(t) are different in the initial period of time, after some time, the sample paths of S(t) and x(t) under different initial values will eventually tend to the same curve, which shows that the boundary equilibrium point $(Y_p(t),0)$ of the system (1.3) is globally attractive.

Fig. 3

Numerical simulations of the solution of system (1.2) and (1.3). a Sample paths of S(t); b Sample paths of x(t); c The phase diagram of S and x

Fig. 4

Numerical simulations of the solution of system (1.2) and (1.3) under different initial values. a Sample paths of S(t) under different initial values; b Sample paths of x(t) under different initial values; c The phase diagram of S and x under different initial values

8 Conclusions

In this paper, we mainly consider the stochastic periodic behavior of a chemostat model with periodic nutrient input and periodic random perturbation. We first prove the existence of global unique positive solution for stochastic non-autonomous periodic chemostat system (Theorem 3.1). Then we prove that system (1.3) has a nontrivial positive periodic solution under some conditions (Theorem 4.1). Meanwhile, we also get the existence of boundary periodic solution $(Y_p(t),0)$ of system (1.3) when $2D>(\sigma _1^*)^2$ and $\frac{m\eta }{a+\eta }-\langle D_1+\frac{1}{2}\sigma _2^2(t)\rangle _T<0$, and we prove $(Y_p(t),0)$ is globally attractive (Theorem 5.1). Here, we should note that these conditions are sufficient conditions, not necessary conditions. Finally, we verify the main results by numerical simulation, and from the simulation results, we can see more intuitively the stochastic periodic behavior of the solution of system (1.2) and (1.3) under different conditions.

From the conclusion of this paper, the existence of natural environmental noise plays a harmful role in the growth of microorganisms. We find that larger noises will lead to the extinction of microorganisms. However, the constructive role of noise in nonlinear systems, such as noise induced resonances [34,35,36], noise enhanced stability [37,38,39], etc., has been extensively investigated theoretically and experimentally recently. For example, In [40], Zu et al. concluded that small white noise can reduce the extinction risk of population by analyzing a stochastic toxin-mediated predator–prey model. Guarcello et al. [41, 42] explored the effect of noise on the ballistic graphene-based Josephson junctions under Gaussian noise and non-Gaussian noise and observed resonant activation and noise induced stability.

From a long-term perspective, we can also study some multi-species competition stochastic chemostat models with periodic nutrient input and periodic perturbation, or consider the influence of color noise on the dynamical behavior of stochastic non-autonomous microbial culture model.