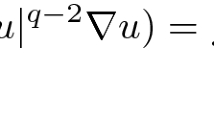A Double Phase Problem with a Nonlinear Boundary Condition

Abstract

In this paper we prove the existence of solutions to a double phase problem with a prescribed nonlinear boundary condition which is nonlinear in nature. The driving nonlinear perturbations obey a suitable condition at the origin and on the boundary. To the best of our knowledge, a double phase measure data problem with nonlinear boundary condition is new and has not been studied yet. The novelty of our work lies in using the well known weak convergence method to guarantee the existence of solutions. We also provide an illustrative example.

1 Introduction

In this paper we shall analyze the existence of solutions to the following measure data problem:

$$\begin{aligned} \left\{ \begin{array}{ll}-\nabla \cdot (|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)&{}=f_1(x,u,\nabla u)+\mu ~~~\text {in}~\Omega \\ (|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\cdot n&{}=f_2(x,u,\nabla u)~~~\text {on}~\partial \Omega ,\end{array} \right. \end{aligned}$$

(1.1)

where $N\ge 2, \ \Omega \subset {\mathbb {R}}^N$ is a bounded domain with a smooth boundary of Hausdorff dimension $(N-1)$, $\mu$ is a positive Radon measure defined over the $\sigma$-algebra of $\Omega$, n is the outward unit normal,

$$\begin{aligned} (\textbf{C}):~~~1<p^+=:\underset{x\in \Omega }{\sup }\{p(x)\}<q^-:=\underset{x\in \Omega }{\inf }\{p(x)\}<N, \end{aligned}$$

$\nu \in L_w^1(\Omega )$ is the weak Marcinkiewicz space, and functions $f_1, f_2$ are of the Carathéodory type and satisfy certain growth conditions at the origin and at infinity.

To the best of our knowledge, a double phase measure data problem with nonlinearity having variable exponent growth and nonlinear boundary condition is new and has not been studied yet. The novelty of our work lies in the usage of the well known weak convergence method to guarantee the existence of solutions to problem (1.1). We recall the definition of the double phase differential operator

$$\begin{aligned} \begin{aligned} -\nabla \cdot (|\nabla u|^{p(x)-2}+\nu (x)|\nabla u|^{q(x)-2}\nabla u)~\text {for all}~u\in W^{1,{\mathcal {D}}(x)}(\Omega ), \end{aligned} \end{aligned}$$

(1.2)

where $W^{1,{\mathcal {D}}(x)}(\Omega )$ is a suitable Musielak–Orlicz Sobolev space, the definition of which will be given in the subsequent section. We observe that when $\underset{\bar{\Omega }}{\inf }\{\nu (x)\}>0$ or when $\nu \equiv 0$, then the operator in (1.2) becomes a weighted (q(x), p(x))-Laplacian or a purely p(x)-Laplacian operator, respectively.

In general, the study of single phase elliptic problems with a source term taken to be a positive Radon measure along with a Dirichlet boundary condition has been of great interest among only a handful of researchers. Therefore we shall first give a brief account of such elliptic problems involving either a measure or an $L^1$ data. While surveying the literature, we have noticed that the problems of this nature have not been studied in great proportions, owing to their mathematical difficulty. However, we would like to bring to the attention of the readers some of the most important work which will help them to get acquainted with the techniques involved in tackling such type of problems that are driven by a measure data.

We begin by referring to the seminal work of Brezis [14] that stands out in this list due to its pioneering efforts. His key observation was that not all measures are suitable to work with and this led to the coining of the term reduced measure. This motivated further development in the field, albeit after a very long time. Véron’s book [41] is a rich documentation of the techniques to tackle the problems driven by measure datum. This acted as a reference point for the researchers which led to an increase in the study of problems of these types. For more information and insight we refer to Bhakta and Marcus [9], Boccardo and Gallouët [10, 11], Brezis et al. [15], Véron et al. [16], Ghosh et al. [21], Giri and Choudhuri [22], Mingione [31], and the references therein. In addition to this, we also direct the attention of the readers with regard to function spaces to Guliyev et al. [25], Guariglia and Silvestrov [24], Guariglia [23], Polidoro and Ragusa [38], and the references therein.

Moving on, we discuss the double phase problem results available in the literature. Zhikov [45] introduced and studied functionals for modelling the strongly anisotropic materials. The functional

$$\begin{aligned} {\mathcal {E}}(u):=\int _{\Omega }(|\nabla u|^p+\nu (x)|\nabla u|^q)dx \end{aligned}$$

has been studied to understand the regularity for isotropic and anisotropic functionals. Some of the other physical applications can be found for example in transonic flow (see Bahrouni et al. [3], Benci et al. [8]) and reaction diffusion systems (see Cherfils et al. [17]). We also refer to Aberqi et al. [1, 2], Baroni et al. [4,5,6,7], Fiscella [20], Marcellini et al. [29, 30], and the references therein. Recently, Manouni et al. [28] have studied a problem similar to (1.1) with constant exponents and $\mu =0$. They proved the existence of multiple solutions to this problem. Very few works pertaining to the double phase operators with a nonlinear boundary conditions exist for the following problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\nabla \cdot (a(x)|\nabla u|^{p(x)-2}\nabla u-\Delta _qu+b(x)|u|^{p-2}u&{}=\lambda f(x,u(x))~\text {in}~\Omega \\ \frac{\partial u}{\partial n_{\theta }}+\beta |\nabla u|^{p-2}u&{}=0~\text {on}~\partial \Omega , \end{array} \right. \end{aligned}$$

(1.3)

Here, $a<q<p<N$, $b\in L^{\infty }(\Omega )$ is a positive potential, $a(x)>0$ a.e. in $\Omega$, and

$$\begin{aligned} \frac{\partial u}{\partial n_{\theta }}=(a(x)|\nabla u|^{p-2}+|\nabla u|^{q-2})\frac{\partial u}{\partial n}, \end{aligned}$$

where n is the outward normal on $\partial \Omega$.

Papageorgiou et al. [33, 35] proved the existence of multiple solutions in the superlinear and resonant case for the following problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\nabla \cdot (a(x)|\nabla u|^{p(x)-2}\nabla u-\Delta _qu+b(x)|u|^{p-2}u&{}=f(x,u(x))~\text {in}~\Omega \\ \frac{\partial u}{\partial n_{\theta }}+\beta |\nabla u|^{p-2}u&{}=0~\text {on}~\partial \Omega , \end{array} \right. \end{aligned}$$

(1.4)

where $1<q<p\le N$ and $a(\cdot )>0$ is a Lipschitz function. Another noteworthy work due to Gasiński and Winkert [18]. We also direct the attention of the reader to Hsini et al. [26], Liu et al. [27], Panda et al. [32], Rădulescu and Repovš [36], Shi et al. [40], Q. Zhang [43], Y. Zhang et al. [44], and the references therein.

We choose the nonlinear perturbations $f_1$, $f_2$ in problem (1.1) as follows

$$\begin{aligned} \begin{aligned} f_1(x,s.\xi )&=f(x,s,\xi )-|s|^{p(x)-2}s-\nu (x)|s|^{q(x)-2}s~\text {a.e. in}~\Omega ,\\ f_2(x,s)&=g(x,s)-\beta |s|^{p(x)-2}s~\text {a.e. in}~\partial \Omega , \end{aligned} \end{aligned}$$

(1.5)

for all $s\in {\mathbb {R}}$ and $\xi \in {\mathbb {R}}^N$, $\beta >0$. Problem (1.1) then becomes

$$\begin{aligned} \left\{ \begin{array}{ll} &{} -\nabla \cdot (|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\\ &{}\quad =f(x,u,\nabla u)-|u|^{p(x)-2}u-\nu (x)|u|^{q(x)-2}u+\mu ~\text {in}~\Omega \\ &{}(|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\cdot n =g(x,u)-\beta |u|^{p(x)-2}u~\text {on}~\partial \Omega . \end{array} \right. \end{aligned}$$

(1.6)

We shall impose the following hypothesis on f, g:

(H):

The perturbations $f:\Omega \times {\mathbb {R}}\times {\mathbb {R}}^N\rightarrow {\mathbb {R}}$, $g:\partial \Omega \times {\mathbb {R}}\times {\mathbb {R}}^N\rightarrow {\mathbb {R}}$ are well known Carathéodory functions with $f(x,0,0)\ne 0$ for a.e. in $\Omega$ and they satisfy the following conditions:

(a):

There exist $\phi _1\in L^{\frac{r_1(x)}{r_1(x)-1}}(\Omega )$, $\phi _2\in L^{\frac{r_2(x)}{r_2(x)-1}}(\Omega )$ and $b_1,b_2,b_3\ge 0$ such that

$$\begin{aligned} \begin{aligned} |f(x,s,\xi )|&\le b_1|\xi |^{p(x)\frac{r_1(x)}{r_1(x)-1}}+b_2|s|^{r_1(x)-1}+\phi _1~\text {a.e. in}~\Omega \\ |g(x,s)|&\le b_3|s|^{p(x)}+\phi _2~\text {a.e. in}~\Omega , \end{aligned} \end{aligned}$$

(1.7)

for every $s\in {\mathbb {R}}$, $\xi \in {\mathbb {R}}^N$, where $1<r_1^+<p^{*^{-}}$ and $1<r_2^+<p_*^{{-}}$. Here, $p_*(x):=\frac{(N-1)p(x)}{N-p(x)}$.

(b):

There exist $z_1\in L^1(\Omega )$, $z_2\in L^1(\partial \Omega )$, and $a_1,a_2,a_3\ge 0$ such that

$$\begin{aligned} \begin{aligned} f(x,s,\xi )s&\le a_1|\xi |^{p(x)}+a_2|s|^{p(x)}+z_1~\text {a.e. in}~\Omega \\ g(x,s)s&\le a_3|s|^{p(x)}+z_2~\text {a.e. in}~\Omega , \end{aligned} \end{aligned}$$

(1.8)

for every $s\in {\mathbb {R}}$, $\xi \in {\mathbb {R}}^N$.

The conditions in hypothesis $(\textbf{H})$ were motivated by the presence of the gradient term. We note that the usual variational techniques do not work and hence we shall use the surjectivity results for pseudomonotone operators in which the first eigenvalue of the Robin and Steklov eigenvalue problems p-Laplacian plays a key role. This requirement led us to use the growth condition (H) to suit the purpose. A prototype example that satisfies $(\textbf{H})$ is $f(x,u,\nabla u)=|\nabla u|^6,~g(x,u)=u$ with $r_1(x)\equiv 3/2,~ p(x)\equiv 2$. However, a nonlinearity of the type $f(x,u,\nabla u)=e^{c|\nabla u|^{p(x)}},~c>0$, does not fall in the category of functions which satisfy $(\textbf{H})$. We remark that problem (1.6) with $1<r_1(x)\le p^*(x),~1<r_2(x)\le p_*(x)$, is still open.

Definition 1.1

A function $u\in W^{1,{\mathcal {D}}(x)}(\Omega )$ is called a weak solution to problem (1.6) if

$$\begin{aligned} \begin{aligned}&\int _{\Omega }(|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\cdot \nabla \varphi dx\\&\qquad +\int _{\Omega }(|u|^{p(x)-2} u+\nu (x)|u|^{q(x)-2}u)\varphi dx\\&\quad =\int _{\Omega }f(x,u,\nabla u)\varphi dx+\int _{\partial \Omega }g(x,u)\varphi dx\\&\qquad -\beta \int _{\partial \Omega }|u|^{p(x)-2}u\varphi dS+\int _{\Omega }\varphi d\mu \end{aligned} \end{aligned}$$

(1.9)

holds for all $\varphi \in W^{1,{\mathcal {D}}(x)}(\Omega )\cap C_{L}(\bar{\Omega })$.

Here, $C_L(\bar{\Omega })$ is the space of Lipschitz continuous functions. By the Rademacher theorem, every Lipschitz continuous function is differentiable a.e. in $\Omega$. The plan of attacking problem (1.6) is to define a sequence of problems which arises due to the existence of a smooth positive sequence of functions $\mu _n$ that converges to $\mu$ in the sense of Definition 2.3. The sequence of problems is as follows:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}(P_n):~ -\nabla \cdot (|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)=&f(x,u,\nabla u)-|u|^{p(x)-2}s\\&-\nu (x)|u|^{q(x)-2}u+\mu _n~\text {in}~\Omega \\ (|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\cdot n=&g(x,u)-\beta |u|^{p(x)-2}u~\text {on}~\partial \Omega . \end{aligned}\right\} \end{aligned} \end{aligned}$$

(1.10)

The following are the main results of this paper.

Theorem 1.1

Suppose that $1<p^+<q^-<N$ and $\nu \in L^1(\Omega )$. Then problem (1.6) has a nontrivial weak solution ${\tilde{u}}\in W^{1,{\mathcal {D}}(x)}(\Omega )\cap L^{\infty }(\Omega ),$ provided that the following properties hold:

• (I) $a_1+a_2(1/\lambda _{1,p(x),\alpha }^R)<1$ and $a_2\alpha (1/\lambda _{1,p(x),\alpha }^R)+a_3<\beta ;$

• (II) $\max \{a_1,a_2\}+a_3(1/\lambda _{1,p(x),\alpha }^R)<1$ and $\beta \ge 0$.

Here, $\lambda _{1,p(x),\alpha }^R$ is the first eigenvalue of the p(x)-Laplacian with the Robin boundary condition with $\alpha >0$ and $\lambda _{1,p(x),\alpha }^S$ is the first eigenvalue of the p(x)-Laplacian with the Steklov boundary condition, see (2.4) and (2.6) respectively.

Theorem 1.2

Suppose that the perturbations $f:\Omega \times {\mathbb {R}}\times {\mathbb {R}}^N\rightarrow {\mathbb {R}}$, $g:\partial \Omega \times {\mathbb {R}}\times {\mathbb {R}}^N\rightarrow {\mathbb {R}}$ in problem (1.6) satisfy hypothesis $(\textbf{H})$. Then problem (1.6) has a solution.

This paper is organized as follows. In Sect. 2 we collect all preliminary data. In Sect. 3 we prove Theorem 1.1. In Sect. 4 we prove Theorem 1.2. In Sect. 5 we give an illustrative example.

2 Preliminaries

In this section we shall gather the key notions and results needed for our proofs. For the rest the readers can consult the comprehensive monograph by Papageorgiou et al. [34]. We shall begin by recalling the definition of the Sobolev space with variable exponent (see e.g. Bonder et al. [13]):

$$\begin{aligned} \begin{aligned} W^{1,r(x)}(\Omega ):=\{u\in W_{\text {loc}}^{1,1}(\Omega )|u\in L^{p(x)}(\Omega )~\text {and}~|\nabla u|\in L^{r(x)}(\Omega )\}, \end{aligned} \end{aligned}$$

(2.1)

where $L^{r(x)}(\Omega )$ is the Lebesgue space equipped with the Luxemburg norm

$$\begin{aligned} \Vert u\Vert _{r(x)}=\inf \left\{ \mu >0\left| \right. \int _{\Omega }\left| \frac{u(x)}{\mu }\right| ^{r(x)}dx\le 1\right\} . \end{aligned}$$

The critical exponent is defined as

$$\begin{aligned} r^*(x)={\left\{ \begin{array}{ll} \frac{Nr(x)}{N-r(x)}&{}~\text {if}~r(x)<N,\\ \infty &{}~\text {if}~r(x)\ge N. \end{array}\right. } \end{aligned}$$

(2.2)

2.1 Properties of the Sobolev Space with Variable Exponents

We recall some of the relevant properties of $W^{1,r(x)}(\Omega )$ which can also be found in Rădulescu and Repovš [39]. When $r^->1$, then the space $W^{1,r(x)}(\Omega )$ is a reflexive uniformly convex Banach space. Furthermore, for any bounded measurable function r, the space $W^{1,r(x)}(\Omega )$ is separable. The corresponding modular function is defined as follows:

$$\begin{aligned} m_{r(x)}(u):=\int _{\Omega }(|\nabla u(x)|^{r(x)}+|u(x)|^{r(x)})dx. \end{aligned}$$

Henceforth, we shall write u instead of u(x) whenever the modular function is used. For properties of the modular function we refer to [39, Section 1.3].

Remark 2.1

By Bonder et al. [13, Proposition 2.2], for $r,{\bar{r}}\in C(\bar{\Omega })$ such that $1\le {\bar{r}}(x)\le r(x)^*$ for all $x\in \bar{\Omega }$, we have $W^{1,{\bar{r}}(x)}(\Omega )\hookrightarrow L^{r(x)}(\Omega )$. Furthermore, if $\underset{\Omega }{\inf }\{{\bar{r}}(x)-r(x)\}>0$ then the embedding is compact. Also, the Poincaré inequality holds even in the variable exponent case (see Diening et al. [19, p. 249, Theorem 8.2.4]).

2.2 Description of the Solution Space

Let ${\mathcal {D}}:\Omega \times [0,\infty )\rightarrow [0,\infty )$ be a function defined by

$$\begin{aligned} {\mathcal {D}}(x,t):=t^{p(x)}+\nu (x)t^{q(x)}. \end{aligned}$$

This allows us to define the modular function by

$$\begin{aligned} m_{{\mathcal {D}}(x)}(u):=\int _{\Omega }{\mathcal {D}}(x,u)dx=\int _{\Omega }(|u|^{p(x)}+\nu (x)|\nabla u|^{q(x)})dx. \end{aligned}$$

Then the Musielak–Orlicz space $L^{{\mathcal {D}}(x)}$ is defined as follows

$$\begin{aligned} L^{{\mathcal {D}}(x)}(\Omega ):=\{u|u:\Omega \rightarrow {\mathbb {R}}~\text {is measurable and}~m_{{\mathcal {D}}(x)}(u)<\infty \}, \end{aligned}$$

and it is equipped with the Luxemburg norm

$$\begin{aligned} \Vert u\Vert _{{\mathcal {D}}(x)}:=\inf \left\{ \mu >0|~m_{{\mathcal {D}}(x)}\left( \frac{u}{\mu }\right) \le 1\right\} , \end{aligned}$$

making $L^{{\mathcal {D}}(x)}(\Omega )$ a reflexive Banach space (see Véron [42, Lemma 18]). We now define the space $W^{1,{\mathcal {D}}(x)}(\Omega )$ in which solutions to problem (1.1) will be searched, as follows:

$$\begin{aligned} W^{1,{\mathcal {D}}(x)}(\Omega ):=\{u\in L^{{\mathcal {D}}(x)}(\Omega )|~|\nabla u|\in L^{{\mathcal {D}}(x)}(\Omega ) \}. \end{aligned}$$

A suitable norm on $W^{1,{\mathcal {D}}(x)}(\Omega )$ is $\Vert u\Vert _{1,{\mathcal {D}}(x)}:=\inf \left\{ \mu >0\mid {\tilde{m}}\left( \frac{u}{\mu }\right) \right\}$, where ${\tilde{m}}(u)=m_{{\mathcal {D}}(x)}(u)+m_{{\mathcal {D}}(x)}(\nabla u)$.

2.3 Some Basic Definitions

We recall a few basic definitions that will be important for the proof of the main result of this paper. Throughout the definitions we let ${\mathcal {A}}:X\rightarrow X^*$ and X be a reflexive Banach space, with $X^*$ denoting the dual space of X. Furthermore, let $\langle \cdot ,\cdot \rangle$ denote its duality pairing.

Definition 2.1

A sequence $(u_n)$ is said to satisfy the $(S+)$ property if $u_n\rightharpoonup u$ and $\underset{n\rightarrow \infty }{\limsup }\langle {\mathcal {A}}u_n,u_n-u\rangle \le 0$ implies ${\mathcal {A}}u_n\rightharpoonup {\mathcal {A}}u$ and $\langle {\mathcal {A}}u_n,u_n\rangle \rightarrow \langle {\mathcal {A}}u,u\rangle$.

Definition 2.2

A sequence $(u_n)\subset X$ is said to be pseudomonotone if $u_n\rightharpoonup u$ in X and $\underset{n\rightarrow \infty }{\limsup }\langle {\mathcal {A}}u_n,u_n-u\rangle \le 0$ imply ${\mathcal {A}}u_n\rightharpoonup {\mathcal {A}}u$ and $\langle {\mathcal {A}}u_n,u_n\rangle \rightarrow \langle {\mathcal {A}}u,u\rangle$.

The reader should note that the classical definition of a pseudomonotone operator says that if $u_n\rightharpoonup u$ in X, $\underset{n\rightarrow \infty }{\limsup }\langle {\mathcal {A}}u_n,u_n-u\rangle \le 0$ implies $\underset{n\rightarrow \infty }{\liminf }\langle {\mathcal {A}}u_n,u_n-v\rangle \ge \langle {\mathcal {A}}u,u-v\rangle$ for all $v\in X$. This agrees with the one given in Definition 2.2 if ${\mathcal {A}}$ is a bounded operator.

We recall a result which will be necessary to establish the existence of solutions.

Theorem 2.1

(Papageorgiou and Winkert [37, Theorem 6.1.57]) Let ${\mathcal {A}}$ be a pseudomonotone operator which is also bounded and coercive, and let $b\in X^*$. Then a solution to the equation ${\mathcal {A}}u=b$ exists.

We further define

$$\begin{aligned} \begin{aligned} \langle {\mathcal {A}}u,\varphi \rangle _{{\mathcal {D}}(x)}&:=\int _{\Omega }(|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\cdot \nabla \varphi dx\\&\qquad +\int _{\Omega }(|u|^{p(x)-2} u+\nu (x)|u|^{q(x)-2}u)\varphi dx \end{aligned} \end{aligned}$$

(2.3)

for all $u,\varphi \in W^{1,{\mathcal {D}}(x)}(\Omega )$, where $\langle \cdot ,\cdot \rangle _{{\mathcal {D}}(x)}$ is the duality pairing of $W^{1,{\mathcal {D}}(x)}(\Omega )$ and $(W^{1,{\mathcal {D}}(x)}(\Omega ))^*$. Under the assumption $(\textbf{C})$ on $p,q,\Omega$, it follows by Crespo et al. [18, Proposition 3.5] that the operator ${\mathcal {A}}$ is bounded, linear and strictly monotone (implying that it is maximal monotone) and is of type $(S+)$. We shall denote the interior of the cone of nonnegative functions of $C^1$ class defined over $\bar{\Omega }$ which consists of strictly positive functions of $C^1$ class by $\mathring{C^1}(\bar{\Omega })$.

Definition 2.3

Let $(\mu _n)$ be a bounded sequence of measures on the space of Radon measures ${\mathcal {M}}(\Omega )$ and let $\Omega$ be a bounded domain in ${\mathbb {R}}^{N}$. We say that $(\mu _n)$ converges weakly in $\Omega$ to a measure $\mu \in {\mathcal {M}}(\Omega )$ if $(\mu _n)$ converges weakly to $\mu \in {\mathcal {M}}(\Omega )$, i.e

$$\begin{aligned} \int _{\Omega }\phi d\mu _n\rightarrow \int _{\Omega }\phi d\mu ,~~~\text {for all}~\phi \in C(\bar{\Omega }). \end{aligned}$$

2.4 The Robin and the Steklov Boundary Conditions

We first recall the Robin boundary condition via the eigenvalue problem driven by the r(x)-Laplacian operator

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{r(x)}u&{}=\lambda |u|^{r(x)-2}u~\text {in}~\Omega \\ |\nabla u|^{r(x)-2}\nabla u\cdot n&{}=-\alpha |u|^{r(x)-2}u~\text {on}~\partial \Omega , \end{array} \right. \end{aligned}$$

(2.4)

where $\alpha >0$. We keep the notations used in Manouni et al. [28] and define

$$\begin{aligned} \lambda _{1,r(x),\alpha }^R:=\underset{\underset{u\ne 0}{W^{1,r(x)}(\Omega ),}}{\inf }\frac{\int _{\Omega }|\nabla u|^{r(x)}dx+\alpha \int _{\partial \Omega }|u|^{r(x)}dS}{\int _{\Omega }|u|^{r(x)}dx}. \end{aligned}$$

(2.5)

We shall further denote by $u_{1,r(x),\alpha }^R$ the normalized positive solution corresponding to the eigenvalue $\lambda _{1,r(x),\alpha }^R$. Here, dS is the infinitesimal surface measure on $\partial \Omega$. It can be proved by the maximum principle that $u\in \mathring{C^1}(\bar{\Omega })$.

The problem driven by r(x)-Laplacian operator with the Steklov boundary condition is as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{r(x)}u&{}=|u|^{r(x)-2}u~\text {in}~\Omega \\ |\nabla u|^{r(x)-2}\nabla u\cdot n&{}=-\lambda |u|^{r(x)-2}u~\text {on}~\partial \Omega . \end{array} \right. \end{aligned}$$

(2.6)

Similarly to the Robin problem, let the smallest eigenvalue be denoted by $\lambda _{1,r(x),\alpha }^{S}>0$ which is isolated, simple and represented by

$$\begin{aligned} \lambda _{1,r(x),\alpha }^S:=\underset{\underset{u\ne 0}{W^{1,r(x)}(\Omega ),}}{\inf }\frac{\int _{\Omega }|\nabla u|^{r(x)}dx+\int _{\Omega }|u|^{r(x)}dS}{\int _{\partial \Omega }|u|^{r(x)}dx}. \end{aligned}$$

(2.7)

As was done earlier, we denote by $u_{1,r(x)}^S$ the normalized eigenfunction which also belongs to $\mathring{C^1}(\bar{\Omega })$. Furthermore, we define $T_f:W^{1,{\mathcal {D}}(x)}(\Omega )\subset L^{r_1(x)}(\Omega )\rightarrow L^{r_1'(x)}$ and $T_g:L^{r_2(x)}(\partial \Omega )\rightarrow L^{r_2'(x)}(\Omega )$ to be the operators of the Nemytskij type pertaining to the functions f and g,  respectively.

3 Proof of Theorem 1.1

We denote by $i^*:L^{r_1(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*$ the adjoint of the inclusion map $i: W^{1,{\mathcal {D}}(x)}(\Omega )\rightarrow L^{r_1(x)}(\Omega )$ and by $j^*:L^{r_2'(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*$ the adjoint of the inclusion map $j: W^{1,{\mathcal {D}}(x)}(\Omega )\rightarrow L^{r_2(x)}(\partial \Omega )$. We further define

$$\begin{aligned} \begin{aligned}&n_f:=i^*\circ {\tilde{N}}_f:W^{1,{\mathcal {D}}(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*\\&\quad N_g:=j^*\circ {\tilde{N}}_g\circ j:W^{1,{\mathcal {D}}(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*. \end{aligned} \end{aligned}$$

(3.1)

Thanks to hypothesis $(\textbf{H})(a)$, the operators in (3.1) are continuous and bounded. We further define $N_{\beta }:L^{p(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*$ as follows:

$$\begin{aligned} N_{\beta }:i_{\beta }^*\circ (\beta |\cdot |^{p(x)-2})\circ i_{\beta }. \end{aligned}$$

(3.2)

We also define

$$\begin{aligned} {\mathcal {F}}_n(u)=\int _{\Omega }ud\mu _n. \end{aligned}$$

Here, $i_{\beta }^*:L^{p(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*$ is the adjoint operator of the embedding $i_\beta {:W^{1,{\mathcal {D}}(x)}}(\Omega )\rightarrow L^{p(x)}(\Omega )$.

This allows us to define an operator ${\mathcal {B}}_n:W^{1,{\mathcal {D}}(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*$ as follows:

$$\begin{aligned} {\mathcal {B}}_n(u):={\mathcal {A}}(u)-N_f(u)-{\mathcal {F}}_n(u)-N_g(u)+N_{\beta }(u). \end{aligned}$$

(3.3)

Again, by the growth condition in $(\textbf{H})(a)$, it is clear that operator ${\mathcal {B}}$ maps bounded sets to bounded sets.

We now prove that operator ${\mathcal {B}}_n$ is pseudomonotone. To this end, we consider a sequence $(u_n)\subset W^{1,{\mathcal {D}}(x)}(\Omega )$ such that

$$\begin{aligned} \begin{aligned} u_j\rightharpoonup u~\text {in}~W^{1,{\mathcal {D}}(x)}(\Omega ),~~\underset{j\rightarrow \infty }{\limsup }\langle {\mathcal {B}}_nu_j,u_j-u\rangle _{\mathcal (D)(x)}\le 0. \end{aligned} \end{aligned}$$

(3.4)

By Remark 2.1, there exists a compact embedding $W^{1,{\mathcal {D}}(x)}(\Omega )\hookrightarrow L^{{\tilde{r}}(x)}$, whenever ${\tilde{r}}^+<p*^{-}$. In combination with (3.4), we obtain

$$\begin{aligned} \begin{aligned} u_j\rightarrow u~\text {in}~L^{r_1(x)}(\Omega ),~~u_j\rightarrow u~\text {in}~L^{r_2(x)}(\partial \Omega )~\text {and}~L^{p(x)}(\partial \Omega ). \end{aligned} \end{aligned}$$

(3.5)

Invoking the growth condition $(\textbf{H})(a)$ in combination with the Hölder inequality, yields

$$\begin{aligned} \begin{aligned}&\int _{\Omega }f(x,u,\nabla u)(u_j-u)dx\le b_1\int _{\Omega }|\nabla u_j|^{p(x)\frac{r_1(x)-1}{r_1(x)}}|u_j-u|dx\\&\quad +b_2\int _{\Omega }|u_j|^{r_1(x)-1}|u_j-u|dx +\int _{\Omega }|\phi _1(x)||u_j-u|dx\\&\quad \le C_1b_1\max \left\{ \Vert |\nabla u_j|\Vert _{p(x)}^{p^-\frac{r_1^--1}{r_1^+}},\Vert |\nabla u_j|\Vert _{p(x)}^{p^+\frac{r_1^+-1}{r_1^-}},\Vert |\nabla u_j|\Vert _{p(x)}^{p^+\frac{r_1^--1}{r_1^+}},\Vert |\nabla u_j|\Vert _{p(x)}^{p^-\frac{r_1^--1}{r_1^+}}\right\} \\&\quad + C_1b_2\max \left\{ \Vert u_j\Vert _{r_1(x)}^{r_1^--1},\Vert u_j\Vert _{r_1(x)}^{r_1^+-1}\right\} +\Vert \phi _1\Vert _{\frac{r_1(x)}{r_1(x)-1}}\Vert u_j-u\Vert _{r_1(x)}\rightarrow 0 \end{aligned} \end{aligned}$$

(3.6)

and

$$\begin{aligned} \begin{aligned}&\int _{\Omega }g(x,u)(u_j-u)dx\le a_3\int _{\partial \Omega }|u_j|^{r_2(x)-1}|u_j-u|dS+\int _{\partial \Omega }|\phi _2(x)||u_j-u|dS\\&\quad \le C_2\left( a_3\max \{\Vert u_j\Vert _{r_2(x),\partial \Omega }^{r_2^-\frac{r_2^-}{r_2^+-1}},\Vert u_j\Vert _{r_2(x),\partial \Omega }^{r_2^+\frac{r_2^+}{r_2^--1}},\Vert u_j\Vert _{r_2(x),\partial \Omega }^{r_2^+\frac{r_2^-}{r_2^+-1}},\Vert u_j\Vert _{r_2(x),\partial \Omega }^{r_2^-\frac{r_2^-}{r_2^+-1}}\}+\Vert \phi _2\Vert _{\frac{r_2(x)}{r_2(x)-1},\partial \Omega }\right) \\&\qquad \times \Vert u_j-u\Vert _{r_2(x),\partial \Omega }\rightarrow 0. \end{aligned} \end{aligned}$$

(3.7)

By the Hölder inequality, we have

$$\begin{aligned} \begin{aligned}&\beta \int _{\partial \Omega }|u_j|^{p(x)-2}u_j(u_j-u)dS\\&\quad \le C_3\beta \max \{\Vert u_j\Vert _{p(x),\partial \Omega }^{p^-\frac{p^-}{p^+-1}},\Vert u_j\Vert _{p(x),\partial \Omega }^{p^+\frac{p^+}{p^--1}},\Vert u_j\Vert _{p(x),\partial \Omega }^{p^+\frac{p^-}{p^+-1}},\Vert u_j\Vert _{p(x),\partial \Omega }^{p^-\frac{p^+}{p^--1}}\}\\&\qquad \times \Vert u_j-u\Vert _{p(x),\partial \Omega }\rightarrow 0. \end{aligned} \end{aligned}$$

(3.8)

By Definition 1.9 of the weak solution and by the estimates derived above, we obtain

$$\begin{aligned} \begin{aligned} \underset{j\rightarrow \infty }{\limsup }\langle {\mathcal {A}}u_j,u_j-u\rangle _{{\mathcal {D}}(x)}=\underset{j\rightarrow \infty }{\limsup }\langle {\mathcal {B}}_n u_j,u_j-u\rangle _{{\mathcal {D}}(x)}\le 0. \end{aligned} \end{aligned}$$

(3.9)

Also, since ${\mathcal {A}}$ is a bounded linear operator, it follows by Crespo et al. [18, Proposition 3.5] that ${\mathcal {A}}$ satisfies the $(S+)$ condition (see Definition 2.1). Thus from (3.8)–(3.9) we get

$$\begin{aligned} u_j\rightarrow u~\text {in}~W^{1,{\mathcal {D}}(x)}(\Omega ). \end{aligned}$$

(3.10)

Since ${\mathcal {B}}_n$ is continuous, we have that ${\mathcal {B}}_n(u_j)\rightarrow {\mathcal {B}}_n(u)$ in $W^{1,{\mathcal {D}}(x)}(\Omega )^*$. This proves that B is indeed pseudomonotone.

We shall now prove that the operator ${\mathcal {B}}_n:W^{1,{\mathcal {D}}(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*$ is coercive. We subdivide the proof into two cases:

Case (i): Suppose that the Robin boundary condition holds. Then for $r(\cdot )=p(\cdot )$ we have by (2.4)–(2.5) that

$$\begin{aligned} \begin{aligned} \int _{\Omega }|u|^{p(x)}dx\le (1/\lambda _{1,r(x),\alpha }^R)\left( \int _{\Omega }|\nabla u|^{p(x)}dx+\alpha \int _{\partial \Omega }|u|^{p(x)}dx\right) \end{aligned} \end{aligned}$$

(3.11)

for all $u\in W^{1,p(x)}(\Omega )$. Note that we have used the definition of $\lambda _{1,r(x)\alpha }^R$ from (3.11). Furthermore, from $(\textbf{H})(b)$, (3.11), and by the properties of the modular function, we have

$$\begin{aligned} \begin{aligned}&\langle {\mathcal {B}}_n(u),u\rangle _{{\mathcal {D}}(x)}=\int _{\Omega }(|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\cdot \nabla udx\\&\qquad +\int _{\Omega }(|u|^{p(x)-2}u+\nu (x)|u|^{q(x)-2}u)udx\\&\qquad -\int _{\Omega }f(x,u,\nabla u)udx-\int _{\Omega }g(x,u)udS+\beta \int _{\partial \Omega }|u|^{p(x)}dS\\&\quad \ge \int _{\Omega }|\nabla u|^{p(x)}dx+\int _{\Omega }\nu (x)|\nabla u|^{q(x)}+\int _{\Omega }|u|^{p(x)}+\int _{\Omega }\nu (x)|u|^{q(x)}dx\\&\qquad -a_1\int _{\Omega }|\nabla u|^{p(x)}dx-a_2\int _{\Omega }|u|^{p(x)dx}-\int _{\Omega }z_1dx-a_3\\&\int _{\partial \Omega }|u|^{p(x)}dx-\int _{\Omega }z_2dx +\beta \int _{\partial \Omega }|u|^{p(x)}dS\\&\quad \ge \int _{\Omega }|\nabla u|^{p(x)}dx+\int _{\Omega }\nu (x)|\nabla u|^{q(x)}+\int _{\Omega }|u|^{p(x)}+\int _{\Omega }\nu (x)|u|^{q(x)}dx\\&\qquad -a_1\int _{\Omega }|\nabla u|^{p(x)}dx-a_2(1/\lambda _{1,r(x),\alpha }^R)\\&\int _{\Omega }|\nabla u|^{p(x)}dx+a_2\alpha (1/\lambda _{1,r(x),\alpha }^R)\int _{\partial \Omega }|u|^{p(x)dx}\\&\qquad -\int _{\Omega }z_1dx-a_3\int _{\partial \Omega }|u|^{p(x)}dx-\int _{\partial \Omega }z_2dx+\beta \int _{\partial \Omega }|u|^{p(x)}dS\\&\quad \ge (1-a_1-a_2(1/\lambda _{1,r(x),\alpha }^R))\left( \int _{\Omega }|\nabla u|^{p(x)}dx+\int _{\Omega }|u|^{p(x)}dx\right) \\&\qquad +\int _{\Omega }\nu (x)|\nabla u|^{q(x)}+\int _{\Omega }\nu (x)|u|^{q(x)}dx\\&\qquad +(\beta -a_2\alpha (1/\lambda _{1,r(x),\alpha }^R)-a_3)\int _{\partial \Omega }|u|^{p(x)}dS-\Vert z_1\Vert _{1}-\Vert z_2\Vert _{1,\partial \Omega }. \end{aligned} \end{aligned}$$

(3.12)

Hence B is indeed a coercive operator.

Case (ii): Suppose that the Steklov boundary condition holds. Again, for $r(\cdot )=p(\cdot )$ we have

$$\begin{aligned} \begin{aligned} \int _{\partial \Omega }|u|^{p(x)}dx\le (1/\lambda _{1,r(x),\alpha }^S)\left( \int _{\Omega }|\nabla u|^{p(x)}dx+\alpha \int _{\Omega }|u|^{p(x)}dx\right) . \end{aligned} \end{aligned}$$

(3.13)

As in Case (i), we choose $u\in W^{1,{\mathcal {D}}(x)}(\Omega )$ such that $\Vert u\Vert >1$. By using $(\textbf{H})(b)$ and (3.13), we get

$$\begin{aligned} \begin{aligned}&\langle {\mathcal {B}}_nu,u \rangle _{{\mathcal {D}}(x)}=\int _{\Omega }(|\nabla u|^{p(x)-2}\nabla u+\nu (x)|\nabla u|^{q(x)-2}\nabla u)\cdot \nabla udx\\&\qquad +\int _{\Omega }(|u|^{p(x)-2}u+\nu (x)|u|^{q(x)-2}u)udx\\&\qquad -\int _{\Omega }f(x,u,\nabla u)udx-\int _{\Omega }g(x,u)udS+\beta \int _{\partial \Omega }|u|^{p(x)}dS\\&\quad \ge \int _{\Omega }|\nabla u|^{p(x)}dx+\int _{\Omega }\nu (x)|\nabla u|^{q(x)}+\int _{\Omega }|u|^{p(x)}+\int _{\Omega }\nu (x)|u|^{q(x)}dx\\&\qquad -a_1\int _{\Omega }|\nabla u|^{p(x)}dx-a_2\int _{\Omega }|u|^{p(x)}dx-\Vert z_1\Vert _{1}-a_3\\&\int _{\partial \Omega }|u|^{p(x)}dS-\Vert z_2\Vert _{1,\partial \Omega }+\beta \int _{\partial \Omega }|u|^{p(x)}dS \end{aligned} \end{aligned}$$

(3.14)

$$\begin{aligned} \begin{aligned}&\ge \int _{\Omega }|\nabla u|^{p(x)}dx+\int _{\Omega }\nu (x)|\nabla u|^{q(x)}+\int _{\Omega }|u|^{p(x)}+\int _{\Omega }\nu (x)|u|^{q(x)}dx\\&\qquad -a_1\int _{\Omega }|\nabla u|^{p(x)}dx-a_2\int _{\Omega }|u|^{p(x)}dx-\Vert z_1\Vert _{1}-\Vert z_2\Vert _{1,\partial \Omega }\\&\qquad -a_3(1/\lambda _{1,r(x),\alpha }^S)\int _{\Omega }|\nabla u|^{p(x)}dx-a_3(1/\lambda _{1,r(x),\alpha }^S)\alpha \\&\int _{\Omega }|u|^{p(x)}dx+\beta \int _{\partial \Omega }|u|^{p(x)}dS\\&\quad \ge (1-\max \{a_1,a_2\}-a_3(1/\lambda _{1,r(x),\alpha }^S))\\&\left( \int _{\Omega }|\nabla u|^{p(x)}dx+\int _{\Omega }|u|^{p(x)}\right) +\int _{\Omega }|\nabla u|^{q(x)}dx\\&\qquad +\int _{\Omega }|u|^{q(x)}-\Vert z_1\Vert _{1}-\Vert z_2\Vert _{1,\partial \Omega }\\&\quad \ge (1-\max \{a_1,a_2\}-a_3(1/\lambda _{1,r(x),\alpha }^S)){\tilde{m}}(u)-\Vert z_1\Vert _{1}-\Vert z_2\Vert _{1,\partial \Omega }. \end{aligned} \end{aligned}$$

As we have concluded in Case (i), the operator ${\mathcal {B}}_n$ is coercive. Thus we have proved that operator ${\mathcal {B}}_n:W^{1,{\mathcal {D}}(x)}(\Omega )\rightarrow W^{1,{\mathcal {D}}(x)}(\Omega )^*$ is coercive, bounded, and pseudomonotone. By applying Theorem 2.1, we establish the existence of ${\tilde{u}}\in W^{1,{\mathcal {D}}(x)}(\Omega )$ such that ${\mathcal {B}}_n({\tilde{u}}_n)=0$ with ${\tilde{u}}_n\ne 0$. The nontriviality of ${\tilde{u}}_n$ follows from $f(x,0,0)\ne 0$ a.e. in $\Omega$. By the definition of ${\mathcal {B}}_n$ we conclude that ${\tilde{u}}_n$ is a nontrivial weak solution to problem (1.6). This completes the proof of Theorem 1.1. $\square$

4 Proof of Theorem 1.2

We shall prove that the sequence of solutions $(u_n)$ converges to $u\in W^{1,{\mathcal {D}}(x)}(\Omega )\cap C_L(\bar{\Omega })$ which in turn, is a solution to problem (1.6). We shall first prove that $(u_n)$ is bounded in $W^{1,{\mathcal {D}}(x)}(\Omega )$. We test the weak formulation of problem (1.6) with $\varphi =u_n$ and assume that a subsequence of $(u_n)$, still denoted by $(u_n)$, is such that $\Vert u_n\Vert \rightarrow \infty$, and we get the following:

$$\begin{aligned} \begin{aligned}&\underset{x\in \Omega }{\inf }\{\nu (x)\}\Vert u_n\Vert _{q(x)}^{q^-}\le \int _{\Omega }(|\nabla u_n|^{p(x)}+\nu (x)|\nabla u_n|^{q(x)}) dx\\&\qquad +\int _{\Omega }(|u_n|^{p(x)} +\nu (x)|u_n|^{q(x)})dx\\&\quad =\int _{\Omega }f(x,u_n,\nabla u_n)u_n dx+\int _{\partial \Omega }g(x,u_n)u_n dx-\beta \int _{\partial \Omega }|u_n|^{p(x)} dS+\int _{\Omega }u_n d\mu _n\\&\quad \le a_1\int _{\Omega }|\nabla u_n|^{p(x)}dx+a_2\int _{\Omega }|u|^{p(x)}dx+\int _{\Omega }z_1u_ndx+\int _{\partial \Omega }a_3|u|^{p(x)}dx\\&\qquad +\int _{\partial \Omega }z_2dx+\int _{\Omega }u_n d\mu _n\\&\quad \le (a_1+C_4a_2)\Vert u_n\Vert _{1,p(x)}^{p^+}+\Vert z_1\Vert _1+\Vert z_2\Vert _{1,\partial \Omega }+MC_5a_3\Vert u_n\Vert _{1,p(x)}^{p^+}. \end{aligned} \end{aligned}$$

(4.1)

Since $p^+<q^-$, we have that

$$\begin{aligned} \begin{aligned} \underset{x\in \Omega }{\inf }\{\nu (x)\} \le&(a_1\!+\!C_4a_2)\frac{\Vert u_n\Vert _{1,p(x)}^{p^+}}{\Vert u_n\Vert _{q(x)}^{q^-}}\!+\!\frac{\Vert z_1\Vert _1}{\Vert u_n\Vert _{q(x)}^{q^-}}+\frac{\Vert z_2\Vert _{1,\partial \Omega }}{\Vert u_n\Vert _{q(x)}^{q^-}}\!+\!MC_5a_3\frac{\Vert u_n\Vert _{p(x)}^{p^+}}{\Vert u_n\Vert _{q(x)}^{q^-}}\rightarrow 0 \end{aligned} \end{aligned}$$

(4.2)

as $n\rightarrow \infty$. This is a contradiction since $\underset{x\in \Omega }{\inf }\{\nu (x)\}>0$. Thus $(u_n)$ is indeed bounded in $W^{1,q(x)}(\Omega )$ and hence bounded in $W^{1,p(x)}(\Omega )$. Therefore $(u_n)$ is bounded in $W^{1,{\mathcal {D}}(x)}(\Omega )\cap C_L(\bar{\Omega })$. Hence $u_n\rightharpoonup u_*$ in $W^{1,{\mathcal {D}}(x)}(\Omega )\cap C_L(\bar{\Omega })$. It remains to establish that $u_*$ is a weak solution to problem (1.6).

The tools at our disposal are: (a) $\mu _n\rightharpoonup \mu$ in the sense of Definition 2.3, (b) $u_n\rightharpoonup u_*$ in $W^{1,{\mathcal {D}}(x)}(\Omega )\cap C_L(\bar{\Omega })$. We shall try to capitalize on these by passing to the limit $n\rightarrow \infty$ in the weak formulation of the problem as defined in Definition 1.9 by testing it with $\varphi =T_ku_n$, where

$$\begin{aligned} T_ku_n(x):=\max \{u_n(x),k\}, \end{aligned}$$

is the truncation of $u_n$. The conditions $(2.1)\text {--}(2.5)$ in Boccardo et al. [12], which are as follows

$$\begin{aligned} \begin{aligned}&|a(x,s,\xi )|\le \beta [k(x)+|s|^{p-1}+|\xi |^{p-1}],\\&|a_0(x,s,\xi )|\le \beta [k(x)+|s|^{p-1}+|\xi |^{p-1}],\\&[a(x,s,\xi )-a(x,s,\xi ^*)][\xi -\xi ^*]\ge 0,~(\xi \ne \xi ^*),\\&a(x,s,\xi )\xi \ge \alpha |\xi |^p,\\&a_0(x,s,\xi )\xi \ge \alpha _0|\xi |^p, \end{aligned} \end{aligned}$$

(4.3)

hold in this case and hence we obtain $T_ku_n\rightarrow T_ku_*$ in $W_0^{1,p(x)}(\Omega )$. By the diagonal argument, we conclude that (up to subsequences) $\nabla u_n$ converges to $\nabla u_*$ in measure, and hence (if required, we can extract another subsequence)

$$\begin{aligned} \nabla u_n\rightarrow \nabla u_*~\text {a.e. in}~\Omega . \end{aligned}$$

(4.4)

Thus for every $\varphi \in W^{1,{\mathcal {D}}(x)}(\Omega )\cap C_L(\bar{\Omega })$, we have

$$\begin{aligned} \begin{aligned} \langle u_*,\varphi \rangle _{{\mathcal {D}}(x)}=\underset{n\rightarrow \infty }{\lim }\langle u_n,\varphi \rangle _{{\mathcal {D}}(x)}=&\underset{n\rightarrow \infty }{\lim }\left( \int _{\Omega }f(x,u_n,\nabla u_n)\varphi dx+\int _{\partial \Omega }g(x,u_n)\varphi dx\right. \\&\left. -\beta \int _{\partial \Omega }|u_n|^{p(x)-2}u_n\varphi dS+\int _{\Omega }\varphi d\mu _n\right) \\ =&\int _{\Omega }f(x,u_*,\nabla u_*)\varphi dx+\int _{\partial \Omega }g(x,u_*)\varphi dx\\&-\beta \int _{\partial \Omega }|u_*|^{p(x)-2}u_*\varphi dS+\int _{\Omega }\varphi d\mu . \end{aligned} \end{aligned}$$

(4.5)

The limiting analysis in (4.5) along with the condition $f(x,0,0)\ne 0$ a.e. in $\Omega$ from (H) proves that $u_*$ is indeed a nontrivial weak solution to (1.6). This completes the proof of Theorem 1.2. $\square$

5 An Illustrative Example

A first look might give the impression that the assumptions on the nonlinear perturbations $f_1$, $f_2$ in problem (1.1) were somewhat restrictive. However, a closer look reveals that these functions are quite widely used in the literature. Some commonly used functions are

$$\begin{aligned} f_1(x,s,\xi )={\left\{ \begin{array}{ll} b_0|s|^{p-2}s,\\ b_1|\xi |^{\frac{pr}{r-1}}+b_2|s|^{r-2}u+\varphi _1(x),\\ b_3|\xi |^{\frac{pr}{r-1}}. \end{array}\right. } \end{aligned}$$

As remarked in Sect. 1, the presence of the gradient term in the nonlinearity $f_1$ disallows the straightforward usage of variational principle. Hence we shall now illustrate the results proved in Theorems 1.1 and 1.2 for the case $\mu =1$ of problem (1.6).

We observe that for a fixed $k>0$, if $\mu _{k}=k^{-1}|\Omega |\sum _{i=1}^{k}\delta _{\alpha _i}$, then $\mu _k$ defines a Radon measure. We further define a sequence of measures

$$\begin{aligned} \mu _{n,k}=k^{-1}|\Omega |\sum _{i=1}^{k}\rho _{1/n}*\mu _k. \end{aligned}$$

Note that $\mu _{n,k}(\Omega )=|\Omega |$. Here, $(\alpha _i)_{i=1}^{k}$ are points that are uniformly distributed in $\Omega$, $(\delta _{\alpha _i})_{i=1}^{k}$ are the Dirac-delta distributions and $\rho _{1/n}$ are the standard mollifiers defined over $\Omega$.

We shall now see that $(\mu _{n,k})$ converges to 1 in the sense of Definition 2.3. This is because

$$\begin{aligned} \begin{aligned}&\underset{n\rightarrow \infty }{\lim }\left| \int _{\Omega }\varphi [\rho _{1/n}*\mu _k-1]\right| dx\\&\quad \le \underset{n\rightarrow \infty }{\lim }\left( \Vert \varphi \Vert _{\infty }\int _{\Omega }|(k^{-1}|\Omega |\sum _{i=1}^{k}\rho _{1/n}(x-\alpha _i)-1)|dx\right) =0 \end{aligned} \end{aligned}$$

(5.1)

for all $\varphi \in C_{L}(\bar{\Omega })$. Thus by Theorem 1.1, for each $(\mu _{n,k})$ there exists a solution, say $u_n$. Furthermore, by Theorem 1.2, we have that $u_n\rightarrow u_*$, where $u_*$ is a solution to (1.6) corresponding to $\mu =1$.