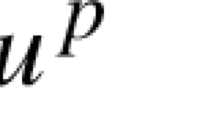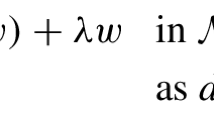1 Introduction

Let (M, g) is a smooth compact Riemannian N-manifolds. In this paper, we investigate the following nonlinear q(m)-Kirchhoff-type problems with Dirichlet boundary condition and with nonlocal terms and logarithmic nonlinearity

$$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} \Phi \bigg (\displaystyle \int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)}\text {dv}_{g}(m)\bigg )\bigg (-\Delta _{q(m)}u\bigg ) + g(m) \vert u \vert ^{\theta p(m)-2}u\ln \vert u \vert \\ \displaystyle = \vert u \vert ^{p(m)-2}u+ \lambda \Psi \bigg (\int _{M}F(m,u)\text {dv}_{g}(m)\bigg )f(m,u) &{} \text { in } M,\\ u=0 &{} \text { on } \Gamma , \end{array}\right. \end{aligned}$$
(1.1)

where \(\lambda \) and \(\theta \) are strictly positive real parameters, \(p(m),q(m) \in C(M)\) and \(F(m,t)=\displaystyle \int _{0}^{t} f(m,s) ds\) where \(d\text {v}_{g}= \sqrt{det(g_{ij})} dm\) is the Riemannian volume element on (M, g), with the \(g_{ij}\) being the components of the Riemannian metric g in the chart and dm is the Lebesgue volume element of \(\mathbb {R}^{N}\).

The operator \(\Delta _{q(m)} u = div\bigg ( \vert \nabla u \vert ^{q(m)-2}u\bigg )\) is referred to as the q(m)-Laplacian and changes into the q-Laplacian when \(q(m) = q\) (a constant). The q-Laplacian operator is \((q-1)\)-homogeneous, meaning that for every \(\mu > 0\), \(\Delta _{q}(\mu u)=\mu ^{q-1} \Delta _{q}( u)\), whereas the q(m)-Laplacian operator is not homogeneous when q(m) is not a constant.

The ability to model various phenomena that emerge in the study of elastic mechanics, electrorheological fluids [21] and image restoration provides a strong motivation for the study of problems involving variable exponent growth conditions [3, 4, 6, 10, 11, 14, 16,17,18,19, 24, 25].

The problem (1.1) is a generalization of a Kirchhoff model. More specifically, Kirchhoff proposed a model given by the equation

$$\begin{aligned} \rho \frac{\partial ^2 u}{\partial t^2}-\left( \frac{P_0}{h}+\left. \frac{E}{2 L} \int _0^L \bigg \vert \frac{\partial u}{\partial m}\right| ^2 d m\right) \frac{\partial ^2 u}{\partial m^2}=0, \end{aligned}$$
(1.2)

where L is the length of the string, h is the area of the cross section, E is the Young modulus of the material, \(\rho \) is the mass density and \(P_{0}\) is the initial tension. A distinguishing feature of Kirchhoff equation (1.2) is that the equation contains a nonlocal coefficient \(\displaystyle \frac{P_0}{h}+\frac{E}{2\,L} \int _0^L\left| \frac{\partial u}{\partial m}\right| ^2 d m\) which depends on the average \(\displaystyle \frac{1}{2\,L} \int _0^L\left| \frac{\partial u}{\partial m}\right| ^2 d m\), and then the equation is no longer a pointwise identity.

The problem (1.1) is known as a bi-nonlocal due to the terms

$$\begin{aligned} \Phi \bigg (\int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)}\text {d}v_{g}(m)\bigg ) \text { and } \Psi \bigg (\int _{M}F(m,u)\text {d}v_{g}(m)\bigg ), \end{aligned}$$

which means that (1.1) is no longer a pointwise identity. This phenomenon poses some mathematical difficulties that are particularly fascinating to study.

The contributions to the paper are as follows. We show that the problem (1.1) admits at least nontrivial weak solutions. We prove also the existence and multiplicity of large energy solutions and small negative energy solutions to the problem (1.1). The arguments are based on the Mountain Pass Theorem, the Fountain and Dual Fountain Theorem and some variational techniques.

The paper consists of four sections. Section 2 contains some important results about Sobolev spaces on Riemannian manifolds. In Sect. 3, we recall the theorems that will be used in the proof of our main results. Section 4 presents our main results, and the proofs of the main results are given in Sect. 5.

2 Preliminaries

In this section, we present some important results about variable exponents Sobolev spaces on Riemannian manifolds, which will be used in the rest of this paper. For more details about Sobolev spaces, fractional function spaces and special functions, we refer to [1, 2, 5, 7,8,9, 12, 13, 15, 20].

Definition 2.1

[12] Given (M, g) a smooth Riemannian manifolds and \(\nabla \) the Levi-Civita connection, for \(u\in C^{\infty }(M)\), then \(\nabla ^{k} u\) denotes the k-th covariant derivative of u. The norm of k-th covariant derivative in local chart is given by the following formula

$$\begin{aligned} \left| \nabla ^{k} u\right| ^{2}=g^{i_{1} j_{1}} \cdots g^{i_{k} j_{k}}\left( \nabla ^{k} u\right) _{i_{1} \cdots i_{k}}\left( \nabla ^{k} u\right) _{j_{1} \cdots j_{k}}, \end{aligned}$$

where the summation convention of Einstein is used.

Definition 2.2

[12] Let (M, g) be a smooth Riemannian manifolds, and \(\gamma :[c, d] \longrightarrow \) M be a curve of class \(C^{1}\). The length of \(\gamma \) is

$$\begin{aligned} L(\gamma )=\int _{a}^{b} \sqrt{g(\gamma (t))\left( \frac{d \gamma }{d t}, \frac{d \gamma }{d t}\right) } d t, \end{aligned}$$

and for \(z, y \in M\), we define the distance \(d_{g}\) by

$$\begin{aligned} d_{g}(z, y)=\inf \{L(\gamma ): \gamma :[c, d] \rightarrow M \text{ such } \text{ that } \gamma (c)=z \text{ and } \gamma (d)=y\}. \end{aligned}$$

Definition 2.3

[12] The variable exponents Sobolev space \(W^{1, q(m)}(M)\) consists of such functions \(u \in L^{q(m)}(M)\) for which \(\nabla ^{j} u \in L^{q(m)}(M)\) for \(j=1,2, \cdots , n\). The norm of u in \(W^{1,q(m)}(M)\) is defined by

$$\begin{aligned} \vert u \vert _{1, q(m)}= \vert u \vert _{q(m)}+\sum _{j=1}^{n}\left| \nabla ^{j} u\right| _{q(m)}. \end{aligned}$$

The space \(W_{0}^{1, q(m)}(M)\) is defined as the closure of \(C_{c}^{\infty }(M)\) in \(W^{1, q(m)}(M)\) with respect to the norm \( \vert \cdot \vert _{1,q(m)}\).

We note \(\mathcal {P}(M)\) the set of all measurable functions \(q(.): M \rightarrow [1, \infty ]\).

Proposition 2.4

[7] (Hölder’s inequality) If \(q(.) \in \mathcal {P}(M)\), then for every \(u \in L^{q(\cdot )}(M)\) and \(v \in L^{q^{\prime }(\cdot )}(M)\) the following inequality holds

$$\begin{aligned} \int _{M} \vert u(m) v(m) \vert \textrm{d} v_{g}(m) \le 2 \vert u \vert _{L^{q(\cdot )}(M)} \cdot \vert v \vert _{L^{q^{\prime }(\cdot )}(M)} \cdot \end{aligned}$$

Proposition 2.5

[7] If \(u \in L^{q(m)}(M),\left\{ u_{n}\right\} \subset L^{q(m)}(M)\), then we have

  1. (1)

    \( \vert u \vert _{q(m)}<1\) (resp. \(\left. =1,>1\right) \Longleftrightarrow \rho _{q(m)}(u)<1\) (resp. \(=1,>1\)).

  2. (2)

    For \(u \in L^{q(m)}(M) \backslash \{0\}, \vert u \vert _{q(m)}=\lambda \Longleftrightarrow \rho _{q(m)}\left( \frac{u}{\lambda }\right) =1\).

  3. (3)

    \( \vert u \vert _{q(m)}<1 \Rightarrow \vert u \vert _{q(m)}^{q^{+}} \le \rho _{q(m)}(u) \le \vert u \vert _{q(m)}^{q^{-}}\).

  4. (4)

    \( \vert u \vert _{q(m)}>1 \Rightarrow \vert u \vert _{q(m)}^{q^{-}} \le \rho _{q(m)}(u) \le \vert u \vert _{q(m)}^{q^{+}}\).

  5. (5)

    \(\lim _{n \rightarrow +\infty }\left| u_{n}-u\right| _{q(m)}=0 \Longleftrightarrow \lim _{n \rightarrow +\infty } \rho _{q(m)}\left( u_{n}-u\right) =0\).

Theorem 2.6

[12] Let M be a compact Riemannian manifolds with a smooth boundary or without boundary and \(q(m), p(m) \in C({\bar{M}}) \cap L^{\infty }(M)\). Assume that

$$\begin{aligned} p(m)<N, \quad p(m)<\frac{N q(m)}{N-q(m)} \text{ for } m \in {\bar{M}}. \end{aligned}$$

Then,

$$\begin{aligned} W^{1, q(m)}(M) \hookrightarrow L^{p(m)}(M), \end{aligned}$$

is a continuous and compact embedding.

Proposition 2.7

[1] If (M, g) is complete, then \(W^{1, q(m)}(M)=W_{0}^{1, q(m)}(M)\).

Remark 2.8

On the Sobolev space \(W_{0}^{1,q(m)}(M)\), we can consider the equivalent norm

$$\begin{aligned} \Vert u \Vert = \vert \nabla u \vert _{q(m)}. \end{aligned}$$

3 Mathematical tools

In this section, we recall the theorems that will be used in the proof of our main results. Let X be a reflexive and separable Banach space. Therefore, there exist \(\left\{ e_{n}\right\} \subset X\) and \(\left\{ e_{n}^{*}\right\} \subset X^{*}\) such that

$$\begin{aligned} X=\overline{{\text {span}}\left\{ e_{n}, n \in \mathbb {N}\right\} }, \quad X^{*}=\overline{{\text {span}}\left\{ e_{n}^{*}, n \in \mathbb {N}\right\} }, \quad \left\langle e_{n}, e_{j}^{*}\right\rangle =\delta _{i, j}, \end{aligned}$$

where \(\delta _{\textrm{i}, j}\) denotes the Kronecker symbol. For \(j\in \mathbb {N}\), we put

$$\begin{aligned} X_{j}=\mathbb {R} e_{j}={\text {span}}\left\{ e_{j}\right\} , \quad Y_{j}=\prod _{i=1}^{j} X_{i}, \quad Z_{j}=\prod _{i=j}^{\infty } X_{i}. \end{aligned}$$

Definition 3.1

A function E is said to satisfy the Palais–Smale condition (PS), if any sequence \((u_{n}) \in X\) such that \((E(u_{n}))\) is bounded and \(E'(u_{n}) \rightarrow 0\) in \(X^{*}\) has a convergent subsequence.

Theorem 3.2

[22](Mountain Pass Theorem). Let X be a Banach space, \(E \in \) \(C^{1}(X, \mathbb {R})\) and \(e \in X\) with \( \Vert e \Vert >r\) for some \(r>0\). Assume that

$$\begin{aligned} \inf _{ \Vert u \Vert =r} E(u)>E(0) \ge E(e). \end{aligned}$$

If E satisfies the (PS) condition at level c, then, c is a critical value of E, where

$$\begin{aligned} c=\inf _{\gamma \in \Gamma } \max _{t \in [0,1]} E(\gamma (t)), \text{ and } \Gamma =\{\gamma \in C([0,1], X): \gamma (0)=0, \gamma (1)=e\} \text{. } \end{aligned}$$

Theorem 3.3

[22](Fountain Theorem) Assume that \(E \in C(X, \mathbb {R})\) is an even functional satisfying the (PS) condition. Moreover, for each \(j\in \mathbb {N}\), there exist \(\gamma _{j}>r_{j}>0\) such that

  1. i

    \(a_{j}=\max _{u \in Y_{j}, \Vert u \Vert =\gamma _{j}} E(u) \le 0\).

  2. ii

    \(b_{j}=\inf _{u \in Z_{j}, \Vert u \Vert =r_{j}} E(u) \rightarrow \infty \), as \(j \rightarrow \infty \).

Then, E has a sequence of critical points \(\left\{ u_{j}\right\} \) such that \(E\left( u_{j}\right) \rightarrow \infty \).

Definition 3.4

A function E is said to satisfy the \((P S)_c^*\) condition (with respect to \(\left( Y_n\right) \) ), if any sequence \(\left( u_{n}\right) \subset X\) such that \(n\rightarrow \infty , u_{n} \in Y_{n}, E\left( u_{n}\right) \rightarrow c\) and \(\left( \left. E\right| _{Y_{n}}\right) ^{\prime }\left( u_{n}\right) \rightarrow 0\), contains a subsequence converging to a critical point of E.

Theorem 3.5

[22](Dual Fountain Theorem) Assume that \(E \in C^1(X, \mathbb {R})\) satisfies \(E(-u)=E(u)\), and for every \(j \ge j_0\), there exist \(\rho _j>r_j>0\) such that

\(({\textbf {B}}_1)\):

\(c_j=\inf _{u \in Z_j, \Vert u \Vert _X=\rho _j} E(u) \ge 0\).

\(({\textbf {B}}_2)\):

\(d_j=\max _{u \in Y_k, \Vert u \Vert _X=r_j} E(u)<0\).

\(({\textbf {B}}_3)\):

\(s_j=\inf _{u \in Z_k, \Vert u \Vert _X \le \rho _j} E(u) \rightarrow 0 \qquad \text { as } \qquad j \rightarrow \infty .\)

\(({\textbf {B}}_4\)):

E satisfies \((P S)_c^*\) condition for every \(c\in [s_{j_0},0)\).

Then E has a sequence of negative critical values converging to 0.

4 Hypotheses and main results

In order to ensure the existence and multiplicity of solutions for the problem (1.1), we assume the following hypotheses:

\((H_{1})\):

\(g: M \longrightarrow \mathbb {R}\) is a continuous function and satisfies the following condition

$$\begin{aligned} b_1\le g(m)\le b_2, \end{aligned}$$

for some positive constants \(b_1\) and \(b_2\).

\((H_{2})\):

\(\Phi :(0,+\infty ) \rightarrow (0,+\infty )\) is a continuous function and satisfies the following condition

$$\begin{aligned} a_{1}t^{\alpha -1}\le \Phi (t) \le a_{2}t^{\alpha -1}, \end{aligned}$$

for all \(t >0\) and \(a_{1}\), \(a_{2}\) real numbers such that \(a_{2}\ge a_{1}> 0\) and \(\alpha >1.\)

\((H_{3})\):

\(\Psi : \mathbb {R} \rightarrow \mathbb {R}\) is a continuous function and there exists positive constant \(\beta >\frac{\alpha q^+}{p^-}\) such that

$$\begin{aligned} t\le {\hat{\Psi }}(t)\le t^{\beta }, \text{ for } t\in \mathbb {R}, \end{aligned}$$
(4.1)

and

$$\begin{aligned} {\hat{\Psi }}(t) \le \Psi (t)t, \text{ for } t> 0, \end{aligned}$$
(4.2)

where \({\hat{\Psi }}(t)=\displaystyle \int _{0}^{t} \Psi (z) d z.\)

\((H_{4})\):

The function \(f: M \times \mathbb {R} \longrightarrow \mathbb {R}\) is continuous such that there exist \(\epsilon >0\) satisfying

$$\begin{aligned} \begin{aligned} \vert f(m,t) \vert \le \epsilon \vert t \vert ^{p(m)-1} \text { for all }(m,t)\in M\times \mathbb {R}, \end{aligned} \end{aligned}$$

with \(p^+<\alpha q^-\).

\((H_{5})\):

There exist \(\eta >0\) and \(A>0\), such that

$$\begin{aligned} \begin{aligned} 0<F(m,t) \le \frac{t}{\eta } f(m,t), \text { for } \vert t \vert \ge A \text { and } m\in M, \end{aligned} \end{aligned}$$

with \(\eta >\max \bigg (\alpha q^+, \displaystyle \frac{a_{2}\alpha (q^+)^\alpha }{a_1 (q^-)^\alpha }, \frac{b_2 \theta p^+}{b_1}\bigg ).\)

\((H_{6})\):
$$\begin{aligned} \theta p(m), p(m)< q^{*}(m)=\left\{ \begin{array}{l} \frac{Nq(m)}{N-q(m)} \qquad \quad \text { if } \qquad q(m)< N, \\ \infty \qquad \quad \qquad \text { if } \qquad q(m) \ge N,\end{array}\right. \end{aligned}$$

and

$$\begin{aligned} 1<p^-\le p\le p^+< \theta p^-\le \theta p\le \theta p^+< (1+\theta ) p^- \le (1+\theta ) p \le (1+\theta ) p^+<\alpha q^-\le \alpha q\le \alpha q^+. \end{aligned}$$
\((H_{7})\):

\(f(m,-t)=-f(m,t)\) for all \(t\in \mathbb {R}\) and \(m\in M\).

Now, we state our main results of this paper.

Theorem 4.1

Assume that the hypotheses \(\left( H_{1}\right) \)-\(\left( H_{6}\right) \) are satisfied, then there exists \(\lambda ^* > 0\) such that for any \(\lambda \in (0, \lambda ^*)\) the problem (1.1) admits at least nontrivial weak solutions.

Theorem 4.2

If the conditions \(\left( H_{1}\right) \)-\(\left( H_{7}\right) \) hold, then for any \(\lambda >0\) the problem (1.1) possesses infinitely many large energy solutions.

Theorem 4.3

If the conditions \(\left( H_{1}\right) \)-\(\left( H_{7}\right) \) hold, then for any \(\lambda >0\) the problem (1.1) possesses infinitely many small negative energy solutions.

5 Proofs of the main results

First, let us give the definition of a weak solution to the problem (1.1).

Definition 5.1

A function \(u \in W_{0}^{1,q(m)}(M)\) is a weak solution of the problem (1.1) iff

$$\begin{aligned} \begin{aligned}&\Phi \big (\int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)} \text {d}v_{g}(m)\big )\int _{M} \vert \nabla u \vert ^{q(m)-2}\nabla u \nabla w \text {d}v_{g}(m)\\ {}&\quad +\int _{M}g(m) \vert u \vert ^{\theta p(m)-2}u \ln \vert u \vert wdv_{g}(m)\\&\quad -\int _{M} \vert u \vert ^{p(m)-2}uwdv_{g}(m)-\lambda \Psi \bigg (\int _{M}F(m,u)\text {d}v_{g}(m)\bigg ) \int _{M}f(m,u) w \text {d}v_{g}(m)=0, \end{aligned} \end{aligned}$$

for all u, w \(\in W_{0}^{1,q(m)}(M)\).

Next, considering the energy function \(E: W_{0}^{1,q(m)}(M) \rightarrow \mathbb {R}\) associated to problem (1.1) defined by

$$\begin{aligned} \begin{aligned} E(u)&={\hat{\Phi }}\bigg (\int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)} \text {d}v_{g}(m)\bigg )+\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}\ln \vert u \vert }{\theta p(m)}\text {d}v_{g}(m)\\&-\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}}{(\theta p(m))^{2}}\text {d}v_{g}(m)-\int _{M}\frac{ \vert u \vert ^{p(m)}}{p(m)}\text {d}v_{g}(m)-\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,u)\text {d}v_{g}(m)\bigg ), \end{aligned} \end{aligned}$$

where \({\hat{\Phi }}(t)=\displaystyle \int _{0}^{t} \Phi (s) ds\) and \({\hat{\Psi }}(t)=\displaystyle \int _{0}^{t} \Psi (s) ds \).

Using some simple computations, we can show that the functional E is well defined and belongs to \(\mathcal {C}^{1}\left( W_0^{1,q(m)}(M), \mathbb {R}\right) \). Furthermore, \(u \in W_{0}^{1,q(m)}(M)\) is a weak solution of the problem (1.1) if and only if u is a critical point of this problem.

The next lemmas give a helpful estimate for logarithmic nonlinear term, which are crucial to our proof.

Lemma 5.2

[23] Let \(p(m) \in \mathcal {C}_{+}({\bar{M}})\). Hence, the following estimate holds:

$$\begin{aligned} \ln t \le \frac{1}{e p(m)} t^{p(m)} \le \frac{1}{e p^{-}} t^{p(m)}, \text{ for } \text{ all } t \in [1,+\infty ). \end{aligned}$$

Proposition 5.3

Let \(u \in W_0^{1,q(m)}(M)\) and \(p(m), \theta p(m) \in \mathcal {C}_{+}({\bar{M}})\), then

$$\begin{aligned} \int _{M} \vert u \vert ^{\theta p(m)} \ln \vert u \vert \text {d} v_{g}(m) \le C vol(M)+ \frac{1}{e p^{-}} \max \left\{ \vert u \vert _{(1+\theta ) p(m)}^{(1+\theta ) p^{+}}, \vert u \vert _{(1+\theta ) p(m)}^{(1+\theta ) p^{-}}\right\} , \end{aligned}$$

where C is positive constant and \(\theta p(m)<(1+ \theta )p(m)<q^{*}(m).\)

Proof

Let \(M_1=\{m \in M: \vert u(m) \vert \le 1\}\) and \(M_2=\{m \in M: \vert u(m) \vert \ge 1\}\). Then,

$$\begin{aligned} \int _{M} \vert u \vert ^{\theta p(m)} \ln \vert u \vert d v_{g}(m)=\int _{M_1} \vert u \vert ^{\theta p(m)} \ln \vert u \vert dv_{g} (m)+\int _{M_2} \vert u \vert ^{\theta p(m)} \ln \vert u \vert d v_{g}(m). \end{aligned}$$

Since \( \vert u(m) \vert \le 1\), there exist \(A>0\) and \(B>0\) such that \( \vert u \vert ^{\theta p(m)}<A\) and \(\ln \vert u \vert <B\). Then,

$$\begin{aligned} \int _{M_1} \vert u \vert ^{\theta p(m)} \ln \vert u \vert d v_{g}(m)<C vol(M). \end{aligned}$$

Using Lemma 5.2, we get

$$\begin{aligned} \begin{aligned} \int _{M_2} \vert u \vert ^{\theta p(m)} \ln \vert u \vert \text {d} v_g(m)&\le \frac{1}{e p^{-}} \int _{M_2} \vert u \vert ^{\theta p(m)+p(m)} \text {d} v_g(m) \\&\le \frac{1}{e p^{-}} \max \left\{ \vert u \vert _{(1+\theta )p(m)^{\prime }}^{(1+\theta )p^{+}} \vert u \vert _{(1+\theta )p(m)}^{(1+\theta )p^{-}}\right\} . \end{aligned} \end{aligned}$$

This implies that

$$\begin{aligned} \begin{aligned} \int _{M} \vert u \vert ^{\theta p(m)} \ln \vert u \vert \text {d} v_g(m)&\le C vol(M) +\frac{1}{e p^{-}} \max \left\{ \vert u \vert _{(1+\theta )p(m)^{\prime }}^{(1+\theta )p^{+}} \vert u \vert _{(1+\theta )p(m)}^{(1+\theta )p^{-}}\right\} . \end{aligned} \end{aligned}$$

\(\square \)

5.1 Proof of Theorem 4.1

In this subsection, we will use Theorem 3.2 in order to prove the existence of nontrivial solutions. The proof of Theorem 4.1 is divided into several lemmas.

Lemma 5.4

Assume that the conditions \(\left( H_{1}\right) \)-\(\left( H_{4}\right) \) and \(\left( H_{6}\right) \) hold, then there exist \(\lambda ^* > 0\), \(\rho >0\) and \(\sigma >0\) such that \(E(u) \ge \sigma \) if \( \Vert u \Vert = \rho \) for any \(\lambda \in (0, \lambda ^*)\).

Proof

From \(\left( H_{4}\right) \), we get

$$\begin{aligned} \vert F(m,t) \vert \le \frac{\epsilon }{p(m)} \vert t \vert ^{p(m)} \text { for all }(m,t)\in M\times \mathbb {R}. \end{aligned}$$
(5.1)

Let \(u\in W_{0}^{1,p(m)}(M)\) such that \( \Vert u \Vert =\rho \in (0,1)\). By \((H_2)\), (4.1), (5.1) and Proposition 3, we get

$$\begin{aligned} E(u)= & {} {\hat{\Phi }}\bigg (\int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)} dv_{g}(m)\bigg ) +\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}\ln \vert u \vert }{\theta p(m)}dv_{g}(m)\\{} & {} -\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}}{(\theta p(m))^{2}}dv_{g}(m)\\{} & {} -\int _{M}\frac{ \vert u \vert ^{p(m)}}{p(m)}dv_{g}(m)-\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,u)dv_{g}(m)\bigg )\\\ge & {} \frac{a_{1}}{\alpha (q^+)^\alpha }\bigg (\int _{M} \vert \nabla u \vert ^{q(m)}dv_{g}(m)\bigg )^\alpha -\frac{b_{2}}{(\theta p^-)^2}\int _{M} \vert u \vert ^{\theta p(m)}dv_{g}(m)\\ {}{} & {} -\frac{1}{p^-}\int _{M} \vert u \vert ^{p(m)}dv_{g}(m)\\{} & {} -\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\bigg (\int _{M} \vert u \vert ^{p(m)}dv_{g}(m)\bigg )^\beta \\\ge & {} \frac{a_{1}}{\alpha (q^+)^\alpha } \Vert u \Vert ^{q^{+}\alpha }-\frac{b_{2}}{(\theta p^-)^2}C^{\theta p^-} \Vert u \Vert ^{\theta p^-}-\frac{1}{p^-}C^{p^-} \Vert u \Vert ^{p^-}-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }C^{\beta p^-} \Vert u \Vert ^{\beta p^-} \\\ge & {} \frac{a_{1}}{\alpha (q^+)^\alpha }\rho ^{q^{+}\alpha }-\frac{b_{2}}{(\theta p^-)^2}C^{\theta p^-}\rho ^{\theta p^-}-\frac{1}{p^-}C^{p^-}\rho ^{ p^-}-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }C^{\beta p^-}\rho ^{\beta p^-} \\\ge & {} \bigg [ \frac{a_{1}}{\alpha (q^+)^\alpha }-\bigg (\frac{b_{2}}{(\theta p^-)^2}C^{\theta p^-}+\frac{1}{p^-}C^{p^-}\bigg )\rho ^{p^- -\alpha q^+}\bigg ]\rho ^{\alpha q^+}-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }C^{\beta p^-}\rho ^{\beta p^-}. \end{aligned}$$

Let us consider,

$$\begin{aligned} {\tilde{\rho }}=\bigg [\frac{ a_{1}}{2\alpha (q^+)^\alpha \bigg (\frac{b_{2}}{(\theta p^-)^2}C^{\theta p^-}+\frac{1}{p^-}C^{p^-}\bigg )}\bigg ]^{\frac{1}{p^- -\alpha q^+}}. \end{aligned}$$

Hence, for any \(u\in W_{0}^{1,p(m)}(M)\) such that \( \Vert u \Vert =\rho \in \bigg (max(0, {{\tilde{\rho }}}),1\bigg )\), since \(p^-<\alpha q^+\), we obtain

$$\begin{aligned} \begin{aligned} E(u)&\ge \bigg [ \frac{a_{1}}{\alpha (q^+)^\alpha } -\bigg (\frac{b_{2}}{(\theta p^-)^2}C^{\theta p^-}+\frac{1}{p^-}C^{p^-}\bigg ) {{\tilde{\rho }}}^{p^-\alpha q^+}\bigg ]\rho ^{\alpha q^+}-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }C^{\beta p^-}\rho ^{\beta p^-}\\&\ge \frac{a_{1}}{2\alpha (q^+)^\alpha }\rho ^{\alpha q^+}-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }C^{\beta p^-}\rho ^{\beta p^-} \\&\ge \bigg (\frac{a_{1}}{2\alpha (q^+)^\alpha }-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }C^{ \beta p^-} \bigg ) \rho ^{\alpha q^+}. \end{aligned} \end{aligned}$$

Hence, if \(\lambda <\lambda ^*:= \frac{a_1 (p^-)^\beta }{2\alpha (q^+)^\alpha \epsilon ^\beta C^{\beta p^-}},\) then \(E(u)\ge \sigma >0.\) \(\square \)

Lemma 5.5

Assume that the conditions \(\left( H_{1}\right) \)-\(\left( H_{6}\right) \) hold, then there exist \(w \in W_{0}^{1,q(m)}(M)\) such that \( \Vert w \Vert >0\) and \(E(w)<0\).

Proof

Let \(u\in W_{0}^{1,q(m)}(M) \backslash \{0\}\). From \((H_5)\), we obtain

$$\begin{aligned} \int _{M}F(m,u) dv_{g}(m)\ge c \int _{ \vert u \vert >A} \vert u \vert ^{\eta } dv_{g}(m), \end{aligned}$$
(5.2)

for some \(c>0\).

By \(\left( H_{1}\right) \), \(\left( H_{2}\right) \), (4.1) and (5.2), we have

$$\begin{aligned} \begin{aligned} E(u)&={\hat{\Phi }}\bigg (\int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)} dv_{g}(m)\bigg )+\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}\ln \vert u \vert }{\theta p(m)}dv_{g}(m)\\ {}&\quad -\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}}{(\theta p(m))^{2}}dv_{g}(m)\\&-\int _{M}\frac{ \vert u \vert ^{p(m)}}{p(m)}dv_{g}(m)-\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,u)dv_{g}(m)\bigg )\\&\le \frac{a_{2}}{\alpha (q^-)^{\alpha }}\bigg (\int _{M} \vert \nabla u \vert ^{q(m)} dv_{g}(m)\bigg )^\alpha +\frac{b_2}{\theta p^-}\int _{M} \vert u \vert ^{\theta p(m)} \ln \vert u \vert dv_{g}(m)\\ {}&-\frac{1}{p^+}\int _{M} \vert u \vert ^{p(m)} dv_{g}(m)-\lambda c\int _{ \vert u \vert > A} \vert u \vert ^{\eta } dv_{g}(m). \end{aligned} \end{aligned}$$

Then fixing \(u \ne 0\) and choosing \(t > 1\), we obtain

$$\begin{aligned} \begin{aligned} E(tu)&\le \frac{a_{2}}{\alpha (q^-)^{\alpha }}\bigg (\int _{M} \vert \nabla tu \vert ^{q(m)} dv_{g}(m)\bigg )^\alpha +\frac{b_2}{\theta p^-}\int _{M} \vert tu \vert ^{\theta p(m)} \ln \vert tu \vert dv_{g}(m)\\&-\frac{1}{p^+}\int _{M} \vert tu \vert ^{p(m)} dv_{g}(m)-c\int _{ \vert tu \vert> A} \vert u \vert ^{\eta } dv_{g}(m)\\&\le \frac{t^{\alpha q^+}a_{2}}{\alpha (q^-)^{\alpha }}\bigg (\int _{M} \vert \nabla u \vert ^{q(m)} dv_{g}(m)\bigg )^\alpha +\frac{b_{2} t^{\theta p^{+}} \ln t}{\theta p^-}\int _{M} \vert u \vert ^{\theta p(m)} dv_{g}(m) \\&+\frac{b_{2} t^{\theta p^{+}}}{\theta p^{-}}\int _{M} \vert u \vert ^{\theta p(m)} \ln \vert u \vert dv_{g}(m)-\frac{t^{p^-}}{p^+} \int _{M} \vert u \vert ^{p(m)} dv_{g}(m)\\ {}&\quad -\lambda ct^{\eta }\int _{ \vert tu \vert>A} \vert u \vert ^{\eta } dv_{g}(m) \\&\le t^{\alpha q^+}\bigg [ \frac{a_{2}}{\alpha (q^-)^{\alpha }}\bigg (\int _{M} \vert \nabla u \vert ^{q(m)} dv_{g}(m)\bigg )^\alpha + \frac{lnt}{t^{\alpha q^+ -\theta p^{+} }}\times \frac{b_{2}}{\theta p^-}\int _{M} \vert u \vert ^{\theta p(m)} dv_{g}(m)\\&+ t^{\theta p^{+} - \alpha q^+ }\frac{ b_{2}}{\theta p^{-}}\int _{M} \vert u \vert ^{\theta p(m)} \ln \vert u \vert dv_{g}(m)-\frac{t^{p^- -\alpha q^+}}{p^+}\int _{M} \vert u \vert ^{p(m)} dv_{g}(m)\\&-\lambda ct^{\eta - \alpha q^+}\int _{ \vert tu \vert > A} \vert u \vert ^{\eta } dv_{g}(m) \bigg ], \end{aligned} \end{aligned}$$

with \(\displaystyle \int _{ \vert tu \vert > A} \vert u \vert ^{\eta } dv_{g}(m) \longrightarrow \rho _{\eta }(u)\) as \(t\longrightarrow +\infty \). Since \(\eta >\alpha q^+\), \(\alpha q^+ >\theta p^+\) and \(\frac{\ln t}{t^{\alpha q^+ -\theta p^{+} }} \longrightarrow 0\) as \(t \longrightarrow + \infty \), we deduce that \(E(tu)\longrightarrow -\infty \) as \(t\longrightarrow + \infty \). Hence, for \(t > 1\) sufficiently large, we can let \(w = tu\) such that \(E(w) <0\). \(\square \)

Lemma 5.6

Suppose that the conditions in Theorem 4.1 hold, then the functional E satisfies the (PS) condition.

Proof

Let \({u_{n}}\) be a Palais–Smale sequence, i.e.,

$$\begin{aligned} E(u_{n}) \text { is bounded and } E'(u_{n})\longrightarrow 0 \qquad { in } \left( W_{0}^{1,q(m)}(M) \right) ^{*}. \end{aligned}$$
(5.3)

We proceed in two steps to prove Lemma 5.6.

\({\textbf {Step 1}}\): By contradiction, we will prove that \({u_{n}}\) is bounded in \(W_{0}^{1,q(m)}(M)\). Let \( \Vert u_{n} \Vert \rightarrow +\infty \), hence \( \Vert u_{n} \Vert > 1\). From \(\left( H_{1}\right) \)-\(\left( H_{2}\right) \), we get

$$\begin{aligned} \begin{aligned}&E(u_{n}) - \frac{1}{\eta } \langle E'(u_{n}),u_{n}\rangle \\&\quad ={\hat{\Phi }}\left( \int _{M} \frac{1}{q(m)} \vert \nabla u_{n}(m) \vert ^{q(m)}\text {d} v_{g}(m)\right) +\int _{M}\frac{g(m) \vert u_n \vert ^{\theta p(m)}\ln \vert u_n \vert }{\theta p(m)}dv_{g}(m)\\&\qquad -\int _{M}\frac{g(m) \vert u_n \vert ^{\theta p(m)}}{(\theta p(m))^{2}}dv_{g}(m) -\int _{M} \frac{ \vert u_n \vert ^{p(m)}}{p(m)} dv_{g}(m) -\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,u_{n})dv_{g}(m)\bigg )\\&\qquad - \frac{1}{\eta }\Phi \left( \int _{M} \frac{1}{q(m)} \vert \nabla u_{n}(m) \vert ^{q(m)}\text {d} v_{g}(m)\right) \int _{M} \vert \nabla u_n \vert ^{q(m)}\text {d} v_{g}(m) \\&\qquad - \frac{1}{\eta }\int _{M}g(m) \vert u_n \vert ^{\theta p(m)}\ln \vert u_n \vert dv_{g}(m)+\frac{1}{\eta }\int _{M} \vert u_n \vert ^{p(m)}dv_{g}(m)\\&\qquad +\frac{\lambda }{\eta }\Psi \bigg (\int _{M}F(m,u_{n})dv_{g}(m)\bigg )\int _{M}f(m,u_n)u_n dv_{g}(m) \\&\quad \ge \big (\frac{a_1}{\alpha (q^+)^\alpha }-\frac{a_2}{\eta (q^-)^{\alpha -1}}\big )\bigg (\int _{M} \vert \nabla u_n \vert ^{q(m)}dv_{g}(m)\bigg )^\alpha \\&\quad + \bigg ( \frac{b_1}{\theta p^+ } - \frac{b_2}{\eta } \bigg )\int _{M} \vert u_n \vert ^{\theta p(m)}\ln \vert u_n \vert dv_{g}(m)\\&\quad - \frac{b_2}{(\theta p^-)^2}\int _{M} \vert u_n \vert ^{\theta p(m)}dv_{g}(m) +\bigg (\frac{1}{\eta }-\frac{1}{p^-}\bigg )\int _{M} \vert u_n \vert ^{p(m)}dv_{g}(m)\\&\quad +\frac{\lambda }{\eta }\Psi \bigg (\int _{M}F(m,u_{n})dv_{g}(m)\bigg )\int _{M}f(m,u_n)u_n dv_{g}(m)-\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,u_{n})dv_{g}(m)\bigg ). \end{aligned} \end{aligned}$$

According to \(\left( H_{5}\right) \), we obtain

$$\begin{aligned} 0<\int _{M}F(m,u_{n}) dv_{g}(m)\le \frac{1}{\eta } \int _{M} f(m,u_{n}) u_{n} dv_{g}(m). \end{aligned}$$

Moreover, by (4.2)

$$\begin{aligned} {\hat{\Psi }}\bigg (\int _{M}F(m,u_{n}) dv_{g}(m) \bigg ) \le \Psi \bigg (\int _{M}F(m,u_{n}) dv_{g}(m)\bigg )\int _{M}F(m,u_{n}) dv_{g}(m)&\nonumber \\ \le \frac{1}{\eta }\Psi \bigg (\int _{M}F(m,u_{n}) dv_{g}(m)\bigg ) \int _{M} f(m,u_{n}) u_{n} dv_{g}(m).&\end{aligned}$$
(5.4)

Then, from (5.4) and since \(\eta >\max \bigg ( \displaystyle \frac{a_{2}\alpha (q^+)^\alpha }{a_1 (q^-)^\alpha }, \frac{b_2 \theta p^+}{b_1}\bigg )\) and \(\eta>\alpha q^+>p^-\), we get

$$\begin{aligned} \begin{aligned} E(u_{n}) - \frac{1}{\eta } \langle E'(u_{n}),u_{n}\rangle&\ge \bigg (\frac{a_1}{\alpha (q^+)^\alpha }-\frac{a_2}{\eta (q^-)^{\alpha -1}}\bigg ) \Vert u \Vert ^{\alpha q^{-}} - \frac{b_2}{(\theta p^-)^2} C^{\theta p^+} \Vert u \Vert ^{\theta p^+}\\&+\bigg (\frac{1}{\eta }-\frac{1}{p^-}\bigg )C^{p^+} \Vert u \Vert ^{p^+}. \end{aligned} \end{aligned}$$

Since \(p^+<\theta p^+<\alpha q^-\) then \(0 \ge + \infty \), we obtain a contradiction. Then \(u_{n}\) is necessarily bounded in \(W_{0}^{1,q(m)}(M)\).

Step 2: Let us now study the strong convergence of \(u_{n}\) in \(W_{0}^{1,q(m)}(M)\). Since \({u_{n}}\) is bounded in \(W_{0}^{1,q(m)}(M)\), there exists a subsequence of \({u_{n}}\), noted \({u_{n}}\), such as \( u_{n} \rightharpoonup u \text { weakly in } W_{0}^{1,q(m)}(M)\). On the other hand, from the compact embeddings, we obtain

$$\begin{aligned} u_{n} \longrightarrow u \text { strongly in } L^{p(m)}(M), p(m) < q^{*}(m). \end{aligned}$$
(5.5)
$$\begin{aligned} u_{n} \longrightarrow u \text { strongly in } L^{(1+\theta ) p(m)}(M), (\theta +1 )p(m)<q^{*}(m). \end{aligned}$$
(5.6)

By (5.3), we get

$$\begin{aligned} \langle E'(u_{n}),u_{n}-u \rangle \longrightarrow 0. \end{aligned}$$
(5.7)

Moreover,

$$\begin{aligned} \begin{aligned}&\Phi \left( \int _{M} \frac{ \vert \nabla u_{n}(m) \vert ^{q(m)}}{q(m)}\text {d} v_{g}(m)\right) \int _{M} \vert \nabla u_n \vert ^{q(m)-2}\nabla u_n (\nabla u_{n}-\nabla u) \text {d} v_{g}(m)\\&=\langle E'(u_{n}),u_{n}-u \rangle +\int _{M} \vert u_n \vert ^{p(m)-2}u_n (u_n- u)dv_{g}(m) \\&-\int _{M}g(m) \vert u_n \vert ^{\theta p(m)-2}u_n \ln \vert u_n \vert (u_n- u) dv_{g}(m)\\&+\lambda \Psi \bigg (\int _{M}F(m,u_{n})dv_{g}(m)\bigg )\int _{M}f(m,u_n)(u_n- u) dv_{g}(m). \end{aligned} \end{aligned}$$

Using the Hölder inequality, we get

$$\begin{aligned} \begin{aligned} \bigg \vert \int _{M} \vert u_{n} \vert ^{p(m)-2}u_{n}\left( u_{n}- u \right) \text {d} v_{g}(m) \bigg \vert&\le \int _{M} \vert u_{n} \vert ^{p(m)-1} \vert \left( u_{n}- u \right) \vert \text {d} v_{g}(m) \\&\le 2 \vert \vert u_{n} \vert ^{p(m)-1} \vert _{\frac{p(m)}{p(m)-1}} \vert u_{n}-u \vert _{p(m)} \\&\le 2 \bigg ( \vert u_{n} \vert _{p(m)}^{p^{+}-1}+ \vert u_{n} \vert _{p(m)}^{p^{+}-1}\bigg ) \vert u_{n}-u \vert _{p(m)}, \end{aligned} \end{aligned}$$

then, by (5.5)

$$\begin{aligned} \bigg \vert \int _{M} \vert u_{n} \vert ^{p(m)-2}u_{n}\left( u_{n}- u \right) \text {d} v_{g}(m) \bigg \vert \longrightarrow 0 \text { as } n\longrightarrow + \infty . \end{aligned}$$
(5.8)

Similarly, from \((H_{4})\), (4.1) and (5.5), we get

$$\begin{aligned} \bigg \vert \Psi \bigg (\int _{M}F(m,u_{n})dv_{g}(m)\bigg )\int _{M} f(m,u_n)\left( u_{n}- u \right) \text {d} v_{g}(m) \bigg \vert \longrightarrow 0 \text { as } n\longrightarrow + \infty .\nonumber \\ \end{aligned}$$
(5.9)

On the other hand, we have

$$\begin{aligned} \begin{aligned}&\int _{M} \bigg \vert \vert u_n \vert ^{\theta p(m)-2} u_n \ln \vert u_n \vert \bigg \vert ^{\frac{(1+\theta ) p(m)}{(1+\theta ) p(m)-1}}dv_{g}(m)\\&\quad =\int _{M_1}\bigg \vert \vert u_n \vert ^{\theta p(m)-2} u_n \ln \vert u_n \vert \bigg \vert ^{\frac{(1+\theta ) p(m)}{(1+\theta ) p(m)-1}} dv_{g}(m)\\&\qquad +\int _{M_2}\bigg \vert \vert u_n \vert ^{\theta p(m)-2} u_n \ln \vert u_n \vert \bigg \vert ^{\frac{(1+\theta ) p(m)}{(1+\theta ) p(m)-1}} dv_{g}(m) \\&\quad \le C vol(M)+ \int _{M_2}\bigg \vert \vert u_n \vert ^{\theta p(m)-2} u_n \ln \vert u_n \vert \bigg \vert ^{\frac{(1+\theta ) p(m)}{(1+\theta ) p(m)-1}} dv_{g}(m), \end{aligned} \end{aligned}$$

where \(M_1=\{m\in M, \vert u_n \vert \le 1\}\) and \(M_2 =\{m\in M, \vert u_n \vert \ge 1\}.\) We can deduce from the continuous embedding \(W_{0}^{1,q(m)}(M) \hookrightarrow L^{(1+\theta ) p(m)}(M)\) and Lemma 5.2 that

$$\begin{aligned} \begin{aligned}&\int _{M}\bigg \vert \vert u_n \vert ^{\theta p(m)-2} u_n \ln \vert u_n \vert \bigg \vert ^{\frac{(1+\theta ) p(m)}{(1+\theta ) p(m)-1}} dv_{g}(m)\\&\le \textrm{C}vol(M)+\frac{1}{(e p^{-})^{\frac{(1+\theta )p^+}{(1+\theta )p^- -1}}}\int _{M} \vert u_n \vert ^{(\theta +1) p(m)} dv_{g}(m)\\&\le \textrm{C}vol(M)+\frac{1}{(e p^{-})^{\frac{(1+\theta )p^+}{(1+\theta )p^- -1}}}\bigg (C^{(1 +\theta ) p^-} \Vert u_n \Vert ^{(1 +\theta ) p^-} +C^{(1 +\theta ) p^+} \Vert u_n \Vert ^{(1 +\theta )p^+}\bigg ). \end{aligned} \end{aligned}$$
(5.10)

The inequality (5.10) implies that

$$\begin{aligned} \left| \vert u_n \vert ^{\theta p(m)-1} \ln \vert u_n \vert \right| _{\frac{(1+\theta ) p(m)}{(1+\theta ) p(m)-1}}\le C. \end{aligned}$$
(5.11)

Using the Hölder inequality, \((H_{1})\), (5.6) and (5.11), we get

$$\begin{aligned} \begin{aligned} \bigg \vert \int _{M}g(m) \vert&u_n \vert ^{\theta p(m)-2} u_n \ln \vert u_n \vert (u_n -u) dv_{g}(m) \bigg \vert \\&\le 2 b_1 \left| \vert u_n \vert ^{p(m)-1} \ln \vert u_n \vert \right| _{\frac{(1+\theta ) p(m)}{(1+\theta ) p(m)-1}} \vert u_n -u \vert _{(1+\theta ) p(m)} \longrightarrow 0 \text{ as } n \longrightarrow +\infty . \end{aligned} \end{aligned}$$
(5.12)

From (5.7), (5.8), (5.9) and (5.12), we get

$$\begin{aligned} \Phi \left( \int _{M} \frac{1}{q(m)} \vert \nabla u_{n}(m) \vert ^{q(m)}\text {d} v_{g}(m)\right) \int _{M} \vert \nabla u_n \vert ^{q(m)-2}\nabla u_n (\nabla u_{n}-\nabla u) d v_{g}(m)\longrightarrow 0. \end{aligned}$$

From condition \((H_{2})\), we get

$$\begin{aligned} \int _{M} \vert \nabla u_n \vert ^{q(m)-2}\nabla u_n (\nabla u_{n}-\nabla u) \text {d} v_{g}(m)\longrightarrow 0 \text { as } n\longrightarrow +\infty . \end{aligned}$$

Similarly, we have

$$\begin{aligned} \int _{M} \vert \nabla u \vert ^{q(m)-2}\nabla u (\nabla u_{n}-\nabla u) \text {d} v_{g}(m)\longrightarrow 0 \text { as } n\longrightarrow +\infty . \end{aligned}$$

According to the following inequalities

$$\begin{aligned} \left| u-v\right| ^s \le \left\{ \begin{array}{l} c_1\left[ \left( \left| u\right| ^{s-2} u-\left| v\right| ^{s-2} v\right) \left( u-v\right) \right] ^{\frac{s}{2}}\left( \left| u\right| ^s+\left| v\right| ^s\right) ^{\frac{2-s}{s}}, 1<s<2, \\ c_2\left( \left| u\right| ^{s-2} u-\left| v\right| ^{s-2} v\right) \left( u-v\right) , s \ge 2, \end{array}\right. \nonumber \\ \end{aligned}$$
(5.13)

for all \(u, v \in \mathbb {R}^N\), where \(c_1\) and \(c_2\) are positive constants depending only on s, we obtain

$$\begin{aligned}{} & {} \int _{M}\left| \nabla u_n-\nabla u\right| ^{q(m)} d v_{g}(m)\\ {}{} & {} \quad \le \int _{M}\left( \left| \nabla u_n\right| ^{q(m)-2} \nabla u_n- \vert \nabla u \vert ^{q(m)-2} \nabla u \right) \left( \nabla u_n-\nabla u\right) \text {d} v_{g}(m). \end{aligned}$$

Hence, \({u_{n}} \longrightarrow u\) strongly in \(W_{0}^{1,q(m)}(M)\). Thus, E satisfies the Palais–Smale condition in \(W_{0}^{1,q(m)}(M)\). \(\square \)

Finally, Lemma 5.4, Lemma 5.5 and Lemma 5.6 lead us to the conclusion that E satisfy the all conditions of the Mountain Pass Theorem. Then, E has at least one nontrivial critical point, i.e., problem (1.1) has a nontrivial weak solutions.

5.2 Proof of Theorem 4.2

We will prove Theorem 4.2 with the help of the Fountain Theorem. According to \(\left( H_{7}\right) \) and Lemma 5.6, \(E\in \mathcal {C}^{1}\left( W_0^{1,q(m)}(M), \mathbb {R}\right) \) is an even functional and satisfies the Palais–Smale condition. Now, we shall verify that E satisfies the conditions (i) and \(({\textbf {ii}})\) of Theorem 3.3.

\(({\textbf {i}})\) In view of \(\left( H_{4}\right) \) and \(\left( H_{5}\right) \), there exist two positive constants \(C_1\) and \(C_2\) such that

$$\begin{aligned} \vert F(m,t) \vert \ge C_1 \vert t \vert ^\eta -C_2 \vert t \vert , \text { for } (m,t)\in M\times \mathbb {R}. \end{aligned}$$
(5.14)

Let \(u \in Y_{j}\) such that \( \Vert u \Vert > 1\). Hence, from \(\left( H_{1}\right) \), \(\left( H_{2}\right) \), (4.1), (5.14) and Proposition 5.3, we obtain

$$\begin{aligned} \begin{aligned} E(u)&={\hat{\Phi }}\bigg (\int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)} dv_{g}(m)\bigg )+\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}\ln \vert u \vert }{\theta p(m)}dv{g}(m)\\&-\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}}{(\theta p(m))^{2}}dv_{g}(m)-\int _{M}\frac{ \vert u \vert ^{p(m)}}{p(m)}dv_{g}(m)-\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,u)dv_{g}(m)\bigg )\\&\le \frac{a_{2}}{\alpha (q^-)^{\alpha }}\bigg (\int _{M} \vert \nabla u \vert ^{q(m)} dv_{g}(m)\bigg )^\alpha +\frac{b_2}{\theta p^-}\int _{M} \vert u \vert ^{\theta p(m)} \ln \vert u \vert dv_{g}(m)\\&-\frac{1}{p^+}\int _{M} \vert u \vert ^{p(m)} dv_{g}(m)-\lambda C_1\int _{M} \vert u \vert ^{\eta } dv_{g}(m)+\lambda C_2 \int _{M} \vert u \vert dv_{g}(m)\\&\le \frac{a_{2}}{\alpha (q^-)^{\alpha }} \Vert u \Vert ^{\alpha q^+} + \frac{b_2}{\theta p^-} C vol(M)+ \frac{b_2}{\theta p^- e p^{-}} \max \bigg \{ \vert u \vert _{(1+\theta ) p(m)}^{(1+\theta ) p^{+}}, \vert u \vert _{(1+\theta ) p(m)}^{(1+\theta ) p^{-}}\bigg \}\\&- \frac{1}{p^+}\min \bigg \{ \vert u \vert _{p(m)}^{p^{+}}, \vert u \vert _{p(m)}^{p^{-}}\bigg \}-\lambda C_1 \vert u \vert _{\eta }^{\eta }+ \lambda C_2 \vert u \vert _1. \end{aligned} \end{aligned}$$

Because \(\dim Y_{j}<\infty \), then all norms are equivalents, so there are four positive constants \(C_3\), \(C_4\), \(C_{5}\) and \(C_6\), such that

$$\begin{aligned} \vert u \vert _{(1+\theta ) p(m)}^{(1+\theta ) p^{\pm }}\le C_3 \Vert u \Vert ^{(1+\theta ) p^{\pm }}, \vert u \vert _{p(m)}^{p^{\pm }}\ge C_4 \Vert u \Vert ^{p^\pm }, \vert u \vert _{\eta }^{\eta }\ge C_5 \Vert u \Vert ^{\eta }, \vert u \vert _1\le C_6 \Vert u \Vert . \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} E(u)&\le \frac{a_{2}}{\alpha (q^-)^{\alpha }} \Vert u \Vert ^{\alpha q^+}+\frac{b_2}{\theta p^-} C vol(M) +\frac{b_2}{\theta p^- e p^{-}} C_3 \Vert u \Vert ^{(1+\theta )p^{+}} -\frac{1}{p^+}C_4 \Vert u \Vert ^{p^-}\\&- \lambda C_1 C_5 \Vert u \Vert ^{\eta }+\lambda C_2 C_6 \Vert u \Vert \\&\le \Vert u \Vert ^{\alpha q^+}\bigg [\frac{a_{2}}{\alpha (q^-)^{\alpha }}+\frac{b_2}{\theta p^-} \frac{C vol(M)}{ \Vert u \Vert ^{\alpha q^+}} +\frac{b_2}{\theta p^- e p^{-}} C_3 \Vert u \Vert ^{(1+\theta )p^{+}-\alpha q^+} \\&-\frac{1}{p^+}C_4 \Vert u \Vert ^{p^- - \alpha q^+} - \lambda C_1 C_5 \Vert u \Vert ^{\eta -\alpha q^+}+\lambda C_2 C_6 \Vert u \Vert ^{1-\alpha q^+}\bigg ]. \end{aligned} \end{aligned}$$

Since \(\eta>\alpha q^+>1\) and \((1+ \theta ) p^+ <\alpha q^+\), we get \(E(u) \longrightarrow - \infty \text { as } \Vert u \Vert \longrightarrow +\infty , \text{ for } \text{ all } u \in Y_{j}.\)

Then, there exists \(\gamma _{j}= \Vert u \Vert \) large enough such that

$$\begin{aligned} a_{j}=\max _{u \in Y_{j}, \Vert u \Vert =\gamma _{j}} E(u)\le 0. \end{aligned}$$

So, the condition \(({\textbf {i}})\) of Theorem 3.3 is satisfied.

(ii) Let \(u \in Z_{j}\) such that \( \Vert u \Vert >1\). According to \((H_{1})\), \((H_{2})\), (4.1) and (5.1), we get

$$\begin{aligned} \begin{aligned} E(u)&={\hat{\Phi }}\bigg (\int _{M}\frac{ \vert \nabla u \vert ^{q(m)}}{q(m)} dv_{g}(m)\bigg )+\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}\ln \vert u \vert }{\theta p(m)}dv_{g}(m)\\&-\int _{M}\frac{g(m) \vert u \vert ^{\theta p(m)}}{(\theta p(m))^{2}}dv_{g}(m)-\int _{M}\frac{ \vert u \vert ^{p(m)}}{p(m)}dv_{g}(m)-\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,u)dv_{g}(m)\bigg )\\&\ge \frac{a_{1}}{\alpha (q^+)^\alpha }\bigg (\int _{M} \vert \nabla u \vert ^{q(m)}dv_{g}(m)\bigg )^\alpha -\frac{b_{2}}{(\theta p^-)^2}\int _{M} \vert u \vert ^{\theta p(m)}dv_{g}(m)\\&-\frac{1}{p^-}\int _{M} \vert u \vert ^{p(m)}dv_{g}(m)-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\bigg (\int _{M} \vert u \vert ^{p(m)}dv_{g}(m)\bigg )^\beta \\&\ge \frac{a_{1}}{\alpha (q^+)^\alpha } \Vert u \Vert ^{\alpha q^-} -\frac{b_{2}}{(\theta p^-)^2}\max \bigg \{ \vert u \vert _{\theta p(m)}^{\theta p^+}, \vert u \vert _{\theta p(m)}^{\theta p^- }\bigg \} -\frac{1}{p^-}\max \bigg \{ \vert u \vert _{p(m)}^{p^-}, \vert u \vert _{p(m)}^{p^+}\bigg \}\\ {}&-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\max \bigg \{ \vert u \vert _{p(m)}^{\beta p^-}, \vert u \vert _{p(m)}^{\beta p^+} \bigg \}. \end{aligned} \end{aligned}$$

Put

$$\begin{aligned} \sigma _{j}=\sup \bigg \{ \vert u \vert _{p(m)}, \Vert u \Vert =1, u \in Z_{j}\bigg \}, \end{aligned}$$
(5.15)

and

$$\begin{aligned} \mu _{j}=\sup \bigg \{ \vert u \vert _{\theta p(m)}, \Vert u \Vert =1, u \in Z_{j} \bigg \}. \end{aligned}$$
(5.16)

Hence,

$$\begin{aligned} \begin{aligned} E(u)&\ge \frac{a_{1}}{\alpha (q^+)^\alpha } \Vert u \Vert ^{\alpha q^-}-\frac{b_{2}}{(\theta p^-)^2}\max \bigg \{ \mu _j^{\theta p^+ } \Vert u \Vert ^{\theta p^+}, \mu _{j}^{\theta p^- } \Vert u \Vert ^{\theta p^- }\bigg \}\\&-\frac{1}{p^-}\max \bigg \{\sigma _j^{p^-} \Vert u \Vert ^{p^-},\sigma _j^{p^+} \Vert u \Vert ^{p^+}\bigg \}-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\max \bigg \{ \sigma _j^{\beta p^-} \Vert u \Vert ^{\beta p^-},\sigma _j^{\beta p^+} \Vert u \Vert ^{\beta p^+} \bigg \}\\&\ge \bigg [\frac{a_{1}}{\alpha (q^+)^\alpha }-\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\sigma _j^{\beta p^+} \Vert u \Vert ^{\beta p^{+} -\alpha q^-}\bigg ] \Vert u \Vert ^{\alpha q^-}-\frac{b_{2}}{(\theta p^-)^2} \mu _j^{\theta p^+} \Vert u \Vert ^{\theta p^+}\\ {}&\quad -\frac{1}{p^-}\sigma _j^{p^+} \Vert u \Vert ^{p^+}. \end{aligned} \end{aligned}$$

Let us define

$$\begin{aligned} r_{j}=\bigg (\frac{a_{1}(p^{-})^{\beta }}{2\lambda \epsilon ^{\beta } \sigma _j^{\beta p^{+}} \alpha (q^+)^\alpha } \bigg )^{\frac{1}{\beta p^{+} -\alpha q^{-}}}. \end{aligned}$$

Since \(\beta p^{+}>\alpha q^{-}\) and \(\lim _{j\longrightarrow +\infty } \sigma _{j}= 0\), then \(r_{j} \longrightarrow +\infty \) as \(j \longrightarrow + \infty \). Hence, for any \(u\in Z_{j}\) with \( \Vert u \Vert =r_{j}\), we get

$$\begin{aligned} \begin{aligned} E(u)&\ge \bigg [\frac{a_{1}}{2\alpha (q^+)^\alpha }-\frac{1}{p^-}\sigma _j^{p^+}r_j^{p^{+}-\alpha q^-} -\frac{b_{2}}{(\theta p^-)^2} \mu _j r_j^{\theta p^+ -\alpha p^-} \bigg ]r_{j}^{\alpha q^-}\longrightarrow +\infty , \end{aligned} \end{aligned}$$

as \(j \rightarrow \infty \), since \(p^{+}<\theta p^+<\alpha q^{-}\) and \(\sigma _j,\mu _{j}\longrightarrow 0\) as \(j\longrightarrow +\infty \).

Then \(\inf _{u \in Z_{j}, \Vert u \Vert =r_{j}} E(u) \rightarrow +\infty \) as \(j \rightarrow \infty \). That is, condition (ii) of Theorem 3.3 is satisfied. This concludes the proof of Theorem 4.2.

5.3 Proof of Theorem 4.3

We will prove Theorem 4.3 with the help of the Dual Fountain Theorem. From condition \(\left( H_{7}\right) \), we see that \(E\in \mathcal {C}^{1}\left( W_0^{1,q(m)}(M),\mathbb {R}\right) \) is an even functional. Now, we shall verify that E satisfies the conditions \(({\textbf {B}}_1)\)-\(({\textbf {B}}_4)\) of Theorem 3.5. \(({\textbf {B}}_1)\) For any \(u\in Z_{j}\), \( \Vert u \Vert <1\), similarly of the proof of Theorem 4.2 (ii), we have

$$\begin{aligned} \begin{aligned} E(u)&\ge \frac{a_{1}}{\alpha (q^+)^\alpha } \Vert u \Vert ^{\alpha q^+}-\frac{b_{2}}{(\theta p^-)^2}\max \bigg \{ \mu _j^{\theta p^+ } \Vert u \Vert ^{\theta p^+}, \mu _{j}^{\theta p^- } \Vert u \Vert ^{\theta p^- }\bigg \}\\&-\frac{1}{p^-}\max \bigg \{\sigma _j^{p^-} \Vert u \Vert ^{p^-},\sigma _j^{p^+} \Vert u \Vert ^{p^+}\bigg \}\\ {}&\quad -\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\max \bigg \{ \sigma _j^{\beta p^-} \Vert u \Vert ^{\beta p^-},\sigma _j^{\beta p^+} \Vert u \Vert ^{\beta p^+} \bigg \}\\&\ge \frac{a_{1}}{\alpha (q^+)^\alpha } \Vert u \Vert ^{\alpha q^+}-\frac{b_{2}}{(\theta p^-)^2} \mu _j^{\theta p^- } \Vert u \Vert ^{\theta p^-} -\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\sigma _j^{\beta p^-} \Vert u \Vert ^{\beta p^{-}} -\frac{1}{p^-}\sigma _j^{p^-} \Vert u \Vert ^{p^-}\\&\ge \frac{a_{1}}{\alpha (q^+)^\alpha } \Vert u \Vert ^{\alpha q^+}-\bigg [\frac{b_{2}}{(\theta p^-)^2} \mu _j^{\theta p^- }+\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\sigma _j^{\beta p^-} +\frac{1}{p^-}\sigma _j^{p^-}\bigg ] \Vert u \Vert ^{p^-}. \end{aligned} \end{aligned}$$
(5.17)

Since \(\sigma _j\) and \(\mu _j\) are null sequences, then

$$\begin{aligned} \rho _j= & {} \bigg [\frac{2\alpha (q^+)^\alpha }{a_1}\bigg (\frac{b_{2}}{(\theta p^-)^2} \mu _j^{\theta p^- }+ \lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\sigma _j^{\beta p^-} +\frac{1}{p^-}\sigma _j^{p^-}\bigg ) \bigg ]^{\frac{1}{\alpha q^+ -p^-}}\\ {}{} & {} \longrightarrow 0 \text { as } j\longrightarrow + \infty . \end{aligned}$$

Then, there exists \(j_0\in \mathbb {N}\) such that \(\rho _{j}<1\) for all \(j\ge j_0\). Hence, for all \(u\in Z_j\) with \( \Vert u \Vert = \rho _j\), \(j\ge j_0\), we have

$$\begin{aligned} E(u)\ge \frac{a_1 }{2\alpha (q^+)^\alpha }\rho _{j}^{\frac{\alpha q^+}{\alpha q^+ -p^-}}\ge 0. \end{aligned}$$

This shows \(({\textbf {B}}_1)\).

\(({\textbf {B}}_2)\) For \(w\in Y_{j}\) with \( \Vert w \Vert = 1\) and \(0<t<\rho _{j}<1\), from \(\left( H_{1}\right) \), \(\left( H_{2}\right) \), (4.1), (5.1) and Proposition 5.3, we get

$$\begin{aligned} \begin{aligned} E(tw)&={\hat{\Phi }}\bigg (\int _{M}\frac{ \vert \nabla tw \vert ^{q(m)}}{q(m)} dv_{g}(m)\bigg )+\int _{M}\frac{g(m) \vert tw \vert ^{\theta p(m)}\ln \vert tw \vert }{\theta p(m)}dv_{g}(m)\\&-\int _{M}\frac{g(m) \vert tw \vert ^{\theta p(m)}}{(\theta p(m))^{2}}dv_{g}(m)-\int _{M}\frac{ \vert tw \vert ^{p(m)}}{p(m)}dv_{g}(m)-\lambda {\hat{\Psi }}\bigg (\int _{M}F(m,tw)dv_{g}(m)\bigg )\\&\le \frac{t^{\alpha q^-}a_{2}}{\alpha (q^-)^{\alpha }}\bigg (\int _{M} \vert \nabla w \vert ^{q(m)} dv_{g}(m)\bigg )^\alpha +\frac{b_{2} t^{\theta p^{-}} \ln t}{\theta p^-}\int _{M} \vert w \vert ^{\theta p(m)} dv_{g}(m)\\&+\frac{b_{2} t^{\theta p^{-}}}{\theta p^{-}}\int _{M} \vert w \vert ^{\theta p(m)} \ln \vert w \vert dv_{g}(m)-\frac{t^{p^+}}{p^+}\int _{M} \vert w \vert ^{p(m)} dv_{g}(m)\\&+\lambda \frac{\epsilon ^\beta t^{ \beta p^-}}{(p^-)^\beta }\bigg (\int _{M} \vert w \vert ^{ p(m)} dv_{g}(m)\bigg )^{\beta } \\&\le \frac{t^{\alpha q^-}a_{2}}{\alpha (q^-)^{\alpha }}\bigg (\int _{M} \vert \nabla w \vert ^{q(m)} dv_{g}(m)\bigg )^\alpha +\frac{b_{2} t^{\theta p^{-}} \ln t}{\theta p^-}\int _{M} \vert w \vert ^{\theta p(m)} dv_{g}(m) \\ {}&+\frac{b_{2} t^{\theta p^{-}}}{\theta p^{-}} \bigg [ Cvol(M)+ \frac{1}{e p^{-}} \int _{M} \vert w \vert ^{(1+\theta ) p(m)}dv_{g}(m)\bigg ]-\frac{t^{p^+}}{p^{+}}\int _{M} \vert w \vert ^{p(m)} dv_{g}(m)\\&+\lambda \frac{\epsilon ^\beta t^{ \beta p^-}}{(p^-)^\beta }\bigg (\int _{M} \vert w \vert ^{ p(m)} dv_{g}(m)\bigg )^{\beta }. \end{aligned} \end{aligned}$$

Since all norms are equivalent, we obtain

$$\begin{aligned} \begin{aligned} E(tw)&\le \frac{t^{\alpha q^-}a_{2}}{\alpha (q^-)^{\alpha }} +\frac{b_{2} t^{\theta p^{-}} \ln t}{\theta p^-}C_1 +\frac{b_{2} t^{\theta p^{-}}}{\theta p^{-}}\bigg [ C vol(M)+ \frac{1}{e p^{-}} C_2\bigg ]-\frac{t^{p^+}}{p^{+}}C_3+ \lambda \frac{\epsilon ^\beta t^{ \beta p^-}}{(p^-)^\beta }C_{4}\\&\le \bigg [t^{\alpha q^{-} - p^{+}} \frac{a_{2}}{\alpha (q^-)^{\alpha }} + t^{\theta p^- -p^+}\ln t \frac{b_{2} }{\theta p^{-}}C_1 +t^{\theta p^- - p^+}\frac{b_{2} }{\theta p^{-}} \bigg [ Cvol(M)+ \frac{1}{e p^{-}} C_2\bigg ]\\&-\frac{1}{p^{+}}C_3+t^{ \beta p^{-}- p^{+}}\lambda \frac{\epsilon ^\beta C_{4}}{(p^-)^\beta }\bigg ] t^{ p^+}. \end{aligned} \end{aligned}$$

Let us put

$$\begin{aligned} \begin{aligned} S(t)&=t^{\alpha q^{-} - p^{+}} \frac{a_{2}}{\alpha (q^-)^{\alpha }} + t^{\theta p^- -p^+} \ln t \frac{b_{2} }{\theta p^{-}}C_1 +t^{\theta p^- - p^+}\frac{b_{2} }{\theta p^{-}} \bigg [ Cvol(M)+ \frac{1}{e p^{-}} C_2\bigg ]\\&-\frac{1}{p^{+}}C_3+t^{ \beta p^{-}- p^{+}}\lambda \frac{\epsilon ^\beta C_{4}}{(p^-)^\beta }. \end{aligned} \end{aligned}$$

Because \(\beta p^->\alpha q^->\theta p^->p^+\), then the function \(t\longrightarrow S(t)\) is strictly negative in a neighborhood of zero. It follows that there exists a \(r_{j}\in (0, \rho _{j})\) such that \(E(u)< 0\), for all \(u\in Y_j\) \( \Vert u \Vert =r_j\). Hence, we get

$$\begin{aligned} d_{j} = \max _{u\in Y_{j}, \Vert u \Vert =r_{j}} E(u) < 0. \end{aligned}$$

\(({\textbf {B}}_3)\) Since \(Y_{j} \cap Z_{j}\ne \emptyset \) and \(r_{j}<\rho _{j}\), we get

$$\begin{aligned} s_{j} = \max _{u\in Z_{j}, \Vert u \Vert \le \rho _{j}} \inf E(u)\le d_{j}= \max _{u\in Y_{j}, \Vert u \Vert =r_{j}} E(u)<0. \end{aligned}$$

By (5.17), for \(w \in Z_{j}\), \( \Vert w \Vert = 1\), \(0\le t \le \rho _{j}<1\) and \(u = tw\), we obtain

$$\begin{aligned} \begin{aligned} E(tw)&\ge \frac{a_{1}}{\alpha (q^+)^\alpha } \Vert tw \Vert ^{\alpha q^+}-\frac{b_{2}}{(\theta p^-)^2} \mu _j^{\theta p^- } \Vert tw \Vert ^{\theta p^-}\\ {}&\quad -\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\sigma _j^{\beta p^-} \Vert tw \Vert ^{\beta p^{-}} -\frac{1}{p^-}\sigma _j^{p^-} \Vert tw \Vert ^{p^-}\\&\ge \frac{a_{1}}{\alpha (q^+)^\alpha } t^{\alpha q^+}-\frac{b_{2}}{(\theta p^-)^2} \mu _j^{\theta p^- } t^{\theta p^-} -\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\sigma _j^{\beta p^-}t^{\beta p^{-}} -\frac{1}{p^-}\sigma _j^{p^-}t^{p^-} \\&\ge -\frac{b_{2}}{(\theta p^-)^2} \mu _j^{\theta p^- } -\lambda \frac{\epsilon ^\beta }{(p^-)^\beta }\sigma _j^{\beta p^-} -\frac{1}{p^-}\sigma _j^{p^-}. \end{aligned} \end{aligned}$$

Then \(s_{j} \longrightarrow 0\) as \(j\longrightarrow + \infty \). So \(({\textbf {B}}_3)\) holds. \(({\textbf {B}}_{4})\) Let \(\left( u_{n}\right) \subset W_0^{1,q(m)}(M)\) such that \(u_{n} \in Y_{n}, E\left( u_{n}\right) \rightarrow {\widetilde{c}}\) and \(\left( \left. E\right| _{Y_{n}}\right) ^{\prime }\left( u_{n}\right) \rightarrow 0\). The boundedness of \(\left\| u_{n}\right\| \) can be obtained in the same manner as in the proof of Lemma 5.6.

Let us prove

$$\begin{aligned} \lim _{n \rightarrow +\infty }\left\langle E^{\prime }\left( u_{n}\right) , u_{n}-u\right\rangle =0. \end{aligned}$$
(5.18)

As \(X=\overline{\cup _{n} Y_{n}}\), we can choose \(v_{n} \in Y_{n}\) such that \(v_{n} \rightarrow u\) strongly in \(W_{0}^{1,q(m)}(M)\). Since \(E_{\mid Y_{n}}^{\prime }\left( u_{n}\right) \longrightarrow 0\) and \(u_{n}-v_{n} \rightarrow 0\) in \(Y_{n}\), (see [5, Proposition 3.5]), then we get

$$\begin{aligned} \lim _{n \rightarrow +\infty }\left\langle E^{\prime }\left( u_{n}\right) , u_{n}-v_{n}\right\rangle =0. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \begin{aligned} \lim _{n \rightarrow +\infty }\left\langle E^{\prime }\left( u_{n}\right) , u_{n}-u\right\rangle =\lim _{n \rightarrow +\infty }\left\langle E^{\prime }\left( u_{n}\right) , u_{n}-v_{n}\right\rangle +\lim _{n \rightarrow +\infty }\left\langle E^{\prime }\left( u_{n}\right) , v_{n}-u\right\rangle =0. \end{aligned} \end{aligned}$$

Moreover,

$$\begin{aligned}{} & {} \Phi \left( \int _{M} \frac{ \vert \nabla u_{n}(m) \vert ^{q(m)}}{q(m)}\text {d} v_{g}(m)\right) \int _{M} \vert \nabla u_n \vert ^{q(m)-2}\nabla u_n (\nabla u_{n}-\nabla u) \text {d} v_{g}(m) \\{} & {} \quad =\langle E'(u_{n}),u_{n}-u \rangle +\int _{M} \vert u_n \vert ^{p(m)-2}u_n (u_n- u)dv_{g}(m)\\{} & {} \qquad -\int _{M}g(m) \vert u_n \vert ^{\theta p(m)-2}u_n \ln \vert u_n \vert (u_n- u) dv_{g}(m)\\{} & {} \qquad +\lambda \Psi \bigg (\int _{M}F(m,u_{n})dv_{g}(m)\bigg )\int _{M}f(m,u_n)(u_n- u) dv_{g}(m). \end{aligned}$$

From (5.7), (5.8), (5.9),(5.12), (5.13) and \((H_2)\), we get \(u_{n} \rightarrow u\). Moreover \(E^\prime (u_n)\longrightarrow E^\prime (u)\).

Let’s now demonstrate below that \(E^{\prime }(u)=0\). Taking arbitrarily \(v_j \in Y_j\) and observe that when \(n \ge j\), we have

$$\begin{aligned} \begin{aligned} \left\langle E^{\prime }(u), v_j\right\rangle&=\left\langle E^{\prime }(u)-E^{\prime }\left( u_{n}\right) , v_j\right\rangle +\left\langle E^{\prime }\left( u_{n}\right) , v_j\right\rangle \\&=\left\langle E^{\prime }(u)-E^{\prime }\left( u_{n}\right) , v_j\right\rangle +\left\langle \left( \left. E\right| _{Y_{n}}\right) ^{\prime }\left( u_{n}\right) , v_j\right\rangle \longrightarrow 0 \text { as } n\longrightarrow +\infty . \end{aligned} \end{aligned}$$

Then, \(\left\langle E^{\prime }(u), v_j\right\rangle =0\) for all \( v_j \in Y_j.\) Therefore, \(E^{\prime }(u)=0\). This proves that J satisfies the \((P S)_c^*\) condition for every \(c \in \mathbb {R}\). So \(({\textbf {B}}_4)\) is satisfied. Hence, the Dual Fountain Theorem leads to the conclusion of Theorem 4.3.