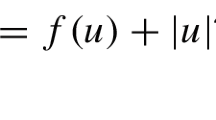Existence of Least-Energy Sign-Changing Solutions for the Schrödinger–Bopp–Podolsky System with Critical Growth

Abstract

In this paper, we study the Schrödinger–Bopp–Podolsky system

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+V(x)u+\phi u=\mu f(u)+u^{5} &{}\text { in } \ \mathbb {R}^{3},\\ -\Delta \phi +a^{2}\Delta ^{2}\phi =4\pi u^{2} &{}\text { in } \ \mathbb {R}^{3}, \end{array}\right. } \end{aligned}$$

thereinto, we request that $a,\ \mu >0$, the function V(x) and f(u) satisfies some specified conditions. By using constraint variational method and quantitative deformation lemma, we derive two results. If $\mu$ is large enough, the system has a least-energy sign-changing solution $u_{\mu }$. Moreover, the energy of the solution is twice as large as that of the ground state solution.

1 Introduction

In this paper, we consider the following Schrödinger–Bopp–Podolsky system

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+V(x)u+\phi u=\mu f(u)+u^{5} &{}\text { in } \ \mathbb {R}^{3},\\ -\Delta \phi +a^{2}\Delta ^{2}\phi =4\pi u^{2} &{}\text { in } \ \mathbb {R}^{3}, \end{array}\right. } \end{aligned}$$

(1.1)

thereinto, we request that $a>0$, which is the Bopp–Podolsky parameter, $\mu >0$, the potential function $V:\mathbb {R}^{3}\rightarrow \mathbb {R}^{+}$ and the nonlinearity $f:\mathbb {R} \rightarrow \mathbb {R}$ satisfies some suitable hypotheses.

The most common Schrödinger–Bopp–Podolsky system is

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta u+V(x)u+K(x)\phi u=f(x,u) &{}\text { in } \ \mathbb {R}^{3},\\ -\Delta \phi +a^{2}\Delta ^{2}\phi =4\pi u^{2} &{}\text { in } \ \mathbb {R}^{3}, \end{array}\right. } \end{aligned}$$

(1.2)

which was first studied in [1] in mathematical literature, and we refer to the recent paper [1,2,3,4,5,6,7,8,9,10,11,12,13,14] for more physical details, we will omit it here.

In recent years, in [1], P. dAvenia and G. Siciliano studied the system (1.2) when V(x) is a constant, $K(x)=q^{2}$ and $f(x,u)=|u|^{p-2}u$. By using variational method, they obtained the existence and nonexistence results. Moreover, they have shown that in the radial case the concentration behaves of the solutions they found. In particular, they take two different approaches to overcoming compactness of the Sobolev embedding $H^{1}(\mathbb {R}^{3})\hookrightarrow L^{s}(\mathbb {R}^{3})(2\le s<6)$: by means of the Splitting lemma; by looking for solutions in the subspace of radial functions of $H^{1}(\mathbb {R}^{3})$, both of which are only available for the case $p\in (2, 6)$. However, the authors do not cover critical cases. In [15], Chen and Tang studied the existence of solutions of system (1.1), by using some new analytic techniques and new inequalities, they found nontrivial solutions, ground state solutions of Nehari–Pohozaev type and ground state solutions of Nehari type in constant potential case. On the other hand, for the case of non-constant potential, they proved that system (1.1) admits ground state solutions for all $\mu >0$ large enough. In [16], Li, Patrizia Pucci and Tang considered the system when $K(x)=q^{2}$ and $f(x,u)=\mu |u|^{p-1}u+|u|^{4}u$. They firstly proved the existence of ground state solutions for the “limit” problem, by using a global compactness lemma, they proved that Palais–Smale condition holds and the existence of ground state solutions. Therefore, the main results of [15] and [16] has extended the existence results in [1] to critical cases. Moreover, in [17] Yang, Chen and Liu considered a class of Schrödinger–Bopp–Podolsky system with critical growth. They proved the existence of nontrivial solution without any growth and Ambrosetti–Rabinowitz conditions.

Based on the above observations, we find that more of the research around the Schrödinger–Bopp–Podolsky system is the ground state solution. Motivated by [15, 18,19,20] and an originate idea of [21], the main purpose of present paper is to investigate the existence of least-energy sign-changing solutions for the critical Schrödinger–Bopp–Podolsky system with subcritical perturbations. And, we suppose that $V:\mathbb {R}^{3}\rightarrow \mathbb {R}^{+}$ and $f:\mathbb {R} \rightarrow \mathbb {R}$ satisfy the following assumptions:

(V):

$V(x)\in C(\mathbb {R}^{3}, ~\mathbb {R}^{+})$ is coercive;

($f_1$):

$f\in C^{1}(\mathbb {R}, ~\mathbb {R})$, $\lim \limits _{|t|\rightarrow 0}\frac{f(t)}{t}=0$ and $\lim \limits _{|t|\rightarrow \infty }\frac{f(t)}{t^{5}}=0$;

($f_2$):

The function $\frac{f(t)}{|t|^{3}}$ is increasing on $(-\infty ,~0)$ and $(0,+\infty )$.

Thus, we can say that, for any fixed $a>0$, a pair $(u,\phi )\in H\times \mathcal {D}$ is a solution of (1.1) if and only if the following equations hold

$$\begin{aligned} \int _{\mathbb {R}^{3}}[\nabla u\cdot \nabla v+V(x)uv]dx+\int _{\mathbb {R}^{3}}\phi uvdx=\int _{\mathbb {R}^{3}}[\mu f(u)+u^{5}]vdx,\ \ \ \&\forall v \in H^{1}(\mathbb {R}^{3}),\\ \int _{\mathbb {R}^{3}}\nabla \phi \cdot \nabla \zeta dx+a^{2}\int _{\mathbb {R}^{3}}\Delta \phi \Delta \zeta dx=4\pi \int _{\mathbb {R}^{3}}\zeta u^{2}dx,\ \ \ \&\forall \zeta \in \mathcal {D}, \end{aligned}$$

where $\mathcal {D}$ and H is a function space that will be introduced in Sect. 2.

Then our results can be stated as follows.

Theorem 1.1

Assume that (V), $(f_1)$ and $(f_2)$ holds, then there exists $\mu ^{*}>0$ such that for all $\mu \ge \mu ^{*}$, the system (1.1) has a least-energy sign-changing solution $u_{\mu }$, which has precisely two nodal domains.

Theorem 1.2

Assume that (V), $(f_1)$ and $(f_2)$ holds, then there exists $\mu ^{**}>0$ such that for all $\mu \ge \mu ^{**}$, the energy of any sign-changing solutions for system (1.1) is strictly larger than two times of the energy of the ground state solution.

Remark 1.3

In fact, there are some differences obviously caused by the nonlocal term, and some good methods of seeking sign-changing solutions for local problems seem not be applicable to nonlocal problems. We borrow the idea from [21], trying to seek a minimizer of the energy function $J_{\mu }$ over the constraint $\mathcal {M}_{\mu }=\{u\in H \text { with } u^{\pm }\ne 0: \langle (J_{\mu })'(u),u^{+}\rangle = \langle (J_{\mu })'(u),u^{-} \rangle =0\}$; then we prove that the minimizer is the sign-changing solution of system (1.1). For the proof of Theorem 1.2, we define the manifold $\mathcal {N}_{\mu }=\{u\in H^{1}(\mathbb {R}^{3})\ \backslash \ \{ 0\}: \langle (J_{\mu })'(u),u\rangle =0\}$, then there exists positive constants $s,\ t$ for $u^{+}$ and $u^{-}$ respectively such that $su^{+}$ and $tu^{-}$ both in $\mathcal {N}_{\mu }$, using the results in [15], we have a ground state solution $v_{\mu }$ with $\mathcal {J}_{\mu }(v_{\mu })=\inf \limits _{\mathcal {N}_{\mu }}\mathcal {J}_{\mu }(u)$, and thus we can compare the energy between sign-changing solutions and ground state solutions by inequalities.

The rest of this paper is organized as follows. In Sect. 2, we present some preliminary notations and Lemmas. In Sect. 3, we prove Theorem 1.1 and Theorem 1.2.

2 Preliminary

In this paper, we use the following notations:

• $H=\{u\in D^{1,2}(\mathbb {R}^{3}):\int _{\mathbb {R}^{3}}V(x)u^{2}dx<\infty \},$ with the norm

  $$\begin{aligned} \Vert u\Vert ^{2}=\int _{\mathbb {R}^{3}}(|\nabla u|^{2}+V(x)u^{2})dx. \end{aligned}$$

• $L^p(\mathbb {R}^3)$ is the usual Lebesgue space endowed with the norm

  $$\begin{aligned} |u|^p_p=\int _{\mathbb {R}^3}|u|^pdx~\text {and}~|u|_{\infty }=\mathop {\mathrm {ess~sup}}\limits _{x\in \mathbb {R}^3}|u(x)|~~ \text {for all}~ p\in [1,~6). \end{aligned}$$

• $C_{i}$ denote a positive constant and is possibly various in different places.

• $\langle \cdot ,\cdot \rangle$ denote action of dual.

• $u^{+}:= \max \{ u(x), 0\}$, $u^{-}:= \min \{ u(x), 0\}.$

• $S~=\inf \limits _{u\in D^{1,2}(\mathbb {R}^{3})}\frac{|\nabla u|_{2}^{2}}{|u|_{6}^{2}}$.

Let $\mathcal {D}$ be the completion of $C_{c}^{\infty }(\mathbb {R}^{3})$ with respect to the norm $\Vert \cdot \Vert _{\mathcal {D}}$ induced by the scalar product

$$\begin{aligned} \langle \varphi ,\psi \rangle _{\mathcal {D}}:=\int _{\mathbb {R}^{3}}\nabla \varphi \cdot \nabla \psi dx+a^{2}\int _{\mathbb {R}^{3}}\Delta \varphi \Delta \psi dx. \end{aligned}$$

Clearly, $\mathcal {D}$ is a Hilbert space continuously embedded into $D^{1,2}(\mathbb {R}^{3})$ and consequently in $L^{6}(\mathbb {R}^{3})$.

Next, we present the following basic results.

Lemma 2.1

(Lemma 3.1, [1]) The space $\mathcal {D}$ is continuously embedded in $L^{\infty }(\mathbb {R}^{3})$.

Lemma 2.2

(Lemma 3.2, [1]) The space $\mathcal {C}_{c}^{\infty }(\mathbb {R}^{3})$ is dense in

$$\begin{aligned} \mathcal {A}:=\{\phi \in D^{1,2}(\mathbb {R}^{3}):\Delta \phi \in L^{2}(\mathbb {R}^{3})\} \end{aligned}$$

normed by $\sqrt{\langle \phi ,\phi \rangle _{\mathcal {D}}}$ and, therefore, $\mathcal {D}=\mathcal {A}$.

In view of the Riesz Theorem, for every fixed $u\in H^{1}(\mathbb {R}^{3})$, there exists a unique solution $\phi _{u}\in \mathcal {D}$ of the second equation in (1.1). Let

$$\begin{aligned} \kappa (x)=\frac{1-e^{-\frac{|x|}{a}}}{|x|}. \end{aligned}$$

We have the following fundamental properties.

Lemma 2.3

(Lemma 3.3, [1]) For all $y\in \mathbb {R}^{3}$, $\kappa (\cdot -y)$ solves in the sense of distributions

$$\begin{aligned} -\Delta \phi +a^{2}\Delta ^{2}\phi =4\pi \delta _{y}. \end{aligned}$$

Moreover,

• (i) if $g\in L_{loc}^{1}(\mathbb {R}^{3})$ and, for a.e. $x\in \mathbb {R}^{3}$, the map $y\in \mathbb {R}^{3} \mapsto \frac{g(y)}{|x-y|}$ is summable, then $\kappa *g\in L_{loc}^{1}(\mathbb {R}^{3})$;

• (ii) if $g\in L^{s}(\mathbb {R}^{3})$ with $1\le s < \frac{3}{2}$, then $\kappa *g\in L^{q}(\mathbb {R}^{3})$ for $q\in (\frac{3s}{3-2s}, ~+\infty ]$.

In both cases $\kappa *g$ solves

$$\begin{aligned} -\Delta \phi +a^{2}\Delta ^{2}\phi =4\pi g \end{aligned}$$

(2.1)

in the sense of distributions, we have the following distributional derivatives

$$\begin{aligned} \nabla (\kappa *g)=(\nabla \kappa )*g \ \ \text { and }\ \ \Delta (\kappa *g)=(\Delta \kappa )*g\ \ \ \ a.e.\text { in } \mathbb {R}^{3}. \end{aligned}$$

For any fixed $u\in H^{1}(\mathbb {R}^{3})$, the unique solution in $\mathcal {D}$ of the second equation in (1.1) is given by

$$\begin{aligned} \phi _{u}:=\kappa *u^{2}. \end{aligned}$$

(2.2)

Then we have the following useful properties.

Lemma 2.4

(Lemma 3.4, [1]) For every $u\in H^{1}(\mathbb {R}^{3})$ we have:

• (1) for every $y\in \mathbb {R}^{3}$, $\phi _{u(\cdot +y)}=\phi _{u}(\cdot +y)$;

• (2) $\phi _{u}\ge 0$;

• (3) for every $s\in (3,+\infty ]$, $\phi _{u}\in L^{s}(\mathbb {R}^{3})\cap \mathcal {C}_{0}(\mathbb {R}^{3})$;

• (4) for every $s\in (3/2,+\infty ]$, $\nabla \phi _{u}=\nabla \kappa *u^{2}\in L^{s}(\mathbb {R}^{3})\cap \mathcal {C}_{0}(\mathbb {R}^{3})$;

• (5) $\phi _{u}\in \mathcal {D}$;

• (6) $\Vert \phi _{u}\Vert _{6}\le C\Vert u\Vert ^{2}$;

• (7) $\phi _{u}$ is the unique minimizer of the functional

  $$\begin{aligned} E(\phi )=\frac{1}{2}\Vert \nabla \phi \Vert _{2}^{2}+\frac{a^{2}}{2}\Vert \Delta \phi \Vert _{2}^{2}-\int _{\mathbb {R}^{3}}\phi u^{2}dx,\ \ \ \ \phi \in \mathcal {D}; \end{aligned}$$

• (8) if $v_{n}\rightharpoonup v$ in $H^{1}(\mathbb {R}^{3})$, then $\phi _{v_{n}}\rightharpoonup \phi _{v}$ in $\mathcal {D}.$

Lemma 2.5

(Theorem 2.1, [22]) If V(x) satisfies (V), then H is compactly embedded in $L^{p}(\mathbb {R}^{3})$ for any $p\in [2,6)$. Especially, for any $p\in [2,6)$, there exists $C>0$ such that

$$\begin{aligned} |u|_{p}\le C\Vert u\Vert ,\ \ \ \forall u\in H. \end{aligned}$$

In view of [1], the energy function of (1.1), defined in $H^{1}(\mathbb {R}^{3}) \times \mathcal {D}$ by

$$\begin{aligned} \mathcal {S}(u,\phi )~=~&\frac{1}{2}\int _{\mathbb {R}^{3}}[|\nabla u|^{2}+V(x)u^{2}]dx+\frac{1}{2}\int _{\mathbb {R}^{3}}\phi u^{2}dx\\&-\frac{1}{16\pi }\Vert \nabla \phi \Vert _{2}^{2}-\frac{a^{2}}{16\pi }\Vert \Delta \phi \Vert _{2}^{2}-\int _{\mathbb {R}^{3}}[\mu F(u)+\frac{1}{6}u^{6}]dx \end{aligned}$$

is continuously differentiable and its critical points correspond to the weak solution of (1.1). In order to avoid the difficulty originated by the strongly indefiniteness of the function $\mathcal {S}$, we apply the reduction procedure used in [1] and get the reduced function

$$\begin{aligned} \mathcal {J}_{\mu }(u)=\frac{1}{2}\int _{\mathbb {R}^{3}}[|\nabla u|^{2}+V(x)u^{2}]dx+\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{u}u^{2}dx-\int _{\mathbb {R}^{3}}[\mu F(u)+\frac{1}{6}u^{6}]dx, \end{aligned}$$

(2.3)

which is of class $\mathcal {C}^{1}$ on H and, for all $u,v\in H$

$$\begin{aligned} \langle (\mathcal {J}_{\mu })'(u),v \rangle =\int _{\mathbb {R}^{3}}[\nabla u \cdot \nabla v+V(x)uv]dx+\int _{\mathbb {R}^{3}}\phi _{u}uvdx-\int _{\mathbb {R}^{3}}[\mu f(u)+u^{5}]vdx, \end{aligned}$$

(2.4)

Remark 2.6

The following statements are equivalent:

• (i) The pair $(u,\phi )\in H\times \mathcal {D}$ is critical point of $\mathcal {S}$, that is $(u,\phi )$ is a solution of (1.1);

• (ii) u is a critical point of $\mathcal {J}_{\mu }$ and $\phi =\phi _{u}$.

Hence, if $u\in H$ is a critical point of $\mathcal {J}_{\mu }$, then the pair $(u,\phi _{u})$ is a solution of (1.1). As we defined before, for the sake of simplicity, in many cases we just say $u\in H$, instead of $(u,\phi _{u})\in H\times \mathcal {D}$, is a solution of (1.1).

Next, we define the manifold

$$\begin{aligned} \mathcal {M}_{\mu }=\{u\in H \text { with } u^{\pm }\ne 0: \langle (J_{\mu })'(u),u^{+}\rangle =\langle (J_{\mu })'(u),u^{-}\rangle =0\}, \end{aligned}$$

and fixed $u\in H$ with $u^{\pm }\ne 0$.

Lemma 2.7

Assume that (V), $(f_1)$ and $(f_2)$ holds, if $u\in H$ with $u^{\pm }\ne 0$, then we have the following results:

• (i) There exists a unique pair $(s_{u},t_{u})\in (0,+\infty )\times (0,+\infty )$ such that $s_{u}u^{+}+t_{u}u^{-}\in \mathcal {M}_{\mu }$ and

  $$\begin{aligned} \mathcal {J}_{\mu }(s_{u}u^{+}+t_{u}u^{-})=\max _{(s,t)\in (0,+\infty )\times (0,+\infty )}J_{\mu }(su^{+}+tu^{-}). \end{aligned}$$

• (ii) If $\langle (\mathcal {J}_{\mu })'(u),u^{\pm }\rangle \le 0$, then $0< s_{u}, t_{u} \le 1$.

Proof

• (i) For any $u\in H$ with $u^{\pm }\ne 0$, to prove that there exists a unique pair $(s_{u},t_{u})\in (0,+\infty )\times (0,+\infty )$ such that $s_{u}u^{+}+t_{u}u^{-}\in \mathcal {M}_{\mu }$ is equivalent to prove that $\langle (J_{\mu })'(s_{u}u^{+}+t_{u}u^{-}),s_{u}u^{+}\rangle =\langle (J_{\mu })'(s_{u}u^{+}+t_{u}u^{-}),t_{u}u^{-}\rangle =0$, which means the following equations have a unique solution:

  $$\begin{aligned} {\left\{ \begin{array}{ll} s^{2}\Vert u^{+}\Vert ^{2}&{}+s^{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2}dx+s^{2}t^{2}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2} d x\\ &{}-\mu s\int _{\mathbb {R}^{3}}f(su^{+}+tu^{-})u^{+} d x -s^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6} d x =0;\\ t^{2}\Vert u^{-}\Vert ^{2}&{}+t^{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{-}|^{2}dx+s^{2}t^{2}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{-}|^{2}dx\\ &{}-\mu t\int _{\mathbb {R}^{3}}f(su^{+}+tu^{-})u^{-} d x-t^{6}\int _{\mathbb {R}^{3}}|u^{-}|^{6} d x =0. \end{array}\right. } \end{aligned}$$

  (2.5)

  $\varvec{Firstly}$, we claim the existence of the pair $(s_{u},t_{u})$. Define

  $$\begin{aligned} g_{u}(s,t)~=s^{2}\Vert u^{+}\Vert ^{2}&+s^{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2}dx+s^{2}t^{2}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2} d x\nonumber \\&-\mu s\int _{\mathbb {R}^{3}}f(su^{+}+tu^{-})u^{+} d x -s^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6} d x; \end{aligned}$$

  (2.6)
  $$\begin{aligned} h_{u}(s,t)~=t^{2}\Vert u^{-}\Vert ^{2}&+t^{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{-}|^{2} d x+s^{2}t^{2}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{-}|^{2} d x \nonumber \\&-\mu t\int _{\mathbb {R}^{3}}f(su^{+}+tu^{-})u^{-} d x -t^{6}\int _{\mathbb {R}^{3}}|u^{-}|^{6} d x. \end{aligned}$$

  (2.7)

  By $(f_1)$, for any $\varepsilon > 0$, there exists $C_{\varepsilon } > 0$, we have

  $$\begin{aligned} |f(t)| \le \varepsilon |t| +C_{\varepsilon }|t|^{5}. \end{aligned}$$

  (2.8)

  Using (2.8) and Sobolev inequality, we get

  $$\begin{aligned} g_{u}(s,s)=&s^{2}\Vert u^{+}\Vert ^{2}+s^{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2} d x+s^{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2} d x \\&-\mu s\int _{\mathbb {R}^{3}}f(su)u^{+} d x -s^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6} d x \\ \ge&s^{2}\Vert u^{+}\Vert ^{2}-\varepsilon \mu s^{2}\int _{\mathbb {R}^{3}}|u^{+}|^{2} d x -C_{\varepsilon }\mu s^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6} d x -s^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6} d x \\ \ge&(1-\varepsilon \mu C_{1})s^{2}\Vert u^{+}\Vert ^{2} - \mu C_{2}s^{6}\Vert u^{+}\Vert ^{6}-C_{3}s^{6}\Vert u^{+}\Vert ^{6}. \end{aligned}$$

  Choosing $\varepsilon > 0$ small enough such that $1-\varepsilon \mu C_{1} > 0$, then $g_{u}(s,s) > 0$ for $s > 0$ small enough. Similarly, we obtain that $h_{u}(t,t) > 0$ for $t > 0$ small enough. By $(f_2)$, we can easily get that:

  $$\begin{aligned} f(t)t \ge 4F(t) > 0, \ \ \ \ t\in (-\infty , 0)\cup (0, +\infty ). \end{aligned}$$

  (2.9)

  By Lemma 2.4 (6), (2.9) and Sobolev inequality, we also have that

  $$\begin{aligned} g_{u}(t,t)=&t^{2}\Vert u^{+}\Vert ^{2}+t^{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2} d x+ t^{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2} d x\\&-\mu t\int _{\mathbb {R}^{3}}f(tu)u^{+} d x -t^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6} d x\\ \le&t^{2}\Vert u^{+}\Vert ^{2}+t^{4}\int _{\mathbb {R}^{3}}\phi _{u}|u^{+}|^{2} d x-t^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6} d x. \end{aligned}$$

  as $t\rightarrow +\infty$, $g_{u}(t,t)\rightarrow -\infty$, which means $g_{u}(t,t) < 0$ for $t > 0$ large enough. Similarly, we obtain that $h_{u}(s,s) < 0$ for $s > 0$ large enough. Assume there exists $0< r < R$ such that

  $$\begin{aligned} g_{u}(r,r)> 0,\ \ \ \ g_{u}(R,R)< 0,\\ h_{u}(r,r) > 0,\ \ \ \ h_{u}(R,R) < 0. \end{aligned}$$

  Thus, we have

  $$\begin{aligned} g_{u}(r,t)> 0,\ \ \ \ g_{u}(R,t)< 0 ,\ \&\forall t\in [r,R].\\ h_{u}(s,r) > 0,\ \ \ \ h_{u}(s,R) < 0 ,\ \&\forall s\in [r,R]. \end{aligned}$$

  Then there exists a pair $(s_{u},t_{u})\in (0,+\infty )\times (0,+\infty )$ such that $g_{u}(s_{u},t_{u}) = 0$ and $h_{u}(s_{u},t_{u}) = 0$, thus $s_{u}u^{+}+t_{u}u^{-}\in \mathcal {M}_{\mu }$.

  $\varvec{Secondly}$, we claim the uniqueness of the pair $(s_{u},t_{u})$. $\varvec{Case\ 1.\ u \in \mathcal {M}_{\mu }.}$ By the definition of manifold, we have

  $$\begin{aligned} \Vert u^{\pm }\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u^{\pm }}|u^{\pm }|^{2} d x +\int _{\mathbb {R}^{3}}\phi _{u^{\mp }}|u^{\pm }|^{2} d x=\mu \int _{\mathbb {R}^{3}} f(u)u^{\pm } d x +\int _{\mathbb {R}^{3}}|u^{\pm }|^{6} d x. \end{aligned}$$

  (2.10)

  Let $(s_{0},t_{0})$ be a pair of suitable numbers such that $s_{0}u^{+}+t_{0}u^{-}\in \mathcal {M}_{\mu }$ with $0< s_{0} \le t_{0}.$ Then we have

  $$\begin{aligned} s_{0}^{2}\Vert u^{+}\Vert ^{2}+s_{0}^{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2}dx&+s_{0}^{2}t_{0}^{2}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2}dx\nonumber \\&=\mu \int _{\mathbb {R}^{3}} f(s_{0}u^{+})s_{0}u^{+}dx+s_{0}^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6}dx. \end{aligned}$$

  (2.11)
  $$\begin{aligned} t_{0}^{2}\Vert u^{-}\Vert ^{2}+t_{0}^{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{-}|^{2}dx&+s_{0}^{2}t_{0}^{2}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{-}|^{2}dx\nonumber \\&=\mu \int _{\mathbb {R}^{3}} f(t_{0}u^{-})t_{0}u^{-}dx+t_{0}^{6}\int _{\mathbb {R}^{3}}|u^{-}|^{6}dx. \end{aligned}$$

  (2.12)

  Operating $\frac{1}{t_{0}^{4}}$(2.12)-(2.10), we have:

  $$\begin{aligned} (\frac{1}{t_{0}^{2}}-1)\Vert u^{-}\Vert ^{2} \ge (t_{0}^{2}-1)\int _{\mathbb {R}^{3}}|u^{-}|^{6}dx+\mu \int _{\mathbb {R}^{3}}[\frac{f(t_{0}u^{-})}{(t_{0}u^{-})^{3}}-\frac{f(u^{-})}{(u^{-})^{3}}](u^{-})^{4} d x. \end{aligned}$$

  (2.13)

  Using $(f_2)$, if $t_{0} > 1$, the inequality is absurd; therefore, we obtain that $0 < s_{0} \le t_{0} \le 1$. Similarly, we also obtain that $s_{0} \ge 1$. Consequently, $s_{0} = t_{0} = 1$.

  $\varvec{Case\ 2.\ u \not \in \mathcal {M}_{\mu }.}$ Suppose that there exists two pairs $(s_{1},t_{1})$, $(s_{2},t_{2})$ such that $v=s_{1}u^{+}+t_{1}u^{-}\in \mathcal {M}_{\mu },$ $w=s_{2}u^{+}+t_{2}u^{-}\in \mathcal {M}_{\mu }.$ Therefore, we have

  $$\begin{aligned} w=s_{2}u^{+}+t_{2}u^{-}=\frac{s_{2}}{s_{1}}s_{1}u^{+}+\frac{t_{2}}{t_{1}}t_{1}u^{-}=\frac{s_{2}}{s_{1}}v^{+}+\frac{t_{2}}{t_{1}}v^{-}. \end{aligned}$$

  Through the analysis in Case 1, we have

  $$\begin{aligned} \frac{s_{2}}{s_{1}}=\frac{t_{2}}{t_{1}}=1, \end{aligned}$$

  so, $s_{1}=s_{2}$, $t_{1}=t_{2}$. The uniqueness is complete.

  $\varvec{Thirdly}$, we claim that the pair $(s_{u},t_{u})$ is a maximum point. For any $u\in H$ with $u^{\pm }\ne 0$, by (2.9), we have

  $$\begin{aligned}&\mathcal {J}_{\mu }(su^{+}+tu^{-})\\ {}&=\frac{1}{2}\int _{\mathbb {R}^{3}}[|\nabla (su^{+}+tu^{-})|^{2}+V(x)(su^{+}+tu^{-})^{2}]dx\\&+\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{su^{+}+tu^{-}}|su^{+}+tu^{-}|^{2}dx -\mu \int _{\mathbb {R}^{3}}F(su^{+}+tu^{-})dx\\&-\frac{1}{6}\int _{\mathbb {R}^{3}}|su^{+}+tu^{-}|^{6}dx\\ =&\frac{s^{2}}{2}\Vert u^{+}\Vert ^{2}+\frac{t^{2}}{2}\Vert u^{-}\Vert ^{2} +\frac{s^{4}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2}dx +\frac{t^{4}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{-}|^{2}dx \\&+\frac{s^{2}t^{2}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{-}|^{2}dx +\frac{s^{2}t^{2}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2}dx\\&-\int _{\mathbb {R}^{3}}\mu F(su^{+}+tu^{-})dx-\frac{s^{6}}{6}|u^{+}|_{6}^{6}-\frac{t^{6}}{6}|u^{-}|_{6}^{6}\\ \le&\frac{s^{2}}{2}\Vert u^{+}\Vert ^{2}+\frac{t^{2}}{2}\Vert u^{-}\Vert ^{2} +\frac{s^{4}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2}dx\\&+\frac{t^{4}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{-}|^{2}dx +\frac{s^{2}t^{2}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{-}|^{2}dx\\&+\frac{s^{2}t^{2}}{4}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2}dx -\frac{s^{6}}{6}|u^{+}|_{6}^{6}-\frac{t^{6}}{6}|u^{-}|_{6}^{6}. \end{aligned}$$

  Obviously, $\mathcal {J}_{\mu }(su^{+}+tu^{-}) \rightarrow -\infty$ as $(s,t)\rightarrow \infty$. Thus, $\mathcal {J}_{\mu }(su^{+}+tu^{-})$ only have a unique maximum point such that

  $$\begin{aligned} \mathcal {J}_{\mu }(s_{u}u^{+}+t_{u}u^{-})=\max _{(s,t)\in (0,+\infty )\times (0,+\infty )}J_{\mu }(su^{+}+tu^{-}). \end{aligned}$$

• (ii) If $\langle (\mathcal {J}_{\mu })'(u),u^{\pm }\rangle \le 0$, by the definition, we have

  $$\begin{aligned} \Vert u^{\pm }\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u}|u^{\pm }|^{2} d x \le \mu \int _{\mathbb {R}^{3}} f(u)u^{\pm } d x +\int _{\mathbb {R}^{3}}|u^{\pm }|^{6} d x. \end{aligned}$$

  For the fixed $u\in H$, by (i), we know that there exists a pair $(s_{u},t_{u})$ such that $s_{u}u^{+}+t_{u}u^{-}\in \mathcal {M}_{\mu }$ with $0 < t_{u} \le s_{u}$, then

  $$\begin{aligned}&s_{u}^{2}\Vert u^{+}\Vert ^{2}+s_{u}^{4}\int _{\mathbb {R}^{3}}\phi _{u}|u^{+}|^{2} d x \\ {}&\ge s_{u}^{2}\Vert u^{+}\Vert ^{2}+s_{u}^{4}\int _{\mathbb {R}^{3}}\phi _{u^{+}}|u^{+}|^{2} d x +s_{u}^{2}t_{u}^{2}\int _{\mathbb {R}^{3}}\phi _{u^{-}}|u^{+}|^{2} d x \\&= \mu \int _{\mathbb {R}^{3}} f(s_{u}u^{+}+t_{u}u^{-})(s_{u}u^{+}) d x+s_{u}^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6}dx . \end{aligned}$$

  It’s similar to the calculation in (i), we omitted it here. We have that

  $$\begin{aligned} (\frac{1}{s_{u}^{2}}-1)\Vert u^{+}\Vert ^{2} \ge (s_{u}^{2}-1)\int _{\mathbb {R}^{3}}|u^{+}|^{6}dx+\mu \int _{\mathbb {R}^{3}}[\frac{f(s_{u}u^{+})}{(s_{u}u^{+})^{3}}-\frac{f(u^{+})}{(u^{+})^{3}}](u^{+})^{4} d x. \end{aligned}$$

  By $(f_2)$, if $s_{u} \ge 1$, the inequality is absurd, thus $0< t_{u} \le s_{u} \le 1.$ The proof is complete.

$\square$

Lemma 2.8

There exists $\rho > 0$ such that $\Vert u^{\pm }\Vert \ge \rho$ for all $u\in \mathcal {M}_{\mu }.$

Proof

$\forall u\in \mathcal {M}_{\mu }$, we have

$$\begin{aligned} \Vert u^{\pm }\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u}|u^{\pm }|^{2} d x = \mu \int _{\mathbb {R}^{3}} f(u)u^{\pm } d x +\int _{\mathbb {R}^{3}}|u^{\pm }|^{6} d x. \end{aligned}$$

By (2.8) and Sobolev inequalities, we have that

$$\begin{aligned} \Vert u^{\pm }\Vert ^{2}&\le \Vert u^{\pm }\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u}|u^{\pm }|^{2} d x = \mu \int _{\mathbb {R}^{3}} f(u)u^{\pm } d x +\int _{\mathbb {R}^{3}}|u^{\pm }|^{6} d x\\&\le \varepsilon \mu \int _{\mathbb {R}^{3}}|u^{\pm }|^{2}dx+C_{\varepsilon }\mu \int _{\mathbb {R}^{3}}|u^{\pm }|^{6}dx +\int _{\mathbb {R}^{3}}|u^{\pm }|^{6}dx\\&\le C_{4}\varepsilon \mu \Vert u^{\pm }\Vert ^{2}+C_{5}\mu \Vert u^{\pm }\Vert ^{6}+C_{6}\Vert u^{\pm }\Vert ^{6}. \end{aligned}$$

Thus

$$\begin{aligned} (1-C_{4}\varepsilon \mu )\Vert u^{\pm }\Vert ^{2} \le C_{5}\mu \Vert u^{\pm }\Vert ^{6}+C_{6}\Vert u^{\pm }\Vert ^{6}. \end{aligned}$$

Choosing $\varepsilon > 0$ such that $1-C_{4}\varepsilon \mu > 0$, then there exists $\rho > 0$, $\Vert u^{\pm }\Vert \ge \rho > 0.$ $\square$

Lemma 2.9

Suppose (V), $(f_1)$ and $(f_2)$ holds, let $c_{\mu }=\inf \limits _{u\in \mathcal {M}_{\mu }}\mathcal {J}_{\mu }$, then we have that $\lim \limits _{\mu \rightarrow \infty }c_{\mu } =0$.

Proof

For any $u\in \mathcal {M}_{\mu }$, using (2.9) and Lemma 2.8, we have

$$\begin{aligned} \mathcal {J}_{\mu }(u)&=\mathcal {J}_{\mu }(u)-\frac{1}{4}\langle (\mathcal {J}_{\mu })'(u),u\rangle \\&=\frac{1}{4}\Vert u\Vert ^{2}+\frac{\mu }{4}\int _{\mathbb {R}^{3}}[f(u)u-4F(u)]dx+\frac{1}{12}\int _{\mathbb {R}^{3}}|u|^{6}dx\\&\ge \frac{1}{4}\Vert u\Vert ^{2}\\&\ge \frac{1}{4}\rho ^{2}>0. \end{aligned}$$

Therefore, $\mathcal {J}_{\mu }(u)$ is bounded below on $\mathcal {M}_{\mu }$. That is $c_{\mu }$ is well-defined. For $\forall u\in H$ with $u^{\pm }\ne 0$, for each $\mu > 0$, by Lemma 2.7, there exists a unique pair $(s_{\mu },t_{\mu })\in (0,+\infty )\times (0,+\infty )$ such that $s_{\mu }u^{+}+t_{\mu }u^{-}\in \mathcal {M}_{\mu }$. Therefore, by (2.9) and Lemma 2.7, we have that

$$\begin{aligned} 0 \le c_{\mu }=\inf _{u\in \mathcal {M}_{\mu }}\mathcal {J}_{\mu }&\le \mathcal {J}_{\mu }(s_{\mu }u^{+}+t_{\mu }u^{-})\\&\le \frac{1}{2}\Vert s_{\mu }u^{+}+t_{\mu }u^{-}\Vert ^{2} +\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{s_{\mu }u^{+}+t_{\mu }u^{-}}|s_{\mu }u^{+}+t_{\mu }u^{-}|^{2}d x\\&\le s_{\mu }^{2}\Vert u^{+}\Vert ^{2}+t_{\mu }^{2}\Vert u^{-}\Vert ^{2}+\frac{1}{2}C_{7}s_{\mu }^{4}\Vert u^{+}\Vert ^{4} +\frac{1}{2}C_{8}t_{\mu }^{4}\Vert u^{-}\Vert ^{4}. \end{aligned}$$

To our end, we just prove that $s_{\mu }\rightarrow 0$ and $t_{\mu }\rightarrow 0$ as $\mu \rightarrow \infty$.

Let $\Phi _{u}=\{ (s_{\mu },t_{\mu })\in (0,+\infty )\times (0,+\infty ): W_{u}(s_{\mu },t_{\mu })=(0,0),\ \mu > 0\},$ where $W_{u}$ is defined as follow: $W_{u}: (0,+\infty )\times (0,+\infty ) \rightarrow \mathbb {R}^{2}$

$$\begin{aligned} W_{u}(s,t)=(\langle (\mathcal {J}_{\mu })'(su^{+}+tu^{-}), su^{+} \rangle , \langle (\mathcal {J}_{\mu })'(su^{+}+tu^{-}), tu^{-} \rangle ). \end{aligned}$$

Then, we have that

$$\begin{aligned} 2s_{\mu }^{2}\Vert u^{+}\Vert ^{2}+&2t_{\mu }^{2}\Vert u^{-}\Vert ^{2}+2C_{9}s_{\mu }^{4}\Vert u^{+}\Vert ^{4}+2C_{10}t_{\mu }^{4}\Vert u^{-}\Vert ^{4}\\&\ge \Vert s_{\mu }u^{+}+t_{\mu }u^{-}\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{s_{\mu }u^{+}+t_{\mu }u^{-}}|s_{\mu }u^{+}+t_{\mu }u^{-}|^{2}dx\\&=\mu \int _{\mathbb {R}^{3}}f(s_{\mu }u^{+}+t_{\mu }u^{-})(s_{\mu }u^{+}+t_{\mu }u^{-})dx +\int _{\mathbb {R}^{3}}|s_{\mu }u^{+}+t_{\mu }u^{-}|^{6}dx\\&\ge s_{\mu }^{6}\int _{\mathbb {R}^{3}}|u^{+}|^{6}dx +t_{\mu }^{6}\int _{\mathbb {R}^{3}}|u^{-}|^{6}dx. \end{aligned}$$

Therefore, $\Phi _{u}$ is bounded. Let $\{\mu _{n}\} \subset (0,\infty )$ be such that $\mu _{n} \rightarrow \infty$ as $n \rightarrow \infty$. Then, there exist $s_{0}$ and $t_{0}$ such that, up to a subsequence, $(s_{\mu _{n}},t_{\mu _{n}})\rightarrow (s_{0},t_{0})$ as $n \rightarrow \infty$. Next, we claim $s_{0}=t_{0}=0$. Suppose, by contradiction, that $s_{0} > 0$ or $t_{0} > 0$. Thanks to $s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-} \in \mathcal {M}_{\mu }$, for any $n \in \mathbb {N}$, we have

$$\begin{aligned} \Vert s_{\mu _{n}}u^{+}&+t_{\mu _{n}}u^{-}\Vert ^{2} +\int _{\mathbb {R}^{3}}\phi _{s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-}}|s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-}|^{2}dx \nonumber \\&=\mu _{n} \int _{\mathbb {R}^{3}}f(s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-})(s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-})dx +\int _{\mathbb {R}^{3}}|s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-}|^{6}dx. \end{aligned}$$

(2.14)

According to $s_{\mu _{n}}u^{+}\rightarrow s_{0}u^{+}$ and $t_{\mu _{n}}u^{-}\rightarrow t_{0}u^{-}$ in H, by (2.8) and (2.9), we have that

$$\begin{aligned}&\int _{\mathbb {R}^{3}}f(s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-})(s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-})dx \nonumber \\ {}&\rightarrow \int _{\mathbb {R}^{3}}f(s_{0}u^{+}+t_{0}u^{-})(s_{0}u^{+}+t_{0}u^{-})dx > 0 \end{aligned}$$

(2.15)

as $n\rightarrow \infty$. So, it follows from $\mu _{n} \rightarrow \infty$ as $n \rightarrow \infty$ and $\{s_{\mu _{n}}u^{+}+t_{\mu _{n}}u^{-}\}$ is bounded in H, combining with (2.14) and (2.15), that we have a contradiction. Hence, $s_{0}=t_{0}=0$. That is, $\lim \limits _{\mu \rightarrow \infty }c_{\mu } =0$. $\square$

Lemma 2.10

There exists $\mu ^{*} > 0$ such that for all $\mu \ge \mu ^{*}$, the infimum $c_{\mu }$ is achieved.

Proof

Supposed that there exists a sequence $\{u_{n}\} \subset \mathcal {M}_{\mu }$ such that $\lim \limits _{n\rightarrow \infty }\mathcal {J}_{\mu }(u_{n}) = c_{\mu }$, obviously, $\{u_{n}\}$ bounded in H. Then by Lemma 2.5, up to a subsequence, there exists a $u_{\mu }\in H$ such that

$$\begin{aligned}&u_{n} \rightharpoonup u_{\mu } \ \ \ \text{ in } H; \end{aligned}$$

(2.16)

$$\begin{aligned}&u_{n} \rightarrow u_{\mu } \ \ \ \text{ in } L^{p}(\mathbb {R}^{3})\ \text { for } p \in (2,6); \end{aligned}$$

(2.17)

$$\begin{aligned}&u_{n}(x) \rightarrow u_{\mu }(x) \ \ \ \text{ a.e. } \text{ in } \mathbb {R}^{3}. \end{aligned}$$

(2.18)

Besides, we also have $u_{n}^{\pm } \rightharpoonup u_{\mu }^{\pm } \text{ in } H,$ $u_{n}^{\pm } \rightarrow u_{\mu }^{\pm } \text{ in } L^{p}(\mathbb {R}^{3})$ and $u_{n}(x)^{\pm } \rightarrow u_{\mu }(x)^{\pm }$ a.e. in $\mathbb {R}^{3}$.

According to Lemma 2.9, there exists $\mu ^{*} > 0$ such that $c_{\mu } < \frac{1}{3}S^{\frac{3}{2}}$ for all $\mu \ge \mu ^{*}$. Fixed $\mu \ge \mu ^{*}$, it follows from Lemma 2.7 that $\mathcal {J}_{\mu }(su_{n}^{+}+tu_{n}^{-}) \le \mathcal {J}_{\mu }(u_{n})$ for all $s,t > 0$.

Therefore, by using Brezis–Lieb Lemma, Fatou’s Lemma and Hardy–Littlewood–Sobolev inequality, we have that

$$\begin{aligned}&\liminf _{n \rightarrow \infty } \mathcal {J}_{\mu }(su_{n}^{+}+tu_{n}^{-})\\ {}&\ge \frac{s^{2}}{2}\lim _{n\rightarrow \infty }(\Vert u_{n}^{+}-u_{\mu }^{+}\Vert ^{2}+\Vert u_{\mu }^{+}\Vert ^{2})+\frac{t^{2}}{2}\lim _{n\rightarrow \infty }(\Vert u_{n}^{-}-u_{\mu }^{-}\Vert ^{2}+\Vert u_{\mu }^{-}\Vert ^{2})\\&+\frac{t^{2}}{4}\liminf _{n\rightarrow \infty }\int _{\mathbb {R}^{3}}\phi _{u_{n}^{-}}|u_{n}^{-}|^{2}dx+\frac{s^{2}}{4}\liminf _{n\rightarrow \infty }\int _{\mathbb {R}^{3}}\phi _{u_{n}^{+}}|u_{n}^{+}|^{2}dx \\&+\frac{s^{2}t^{2}}{4}\liminf _{n\rightarrow \infty }\int _{\mathbb {R}^{3}}\phi _{u_{n}^{+}}|u_{n}^{-}|^{2}dx+\frac{s^{2}t^{2}}{4}\liminf _{n\rightarrow \infty }\int _{\mathbb {R}^{3}}\phi _{u_{n}^{-}}|u_{n}^{+}|^{2}dx \\&-\limsup _{n\rightarrow \infty }\mu \int _{\mathbb {R}^{3}}F(su_{n}^{+}+tu_{n}^{-})dx-\frac{s^{6}}{6}\lim _{n\rightarrow \infty }(|u_{n}^{+}-u_{\mu }^{+}|_{6}^{6}+|u_{\mu }^{+}|_{6}^{6})\\&-\frac{t^{6}}{6}\lim _{n\rightarrow \infty }(|u_{n}^{-}-u_{\mu }^{-}|_{6}^{6}+|u_{\mu }^{-}|_{6}^{6})\\&\ge \mathcal {J}_{\mu }(su_{\mu }^{+}+tu_{\mu }^{-})+\frac{s^{2}}{2}\lim _{n\rightarrow \infty }\Vert u_{n}^{+}-u_{\mu }^{+}\Vert ^{2}+\frac{t^{2}}{2}\lim _{n\rightarrow \infty }\Vert u_{n}^{-}-u_{\mu }^{-}\Vert ^{2}\\&-\frac{s^{6}}{6}\lim _{n\rightarrow \infty }|u_{n}^{+}-u_{\mu }^{+}|_{6}^{6} -\frac{t^{6}}{6}\lim _{n\rightarrow \infty }|u_{n}^{-}-u_{\mu }^{-}|_{6}^{6} \end{aligned}$$

Letting $A_{1}=\lim \limits _{n\rightarrow \infty }\Vert u_{n}^{+}-u_{\mu }^{+}\Vert ^{2},$ $A_{2}=\lim \limits _{n\rightarrow \infty }\Vert u_{n}^{-}-u_{\mu }^{-}\Vert ^{2},$ $B_{1}=\lim \limits _{n\rightarrow \infty }|u_{n}^{+}-u_{\mu }^{+}|_{6}^{6},$ and $B_{2}=\lim \limits _{n\rightarrow \infty }|u_{n}^{-}-u_{\mu }^{-}|_{6}^{6}.$ Then we have that

$$\begin{aligned} \mathcal {J}_{\mu }(su_{\mu }^{+}+tu_{\mu }^{-})+\frac{s^{2}}{2}A_{1}+\frac{t^{2}}{2}A_{2}-\frac{s^{6}}{6}B_{1}-\frac{t^{6}}{6}B_{2} \le c_{\mu }. \end{aligned}$$

(2.19)

for all $s> 0$ and $t> 0$.

$\varvec{Firstly}$, we prove that $u_{\mu }^{\pm }\ne 0.$

Since the situation $u_{\mu }^{-} \ne 0$ is analogous, we just prove $u_{\mu }^{+} \ne 0$. By contradiction, we suppose $u_{\mu }^{+} = 0$. Hence, let $t>0$ small enough in (2.19).

$\varvec{Case\ 1:\ A_{1}=0.}$

In this case, we can induce that $u_{n}^{+} \rightarrow u_{\mu }^{+}$ in H. By lemma 2.8, we obtain $\Vert u_{\mu }^{+}\Vert \ge \rho > 0$. Obviously, we have a contradiction.

$\varvec{Case\ 2:\ A_{1}>0.}$

If $B_{1}=0$, from above, we have that $\frac{s^{2}}{2}A_{1} \le c_{\mu }$ for all $s>0$, this is absurd.

If $B_{1}>0$, we can induce that

$$\begin{aligned} \frac{s^{2}}{2}A_{1}-\frac{s^{6}}{6}B_{1}\le c_{\mu }. \end{aligned}$$

By the definition of S, we have that $B_{1}^{\frac{1}{3}}S\le A_{1}$, thus we induce that

$$\begin{aligned} \frac{s^{2}}{2}A_{1}-\frac{s^{6}}{6S^{3}}A_{1}^{3}\le \frac{s^{2}}{2}A_{1}-\frac{s^{6}}{6}B_{1}\le c_{\mu }. \end{aligned}$$

It is easy to see that $\frac{1}{3}S^{\frac{3}{2}}=\max \limits _{s\ge 0}\{\frac{s^{2}}{2}A_{1}-\frac{s^{6}}{6\,S^{3}}A_{1}^{3}\}.$ So we can get that

$$\begin{aligned} \frac{1}{3}S^{\frac{3}{2}} \le \frac{s^{2}}{2}A_{1}-\frac{s^{6}}{6}B_{1} \le c_{\mu } <\frac{1}{3}S^{\frac{3}{2}}\ \ \ \ \text {for all}\ \mu \ge \mu ^{*}, \end{aligned}$$

which is contradiction. Therefore, $u_{\mu }^{\pm }\ne 0$.

$\varvec{Secondly}$, we prove that $A_{1}=A_{2}=0.$

Since the situation $A_{2}=0$ is analogous, we just prove $A_{1}=0$. By contradiction, we suppose $A_{1}>0$.

By the definition of $\{u_{n}\} \subset \mathcal {M}_{\mu }$, we have that

$$\begin{aligned} \langle (\mathcal {J}_{\mu })'(u_{n}), u_{n}^{+}\rangle =\langle (\mathcal {J}_{\mu })'(u_{n}), u_{n}^{-}\rangle =0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \Vert u_{n}^{+}\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u_{n}}|u_{n}^{+}|^{2}dx-\mu \int _{\mathbb {R}^{3}}f(u_{n}^{+})u_{n}^{+}dx -\int _{\mathbb {R}^{3}}|u_{n}^{+}|^{6}dx=0. \end{aligned}$$

(2.20)

$$\begin{aligned} \Vert u_{n}^{-}\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u_{n}}|u_{n}^{-}|^{2}dx-\mu \int _{\mathbb {R}^{3}}f(u_{n}^{-})u_{n}^{-}dx -\int _{\mathbb {R}^{3}}|u_{n}^{-}|^{6}dx=0. \end{aligned}$$

(2.21)

Therefore, by using Brezis–Lieb Lemma, Fatou’s Lemma and Hardy–Littlewood–Sobolev inequality and (2.20), we can deduce that

$$\begin{aligned} 0=&\lim \limits _{n\rightarrow \infty }[\Vert u_{n}^{+}\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u_{n}}|u_{n}^{+}|^{2}dx-\mu \int _{\mathbb {R}^{3}}f(u_{n}^{+})u_{n}^{+}dx -\int _{\mathbb {R}^{3}}|u_{n}^{+}|^{6}dx]\\ =&\lim \limits _{n\rightarrow \infty }(\Vert u_{n}^{+}-u_{\mu }^{+}\Vert ^{2}+\Vert u_{\mu }^{+}\Vert ^{2})+\lim \limits _{n\rightarrow \infty }\int _{\mathbb {R}^{3}}\phi _{u_{n}}|u_{n}^{+}|^{2}dx-\lim \limits _{n\rightarrow \infty }\mu \int _{\mathbb {R}^{3}}f(u_{n}^{+})u_{n}^{+}dx \\&-\lim \limits _{n\rightarrow \infty }\int _{\mathbb {R}^{3}}(|u_{n}^{+}-u_{\mu }^{+}|^{6}+|u_{\mu }^{+}|^{6})dx\\ =&A_{1}+\Vert u_{\mu }^{+}\Vert ^{2}+\int _{\mathbb {R}^{3}}\phi _{u_{\mu }}|u_{\mu }^{+}|^{2}dx-\mu \int _{\mathbb {R}^{3}}f(u_{\mu }^{+})u_{\mu }^{+}dx-B_{1}-|u_{\mu }^{+}|_{6}^{6}\\ =&A_{1}-B_{1}+\langle (\mathcal {J}_{\mu })'(u_{\mu }), u_{\mu }^{+}\rangle . \end{aligned}$$

By (2.16), we have that $\langle (\mathcal {J}_{\mu })'(u_{\mu }), u_{\mu }^{+}\rangle \le 0,$ thus

$$\begin{aligned} A_{1}-B_{1}\ge 0, \end{aligned}$$

which means

$$\begin{aligned} A_{1}\ge B_{1}. \end{aligned}$$

(2.22)

Since the equation (2.21) is analogous, we also can induce that

$$\begin{aligned} A_{2}\ge B_{2} \end{aligned}$$

(2.23)

So combining with (2.19), we have

$$\begin{aligned} c_{\mu }&\ge \mathcal {J}_{\mu }(su_{\mu }^{+}+tu_{\mu }^{-})+ \frac{s^{2}}{2}A_{1}+\frac{t^{2}}{2}A_{2}-\frac{s^{6}}{6}B_{1}-\frac{t^{6}}{6}B_{2}\\&\ge \mathcal {J}_{\mu }(su_{\mu }^{+}+tu_{\mu }^{-})+(\frac{s^{2}}{2}-\frac{s^{6}}{6})A_{1} +(\frac{t^{2}}{2}-\frac{t^{6}}{6})A_{2}. \end{aligned}$$

There exists $(\overline{s},\overline{t})\in (0,+\infty )\times (0,+\infty )$ such that $\frac{s^{2}}{2}-\frac{s^{6}}{6}>0$ and $\frac{t^{2}}{2}-\frac{t^{6}}{6}> 0$. Thus

$$\begin{aligned} c_{\mu }&\ge \mathcal {J}_{\mu }(su_{\mu }^{+}+tu_{\mu }^{-})+(\frac{s^{2}}{2}-\frac{s^{6}}{6})A_{1} +(\frac{t^{2}}{2}-\frac{t^{6}}{6})A_{2}\\&> \mathcal {J}_{\mu }(su_{\mu }^{+}+tu_{\mu }^{-})\\&\ge c_{\mu } \end{aligned}$$

That is, we have a contradiction. Therefore, we deduce that $A_{1}=A_{2}=0.$

$\varvec{Lastly}$, we prove that $c_{\mu }$ is achieved.

For $u_{\mu }^{\pm }\ne 0$, according to Lemma 2.7, there exists a pair $(s_{u_{\mu }},t_{u_{\mu }})\in (0,\infty )\times (0,\infty )$ such that $\widetilde{u}=s_{u_{\mu }}u_{\mu }^{+}+t_{u_{\mu }}u_{\mu }^{-}\in \mathcal {M}_{\mu }.$ Furthermore, it is obviously that $\langle (\mathcal {J}_{\mu })'(u),u_{\mu }^{\pm } \rangle \le 0$, so $0< s_{u_{\mu }},t_{u_{\mu }} \le 1.$

Since $\widetilde{u}_{\mu }=s_{u_{\mu }}u_{\mu }^{+}+t_{u_{\mu }}u_{\mu }^{-}\in \mathcal {M}_{\mu }$ and $B_{1}=B_{2}=0,$ the norm of H is lower semicontinuous, we have that

$$\begin{aligned} c_{\mu } \le&\mathcal {J}_{\mu }(\widetilde{u}_{\mu })-\frac{1}{4}\langle (\mathcal {J}_{\mu })'(\widetilde{u}_{\mu }),\widetilde{u}_{\mu } \rangle \\ \le&\frac{1}{4}\Vert u_{\mu }\Vert ^{2}+\frac{1}{12}\int _{\mathbb {R}^{3}}|u_{\mu }|^{6}dx+\frac{\mu }{4}\int _{\mathbb {R}^{3}}[f(u_{\mu })u_{\mu } -4F(u_{\mu })]dx\\ \le&\liminf _{n\rightarrow \infty }[\mathcal {J}_{\mu }(u_{n})-\frac{1}{4}\langle (\mathcal {J}_{\mu })'(u_{n}),u_{n} \rangle ]=c_{\mu }. \end{aligned}$$

So, we have that $s_{u_{\mu }}=t_{u_{\mu }}=1$, which means $u_{\mu }\in \mathcal {M}_{\mu }$, and $\mathcal {J}_{\mu }(u_{\mu })=c_{\mu }.$

The proof is complete. $\square$

3 The proof of main results

Proof of Theorem 1.1

Thanks to Lemma 2.10, we just prove that the minimizer $u_{\mu }$ for $c_{\mu }$ is indeed a sign-changing solution of system (1.1). Since $u_{\mu } \in \mathcal {M}_{\mu }$, according to Lemma 2.7, we have that

$$\begin{aligned} \mathcal {J}_{\mu }(s u_{\mu }^{+}+t u_{\mu }^{-})<\mathcal {J}_{\mu }(u_{\mu }^{+}+u_{\mu }^{-})=c_{\mu },\ \ \text { for } (s,t)\in (0,\infty )\times (0,\infty )\backslash (1,1). \end{aligned}$$

(3.1)

If $(\mathcal {J}_{\mu })'(u_{\mu })\ne 0$, then there exist $\delta > 0$ and $\theta > 0$ such that $\Vert \mathcal {J}_{\mu }'(v)\Vert \ge \theta$, for all $\Vert v-u_{\mu }\Vert \le 3\delta .$

Choosing $\sigma \in (0,\min \{ \frac{1}{2},\frac{\delta }{\sqrt{2}\Vert u_{\mu }\Vert } \} ).$ Let $D:= (1-\sigma ,1+\sigma )\times (1-\sigma ,1+\sigma )$ and $g(s,t)=su_{\mu }^{+}+tu_{\mu }^{-}$, $(s,t)\in D.$ In view of (3.1), it is easy to see that

$$\begin{aligned} \overline{c_{\mu }}:=\max _{\partial D}\mathcal {J}\circ g < c_{\mu }. \end{aligned}$$

(3.2)

Let $\varepsilon := \min \{ \frac{(\overline{c_{\mu }}-c_{\mu })}{2},\frac{\theta \delta }{8} \}$ and $S_{\delta }:=B(u_{\mu },\delta ),$ according to Lemma 2.3 in [23], there exists a deformation $\eta \in C([0,1]\times H,H)$ such that

• (a) $\eta (1,v)=v$ if $v\notin (\mathcal {J}_{\mu })^{-1}([c_{\mu }-2\varepsilon ,c_{\mu }+2\varepsilon ]\cap S_{2\delta });$

• (b) $\eta (1,\mathcal {J}_{\mu }^{c_{\mu }+\varepsilon }\cap S_{2\delta })\subset \mathcal {J}_{\mu }^{c_{\mu }-\varepsilon };$

• (c) $\mathcal {J}_{\mu }(\eta (1,v)) \le \mathcal {J}_{\mu }(v)$ for all $v\in H.$

$\varvec{Firstly}$, we prove that

$$\begin{aligned} \max _{(s,t)\in \overline{D}}\mathcal {J}_{\mu }(\eta (1,g(s,t))) < c_{\mu }. \end{aligned}$$

(3.3)

In fact, follows from Lemma 2.7 that $\mathcal {J}_{\mu }(g(s,t)) \le c_{\mu } < c_{\mu }+\varepsilon .$ That is, $g(s,t)\in \mathcal {J}_{\mu }^{ c_{\mu }+\varepsilon }.$ On the other hand, we have

$$\begin{aligned} \Vert g(s,t)-u_{\mu }\Vert ^{2}=&\Vert (s-1)u_{\mu }^{+}+(t-1)u_{\mu }^{-}\Vert ^{2}\\ \le&2(s-1)^{2}\Vert u_{\mu }^{+}\Vert ^{2}+2(t-1)^{2}\Vert u_{\mu }^{-}\Vert ^{2} \\ \le&2\sigma ^{2} \Vert u_{\mu }\Vert ^{2}\le \delta ^{2}, \end{aligned}$$

which shows that $g(s,t)\in S_{\delta }$ for all $(s,t)\in \overline{D}.$

According (b), we can know that $\mathcal {J}_{\mu }(\eta (1,g(s,t))) < c_{\mu }-\varepsilon .$ Hence (3.3) holds.

$\varvec{Secondly}$, we need to prove that $\eta (1,g(D)) \cap \mathcal {M}_{\mu } \ne \emptyset .$

Let $h(s,t)=\eta (1,g(s,t))$ and

$$\begin{aligned} \Psi _{0}(s,t)&:=(\langle (\mathcal {J}_{\mu })'(g(s,t)),u_{\mu }^{+} \rangle , \langle (\mathcal {J}_{\mu })'(g(s,t)),u_{\mu }^{-} \rangle )\\&:=(\varphi ^{1}(s,t),\varphi ^{2}(s,t)),\\ \Psi _{1}(s,t)&:=(\frac{1}{s}\langle (\mathcal {J}_{\mu })'(h(s,t)),h(s,t)^{+} \rangle , \frac{1}{t}\langle (\mathcal {J}_{\mu })'(h(s,t)),h(s,t)^{-} \rangle ). \end{aligned}$$

By direct calculation, we have that

$$\begin{aligned} \frac{\partial \varphi ^{1}(s,t)}{\partial s}|_{(1,1)}=&\Vert u_{\mu }^{+}\Vert ^{2}+3\int _{\mathbb {R}^{3}}\phi _{u_{\mu }^{+}}|u_{\mu }^{+}|^{2}dx +\int _{\mathbb {R}^{3}}\phi _{u_{\mu }^{-}}|u_{\mu }^{+}|^{2}dx\\&-\mu \int _{\mathbb {R}^{3}}f'(u_{\mu }^{+})|u_{\mu }^{+}|^{2}dx-5\int _{\mathbb {R}^{3}}|u_{\mu }^{+}|^{6}dx.\\ \frac{\partial \varphi ^{1}(s,t)}{\partial t}|_{(1,1)}=&2\int _{\mathbb {R}^{3}}\phi _{u_{\mu }^{-}}|u_{\mu }^{+}|^{2}dx.\\ \frac{\partial \varphi ^{2}(s,t)}{\partial s}|_{(1,1)}=&2\int _{\mathbb {R}^{3}}\phi _{u_{\mu }^{+}}|u_{\mu }^{-}|^{2}dx.\\ \frac{\partial \varphi ^{2}(s,t)}{\partial t}|_{(1,1)}=&\Vert u_{\mu }^{-}\Vert ^{2}+3\int _{\mathbb {R}^{3}}\phi _{u_{\mu }^{-}}|u_{\mu }^{-}|^{2}dx +\int _{\mathbb {R}^{3}}\phi _{u_{\mu }^{+}}|u_{\mu }^{-}|^{2}dx\\&-\mu \int _{\mathbb {R}^{3}}f'(u_{\mu }^{-})|u_{\mu }^{-}|^{2}dx-5\int _{\mathbb {R}^{3}}|u_{\mu }^{-}|^{6}dx. \end{aligned}$$

Let

$$\begin{aligned} M= \begin{bmatrix} \frac{\partial \varphi ^{1}(s,t)}{\partial s}|_{(1,1)} &{} \frac{\partial \varphi ^{2}(s,t)}{\partial s}|_{(1,1)} \\ \frac{\partial \varphi ^{1}(s,t)}{\partial t}|_{(1,1)} &{} \frac{\partial \varphi ^{2}(s,t)}{\partial t}|_{(1,1)} \end{bmatrix} \end{aligned}$$

By using $(f_2)$ and $u_{\mu }\in \mathcal {M}_{\mu }$, we have that $\text {det} M > 0.$ Since $\Psi _{0}$ is a $C^{1}$ function and (1, 1) is the unique isolated zero point of $\Psi _{0}$, by using the degree theory, we deduce that deg($\Psi _{0},D,0$)=1.

So, combining (3.2) with (a), we obtain that $g(s,t)=h(s,t)$ on $\partial D.$ Consequently, deg($\Psi _{1},D,0$)=1. That is $\Psi _{1}(s_{0},t_{0})=0$ for some $(s_{0},t_{0})\in D,$ so that $\eta (1,g(s_{0},t_{0}))=h(s_{0},t_{0}) \in \mathcal {M}_{\mu }.$ By (3.3), we have a contradiction. Therefore we conclude that $u_{\mu }$ is a sign-changing solution for system (1.1).

$\varvec{Finally}$, we prove that $u_{\mu }$ has exactly two nodal domains.

To this end, we assume by contradiction that $u_{\mu }=u_{1}+u_{2}+u_{3}$ with $u_{i}\ne 0, u_{1}\ge 0, u_{2}\le 0, \text {suppt}\ {u_{i}}\cap \text {suppt}\ {u_{j}}=\emptyset \ \text { for } i\ne j,\ i,\ j=1,2,3$ and $\langle (\mathcal {J}_{\mu })'(u_{\mu }),u_{i} \rangle =0$ for $i=1,2,3.$

Setting $v:=u_{1}+u_{2}$, we have that $v^{+}=u_{1}$ and $v^{-}=u_{2}$, i.e., $v^{\pm }\ne 0.$ Then, there exists a unique pair $(s_{v},t_{v})$ of positive numbers such that $s_{v}v^{+}+t_{v}v^{-}=s_{v}u_{1}+t_{v}u_{2}\in \mathcal {M}_{\mu }.$ So, $\mathcal {J}_{\mu }(s_{v}u_{1}+t_{v}u_{2}) \ge c_{\mu }.$

Moreover, since $\langle (\mathcal {J}_{\mu })'(u_{\mu }),u_{i} \rangle =0,$ we obtain that $\langle (\mathcal {J}_{\mu })'(v),v^{+} \rangle < 0.$ According to Lemma 2.7, we have that $(s_{v},t_{v})\in (0,1]\times (0,1].$ On the other hand, we also have that

$$\begin{aligned} 0= \frac{1}{4}\langle (\mathcal {J}_{\mu })'(u),u_{3}\rangle =&\frac{1}{4}\Vert u_{3}\Vert ^{2}+\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{u_{1}}|u_{3}|^{2}dx +\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{u_{2}}|u_{3}|^{2}dx \\&+\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{u_{3}}|u_{3}|^{2}dx-\frac{\mu }{4}\int _{\mathbb {R}^{3}}f(u_{3})u_{3}dx -\frac{1}{4}\int _{\mathbb {R}^{3}}|u_{3}|^{6}dx\\ <&\mathcal {J}_{\mu }(u_{3})+\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{u_{1}}|u_{3}|^{2}dx +\frac{1}{4}\int _{\mathbb {R}^{3}}\phi _{u_{2}}|u_{3}|^{2}dx. \end{aligned}$$

Then, by (2.9), we have that

$$\begin{aligned} c_{\mu }\le \mathcal {J}_{\mu }(s_{v}u_{1}+t_{v}u_{2})=&\mathcal {J}_{\mu }(s_{v}u_{1}+t_{v}u_{2})-\frac{1}{4}\langle (\mathcal {J}_{\mu })'(s_{v}u_{1}+t_{v}u_{2}), s_{v}u_{1}+t_{v}u_{2} \rangle \\ \le&\frac{1}{4}(\Vert u_{1}\Vert ^{2}+\Vert u_{2}\Vert ^{2})+\frac{1}{12}\int _{\mathbb {R}^{3}}(|u_{1}|^{6}+|u_{2}|^{6})dx \\&+\frac{\mu }{4}\int _{\mathbb {R}^{3}}[f(u_{1})u_{1}-4F(u_{1})+f(u_{2})u_{2}-4F(u_{2})]dx\\ =&\mathcal {J}_{\mu }(u_{1}+u_{2})-\frac{1}{4}\langle (\mathcal {J}_{\mu })'(u_{1}+u_{2}), u_{1}+u_{2} \rangle \\ <&\mathcal {J}_{\mu }(u)=c_{\mu }. \end{aligned}$$

which is a contradiction, this is, $u_{3}=0$ and $u_{\mu }$ has exactly two nodal domains. $\square$

By Theorem 1.1, we obtain a least-energy sign-changing solution $u_{\mu }$ of system (1.1). Next, we prove that the energy of $u_{\mu }$ is strictly larger than two times the least energy.

Proof of Theorem 1.2

Firstly, we define the manifold

$$\begin{aligned} \mathcal {N}_{\mu }=\{ u\in H\ \backslash \ \{0\} \ | \langle (\mathcal {J}_{\mu })'(u), u \rangle =0 \}; \end{aligned}$$

$$\begin{aligned} c_{\mu }^{*}=\inf _{u\in \mathcal {N}_{\mu }}\mathcal {J}_{\mu }(u). \end{aligned}$$

Similar to the proof of Lemma 2.10, there exists $\mu _{1}^{*}> 0$, there is $v_{\mu }\in \mathcal {N}_{\mu }$ such that $\mathcal {J}_{\mu }(v_{\mu })=c_{\mu }^{*} > 0.$ By standard arguments, the critical points of the functional $\mathcal {J}_{\mu }$ on $\mathcal {N}_{\mu }$ are critical points of $\mathcal {J}_{\mu }$ on H. Thus, we obtain that $v_{\mu }$ is the ground state solution of system (1.1). Details for [15], here we omitted it.

Let $\mu ^{**}=\max \{ \mu ^{*},\mu _{1}^{*} \}$, suppose that $u_{\mu }=u_{\mu }^{+}+u_{\mu }^{-}.$ As the proof of Lemma 2.7, there exists $0 <s_{u_{\mu }},t_{u_{\mu }} \le 1$ such that $s_{u_{\mu }}u_{\mu }^{+}\in \mathcal {N}_{\mu }$ and $t_{u_{\mu }}u_{\mu }^{-}\in \mathcal {N}_{\mu }.$

Therefore, in view of Lemma 2.7, we have that

$$\begin{aligned} 2c_{\mu }^{*} \le \mathcal {J}_{\mu }(s_{u_{\mu }}u_{\mu }^{+})+\mathcal {J}_{\mu }(t_{u_{\mu }}u_{\mu }^{-}) \le \mathcal {J}_{\mu }(s_{u_{\mu }}u_{\mu }^{+}+t_{u_{\mu }}u_{\mu }^{-}) < \mathcal {J}_{\mu }(u_{\mu }^{+}+u_{\mu }^{-})=c_{\mu }. \end{aligned}$$

which shows that $c_{\mu }> 2c_{\mu }^{*}$ and $c_{\mu }^{*} > 0$ cannot be achieved by a sign-changing solutions in H. The prove is complete. $\square$