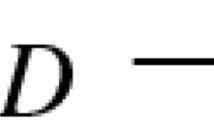${\mathcal {F}}$-Copartial Morphisms

Abstract

In this paper, first we give the definition of ${\mathcal {F}}$-copartial morphisms with an additive exact substructure ${\mathcal {F}}$ of an exact structure ${\mathcal {E}}$ in an additive category ${\mathcal {A}}$. Then, we study many properties of ${\mathcal {F}}$-copartial morphisms. Moreover, we define ${\mathcal {F}}$-copartial morphisms with a pure-exact structure ${\mathcal {F}}$ and with a finite pure-exact structure ${\mathcal {F}}$ in the category of modules over a ring and call them copartial morphisms and finitely copartial morphisms, respectively. We also investigate the relations between them and give the new characterizations of finitely (singly) pure-projective modules, flat modules and finitely (singly) projective modules with copartial morphisms and finitely copartial morphisms. Finally, we define $\mu$-partial morphisms for a defining matrix $\mu$ and give a new characterization of semi-compact modules with $\mu$-partial morphisms.

1 Introduction

The notion of exact categories was originally due to Quillen (see, [21]). The theory of exact categories is a generalization of abelian categories, and they play a quite useful role in Representation Theory, Algebraic Geometry, Algebraic Analysis and Algebraic K-Theory. On the other hand, exact categories are applicable in the study of filtered objects and tilting theory while the classical theory of abelian theories does not apply. This theory was developed by Bühler, Fu, Gillespie, Hovey, Keller, Krause, Neeman, Šťovíček and possibly others, see [3, 7, 8, 11, 13, 14, 17, 18] and [20] and so on.

Recall that a short exact sequence of right R-modules is called pure if it remains exact upon tensoring by any left module. Pure-injective modules are modules which are injective with respect to pure-exact sequences. Purity is a considerable interest for logicians that are interested in the model theory of modules. Partial morphisms were introduced by Ziegler in [24] by using model theory, in order to prove existence of pure-injective envelopes. Ziegler realized that pure-injective modules extend other types of morphisms and called those morphisms as partial morphisms. Partial morphisms were also studied by Monari Martinez in [16] through algebraic methods. She gave a matrix-theoretic reformulation of partial morphisms by using system of linear equations. But this algebraic translation of the notion of partial morphisms does not shed much light about their role in the categorical study of purity. In [5], Cortés-Izurdiaga, Guil Asensio, Kalebog̃az and Srivastava gave a categorical definition of this concept which can be stated in any additive exact category. They first defined the partial morphisms introduced by Ziegler in [24] in the module category over a ring. Then, they gave the characterization of partial morphisms by using pushout: a homomorphism $f:K\longrightarrow N$ is partial morphism with respect to the inclusion u of K in a module M if and only if the induced morphism $\text{ Ext}^{1}{(-,f)}$ transforms u in a pure monomorphism. So it allowed them to define partial morphisms with respect to an additive exact substructure ${\mathcal {F}}$ of an exact structure ${\mathcal {E}}$ in an additive category ${\mathcal {A}}$, and they called them ${\mathcal {F}}$-partial morphisms. As a dual notion of ${\mathcal {F}}$-partial morphisms, in Sect. 2, we first define ${\mathcal {F}}$-copartial morphisms with an additive exact substructure ${\mathcal {F}}$ of an exact structure ${\mathcal {E}}$ in an additive category ${\mathcal {A}}$ (Definition 2.1). The first aim of this paper is to study the main properties of ${\mathcal {F}}$-copartial morphisms (Proposition 2.5 and Proposition 2.7). Then, we show that ${\mathcal {F}}$-copartial morphisms characterize ${\mathcal {F}}$-projective objects (i.e., objects which are projective with respect to ${\mathcal {F}}$-deflations) (Theorem 2.10). In this section, we reveal the close relationship between ${\mathcal {F}}$-copartial morphisms with ${\mathcal {F}}$-phantom morphisms (see [7] for the definition and the main properties of phantom morphisms with respect to the exact substructure ${\mathcal {F}}$). We also study ${\mathcal {E}}_{{\mathcal {X}}}$-copartial and ${\mathcal {E}}^{{\mathcal {X}}}$-copartial morphisms for a given class of objects ${\mathcal {X}}$ where ${\mathcal {E}}_{{\mathcal {X}}}$ (${\mathcal {E}}^{{\mathcal {X}}}$) is denote the exact structure consisting of all conflations $A\longrightarrow B\longrightarrow C$ which are $\text{ Hom }{(X,-)}$-exact (respectively, $\text{ Hom }{(-,X)}$-exact) for every $X\in {\mathcal {X}}$ (Proposition 2.12 and Proposition 2.13). Then, we characterize the objects of M that every deflation end with M is an ${\mathcal {F}}$-deflation by using ${\mathcal {F}}$-copartial morphisms (Theorem 2.14).

Let R be a ring and let A, C be left R-modules and $f:A\longrightarrow C$ be an epimorphism. It is well known that f is called M-pure if $\text{ Hom}_R(M,f): \text{ Hom}_R(M,A)\longrightarrow \text{ Hom}_R(M,C)$ is an epimorphism. An epimorphism f is called pure if f is M-pure for all finitely presented left R-modules M from [22] and an epimorphism f is called finitely (singly) split if f is M-pure for all finitely generated (cyclic) left R-modules M from [1]. We note that the exact structure ${\mathcal {E}}_{\mathcal {P}}$ is called $\textit{pure-exact structure}$ if ${\mathcal {P}}$ is the class of all finitely presented left R-modules and ${\mathcal {E}}_{\mathcal {P}}$ is called $\textit{finite (single) pure-exact structure}$ if ${\mathcal {P}}$ is the class of all finitely generated (cyclic) left R-modules. As an application of ${\mathcal {F}}$-copartial morphisms to pure-exact structure ${\mathcal {F}}$ on the category of left R-modules over a ring R, we define copartial morphisms (Definition 2.16) and give some results on copartial morphisms. Copartial morphisms are exactly the dual versions of Ziegler partial morphisms. We give a new characterization of pure-projective modules (M is called pure-projective if every pure epimorphism onto M splits) by using copartial morphisms. In Sect. 3, we study another application of ${\mathcal {F}}$-copartial morphisms to finite (single) pure-exact structure ${\mathcal {F}}$ on the category of left R-modules over a ring R. We call them finitely (singly) copartial morphisms (Definition 3.2). In [15], Mao called a morphism $\alpha :M\longrightarrow N$ finitely phantom if the restriction of $\alpha$ to every finitely generated submodule of M factors through a projective left R-module and he called a morphism $\alpha :M\longrightarrow N$ Mittag–Leffler if for each morphism $\beta :F\longrightarrow M$ with F finitely generated, there exists a finitely presented left R-module L, $\varphi :F\longrightarrow L$ and $\gamma :L\longrightarrow M$ such that $\alpha \beta =\alpha \gamma \varphi$. In this paper, we relate finitely copartial morphisms to finitely phantom morphisms and Mittag–Leffler morphisms (Corollary 3.3 and Proposition 3.4). Another purpose of this paper is to investigate the relations between copartial morphisms and finitely (singly) copartial morphisms. It is obvious that every finitely (singly) copartial morphism is copartial morphism. In this work, we discuss when every copartial morphism is finitely (singly) copartial (Proposition 3.8). In [1], finitely (singly) pure-projective modules were defined. Azumaya called a left R-module M finitely (singly) pure-projective if every pure epimorphism onto M is finitely (singly) split. We also give new characterizations of finitely (singly) pure-projective modules, flat modules and finitely (singly) projective modules with copartial morphisms and with finitely (singly) copartial morphisms (Theorem 3.11, Corollary 3.15, Corollary 3.17). In this section, we show that some of our results are extensions of the results proven by Azumaya in [1] and Mao in [15]. Our new characterizations also allow us to give some categorical proofs of some results in [1].

For an R-module M and for any index set I, $M^I$ means I-times direct product and $M^{(I)}$ means I-times direct sum of M. Each element of $M^I$ can be regarded as a row vector with entries in M (we denote them by $(x_i)$ whose i-th entry is $x_i$ for each $i\in I$) and each element of $M^{(I)}$ can be regarded as a column vector with entries in M (we denote them by $[x_i]$ whose i-th entry is $x_i$ for each $i\in I$) according to the context. If n is a positive integer, $M^n$ is defined to be $M^I=(M^{(I)})$ where $I=\{1,\ 2,\ ...,\ n\}$. Let I and J be two index sets and let $\mu = [a_{ij}]$ be a row-finite $I\times J$ matrix over R. For each row vector $(r_i)\in R^{(I)}$, the product $(r_i)\mu = \sum _i r_i a_{ij}$ is in $R^{(J)}$, and one defines a left R-homomorphism $\mu : R^{(I)}\longrightarrow R^{(J)}$ as $(r_i)\longrightarrow (r_i)\mu$. The cokernel of this homomorphism is denoted by $Coker(\mu )$. For a left R-module M, in [1], Azumaya called $\mu$ is a defining matrix of M (or $\mu$ defines M) if $Coker(\mu ) \cong M$. In the last section of this paper, in Sect. 4, we define $\mu$-partial morphisms for a defining matrix $\mu$ in the module category as an extension of Ziegler partial morphism studied in [5]. By using $\mu$-partial morphisms, we give a new characterization of semi-compact modules which is investigated in [2] (Proposition 4.6).

All rings in this paper are associative with unit and all modules are unitary. Throughout the paper, we fix an exact category (${\mathcal {A}}$;${\mathcal {E}}$) for an additive category ${\mathcal {A}}$ with a distinguished class ${\mathcal {E}}$ of kernel–cokernel pairs which play the role of short exact sequences and an additive exact substructure ${\mathcal {F}}$. Given a ring R, R-Mod is the category of left modules over R whose objects are all left modules over R and morphisms are all module homomorphisms between left R-modules.

2 ${\mathcal {F}}$-Copartial Morphisms

Let ${\mathcal {A}}$ be an additive category. A kernel–cokernel pair (i, p) in ${\mathcal {A}}$ is a pair of composable morphisms

such that i is a kernel of p and p is a cokernel of i. If a class ${\mathcal {E}}$ of kernel–cokernel pairs on ${\mathcal {A}}$ is fixed, an admissible monomorphism is a morphism i for which there exists a morphism p such that $(i, p)\in {\mathcal {E}}$. Similarly, an admissible epimorphism is a morphism p for which there exists a morphism i such that $(i, p)\in {\mathcal {E}}$.

An exact structure on ${\mathcal {A}}$ is a class ${\mathcal {E}}$ of kernel–cokernel pairs which is closed under isomorphisms and satisfies the following axioms

E0:

For every object $A\in {\mathcal {A}}$, the identity morphism $1_A$ is an admissible monomorphism.

$\text {E0}^{\text {op}}$:

For every object $A\in {\mathcal {A}}$, the identity morphism $1_A$ is an admissible epimorphism.

E1:

The class of admissible monomorphisms is closed under composition.

$\text {E1}^{\text {op}}$:

The class of admissible epimorphisms is closed under composition.

E2:

The pushout of an admissible monomorphism along an arbitrary morphism exists and yields an admissible monomorphism, that is, for any admissible monomorphism $i:A\longrightarrow B$ and any morphism $f:A\longrightarrow B^{\prime }$, there is a pushout diagram;

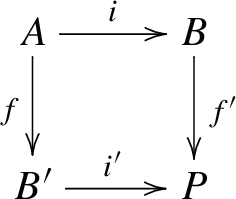
with $i^{\prime }$ an admissible monomorphism.

[${\text {E2}^{\text {op}}}$:

] The pullback of an admissible epimorphism along an arbitrary morphism exists and yields an admissible epimorphism, that is, for any admissible epimorphism $p:B\longrightarrow C$ and any morphism $g:B^{\prime }\longrightarrow C$ there is a pullback diagram;

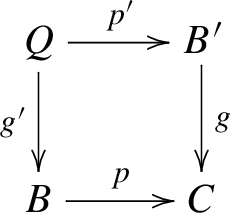
with $p^{\prime }$ an admissible epimorphism.

An exact category is a pair $({\mathcal {A}}, {\mathcal {E}})$ consisting of an additive category ${\mathcal {A}}$ and an exact structure ${\mathcal {E}}$ on ${\mathcal {A}}$. Elements of ${\mathcal {E}}$ are called short exact sequences. Keller [13] uses conflation, inflation and deflation for what we call short exact sequence, admissible monomorphism and admissible epimorphism, respectively. Throughout the paper, we also use this terminology. Let A be an object of ${\mathcal {A}}$. An admissible quotient of A is a quotient object U of an object A such that one (and any) quotient map $p:A\longrightarrow U$ is a deflation.

An exact substructure ${\mathcal {F}}$ of ${\mathcal {E}}$ is an exact structure on ${\mathcal {A}}$ such that each conflation in ${\mathcal {F}}$ (which we shall call ${\mathcal {F}}$-conflation) is a conflation in ${\mathcal {E}}$. Inflations, deflations and admissible quotient objects with respect to ${\mathcal {F}}$ will be called ${\mathcal {F}}$-inflations, ${\mathcal {F}}$-deflations and $\mathcal F$-admissible quotient objects, respectively.

Partial morphisms are first defined by Ziegler in Model Theory of Modules in [24]. In [5], Cortés-Izurdiaga, Guil Asensio, Kalebog̃az, Srivastava give a categorical definition of partial morphisms relative to the pure-exact structure in the module category by using pushout. Then, they extend the notion of partial morphisms to any additive exact category $({\mathcal {A}}, {\mathcal {E}})$. And they call ${\mathcal {F}}$-partial morphism to the partial morphism with respect to an additive substructure ${\mathcal {F}}$ of an exact structure ${\mathcal {E}}$ in an additive category ${\mathcal {A}}$. As a dual of this notion, we begin with defining the ${\mathcal {F}}$-copartial morphisms as follows:

Definition 2.1

Let X and Y be objects of ${\mathcal {A}}$. An ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) f from X to Y is a morphism $f:X\longrightarrow U$ where U is an admissible quotient of Y with quotient map $p:Y\longrightarrow U$, such that in the pullback of f along p;

$\overline{p}$ is an ${\mathcal {F}}$-deflation (respectively, $\overline{p}$ and $\overline{f}$ are ${\mathcal {F}}$-deflations). We shall call the quotient object U the codomain of f.

Remark 2.2

The definition of ${\mathcal {F}}$-copartial morphism does not depend on the selected quotient morphism of $p:Y\longrightarrow U$. Let $v : Y \longrightarrow V$ be an equivalent epimorphism to $p : Y \longrightarrow U$. That means there exists an isomorphism $w : U \longrightarrow V$ such that $wp = v$, then f is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) if and only if wf is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism).

Next lemma is used in the rest of the paper. It is a special case of the dual of the Obscure Axiom [3, Proposition 2.16].

Lemma 2.3

Let X, Y, Z be objects of ${\mathcal {A}}$. If an ${\mathcal {F}}$-deflation $f:Z\longrightarrow Y$ factors through a deflation $p:X\longrightarrow Y$ as follows:

then p is an ${\mathcal {F}}$-deflation too.

Proof

Let $i:K\longrightarrow X$ be the kernel of p. If we take the pullback g along i, we get the following commutative diagram:

Since f is an ${\mathcal {F}}$-deflation and $\overline{i}$ is the kernel of f, then $\overline{i}$ is an ${\mathcal {F}}$-inflation. Since the left square is pushout by [19, Example 3, page 93], i is also an ${\mathcal {F}}$-inflation. Thus, p is an ${\mathcal {F}}$-deflation. $\square$

One of the main purposes of this paper is to develop this new subject of ${\mathcal {F}}$-copartial morphisms for some exact substructure ${\mathcal {F}}$. Now we give some basic properties of F-copartial morphisms. Some of them are the duals of the results that obtained in [5]. So we give some of them without any proofs.

Lemma 2.4

Let Y be an object of ${\mathcal {A}}$, U an admissible quotient of Y with the quotient map $p:Y\longrightarrow U$ and f an ${\mathcal {F}}$-copartial morphism from any object X of ${\mathcal {A}}$ to Y with codomain U. If f is an ${\mathcal {F}}$-deflation, then p is an ${\mathcal {F}}$-deflation.

Proof

Let us take the pullback of f along p. Then, we get the following commutative diagram:

with $f\overline{p}=p\overline{f}$. Since f is an ${\mathcal {F}}$-copartial morphism, $\overline{p}$ is an ${\mathcal {F}}$-deflation. As the morphism f is an ${\mathcal {F}}$-deflation, the composition $f\overline{p}$ is also an ${\mathcal {F}}$-deflation. Then, p is also an ${\mathcal {F}}$-deflation by Lemma 2.3. $\square$

Proposition 2.5

Let X, Y, Z be objects of ${\mathcal {A}}$ and U, an admissible quotient of Y with the quotient morphism $p:Y\longrightarrow U$.

• 1. p is an ${\mathcal {F}}$-deflation if and only if for any object X of ${\mathcal {A}}$, every morphism $f:X\longrightarrow U$ is ${\mathcal {F}}$-copartial from X to Y with codomain U.

  Moreover, suppose that p be an ${\mathcal {F}}$-deflation. A morphism $f:X\longrightarrow U$ is an ${\mathcal {F}}$-deflation if and only if f is an ${\mathcal {F}}$-copartial isomorphism from X to Y with codomain U.

• 2. If $f:X\longrightarrow U$ is a morphism, then f defines an ${\mathcal {F}}$-copartial isomorphism from X to Y with codomain U if and only if f is a deflation, f is an ${\mathcal {F}}$-copartial morphism from X to Y with codomain U and p is an ${\mathcal {F}}$-copartial morphism from Y to X with codomain U.

• 3. Let

  

  be a conflation whose cokernel is $p:Y\longrightarrow U$. Then, a morphism $f:X\longrightarrow U$ defines an ${\mathcal {F}}$-copartial morphism from X to Y with codomain U if and only if Ext$(f,A)(\eta )\in {\mathcal {F}}$.

• 4. If $f:X\longrightarrow U$ is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) from X to Y with codomain U and g is any morphism (respectively, ${\mathcal {F}}$-deflation) from Z to X, then fg is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) from Z to Y with codomain U.

• 5. If $f:X\longrightarrow Z$ is an ${\mathcal {F}}$-deflation and $g:Z\longrightarrow U$ is any morphism such that the composition gf is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) from X to Y with codomain U, then g is also an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) from Z to Y with codomain U.

• 6. If f and g are ${\mathcal {F}}$-copartial morphisms from X to Y with codomain U, then $f+g$ is an ${\mathcal {F}}$-copartial morphism from X to Y.

• 7. If $f:X\longrightarrow U$ is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) from X to Y with codomain U and $g:Z\longrightarrow Y$ is an ${\mathcal {F}}$-deflation, then f is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism) from X to Z with codomain U.

• 8. If $f:X\longrightarrow U$ be any morphism such that pullback of f along p as in the following commutative diagram:

  

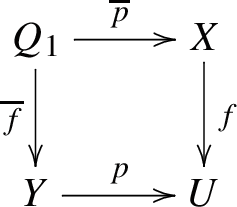
  then $g:Z\longrightarrow X$ is an ${\mathcal {F}}$-copartial morphism from Z to $Q_1$ with codomain X if and only if fg is an ${\mathcal {F}}$-copartial morphism from Z to Y with codomain U.

Proof

(1) Let $p:Y\longrightarrow U$ be an ${\mathcal {F}}$-deflation and f be any morphism from an object X to U. The pullback along any ${\mathcal {F}}$-deflation is an ${\mathcal {F}}$-deflation, so that any morphism $f:X\longrightarrow U$ is an ${\mathcal {F}}$-copartial morphism. Conversely, if we take $X=U$, then $p:Y\longrightarrow U$ is an ${\mathcal {F}}$-deflation by Lemma 2.4.

Moreover, as a consequence of Lemma 2.3, f is an ${\mathcal {F}}$-deflation if and only if it is an ${\mathcal {F}}$-copartial isomorphism.

The proofs of (2), (3), (4), (6) and (7) are the duals of Proposition 2.5 in [5].

(5) Let $f:X\longrightarrow Z$ be an ${\mathcal {F}}$-deflation and $g:Z\longrightarrow U$ be any morphism such that gf is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism). If we take the pullbacks of g along p and f along $\overline{p}$, then we get the following commutative diagram:

The outer diagram is also the pullback of gf along p. Since gf is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism), then $p^{\prime }$ is an ${\mathcal {F}}$-deflation (respectively, $p^{\prime }$ and $\overline{g}f^{\prime }$ are ${\mathcal {F}}$-deflations). Then, by Lemma 2.3, $\overline{p}$ is an ${\mathcal {F}}$-deflation (respectively, $\overline{p}$ and $\overline{g}$ are ${\mathcal {F}}$-deflations) since f is an ${\mathcal {F}}$-deflation. Thus, g is an ${\mathcal {F}}$-copartial morphism (respectively, ${\mathcal {F}}$-copartial isomorphism).

(8) Suppose that $g:Z\longrightarrow X$ be an ${\mathcal {F}}$-copartial morphism. Let us take the pullback of g along $\overline{p}$. Then, we get the following commutative diagram with the outer diagram is the pullback of fg along p:

Since g is an ${\mathcal {F}}$-copartial morphism, then $p^{\prime }$ is an ${\mathcal {F}}$-deflation. So fg is an ${\mathcal {F}}$-copartial morphism from Z to Y with codomain U.

Converse is clear. $\square$

Corollary 2.6

Let Y be an object of ${\mathcal {A}}$ and U an admissible quotient of Y with the quotient map $p:Y\longrightarrow U$. $1_{U}$ is an ${\mathcal {F}}$-copartial morphism from U to Y with codomain U if and only if p is an ${\mathcal {F}}$-deflation.

Now we give some properties of ${\mathcal {F}}$-copartial morphisms (${\mathcal {F}}$-copartial isomorphisms) in a commutative diagram as follows:

Proposition 2.7

Consider the following commutative diagram with two conflations:

• 1. If $g_1:B\longrightarrow C$ is an ${\mathcal {F}}$-deflation, then $\gamma$ is an ${\mathcal {F}}$-copartial morphism from C to Y with codomain Z.

• 2. If $g_1:B\longrightarrow C$ and $\varphi :B\longrightarrow Y$ are ${\mathcal {F}}$-deflations, then $\gamma$ is an ${\mathcal {F}}$-copartial isomorphism from C to Y with codomain Z.

Proof

(1) Let us take the pullback of $\gamma$ along $g_2$. Then, we get the following commutative diagram:

By the universal property of pullback, we get the morphism $h:B\longrightarrow Q$ with $\overline{g_2} h= g_1$ and $\overline{\gamma } h=\varphi$. So $\overline{g_2}$ is an ${\mathcal {F}}$-deflation by Lemma 2.3. Therefore, $\gamma$ is an ${\mathcal {F}}$-copartial morphism from C to Y with codomain Z.

(2) Let us take the pullback of $\gamma$ along $g_2$. Then, we get the following commutative diagram:

By the universal property of pullback, we get the morphism $h:B\longrightarrow Q$ with $\overline{g_2} h= g_1$ and $\overline{\gamma } h=\varphi$. So $\overline{g_2}$ and $\overline{\gamma }$ are ${\mathcal {F}}$-deflations by Lemma 2.3. Therefore, $\gamma$ is an ${\mathcal {F}}$-copartial isomorphism from C to Y with codomain Z. $\square$

Corollary 2.8

Let X and Y be objects of ${\mathcal {A}}$ and U an admissible quotient of Y with the quotient map $p:Y\longrightarrow U$ and $f:X\longrightarrow U$ be a morphism. If there exists a morphism $g:X\longrightarrow Y$ such that $pg=f$, then f is an ${\mathcal {F}}$-copartial morphism from X to Y with codomain U.

Given P an object of ${\mathcal {A}}$ and $p:A\longrightarrow C$ an deflation. Recall that P is called p-projective (or projective with respect to p) if for each morphism $f:P\longrightarrow C$ there exist a morphism $g:P\longrightarrow A$ with $pg=f$. P is said that projective object in ${\mathcal {A}}$ if it is projective with respect to each deflation. Projective objects with respect to ${\mathcal {F}}$-deflations will be called ${\mathcal {F}}$-projective objects. We shall say that ${\mathcal {A}}$ has enough projective objects if for each objects A in ${\mathcal {A}}$, there exists a deflation $P\longrightarrow A$ with a projective object P in ${\mathcal {A}}$. After these definitions, we can give the duals of Proposition 2.5 (4) and Theorem 2.8 in [5].

Proposition 2.9

Let Y be an object of ${\mathcal {A}}$, U an admissible quotient of Y with the quotient map $p:Y\longrightarrow U$ and f an ${\mathcal {F}}$-copartial morphism from any object X of ${\mathcal {A}}$ to Y with codomain U. Then,

• 1. If there exists $h:Y\longrightarrow X$ such that $fh=p$, then f is an ${\mathcal {F}}$-copartial isomorphism.

• 2. The converse of (1) is true if Y is ${\mathcal {F}}$-projective.

Proof

The proof is the dual of the proof of Proposition 2.5 (4) in [5]. $\square$

In the next theorem, we give a characterization of ${\mathcal {F}}$-projective objects by ${\mathcal {F}}$-copartial morphisms.

Theorem 2.10

An object X of ${\mathcal {A}}$ is ${\mathcal {F}}$-projective if and only if any ${\mathcal {F}}$-copartial morphism f from X to any object Y with codomain U, where U is any admissible quotient of Y with the quotient map $p:Y\longrightarrow U$, extends to a morphism $g:X\longrightarrow Y$.

Proof

If X is an ${\mathcal {F}}$-projective object and f is an ${\mathcal {F}}$-copartial morphism from X to Y, we can get the following pullback:

with an ${\mathcal {F}}$-deflation $\overline{p}$. Because of the ${\mathcal {F}}$-projectivity of X, there exists a morphism $w:X\longrightarrow Q$ such that $1_X=\overline{p}w$. Then, $\overline{f}w$ is a morphism from X to Y with $f=p\overline{f}w$.

Conversely, if $v:Y\longrightarrow V$ is an ${\mathcal {F}}$-deflation and $f:X\longrightarrow V$ is any morphism, then by Proposition 2.5 (1), f is an ${\mathcal {F}}$-copartial morphism from X to Y. By hypothesis, there exists $g:X\longrightarrow Y$ such that $vg=f$. Then, X is an ${\mathcal {F}}$-projective object. $\square$

Phantom morphisms were introduced by Gnacadja [9] in the category of modules over a finite group ring and studied by Herzog [10] for a general module category. In [7], phantom morphisms with respect to the exact substructure ${\mathcal {F}}$ have been defined. A morphism $f:X\longrightarrow A$ is called ${\mathcal {F}}$-phantom if the pullback of any conflation (end with A) along f gives a conflation that belongs to ${\mathcal {F}}$ (equivalently if $\text{ Ext }{(f,B)}\in {\mathcal {F}}$ for each conflation of the form $\eta :B\longrightarrow C\longrightarrow A$).

In the next corollary, we characterize ${\mathcal {F}}$-phantom morphisms in terms of ${\mathcal {F}}$-copartial morphisms as follows.

Corollary 2.11

Let $f:X\longrightarrow U$ be a morphism in ${\mathcal {A}}$. f is an ${\mathcal {F}}$-phantom morphism if and only if for every admissible quotient map $p:Y\longrightarrow U$ f is an ${\mathcal {F}}$-copartial morphism from X to Y with codomain U.

Proof

Let $f:X\longrightarrow U$ be an ${\mathcal {F}}$-phantom morphism and $p:Y\longrightarrow U$ be an admissible quotient map. Let $i:K\longrightarrow Y$ be the kernel of p. Then, $\text{ Ext }{(f,K)}\in {\mathcal {F}}$ by the definition of ${\mathcal {F}}$-phantom morphism. So the pullback of f along p is an ${\mathcal {F}}$-deflation. Therefore, f is an ${\mathcal {F}}$-copartial morphism. We can get the converse by the similar way. $\square$

Given a class ${\mathcal {X}}$ of objects, ${\mathcal {E}}_{{\mathcal {X}}}$ is the class of all $\text{ Hom}_{{\mathcal {A}}}({\mathcal {X}},-)$-exact conflations, i.e., those conflations

$$\begin{aligned} A\longrightarrow C\longrightarrow B \end{aligned}$$

such that

$$\begin{aligned} \text{ Hom}_{{\mathcal {A}}}(X,A)\longrightarrow \text{ Hom}_{{\mathcal {A}}}(X,C)\longrightarrow \text{ Hom}_{{\mathcal {A}}}(X,B) \end{aligned}$$

is a short exact sequence in the category of abelian groups for each $X\in {\mathcal {X}}$. Dually, ${\mathcal {E}}^{{\mathcal {X}}}$ is the class of all $\text{ Hom}_{{\mathcal {A}}}(-,{\mathcal {X}})$-exact conflations, that is, those conflations

$$\begin{aligned} A\longrightarrow C\longrightarrow B \end{aligned}$$

such that

$$\begin{aligned} \text{ Hom}_{{\mathcal {A}}}(B,X)\longrightarrow \text{ Hom}_{{\mathcal {A}}}(C,X)\longrightarrow \text{ Hom}_{{\mathcal {A}}}(A,X) \end{aligned}$$

is a short exact sequence in the category of abelian groups for each $X\in {\mathcal {X}}$. Both ${\mathcal {E}}_{{\mathcal {X}}}$ and ${\mathcal {E}}^{{\mathcal {X}}}$ are exact substructures of ${\mathcal {E}}$ from [3, Exercise 5.6].

Now we will give the characterizations of ${\mathcal {E}}^{{\mathcal {X}}}$-copartial and ${\mathcal {E}}_{{\mathcal {X}}}$-copartial morphisms for a given class of objects X.

Proposition 2.12

Let ${\mathcal {X}}$ be a class of objects, X and Y be two objects of ${\mathcal {A}}$, U an admissible quotient of Y with the quotient map $p:Y\longrightarrow U$ and $f:X\longrightarrow U$ be a morphism. Then, the followings are equivalent:

• 1. f is an ${\mathcal {E}}_{{\mathcal {X}}}$-copartial morphism from X to Y with codomain U.

• 2. For each morphism $g:Z\longrightarrow X$ with $Z\in {\mathcal {X}}$, there exists $h:Z\longrightarrow Y$ with $ph=fg$.

Proof

Proof is the dual of Proposition 2.10 in [5]. $\square$

Proposition 2.13

Suppose that there exists enought injective objects. Let ${\mathcal {X}}$ be a class of objects, X and Y be two objects of ${\mathcal {A}}$, U an admissible quotient of Y with the quotient map $p:Y\longrightarrow U$ and $f:X\longrightarrow U$ be a morphism. Then, the followings are equivalent:

• 1. f is an ${\mathcal {E}}^{{\mathcal {X}}}$-copartial morphism.

• 2. For each commutative diagram

  

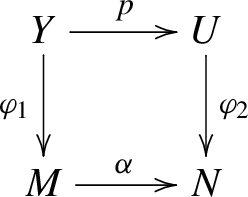
  in which $\text{ Ker }{\alpha }\in {\mathcal {X}}$, there exists $g:X\longrightarrow M$ such that $\alpha g= \varphi _2 f$.

Proof

Proof is the dual of Proposition 2.11 in [5]. $\square$

Now we will characterize the objects of M that every deflation end with M is an ${\mathcal {F}}$-deflation.

Theorem 2.14

Let M be an object of ${\mathcal {A}}$. Every deflation end with M is an ${\mathcal {F}}$-deflation if and only if for any object N and its quotient object U with the quotient map $p:N\longrightarrow U$, every morphism from M to U is an ${\mathcal {F}}$-copartial morphism from M to N with codomain U.

Proof

Let every deflation end with M is an ${\mathcal {F}}$-deflation and let for an object N and its quotient U with a deflation $p:N\longrightarrow U$, f be a morphism from M to U. If we take the pullback of f along p, we get the following commutative diagram:

By assumption, $\overline{p}:Q\longrightarrow M$ is an ${\mathcal {F}}$-deflation. So f is an ${\mathcal {F}}$-copartial morphism from M to Y with codomain U.

For the converse, let us take a deflation $p:A\longrightarrow M$. By assumption, $1_M$ is an ${\mathcal {F}}$-copartial morphism from M to A with codomain M. Then, by Corollary 2.6p is an ${\mathcal {F}}$-deflation. $\square$

Proposition 2.15

Let M and $M^{\prime }$ be objects of ${\mathcal {A}}$ and let there be an ${\mathcal {F}}$-deflation $u:M\longrightarrow M^{\prime }$. If any deflation end with M is an ${\mathcal {F}}$-deflation, then any deflation end with $M^{\prime }$ is an ${\mathcal {F}}$-deflation.

Proof

For an object N and its quotient object U with the quotient map $p:N\longrightarrow U$, let us take a morphism f from $M^{\prime }$ to U. Then, we get the following commutative diagram by taking pullbacks of f along p and of u along $\overline{p}$:

By assumption, the deflation $p^{\prime }:Q_2\longrightarrow M$ is an ${\mathcal {F}}$-deflation. Then, $\overline{p}$ is also an ${\mathcal {F}}$-deflation by Lemma 2.3. Therefore, f is an ${\mathcal {F}}$-copartial morphism. By Theorem 2.14, any deflation end with $M^{\prime }$ is an ${\mathcal {F}}$-deflation. $\square$

Let R be a ring, A and C be left R-modules and $f: A \longrightarrow C$ be an epimorphism. f is called pure epimorphism if $\text{ Hom}_{R}(M, f): Hom_{R}(M, A)\longrightarrow \text{ Hom}_{R}(M, C)$ is an epimorphism for all finitely presented left R-modules M. Let B be the kernel of f. Then by the theorem of Fieldhouse [6] and Warfield [22], f is pure if and only if B is pure in A in the sense that the natural homomorphism $N\otimes _{R} B\longrightarrow N \otimes _{R} A$ derived from the inclusion map $B\longrightarrow A$ is a monomorphism for all right R-modules N. Moreover, by Cohn’s theorem in [4], this is equivalent to the condition that every finite system of linear equations over B which is solvable in A is also solvable in B. On the other hand, for every commutative diagram

with $n,m\in {\mathbb {N}}$, there exists a morphism $h:R^{(n)}\longrightarrow B$ with $hg=f$ if and only if $u: B\longrightarrow A$ is a pure monomorphism (B is pure in A) from [23]. The conflation $B\longrightarrow A\longrightarrow C$ is called pure conflation if f is a pure epimorphism (or u is a pure monomorphism).

Definition 2.16

An ${\mathcal {F}}$-copartial morphism (${\mathcal {F}}$-copartial isomorphism) with a pure-exact substructure ${\mathcal {F}}$ in the category of R-Mod is called copartial morphism (copartial isomorphism). That means:

Let X and Y be left R-modules. A copartial morphism (respectively, copartial isomorphism) f from X to Y is a morphism $f:X\longrightarrow U$ where U is a quotient of Y with quotient map $p:Y\longrightarrow U$, such that in the pullback of f along p;

$\overline{p}$ is a pure epimorphism (respectively, $\overline{p}$ and $\overline{f}$ are pure epimorphisms). We shall call the quotient module U the codomain of f.

Remark 2.17

If ${\mathcal {P}}$ is the class of all finitely presented modules, the exact structure ${\mathcal {E}}_{{\mathcal {P}}}$ consists of all pure conflations and it is called pure-exact structure on R-Mod. And as a consequence of Proposition 2.12, ${\mathcal {E}}_{{\mathcal {P}}}$-copartial morphisms are exactly the copartial morphisms for the class of all finitely presented modules ${\mathcal {P}}$ in R-Mod.

The projective objects with respect to pure-exact sequences on R-Mod are called pure-projective modules (see [23]). As a corollary of Theorem 2.10, we get that the new characterization of pure-projective modules by copartial morphisms.

Corollary 2.18

An R-module P is pure-projective if and only if any copartial morphism from P to any module X with codomain U, where U is any quotient of X, extends to a morphism $g:P\longrightarrow X$.

Now we give some applications of ${\mathcal {F}}$-copartial morphisms to the pure-exact structure ${\mathcal {F}}$ that we will use them in the rest of this paper.

Corollary 2.19

Let X, Y and U be left R-modules with an epimorphism $p:Y\longrightarrow U$. $1_U$ is a copartial morphism from U to Y with codomain U if and only if p is a pure epimorphism.

Corollary 2.20

Let X, Y be left R-modules and $p:Y\longrightarrow U$ be an epimorphism. If $f:X\longrightarrow U$ is a copartial morphism (respectively, copartial isomorphism) from X to Y with codomain U and $g: Z\longrightarrow X$ be any morphism (respectively, pure epimorphism), then fg is an copartial morphism (respectively, copartial isomorphism) from Z to Y with codomain U.

3 Finitely Copartial Morphisms

Let M be a left R-module. Let A, C be left R-modules and $f:A\longrightarrow C$ an epimorphism. The epimorphism f is called M-pure if $\text{ Hom}_R(M,f):\text{ Hom}_R(M,A)\longrightarrow \text{ Hom}_R(M,C)$ is an epimorphism or in other words for each homomorphism $\psi :M\longrightarrow C$ there exists a homomorphism $\varphi :M\longrightarrow A$ such that $f\varphi =\psi$ (see [1]). Thus, an epimorphism $f:A\longrightarrow C$ is called pure if f is M-pure for all finitely presented left R-modules M. In Sect. 2, we also recall some other equivalent conditions of pure epimorphisms. In [1], Azumaya replaces the class of finitely presented modules with the class of finitely generated modules in the definition of purity and the author yields a series of some meaningful results.

Let A, C be left R-modules and $f:A\longrightarrow C$ be an epimorphism. In [1], they called f finitely (singly) split if f is M-pure for all finitely generated (cyclic) R-modules M, that means, f is finitely (singly) split if $\text{ Hom }(M, f):\text{ Hom }(M, A)\longrightarrow \text{ Hom }(M, C)$ is an epimorphism for all finitely generated (cyclic) left R-modules M. Clearly, every finitely split epimorphism is both pure and singly split. Let B be a submodule of A. They said that A is a finite (single) extension of B if the factor module A/B is finitely generated (cyclic) and B is finitely (singly) split in A if, for every submodule $A^{\prime }$ of A which is a finite (single) extension of B, B is a direct summand of $A^{\prime }$.

For an R-module M and for any index set I, $M^I$ means I-times direct product and $M^{(I)}$ means I-times direct sum of M. Each element of $M^I$ can be regarded as a row vector with entries in M (we denote them by $(x_i)$ whose i-th entry is $x_i$ for each $i\in I$) and each element of $M^{(I)}$ can be regarded as a column vector with entries in M (we denote them by $[x_i]$ whose i-th entry is $x_i$ for each $i\in I$). If n is a positive integer, $M^n$ is defined to be $M^I=(M^{(I)})$ where $I=\{1,\ 2,\ ...,\ n\}$. Let I and J be two index sets, and let $\mu = [a_{ij}]$ be a row-finite $I\times J$ matrix over R. For each row vector $(r_i)\in R^{(I)}$, the product $(r_i)\mu = \sum _i r_i a_{ij}$ is in $R^{(J)}$ and this gives a left R-homomorphism $\mu : R^{(I)}\longrightarrow R^{(J)}$ with the mapping $(r_i)\longrightarrow (r_i)\mu$. The cokernel of this homomorphism is denoted by $Coker(\mu )$. For a left R-module M, in [1], Azumaya called $\mu$ is a defining matrix of M (or $\mu$ defines M) if $Coker(\mu ) \cong M$, i.e., if there is an exact sequence:

where $\theta$ is an epimorphism.

Let M be any left R-module. For an index J, let $[u_j|j\in J]$ be a system of generators of M. Then, the mapping $(s_j)\longrightarrow (s_j)[u_j]$ defines an epimorphism $R^{(J)} \longrightarrow M$. For an index set I, let $[\mu _i|i\in I]$ be a system of generators of the kernel of this epimorphism, and let $\mu$ be the (row-finite) $I\times J$ matrix whose i-th row is $\mu _i$ for each $i\in I$. Then, the mapping $(r_i)\longrightarrow (r_i) \mu = \sum r_i\mu _i$ gives an epimorphism from $R^{(I)}$ onto the kernel. Therefore, we have an exact sequence

and so $\mu$ is a defining matrix of M. The matrix depends on the choice of generators $[u_j]$ and $[\mu _i]$. Thus, defining matrices of M are not necessarily unique. It is obvious that M is finitely generated or cyclic if and only if M has a defining matrix of finite columns or of single column, respectively, while M is finitely presented if and only if M has a defining matrix of finite rows and columns, i.e., a finite matrix.

Let $\mu = [a_{ij}]$ be any row-finite $I\times J$ matrix over R and V a left R-module. By a system of linear equations for $\mu$in V, we mean a system of linear equations of the form $\sum _j a_{ij}x_{j} = v_i$ for $i\in I$, where $[v_i]$ is a given vector in $V^{I}$. Let A be a left R-module and B a submodule of A with inclusion $u:B\longrightarrow A$ and $\mu$ be a defining matrix of any module. In [1], they called that B is $\mu$-pure in A (or u is $\mu$-pure monomorphism) if a system of linear equations for $\mu$ in B is solvable in B whenever it is solvable in A.

Corollary 3.1

Let $u:B\longrightarrow A$ be a monomorphism. Then the following conditions are equivalent:

• 1. u is a $\mu$-pure monomorphism (B is $\mu$-pure in A) for all matrices $\mu$ of finite (single) column over R.

• 2. For any commutative diagram with $m\in {\mathbb {N}}$;

  

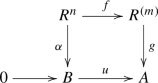
  there exists a homomorphism $h: R^{(m)}\longrightarrow B$ such that $hf=\alpha$.

Let M be a left R-module, $\mu$ be a defining matrix of M and $f:A\longrightarrow C$ be an epimorphism with kernel B. In [1, Proposition 1], Azumaya proved that f is M-pure if and only if B is $\mu$-pure in A. In [1, Page 119], he had the theorem of Cohn, Fieldhouse and Warfield that f is a pure epimorphism if and only if B is pure in A if and only if B is $\mu$-pure in A for all finite matrices $\mu$ over R. Then, in [1, Theorem 3], he also proved that f is a finitely (singly) split epimorphism if and only if B is $\mu$-pure in A for all matrices $\mu$ of finite columns (single column) over R and B is finitely (singly) split in A.

In this paper, we called the conflation $B\longrightarrow A\longrightarrow C$ is $\mu$-pure conflation if u is $\mu$-pure monomorphism (or f is M-pure epimorphism). $\mu$-pure conflations for all finite matrices $\mu$ over R in R-Mod are coincide with pure-exact sequences. We call a conflation finite (single) pure conflation if it is a $\mu$-pure conflation for all matrices $\mu$ of finite columns (one column) over R in R-Mod.

If ${\mathcal {P}}$ is the class of all finitely generated (cyclic) modules, the exact structure ${\mathcal {E}}_{{\mathcal {P}}}$ consists of all finite (single) pure conflations and in this paper we call this exact structure finite (single) pure-exact structure on R-Mod. As an another application of ${\mathcal {F}}$-copartial morphisms to finite pure-exact structure ${\mathcal {F}}$ on the category of R-Mod, we give the following definition. One of the purposes of this paper is to investigate of ${\mathcal {F}}$-copartial morphisms with finite (single) pure-exact structure ${\mathcal {F}}$ on R-Mod.

Definition 3.2

An ${\mathcal {F}}$-copartial morphism (${\mathcal {F}}$-copartial isomorphism) with the finite (single) pure-exact structure ${\mathcal {F}}$ in the category of R-Mod is called finitely (singly) copartial morphism (finitely (singly) copartial isomorphism). That means,

Let X and Y be left R-modules. A finitely (singly) copartial morphism (finitely (singly) copartial isomorphism) f from X to Y is a morphism $f:X\longrightarrow U$ where U is a quotient of Y with a quotient map $p:Y\longrightarrow U$, such that pullback of f along p:

$\overline{p}$ is a finitely (singly) split epimorphism (respectively, $\overline{p}$ and $\overline{f}$ are finitely (singly) split epimorphisms). We shall call the quotient module U the codomain of f.

In [15], a morphism $\alpha :M\longrightarrow N$ of left R-modules is called a finitely phantom morphism if for each morphism $\beta :F\longrightarrow M$ with F finitely generated, the composition $\alpha \beta$ factors through a projective (or free) left R-module, or equivalently if the restriction of $\alpha$ to every finitely generated submodule of M factors through a projective left R-module. If we take ${\mathcal {F}}$ as a finite pure-exact structure on R-Mod in Lemma 2.11, we get the following corollary by using [15, Theorem 2.5].

Corollary 3.3

Let X and U be left R-modules and $f:X\longrightarrow U$ be any morphism. f is a finitely phantom morphism if and only if for any epimorphism $p:Y\longrightarrow U$ f is a finitely copartial morphism from X to Y with codomain U.

Recall that a morphism $\alpha :M\longrightarrow N$ is called a Mittag–Leffler morphism if for each morphism $\beta :F\longrightarrow M$ with F finitely generated, there exists a finitely presented left R-module L, $\varphi :F\longrightarrow L$ and $\gamma :L\longrightarrow M$ such that $\alpha \beta =\alpha \gamma \varphi$.

Proposition 3.4

Let X, Y and U be left R-modules and $f:X\longrightarrow U$ be any morphism. If f is a Mittag–Leffler morphism, then for any pure epimorphism $p:Y\longrightarrow U$ f is a finitely copartial morphism from X to Y with codomain U.

Proof

Let $f:X\longrightarrow U$ be a Mittag–Leffler morphism and $p:Y\longrightarrow U$ be a pure epimorphism. If we take the pullback f along p, we get the following commutative diagram:

Now to show that $\overline{p}$ is a finitely split epimorphism, take a finitely generated module F and a morphism $g:F\longrightarrow X$. Since f is a Mittag–Leffler morphism, there exists a finitely presented module A, $\alpha :A\longrightarrow X$ and $\beta :F\longrightarrow A$ such that $fg=f\alpha \beta$. Since p is a pure epimorphism and A is a finitely presented module, there exists a morphism $h:A\longrightarrow Y$ such that $ph=f\alpha$. Then, we get that $ph\beta =f\alpha \beta =fg$. By the universal property of pullback, there exists a morphism $\varphi :F\longrightarrow Q$ such that $g=\overline{p}\varphi$. Therefore, $\overline{p}$ is finitely split, so f is a finitely copartial morphism. $\square$

Proposition 3.5

Let X, Y and U be left R-modules and $f:X\longrightarrow U$ be any epimorphism. If for any epimorphism $p:Y\longrightarrow U$ f is a finitely copartial morphism from X to Y with codomain U, then f is a Mittag–Leffler morphism.

Proof

By [15, Theorem 2.13, $(1)\Longrightarrow (3)$] and by Corollary 3.3 . $\square$

Remark 3.6

Let X, Y be left R-modules and U be a quotient of Y. Every finitely copartial morphism from X to Y with codomain U is copartial morphism from X to Y with codomain U. But the converse is not true.

Example 3.7

Let F be a field, $R=\prod _{i=1}^{\infty }F$ and $I=\bigoplus _{i=1}^{\infty }F$. Then, R/I is a flat R-module but it is not finitely projective by [12, page 1611]. Thus, the identitiy map $1_{R/I}$ is a copartial morphism which is not finitely copartial.

Proposition 3.8

Let R be a ring. Then, the following are equivalent:

• 1. R is left Noetherian.

• 2. Every copartial morphism is finitely copartial.

• 3. Every copartial morphism is singly copartial.

Proof

$(1)\Longrightarrow (2)$ Let $f:X\longrightarrow U$ be a copartial morphism and let $p:Y\longrightarrow U$ be an epimorphism. If we take the pullback of f along p, we get the following commutative diagram:

with $\overline{p}$ is a pure epimorphism. So $\overline{p}$ is finitely split by [1, Proposition 6]. Thus, f is a finitely copartial morphism.

$(2)\Longrightarrow (3)$ Clear.

$(3)\Longrightarrow (1)$ Let L be a left ideal of R. We will show that L is finitely generated. Let us take an epimorphism $p:X\longrightarrow U$ and any copartial morphism f from R/L to any module X with codomain U. Then, take the pullback of f along p:

Since f is copartial, by assumption (3) it is singly copartial. So $\overline{p}$ is singly split. Since R/L is cyclic, there exists $h:R/L\longrightarrow Q$. So we can extend copartial morphism f to a morphism from R/L to X. By Corollary 2.18, R/L is pure-projective. So R/L is finitely presented. By [19, Proposition 3.2, page 11], L is finitely generated. Thus, R is Noetherian. $\square$

If we apply Lemma 2.4, Proposition 2.5 (5) to a finite (single) pure-exact structure ${\mathcal {F}}$, we get the following corollaries to use in the sequel.

Corollary 3.9

Let X and Y be left R-modules, U be a quotient of Y with the quotient map $p:Y\longrightarrow U$ and f be a finitely (singly) copartial morphism from X to Y with codomain U. If f is finitely (singly) split, then p is finitely (singly) split.

Corollary 3.10

Let X and Y be left R-modules and U be a quotient of Y with the quotient map $p:Y\longrightarrow U$. If $f:X\longrightarrow Z$ is a finitely split epimorphism and $g:Z\longrightarrow U$ is any morphism such that gf is a finitely copartial morphism from X to Y with codomain U, then g is also a finitely copartial morphism from Z to Y with codomain U.

Let M be a left R-module. Recall that M is called pure-projective if every pure epimorphism onto M splits. A ring R is called left pure-semisimple if each left R-module is pure-projective. In [1], Azumaya called M finitely (singly) pure-projective if every pure epimorphism onto M is finitely (singly) split. It is clear that every pure-projective module is finitely pure-projective.

Now we give a new characterization of finitely pure-projective modules with copartial morphisms:

Theorem 3.11

Let P be a left R-module. P is finitely pure-projective if and only if every copartial morphism from P to any module X with codomain U, where U is a quotient of X, is a finitely copartial morphism from P to X with codomain U.

Proof

Let P be finitely pure-projective and f be a copartial morphism from P to X with codomain U, where U is a quotient of X with quotient map $p:X\longrightarrow U$. Then, we get the following commutative diagram by taking pullback of f along p:

with pure epimorphism $\overline{p}$. As P is finitely pure-projective, $\overline{p}$ is a finitely split epimorphism. Thus, f is a finitely copartial morphism from P to X with codomain U.

Conversely, let us take a pure epimorphism p from A to P. Since p is a pure-epimorphism, $1_P$ is a copartial morphism by Corollary 2.19. By assumption, $1_P$ is a finitely copartial morphism. Then, p is finitely split by Lemma 3.9. Therefore, P is a finitely pure-projective module. $\square$

Proposition 3.12

The following are equivalent for the ring R:

• 1. R is left Noetherian.

• 2. Any left R-module M is finitely pure-projective.

• 3. Any left R-module M is singly pure-projective.

Proof

By Theorem 3.11 and Proposition 3.8. $\square$

Corollary 3.13

A left Noetherian ring R is left pure-semisimple if and only if every finitely (singly) pure-projective module is pure-projective.

Proof

It is clear from Proposition 3.12. $\square$

In the next proposition, we give the alternative proof for [1, Corollary 8], by using Theorem 3.11.

Proposition 3.14

Let P an $P^{\prime }$ be left R-modules, and let there be a finitely (singly) split epimorphism $u:P\longrightarrow P^{\prime }$. If P is finitely (singly) pure-projective, then so is $P^{\prime }$ too.

Proof

Let f be any copartial morphism from $P^{\prime }$ to Y with codomain U with an epimorphism $p:Y\longrightarrow U$. By Corollary 2.20, fu is a copartial morphism from P to Y with codomain U. Since P is finitely (singly) pure-projective, then fu is a finitely (singly) copartial morphism. So f is a finitely (singly) copartial morphism from $P^{\prime }$ to Y with codomain U by Corollary 3.10. Thus, $P^{\prime }$ is finitely (singly) pure-projective. $\square$

Let M be a left R-module. M is called flat if for any right R-module A and a submodule B of A the natural homomorphism $\kappa \otimes M: B \otimes _{R} M \longrightarrow A \otimes _{R} M$ is a monomorphism, where $\kappa$ is the inclusion map $B\longrightarrow A$. The flatness for M is equivalent to the condition that every epimorphism onto M is pure in [19, Proposition 11.1, page 371]. And recall that M is called finitely (singly) projective if every epimorphism onto M is finitely (singly) split (see [1]). Clearly, M is finitely projective if and only if M is flat and finitely pure-projective.

If ${\mathcal {F}}$ is a pure-exact structure on R-Mod category, Theorem 2.14 gives us the characterization of flat modules and Proposition 2.15 gives us the result of Wisbauer (see [23, 36.1]) as follows.

Corollary 3.15

M is a flat R-module if and only if for any module N and its quotient U with an epimorphism $p:N\longrightarrow U$, every morphism from M to U is a copartial morphism from M to N with codomain U.

Corollary 3.16

Let M and $M^{\prime }$ be R-modules, and let there be a pure epimorphism $M\longrightarrow M^{\prime }$. If M is flat, then so is $M^{\prime }$ too.

If ${\mathcal {F}}$ is a finite pure-exact structure on R-Mod category, Theorem 2.14 gives us the characterization of finitely projective modules and Proposition 2.15 gives us the results of Azumaya (see [1, Corollary 13 and Proposition 15]) as follows.

Corollary 3.17

M is a finitely (singly) projective R-module if and only if for any module N and its quotient U with an epimorphism $p:N\longrightarrow U$, every morphism from M to U is a finitely (singly) copartial morphism from M to N with codomain U.

Corollary 3.18

Let M and $M^{\prime }$ be R-modules, and let there be a finitely (singly) split epimorphism $M\longrightarrow M^{\prime }$. If M is finitely (singly) projective, then so is $M^{\prime }$ too.

Corollary 3.19

Let R be a left Noetherian ring. Then, every flat left R-module is finitely projective.

Proof

By Proposition 3.8, Corollary 3.15 and Corollary 3.17. $\square$

4 $\mu$-partial Morphisms

To give the dual notion of finitely (singly) copartial morphism in R-Mod category, first we define $\mu$-partial morphisms for a defining matrix $\mu$. $\mu$-partial morphisms are extensions of the partial morphisms that mention in [5].

Definition 4.1

Let X, Y be left R-modules and $\mu$ be a defining matrix of any module. A $\mu$-partial morphism (respectively, $\mu$-partial isomorphism) f from X to Y is a morphism $f:U\longrightarrow Y$ where U is a submodule of X with an inclusion $u:U\longrightarrow X$ such that in the pushout of f along u,

$\overline{u}$ is a $\mu$-pure monomorphism (respectively, $\overline{u}$ and $\overline{f}$ are $\mu$-pure monomorphisms). We shall call U the domain of f.

Remark 4.2

$\mu$-partial morphisms for all finite matrices $\mu$ over R in R-Mod category are partial morphisms in the sense of Ziegler which are studied in [5]. $\mu$-partial morphisms for all matrices $\mu$ of finite columns (one column) over R in R-Mod category are just the dual versions of finite (singly) copartial morphisms.

In [1], it is defined that Q is finitely (singly) pure-injective if Q is finitely (singly) split in every pure extension of Q. Clearly, it is equivalent to condition that Q is direct summand of every finite (single) pure-extension of Q. On the other hand, in [1] Q is called finitely (singly) compact if Q satisfies the condition of the algebraic compactness for all row finite matrices of finite (single) column(s). (instead of all row finite matrices).

Proposition 4.3

Let M be a left R-module. M is finitely (singly) pure-injective if and only if every pure monomorphism start with M is a $\mu$-pure monomorphism for all matrices $\mu$ of finite columns (one column).

Proof

It is clear from [1, Theorem 3]. $\square$

We can give the characterization of finitely (singly) pure-injective left R-modules with $\mu$-partial morphisms.

Proposition 4.4

Let Q be a left R-module. Q is finitely (singly) pure-injective if and only if every partial morphism from any module X to Q with domain U, where U is a submodule of X, is $\mu$-partial morphism from X to Q with domain U for all matrices $\mu$ of finite columns (one column).

Proof

Let f be a partial morphism from X to Q with domain U. If we take the pushout of f along u, we get the following commutative diagram:

with $\overline{u}$ is a pure-monomorphism. Since Q is finitely (singly) pure-injective, $\overline{u}$ is a $\mu$-pure monomorphism for all matrices $\mu$ of finite columns (one column) over R by Proposition 4.3. Therefore, f is $\mu$-partial morphism from X to Q with domain U for all matrices $\mu$ of finite columns (one column).

Conversely, let us take a pure monomorphism $u:Q\longrightarrow A$ start with Q. Then, $1_Q$ is a partial morphism from A to Q with domain Q from [5, Proposition 5]. By assumption, $1_Q$ is a $\mu$-partial morphism for all matrices $\mu$ of finite columns (one column). By the Obscure Axiom in [3], u is $\mu$-pure monomorphism for all matrices $\mu$ of finite columns (one column). Therefore, Q is finitely (singly) pure-injective from Proposition 4.3. $\square$

In [2, Theorem 1.8], they give some characterizations of semi-compact modules. We give some of them in the following:

Corollary 4.5

Let M be a left R-module. Then the followings are equivalent:

• 1. M is semi-compact.

• 2. M is singly pure-injective.

• 3. Every pure monomorphism start with M is singly split monomorphism.

Now, as a consequence of all these results we can give a new characterization of semi-compact modules:

Proposition 4.6

Let Q be an R-module. Q is semi-compact if and only if every partial morphism from any module X to Q with domain U, where U is a submodule of X is $\mu$-partial morphism for all matrices $\mu$ of one column from X to Q with domain U.