1 Introduction

In recent decades, the backward heat conduction problem (BHCP) [15, 16, 23, 40] is very important in environmental science, energy development, fluid mechanics and electronic science. It aims at detecting the previous status of physical field from its present information. It is well known that such a problem is severely ill-posed in the Hadamard sense [5, 37]. That is to say, a small perturbation of the measurements may cause a large change in the solution. At present, there are a lot of research achievements on the BHCP of deterministic situation.

On the one hand, the classical convection–diffusion model is the parabolic equation \(\frac{\partial u}{\partial t}+\nu \nabla u=D\triangle u,\,x\in D\subset {\mathbb {R}}^d,\,t>0\). The backward problem for this equation has been studied extensively. Chen and Liu [3] used a new regularization method to give the regularized solution. The new regularization method is considered with both the number of truncation terms and the approximation accuracy for the final data as multiple regularization parameters. H\(\grave{a}\)o and Nguyen [11] gave a convergence estimate in the sense of \(L^p\)-norm by a mollification method for the BHCP, where \(p\in (1,\infty )\). Cheng et al. [4] proved the uniqueness of the mild solution for the parabolic equations and applied the discrete Tikhonov regularization method with the generalized cross validation rule to obtain a stable numerical approximation to the initial value. Li et al. [21] used the Carleman estimation to get the conditional stability for such a kind of problem. More related works are available to references [2, 9, 12,13,14, 17, 22, 26,27,28,29, 36, 41].

On the other hand, the time-fractional diffusion equation has attracted the attention of many scholars recently. Wang and Liu [38] considered a backward problem for a time-fractional diffusion process with inhomogeneous media of which the regularization method is same as [3]. Wei and Zhang [39] discussed the backward problem for a time-fractional diffusion-wave equation in a bounded domain and gave the existence, uniqueness and conditional stability. Then, Floridial and Yamamoto [7] improved the theoretical achievements of [39]. Tuan et al. [30] studied a backward problem for a nonlinear fractional diffusion equation and used a filter regularization method to approximate the solution.

With the rapid development of science and technology, more and more scholars realize that the mathematical physical system is inevitably accompanied by random disturbances, which motivates us to add random terms to certain mathematical models. For the direct problem, Foondun [6] considered a stochastic time-fractional diffusion equation (STFDE) over a bounded domain. In [33], random Rayleigh–Stokes equations with Riemann–Liouville fractional derivatives were studied, and the existence and uniqueness of solutions corresponding to two different source terms were discussed. Thach et al. [34, 35] discussed random pseudo-parabolic equations with fractional Caputo derivations for different Hurst parameters and gave the existence, uniqueness and continuity of mild solutions. For the inverse problem, Lv [18] gave a global Carleman estimation for stochastic parabolic equation and studied two kinds of inverse problems. Li and Wang considered an inverse random source problem for the Helmholtz equation driven by a fractional Gaussian field [19] and the time-harmonic Maxwell’s equations driven by a centered complex-valued Gaussian vector field with correlated components [20]. Gong et al. [10] considered an inverse random source problem for the STFDE and proved the uniqueness of inverse source problem by the variance of the Fourier transform of the boundary data. About the backward problem, Peng et al. [25] dealt with a nonlocal backward problem for a STFDE and obtained some properties of backward problem with the nonlocally terminal value term. Feng et al. [8] studied a STFDE with the source \(f(x)h(t)+g(x){\dot{B}}^H(t)\) driven by fractional Brownian motion (fBm) and reconstructed f(x) and \(|g(x)|\) from the statistics of the final data \(u(x, T, \omega )\). Tuan et al. [32] studied two terminal value problems for bi-parabolic equations driven by Wiener process and fBm (\(H\in (\frac{1}{2},1)\)) and discussed existence and instability of the mild solution. However, to the best of our knowledge, there has not been such work about the stochastic convection–diffusion equation. This is our motivation for this work. In detail, we study the following backward problem for the stochastic convection–diffusion equation driven by fBm:

$$\begin{aligned} \left\{ \begin{aligned}&u_t(x,t)+u_x(x,t)-u_{xx}(x,t)=F(x,t),&(x,t)\in D\times (0,T),\\&u(x,t)=0,&(x,t)\in \partial D\times [0,T],\\&u(x,T)=g(x),&x\in {\overline{D}}, \end{aligned} \right. \end{aligned}$$
(1.1)

where \(D=(0,1)\) and the random source is assumed as

$$\begin{aligned} F(x,t)=f(x)h(t)+\sigma (x){\dot{B}}^H(t). \end{aligned}$$

Here, f(x) and \(\sigma (x)\) are deterministic functions with compact supports contained in D, h(t) is also a deterministic function, \(B^H(t)\) is the fBm with the Hurst index \(H\in (0,1)\) and \({\dot{B}}^H(t)\) can be roughly understood as the derivative of \(B^H(t)\) with respect to the time t. When \(H=\frac{1}{2}\), the fBm reduces to the classical Brownian motion and \({\dot{B}}^H(t)\) becomes the white noise. Since the source F(x, t) is a random field with low regularity, it is a distribution instead of a function. Moreover, the direct problem has been discussed in [42]. This paper will discuss the regularity and instability of the mild solution of the backward problem (1.1).

It is known that the operator \(\frac{\partial }{\partial x} - \frac{\partial ^2}{\partial x^2}\) with the homogeneous Dirichlet boundary condition has an eigensystem \(\{\lambda _n, e_n\}_{n=1}^{\infty }\), where \(\lambda _n=\frac{1}{4}+n^2\pi ^2\), \(e_n(x)=\sqrt{2}e^{\frac{x}{2}}\sin (n\pi x)\). The eigenvalues satisfy \(0<\lambda _1\le \lambda _2\le \cdots \le \lambda _n\le \cdots \) with \( \lambda _n\rightarrow \infty \) as \(n\rightarrow \infty \). And the eigenfunctions \(\{e_n\}_{n=1}^{\infty }\) are a complete orthonormal basis weighted by \(e^{-x}\) over \(L^2(D)\). Here, the corresponding weighted space is called \({\widetilde{L}}^2(D)\). Specifically,

$$\begin{aligned} {\widetilde{L}}^2(D)=\{v \in L^2(D)\big |\int _De^{-x}v^2(x)dx<\infty \}. \end{aligned}$$

In this paper, \((\cdot ,\cdot )\) is defined as \((f,g)=\int _De^{-x}f(x)g(x)dx\) and \(\Vert \cdot \Vert \) denotes the \({\widetilde{L}}^2(D)\)-norm, i.e., \(\Vert f(\cdot )\Vert :=(\int _De^{-x}f^2(x)dx)^{\frac{1}{2}}<\infty \), for any functions \(f(x),g(x) \in L^2(D)\). Moreover,

$$\begin{aligned} f(x)=\sum _{n=1}^{\infty }f_ne_n(x), \quad f_n=(f,e_n)=\int _D e^{-x}f(x)e_n(x)dx. \end{aligned}$$

The outline of this paper is as follows. In Sect. 2, we firstly provide the mild solution of this problem and some useful lemmas. The regularity of the mild solution and instability of the problem are proved in Sect. 3. In Sect. 4, we propose a truncated regularization method and give a convergence estimation under an a-priori regularization parameter choice rule. At last, some numerical examples are presented in Sect. 5.

2 Preliminaries

In this section, we introduce some useful definitions and lemmas.

Definition 1

\((\Omega , {\mathcal {F}}, {\mathbb {P}})\) is called a complete probability space, if \(\Omega \) is a sample space, \({\mathcal {F}}\) is a \(\sigma \)-algebra on \(\Omega \), and \({\mathbb {P}}: {\mathcal {F}}\rightarrow [0,1]\) is a probability measure on the measurable space \((\Omega , {\mathcal {F}})\).

For a random variable X defined on the probability space \((\Omega , {\mathcal {F}}, {\mathbb {P}})\), the expectation of X is defined by \({\mathbb {E}}(X)=\int _{\Omega }X(\omega )d{\mathbb {P}}(\omega )\). Then, the variance of X is \({\mathbb {V}}(X)={\mathbb {E}}(X-{\mathbb {E}}(X))^2 = {\mathbb {E}}(X^2)-({\mathbb {E}}(X))^2\). Moreover, for two random variables X and Y, the covariance of X and Y is \(\text {Cov}(X,Y)={\mathbb {E}}[(X-{\mathbb {E}}(X))(Y-{\mathbb {E}}(Y))]\). In the sequel, the dependence of random variables on the sample \(\omega \in \Omega \) will be omitted unless it is necessary to avoid confusion.

Definition 2

[24] A Gaussian process \(B^H=\{B^H(t), t\ge 0\}\) is called fractional Brownian motion of Hurst parameter \(H\in (0,1)\) if it has mean zero and the covariance function

$$\begin{aligned} R(t,s)={\mathbb {E}}[B^H(t)B^H(s)]=\frac{1}{2}\left( t^{2H}+s^{2H}-|{t-s}|^{2H}\right) . \end{aligned}$$

Particularly, if \(H=\frac{1}{2}\), \(B^H\) becomes the standard Brownian motion and is usually denoted by W which covariance function turns to be \(R(t,s)=t\wedge s\).

The fBm \(B^H\) with \(H\in (0,1)\) has a Wiener integral representation

$$\begin{aligned} B^H(t)=\int _0^tK_H(t,s)dW(s), \end{aligned}$$

where \(K_H\) is a square integrable kernel and W is the standard Brownian motion.

For a fixed interval [0, T], denote by \({\mathcal {E}}\) the space of step functions on [0, T] and by \({\mathcal {H}}\) the closure of \({\mathcal {E}}\) with respect to the product

$$\begin{aligned} \langle \chi _{[0, t]}, \chi _{[0, s]}\rangle _{{\mathcal {H}}}=R(t, s), \end{aligned}$$

where \(\chi _{[0, t]}\) and \(\chi _{[0, s]}\) are the characteristic functions. For \(\psi (t),\phi (t)\in {\mathcal {H}}\), it follows from the Itô isometry that

  1. (1)

    If \(H\in (0,\frac{1}{2})\),

    $$\begin{aligned}&{\mathbb {E}}\left[ \int _0^t\psi (s)\mathrm{d}B^H(s)\int _0^t\phi (s)\mathrm{d}B^H(s)\right] \nonumber \\&\quad =\int _0^t\left[ K_H(t,\tau )\psi (\tau )+\int _\tau ^t(\psi (u)-\psi (\tau ))\frac{\partial K_H(u,\tau )}{\partial u}du\right] \nonumber \\&\qquad \cdot \left[ K_H(t,\tau )\phi (\tau )+\int _\tau ^t(\phi (u)-\phi (\tau ))\frac{\partial K_H(u,\tau )}{\partial u}du\right] d\tau , \end{aligned}$$
    (2.1)

    where

    $$\begin{aligned}&K_H(t,\tau )\\&=C_H\left[ \left( \frac{t}{\tau }\right) ^{H-\frac{1}{2}}(t-\tau )^{H-\frac{1}{2}}-(H-\frac{1}{2})\tau ^{\frac{1}{2}-H}\int _\tau ^t u^{H-\frac{3}{2}}(u-\tau )^{H-\frac{1}{2}}du\right] , \end{aligned}$$

    and \(C_H=\left( \frac{2H}{(1-2H)\beta (1-2H,H+\frac{1}{2})}\right) ^{\frac{1}{2}}\) with \(\beta (p,q)=\int _0^1t^{p-1}(1-t)^{q-1}\mathrm{d}t\). Since

    $$\begin{aligned} \frac{\partial K_H(u,\tau )}{\partial u}=C_H(H-\frac{1}{2})\left( \frac{u}{\tau }\right) ^{H-\frac{1}{2}}(u-\tau )^{H-\frac{3}{2}}, \end{aligned}$$

    obviously, \(K_H(u,\tau )>0\) and it is decreasing monotonically with respect to u,   for \(H\in (0,\frac{1}{2}), 0<\tau <u\).

  2. (2)

    If \(H=\frac{1}{2}\),

    $$\begin{aligned}&{\mathbb {E}}\left[ \int _0^t\psi (s)\mathrm{d}B^H(s)\int _0^t\phi (s)\mathrm{d}B^H(s)\right] ={\mathbb {E}}\left[ \int _0^t\psi (s)dW(s)\int _0^t\phi (s)dW(s)\right] \nonumber \\&\quad =\int _0^t\psi (s)\phi (s)\mathrm{d}s. \end{aligned}$$
    (2.2)
  3. (3)

    If \(H\in (\frac{1}{2},1)\),

    $$\begin{aligned} {\mathbb {E}}\left[ \int _0^t\psi (s)\mathrm{d}B^H(s)\int _0^t\phi (s)\mathrm{d}B^H(s)\right] =\alpha _H\int _0^t\int _0^t\psi (r)\phi (u)|{r-u}|^{2H-2}dudr, \end{aligned}$$
    (2.3)

    where \(\alpha _H=H(2H-1)\).

Lemma 2.1

For \(l\geqslant 0\), \(0<z_1<z_2<t\), and \(H\in (\frac{1}{2},1)\), we have

$$\begin{aligned} \int _0^t\int _0^t(t-z_1)^l(t-z_2)^l|{z_1-z_2}|^{2H-2}\mathrm{d}z_1\mathrm{d}z_2\lesssim t^{2H+2l}. \end{aligned}$$

Hereinafter, \(a\lesssim b\) or \(a\gtrsim b\) stands for \(a\leqslant Cb\) or \(a\geqslant Cb\), where \(C>0\) is a constant and its specific value is not required but should be clear from the context.

Proof

Using the binomial expansion, we can obtain that

$$\begin{aligned}&\int _0^t\int _0^t(t-z_1)^l(t-z_2)^l|{z_1-z_2}|^{2H-2}\mathrm{d}z_1\mathrm{d}z_2\\&\quad =2\int _0^t\int _{z_2}^t(t-z_1)^l(t-z_2)^l(z_1-z_2)^{2H-2}\mathrm{d}z_1\mathrm{d}z_2\\&\quad =2\int _0^t\int _0^{z_2}z_1^lz_2^l(z_2-z_1)^{2H-2}\mathrm{d}z_1\mathrm{d}z_2\\&\quad =2\int _0^t\int _0^{z_2}z_1^lz_2^l\sum _{p=0}^{\infty }(-1)^p{2H-2\atopwithdelims ()p}z_1^p z_2^{2H-2-p}\mathrm{d}z_1\mathrm{d}z_2\\&\quad =2\sum _{p=0}^{\infty }\int _0^t\int _0^{z_2}(-1)^p{2H-2\atopwithdelims ()p}z_1^{l+p} z_2^{2H-2-p+l}\mathrm{d}z_1\mathrm{d}z_2\\&\quad =2\sum _{p=0}^{\infty }(-1)^p{2H-2\atopwithdelims ()p}\frac{1}{l+1+p}\int _0^tz_2^{2H-1+2l}\mathrm{d}z_2\\&\quad =2\sum _{p=0}^{\infty }(-1)^p{2H-2\atopwithdelims ()p}\frac{1}{(l+1+p)(2H+2l)}t^{2H+2l}\\&\qquad \lesssim t^{2H+2l}. \end{aligned}$$

\(\square \)

Lemma 2.2

By the method of separation of variables, the solution of problem (1.1) can be written in the form \(u(x,t)=\sum _{n\in {\mathbb {Z}}^+}(u(\cdot ,t),e_n)e_n(x)=:\sum _{n\in {\mathbb {Z}}^+}u_n(t)e_n(x)\), where

$$\begin{aligned} u_n(t)=\Big (g_n\psi _n(T)-\int _t^Tf_nh(s)\psi _n(s)\mathrm{d}s-\int _t^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )\psi _n(-t). \end{aligned}$$
(2.4)

Here, \({\psi _n(s):=e^{\lambda _ns}},\,\lambda _n=\frac{1}{4}+n^2\pi ^2,\,g_n=(g,e_n),\, f_n=(f,e_n),\,\sigma _n=(\sigma ,e_n)\).

Definition 3

For any \(p>0\), we introduce the following space:

$$\begin{aligned} {\widetilde{H}}^p:= \{v\in {\widetilde{L}}^2(D)\,such\,\,that\,\, \Vert v\Vert ^2_{{\widetilde{H}}^p}:=\sum _{n\in \mathbb {Z^+}}\lambda _n^{2p}(v,e_n)^2<\infty \}. \end{aligned}$$

Particularly, if \(p=0\), then \({\widetilde{H}}^p\) turns to \({\widetilde{L}}^2\).

Definition 4

[31]Let X be a Sobolev space. We introduce the following space: \(L^P(\Omega ,X):=\{\rho \, is \,X-valued \,\,random \,\,variable \,\,on \,\Omega : \Vert \rho \Vert ^p_{L^p(\Omega ,X)}:={\mathbb {E}}\Vert \rho \Vert ^p_X<\infty \},\,p\geqslant 1\).

Definition 5

In order to prove some properties of the solutions, for two nonnegative numbers b and p, let us attempt to introduce a space called the Gevrey-type space [1]:

$$\begin{aligned} V^b_p:=\{f\in {\widetilde{L}}^2(D), such\,\,that\, \Vert f\Vert ^2_{V^b_p}:=\sum _{n\in \mathbb {Z^+}}\lambda _n^{2p}e^{2b\lambda _n}(f,e_n)^2<\infty \}. \end{aligned}$$

We note that if \(b=0\), then \(V^b_p\) turns to \({\widetilde{H}}^p\); if \(b=p=0\), then \(V^b_p\) turns to \({\widetilde{L}}^2\).

Moreover, we will analyze our problem under the following assumption.

Assumption 1

Let \(H\in (0,1)\) and f, \(\sigma \) and \(g \in {\widetilde{L}}^2(D)\). Moreover, assume that \(h\in L^{\infty }(0,T)\) is a nonnegative function and its support has a positive measure, i.e., \(h>C_h>0\).

3 The Properties of the Problem

3.1 The Regularity of the Solution

In this section, we attempt to find the spaces where we obtain the regularity of the mild solution to the problem. Before obtaining the result, we need the following strong assumptions for the data \(\{g, f, \sigma \}\).

Assumption 2

Let \(p\geqslant 0\), we set \(g(x),\,f(x),\,\sigma (x)\in V^T_{p+1}\subset V^T_p\).

Before giving the main theorem for the regularity of solution, let us give some important lemmas. From (2.4), if we set \(I_1(t,T):=\sum _{n\in {\mathbb {Z}}^+}\psi _n(T-t)(\cdot ,e_n)e_n\), \(I_2(t,s):=\sum _{n\in {\mathbb {Z}}^+}\psi _n(s-t)(\cdot ,e_n)e_n\), then

$$\begin{aligned} u(\cdot ,t)=I_1(t,T)g-\int _t^Th(s)I_2(t,s)fds-\int _t^TI_2(t,s)\sigma \mathrm{d}B^H(s). \end{aligned}$$

Lemma 3.1

For the convenience of subsequent calculation, we first give an estimation formula

$$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \\&\lesssim \left\{ \begin{aligned}&e^{2\lambda _n(T-t)}(T+T^{2H}+\lambda _n^2T^{2H+2}),\quad \text {for}\,\,H\in (0,\frac{1}{2}),\\&e^{2\lambda _n(T-t)}T^{2H},\quad \text {for}\,\,H\in [\frac{1}{2},1). \end{aligned} \right. \end{aligned}$$

Proof

We discuss the cases \(H\in (0,\frac{1}{2}), H=\frac{1}{2}\) and \(H\in (\frac{1}{2},1)\) separately, since the covariance operator of \(B^H\) has different forms in these three cases.

  1. (1)

     For \(H\in (0,\frac{1}{2})\), according to (2.1), we have

    $$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \nonumber \\&={\mathbb {E}}\left[ \Big (\int _0^T1_{[t,T]}(s)\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \nonumber \\&=\int _0^T\Big [K_H(T,s)1_{[t,T]}(s)\psi _n(s-t)\nonumber \\&\qquad +\int _s^T\big (1_{[t,T]}(u)\psi _n(u-t)-1_{[t,T]}(s)\psi _n(s-t)\big )\frac{\partial K_H(u,s)}{\partial u}du\Big ]^2\mathrm{d}s\nonumber \\&=\int _0^t\Big (\int _t^T\psi _n(u-t)\frac{\partial K_H(u,s)}{\partial u}du\Big )^2\mathrm{d}s\nonumber \\&\qquad +\int _t^T\left[ K_H(T,s)\psi _n(s-t)+\int _s^T(\psi _n(u-t)-\psi _n(s-t))\frac{\partial K_H(u,s)}{\partial u}du\right] ^2\mathrm{d}s\nonumber \\&=:N_1+N_2. \end{aligned}$$
    (3.1)

    For \(N_1\), using the Hölder inequality, we have

    $$\begin{aligned} N_1&=\int _0^t\Big (\int _t^Te^{\lambda _n(u-t)}C_H(H-\frac{1}{2})\left( \frac{u}{s}\right) ^{H-\frac{1}{2}}(u-s)^{H-\frac{3}{2}}du\Big )^2\mathrm{d}s\nonumber \\&\leqslant C_H^2e^{2\lambda _n(T-t)}(T-t)\int _0^t\int _t^T\left( \frac{u}{s}\right) ^{2H-1}(u-s)^{2H-3}duds\nonumber \\&\lesssim e^{2\lambda _n(T-t)}(T-t). \end{aligned}$$
    (3.2)

    Before we talk about \(N_2\), let us give the following estimation for \(K_H(T,s), 0<s<T\).

    $$\begin{aligned}&\int _s^Tu^{H-\frac{3}{2}}(u-s)^{H-\frac{1}{2}}du\nonumber \\&=\int _s^Tu^{2H-2}\left[ \sum _{p=0}^{\infty }{H-\frac{1}{2}\atopwithdelims ()p}\left( -\frac{s}{u}\right) ^p\right] du\nonumber \\&=\sum _{p=0}^{\infty }{H-\frac{1}{2}\atopwithdelims ()p}(-1)^ps^p\frac{T^{2H-1-p}-s^{2H-1-p}}{2H-1-p}\nonumber \\&\leqslant (T^{2H-1}-s^{2H-1})\sum _{p=0}^{\infty }{H-\frac{1}{2}\atopwithdelims ()p}\frac{(-1)^p}{2H-1-p}\nonumber \\&\lesssim s^{2H-1}-T^{2H-1}\nonumber \\&\leqslant s^{2H-1}. \end{aligned}$$
    (3.3)

    This implies

    $$\begin{aligned} K_H^2(T,s)&=C^2_H\left[ \left( \frac{T}{s}\right) ^{H-\frac{1}{2}}(T-s)^{H-\frac{1}{2}}+(\frac{1}{2}-H)s^{\frac{1}{2}-H}\int _s^Tu^{H-\frac{3}{2}}(u-s)^{H-\frac{1}{2}}du\right] ^2\nonumber \\&\lesssim C^2_H\left[ (T-s)^{H-\frac{1}{2}}+s^{H-\frac{1}{2}}\right] ^2. \end{aligned}$$
    (3.4)

    Therefore, for \(N_2\),

    $$\begin{aligned} N_2&=\int _t^T\Big [K_H(T,s)\psi _n(s-t)\\&\quad +\int _s^T(\psi _n(u-t)-\psi _n(s-t))C_H(H-\frac{1}{2})\left( \frac{u}{s}\right) ^{H-\frac{1}{2}}(u-s)^{H-\frac{3}{2}}du\Big ]^2\mathrm{d}s\\&\leqslant \int _t^TK_H^2(T,s)\psi _n^2(s-t)\mathrm{d}s\\&\quad +\int _t^T\Big (\int _s^T(\psi _n(u-t)-\psi _n(s-t))C_H(H-\frac{1}{2})\left( \frac{u}{s}\right) ^{H-\frac{1}{2}}(u-s)^{H-\frac{3}{2}}du\Big )^2\mathrm{d}s\\&{=}{:} N_{21}+N_{22}. \end{aligned}$$

    Here, about \(N_{21}\), using (3.4), it follows that

    $$\begin{aligned} N_{21}&\lesssim \int _t^T((T-s)^{H-\frac{1}{2}}+s^{H-\frac{1}{2}})^2e^{2\lambda _n(s-t)}\mathrm{d}s\nonumber \\&\lesssim \int _t^T((T-s)^{2H-1}+s^{2H-1})e^{2\lambda _n(s-t)}\mathrm{d}s\nonumber \\&\leqslant e^{2\lambda _n(T-t)}\int _t^T((T-s)^{2H-1}+s^{2H-1})\mathrm{d}s\nonumber \\&\lesssim e^{2\lambda _n(T-t)}((T-t)^{2H}+T^{2H}-t^{2H})\nonumber \\&\lesssim e^{2\lambda _n(T-t)}T^{2H}. \end{aligned}$$
    (3.5)

    Similarly,

    $$\begin{aligned} N_{22}&\leqslant C_H^2(H-\frac{1}{2})^2\int _t^T\int _s^T(T-s)(\psi _n^{'}(\xi -t))^2(u-s)^2\left( \frac{u}{s}\right) ^{2H-1}\nonumber \\&\quad (u-s)^{2H-3}duds,\,\,\text {where}\,\,\xi \in (s,u)\nonumber \\&\leqslant C_H^2(T-t)\lambda _n^2e^{2\lambda _n(\xi ^*-t)}\int _t^T\int _s^T(u-s)^{2H-1}duds,\,\,\text {where}\,\,\xi ^*\in (t,T)\nonumber \\&=\frac{(T-t)^{2H+2}}{2H(2H+1)}C_H^2\lambda _n^2e^{2\lambda _n(\xi ^*-t)}\nonumber \\&\lesssim \lambda _n^2(T-t)^{2H+2}e^{2\lambda _n(T-t)}. \end{aligned}$$
    (3.6)

    Therefore, combining (3.2), (3.5) and (3.6),

    $$\begin{aligned} {\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right]&\leqslant N_1+N_2\\&\lesssim (T-t)e^{2\lambda _n(T-t)}+T^{2H}e^{2\lambda _n(T-t)}\\&\quad +\lambda _n^2(T-t)^{2H+2}e^{2\lambda _n(T-t)}\\&\leqslant e^{2\lambda _n(T-t)}(T+T^{2H}+\lambda _n^2T^{2H+2}). \end{aligned}$$
  2. (2)

     For \(H=\frac{1}{2}\), according to Itô isometry (2.2), we have

    $$\begin{aligned} {\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \leqslant e^{2\lambda _n(T-t)}T. \end{aligned}$$
  3. (3)

     For \(H\in (\frac{1}{2},1)\), by (2.3) and Lemma 2.1, we have

    $$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \\&={\mathbb {E}}\left[ \Big (\int _0^T1_{[t,T]}(s)\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \\&=\alpha _H\int _0^T\int _0^T1_{[t,T]}(r)\psi _n(r-t)\cdot 1_{[t,T]}(u)\psi _n(u-t)\mid {r-u}\mid ^{2H-2}dudr\\&=\alpha _H\int _t^T\int _t^T\psi _n(r-t)\psi _n(u-t)\mid {r-u}\mid ^{2H-2}dudr\\&\lesssim e^{2\lambda _n(T-t)}T^{2H}. \end{aligned}$$

Making an arrangement for the above estimations, we obtain

$$\begin{aligned} {\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \lesssim \left\{ \begin{aligned}&e^{2\lambda _n(T-t)}(T+T^{2H}+\lambda _n^2T^{2H+2}),\,\text {for}\, H\in (0,\frac{1}{2}),\\&e^{2\lambda _n(T-t)}T^{2H}, \,\text {for}\, H\in [\frac{1}{2},1). \end{aligned} \right. \end{aligned}$$
(3.7)

\(\square \)

Remark 3.2

Similar to the above calculation methods, for \(\delta \geqslant 0\), we easily get

$$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _{t+\delta }^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \lesssim \left\{ \begin{aligned}&e^{2\lambda _n(T-t)}(T+T^{2H}+\lambda _n^2T^{2H+2}),\,\text {for}\, H\in (0,\frac{1}{2}),\\&e^{2\lambda _n(T-t)}T^{2H}, \,\text { for}\, H\in [\frac{1}{2},1). \end{aligned} \right. \end{aligned}$$
(3.8)
$$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^{t+\delta }\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \lesssim \left\{ \begin{aligned}&e^{2\lambda _n\delta }(\delta +\delta ^{2H}+\lambda _n^2\delta ^{2H+2}),\,\text {for}\, H\in (0,\frac{1}{2}),\\&e^{2\lambda _n\delta }\delta ^{2H}, \,\text {for}\, H\in [\frac{1}{2},1). \end{aligned} \right. \end{aligned}$$
(3.9)

Lemma 3.3

Let \(p\geqslant 0\), \(t\in (0,T)\) and assume that g satisfies Assumption 2. Then, if \(\delta \geqslant 0\) is small enough, there hold

  1. (1)

     \(\Vert I_1(t,T)g\Vert _{{\widetilde{H}}^p}\leqslant \Vert g\Vert _{V^T_p}\);

  2. (2)

     \(\Vert (I_1(t+\delta ,T)-I_1(t,T))g\Vert _{{\widetilde{H}}^p}\leqslant \delta \Vert g\Vert _{V^T_{p+1}}\).

Proof

Using Definitions 3 and 5, we can obtain that

  1. (1)
    $$\begin{aligned} \Vert I_1(t,T)g\Vert ^2_{{\widetilde{H}}^p}&=\sum _{n\in {\mathbb {Z}}^+}\lambda _n^{2p}(I_1(t,T)g,e_n)^2\\&=\sum _{n\in {\mathbb {Z}}^+}\lambda _n^{2p}e^{2\lambda _n(T-t)}(g,e_n)^2\\&\leqslant \sum _{n\in {\mathbb {Z}}^+}\lambda _n^{2p}e^{2\lambda _nT}(g,e_n)^2\\&=\Vert g\Vert ^2_{V^T_p}. \end{aligned}$$
  2. (2)

    Similarly,

    $$\begin{aligned}&\Vert \big (I_1(t+\delta ,T)-I_1(t,T)\big )g\Vert ^2_{{\widetilde{H}}^p}\\&=\sum _{n\in {\mathbb {Z}}^+}\lambda _n^{2p}\big ((I_1(t+\delta ,T)-I_1(t,T))g,e_n\big )^2\\&=\sum _{n\in {\mathbb {Z}}^+}\lambda _n^{2p}(g,e_n)^2\big (e^{\lambda _n(T-t-\delta )}-e^{\lambda _n(T-t)}\big )^2. \end{aligned}$$

By mean value theorem of differentiation, we have

$$\begin{aligned} \Vert \big (I_1(t+\delta ,T)-I_1(t,T)\big )g\Vert ^2_{{\widetilde{H}}^p}&\leqslant \delta ^2\sum _{n\in {\mathbb {Z}}^+}\lambda _n^{2(p+1)}(g,e_n)^2e^{2\lambda _nT}=\delta ^2\Vert g\Vert ^2_{V^T_{p+1}}. \end{aligned}$$

\(\square \)

Lemma 3.4

Let \(t,s\in (0,T)\), \({\delta \geqslant 0}\) and assume that f satisfies Assumption 2, we get

  1. (1)

     \(\Vert I_2(t,s)f\Vert _{{\widetilde{H}}^p}\leqslant \Vert f\Vert _{V^T_p}\);

  2. (2)

     \(\Vert (I_2(t+\delta ,s)-I_2(t,s))f\Vert _{{\widetilde{H}}^p}\leqslant \delta \Vert f\Vert _{V^T_{p+1}}\).

Proof

The proof is similar to Lemma 3.3. \(\square \)

Remark 3.5

The mild solution and inverse problem may not be stable because \(e^{2\lambda _n(T-t)}\) goes to infinity rapidly as \(n\rightarrow \infty \), so we restrict f and g in Assumption 2.

Lemma 3.6

Let \(\delta \geqslant 0\) is small enough, and assuming that f and h satisfy Assumptions 1 and 2, we have

$$\begin{aligned} \left\| \int _{t+\delta }^Th(s)I_2(t+\delta ,s)fds-\int _t^Th(s)I_2(t,s)fds\right\| _{{\widetilde{H}}^p}\lesssim \delta (T+1)\Vert h\Vert _{L^\infty (0,T)}\Vert f\Vert _{V^T_{p+1}}. \end{aligned}$$

Proof

Using the triangle inequality and Lemma 3.4, we have

$$\begin{aligned}&\big \Vert \int _{t+\delta }^Th(s)I_2(t+\delta ,s)fds-\int _t^Th(s)I_2(t,s)fds\big \Vert _{{\widetilde{H}}^p}\\&\quad =\big \Vert \int _{t+\delta }^Th(s)(I_2(t+\delta ,s)-I_2(t,s))fds\\&\qquad +\int _{t+\delta }^Th(s)I_2(t,s)fds-\int _t^Th(s)I_2(t,s)fds\big \Vert _{{\widetilde{H}}^p}\\&\quad \leqslant \big \Vert \int _{t+\delta }^Th(s)(I_2(t+\delta ,s)-I_2(t,s))fds\big \Vert _{{\widetilde{H}}^p}+\big \Vert \int _t^{t+\delta }h(s)I_2(t,s)fds\big \Vert _{{\widetilde{H}}^p}\\&\quad \leqslant \Vert h\Vert _{L^\infty (0,T)}\int _{t+\delta }^T\big \Vert (I_2(t+\delta ,s)-I_2(t,s))f\big \Vert _{{\widetilde{H}}^p}\mathrm{d}s\\&\qquad +\Vert h\Vert _{L^\infty (0,T)}\int _t^{t+\delta }\big \Vert I_2(t,s)f\big \Vert _{{\widetilde{H}}^p}\mathrm{d}s\\&\quad \leqslant \delta T\Vert h\Vert _{L^\infty (0,T)}\Vert f\Vert _{V^T_{p+1}}+\delta \Vert h\Vert _{L^\infty (0,T)}\Vert f\Vert _{V^T_p}\\&\quad \leqslant \delta (T+1)\Vert h\Vert _{L^\infty (0,T)}\Vert f\Vert _{V^T_{p+1}}. \end{aligned}$$

\(\square \)

Lemma 3.7

Let \(\delta \geqslant 0\) is small enough, and assuming that \(\sigma \) satisfies Assumption 2, there holds

$$\begin{aligned} \big \Vert \int _{t+\delta }^TI_2(t+\delta ,s)\sigma \mathrm{d}B^H(s)-\int _t^TI_2(t,s)\sigma \mathrm{d}B^H(s)\big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\lesssim \delta ^H\Vert \sigma \Vert _{V^T_{p+2}}. \end{aligned}$$

Proof

According to the triangle inequality of the norm, we have

$$\begin{aligned}&\Big \Vert \int _{t+\delta }^TI_2(t+\delta ,s)\sigma \mathrm{d}B^H(s)-\int _t^TI_2(t,s)\sigma \mathrm{d}B^H(s)\Big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\\&\quad =\Big \Vert \int _{t+\delta }^T(I_2(t+\delta ,s)-I_2(t,s))\sigma \mathrm{d}B^H(s)\\&\qquad +\int _{t+\delta }^TI_2(t,s)\sigma \mathrm{d}B^H(s)-\int _t^TI_2(t,s)\sigma \mathrm{d}B^H(s)\Big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\\&\quad \leqslant \Big \Vert \int _{t+\delta }^T(I_2(t+\delta ,s)-I_2(t,s))\sigma \mathrm{d}B^H(s)\Big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\\&\qquad +\Big \Vert \int _t^{t+\delta }I_2(t,s)\sigma \mathrm{d}B^H(s)\Big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\\&\quad {=}{:} S_1+S_2. \end{aligned}$$

For \(S_1\), by Definition 4, it follows that

$$\begin{aligned} S_1^2&=\Big \Vert \int _{t+\delta }^T(I_2(t+\delta ,s)-I_2(t,s))\sigma \mathrm{d}B^H(s)\Big \Vert ^2_{L^2(\Omega ,{\widetilde{H}}^p)}\\&={\mathbb {E}}\left[ \Big \Vert \int _{t+\delta }^T(I_2(t+\delta ,s)-I_2(t,s))\sigma \mathrm{d}B^H(s)\Big \Vert ^2_{{\widetilde{H}}^p}\right] \\&=\sum _{n\in \mathbb {Z^+}}{\mathbb {E}}\left[ \Big \Vert \int _{t+\delta }^T(e^{\lambda _n(s-t-\delta )}-e^{\lambda _n(s-t)})(\sigma ,e_n)e_ndB^H(s)\Big \Vert ^2_{{\widetilde{H}}^p}\right] \\&=\sum _{n\in \mathbb {Z^+}}{\mathbb {E}}\left[ \left( \int _{t+\delta }^T(e^{\lambda _n(s-t-\delta )}-e^{\lambda _n(s-t)})\mathrm{d}B^H(s)\right) ^2\right] \Vert (\sigma ,e_n)e_n\Vert ^2_{{\widetilde{H}}^p}. \end{aligned}$$

Using mean value theorem of differentiation and (3.8), we have the following estimate

$$\begin{aligned} S_1^2&=\sum _{n\in \mathbb {Z^+}}{\mathbb {E}}\left[ \left( \int _{t+\delta }^T-\delta \lambda _ne^{\lambda _n(\xi -t)}\mathrm{d}B^H(s)\right) ^2\right] \lambda _n^{2p}(\sigma ,e_n)^2,\,(\xi \in (s-\delta ,s))\nonumber \\&=\sum _{n\in \mathbb {Z^+}}\delta ^2\lambda _n^2{\mathbb {E}}\left[ \left( \int _{t+\delta }^Te^{\lambda _n(\xi -t)}\mathrm{d}B^H(s)\right) ^2\right] \lambda _n^{2p}(\sigma ,e_n)^2\nonumber \\&\lesssim \left\{ \begin{aligned}&\delta ^2\sum _{n\in \mathbb {Z^+}}\lambda _n^{2(p+1)}e^{2\lambda _nT}(T+T^{2H}+\lambda _n^2T^{2H+2})(\sigma ,e_n)^2,\,\text {for}\, H\in (0,\frac{1}{2})\nonumber \\&\delta ^2T^{2H}\sum _{n\in \mathbb {Z^+}}\lambda _n^{2(p+1)}e^{2\lambda _nT}(\sigma ,e_n)^2,\,\text {for}\, H\in [\frac{1}{2},1)\nonumber \end{aligned} \right. \\&\lesssim \delta ^2\Vert \sigma \Vert ^2_{V^T_{p+2}}. \end{aligned}$$
(3.10)

Similarly, for \(S_2\), there holds

$$\begin{aligned} S_2^2&=\Big \Vert \int _t^{t+\delta }I_2(t,s)\sigma \mathrm{d}B^H(s)\Big \Vert ^2_{L^2(\Omega ,{\widetilde{H}}^p)}\\&=\sum _{n\in \mathbb {Z^+}}\Big \Vert \int _t^{t+\delta }e^{\lambda _n(s-t)}(\sigma ,e_n)e_n \mathrm{d}B^H(s)\Big \Vert ^2_{L^2(\Omega ,{\widetilde{H}}^p)}\\&=\sum _{n\in \mathbb {Z^+}}{\mathbb {E}}\left[ \left( \int _t^{t+\delta }e^{\lambda _n(s-t)}\mathrm{d}B^H(s)\right) ^2\right] \Vert (\sigma ,e_n)e_n\Vert ^2_{{\widetilde{H}}^p}\\&=\sum _{n\in \mathbb {Z^+}}{\mathbb {E}}\left[ \left( \int _t^{t+\delta }e^{\lambda _n(s-t)}\mathrm{d}B^H(s)\right) ^2\right] \lambda _n^{2p}(\sigma ,e_n)^2. \end{aligned}$$

By (3.9), we have

$$\begin{aligned} S_2^2&\leqslant \left\{ \begin{aligned}&\sum _{n\in \mathbb {Z^+}}e^{2\lambda _n\delta }(\delta +\delta ^{2H}+\lambda _n^2\delta ^{2H+2})\lambda _n^{2p}(\sigma ,e_n)^2,\,\text {for}\, H\in (0,\frac{1}{2})\nonumber \\&\sum _{n\in \mathbb {Z^+}}e^{2\lambda _n\delta }\delta ^{2H}\lambda _n^{2p}(\sigma ,e_n)^2, \,\text {for}\, H\in [\frac{1}{2},1)\nonumber \end{aligned} \right. \\&\lesssim \delta ^{2H}\sum _{n\in \mathbb {Z^+}}e^{2\lambda _nT}\lambda _n^{2p+2}(\sigma ,e_n)^2\nonumber \\&\leqslant \delta ^{2H}\Vert \sigma \Vert ^2_{V^T_{p+1}}. \end{aligned}$$
(3.11)

Therefore, combining (3.10) and (3.11), we have

$$\begin{aligned}&\Big \Vert \int _{t+\delta }^TI_2(t+\delta ,s)\sigma \mathrm{d}B^H(s)-\int _t^TI_2(t,s)\sigma \mathrm{d}B^H(s)\Big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\\&\leqslant \delta \Vert \sigma \Vert _{V^T_{p+2}}+\delta ^H\Vert \sigma \Vert _{V^T_{p+1}}\\&\lesssim \delta ^H\Vert \sigma \Vert _{V^T_{p+2}}. \end{aligned}$$

\(\square \)

Theorem 3.8

Let \(\delta \geqslant 0\). Assuming f, g and \(\sigma \) satisfy Assumption 2, then

$$\begin{aligned} \Vert u(\cdot ,t+\delta )-u(\cdot ,t)\Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\leqslant C_\delta (\Vert g\Vert _{V^T_{p+1}}+\Vert f\Vert _{V^T_{p+1}}+\Vert \sigma \Vert _{V^T_{p+2}}), \end{aligned}$$

where \(C_\delta =\max \{\delta ,\delta (T+1)\Vert h\Vert _{L^\infty (0,T)}, \delta ^H\}\).

Proof

Using the triangle inequality, it follows that

$$\begin{aligned}&\Vert u(\cdot ,t+\delta )-u(\cdot ,t)\Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\\&\quad =\Big \Vert I_1(t+\delta ,T)g-\int _{t+\delta }^Th(s)I_2(t+\delta ,s)fds-\int _{t+\delta }^TI_2(t+\delta ,s)\sigma \mathrm{d}B^H(s)\\&\qquad -\Big (I_1(t,T)g-\int _t^Th(s)I_2(t,s)fds-\int _t^TI_2(t,s)\sigma \mathrm{d}B^H(s)\Big )\Big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\\&\quad \leqslant \Vert (I_1(t+\delta ,T)-I_1(t,T))g\Vert _{{\widetilde{H}}^p}\\&\qquad +\Big \Vert \int _{t+\delta }^Th(s)I_2(t+\delta ,s)fds-\int _t^Th(s)I_2(t,s)fds\Big \Vert _{{\widetilde{H}}^p}\\&\qquad +\Big \Vert \int _{t+\delta }^TI_2(t+\delta ,s)\sigma \mathrm{d}B^H(s)-\int _t^TI_2(t,s)\sigma \mathrm{d}B^H(s)\Big \Vert _{L^2(\Omega ,{\widetilde{H}}^p)}. \end{aligned}$$

Combining Lemmas 3.3(2), 3.6 and 3.7, it is easy to draw the conclusion. \(\square \)

3.2 The Instability of the Problem

In this section, we will analyze the instability of u(x, t) by the expectation and variance of \(u_n(t)\). From (2.4), we have

$$\begin{aligned} {\mathbb {E}}(u_n(t))&=g_n\psi _n(T-t)-f_n\int _t^Th(s)\psi _n(s-t)\mathrm{d}s.\\ {\mathbb {V}}ar(u_n(t))&=\sigma _n^2{\mathbb {E}}\left[ \left( \int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\right) ^2\right] . \end{aligned}$$

3.2.1 The Expectation \({\mathbb {E}}(u_n(t))\)

Here, we consider two special cases. On the one hand, if \(f\equiv 0\), , then \(f_n=0\). It follows that

$$\begin{aligned} \psi _n(T-t)\rightarrow \infty ,\,\,\text {as}\,\,n\rightarrow \infty ,\,\mathrm then\,\, {\mathbb {E}}(u_n(t))\rightarrow \infty . \end{aligned}$$

On the other hand, if \(g\equiv 0\), then \(g_n=0\). Using mean value theorem of integrals and Assumption 1, we have

$$\begin{aligned} \int _t^Th(s)\psi _n(s-t)\mathrm{d}s&=\psi _n(\xi )\int _t^Th(s)\mathrm{d}s\geqslant C_h\psi _n(\xi )(T-t)\\ \rightarrow&\infty ,\,\,\text {as}\,\,n\rightarrow \infty \,(\xi \in (0,T-t)), \end{aligned}$$

then \({\mathbb {E}}(u_n(t))\rightarrow \infty \).

3.2.2 The Variance \({\mathbb {V}}ar(u_n(t))\)

We would separately talk about \({\mathbb {V}}ar(u_n(t))\) for different H.

  1. (1)

     For the case \(H\in (0,\frac{1}{2})\), by (3.1),

    $$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \\&\quad =\int _0^t\Big (\int _t^T\psi _n(u-t)\frac{\partial K_H(u,s)}{\partial u}du\Big )^2\mathrm{d}s\\&\qquad +\int _t^T\left[ K_H(T,s)\psi _n(s-t)+\int _s^T(\psi _n(u-t)-\psi _n(s-t))\frac{\partial K_H(u,s)}{\partial u}du\right] ^2\mathrm{d}s\\&\quad {=}{:} N_1+N_2. \end{aligned}$$

    For \(N_1\),

    $$\begin{aligned} N_1&=\int _0^t\Big (\int _t^T\psi _n(u-t)C_H(H-\frac{1}{2})(\frac{u}{s})^{H-\frac{1}{2}}(u-s)^{H-\frac{3}{2}}du\Big )^2\mathrm{d}s\\&=C_H^2(H-\frac{1}{2})^2\int _0^t\Big (\int _t^Te^{(\frac{1}{4}+n^2\pi ^2)(u-t)}(\frac{u}{s})^{H-\frac{1}{2}}(u-s)^{H-\frac{3}{2}}du\Big )^2\mathrm{d}s\\&\geqslant C_H^2(H-\frac{1}{2})^2(\frac{1}{4}+n^2\pi ^2)\int _0^t\Big (\int _t^T(u-t)(\frac{u}{s})^{H-\frac{1}{2}}(u-s)^{H-\frac{3}{2}}du\Big )^2\mathrm{d}s, \end{aligned}$$

    where \(\int _0^t\Big (\int _t^T(u-t)(\frac{u}{s})^{H-\frac{1}{2}}(u-s)^{H-\frac{3}{2}}du\Big )^2\mathrm{d}s\) is a normal integral; therefore, \(N_1\rightarrow \infty ,\,\,\text {as}\,\,n\rightarrow \infty \). Since \(N_2\geqslant 0\),

    $$\begin{aligned} {\mathbb {E}}\left[ \left( \int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\right) ^2\right] =N_1+N_2\rightarrow \infty ,\,\,\text {as}\,\, n\rightarrow \infty . \end{aligned}$$
  2. (2)

     For the case \(H=\frac{1}{2}\), by (2.2) and mean value theorem, we have

    $$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \\&=\psi _n(\xi )(T-t)\rightarrow \infty ,\,\,\text {as}\,\, n\rightarrow \infty \quad (\xi \in (0,2T-2t)). \end{aligned}$$
  3. (3)

     For the case \(H\in (\frac{1}{2},1)\), similarly, by (2.3)

    $$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \\&\quad =\alpha _H\psi _n(\xi _1)\psi _n(\xi _2)\int _t^T\int _t^T\mid {r-u}\mid ^{2H-2}\mathrm{d}r\mathrm{d}u\,\,(\xi _1, \xi _2\in (0,2T-2t))\\&\quad =2\alpha _H\frac{(T-t)^{2H}}{2H(2H-1)}\psi _n(\xi _1)\psi _n(\xi _2)\rightarrow \infty ,\,\,\text {as}\,\, n\rightarrow \infty . \end{aligned}$$

    Above all, we can conclude that this problem is instability.

4 The Regularized Solution of the Problem

The instability means the small error in the high-frequency components for \(g^\delta , f^\delta \) and \(\sigma ^\delta \) will be amplified by the factor \(\psi _n(t)\), so we need some regularization methods to compute \(u(x,t), t\in (0,1)\) from measured data \(g^\delta , f^\delta \) and \(\sigma ^\delta \). Here, we adopt the truncated regularization method to establish the regularized solution for u(x, t) in (1.1). If the noisy data \(g^{\delta }, f^{\delta }\) and \(\sigma ^{\delta }\) satisfy

$$\begin{aligned} \Vert g^\delta -g\Vert \leqslant \delta , \quad \Vert f^\delta -f\Vert \leqslant \delta , \quad \Vert \sigma ^\delta -\sigma \Vert \leqslant \delta , \end{aligned}$$
(4.1)

where the constant \(\delta \geqslant 0\) is a noise level, then the regularized solution \(u^{M,\delta }\) is defined as

$$\begin{aligned} u^{M,\delta }(x,t)&=\sum _{n=1}^M\Big [g_n^\delta \psi _n(T)\\&\quad -\int _t^Tf_n^\delta h(s)\psi _n(s)\mathrm{d}s-\int _t^T\sigma _n^\delta \psi _n(s)\mathrm{d}B^H(s)\Big ]\psi _n(-t)e_n(x). \end{aligned}$$

In addition, we set

$$\begin{aligned} u^M(x,t)&=\sum _{n=1}^M\Big [g_n\psi _n(T)\\&\quad -\int _t^Tf_n h(s)\psi _n(s)\mathrm{d}s-\int _t^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big ]\psi _n(-t)e_n(x). \end{aligned}$$

To obtain the error estimation between u and \(u^{M,\delta }\), the a-priori bound L on the mild solution is needed. In detail, we set

$$\begin{aligned}&\Vert u(\cdot ,0)\Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}\nonumber \\&\quad ={\mathbb {E}}\Big [\sum _{n=1}^\infty \Big (g_n\psi _n(T)-\int _0^Th(s)f_n\psi _n(s)\mathrm{d}s-\int _0^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )^2\Big ]\nonumber \\&\quad \lesssim \sum _{n=1}^\infty (g_n\psi _n(T))^2+\sum _{n=1}^\infty \Big (\int _0^Th(s)f_n\psi _n(s)\mathrm{d}s\Big )^2\nonumber \\&\qquad +\sum _{n=1}^\infty {\mathbb {E}}\left[ \Big (\int _0^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] \nonumber \\&\quad \leqslant L^2. \end{aligned}$$
(4.2)

Theorem 4.1

For \(H\in [\frac{1}{2},1)\), let M be a positive integer number. Assume that the a-priori bound (4.2) and the noise level (4.1) hold. Then,

$$\begin{aligned} \big \Vert u^{M,\delta }(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}&\lesssim \psi _M(2T-2t)\delta ^2\\&\quad +\psi _M(-2t)L^2,\quad \text {for}\quad 0<t<T. \end{aligned}$$

Proof

According to the triangle inequality, we get

$$\begin{aligned}&\big \Vert u^{M,\delta }(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}\nonumber \\&\quad \lesssim \big \Vert u^{M,\delta }(\cdot ,t)-u^M(\cdot ,t)\big \Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}+\big \Vert u^M(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}\nonumber \\&\qquad {=}{:} I_1+I_2. \end{aligned}$$
(4.3)

For \(I_1\),

$$\begin{aligned} I_1&={\mathbb {E}}\Big \Vert \sum _{n=1}^M\Big [(g_n^\delta -g_n)\psi _n(T)-\int _t^T(f_n^\delta -f_n) h(s)\psi _n(s)\mathrm{d}s\nonumber \\&\quad -\int _t^T(\sigma _n^\delta -\sigma _n)\psi _n(s)\mathrm{d}B^H(s)\Big ]\psi _n(-t)e_n(\cdot )\Big \Vert ^2\nonumber \\&\lesssim \sum _{n=1}^M((g_n^\delta -g_n)\psi _n(T-t))^2+\sum _{n=1}^M\Big (\int _t^T(f_n^\delta -f_n)h(s)\psi _n(s-t)\mathrm{d}s\Big )^2\nonumber \\&\quad +\sum _{n=1}^M{\mathbb {E}}\left[ \Big (\int _t^T(\sigma _n^\delta -\sigma _n)\psi _n(s-t)\mathrm{d}B^H(s)\Big )^2\right] \nonumber \\&{=}{:} J_1(t,T)+J_2(t,T)+J_3(t,T). \end{aligned}$$

Here,

$$\begin{aligned} J_1(t,T)\leqslant \psi _M^2(T-t)\sum _{n=1}^\infty (g_n^\delta -g_n)^2\leqslant \delta ^2\psi _M(2T-2t). \end{aligned}$$

If Assumption 1 and the noise level (4.1) hold, then

$$\begin{aligned} J_2(t,T)&\leqslant \psi _M^2(T-t)\Vert h\Vert ^2_{L^\infty (0,T)}(T-t)^2\sum _{n=1}^\infty (f_n^\delta -f_n)^2\nonumber \\&\leqslant \delta ^2\psi _M(2T-2t)\Vert h\Vert ^2_{L^\infty (0,T)}(T-t)^2. \end{aligned}$$

Since

$$\begin{aligned} J_3(t,T)=\sum _{n=1}^M(\sigma _n^\delta -\sigma _n)^2{\mathbb {E}}\left[ \left( \int _t^T\psi _n(s-t)\mathrm{d}B^H(s)\right) ^2\right] , \end{aligned}$$

from (3.7), we have

$$\begin{aligned} J_3(t,T)\lesssim \delta ^2e^{2\lambda _M(T-t)}T^{2H}\lesssim \delta ^2\psi _M(2T-2t), \,\,\text {for}\,\, H\in [\frac{1}{2},1). \end{aligned}$$

Therefore,

$$\begin{aligned} I_1\lesssim \delta ^2\psi _M(2T-2t)(2+(T-t)^2\Vert h\Vert ^2_{L^\infty (0,T)}). \end{aligned}$$
(4.4)

For \(I_2\) in (4.3), there exists

$$\begin{aligned} I_2&={\mathbb {E}}\left[ \sum _{n=M+1}^\infty \Big (g_n\psi _n(T)-\int _t^Th(s)f_n\psi _n(s)\mathrm{d}s-\int _t^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )^2\psi _n(-2t)\right] \nonumber \\&\lesssim \sum _{n=M+1}^\infty (g_n\psi _n(T-t))^2\psi _n(-2t)+\sum _{n=M+1}^\infty \Big (\int _t^Th(s)f_n\psi _n(s)\mathrm{d}s\Big )^2\psi _n(-2t)\nonumber \\&\quad +\sum _{n=M+1}^\infty {\mathbb {E}}\left[ \Big (\int _t^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] \psi _n(-2t)\nonumber \\&{=}{:} K_1+K_2+K_3. \end{aligned}$$
(4.5)

For \(K_1\),

$$\begin{aligned} K_1\leqslant \psi _M(-2t)\sum _{n=1}^\infty (g_n\psi _n(T))^2. \end{aligned}$$
(4.6)

For \(K_2\),

$$\begin{aligned} K_2\leqslant \psi _M(-2t)\sum _{n=1}^\infty \Big (\int _0^Th(s)f_n\psi _n(s)\mathrm{d}s\Big )^2. \end{aligned}$$
(4.7)

For \(K_3\),

$$\begin{aligned}&\sum _{n=M+1}^\infty {\mathbb {E}}\left[ \Big (\int _t^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] \psi _n(-2t)\\&\quad =\sum _{n=M+1}^\infty \sigma _n^2\psi _n(-2t){\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] . \end{aligned}$$

We need to compute \({\mathbb {E}}\left[ \Big (\int _t^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] \) for \(H=\frac{1}{2}\) and \(H\in (\frac{1}{2},1)\), respectively.

  1. (1)

     For \(H=\frac{1}{2}\),

    $$\begin{aligned}&{\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] =\int _t^T\psi _n(2s)\mathrm{d}s\leqslant \int _0^T\psi _n(2s)\mathrm{d}s\nonumber \\&\quad ={\mathbb {E}}\left[ \Big (\int _0^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] . \end{aligned}$$
    (4.8)
  2. (2)

     For \(H\in (\frac{1}{2},1)\),

    $$\begin{aligned}&{\mathbb {E}}\left[ (\int _t^T\psi _n(s)\mathrm{d}B^H(s))^2\right] \nonumber \\&\quad =\int _t^T\int _t^T\psi _n(r)\psi _n(u)\mid {r-u}\mid ^{2H-2}\mathrm{d}r\mathrm{d}u\nonumber \\&\quad \leqslant \int _0^T\int _0^T\psi _n(r)\psi _n(u)\mid {r-u}\mid ^{2H-2}\mathrm{d}r\mathrm{d}u\nonumber \\&\quad ={\mathbb {E}}\left[ \Big (\int _0^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] . \end{aligned}$$
    (4.9)

From (4.8)–(4.9), it concludes that

$$\begin{aligned} K_3\leqslant \psi _M(-2t)\sum _{n=1}^\infty {\mathbb {E}}\left[ \Big (\int _0^T\sigma _n\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] ,\,\text {for}\,\,H\in [\frac{1}{2},1). \end{aligned}$$
(4.10)

Plunging (4.6), (4.7) and (4.10) into (4.5), we have

$$\begin{aligned} I_2\leqslant \psi _M(-2t)L^2. \end{aligned}$$
(4.11)

Summing up (4.4) and (4.11), we can conclude that

$$\begin{aligned}&\big \Vert u^{M,\delta }(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}\\&\quad \lesssim \delta ^2\psi _M(2T-2t)\{1+(T-t)^2\Vert h\Vert ^2_{L^\infty (0,T)}+T^{2H}\}+\psi _M(-2t)L^2\\&\quad \lesssim \delta ^2\psi _M(2T-2t)+\psi _M(-2t)L^2. \end{aligned}$$

\(\square \)

Remark 4.2

Particularly, if we choose \(M=\lceil (\frac{4\ln (\frac{L}{\delta })-T}{4T\pi ^2})^{\frac{1}{2}}\rceil \), then

$$\begin{aligned} \big \Vert u^{M,\delta }(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}\lesssim L^{2(1-\frac{t}{T})}\delta ^{2\frac{t}{T}}\rightarrow 0,\,\,\text {as}\,\,\delta \rightarrow 0. \end{aligned}$$

Remark 4.3

For \(H\in (0,\frac{1}{2})\), since the covariance is negatively correlated, the inequality

$$\begin{aligned} {\mathbb {E}}\left[ \Big (\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] \lesssim {\mathbb {E}}\left[ \Big (\int _0^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\right] \end{aligned}$$

may not be true anymore. In detail,

$$\begin{aligned}&{\mathbb {E}}\Big [\Big (\int _0^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\Big ]\\&\quad ={\mathbb {E}}\Big [\Big (\int _0^t\psi _n(s)\mathrm{d}B^H(s)+\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\Big ]\\&\quad ={\mathbb {E}}\Big [\Big (\int _0^t\psi _n(s)\mathrm{d}B^H(s)\Big )^2\Big ]+{\mathbb {E}}\Big [\Big (\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big )^2\Big ]\nonumber \\&\qquad +2{\mathbb {E}}\Big [\int _0^t\psi _n(s)\mathrm{d}B^H(s)\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big ]. \end{aligned}$$

Because  \({\mathbb {E}}\Big [\int _0^t\psi _n(s)\mathrm{d}B^H(s)\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big ]<0\) for \(H\in (0,\frac{1}{2})\), there is no guarantee that

$$\begin{aligned} {\mathbb {E}}\Big [\Big (\int _0^t\psi _n(s)\mathrm{d}B^H(s)\Big )^2\Big ]+2{\mathbb {E}}\Big [\int _0^t\psi _n(s)\mathrm{d}B^H(s)\int _t^T\psi _n(s)\mathrm{d}B^H(s)\Big ]\geqslant 0. \end{aligned}$$

To obtain the error estimation of regularized solution and exact solution for \(H\in (0,1)\), we give another a-prior bound at any time as:

$$\begin{aligned} \Vert u(\cdot ,t)\Vert _{L^2(\Omega ,{\widetilde{H}}^p)}\leqslant L_1. \end{aligned}$$
(4.12)

Then, using Definition 4, we have

$$\begin{aligned}&\big \Vert u^{M}(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega , {\widetilde{L}}^2(D))}\nonumber \\&\quad =\sum _{n>M}\lambda _n^{2p}\lambda _n^{-2p}{\mathbb {E}}|(u(\cdot ,t),e_n)|^2\nonumber \\&\quad \leqslant \lambda _M^{-2p}\Vert u(\cdot ,t)\Vert ^2_{L^2(\Omega , {\widetilde{H}}^p)}\nonumber \\&\quad =\lambda _M^{-2p}L_1^2. \end{aligned}$$
(4.13)

Theorem 4.4

For \(H\in (0,1)\), \(M>0\) is a integer number. Assume that the a-priori bound (4.12) and the noise level (4.1) hold. We have

$$\begin{aligned} \big \Vert u^{M,\delta }(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega ,{\widetilde{L}}^2(D))}\lesssim \psi _M(2T-2t)\delta ^2+\lambda _M^{-2p}L_1^2,\quad \text {for}\quad 0<t<T. \end{aligned}$$

Proof

Combining (4.4) and (4.13), we can easily get the conclusion. \(\square \)

Particularly, if we choose \(M=\lceil (\frac{4\ln (\frac{L_1}{\delta })}{2(T-t)\pi ^2})^{\frac{1}{2}}\rceil \), then

$$\begin{aligned} \big \Vert u^{M,\delta }(\cdot ,t)-u(\cdot ,t)\big \Vert ^2_{L^2(\Omega ,{\widetilde{L}}^2(D))}\lesssim L_1\delta +\left( \frac{2(T-t)}{\ln (\frac{L_1}{\delta })}\right) ^{2p}L_1^2\rightarrow 0,\,\,\text {as}\,\,\delta \rightarrow 0. \end{aligned}$$
Fig. 1
figure 1

The reconstruction results for \(t =0\) from noisy measurement data at T=0.5 for the problem with \(M=1\)

Full size image
Fig. 2
figure 2

The exact and approximated solutions for the problem with \(T=0.8, M=1\), (left): one path, (right): the expectation

Full size image

5 Numerical Experiments

In this section, we make some numerical implementations on our inversion scheme. Since the backward problem is ill-posed, we use the truncated regularization method to obtain the regularization solution by the finial value \(u(x,T,\omega )\), where the \(u(x,T,\omega )\) is given in the direct problem, and we truncate the above series by the first M terms as a regularization. Let \(N_x\) and \(N_t\) be the number of discrete points in the spatial and temporal directions, respectively, and \(x_i=(i-1)h_x,i=1,2,\ldots ,N_x,t_j=(j-1)h_t,j=1,2,\cdots ,N_t\), where \(h_x\) and \(h_t\) are the steps in the spatial direction and time direction, respectively. We solve the direct problem using the following finite difference scheme:

$$\begin{aligned} \frac{u^{j+1}_i-u^j_i}{h_t}+\frac{u^j_{i+1}-u^j_{i-1}}{2h_x}-\frac{u^j_{i+1}-2u^j_i+u^j_{i-1}}{h_x^2}=F(x_i,t_j), \end{aligned}$$

Here, \(F(x_i,t_j)=f(x_i)h(t_j)+\sigma (x_i)\frac{B^H(t_{j+1})-B^H(t_j)}{h_t}\); the initial boundary value condition is discretized as \(u^j_1=0,u^j_{N_x}=0,u^1_i=g(x_i)\). In this paper, we choose \(N_x=101\), \(N_t=2^{15}+1\), \(T=1\) and sample paths \(P=1000\), and some known functions in (2.4) are chosen as

$$\begin{aligned} f(x)=\sin (x)\cos (\pi x/2),\quad \sigma (x)=x(1-x),\quad h(t)=1. \end{aligned}$$

Moreover, the data \(f, \sigma \) and g are assumed to be polluted by a uniformly distributed noise with level \(\delta \). The parameters M, H and T may vary in different experiments.

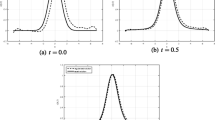
Figure 1 shows the results of the backward problem with different \(T, M, H and \delta \), which tells us that the recovery would be more accurate if \(\delta \geqslant 0\) is smaller. Based on the results, it can be observed that the regularized results are also acceptable for only one path when \(T=0.5\). Of course, this conclusion can be drawn intuitively from Fig. 2.

6 Conclusion

In this paper, we have studied a backward problem for convection–diffusion equation driven by fBm with Hurst index \(H\in (0,1)\). We obtain the regularity of mild solution and discuss the ill-posedness for the backward problem. The truncated regularization method is introduced to approximate the solution of the problem. Under the a-priori assumption, we obtain the convergence estimate in \({\widetilde{L}}^2\) norm. Finally, numerical implementations are presented to show the validity of our theorem analysis. However, for this stochastic backward problem, we are not sure if the uniqueness is true. Hope we can do something about it in future.