1 Introduction

Human immunodeficiency virus (HIV) is a chronic disease which weakens the immune system, leading to increased susceptibility to a wide range of infections and some types of cancer [46]. An important biomarker to measure HIV disease progression is HIV viral load (VL), the number of copies of actively replicating HIV virus in an individual [42]. By the US Health and Human Services guideline, if the number of copies is less than or equal to 200 per milliliter of blood, VL is classified as undetectable; otherwise, it is classified as detectable [14]. To date, there is no cure for HIV but the suppression of VL to undetectable levels improves physical functioning, reduces opportunistic infections, reduces HIV related mortality, and is associated with a substantial decrease in the probability of transmitting HIV to others [6, 10, 15]. Not only is suppressing VL important on an individual level, it also has the potential to decrease HIV incidence rates in a community because of reduced infectivity [10, 13]. Consequently, the focus of care has shifted from survival to improving health outcomes and the success of highly active antiretroviral therapy (ART) to suppress VL to undetectable levels for prolonged periods of time has transformed HIV into a manageable chronic disease [42].

To gain insight into the HIV endemic, survival models of patient VL may be an effective way since traditional regression models are not able to handle censored data directly. Additionally, these models can be used to assess the effect of various factors and treatments on VL suppression. The commonly used form of survival model can be written as

$$\begin{aligned} \lambda (t) = \lambda _{0}(t) e^{x_{i}\beta } \end{aligned}$$

where \(\lambda _{0}(t)\) is the baseline hazard function, \(x_{i}\) is the set of covariates, and \(\beta \) are parameters estimating covariate effects on hazard. In semi-parametric survival models, the regression coefficients are estimated leaving the baseline hazard unspecified. For example, the Cox Proportional Hazards (PH) model [11] introduced the use of the partial-likelihood function to estimate the coefficients without needing to characterize the baseline Hazard Rate. To avoid making distributional assumptions about the baseline hazard, several studies used nonparametric methods to correct for censoring [18, 31, 34, 35]. However, this can also be disadvantageous since assuming an underlying distribution naturally smooths the data so that censoring has less impact on parameter estimates.

While the parametric survival models can be advantageous in many respect, a well-suited parametric distribution for baseline hazard generally ensures more precise estimation of hazard parameters when compared to the semi-parametric counterpart. However, such benefits also come with a very commonly faced challenge for the applied researchers of selecting the appropriate parametric distribution. This gets even more challenging in cases where the data present characteristics, e.g., left censored time-to-events, heavy-tailed event time density, not very frequently studied in related literature. Given the importance of choosing right distribution in a parametric survival model, any guidance on choosing well-fitting parametric distributions can be a useful addition to the related literature helping applied researchers.

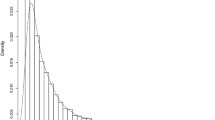
There have been several studies (e.g., [23, 24, 39]) that studied the comparative fits of various distributions to the right-censored and interval-censored lifetime data. However, there are no known recommendations or exploration in the literature on guiding the optimal choice of distribution to use while modeling left-censored time-to-event with heavy-tailed event times. These data features not rare in chronic disease biomarker settings, e.g., HIV VL as discussed in above and characterized further in below (see Fig. 1).

Among the very limited studies in literature analyzing time-to-event of HIV VL suppression, it may be notable that [40] applied a lognormal survival model using a fully parametric approach to take into account the left-censored HIV VL counts. The choice of lognormal distribution was guided by a previous work of [17] based on the estimated lognormal survival distribution function was contained within the 95% confidence interval of nonparametric Kaplan–Meier estimate. Despite [40] presented sensitivity analysis by comparing the lognormal survival model to a univariate mixed model and a Cox PH model, it was not known if any other survival distributions could provide a better fit to the data.

While analyzing left-censored event time data, a further challenge can be the use of the appropriate hazard function for estimation of event risk. The common and widely used estimate of time-to-event risk, Hazard Rate (HR), is appropriate for using with right-censored lifetime data and may be very unstable if used for analyzing left-censored event time risk [43]. A more appropriate choice of estimating left-censored time-to-event risk can be the Reversed Hazard Rate (RHR) [43].

Since its introduction in 1963 [2], the RHR has been used in various applications and several articles [5, 12, 16, 20, 28, 29, 36, 37] studying the properties of the RHR function and devising methodologies based on it to analyze left-censored lifetime data are found in the literature. One recent development is the Parametric Reversed Hazards (PRH) model based on the RHR to be applied to left-censored lifetime data [43]. In this formulation [43], the lifetime random variable was assumed to be distributed as inverted Weibull.

Fig. 1
figure 1

Density of observed and simulated data

Full size image

This current study derives the PRH model for a variety of distributions which may be appropriate for left-censored heavy-tailed data including the Exponential, Log-normal, Inverse Gaussian, Log-logistic, Gompertz–Makeham, Gamma, Generalized Gamma, Inverse Gamma, Generalized Inverse Gamma, Weibull, Inverse Weibull, Generalized Inverse Weibull, Modified Weibull, Flexible Weibull, Power Generalized Weibull, and Marshal–Olkin distributions. Extensive statistical simulations are used to assess the performance of the derived PRH models and compare these to establish a guideline for which distribution/s would “best” fit left-censored, heavy-tailed HIV VL data. We applied the selected best performing model to the South Carolina Enhanced HIV/AIDS Reporting Surveillance System (SC eHARS) data to explain effects of different demographic, social, and treatment factors on patients’ VL transition from detectable-to-undetectable levels. Recommendations from this study may help researchers apply more accurate models for this type of censoring, specifically in HIV VL-related studies where left censoring may be a common occurrence and the data demonstrate considerably uncommon features, e.g., being heavy-tailed.

2 The Parametric Reverse Hazards model

The Parametric Reversed Hazard (PRH) model [43] is a fully parametric model based on the Reversed Hazard Rate (RHR) for the analysis of left-censored data. The Hazard Rate (HR) used for analyzing more common right-censored time-to-event data is defined as the instantaneous rate of an event in an infinitesimal time width, \(\varDelta t\), following an event free time t and expressed mathematically as

$$\begin{aligned} \lambda (t) = \lim _{\varDelta t \rightarrow 0} \frac{P(T \le t + \varDelta t | T \le t)}{\varDelta t} \end{aligned}$$

Unlike the above, RHR of T is the instantaneous rate of the event occurring in an infinitesimal time width, \(\varDelta t\), preceding t, given that the event occurred before time t. It is defined as

$$\begin{aligned} \lambda _r(t) = \lim _{\varDelta t \rightarrow 0} \frac{P(t - \varDelta t \le T | T \le t)}{\varDelta t} \end{aligned}$$

In terms of the distribution function, F(t), and probability density function, f(t), the RHR function can be written as

$$\begin{aligned} \lambda _r(t) = \frac{f(t)}{F(t)} \end{aligned}$$

By letting X be a \(p \times 1\) vector of covariates, we can now define the PRH model as

$$\begin{aligned} \lambda _r(t | X) = \lambda _{r0}(t) g(\beta ; X) \end{aligned}$$

where \(\lambda _{0}(t)\) is the baseline RHR, \(g(\beta ; X)\) is a nonnegative function of X and \(\beta \) (a \(p \times 1\) vector of regression parameters), and \(\lambda (t | X)\) is the RHR of T given the covariates X.

The PRH model can also be expressed in terms of the distribution function as

$$\begin{aligned} F(t | X) = F_{0}(t)^{g(\beta ; X)} \end{aligned}$$

where F(t|X) is the distribution function of T given X and \(F_{0}(t)\) is the baseline distribution function in the absence of covariates.

Suppose that the lifetime random variable T is randomly left-censored by Z. In practice, we may observe the vectors \((Y, \delta , X)\), where \(Y =\) max(T, Z) and \(\delta = I(T = Y)\) with I(.) being the indicator function. The likelihood function can then be written as

$$\begin{aligned} L(\beta , y) = \prod _{i = 1}^{n} f(y_{i} | x_{i})^{\delta _{i}} F(y_{i} | x_{i})^{1 - \delta _{i}} \end{aligned}$$

Using this general notation, we show the derivation assuming Generalized Inverse Weibull as the baseline hazard distribution. See supplementary materials for model derivations for the other baseline hazard distributions.

When the lifetime random variable follows a Generalized Inverse Weibull distribution, the baseline distribution function is given by

$$\begin{aligned} F_{0}(t) = e^{-\gamma \left( \frac{\lambda }{t} \right) ^{\alpha } } , \; \; \; t> 0; \alpha , \gamma , \lambda > 0 \end{aligned}$$

The baseline RHR of T is then obtained as

$$\begin{aligned} \lambda _{0}(t) = \alpha \gamma \lambda ^{\alpha } t^{-(\alpha -1)} \end{aligned}$$

In the presence of the covariates X, we have

$$\begin{aligned} \lambda (t | X)&= \alpha \gamma \lambda ^{\alpha } t^{-(\alpha -1)} e^{x_i \beta } \\ F(t | X)&= \left[ e^{-\gamma \left( \frac{\lambda }{t} \right) ^{\alpha } } \right] ^{\exp (x_{i}\beta )} \\ f(t | X)&= \alpha \gamma \lambda ^{\alpha } t^{-(\alpha -1)} e^{x_i \beta } \left[ e^{-\gamma \left( \frac{\lambda }{t} \right) ^{\alpha } } \right] ^{\exp (x_{i}\beta )} \end{aligned}$$

From these, the likelihood and the log-likelihood functions are obtained as

$$\begin{aligned} L(\alpha , \gamma , \lambda , t) = \prod _{i = 1}^{n} \left[ \alpha \gamma \lambda ^{\alpha } t_{i}^{-(\alpha -1)} e^{x_i \beta } \right] ^{\delta _i} \left[ e^{-\gamma \left( \frac{\lambda }{t_i} \right) ^{\alpha } } \right] ^{\exp (x_{i}\beta )} \\ \begin{aligned} l(\alpha , \gamma , \lambda , t) = \sum _{i = 1}^{n} \delta _{i} x_{i}\beta + \sum _{i = 1}^{n} \delta _{i} \ln \alpha + \sum _{i = 1}^{n} \delta _{i} \ln \gamma + \sum _{i = 1}^{n} \delta _{i} \alpha \ln \lambda \\ - (\alpha - 1)\sum _{i = 1}^{n} \delta _{i} \ln t_i - \sum _{i = 1}^{n} \gamma \left( \frac{\lambda }{t_i} \right) ^{\alpha } e^{x_i \beta } \end{aligned} \end{aligned}$$

Similar derivations for several other distributions including the Exponential, Log-normal, Inverse Gaussian, Log-logistic, Gompertz–Makeham, Gamma, Generalized Gamma, Inverse Gamma, Generalized Inverse Gamma, Weibull, Inverse Weibull, Modified Weibull, Flexible Weibull, Power Generalized Weibull, and Marshal–Olkin distributions are provided in supplementary materials.

3 Simulation Study

We used the SC eHARS HIV VL data, further described in the next section, as a real-life example of such data and simulate data with similar distribution for the time to transit from detectable VL to undetectable VL state after HIV diagnosis. Figure 1 presents the density of time to transition from detectable-to-undetectable VL transition for both observed data and a randomly selected set of simulated data showing similarities in densities. The time to detectable-to-undetectable VL transition data were simulated from a Skewed Normal distribution with location, scale, and shape parameters, respectively, as 5, 30, 50. Different parameters were tested under the Skewed Normal distribution using a trial-and-error approach until the simulated data matched as close as possible to the SC VL data.

To assess the model fits best, we used information criteria including

  1. 1.

    Akaike Information Criterion (AIC) rewards goodness of fit but penalizes the model for increasing the number of estimated parameters:

    $$\begin{aligned} AIC = 2k - 2\ln (L) \end{aligned}$$
  2. 2.

    Bayesian Information Criterion (BIC), which uses a larger penalty than AIC:

    $$\begin{aligned} BIC = k\ln (n) - 2\ln (L) \end{aligned}$$
  3. 3.

    Corrected Akaike Information Criterion (AICC), which corrects the AIC for overfitting of the data in cases where the sample size is relatively small compared to the number of parameters in the model:

    $$\begin{aligned} AICC = AIC + (2k(k+1))/(n-k-1) \end{aligned}$$
  4. 4.

    Hannan–Quinn Information Criterion (HQIC), which is often cited in the literature but, unlike AIC, it is not asymptotically efficient:

    $$\begin{aligned} HQIC = 2k\ln (\ln (n)) - 2\ln (L) \end{aligned}$$
  5. 5.

    Bozdogan’s Consistent Akaike Information Criterion (CAIC), is another adjusted form of AIC which is consistent:

    $$\begin{aligned} CAIC = k(\ln (n)+1) - 2\ln (L) \end{aligned}$$

Where k is the number of parameters to be estimated, L is the maximum value of the likelihood function, and n is the number of observations. The model with the smallest average AIC, BIC, AICC, HQIC, and CAIC value was determined to be the model with the best fit. The simulation studies were conducted using the Statistical Computing Software, R version 3.2.5. The summaries of the simulation results are presented in Tables 1, 2, 3.

Table 1 summarizes the results for the simulated data with a censoring rate of 20%, Table 2 for data with censoring rate of 30%, and Table 3 for data with censoring rate 40%. From these tables, it is clear that the Generalized Inverse Weibull distribution consistently performs the best, having the lowest average AIC, BIC, AICC, HQIC, and CAIC. Following closely behind in performance are the Log-Logistic, Log-Normal, Inverse Gaussian, and Gamma distributions, respectively. This is consistent across all censoring rates and sample sizes. The consistently worst performing distributions are the Modified Weibull, Inverse Weibull, Inverse Gamma, Power Generalized Weibull, and Exponential distributions, respectively.

Table 1 Average summary measures across 5000 simulations from simulation study with censoring rate 20%
Full size table
Table 2 Average summary measures across 5000 simulations from simulation study with censoring rate 30%
Full size table
Table 3 Average summary measures across 5000 simulations from simulation study with censoring rate 40%
Full size table

4 Application to SC eHARS Data

The HIV endemic disproportionately impacts the Southern states in the US in terms of the overall number of people living with HIV/AIDS (PLWHA), and survival rates after diagnosis [33]. SC, like many Southern states, ranks high for poverty, unemployment, and low educational completion which are all characteristics that may promote disease transmission. The number of PLWHA in SC has increased from 12,089 in 2004 to 16,311 in 2014 [38]. Studies on retention in HIV care found that a large proportion of PLWHA in SC failed to remain in care on a regular basis [30, 41]. Given the HIV burden in SC and the need to focus on retention in HIV care within the context of the National HIV/AIDS Strategy goals, it is important to identify factors which suppress VL. Identifying these factors will assist in developing targeted strategies to reduce the HIV burden in SC.

Since January 2004, all health care providers, hospitals, and laboratories in SC are legally mandated to report all CD4 count and VL measurements to the SC Department of Health and Environmental Control (DHEC) [7]. These data are stored in the SC eHARS database along with the patient’s socio-demographic characteristics. The quality rating of the SC eHARS database exceeds the CDC minimum standards of reporting timeliness with 95% of new cases being reported within 6 months of HIV diagnosis and 98% of all HIV cases reported [44]. Our sample consisted of 6,221 residents in SC who were aged \(\ge 13\) years or older; diagnosed or living with HIV infection between January 1, 2005, and December 31, 2013; had detectable VL at the start of the study period; had at least two reported VL values during the study period.

This study applies the best model as determined from the simulation study to left-censored heavy-tailed HIV VL data from South Carolina. The aim of applying the PRH model to this dataset is to explain the risk behavior of transitioning from detectable VL to undetectable VL. Patients with undetectable VL at the beginning of the study were defined as being left-censored. Covariates that were assessed include gender (male or female), race (White, Black, or other), HIV risk exposure group (heterosexual, men who have sex with men, or other), place of residence (rural or urban), age at baseline, initial treatment regimen (single tablet regimen, multiple tablet regimen), and baseline CD4 count (200 or less, 201 to 350, 351 to 500, or more than 500). Note that HIV risk exposure group refers to how the patient was first exposed to HIV with options including heterosexual HIV infected partner, men who have sex with other men, injecting drug user, no identifiable risk, and no risk reported. Results from the PRH model are presented and discussed in the next section.

Of the individuals in our sample, 1703 (27%) had an undetectable VL at the beginning of the observation period, so they were considered as being left-censored (Table 4). Mean age of the sample at baseline was 40.0 years (range = 14.8–81.6). The majority of subjects were male (n = 3657, 58.8%), Black (n = 4966, 79.8%), and lived in an urban county when diagnosed with HIV (n = 4208, 67.6%). The CD4 count at the beginning of the study was less than 200 cells/mm3 for just over one third of the individuals (34.03%). Almost half of the sample had missing treatment regimen (n = 2928, 47.1%).

Table 4 Characteristics of persons living with HIV in South Carolina, 2005-2013
Full size table

The Generalized Inverse Weibull distribution, which was found to be the best performing distribution from the simulation study, is applied to analyze the left-censored SC eHARS data time-to-event data for detectable-to-undetectable VL transition. Table 5 shows the results of the estimated PRH model using a Generalized Inverse Weibull distribution. Information on treatment regimen is a very important variable to use in our model to assess which type of treatment has the most, if any, impact on the transition from detectable-to-undetectable VL. However, this information is missing in almost 50% of the subjects in our sample. Thus, we fit the model without this starting treatment regimen information (Model 1) and then we fit a second model with reduced sample size after including the treatment variable in the model (Model 2). It should be noted that if there was not such a large proportion of missing values in the treatment variable, we would fit only one model, Model 2.

While several covariates have been shown to have an effect on the time-to-event of transitioning from detectable-to-undetectable VL level, the significant change in behavior of some of these covariates comparing the model incorporating the treatment variable compared to the model without this important factor suggests that an interaction may be present between treatment regimen and each of the other covariates. Additional models were run testing for these interactions. The only statistically significant interaction found was between treatment regimen and age, the results of which are shown in Table 6.

Table 5 Estimated Reverse Hazard Rates (HR) using Generalized Inverse Weibull Reverse Hazard model (without interactions) of SC adult HIV patients
Full size table
Table 6 Estimated Reverse Hazard Rates using Generalized Inverse Weibull Reverse Hazard model (with interactions) of SC adult HIV patients
Full size table

The final model is shown in Table 6. Males are 1.11 times more likely to reach undetectable levels faster than their female counterparts (95% CI 1.00, 1.24). White individuals are 1.53 times more likely to reach undetectable levels faster than Black individuals (95% CI 1.40, 1.67). Other races are 0.86 times less likely to reach undetectable levels faster than Black individuals, though this finding is not significant (95% CI 0.63, 1.16). Risk of exposure, place of residence (rural vs urban), and CD4 count do not seem to have any statistically significant impact on the time taken to transition from detectable-to-undetectable VL levels. The significant interaction between treatment regimen and age highlights that older people living with HIV/AIDS are 0.97 times less likely to reach undetectable levels faster than their younger counterparts (95% CI 0.97, 0.98).

5 Discussion

The current study derived several extensions of the PRH model and conducted extensive simulation studies to evaluate the usefulness of parametric regression models based on the Reversed Hazard Rate for analyzing left-censored heavy-tailed HIV viral load time-to-event data. Simulation studies suggested the best distribution to use under the PRH model is the Generalized Inverse Weibull distribution followed in order of performance by Log-Logistic, Log-Normal, Inverse Gaussian, and Gamma distributions.

Application of this best performing model on the SC eHARS data revealed important factors on the time to transition from detectable-to-undetectable viral load levels. Males were found to be more likely to reach undetectable levels faster than females. This trend is also evident in several recent studies [4, 7, 25]. A possible reason for this disparity may be attributed to the higher rates of treatment adherence among males compared to females. Though some studies did not find an association between gender and treatment adherence, a meta-analysis [22] of 207 studies concluded that males adhere more to ART than females.

White individuals are more likely to reach undetectable levels faster than Black individuals. This is supported by several studies which show that Black individuals are disproportionately affected by HIV/AIDS as they tend to have poorer access to health care, are less likely to receive treatment, less likely to adhere to treatment, and less likely to survive HIV/AIDS [4, 7,8,9, 19, 27, 32].

This study did not find any statistically significant association between place of residence and time to transition from detectable-to-undetectable VL levels. This may seem in contrary to the expectation that individuals who live in urban areas would be more likely to reach undetectable levels faster than those who live in rural areas due to the typically increased access to health care and higher range of specialists available to people living with HIV/AIDS in urban areas [44, 45]. However, other studies (e.g.,[9]) have also reported analyses supporting the current study reporting no significant effect of place of residence on detectable-to-undetectable VL transition.

Finally, the interaction between drug regimen and age highlights that older people who are on a multiple treatment regimen are likely to reach undetectable levels slower than their younger counterparts. There are mixed findings on this in the existing literature. Young people with HIV tend to have delayed diagnosis and thus higher VL at baseline. One study [7] suggests that this along with underutilization of health care due to HIV-related stigma explains their finding that younger people with HIV reach undetectable levels slower than their older counterparts. A possible explanation of our result may be that older people are not as adherent to treatment [22] or perhaps they have a co-existing morbidity which effects the rate at which they reach undetectable levels.

There are several limitations of the SC eHARS database. Data on VL and CD4 count measurements were not available for those who dropped out of medical care after initial diagnosis—this includes those who passed away, moved to a different state, etc. Additionally, persons living with HIV/AIDS who have not been diagnosed were not captured in this database. The database also does not include information on morbidities which may be co-existing with HIV/AIDS which can impact the effect of drug regimens, especially in older people. Since the interaction between age and drug regimen is found to be statistically significant to have an impact on the VL transition, co-existing conditions warrant further exploration. These limitations may have resulted in not finding an association with factors we would expect based on prior research.

Regardless of these limitations, the application to the SC eHARS database provides important information on the trajectories of VL in SC over time. The results obtained in this study can be used to direct researchers in applying more accurate models when studying similar databases. We recommend that the Generalized Inverse Weibull PRH model be used for analyses involving skewed, left-censored heavy-tailed HIV VL data.