1 Introduction

It is well known that one can rarely compute an exact solution of the boundary-value problem describing a fluid flow. This can be done only if we start with very simplified mathematical models and consider the flow domains with ideal geometries, i.e., with no distortions. However, in real-life applications, the domain boundary can contain small irregularities such as rugosities and dents, being far from the ideal one. These kinds of problems are usually very challenging from the mathematical point of view and are commonly treated numerically (see, e.g., [11]). The main reason lies in the fact that the introduction of the small parameter in the boundary perturbation forces us to perform very tedious change of variables. In view of that, one cannot find many analytical results on the subject throughout the literature, both engineering and mathematical.

Many different empirical laws have been employed in order to describe the filtration of a fluid through a porous medium. One of the more widely used is the Darcy–Brinkman law (see, e.g., [2, 4, 15, 24]), representing a natural extension of the Darcy law (see [5]) which is not capable of taking into account the classical no-slip boundary condition on the walls of the domain. For this reason, the Darcy–Brinkman law is more suitable for numerical simulations of fluid flows through a porous medium.

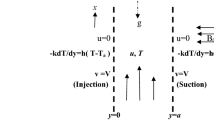
In this paper, we consider a magnetohydrodynamic (MHD) flow through a channel filled with a porous medium. The MHD flow of a viscous incompressible conducting fluid through a porous medium naturally arises both in natural settings (e.g., plasma dynamics and astrophysics), as well as in the engineering applications (e.g., nuclear engineering and metallurgy). For that reason, MHD flow problems have been a subject of investigation over a long period of time, starting from the pioneering work of Hartmann [10] to more recent papers that influenced our work (see [6, 9, 12, 13, 23, 25, 27,28,29]). In the present paper, we assume that the porous medium flow in the channel is under the action of the transverse magnetic field, leading to the following boundary-value problem:

$$\begin{aligned} \begin{aligned}&\mu _{e} \Delta \mathbf {u}^{*}-\frac{\mu }{K}\mathbf {u}^{*}-\sigma B_{0}^2 {u}_{x^{*}}^{*} \mathbf {e}_{1}=\nabla p^{*},\\&\text{ div } \mathbf {u}^{*}=\mathbf {0} \text{ in }\ \Omega _{\varepsilon }^{*}. \end{aligned} \end{aligned}$$
(1.1)

Here, \(\mathbf {u}^{*}=({u}_{x^{*}}^{*},{u}_{y^{*}}^{*})\) and \(p^{*}\) denote the (dimensional) filter velocity and pressure. Furthermore, \(\mu \) is the physical viscosity of the fluid, \(\mu _{e}\) denotes the effective viscosity for the Brinkman term, K stands for the permeability of the porous medium, \(\sigma \) is the conductivity of the fluid, while \(B_{0}\) represents the uniform magnetic field. Hereinafter, we denote by \((\mathbf {e}_1,\mathbf {e}_2)\) the standard Cartesian basis. Since we are dealing with a second-order PDE for the velocity, Eq. (1.1)\(_{1}\) can handle the presence of a boundary on which the no-slip condition is imposed. In this way, the above system is capable of successfully describing numerous situations naturally arising in the applications.

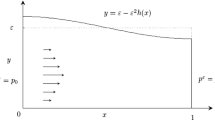
The goal of this work is to investigate the influence of the slightly perturbed channel wall and the MHD effects on the effective flow. We start from a rectangular domain \((0,H)^2\) and apply a small perturbation of magnitude \(\varepsilon \) on the upper part of the boundary. In view of that, the considered domain has the following form:

$$\begin{aligned} \Omega _{\varepsilon }^{*}=\Big \{ (x^{*},y^{*}) \in \mathbb {R}^2 :\ 0<x^{*}<H,\ 0<y^{*}<H-\lambda h\Big ( \frac{x^{*}}{H}\Big ) \Big \}. \end{aligned}$$

Let \(\varepsilon =\frac{\lambda }{H} \ll 1\) be a small positive parameter (\(0 < \varepsilon \ll 1\)), while h is assumed to be an arbitrary smooth function of \(\mathcal {O}(1)\) magnitude. For the purpose of our analysis, we need to work in a non-dimensional setting. Thus, we normalize the physical variables by H and the velocity by \(\frac{GH^2}{\mu _{e}}\), where G denotes the pressure gradient. In other words, we introduce the new variables:

$$\begin{aligned} x=\frac{x^{*}}{H},\ y=\frac{y^{*}}{H},\ u=\frac{u^{*}}{\frac{GH^2}{\mu _{e}}}. \end{aligned}$$

As a consequence, the dimensionless form of the system (1.1) reads as follows:

$$\begin{aligned} \begin{aligned}&\Delta \mathbf {u}-k^2 \mathbf {u}-M^2 u_x \mathbf {e}_{1}=\nabla p, \\&\text{ div } \mathbf {u}=\mathbf {0} \text{ in }\ \Omega _{\varepsilon }, \end{aligned} \end{aligned}$$

now posed in the domain (see Fig. 1)

$$\begin{aligned} \Omega _{\varepsilon }=\{ (x,y) \in \mathbb {R}^2 :\ 0<x<1,\ 0<y<1-\varepsilon h(x) \}. \end{aligned}$$

Here, we have the non-dimensional parameter \(k=H\sqrt{\frac{\mu }{\mu _{e}K}}\) characterizing the porous medium and the Hartmann number \(M=HB_{0}\sqrt{\frac{\sigma }{\mu _{e}}}\) taking into account the MHD effects.

Fig. 1
figure 1

The domain after non-dimensionalization

Full size image

The paper is organized as follows. In Sect. 2, we present the problem settings, namely the perturbed domain under consideration and the governing system of equations for the MHD flow with the corresponding boundary conditions. In Sect. 3, assuming that \(h<0\) on \(\langle 0,1 \rangle \), we derive the effective boundary conditions at the upper boundary of the domain by using the Taylor series approach with respect to y. We then seek the solution of the problem using the method of formal asymptotic expansions and compute the first two terms in the expansion. Since the terms are given as explicit expressions, we easily verify that they take into account the effects of the boundary perturbation as well as the effects of the imposed magnetic field through the presence of the boundary perturbation function h and the Hartmann number M, respectively. The nonlocal effects of the boundary perturbation depend on the value of the Hartmann number and this is visually presented in Sect. 3.3. Finally, in Sect. 4, we provide a rigorous mathematical justification of the formally derived model from Sect. 3. In order to accomplish that, we apply the idea originally proposed in [17]. We first prove that the solution obtained in Sect. 3 is asymptotically the same as the one obtained for a general function h. The model is then justified in a classical way, via error estimates in suitable norms for the difference between the original solution and the obtained asymptotic approximation.

We conclude the Introduction by providing more bibliographic remarks on the subject. The effects of periodically corrugated walls on the fluid flow (without porous structure) have been investigated in [1, 3, 14, 22, 26]. Fluid flow through domain \(\Omega _{\varepsilon }\) with small (not necessarily periodic) boundary perturbation has been addressed in [16,17,18,19,20], for different regimes of the flow. Finally, the inertial effects on the MHD flow within the channel with periodically corrugated walls have been studied in [21].

2 Problem Settings

As discussed in Sect. 1, we consider the following domain:

$$\begin{aligned} \Omega _{\varepsilon }=\{ (x,y) \in \mathbb {R}^2 :\ 0<x<1,\ 0<y<1-\varepsilon h(x) \}, \end{aligned}$$

where \(\varepsilon >0\) is a small parameter and \(h \in C^{\infty }(0,1)\) an arbitrary smooth boundary perturbation function. The MHD flow in the domain with the perturbed boundary \(\Omega _{\varepsilon }\) is modeled by the (dimensionless) MHD extension of the Darcy–Brinkman equation given by the following system of equations:

$$\begin{aligned} \begin{aligned}&\Delta \mathbf {u}^{\varepsilon }-k^2 \mathbf {u}^{\varepsilon }-M^2 u_x^{\varepsilon } \mathbf {e}_{1}=\nabla p^{\varepsilon }, \\& \text{ div } \mathbf {u}^{\varepsilon }=\mathbf {0} \text{ in }\ \Omega _{\varepsilon }, \end{aligned} \end{aligned}$$
(2.1)

where \(\mathbf {u}^{\varepsilon }=(u_{x}^{\varepsilon },u_{y}^{\varepsilon })\) is the unknown fluid velocity and \(p^{\varepsilon }\) the pressure, while \(k=H\sqrt{\frac{\mu }{\mu _{e}K}}\) and \(M=HB_{0}\sqrt{\frac{\sigma }{\mu _{e}}}\) are the non-dimensional parameters.

In order to complete the problem, we need to add suitable boundary conditions. We impose the standard no-slip boundary conditions on the upper and lower boundary and prescribe the (dimensionless) values of pressures \(p_{0},p_{1}\) (\(p_{1}<p_{0}\)) on the lateral ends of the channel. More precisely:

$$\begin{aligned} \begin{aligned}&\mathbf {u}^{\varepsilon }=\mathbf {0}, \text{ for }\ y=0,\ y=1-\varepsilon h, \\&u_{y}^{\varepsilon }=0, \text{ for }\ x=0,1, \\&p^{\varepsilon }=p_{i}, \text{ for }\ x=i \in \{ 0,1 \}. \end{aligned} \end{aligned}$$
(2.2)

The well-posedness of the problem (2.1)–(2.2) can be established following the standard arguments, see, e.g., [8].

In this paper, we will focus on investigating the asymptotic behavior of the flow described by the problem (2.1)–(2.2), as \(\varepsilon \rightarrow 0\).

3 Asymptotic Analysis

In the following, we follow the approach provided in [19].

In this section, we will derive the effective boundary conditions on the perturbed upper part of the boundary. In order to simplify the notation, we will assume that the boundary perturbation function h is negative, i.e., that \(h<0\) on \(\langle 0,1 \rangle \). This is assumed so that our solution \((\mathbf {u}^{\varepsilon },p^{\varepsilon })\) of (2.1)–(2.2) is defined on the rectangle denoted by \(\Omega =\{ (x,y)\in \mathbb {R}^{2} :\ 0<x<1,\ 0<y<1 \} \subset \Omega ^{\varepsilon }\) and we can directly use the formal Taylor series approach. More precisely, we will expand the velocity \(\mathbf {u}^{\varepsilon }\) with respect to y near the upper boundary \(y=1\). It is important to emphasize at this point that the derived results are valid for a general function h and this can be rigorously justified by proving that the obtained asymptotic approximation in this section is asymptotically the same as the one obtained with no constraints on the boundary function h (see Sect. 4.1).

We formally expand in the following way:

$$\begin{aligned} \mathbf {u}^{\varepsilon }(x,y)=\sum _{j=0}^{\infty } \frac{1}{j!} \frac{\partial ^j \mathbf {u}^{\varepsilon }}{\partial y^j}(x,1)(y-1)^{j}. \end{aligned}$$

We deduce from (2.2)\(_{1}\) the following:

$$\begin{aligned} \mathbf {0}=\mathbf {u}^{\varepsilon }(x,1-\varepsilon h)=\mathbf {u}^{\varepsilon }(x,1)-\varepsilon \frac{\partial \mathbf {u}^{\varepsilon }}{\partial y}(x,1)h+\frac{\varepsilon ^2}{2}\frac{\partial ^2 \mathbf {u}^{\varepsilon }}{\partial y^2}(x,1)h^2-\dots . \end{aligned}$$
(3.1)

We seek the solution of the governing problem (2.1)–(2.2) in the form of a power series in terms of the small parameter \(\varepsilon \):

$$\begin{aligned} \begin{aligned} \mathbf {u}^{\varepsilon }(x,y)&=\mathbf {V}^{0}(x,y)+\varepsilon \mathbf {V}^{1}(x,y)+\varepsilon ^2 \mathbf {V}^{2}(x,y)+\dots , \\ p^{\varepsilon }(x,y)&=Q^{0}(x,y)+\varepsilon Q^{1}(x,y)+\varepsilon ^2 Q^{2}(x,y)+\dots . \end{aligned} \end{aligned}$$
(3.2)

In order to derive the boundary conditions at \(y=1\), we substitute (3.2) into (3.1) and obtain the following identity:

$$\begin{aligned} \begin{aligned} \mathbf {0}=&\mathbf {V}^{0}(x,1)+\varepsilon \Big ( \mathbf {V}^{1}(x,1)-h \frac{\partial \mathbf {V}^{0}}{\partial y}(x,1) \Big ) \\&+\varepsilon ^2 \Big ( \mathbf {V}^{2}(x,1)-h \frac{\partial \mathbf {V}^{1}}{\partial y}(x,1)+\frac{h^2}{2}\frac{\partial ^2 \mathbf {V}^{0}}{\partial y}(x,1) \Big )+\dots . \end{aligned} \end{aligned}$$

We thus obtain the following boundary conditions:

$$\begin{aligned} \mathbf {V}^{0}(x,1)=\mathbf {0}, \mathbf {V}^{1}(x,1)=h(x) \frac{\partial \mathbf {V}^{0}}{\partial y}(x,1). \end{aligned}$$

The divergence-free condition is given by:

$$\begin{aligned} \text{ div }\mathbf {V}^{0}=\frac{\partial V_{x}^{0}}{\partial x}+\frac{\partial V_{y}^{0}}{\partial y}=0, \end{aligned}$$

and we obtain the following at \(y=1\):

$$\begin{aligned} \frac{\partial V_{x}^{0}}{\partial x}(x,1)+\frac{\partial V_{y}^{0}}{\partial y}(x,1)=0. \end{aligned}$$

Since \(\frac{\partial V_{x}^{0}}{\partial x}(x,1)=0\), we now obtain that \(\frac{\partial V_{y}^{0}}{\partial y}(x,1)=0\) and conclude:

$$\begin{aligned} \begin{aligned}&V_{x}^{0}(x,1)=0, V_{y}^{0}(x,1)=0, \\&V_{x}^{1}(x,1)=h(x)\frac{\partial V_{x}^{0}}{\partial y}(x,1) V_{y}^{1}(x,1)=0. \end{aligned} \end{aligned}$$

3.1 Zero-Order Approximation

Substituting the asymptotic expansions (3.2) into the system of Eq. (2.1) and taking into account the boundary conditions, we obtain the following problem posed in the \(\varepsilon \)-independent domain \(\Omega \):

$$\begin{aligned} \begin{aligned}&1:\Delta \mathbf {V}^{0}-k^2 \mathbf {V}^{0}-M^2 V_x^{0} \mathbf {e}_{1}=\nabla Q^{0} \text{ in }\ \Omega ,\\&1 :\text{ div } \mathbf {V}^{0}=0 \text{ in }\ \Omega ,\\&1 :\mathbf {V}^{0}(x,0)=\mathbf {0}, \mathbf {V}^{0}(x,1)=\mathbf {0},\\&1 :\ V_{y}^{0}(0,y)=0, V_{y}^{0}(1,y)=0, Q^{0}(0,y)=p_{0}, Q^{1}(1,y)=p_{1}. \end{aligned} \end{aligned}$$
(3.3)

The solution of the problem (3.3) is given in the following form:

$$\begin{aligned} \mathbf {V}^{0}=\mathbf {V}^{0}(y)=V_{x}^{0}(y) \mathbf {e}_{1}, Q^{0}=Q^{0}(x). \end{aligned}$$
(3.4)

Due to the pressure boundary conditions (3.3)\(_{4}\), \(Q^{0}\) is given in the following form:

$$\begin{aligned} Q^{0}(x)=p_{0}+(p_{1}-p_{0})x. \end{aligned}$$
(3.5)

Taking into account (3.4)–(3.5), we obtain from (3.3) the following:

$$\begin{aligned} \frac{\partial ^2 V_{x}^{0}}{\partial y^2}-k^2 V_{x}^{0}-M^2 V_{x}^{0}=p_{1}-p_{0}, \end{aligned}$$

leading to

$$\begin{aligned} \frac{\partial ^2 V_{x}^{0}}{\partial y^2}-(k^2+M^2)V_{x}^{0}=p_{1}-p_{0}. \end{aligned}$$

The zero-order velocity approximation \(V_{x}^{0}\) is thus given in the following form:

$$\begin{aligned} V_{x}^{0}(y)= & {} \frac{p_{1}-p_{0}}{k^2+M^2}\left( \frac{1-\cosh \left( \sqrt{k^2+M^2}\right) }{\sinh \left( \sqrt{k^2+M^2}\right) } \sinh \left( y \sqrt{k^2+M^2}\right) +\cosh \left( y \sqrt{k^2+M^2}\right) -1\right) .\nonumber \\ \end{aligned}$$
(3.6)

It is important to emphasize at this point that the zero-order approximation of the velocity given by (3.6) contains the effects of the imposed magnetic field appearing through the presence of the Hartmann number M. However, we do not observe any effects of the boundary perturbation h, and thus we need to continue our computation by looking at the next-order term in the expansion.

3.2 First-Order Corrector

Let us now compute the first-order velocity and pressure corrector \((\mathbf {V}^{1},Q^{1})\). We obtain:

$$\begin{aligned} \begin{aligned}&\varepsilon : \Delta \mathbf {V}^{1}-k^2 \mathbf {V}^{1}-M^2 V_x^{1} \mathbf {e}_{1}=\nabla Q^{1} \text{ in }\ \Omega , \\&\varepsilon : \text{ div } \mathbf {V}^{1}=0, \\&\varepsilon : \mathbf {V}^{1}(x,0)=\mathbf {0}, V_{x}^{1}(x,1)=h(x) \frac{\partial V_{x}^{0}}{\partial y}(x,1), V_{y}^{1}(x,1)=0, \\&\varepsilon :\ V_{y}^{1}(0,y)=0, V_{y}^{1}(1,y)=0, Q^{1}(0,y)=0, Q^{1}(1,y)=0. \end{aligned} \end{aligned}$$
(3.7)

We expand the unknown functions in the form of the trigonometric Fourier series:

$$\begin{aligned} \begin{aligned}&V_{x}^{1}=\sum _{j=0}^{\infty } a_{j}(y)\cos (j \pi x), \\&V_{y}^{1}=\sum _{j=1}^{\infty } b_{j}(y)\sin (j \pi x), \\&Q^{1}=\sum _{j=1}^{\infty } c_{j}(y) \sin (j \pi x). \end{aligned} \end{aligned}$$
(3.8)

Furthermore, we expand the given boundary function h in the following way:

$$\begin{aligned} h(x)=\frac{h_{0}}{2}+\sum _{j=1}^{\infty } h_{j}\cos ( j \pi x), h_{j}=2 \int _{0}^{1} h(t) \cos (j \pi t)dt. \end{aligned}$$
(3.9)

It is important to notice at this point that the expansions (3.8) automatically satisfy the boundary conditions (3.7)\(_{4}\). We now deduce from the boundary conditions (3.7)\(_{3}\) the following:

$$\begin{aligned} \begin{aligned}&0=V_{x}^{1}(x,0) \Rightarrow a_{j}(0)=0,\ j \ge 0, \\&0=V_{y}^{1}(x,0) \Rightarrow b_{j}(0)=0,\ j \ge 1, \\&0=V_{y}^{1}(x,1) \Rightarrow b_{j}(1)=0,\ j \ge 1. \end{aligned} \end{aligned}$$
(3.10)

The condition for \(V_{x}^{1}\) at \(y=1\) reads:

$$\begin{aligned} \begin{aligned}&V_{x}^{1}(x,1)=h(x) \frac{\partial V_{x}^{0}}{\partial y}(1), \end{aligned} \end{aligned}$$

leading to:

$$\begin{aligned} \sum _{j=0}^{\infty } a_{j}(1)\cos (j \pi x)=\frac{h_{0}}{2}\frac{\partial V_{x}^{0}}{\partial y}(1)+\sum _{j=1}^{\infty } h_{j} \cos (j \pi x) \frac{\partial V_{x}^{0}}{\partial y}(1), \end{aligned}$$

and we obtain:

$$\begin{aligned} a_{0}(1)=\frac{h_{0}}{2}\frac{\partial V_{x}^{0}}{\partial y}(1), a_{j}(1)=h_{j}\frac{\partial V_{x}^{0}}{\partial y}(1), j \ge 1. \end{aligned}$$
(3.11)

It is important to note that there holds:

$$\begin{aligned} \frac{\partial V_{x}^{0}}{\partial y}(1)=\frac{p_{1}-p_{0}}{\sqrt{k^2+M^2}}\left( \frac{1-\cosh \left( \sqrt{k^2+M^2}\right) }{\sinh \left( \sqrt{k^2+M^2}\right) }\cosh \left( \sqrt{k^2+M^2}\right) +\sinh \left( \sqrt{k^2+M^2}\right) \right) . \end{aligned}$$
(3.12)

Now, plugging (3.8) into the problem (3.7) satisfied by \((\mathbf {V}^{1},Q^{1})\), we obtain:

$$\begin{aligned}&-\sum _{j=0}^{\infty } a_{j}(y)(j\pi )^2 \cos (j\pi x)+\sum _{j=0}^{\infty } a_{j}''(y)\cos (j \pi x)-\left( k^2+M^2\right) \sum _{j=0}^{\infty }a_{j}(y)\cos (j \pi x)\nonumber \\&\quad =\sum _{j=1}^{\infty } c_{j}(y) (j\pi ) \cos ( j \pi x),\nonumber \\&\quad -\sum _{j=1}^{\infty } b_{j}(y) (j\pi )^2 \sin (j\pi x)+\sum _{j=1}^{\infty } b_{j}''(y)\sin (j\pi x)-k^2 \sum _{j=1}^{\infty } b_{j}(y) \sin (j \pi x)\nonumber \\&\quad =\sum _{j=1}^{\infty } c_{j}'(y)\sin (j\pi x),\nonumber \\&\quad -\sum _{j=0}^{\infty } a_{j}(y)(j\pi )\sin (j\pi x)+\sum _{j=1}^{\infty } b_{j}'(y) \sin (j \pi x)=0. \end{aligned}$$
(3.13)

We now obtain from (3.13) the following identities:

$$\begin{aligned} \begin{aligned}&a_{0}''-(k^2+M^2)a_{0}=0, \\&a_{j}''-j^2\pi ^2 a_{j}-\left( k^2+M^2\right) a_{j}=j \pi c_{j},\ j \ge 1,\\&b_{j}''-j^2\pi ^2 b_{j}-k^2 b_{j}=c_{j}',\ j \ge 1,\\&-j \pi a_{j}+b_{j}'=0,\ j \ge 1. \end{aligned} \end{aligned}$$
(3.14)

We directly deduce from (3.14)\(_{1}\):

$$\begin{aligned} a_{0}(y)=A \cosh \left( \sqrt{k^2+M^2}y\right) +B \sinh \left( \sqrt{k^2+M^2}y\right) . \end{aligned}$$

Taking into account the boundary conditions (3.10)\(_{1}\) and (3.11)–(3.12), we obtain:

$$\begin{aligned} a_{0}(y)=\frac{h_{0}}{2}\frac{p_{1}-p_{0}}{\sqrt{k^2+M^2}}\frac{\cosh \left( \sqrt{k^2+M^2}\right) -1}{\sinh ^2\left( \sqrt{k^2+M^2}\right) }\sinh \left( \sqrt{k^2+M^2}y\right) . \end{aligned}$$

We now obtain from (3.14)\(_{4}\) the following:

$$\begin{aligned} a_{j}=\frac{1}{j\pi }b_{j}', j \ge 1. \end{aligned}$$
(3.15)

From (3.15) and (3.14)\(_{2}\), we get:

$$\begin{aligned} \frac{1}{j\pi }b_{j}'''-j^2\pi ^2 \frac{1}{j\pi } b_{j}'-\left( k^2+M^2\right) \frac{1}{j\pi }b_{j}'=j\pi c_{j}, j \ge 1, \end{aligned}$$

from which we directly obtain:

$$\begin{aligned} c_{j}=\frac{1}{j^2\pi ^2}b_{j}^{'''}-b_{j}'-\left( k^2+M^2\right) \frac{1}{j^2\pi ^2}b_{j}'. \end{aligned}$$
(3.16)

Now, from (3.16) and (3.14)\(_{3}\), we have:

$$\begin{aligned} b_{j}''-j^2 \pi ^2 b_{j}-k^2 b_{j}=\frac{1}{j^2 \pi ^2}b_{j}^{(4)}-b_{j}''-\frac{1}{j^2\pi ^2}\left( k^2+M^2\right) b_{j}'', \end{aligned}$$

which can be rewritten in the following way:

$$\begin{aligned} b_{j}^{(4)}-2j^2 \pi ^2 b_{j}''-\left( k^2+M^2\right) b_{j}''+\left( j^4\pi ^4+k^2j^2\pi ^2\right) b_{j}=0. \end{aligned}$$
(3.17)

The solution of (3.17) is given in the following form:

$$\begin{aligned} b_{j}(y)=C_{j}\sinh (\lambda _{j}y)+D_{j}\cosh (\lambda _{j}y)+E_{j}\sinh (\mu _{j}y)+F_{j}\cosh (\mu _{j}y), \end{aligned}$$
(3.18)

where

$$\begin{aligned} \begin{aligned} \lambda _{j}&=\frac{\sqrt{-\sqrt{4\pi ^2j^2M^2+k^4+2k^2M^2+M^4}+2\pi ^2j^2+k^2+M^2}}{\sqrt{2}}, \\ \mu _{j}&=\frac{\sqrt{\sqrt{4\pi ^2j^2M^2+k^4+2k^2M^2+M^4}+2\pi ^2j^2+k^2+M^2}}{\sqrt{2}}. \end{aligned} \end{aligned}$$

We now obtain from the boundary conditions (3.10)\(_{2}\) and (3.10)\(_{3}\) the following:

$$\begin{aligned} \begin{aligned}&D_{j}+F_{j}=0, \\&C_{j}\sinh (\lambda _{j})+D_{j}\cosh (\lambda _{j})+E_{j}\sinh (\mu _{j})+F_{j}\cosh (\mu _{j})=0. \end{aligned} \end{aligned}$$
(3.19)

From (3.15), we now have:

$$\begin{aligned} a_{j}= & {} \frac{C_{j}\lambda _{j}}{j\pi }\cosh (\lambda _{j}y)+\frac{D_{j}\lambda _{j}}{j\pi }\sinh (\lambda _{j}y)\nonumber \\&+\frac{E_{j}\mu _{j}}{j\pi }\cosh (\mu _{j}y)+\frac{F_{j}\mu _{j}}{j\pi }\sinh (\mu _{j}y). \end{aligned}$$
(3.20)

Taking into account the boundary conditions (3.10)\(_{1}\) and (3.11), we obtain:

$$\begin{aligned} \begin{aligned}&C_{j}\lambda _{j}+E_{j}\mu _{j}=0, \\&C_{j}\lambda _{j}\cosh (\lambda _{j})+D_{j}\lambda _{j}\sinh (\lambda _{j})+E_{j}\mu _{j}\cosh (\mu _{j})+F_{j}\mu _{j}\sinh (\mu _{j})\\&\quad =j\pi h_{j}\frac{\partial V_{x}^{0}}{\partial y}(1). \end{aligned} \end{aligned}$$
(3.21)

We now obtain from (3.19) and (3.21):

$$\begin{aligned} C_{j}&=\frac{\begin{array}{ll} &{}j \pi h_{j} \frac{p_{1}-p_{0}}{k^2+M^2}\left( \frac{1-\cosh \left( \sqrt{k^2+M^2}\right) }{\sinh \left( \sqrt{k^2+M^2}\right) }\cosh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}+\sinh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}\right) \\ &{}\quad \times \frac{\mu _{j}\cosh (\mu _{j})-\mu _{j}\cosh (\lambda _{j})}{\mu _{j}\sinh (\lambda _{j})-\lambda _{j}\sinh (\mu _{j})} \end{array}}{\lambda _{j}\sinh (\lambda _{j})-\mu _{j}\sinh (\mu _{j})-\lambda _{j}\mu _{j} \frac{\left( \cosh (\mu _{j})-\cosh (\lambda _{j})\right) ^2}{\mu _{j}\sinh (\lambda _{j})-\lambda _{j}\sinh (\mu _{j})}}, \nonumber \\ D_{j}&=\frac{j \pi h_{j} \frac{p_{1}-p_{0}}{k^2+M^2}\left( \frac{1-\cosh \left( \sqrt{k^2+M^2}\right) }{\sinh \left( \sqrt{k^2+M^2}\right) }\cosh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}+\sinh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}\right) }{\lambda _{j}\sinh (\lambda _{j})-\mu _{j}\sinh (\mu _{j})-\lambda _{j}\mu _{j} \frac{\left( \cosh (\mu _{j})-\cosh (\lambda _{j})\right) ^2}{\mu _{j}\sinh (\lambda _{j})-\lambda _{j}\sinh (\mu _{j})}}, \nonumber \\ E_{j}&=-\frac{\lambda _{j}}{\mu _{j}}\frac{\begin{array}{ll} &{}j \pi h_{j} \frac{p_{1}-p_{0}}{k^2+M^2}\left( \frac{1-\cosh \left( \sqrt{k^2+M^2}\right) }{\sinh \left( \sqrt{k^2+M^2}\right) }\cosh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}+\sinh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}\right) \\ &{}\quad \times \frac{\mu _{j}\cosh (\mu _{j})-\mu _{j}\cosh (\lambda _{j})}{\mu _{j}\sinh (\lambda _{j})-\lambda _{j}\sinh (\mu _{j})} \end{array}}{\lambda _{j}\sinh (\lambda _{j})-\mu _{j}\sinh (\mu _{j})-\lambda _{j}\mu _{j} \frac{\left( \cosh (\mu _{j})-\cosh (\lambda _{j})\right) ^2}{\mu _{j}\sinh (\lambda _{j})-\lambda _{j}\sinh (\mu _{j})}}, \nonumber \\ F_{j}&=-\frac{j \pi h_{j} \frac{p_{1}-p_{0}}{k^2+M^2}\left( \frac{1-\cosh \left( \sqrt{k^2+M^2}\right) }{\sinh \left( \sqrt{k^2+M^2}\right) }\cosh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}+\sinh \left( \sqrt{k^2+M^2}\right) \sqrt{k^2+M^2}\right) }{\lambda _{j}\sinh (\lambda _{j})-\mu _{j}\sinh (\mu _{j})-\lambda _{j}\mu _{j} \frac{\left( \cosh (\mu _{j})-\cosh (\lambda _{j})\right) ^2}{\mu _{j}\sinh (\lambda _{j})-\lambda _{j}\sinh (\mu _{j})}}. \end{aligned}$$
(3.22)

Finally, we obtain the expression for \(c_{j}\) from (3.16) and (3.18):

$$\begin{aligned} \begin{aligned} c_{j}&=\Big (\frac{C_{j}\lambda _{j}^3}{j^2\pi ^2}-C_{j}\lambda _{j} -\frac{k^2+M^2}{j^2\pi ^2}C_{j}\lambda _{j}\Big )\cosh (\lambda _{j}y)\\&\quad +\Big (\frac{D_{j}\lambda _{j}^3}{j^2\pi ^2}-D_{j}\lambda _{j} -\frac{k^2+M^2}{j^2\pi ^2}D_{j}\lambda _{j}\Big )\sinh (\lambda _{j}y)\\&\quad +\Big (\frac{E_{j}\mu _{j}^{3}}{j^2 \pi ^2}-E_{j}\mu _{j} -\frac{k^2+M^2}{j^2\pi ^2}E_{j}\mu _{j}\Big )\cosh (\mu _{j}y)\\&\quad +\Big (\frac{F_{j}\mu _{j}^3}{j^2\pi ^2}-F_{j}\mu _{j} -\frac{k^2+M^2}{j^2\pi ^2}F_{j}\mu _{j}\Big )\sinh (\mu _{j}y). \end{aligned} \end{aligned}$$
(3.23)

This completes the formal derivation of the effective model describing the MHD flow through a channel filled with a porous medium with slightly perturbed boundary. Our asymptotic approximation takes the form:

(3.24)

3.3 Numerical Example

Let us note at this point that the first-order asymptotic approximation derived in the previous section (see 3.24) is given in explicit form. For this reason, we now visually present our asymptotic solution in order to indicate how the flow adjusts to the presence of the small boundary perturbation with regard to the Hartmann number M. In view of that, we use the boundary perturbation function

$$\begin{aligned} h(x)=-\cos \Big ( \frac{\pi x}{2}\Big ), \end{aligned}$$

and take the pressure drop \(p_{1}-p_{0}=-1\). The porous medium parameter k is set to 1, while the Hartmann number takes the following values: \(M=0,2,4,6\). We compute the corrector approximations up to \(j=10\) in (3.8), since increasing j provides no significant improvements. The same is done for the function h in (3.9), where the coefficient \(h_{j}\) are computed using the numerical integration in MATLAB.

In order to clearly observe the effects of small boundary perturbation, we present corresponding 3D figures of the velocity corrector \(V_{x}^{1}\) computed in Sect. 3.2 for different values of the Hartmann number M (see Figs. 2 and 3). We see that the correctors acknowledge the effects of the slightly perturbed boundary and that those effects are not just local. Moreover, we see that increasing the value of the Hartmann number M decreases the overall magnitude of the velocity and that the boundary perturbation effects are more localized near \(y=1\).

In view of that, we further depict the x-component of the velocity approximation given by (3.24). The effects can be clearly observed for \(\varepsilon =0.1\) (see Figs. 4 and 5). We again confirm that increasing the value of the Hartmann number M decreases the overall magnitude of the velocity approximation and that the boundary perturbation effects are more localized near \(y=1\).

In order to provide a more detailed visualization of the presented figures, we present the 3D figures of the velocity corrector \(V_{y}^{1}\) and pressure corrector \(Q^{1}\) with the 2D velocity profiles of the velocity corrector \(V_{x}^{1}\) and \(V_{y}^{1}\) along with the x-component of the velocity approximation given by (3.24) for fixed values x and y in Appendix A (see Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21).

Fig. 2
figure 2

Velocity corrector \(V_{x}^{1}\) with Hartmann number \(M=0\) (left) and \(M=2\) (right)

Full size image
Fig. 3
figure 3

Velocity corrector \(V_{x}^{1}\) with Hartmann number \(M=4\) (left) and \(M=6\) (right)

Full size image
Fig. 4
figure 4

Velocity approximation (x-component) with Hartmann number \(M=0\) (left) and \(M=2\) (right) and \(\varepsilon =0.1\)

Full size image
Fig. 5
figure 5

Velocity approximation (x-component)with Hartmann number \(M=4\) (left) and \(M=6\) (right) and \(\varepsilon =0.1\)

Full size image

4 Rigorous Justification

4.1 Transformed Problem

In order to evaluate the difference between the original solution and the asymptotic one in terms of the small parameter \(\varepsilon \), the governing problem (2.1)–(2.2) needs to be transformed and written in an \(\varepsilon \)-independent domain \(\Omega =(0,1)^2\). To accomplish that, we introduce a new variable:

$$\begin{aligned} z=\frac{y}{1-\varepsilon h}, \end{aligned}$$

and the new unknown functions

$$\begin{aligned} \mathbf {U}^{\varepsilon }(x,z)=\mathbf {u}^{\varepsilon }(x,z(1-\varepsilon h(x))), P^{\varepsilon }(x,z)=p^{\varepsilon }(x,z(1-\varepsilon h(x))). \end{aligned}$$

Let us note that there hold the following identities:

$$\begin{aligned} \begin{aligned} \frac{\partial z}{\partial x}&=\frac{\varepsilon yh'}{(1-\varepsilon h)^2}=\frac{\varepsilon zh'}{1-\varepsilon h}, \\ \frac{\partial z}{\partial y}&=\frac{1}{1-\varepsilon h}, \\ \frac{\partial ^2 z}{\partial x^2}&=\frac{y \varepsilon h''(1-\varepsilon h)+2y \varepsilon ^2 (h')^2}{(1-\varepsilon h)^2}=\varepsilon \frac{zh''}{1-\varepsilon h}+2\varepsilon ^2 \frac{z(h')^2}{(1-\varepsilon h)^2}. \end{aligned} \end{aligned}$$

In view of that, the partial derivatives in new variables read:

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial x} \rightarrow \frac{\partial }{\partial x}+\frac{\partial z}{\partial x}\frac{\partial }{\partial z}=\frac{\partial }{\partial x}+\varepsilon \frac{zh'}{1-\varepsilon h}\frac{\partial }{\partial z}=\frac{\partial }{\partial x}+\varepsilon zh'\sum _{j=0}^{\infty } \varepsilon ^{j}h^{j} \frac{\partial }{\partial z}, \\&\frac{\partial }{\partial y} \rightarrow \frac{\partial z}{\partial y}\frac{\partial }{\partial z}=\frac{1}{1-\varepsilon h}\frac{\partial }{\partial z}=\sum _{j=0}^{\infty } \varepsilon ^{j}h^{j} \frac{\partial }{\partial z}, \\&\frac{\partial ^2}{\partial x^2} \rightarrow \left( \frac{\partial }{\partial x}+\frac{\partial z}{\partial x}\frac{\partial }{\partial z}\right) \left( \frac{\partial }{\partial x}+\frac{\partial z}{\partial x}\frac{\partial }{\partial z}\right) \\&=\frac{\partial ^2 }{\partial x^2}+\frac{\partial ^2 z}{\partial x^2} \frac{\partial }{\partial z}+2 \frac{\partial z}{\partial x}\frac{\partial ^2 }{\partial z \partial x}+\left( \frac{\partial z}{\partial x}\right) ^2 \frac{\partial ^2}{\partial z^2} \\&=\frac{\partial ^2 }{\partial x^2}+\left( \varepsilon zh'' \frac{\partial }{\partial z}+2zh'\frac{\partial ^2 }{\partial z \partial x}\right) \\&+\sum _{j=2}^{\infty } \varepsilon ^{j}h^{j-2}\left[ z\left( h''h+2(j-1)(h')^2\right) \frac{\partial }{\partial z}+2zh'h\frac{\partial ^2}{\partial z \partial x}\right. \\&\left. +(zh')^2(j-1)\frac{\partial ^2}{\partial z^2}\right] , \\&\frac{\partial ^2}{\partial y^2} \rightarrow \frac{1}{(1-\varepsilon h)^2}\frac{\partial ^2}{\partial z^2}=\sum _{j=0}^{\infty } \varepsilon ^{j}(j+1)h^{j}\frac{\partial ^2 }{\partial z^2}. \end{aligned} \end{aligned}$$

Taking into account the above change of variables, the system (2.1)–(2.2) becomes:

$$\begin{aligned}&\frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial x^2}+\frac{1+\varepsilon ^2 z^2 (h')^2}{(1-\varepsilon h)^2} \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z^2}+\frac{2\varepsilon zh'}{1-\varepsilon h}\frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z \partial x}+\frac{\varepsilon z}{1-\varepsilon h}\left( h''+\frac{2\varepsilon (h')^2}{1-\varepsilon h}\right) \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z}\nonumber \\&-k^2\mathbf {U}^{\varepsilon }-M^2 U_x^{\varepsilon }\mathbf {e}_{1}\nonumber \\&\quad =\left( \frac{\partial P^{\varepsilon }}{\partial x}+\frac{\varepsilon zh'}{1-\varepsilon h}\frac{\partial P^{\varepsilon }}{\partial z}\right) \mathbf {e}_{1}+\frac{1}{1-\varepsilon h}\frac{\partial P^{\varepsilon }}{\partial z}\mathbf {e}_{2} \text{ in }\ \Omega , \nonumber \\&\frac{\partial U_{x}^{\varepsilon }}{\partial x}+\frac{\varepsilon zh'}{1-\varepsilon h}\frac{\partial U^{\varepsilon }_{x}}{\partial z}+\frac{1}{1-\varepsilon h}\frac{\partial U_{y}^{\varepsilon }}{\partial z}=0 \text{ in }\ \Omega ,\nonumber \\&\mathbf {U}^{\varepsilon }(x,0)=\mathbf {U}^{\varepsilon }(x,1)=\mathbf {0}, U_{y}^{\varepsilon }(0,z)=U_{y}^{\varepsilon }(1,z)=0,\nonumber \\&P^{\varepsilon }(0,z)=p_{0},\ P^{\varepsilon }(1,z)=p_{1}, \end{aligned}$$
(4.1)

where \(\mathbf {U}^{\varepsilon }=(U^{\varepsilon }_{x},U^{\varepsilon }_{y})\).

We expand the solution \((\mathbf {U}^{\varepsilon },P^{\varepsilon })\) of problem (4.1) in the form of a power series in terms of the small parameter \(\varepsilon \) in the following way:

$$\begin{aligned} \begin{aligned}&\mathbf {U}^{\varepsilon }=\mathbf {U}^{0}+\varepsilon \mathbf {U}^{1}+\varepsilon ^{2} \mathbf {U}^{2}+\dots , \\&P^{\varepsilon }=P^{0}+\varepsilon P^{1}+\varepsilon ^2 P^{2}+\dots . \end{aligned} \end{aligned}$$
(4.2)

In the following, we identify the problems for \((\mathbf {U}^{j},P^{j})\), \(j=0,1\) and link its solutions with corresponding \((\mathbf {V}^{j},Q^{j})\) computed in Sect. 3.

Plugging the expansions (4.2) into the system of Eq. (4.1), we obtain the following problem for \((\mathbf {U}^{0},P^{0})\):

$$\begin{aligned} \begin{aligned}&1 : \Delta _{xz}\mathbf {U}^{0}-k^2 \mathbf {U}^{0}-M^2 U_x^{0}\mathbf {e}_{1}=\nabla _{xz}P^{0} \text{ in }\ \Omega ,\\&1 : \text{ div}_{xz} \mathbf {U}^{0}=0 \text{ in }\ \Omega ,\\&1 :\mathbf {U}^{0}(x,0)=\mathbf {U}^{0}(x,1)=\mathbf {0},\\&1 :U_{y}^{0}(0,z)=U_{y}^{0}(1,z)=0, P^{0}(0,z)=p_{0}, P^{0}(1,z)=p_{1}, \end{aligned} \end{aligned}$$
(4.3)

where we use the usual notation \(\Delta _{xz} \phi =\frac{\partial ^2 \phi }{\partial x^2}+\frac{\partial ^2 \phi }{\partial z^2}\), \(\nabla _{xz} \Phi =\frac{\partial \phi }{\partial x}\mathbf {e}_{1}+\frac{\partial \phi }{\partial z}\mathbf {e}_{2}\), \(\text{ div}_{xz} \mathbf {W}=\frac{\partial W_{x}}{\partial x}+\frac{\partial W_{y}}{\partial z}\). Comparing problem (4.3) with the one satisfied by \((\mathbf {V}^{0},Q^{0})\) given by (3.3), we deduce that \(\mathbf {V}^{0}(x,y)=\mathbf {U}^{0}(x,y)\), \(Q^{0}(x,y)=P^{0}(x,y)\).

The first-order corrector \((\mathbf {U}^{1},P^{1})\) is the solution of the following problem:

$$\begin{aligned} \begin{aligned}&\varepsilon :\Delta _{xz} \mathbf {U}^{1}+2h \frac{\partial ^2 \mathbf {U}^{0}}{\partial z^2}+2zh' \frac{\partial ^2 \mathbf {U}^{0}}{\partial z \partial x}+zh'' \frac{\partial \mathbf {U}^{0}}{\partial z}-k^2 \mathbf {U}^{1}-M^2 U_x^{1}\mathbf {e}_{1} \\& =\left( \frac{\partial P^{1}}{\partial x}+zh'\frac{\partial P^{0}}{\partial z}\right) \mathbf {e}_{1}+\left( \frac{\partial P^{1}}{\partial z}+h \frac{\partial P^{0}}{\partial z}\right) \mathbf {e}_{2} \text{ in }\ \Omega , \\&\varepsilon : \frac{\partial U_{x}^{1}}{\partial x}+zh' \frac{\partial U_{x}^{0}}{\partial z}+\frac{\partial U_{y}^{1}}{\partial z}+h \frac{\partial U_{y}^{0}}{\partial z}=0 \text{ in }\ \Omega , \\&\varepsilon : \mathbf {U}^{1}(x,0)=\mathbf {U}^{1}(x,1)=\mathbf {0}, \\&\varepsilon : U_{y}^{1}(0,z)=U_{y}^{1}(1,z)=0, P^{1}(0,z)=P^{1}(1,z)=0. \end{aligned} \end{aligned}$$
(4.4)

Taking into account (3.4) and (3.6), the problem for \((\mathbf {U}^{1},P^{1})\) reduces to:

$$\begin{aligned}&\Delta _{xz} U_{x}^{1}-k^2 U_{x}^{1}-M^2U_{x}^{1}\\&\quad =\frac{\partial P^{1}}{\partial x}-\frac{zh''(p_{1}-p_{0})}{\sqrt{k^2+M^2}}\\&\quad \times \Big (\frac{1-\cosh (\sqrt{k^2+M^2})}{\sinh (\sqrt{k^2+M^2})}\cosh (\sqrt{k^2+M^2}z) +\sinh (\sqrt{k^2+M^2}z)\Big )\\&\qquad -2h (p_{1}-p_{0})\Big (\frac{1-\cosh (\sqrt{k^2+M^2})}{\sinh (\sqrt{k^2+M^2})}\sinh (\sqrt{k^2+M^2}z)\\&\qquad +\cosh (\sqrt{k^2+M^2}z)\Big ) \text{ in }\ \Omega ,\\&\Delta _{xz}U_{y}^{1}-k^2 U_{y}^{1}=\frac{\partial P^{1}}{\partial z} \text{ in }\ \Omega ,\\&\text{ div}_{xz}\mathbf {U}^{1}\\&\quad =-\frac{(p_{1}-p_{0})zh'}{\sqrt{k^2+M^2}} \Big (\frac{1-\cosh (\sqrt{k^2+M^2)}}{\sinh (\sqrt{k^2+M^2})}\cosh (\sqrt{k^2+M^2}z)\\&\qquad +\sinh (\sqrt{k^2+M^2}z)\Big ) \text{ in }\ \Omega ,\\&\mathbf {U}^{1}(x,0)=\mathbf {U}^{1}(x,1)=\mathbf {0},\\&U_{y}^{1}(0,z)=U_{y}^{1}(1,z)=0, P^{1}(0,z)=P^{1}(1,z)=0. \end{aligned}$$

If we compare the problem (4.4) with the problem (3.7) satisfied by \((\mathbf {V}^{1},Q^{1})\), we observe that additional terms have appeared in the governing equations. This appears due to the change of variables. As a result, we cannot explicitly compute \(\mathbf {U}^{1}\), but we can make a connection with \(\mathbf {V}^{1}\). It is straightforward to verify that there holds:

$$\begin{aligned} \mathbf {V}^{1}(x,y)&=\mathbf {U}^{1}(x,y) +\frac{yh(p_{1}-p_{0})}{\sqrt{k^2+M^2}}\Big (\frac{1-\cosh (\sqrt{k^2+M^2})}{\sinh (\sqrt{k^2+M^2})}\cosh (\sqrt{k^2+M^2}y)\nonumber \\&\quad +\sinh (\sqrt{k^2+M^2}y)\Big )\mathbf {e}_{1},\nonumber \\ Q^{1}(x,y)&=P^{1}(x,y). \end{aligned}$$
(4.5)

We clearly see from (4.5) that \(\mathbf {V}^{1} \ne \mathbf {U}^{1}\), implying that the two asymptotic approximation \(\mathbf {V}^{0}+\varepsilon \mathbf {V}^{1}\) and \(\mathbf {U}^{0}+\varepsilon \mathbf {U}^{1}\) are not equal. However, it can be shown that these two approximations are asymptotically the same since there holds the following identity:

$$\begin{aligned}&\mathbf {U}^{0}(x,z)+\varepsilon \mathbf {U}^{1}(x,z)\\&\quad =\mathbf {U}^{0}(x,y+\varepsilon yh(x))+\varepsilon \mathbf {U}^{1}(x,y)+\mathcal {O}(\varepsilon ^2) \\&\quad =\mathbf {U}^{0}(x,y)+\varepsilon \left( \mathbf {U}^{1}(x,y)+yh(x)\frac{\partial \mathbf {U}^{0}}{\partial y}(x,y)\right) +\mathcal {O}(\varepsilon ^2) \\&\quad =\mathbf {U}^{0}(x,y)+\varepsilon \frac{yh(x)(p_{1}-p_{0})}{\sqrt{k^2+M^2}}\\&\quad \times \left( \frac{1-\cosh \left( \sqrt{k^2+M^2}\right) }{\sinh \left( \sqrt{k^2+M^2}\right) }\cosh \left( \sqrt{k^2+M^2}y\right) +\sinh (\sqrt{k^2+M^2}y)\right) \mathbf {e}_{1}\\&\qquad +\varepsilon \mathbf {U}^{1}(x,y)+\mathcal {O}(\varepsilon ^2) \\&\quad =\mathbf {V}^{0}(x,y)+\varepsilon \mathbf {V}^{1}(x,y)+\mathcal {O}(\varepsilon ^2). \end{aligned}$$

For this reason, in order to rigorously justify the asymptotic approximation \((\mathbf {V}^{0}+\varepsilon \mathbf {V}^{1},Q^{0}+\varepsilon Q^{1})\) computed in Sect. 3, it is sufficient to derive error estimates for \((\mathbf {U}^{0}+\varepsilon \mathbf {U}^{1},P^{0}+\varepsilon P^{1})\).

4.2 Error Estimates

In order to rigorously justify our model, we need to evaluate the difference between the original solution \((\mathbf {U}^{\varepsilon },P^{\varepsilon })\) of the transformed problem (4.1) and the corresponding asymptotic approximation \(\mathbf {U}_{approx}^{\varepsilon }=\mathbf {U}^{0}+\varepsilon \mathbf {U}^{1}\).

To achieve this, we need the following technical results (see, e.g., [7]):

Lemma 4.1

There exists a constant C, independent of \(\varepsilon \), such that there holds the estimate:

$$\begin{aligned} \vert \vert \varphi ^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \vert \vert \nabla \varphi ^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \end{aligned}$$
(4.6)

for any \(\varphi ^{\varepsilon } \in H^{1}(\Omega )\) such that \(\varphi ^{\varepsilon }\) for \(z=0,1\).

Lemma 4.2

The problem

$$\begin{aligned} \begin{aligned}&\text{ div } \varphi ^{\varepsilon }=f^{\varepsilon } \in L_{0}^{2}(\Omega ) \text{ in }\ \Omega , \\& \varphi ^{\varepsilon }=0 \text{ on }\ \partial \Omega , \end{aligned} \end{aligned}$$

has a solution \(\varphi ^{\varepsilon } \in H_{0}^{1}(\Omega )\) such that there hold the estimates:

$$\begin{aligned} \vert \vert \nabla \varphi ^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \vert \vert f^{\varepsilon } \vert \vert _{L^{2}(\Omega )}. \end{aligned}$$

In the following, we derive the a priori estimates for the velocity \(\mathbf {U}^{\varepsilon }\).

Proposition 4.1

Let \((\mathbf {U}^{\varepsilon },P^{\varepsilon })\) be the solution of problem (4.1). Then, there hold the following estimates:

$$\begin{aligned} \begin{aligned}&\vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C. \end{aligned} \end{aligned}$$
(4.7)

Proof

Let us recall that the system satisfied by the original solution \((\mathbf {U}^{\varepsilon },P^{\varepsilon })\) reads:

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial x^2}+\frac{1+\varepsilon ^2 z^2 (h')^2}{(1-\varepsilon h)^2} \frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z^2}+\frac{2\varepsilon zh'}{1-\varepsilon h}\frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z \partial x}\\&\quad +\frac{\varepsilon z}{1-\varepsilon h}\left( h''+\frac{2\varepsilon (h')^2}{1-\varepsilon h}\right) \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z}-k^2\mathbf {U}^{\varepsilon }-M^2 U_x^{\varepsilon }\mathbf {e}_{1}\\&\quad =\left( \frac{\partial P^{\varepsilon }}{\partial x}+\frac{\varepsilon zh'}{1-\varepsilon h}\frac{\partial P^{\varepsilon }}{\partial z}\right) \mathbf {e}_{1}+\frac{1}{1-\varepsilon h}\frac{\partial P^{\varepsilon }}{\partial z}\mathbf {e}_{2} \text{ in }\ \Omega ,\\&\frac{\partial U_{x}^{\varepsilon }}{\partial x}+\frac{\varepsilon zh'}{1-\varepsilon h}\frac{\partial U_{x}}{\partial z}+\frac{1}{1-\varepsilon h}\frac{\partial U_{y}^{\varepsilon }}{\partial z}=0 \text{ in }\ \Omega ,\\&\mathbf {U}^{\varepsilon }(x,0)=\mathbf {U}^{\varepsilon }(x,1)=\mathbf {0}, U_{y}^{\varepsilon }(0,z)=U_{y}^{\varepsilon }(1,z)=0, P^{\varepsilon }(0,z)=p_{0},\ P^{\varepsilon }(1,z)=p_{1}, \end{aligned} \end{aligned}$$
(4.8)

We introduce \(\mathbf {z}^{\varepsilon }\) as the solution of the following auxiliary problem:

$$\begin{aligned} \begin{aligned}&\text{ div } \mathbf {z}^{\varepsilon }=P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }:=f^{\varepsilon } \text{ in }\ \Omega , \\&\mathbf {z}^{\varepsilon }=\mathbf {0} \text{ on }\ \partial \Omega . \end{aligned} \end{aligned}$$
(4.9)

Due to Lemma 4.2 and since \(\int _{\Omega }f^{\varepsilon }=0\), problem (4.9) admits at least one solution satisfying the following estimate:

$$\begin{aligned} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert \le C \Big \vert \Big \vert P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )}. \end{aligned}$$
(4.10)

We now multiply (4.8) by \(\mathbf {z}^{\varepsilon }\) and integrate over \(\Omega \) to obtain:

$$\begin{aligned} \begin{aligned}&\Big \vert \Big \vert P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )}^2\\&\quad \le \int _{\Omega } \nabla \mathbf {U}^{\varepsilon } \nabla \mathbf {z}^{\varepsilon }-\int _{\Omega } \frac{2\varepsilon h-\varepsilon ^2h^2+\varepsilon ^2 z^2(h')^2}{(1-\varepsilon h)^2} \frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z^2}\mathbf {z}^{\varepsilon }\\&\qquad -\int _{\Omega } \frac{2\varepsilon zh'}{1-\varepsilon h} \frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z \partial x}\mathbf {z}^{\varepsilon } \\&\qquad -\int _{\Omega } \frac{\varepsilon z}{1-\varepsilon h}\Big (h''+\frac{2 \varepsilon (h')^2}{1-\varepsilon h}\Big ) \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z}\mathbf {z}^{\varepsilon }+\int _{\Omega }k^2 \mathbf {U}^{\varepsilon } \mathbf {z}^{\varepsilon }+\int _{\Omega }M^2 U_x^{\varepsilon } \mathbf {e}_{1}\mathbf {z}^{\varepsilon } \\&\qquad -\int _{\Omega } \frac{\varepsilon zh'}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big ) \frac{\partial \mathbf {z}^{\varepsilon }}{\partial z}\mathbf {e}_{1}\\&\qquad -\int _{\Omega } \frac{\varepsilon h'}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big ) \mathbf {z}^{\varepsilon }\mathbf {e}_{1} \\&\qquad -\int _{\Omega }\varepsilon h\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big ) \frac{\partial \mathbf {z}^{\varepsilon }}{\partial z}\mathbf {e}_{2}. \end{aligned} \end{aligned}$$
(4.11)

Let us now estimate the terms on the right-hand side of (4.11) using Poincare’s inequality (4.6) and the estimate (4.10):

$$\begin{aligned}&\Big \vert \int _{\Omega } \nabla \mathbf {U}^{\varepsilon } \nabla \mathbf {z}^{\varepsilon } \Big \vert \\&\quad \le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \Big \vert \Big \vert P^{\varepsilon }\\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )},\\ {}&\varepsilon \Big \vert \int _{\Omega } \frac{2h-\varepsilon h^2+\varepsilon z^2 (h')^2}{(1-\varepsilon h)^2}\frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z^2}\mathbf {z}^{\varepsilon } \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \Big \vert \Big \vert P^{\varepsilon }\\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )},\\&\varepsilon \Big \vert \int _{\Omega } \frac{2zh'}{1-\varepsilon h} \frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z \partial x} \mathbf {z}^{\varepsilon } \Big \vert \nonumber \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \Big \vert \Big \vert P^{\varepsilon }\\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )}, \\&\varepsilon \Big \vert \int _{\Omega } \frac{z}{1-\varepsilon h}\Big (h''+\frac{2\varepsilon (h')^2}{1-\varepsilon h}\Big ) \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z}\mathbf {z}^{\varepsilon } \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \Big \vert \Big \vert P^{\varepsilon }\\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )},\\&k^2 \Big \vert \int _{\Omega } \mathbf {U}^{\varepsilon } \mathbf {z}^{\varepsilon } \Big \vert \\&\quad \le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \Big \vert \Big \vert P^{\varepsilon }\\ \end{aligned}$$
$$\begin{aligned}&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )},\nonumber \\&M^2 \Big \vert \int _{\Omega } U_x^{\varepsilon } \mathbf {e}_{1} \mathbf {z}^{\varepsilon } \Big \vert \nonumber \\&\quad \le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \Big \vert \Big \vert P^{\varepsilon }\nonumber \\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )},\nonumber \\&\varepsilon \Big \vert \int _{\Omega } \frac{zh'}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big ) \frac{\partial \mathbf {z}^{\varepsilon }}{\partial z}\mathbf {e}_{1} \Big \vert \nonumber \\&\quad \le C \varepsilon \Big \vert \Big \vert P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \varepsilon \Big \vert \Big \vert P^{\varepsilon }\nonumber \\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )}^{2},\nonumber \\&\varepsilon \Big \vert \int _{\Omega } \frac{h'}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P\Big ) \mathbf {z}^{\varepsilon }\mathbf {e}_{1} \Big \vert \nonumber \\&\quad \le C \varepsilon \Big \vert \Big \vert P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \varepsilon \Big \vert \Big \vert P^{\varepsilon }\nonumber \\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )}^{2},\nonumber \\&\varepsilon \Big \vert \int _{\Omega } \frac{h}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P \Big ) \frac{\partial \mathbf {z}^{\varepsilon }}{\partial z}\mathbf {e}_{2} \Big \vert \nonumber \\&\quad \le C \varepsilon \Big \vert \Big \vert P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {z}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \varepsilon \Big \vert \Big \vert P^{\varepsilon }\nonumber \\&\qquad -\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )}^{2}. \end{aligned}$$
(4.12)

Now, for sufficiently small \(\varepsilon \), we obtain from (4.11)–(4.12) the following estimate:

$$\begin{aligned} \Big \vert \Big \vert P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )} \le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}. \end{aligned}$$
(4.13)

Multiplying (4.8) by \(\mathbf {U}^{\varepsilon }\) and integrating over \(\Omega \) yields:

$$\begin{aligned} \begin{aligned}&k^2\int _{\Omega } \vert \mathbf {U}^{\varepsilon } \vert ^2+M^2 \int _{\Omega } \vert U_{x} \vert ^2+\int _{\Omega } \vert \nabla \mathbf {U}^{\varepsilon } \vert ^2\\&\quad =\int _{\Omega } \frac{2\varepsilon h-\varepsilon ^2 h^2+\varepsilon ^2 z^2 (h')^2}{(1-\varepsilon h)^2} \frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z^2} \mathbf {U}^{\varepsilon } -\varepsilon \int _{\Omega }\frac{zh'}{1-\varepsilon h}\frac{\partial \mathbf {U}^{\varepsilon }}{\partial x}\frac{\partial \mathbf {U}^{\varepsilon }}{\partial z} \\&\qquad -\varepsilon \int _{\Omega }\frac{h'}{1-\varepsilon h}\frac{\partial \mathbf {U}^{\varepsilon }}{\partial x}\mathbf {U}^{\varepsilon }-\varepsilon \int _{\Omega }\Big (\frac{h''(x)}{1-\varepsilon h}+\frac{\varepsilon (h'(x))^2}{(1-\varepsilon h)^2}\Big )\frac{\partial \mathbf {U}^{\varepsilon }}{\partial z} \mathbf {U}^{\varepsilon } \\&\qquad -\varepsilon \int _{\Omega } \frac{zh'}{1-\varepsilon h}\frac{\partial \mathbf {U}^{\varepsilon }}{\partial z}\frac{\partial \mathbf {U}^{\varepsilon }}{\partial x}+\int _{\Omega }\frac{\varepsilon z}{1-\varepsilon h}\Big (h''+\frac{2\varepsilon (h')^2}{1-\varepsilon h}\Big )\frac{\partial \mathbf {U}^{\varepsilon }}{\partial z}\mathbf {U}^{\varepsilon } \\&\qquad +\Big (p_{0}-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big )\int _{\Sigma _{0}^{\varepsilon }} \mathbf {U}^{\varepsilon } \cdot \mathbf {e}_{1}-\Big (p_{1}-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big )\int _{\Sigma _{1}^{\varepsilon }} \mathbf {U}^{\varepsilon } \cdot \mathbf {e}_{1} \\&\qquad +\int _{\Omega }\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big ) \text{ div }\mathbf {U}^{\varepsilon }-\varepsilon \int _{\Omega } \frac{zh'}{1-\varepsilon h}\frac{\partial }{\partial z}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big )\mathbf {U}^{\varepsilon }\mathbf {e}_{1} \\&\qquad -\varepsilon \int _{\Omega } \frac{h}{1-\varepsilon h}\frac{\partial }{\partial z}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big )\mathbf {U}^{\varepsilon }\mathbf {e}_{2}, \end{aligned} \end{aligned}$$
(4.14)

where \(\Sigma _{i}^{\varepsilon }=\{i\} \times \langle 0,\varepsilon \rangle \), \(i=0,1\).

We now have the following identity (using (4.8)\(_{2}\)):

$$\begin{aligned} \begin{aligned}&\int _{\Omega }\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big )\text{ div }\mathbf {U}^{\varepsilon }-\varepsilon \int _{\Omega } \frac{zh'}{1-\varepsilon h}\frac{\partial }{\partial z}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big ) U_{x}^{\varepsilon }\\&\quad -\varepsilon \int _{\Omega } \frac{h}{1-\varepsilon h}\frac{\partial }{\partial z}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big ) U_{y}^{\varepsilon } \\&\quad =\int _{\Omega }\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big ) \text{ div }\mathbf {U}^{\varepsilon }+\varepsilon \int _{\Omega }\frac{h'}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big )U_{x}^{\varepsilon } \\&\qquad +\varepsilon \int _{\Omega } \frac{zh'}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big )\frac{\partial U_{x}^{\varepsilon }}{\partial z}+\varepsilon \int _{\Omega }\frac{h}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big ) \frac{\partial U_{y}^{\varepsilon }}{\partial z} \\&\quad =\varepsilon \int _{\Omega }\frac{h'}{1-\varepsilon h}\Big (P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\Big )U_{x}^{\varepsilon }. \end{aligned} \end{aligned}$$

We now estimate the right hand side of (4.14) using Poincare’s inequality (4.6) and (4.13):

$$\begin{aligned}&\varepsilon \Big \vert \int _{\Omega } \frac{2h-\varepsilon h^2+\varepsilon z^2 (h')^2}{(1-\varepsilon h)^2} \frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z^2} \mathbf {U}^{\varepsilon } \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \\&\varepsilon \Big \vert \int _{\Omega } \frac{zh'}{1-\varepsilon h} \frac{\partial \mathbf {U^{\varepsilon }}}{\partial x} \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z} \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \\&\varepsilon \Big \vert \int _{\Omega } \frac{h'}{1-\varepsilon h} \frac{\partial \mathbf {U}^{\varepsilon }}{\partial x} \mathbf {U}^{\varepsilon } \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \\&\varepsilon \Big \vert \int _{\Omega } \Big (\frac{h''(x)}{1-\varepsilon h}+\frac{\varepsilon (h'(x))^2}{(1-\varepsilon h)^2} \Big )\frac{\partial \mathbf {U}^{\varepsilon }}{\partial z} \mathbf {U}^{\varepsilon } \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \\&\varepsilon \Big \vert \int _{\Omega } \frac{zh'}{1-\varepsilon h} \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z} \frac{\partial \mathbf {U}^{\varepsilon }}{\partial x} \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \\&\varepsilon \Big \vert \int _{\Omega } \frac{z}{1-\varepsilon h} \Big (h''+\frac{2\varepsilon (h')^2}{1-\varepsilon h}\Big ) \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z} \mathbf {U}^{\varepsilon } \Big \vert \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \\&\Big \vert \Big (p_{0}-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big )\int _{\Sigma _{0}^{\varepsilon }} \mathbf {U}^{\varepsilon } \cdot \mathbf {e}_{1}-\Big (p_{1}-\frac{1}{\vert \Omega \vert }\int _{\Omega }P^{\varepsilon }\Big ) \int _{\Sigma _{1}^{\varepsilon }}\mathbf {U}^{\varepsilon } \cdot \mathbf {e}_{1} \Big \vert \\&\quad \le \int _{\Omega } \Big \vert \text{ div }\Big (p_{0}-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon }\\&\quad +(p_{1}-p_{0})x\Big )\mathbf {U}^{\varepsilon } \Big \vert \le C \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \\&\varepsilon \Big \vert \int _{\Omega } \frac{h'}{1-\varepsilon h} \Big ( P^{\varepsilon } - \frac{1}{\vert \Omega \vert } \int _{\Omega } P^{\varepsilon } \Big ) U_{x}^{\varepsilon } \Big \vert \\&\quad \le C \varepsilon \Big \vert \Big \vert P^{\varepsilon }-\frac{1}{\vert \Omega \vert } \int _{\Omega }P^{\varepsilon } \Big \vert \Big \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \\&\quad \le C \varepsilon \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \end{aligned}$$

and now, for sufficiently small \(\varepsilon \), we obtain:

$$\begin{aligned} \vert \vert \nabla \mathbf {U}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}. \le C, \end{aligned}$$

thus obtaining estimate (4.7). This completes our proof. \(\square \)

Theorem 4.1

Let \((\mathbf {U}^{\varepsilon },P^{\varepsilon })\) be the solution of the transformed problem (4.1), and let \(\mathbf {U}_{approx}^{\varepsilon }=\mathbf {U}^{0}+\varepsilon \mathbf {U}^{1}\), \(P_{approx}^{\varepsilon }=P^{0}+\varepsilon P^{1}\) be the asymptotic solution provided in Sect. 4.1. Then, there hold the following estimates:

$$\begin{aligned} \begin{aligned} \vert \vert \mathbf {U}^{\varepsilon }-\mathbf {U}_{approx}^{\varepsilon } \vert \vert _{H^{1}(\Omega )}&\le C \varepsilon ^2, \\ \vert \vert P^{\varepsilon }-P_{approx}^{\varepsilon } \vert \vert _{L^{2}(\Omega ) / \mathbb {R}}&\le C \varepsilon ^2. \end{aligned} \end{aligned}$$
(4.15)

Proof

Let us denote the difference between the original solution and the computed asymptotic approximation by:

$$\begin{aligned} \mathbf {R}^{\varepsilon }=\mathbf {U}^{\varepsilon }-\mathbf {U}_{approx}^{\varepsilon }, r^{\varepsilon }=P^{\varepsilon }-P_{approx}^{\varepsilon }. \end{aligned}$$

Let us recall that the system satisfied by the original solution \((\mathbf {U}^{\varepsilon },P^{\varepsilon })\) reads:

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial x^2}+\frac{1+\varepsilon ^2 z^2 (h')^2}{(1-\varepsilon h)^2} \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z^2}+\frac{2\varepsilon zh'}{1-\varepsilon h}\frac{\partial ^2 \mathbf {U}^{\varepsilon }}{\partial z \partial x}\\&\ +\frac{\varepsilon z}{1-\varepsilon h}\Big (h''+\frac{2\varepsilon (h')^2}{1-\varepsilon h}\Big ) \frac{\partial \mathbf {U}^{\varepsilon }}{\partial z}-k^2\mathbf {U}^{\varepsilon }-M^2 U_x^{\varepsilon }\mathbf {e}_{1} \\&\quad =\Big ( \frac{\partial P^{\varepsilon }}{\partial x}+\frac{\varepsilon zh'}{1-\varepsilon h}\frac{\partial P^{\varepsilon }}{\partial z}\Big )\mathbf {e}_{1}+\frac{1}{1-\varepsilon h}\frac{\partial P^{\varepsilon }}{\partial z}\mathbf {e}_{2} \text{ in }\ \Omega , \\&\frac{\partial U_{x}^{\varepsilon }}{\partial x}+\frac{\varepsilon zh'}{1-\varepsilon h}\frac{\partial U_{x}}{\partial z}+\frac{1}{1-\varepsilon h}\frac{\partial U_{y}^{\varepsilon }}{\partial z}=0 \text{ in }\ \Omega ,\\&\mathbf {U}^{\varepsilon }(x,0)=\mathbf {U}^{\varepsilon }(x,1)=\mathbf {0}, U_{y}^{\varepsilon }(0,z)=U_{y}^{\varepsilon }(1,z)=0, P^{\varepsilon }(0,z)=p_{0},\ P^{\varepsilon }(1,z)=p_{1}, \end{aligned} \end{aligned}$$
(4.16)

The system satisfied by our asymptotic approximation \((\mathbf {U}_{approx}^{\varepsilon },P_{approx}^{\varepsilon })\), where \(\mathbf {U}_{approx}^{\varepsilon }=\mathbf {U}^{0}+\varepsilon \mathbf {U}^{1}\), \(P^{\varepsilon }=P^{0}(x,y)+\varepsilon P^{1}(x,y)\), is given by the following:

$$\begin{aligned} \begin{aligned}&\Delta _{xz}\mathbf {U}_{approx}^{\varepsilon }+2h \varepsilon \frac{\partial ^2 \mathbf {U}^{0}}{\partial z^2}+2\varepsilon zh' \frac{\partial ^2 \mathbf {U}^{0}}{\partial z \partial x}+\varepsilon zh'' \frac{\partial \mathbf {U}^{0}}{\partial z}\\&\ -k^2 \mathbf {U}_{approx}^{\varepsilon }-M^2 U_{approx,x}^{\varepsilon }\mathbf {e}_{1} \\&\quad =\Big ( \frac{\partial P_{approx}^{\varepsilon }}{\partial x}+\varepsilon zh' \frac{\partial P^{0}}{\partial z}\Big )\mathbf {e}_{1}+\Big ( \frac{\partial P_{approx}^{\varepsilon }}{\partial z}+\varepsilon h \frac{\partial P^{0}}{\partial z}\Big ) \mathbf {e}_{2} \text{ in }\ \Omega , \\&\quad \frac{\partial U_{approx,x}^{\varepsilon }}{\partial x}+\varepsilon zh' \frac{\partial U_{x}^{0}}{\partial z}+\frac{\partial U_{approx,y}^{\varepsilon }}{\partial z}+\varepsilon h \frac{\partial U_{y}^{0}}{\partial z}=0 \text{ in }\ \Omega , \\&\quad \mathbf {U}_{approx}^{\varepsilon }(x,0)=\mathbf {U}_{approx}^{\varepsilon }(x,1)=\mathbf {0}, U_{approx,y}^{\varepsilon }(0,z)=U_{approx,y}^{\varepsilon }(1,z)\\&\quad =0, P_{approx}^{\varepsilon }(0,z)=p_{0}, P_{approx}^{\varepsilon }(1,z)=p_{1}. \end{aligned} \end{aligned}$$
(4.17)

Now, subtracting (4.16) and (4.17), we obtain the system satisfied for \((\mathbf {R}^{\varepsilon },r^{\varepsilon })\):

$$\begin{aligned} \begin{aligned}&\Delta _{xz}\mathbf {R}^{\varepsilon }+\varepsilon \Big ( 2h \frac{\partial ^2 \mathbf {R}^{\varepsilon }}{\partial z^2}+2zh' \frac{\partial ^2 \mathbf {R}^{\varepsilon }}{\partial z \partial x}+zh'' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}\Big )-k^2 \mathbf {R}^{\varepsilon }-M^2 R_x^{\varepsilon } \mathbf {e}_{1} \\&\quad =\nabla _{xz} r^{\varepsilon }+\varepsilon \Big ( zh' \frac{\partial r^{\varepsilon }}{\partial z}\mathbf {e}_{1}+h \frac{\partial r^{\varepsilon }}{\partial z}\mathbf {e}_{2}\Big )+\mathbf {E}^{\varepsilon }\ \text{ in }\ \Omega , \\&\text{ div}_{xz}\mathbf {R}^{\varepsilon }+\varepsilon \Big ( zh' \frac{\partial R_{x}^{\varepsilon }}{\partial z}+h \frac{\partial R_{y}^{\varepsilon }}{\partial z}\Big )=\beta ^{\varepsilon }\ \text{ in }\ \Omega , \\&\mathbf {R}^{\varepsilon }(x,0)=\mathbf {0}, \mathbf {R}^{\varepsilon }(x,1)=\mathbf {0}, \\&R_{y}^{\varepsilon }(0,z)=0, R_{y}^{\varepsilon }(1,z)=0, r^{\varepsilon }(0,z)=0, r^{\varepsilon }(1,z)=0, \end{aligned} \end{aligned}$$
(4.18)

where \(\vert \vert \mathbf {E}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}=\mathcal {O}(\varepsilon ^2)\), \(\vert \vert \beta ^{\varepsilon } \vert \vert _{L^{2}(\Omega )}=\mathcal {O}(\varepsilon ^2)\).

Now, we introduce \(\mathbf {w}^{\varepsilon }\) as the solution of the following auxiliary problem:

$$\begin{aligned} \begin{aligned}&\text{ div } \mathbf {w}^{\varepsilon }=r^{\varepsilon }\ \text{ in }\ \Omega , \\& \mathbf {w}^{\varepsilon }=\mathbf {0} \text{ on }\ \partial \Omega . \end{aligned} \end{aligned}$$
(4.19)

Due to Lemma 4.2 and assuming \(\int _{\Omega } r^{\varepsilon }=0\), problem (4.19) admits at least one solution satisfying the following estimate:

$$\begin{aligned} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega ^{\varepsilon })} \le C \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}. \end{aligned}$$
(4.20)

We now multiply (4.18) with \(\mathbf {w}^{\varepsilon }\) and integrate over \(\Omega \) to obtain:

$$\begin{aligned} \begin{aligned}&\vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2\\&\quad =\int _{\Omega } \nabla \mathbf {R}^{\varepsilon } \nabla \mathbf {w}^{\varepsilon }+\varepsilon \int _{\Omega } 2h \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}\frac{\partial \mathbf {w}^{\varepsilon }}{\partial z}+\varepsilon \int _{\Omega } 2h' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial x}\mathbf {w}^{\varepsilon }+\varepsilon \int _{\Omega }2h'z \frac{\partial \mathbf {R}^{\varepsilon }}{\partial x}\frac{\partial \mathbf {w}^{\varepsilon }}{\partial z} \\&\qquad -\varepsilon \int _{\Omega }zh'' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}\mathbf {w}^{\varepsilon }+k^2 \int _{\Omega } \mathbf {R}^{\varepsilon } \mathbf {w}^{\varepsilon }+M^2 \int _{\Omega } R_x^{\varepsilon } \mathbf {e}_{1} \mathbf {w}^{\varepsilon } \\&\qquad -\varepsilon \int _{\Omega } zh' r^{\varepsilon } \frac{\partial \mathbf {w}^{\varepsilon }}{\partial z}\mathbf {e}_{1}-\varepsilon \int _{\Omega } h'r^{\varepsilon } \mathbf {w}^{\varepsilon }\mathbf {e}_{1} -\varepsilon \int _{\Omega }hr^{\varepsilon } \frac{\partial \mathbf {w}^{\varepsilon }}{\partial z}\mathbf {e}_{2}+\int _{\Omega }\mathbf {E}^{\varepsilon } \mathbf {w}^{\varepsilon }. \end{aligned} \end{aligned}$$
(4.21)

Let us now estimate the terms on the right-hand side of (4.21) using Poincare’s inequality (4.6) and the estimate (4.20):

$$\begin{aligned} \Big \vert \int _{\Omega } \nabla \mathbf {R}^{\varepsilon } \nabla \mathbf {w}^{\varepsilon } \Big \vert&\le \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \nonumber \\ \varepsilon \Big \vert \int _{\Omega } 2h \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z} \frac{\partial \mathbf {w}^{\varepsilon }}{\partial z} \Big \vert&\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \nonumber \\ \varepsilon \Big \vert \int _{\Omega } 2h' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial x}\mathbf {w}^{\varepsilon } \Big \vert&\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \nonumber \\ \varepsilon \Big \vert \int _{\Omega } 2h'z \frac{\partial \mathbf {R}^{\varepsilon }}{\partial x} \frac{\partial \mathbf {w}^{\varepsilon }}{\partial z} \Big \vert&\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \nonumber \\ \varepsilon \Big \vert \int _{\Omega } zh'' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}\mathbf {w}^{\varepsilon } \Big \vert&\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\le C \varepsilon \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \nonumber \\ k^2 \Big \vert \int _{\Omega } \mathbf {R}^{\varepsilon } \mathbf {w}^{\varepsilon } \Big \vert&\le C \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \nonumber \\ M^2 \Big \vert \int _{\Omega } R_x^{\varepsilon }\mathbf {e}_{1}\mathbf {w}^{\varepsilon } \Big \vert&\le C \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}\vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \\ \varepsilon \Big \vert \int _{\Omega }zh'r^{\varepsilon } \frac{\partial \mathbf {w}^{\varepsilon }}{\partial z}\mathbf {e}_{1} \Big \vert&\le C \varepsilon \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \nonumber \\&\le C \varepsilon \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^{2}, \nonumber \\ \varepsilon \Big \vert \int _{\Omega } h'r^{\varepsilon } \mathbf {w}^{\varepsilon } \mathbf {e}_{1} \Big \vert&\le C \varepsilon \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \nonumber \\&\le C \varepsilon \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \nonumber \\ \varepsilon \Big \vert \int _{\Omega } h'r^{\varepsilon } \frac{\partial \mathbf {w}^{\varepsilon }}{\partial z} \mathbf {e}_{2} \Big \vert&\le C \varepsilon \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}, \nonumber \\&\le C \varepsilon \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}^2, \nonumber \\ \Big \vert \int _{\Omega } \mathbf {E}^{\varepsilon } \mathbf {w}^{\varepsilon } \Big \vert&\le C\vert \vert \mathbf {E} \vert \vert _{L^{2}(\Omega )} \vert \vert \nabla \mathbf {w} \vert \vert _{L^{2}(\Omega )} \le C \varepsilon ^2 \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )}. \nonumber \end{aligned}$$
(4.22)

Now, for sufficiently small \(\varepsilon \), we obtain from (4.21)–(4.22) the following estimate:

$$\begin{aligned} \vert \vert r^{\varepsilon } \vert \vert _{L^{2}(\Omega )} \le C ( \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega )}+\varepsilon ^2). \end{aligned}$$
(4.23)

We now multiply (4.18) by \(\mathbf {R}^{\varepsilon }\) and integrate over \(\Omega \) to obtain:

$$\begin{aligned} \begin{aligned}&k^2 \int _{\Omega } \vert \mathbf {R}^{\varepsilon } \vert ^2+M^2 \int _{\Omega } \vert R_{x}^{\varepsilon } \vert ^2+\int _{\Omega } \vert \nabla \mathbf {R}^{\varepsilon } \vert ^2\\&\quad =-\varepsilon \int _{\Omega }2h \frac{\partial \mathbf {R}^{\varepsilon }}{ \partial z} \frac{\partial \mathbf {R}^{\varepsilon }}{ \partial z}-\varepsilon \int _{\Omega }zh'' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}\mathbf {R}^{\varepsilon }-\varepsilon \int _{\Omega }zh' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}\frac{\partial \mathbf {R}^{\varepsilon }}{\partial x} \\&\qquad -\varepsilon \int _{\Omega }h' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial x}\mathbf {R}^{\varepsilon }-\varepsilon \int _{\Omega }zh' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial x} \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}+\varepsilon \int _{\Omega }zh'' \frac{\partial \mathbf {R}^{\varepsilon }}{\partial z}\mathbf {R}^{\varepsilon } \\&\qquad +\int _{\Omega }r^{\varepsilon } \text{ div } \mathbf {R}^{\varepsilon } -\varepsilon \int _{\Omega } zh'\frac{\partial r^{\varepsilon }}{\partial z}\mathbf {e}_{1} \mathbf {R}^{\varepsilon }-\varepsilon \int _{\Omega }h \frac{\partial r^{\varepsilon }}{\partial z}\mathbf {e}_{2} \mathbf {R}^{\varepsilon }-\int _{\Omega } \mathbf {E}^{\varepsilon } \mathbf {R}^{\varepsilon }. \end{aligned} \end{aligned}$$
(4.24)

We now use the following identity (see (4.18)\(_{2}\)):

$$\begin{aligned}&\int _{\Omega }r^{\varepsilon } \text{ div } \mathbf {R}^{\varepsilon }-\varepsilon \int _{\Omega }zh' \frac{\partial r^{\varepsilon }}{\partial z}\mathbf {e}_{1}\mathbf {R}^{\varepsilon }-\varepsilon \int _{\Omega }h \frac{\partial r^{\varepsilon }}{\partial z}\mathbf {e}_{2}\mathbf {R}^{\varepsilon }\\&\quad =\int _{\Omega }r^{\varepsilon } \text{ div }\mathbf {R}^{\varepsilon }+\varepsilon \int _{\Omega }r^{\varepsilon }h' \mathbf {R}^{\varepsilon }\mathbf {e}_{1}+\varepsilon \int _{\Omega }r^{\varepsilon }zh' \frac{\partial R_{x}^{\varepsilon }}{\partial z}+\varepsilon \int _{\Omega }r^{\varepsilon }h\frac{\partial R_{y}^{\varepsilon }}{\partial z}\\&\quad =\int _{\Omega } \beta ^{\varepsilon } r^{\varepsilon }+ \varepsilon \int _{\Omega }r^{\varepsilon }h'\mathbf {R}^{\varepsilon } \mathbf {e}_{1}. \end{aligned}$$

We now estimate the right hand side in (4.24) using Poincare’s inequality 4.6 and (4.23):

and now, for sufficiently small \(\varepsilon \), we obtain:

$$\begin{aligned} \vert \vert \nabla \mathbf {R}^{\varepsilon } \vert \vert _{L^{2}(\Omega ^{\varepsilon })}\le C \varepsilon ^2, \end{aligned}$$
(4.25)

yielding the estimate (4.15)\(_{1}\). Finally, from (4.23) and (4.25) we obtain the estimate (4.15)\(_{2}\). \(\square \)