1 Introduction

For a simple undirected graph G, let A(G) denote its adjacency matrix and D(G) denote the diagonal matrix of its degrees. The matrices \(L(G)=D(G)-A(G)\) and \(Q(G)=D(G)+A(G)\) are called the Laplacian matrix and the signless Laplacian matrix (or the Q-matrix) of G, respectively. The largest eigenvalues of A(G), L(G) and Q(G) are called the spectral radius (denoted by \(\rho (G)\)), the Laplacian spectral radius (denoted by \(\mu (G)\)) and the signless Laplacian spectral radius (denoted by q(G)) of G, respectively.

The investigation on the upper or lower bounds of the spectral radius, the Laplacian spectral radius and the signless Laplacian spectral radius of a graph is an important topic in the theory of graph spectra. For the related results, one may refer to [1, 12, 14, 21, 23, 24, 26] and the references therein. The problem of characterizing the graphs with maximal spectral radius among all graphs with a prescribed number of edges has been studied extensively (see, e.g., [1, 2, 8, 18, 20, 22, 25, 26]). Recently, Zhai et al. [27] characterized the graph with the largest signless Laplacian spectral radius among all graphs with given size and clique number. As applications, they determined the graph with maximal signless Laplacian spectral radius among all graphs with given size and among all graphs with given size and chromatic number, respectively. Zhai et al. [28] determined the largest Q-spectral radius of graphs with given size and matching number, and characterized the corresponding extremal graphs completely.

In this paper, we further study the problem of characterizing graphs under edge-condition restriction with maximal signless Laplacian spectral radius. For a graph G, let \(\Delta = \Delta (G)\) denote the maximum degree of G. We first give an upper bound on the signless Laplacian spectral radius of a connected graph with fixed size m.

Theorem 1.1

Let \(k\ge 1\), G be a connected graph with fixed size m and maximum degree \(\Delta \le m-k\). If \(m \ge 3k\), then

$$\begin{aligned} q(G)\le m-k+1+\frac{2k}{m-k}, \end{aligned}$$

and the equality holds if and only if \(G=K_4\) or \(K_3\).

Cvetković [3] proposed twelve directions for further research in the theory of graph spectra, one of which is “classifying and ordering graphs.” From then on, ordering graphs with various properties by their spectra, especially by their largest eigenvalues, becomes an attractive topic. There are many results on ordering graphs by their spectral radii and by their signless Laplacian spectral radii. For related reference, one may see [14, 21] and the references therein. Liu, Liu and Cheng [15] proved that for two connected graphs \(G_1\) and \(G_2\) with n vertices and m edges, if \(\Delta (G_1)\ge m-\frac{n-3}{2}\) and \(\Delta (G_1)>\Delta (G_2)\), then \(q(G_1)>q(G_2)\). Employing Theorem 1.1, we can prove the following theorem.

Theorem 1.2

Let \(G_1\) and \(G_2\) be two connected graphs with fixed size \(m\ge 4\). If \(\Delta (G_1)>\Delta (G_2)\) and \(\Delta (G_1)\ge \frac{2m}{3}+1\), then \(q(G_1)>q(G_2).\)

Employing Theorem 1.2 , we can determine the graphs with maximal signless Laplacian spectral radius among many classes of graphs with a prescribed number of edges. For example, let \(K_{\omega }^*\) denote the connected graph of size m obtained by adding some pendant edges to a vertex of the complete graph \(K_{\omega }\). Clearly, \(K_{\omega }^*\) is the unique graph with the largest maximum degree among all graphs with size m and clique number \(\omega \ge 2\), and \(\Delta (K_{\omega }^*)=m-\frac{1}{2}(\omega -1)(\omega -2)\). Let \(\Delta (K_{\omega }^*)\ge \frac{2}{3}m+1\). By Theorem 1.2, we have the following corollary, which is the weaker form of the main theorem of Zhai et al. in [27].

Corollary 1.3

Let G be a connected graph with size \(m\ge \max \{\frac{3}{2}(\omega -1)(\omega -2)+3,4\}\) and clique number \(\omega \ge 2\). If G is a graph without isolated vertices, then \(q(G) \le q(K_{\omega }^*)\) with equality if and only if \(G=K_{\omega }^*\).

In particular, let \(\omega =2\), we have the following corollary, which is also a result of Zhai et al. in [27].

Corollary 1.4

Let G be a connected graph with \(m\ge 4\) edges. Then \(q(G) \le q(K_{1, m})\), and the equality holds if and only if \(G=K_{1, m}\).

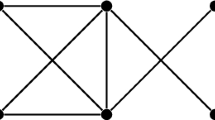
The diameter of a graph G is the maximum distance between any two vertices of G. Let m, d, p be integers with \(2 \le p \le d \le m-1\), and \(T_{m, d, p}\) denote the graph (shown in Fig. 1) obtained from a path \(P_{d+1}=v_1v_2\ldots v_{d+1}\) by adding \(m-d\) pendant edges to the vertex \(v_p\). Clearly, \(T_{m, d, p}\) is the graphs with the largest maximum degree among all graphs of size m and diameter d, and \(\Delta (T_{m, d, p})=m-d+2\). Let \(\Delta (T_{m, d, p})\ge \frac{2}{3}m+1\). By Theorem 1.2 and Lemma 2.7, we have the following corollary.

Corollary 1.5

Let G be a connected graph with fixed size m and diameter \(d \ge 3\). If \(m\ge 3(d-1)\) and \(G\ne T_{m,d,p}\), then

$$\begin{aligned} q(G)< q(T_{m,d,2})<q(T_{m,d,3})< \cdots <q(T_{m,d,\lfloor \frac{d}{2} \rfloor +1}). \end{aligned}$$

Furthermore, we weak the condition \(m\ge 3(d-1)\) in Corollary 1.5 by proving the following theorem.

Theorem 1.6

Let G be a connected graph with fixed size m and diameter d. If \(m\ge d+3\) and \(G\ne T_{m,d,p}\), then

$$\begin{aligned} q(G)< q(T_{m,d,2})<q(T_{m,d,3})< \cdots <q(T_{m,d,\lfloor \frac{d}{2} \rfloor +1}). \end{aligned}$$

Finally, we show that the above results also hold for the Laplacian spectral radius of a graph with a prescribed number of edges.

The rest of this paper is organized as follows. In Sect. 2, we recall some useful notions and Lemmas used further. In Sect. 3, we give the proofs of Theorems 1.1 and 1.2, respectively. In Sect. 4, we give the proof of Theorem 1.6. In Sect. 5, we give similar results on the Laplacian spectral radius of a graph with a prescribed number of edges.

2 Preliminary Lemmas

Denote by \(C_n\) and \(P_n\) the cycle and the path of order n, respectively. For \(v\in V(G),\) \(N_G(v)\) denotes the set of all neighbors of vertex v in G, and \(d(v)=|N_G(v)|\) denotes the degree of vertex v in G. The average degree of the neighbors of \(v_i\) is \(m(v_i)=\frac{1}{d(v_i)}\sum _{v_iv_j \in E(G)} d(v_j)\). Let \(G-xy\) denote the graph obtained from G by deleting the edge \(xy\in E(G).\) Similarly, \(G+xy\) is the graph obtained from G by adding an edge \(xy\notin E(G),\) where \(x, y\in V(G).\) A pendant vertex of G is a vertex of degree 1, and a pendant edge of G is an edge incident with a pendant vertex.

In order to complete the proofs of our main results, we need the following lemmas.

Lemma 2.1

([4]) Let G be a connected graph with \(n\ge 2\) vertices. Then \(q(G)\ge \Delta +1\) with equality if and only if G is the star \(K_{1,\, n-1}\).

Lemma 2.2

([5]) Let G be a graph on n vertices. Then

$$\begin{aligned} q(G)\le \max \{\,d(u)+d(v)\,|\,\, uv\in E(G)\,\}. \end{aligned}$$

If G is connected, then the equality holds if and only if G is regular or semi-regular bipartite.

Lemma 2.3

([7, 9]) Let G be a graph on n vertices. Then

$$\begin{aligned} q(G)\le \max \{\,d(u)+m(u)\,|\,\, u\in V(G)\,\}, \end{aligned}$$

and the equality holds if and only if G is either a regular graph or a semi-regular bipartite graph.

Remark 2.4

In 1998, Merris [17] first obtained this type inequality for the Laplacian spectral radius of a graph.

Lemma 2.5

([13, 19]) Let G be a connected graph. Then

$$\begin{aligned} q(G)\le \max _{uv\in E(G)}\left\{ \frac{d(u)(d(u)+m(u))+d(v)(d(v)+m(v))}{d(u)+d(v)}\right\} . \end{aligned}$$

Lemma 2.6

([11]) Let G be a connected graph, u and v be two vertices of G. Suppose that \(v_i\in N_G(v)\setminus N_G(u)\) \((1\le i\le s)\) and \(x =(x_1, x_2, \ldots , x_n)^T\) is the Perron vector of Q(G), where \(x_i\) corresponds to the vertex \(v_i\) \((1\le i \le n)\). Let \(G^*\) be the graph obtained from G by deleting the edges \(vv_i\) and adding the edges \(uv_i\) \((1\le i\le s)\). If \(x_u\ge x_v\) then \(q(G)<q(G^*)\).

Lemma 2.7

([6]) Let \(G(k,l)~(k,l \ge 0)\) be the graph obtained from a nontrivial connected graph G by attaching pendant paths of lengths k and l at some vertex v. If \(k \ge l \ge 1\), then

$$\begin{aligned} q(G(k,l))>q(G(k+1,l-1)). \end{aligned}$$

Lemma 2.8

([10]) Let \(d \ge 3\), \(m \ge d+2\), and \({\mathcal {T}}_{m,d}\) be the set of all trees with m edges and diameter d. If \(T\in {\mathcal {T}}_{m,d}\setminus \{T_{m,d,\lfloor \frac{d}{2} \rfloor +1},~ T_{m,d,\lfloor \frac{d}{2} \rfloor }, \ldots , T_{m,d,3},~ T_{m,d,2}\}\), then

$$\begin{aligned} \mu (T)<\mu (T_{m,d,2})<\mu (T_{m,d,3})<\cdots<\mu (T_{m,d,\lfloor \frac{d}{2} \rfloor })<\mu (T_{m,d,\lfloor \frac{d}{2} \rfloor +1}). \end{aligned}$$

3 The Proofs of Theorems 1.1 and 1.2

The proof of Theorem 1.1

Suppose that G is a connected graph of size m with \(\Delta =\Delta (G) \le m-k\). If \(m=3\) or 4, noting that \(m\ge 3k\), we know that \(k=1\). If \(m=3\), then \(G=K_3\) or \(P_4\). It is easy to see that \(q(G)\le 4\) with the equality if and only if \(G=K_3\). If \(m=4\), by computation with computer, we can verify that \(q(G)< \frac{14}{3}\). Namely, in the above two cases, Theorem 1.1 holds.

Next we always assume that \(m\ge 5\). Let w be a vertex of G such that

$$\begin{aligned} \max _{u\in V(G)}\left\{ d(u)+m(u)\right\} =d(w)+m(w)=d(w)+\frac{1}{d(w)}\sum _{wv\in E(G)}d(v). \end{aligned}$$

Then \(1 \le d(w) \le \Delta \). By Lemma 2.3, we have

$$\begin{aligned} q(G)\le \max _{u\in V(G)}\left\{ d(u)+m(u)\right\} =d(w)+\frac{1}{d(w)}\sum _{wv\in E(G)}d(v). \end{aligned}$$
(1)

If \(d(w)=1\), by (1), we have

$$\begin{aligned} q(G) \le 1+d(v)\le 1+\Delta \le m-k+1< m-k+1+\frac{2k}{m-k}. \end{aligned}$$

If \(d(w)=2\), by (1), we have

$$\begin{aligned} q(G) \le 2+\frac{m+1}{2} \le m-k+1+\frac{2k}{m-k} \end{aligned}$$

for \(m\ge 3k\). If the equality holds, then \(m=3k\) and \(k=1\). This contradicts \(m\ge 5\). Therefore, the equality cannot hold.

If \(3\le d(w)\le \Delta \le m-k\), noting that

$$\begin{aligned} \sum _{wv\in E(G)}d(v)\le d(w)+2(m-d(w))=2m-d(w), \end{aligned}$$
(2)

by (1), we have

$$\begin{aligned} q(G)\le d(w)+\frac{2m}{d(w)}-1. \end{aligned}$$

Let \(f(x)=x+\frac{2m}{x}.\) By mathematical analysis, it is easy to see that the function f(x) is strictly decreasing for \(0 < x \le \sqrt{2m}\) and strictly increasing for \(x \ge \sqrt{2m}\). It follows that its maximum in any closed interval is attained at one of the ends of this interval. Then we have

$$\begin{aligned} q(G)\le d(w)+\frac{2m}{d(w)}-1\le \max \left\{ 3+\frac{2m}{3},\,\, \Delta +\frac{2m}{\Delta }\right\} -1. \end{aligned}$$
(3)

Case 1 \(\Delta \ge \frac{2m}{3}\). Noting that \(\sqrt{2m} < \frac{2m}{3} \le \Delta \le m-k\), we have that \(\Delta \) and \(m-k\) are in the same monotonic interval of f(x). By (3), we have

$$\begin{aligned} q(G)\le \Delta +\frac{2m}{\Delta }-1\le m-k+1+\frac{2k}{m-k}. \end{aligned}$$

If the equality holds, then \(\Delta =m-k\) and the equality in (2) holds. And by Lemma 2.3, we have G is a regular graph and \(d(w)=m-k\). This implies that \((m-k)(m-k+1)=2m\). Namely \(m^2-(2k+1)m+k^2-k=0\). This contradicts \(m\ge 5\) and \(m \ge 3k\). Therefore, the equality cannot hold.

Case 2 \(3\le \Delta <\frac{2m}{3}\). In this case, we have \(3<\sqrt{2m}< \frac{2m}{3} \le m-k\). It follows that \(\frac{2m}{3}\) and \(m-k\) are in the same monotonic interval of f(x). Noting that \( f(3)=f(\frac{2m}{3})=\frac{2m}{3}+3\), we have \(f(\Delta ) \le f(3)=f\left( \frac{2m}{3}\right) \). By (3), we have

$$\begin{aligned} q(G)\le f(3)-1=f\left( \frac{2m}{3}\right) -1\le f(m-k)-1= m-k+1+\frac{2k}{m-k}. \end{aligned}$$

If the equality holds, then \(m=3k\) and \(\Delta =3\). And by Lemma 2.3, we have G is a regular graph and \(d(w)=3\). It follows that \(G=K_4\). If \(G=K_4\), then the equality holds clearly.

Combining the above arguments, we complete the proof. \(\square \)

The proof of Theorem 1.2

Let \(\Delta (G_1)=m-k_1\) and \(\Delta (G_2)=m-k_2\). Since \(\Delta (G_1)>\Delta (G_2)\) and \(\Delta (G_1)\ge \frac{2m}{3}+1\), it follows that \(k_1<k_2\) and \(k_1\le \frac{1}{3}m-1\). Let \(l=\min \{k_2, [\frac{1}{3}m]\}\). Then \(l\ge k_1+1\).

If \(k_1=0\), then \(k_2\ge 1\), \(G_1=K_{1, m}\) and \(q(G_1)=m+1\). Noting that \(\Delta (G_2)\le m-1\), by Theorem 1.1, we have

$$\begin{aligned} q(G_2)\le m+\frac{2}{m-1} \le m+ \frac{2}{3}< m+1=q(G_1) \end{aligned}$$

for \(m \ge 4\).

If \(k_1\ge 1\), noting that \(\Delta (G_2)=m-k_2\le m-l\) and \(l\le \frac{1}{3}m\), by Theorem 1.1 and Lemma 2.1, we have

$$\begin{aligned} q(G_2)\le m-l+2\le m-k_1+1<q(G_1). \end{aligned}$$

This completes the proof. \(\square \)

4 The Proof of Theorem 1.6

Fig. 1
figure 1

\(T_{m,\, d,\,p}\)

Full size image
Fig. 2
figure 2

\(G_m(r, k, l)\)

Full size image
Fig. 3
figure 3

\(G_m(r, k+l, 0)\)

Full size image

Proof

Let \({\mathcal {G}}(m, d)\) denote the set of all connected graphs with fixed size m and diameter d. Clearly, \(T_{m,\, d, \, p}\in {\mathcal {G}}(m, d)\) for \(2 \le p \le d \le n-1\). It is easy to check that Theorem 1.6 holds for \(d=2\). Next we always assume that \(d \ge 3\).

By Lemma 2.7, we have

$$\begin{aligned} q(T_{m,d,2})<q(T_{m,d,3})< \cdots <q(T_{m,d,\lfloor \frac{d}{2} \rfloor +1}). \end{aligned}$$

For \(G\in {\mathcal {G}}(m, d)\setminus \{T_{m,\, d,\,p}\,|\, 2\le p\le \lfloor d/2\rfloor +1\,\}\) and \(v_iv_j\in E(G)\), we claim that at least \(d-3\) edges of G are neither adjacent to \(v_i\) nor adjacent to \(v_j\). Therefore

$$\begin{aligned} d_i+d_j\le m-(d-3)+1=m-d+4. \end{aligned}$$

If \(d_i+d_j\le m-d+3\) for any edge \(v_iv_j\in E(G)\), by Lemma 2.2, we have

$$\begin{aligned} q(G)\le \max \{d_i+d_j\,|\,v_iv_j\in E(G)\}\le m-d+3. \end{aligned}$$

By Lemma 2.1, we have \(q(T_{m,\, d,\,2})>m-d+3\). Therefore \(q(G)<q(T_{m,\, d, \, 2}).\)

If there exists an edge \(v_iv_j\in E(G)\), without loss of generality, we may assume that \(i=1\) and \(j=2\) such that \(d_1+d_2=m-d+4\), then G must be one of the graphs \(G_m(r, k, l)\) (see Fig. 2), where all k, l, r are nonnegative integers, and \(d_1=k+r+2, d_2=l+r+2, 2r+k+l=m-d\).

Case 1 \(r=0\). In this case, G is a tree. Noting that L(G) and Q(G) are unitarily similar for a bipartite graph, by Lemma 2.8 , we have \(q(G)<q(T_{m,\, d, \, 2})\).

Case 2 \(r\ge 1\). Applying Lemma 2.6 to \(v_1\) and \(v_2\), we have

$$\begin{aligned} q(G)=q(G_m(r,k,l))\le q(G_m(r,k+l,0)), \end{aligned}$$

where \(G_m(r, k+l, 0)\) is shown in Fig. 3.

For \(G_m(r, k+l, 0)\), we have

$$\begin{aligned} d_1=m-d-r+2,d_2=r+2,d_1m_1\le m-d+r+4, d_2m_2 \le m-d+r+4. \end{aligned}$$

Direct computation shows that

$$\begin{aligned} \frac{d_1(d_1+m_1)+d_2(d_2+m_2)}{d_1+d_2}\le & {} m-d+3+\frac{2r^2-2(m-d-1)r+4+d-m}{m-d+4}\\\le & {} m-d+3~~~~~~~~~~~~ \end{aligned}$$

for \(m\ge d+3\) and \(1 \le r \le \frac{m-d}{2}\). It is easy to verify that

$$\begin{aligned} \frac{d_u(d_u+m_u)+d_v(d_v+m_v)}{d_u+d_v} \le m-d+3 \end{aligned}$$

for any other edge \(uv \in E(G_m(r, k+l, 0))\). It follows from Lemma 2.5 that

$$\begin{aligned} q(G)\le q(G_m(r, k+l, 0)) \le m-d+3 < q(T_{m,\,d,\,2}). \end{aligned}$$

Combining the above arguments, we complete the proof. \(\square \)

5 The Similar Results on the Laplacian Spectral Radius of a Graph with Fixed Size

For a connected graph G of order \(n\ge 2\), it is well known that \(\mu (G)\le q(G)\) with equality if and only if G is bipartite and \(\mu (G)\ge \Delta +1\) with equality if and only if \(\Delta (G)=n-1\). By a similar reasoning as the proofs of Theorems 1.1 and 1.2, we can obtain the following theorems and corollaries on the Laplacian spectral radius of a graph with fixed size.

Theorem 5.1

Let \(k\ge 1\), G be a connected graph with fixed size m and maximum degree \(\Delta \le m-k\). If \(m \ge 3k\), then

$$\begin{aligned} \mu (G)< m-k+1+\frac{2k}{m-k}. \end{aligned}$$

Theorem 5.2

Let \(G_1\) and \(G_2\) be two connected graphs with size \(m\ge 4\). If \(\Delta (G_1)>\Delta (G_2)\) and \(\Delta (G_1)\ge \frac{2m}{3}+1\), then \(\mu (G_1)>\mu (G_2).\)

Corollary 5.3

Let G be a graph with clique number \(\omega \ge 2\) and size \(m\ge \frac{3}{2}(\omega -1)(\omega -2)+3\). If G is a graph without isolated vertices, then \(\mu (G) \le \mu (K_{\omega }^*)\), with equality if and only if \(G=K_{\omega }^*\).

Corollary 5.4

Let G be a graph of size \(m\ge 3\). If G is a graph without isolated vertices, then \(\mu (G) \le \mu (K_{1, m})\), with equality if and only if \(G=K_{1, m}\).

By a similar reasoning as the proof of Theorem 1.6, we can prove the following theorem.

Theorem 5.5

Let G be a connected graph with fixed size m and diameter d. If \(m\ge d+3\) and \(G\ne T_{m,d,p}\), then

$$\begin{aligned} \mu (G)< \mu (T_{m,d,2})<\mu (T_{m,d,3})< \cdots <\mu (T_{m,d,\lfloor \frac{d}{2} \rfloor +1}). \end{aligned}$$

Remark 5.6

While this paper was under review, we realized that Lou, Guo, and Wang [16] independently proved the main conclusions of Theorems 1.6 and 5.5 with different methods.