Relaxed DP-3-Coloring of Planar Graphs Without Some Cycles

Abstract

Dvořák and Postle introduced the concept of DP-coloring to overcome some difficulties in list coloring. Sittitrai and Nakprasit combined DP-coloring and defective list coloring to define a new coloring—relaxed DP-coloring. For relaxed DP-coloring, Sribunhung et al. proved that planar graphs without 4- and 7-cycles are DP-(0, 2, 2)-colorable. Li et al. proved that planar graphs without 4, 8-cycles or 4, 9-cycles are DP-(1, 1, 1)-colorable. Lu and Zhu proved that planar graphs without 4, 5-cycles, or 4, 6-cycles, or 4, 7-cycles are DP-(1, 1, 1)-colorable. In this paper, we show that planar graphs without 4, 6-cycles or 4, 8-cycles are DP-(0, 2, 2)-colorable.

1 Introduction

All graphs in this paper are simple and undirected. Assume G is a plane graph, we use V(G), E(G), F(G), and $\delta (G)$ to denote its vertex set, edge set, face set, and minimum degree in the graph G, respectively. We use d(x) to denote the degree of x for each $x \in V(G) \cup F(G)$. We say that u is a d-vertex, $d^{+}$-vertex, or $d^{-}$-vertex if $d(u) = d$, $d(u) \ge d$, or $d(u) \le d$, respectively. Let b(f) be the boundary of a face f and write $f = [v_{1}v_{2}\dots v_{d}]$, where $v_{1}, v_{2}, \dots , v_{d}$ are the boundary vertices of f in a cyclic order. If $d(f)=k$ ($d(f)\ge k$ or $d(f)\le k$), then we call f a k-face ($k^+$-face or $k^-$-face) of G. A face is called a simple face if its boundary is a cycle. A cycle of length k is called a k-cycle, and a 3-cycle is usually called as a triangle. Two cycles or faces are adjacent if they share at least one edge, or their boundaries share at least one edge, respectively. Two adjacent cycles (or faces) $C_{1}$ and $C_{2}$ are normally adjacent if $|V(C_{1})\cap V(C_{2})| = 2$.

We say that L is a k-list assignment for a graph G if it assigns a list L(v) to each vertex v of G with $|L(v)| \ge k$. If G has a proper coloring $\phi$ such that $\phi (v) \in L(v)$ for each vertex v, then we say that G is L-colorable. A graph G is k-choosable if it is L-colorable for any k-list assignment L. The list chromatic number of G, denoted by $\chi _{\ell }(G)$, is the smallest integer k such that G is k-choosable.

Dvořák and Postle [2] introduced a generalization of list coloring. Let G be a graph and L be a list assignment on V(G). A graph $H_{L}$, simply write H, is said to be a cover of G if it satisfies all the following two conditions.

• (i) The vertex set of H is $\bigcup _{u\in V(G)}(\{u\}\times L(u))=\{(u, c): u \in V(G), c\in L(u)\}$.

• (ii) The edge set of H is ${\mathscr {M}} = \bigcup _{uv \in E(G)} {\mathscr {M}}_{uv}$, where ${\mathscr {M}}_{uv}$ is a matching between the sets $\{u\} \times L(u)$ and $\{v\} \times L(v)$.

Let T be a subset of V(H). If $|T \cap (\{u\}\times L(u)) | = 1$ for each vertex u in G, then T is called a transversal of H. When a transversal is independent, it is a DP-coloring. If every cover H of G with a k-assignment L has a DP-coloring, then the least number k is the DP-chromatic number of G, denoted by $\chi _{DP}(G)$. Note that DP-coloring is a generalization of list coloring. This implies that $\chi _{\ell }(G) \le \chi _{DP}(G)$. Chen et al. [1] proved that every planar graph without 4-cycles adjacent to 6-cycles is DP-4-colorable. Recently, it is proved that every planar graph is DP-4-colorable if it does not contain i-cycles adjacent to j-cycles for distinct i and j from $\{3, 4, 5, 6\}$, see [1, 6, 10, 12]. More sufficient conditions for a planar graph to be DP-4-colorable, see [3, 9, 11, 15].

In [14], Sittitrai and Nakprasit combined DP-coloring and relaxed list coloring (defective list coloring) into a new coloring as follows. Let H be a cover of a graph G with a k-assignment L. A transversal T of H is a $(d_{1}, d_{2}, \dots d_{k})$-coloring if every $(v, i) \in T$ has degree at most $d_{i}$ in H[T]. For any k-assignment L and any cover $H_{L}$, if $H_{L}$ has a $(d_{1}, d_{2}, \dots , d_{k})$-coloring, then we say G is DP-$(d_{1}, d_{2}, \dots d_{k})$-colorable. For defective DP-coloring, we refer the readers to [4, 5, 7].

Li et al. [8] proved that every planar graph without 4, 8-cycles, or 4, 9-cycles is DP-(1, 1, 1)-colorable. Lu and Zhu [13] proved that every planar graph without 4, 5-cycles, or 4, 6-cycles, or 4, 7-cycles is DP-(1, 1, 1)-colorable. Sribunhung et al. [16] proved that every planar graph without 4, 7-cycles is DP-(0, 2, 2)-colorable. In this paper, we prove that every planar graph without 4, 6-cycles, or 4, 8-cycles is DP-(0, 2, 2)-colorable.

To prove the conclusion, we need some new definitions. Suppose B is a condition imposed on ordered vertices. A DP-B-coloring of $H_{L}$ is a transversal T with ordered vertices from left to right such that each $(v, c) \in T$ satisfies condition B imposed on each element of H. Suppose T is a transversal of a cover H of G. We say that T is a DP-$B_{A}$-coloring if the vertices in T can be ordered from left to right such that:

• (i) For each $(v, 1)\in T$, (v, 1) has no neighbor on the left.

• (ii) For each $(v, c)\in T$ where $c \ne 1$, (v, c) has at most one neighbor on the left and that neighbor (if it exists) is adjacent to at most one vertex on the left of (v, c).

We say that G is DP-$B_{A}$-k-colorable if every cover $H_{L}$ of a graph G with a k-assignment L has a DP-$B_{A}$-coloring.

A graph is a linear forest if it is a forest with maximum degree at most two. It is easy to prove that a transversal T is a DP-$B_{A}$-coloring only if H[T] is a linear forest and $\{(v, c) \in T: c = 1\}$ is independent in H. But the inverse is not true. For example, $T = \{(x, 1), (y, 2), (z, 1)\}$, where (y, 2) is adjacent to (x, 1) and (z, 1) in H. Observe that T has no desired ordering as in the definition DP-$B_{A}$-coloring.

Theorem 1.1

Every planar graph without 4- and 8-cycles is DP-$B_{A}$-3-colorable.

Corollary 1.2

If G is a planar graph without 4- and 8-cycles, then

• (i) G is DP-(0, 2, 2)-colorable.

• (ii) V(G) can be partitioned into three sets in which each of them induces a linear forest and one of them is an independent set.

Theorem 1.3

Every planar graph without 4- and 6-cycles is DP-$B_{A}$-3-colorable.

Corollary 1.4

If G is a planar graph without 4- and 6-cycles, then

• (i) G is DP-(0, 2, 2)-colorable.

• (ii) V(G) can be partitioned into three sets in which each of them induces a linear forest and one of them is an independent set.

In order to prove results on DP-$B_{A}$-3-colorable graphs, Sribunhung et al. [16] gave some structural results.

Lemma 1.5

(Sribunhung et al. [16]) If G is not DP-$B_{A}$-3-colorable, but all its proper induced subgraphs are DP-$B_{A}$-3-colorable, then $\delta (G) \ge 3$.

Lemma 1.6

(Sribunhung et al. [16]) Suppose G is not DP-$B_{A}$-3-colorable, but all its proper induced subgraphs are DP-$B_{A}$-3-colorable. If a 3-vertex u in G is adjacent to a 3-vertex, then u has two $5^+$-neighbors. Moreover, if x is a 5-neighbor of u, then x has a $4^+$-neighbor.

We say that a 3-vertex is bad if it is adjacent to another 3-vertex; otherwise, it is a good 3-vertex.

2 Plane Graphs without 4- and 8-Cycles

Firstly, we give some structural results on plane graphs without 4- and 8-cycles.

Lemma 2.1

Let G be a plane graph without 4- and 8-cycles. Then the following statements hold.

• (i) There are no adjacent 3-faces.

• (ii) If a 3-face is adjacent to a 5-face, then they are normally adjacent.

• (iii) If $\delta (G)\ge 3$ and a 3-face is adjacent to a 6-face, then they are normally adjacent.

• (iv) If $\delta (G)\ge 3$, then each 7-face is not adjacent to any 3-face.

• (v) If $\delta (G)\ge 3$, then there are no adjacent 5-faces.

• (vi) If $\delta (G)\ge 3$, then each 5-face is adjacent to at most two 3-faces.

• (vii) If $\delta (G)\ge 3$, then each 6-face is adjacent to at most one 3-face.

Proof

• (i) If two 3-faces are adjacent, then G has a 4-cycle, a contradiction.

• (ii) Suppose to the contrary that a 5-face $[v_{1}v_{2}v_{3}v_{4}v_{5}]$ is adjacent to a 3-face $[v_1v_2u]$. Since they are not normally adjacent, $u \in \{v_{3}, v_{4}, v_{5}\}$. Then the 5-cycle has a chord, a contradiction.

• (iii) Suppose that a 6-face f is not a simple face. Then its boundary consists of two triangles. Let $f = [u'vuwvw']$ be a 6-face, where [uvw] and $[u'vw']$ are two triangles. Observe that G has no adjacent triangles. Suppose that f is adjacent to a 3-face. Then either [uvw] or $[u'vw']$ bounds a 3-face, and then there are at least two 2-vertices, a contradiction.

  So we may assume that the 6-face f is a simple face. Suppose to the contrary that $f = [v_{1}v_{2}v_{3}v_{4}v_{5}v_6]$ is not normally adjacent to a 3-face $[v_1v_2u]$. Then $u \in \{v_{3}, v_{4}, v_{5}, v_{6}\}$. By symmetry, we need to consider two cases: $u = v_{3}$ or $u = v_{4}$. If $u = v_{4}$, then $[v_{1}v_{2}v_{3}v_{4}]$ is a 4-cycle, a contradiction. It follows that $u=v_3$. Since $[v_{1}v_{2}v_{3}]$ is a 3-face, we have that $v_{2}$ is a 2-vertex, a contradiction.

• (iv) Assume that a 7-face $f_{1}$ is adjacent to a 3-face $f_{2}$. Observe that $f_{1}$ must be a simple face; otherwise, there is a 4-cycle in the boundary of $f_{1}$, a contradiction. Since $\delta (G) \ge 3$ and G does not have 4-cycle, $f_{1}$ and $f_{2}$ are normally adjacent. Now, $b(f_{1}) \cup b(f_{2})$ contains an 8-cycle, a contradiction.

• (v) Suppose to the contrary that a 5-face $[v_{1}v_{2}v_{3}v_{4}v_{5}]$ is adjacent to a 5-face $[v_{1}v_{2}uvw]$. Since there is no 8-cycle, $\{u, v, w\} \cap \{v_{3}, v_{4}, v_{5}\} \ne \emptyset$. Since $\delta (G) \ge 3$ and $[v_{1}v_{2}v_{3}v_{4}v_{5}]$ has no chord, we have $\{u, w\} \cap \{v_{3}, v_{4}, v_{5}\} = \emptyset$. By symmetry, we can obtain that $\{v_{3}, v_{5}\} \cap \{u, v, w\} = \emptyset$. If $v = v_{4}$, then $[vuv_{2}v_{3}]$ is a 4-cycle, a contradiction.

• (vi) Suppose to the contrary that a 5-face f is adjacent to three 3-faces. If those three 3-faces share vertices outside f, then G has a 4-cycle, a contradiction. Then the boundaries of these four faces form an 8-cycle, a contradiction. Thus, each 5-face is adjacent to at most two 3-faces.

• (vii) Suppose to the contrary that a 6-face f is adjacent to two 3-faces. If those two 3-faces share vertices outside f, then G has a 4-cycle, a contradiction. Then the boundaries of these three faces form an 8-cycle, a contradiction. Thus, each 6-face is adjacent to at most one 3-face. $\square$

Next, we prove the main result—Theorem 1.1.

Suppose to the contrary that G is a minimum counterexample to the statement. By Lemma 1.5, the minimum degree of G is at least three.

A 3-vertex is special if it is incident with a 3-face, a 5-face, and a 6-face.

Lemma 2.2

Let v be a 3-vertex. If v is incident with a 3-face $f_{1} = [vv_{1}v_{2}]$, a 5-face $f_{2} = [vv_{2}v_{3}v_{4}v_{5}]$, and a 6-face $f_{3} = [vv_{5}v_{6}v_{7}v_{8}v_{1}]$, then each of the following holds.

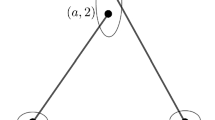
• (i) There is only one possibility for the special 3-vertex v, as shown in Fig. 1, where $v_{4}$ and $v_{7}$ are identical. Furthermore, $f_{2}$ is adjacent to exactly one 3-face, say $f_{1}$.

• (ii) There is no other special 3-vertex on the boundary of $f_{2}$.

Fig. 1

Some cases in Lemma 2.2. Note that $[v_{4}v_{5}v_{6}]$ does not bound a 3-face

Proof

(i) By Lemma 2.1(ii) and (iii), $f_{1}$ and $f_{2}$ are normally adjacent, $f_{1}$ and $f_{3}$ are normally adjacent. Note that the 6-face $f_{3}$ is adjacent to the 3-face $f_{1}$, the boundary of $f_{3}$ is a 6-cycle. Then $\{v, v_{1}, v_{2}\}$ and $\{v_{3}, v_{4}, v_{5}\}$ are disjoint, $\{v, v_{1}, v_{2}\}$ and $\{v_{5}, v_{6}, v_{7}, v_{8}\}$ are disjoint. If $\{v_{3}, v_{4}\}$ and $\{v_{6}, v_{7}, v_{8}\}$ are disjoint, $[v_{1}v_{2}\dots v_{8}]$ is an 8-cycle, a contradiction. So we may assume that $\{v_{3}, v_{4}\} \cap \{v_{6}, v_{7}, v_{8}\} \ne \emptyset$. If $v_{3} \in \{v_{6}, v_{7}, v_{8}\}$, then there is a 4-cycle, a contradiction. It follows that $v_{3} \notin \{v_{6}, v_{7}, v_{8}\}$. If $v_{4} = v_{8}$, then $[vv_{1}v_{8}v_{5}]$ is a 4-cycle, a contradiction. It is observed that $v_{4} \ne v_{6}$, for otherwise $v_{5}$ is a 2-vertex. Therefore, $v_{4}$ and $v_{7}$ are identical. Note that the 3-cycle $[v_{4}v_{5}v_{6}]$ does not bound a 3-face, for otherwise $v_{6}$ is a 2-vertex. Moreover, $v_{4}v_{5}$ cannot be incident with a 3-face; otherwise, there exists a 4-cycle with a chord $v_{4}v_{5}$. It is observed that $vv_{2}$ and $v_{4}v_{5}$ are is triangles; thus, no other edge on $f_{2}$ is contained in a triangle, for otherwise there exists an 8-cycle. It follows that $f_{2}$ is adjacent to exactly one 3-face.

(ii) Since every special 3-vertex is incident with a 3-face, the possible other special 3-vertex on $f_{2}$ is $v_{2}$. By Lemma 2.2(i), if $v_{2}$ is a special 3-vertex, then $v_{4}$ should be identified with a vertex on the 6-face incident with $v_{2}$, and $v_{3}v_{4}$ should be contained in a triangle, but this is impossible. $\square$

Let $\mu (x)=d(x)-4$ be the initial charge of a vertex or a face x, and let $\mu ^{*}(x)$ denote the final charge of x after the discharging process. By the Euler’s formula, $|V(G)| - |E(G)| + |F(G)| =2$ and $\sum _{v\in V(G)}d(v)=\sum _{f\in F(G)}d(f)=2|E(G)|$, we can derive the following identity: $\sum _{x\in V(G)\bigcup F(G)}\mu (x)=-8$. By the following discharging rules, we shall finally get $\mu ^{*}(x) \ge 0$ for all $x \in V(G) \cup F(G)$. Thus a contradiction is obtained and the proof is completed.

The discharging rules are as follows:

R1:

Each $5^+$-vertex gives $\frac{1}{4}$ to each adjacent bad 3-vertex.

R2:

Each $5^+$-face gives $\frac{1}{3}$ to each adjacent 3-face.

R3:

Each 5-face gives $\frac{1}{6}$ to each incident good 3-vertex and $\frac{1}{12}$ to each incident bad 3-vertex.

R4:

Let f be a 6-face or 7-face. Then f gives $\frac{1}{2}$ to each incident good 3-vertex and $\frac{1}{4}$ to each incident bad 3-vertex.

R5:

Each $8^+$-face gives $\frac{5}{6}$ to each incident good 3-vertex and $\frac{5}{12}$ to each incident bad 3-vertex.

Let $\beta (f)$ be the final charge of a 5-face f after applying the rules R1–R5.

R6:

If v is a special 3-vertex, then the incident 5-face f additionally sends $\beta (f)$ to v.

Now, we give a lower bound of $\beta (f)$ in R6.

Lemma 2.3

If f is a 5-face which is incident with a special 3-vertex, then $\beta (f) \ge \frac{1}{3}$.

Proof

By Lemma 2.2(i), the 5-face is adjacent to exactly one 3-face. If the 5-face is incident with at most two 3-vertices, then $\beta (f) \ge 1 - \frac{1}{3} - \frac{1}{6} \times 2 = \frac{1}{3}$ by R2 and R3. If the 5-face is incident with at least three 3-vertices, then the 5-face is incident with exactly three 3-vertices in which two of them are bad 3-vertices by Lemma 1.6. It follows that $\beta (f) \ge 1 -\frac{1}{3} - \frac{1}{6} - \frac{1}{12} \times 2 = \frac{1}{3}$ by R2 and R3. $\square$

Recall that every vertex v is a $3^{+}$-vertex.

Consider a good 3-vertex v. If v is incident with at least two $6^{+}$-faces, then $\mu ^{*}(v) \ge \mu (v) + \frac{1}{2} \times 2 = 0$ by R4 and R5. So we may assume that v is incident with at least two $5^{-}$-faces. By Lemma 2.1(v) and (i), v is incident with a 3-face and a 5-face. If v is incident with an $8^+$-face, then $\mu ^{*}(v) = \mu (v) + \frac{1}{6} + \frac{5}{6} = 0$ by R3 and R5. Otherwise, v is incident with a 3-face, a 5-face f, and a 6-face by Lemma 2.1(iv), i.e., v is a special 3-vertex. Then $\mu ^{*}(v) = \mu (v) + \frac{1}{6} + \frac{1}{2} + \beta (f) \ge 0$ by R3, R4, R6, and Lemma 2.3.

Consider a bad 3-vertex v. By Lemma 1.6, v is adjacent to two $5^{+}$-vertices. If v is incident with at least two $6^+$-faces, then $\mu ^{*}(v) \ge \mu (v) + \frac{1}{4} \times 2 + \frac{1}{4} \times 2 = 0$ by R1, R4, and R5. Then v is incident with at least two $5^{-}$-faces. By Lemma 2.1(v) and (i), v is incident with a 3-face and a 5-face. If v is incident with an $8^+$-face, then $\mu ^{*}(v) = \mu (v) + \frac{1}{4} \times 2 + \frac{1}{12} + \frac{5}{12} = 0$ by R1, R3, and R5. Otherwise, v is incident with a 3-face, a 5-face f, and a 6-face by Lemma 2.1(iv), i.e., v is a special 3-vertex. Then $\mu ^{*}(v) = \mu (v) + \frac{1}{4} \times 2 + \frac{1}{12} + \frac{1}{4} + \beta (f) > 0$ by R1, R3, R4, R6, and Lemma 2.3.

If v is a 4-vertex, then it is not involved in a discharging process and thus $\mu ^{*}(v)=\mu (v)=0$.

Consider a 5-vertex v. If v is adjacent to a bad 3-vertex, say u, then v has a $4^+$-neighbor by Lemma 1.6. Consequently, v is adjacent to at most four bad 3-vertices. Then $\mu ^{*}(v) \ge \mu (v) - \frac{1}{4} \times 4 = 0$ by R1.

Consider a d-vertex v where $d \ge 6$. Then $\mu ^{*}(v)\ge \mu (v) - d \times \frac{1}{4} = (d - 4) - d \times \frac{1}{4} > 0$ by R1.

Let f be a k-face.

• ${k = 3}$. It follows from Lemma 2.1(i) that f is adjacent to three $5^{+}$-faces, and $\mu ^{*}(f) = \mu (f) + 3 \times \frac{1}{3} = 0$ by R2.

• ${k = 4}$. Since G does not contain a 4-cycle, it does not contain a 4-face.

• ${k = 5}$. It follows from Lemma 2.1(vi) that f is adjacent to at most two 3-faces. Suppose that f is incident with a special 3-vertex. By Lemma 2.2(ii), f is incident with exactly one special 3-vertex. By R6 and Lemma 2.3, we get $\mu ^{*}(f) = 0$. So we may assume that f is not incident with a special 3-vertex. If f is incident with at most two 3-vertices, then $\mu ^{*}(f) \ge \mu (f) - \frac{1}{3} \times 2 - \frac{1}{6} \times 2 = 0$ by R2 and R3. If f is incident with at least three 3-vertices, then f is incident with exactly three 3-vertices in which two of them are bad 3-vertices by Lemma 1.6. It follows that $\mu ^{*}(f) \ge \mu (f) - \frac{1}{3} \times 2 - \frac{1}{6} - \frac{1}{12} \times 2 = 0$ by R2 and R3.

• ${k = 6}$. It follows from Lemma 2.1(vii) that f is adjacent to at most one 3-face. If f is incident with at most three 3-vertices, then $\mu ^{*}(f) \ge \mu (f) - \frac{1}{3} - \frac{1}{2} \times 3 = \frac{1}{6} > 0$ by R2 and R4. If f is incident with at least four 3-vertices, then f is incident with exactly four 3-vertices in which all of them are bad 3-vertices by Lemma 1.6. It follows that $\mu ^{*}(f) \ge \mu (f) - \frac{1}{3} - \frac{1}{4} \times 4 = \frac{2}{3} > 0$ by R2 and R4.

• ${k = 7}$. If f is not a simple face, then G contains a 4-cycle, a contradiction. So we may assume that f is a simple face. Then f is bounded by a 7-cycle. It follows from Lemma 2.1(iv) that f is not adjacent to any 3-face. By Lemma 1.6, f is incident with at most four 3-vertices. It follows that $\mu ^{*}(f) \ge \mu (f) - \frac{1}{2} \times 4 > 0$ by R4.

• ${k = 8}$. If f is a simple face, then G contains an 8-cycle, a contradiction. So f is not a simple face, its boundary consists of a 3-cycle and a 5-cycle, or two 3-cycles and a cut edge. It follows from Lemma 2.1(i) and (vi) that f is adjacent to at most two 3-faces. By Lemma 1.6, f is incident with at most five 3-vertices. If f is incident with at most four 3-vertices, then $\mu ^{*}(f) \ge \mu (f) - \frac{1}{3} \times 2 - \frac{5}{6} \times 4 = 0$ by R2 and R5. If f is incident with five 3-vertices, then at least four of the 3-vertices are bad by Lemma 1.6. It follows that $\mu ^{*}(f) \ge \mu (f) - \frac{1}{3} \times 2 - \frac{5}{6} - \frac{5}{12} \times 4 = \frac{5}{6} > 0$ by R2 and R5.

• ${k \ge 9}$. It follows from Lemma 2.1(i) that a 3-vertex is incident with at least two $4^+$-faces. If f is a 9-face incident with exactly four good 3-vertices, then f is adjacent to at most five 3-faces and f is not incident with a bad 3-vertex, thus $\mu ^{*}(f) \ge \mu (f)-\frac{1}{3}\times 5-\frac{5}{6}\times 4 = 0$ by R2 and R5. So we may assume that f is not a 9-face incident with exactly four good 3-vertices. In what follows, if f is a 9-face, then it is incident with at most three good 3-vertices.

Let $v_{1}, v_{2}, \dots , v_{k}$ be the vertices on the boundary of f, and let $f_i$ be the face sharing an edge $v_iv_{i+1}$ with f, where all the subscripts are taken modulo k. In order to easily check the final charge of f, we treat some transfer from an element to another element via some agents. Firstly, f sends $\frac{1}{2}$ to each vertex $v_{i}$ and sends an extra $\frac{1}{6}$ to each good 3-vertex $v_{i}$. Next, $v_{i}$ may play the role of agent. If $f_{i}$ is a 3-face, then the agent $v_{i}$ sends $\frac{1}{6}$ to $f_{i}$, and the agent $v_{i+1}$ sends $\frac{1}{6}$ to $f_{i}$, which corresponds to R2 that f sends $2 \times \frac{1}{6} = \frac{1}{3}$ to $f_{i}$.

Suppose that $v_{i}$ is a 3-vertex incident with $4^{+}$-vertices $v_{i-1}$ and $v_{i+1}$. Then the agent $v_{i-1}$ sends $\frac{1}{4}$ to $v_{i}$ if $f_{i-1}$ is a $4^{+}$-face; otherwise, the agent $v_{i-1}$ sends $\frac{1}{4} - \frac{1}{6}$ to $v_{i}$. Similarly, the agent $v_{i+1}$ sends $\frac{1}{4}$ or $\frac{1}{4} - \frac{1}{6}$ to $v_{i}$. Note that the 3-vertex $v_{i}$ is incident with at most one 3-face; thus, f sends at least $(\frac{1}{2} - \frac{1}{6}) + \frac{1}{6} + \frac{1}{4} + (\frac{1}{4} - \frac{1}{6}) = \frac{5}{6}$ to $v_{i}$, which corresponds to the first part of R5.

Suppose that $v_{i}$ is a 3-vertex, and one of $v_{i-1}$ and $v_{i+1}$ is also a 3-vertex. By symmetry, let $v_{i+1}$ be a 3-vertex. Then the agent $v_{i-1}$ sends $\frac{1}{4}$ or $\frac{1}{4} - \frac{1}{6}$ to $v_{i}$, and then f sends at least $(\frac{1}{2} - \frac{1}{6}) + (\frac{1}{4} - \frac{1}{6}) = \frac{5}{12}$ in total to $v_{i}$, which corresponds to the second part in R5.

For each $4^{+}$-vertex $v_{i}$, when it plays the role of agent, it receives $\frac{1}{2}$ from f and gives at most $2(\frac{1}{4} - \frac{1}{6}) + 2 \times \frac{1}{6} = \frac{1}{2}$.

So we can treat f sends $\frac{1}{2}$ to each vertex $v_{i}$, and $v_{i}$ maybe plays the role of agent to redistribute at most $\frac{1}{2}$ to incident 3-faces and 3-vertices; additionally, f sends an extra $\frac{1}{6}$ to each good 3-vertices.

If f is a 9-face incident with at most three good 3-vertices, then $\mu ^{*}(f)\ge \mu (f)-\frac{1}{2} \times 9 - \frac{1}{6} \times 3 = 0$. If f is a $10^+$-face, then f is incident with at most $\frac{k}{2}$ good 3-vertices, and then $\mu ^{*}(f) \ge \mu (f) - \frac{1}{2} \times k -\frac{1}{6} \times \frac{k}{2} = \frac{1}{6} > 0$.

This completes the proof.

3 Plane Graphs without 4- and 6-Cycles

In this section, we prove the second main result—Theorem 1.3.

Assume that G is a counterexample to Theorem 1.3, but all of its proper induced subgraphs are DP-$B_{A}$-3-colorable. By Lemma 1.5, the minimum degree of G is at least three. Since G has no 4- or 6-cycles, the following statements hold.

Lemma 3.1

A 3-face is not adjacent to a $6^{-}$-face.

Proof

If two 3-faces are adjacent, then G has a 4-cycle, a contradiction.

Suppose that a 5-face $[v_{1}v_{2}v_{3}v_{4}v_{5}]$ is adjacent to a 3-face $[v_1v_2u]$. Since there is no 6-cycle, $u \in \{v_{3}, v_{4}, v_{5}\}$. But the 5-cycle has a chord, then there is a 4-cycle, a contradiction.

Since there is no 6-cycle in G, the boundary of a 6-face consists of two triangles. Let $f = [u'vuwvw']$ be a 6-face, where [uvw] and $[u'vw']$ are two triangles. Observe that G has no adjacent triangles. Suppose that f is adjacent to a 3-face. Then either [uvw] or $[u'vw']$ bounds a 3-face, and then there are at least two 2-vertices, a contradiction. $\square$

We once again use the discharging method to complete the proof. Let $\mu (x)=d(x)-4$ be the initial charge of a vertex or a face x, and let $\mu ^{*}(x)$ denote the final charge of x after the discharging procedure. According to the Euler’s formula and handshaking theorem, the sum of the initial charge is $-8$. By the following discharging rules, we should finally get $\mu ^{*}(x)\ge 0$ for all $x\in V(G)\cup F(G)$. Thus a contradiction is obtained and the counterexample does not exist.

The discharging rules are as follows:

R1:

Each $5^+$-vertex gives $\frac{1}{4}$ to each adjacent bad 3-vertex.

R2:

Each $7^+$-face gives $\frac{1}{3}$ to each adjacent 3-face.

R3:

Each 5-face gives $\frac{1}{3}$ to each incident good 3-vertex and $\frac{1}{6}$ to each incident bad 3-vertex.

R4:

Each $6^+$-face gives $\frac{1}{2}$ to each incident good 3-vertex and $\frac{1}{4}$ to each incident bad 3-vertex.

Recall that every vertex v is a $3^+$-vertex.

Consider a good 3-vertex v. If v is not incident with a 3-face, then v is incident with three $5^+$-faces; thus, $\mu ^{*}(v) \ge \mu (v) + \frac{1}{3} \times 3 = 0$ by R3 and R4. If v is incident with a 3-face, then the other two faces are $7^+$-faces by Lemma 3.1; thus, $\mu ^{*}(v) = \mu (v) + \frac{1}{2} \times 2 = 0$ by R4.

Consider a bad 3-vertex v. If v is not incident with a 3-face, then v is incident with three $5^+$-faces; thus, $\mu ^{*}(v) \ge \mu (v) + \frac{1}{4} \times 2 + \frac{1}{6} \times 3 = 0$ by R1, R3, and R4. If v is incident with a 3-face, then the other two faces are $7^+$-faces by Lemma 3.1, and then $\mu ^{*}(v) = \mu (v)+\frac{1}{4} \times 2 + \frac{1}{4} \times 2 = 0$ by R1 and R4.

If v is a 4-vertex, then it does not involve in a discharging process and then $\mu ^{*}(v)=\mu (v)=0$.

Consider a 5-vertex v. If v is adjacent to a bad 3-vertex, say u, then v has a $4^+$-neighbor by Lemma 1.6. Consequently, v is adjacent to at most four bad 3-vertices. Then $\mu ^{*}(v) \ge \mu (v) - 4 \times \frac{1}{4} = 0$ by R1.

Consider a d-vertex v where $d \ge 6$. Then $\mu ^{*}(v)\ge \mu (v) - d \times \frac{1}{4} = (d - 4) - d \times \frac{1}{4} > 0$ by R1.

Let f be a k-face.

• $\varvec{k = 3}$. It follows from Lemma 3.1 that f is adjacent to three $7^{+}$-faces. Thus $\mu ^{*}(f)=\mu (f)+3\times \frac{1}{3}=0$ by R2.

• $\varvec{k = 4}$. Since G does not contain a 4-cycle, it does not contain a 4-face.

• $\varvec{k = 5}$. It follows from Lemma 3.1 that f is not adjacent to any 3-face. If f is incident with at most two 3-vertices, then $\mu ^{*}(f) \ge \mu (f) - \frac{1}{3} \times 2 > 0$ by R3. If f is incident with at least three 3-vertices, then it is incident with exactly three 3-vertices in which two of them are bad 3-vertices by Lemma 1.6. It follows that $\mu ^{*}(f) \ge \mu (f) - \frac{1}{6} \times 2 - \frac{1}{3} > 0$ by R3.

• $\varvec{k = 6}$. It follows from Lemma 3.1 that f is not adjacent to a 3-face. Since there are no 6-cycles in G, the boundary of f consists of two triangles, and f is incident with at most four 3-vertices. If f is incident with at most three 3-vertices, then $\mu ^{*}(f) \ge \mu (f) - \frac{1}{2} \times 3 = \frac{1}{2} > 0$ by R4. If f is incident with four 3-vertices, then each 3-vertex is bad; thus, $\mu ^{*}(f)=\mu (f)-\frac{1}{4}\times 4=1>0$ by R4.

• $\varvec{k \ge 7}$. Similar to the proof in Theorem 1.1, we can treat f sends $\frac{3}{7}$ to each incident vertex and redistribute at most $\frac{3}{7}$ to incident 3-faces and 3-vertices. Thus, $\mu ^{*}(f) \ge \mu (f) - \frac{3}{7} \times k \ge 0$.

This completes the proof.