Riemann Problem and Wave Interactions for a Temple-class Hyperbolic System of Conservation Laws

Abstract

The exact solutions of the Riemann problem for a Temple-class hyperbolic system of conservation laws consisting of three scalar equations are obtained in fully explicit forms, in which all the state variables may contain Dirac delta functions simultaneously under some suitable Riemann initial data. The generalized Rankine–Hugoniot conditions and the over-compressive entropy condition are derived for such very singular delta shock wave solution. We also prove rigorously this delta shock wave solution satisfying the system in the sense of distributions. Moreover, three typical cases for the delta shock interaction problem are provided in order to illustrate some interesting nonlinear wave phenomena. In addition, some numerical simulations are offered to confirm the theoretical results.

1 Introduction

In this paper, we are concerned with the following hyperbolic system of conservation laws

$$\begin{aligned} \begin{array}{c} \left\{ \begin{aligned} &{}u_t+(u\phi (au+bv+cw))_x=0, \\ &{}v_t+(v\phi (au+bv+cw))_x=0, \\ &{}w_t+(w\phi (au+bv+cw))_x=0, \end{aligned}\right. \end{array} \end{aligned}$$

(1.1)

subjected to the Riemann-type initial conditions given by

$$\begin{aligned} (u,v,w)(x,0)= \left\{ \begin{aligned}&(u_{-},v_{-},w_{-}),&x<0,\\&(u_{+},v_{+},w_{+}),&x>0. \end{aligned} \right. \end{aligned}$$

(1.2)

For convenience, let $\phi {(r)}$ be a given smooth function of the combined state variable $r=au+bv+cw$ satisfying $a^{2}+b^{2}+c^{2}\not =0$, with a, b and c being given constants. It is shown that the system (1.1) has only two different eigenvalues $\lambda _1=\phi (r)$ and $\lambda _2=\phi (r)+r\phi '(r)$, in which $\lambda _1$ is fold two times and the elementary waves associated with $\lambda _1$ are coincident. In this work, we restrict ourselves to the following reasonable assumptions [1]:

$$\begin{aligned} \phi '(r)>0,\quad (r\phi (r))''>0,\quad \phi (0)=0, \end{aligned}$$

(1.3)

which means that the system (1.1) is non-strictly (or weakly) hyperbolic because r may be positive or negative. It is evident to find that the shock curve has the same expression as the rarefaction one, so the system (1.1) belongs to the so-called hyperbolic system of Temple class [2, 3].

It is obvious that the system (1.1) is also a reasonable generalization of the following general $2\times 2$ Keyfitz–Kranzer system [4]

$$\begin{aligned} \left\{ \begin{aligned} u_t+(u\phi (u,v))_x=0,\\ v_t+(v\phi (u,v))_x=0, \end{aligned}\right. \end{aligned}$$

(1.4)

which has been extensively addressed in [5,6,7,8] for example. It should be emphasized that the system (1.4) was first introduced by Keyfitz and Kranzer [4] to discuss the wave propagation problem for an idealized nonlinear elastic string model, in which $\phi (u,v)=\phi (r)$ was a given smooth function of $r=\sqrt{u^{2}+v^{2}}$. Moreover, the admissibility criteria of solutions and the propagation and cancellation of initial oscillations for the system (1.4) were well considered by Chen [5]. The existence, uniqueness and stability of the Cauchy problem for the extended Keyfitz–Kranzer system were also consider by Freistuhler [6] under some suitable initial conditions. In addition, the system (1.4) was also adopted by Kearsley and Reiff [7] to interpret some characteristics of solar wind in magnetohydrodynamic. Very recently, some detailed examples for the system (1.4) have been provided and illustrated by Betancourt et al. [8]. To the end, it is necessary to point out that the asymmetric Keyfitz–Kranzer system has also been proposed by Lu recently, please refer to [9,10,11] for details. It should be stressed that Yang and Zhang [1] investigated a special form of $2\times 2$ Keyfitz–Kranzer system as follows:

$$\begin{aligned} \left\{ \begin{aligned} u_t+(\phi u)_x=0,\\ v_t+(\phi v)_x=0, \end{aligned}\right. \end{aligned}$$

(1.5)

where $\phi =\phi (r)$ is a given smooth function of $r=au+bv$ satisfying $a^2+b^2\ne 0$, where a and b are constants. It was shown in [1] that both the two state variables u and v contain Dirac delta function simultaneously. Furthermore, they [12] also considered the Riemann problem for the system (1.5) when $\phi =\phi (r)$ is a given smooth function of $r=\frac{u}{v}$, in which some new interesting nonlinear wave phenomena were discovered. Subsequently, Shen [13] considered the interaction problem of delta shock wave for the system (1.5) with $\phi (u,v)=\phi (uv)$. Very recently, De la Cruz et al. [14] have investigated the interaction between delta shock waves and contact discontinuities for a nonsymmetric Keyfitz–Kranzer system by using the method of splitting $\delta$-function together with the method of characteristics, please also see the related study about this nonsymmetric Keyfitz–Kranzer system under the viscosity term [15] or the Coulomb-like friction term [16].

Inspired by the above-mentioned work, it is very natural and expected to investigate the extended Keyfitz–Kranzer system (1.1), which belongs to the so-called Temple-class hyperbolic system of conservation laws. More precisely, the system (1.1) is also a special case of the $n\times n$ symmetric Keyfitz–Kranzer system introduced by Freistuhler [6] when $n=3$ and $r=au+bv+cw$ are taken. In addition, it is also interesting to mention that the triple-component nonlinear chromatography system is a special case of our system (1.1) by taking $\phi {(r)}=1+\frac{1}{1+r}$ and then transforming appropriately, please see Eqs. (3.14)–(3.15) in [17] and Eq. (1.1) in [18]. In the current work, the first task is to solve the exact solutions of the Riemann problem (1.1) and (1.2) for all the possible cases under the assumptions (1.3). It is noticed interestingly that five kinds of Riemann solutions are constructed in fully explicit forms for the Riemann problem (1.1) and (1.2) by using the combination of classical waves including shock wave, rarefaction wave and contact discontinuity with the help of the analysis in the phase plane. Moreover, it is discovered that if $r_-\ge 0 \ge r_+$, then the Riemann problem (1.1) and (1.2) admits a delta shock wave solution, in which Dirac delta functions are included in all the state variables u, v and w at the same time. Moreover, we extract the generalized Rankine–Hugoniot conditions to describe the relationship among the location, the wave speed, the strength and the assignment of the state variables u, v and w on such delta shock front. In order to guarantee the uniqueness of delta shock wave solution, the over-compressive entropy condition is also proposed, which shows that all the characteristic lines on the both sides enter the delta shock front. To the end, we can also prove strictly that such delta shock wave solution satisfies the system (1.1) in the sense of distributions. In addition, we also simulate the delta shock wave solution of the Riemann problem (1.1) and (1.2) for the different cases of a, b and c by employing the upwind scheme. It is shown clearly that the numerical results are in complete agreement with our theoretical analysis. To the end, it is of interest to note that the Riemann solutions for the system (1.1) share the similar structures of Riemann solutions for a simplified thin film model [19]. However, it should be stressed that the Dirac delta functions are developed in all the state variables u, v and w simultaneously in the current work, which is completely different from that in [19] where the Dirac delta function is only developed in the single state variable v.

At the present time, the concept of delta shock wave has been widely recognized and accepted in the hyperbolic theory of conservation laws, which refers to the form of standard Dirac $\delta$-measure supported upon a shock front. In general, the concept of delta shock wave is a reasonable generalization and extension of the concept of normal shock wave due to more excessive compressibility of delta shock wave than that of shock wave. More precisely, the number of characteristic lines breaking into the delta shock front is usually more than the number of characteristic lines incoming the normal shock front. To the end, it is necessary to address that the concept of delta shock wave is different from that of delta wave which often appears in the current literature. In fact, the concept of delta wave only refers to the form of standard Dirac $\delta$-measure involved in a solution but it is not necessarily superimposed on the shock front, which is boarder than the concept of delta shock wave. However, it often leads to some confusion and abuse in the current literature.

With the Riemann solutions in hand, it is very significant and also natural to concern with the interaction problem of delta shock wave with other classical waves for the system (1.1). For this purpose, we consider the initial condition consisting of three piecewise constant states as follows:

$$\begin{aligned} (u,v,w)(x,0)= \left\{ \begin{aligned}&(u_-,v_-,w_-),&-\infty<x<-\varepsilon ,\\&(u_m,v_m,w_m),&-\varepsilon<x<\varepsilon ,\\&(u_+,v_+,w_+),&\varepsilon<x<+\infty , \end{aligned}\right. \end{aligned}$$

(1.6)

where $\varepsilon$ is a sufficiently small positive number. More precisely, we consider the interaction between a delta shock wave $\delta S$ starting from $(-\varepsilon ,0)$ when $r_-\ge 0 \ge r_m$ and a shock wave S followed by a contact discontinuity J when $r_+ < r_m \le 0$, a composite wave JR consisting of a contact discontinuity J attached on the wave back of the rarefaction wave R when $r_m=0$ or another delta shock wave $\delta S$ starting from $(\varepsilon ,0)$ when $r_m \ge 0 \ge r_+$, respectively. The strength of delta shock wave is obtained explicitly by using the split delta function method proposed by Nedeljkov [20,21,22] in the construction of the global solution to the double Riemann problem (1.1) and (1.6).

In what follows, let us briefly review the split delta function method for the reason that we will make use of such method heavily to deal with the wave interaction problem. For convenience, let us denote the notations $R^{2}_{+}=(-\infty ,+\infty )\times (0,+\infty )$ and $\overline{R^{2}_{+}}=(-\infty ,+\infty )\times [0,+\infty )$. Let $\Gamma$ be a piecewise smooth boundary curve to separate the two disjoint open sets $\Omega _{1}$ and $\Omega _{2}$, where $\overline{\Omega _{1}}\cup \overline{\Omega _{2}}=\overline{R^{2}_{+}}$ and $\Omega _{1} \cap \Omega _{2}=\emptyset$. Let ${\mathcal {C}}(\Omega _{i})$ be a space of bounded and continuous real-valued functions endowed with the $L^{\infty }$-norm and further let ${\mathcal {M}}(\Omega _{i})$ be the space of measures on $\Omega _{i}$, where $i=1,2$. Let us consider the following two spaces ${\mathcal {C}}_{\Gamma }=\mathcal {C}(\Omega _{1})\times {\mathcal {C}}(\Omega _{2})$ and $\mathcal {M}_{\Gamma }={\mathcal {M}}(\Omega _{1})\times \mathcal {M}(\Omega _{2})$, then the product of $G=(G_{1},G_{2})\in \mathcal {C}_{\Gamma }$ and $D=(D_{1},D_{2})\in {\mathcal {M}}_{\Gamma }$ can be defined by an element $GD=(G_{1}D_{1},G_{2}D_{2})\in \mathcal {M}_{\Gamma }$, in which $G_{i}D_{i}~(i=1,2)$ can be defined by the common product between a continuous function and a measure. Each measure on $\overline{\Omega _{i}}$ is regarded as a measure on $\overline{R^{2}_{+}}$ with support in $\overline{\Omega _{i}}$. Following up this way, we arrive at a mapping $m:{M}_{\Gamma }\rightarrow {M}(\overline{R^{2}_{+}})$ by taking $m(D)=D_{1}+D_{2}$. Moreover, one further has $m(GD)=G_{1}D_{1}+G_{2}D_{2}$. For instance, if the following typical Dirac delta function $\delta (x-\gamma (t))\in \mathcal {M}(\overline{R^{2}_{+}})$ along a piecewise smooth curve $x=\gamma (t)$ is split in the non-unique manner into a left-hand component $D^{-}\in {\mathcal {M}}(\Omega _{1})$ and a right-hand one $D^{+} \in {\mathcal {M}}(\Omega _{2})$, then it holds that

$$\begin{aligned} \delta (x-\gamma (t))=\beta _{-}(t)D^{-}+\beta _{+}(t)D^{+}\ \ \mathrm{with} \ \ \beta _{-}(t)+\beta _{+}(t)=1. \end{aligned}$$

In summary, the concept of solution used in the current work can be illustrated in the following way: perform the multiplication and composition operations in the space ${M}_{\Gamma }$ and subsequently take the mapping $m:{M}_{\Gamma }\rightarrow {M}(\overline{R^{2}_{+}})$ before differentiating in the traditional space of distributions.

In this work, it is of very interest to mention that the delta shock wave $\delta S$ is separated into a delta contact discontinuity $\delta J$ and a shock wave S when it begins to penetrate the composite wave JR. Subsequently, the shock wave begins to penetrate rarefaction wave R. As a result, if $r_->r_+>0$, then the shock wave S is able to cancel the whole rarefaction wave R completely in finite time. Otherwise, if $r_+>r_-\ge 0$, then the shock wave S cannot penetrate R completely and finally takes the line $x=\varepsilon +(\phi (r_-)+r_-\phi _r(r_-))t$ as the asymptotic line. It should be mentioned that the interaction problem of delta shock wave has been extensively investigated such as in [23,24,25,26,27,28,29,30,31] for different hyperbolic systems of conservation laws, which is the basis in the construction of the Riemann solutions for the two-dimensional and multi-dimensional situations [32].

The paper is organized as follows: In Sect. 2, we construct the solutions of the Riemann problem (1.1) and (1.2) for all the possible cases under the assumptions (1.3). In particular, when the condition $r_-\ge 0\ge r_+$ is satisfied, delta shock wave will appear in the solution of the Riemann problem (1.1) and (1.2). We clarify the generalized Rankine–Hugoniot conditions and over-compressive entropy condition for this delta shock wave, which can be used to solve the delta shock wave solution of the Riemann problem (1.1) and (1.2). In Sect. 3, we study the interaction problem of delta shock wave with other classical waves for the system (1.1). Then, the global solutions of the double Riemann problem (1.1) and (1.6) are constructed explicitly for three typical cases. Furthermore, we pay attention to the limiting problem whether the solutions of the double Riemann problem (1.1) and (1.6) are identical with the corresponding ones of (1.1) and (1.2) or not when $\varepsilon \rightarrow 0$. In the end, we present some representative numerical results for the delta shock wave solution of the Riemann problem (1.1) and (1.2) in Sect. 4.

2 The Riemann Problem (1.1) and (1.2)

In order to solve the Riemann problem (1.1) and (1.2) for all kinds of situations, the process can be divided into the following three subsections. In the first subsection, we consider the elementary waves for the system (1.1). Subsequently, we construct the solutions of Riemann problem (1.1) and (1.2) for five different cases as follows: (1) $r_+<r_-<0$, (2) $r_-<r_+\le 0$, (3) $r_-<0<r_+$, (4) $0\le r_-<r_+$ and (5) $0<r_+<r_-$ by using the combinations of elementary waves. To the end, it is found that delta shock wave appears in the solution of the Riemann problem (1.1) and (1.2) in the case of $r_+\le 0\le r_-$, in which the generalized Rankine–Hugoniot relations and entropy condition are deduced for such delta shock wave.

2.1 Elementary Waves for the System (1.1)

In this subsection, we are concerned with the classical waves of the system (1.1). The eigenvalues of system (1.1) are as follows

$$\begin{aligned} \lambda _{1}=\phi ,\quad \lambda _{2}=\phi +r\phi ', \end{aligned}$$

(2.1)

where $\lambda _1$ is a double eigenvalue, which means that the two elementary waves corresponding to $\lambda _1$ are coincident. The right eigenvectors corresponding to $\lambda _1$ and $\lambda _2$ are $\overrightarrow{r_{1}}^1=(b,-a,0)^T$, $\overrightarrow{r_{1}}^2=(c,0,-a)^T$ and $\overrightarrow{r_{2}}=(u,v,w)^T$, respectively. Let the notation $\nabla =(\frac{\partial }{\partial u},\frac{\partial }{\partial v},\frac{\partial }{\partial w})$ be the gradient operator, then it is easy to check that

$$\begin{aligned} \nabla \lambda _{1}\cdot \overrightarrow{r_{1}}^1\equiv 0,\quad \nabla \lambda _{1}\cdot \overrightarrow{r_{1}}^2\equiv 0,\quad \nabla \lambda _{2}\cdot \overrightarrow{r_{2}}=r(r\phi )'', \end{aligned}$$

which allows us to know that $\lambda _{1}$ is linearly degenerate and $\lambda _{2}$ is genuinely nonlinear provided that $r(r\phi )''\ne 0$. Let us denote the curved surface $\Sigma =\{(u,v,w)|\lambda _{1}=\lambda _{2}\}=\{(u,v,w)|r\phi '(r)=0\}$ in the (u, v, w) state space, then the strict hyperbolicity of the system (1.1) fails on such curved surface $\Sigma$. It should be addressed here that our assumptions (1.3) are in full coincide with those in [1, 4]. In the assumptions (1.3), the monotonicity condition $\phi '(r)>0$ makes us to judge the ordering relation between $\lambda _{1}$ and $\lambda _{2}$ obviously. Then, the second condition $(r\phi (r))''>0$ enables us to ensure that the $\lambda _{2}$-characteristic field is genuinely nonlinear when $r\ne 0$. In addition, this condition also allows us to derive the monotonicity of $\phi (r)+r\phi '(r)$ with respect to r immediately, such that the state variables r and then (u, v, w) in the interior of the front (or back) rarefaction wave fan can be determined uniquely by (2.4) [or (2.5)] later. Of course we may assume $(r\phi (r))''<0$ instead of $(r\phi (r))''>0$ and the problem can be dealt with similarly. Finally, the last condition $\phi (0)=0$ is trivial for the convenience of computation. As a consequence, the elementary waves in connection with $\lambda _{1}$ is contact discontinuities as well as the elementary waves in connection with $\lambda _{2}$ is either shock waves or rarefaction waves. From (2.1), we can get $\lambda _1>\lambda _2$ if $r<0$ and $\lambda _1<\lambda _2$ if $r>0$, thus the system (1.1) is non-strictly (or weakly) hyperbolic.

In the following, we need to consider the classical waves including rarefaction wave, shock wave and contact discontinuity, which have a given left state $(u_-,v_-,w_-)$ and a variant right state (u, v, w). Now, let us use self-similar transformation $\xi =\frac{x}{t}$ to find the continuous solution of this form $(u,v,w)(x,t)=(u,v,w)(\xi )$, then the Riemann problem (1.1) and (1.2) turns out to be

$$\begin{aligned}&-\xi u_{\xi }+(\phi u)_{\xi }=0, \quad -\xi v_{\xi }+(\phi v)_{\xi }=0, \nonumber \\&\qquad -\xi w_{\xi }+(\phi w)_{\xi }=0, \quad (u,v,w)(\pm \infty )=\left( u_\pm ,v_\pm ,w_\pm \right) . \end{aligned}$$

(2.2)

For smooth solution, (2.2) is reduced to

$$\begin{aligned} \left( \begin{array}{ccc} au\phi '+\phi -\xi &{} bu\phi ' &{} cu\phi ' \\ av\phi ' &{} bv\phi '+\phi -\xi &{} cv\phi ' \\ aw\phi ' &{} bw\phi ' &{} cw\phi '+\phi -\xi \\ \end{array} \right) \left( \begin{array}{c} du \\ dv \\ dw \\ \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) . \end{aligned}$$

(2.3)

Except for constant states (general solutions), plugging $\xi =\lambda _1=\phi$ into (2.3) yields $adu+bdv+cdw=0$, thus the contact discontinuity is given by

$$\begin{aligned} J\left( u_-,v_-,w_-\right) :\quad \xi =\phi (r)=\phi (r_-),\quad au+bv+cw=au_-+bv_-+cw_-. \end{aligned}$$

Similarly, inserting $\xi =\lambda _2=\phi +r\phi '$ into (2.3) leads to $\frac{\mathrm {d}u}{u}=\frac{\mathrm {d}v}{v}=\frac{\mathrm {d}w}{w}$, together with the condition $\lambda _2(r_-)<\lambda _2(r)$, such that the rarefaction wave curve is shown as

$$\begin{aligned} R\left( u_-,v_-,w_-\right) :\quad \xi =\phi +r\phi ',\quad \frac{u}{u_-}=\frac{v}{v_-}=\frac{w}{w_-}=\frac{r}{r_-},\quad r_-<r. \end{aligned}$$

We now turn our attention to the study of discontinuous solutions of Riemann problem (1.1) and (1.2). In what follows, the notation $[h]=h(x(t)+0,t)-h(x(t)-0,t)$ is used to denote the jump of h across the discontinuity $x=x(t)$. Let $(u_-,v_-,w_-)$ and (u, v, w) be connected by a shock wave or a contact discontinuity with the jump speed $\sigma$, then the Rankine–Hugoniot conditions are given by

$$\begin{aligned} \sigma [u]=[\phi u],\quad \sigma [v]=[\phi v],\quad \sigma [w]=[\phi w], \end{aligned}$$

which is simplified into

$$\begin{aligned}&\left( \begin{array}{ccc} \phi (r_-)+au_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-}-\sigma &{} bu_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-} &{} cu_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-} \\ av_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-} &{} \phi (r_-)+bv_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-}-\sigma &{} cv_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-} \\ aw_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-} &{} bw_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-} &{} \phi (r_-)+cw_+\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-}-\sigma \\ \end{array} \right) \\&\qquad \left( \begin{array}{c} {[}u{]} \\ {[}v{]} \\ {[}w{]} \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array}\right) . \end{aligned}$$

By a tedious but trivial calculation, it is shown that shock wave curve originating from the given left state $(u_-,v_-,w_-)$ is given by

$$\begin{aligned} S\left( u_-,v_-,w_-\right) :\quad \sigma= & {} \frac{r\phi (r)-r_-\phi (r_-)}{r-r_-},\\ \frac{u}{u_-}= & {} \frac{v}{v_-}=\frac{w}{w_-}=\frac{r}{r_-},\quad 0<r<r_-,\quad r<r_-<0. \end{aligned}$$

It is evident to see that the expression of shock wave curve is the same as that of rarefaction one in the (u, v, w) state space, so that the system (1.1) belongs to the well-known Temple type [2, 3].

Fig. 1

The elementary wave curves for the Riemann problem (1.1) and (1.2) are displayed in the projected $(au+bv,w)$ phase plane, where a represents the condition $r_-<0$ and b stands for the condition $r_->0$ with $r_+>0$

2.2 Classical Riemann Solutions

In this subsection, it is expected to construct the solutions of the Riemann problem (1.1) and (1.2) by using the combinations of the above elementary waves. By virtue of the projected $(au+bv,w)$ phase plane in Fig. 1, our discussion can be divided into five cases as follows:

(1) If $r_+<r_-<0$, then the Riemann solution is displayed as $\overleftarrow{S}+J$ given by

$$\begin{aligned} (u,v,w)(x,t)= \left\{ \begin{aligned}&(u_-,v_-,w_-), \quad x\le \frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}t, \\&\left( \frac{r_+u_-}{r_-},\frac{r_+v_-}{r_-},\frac{r_+w_-}{r_-}\right) , \quad \frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}t<x<\phi (r_+)t,\\&(u_+,v_+,w_+), \quad \phi (r_+)t\le x. \end{aligned}\right. \end{aligned}$$

(2) If $r_-<r_+<0$, then the Riemann solution is represented as $\overleftarrow{R}+J$ in the form

$$\begin{aligned} (u,v,w)(x,t)= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) , \quad x<\left( \phi (r_-)+r_-\phi '(r_-)\right) t,\\&\overleftarrow{R}(u,v,w), \quad \left( \phi (r_-)+r_-\phi '(r_-)\right) t\le x\le \left( \phi (r_+)+r_+\phi '(r_+)\right) t,\\&\left( \frac{r_+u_-}{r_-},\frac{r_+v_-}{r_-},\frac{r_+w_-}{r_-}\right) , \quad \left( \phi (r_+)+r_+\phi '(r_+)\right) t<x<\phi (r_+)t,\\&\left( u_+,v_+,w_+\right) , \quad \phi (r_+)t\le x, \end{aligned}\right. \end{aligned}$$

where the varying state in the wave fan of $\overleftarrow{R}(u,v,w)$ is determined by

$$\begin{aligned} \frac{x}{t}=\phi (r)+r\phi '(r),\quad \frac{u}{u_-}=\frac{v}{v_-}=\frac{w}{w_-}. \end{aligned}$$

(2.4)

(3) If $r_-<0<r_+$, then the Riemann solution is represented as $\overleftarrow{R}+J+\overrightarrow{R}$ given by

$$\begin{aligned} (u,v,w)(x,t)= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) , \quad x<\left( \phi (r_-)+r_-\phi '(r_-)\right) t,\\&\overleftarrow{R}(u,v,w), \quad \left( \phi (r_-)+r_-\phi '(r_-)\right) t\le x<0,\\&(0,0,0), \quad x=0,\\&\overrightarrow{R}(u,v,w), \quad 0<x\le \left( \phi (r_+)+r_+\phi '(r_+)\right) t,\\&\left( u_+,v_+,w_+\right) , \quad \left( \phi (r_+)+r_+\phi '(r_+)\right) t<x, \end{aligned}\right. \end{aligned}$$

where the state in $\overleftarrow{R}(u,v,w)$ is also given by (2.4) and the state in $\overrightarrow{R}(u,v,w)$ can be calculated by

$$\begin{aligned} \frac{x}{t}=\phi (r)+r\phi '(r),\quad \frac{u}{u_+}=\frac{v}{v_+}=\frac{w}{w_+}. \end{aligned}$$

(2.5)

(4) If $r_+>r_-\ge 0$, then the Riemann solution is expressed as $J+\overrightarrow{R}$ in the form

$$\begin{aligned} (u,v,w)(x,t)= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) , \quad x\le \phi (r_-)t,\\&\left( \frac{r_-u_+}{r_+},\frac{r_-v_+}{r_+},\frac{r_-w_+}{r_+}\right) , \quad \phi (r_-)t<x<(\phi (r_-)+r_-\phi '(r_-))t,\\&\overrightarrow{R}(u,v,w), \quad \left( \phi (r_-)+r_-\phi '(r_-)\right) t\le x\le \left( \phi (r_+)+r_+\phi '(r_+)\right) t,\\&\left( u_+,v_+,w_+\right) , \quad \left( \phi (r_+)+r_+\phi '(r_+)\right) t<x, \end{aligned}\right. \end{aligned}$$

where the state $\overrightarrow{R}(u,v,w)$ is also given by (2.5).

(5) If $r_->r_+>0$, then the Riemann solution is expressed as $J+\overrightarrow{S}$, which is given by

$$\begin{aligned} (u,v,w)(x,t)= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) , \quad x\le \phi (r_-)t,\\&\left( \frac{r_-u_+}{r_+},\frac{r_-v_+}{r_+},\frac{r_-w_+}{r_+}\right) ,\quad \phi (r_-)t<x<\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}t,\\&\left( u_+,v_+,w_+\right) , \quad \frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}t\le x. \end{aligned}\right. \end{aligned}$$

(2.6)

2.3 Delta Shock Wave Solution

In this subsection, motivated by [1], it will be shown that delta shock wave appears in the solution of the Riemann problem (1.1) and (1.2) for the case $r_-\ge 0\ge r_+$ (see Fig. 2), which also satisfies the system (1.1) in the sense of distributions. For the boundary case $r_->0=r_+$, let us consider the limiting solution $(u,v,w)(\xi )$ when $r_-$ is fixed, $r_->0$ and $r_+\rightarrow 0^+$. When $r_->r_+>0$, the solution is expressed as $J+\overrightarrow{S}$ shown in Fig. 3. By (2.6), the intermediate state is $(u_*,v_*,w_*)=\left( \frac{r_-u_+}{r_+},\frac{r_-v_+}{r_+},\frac{r_-w_+}{r_+}\right)$. Therefore, one has

$$\begin{aligned} \lim _{r_+ \rightarrow 0^+}u_*=\lim _{r_+\rightarrow 0^+}v_*=\lim _{r_+ \rightarrow 0^+}w_*=+\infty , \end{aligned}$$

when $u_+,v_+,w_+>0$. In addition, it is found that the speed of $\overrightarrow{S}$ tends to that of contact discontinuity J, which means that $\overrightarrow{S}$ and J overlap to form a new nonlinear hyperbolic wave.

Fig. 2

For the condition $r_-\ge 0\ge r_+$, $\delta S$ must be developed in the domain $\Omega =\{(x,t)\big |\lambda _1(r_+)t\le x\le \lambda _1(r_-)t, t>0\}$

Fig. 3

For the case $r_->r_+>0$, the solution consisting of $J+\overrightarrow{S}$ is shown on the left-hand side in the projected $(au+bv,w)$ phase plane and on the right-hand side on the (x, t) plane when $r_+\rightarrow 0^+$, where $r_*=au_*+bv_*+cw_*$

Subsequently, let us calculate the total quantities of u, v, w and r as $r_+ \rightarrow 0^+$. It follows from the first equation of (2.2) that

$$\begin{aligned} 0= & {} \int _{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}-\xi du+d(\phi u) =(-\xi u)\big |_{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}\\&+ \int _{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}u\mathrm{{d}}\xi +(\phi u)\big |_{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}, \end{aligned}$$

which gives that if $u_+\ne 0$

$$\begin{aligned} \begin{aligned} \lim _{r_+\rightarrow 0^+}\int _{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}u(\xi )\mathrm{{d}}\xi&=\lim _{r_+\rightarrow 0^+}\left( \frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}u_+-\phi (r_-)u_- \right. \\&\quad \left. -\phi (r_+)u_++\phi (r_-)u_-\right) =\phi (r_-)u_+\ne 0. \end{aligned} \end{aligned}$$

(2.7)

Similarly, from the second and third equations of (2.2), if $v_+\ne 0$ and $w_+\ne 0$, then we can get

$$\begin{aligned}&\lim _{r_+\rightarrow 0^+}\int _{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}v(\xi )\mathrm{{d}}\xi =\phi (r_-)v_+\ne 0, \nonumber \\&\quad \lim _{r_+\rightarrow 0^+}\int _{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}w(\xi )\mathrm{{d}}\xi =\phi (r_-)w_+\ne 0. \end{aligned}$$

(2.8)

Thus, it is calculated by

$$\begin{aligned} \lim _{r_+\rightarrow 0^+}\int _{\xi =\phi (r_-)-0}^{\xi =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}+0}(au+bv+cw)(\xi )\mathrm{{d}}\xi =\lim _{r_+\rightarrow 0^+}\phi (r_-)r_+\equiv 0. \end{aligned}$$

(2.9)

Equations (2.7) and (2.8) show that $u(\xi )$, $v(\xi )$ and $w(\xi )$ have the same singularity as a weighted Dirac delta function at $\xi =\phi (r_-)$ while (2.9) implies that r is still bounded. In addition, the inequality

$$\begin{aligned} \lambda _2(r_+)=\lambda _1(r_+)<\sigma _\delta =\phi (r_-)=\lambda _1(r_-)<\lambda _2(r_-), \end{aligned}$$

is established, where $\sigma _\delta$ is the wave speed of delta shock wave. In addition, the limiting situation can also be considered similarly for the other boundary case $r_+<0=r_-$.

For the case $r_->0>r_+$, it will be shown that the Riemann solution of (1.1) and (1.2) admits a delta shock wave with the wave speed $\sigma _\delta =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}$ satisfying

$$\begin{aligned} \lambda _2(r_+)<\lambda _1(r_+)<\sigma _\delta<\lambda _1(r_-)<\lambda _2(r_-). \end{aligned}$$

And if $u_+v_--u_-v_+\ne 0$, $u_+w_--u_-w_+\ne 0$ and $v_+w_--v_-w_+\ne 0$, then we have

$$\begin{aligned}&\int _{\sigma _\delta -0}^{\sigma _\delta +0}u(\xi )\mathrm{{d}}\xi =\sigma _\delta (u_+-u_-)\\&\quad -(u_+\phi (r_+)-u_-\phi (r_-)) =M(u_+(bv_-+cw_-)-u_-(bv_++cw_+))\ne 0,\\&\int _{\sigma _\delta -0}^{\sigma _\delta +0}v(\xi )\mathrm{{d}}\xi =\sigma _\delta (v_+-v_-)\\&\quad -(v_+\phi (r_+)-v_-\phi (r_-)) =M(v_+(au_-+cw_-)-v_-(au_++cw_+))\ne 0,\\&\int _{\sigma _\delta -0}^{\sigma _\delta +0}w(\xi )\mathrm{{d}}\xi =\sigma _\delta (w_+-w_-)\\&\quad -(w_+\phi (r_+)-w_-\phi (r_-)) =M(w_+(au_-+bv_-)-w_-(au_++bv_+))\ne 0, \end{aligned}$$

with $M=\frac{\phi (r_+)-\phi (r_-)}{r_+-r_-}$, and

$$\begin{aligned} \int _{\sigma _\delta -0}^{\sigma _\delta +0}(au+bv+cw)(\xi )\mathrm{{d}}\xi \equiv 0. \end{aligned}$$

(2.10)

As a result, for the case $r_-\ge 0\ge r_+$, the Riemann solution of (1.1) and (1.2) can be constructed by introducing the concept of delta shock wave, which is a discontinuity at $\xi =\sigma _\delta =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}$ satisfying

$$\begin{aligned} \lambda _2(r_+)\le \lambda _1(r_+)\le \sigma _\delta \le \lambda _1(r_-)\le \lambda _2(r_-). \end{aligned}$$

Next, it will be shown that the above delta shock wave is a solution satisfying the system (1.1) in the sense of distributions. For this purpose, such as in [33, 34], the two-dimensional weighted $\delta$-measure $\beta _i(t)\delta _\Gamma ~(i=1,2,3)$ supported on a smooth curve $\Gamma =\{(x,t)|x=x(t), 0\le t<+\infty \}$ can be defined by

$$\begin{aligned} \langle \beta _i(t)\delta _\Gamma , \varphi (x,t)\rangle =\int _{0}^{+\infty }\beta _i(t)\varphi (x(t),t)\mathrm{{d}}t, \end{aligned}$$

for any test function $\varphi (x,t)\in C_{0}^{\infty }(R\times R_+)$.

With the above definition, in the case of $r_-\ge 0\ge r_+$, the delta shock wave solution of the Riemann problem (1.1) and (1.2) can be expressed as

$$\begin{aligned} u(x,t)= & {} u_-+[u]H(x-\sigma _\delta t)+\beta _1(t),\quad v(x,t)=v_-+[v]H(x-\sigma _\delta t)+\beta _2(t),\\ w(x,t)= & {} w_-+[w]H(x-\sigma _\delta t)+\beta _3(t), \end{aligned}$$

in which $\Gamma =\{(\sigma _\delta t,t):0\le t<+\infty \}$, $\beta _1(t)=(\sigma _\delta [u]-[u\phi (r)])t$, $\beta _2(t)=(\sigma _\delta [v]-[v\phi (r)])t$, $\beta _3(t)=(\sigma _\delta [w]-[w\phi (r)])t$ and H(x) is the Heaviside function. The delta shock wave solution (u, v, w) constructed as above should satisfy

$$\begin{aligned} \langle u,\varphi _t\rangle +\langle u\phi ,\varphi _x\rangle =0,\quad \langle v,\varphi _t\rangle +\langle v\phi ,\varphi _x\rangle =0,\quad \langle w,\varphi _t\rangle +\langle w\phi ,\varphi _x\rangle =0, \end{aligned}$$

(2.11)

for all test functions $\varphi (x,t)\in C_0^{+\infty }(R\times R_+)$, in which

$$\begin{aligned} \langle u,\varphi \rangle= & {} \int _0^{+\infty }\int _{-\infty }^{+\infty }u_0\varphi \mathrm{{d}}x\mathrm{{d}}t+\langle \beta _1(t)\delta _{\Gamma },\varphi \rangle , \\ \langle u\phi ,\varphi \rangle= & {} \int _0^{+\infty }\int _{-\infty }^{+\infty }u_0\phi (r_0)\varphi \mathrm{{d}}x\mathrm{{d}}t+\langle \sigma _\delta \beta _1(t)\delta _{\Gamma },\varphi \rangle , \end{aligned}$$

with $u_0=u_-+[u]H(x-\sigma _\delta t)$ and $\phi (r_0)=\phi (r_-)+[\phi (r)]H(x-\sigma _\delta t)$ where $r_0=au_0+bv_0+cw_0$. The similar notations and conclusions are also performed on the last two equations of (2.11) without explanation any more.

Theorem 2.1

For the case $r_-\ge 0\ge r_+$, the Riemann problem (1.1) and (1.2) admits a delta shock wave solution in the form

$$\begin{aligned} (u,v,w)(x,t)= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) ,\quad x<\sigma _\delta t,\\&\left( \beta _1(t),\beta _2(t),\beta _3(t)\right) \delta \left( x-\sigma _\delta t\right) ,\quad x=\sigma _\delta t,\\&\left( u_+,v_+,w_+\right) ,\quad x>\sigma _\delta t, \end{aligned}\right. \end{aligned}$$

(2.12)

where

$$\begin{aligned} \begin{aligned} \sigma _\delta&=\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-},\\ \beta _1(t)&=M(u_+(bv_-+cw_-)-u_-(bv_++cw_+))t,\\ \beta _2(t)&=M(v_+(au_-+cw_-)-v_-(au_++cw_+))t,\\ \beta _3(t)&=M(w_+(au_-+bv_-)-w_-(au_++bv_+))t. \end{aligned} \end{aligned}$$

(2.13)

The delta shock wave solution (2.12) in connection with (2.13) also satisfies the generalized Rankine–Hugoniot conditions

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{{d}}x}{\mathrm{{d}}t}=\phi (r)\big |_{x=x(t)}=\sigma _\delta ,\quad&\frac{\mathrm{{d}}\beta _1(t)}{\mathrm{{d}}t}=\sigma _\delta [u]-[u\phi (r)],\\&\frac{\mathrm{{d}}\beta _2(t)}{\mathrm{{d}}t}=\sigma _\delta [v]-[v\phi (r)],\quad&\frac{\mathrm{{d}}\beta _3(t)}{\mathrm{{d}}t}=\sigma _\delta [w]-[w\phi (r)]. \end{aligned}\right. \end{aligned}$$

(2.14)

and the over-compressive entropy condition

$$\begin{aligned} \lambda _2(r_+)\le \lambda _1(r_+)\le \sigma _\delta \le \lambda _1(r_-)\le \lambda _2(r_-). \end{aligned}$$

Proof

Let us first check that the above constructed delta shock wave solution (2.12) in connection with (2.13) should satisfy the system (1.1) in the sense of distributions. Based on the definition of Schwartz distributions, this is equivalent to proving that it should satisfy

$$\begin{aligned}&\int _0^{+\infty }\int _{-\infty }^{+\infty }\left( u\varphi _t+u\phi (r)\varphi _x\right) \mathrm{{d}}x\mathrm{{d}}t=0,\quad \int _0^{+\infty }\int _{-\infty }^{+\infty }\left( v\varphi _t+v\phi (r)\varphi _x\right) \mathrm{{d}}x\mathrm{{d}}t=0,\nonumber \\&\quad \int _0^{+\infty }\int _{-\infty }^{+\infty }\left( w\varphi _t+w\phi (r)\varphi _x\right) \mathrm{{d}}x\mathrm{{d}}t=0. \end{aligned}$$

(2.15)

Without loss of generality, assume that $\sigma _\delta >0$, then we have

$$\begin{aligned} \begin{aligned}&\int _{0}^{+\infty }\int _{-\infty }^{+\infty }\left( u\varphi _t+u\phi (r)\varphi _x\right) u\mathrm{{d}}x\mathrm{{d}}t\\&\quad =\int _{0}^{+\infty }\int _{0}^{\frac{x}{\sigma _\delta }}u_+\varphi _t \mathrm{{d}}t \mathrm{{d}}x\\&\qquad +\int _{0}^{+\infty }\int _{\frac{x}{\sigma _\delta }}^{+\infty }u_-\varphi _t \mathrm{{d}}t \mathrm{{d}}x+\int _{0}^{+\infty }\int _{-\infty }^{\sigma _\delta t}u_-\phi (r_-)\varphi _x \mathrm{{d}}x\mathrm{{d}}t\\&\qquad +\int _{0}^{+\infty }\int _{\sigma _\delta t}^{+\infty }u_+\phi (r_+)\varphi _x \mathrm{{d}}x \mathrm{{d}}t\\&\qquad +\int _{0}^{+\infty }M\left( u_+\left( bv_-+cw_-\right) -u_-\left( bv_++cw_+\right) \right) t\mathrm{{d}}\varphi \\&\quad =\int _{0}^{+\infty }u_+\varphi \left( x,\frac{x}{\sigma _\delta }\right) \mathrm{{d}}x-\int _{0}^{+\infty }u_-\varphi \left( x,\frac{x}{\sigma _\delta }\right) \mathrm{{d}}x\\&\qquad +\int _{0}^{+\infty }u_-\phi (r_-)\varphi \left( \sigma _\delta t,t\right) \mathrm{{d}}t-\int _{0}^{+\infty }u_+\phi (r_+)\varphi \left( \sigma _\delta t,t\right) \mathrm{{d}}t\\&\qquad -\int _{0}^{+\infty }M\left( u_+\left( bv_-+cw_-\right) -u_-\left( bv_++cw_+\right) \right) \varphi \mathrm{{d}}t\\&\quad =\int _{0}^{+\infty }\left( \sigma _\delta \left( u_+-u_-\right) +u_-\phi (r_-)-u_+\phi (r_+) \right. \\&\qquad \left. -M\left( u_+\left( bv_-+cw_-\right) -u_-\left( bv_++cw_+\right) \right) \right) \varphi \mathrm{{d}}t=0. \end{aligned} \end{aligned}$$

Similarly, one also has

$$\begin{aligned}&\int _0^{+\infty }\int _{-\infty }^{+\infty }(v\varphi _t+v\phi (r)\varphi _x)\mathrm{{d}}x\mathrm{{d}}t\\&\quad =\int _{0}^{+\infty }(\sigma _\delta (v_+-v_-)+u_-\phi (r_-)-v_+\phi (r_+)\\&\qquad -M\left( v_+(au_-+cw_-)-v_-\left( au_++cw_+\right) \right) \varphi \mathrm{{d}}t=0,\\&\quad \int _0^{+\infty }\int _{-\infty }^{+\infty }(w\varphi _t+w\phi (r)\varphi _x)\mathrm{{d}}x\mathrm{{d}}t\int _{0}^{+\infty }(\sigma _\delta (w_+-w_-)\\&\qquad +w_-\phi (r_-)-w_+\phi (r_+)-M(w_+(au_-+bv_-)-w_-(au_++bv_+))\varphi \mathrm{{d}}t=0. \end{aligned}$$

From the above, we can see that (2.12) in connection with (2.13) is indeed the piecewise smooth Riemann solution of (1.1) and (1.2) in the sense of distributions. In addition, we obtain the relations (2.14), which is said to be the generalized Rankine–Hugoniot conditions of delta shock wave. In order to ensure the uniqueness, the delta entropy condition

$$\begin{aligned} \lambda _2(r_+)\le \lambda _1(r_+)\le \sigma _\delta \le \lambda _1(r_-)\le \lambda _2(r_-), \end{aligned}$$

(2.16)

should be proposed, which means that all characteristic lines on both sides of delta shock front are outgoing here.

Now, we employ the generalized Rankine–Hugoniot conditions (2.14) to solve the Riemann problem (1.1) and (1.2) with the initial data $x(0)=0$, $\beta _1(0)=0$, $\beta _2(0)=0$ and $\beta _3(0)=0$, then (2.12) in connection with (2.13) can be obtained directly by a trivial calculation. We also check that $\sigma _\delta (t)$ exactly satisfies the delta entropy condition (2.16), which guarantees the uniqueness of our obtained solution (2.12) together with (2.13). The proof is completed. $\square$

It can be seen from the inequality (2.16) clearly that the delta shock wave is more compressible than the normal shock wave in the sense that more characteristic lines enter such delta shock front, so that delta shock wave can be regarded as an over-compressible shock wave from the physical viewpoint. It should be addressed here that our current study is focused on the Riemann problem (1.1) and (1.2) only, thus we only need the over-compressible delta entropy condition (2.16). If the uniqueness of Radon measure solution for the Cauchy problem is considered under some suitable initial data, then one may refer to some more elaborate entropy and admissibility conditions [35,36,37,38,39] for example.

In summary, the solutions of the Riemann problem (1.1) and (1.2) can be constructed explicitly for the situation $abc<0$ as follows:

$$\begin{aligned}&(1) \ \overleftarrow{S}+J \ \ \left( r_+<r_-<0\right) , \quad (2) \ \overleftarrow{R}+J \ \ \left( r_-<r_+\le 0\right) , \quad (3) \ \overleftarrow{R}+J+\overrightarrow{R} \ \ \left( r_-<0<r_+\right) , \\&\qquad (4) \ J+\overrightarrow{R} \ \ \left( 0\le r_-<r_+\right) , \quad (5) \ J+\overrightarrow{S} \ \ \left( 0<r_+<r_-\right) , \quad (6) \ \delta S \ \ \left( r_+\le 0\le r_-\right) . \end{aligned}$$

Similarly, the solutions of the Riemann problem (1.1) and (1.2) for the situation $abc>0$ can be treated in the same as those for the situation $abc<0$.

3 Interactions of Delta Shock Waves with Classical Waves

In this section, in order to discover new nonlinear wave phenomena, it is expected to study the wave interaction problem for the system (1.1) when delta shock wave is involved. More specifically, our discussion is divided into the following seven different cases, according to the different wave combinations from $(-\varepsilon ,0)$ and $(\varepsilon ,0)$ as follows:

$$\begin{aligned}&(1) \ \delta S \ \ \mathrm{and} \ \ \overleftarrow{S}+J; \quad (2) \ \delta S \ \ \mathrm{and} \ \ J+\overleftarrow{R}; \quad (3) \ \delta S \ \ \mathrm{and} \ \ \overleftarrow{R}+J+\overrightarrow{R}; \quad (4) \ J+\overrightarrow{S} \ \ \mathrm{and} \ \ \delta S; \\&\qquad (5) \ \overrightarrow{R}+J \ \ \mathrm{and} \ \ \delta S; \quad (6) \ \overleftarrow{R}+J+\overrightarrow{R} \ \ \mathrm{and} \ \ \delta S; \quad (7) \ \delta S \ \ \mathrm{and} \ \ \delta S. \end{aligned}$$

It is noticed that (1) is similar to (4), (2) is similar to (5) as well as (3) is similar to (6) by symmetry. Thus, we need only to consider the cases (1), (2), (3) and (7). Due to the fact that the function $\phi$ is undetermined, it is impossible to calculate the wave interactions for the cases (2) and (3) in fully explicit forms. It is worthwhile to mention that the composite wave JR can be seen as the simplification of both $\overleftarrow{R}+J+\overrightarrow{R}$ and $J+\overleftarrow{R}$, in which a contact discontinuity J is attached on the wave back of the rarefaction wave R. For the sake of brevity, the current work is only concerned with the following three typical cases: (1) $\delta S$ and $\overleftarrow{S}+J$, (2) $\delta S$ and a composite wave JR as well as (3) $\delta S$ and $\delta S$, for the reason that it is adequate to discover nonlinear wave phenomena for the system (1.1) by studying the above three cases.

Fig. 4

The interaction between $\delta S$ and $\overleftarrow{S}+J$ is shown in the (x, t) plane when $r_+<r_m\le 0\le r_-$

Case 1 $\delta S$ and $\overleftarrow{S}+J$.

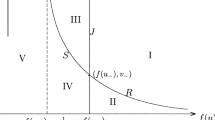
In this case, we study the interaction of delta shock wave $\delta S$ starting from $(-\varepsilon ,0)$ with the backward shock wave $\overleftarrow{S}$ plus the contact discontinuity J starting from $(\varepsilon ,0)$. The occurrence of this case depends on the condition $r_+<r_m\le 0\le r_-$, where $r_m=au_m+bv_m+cw_m$ (see Fig. 4).

The wave speed of $\delta S$ is $\sigma _{\delta 1}=\frac{r_m\phi (r_m)-r_-\phi (r_-)}{r_m-r_-}$, the wave speed of $\overleftarrow{S}$ is $\sigma =\frac{r_+\phi (r_+)-r_m\phi (r_m)}{r_+-r_m}$. From the assume $(r\phi (r))''>0$, we know that $\delta S_1$ will overtake $\overleftarrow{S}$ at a finite time. The intersection $(x_1,t_1)$ is determined by

$$\begin{aligned} x_1=\sigma _{\delta 1}t_1-\varepsilon =\sigma t_1+\varepsilon , \end{aligned}$$

which implies that

$$\begin{aligned} \left( x_1,t_1\right) = \left( \frac{\varepsilon \left( \sigma _{\delta 1} +\sigma \right) }{\sigma _{\delta 1}-\sigma }, \frac{2\varepsilon }{\sigma _{\delta 1}-\sigma }\right) . \end{aligned}$$

(3.1)

The new initial data will be formulated at the intersection $(x_1,t_1)$ as follows:

$$\begin{aligned} (u,v,w)\big |_{t=t_1}= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) ,\quad x<x_1 \\&\left( u_*,v_*,w_*\right) ,\quad x>x_1 \end{aligned} \right\} +\left( \beta _1(t_1),\beta _2(t_1),\beta _3(t_1)\right) \delta \left( x_1,t_1\right) , \end{aligned}$$

where the intermediate state between $\overleftarrow{S}$ and J can be easily obtained by $(u_*,v_*,w_*)=(\frac{r_+u_m}{r_m},\frac{r_+v_m}{r_m},\frac{r_+w_m}{r_m})$. The strengths $\beta _1(t_1)$, $\beta _2(t_1)$ and $\beta _3(t_1)$ can be calculated by

$$\begin{aligned} \left\{ \begin{aligned} \beta _1\left( t_1\right) =M_1\left( u_m\left( bv_-+cw_-\right) -u_-\left( bv_m+cw_m\right) \right) t_1,\\ \beta _2\left( t_1\right) =M_1\left( v_m\left( au_-+cw_-\right) -v_-\left( au_m+cw_m\right) \right) t_1,\\ \beta _3\left( t_1\right) =M_1\left( w_m\left( au_-+bv_-\right) -w_-\left( au_m+bv_m\right) \right) t_1, \end{aligned}\right. \end{aligned}$$

(3.2)

where

$$\begin{aligned} M_1=\frac{\phi \left( r_m\right) -\phi \left( r_-\right) }{r_m-r_-}. \end{aligned}$$

A new delta shock wave will be generated after the interaction of $\delta S_1$ and $\overleftarrow{S}$, let us denote it by $\delta S_2$. Before $\delta S_2$ meets the contact discontinuity J, the solution can be expressed as

$$\begin{aligned} \left\{ \begin{aligned}&u(x,t)=u_-+\left( u_*-u_-\right) H+\beta _{1-}(t)D^-+\beta _{1+}(t)D^+,\\&v(x,t)=v_-+\left( v_*-v_-\right) H+\beta _{2-}(t)D^-+\beta _{2+}(t)D^+,\\&w(x,t)=w_-+\left( w_*-w_-\right) H+\beta _{3-}(t)D^-+\beta _{3+}(t)D^+, \end{aligned}\right. \end{aligned}$$

(3.3)

where $\beta _1(t)D=\beta _{1-}(t)D^-+\beta _{1+}(t)D^+$, $\beta _2(t)D=\beta _{2-}(t)D^-+\beta _{2+}(t)D^+$ and $\beta _3(t)D=\beta _{3-}(t)D^-+\beta _{3+}(t)D^+$ are expressed by using the split delta functions, in which all of them are supported on the line $x=x_1+(t-t_1)\sigma _{\delta 2}$ with $\sigma _{\delta 2}=\frac{r_*\phi (r_*)-r_-\phi (r_-)}{r_*-r_-}$ being the wave speed of $\delta S_2$ and $r_*=au_*+bv_*+cw_*=r_+$. $D^-$ is delta measure on the set $\overline{R\times R_+}\bigcap \{(x,t)|x\le x_1+(t-t_1)\sigma _{\delta 2}\}$ and $D^+$ is delta measure on the set $\overline{R\times R_+}\bigcap \{(x,t)|x\ge x_1+(t-t_1)\sigma _{\delta 2}\}$.

From (3.3), we can get

$$\begin{aligned} u_t= & {} \left( -\sigma _{\delta 2}\left( u_*-u_-\right) +\beta '_{1-}(t)+\beta '_{1+}(t)\right) \delta -\sigma _{\delta 2}\left( \beta _{1-}(t)+\beta _{1+}(t)\right) \delta ', \end{aligned}$$

(3.4)

$$\begin{aligned} (\phi u)_x= & {} \left( \phi \left( r_*\right) u_*-\phi \left( r_-\right) u_-\right) \delta +\left( \phi \left( r_-\right) \beta _{1-}(t)+\phi \left( r_*\right) \beta _{1+}(t)\right) \delta '. \end{aligned}$$

(3.5)

By substituting (3.4) and (3.5) into the first equation of (1.1) and then comparing the coefficients of $\delta$ and $\delta '$, we can get

$$\begin{aligned}&-\sigma _{\delta 2}\left( u_*-u_-\right) +\beta '_{1-} +\beta '_{1+}+\phi \left( r_*\right) u_*-\phi \left( r_-\right) u_-=0, \end{aligned}$$

(3.6)

$$\begin{aligned}&\phi \left( r_-\right) \beta _{1-}(t)+\phi \left( r_*\right) \beta _{1+}(t) -\sigma _{\delta 2}\left( \beta _{1-}(t)+\beta _{1+}(t)\right) =0, \end{aligned}$$

(3.7)

with the initial condition $\beta _1(t_1)$. By (3.5), we can obtain

$$\begin{aligned} \beta _1(t)=\beta _{1-}(t)+\beta _{1+}(t) =\beta _1\left( t_1\right) +M_*\left( u_*\left( bv_-+cw_-\right) -u_-\left( bv_*+cw_*\right) \right) \left( t-t_1\right) . \end{aligned}$$

(3.8)

Similarly, we can also get $\beta _2(t)$ and $\beta _3(t)$ as follows:

$$\begin{aligned} \beta _2(t)= & {} \beta _{2-}(t)+\beta _{2+}(t)=\beta _2\left( t_1\right) \nonumber \\&+\,M_*\left( v_*\left( au_-+cw_-\right) -v_-\left( au_*+cw_*\right) \right) \left( t-t_1\right) , \end{aligned}$$

(3.9)

$$\begin{aligned} \beta _3(t)= & {} \beta _{3-}(t)+\beta _{3+}(t) =\beta _3\left( t_1\right) +M_*\left( w_*\left( au_-+bv_-\right) \right. \nonumber \\&\left. -w_-\left( au_*+bv_*\right) \right) \left( t-t_1\right) , \end{aligned}$$

(3.10)

which is the strength of $\delta S_2$ before the occurrence of the interaction of $\delta S_2$ and J and $M_*=\frac{\phi (r_*)-\phi (r_-)}{r_*-r_-}$. Obviously,

$$\begin{aligned} \begin{aligned} \beta _{1-}(t)&=\frac{r_-}{r_--r_*}\beta _1(t),\quad \beta _{1+}(t)=\frac{-r_*}{r_--r_*}\beta _1(t),\quad \beta _{2-}(t)=\frac{r_-}{r_--r_*}\beta _2(t),\\ \beta _{2+}(t)&=\frac{-r_*}{r_--r_*}\beta _2(t),\quad \beta _{3-}(t)=\frac{r_-}{r_--r_*}\beta _3(t),\quad \beta _{3+}(t)=\frac{-r_*}{r_--r_*}\beta _3(t). \end{aligned} \end{aligned}$$

Then, $\delta S_2$ and J will intersect at the point $(x_2,t_2)$ which can be calculated by

$$\begin{aligned} x_2=\sigma _{\delta 2}\left( t_2-t_1\right) +x_1=\tau t_2+\varepsilon , \end{aligned}$$

where $\tau =\phi (r_+)=\phi (r_*)$ is the wave speed of contact discontinuity J. Then, we can obtain

$$\begin{aligned} \left( x_2,t_2\right) =\left( \frac{\sigma _{\delta 2}\tau t_1+\sigma _{\delta 2}\varepsilon -\tau x_1}{\sigma _{\delta 2}-\tau }, \frac{\varepsilon +\sigma _{\delta 2}t_1-x_1}{\sigma _{\delta 2}-\tau }\right) . \end{aligned}$$

(3.11)

After the time $t_2$, $\delta S_2$ will pass through J with the same wave speed as before and only changes the strength, which can be calculated by

$$\begin{aligned} \beta _1(t)= & {} \beta _1\left( t_2\right) +M\left( u_+\left( bv_-+cw_-\right) -u_-\left( bv_++cw_+\right) \right) \left( t-t_2\right) , \\ \beta _2(t)= & {} \beta _2\left( t_2\right) +M\left( v_+\left( au_-+cw_-\right) -v_-\left( au_++cw_+\right) \right) \left( t-t_2\right) , \end{aligned}$$

and

$$\begin{aligned} \beta _3(t)=\beta _3\left( t_2\right) +M\left( w_+\left( au_-+bv_-\right) -w_-\left( au_++bv_+\right) \right) \left( t-t_2\right) , \end{aligned}$$

where $\beta _1(t_2)$, $\beta _2(t_2)$ and $\beta _3(t_2)$ can be calculated by (3.8), (3.9) and (3.10) when $t=t_2$, respectively. It is easy to check that $(x_1,t_1)$ and $(x_2,t_2)$ tend to (0, 0) as $\varepsilon \rightarrow 0$ from (3.1) and (3.11). Moreover, $\beta _i(t_j)~(i=1,2,3,j=1,2)$ tends to 0 as $\varepsilon \rightarrow 0$ from (3.2), (3.8), (3.9) and (3.10), respectively. Thus, the limit $\varepsilon \rightarrow 0$ of the solution of the double Riemann problem (1.1) and (1.6) is still a single delta shock wave, which is exactly the corresponding solution of the Riemann problem (1.1) and (1.2) in this case.

Fig. 5

The interaction between $\delta S$ and composite wave JR is displayed in the (x, t) plane under the condition $r_->r_+>r_m=0$ in a and the condition $r_+>r_-\ge r_m=0$ in b, respectively

Case 2 $\delta S$ and composite wave JR

For this case, we consider the interaction of the delta shock wave $\delta S_1$ starting from $(-\varepsilon ,0)$ and the composite wave JR starting from $(\varepsilon ,0)$, which relies on the condition $r_-\ge 0=r_m$ and $r_+>0=r_m$. (see Fig. 5). More precisely, when t is small enough before the interaction of $\delta S_1$ and JR happens, the solution can be expressed in the following form:

$$\begin{aligned} (u,v,w)= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) , \quad x<\phi (r_-)t-\varepsilon ,\\&\left( \beta _1(t),\beta _2(t),\beta _3(t)\right) \delta \left( x-\phi (r_-)t-\varepsilon \right) , \quad x=\phi (r_-)t-\varepsilon ,\\&\left( u_m,v_m,w_m\right) , \quad \phi (r_-)t-\varepsilon<x<\varepsilon ,\\&\overrightarrow{R}(u,v,w), \quad \varepsilon \le x\le \left( \phi (r_+)+r_+\phi _r(r_+)\right) t +\varepsilon ,\\&\left( u_+,v_+,w_+\right) , \quad \left( \phi (r_+)+r_+\phi _r(r_+)\right) t+\varepsilon <x, \end{aligned}\right. \end{aligned}$$

(3.12)

where $\beta _1(t),\beta _2(t),\beta _3(t)$ can be calculated by

$$\begin{aligned} \left\{ \begin{aligned} \beta _1(t)=M_1\left( u_m\left( bv_-+cw_-\right) -u_-\left( bv_m+cw_m\right) \right) t,\\ \beta _2(t)=M_1\left( v_m\left( au_-+cw_-\right) -v_-\left( au_m+cw_m\right) \right) t,\\ \beta _3(t)=M_1\left( w_m\left( au_-+bv_-\right) -w_-\left( au_m+bv_m\right) \right) t, \end{aligned}\right. \end{aligned}$$

and the state in $\overrightarrow{R}(u,v,w)$ can be calculated by

$$\begin{aligned} \frac{x-\varepsilon }{t}=\phi (r)+r\phi '(r),\quad \frac{u}{u_+}=\frac{v}{v_+}=\frac{w}{w_+}. \end{aligned}$$

(3.13)

Theorem 3.1

If $r_m=0$ is taken for the double Riemann problem (1.1) and (1.6), then there are a delta shock wave starting from $(-\varepsilon ,0)$ and a composite wave JR starting from $(\varepsilon ,0)$. The delta shock wave $\delta S$ is decomposed into a delta contact discontinuity $\delta J$ and a shock wave $\overrightarrow{S}$ when $\delta S$ meets the composite wave JR. Moreover, the shock wave $\overrightarrow{S}$ is able to penetrate the whole rarefaction wave $\overrightarrow{R}$ completely when $r_->r_+>0$ or cannot penetrate $\overrightarrow{R}$ completely and finally takes the line $x=\varepsilon +(\phi (r_-)+r_-\phi '(r_-))t$ as the asymptotic line when $r_+>r_-\ge 0$.

Proof

The wave speeds of $\delta S$ and J are given by $\sigma _\delta =\phi (r_-)$ and $\tau =\phi (r_m)=0$, respectively. Hence, we can get $\phi (r_-)>\phi (0)=0$ on account of $\phi '(r)>0$. They will meet at the point $(x_1,t_1)=(\varepsilon ,\frac{2\varepsilon }{\phi (r_-)})$, in which the strengths $\beta _1(t_1)$, $\beta _2(t_1)$ and $\beta _3(t_1)$ of $\delta S$ can be calculated according to (3.2) when $r_m=0$. A new Riemann problem is formed at $(x_1,t_1)$ when $\delta S$ and JR start to interact. It is known from (3.12) that the continuously varying right state in $\overrightarrow{R}(u,v,w)$ is also calculated by (3.13), in which the state (u, v, w) changes from $(u_m,v_m,w_m)$ to $(u_+,v_+,w_+)$. Then, we consider the local Riemann problem at the point $(x_1,t_1)$ with the initial data

$$\begin{aligned} (u,v,w)\big |_{t=t_1}= \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) , \quad x<x_1\\&(u,v,w), \quad x>x_1 \end{aligned} \right\} +\left( \beta _1(t_1),\beta _2(t_1),\beta _3(t_1)\right) \delta \left( x_1,t_1\right) , \end{aligned}$$

(3.14)

in which the composite wave JR is separated into a series of non-entropy waves as in [21].

Actually, we can construct the solution of the local Riemann problem (1.1) and (3.14) in the form

$$\begin{aligned} (u,v,w)(x,t)= & {} \left\{ \begin{aligned}&\left( u_-,v_-,w_-\right) , \quad x<\phi (r_-)t-\varepsilon \\&\left( \frac{r_-u}{r},\frac{r_-v}{r},\frac{r_-w}{r}\right) , \quad \phi (r_-)t-\varepsilon<x<x(t)\\&(u,v,w), \quad x(t)<x \end{aligned} \right\} \nonumber \\&\quad +\left( \beta _1(t_1),\beta _2(t_1),\beta _3(t_1)\right) \delta \left( x+\varepsilon -\phi (r_-)t\right) , \end{aligned}$$

(3.15)

where

$$\begin{aligned} x(t)=x_1+\frac{r\phi (r)-r_-\phi (r_-)}{r-r_-}(t-t_1). \end{aligned}$$

In the following, let us prove that (3.15) is really a weak solution of the local Riemann problem (1.1) and (3.14) in the sense of distributions. For convenience, let us introduce the notation $\Gamma =\left\{ (x,t)\big |x=\phi (r_-)t-\varepsilon ,~t>t_1\right\}$. For every $\varphi \in C^\infty _0(R\times R_+)$, if $\mathrm {supp}\varphi \bigcap \Gamma =\emptyset$, then (3.15) obviously satisfies the system (1.1). Otherwise, it is expected to examine that (3.15) still satisfies (2.11) in the local neighborhood of $\Gamma$, which is a weak formulation of (1.1). By calculating, we know that

$$\begin{aligned} \left\{ \begin{aligned} u_t+(\phi u)_x&=-\phi (r_-)\left( (\frac{r_-u}{r}-u_-)\delta +\beta _1(t_1)\delta '\right) \\&\quad +\left( \frac{r_-u\phi (r_-)}{r}-u_-\phi (r_-)\right) \delta +\phi (r_-)\beta _1(t_1)\delta '=0,\\ v_t+(\phi v)_x&=-\phi (r_-)\left( (\frac{r_-v}{r}-v_-)\delta +\beta _2(t_1)\delta '\right) \\&\quad +\left( \frac{r_-v\phi (r_-)}{r}-v_-\phi (r_-)\right) \delta +\phi (r_-)\beta _2(t_1)\delta '=0,\\ w_t+(\phi w)_x&=-\phi (r_-)\left( (\frac{r_-w}{r}-w_-)\delta +\beta _3(t_1)\delta '\right) \\&\quad +\left( \frac{r_-w\phi (r_-)}{r}-w_-\phi (r_-)\right) \delta +\phi (r_-)\beta _3(t_1)\delta '=0, \end{aligned}\right. \end{aligned}$$

(3.16)

holds in the local neighborhood of $\Gamma$ in the sense of distributions, where $\delta$ and $\delta '$ are the functions of $x+\varepsilon -\phi (r_-)t$.

It is seen from (3.15) that the Dirac delta function is supported on $\Gamma$, which is called as the delta contact discontinuity $\delta J$ in [21]. Specifically, $\delta S$ is separated into $\delta J$ and S with the state $(u_*,v_*,w_*)=(\frac{r_-u_+}{r_+},\frac{r_-v_+}{r_+},\frac{r_-w_+}{r_+})$ between them after $t_1$. Accordingly, it is necessary to provide the physical interpretation of delta contact discontinuity for the sake of intuition. It is evident to find that the Dirac delta function propagates along the front of the former contact discontinuity $\Gamma$ with the invariant strength and propagation speed in the physical (x, t) plane. In other words, this delta contact discontinuity $\delta J$ proceeds to move forward with the invariant propagation speed $\phi (r_-)$ and strength (or weight) $(\beta _1(t_1),\beta _2(t_1),\beta _3(t_1))$ of Dirac delta functions for the state variables (u, v, w). This is attributed to the intuitive observation that all the matter on both sides of the front $\Gamma$ of the delta contact discontinuity $\delta J$ shares the same propagation speed $\phi (r_-)$ such that the over-compressibility entropy condition is lost on such $\delta J$ after the time $t_1$. On the other hand, the aggregated matter at the point $(x_1,t_1)$ is impossible to disappear suddenly and thus moves forward along with the front $\Gamma$ of the delta contact discontinuity $\delta J$ after the time $t_1$. As a consequence, it is found clearly that our constructed local solution (3.15) is not only admissible from the above verification but also reasonable from the above physical explanation. At present, there is no general uniqueness result for the delta contact discontinuity $\delta J$ constructed in (3.15). However, such delta contact discontinuity is introduced in a manner to continue the solution after the point $(x_1,t_1)$ where the delta shock wave loses its over-compressibility.

Hereafter, $\delta J$ continues to propagate forward with the strengths $\beta _1(t_1)$, $\beta _2(t_1)$ and $\beta _3(t_1)$ and speed $\phi (r_-)$. The shock wave during the process of penetration is calculated by

$$\begin{aligned} \sigma =\frac{ \mathrm{{d}}x}{ \mathrm{{d}}t}=\frac{r\phi (r)-r_-\phi (r_-)}{r-r_-},\quad \frac{x-\varepsilon }{t}=\phi (r)+r\phi '(r), \end{aligned}$$

(3.17)

with r varying from 0 to $r_+$ and the initial condition $x(t_1)=x_1$. It is deduced from (3.15) that $\sigma \big |_{t=t_1}=\phi (r_-)$, and $\frac{\mathrm {d^2}x}{ \mathrm{{d}}t^2}=-\frac{((r\phi )'(r-r_-)-(r\phi (r)-r_-\phi (r_-)))^2}{(r-r_-)^3(r\phi )''t}$. When $r_->r_+>0$, S will penetrate the whole R in finite time, and the intersection point is determined by (3.17) together with the line of the wave back of R given by $\frac{x-\varepsilon }{t}=\phi (r_+)+r_+\phi '(r_+)$. Finally, the shock wave continues to propagate forward with the speed $\sigma =\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}$. Otherwise, when $r_+>r_-\ge 0$, S cannot penetrate R completely and finally takes the line $x=\varepsilon +(\phi (r_-)+r_-\phi '(r_-))t$ as the asymptotic line.

It is easy to check that $(x_1,t_1)=(\varepsilon ,\frac{2\varepsilon }{\phi (r_-)})$ tends to (0, 0) as $\varepsilon \rightarrow 0$. Moreover, $\beta _i(t_1)~(i=1,2,3)$ tends to 0 as $\varepsilon \rightarrow 0$ from (3.2) when $r_m=0$, respectively. Thus, the limit $\varepsilon \rightarrow 0$ of the solution of the double Riemann problem (1.1) and (1.6) is either a delta contact discontinuity plus a shock wave when $r_->r_+>0$ or a delta contact discontinuity plus a rarefaction wave when $r_+>r_-\ge 0$, which corresponds to the Riemann solution of (1.1) and (1.2) under the same Riemann initial data (1.2). The proof is completed. $\square$

Case 3 $\delta S$ and $\delta S$.

In this case, let us focus on the interaction of two delta shock waves starting from $(-\varepsilon ,0)$ and $(\varepsilon ,0)$, respectively. The occurrence of this case relies on the condition $r_-\ge r_m=0\ge r_+$(see Fig. 6). The wave speeds of $\delta S_1$ and $\delta S_2$ are calculated by $\sigma _{\delta 1}=\frac{r_-\phi (r_-)-r_m\phi (r_m)}{r_--r_m}=\phi (r_-)$ and $\sigma _{\delta 2}=\frac{r_+\phi (r_+)-r_m\phi (r_m)}{r_+-r_m}=\phi (r_+)$, respectively. Thus, it is easy to check that $\delta S_1$ will overtake $\delta S_2$ at a finite time. By virtue of $\phi '>0$, the intersection point can be calculated by $(x_1,t_1)=(\frac{(\sigma _{\delta 1}+\sigma _{\delta 2})\varepsilon }{\sigma _{\delta 1}-\sigma _{\delta 2}},\frac{2\varepsilon }{\sigma _{\delta 1}-\sigma _{\delta 2}})$ and the strengths at $(x_1,t_1)$ are given by

$$\begin{aligned} \beta _1(t_1)=\beta _{1-}(t_1)+\beta _{1+}(t_1),\quad \beta _2(t_1)=\beta _{2-}(t_1)+\beta _{2+}(t_1),\quad \beta _3(t_1)=\beta _{3-}(t_1)+\beta _{3+}(t_1), \end{aligned}$$

in which

$$\begin{aligned} \left\{ \begin{aligned}&\beta _{1-}(t_1)=M_1(u_m(bv_-+cw_-)-u_-(bv_m+cw_m))t_1, \\&\beta _{1+}(t_1)=M_2(u_+(bv_m+cw_m)-u_m(bv_++cw_+))t_1,\\&\beta _{2-}(t_1)=M_1(v_m(au_-+cw_-)-v_-(au_m+cw_m))t_1, \\&\beta _{2+}(t_1)=M_2(v_+(au_m+cw_m)-v_-(au_++cw_+))t_1,\\&\beta _{3-}(t_1)=M_1(w_m(au_-+bv_-)-w_-(au_m+bv_m))t_1, \\&\beta _{3+}(t_1)=M_2(w_+(au_m+bv_+)-w_-(au_++bv_+))t_1, \end{aligned}\right. \end{aligned}$$

together with

$$\begin{aligned} M_2=\frac{\phi (r_+)-\phi (r_m)}{r_+-r_m}. \end{aligned}$$

Fig. 6

The interaction between two delta shock waves is shown in the (x, t) plane when $r_-\ge r_m=0\ge r_+$

Now, the Riemann problem is formulated at $(x_1,t_1)$, which can be dealt with similarly to Case 1. A new delta shock wave $\delta S_3$ will be generated after the coalescence of $\delta S_1$ and $\delta S_2$ at $(x_1,t_1)$, whose wave speed is $\sigma _{\delta 3}=\frac{r_+\phi (r_+)-r_-\phi (r_-)}{r_+-r_-}$ and whose strengths are given, respectively, by

$$\begin{aligned} \left\{ \begin{aligned} \beta _1(t)=\beta _1\left( t_1\right) +M\left( u_+\left( bv_-+cw_-\right) -u_-\left( bv_++cw_+\right) \right) \left( t-t_1\right) ,\\ \beta _2(t)=\beta _2\left( t_1\right) +M\left( v_+\left( au_-+cw_-\right) -v_-\left( au_++cw_+\right) \right) \left( t-t_1\right) ,\\ \beta _3(t)=\beta _3\left( t_1\right) +M\left( w_+\left( au_-+bv_-\right) -w_-\left( au_++bv_+\right) \right) \left( t-t_1\right) . \end{aligned}\right. \end{aligned}$$

It is evident to conclude that the interaction of two delta shock waves still gives rise to a single delta shock wave. It is clear that $(x_1,t_1)\rightarrow 0$ and $\beta _i(t_1)\rightarrow 0~(i=1,2,3)$ as $\varepsilon \rightarrow 0$. Hence, the limit $\varepsilon \rightarrow 0$ of solution of the double Riemann problem (1.1) and (1.6) is just the corresponding delta shock wave solution of the Riemann problem (1.1) and (1.2) under the same Riemann initial data (1.2).

4 Numerical Simulation for Delta Shock Waves

In this section, we present some representative numerical results for delta shock wave solution of the Riemann problem (1.1) and (1.2) mentioned in Sect. 2.3. Many more numerical tests have been performed to make sure that what are not numerical artifacts. Let us take $\phi (r)=r$ to simplify the system (1.1). Moreover, we employ the upwind scheme and $CFL=0.25$ to discretize the system (1.1) with $\phi (r)=r$. According to different signal of a, b and c, eight numerical solutions are shown in detail. In what follows, all the chosen values of a, b, c and $(u_\pm ,v_\pm ,w_\pm )$ should satisfy the condition $r_+\le 0\le r_-$.

Fig. 7

Numerical results of u, v, w and r for $a=0.1$, $b=0.3$ and $c=0.2$

For the case $a=0.1$, $b=0.3$ and $c=0.2$, we can take the initial data as follows:

$$\begin{aligned} u_-=0.21,\quad v_-=0.32,\quad w_-=0.2,\quad u_+=0.31,\quad v_+=0.1,\quad w_+=-0.36, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 7.

Fig. 8

Numerical results of u, v, w and r for $a=0.1$, $b=-0.1$ and $c=0.3$

For the case $a=0.1$, $b=-0.1$ and $c=0.3$, we can choose the following initial data:

$$\begin{aligned} u_-=2.1,\quad v_-=2.14,\quad w_-=1.0,\quad u_+=2.9,\quad v_+=3.24,\quad w_+=0.1, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 8.

Fig. 9

Numerical results of u, v, w and r for $a=0.2$, $b=0.2$ and $c=-0.1$

For the case $a=0.2$, $b=0.2$ and $c=-0.1$, we can choose the following initial data are taken as:

$$\begin{aligned} u_-=0.33,\quad v_-=0.2,\quad w_-=0.2,\quad u_+=0.12,\quad v_+=0.11,\quad w_+=0.5, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 9.

Fig. 10

Numerical results of u, v, w and r for $a=0.3$, $b=-0.2$ and $c=-0.1$

For the case $a=0.3$, $b=-0.2$ and $c=-0.1$, we can select initial data as below:

$$\begin{aligned} u_-=0.24,\quad v_-=0.08,\quad w_-=0.13,\quad u_+=0.2,\quad v_+=0.25,\quad w_+=0.12, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 10.

Fig. 11

Numerical results of u, v, w and r for $a=-0.1$, $b=0.2$ and $c=0.1$

For the case $a=-0.1$, $b=0.2$ and $c=0.1$, we can choose the initial data as follows:

$$\begin{aligned} u_-=0.21,\quad v_-=0.42,\quad w_-=0.21,\quad u_+=0.65,\quad v_+=0.2,\quad w_+=0.1, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 11.

For the case $a=-0.3$, $b=-0.1$ and $c=0.2$, we can take the initial data in the following form:

$$\begin{aligned} u_-=0.3,\quad v_-=0.3,\quad w_-=1.64,\quad u_+=0.21,\quad v_+=0.32,\quad w_+=0.42, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 12.

Fig. 12

Numerical results of u, v, w and r for $a=-0.3$, $b=-0.1$ and $c=0.2$

Fig. 13

Numerical results of u, v, w and r for $a=-0.5$, $b=0.2$ and $c=-0.1$

For the case $a=-0.5$, $b=0.2$ and $c=-0.1$, we take the initial data as below:

$$\begin{aligned} u_-=0.01,\quad v_-=0.7,\quad w_-=0.1,\quad u_+=0.03,\quad v_+=0.02,\quad w_+=0.03, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 13.

Fig. 14

Numerical results of u, v, w and r for $a=-0.1$, $b=-0.2$ and $c=-0.1$

For the case $a=-0.1$, $b=-0.2$ and $c=-0.1$, we can select the following data:

$$\begin{aligned} u_-=0.25,\quad v_-=-1.65,\quad w_-=0.25,\quad u_+=0.27,\quad v_+=-0.2,\quad w_+=0.26, \end{aligned}$$

and present the numerical results at $t=2$ in Fig. 14.

It can be observed from Figs. 7, 8, 9, 10, 11, 12, 13 and 14 that all the state variables u, v and w develop a weighted Dirac delta function, while r is always bounded variation and develops a classical shock wave. This is consistent with the results of our theoretical analysis in Sect. 2.3.