On Modification of Certain Exponential Type Operators Preserving Constant and $e^{-x}$

Abstract

The key goal of this article is to propose a modification of certain exponential type operators defined by Ismail and May. Particularly, we concentrate on a sequence of operators that preserve $e^{-x}$ and constant functions. We find the moments of these modified operators using the concept of moment generating function with the help of Mathematica software. We show uniform convergence of these modified operators and analyze the asymptotic behaviour with a Voronovskaya type theorem. We also illustrate via graphs that our modified operators approximate better than the original operators for certain family of functions. Finally, we show the convergence of these modified operators graphically using Mathematica Software.

1 Introduction

In 2003, King [15] gained recognition for the modification of Bernstein operators which preserve test functions $e_{0}$ and $e_{2}$ on [0, 1]. Later King grabbed researchers attention in this direction and they put forward many relevant studies. Until now, many researchers have done outstanding research in this direction by defining operators which preserve $e_{0}$ and $e_{2},$ $e_{2}+a e_{1}$ for $a>0,$ linear functions, exponential functions, etc. Depending on the ultimate goal of this paper, we will keep this study small and focus on the preservation of exponential functions only. As far as we are aware, the study of preservation of exponential functions is in its early stages. Here we represent some most recent references which are relevant to this study.

In 2017, Acar et al. [2] presented a modification of Szász-Mirakyan operators that preserve $e^{2ax}$, $a>0$. They showed a comparison of modified operators with the Szász-Mirakyan operators and discussed shape preservation properties. They also estimated error in terms of first-order modulus of continuity using a natural transformation. Aral et al. [4] extended the study of these modified operators [2] and proved the usefulness of these operators from a computational point of view. Acar et al. [1] introduced Szász–Mirakyan operators that fixes $e^{ax}$ and $e^{2ax}$ with $a>0$ simultaneously and defined a new weighted modulus of smoothness to establish the approximation order. Also they gave some saturation result to confirm the goodness of the estimates for modified operators. In past four years, using the same theory, many researchers have modified a lot of operators like Bernstein [3], Stancu type Szász–Mirakyan–Durrmeyer Operators [14], Baskakov–Szász–Mirakyan [9], Baskakov–Schurer–Szász–Stancu [19], Baskakov–Schurer–Szász [21], Phillips operators [10, 20]. Deo et al. [6, 7]) proposed sequence of operators using King’s approach which provides better rate of convergence than the Szász–Mirakyan Durrmeyer and Baskakov Durrmeyer operators. In 2018, Yilmaz et al. [22] modified Baskakov–Kantorovich operators and gave a sequence of operators which preserve $e^{-x}$ and constant functions. The overall goal of this article is to propose the modification of the operators [13] preserving $e^{-x}$ and constant functions.

We organise this article in the following manner. In Sect.  2, we discuss the technique to construct the operators. In Sect. 3, we find the moment and central moment of modified operators using the concept of mgf. In Sect. 4, we show uniform convergence and analyze the asymptotic behaviour with a Voronovskaya type theorem. In Sect. 5, we gave a result and supporting graphs to prove the goodness of modified operators. In Sect. 6, we show the convergence using graphical approach.

2 Construction of the Operators

May [17] has done excellent work by defining exponential operators ${\mathcal {L}}_{n}$ as

$$\begin{aligned} {{\mathcal {L}}_{n}}(f;x) = \int \limits _{ - \infty }^\infty {{\mathcal {W}}(n ,x,t)f(t)\mathrm{d}t,} \end{aligned}$$

where ${\mathcal {W}}$ is the kernel which satisfies two conditions given as follows:

• 1. ${{\mathcal {L}}_{n}}(1;x) = 1$ normalisation condition.

• 2. $\frac{\partial }{{\partial x}}{\mathcal {W}}(n ,x,t) = \frac{(t - x)n }{{p(x)}}{\mathcal {W}}(n ,x,t)$, where p(x) is analytic and positive for $x\in {(-\infty , \infty )}$.

This work was carried forward by Ismail and May [13]. They considered a couple of more exponential operators and investigated their convergence properties. Using above definition, they regained some familiar operators like Bernstein operators, Szász operators, etc. and constructed some new operators which were later studied in [11, 16, 18]. Among these new operators defined in [13], one operator is given as

$$\begin{aligned} {{\mathcal {T}}_n}\left( {f;x} \right) = {e^{ - n\sqrt{x} }}\left\{ {f\left( 0 \right) +n\int \limits _0^\infty {{e^{ - nt/\sqrt{x} }}} {t^{ - 1/2}}{I_1}\left( {2n\sqrt{t} } \right) f\left( t \right) \mathrm{d}t } \right\} \end{aligned}$$

(2.1)

where $I_{1}$ is modified Bessel’s function of first kind defined as

$$\begin{aligned} {I_m}\left( z \right) = \sum \limits _{j = 0}^\infty {\frac{{{{\left( {\frac{z}{2}} \right) }^{m + 2j}}}}{{j!\Gamma \left( {m + j+ 1} \right) }}} \end{aligned}$$

Gupta [11] calculated the moments, central moments and obtain convergence estimate and some direct results for the operators given in 2.1.

In this article, our aim is to construct operators preserving $e_{0}$ and $e^{-x}$. We presume operators (2.1) preserve $e^{-x}$, then

$$\begin{aligned} {{\mathcal {T}}_n}\left( {{e^{ - t}};x} \right)&= {e^{ - n\sqrt{{\varrho _n}\left( x \right) } }}\left\{ {1+n\int \limits _0^\infty {{e^{ - nt/\sqrt{{\varrho _n}\left( x \right) } }}} {t^{ - 1/2}}\sum \limits _{j = 0}^\infty {\frac{{{{\left( {n\sqrt{t} } \right) }^{1 + 2j}}}}{{j!\Gamma \left( {j + 2} \right) }}{e^{ - t}}\mathrm{d}t} } \right\} \\&= {e^{ - n\sqrt{{\varrho _n}\left( x \right) } }}\left\{ {1+\sum \limits _{j = 0}^\infty {\frac{{{n^{2\left( {1 + j} \right) }}}}{{j!\Gamma \left( {j + 2} \right) }}\int \limits _0^\infty {{e^{ - \left( {\frac{{nt + \sqrt{{\varrho _n}\left( x \right) t} }}{{\sqrt{{\varrho _n}\left( x \right) } }}} \right) }}} } {t^j}\mathrm{d}t} \right\} \\&= {e^{ - n\sqrt{{\varrho _n}\left( x \right) } }}\left\{ {{{\sum \limits _{j = 0}^\infty {\frac{{{n^{2\left( {1 + j} \right) }}}}{{j!\Gamma \left( {j + 2} \right) }}\left( {\frac{{\sqrt{{\varrho _n}\left( x \right) } }}{{n + \sqrt{{\varrho _n}\left( x \right) } }}} \right) } }^{j + 1}}\int \limits _0^\infty {{e^{ - u}}{u^j}\mathrm{d}u} + 1} \right\} \\&= {e^{ - n\sqrt{{\varrho _n}\left( x \right) } }}\left\{ {{{1+\sum \limits _{j = 0}^\infty {\frac{{{n^{2\left( {1 + j} \right) }}}}{{\left( {j + 1} \right) !}}\left( {\frac{{\sqrt{{\varrho _n}\left( x \right) } }}{{n + \sqrt{{\varrho _n}\left( x \right) } }}} \right) } }^{j + 1}} } \right\} \\&= {e^{ - n\sqrt{{\varrho _n}\left( x \right) } }}\left\{ {{{\sum \limits _{j = 0}^\infty {\frac{1}{{j!}}\left( {\frac{{{n^2}\sqrt{{\varrho _n}\left( x \right) } }}{{n + \sqrt{{\varrho _n}\left( x \right) } }}} \right) } }^j}} \right\} \\&= {e^{\frac{{ - n{\varrho _n}\left( x \right) }}{{n + \sqrt{{\varrho _n}\left( x \right) } }}}} \end{aligned}$$

Taking into account ${{\mathcal {T}}_n}\left( {{e^{ - t}};x} \right) ={e^{ - x}}$, then we can find without hesitation

$$\begin{aligned} {\varrho _n}\left( x \right) =\frac{x^{3/2} \sqrt{4 n^2+x}+2 n^2 x+x^2}{2 n^2} \end{aligned}$$

(2.2)

For $x\in {\mathbb {R}}_{\ge }$ where ${\mathbb {R}}_{\ge }=[0,\infty ),$ We consider the following modified form of operators (2.1)

$$\begin{aligned} {\mathcal {\ddot{T}}_n}\left( {f;x} \right) = {e^{ - n\sqrt{{\varrho _n}\left( x \right) } }}\left\{ {f\left( 0 \right) +n\int \limits _0^\infty {{e^{ - nt/\sqrt{{\varrho _n}\left( x \right) } }}} {t^{ - 1/2}}{I_1}\left( {2n\sqrt{t} } \right) f\left( t \right) \mathrm{d}t } \right\} \end{aligned}$$

(2.3)

where ${\varrho _n}\left( x \right)$ is given as above.

3 Preliminaries

After simple calculations, the mgf of the operators (2.3) may be given as

$$\begin{aligned} {\mathcal {\ddot{T}}_n}\left( {{e^{\phi t}};x} \right) = {e^{\frac{{n\phi {\varrho _n}\left( x \right) }}{{n - \phi \sqrt{{\varrho _n}\left( x \right) } }}}} \end{aligned}$$

(3.1)

Since the moments are related with the mgf, the m-th moment ${\mathcal {\ddot{T}}_n}\left( {{e_m};x} \right) ,{e_m}(t) = {t^m}\left( {m \in {\mathbb {N}} \cup \left\{ 0 \right\} } \right)$ may be obtained by the following relation:

$$\begin{aligned} {\mathcal {\ddot{T}}_n}\left( {{e_m};x} \right) = {\left[ {\frac{{{\partial ^m}}}{{\partial {\phi ^m}}}{\mathcal {\ddot{T}}_n}\left( {{e^{\phi t}};x} \right) } \right] _{\phi = 0}} = {\left[ {\frac{{{\partial ^m}}}{{\partial {\phi ^m}}}\left( {{e^{\frac{{n\phi {\varrho _n}\left( x \right) }}{{n - \phi \sqrt{{\varrho _n}\left( x \right) } }}}}} \right) } \right] _{\phi = 0}} \end{aligned}$$

Employing Mathematica, the expansion of above expression in powers of $\phi$ may be given as:

$$\begin{aligned}&{\mathcal {\ddot{T}}_n}\left( {{e^{\phi t}};x} \right) \nonumber \\&={{e^{\frac{{n\phi {\varrho _n}\left( x \right) }}{{n - \phi \sqrt{{\varrho _n}\left( x \right) } }}}}}\nonumber \\&=1+\phi {\varrho _n}\left( x \right) +\phi ^2 \left( \frac{{\varrho _n}\left( x \right) ^{3/2}}{n}+\frac{{\varrho _n}\left( x \right) ^2}{2}\right) +\phi ^3 \left( \frac{{\varrho _n}\left( x \right) ^2}{n^2}+\frac{{\varrho _n}\left( x \right) ^{5/2}}{n}+\frac{{\varrho _n}\left( x \right) ^3}{6}\right) \nonumber \\&\quad +\frac{\phi ^4 \left( n^3 {\varrho _n}\left( x \right) ^4+12 n^2 {\varrho _n}\left( x \right) ^{7/2}+36 n {\varrho _n}\left( x \right) ^3+24 {\varrho _n}\left( x \right) ^{5/2}\right) }{24 n^3}+O\left( \phi ^5\right) \end{aligned}$$

(3.2)

Also, by change of scale property of mgf, if we expand ${e^{ - \phi t}}{\mathcal {\ddot{T}}_n}\left( {{e^{\phi t}};x} \right)$ in powers of $\phi ,$ the central moment of m-th order ${\nu _m}\left( x \right) = {\mathcal {\ddot{T}}_n}\left( {{{\left( {t - x} \right) }^m};x} \right)$ can be obtained by collecting the coefficient of $\frac{{{\phi ^m}}}{{m!}}$.

$$\begin{aligned}&{e^{ - \phi t}}{\mathcal {\ddot{T}}_n}\left( {{e^{\phi t}};x} \right) \nonumber \\&={{e^{ - \phi x + \frac{{n\phi {\varrho _n}\left( x \right) }}{{n - \phi \sqrt{{\varrho _n}\left( x \right) } }}}}}\nonumber \\&=1+\phi ({\varrho _n}\left( x \right) -x)+\phi ^2 \left( \frac{{\varrho _n}\left( x \right) ^{3/2}}{n}+\frac{x^2}{2}-x {\varrho _n}\left( x \right) +\frac{{\varrho _n}\left( x \right) ^2}{2}\right) \nonumber \\&\quad +\phi ^3 \left( \frac{{\varrho _n}\left( x \right) ^2}{n^2}-\frac{x {\varrho _n}\left( x \right) ^{3/2}}{n}+\frac{{\varrho _n}\left( x \right) ^{5/2}}{n}-\frac{x^3}{6}+\frac{x^2 {\varrho _n}\left( x \right) }{2}-\frac{x {\varrho _n}\left( x \right) ^2}{2}+\frac{{\varrho _n}\left( x \right) ^3}{6}\right) \nonumber \\&\quad +{\phi ^4}\frac{{\left[ \begin{array}{l} {n^3}{x^4} - 4{n^3}{x^3}{\varrho _n}\left( x \right) + 6{n^3}{x^2}{\varrho _n}{\left( x \right) ^2} - 4{n^3}x{\varrho _n}{\left( x \right) ^3} + {n^3}{\varrho _n}{\left( x \right) ^4} + 12{n^2}{x^2}{\varrho _n}{\left( x \right) ^{3/2}}\\ - 24{n^2}x{\varrho _n}{\left( x \right) ^{5/2}} + 12{n^2}{\varrho _n}{\left( x \right) ^{7/2}} - 24nx{\varrho _n}{\left( x \right) ^2} + 36n{\varrho _n}{\left( x \right) ^3} + 24{\varrho _n}{\left( x \right) ^{5/2}} \end{array} \right] }}{{24{n^3}}}\nonumber \\&\quad +O\left( \phi ^5\right) \end{aligned}$$

(3.3)

Lemma 3.1

Following the above argument, we can find the first four moments as follows:

$$\begin{aligned} {\mathcal {\ddot{T}}}_{n}\left( {{e_0};x} \right)&= 1\\ {\mathcal {\ddot{T}}}_{n}\left( {{e_1};x} \right)&= {\varrho _n}\left( x \right) \\ {\mathcal {\ddot{T}}}_{n}\left( {{e_2};x} \right)&= {\left( {{\varrho _n}\left( x \right) } \right) ^2} + \frac{{2{{\left( {{\varrho _n}\left( x \right) } \right) }^{3/2}}}}{n}\\ {\mathcal {\ddot{T}}}_{n}\left( {{e_3};x} \right)&= {\left( {{\varrho _n}\left( x \right) } \right) ^3} + \frac{{6{{\left( {{\varrho _n}\left( x \right) } \right) }^{5/2}}}}{n} + \frac{{6{{\left( {{\varrho _n}\left( x \right) } \right) }^2}}}{{n{}^2}}\\ {\mathcal {\ddot{T}}}_{n}\left( {{e_4};x} \right)&= {\left( {{\varrho _n}\left( x \right) } \right) ^4} + \frac{{12{{\left( {{\varrho _n}\left( x \right) } \right) }^{7/2}}}}{n} + \frac{{36{{\left( {{\varrho _n}\left( x \right) } \right) }^3}}}{{n{}^2}} + \frac{{24{{\left( {{\varrho _n}\left( x \right) } \right) }^{5/2}}}}{{n{}^3}} \end{aligned}$$

Lemma 3.2

Using (3.3), we have the central moments of the modified operator (2.3) as:

$$\begin{aligned} {\nu _1}\left( x \right)&= {\varrho _n}\left( x \right) - x\\ {\nu _2}\left( x \right)&= {\left( {{\varrho _n}\left( x \right) - x} \right) ^2} + \frac{{2{{\left( {{\varrho _n}\left( x \right) } \right) }^{3/2}}}}{n}\\ {\nu _3}\left( x \right)&= {\left( {{\varrho _n}\left( x \right) } \right) ^3} + \frac{{6{{\left( {{\varrho _n}\left( x \right) } \right) }^{5/2}}}}{n}+ \left( {\frac{6}{{n{}^2}} - 3x} \right) {\left( {{\varrho _n}\left( x \right) } \right) ^2} \\&\quad - \frac{{6x{{\left( {{\varrho _n}\left( x \right) } \right) }^{3/2}}}}{n} + 3{x^2}{\varrho _n}\left( x \right) - {x^3}\\ {\nu _4}\left( x \right)&= {\left( {{\varrho _n}\left( x \right) } \right) ^4} + \frac{{12{{\left( {{\varrho _n}\left( x \right) } \right) }^{7/2}}}}{n} + \left( {\frac{{36}}{{n{}^2}} - 4x} \right) {\left( {{\varrho _n}\left( x \right) } \right) ^3} + \left( {\frac{{24}}{{n{}^3}} - \frac{{24x}}{n}} \right) {\left( {{\varrho _n}\left( x \right) } \right) ^{5/2}}\\&+ \left( {\frac{6}{{n{}^2}} + 6{x^2}} \right) {\left( {{\varrho _n}\left( x \right) } \right) ^2} + \frac{{12{x^2}{{\left( {{\varrho _n}\left( x \right) } \right) }^{3/2}}}}{n} - 4{x^3}{\varrho _n}\left( x \right) + {x^4} \end{aligned}$$

Also,

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } n{\nu _1}\left( x \right) = \mathop {\lim }\limits _{n \rightarrow \infty } n\left[ {{\varrho _n}\left( x \right) - x} \right] = {x^{3/2}} \end{aligned}$$

and

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } n{\nu _2}\left( x \right) = \mathop {\lim }\limits _{n \rightarrow \infty } n\left[ {{{\left( {{\varrho _n}\left( x \right) - x} \right) }^2} + \frac{{2{{\left( {{\varrho _n}\left( x \right) } \right) }^{3/2}}}}{n}} \right] = 2{x^{3/2}} \end{aligned}$$

4 Main Result

Let us represent the subspace of real-valued continuous functions having finite limit at infinity equipped with uniform norm by ${C^*}({\mathbb {R}}_{\ge }).$ Boyanov [5] gave approximation properties of a function in an infinite interval. Later, Holhoş [12] verified the next theorem to find the rate of convergence of a function quantitatively.

Theorem

Let ${{\mathcal {L}}_n}:{C^*}({\mathbb {R}}_{\ge }) \rightarrow {C^*}({\mathbb {R}}_{\ge })$ be the sequence of linear positive operators and

$$\begin{aligned} {\left\| {{{\mathcal {L}}_n}\left( {{e_0}} \right) - 1} \right\| _{{\mathbb {R}}_{\ge }}} = {\beta _n},\\ {\left\| {{{\mathcal {L}}_n}\left( {{e^{ - t}}} \right) - {e^{ - x}}} \right\| _{{\mathbb {R}}_{\ge }}} = {\gamma _n},\\ {\left\| {{{\mathcal {L}}_n}\left( {{e^{ - 2t}}} \right) - {e^{ - 2x}}} \right\| _{{\mathbb {R}}_{\ge }}} = {\delta _n}. \end{aligned}$$

then

$$\begin{aligned}{\left\| {{{\mathcal {L}}_n}f - f} \right\| _{{\mathbb {R}}_{\ge }}} \le {\beta _n}{\left\| f \right\| _{{\mathbb {R}}_{\ge }}} + (2 + {\beta _n}){\omega ^*}(f,\sqrt{{\beta _n} + 2{\gamma _n} + {\delta _n}} ).\end{aligned}$$

The modulus of continuity is defined as:

$$\begin{aligned} {\omega ^*}(\hslash ,\delta ) = \mathop {sup}\limits _{\begin{array}{c} \scriptstyle \left| {{e^{ - t}} - {e^{ - x}}} \right| \le \delta \\ \scriptstyle x,t > 0 \end{array}} \left| {\hslash \left( t \right) - \hslash \left( x \right) } \right| \end{aligned}$$

with the property

$$\begin{aligned} \left| {\hslash \left( t \right) - \hslash \left( x \right) } \right| \le \left( {1 + \frac{{{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2}}}{{{\delta ^2}}}} \right) {\omega ^ * }\left( {\hslash ,\delta } \right) ,\;\;\delta > 0 \end{aligned}$$

(4.1)

In next theorem we give quantitative estimate for proposed operators as an application of above-mentioned theorem.

Theorem 4.1

For $f \in {C^ * }({\mathbb {R}}_{\ge }),$ we have

$$\begin{aligned}{\left\| {\mathcal {\ddot{T}}_{n}f - f} \right\| _{({\mathbb {R}}_{\ge })}} \le 2{\omega ^ * }\left( {f,\sqrt{{\delta _n}} } \right) .\end{aligned}$$

Here ${\mathcal {\ddot{T}}_{n}f}$ converges to f uniformly and ${\delta _n} \rightarrow 0$ as $n \rightarrow \infty$

Proof

The operators preserve $e^{-x}$ as well as constant functions so ${\beta _n} = {\gamma _n} = 0.$ we only have to evaluate ${\delta _n}.$ From (3.2), we have

$$\begin{aligned} \mathcal {\ddot{T}}_{n}\left( {{e^{ - 2t}};x} \right) = {e^{\frac{{ - 2n{\varrho _n}\left( x \right) }}{{n + 2\sqrt{{\varrho _n}\left( x \right) } }}}} \end{aligned}$$

where

$$\begin{aligned} {\varrho _n}\left( x \right) = \frac{{2{n^2}x + {x^2} + {x^{3/2}}\sqrt{4{n^2} + x} }}{{2{n^2}}}. \end{aligned}$$

Using mathematica, we will get

$$\begin{aligned} \mathcal {\ddot{T}}_{n}\left( {{e^{ - 2t}};x} \right) = {e^{ - 2x}} + \frac{{\left( {2{e^{ - 2x}}} \right) {x^{3/2}}}}{n} + \frac{{\left( {{e^{ - 2x}}{x^2}} \right) (2x - 3)}}{{{n^2}}} + O\left( {{{\left( {\frac{1}{n}} \right) }^3}} \right) \end{aligned}$$

Since

$$\begin{aligned} \mathop {sup}\limits _{x \in {\mathbb {R}}_{\ge }} {x^{3/2}}{e^{ - 2x}} = \frac{{3\sqrt{3} }}{{8{e^{3/2}}}},\mathop {sup}\limits _{x \in {\mathbb {R}}_{\ge }} {x^2}{e^{ - 2x}} = \frac{1}{{{e^2}}} \end{aligned}$$

and

$$\begin{aligned} \mathop {Sup}\limits _{x \in {\mathbb {R}}_{\ge }} {x^3}{e^{ - 2x}} = \frac{{27}}{{8{e^3}}} \end{aligned}$$

So we get

$$\begin{aligned} {\delta _n}&= {\left\| {\mathcal {\ddot{T}}_{n}\left( {{e^{ - 2t}}} \right) - {e^{ - 2x}}} \right\| _{{\mathbb {R}}_{\ge }}}\\&= \mathop {sup}\limits _{x \in {\mathbb {R}}_{\ge }} \left| {\mathcal {\ddot{T}}_{n}\left( {{e^{ - 2t}}} \right) - {e^{ - 2x}}} \right| \\&\le \frac{1}{n}\left( {\frac{{3\sqrt{3} }}{{4{e^{3/2}}}}} \right) + \frac{1}{{{n^2}}}\left( {\frac{3}{{{e^2}}} + \frac{{27}}{{4{e^3}}}} \right) + O\left( {{{\left( {\frac{1}{n}} \right) }^3}} \right) \\&\le O\left( {\frac{1}{n}} \right) \rightarrow 0 \; \text {as}\; n \rightarrow \infty \end{aligned}$$

$\square$

Remark 4.1

Using Mathematica and Lemma 3.2, we have

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } {n^2}{\nu _4}\left( x \right)&= \mathop {\lim }\limits _{n \rightarrow \infty } {n^2}\left[ {{{\left( {{\varrho _n}\left( x \right) } \right) }^4} + \frac{{12{{\left( {{\varrho _n}\left( x \right) } \right) }^{7/2}}}}{n} + \left( {\frac{{36}}{{n{}^2}} - 4x} \right) {{\left( {{\varrho _n}\left( x \right) } \right) }^3}} \right. \\&\quad + \left( {\frac{{24}}{{n{}^3}} - \frac{{24x}}{n}} \right) {\left( {{\varrho _n}\left( x \right) } \right) ^{5/2}}\left. + \left( {\frac{6}{{n{}^2}} + 6{x^2}} \right) {{\left( {{\varrho _n}\left( x \right) } \right) }^2} \right. \\&\quad \left. + \frac{{12{x^2}{{\left( {{\varrho _n}\left( x \right) } \right) }^{3/2}}}}{n} - 4{x^3}{\varrho _n}\left( x \right) + {x^4} \right] \\&= 12{x^3} \end{aligned}$$

and

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } {n^2}{\mathcal {\ddot{T}}_n}\left( {{{\left( {{e^{ - x}} - {e^{ - t}}} \right) }^4};x} \right)&= \mathop {\lim }\limits _{n \rightarrow \infty } {n^2}{\mathcal {\ddot{T}}_n}\left( {\sum \limits _{j = 0}^4 {\left( \begin{array}{l} 4\\ j \end{array} \right) {{\left( {{e^{ - x}}} \right) }^j}{{\left( {{e^{ - t}}} \right) }^{4 - j}}} } \right) \\&= \mathop {\lim }\limits _{n \rightarrow \infty } {n^2}\sum \limits _{j = 0}^4 {\left( \begin{array}{l} 4\\ j \end{array} \right) {{e^{ - jx}}}{\mathcal {\ddot{T}}_n}\left( {{e^{ - \left( {4 - j} \right) t}};x} \right) } \\&= \mathop {\lim }\limits _{n \rightarrow \infty } {n^2}\sum \limits _{j = 0}^4 {\left( \begin{array}{l} 4\\ j \end{array} \right) {{e^{ - jx}}}{e^{\frac{{ - \left( {4 - j} \right) n{\varrho _n}\left( x \right) }}{{\left( {n + \left( {4 - j} \right) \sqrt{{\varrho _n}\left( x \right) } } \right) }}}}} \\&= 12{e^{ - 4x}}{x^3} \end{aligned}$$

Theorem 4.2

For $x \in {\mathbb {R}}_{\ge },$ and $f,f'' \in {C^ * }({\mathbb {R}}_{\ge })$ we have

$$\begin{aligned}&\left| {n\left[ {\mathcal {\ddot{T}}_{n}\left( {f;x} \right) - f\left( x \right) } \right] - {x^{3/2}}\left[ {f'\left( x \right) + f''\left( x \right) } \right] } \right| \\&\le \left| {{a_n}\left( x \right) } \right| \left| {f'\left( x \right) } \right| + \left| {{b_n}\left( x \right) } \right| \left| {f''\left( x \right) } \right| + 2{\omega ^ * }\left( {f'',\delta } \right) \left( {\left( {2{b_n}\left( x \right) + {x^{3/2}}} \right) + {c_n}\left( x \right) } \right) \end{aligned}$$

Proof

By Taylor’s expansion we have

$$\begin{aligned}f\left( t \right) = f\left( x \right) + \left( {t - x} \right) f'\left( x \right) + \frac{1}{2}{\left( {t - x} \right) ^2}f''\left( x \right) + \ddot{r}\left( {t,x} \right) {\left( {t - x} \right) ^2}\end{aligned}$$

where

$$\begin{aligned}\ddot{r}\left( {t,x} \right) = \frac{{f''\left( \mu \right) - f''\left( x \right) }}{2},\;\;\;\;x<\mu <t.\end{aligned}$$

From Lemma 3.2 and applying ${\mathcal {\ddot{T}}_{n}}$ to both sides of the above expression, we have

$$\begin{aligned}&\left| {\mathcal {\ddot{T}}_{n}\left( {f;x} \right) - f\left( x \right) - {\nu _1}\left( x \right) f'\left( x \right) - \frac{1}{2}{\nu _2}\left( x \right) f''\left( x \right) } \right| \le \left| {\mathcal {\ddot{T}}_{n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) } \right| . \end{aligned}$$

Using Lemma 3.2

$$\begin{aligned}&\left| {n\left[ {\mathcal {\ddot{T}}_{n}\left( {f;x} \right) - f\left( x \right) } \right] - \left( {{x^{3/2}}} \right) f'\left( x \right) - \frac{1}{2}\left( {2{x^{3/2}}} \right) f''\left( x \right) } \right| \\&\le \left| {n\left( {{\nu _1}\left( x \right) } \right) - \left( {{x^{3/2}}} \right) } \right| \left| {f'\left( x \right) } \right| + \frac{1}{2}\left| {n\left( {{\nu _2}\left( x \right) } \right) - \left( {2{x^{3/2}}} \right) } \right| \left| {f''\left( x \right) } \right| \\&+ \left| {n\mathcal {\ddot{T}}_{n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) } \right| . \end{aligned}$$

Taking ${a_n}\left( x \right) = n\left( {{\nu _1}\left( x \right) } \right) - \left( {{x^{3/2}}} \right)$ and ${b_n}\left( x \right) = \frac{1}{2}\left| {n\left( {{\nu _2}\left( x \right) } \right) - \left( {2{x^{3/2}}} \right) } \right| ,$ we get

$$\begin{aligned}&\left| {n\left[ {\mathcal {\ddot{T}}_{n}\left( {f;x} \right) - f\left( x \right) } \right] - \left( {{x^{3/2}}} \right) \left[ {f'\left( x \right) + f''\left( x \right) } \right] } \right| \\&\le \left| {{a_n}\left( x \right) } \right| \left| {f'\left( x \right) } \right| + \left| {{b_n}\left( x \right) } \right| \left| {f''\left( x \right) } \right| + \left| {n\mathcal {\ddot{T}}_{n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) } \right| . \end{aligned}$$

For completion of the proof, we need to evaluate $\left| {n\mathcal {\ddot{T}}_{n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) } \right| .$ Applying inequality (4.1), we get

$$\begin{aligned} \left| {\ddot{r}\left( {t,x} \right) } \right| \le \left( {1 + \frac{{{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2}}}{{{\delta ^2}}}} \right) {\omega ^ * }\left( {f'',\delta } \right) \end{aligned}$$

Two inequality $\left| {\ddot{r}\left( {t,x} \right) } \right| \le 2{\omega ^ * }\left( {f'',\delta } \right)$ and $\left| {\ddot{r}\left( {t,x} \right) } \right| \le \frac{{2{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2}}}{{{\delta ^2}}}{\omega ^ * }\left( {f'',\delta } \right)$ holds for the case $\left| {{e^{ - t}} - {e^{ - x}}} \right| \le \delta$ and $\left| {{e^{ - t}} - {e^{ - x}}} \right| > \delta$ respectively.

Thus

$$\begin{aligned}\left| {\ddot{r}\left( {t,x} \right) } \right| \le 2\left( {1 + \frac{{{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2}}}{{{\delta ^2}}}{\omega ^ * }\left( {f'',\delta } \right) } \right) \end{aligned}$$

Using above argument and Cauchy Schwarz inequality, we get

$$\begin{aligned}&n\mathcal {\ddot{T}}_{n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) \\&\le n\mathcal {\ddot{T}}_{n}\left( {2\left( {1 + \frac{{{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2}}}{{{\delta ^2}}}{\omega ^ * }\left( {f'',\delta } \right) } \right) {{\left( {t - x} \right) }^2};x} \right) \\&= 2n\left( {{\nu _2}\left( x \right) } \right) {\omega ^ * }\left( {f'',\delta } \right) + \frac{{2n}}{{{\delta ^2}}}{\omega ^ * }\left( {f'',\delta } \right) \mathcal {\ddot{T}}_{n}\left( {{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2}{{\left( {t - x} \right) }^2};x} \right) \\&= 2{\omega ^ * }\left( {f'',\delta } \right) \left[ {n\left( {{\nu _2}\left( x \right) } \right) + {\left( {{n^2}{\nu _4}\left( x \right) } \right) ^{1/2}}{\left( {{n^2}{{\ddot{{\mathcal {T}}}}_n}\left( {{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2};x} \right) } \right) ^{1/2}}} \right] . \end{aligned}$$

We complete the proof by choosing $\delta = \frac{1}{{\sqrt{n} }}$ and ${c_n}\left( x \right) = {\left( {{n^2}{\nu _4}\left( x \right) } \right) ^{1/2}}{\left( {{n^2}{{\ddot{{\mathcal {T}}}}_n}\left( {{{\left( {{e^{ - t}} - {e^{ - x}}} \right) }^2};x} \right) } \right) ^{1/2}}.$ $\square$

Theorem 4.3

Let $x\in {\mathbb {R}}_{\ge }$ and $f,f'' \in {C^ * }({\mathbb {R}}_{\ge }).$ Then we have

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } n\left[ {{\mathcal {\ddot{T}}_n}\left( {f;x} \right) - f\left( x \right) } \right] = {x^{3/2}}\left[ {f'\left( x \right) + f''\left( x \right) } \right] \end{aligned}$$

(4.2)

Proof

By the Taylor’s expansion of f, we have

$$\begin{aligned} f\left( t \right) = f\left( x \right) + \left( {t - x} \right) f'\left( x \right) + \frac{1}{2}{\left( {t - x} \right) ^2}f''\left( x \right) + \ddot{r}\left( {t,x} \right) {\left( {t - x} \right) ^2} \end{aligned}$$

(4.3)

where

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow x} \ddot{r}\left( {t,x} \right) = 0. \end{aligned}$$

From Lemma 3.2 and applying $\ddot{T}_{n}$ to (4.3), we get

$$\begin{aligned}\mathcal {\ddot{T}}_{n}\left( {f;x} \right) - f\left( x \right) = {\nu _1}\left( x \right) f'\left( x \right) + \frac{1}{2}{\nu _2}\left( x \right) f''\left( x \right) + \mathcal {\ddot{T}}_{n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) .\end{aligned}$$

Making use of Cauchy Schwarz inequality, we have

$$\begin{aligned} {\mathcal {\ddot{T}}_n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) \le \sqrt{{\mathcal {\ddot{T}}_n}\left( {{\ddot{r}^2}\left( {t,x} \right) ;x} \right) {\mathcal {\ddot{T}}_n}\left( {{{\left( {t - x} \right) }^4};x} \right) } \end{aligned}$$

(4.4)

Also, we have

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } {\mathcal {\ddot{T}}_n}\left( {\ddot{r}^{2}\left( {t,x} \right) ;x} \right) = 0. \end{aligned}$$

(4.5)

From (4.4) and (4.5), we get

$$\begin{aligned}\mathop {\lim }\limits _{n \rightarrow \infty } n{\mathcal {\ddot{T}}_n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) = 0.\end{aligned}$$

Thus we get

$$\begin{aligned}&\mathop {\lim }\limits _{n \rightarrow \infty } n\left[ {{\mathcal {\ddot{T}}_n}\left( {f;x} \right) - f\left( x \right) } \right] \\&= \mathop {\lim }\limits _{n \rightarrow \infty } n\left[ {{\nu _1}\left( x \right) f'\left( x \right) + \frac{1}{2}{\nu _2}\left( x \right) f''\left( x \right) + {\mathcal {\ddot{T}}_n}\left( {\ddot{r}\left( {t,x} \right) {{\left( {t - x} \right) }^2};x} \right) } \right] \\&= {x^{3/2}}\left[ {f'\left( x \right) + f''\left( x \right) } \right] \end{aligned}$$

$\square$

Let us represent the class of bounded and uniform continuous functions on ${\mathbb {R}}_{\ge }$ equipped with sup norm by $C_{B}({\mathbb {R}}_{\ge }).$ For a function $g\in C_{B}({\mathbb {R}}_{\ge }),$ the first and second-order modulus of continuity is given by ${\omega _p}\left( {g,\delta } \right) = \mathop {\sup }\limits _{x \in {\mathbb {R}}_{\ge }} \mathop {\sup }\limits _{0 \le h \le \delta } \left| {\triangle _h^pg\left( x \right) } \right|$ for $p=1$ and $p=2$, respectively. Further, The Peetre’s K-functional and its relation with ${\omega _2}\left( {g,\delta } \right)$ for a function $\hslash \in C_B^2({\mathbb {R}}_{\ge }) = \left\{ {\hslash \in {C_B}({\mathbb {R}}_{\ge }):\hslash ',\hslash '' \in {C_B}({\mathbb {R}}_{\ge })} \right\}$ is given as:

$$\begin{aligned} {K_2}\left( {g,\delta } \right) = \mathop {\inf }\limits _{\hslash \in C_B^2({\mathbb {R}}_{\ge })} \left\{ {\left\| {g - \hslash } \right\| + \delta \left\| {\hslash } \right\| ,\left( {\delta > 0} \right) } \right\} , \end{aligned}$$

and

$$\begin{aligned} {K_2}(g;\delta ) \le {\mathcal {M}}{\omega _2}(g;\sqrt{\delta }) \end{aligned}$$

respectively.

Theorem 4.4

Let $f\in C_{B}({\mathbb {R}}_{\ge }).$ Then, for all $x\in {\mathbb {R}}_{\ge },$ there exists a positive constant ${\mathcal {M}}$ such that

$$\begin{aligned} \left| {{\mathcal {\ddot{T}}_n}\left( {f;x} \right) - f\left( x \right) } \right| \le {\mathcal {M}}{\omega _2}\left( {f,\frac{1}{2}\sqrt{{\nu _2}\left( x \right) + \frac{{{{\left( {{\varrho _n}\left( x \right) - x} \right) }^2}}}{2}} } \right) + \omega \left( {f,\left( {{\varrho _n}\left( x \right) - x} \right) } \right) \end{aligned}$$

Proof

We construct the auxiliary operators ${{\mathbb {T}}_n}:{C_B}({\mathbb {R}}_{\ge }) \rightarrow {C_B}({\mathbb {R}}_{\ge })$

$$\begin{aligned} {{\mathbb {T}}_n}\left( {f;x} \right) = {\mathcal {\ddot{T}}_n}\left( {f;x} \right) + f\left( x \right) - f\left( {{\varrho _n}\left( x \right) } \right) , \end{aligned}$$

where $\varrho _{n}(x)$ is given in 2.2. For the operators 2.3, we have

$$\begin{aligned} \left\| {{\mathcal {\ddot{T}}_n}\left( {f;x} \right) } \right\| \le \left\| f \right\| \end{aligned}$$

implies

$$\begin{aligned} \left\| {{{\mathbb {T}}_n}\left( {f;x} \right) } \right\| \le \left\| {{\mathcal {\ddot{T}}_n}\left( {f;x} \right) } \right\| + 2\left\| f \right\| \le 3\left\| f \right\| \end{aligned}$$

(4.6)

Also the Taylor expansion for $\hbar \in C_B^2({\mathbb {R}}_{\ge })$ is given as

$$\begin{aligned}\hbar \left( t \right) = \hbar \left( x \right) + \left( {t - x} \right) \hbar '\left( x \right) + \int \limits _x^t {\left( {t - \mu } \right) } \hbar ''\left( \mu \right) \mathrm{d}\mu ,x \in {\mathbb {R}}_{\ge }\end{aligned}$$

Applying Cauchy schwarz inequality and ${{\mathbb {T}}_n}$ to the both sides of above equation, we get

$$\begin{aligned} \left| {{{\mathbb {T}}_n}\left( {\hbar ;x} \right) - \hbar \left( x \right) } \right|&= \left| {{{\mathbb {T}}_n}\left( {\int \limits _x^t {\left( {t - \mu } \right) } \hbar ''\left( \mu \right) \mathrm{d}\mu ;x} \right) } \right| \nonumber \\&\le \left| {{\mathcal {\ddot{T}}_n}\left( {\int \limits _x^t {\left( {t - \mu } \right) } \hbar ''\left( \mu \right) \mathrm{d}\mu ;x} \right) } \right| + \left| {\int \limits _x^{{\varrho _n}\left( x \right) } {\left( {{\varrho _n}\left( x \right) - \mu } \right) \hbar ''\left( \mu \right) \mathrm{d}\mu } } \right| \nonumber \\&\le \left\| {\hbar ''} \right\| \left( {{\nu _2}\left( x \right) + \frac{{{{\left( {{\varrho _n}\left( x \right) - x} \right) }^2}}}{2}} \right) . \end{aligned}$$

(4.7)

Using the estimates from Eqs. (4.6) and 4.7, we get

$$\begin{aligned} \left| {{\mathcal {\ddot{T}}_n}\left( {f;x} \right) - f\left( x \right) } \right|&\le \left| {{{\mathbb {T}}_n}\left( {f - \hbar ;x} \right) - \left( {f - \hbar } \right) \left( x \right) } \right| + \left| {f\left( {{\varrho _n}\left( x \right) } \right) - f\left( x \right) } \right| + \left| {{{\mathbb {T}}_n}\left( {\hbar ;x} \right) - \hbar \left( x \right) } \right| \\&\le 4\left\| {f - \hbar } \right\| + \left( {{\nu _2}\left( x \right) + \frac{{{{\left( {{\varrho _n}\left( x \right) - x} \right) }^2}}}{2}} \right) \left\| {\hbar ''} \right\| + \left| {f\left( {{\varrho _n}\left( x \right) } \right) - f\left( x \right) } \right| \\&\le 4{K_2}\left( {f,\frac{1}{4}\left( {{\nu _2}\left( x \right) + \frac{{{{\left( {{\varrho _n}\left( x \right) - x} \right) }^2}}}{2}} \right) } \right) + \left| {f\left( {{\varrho _n}\left( x \right) } \right) - f\left( x \right) } \right| \\&\le {\mathcal {M}}{\omega _2}\left( {f,\frac{1}{2}\sqrt{\left( {{\nu _2}\left( x \right) + \frac{{{{\left( {{\varrho _n}\left( x \right) - x} \right) }^2}}}{2}} \right) } } \right) + \omega \left( {f,\left( {{\varrho _n}\left( x \right) - x} \right) } \right) \end{aligned}$$

$\square$

5 Comparison with $T_{n}$

In the next theorem, using the asymptotic formulae satisfied by ${\mathcal {T}}_{n}$ and $\mathcal {\ddot{T}}_{n}$, we show that for a particular class of functions the newly constructed operators $\mathcal {\ddot{T}}_{n}$ approximate better than the original operator ${\mathcal {T}}_{n}.$

Theorem 5.1

Let $f\in C^{2}({\mathbb {R}}_{\ge }).$ Assume that there exist $n_{0} \in {\mathbb {N}},$ such that

$$\begin{aligned} f\left( x \right) \le {{\mathcal {\ddot{T}}}_n}\left( {f;x} \right) \le {\mathcal {T}}\left( {f;x} \right) \;\;\forall n \ge {n_0},\;\;x \in {\mathbb {R}}_{>} \;\text {where}\; {\mathbb {R}}_{>}= \left( {0,\infty } \right) \end{aligned}$$

(5.1)

then

$$\begin{aligned} f''\left( x \right) \ge - f'\left( x \right) \ge 0,x \in {\mathbb {R}}_{>} \end{aligned}$$

(5.2)

In particular $f''\left( x \right) \ge 0.$

Contrarily, if (5.2) holds with strict inequalities for a given $x \in {\mathbb {R}}_{>},$ there exist $n_{0} \in {\mathbb {N}},$ such that for $n \ge {n_0}$

$$\begin{aligned} f\left( x \right)< {{\mathcal {\ddot{T}}}_n}\left( {f;x} \right) < {\mathcal {T}}\left( {f;x} \right) \end{aligned}$$

(5.3)

Proof

From(5.1) we have

$$\begin{aligned} 0 \le n({{\mathcal {\ddot{T}}}_n}\left( {f;x} \right) - f\left( x \right) ) \le n({\mathcal {T}}\left( {f;x} \right) - f\left( x \right) )\;\;\forall n \ge {n_0},\;\;x \in {\mathbb {R}}_{>} \end{aligned}$$

considering an asymptotic formula which is held by operators ${\mathcal {T}}_{n}$ defined in [11].

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow \infty } n({\mathcal {T}}\left( {f;x} \right) - f\left( x \right) ) = {x^{3/2}} f''\left( x \right) . \end{aligned}$$

Now considering (4.2) and above equation, we get

$$\begin{aligned} 0 \le - f'\left( x \right) \le f''\left( x \right) . \end{aligned}$$

Contrarily, if (5.2) holds with strict inequality for a given $x \in {\mathbb {R}}_{>},$ then

$$\begin{aligned}&\quad 0< {x^{3/2}}\left( {f''\left( x \right) + f'\left( x \right) } \right)< {x^{3/2}}f''\left( x \right) \\&\Rightarrow 0< \mathop {\lim }\limits _{n \rightarrow \infty } n({{\mathcal {\ddot{T}}}_n}\left( {f;x} \right) - f\left( x \right) )< x\mathop {\lim }\limits _{n \rightarrow \infty } n({\mathcal {T}}\left( {f;x} \right) - f\left( x \right) )\\&\Rightarrow f(x)< {{\mathcal {\ddot{T}}}_n}\left( {f;x} \right) < {\mathcal {T}}\left( {f;x} \right) . \end{aligned}$$

This is the required result. $\square$

Fig. 1

Comparison of modified operators $\mathcal {\ddot{T}}_{n}$ with original operators ${\mathcal {T}}_{n}$

Table 1 Evaluation of error for the operators $\mathcal {\ddot{T}}_{n}$ and ${\mathcal {T}}_{n}$

Example 5.1

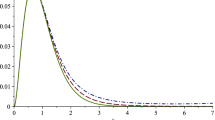
This example is the graphical representation for the fact that for a function f which satisfies Eq. (5.2), the modified operators $\mathcal {\ddot{T}}_{n}$ converges better than the original operators ${\mathcal {T}}_n.$ We can check that for the function $f(x)=e^{-5x},$ (5.2) holds with strict inequalities. In the following Figure, we have drawn the graph of f (Gray), $\mathcal {\ddot{T}}_{n}(f;x)$ (Green), ${\mathcal {T}}_n(f;x)$ (Orange) and in the following Table we have estimated the error for the operators $\mathcal {\ddot{T}}_{n}(f;x)$ and ${\mathcal {T}}_n(f;x).$ One can easily see from Fig. 1 and Table 1 that $\mathcal {\ddot{T}}_{n}$ converges better than ${\mathcal {T}}_n(f;x)$ for the class of functions which satisfies 5.2.

Fig. 2

The convergence of operators ${\mathcal {\ddot{T}}_n}$ to the function $f(x)=5{\mathop {\hbox {cos}}\nolimits } \left( x \right) - x{e^{\frac{x}{{20}}}}$ for $n=20, 50, 100$

Table 2 Evaluation of error for $f(x)=5{\mathop {\hbox {cos}}\nolimits } \left( x \right) - x{e^{\frac{x}{{20}}}}$ for $n=10, 20, 50,100$

Fig. 3

Graphical representation of absolute error of operators ${\mathcal {\ddot{T}}_n}$ to the function $f(x)=5{\mathop {\hbox {cos}}\nolimits } \left( x \right) - x{e^{\frac{x}{{20}}}}$ for $n=10, 20, 50,100$. The error clearly is converging to zero for the given function

6 Convergence Graphs and Error Estimation Table

Example 6.1

For $n= 10, 20, 100$ the approximation for the function $f(x)=5{\mathop {\hbox {cos}}\nolimits } \left( x \right) - x{e^{\frac{x}{{20}}}}$ by the operators $\mathcal {\ddot{T}}_{n}\left( {f;x} \right)$ is illustrated in Fig. 2. Further, in Table 2, we estimated the absolute error $\ddot{E}_{n}= \left| \mathcal {\ddot{T}}_{n}\left( {f;x} \right) - f(x) \right|$ for different values of n and given the corresponding graph for error depicting the convergence in Fig. 3. It can be clearly seen from Figs. 2, 3 and from Table 2 that for larger values of n the proposed operator (2.3) converges to f(x).