1 Introduction

Mathematical modeling of processes in epidemiology has played significant role in both foreseeing the transmission dynamics of infectious diseases and allowing public health policy makers to optimize the use of limited resources [2, 4, 5]. The concept of compartmental model is from the classical SIR model proposed by Kermack and McKendrick [13], in which the total population (N) is divided into three compartments: the susceptible individuals (S), the infectious individuals (I), and the recovered individuals (R). Later, many epidemic models are inspired and wildly used, by considering different compartments based on the epidemiological status of individuals and incorporating various control strategies, such as isolation, vaccination, treatment, and so on. Tremendous compartmental models are formulated and investigated even now, to mimic the spread of infectious diseases, for instance, SEIR [16, 23], SICA [19], n-group SIR model[22], and so on[21]. Motivated by previous compartmental models, we study a SEIRS model, with diagnosed and undiagnosed infectious compartments, which contribute differently to new infections. We consider a general incidence rate which can be specified to characterize transmission dynamics in various scenarios. Moreover, we incorporate the isolation rate as a time-dependent function, which may simulate the situation of different response stages.

Optimal control is a branch of applied mathematics developed to find optimal ways to control a dynamical system [8, 11]. In optimal control theory, the Pontryagin’s Maximum Principle [17] is a classical result, used to find the best possible control for taking a dynamical system from one state to another. It’s necessary for any optimal control along with the optimal state trajectory to satisfy a Hamiltonian system, which is a two-point boundary value problem, with a minimization condition on the Hamiltonian. In recent years, numerous applications of optimal control problem in infectious disease modeling deal with finding control laws for dynamical systems over a period of time such that an objective functional is optimized [1, 3, 15, 18, 20, 24]. Here, we consider the time-dependent isolation rate as a control and derive the theoretic optimal control, which is then simulated with a specified setting of parameters.

In this paper, we consider an SEIRS epidemic model, incorporating appropriate compartments, such as isolated exposed class and diagnosed class, relevant to interventions. In the model, we use a general nonlinear decreasing function \(\beta (I)\) as the effective contact rate and a time-dependent isolated proportion q(t), which later will be considered as a control. The paper is organized as follows. In Sect. 2, the compartmental model is formulated; in Sect. 3, the isolated proportion q(t) is set to a constant q and the qualitative analyses are carried out in terms of the basic reproduction number \(\mathscr {R}_0\). The sensitivity of \(\mathscr {R}_0\) with respect to model parameters is studied using the normalized forward sensitivity index; in Sect. 4, the optimal control problem of the epidemic is investigated and solved by applying the Pontryagin’s Maximum Principle; in Sect. 5, numerical simulations are performed to explore and extend the theoretical results obtained. The paper ends up with a conclusion.

2 Model Formulation

The total population N is divided into six compartments, depending on the epidemiological status of individuals: the susceptible individuals, S; the exposed individuals but not isolated, E; the isolated exposed individuals, \(E_q\); the undiagnosed infectious individuals, I; the diagnosed individuals, D; and the recovered individuals, R. Here, we assume that only the exposed but not isolated individuals and the undiagnosed infectious individuals can infect the susceptible individuals. Moreover, we introduce a non-linear function \(\beta (I)\) describing the effective contact rate, which mimics the self-consciousness formulated in the transmission of disease due to the media effect. The dynamical flow of the disease transmission between compartments is depicted in Fig. 1.

Fig. 1
figure 1

Diagram of the SEIRS model. Susceptible individuals are infected by undiagnosed infectious individuals and become exposed; part of the exposed individuals are isolated and become diagnosed infectious, who are not able to infect others; the other part of the exposed individuals are not isolated and become undiagnosed infectious; the undiagnosed infectious individuals either get diagnosed or get recovered and the diagnosed infectious individuals get recovered; the recovered individuals will lose immunity and be susceptible again. A constant recruitment rate of susceptible individuals and a natural death rate of all individuals are considered. For simplicity, no death from disease cause is included

Full size image

The epidemic model is given by the following system of ordinary differential equations according to Fig. 1:

$$\begin{aligned} S'(t)&=\Lambda -\beta (I(t))S(t)I(t)+\phi R(t)-{\mathrm {d}}S(t), \end{aligned}$$
(2.1a)
$$\begin{aligned} E'(t)&=\beta (I(t))S(t)I(t)(1-q(t))-\tau E(t)-{\mathrm {d}}E(t), \end{aligned}$$
(2.1b)
$$\begin{aligned} E_q'(t)&=\beta (I(t))S(t)I(t)q(t)-\delta _2 E_q(t)-{\mathrm {d}}E_q(t), \end{aligned}$$
(2.1c)
$$\begin{aligned} I'(t)&=\tau E(t)-\delta _1 I(t)-r_1 I(t)-{\mathrm {d}}I(t), \end{aligned}$$
(2.1d)
$$\begin{aligned} D'(t)&=\delta _1 I(t)+\delta _2 E_q(t)-r_2D(t)-{\mathrm {d}}D(t), \end{aligned}$$
(2.1e)
$$\begin{aligned} R'(t)&=r_1 I(t)+r_2 D(t)-\phi R(t)-{\mathrm {d}}R(t), \end{aligned}$$
(2.1f)

under initial conditions

$$\begin{aligned} S(0)>0, \quad E(0),~E_q(0),~I(0),~D(0),~R(0)\ge 0,\quad E(0)+E_q(0)+I(0)>0. \end{aligned}$$
(2.2)

The effective contact rate \(\beta (I)\) satisfies

$$\begin{aligned} \beta (0) = \beta _0,~\beta (I)>0,~\beta '(I)<0. \end{aligned}$$
(2.3)

It’s obvious that \(0<\beta (I)\le \beta _0\), for \(I\ge 0\). Note that, many types of \(\beta (I)\) satisfying (2.3) have already been proposed, such as \(\beta _0/(1+kI)\) , \(\beta _0/(1+\alpha I^2)\), and so on [7, 25]. Moreover, we denote the isolated proportion as q(t) and let \(0\le q(t)\le q_{max}<1\). All the parameters involved in system (2.1) are listed in Table 1.

Table 1 Model parameters
Full size table

Let the total population \(N(t) = S(t)+E(t)+E_q(t)+I(t)+D(t)+R(t)\), governed by the following equation:

$$\begin{aligned} \begin{array}{lll} N'(t)= & {} \Lambda -dN(t), \end{array} \end{aligned}$$
(2.4)

which leads to

$$\begin{aligned} \lim _{t\rightarrow +\infty }N(t)= \Lambda /d, \end{aligned}$$
(2.5)

no matter what initial total population size N(0) is. Therefore, it allows us to attack the dynamics of system (2.1) in the following feasible positively invariant region:

$$\begin{aligned} \Sigma = \{(S,E,E_q,I,D,R)\in \mathbb {R}_+^6:~ S+E+E_q+I+D+R=\Lambda /d\}. \end{aligned}$$
(2.6)

3 Dynamical Results with \(q(t) = q\) (Constant)

In this section, by setting \(q(t)=q\), which means the isolated proportion of exposed individuals is a constant, we discuss the dynamical behaviors of the following system:

$$\begin{aligned} S'(t)&=\Lambda -\beta (I(t))S(t)I(t)+\phi R(t)-{\mathrm {d}}S(t), \end{aligned}$$
(3.1a)
$$\begin{aligned} E'(t)&= \beta (I(t))S(t)I(t)(1-q)-\tau E(t)-{\mathrm {d}}E(t), \end{aligned}$$
(3.1b)
$$\begin{aligned} E_q'(t)&= \beta (I(t))S(t)I(t)q-\delta _2 E_q(t)-{\mathrm {d}}E_q(t), \end{aligned}$$
(3.1c)
$$\begin{aligned} I'(t)&= \tau E(t)-\delta _1 I(t)-r_1 I(t)-{\mathrm {d}}I(t), \end{aligned}$$
(3.1d)
$$\begin{aligned} D'(t)&= \delta _1 I(t)+\delta _2 E_q(t)-r_2D(t)-{\mathrm {d}}D(t), \end{aligned}$$
(3.1e)
$$\begin{aligned} R'(t)&= r_1 I(t)+r_2 D(t)-\phi R(t)-{\mathrm {d}}R(t), \end{aligned}$$
(3.1f)

under initial condition (2.2), in feasible region defined by (2.6).

3.1 Disease-Free Equilibrium and Basic Reproduction Number

It can be verified that region \(\Sigma \) is positively invariant and globally attracting in \(\mathbb {R}_+^6\), with respect to model (3.1). This guarantees that the model is well posed and biologically meaningful.

The disease-free equilibrium of system (3.1) can be obtained from the following equations

$$\begin{aligned} \left\{ \begin{array}{l} E = 0,~E_q = 0,~I = 0,~ D=0,~ R=0,\\ \Lambda -dS_0 = 0, \end{array} \right. \end{aligned}$$
(3.2)

namely, there always exists a unique disease-free equilibrium \(E_0\),

$$\begin{aligned} E_0=(S_0,0,0,0,0,0)^T = (\Lambda /d,0,0,0,0,0)^T, \end{aligned}$$
(3.3)

where \(S_0 = \Lambda /d\).

Next, following the method of the next-generation matrix for deterministic compartmental models by van den Driessche and Watmough [10], we calculate the basic reproduction number \(\mathscr {R}_0\).

Using the same notation as in [10], we denote \(x(t) = (E(t),E_q(t),I(t),D(t),R(t),\) \(S(t))^T\), and \(x_0 = (0,0,0,0,0,S_0)^T\). We rewrite system (3.1) as

$$\begin{aligned} \displaystyle \frac{{\mathrm {d}}x}{{\mathrm {d}}t}=\mathscr {F}(x)-\mathscr {V}(x), \end{aligned}$$
(3.4)

where

$$\begin{aligned} \mathscr {F}(x) = (\beta (I)SI(1-q),\beta (I)SIq,0,0,0,0)^T, \end{aligned}$$
(3.5)

and

$$\begin{aligned} \mathscr {V}(x) = \left( \begin{matrix} (\tau +d)E\\ (\delta _2+d)E_q\\ (\delta _1+r_1+d)I-\tau E\\ (r_2+d)D-\delta _1I-\delta _2E_q\\ (\phi +d)R-r_1 I-r_2 D\\ \beta (I)SI-\Lambda -\phi R+dS \end{matrix} \right) . \end{aligned}$$
(3.6)

Taking the \(Fr\acute{e}chet\) derivatives of \(\mathscr {F}(x)\) and \(\mathscr {V}(x)\), and evaluating them at \(x_0\), we find

$$\begin{aligned} F = \left( \begin{matrix} 0&{}0&{}\beta _0S_0(1-q)&{}0\\ 0&{}0&{}\beta _0S_0q&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0, \end{matrix} \right) , \quad V = \left( \begin{matrix} \tau +d&{}0&{}0&{}0\\ 0&{}\delta _2+d&{}0&{}0\\ -\tau &{}0&{}\delta _1+r_1+d&{}0\\ 0&{}-\delta _2&{}-\delta _1&{}r_2+d \end{matrix} \right) , \end{aligned}$$
(3.7)

where F is nonnegative and V is non-singular. Additionally,

Therefore, \(FV^{-1}\) is nonnegative and the basic reproduction number \(\mathscr {R}_0\) is given as follows:

$$\begin{aligned} \mathscr {R}_0=\rho (FV^{-1})=\frac{\Lambda \beta _0\tau (1-q)}{d(\tau +d)(\delta _1+r_1+d)}. \end{aligned}$$
(3.8)

Moreover, we then have the following theorem [10].

Theorem 1

The disease-free equilibrium \(E_0\) of system (3.1) is locally asymptotically stable when \(\mathscr {R}_0<1\), and unstable when \(\mathscr {R}_0>1\).

3.2 Global Stability of Disease-Free Equilibrium

Now, we prove the global stability of disease-free equilibrium \(E_0\) by considering following Lyapunov function:

$$\begin{aligned} V(E(t),I(t))=\tau E(t)+(\tau +d)I(t), \end{aligned}$$
(3.9)

where \(V\ge 0\) in \(\Sigma \) and \(V=0\) if and only if \((E,I) = (0,0)\). Recall that \(0<\beta (I)\le \beta _0\) and \(0<S\le S_0\). Differentiating V along the solutions of (3.1) yields

$$\begin{aligned} \begin{array}{lll} \displaystyle \left. \frac{{\mathrm {d}}V}{{\mathrm {d}}t}\right| _(3.1)(E(t),I(t))&{}=&{}\tau E'(t)+(\tau +d)I'(t) \\ &{}=&{}\tau \beta (I)SI(1-q)-(\delta _1+r_1+d)(\tau +d)I \\ &{}\le &{}\tau \beta _0S_0I(1-q)-(\delta _1+r_1+d)(\tau +d)I \\ &{}=&{}(\delta _1+r_1+d)(\tau +d)(\mathscr {R}_0-1)I \\ &{}\le &{}0, \end{array} \end{aligned}$$
(3.10)

when \(\mathscr {R}_0\le 1\). Moreover, \(V'=0\) if and only if \(\mathscr {R}_0=1\) and evaluated at \(E^0\). By LaSalle’s Invariance Principle [14], we have the following result:

$$\begin{aligned} \lim _{t\rightarrow +\infty }(E(t),E_q(t),I(t),D(t),R(t),S(t))^T = (0,0,0,0,0,S_0)^T. \end{aligned}$$
(3.11)

Theorem 2

The disease-free equilibrium \(E_0\) is globally asymptotically stable when \(\mathscr {R}_0\le 1\), and unstable when \(\mathscr {R}_0>1\).

3.3 Existence and Uniqueness of Endemic Equilibrium

To calculate the endemic equilibrium, let the right-hand side of system (3.1) be zero and \(I^*\ne 0\), such that

$$\begin{aligned} \Lambda -\beta (I^*)S^*I^*+\phi R^*-dS^*&= 0, \end{aligned}$$
(3.12a)
$$\begin{aligned} \beta (I^*)S^*I^*(1-q)-(\tau +d)E^*&= 0, \end{aligned}$$
(3.12b)
$$\begin{aligned} \beta (I^*)S^*I^*q-(\delta _2+d)E_q^*&= 0, \end{aligned}$$
(3.12c)
$$\begin{aligned} \tau E^*-(\delta _1+r_1+d)I^*&= 0, \end{aligned}$$
(3.12d)
$$\begin{aligned} \delta _1 I^*+\delta _2 E_q^*-(r_2+d)D^*&= 0 , \end{aligned}$$
(3.12e)
$$\begin{aligned} r_1 I^*+r_2 D^*-(\phi +d)I^*&= 0 . \end{aligned}$$
(3.12f)

From (3.12b)-(3.12f), we have

$$\begin{aligned} E^*&= \frac{\delta _1+r_1+d}{\tau }I^*, \end{aligned}$$
(3.13a)
$$\begin{aligned} S^*&= \frac{(\tau +d)(\delta _1+r_1+d)}{(1-q)\tau \beta (I^*)}, \end{aligned}$$
(3.13b)
$$\begin{aligned} E_q^*&=\frac{q(\tau +d)(\delta _1+r_1+d)}{(\delta _2+d)(1-q)\tau }I^*, \end{aligned}$$
(3.13c)
$$\begin{aligned} D^*&=\left[ \frac{\delta _2 q(\tau +d)(\delta _1+r_1+d)}{(r_2+d)(\delta _2+d)(1-q)\tau } +\frac{\delta _1}{r_2+d}\right] I^* \end{aligned}$$
(3.13d)

and

$$\begin{aligned} R^*=\left[ \frac{r_1}{\phi +d}+\frac{r_2\delta _2 q(\tau +d)(\delta _1+r_1+d)}{(\phi +d)(r_2+d)(\delta _2+d)(1-q)\tau }+\frac{r_2\delta _1}{(\phi +d)(r_2+d)}\right] I^*. \end{aligned}$$
(3.14)

In the bounded region (2.6), we have

$$\begin{aligned} S^* = \Lambda /d-(\beta (I^*)S^*I^*/d-\phi R^*/d)\le \Lambda /d, \end{aligned}$$
(3.15)

and

$$\begin{aligned} \begin{array}{lll} 0&{}\le &{} \beta (I^*)S^*I^*/d-\phi R^*/d \\ ~&{}=&{} MI^*, \end{array} \end{aligned}$$
(3.16)

where

$$\begin{aligned} \begin{array}{lll} M &{} =&{} \displaystyle \frac{(\tau +d)(\delta _1+r_1+d)}{(1-q)\tau }-\phi \left[ \frac{r_1}{\phi +d}+\frac{r_2\delta _2 q(\tau +d)(\delta _1+r_1+d)}{(\phi +d)(r_2+d)(\delta _2+d)(1-q)\tau } \right. \\ &{}&{} \displaystyle \left. +\frac{r_2\delta _1}{(\phi +d)(r_2+d)}\right] \ge 0. \end{array} \end{aligned}$$
(3.17)

Substituting \(S^*,~E^*,~E_q^*,~I^*,~D^*\) and \(R^*\) into (3.12a), we have

$$\begin{aligned} f(I^*)\triangleq \Lambda -M I^*-\frac{(\tau +d)(\delta _1+r_1+d)}{(1-q)\tau \beta (I^*)}=0. \end{aligned}$$
(3.18)

Directly, when \(\mathscr {R}_0>1\)

$$\begin{aligned} f(0) = \Lambda -\frac{(\tau +d)(\delta _1+r_1+d)}{(1-q)\tau \beta _0}=\frac{(\tau +d)(\delta _1+r_1+d)}{(1-q)\tau \beta _0}\times \left( \mathscr {R}_0-1\right) >0, \end{aligned}$$
(3.19)

and

$$\begin{aligned} \frac{{\mathrm {d}}f(I^*)}{{\mathrm {d}}I^*} = -M+\frac{(\tau +d)(\delta _1+r_1+d)}{(1-q)\tau \beta ^2(I^*)}\times \beta '(I^*)\le 0. \end{aligned}$$
(3.20)

Therefore, from the sketch of function \(f(I^*)\) with respect to \(I^*\), there exists a unique \(I^*>0\) in \(\Sigma \), if and only if \(\mathscr {R}_0>1\).

Theorem 3

System (3.1) exists a unique endemic equilibrium \(E_*=(S^*,E^*,E_q^*,I^*,D^*,\) \(R^*)^T\) when \(\mathscr {R}_0>1\), and a unique disease-free equilibrium \(E_0=(S_0,0,0,0,0,0)^T\) when \(\mathscr {R}_0\le 1\).

3.4 Uniformly Persistent

Now, we establish the uniform persistence for system (3.1) when \(\mathscr {R}_0>1\), by applying the following Lemma of Zhao [27].

Lemma 1

[27] Let \(\phi _t\): \(X\rightarrow ~X\) be a semiflow and \(X_0\subset X\) an open set. Define \(\partial X_0=X\backslash X_0\), and \(M_\partial =\{x\in \partial X_0: ~ \phi _tx\in \partial X_0,~t\ge 0\}\). Assume that

  1. (I)

    \(\phi _t X_0\subset X_0\) and \(\phi _t\) has a global attractor A;

  2. (II)

    there exists a finite sequence of \(\mathscr {M}=\{M_1,\ldots ,~M_k\}\) of disjoint, compact, and isolated invariant sets in \(\partial X_0\) such that

    1. (i)

      \(\Omega (M_\partial ):=\cup _{x\in M_\partial }\omega (x)\subset \cup _{i=1}^k M_i\);

    2. (ii)

      no subset of \(\mathscr {M}\) forms a cycle in \(\partial X_0\);

    3. (iii)

      \(M_i\) is isolated in X;

    4. (iv)

      \(W^s(M_i)\cap X_0={\emptyset }\) , where \(W^s(M_i)=\{x\in X_0:~\omega (x)\subset M_i\}\), for each \(1\le i\le k\).

Then, \(\phi _t\) is uniformly persistent with respect to \((X_0,\partial X_0)\), namely, there exists \(\eta >0\), such that \(\displaystyle \liminf _{t\rightarrow +\infty }d(\phi _tx,\partial X_0)\ge \eta \) for \(x\in X_0\).

Theorem 4

If \(\mathscr {R}_0>1\), then system (3.1) is uniformly persistent, namely, there exists \(\eta >0\), such that \(\displaystyle \liminf _{t\rightarrow +\infty }\{S(t),E(t),E_q(t),I(t),D(t),R(t)\}\ge \eta \), under initial conditions S(t), E(t), \(E_q(t)\), I(t), D(t), \(R(t)>0\).

Proof

Choose \(X=\mathbb {R}_+^6\), \(X_0 = \{(S,E,E_q,I,D,R)\in X,~ E+E_q+I+D+R>0\}\), and \(\partial X_0 = X\backslash X_0= \{(S,E,E_q,I,D,R)\in X,~ E=E_q=I=D=R=0\}\). Let \(\phi _t\) be the semiflow induced by the solutions of system (3.1). It’s easy to verify that \(\phi _t X_0\subset X_0\) and \(\phi _t\) is ultimately bounded in \(X_0\), which implies that there always exists a global attractor for \(\phi _t\). \(E_0\) is the unique boundary equilibrium on \(\partial X_0\), and it’s globally stable on \(\partial X_0\). Let \(M_1=\{E_0\}\) and \(\mathscr {M}=\{M_1\}\). Then \(\cup _{x\in M_\partial }\omega (x)=M_1\) and no subset of \(\mathscr {M}\) forms a cycle in \(\partial X_0\). If \(\mathscr {R}_0>1\), then \(E_0\) is unstable in \(X_0\), which guarantees conditions (iii) and (iv) are satisfied. Therefore, applying Lemma 1, the proof is complete. \(\square \)

3.5 Sensitivity of the Basic Reproduction Number

The sensitivity of the basic reproduction number \(\mathscr {R}_0\) is an important issue, because it determines the model robustness to parameter values. Next, we discuss the sensitivity of \(\mathscr {R}_0\) with respect to model parameters measured by the so-called sensitivity index. More specifically, the impact of \(\beta _0,~q,~\delta _1,~\delta _2\) on \(\mathscr {R}_0\) is investigated, respectively.

Definition 1

[9, 26] The normalized forward sensitivity index of a variable v that depends differentiably on a parameter p is defined by

$$\begin{aligned} \mathscr {Y}_p^v:=\frac{\partial v}{\partial p}\times \frac{p}{|v|}. \end{aligned}$$
(3.21)

Remark 1

If \(\mathscr {Y}_p^v=+1\), then an increase (decrease) of p by \(x\%\) increases (decreases) v by \(x\%\). If \(\mathscr {Y}_p^v=-1\), then an increase (decrease) of p by \(x\%\) decreases (increases) v by \(x\%\).

It follows directly from (3.8) and (3.21),

$$\begin{aligned} \begin{array}{c} \displaystyle \mathscr {Y}_{\beta _0}^{\mathscr {R}_0}:=\frac{\partial \mathscr {R}_0}{\partial \beta _0}\times \frac{\beta _0}{|\mathscr {R}_0|}=1, \\ \displaystyle \mathscr {Y}_{q}^{\mathscr {R}_0}:=\frac{\partial \mathscr {R}_0}{\partial q}\times \frac{q}{|\mathscr {R}_0|}=-\frac{q}{1-q}, \\ \displaystyle \mathscr {Y}_{\delta _1}^{\mathscr {R}_0}:=\frac{\partial \mathscr {R}_0}{\partial \delta _1}\times \frac{\delta _1}{|\mathscr {R}_0|}=-\frac{\delta _1}{\delta _1+r_1+d}, \\ \displaystyle \mathscr {Y}_{\delta _2}^{\mathscr {R}_0}:=\frac{\partial \mathscr {R}_0}{\partial \delta _2}\times \frac{\delta _2}{|\mathscr {R}_0|}=0. \\ \end{array} \end{aligned}$$
(3.22)

From the signs of the normalized forward sensitivity index, we conclude that the basic reproduction number \(\mathscr {R}_0\) increases with \(\beta _0\), and decreases with \(\delta _1\) and q, respectively; whereas, \(\delta _2\) has no impact on the values of \(\mathscr {R}_0\). Note that the most sensitive parameter p it corresponds the largest absolute value of normalized forward sensitivity index, which indicates: if \(0<q<1/2\), then \(\beta _0\) is the most sensitive parameter under consideration; if \(1/2<q<1\), then q is the most sensitive parameter. Moreover, increasing the isolated proportion q and the transition rate \(\delta _1\) of the undiagnosed infectious individuals to the diagnosed class can decrease \(\mathscr {R}_0\), but changing the transition rate \(\delta _2\) of the isolated exposed individuals to the diagnosed class cannot alter the value of \(\mathscr {R}_0\). Actually, we can decrease \(\mathscr {R}_0\) until it’s no greater than 1, which indicates that the infection will die out in long run, by letting \(q\ge q^c\) or \(\delta _1\ge \delta _1^c\), where

$$\begin{aligned} q^c=1-\frac{d(\tau +d)(\delta _1+r_1+d)}{\Lambda \beta _0\tau },\quad \delta _1^c = \frac{\Lambda \beta _0\tau (1-q)}{d(\tau +d)}-r_1-d. \end{aligned}$$
(3.23)

4 Optimal Control Problem with q(t) (Non-constant)

In this section, we present the optimal control problem of the epidemic, aiming to find the optimal value \(q^*\) of the control q(t), such that the associated state trajectories \(S^*,E^*,E_q^*,I^*,D^*,R^*\) are the solutions of system (2.1) in the time interval [0, T] with initial conditions (2.2), and minimize the objective functional given as follows:

$$\begin{aligned} J(q(\cdot ))=\int _{0}^{T}\left[ m_1 I(t)+m_2 D(t)+m_3q^2(t)\right] dt, \end{aligned}$$
(4.1)

where \(m_1,~m_2\) and \(m_3\) are given constant weights, measuring the number of infectious individuals I, the number of diagnosed infectious individuals D and the cost of the intervention associated to the control q(t), respectively. To be clear, the weight parameters \(m_1,~m_2\) and \(m_3\) are to be chosen according to different optimal control scenarios, such as to increase weight \(m_1\) in order to emphasize the number of infectious individuals in the objective functional. The set of admissible control function is given by

$$\begin{aligned} \Omega =\{q(\cdot )\in L^\infty (0,T)|0\le q(t)\le q_{max},~\forall t\in [0,T]\}. \end{aligned}$$
(4.2)

We consider the optimal control problem of determining \((S^*(\cdot ),E^*(\cdot ),E_q^*(\cdot ),I^*(\cdot ),\) \(D^*(\cdot ), R^*(\cdot ))\), associated to an admissible control \(q^*(\cdot )\in \Omega \) in the time interval [0, T], satisfying system (2.1), with initial conditions (2.2) and minimizing the cost functional (4.1), namely,

$$\begin{aligned} J(q^*(\cdot ))=\min _{\Omega }J(g(\cdot )). \end{aligned}$$
(4.3)

It’s obvious that the integrand of the cost functional J is concave with respect to the control q. The control system (2.1) is Lipschitz with respect to the state variables \((S,E,E_q,I,D,R)\). These properties ensure the existence of an optimal control \(q^*(\cdot )\) of the optimal control problem (see [8] for details).

According to the Pontryagin’s Maximum Principle [17], if \(q^*(\cdot )\) is an optimal control for problem (2.1), (4.3) with the initial conditions given in (2.2) and fixed final time \(T>0\), then there exists a nontrivial absolutely continuous mapping \(\lambda :~[0,T]\rightarrow \mathbb {R}^6\), \(\lambda (t)=(\lambda _1(t),\lambda _2(t),\lambda _3(t),\lambda _4(t),\lambda _5(t),\lambda _6(t))\), called adjoint vector, such that

$$\begin{aligned} S'=\frac{\partial H}{\partial \lambda _1},~E'=\frac{\partial H}{\partial \lambda _2},~E_q'=\frac{\partial H}{\partial \lambda _3},~I'=\frac{\partial H}{\partial \lambda _4},~D'=\frac{\partial H}{\partial \lambda _5},~R'=\frac{\partial H}{\partial \lambda _6},~ \end{aligned}$$
(4.4)

and

$$\begin{aligned} \lambda _1'=-\frac{\partial H}{\partial S},~\lambda _2'=-\frac{\partial H}{\partial E},~\lambda _3'=-\frac{\partial H}{\partial E_q},~\lambda _4'=-\frac{\partial H}{\partial I},~\lambda _5'=-\frac{\partial H}{\partial D},~\lambda _6'=-\frac{\partial H}{\partial R},~ \end{aligned}$$
(4.5)

where function H defined by

$$\begin{aligned} \begin{array}{lll} H&{}=&{}H(S(t),E(t),E_q(t),I(t),D(t),R(t),q(t)) \\ &{}=&{}m_1I(t)+m_2D(t)+m_3q^2(t) \\ &{}&{}+\lambda _1(t)(\Lambda -\beta (I(t))S(t)I(t)+\phi R(t)-dS(t)) \\ &{}&{}+\lambda _2(t)(\beta (I(t))S(t)I(t)(1-q(t))-\tau E(t)-dE(t)) \\ &{}&{}+\lambda _3(t)(\beta (I(t))S(t)I(t)q(t)-\delta _2 E_q(t)-dE_q(t)) \\ &{}&{} +\lambda _4(t)(\tau E(t)-\delta _1 I(t)-r_1 I(t)-dI(t)) \\ &{}&{}+\lambda _5(t)(\delta _1 I(t)+\delta _2 E_q(t)-r_2D(t)-dD(t)) \\ &{}&{}+\lambda _6(t)(r_1 I(t)+r_2 D(t)-\phi R(t)-dR(t)) \end{array} \end{aligned}$$
(4.6)

is called the Hamiltonian, and the minimization condition

$$\begin{aligned} \begin{array}{ll} &{}H(S^*(t),E^*(t),E_q^*(t),I^*(t),D^*(t),R^*(t),q^*(t)) \\ =&{}\displaystyle \min _{0\le q\le q_{max}}H(S^*(t),E^*(t),E_q^*(t),I^*(t),D^*(t),R^*(t),q) \end{array} \end{aligned}$$
(4.7)

holds almost everywhere on [0, T]. Moreover, the transversality conditions

$$\begin{aligned} \lambda _i(T)=0,\qquad i = 1,\ldots ,6, \end{aligned}$$
(4.8)

hold.

Applying the Pontryagin’s Maximum Principle to the optimal control problem (2.1), (4.3), the following theorem is derived.

Theorem 5

The optimal control problem (2.1), (4.3) with the initial conditions given in (2.2) and fixed final time T admits a unique optimal solution \((S^*(\cdot ),E^*(\cdot ),E_q^*(\cdot ),\) \(I^*(\cdot ),D^*(\cdot )\), \(R^*(\cdot ))\), associated to the optimal control \(q^*(\cdot )\in \Omega \) on [0, T] described by

$$\begin{aligned} q^*(t)=\min \left\{ \max \left\{ 0,\frac{\beta (I^*(t))S^*(t)I^*(t)(\lambda _2(t)-\lambda _3(t))}{2m_3}\right\} ,q_{max}\right\} , \end{aligned}$$
(4.9)

where the adjoint functions satisfy

$$\begin{aligned} { \left\{ \begin{array}{ll} \lambda '_1(t)=&{}\lambda _1(t)(\beta (I(t))I(t)+d)-\lambda _2(t)\beta (I(t))I(t)(1-q(t)) \\ &{}-\lambda _3(t)\beta (I(t))I(t)q(t), \\ \lambda '_2(t)=&{}\lambda _2(t)(\tau +d)-\lambda _4(t)\tau , \\ \lambda '_3(t)=&{}\lambda _3(t)(\delta _2+d)-\lambda _5(t)\delta _2, \\ \lambda '_4(t)=&{}\lambda _1(t)[\beta (I(t))S(t)+\beta '(I(t))S(t)I(t)] \\ &{}\quad -\lambda _3(t)[\beta (I(t))S(t)+\beta '(I(t))S(t)I(t)]q(t) \\ &{}\quad -\lambda _2(t)[\beta (I(t))S(t)+\beta '(I(t))S(t)I(t)](1-q(t)) \\ &{}\quad +\lambda _4(t)(\delta _1+r_1+d)-\lambda _5(t)\delta _1-\lambda _6(t) r_1-m_1, \\ \lambda '_5(t)=&{}\lambda _5(t)(r_2+d)-\lambda _6(t)r_2-m2, \\ \lambda '_6(t)=&{}-\lambda _1(t)\phi +\lambda _6(t)(\phi +d), \end{array} \right. } \end{aligned}$$
(4.10)

subject to the transversality conditions \(\lambda _i(T)=0,~i=1,\ldots ,6\).

Proof

Existence of an optimal control solution \((S^*,E^*,E_q^*,I^*,D^*,R^*)\) associated to an optimal control \(q^*\) comes from the convexity of the integrand of the cost functional J with respect to the control q, and the Lipschitz property of the state system with respect to state variables \((S,E,E_q,I,D,R)\). From \(\displaystyle \frac{\partial H}{\partial q}(S^*,E^*,E_q^*,I^*,D^*,R^*,q)=0\), we have

$$\begin{aligned} 2m_3q-\lambda _2(t)\beta (I^*(t))S^*(t)I^*(t)+\lambda _3(t)\beta (I^*(t)S^*(t)I^*(t))=0, \end{aligned}$$
(4.11)

and

$$\begin{aligned} q(t)=\frac{\beta (I^*(t))S^*(t)I^*(t)(\lambda _2(t)-\lambda _3(t))}{2m_3}. \end{aligned}$$
(4.12)

Therefore, the final expression of the optimal control \(q^*(t)\) is defined by (4.9).

System (4.10) is derived from the Pontryagin’s Maximum Principle and the optimal control (4.9) comes from the minimization condition (4.7). For some final time \(T>0\), the optimal control by (4.9) is unique due to the boundedness of the state and adjoint functions, and the Lipschitz property of system (2.1) and system (4.10). \(\square \)

Remark 2

Detailed theory is referred to [11, 12, 18].

5 Numerical Results

The following specified form of \(\beta (I)\) (as in [7]) is chosen to illustrate the obtained theoretical results for system (2.1):

$$\begin{aligned} \beta (I) = \frac{\beta _0}{1+kI}, \end{aligned}$$
(5.1)

where \(\beta (I)\) satisfies condition (2.3), and \(\beta _0,~k>0\).

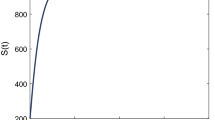
First, we consider the dynamical behaviors of system (3.1) with constant isolated proportion q. The parameter values are listed in Table 2, which may to some extent characterize the flu transmission dynamics. The initial number of individuals in each compartment is given by \( E(0)=800,~E_q(0)=200,~I(0)=100,~D(0)=100,~R(0)=50\), and \(S(0) = \Lambda /d-E(0)-E_q(0)-I(0)-D(0)-R(0)\). The simulation results show: Fig. 2a presents the global asymptotic stability of the disease-free equilibrium with \(\mathscr {R}_0<1\); Fig. 2b presents the global asymptotic stability of the endemic equilibrium with \(\mathscr {R}_0>1\).

Next, we investigate the numerical solution of the optimal problem studied in Sect. 4. The optimal control given by Theorem 5 is computed numerically by implementing a forward-backward fourth-order Runge–Kutta method[6, 15]. Following the method in [6], system (2.1) is solved with a guess for the control over time interval [0, T], using a forward fourth-order Runge–Kutta scheme and the transversal condition (4.8); the adjoint system (4.10) is solved by backward fourth-order Runge–Kutta scheme using the current iteration solution of system (2.1). The controls are updated by using the expression given by (4.9). In this simulation, we consider \(q_{max} = 0.5\) and \(T=40\); namely, the set of admissible controls is given by

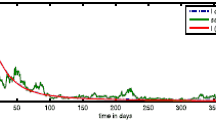
$$\begin{aligned} \Omega =\{q(\cdot )\in L^\infty (0,40)|0\le q(t)\le 0.5,~\forall t\in [0,40]\}. \end{aligned}$$
(5.2)

Let \(m_1=m_2=1\) and \(m_3=500\). The numerical solution of the optimal control \(q^*\) is given in Fig. 3a, as well as the comparison of solutions of system (2.1) with and without control.

Table 2 Parameter values assigned in simulations
Full size table
Fig. 2
figure 2

Illustration of the dynamical nature of the infected compartments, namely \(E(t),~E_q(t),~I(t)\) and D(t): a \(\mathscr {R}_0 = 0.3939<1\) with \(\beta _0= 2\times 10^{-6}\); b \(\mathscr {R}_0 = 3.9391>1\) with \(\beta _0= 2\times 10^{-5}\)

Full size image
Fig. 3
figure 3

a Optimal control \(q^*(t)\); b Comparison: solutions of system (2.1) with optimal control \(q^*(t)\) versus solutions without control \(q(t)=0\)

Full size image

6 Conclusion

In this paper, an SEIRS epidemic model is formulated, incorporating appropriate compartments such as isolated exposed class and diagnosed class, relevant to interventions. The dynamical behaviors and the optimal control problem of the model are investigated.

On one hand, the isolated proportion of exposed individuals is set to a constant q. The dynamical behaviors of system (3.1) are discussed. The basic reproduction number \(\mathscr {R}_0\) is derived by the next-generation matrix method, which is crucial to the global dynamics of the model. The qualitative analyses are carried out in terms of \(\mathscr {R}_0\). The system only has a globally asymptotically stable disease-free equilibrium when \(\mathscr {R}_0\le 1\), and it implies that the disease eventually dies out; the system has a unique endemic equilibrium when \(\mathscr {R}_0>1\), and the disease becomes uniformly persistent in the long run. The sensitivity of the basic reproduction number with respect to model parameters is studied by the normalized forward sensitivity index. As we can see, \(\beta _0\) is the most sensitive parameter under consideration, and \(\mathscr {R}_0\) increases with \(\beta _0\) and decreases with \(\delta _1\) and q, respectively, whereas \(\delta _2\) has no impact on the value of \(\mathscr {R}_0\). Moreover, we give the critical values \(q^c\) and \(\delta _1^c\), in order to ensure \(\mathscr {R}_0\le 1\).

On the other hand, the paper investigates the optimal control problem of the epidemic, aiming to find the optimal value \(q^*\) of the control q(t). The celebrated Pontryagin’s Maximum Principle is applied to optimal control problem and an explicit expression of the optimal control is presented. The numerical solution of the optimal control is computed by implementing a forward-backward fourth-order Runge–Kutta method. Furthermore, the simulation results indicate that using the optimal control measure, the number of the infectious individuals undiagnosed and the diagnosed individuals diminish.

The time-dependent isolation rate may be able to depict the scenarios with different intervention response stages, such as due to the delayed public awareness of disease transmission. The optimal control suggests a reasonable isolation rate function to minimize the number of both the diagnosed and undiagnosed individuals, as well as the cost of intervention, which can give some suggestions to control the disease transmission dynamics.