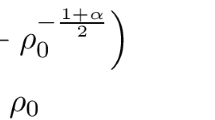The Perturbed Riemann Problem for a Macroscopic Production Model with Chaplygin Gas

Abstract

The exact Riemann solutions for a macroscopic production model under the equation of state given by the Chaplygin gas are solved explicitly for all possible Riemann initial data. It is discovered interestingly that a composite hyperbolic wave is involved in Riemann solution under some specially designated initial conditions, which is made up of a rarefaction wave and a delta contact discontinuity attached on the wave front of the rarefaction wave. Furthermore, the constructions of global solutions to the perturbed Riemann problem for this system are also displayed in completely explicit forms when the initial data are taken to be three piecewise constant states under some suitable restrictive conditions by using the method of characteristics. During the process of constructing global solutions, the interactions of elementary waves are studied in detail. Moreover, it is proved rigorously that Riemann solutions are stable with respect to the specific small perturbations of Riemann initial data.

1 Introduction

In recent years, the macroscopic production models have become one of the important research topics in the study of production planning and control in the manufacturing industry. In the previous stage, the fluid-like continuous models [1, 2] have been introduced to model high-volume product flows, which can be used to depict the product flow by using discrete event simulations in an accumulated way. The most widely used model is a scalar conservation law under appropriate assumptions on the flux function which is called as a clearing function for the product flow. In general, a given clearing function describes the averaged sample data, but cannot illustrate the data diffusion. In order to solve this problem, the following macroscopic production model [3] consisting of two conservation laws is proposed in the form

$$\begin{aligned} \left\{ \begin{array}{l} \rho _{t}+(\rho u)_{x}=0, \\ \Big (\rho u\big (1+P(\rho )\big )\Big )_{t}+\Big (\rho u^{2}\big (1+P(\rho )\big )\Big )_{x}=0, \end{array}\right. \end{aligned}$$

(1.1)

in which $\rho$ and u are used to represent the product density and velocity, respectively, which are often required to be non-negative. In addition, t and x express the time and the production stage (or the degree of completion) to describe the work-in-progress and the pressure term P refers to the anticipated factor in the production line which is usually given by the equation of state $P=P(\rho )$.

It is of great interest to notice that some interesting nonlinear phenomena were observed in [3] when the pressure term was taken as $P(\rho )=\rho$. Especially, it was obtained in [4] that the delta standing wave was also involved in Riemann solutions for system (1.1) under this pressure term $P(\rho )=\rho$. In fact, the singularity of $\delta -$concentration was also investigated in [5, 6] which can be used to illustrate some extreme situations in the production line. Nowadays, it was known in [7,8,9,10,11] that delta shock wave is involved in Riemann solutions for the isentropic Chaplygin gas dynamical system. It is worthwhile to mention that the equation of state for the Chaplygin gas is taken to be the negative pressure $P(\rho )=-\frac{1}{\rho }$, which often happens in the product flow. Actually, this equation of state $P(\rho )=-\frac{1}{\rho }$ was also used in the AR traffic flow model to describe some complicated traffic phenomena well [12]. It is known that the behaviors of the macroscopic production model (1.1) are very similar to those of the AR traffic flow model. Thus, it is natural to introduce the equation of state for the Chaplygin gas $P(\rho )=-\frac{1}{\rho }$ into the macroscopic production model (1.1) in order to discover some new interesting nonlinear phenomena. In the current paper, from the viewpoint of hyperbolic systems of conservation laws, it is also of great interest to consider system (1.1) under the equation of state $P(\rho )=-\frac{1}{\rho }$ given by the Chaplygin gas, which is rewritten precisely as

$$\begin{aligned} \left\{ \begin{array}{l} \rho _{t}+(\rho u)_{x}=0, \\ (\rho u-u)_{t}+(\rho u^{2}-u^{2})_{x}=0. \end{array}\right. \end{aligned}$$

(1.2)

In order to develop wave analysis, we first draw our attention on system (1.2) with the following Riemann-type initial condition

$$\begin{aligned} (\rho ,u)(x,0)=\left\{ \begin{array}{ll} (\rho _{-},u_{-}), &{} x<0,\\ (\rho _{+},u_{+}), &{} x>0. \end{array} \right. \end{aligned}$$

(1.3)

The Riemann problem is a special initial value problem with the initial condition consisting of two constant states separated by the origin. It is one of the most fundamental problems in the field of nonlinear hyperbolic systems of conservation laws. The structures of Riemann solutions can be used well to describe the various and complicated nonlinear phenomena and are also regarded as the basic for numerical schemes, for the reason that Riemann solutions are served as the basic building blocks of constructing solutions to the general initial value problem by employing the random choice method. It is of great interest to develop numerical methods such as Godunov methods or even Riemann-free methods [13,14,15,16,17,18], which are based on the constructions of Riemann solutions in details. Thus, the constructions of Riemann solutions for different hyperbolic systems of conservation laws are very important and also have attracted the attention of researchers from analytical and numerical aspects.

It is not difficult to get that system (1.2) owns two real and different eigenvalues $\lambda _{1}=u-\frac{\displaystyle u}{\displaystyle \rho -1}$ and $\lambda _{2}=u$. Obviously, the line $\rho =1$ is a singular curve in the quarter $(\rho ,u)$ phase plane. In the present paper, we restrict ourselves into the region $\Omega =\{(\rho ,u)| \rho>1, u>0 \}$, such that $\lambda _{1}<\lambda _{2}$ and then the system (1.2) is strictly hyperbolic in this region $\Omega$. In fact, the other region $\{(\rho ,u)| 0<\rho <1, u>0 \}$ can be dealt with similarly. It is worthwhile to notice that the shock curve shares the same expression formula with the rarefaction one in the quarter $(\rho ,u)$ phase plane, namely system (1.2) belongs to the so-called Temple class [19,20,21]. Furthermore, it is of great interest to observe that a composite wave is involved in Riemann solution of (1.2) and (1.3) under certain initial condition $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$, which is made up of a rarefaction wave and a delta contact discontinuity attached on the wave front of rarefaction wave. In the current paper, we only construct possible solution of the Riemann problem (1.2) and (1.3) for this certain initial condition and the uniqueness problem is still unsolved and left for the future work. In addition, it is well known that delta shock wave should be introduced in order to solve Riemann problems for some weak hyperbolic conservation systems and the theory of delta shock wave has been well established and developed in recent years, see [22,23,24,25,26,27,28] for examples. However, as far as we know, our constructed composite wave solution with the singularity of delta function cannot be found in any Riemann solution but only appears in the study [29,30,31] of wave interaction between a delta shock wave with a rarefaction wave for some hyperbolic systems of conservation laws.

It is well known that Riemann solutions of (1.2) and (1.3) cannot illustrate the dynamic pictures of system (1.2) in all the situations. In order to capture some more complicated nonlinear phenomena, it is necessary to investigate the perturbed (or double) Riemann problem for system (1.2) with the following constant states in three pieces

$$\begin{aligned} (\rho ,u)(x,0)=\left\{ \begin{array}{ll} (\rho _{-},u_{-}), &{} -\infty<x<0, \\ (\rho _{m},u_{m}), &{} 0<x<\varepsilon , \\ (\rho _{+},u_{+}), &{} \varepsilon<x<+\infty , \end{array} \right. \end{aligned}$$

(1.4)

where $\varepsilon$ is taken to be a adequately small positive number. In order to construct the global solutions to the perturbed Riemann problem (1.2) and (1.4), we need to deal with the problem of wave interactions carefully. Due to the fact that the uniqueness problem is unsolved when $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$, we restrict ourselves to only consider the interactions of elementary waves including shock wave, rarefaction wave and contact discontinuity. For this purpose, it is required that the initial condition (1.4) should satisfy $u_{m}>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$ and $u_{+}>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$ simultaneously. Thanks to system (1.2) with special structure of Temple class, the global solutions of (1.2) and (1.4) are constructed in fully explicit forms by using the method of characteristics. As a consequence, it is evident to show that the limits of perturbed Riemann solutions of (1.2) and (1.4) converge to the corresponding ones of (1.2) and (1.3) when the perturbation parameter $\varepsilon$ approaches zero. That is to say, Riemann solutions of (1.2) and (1.3) are stable with respect to certain small perturbation of initial condition given by (1.4) where $\varepsilon$ is regarded as the so-called perturbation parameter. It should be stressed that the initial condition taken in the form (1.4) has been intensively used to investigate the problem of wave interactions [32,33,34,35,36,37,38] for various hyperbolic systems of conservation laws.

The rest of this paper is organized in the following way. In Sect. 2, we investigate the general properties and elementary waves for system (1.2) and then solve exact Riemann solutions of (1.2) and (1.3) for all possible initial conditions. In Sect. 3, the perturbed Riemann solutions of (1.2) and (1.4) are constructed by studying all the occurring wave interactions under the two restrictive conditions $u_{m}>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$ and $u_{+}>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$. Finally, the limit $\varepsilon \rightarrow 0$ is taken, which allows us to get stabilities of Riemann solutions with respect to this special perturbation of initial condition and then the conclusion is drawn in Sect. 4.

2 Riemann Solutions of (1.2) and (1.3)

In this section, we firstly present some basic characteristics for system (1.2). Then, we construct Riemann solutions of (1.2) and (1.3) when the initial condition (1.3) lies in the region $\Omega =\{(\rho ,u)| \rho>1, u>0 \}$. System (1.2) admits the following quasi-linear form

$$\begin{aligned} \left( \begin{array}{cc} 1 &{} 0 \\ u &{} \rho -1\\ \end{array} \right) \left( \begin{array}{cc} \rho \\ u \\ \end{array} \right) _{t} + \left( \begin{array}{cc} u &{} \rho \\ u^{2} &{} 2(\rho -1) u\\ \end{array} \right) \left( \begin{array}{cc} \rho \\ u \\ \end{array} \right) _{x}= \left( \begin{array}{cc} 0\\ 0\\ \end{array} \right) . \end{aligned}$$

The eigenvalues are represented as

$$\begin{aligned} \lambda _{1}=u-\frac{\displaystyle u}{\displaystyle \rho -1},\qquad \lambda _{2}=u. \end{aligned}$$

(2.1)

It is evident that system (1.2) is strictly hyperbolic in the region $\Omega$. The corresponding right eigenvectors for $\lambda _{i} (i=1,2)$ are given, respectively, by $\overrightarrow{r_{1}}=(\rho (\rho -1),-u)^{T}$ and $\overrightarrow{r_{2}}=(1,0)^{T}$. A simple calculation shows that $\nabla \lambda _{1}\cdot \overrightarrow{r_{1}}=\frac{2u}{\rho -1}\ne 0$ in the region $\Omega$ and $\nabla \lambda _{2}\cdot \overrightarrow{r_{2}}\equiv 0$, in which $\nabla =(\frac{\displaystyle \partial }{\displaystyle \partial \rho },\frac{\displaystyle \partial }{\displaystyle \partial u})$. So, it is easily shown that the first characteristic field is genuinely nonlinear in the region $\Omega$ and the second characteristic field is always linearly degenerate. As a consequence, the wave of $\lambda _{1}-$family is either shock wave or rarefaction wave as well as the wave of $\lambda _{2}-$family is always contact discontinuity. For convenience, we use the notations S, R and J, respectively, to stand for shock wave, rarefaction wave and contact discontinuity in the current paper. In addition, the Riemann invariants along the characteristic fields are chosen, respectively, as $u-\frac{\displaystyle u}{\displaystyle \rho }$ and u.

To solve self-similar Riemann solutions of the form $(\rho ,u)(x,t)=(\rho ,u)(\xi )$ with $\xi =\frac{x}{t}$, the Riemann problem (1.2) and (1.3) is reduced to

$$\begin{aligned} \left\{ \begin{array}{l} -\xi \rho _{\xi }+(\rho u)_{\xi }=0, \\ -\xi (\rho u-u)_{\xi }+(\rho u^{2}-u^{2})_{\xi }=0, \end{array}\right. \end{aligned}$$

(2.2)

with the boundary conditions $(\rho ,u)(\pm \infty )=(\rho _{\pm },u_{\pm })$. For smooth solutions, system (2.2) is rewritten as

$$\begin{aligned} \left( \begin{array}{cc} u-\xi &{} \rho \\ -\xi u+u^{2} &{} -\xi (\rho -1)+2(\rho -1)u \\ \end{array} \right) \left( \begin{array}{cc} \rho \\ u \\ \end{array} \right) _{\xi }= \left( \begin{array}{cc} 0\\ 0\\ \end{array} \right) . \end{aligned}$$

It provides not only general solution (constant state), but also singular solution. It should be pointed out that a rarefaction wave is a piecewise smooth continuous solution of (2.2). Let the left state $(\rho _{-},u_{-})$ be a fixed point in the region $\Omega$, then we get the 1-rarefaction curve originating from $(\rho _{-},u_{-})$ as follows:

$$\begin{aligned} R(\rho _{-},u_{-}): \xi =\lambda _{1}=u-\frac{\displaystyle u}{\displaystyle \rho -1}, \qquad u-\frac{\displaystyle u}{\displaystyle \rho }=u_--\frac{\displaystyle u_{-}}{\displaystyle \rho _{-}}, \qquad \rho >\rho _{-}, \quad u<u_{-}. \end{aligned}$$

(2.3)

It is worth mentioning that if the given left state $(\rho _{-},u_{-})$ lies in the region $\Omega$, then the 1-rarefaction curve has the line $u=u_--\frac{\displaystyle u_{-}}{\displaystyle \rho _{-}}$ as its asymptote. By differentiating $\rho$ with respect to u in (2.3), we find that

$$\begin{aligned} \frac{\displaystyle d\rho }{\displaystyle du}=\frac{\displaystyle -\rho _{-}(\rho _{-}-1)u_{-}}{\displaystyle \big (\rho _{-}u-(\rho _{-}-1)u_{-}\big )^{2}}<0,\qquad \frac{\displaystyle d^{2}\rho }{\displaystyle du^{2}}=\frac{\displaystyle 2\rho _-^{2}(\rho _{-}-1)u_{-}}{\displaystyle \big (\rho _{-}u-(\rho _{-}-1)u_{-}\big )^{3}}=\frac{\displaystyle 2\rho ^{3}(\rho _{-}-1)u_{-}}{\displaystyle \rho _{-} u^{3}}>0, \end{aligned}$$

which implies that the 1-rarefaction curve is convex in $\Omega$.

The R-H conditions at a discontinuous curve $x=x(t)$ are given by

$$\begin{aligned} \left\{ \begin{array}{l} \sigma [\rho ]=[\rho u], \\ \sigma [\rho u-u]=[\rho u^{2}-u^{2}], \end{array}\right. \end{aligned}$$

(2.4)

where $\sigma =\frac{\displaystyle dx}{\displaystyle dt}$ is the velocity of discontinuity and $[\rho ]=\rho _{r}-\rho _{l}$ with $\rho _{l}=\rho (x(t)-0,t)$ and $\rho _{r}=\rho (x(t)+0,t)$ is the jump of $\rho$ across the discontinuity, etc. On the one hand, if $\sigma =0$, then we can only obtain a constant state solution. On the other hand, if $\sigma \ne 0$, then eliminating $\sigma$ in (2.4) yields

$$\begin{aligned} (\rho _{r} u_{r}-u_{r}-\rho _{l} u_{l}+u_{l})(\rho _{r} u_{r}-\rho _{l} u_{l}) =(\rho _{r}-\rho _{l})(\rho _{r}u^{2}_{r}-u^{2}_{r}-\rho _{l}u^{2}_{l}+u^{2}_{l}), \end{aligned}$$

which is simplified into

$$\begin{aligned} (u_{l}-u_{r})\Big (\rho _{r}u_{l}(\rho _{l}-1)-\rho _{l}u_{r}(\rho _{r}-1)\Big )=0. \end{aligned}$$

On the one hand, if $u_{l}\ne u_{r}$, then we have $u_l-\frac{u_{l}}{\rho _{l}}=u_r-\frac{u_{r}}{\rho _{r}}$. We then find $\rho _{l}>\rho _{r}$ by using the Lax entropy conditions. Therefore, let the left state $(\rho _{l},u_{l})=(\rho _{-},u_{-})$ be fixed in the region $\Omega$, then the 1-shock curve originating from $(\rho _{-},u_{-})$ is expressed as

$$\begin{aligned} S(\rho _{-},u_{-}): \sigma =\frac{\displaystyle \rho u-\rho _{-} u_{-}}{\displaystyle \rho -\rho _{-}}, \qquad u-\frac{\displaystyle u}{\displaystyle \rho }=u_--\frac{\displaystyle u_{-}}{\displaystyle \rho _{-}}, \qquad \rho <\rho _{-}, \quad u>u_{-}. \end{aligned}$$

(2.5)

If the given left state $(\rho _{-},u_{-})$ lies in $\Omega$, then the 1-shock curve has the line $\rho =1$ as its asymptote. On the other hand, if $u_{l}= u_{r}$, then one has $\sigma =u_{l}=u_{r}$. Therefore, the curve of contact discontinuity starting from the given left state $(\rho _{-},u_{-})$ is represented as

$$\begin{aligned} J(\rho _{-},u_{-}):\tau =u=u_{-}. \end{aligned}$$

(2.6)

In summary, if the given left state $(\rho _{-},u_{-})$ lies in the region $\Omega$, then the set of states consist of 1-shock curve $S(\rho _{-},u_{-})$, 1-rarefaction curve $R(\rho _{-},u_{-})$ and 2-contact discontinuity curve $J(\rho _{-},u_{-})$ (see Fig. 1). Then the unique global Riemann solution of (1.2) and (1.3) can be constructed in terms of the right state $(\rho _{+},u_{+})$ in the different parts I, II and III of the region $\Omega$.

More specifically, if $u_{-}<u_{+}$, then the Riemann solution of (1.2) and (1.3) can be expressed by the symbol $S+J$ in the following form (see Fig. 2a)

$$\begin{aligned} (\rho ,u)(x,t)=\left\{ \begin{array}{ll} (\rho _{-},u_{-}), &{} \frac{x}{t}<\sigma ,\\ (\rho _{*},u_{*}), &{} \sigma<\frac{x}{t}<\tau ,\\ (\rho _{+},u_{+}), &{} \frac{x}{t}>\tau , \end{array} \right. \end{aligned}$$

(2.7)

in which the intermediate state $(\rho _{*},u_{*})$ is given by

$$\begin{aligned} (\rho _{*},u_{*})=\Bigg (\frac{\displaystyle \rho _{-} u_{+}}{\displaystyle \rho _{-}u_{+}-(\rho _{-}-1)u_{-}},u_{+}\Bigg ), \end{aligned}$$

(2.8)

and the wave speeds of S and J are computed, respectively, by

$$\begin{aligned} \sigma =\frac{\displaystyle \rho _{*}u_{*}-\rho _{-}u_{-}}{\displaystyle \rho _{*}-\rho _{-}} =\frac{\displaystyle (\rho _{-}-1)u_{-}-u_{+}}{\displaystyle \rho _{-}-1}=u_--\frac{\displaystyle u_+}{\displaystyle \rho _--1},\qquad \tau =u_{+}. \end{aligned}$$

(2.9)

Fig. 1

The $(\rho ,u)$ phase plane for the Riemann problem (1.2) and (1.3) is shown for the given left state $(\rho _{-},u_{-})$ located in the region $\Omega =\{(\rho ,u)| \rho>1, u>0 \}$, in which the rarefaction curve $R(\rho _{-},u_{-})$ takes the line $u=u_--\frac{\displaystyle u_{-}}{\displaystyle \rho _{-}}$ and the shock curve $S(\rho _{-},u_{-})$ takes the line $\rho =1$ as their asymptotic lines, respectively

Fig. 2

The constructions of solutions to the Riemann problem (1.2) and (1.3) are displayed for all kinds of initial conditions

If $\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}<u_{+}<u_{-}$, then the Riemann solution of (1.2) and (1.3) can be expressed by the symbol $R+J$ in the following form (see Fig. 2b)

$$\begin{aligned} (\rho ,u)(x,t)=\left\{ \begin{array}{ll} (\rho _{-},u_{-}), &{} \frac{x}{t}<\lambda _{1}(\rho _{-},u_{-}),\\ (\rho ,u), &{}\lambda _{1}(\rho _{-},u_{-})<\frac{x}{t}<\lambda _{1}(\rho _{*},u_{*}),\\ (\rho _{*},u_{*}), &{}\lambda _{1}(\rho _{*},u_{*})<\frac{x}{t}<\tau ,\\ (\rho _{+},u_{+}), &{} \frac{x}{t}>\tau , \end{array} \right. \end{aligned}$$

(2.10)

in which $(\rho _{*},u_{*})$ is also given by (2.8) and the state $(\rho ,u)$ in the rarefaction wave fan follows from (2.3) that

$$\begin{aligned} (\rho ,u)=\Bigg (\frac{\displaystyle (\rho _{-}-1) u_{-}+\sqrt{(\rho _{-}-1)^{2} u_{-}^{2}-\frac{\rho _{-}(\rho _{-}-1)u_{-}x}{t}}}{\displaystyle \sqrt{(\rho _{-}-1)^{2} u_{-}^{2}-\frac{\rho _{-}(\rho _{-}-1)u_{-}x}{t}}},\frac{\displaystyle (\rho _{-}-1)u_{-} +\sqrt{(\rho _{-}-1)^{2} u_{-}^{2}-\frac{\rho _{-}(\rho _{-}-1)u_{-}x}{t}}}{\displaystyle \rho _{-}}\Bigg ). \end{aligned}$$

(2.11)

In the end, we need to consider the case $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$. Before solving it, we shall focus on the limit of Riemann solution (2.10) when $u_{+}\rightarrow \Big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\Big )_{+}$ is taken. In terms of $u_{-}>0$ and $\rho _{-}>1$, it follows from (2.8) that

$$\begin{aligned}&\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}}\rho _{*} =\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}}\Bigg (\frac{\displaystyle \rho _{-} u_{+}}{\displaystyle \rho _{-}u_{+}-(\rho _{-}-1)u_{-}}\Bigg ) =+\infty ,\\&\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}}u_{*} =\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}}u_{+}=\frac{\displaystyle (\rho _{-}-1) u_{-}}{\displaystyle \rho _{-}}, \end{aligned}$$

which allows us to conclude that the singularity is formed for the state variable $\rho$ in the limiting $u_{+}\rightarrow \Big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\Big )_{+}$ situation. It then follows from (2.7) combining with (2.8) that

$$\begin{aligned}&\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}}\lambda _{1}(\rho _{*},u_{*}) =\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}} \Big (u_{*}-\frac{\displaystyle u_{*}}{\displaystyle \rho _{*}-1}\Big ) =\frac{\displaystyle (\rho _{-}-1)u_{-}}{\displaystyle \rho _{-}},\\&\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}}\tau =\lim _{u_{+}\rightarrow \big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\big )_{+}}u_{+} =\frac{\displaystyle (\rho _{-}-1)u_{-}}{\displaystyle \rho _{-}}. \end{aligned}$$

As a result, it is not difficult to see that the front of rarefaction wave R and the contact discontinuity J coincide with each other on the line $x=\Big (\frac{\displaystyle (\rho _{-}-1)u_{-}}{\displaystyle \rho _{-}}\Big )t$ and the density between them tends to $+\infty$ in the limiting $u_{+}\rightarrow \Big (\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}\Big )_{+}$ situation. Thus, if the initial condition (1.3) satisfies the special requirement $u_{+}=\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$, we can construct a composite wave $R\delta J$, which is made up of a rarefaction wave R and a delta contact discontinuity $\delta J$ attached on the wave front of R. More specifically, when $u_{+}=\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$, the Riemann solution of (1.2) and (1.3) may be displayed in the form

$$\begin{aligned} (\rho ,u)(x,t)=\left\{ \begin{array}{ll} (\rho _{-},u_{-}), &{} \frac{x}{t}<\lambda _{1}(\rho _{-},u_{-}),\\ (\rho ,u), &{}\lambda _{1}(\rho _{-},u_{-})<\frac{x}{t}<u_{+},\\ (+\infty ,u_{+}), &{}\frac{x}{t}=u_{+},\\ (\rho _{+},u_{+}), &{} \frac{x}{t}>u_{+}, \end{array} \right. \end{aligned}$$

(2.12)

in which the state $(\rho ,u)$ in the rarefaction wave fan R is also calculated by (2.11).

Motivated by the above detailed observation on the construction of Riemann solution for the special case $u_{+}=\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$, we plan to construct possible Riemann solution of (1.2) and (1.3) when $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$. It is not difficult to get that

$$\begin{aligned} \lambda _{1}(\rho _{+},u_{+})<\lambda _{2}(\rho _{+},u_{+})<\frac{\displaystyle (\rho _{-}-1)u_{-}}{\displaystyle \rho _{-}}, \end{aligned}$$

which means that all the characteristic lines on the right-hand side of the contact discontinuity $x=\frac{(\rho _{-}-1)u_{-}t}{\rho _{-}}$ will enter the line of this contact discontinuity. Thus, the delta contact discontinuity is formed whose mass only comes from the particles on the right-hand side. Different from delta shock wave, the left-hand side of contact discontinuity is rarefaction wave and thus the strength of delta contact discontinuity cannot be solved by the so-called generalized Rankine–Hugoniot relations of delta shock wave. But we notice that mass only comes from the particles on the right-hand side. Hence, we calculate the strength of delta contact discontinuity by using the density multiplying by the difference between the speed of the particles and the speed of delta contact discontinuity as

$$\begin{aligned} \beta (t)=\rho _{+}\Big (\frac{\displaystyle (\rho _{-}-1)u_{-}}{\displaystyle \rho _{-}}-u_{+}\Big )t. \end{aligned}$$

Therefore, when $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$, we can construct the possible Riemann solution of (1.2) and (1.3) by using the composite wave $R\delta J$, which is given by (see Fig. 2c)

$$\begin{aligned} (\rho ,u)(x,t)=\left\{ \begin{array}{ll} (\rho _{-},u_{-}), &{} \frac{x}{t}<\lambda _{1}(\rho _{-},u_{-}),\\ (\rho ,u), &{}\lambda _{1}(\rho _{-},u_{-})<\frac{x}{t}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}},\\ (\beta (t)\delta (x-\frac{(\rho _{-}-1)u_{-}t}{\rho _{-}}),\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}), &{}\frac{x}{t}=\frac{(\rho _{-}-1)u_{-}}{\rho _{-}},\\ (\rho _{+},u_{+}), &{} \frac{x}{t}>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}. \end{array} \right. \end{aligned}$$

(2.13)

It should be mentioned that the delta shock wave is an over-compressive shock wave in the sense that it is usually an isolated discontinuity to connect the left state and the right state directly for the Riemann problem. In other words, the delta shock wave is surrounded by the two constant states on both sides of it. By comparison, in the wave fan of $R\delta J$, the delta contact discontinuity $\delta J$ is attached on the wave front of R, namely $\delta J$ is surrounded by a rarefaction wave on the left-hand side and a constant state on the right-hand side. Different from the delta shock wave, it is impossible to use the generalized Rankine–Hugoniot relations to calculate the strength of $\delta J$ for the reason that the left-hand side of it is a rarefaction wave and the density $\rho$ in the characteristic line of the rarefaction wave R tends to $+\infty$ if the characteristic line tends closer and closer to the line of $\delta J$. In the current work, the strength $\beta (t)$ in (2.13) is obtained by virtue of the fact that all of the mass gathering together on the line of $\delta J$ only comes from the particles on the right-hand side of it. It is of great interest to notice that the solution consisting of delta shock wave surrounded by two rarefaction waves on both sides of delta shock line has been constructed in [39] recently, which is similar to the composite wave $R\delta J$ in this paper. In conclusion, the Riemann solutions of (1.2) and (1.3) are constructed fully for all the possible cases, namely $S+J$ for $u_{-}<u_{+}$, $R+J$ for $\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}<u_{+}<u_{-}$, as well as $R\delta J$ for $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$.

3 Wave Interactions

It is remarked that system (1.2) is attributed to Temple class whose wave interactions have relatively simple structures. Due to the fact that we can only use the composite wave $R\delta J$ to construct possible Riemann solution of (1.2) and (1.3) when $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$, whose uniqueness is still unsolved. Thus, we restrict ourselves to only consider the interactions of elementary waves including shock wave, rarefaction wave and contact discontinuity. For this purpose, we are dedicated to the special initial value problem for system (1.2) with the constant states in three pieces (1.4) which should satisfy $u_{m}>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$ and $u_{+}>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$ simultaneously. In brief, our main purpose in this section is to construct global solutions of the perturbed Riemann problem (1.2) and (1.4) by using the method of characteristics when the composite wave $R\delta J$ is not involved. In this respect, there exist four cases according to the different combinations of waves originating from the two initial points (0, 0) and $(\varepsilon ,0)$ as follows:

$$\begin{aligned} (1)~S+J~~\text {and}~~S+J, \quad (2)~R+J~~\text {and}~~R+J, \quad (3)~R+J~~\text {and}~~S+J, \quad (4)~S+J~~\text {and}~~R+J. \end{aligned}$$

In addition, by taking the initial condition (1.4), we can further consider whether the limits $\varepsilon \rightarrow 0$ of solutions of (1.2) and (1.4) are in accordance with the corresponding ones of (1.2) and (1.3) or not.

Fig. 3

The interaction between $S+J$ and $S+J$ is shown when $\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}<u_{-}<u_{m}<u_{+}$

Case 1. $S+J$ and $S+J$

In this work, we begin by taking into account the case that there are a shock wave followed by a contact discontinuity emitting from the initial points (0,0) and $(\varepsilon ,0)$, respectively. For the sake of convenience, we use $S_{1},$ $J_{2}$ and $S_{3},$ $J_{4}$ to denote them, respectively (see Fig. 3). In this case, when the time t is adequately small, the solution of (1.2) and (1.4) can be abbreviated by using the symbols as

$$\begin{aligned} (u_{-},v_{-})+S_{1}+(u_{1},v_{1})+J_{2}+(u_{m},v_{m})+S_{3}+(u_{2},v_{2}) +J_{4}+(u_{+},v_{+}), \end{aligned}$$

where $``+''$ stands for “followed by”. Obviously, the occurrence of this case depends on the conditions $\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}<u_{-}<u_{m}<u_{+}$. By virtue of (2.8), the intermediate states $(\rho _{1},u_{1})$ and $(\rho _{2},u_{2})$ can be given, respectively, by

$$\begin{aligned} (\rho _{1},u_{1})=\Bigg (\frac{\displaystyle \rho _{-} u_{m}}{\displaystyle \rho _{-}u_{m}-(\rho _{-}-1) u_{-}},u_{m}\Bigg ),\qquad (\rho _{2},u_{2})=\Bigg (\frac{\displaystyle \rho _{m} u_{+}}{\displaystyle \rho _{m}u_{+}-(\rho _{m}-1) u_{m}},u_{+}\Bigg ). \end{aligned}$$

(3.1)

Proposition 3.1

The contact discontinuity $J_{2}$ collides with the shock wave $S_{3}$ in finite time. Subsequently, the interaction between $J_{2}$ and $S_{3}$ gives rise to a new shock wave $S_{5}$ and a new contact discontinuity $J_{6}$, respectively. Finally, the two shock waves $S_{1}$ and $S_{5}$ coalesce into a new shock wave $S_{7}$ as well as the two contact discontinuities $J_4$ and $J_6$ are parallel with each other.

Proof

It is evident that the wave speeds of $J_{2}$ and $S_{3}$ are given, respectively, by

$$\begin{aligned} \tau _{2}=u_{m},\qquad \sigma _{3}=\frac{\displaystyle (\rho _{m}-1) u_{m}-u_{+}}{\displaystyle \rho _{m}-1}=u_m-\frac{\displaystyle u_+}{\displaystyle \rho _m-1}. \end{aligned}$$

(3.2)

Taking into account $\rho >1$ and $u>0$, we have

$$\begin{aligned} \tau _{2}-\sigma _{3}=\frac{u_{+}}{\rho _{m}-1}>0, \end{aligned}$$

which implies that $\tau _{2}>\sigma _{3}$. Therefore, $J_{2}$ collides with $S_{3}$ in finite time. The point of intersection $(x_{1},t_{1})$ is determined by

$$\begin{aligned} \left\{ \begin{array}{ll} x_{1}=\tau _{2}t_{1}=u_{m}t_{1}, \\ x_{1}-\varepsilon =\sigma _{3}t_{1}=\Big (u_m-\frac{\displaystyle u_+}{\displaystyle \rho _m-1}\Big )t_{1}, \end{array}\right. \end{aligned}$$

which yields

$$\begin{aligned} (x_{1},t_{1})=\Bigg (\frac{\displaystyle (\rho _{m}-1)u_{m}\varepsilon }{\displaystyle u_{+}},\frac{\displaystyle (\rho _{m}-1)\varepsilon }{\displaystyle u_{+}}\Bigg ). \end{aligned}$$

(3.3)

Obviously, $J_{2}$ and $S_{3}$ intersect at a finite time when a new Riemann problem is formed. At the time $t=t_{1}$, we again have a Riemann problem for system (1.2) subject to the Riemann-type initial data $(\rho _{1},u_{1})$ and $(\rho _{2},u_{2})$. On account of the relations $\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}<u_{-}<u_{1}=u_{m}<u_{+}=u_{2}$, the Riemann solution at the point $(x_{1},t_{1})$ is still a shock wave followed by a contact discontinuity, which are denoted with $S_{5}$ and $J_{6}$, respectively. Moreover, the intermediate state $(\rho _{3},u_{3})$ between $S_{5}$ and $J_{6}$ can also be obtained by

$$\begin{aligned} (\rho _{3},u_{3})=\Bigg (\frac{\displaystyle \rho _{1} u_{2}}{\displaystyle \rho _{1}u_{2}-(\rho _{1}-1) u_{1}},u_{2}\Bigg )=\Bigg (\frac{\displaystyle \rho _{-} u_{+}}{\displaystyle \rho _{-}u_{+}-(\rho _{-}-1) u_{-}},u_{+}\Bigg ). \end{aligned}$$

(3.4)

By using (3.1) and (3.4), it is not difficult to achieve the wave speeds of $S_{5}$ and $J_{6}$ as

$$\begin{aligned} \sigma _{5}=\frac{\displaystyle \rho _{1}u_{1}-\rho _{3}u_{3}}{\displaystyle \rho _{1}-\rho _{3}}=u_{m}+u_{+}-\frac{\displaystyle \rho _{-}u_{m}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}},\qquad \tau _{6}=u_{+}. \end{aligned}$$

(3.5)

On the one hand, one has

$$\begin{aligned} \begin{aligned} \sigma _{5}-\sigma _{3}&=u_{m}+u_{+}-\frac{\displaystyle \rho _{-} u_{m}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}-\Big (u_m-\frac{\displaystyle u_{+}}{\displaystyle \rho _{m}-1}\Big ) =\frac{\displaystyle \rho _{m}(\rho _{-}-1)u_{-}-\rho _{-}(\rho _{m}-1)u_{m}}{\displaystyle (\rho _{m}-1) (\rho _{-}-1)u_{-}}u_{+}\\&=\frac{\displaystyle \rho _m\rho _-\bigg (u_--\frac{u_-}{\rho _-}-\Big (u_m-\frac{u_m}{\rho _m}\Big )\bigg )}{\displaystyle (\rho _m-1)(\rho _--1)u_-} =\frac{\displaystyle \rho _m\rho _-\bigg (u_1-\frac{u_1}{\rho _1}-\Big (u_m-\frac{u_m}{\rho _m}\Big )\bigg )}{\displaystyle (\rho _m-1)(\rho _--1)u_-}\\&=\frac{\displaystyle \rho _m\rho _-\Big (\frac{1}{\rho _m}-\frac{1}{\rho _1}\Big )u_m}{\displaystyle (\rho _m-1)(\rho _--1)u_-}<0, \end{aligned} \end{aligned}$$

which permits us to see that the shock wave reduces the speed forwards (or add up the speed backwards) when across the contact discontinuity. On the other hand, it is evident that $0<\tau _{2}=u_{m}<u_{+}=\tau _{6}$, which means that the contact discontinuity adds up the speed forwards when across the shock wave. Eventually, $J_{4}$ is parallel to $J_{6}$ due to the relation $\tau _{4}=\tau _{6}=u_{+}$.

In the following, we consider the interaction between $S_{1}$ and $S_{5}$. The wave speed of $S_{1}$ is given by $\sigma _{1}=u_{-}-\frac{\displaystyle u_{m}}{\displaystyle \rho _{-}-1}$. Comparing with $\sigma _{5}$ in (3.5), we have

$$\begin{aligned} \begin{aligned} \sigma _{5}-\sigma _{1}&=u_{m}+u_{+}-\frac{\displaystyle \rho _{-} u_{m}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}-\Big (u_--\frac{\displaystyle u_{m}}{\displaystyle \rho _{-}-1}\Big ) =(u_{m}+u_{+}-u_{-})+\frac{\displaystyle u_{m}(u_{-}-\rho _{-}u_{+})}{\displaystyle (\rho _{-}-1)u_{-}}\\&=\Bigg (1+\frac{\displaystyle u_{-}-\rho _{-}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}} \Bigg )u_{m}+(u_{+}-u_{-}) =\frac{\displaystyle \rho _{-}u_{m}(u_{-}-u_{+})}{\displaystyle (\rho _{-}-1)u_{-}}+(u_{+}-u_{-})\\&=(u_{-}-u_{+})\Bigg (\frac{\displaystyle \rho _{-}u_m}{\displaystyle (\rho _{-}-1)u_{-}}-1\Bigg )<0. \end{aligned} \end{aligned}$$

In other words, the shock wave $S_{1}$ catches up with the shock wave $S_{5}$ in finite time. The point of intersection $(x_{2},t_{2})$ is determined by

$$\begin{aligned} \left\{ \begin{array}{ll} x_{2}=\sigma _{1}t_{2}=\Big (u_{-}-\frac{\displaystyle u_{m}}{\displaystyle \rho _{-}-1}\Big )t_{2}, \\ x_{2}-x_{1}=\sigma _{5}(t_{2}-t_{1})=\Bigg (u_{m}+u_{+}-\frac{\displaystyle \rho _{-} u_{m}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}\Bigg )(t_{2}-t_{1}), \end{array}\right. \end{aligned}$$

where $(x_{1},t_{1})$ is given by (3.3). Then, we have

$$\begin{aligned} (x_2,t_2)=\Bigg (\frac{(\rho _m-1)\big ((\rho _--1)u_--u_m\big )\varepsilon }{(\rho _--1)(u_+-u_-)},\frac{(\rho _m-1)\varepsilon }{u_+-u_-}\Bigg ). \end{aligned}$$

(3.6)

It follows from (3.4) that

$$\begin{aligned} u_{3}-\frac{\displaystyle u_{3}}{\displaystyle \rho _{3}}=u_{+}-\frac{\displaystyle \rho _{-}u_{+}-(\rho _{-}-1) u_{-}}{\displaystyle \rho _{-}}=u_--\frac{\displaystyle u_{-}}{\displaystyle \rho _{-}}. \end{aligned}$$

Hence, it is concluded that the two states $(\rho _{-},u_{-})$ and $(\rho _{3},u_{3})$ can be connected by a single shock wave $S_{7}$, whose wave speed is $\sigma _{7}=u_{-}-\frac{\displaystyle u_{+}}{\displaystyle \rho _{-}-1}$. That is to say, the two shock waves $S_{1}$ and $S_{5}$ coalesce into a new shock wave $S_{7}$. Comparing with $\sigma _{1}$ and $\sigma _{5}$, we have

$$\begin{aligned} \sigma _{1}-\sigma _{7}=u_{-}-\frac{\displaystyle u_{m}}{\displaystyle \rho _{-}-1}-\Big (u_{-}-\frac{\displaystyle u_{+}}{\displaystyle \rho _{-}-1}\Big )=\frac{\displaystyle u_{+}-u_{m}}{\displaystyle \rho _{-}-1}>0, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \sigma _{5}-\sigma _{7}&=u_{m}+u_{+}-\frac{\displaystyle \rho _{-} u_{m}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}-\Big (u_{-}-\frac{\displaystyle u_{+}}{\displaystyle \rho _{-}-1}\Big ) =(u_{m}+u_{+}-u_{-})+\frac{\displaystyle u_{+}(u_{-}-\rho _{-}u_{m})}{\displaystyle (\rho _{-}-1)u_{-}}\\&=\Bigg (1+\frac{\displaystyle u_{-}-\rho _{-}u_{m}}{\displaystyle (\rho _{-}-1)u_{-}} \Bigg )u_{+}+(u_{m}-u_{-}) =\frac{\displaystyle \rho _{-}u_{+}(u_{-}-u_{m})}{\displaystyle (\rho _{-}-1)u_{-}}+(u_{m}-u_{-})\\&=\frac{\displaystyle (u_{-}-u_{m})(\rho _{-}(u_{+}-u_{-})+u_{-})}{\displaystyle (\rho _{-}-1)u_{-}}<0, \end{aligned} \end{aligned}$$

in which the inequalities $u_{-}<u_{m}<u_{+}$ and $\rho _{-}>1$ have been used. As a consequence, $\sigma _5<\sigma _7<\sigma _1$ can be established, namely the wave speed of $S_7$ is between those of $S_1$ and $S_5$. With the help of the above calculations and discussions, we can draw Fig. 3 to illustrate this case in detail. The proof of this proposition is completed. $\square$

Case 2. $R+J$ and $R+J$

Secondly, we focus on the situation that there are a rarefaction wave followed by a contact discontinuity emitting from the initial points (0,0) and $(\varepsilon ,0)$, respectively. For the sake of convenience, we use $R_{1},$ $J_{2}$ and $R_{3},$ $J_{4}$ to denote them, respectively (see Fig. 4). For t adequately small, the solution of (1.2) and (1.4) is abbreviated as

$$\begin{aligned} (u_{-},v_{-})+R_{1}+(u_{1},v_{1})+J_{2}+(u_{m},v_{m})+R_{3}+(u_{2},v_{2})+J_{4}+(u_{+},v_{+}). \end{aligned}$$

The occurrence of this case depends on the conditions $\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}<u_{+}<u_{m}<u_{-}$. Remark that the intermediate states $(\rho _{1},u_{1})$, $(\rho _{2},u_{2})$ and $(\rho _{3},u_{3})$ are the same as those in Case 1.

Fig. 4

The interaction between $R+J$ and $R+J$ is shown when $\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}<u_{+}<u_{m}<u_{-}$

Proposition 3.2

The contact discontinuity $J_{2}$ collides with the wave back of the rarefaction wave $R_{3}$ in finite time. Subsequently, the interaction between $J_{2}$ and $R_{3}$ gives rise to a new rarefaction wave $R_{5}$ and a new contact discontinuity $J_{7}$, respectively. In the end, the wave front of $R_{1}$ is parallel to the wave back of $R_{5}$ as well as $J_4$ is parallel to $J_7$, respectively.

Proof

It suffices to show that the wave speeds of $J_{2}$ and the wave back of $R_{3}$ are given, respectively, by

$$\begin{aligned} \tau _{2}=u_{m},\qquad \xi _{3}(\rho _{m},u_{m})=u_m-\frac{\displaystyle u_{m}}{\displaystyle \rho _{m}-1}. \end{aligned}$$

(3.7)

We then get

$$\begin{aligned} \tau _{2}-\xi _{3}(\rho _{m},u_{m})=\frac{\displaystyle u_{m}}{\displaystyle \rho _{m}-1}>0, \end{aligned}$$

which implies that $J_{2}$ collides with the wave back of $R_{3}$ in finite time. The point of intersection $(x_{1},t_{1})$ is determined by

$$\begin{aligned} \left\{ \begin{array}{ll} x_{1}=\tau _{2}t_{1}=u_{m}t_{1}, \\ x_{1}-\varepsilon =\xi _{3}(\rho _{m},u_{m})t_{1}=\Big (u_m-\frac{\displaystyle u_{m}}{\displaystyle \rho _{m} -1}\Big )t_{1}, \end{array}\right. \end{aligned}$$

which yields

$$\begin{aligned} (x_{1},t_{1})=\Bigg ((\rho _{m}-1)\varepsilon ,\frac{\displaystyle (\rho _{m}-1)\varepsilon }{\displaystyle u_{m}}\Bigg ). \end{aligned}$$

(3.8)

We find that $J_{2}$ and the wave back of $R_{3}$ intersect at a finite time. Subsequently, $J_{2}$ begins to penetrate the rarefaction wave $R_{3}$ after $t_{1}$, which is recorded as $J_{6}$ in the process of penetration. The expression of $J_{6}$ during the penetrating process is computed by

$$\begin{aligned} \frac{\displaystyle dx}{\displaystyle dt}=u, \qquad \frac{\displaystyle x-\varepsilon }{\displaystyle t}=u-\frac{\displaystyle u}{\displaystyle \rho -1},\qquad u-\frac{\displaystyle u}{\displaystyle \rho }=u_m-\frac{\displaystyle u_{m}}{\displaystyle \rho _{m}}, \qquad x(t_{1})=x_{1}. \end{aligned}$$

(3.9)

Differentiating the second equation in (3.9) with respect to t, we have

$$\begin{aligned} u=\frac{\displaystyle dx}{\displaystyle dt}=\frac{\displaystyle (\rho -2) u}{\displaystyle \rho -1}+\frac{\displaystyle (\rho -2)t}{\displaystyle \rho -1}\frac{\displaystyle du}{\displaystyle dt} +\frac{\displaystyle ut}{\displaystyle (\rho -1)^{2}}\frac{\displaystyle d\rho }{\displaystyle dt}, \end{aligned}$$

which is simplified into

$$\begin{aligned} u=(\rho -2)t \frac{\displaystyle du}{\displaystyle dt}+\frac{\displaystyle ut}{\displaystyle \rho -1}\frac{\displaystyle d\rho }{\displaystyle dt}. \end{aligned}$$

(3.10)

Differentiating the third equation in (3.9) with respect to t yields

$$\begin{aligned} \frac{\displaystyle du}{\displaystyle dt}+\frac{\displaystyle u}{\displaystyle \rho (\rho -1)}\frac{\displaystyle d\rho }{\displaystyle dt}=0. \end{aligned}$$

(3.11)

Which, together with (3.10), gives

$$\begin{aligned} \frac{\displaystyle du}{\displaystyle dt}+\frac{1}{\rho t} \Big (u- (\rho -2)t \frac{\displaystyle du}{\displaystyle dt}\Big )=0, \end{aligned}$$

such that one has

$$\begin{aligned} \frac{\displaystyle du}{\displaystyle dt}=-\frac{\displaystyle u}{\displaystyle 2t}. \end{aligned}$$

Hence, we can get

$$\begin{aligned} \frac{\displaystyle dx}{\displaystyle dt}=u=u_m \sqrt{\frac{\displaystyle t_1}{\displaystyle t}}. \end{aligned}$$

As a result, the curve of $J_{6}$ is expressed as

$$\begin{aligned} x=2u_m \sqrt{t_1 t }+x_1-2u_mt_1. \end{aligned}$$

(3.12)

In the end, by combining (3.12) together with the line of wave back of $R_{3}$ given by

$$\begin{aligned} x_{2}-\varepsilon =\Big (u_{2}-\frac{\displaystyle u_2}{\displaystyle \rho _{2}-1}\Big )t_{2}. \end{aligned}$$

The end point of $J_{6}$ passing through $R_{3}$ can be obtained as

$$\begin{aligned} (x_{2},t_{2})=\Bigg (\frac{\displaystyle (\rho _m-1)(\rho _mu_++2u_m)\varepsilon }{\displaystyle 2(\rho _m-1) u_m-\rho _mu_+}, \frac{\displaystyle \rho _m^2(\rho _m-1)u_m\varepsilon }{\displaystyle \big (2(\rho _m-1)u_m-\rho _mu_+\big )^2}\Bigg ). \end{aligned}$$

(3.13)

There is no doubt that the two states $(\rho _2,u_2)$ and $(\rho _3,u_3)$ can be connected by the contact discontinuity $J_{7}$ for the reason that $u_{3}=u_{2}=u_{+}$. In the end, it is evident that the two contact discontinuities $J_{4}$ and $J_{7}$ are parallel with each other due to the fact that the wave speeds of $J_{7}$ and $J_{4}$ are the same as $\tau _{7}=\tau _{4}=u_{+}$. The proof is finished. $\square$

Case 3. $R+J$ and $S+J$

Thirdly, we are devoted to the case that there are a rarefaction wave followed by a contact discontinuity emitting from the origin (0,0) and a shock wave followed by a contact discontinuity emitting from the initial point $(\varepsilon ,0)$, respectively. As before, we use $R_{1},$ $J_{2}$ and $S_{3},$ $J_{4}$ to stand for them, respectively. For t adequately small, the solution of (1.2) and (1.4) can be symbolized as (see Figs. 5 and 6)

$$\begin{aligned} (u_{-},v_{-})+R_{1}+(u_{1},v_{1})+J_{2}+(u_{m},v_{m})+S_{3}+(u_{2},v_{2}) +J_{4}+(u_{+},v_{+}). \end{aligned}$$

The occurrence of this case depends on the conditions $\frac{(\rho _--1)u_-}{\rho _-}<u_{m}<u_{-}$ and $\frac{(\rho _--1)u_-}{\rho _-}<u_{m}<u_{+}$. Similarly, the intermediate states $(\rho _{1},u_{1})$, $(\rho _{2},u_{2})$ and $(\rho _{3},u_{3})$ and the point of intersection $(x_{1},t_{1})$ are also calculated in the same formulae as before and then a new Riemann problem is formed at the time $t_{1}$.

Proposition 3.3

The wave front of the rarefaction wave $R_{1}$ catches up with the shock wave $S_{5}$ in finite time. More specifically, $S_{5}$ is able to penetrate the whole $R_{1}$ thoroughly when $u_{-}<u_{+}$ or not when $u_{-}>u_{+}$. Moreover, the two contact discontinuities $J_4$ and $J_6$ are parallel with each other.

Fig. 5

The interaction between $R+J$ and $S+J$ is shown when $\frac{(\rho _--1)u_-}{\rho _-}<u_{m}<u_{+}<u_{-}$, in which $S_{5}$ cannot penetrate the whole $R_{1}$ in finite time and ultimately has the line $x=\Bigg (\frac{\big (2(\rho _{-}-1)u_{-}-\rho _{-}u_{+}\big )u_{+}}{(\rho _{-}-1)u_{-}}\Bigg )t$ as its asymptote

Fig. 6

The interaction between $R+J$ and $S+J$ is shown when $\frac{(\rho _--1)u_-}{\rho _-}<u_{m}<u_{-}<u_{+}$, in which $S_{5}$ is able to penetrate the whole $R_{1}$ completely

Proof

The wave speeds of the wave front of $R_{1}$ and $S_{5}$ are as follows:

$$\begin{aligned} \xi _{1}(\rho _{1},u_{1})=\frac{\displaystyle (\rho _{1}-2) u_{1}}{\displaystyle \rho _{1}-1}=2u_{m}-\frac{\displaystyle \rho _{-}u_{m}^{2}}{\displaystyle (\rho _{-}-1)u_{-}},\qquad \sigma _{5}=u_{m}+u_{+}-\frac{\displaystyle \rho _{-}u_{m}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}. \end{aligned}$$

(3.14)

Then, we have

$$\begin{aligned} \begin{aligned} \xi _{1}(\rho _{1},u_{1})-\sigma _{5}&=2u_{m}-\frac{\displaystyle \rho _{-}u_{m}^{2}}{\displaystyle (\rho _{-}-1)u_{-}}-(u_{m}+u_{+})+\frac{\displaystyle \rho _{-} u_{m}u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}\\&=(u_{m}-u_{+})\Big (1-\frac{\displaystyle \rho _{-} u_{m}}{\displaystyle (\rho _{-}-1)u_{-}}\Big )>0, \end{aligned} \end{aligned}$$

which permits us to get $\xi _{1}(\rho _{1},u_{1})>\sigma _{5}$. Hence, the wave front of $R_{1}$ catches up with $S_{5}$ in finite time and then the point of intersection $(x_{2},t_{2})$ is determined by

$$\begin{aligned} \left\{ \begin{array}{ll} x_{2}=\xi _{1}(\rho _{1},u_{1})t_{2}=\Big (2u_{m}-\frac{\displaystyle \rho _{-}u_{m}^{2}}{\displaystyle (\rho _{-}-1)u_{-}}\Big )t_{2}, \\ x_{2}-x_{1}=\sigma _{5}(t_{2}-t_{1})=\Big (u_{m}+u_{+}-\frac{\displaystyle \rho _{-}u_{m} u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}\Big )(t_{2}-t_{1}), \end{array}\right. \end{aligned}$$

which yields

$$\begin{aligned} (x_2,t_2)=\Bigg (\frac{(\rho _m-1)\big (2(\rho _--1)u_--\rho _-u_m\big ) u_m\varepsilon }{(\rho _--1)u_-(u_+-u_m)},\frac{(\rho _m-1)\varepsilon }{u_+-u_m}\Bigg ). \end{aligned}$$

(3.15)

Analogously, $S_{5}$ begins to penetrate $R_{1}$ after $t_{2}$, which is recorded as $S_{7}$ in the process of penetration. The expression of $S_{7}$ during the penetrating process is able to be computed by

$$\begin{aligned} \frac{\displaystyle dx}{\displaystyle dt}=u-\frac{\displaystyle u_+}{\displaystyle \rho -1}, \qquad \frac{\displaystyle x}{\displaystyle t}=u-\frac{\displaystyle u}{\displaystyle \rho -1},\qquad u-\frac{\displaystyle u}{\displaystyle \rho }=u_--\frac{\displaystyle u_{-}}{\displaystyle \rho _{-}}, \qquad x(t_{2})=x_{2}. \end{aligned}$$

(3.16)

Differentiating the second equation in (3.16) with respect to t, we have

$$\begin{aligned} u-\frac{\displaystyle u_+}{\displaystyle \rho -1}=\frac{\displaystyle dx}{\displaystyle dt}=\frac{\displaystyle (\rho -2) u}{\displaystyle \rho -1}+\frac{\displaystyle (\rho -2)t}{\displaystyle \rho -1}\frac{\displaystyle du}{\displaystyle dt}+\frac{\displaystyle ut}{\displaystyle (\rho -1)^{2}}\frac{\displaystyle d\rho }{\displaystyle dt}, \end{aligned}$$

which is simplified into

$$\begin{aligned} u-u_+=(\rho -2)t\frac{\displaystyle du}{\displaystyle dt}+\frac{\displaystyle ut}{\displaystyle (\rho -1)}\frac{\displaystyle d\rho }{\displaystyle dt}. \end{aligned}$$

(3.17)

Differentiating the third equation in (3.16) with respect to t yields

$$\begin{aligned} \frac{\displaystyle du}{\displaystyle dt}+\frac{\displaystyle u}{\displaystyle \rho (\rho -1)}\frac{\displaystyle d\rho }{\displaystyle dt}=0. \end{aligned}$$

(3.18)

Which, together with (3.17), gives

$$\begin{aligned} \frac{\displaystyle du}{\displaystyle dt}+\frac{\displaystyle 1}{\displaystyle \rho t}\Big (u-u_+-(\rho -2)t\frac{\displaystyle du}{\displaystyle dt}\Big )=0, \end{aligned}$$

such that one has

$$\begin{aligned} \frac{\displaystyle du}{\displaystyle dt}=-\frac{\displaystyle u-u_+}{\displaystyle 2t}. \end{aligned}$$

Hence, we can get

$$\begin{aligned} \frac{\displaystyle dx}{\displaystyle dt}=u-\frac{\displaystyle u_+}{\displaystyle \rho -1}=\frac{\displaystyle (\rho _--1)u_--\rho _-u_+}{\displaystyle (\rho _--1)u_-}u+u_+ =\frac{\displaystyle (\rho _--1)u_--\rho _-u_+}{\displaystyle (\rho _--1)u_-}\Big ((u_m-u_+)\sqrt{\frac{t_2}{t}}+u_+\Big )+u_+. \end{aligned}$$

As a result, the curve of $S_7$ is expressed as

$$\begin{aligned} x= & {} \frac{\big (2(\rho _--1)u_--\rho _-u_+\big )u_+t}{(\rho _--1)u_-}\nonumber \\&-\frac{2\big ((\rho _--1)u_--\rho _-u_+\big )\sqrt{(\rho _m-1)(u_+-u_m)\varepsilon t}}{(\rho _--1)u_-} +\frac{\rho _-(\rho _m-1)(u_m-u_+)\varepsilon }{(\rho _--1)u_-}.\qquad \quad \end{aligned}$$

(3.19)

In the end, by combining (3.19) together with the line of wave back of $R_3$ given by

$$\begin{aligned} x_{3}=\Big (u_{-}-\frac{\displaystyle u_-}{\displaystyle \rho _{-}-1}\Big )t_{3}. \end{aligned}$$

There are two situations in the process of penetration:

• (1) If $u_{-}>u_{+}$, then $S_{7}$ cannot penetrate $R_{1}$ completely and ultimately has the line $x=\Bigg (\frac{\displaystyle \big (2(\rho _{-}-1)u_{-}-\rho _{-}u_{+}\big )u_{+}}{\displaystyle (\rho _{-}-1)u_{-}}\Bigg )t$ as its asymptote.

• (2) If $u_{-}<u_{+}$, then $S_{7}$ has the ability to penetrate the whole rarefaction wave $R_{1}$ completely at a point $(x_{3},t_{3})$ and then be denoted with a new shock wave $S_{8}$ after penetration, whose wave speed is given by $\sigma _{8}=u_{-}-\frac{\displaystyle u_{+}}{\displaystyle \rho _{-}-1}.$ It suffices to get

  $$\begin{aligned} (x_3,t_3)=\Bigg (\frac{(\rho _--2)(\rho _m-1)(u_+-u_m)u_-\varepsilon }{(\rho _--1)(u_+-u_-)^2},\frac{(\rho _m-1)(u_+-u_m)\varepsilon }{(u_+-u_-)^2}\Bigg ). \end{aligned}$$

  (3.20)

  As before, the two contact discontinuities $J_4$ and $J_6$ are also parallel. $\square$

Case 4. $S+J$ and $R+J$

In the end, we shall focus our attention on the situation that there are a shock wave followed by a contact discontinuity emitting from the initial point (0,0) and a rarefaction wave followed by a contact discontinuity emitting from the initial point $(\varepsilon ,0)$, respectively. Similarly, we use $S_{1},$ $J_{2}$ and $R_{3},$ $J_{4}$ to denote them, respectively. For t adequately small, the solution of (1.2) and (1.4) can be symbolized as

$$\begin{aligned} (u_{-},v_{-})+S_{1}+(u_{1},v_{1})+J_{2}+(u_{m},v_{m})+R_{3}+(u_{2},v_{2})+J_{4}+(u_{+},v_{+}). \end{aligned}$$

The occurrence of this case depends on the conditions $\frac{(\rho _--1)u_-}{\rho _-}<u_{-}<u_{m}$ and $\frac{(\rho _--1)u_-}{\rho _-}<u_{+}<u_{m}$. Precisely, all the intermediate states are calculated in the same way as before. It is noted that the process of $J_{2}$ penetrating $R_{3}$ is the same as that in Case 2. Finally, we need to consider how does the shock wave $S_{1}$ to penetrate the non-centered rarefaction wave $R_{5}$. The analytic calculation is impossible due to the fact that the rarefaction wave $R_{5}$ is non-centered. But we notice that both $S_{1}$ and $R_{5}$ belong to the wave of $\lambda _{1}-$family. Thus, we can judge that $S_{1}$ is able to cancel $R_{5}$ when $u_{-}<u_{+}$ or cannot penetrate $R_{5}$ completely when $u_{-}>u_{+}$. In fact, this situation is similar to that in Case 3. In other words, the wave interaction in Case 4 is just the combination of those in Cases 2 and 3. Hence, we only describe the process and omit the details here.

4 Conclusion

The wave interaction problems for system (1.2) have been well investigated in fully explicit forms by using the method of characteristics, including shock wave, rarefaction wave and contact discontinuity. Based on the above results, we can construct the global solutions to the perturbed Riemann problem (1.2) and (1.4) under the assumption $min (u_{m},u_{+})>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$ such that the composite wave $R\delta J$ is not involved. It is evident to see that the limits $\varepsilon \rightarrow 0$ of solutions of (1.2) and (1.4) tend to the corresponding ones of (1.2) and (1.3) by analyzing the above four cases in detail. As a consequence, it is verified strictly that the Riemann solutions of (1.2) and (1.3) are stable with respect to the specific small perturbations (1.4) of Riemann initial data under the assumption $min (u_{m},u_{+})>\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$.

It should be stressed that the composite wave $R\delta J$ is involved in the Riemann solution of (1.2) and (1.3) when the initial condition (1.3) satisfies $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$. This is a new kind of singular hyperbolic wave which has not been paid enough attention in current literatures. There are still some interesting, but difficult problems needed to be considered. The first concern is that our constructed composite wave $R\delta J$ is the uniqueness Riemann solution of (1.2) and (1.3) or not when $0<u_{+}<\frac{(\rho _{-}-1)u_{-}}{\rho _{-}}$. The second concern is that the composite wave $R\delta J$ is stable or not under some small perturbations of Riemann initial data (1.3) such as the perturbation (1.4). We plan to consider these interesting but difficult problems in our future work.