Some Results About the Reliability of Folded Hypercubes

Abstract

In this paper we investigate some reliability measures, including super-connectivity, cyclic edge connectivity, etc., in the folded hypercubes.

1 Introduction

Suppose that $\Gamma$ is a finite, simple and undirected graph. We use $V(\Gamma )$, $E(\Gamma )$, $A(\Gamma )$ and $\mathrm{Aut}(\Gamma )$ for showing the vertex set, edge set, arc set and the automorphism group of $\Gamma$, respectively. We say that $\Gamma$ is vertex-transitive, edge-transitive and arc-transitive if $\mathrm{Aut}(\Gamma )$ acts transitive on $V(\Gamma )$, $E(\Gamma )$, $A(\Gamma )$, respectively.

We remind that hypercube $Q_n$ is a graph with $2^n$ vertices, each vertex with a distinct binary string $x_1x_2\cdots x_n$ on the set $\{0, 1\}$. Two vertices are linked by an edge if and only if their strings differ in exactly one bit. It is well known that $Q_n$ is an arc-transitive graph. As a variant of the hypercube, the n-dimensional folded hypercube $FQ_n$, proposed first by El-Amawy and Latifi [1], is a graph obtained from the hypercube $Q_n$ by adding an edge, called a complementary edge, between any two vertices $x = (x_1x_2\cdots x_n)$ and $\overline{x} = (\overline{x_1}\ \overline{x_2} \cdots \overline{x_n})$, where $\overline{x_i} = 1 - x_i$. The graphs shown in Figs. 1 and 2 are $FQ_3$ and $FQ_4$, respectively. By an easy observation, $FQ_n$ is an $(n+1)$-regular and its order is $2^n$. Like $Q_n$, $FQ_n$ is arc-transitive (see [15]). Also by [1], it has diameter of $\lceil n/2\rceil$ which is smaller than the diameter of $Q_n$. In the literature, $FQ_n$ has received considerable attention, and a lot of its properties have been investigated. For example see ([7,8,9, 13, 22, 23, 25, 29, 34]).

Fig. 1

($FQ_3$)

Fig. 2

($FQ_4$)

Zhou et al. (see [33]) studied some reliability measures such as super-connectivity, cyclically connectivity in the balanced hypercube by using its symmetric properties. In this paper we get the similar results for n-dimensional folded hypercube $FQ_n$.

2 Preliminaries

In this section, we give some terminology and notation. For notation and terminology not define here we follow [3].

Let n be a positive integer. Denote by $C_n$ the cyclic graph of order n. For a vertex v in a graph $\Gamma$, use $N_\Gamma (v)$ to denote the neighborhood of v, that is, the set of vertices adjacent to v. Also for a positive integer m, $mK_1$ represents the null graph with m vertices and a graph is trivial if it is a vertex.

The vertex-connectivity of a graph $\Gamma$ denoted by $\kappa (\Gamma )$ is the minimum number of vertices whose removal results in a disconnected graph or a trivial graph. Similarly, we can define edge-connectivity of a graph $\Gamma$ which is denoted by $\lambda (\Gamma )$. In fact $\kappa (\Gamma )$ and $\lambda (\Gamma )$ are two important factors for measuring the reliability of an interconnection network. Also a larger $\kappa (\Gamma )$ or $\lambda (\Gamma )$ means that the network $\Gamma$ is more reliable. It is well known that $\kappa (\Gamma )\le \lambda (\Gamma )\le \delta (\Gamma )$, where $\delta (\Gamma )$ is the minimum degree of $\Gamma$. A graph is said to be super-$\kappa$(resp. super-$\lambda$), if any minimum vertex-cut (resp. edge-cut) isolates a vertex.

In order to estimate more precisely the reliability, Esfahanian and Hakimi introduce such a kind of edge cut in  [6] that separates a connected graph into a disconnected one without isolated vertices. With the properties of restricted edge connectivity, Li analyzed the reliability of circulant graphs in  [11] and improved Bauer’s result. For more accurate results, Ou et al. introduce the concepts of m-restricted edge cut and m-restricted edge connectivity in  [6, 16, 17, 27]. An edge set F is an m-restricted edge cut of a connected graph G if $G-F$ is disconnected and each component of $G-F$ contains at least m vertices (see [6]). Let $\lambda ^{(m)}(G)$ be the minimum size of all m-restricted edge cuts and $\xi _m(G)=\mathrm{min}\{|\omega (U)|: |U|=m \ \mathrm{and} G[U] \mathrm{is}\ \mathrm{connected}\}$ where $\omega (U)$ is the set of edges with exactly one end vertex in U and G[U] is the subgraph of G induced by U. A graph G is $\lambda ^{(m)}$-graph if $\lambda ^{(m)}(G)=\xi _m(G)$. Also $\lambda ^{(m)}(G)$ is called m-restricted edge connectivity of graph G. Moreover, a graph is called super-m-restrict edge connected, in short, super-$\lambda ^{(m)}$ if every minimum edge cut isolates one component G[U] with $|U|=m$. In the special case, a set F of edges of a connected graph G is said to be a restricted edge-cut, if its removal disconnects G, and $G-F$ contains no isolated vertices. If G has at least one restricted edge-cut, the restricted edge-connectivity of G, denoted by $\lambda ^{'}(G)$, is then defined to be the minimum cardinality over all restricted edge-cuts of G. Moreover, a graph $\Gamma$ is called super-restricted edge-connected, in short, super-$\lambda ^{'}$ if every minimum restricted edge cut isolates one component of size 2 . The super-restricted edge-connectivity of many interconnection networks has been studied (see [5, 11, 12, 19, 24, 33]).

Similarly, if V is a vertex set then m-restricted cut, m-restricted connectivity and super-m-restricted connectivity ( in the special case super-$\kappa ^{'}$) are defined analogously.

For a graph $\Gamma$, an edge set F is a cyclic edge-cut if $\Gamma -F$ is disconnected and at least two of its components contain cycles. Clearly, a graph has a cyclic edge-cut if and only if it has two vertex-disjoint cycles. For a cyclically separable graph G, the cyclic edge-connectivity of $\Gamma$, denoted by $\lambda _c(\Gamma )$, is defined as the cardinality of a minimum cyclic edge-cut of $\Gamma$. Cyclic edge-connectivity plays an important role in many classic fields of graph theory such as measure of network reliability. A graph $\Gamma$ is said to be super-$\lambda _c$, if the removal of any minimum cyclic edge-cut of $\Gamma$ results in a component which is a shortest cycle of $\Gamma$. The cyclic edge-connectivity of many interconnection networks has been studied (see [18, 21, 28, 30,31,32]).

Suppose that $\Gamma$ and $\Delta$ are two graphs. The lexicographic product of $\Gamma$ and $\Delta$ which is denoted by $\Gamma [\Delta ]$ is a graph with vertex set $V(\Gamma )\times V(\Delta )$ and two vertices $(u_1, v_1)$, $(u_2, v_2) \in V(\Gamma )\times V(\Delta )$ are adjacent in $\Gamma [\Delta ]$ whenever either $u_1$ is adjacent to $u_2$ in $\Gamma$, or $u_1=u_2$ and $v_1$ is adjacent to $v_2$ in $\Delta$.

Let $\Gamma$ and H be two graphs. The lexicographic product $\Gamma [H]$ is defined as the graph with vertex set $V(\Gamma )\times V(H)$, and for any two vertices $(u_1, v_1)$, $(u_2, v_2) \in V(\Gamma )\times V(H)$, they are adjacent in $\Gamma [H]$ if and only if either $u_1$ is adjacent to $u_2$ in $\Gamma$, or $u_1=u_2$ and $v_1$ is adjacent to $v_2$ in H.

Proposition 2.1

([14, 20]) Let $\Gamma$ be a connected graph which is both vertex-transitive and edge-transitive. Then $\kappa (\Gamma )=\delta (\Gamma )$, and moreover, $\Gamma$ is not super-$\kappa$ if and only if $\Gamma \cong C_n[mK_1]$ $(n\ge 6)$ or $L(Q_3)[mK_1]$, where $L(Q_3)$ is the line graph of three-dimensional hypercube $Q_3$.

The following results are about the connectivity of edge-transitive graphs.

Proposition 2.2

([2, 11, 19, 30, 31]) Let $\Gamma$ be a k($k\ge 3$)-regular edge-transitive graph. Then

• (1) $\Gamma$ is super-$\lambda$.

• (2) $\lambda ^{'}(\Gamma )=2k-2$.

• (3) $\Gamma$ is not super-$\lambda ^{'}$ if and only if $\Gamma$ is isomorphic to the three-dimensional hypercube $Q_3$ or to a four-valent edge-transitive graph of girth 4.

• (4) If $\Gamma$ is not isomorphic to $K_4$, $K_5$ or $K_{3, 3}$ then $\lambda _c(\Gamma )=g(k-2)$, where g is the girth of $\Gamma$.

By [32][Theorem 3.4] we have the following result.

Proposition 2.3

Let $\Gamma$ be a k($k\ge 3$)-regular edge-transitive graph of girth g. Suppose that $\Gamma$ is not isomorphic to $K_4$, $K_5$ or $K_{3, 3}$. If $\Gamma$ is not super-$\lambda _c$, then $(g, k)=(6, 3), (4, 4), (4, 5), (4, 6)$ or (3, 6). Furthermore, $C_n[2K_1]$ $(n\ge 4)$ is non-super-$\lambda _c$, and if $(g, k)=(4, 6)$ or $(g, k)=(4, 5)$ then $|\Gamma |=16$ or $|\Gamma |=12$, respectively.

3 Reliability Evaluation of Folded Hypercube

The reliability of an interconnection network is an important issue for multiprocessor systems. In this section we study some reliability measures, say, super-connectivity, cyclic connectivity, etc., in folded hypercube. For the folded hypercubes, in [1] it was shown that $\kappa (FQ_n) = n + 1$. However, by [15], we know that $FQ_n$ is arc-transitive. Thus by Proposition 2.1, $\kappa (FQ_n)=\delta (FQ_n)=n+1$. In the following we obtain the stronger result which states $FQ_n$ is super-k for $n\ge 2$.

Theorem 3.1

$FQ_n$ is super-k if and only if $n\ge 2$.

Proof

If $n=2$ then $FQ_n$ is a complete graph $K_4$. Clearly, it is super-k. In what follows, assume that $n\ge 3$. Suppose to contrary that is $FQ_n$ is not super-k. Since $FQ_n$ is both vertex-transitive and edge-transitive, from Proposition 2.1 it follows that $FQ_n\cong C_l[mK_1]$ $(l\ge 6)$ or $L(Q_3)[mK_1]$. First suppose that $FQ_n\cong C_l[mK_1]$ $(l\ge 6)$. We know that $\kappa (FQ_n)=n+1$. Also by [26][Theorems 1], $\kappa (C_l[mK_1])=2m$ and so $n+1=2m$. Moreover, since $|V(C_l[mK_1])|=|V(FQ_n)|$, it follows that $2^n=ml$. Thus m and l are even. By [1] we know that $\mathrm{diam}(FQ_n)=\lceil n/2 \rceil$. Also we know that $\mathrm{diam}(C_l[mK_1])=l/2$ (see [10]). Now $l/2=\lceil n/2 \rceil$ and so $\lceil n/2 \rceil =\lceil 2m-1/2 \rceil =m=l/2$. Now $2^n=2m^2$ and we may suppose that $m=2^k$ for some $k\ge 0$. If $k=1$ then $m=2$ and $l=4$, a contradiction. Thus $k\ge 2$. By $2^n=2m^2=22^{2k}=2^{2k+1}$ we have $n=2k+1$. Now by $n=2m-1$ we have $2k+1=2^{k+1}-1$. Thus $2^k=k+1$, a contradiction. Now suppose that $FQ_n\cong L(Q_3)[mK_1]$. Thus, the number of vertices of these graphs is same and so $2^n=12m$, a contradiction. $\square$

In the following theorem we show that the delation of any minimum edge-cut of $FQ_n$ isolates a vertex.

Theorem 3.2

$FQ_n$ is super-$\lambda$ if and only if $n\ge 3$.

Proof

If $n=2$ then $FQ_2$ is a complete graph $K_4$. Clearly, it is not super-$\lambda$. Suppose that $n\ge 3$. Thus the valency of $FQ_n$ is at least 4. Since $FQ_n$ is edge-transitive, the theorem follows from Proposition 2.2(1). $\square$

From this theorem we immediately have the following corollary.

Corollary 3.3

For $n\ge 2$, $\lambda (FQ_n)=n+1$.

In [23][Theorem 3] Xu et al. proved that the restricted edge-connectivity of $FQ_n$ is 2n. Here we present a simple proof for this result.

Theorem 3.4

For $n\ge 2$, $\lambda ^{'}(FQ_n)=2n$.

Proof

If $n=2$ then $FQ_2$ is a complete graph $K_4$. Clearly, $\lambda ^{'}(FQ_2)=4$. Thus we may suppose that $n\ge 3$. Therefore $FQ_n$ has valency $n+1\ge 4$. Now since $FQ_n$ is edge-transitive, the theorem follows from Proposition 2.2. $\square$

In the following theorem we show that every minimum edge-cut of $FQ_n$ $(n\ge 3)$ isolates an edge.

Theorem 3.5

$FQ_n$ is super-$\lambda ^{'}$ if and only if $n\ne 3$.

Proof

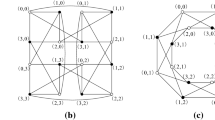
If $n=2$ then clearly $FQ_2$ is super-$\lambda ^{'}$. Also if $n=3$ then again it is easy to see that $FQ_3$ is not super-$\lambda ^{'}$ (see Fig. 1). Thus we may suppose that $n\ge 4$. Therefore $FQ_n$ has valency $n\ge 5$. We know that $FQ_n$ is edge-transitive. By Proposition 2.2$FQ_n$ is not super-$\lambda ^{'}$ if and only if it is isomorphic to the three-dimensional hypercube $Q_3$ or a four-valent edge-transitive graph of girth 4. Since $FQ_n$ $(n\ge 4)$ has valency at least 5 it implies that $FQ_n\cong Q_3$. Also if $FQ_n\cong Q_3$ then $n=3$. But we know that $Q_3$ has valency three, but the valency of $FQ_3$ is four, a contradiction. Therefore $FQ_n$ is super-$\lambda ^{'}$ for $n\ge 2$. $\square$

The following theorem shows that for $n\ge 3$, every minimum cyclic edge-cut of $FQ_n$ isolates a shortest cycle.

Theorem 3.6

$FQ_n$ is super-$\lambda _c$ if and only if $n\ne 2$.

Proof

If $n=2$ then clearly $FQ_2$ is not super-$\lambda _c$. Also if $n=3$ or $n = 4$ then it is easy to see that $FQ_3$ is super-$\lambda _c$. Thus we may suppose that $n\ge 5$. We know that $FQ_n$ has order $2^n$ and valency $n+1$. Thus $FQ_n$ is not isomorphic to $K_3$, $K_4$ or $K_{3, 3}$. Suppose to contrary that $FQ_n$ is not super-$\lambda _c$. By Proposition 2.3, $n+1 \in \{3, 4, 5, 6 \}$. Suppose that $n+1=3$ or $n+1=4$ then $n=2$ or $n=3$, a contradiction. If $n+1=5$ or $n+1=6$ then $n=4$ or $n=5$. Now by Proposition 2.3, $FQ_4$ or $FQ_5$ has 12 or 16 vertices, a contradiction.

In the following theorem we show that for $n\ge 3$, by removing $4(n-1)$ edges from $FQ_n$ we obtain a disconnected graph which has at least two components containing cycle. $\square$

Theorem 3.7

For $n\ge 3$, $\lambda _c(FQ_n)=4(n-1)$.

Proof

Since $FQ_n$ has at least 8 vertices it is not isomorphic to $K_3$, $K_4$ and $K_{3, 3}$. By [22][Theorems 3.3] we know that $FQ_n$ has girth 4. Now by Proposition 2.2$\lambda _c(FQ_n)=4(n+1-2)=4(n-1)$. $\square$

Theorem 3.8

$FQ_n$ $(n\ge 8)$ is super-$\kappa ^{'}$.

Proof

By [4, 34], we know that $\kappa _2 \ge \kappa _1$. Suppose that $FQ_n$ for $(n\ge 8)$ is not super-$\kappa ^{'}$. Thus there is a restricted cut S of order $\kappa _1$, but the cut is not the neighborhood of any edge. That is, S is also a 3-restricted cut. Thus $|S|\ge \kappa _2$, a contradiction. $\square$