Some Results on the 3-Vertex-Rainbow Index of a Graph

Abstract

Let G be a nontrivial connected graph with a vertex-coloring c: $V(G)\rightarrow \{1,2,\ldots ,q\},q\in N$. For a set $S\subseteq V(G)$ and $|S|\ge 2$, a subtree T of G satisfying $S\subseteq V(T)$ is said to be an S-Steiner tree or simply S-tree. The S-tree T is called a vertex-rainbow S-tree if the vertices of $V(T)\setminus S$ have distinct colors. Let k be a fixed integer with $2\le k\le |V(G)|$, if every k-subset S of V(G) has a vertex-rainbow S-tree, then G is said to be vertex-rainbow k-tree connected. The k-vertex-rainbow index of G, denoted by $rvx_{k}(G)$, is the minimum number of colors that are needed in order to make G vertex-rainbow k-tree connected. In this paper, we study the 3-vertex-rainbow index of unicyclic graphs and complementary graphs, respectively.

1 Introduction

All graphs considered in this paper are simple, finite and undirected. We follow the notation and terminology of [1] for those not described here. In recent years, colored notions of connectivity in graphs become a new and active subject in graph theory. Stating from rainbow connection, rainbow-vertex connection and total rainbow connection appeared later. Many researchers are working in this field, and a lot of papers have been published in journals, see [2, 3, 5,6,7,8,9,10,11,12, 15,16,17,18,19, 21] for details. The reader also can see [14] for dynamic survey and [13] for a new monograph on this topic.

The concept of rainbow path was generalized to rainbow tree by Chartrand et al. [4]. For every set S of V(G) and $|S|\ge 2$, a subtree T of G such that $S\subseteq V(T)$ is called an S-Steiner tree or simply S-tree. For every set S of V(G), an S-tree is called a rainbow S-tree if any two edges of the tree are assigned distinct colors. Let k be a fixed integer with $2\le k\le |V(G)|$, the edge-coloring c of G is said to be a k-rainbow coloring if for every set S of k vertices of G, there exists a rainbow S-tree. The k-rainbow index of a connected graph, denoted by $rx_{k}(G)$, is the minimum number of colors that are required in a k-rainbow coloring of G.

As a natural counterpart of the k-rainbow index, Mao introduced the concept of k-vertex-rainbow index $rvx_{k}(G)$ and investigated the Nordhaus–Gaddum problem with $k=3$ in [20]. An S-tree T is called a vertex-rainbow S-tree or a vertex-rainbow tree connecting S if no two vertices of $V(T)\backslash S$ share same color. Let k be a fixed integer with $2\le k\le |V(G)|$, the vertex-coloring c of G is said to be a k-vertex-rainbow coloring if for every set S of k vertices of G, there exists a vertex-rainbow S-tree. If such vertex-coloring c exists, then G is called vertex-rainbow k-tree connected. The k-vertex-rainbow index of a connected graph, denoted by $rvx_{k}(G)$, is the minimum number of colors that are needed in a k-vertex-rainbow coloring of G.

In 2010, Chartrand et al. [4] considered the 3-rainbow index of unicyclic graphs. In Sect. 2, we investigated the 3-vertex-rainbow index of unicyclic graphs. Moreover, we studied the 3-vertex-rainbow index of complementary graphs in Sect. 3.

2 The 3-Vertex-Rainbow Index of Unicyclic Graphs

For a subset X of V(G), we use G[X] to denote the induced subgraph by X. The distance between two vertices u and v in a connected graph G, denoted by d(u, v), is the length of a shortest u-v path in G. The eccentricity of a vertex v is defined as $\mathrm{ecc}_{G}(v):=\mathrm{max}_{x\in V(G)}d(v,x)$. The Steiner distance d(S) of a set S of V(G) is the minimum number of edge of a tree in G containing S. The Steiner k-diameter $\mathrm{sdiam}_{k}(G)$ of G is the maximum Steiner distance of S among all sets S with k vertices in G. In [20], Mao obtained the following results.

Proposition 2.1

[20] Let G be a nontrivial connected graph of order n. Then, $rvx_{k}(G)=0$ if and only if $sdiam_{k}(G)=k-1$.

Proposition 2.2

[20] Let G be a nontrivial connected graph of order n ($n\ge 5$), and let k be an integer with $2\le k\le n$. Then, $0\le rvx_{k}(G)\le n-2$.

Let $G_{1}=C_{1}\cup C_{2}\cup \{uv\}$, where $C_{1}=uu_{1}u_{2}\ldots u_{i}u$ and $C_{2}=vv_{1}v_{2}\ldots v_{j}v$. For every k-subset S of $\{u_{1},u_{2},\ldots ,u_{i},v_{1},v_{2},\ldots ,v_{j}\}$ satisfying $S\cap \{u_{1},u_{2},\ldots ,u_{i}\}\ne \emptyset$ and $S\cap \{v_{1},v_{2},\ldots ,v_{j}\}\ne \emptyset$, we know that every S-tree contains the two cut vertices u and v. The following observation holds.

Observation 2.3

Let G be a connected graph of order n containing two cut vertices u and v. For each integer k with $2\le k\le n$, every k-vertex-rainbow coloring of G must assign distinct colors to u and v.

In [4], Chartrand et al. proved that the 3-rainbow index of cycles is $n-1$ for $n=3$, or $n-2$ for $n\ge 4$. Now we consider the 3-vertex-rainbow index of cycles.

Theorem 2.4

For integer n,

$$\begin{aligned} rvx_{3}(C_{n})= {\left\{ \begin{array}{ll} 0&{}\mathrm { if } \quad 3\le n\le 4,\\ n-4&{}\mathrm { if }\quad n\ge 5. \end{array}\right. } \end{aligned}$$

Proof

For $3\le n\le 4$, by Proposition 2.1, we have $rvx_{3}(C_{3})=0$ and $rvx_{3}(C_{4})=0$.

For $n=5$, we assign one color to all vertices of $C_{5}$. Thus, $rvx_{3}(C_{5})\le 1$. Since $\mathrm{sdiam}_{3}(C_{5})=3$, we have $rvx_{3}(C_{5})\ge 1$, and so $rvx_{3}(C_{5})=1=n-4$.

For $n=6$, we assign a vertex-coloring c to $C_{6}$ as follows: $c(v_{1})=c(v_{2})=c(v_{3})=c(v_{6})=1,c(v_{4})=c(v_{5})=2$. It is easy to verify that $C_{6}$ is vertex-rainbow 3-tree connected with the above vertex-coloring, and so $rvx_{3}(C_{6})\le 2$. Since every tree connecting $\{v_{1},v_{3},v_{5}\}$ has size at least 4, every tree has at least two vertices which are different from $\{v_{1},v_{3},v_{5}\}$. Note that $rvx_{3}(C_{6})\ge 2$. Thus $rvx_{3}(C_{6})=2=n-4$.

For $n\ge 7$, let $C_{n}:v_{1},v_{2},\ldots ,v_{n},v_{n+1}=v_{1}$. Assign a vertex-coloring c to $C_{n}$ as follows: $c(v_{1})=c(v_{4})=c(v_{7})=1,c(v_{2})=c(v_{5})=2$ and $c(v_{3})=c(v_{6})=3$ if $n=7$; $c(v_{i})=i$ for $1\le i\le n-4$ and $c(v_{i})=i-n+4$ for $n-3\le i\le n$ if $n\ge 8$. For $n=7$, we can check that the coloring c is a 3-vertex-rainbow coloring, and thus, $rvx_{3}(C_{7})\le 3=n-4$. For $n\ge 8$, we need to show that there exists a vertex-rainbow tree connecting any three different vertices $v_{i},v_{j}$ and $v_{z}$ of $C_{n}$, where $1\le i<j<z\le n$. Let $S=\{v_{i},v_{j},v_{z}\}$. Without loss of generality, we verify $rvx_{3}(C_{n})\le n-4$ by considering the following four cases.

${\mathbf {Case~1}}$ $v_{i},v_{j}$ and $v_{z}$ are three distinct vertices of the path $P=v_{1}v_{2}\ldots v_{n-4}$ ($P=v_{5}v_{6}\ldots v_{n}$), where $1\le i< j<z\le n-4$ ($5\le i< j<z\le n$). Obviously, there is a vertex-rainbow S-tree $T=v_{i}\ldots v_{j}\ldots v_{z}$, and so $rvx_{3}(C_{n})\le n-4$.

${\mathbf {Case~2}}$ Two vertices of S which lie on the path $P=v_{1}v_{2}\ldots v_{n-4}$, and the remaining vertex of S lies on the path $P^{'}=v_{n-3}v_{n-2}v_{n-1}v_{n}$. Let $1\le i< j\le 4$ and $n-3\le z\le n$. If $i=1$ and $j=2$, then there exists a vertex-rainbow S-tree T, where $T=v_{z}\ldots v_{i}v_{j}$. If $i=1,j=3$ and $n-2\le z\le n$, then there exists a vertex-rainbow S-tree T, where $T=v_{z}\ldots v_{i}v_{2}v_{j}$. If $i=1,j=3$ and $z=n-3$, then there exists a vertex-rainbow S-tree T, where $T=v_{i}v_{2}v_{j}v_{4}\ldots v_{z}$. If $i=1$ and $j=4$, then there exists a vertex-rainbow S-tree T, where $T=v_{j}v_{5}\ldots v_{z}\ldots v_{i}$. If $i=2$ and $j=3$, then there exists a vertex-rainbow S-tree T, where $T=v_{z}\ldots v_{1}v_{i}v_{j}$. If $i=2,j=4$ and $n-3\le z\le n-1$, then there exists a vertex-rainbow S-tree T, where $T=v_{i}v_{3}v_{j}v_{5}\ldots v_{z}$. If $i=2,j=4$ and $z=n$, then there exists a vertex-rainbow S-tree T, where $T=v_{z}v_{1}v_{i}v_{3}v_{j}$. If $i=3$ and $j=4$, then there exists a vertex-rainbow S-tree T, where $T=v_{i}v_{j}v_{5}\ldots v_{z}$. Let $1\le i\le 4,5\le j\le n-4$ and $n-3\le z\le n$. If $n-3\le z\le n-2$, then there exists a vertex-rainbow S-tree T, where $T=v_{i}\ldots v_{j}\ldots v_{z}$. If $i=1$ and $z=n-1$, then there exists a vertex-rainbow S-tree T, where $T=v_{j}\ldots v_{z}\ldots v_{i}$. If $2\le i\le 4$ and $z=n-1$, then there exists a vertex-rainbow S-tree T, where $T=v_{i}\ldots v_{j}\ldots v_{z}$. If $z=n$, then there exists a vertex-rainbow S-tree T, where $T=v_{z}\ldots v_{i}\ldots v_{j}$. Let $5 \le i<j \le n-4$ and $n-3 \le z \le n$. Then, there exists a vertex-rainbow S-tree T, where $T=v_{i}\ldots v_{j}\ldots v_{z}$. Hence, $rvx_{3}(C_{n})\le n-4$.

$\mathbf {Case~3}$ One vertex of $\{v_{i},v_{j},v_{z}\}$ which lies on the path $P=v_{1}v_{2}\ldots v_{n-4}$ and the remaining vertices of $\{v_{i},v_{j},v_{z}\}$ lie on the path $P^{'}=v_{n-3}v_{n-2}v_{n-1}v_{n}$. Let $1 \le i\le 4$ and $n-3 \le j<z \le n$. Then, an argument similar to the one used in the proof of $1\le i<j\le 4$ and $n-3\le z\le n$. Let $5\le i\le n-4$ and $n-3\le j<z\le n$. Then, there exists a vertex-rainbow S-tree T, where $T=v_{i}\ldots v_{j}\ldots v_{z}$. Thus, $rvx_{3}(C_{n})\le n-4$.

$\mathbf {Case~4}$ $v_{i},v_{j}$ and $v_{z}$ are three distinct vertices of the path $P=v_{n-3}v_{n-2}v_{n-1}v_{n}$, where $n-3\le i<j<z\le n$. Thus, there exists a vertex-rainbow S-tree T, where $T=v_{i}\ldots v_{j}\ldots v_{z}$. Therefore, $rvx_{3}(C_{n})\le n-4$.

Next, we verify that $rvx_{3}(C_{n})\ge n-4$ by proving the following three claims.

${\mathbf {Claim~1}}$ No five vertices of $C_{n}$ can be colored the same.

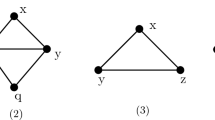
Proof Suppose that $c(v_{i})=c(v_{j})=c(v_{m})=c(v_{p})=c(v_{q})$, where $1\le i<j<m<p<q\le n$. According to the adjacency of vertices of $\{v_{i},v_{j},v_{m},v_{p},v_{q}\}$, we only need to consider the seven types of $\{H_{1},H_{2},H_{3},H_{4},H_{5},H_{6},H_{7}\}$ shown in Fig. 1. (For all the graphs of this paper, if two vertices of a graph are joined by a solid line, then the two vertices are said to be adjacent.) Let $S=\{v_{g},v_{h},v_{m}\}$. Then, any tree connecting S is not a vertex-rainbow S-tree, a contradiction. This completes the proof of the Claim 1. $\square$

Fig. 1

Seven types of claim 2

${\mathbf {Claim~2}}$ At most one pair of four vertices of $C_{n}$ can be colored the same. Moreover, the four vertices share same color if and only if $P_{4}$ contains them, and other vertices have distinct colors.

Proof Suppose that there are two pairs $\pi _{1}=\{v_{i},v_{j},v_{p},v_{q}\}$ and $\pi _{2}=\{v_{a},v_{b},v_{c},v_{d}\}$ of vertices, where the colors of four of the eight vertices are the same if and only if the four vertices belong to the same pair with $i<j<p<q$ and $a<b<c<d$. If $v_{i},v_{j},v_{p}$ and $v_{q}$ are four internally distinct vertices of the path $P=v_{a}\ldots v_{b}$, then there is no vertex-rainbow S-tree, where $S=\{v_{i},v_{b},v_{q}\}$. If $v_{i},v_{j}$ and $v_{p}$ are three internally distinct vertices of the path $P=v_{a}\ldots v_{b}$, $v_{q}$ is an internal vertex of the path $P^{'}=v_{b}\ldots v_{c}\ldots v_{d}\ldots v_{a}$, then there is no vertex-rainbow tree connecting $\{v_{i},v_{b},v_{q}\}$. If $v_{i}$ and $v_{j}$ are two internally distinct vertices of the path $P=v_{a}\ldots v_{b}$, $v_{p}$ and $v_{q}$ are two internally distinct vertices of the path $P^{'}=v_{b}\ldots v_{c}\ldots v_{d}\ldots v_{a}$, then there is no vertex-rainbow tree connecting $\{v_{i},v_{c},v_{q}\}$. If $v_{i},v_{j},v_{p}$ and $v_{q}$ are four internally distinct vertices of the paths $P=v_{a}\ldots v_{b},P^{'}=v_{b}\ldots v_{c},P^{''}=v_{c}\ldots v_{d}$ and $P^{'''}=v_{d}\ldots v_{a}$, respectively, then there is no vertex-rainbow S-tree, where $S=\{v_{i},v_{c},v_{q}\}$.

Without loss of generality, assume that $\pi _{1}=\{v_{i},v_{j},v_{p},v_{q}\}$ satisfies $c(v_{i})=c(v_{j})=c(v_{p})=c(v_{q})$. Next, we verify that the four vertices of $\pi _{1}$ can be colored the same if and only if $P_{4}$ contains $\pi _{1}$, and the others have distinct colors. Consider the four graphs $G_{1},G_{2},G_{3}$ and $G_{4}$ shown in Fig. 2. For the type shown in $G_{1}$, there is no vertex-rainbow tree connecting $\{v_{g},v_{j},v_{h}\}$; In $G_{2},G_{3}$ and $G_{4}$, there is no vertex-rainbow tree connecting $\{v_{g},v_{h},v_{f}\}$. If $P_{4}$ contains $\pi _{1}$, then we can check that there exists a vertex-rainbow tree connecting any three distinct vertices of $C_{n}$. Suppose that there exist two distinct vertices $v_{a}$ and $v_{b}$ satisfying $c(v_{a})=c(v_{b})$. By Claim 1, we have $c(v_{a})\ne c(v_{i})$. According to the adjacency of vertices of $\{v_{i},v_{j},v_{p},v_{q},v_{a},v_{b}\}$, we consider the graphs $G_{5},G_{6},G_{7},G_{8}$ and $G_{9}$ in Fig. 2. For the type shown in $G_{5}$, there is no vertex-rainbow tree connecting $\{v_{i},v_{j},v_{g}\}$; In $G_{6}$, there is no vertex-rainbow tree connecting $\{v_{i},v_{q},v_{g}\}$; In $G_{7},G_{8}$ and $G_{9}$, there is no vertex-rainbow tree connecting $\{v_{j},v_{g},v_{f}\}$, a contradiction. This completes the proof of the Claim 2. $\square$

Fig. 2

Nine types of Claim 2

${\mathbf {Claim~3}}$ If there are not four vertices of $C_{n}$ with the same color, then one of the following cases holds.

• (i) At most two pairs of three vertices of $C_{n}$ can be colored the same and other vertices must be colored the different.

• (ii) If $C_{n}$ contains only one pair of three vertices with the same color, then other vertices contain at most two pairs of two vertices where the vertices in each pair can be colored the same.

• (iii) At most four pairs of two vertices of $C_{n}$ satisfy that any two vertices of $C_{n}$ have the same color if and only if the two vertices in the same pair.

Proof (i) Let $\pi _{1}=\{v_{a},v_{a}^{'},v_{a}^{''}\}$ and $\pi _{2}=\{v_{b},v_{b}^{'},v_{b}^{''}\}$ which satisfy $c(v_{a})=c(v_{a}^{'})=c(v_{a}^{''})$ and $c(v_{b})=c(v_{b}^{'})=c(v_{b}^{''})$, where the vertices of $\pi _{1}$ ($\pi _{2}$) are encountered in the clockwise order $v_{a},v_{a}^{'},v_{a}^{''}$ ($v_{b},v_{b}^{'},v_{b}^{''}$) in $C_{n}$. Since $n\ge 7$, we know that there exists a vertex $v_{g}\not \in \pi _{1}\cup \pi _{2}$. There is a vertex-rainbow tree connecting any three distinct vertices if and only if the following two cases hold: (1) $v_{b}$ and $v_{b}^{'}$ are two internally distinct vertices of the path $P=v_{a}\ldots v_{a}^{'}$, $v_{b}^{''}$ and $v_{g}$ are the internal vertices of the paths $P^{'}=v_{a}^{'}\ldots v_{a}^{''}$ and $P^{''}=v_{a}^{'}\ldots v_{b}^{''}$, respectively; (2) $v_{b}$ and $v_{b}^{'}$ are two internally distinct vertices of the path $P=v_{a}\ldots v_{a}^{'}$, $v_{b}^{''}$ and $v_{g}$ are the internal vertices of the paths $P^{'}=v_{a}^{''}\ldots v_{a}$ and $P^{''}=v_{b}^{''}\ldots v_{a}$, respectively. (Isomorphism is no longer discussed.) If $v_{b}$ and $v_{b}^{'}$ are the internal vertices of the path $P=v_{a}\ldots v_{a}^{'}$, $v_{b}^{''}$ is the internal vertex of $P^{'}=v_{a}^{'}\ldots v_{a}^{''}\ldots v_{a}$, and the location of $v_{g}$ that is different from (1) and (2), then we can check that there exists a set $S^{'}$ of three vertices, any tree connecting $S^{'}$ is not vertex-rainbow. If $v_{b},v_{b}^{'}$ and $v_{b}^{''}$ are three internally distinct vertices of the path $P=v_{a}\ldots v_{a}^{'}$, then any tree connecting $\{v_{b},v_{a}^{'},v_{g}\}$ is not vertex-rainbow. If $v_{b},v_{b}^{'}$ and $v_{b}^{''}$ are the internal vertices of the paths $P=v_{a}\ldots v_{b}\ldots v_{a}^{'}$, $P^{'}=v_{a}^{'}\ldots v_{b}^{'}\ldots v_{a}^{''}$ and $P^{''}=v_{a}^{''}\ldots v_{b}^{''}\ldots v_{a}$, respectively, then any tree connecting $\{v_{a},v_{a}^{'},v_{a}^{''}\}$ is not vertex-rainbow.

Let $v_{b}$ and $v_{b}^{'}$ be two internally distinct vertices of the path $P=v_{a}\ldots v_{a}^{'}$, $v_{b}^{''}$ be an internal vertex of the path $P^{'}=v_{a}^{'}\ldots v_{a}^{''}\ldots v_{a}$. Suppose $\pi _{3}=\{v_{c},v_{c}^{'},v_{c}^{''}\}$, where $c(v_{c})=c(v_{c}^{'})=c(v_{c}^{''})\ne c(v_{a})\ne c(v_{b})$, and the vertices in $\pi _{3}$ are encountered in the clockwise order $v_{c},v_{c}^{'},v_{c}^{''}$ in $C_{n}$. Assume that $v_{c},v_{c}^{'}$ and $v_{c}^{''}$ are three internal vertices of the path $P=v_{a}\ldots v_{b}^{'}\ldots v_{a}^{'}$. Then, any tree connecting $\{v_{a},v_{c}^{''},v_{b}^{''}\}$ is not vertex-rainbow. Assume that $v_{c},v_{c}^{'}$ and $v_{c}^{''}$ are three internal vertices of the path $P=v_{a}^{'}\ldots v_{a}^{''}$. Then, any tree connecting $\{v_{a},v_{c},v_{b}^{''}\}$ is not vertex-rainbow. Assume that $v_{c},v_{c}^{'}$ and $v_{c}^{''}$ are three internal vertices of the path $P=v_{a}^{''}\ldots v_{a}$. Then, any tree connecting $\{v_{a},v_{c},v_{b}^{''}\}$ is not vertex-rainbow. Assume that $v_{c}$ and $v_{c}^{'}$ are two internal vertices of the path $P=v_{a}\ldots v_{b}^{'}\ldots v_{a}^{'}$, $v_{c}^{''}$ is an internal vertex of the path $P^{'}=v_{a}^{'}\ldots v_{a}^{''}\ldots v_{a}$. If $v_{c}$ and $v_{c}^{'}$ are two internal vertices of the path $P=v_{a}\ldots v_{b}\ldots v_{b}^{'}$, then any tree connecting $\{v_{a},v_{b}^{'},v_{c}^{''}\}$ is not vertex-rainbow. If $v_{c}$ is the internal vertex of the path $P=v_{a}\ldots v_{b}^{'}\ldots v_{a}^{'}$ and $v_{c}^{'}$ is the internal vertex of the path $P^{'}=v_{b}^{'}\ldots v_{a}^{'}$, then any tree connecting $\{v_{a},v_{c}^{'},v_{c}^{''}\}$ is not vertex-rainbow. Assume that $v_{c}$ and $v_{c}^{'}$ are two internal vertices of the path $P=v_{a}^{'}\ldots v_{a}^{''}$, $v_{c}^{''}$ is an internal vertex of the path $P^{'}=v_{a}^{''}\ldots v_{a}\ldots v_{a}^{'}$. Then, any tree connecting $\{v_{a},v_{a}^{'},v_{b}^{''}\}$ is not vertex-rainbow. Assume that $v_{c}$ and $v_{c}^{'}$ are two internal vertices of the path $P=v_{a}^{''}\ldots v_{a}$, $v_{c}^{''}$ is an internal vertex of the path $P^{'}=v_{a}\ldots v_{a}^{'}\ldots v_{a}^{''}$. Then, there is no vertex-rainbow tree connecting $\{v_{a},v_{a}^{'},v_{b}^{''}\}$. Assume that $v_{c},v_{c}^{'}$ and $v_{c}^{''}$ are the internal vertices of the paths $P=v_{a}\ldots v_{a}^{'}, P^{'}=v_{a}^{'}\ldots v_{a}^{''}$ and $P^{''}=v_{a}^{''}\ldots v_{a}$, respectively. Then, any tree connecting $\{v_{a},v_{a}^{'},v_{c}\}$ is not vertex-rainbow. Assume that $v_{c},v_{c}^{'}$ and $v_{c}^{''}$ are the internal vertices of the paths $P=v_{a}^{'}\ldots v_{a}^{''}$, $P^{'}=v_{a}^{''}\ldots v_{a}$ and $P^{''}=v_{a}\ldots v_{a}^{'}$, respectively. Then, any tree connecting $\{v_{a},v_{a}^{'},v_{c}^{''}\}$ is not vertex-rainbow. Assume that $v_{c},v_{c}^{'}$ and $v_{c}^{''}$ are the internal vertices of the paths $P=v_{a}^{''}\ldots v_{a}$, $P^{'}=v_{a}\ldots v_{a}^{'}$ and $P^{''}=v_{a}^{'}\ldots v_{a}^{''}$, respectively. Then, any tree connecting $\{v_{a},v_{a}^{'},v_{c}^{'}\}$ is not vertex-rainbow, a contradiction.

Next, we verify that other vertices must be colored different. Note that $v_{b}$ and $v_{b}^{'}$ are two internal vertices of the path $P=v_{a}\ldots v_{a}^{'}$, and $v_{b}^{''}$ is the internal vertex of the path $P^{'}=v_{a}^{'}\ldots v_{a}^{''}\ldots v_{a}$. Suppose that $\pi _{4}=\{v_{d},v_{d}^{'}\}$ satisfies $c(v_{d})=c(v_{d}^{'})$, and the vertices of $\pi _{4}$ are encountered in the clockwise order $v_{d},v_{d}^{'}$ in $C_{n}$. Let $v_{d}$ and $v_{d}^{'}$ be two internal vertices of the path $P=v_{a}\ldots v_{b}^{'}\ldots v_{a}^{'}$. If at least one vertex of $\{v_{d},v_{d}^{'}\}$ is the internal vertex of the path $P=v_{a}\ldots v_{b}$, then there is no vertex-rainbow tree connecting $\{v_{d},v_{d}^{'},v_{a}^{'}\}$. If $v_{d}$ and $v_{d}^{'}$ are the internal vertices of the path $P=v_{b}\ldots v_{b}^{'}$, then there is no vertex-rainbow tree connecting $\{v_{d},v_{a},v_{a}^{'}\}$. If $v_{d}$ and $v_{d}^{'}$ are the internal vertices of the path $P=v_{b}^{'}\ldots v_{a}^{'}$, then there is no vertex-rainbow tree connecting $\{v_{a},v_{a}^{'},v_{b}^{'}\}$. If $v_{d}$ and $v_{d}^{'}$ are the internal vertices of the paths $P=v_{b}\ldots v_{b}^{'}$ and $P^{'}=v_{b}^{'}\ldots v_{a}^{'}$, respectively, then there is no vertex-rainbow tree connecting $\{v_{d},v_{a},v_{a}^{'}\}$. Let $v_{d}$ and $v_{d}^{'}$ be two internal vertices of the path $P=v_{a}^{'}\ldots v_{a}^{''}$. Then, there is no vertex-rainbow tree connecting $\{v_{a},v_{a}^{'},v_{a}^{''}\}$. Let $v_{d}$ and $v_{d}^{'}$ be two internal vertices of the path $P=v_{a}^{''}\ldots v_{a}$. Then, any tree connecting $\{v_{a},v_{a}^{'},v_{a}^{''}\}$ is not vertex-rainbow. Let $v_{d}$ and $v_{d}^{'}$ be the internal vertices of the paths $P=v_{a}\ldots v_{a}^{'}$ and $P^{'}=v_{a}^{'}\ldots v_{a}^{''}\ldots v_{a}$, respectively. If $v_{d}$ is the internal vertex of the path $P=v_{a}\ldots v_{b}$, then there is no vertex-rainbow tree connecting $\{v_{d},v_{d}^{'},v_{a}^{'}\}$. If $v_{d}$ is the internal vertex of the path $P=v_{b}\ldots v_{b}^{'}$, then there is no vertex-rainbow tree connecting $\{v_{a},v_{a}^{'},v_{d}\}$. If $v_{d}$ is the internal vertex of the path $P=v_{b}^{'}\ldots v_{a}^{'}$, then there is no vertex-rainbow tree connecting $\{v_{a},v_{b}^{''},v_{d}\}$. Let $v_{d}$ and $v_{d}^{'}$ be the internal vertices of the paths $P=v_{a}^{'}\ldots v_{a}^{''}$ and $P^{'}=v_{a}^{''}\ldots v_{a}$, respectively. Then, there is no vertex-rainbow tree connecting $\{v_{b},v_{d},v_{d}^{'}\}$. Let $v_{d}$ and $v_{d}^{'}$ be the internal vertices of the paths $P=v_{a}^{'}\ldots v_{a}^{''}$ and $P^{'}=v_{a}\ldots v_{b}^{'}\ldots v_{a}^{'}$, respectively, or $v_{d}$ and $v_{d}^{'}$ be the internal vertices of the paths $P=v_{a}^{''}\ldots v_{a}$ and $P^{'}=v_{a}\ldots v_{a}^{'}\ldots v_{a}^{''}$, respectively. By the above similar argument, we can find a set of three vertices, and there is no vertex-rainbow tree connecting it, a contradiction.

(ii) Let $\pi _{1}=\{v_{a},v_{a}^{'},v_{a}^{''}\}$ such that $c(v_{a})=c(v_{a}^{'})=c(v_{a}^{''})$. To the contrary, assume that there exist three pairs $\pi _{2}=\{v_{b},v_{b}^{'}\},\pi _{3}=\{v_{c},v_{c}^{'}\}$ and $\pi _{4}=\{v_{d},v_{d}^{'}\}$ of vertices where the colors of two of the six vertices are the same if and only if the two vertices belong to the same pair. Let $\{v_{i_{1}},v_{i_{2}},v_{i_{3}},v_{i_{4}},v_{i_{5}},v_{i_{6}}\}= \{v_{b},v_{b}^{'},v_{c},v_{c}^{'},v_{d},v_{d}^{'}\}$, where $i_{1}<i_{2}<i_{3}<i_{4}<i_{5}<i_{6}$. If $v_{a},v_{a}^{'}$ and $v_{a}^{''}$ are the internal vertices of the path $P=v_{i_{1}}\ldots v_{i_{2}}$, then any tree connecting $\{v_{a},v_{i_{1}},v_{i_{2}}\}$ is not vertex-rainbow. If $v_{a}$ and $v_{a}^{'}$ are the internal vertices of the path $P=v_{i_{1}}\ldots v_{i_{2}}$, $v_{a}^{''}$ is the internal vertex of the path $P^{'}=v_{i_{2}}\ldots v_{i_{3}}\ldots v_{i_{6}}\ldots v_{i_{1}}$, then any tree connecting $\{v_{a}^{''},v_{i_{1}},v_{i_{2}}\}$ is not vertex-rainbow. If $v_{a}$ is the internal vertex of the path $P=v_{i_{1}}\ldots v_{i_{2}}$, $v_{a}^{'}$ and $v_{a}^{''}$ are the internal vertices of the paths $P^{'}=v_{i_{2}}\ldots v_{i_{3}}$ and $P^{''}=v_{i_{3}}\ldots v_{i_{6}}\ldots v_{i_{1}}$, respectively, then any tree connecting $\{v_{i_{1}},v_{i_{2}},v_{i_{3}}\}$ is not vertex-rainbow. If $v_{a}$ is the internal vertex of the path $P=v_{i_{1}}\ldots v_{i_{2}}$, $v_{a}^{'}$ and $v_{a}^{''}$ are the internal vertices of the paths $P^{'}=v_{i_{3}}\ldots v_{i_{4}}$ and $P^{''}=v_{i_{4}}\ldots v_{i_{6}}\ldots v_{i_{1}}$, respectively, then any tree connecting $\{v_{i_{1}},v_{i_{2}},v_{i_{4}}\}$ is not vertex-rainbow, a contradiction.

(iii) Suppose that there are five pairs $\pi _{1}=\{v_{a},v_{a}^{'}\},\pi _{2}=\{v_{b},v_{b}^{'}\}, \pi _{3}=\{v_{c},v_{c}^{'}\},\pi _{4}=\{v_{d},v_{d}^{'}\}$ and $\pi _{5}=\{v_{e},v_{e}^{'}\}$ of vertices where the colors of two of the ten vertices are the same if and only if the two vertices belong to the same pair. Let $\{v_{i_{1}},v_{i_{2}},v_{i_{3}},v_{i_{4}},v_{i_{5}}, v_{i_{6}},v_{i_{7}},v_{i_{8}},v_{i_{9}},v_{i_{10}} \} =\{v_{a},v_{a}^{'},v_{b},v_{b}^{'},v_{c},v_{c}^{'},v_{d}, v_{d}^{'},v_{e},v_{e}^{'}\}$, where $i_{1}<i_{2}<\ldots <i_{10}$. Without loss of generality, we consider the two trees $T_{1}=v_{i_{1}}\ldots v_{i_{2}}\ldots v_{i_{3}}\ldots v_{i_{4}}\ldots v_{i_{5}}\ldots v_{i_{6}}\ldots v_{i_{7}}$ and $T_{2}=v_{i_{4}}\ldots v_{i_{5}}\ldots v_{i_{6}}\ldots v_{i_{7}}\ldots v_{i_{8}}\ldots v_{i_{9}}\ldots v_{i_{10}}\ldots v_{i_{1}}$. Let $S=\{v_{i_{1}},v_{i_{4}},v_{i_{7}}\}$. We prove (iii) by consider the following two cases.

$\mathbf {Case~1}$ Two vertices of the set S can be colored the same. Without loss of generality, we assume that $c(v_{i_{4}})=c(v_{i_{7}})\ne c(v_{i_{1}})$. Denote $S_{1}=\{v_{i_{5}},v_{i_{6}},v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$. Since $c(v_{i_{4}})=c(v_{i_{7}})$, we know that at most four colors are assigned to $S_{1}$; obviously, $T_{2}$ is not a vertex-rainbow S-tree. Suppose $c(v_{i_{1}})=c(v_{i_{j}})$ with $8\le j\le 10$. If $c(v_{i_{5}})\ne c(v_{i_{6}})$, then we have $c(v_{i_{2}})=c(v_{i_{3}})$, or only one color of $\{v_{i_{2}},v_{i_{3}}\}$ is among the colors that are assigned to $\{v_{i_{5}},v_{i_{6}}\}$ and the another color of $\{v_{i_{2}},v_{i_{3}}\}$ is among the colors that are assigned to $\{v_{i_{8}},v_{i_{9}},v_{i_{10}}\}\setminus \{v_{i_{j}}\}$, or the two colors of $\{v_{i_{2}},v_{i_{3}}\}$ are among the colors that are assigned to $\{v_{i_{5}},v_{i_{6}}\}$, and so there is no vertex-rainbow S-tree. If $c(v_{i_{5}})=c(v_{i_{6}})$, then there are two colors are assigned to $\{v_{i_{2}},v_{i_{3}},v_{i_{8}},v_{i_{9}},v_{i_{10}}\}\setminus \{v_{i_{j}}\}$, and so there is no vertex-rainbow S-tree. Suppose $c(v_{i_{1}})=c(v_{i_{5}})$. If $c(v_{i_{6}})=c(v_{i_{j}})$ and $c(v_{i_{2}})=c(v_{i_{3}})$, where $8\le j\le 10$, then there is no vertex-rainbow S-tree. If $c(v_{i_{6}})=c(v_{i_{j}})$, where $8\le j\le 10$, then the colors that are assigned to $\{v_{i_{2}},v_{i_{3}}\}$ are among the colors that are assigned to $\{v_{i_{8}},v_{i_{9}},v_{i_{10}}\}\setminus \{v_{i_{j}}\}$, and so there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{6}},v_{i_{j}}\}$. If $c(v_{i_{6}})\ne c(v_{i_{j}})$, where $8\le j\le 10$, then there are two vertices of $\{v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$ having the same color and the color of $v_{i_{6}}$ is among the colors that are assigned to $\{v_{i_{2}},v_{i_{3}}\}$, and so there is no vertex-rainbow S-tree. Suppose $c(v_{i_{1}})=c(v_{i_{6}})$. If $c(v_{i_{5}})=c(v_{i_{8}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{5}},v_{i_{8}}\}$. If $c(v_{i_{5}})=c(v_{i_{9}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{4}},v_{i_{7}},v_{i_{10}}\}$. If $c(v_{i_{5}})=c(v_{i_{10}})$ and $c(v_{i_{2}})=c(v_{i_{8}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{2}},v_{i_{5}},v_{i_{8}}\}$. If $c(v_{i_{5}})=c(v_{i_{10}})$ and $c(v_{i_{2}})=c(v_{i_{9}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{1}},v_{i_{3}},v_{i_{8}}\}$. If $c(v_{i_{5}})=c(v_{i_{10}})$ and $c(v_{i_{2}})=c(v_{i_{3}})$, then there is no vertex-rainbow S-tree. If $c(v_{i_{5}})\ne c(v_{i_{j}})$, where $8\le j\le 10$, then there are two vertices of $\{v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$ having the same color, and the color of $v_{i_{5}}$ is among the colors that are assigned to $\{v_{i_{2}},v_{i_{3}}\}$, and so there is no vertex-rainbow S-tree. Suppose $c(v_{i_{1}})=c(v_{i_{2}})$ ($c(v_{i_{1}})=c(v_{i_{3}})$). We can check that there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{6}},v_{i_{10}}\}$ ($\{v_{i_{2}},v_{i_{4}},v_{i_{10}}\}$), a contradiction.

$\mathbf {Case~2}$ No vertex of S can be colored the same. Moreover, we have the following four subcases.

$\mathbf {Subcase~2.1}$ $T_{2}$ is vertex-rainbow, and $T_{1}$ is not vertex-rainbow. Note that at least one color of $\{v_{i_{2}},v_{i_{3}}\}$ is among the colors that are assigned to $\{v_{i_{5}},v_{i_{6}}\}$. Suppose $c(v_{i_{2}})=c(v_{i_{5}})$. Then, the colors that are assigned to S are among the colors that are assigned to $\{v_{i_{6}},v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$. If $c(v_{i_{2}})=c(v_{i_{5}})$ and $c(v_{i_{6}})=c(v_{i_{7}})$, then any tree connecting $\{v_{i_{2}},v_{i_{5}},v_{i_{8}}\}$ is not vertex-rainbow. If $c(v_{i_{2}})=c(v_{i_{5}})$ and $c(v_{i_{6}})=c(v_{i_{j}})$, where $8\le j\le 10$, then any tree connecting $\{v_{i_{1}},v_{i_{3}},v_{i_{6}}\}$ is not vertex-rainbow. Suppose $c(v_{i_{2}})=c(v_{i_{6}})$. Then, the colors are assigned to $\{v_{i_{1}},v_{i_{3}},v_{i_{4}},v_{i_{7}}\}$ are among the colors that are assigned to $\{v_{i_{5}},v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$, we know that one of vertices of $\{v_{i_{1}},v_{i_{3}},v_{i_{4}},v_{i_{7}}\}$ has the same color as the vertex $v_{i_{5}}$. If $c(v_{i_{2}})=c(v_{i_{6}}),c(v_{i_{1}})=c(v_{i_{5}})$ and $c(v_{i_{7}})=c(v_{i_{10}})$, then any tree connecting $\{v_{i_{2}},v_{i_{6}},v_{i_{9}}\}$ is not vertex-rainbow. If $c(v_{i_{2}})=c(v_{i_{6}}),c(v_{i_{1}})=c(v_{i_{5}})$ and $c(v_{i_{7}})=c(v_{i_{l}})$, where $8\le l\le 9$, then any tree connecting $\{v_{i_{2}},v_{i_{6}},v_{i_{10}}\}$ is not vertex-rainbow. If $c(v_{i_{2}})=c(v_{i_{6}})$ and $c(v_{i_{3}})=c(v_{i_{5}})$, then any tree connecting $\{v_{i_{2}},v_{i_{6}},v_{i_{9}}\}$ is not vertex-rainbow. If $c(v_{i_{2}})=c(v_{i_{6}})$ and $c(v_{i_{4}})=c(v_{i_{5}})$, then any tree connecting $\{v_{i_{2}},v_{i_{6}},v_{i_{9}}\}$ is not vertex-rainbow. If $c(v_{i_{2}})=c(v_{i_{6}})$ and $c(v_{i_{5}})=c(v_{i_{7}})$, then any tree connecting $\{v_{i_{2}},v_{i_{4}},v_{i_{8}}\}$ is not vertex-rainbow, a contradiction.

$\mathbf {Subcase~2.2}$ Both $T_{1}$ and $T_{2}$ are vertex-rainbow. Obviously, the colors that are assigned to $\{v_{i_{2}},v_{i_{3}}\}$ are among the colors that are assigned to $\{v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$, and the colors that are assigned to S are among the colors that are assigned to $\{v_{i_{5}},v_{i_{6}},v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$. For $c(v_{i_{1}})=c(v_{i_{10}})$, we know that the colors of $\{v_{i_{4}},v_{i_{7}}\}$ are same with the colors that are assigned to $\{v_{i_{5}},v_{i_{6}}\}$. Then, there is no vertex-rainbow tree connecting $\{v_{i_{2}},v_{i_{5}},v_{i_{9}}\}$. For $c(v_{i_{1}})=c(v_{i_{9}})$ ($c(v_{i_{1}})=c(v_{i_{8}})$), we have a similar argument with $c(v_{i_{1}})=c(v_{i_{10}})$. Then, there is no vertex-rainbow tree connecting $\{v_{i_{2}},v_{i_{8}},v_{i_{10}}\}$ ($\{v_{i_{1}},v_{i_{4}},v_{i_{8}}\}$). For $c(v_{i_{1}})=c(v_{i_{6}})$, we can find that one of vertices of $\{v_{i_{4}},v_{i_{7}}\}$ has the same color with the vertex $v_{i_{5}}$. If $c(v_{i_{1}})=c(v_{i_{6}}),c(v_{i_{2}})=c(v_{i_{10}})$ ($c(v_{i_{2}})=c(v_{i_{9}})$) and $c(v_{i_{4}})=c(v_{i_{5}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{6}},v_{i_{8}}\}$. If $c(v_{i_{1}})=c(v_{i_{6}}),c(v_{i_{2}})=c(v_{i_{10}})$ ($c(v_{i_{2}})=c(v_{i_{9}})$) and $c(v_{i_{7}})=c(v_{i_{5}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{6}},v_{i_{8}}\}$. If $c(v_{i_{1}})=c(v_{i_{6}}),c(v_{i_{2}})=c(v_{i_{8}})$ and $c(v_{i_{4}})=c(v_{i_{5}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{7}},v_{i_{10}}\}$. If $c(v_{i_{1}})=c(v_{i_{6}}),c(v_{i_{2}})=c(v_{i_{8}})$ and $c(v_{i_{7}})=c(v_{i_{5}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{1}},v _{i_{4}},v_{i_{8}}\}$. For $c(v_{i_{1}})=c(v_{i_{5}})$, we can find one of vertices of $\{v_{i_{4}},v_{i_{7}}\}$ has the same color with the vertex $v_{i_{6}}$. If $c(v_{i_{1}})=c(v_{i_{5}}),c(v_{i_{2}})=c(v_{i_{10}})$ ($c(v_{i_{2}})=c(v_{i_{9}})$) and $c(v_{i_{4}})=c(v_{i_{6}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{5}},v_{i_{8}}\}$. If $c(v_{i_{1}})=c(v_{i_{5}}),c(v_{i_{2}})=c(v_{i_{10}})$ ($c(v_{i_{2}})=c(v_{i_{9}})$) and $c(v_{i_{7}})=c(v_{i_{6}})$, then any tree connecting $\{v_{i_{3}},v_{i_{5}},v_{i_{8}}\}$ is not vertex-rainbow. If $c(v_{i_{1}})=c(v_{i_{5}}),c(v_{i_{2}})=c(v_{i_{8}})$ and $c(v_{i_{4}})=c(v_{i_{6}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{3}},v_{i_{7}},v_{i_{10}}\}$. If $c(v_{i_{1}})=c(v_{i_{5}}),c(v_{i_{2}})=c(v_{i_{8}})$ and $c(v_{i_{7}})=c(v_{i_{6}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{1}},v_{i_{4}},v_{i_{8}}\}$, a contradiction.

$\mathbf {Subcase~2.3}$ $T_{2}$ is not vertex-rainbow, and $T_{1}$ is vertex-rainbow. We have $c(v_{i_{2}})\ne c(v_{i_{3}})\ne c(v_{i_{5}})\ne c(v_{i_{6}})$, and there are two vertices of $\{v_{i_{8}},v_{i_{9}},v_{i_{10}}\}$ having the same color. Therefore. the colors that are assigned to S are among the colors that are assigned to $\{v_{i_{2}},v_{i_{3}},v_{i_{5}},v_{i_{6}}\}$. If $c(v_{i_{8}})=c(v_{i_{9}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{4}},v_{i_{7}},v_{i_{10}}\}$. If $c(v_{i_{9}})=c(v_{i_{10}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{1}},v_{i_{4}},v_{i_{8}}\}$. If $c(v_{i_{8}})=c(v_{i_{10}})$, then there is no vertex-rainbow tree connecting $\{v_{i_{1}},v_{i_{7}},v_{i_{9}}\}$, a contradiction.

$\mathbf {Subcase~2.4}$ Neither $T_{1}$ nor $T_{2}$ is vertex-rainbow. Consider the tree $T_{3}=v_{i_{7}}\ldots v_{i_{8}}\ldots v_{i_{9}} \ldots v_{i_{10}}\ldots v_{i_{1}}\ldots v_{i_{2}}\ldots v_{i_{3}}\ldots v_{i_{4}}$. Assume that $T_{3}$ is vertex-rainbow. Note that $T_{1}$ is not vertex-rainbow, and so an argument similar to the one used in the proof of Subcase 2.1 shows a contradiction.

Combining the above three claims, we have $rvx_{3}(C_{n})\ge n-4$, and hence $rvx_{3}(C_{n})=n-4$.$\square$

The girth of a graph G with some cycles, denoted by g(G) or simply g, is the length of the smallest cycle in G. Let $N_{k}=\{1,2,\ldots ,k\}$ for each positive integer k, and $d(v,H)=min\{d_{G}(v,x):x\in V(H)\}$, where H is a subgraph of a connected graph G and $v\in V(G)\backslash V(H)$. Now we determine the 3-vertex-rainbow index of all unicyclic graphs that are not cycles.

Theorem 2.5

If G is a unicyclic graph of order $n\ge 4$ and $3\le g(G)\le 4$ that is not a cycle, then $rvx_{3}(G)\le n-3$, and the bound is tight.

Proof

Let $G^{'}$ be a subgraph of G , where $V(G^{'})=\{v_{1},v_{2},v_{3},v_{4},\ldots ,v_{t}\}$, $E(G^{'})=\{v_{1}v_{2},v_{2}v_{3}, v_{1}v_{3},v_{i}v_{i+1}|3\le i\le t-1\}$ for $g(G)=3$, or $E(G^{'})=\{v_{1}v_{2},v_{2}v_{3},v_{3}v_{4},v_{1}v_{4},v_{i}v_{i+1}|4\le i\le t-1\}$ for $g(G)=4$, and $d_{G}(v_{t})=1$. Let $V(G)\setminus V(G^{'})=\{v_{t+1},v_{t+2},\ldots ,v_{n}\}$. Suppose that there are $h_{1}+1$ leaves in G, denote $h=h_{1}+1$ (May be $h_{1}=0$). Assign a vertex-coloring c to $G^{'}$ as follows: $c(v_{i})=i-2$ for $4\le i\le t-1$ and other vertices with color 1. We can find that $G^{'}$ is vertex-rainbow 3-tree connected with $3\le g(G)\le 4$, thus $rvx_{3}(G^{'})\le t-3$. For $g(G)=3$, we know that $G^{'}$ contains $t-3$ cut vertices. Then, by Observation 2.3, $rvx_{3}(G^{'})\ge t-3$. Therefore, $rvx_{3}(G^{'})=t-3$. For $g(G)=4$, assume that $rvx_{3}(G^{'})\le t-4$, by Observation 2.3, we assign $t-4$ colors to the cut vertices of $G^{'}$. Then, the colors that are assigned to $\{v_{1},v_{2},v_{3},v_{t}\}$ are among the colors that are assigned to $\{v_{4},v_{5},\ldots ,v_{t-1}\}$. If $c(v_{1})=c(v_{3})=c(v_{4})$, then there is no vertex-rainbow tree connecting $\{v_{2},v_{t-1},v_{t}\}$. If $c(v_{3})=c(v_{4})\ne c(v_{1})$ and $c(v_{1})\ne c(v_{t-1})$, then there is no vertex-rainbow tree connecting $\{v_{2},v_{t-1},v_{t}\}$. If $c(v_{3})=c(v_{4})\ne c(v_{1})$ and $c(v_{1})=c(v_{t-1})$, then there is no vertex-rainbow tree connecting $\{v_{2},v_{t-2},v_{t}\}$. If $c(v_{1})=c(v_{4})\ne c(v_{3})$, then we draw a same conclusion with $c(v_{3})=c(v_{4})\ne c(v_{1})$. If $c(v_{1})\ne c(v_{4})$ and $c(v_{3})\ne c(v_{4})$, then there is no vertex-rainbow tree connecting $\{v_{2},v_{4},v_{t}\}$. Therefore, $rvx_{3}(G^{'})\ge t-3$. Hence, $rvx_{3}(G^{'})=t-3$. Next, we assign color 1 to the leaves of G, and colors $t-2,t-1,t,t+1,\ldots ,n-3-h_{1}$ to the cut vertices in G but not in $G^{'}$.

Suppose $g(G)=3$. Let $d(v_{1})=d(v_{2})=2$ and $d(v_{3})\ge 3$. Then, by checking the given 3-vertex-rainbow coloring, we have $rvx_{3}(G)=n-3-h_{1}=n-2-h$, where $h\ge 1$. Let $d(v_{1})=2$ and $d(v_{2})\ge 3$. Thus, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{2})$, we assign a new color $n-2-h_{1}$ to the cut vertex $v_{2}$ instead of the color 1; otherwise, any tree connecting $\{v_{4},v_{5},v_{m}\}$ is not vertex-rainbow, and so $rvx_{3}(G)=n-2-h_{1}=n-1-h$, where $h\ge 2$. Let $d(v_{1})\ge 3$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{1})$, and we assign a new color $n-2-h_{1}$ to the cut vertex $v_{1}$ instead of the color 1; otherwise, any tree connecting $\{v_{4},v_{5},v_{m}\}$ is not vertex-rainbow. Assume that there exists another leaf $v_{m_{1}}$ satisfying $d(v_{m_{1}},C)=d(v_{m_{1}},v_{j})$, where $2\le j\le 3$. Then, we must assign a new color $n-1-h_{2}$ to the cut vertex $v_{j}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{4}\}$. Therefore, $rvx_{3}(G)=n-1-h_{2}=n-h$ with $h\ge 3$. If $h=1$, then $G=G^{'}$, and so $rvx_{3}(G)=n-3$. Finally, we have $rvx_{3}(G)\le n-3$, and $G=G^{'}$ is a tight example.

Suppose $g(G)=4$. Let $d(v_{1})=d(v_{2})=d(v_{3})=2$ and $d(v_{4})\ge 3$. Then, by checking the given 3-vertex-rainbow coloring, we have $rvx_{3}(G)=n-3-h_{1}=n-2-h$, where $h\ge 1$. Let $d(v_{1})=d(v_{2})=2$ and $d(v_{3})\ge 3$. Then, $rvx_{3}(G)=n-3-h_{1}=n-2-h$ by checking the given 3-vertex-rainbow coloring, where $h\ge 1$. Let $d(v_{1})=2$ and $d(v_{2})\ge 3$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{2})$, and so we must assign a new color $n-2-h_{1}$ to the cut vertex $v_{2}$ instead of the color 1, otherwise, any tree connecting $\{v_{4},v_{5},v_{m}\}$ is not vertex-rainbow. Thus, $rvx_{3}(G)=n-2-h_{1}=n-1-h$, where $h\ge 2$. Let $d(v_{1})\ge 3$. If $d(v_{2})=d(v_{3})=1$, then $rvx_{3}(G)=n-3-h_{1}=n-2-h$ with $h\ge 2$. If $d(v_{j})\ge 3$, where $2\le j\le 3$, then there exist two leaves $v_{m}$ and $v_{m_{1}}$ satisfying $d(v_{m},C)=d(v_{m},v_{1})$ and $d(v_{m_{1}},C)=d(v_{m_{1}},v_{j})$. Note that we must color $v_{1}$ with a new color $n-2-h_{1}$ instead of color 1; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{t}\}$, and so $rvx_{3}(G)=n-2-h_{1}=n-1-h$ with $h\ge 3$. If $d(v_{2})=d(v_{3})\ge 3$, then there exist three leaves $v_{m},v_{m_{1}}$ and $v_{m_{2}}$ satisfying $d(v_{m},C)=d(v_{m},v_{1}),d(v_{m_{1}},C)=d(v_{m_{1}},v_{2})$ and $d(v_{m_{2}},C)=d(v_{m_{2}},v_{3})$. In order to ensure there exists a vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{m_{2}}\}$, we assign the new colors $n-2-h_{1}$ and $n-1-h_{1}$ to $v_{1}$ and $v_{2}$, respectively, and so $rvx_{3}(G)=n-1-h_{1}=n-h$, where $h\ge 4$. For $h=1$, we have $rvx_{3}(G)=n-3$. Finally, $rvx_{3}(G)\le n-3$, and $G=G^{'}$ is a tight example. $\square$

Theorem 2.6

If G is a unicyclic graph of order $n\ge 6$ and girth 5 that is not a cycle, then $rvx_{3}(G)\le n-4$, and the bound is tight.

Proof

Let $G^{'}$ be a subgraph of G , where $V(G^{'})=\{v_{1},v_{2},\ldots ,v_{t}\}$, $E(G^{'})=\{v_{1}v_{2},v_{2}v_{3},v_{3}v_{4}, v_{4}v_{5},v_{1}v_{5},v_{i}v_{i+1}|5\le i\le t-1\}$ and $d_{G}(v_{t})=1$. Let $V(G)\setminus V(G^{'})=\{v_{t+1},v_{t+2},\ldots ,v_{n}\}$. Suppose that there are $h_{1}+1$ leaves in G, and denote $h=h_{1}+1$. Assign a vertex-coloring c to $G^{'}$ as follows: $c(v_{i})=i-3$ for $5\le i\le t-1$, and other vertices with color 1. By checking the given vertex-coloring, we have $rvx_{3}(G^{'})\le t-4$. To the contrary, assume that $rvx_{3}(G^{'})\le t-5$. Let $X_{1}=\{v_{1},v_{2},v_{3},v_{4},v_{t}\}$ and $X_{2}=\{v_{5},v_{6},\ldots ,v_{t-1}\}$, by Observation 2.3, we have the colors that are assigned to $X_{1}$ are among the colors that are assigned to $X_{2}$. Then, there is no vertex-rainbow tree connecting $\{v_{1},v_{3},v_{t}\}$, and so $rvx_{3}(G^{'})\ge t-4$. Hence, $rvx_{3}(G^{'})=t-4$. Moreover, an argument similar to the one used in the proof of Theorem 2.5 shows that $rvx_{3}(G)\le n-4$. Finally, $rvx_{3}(G)\le n-4$, and $G=G^{'}$ is a tight example. $\square$

Theorem 2.7

If G is a unicyclic graph of order $n\ge 7$ and girth at least 6 that is not a cycle, then $rvx_{3}(G)\le n-5$, and the bound is tight.

Proof

Let $G^{'}$ be a subgraph of G with $V(G^{'})=\{v_{1},v_{2},\ldots ,v_{g},v_{g+1},\ldots ,v_{t}\}$ and $E(G^{'})=\{v_{1}v_{g},v_{i}v_{i+1}|1\le i\le t-1\}$, where $g\ge 6$ and $d_{G}(v_{t})=1$. Let $V(G)\setminus V(G^{'})=\{v_{t+1},v_{t+2},\ldots , v_{n}\}$. Suppose that there are $h_{1}+1$ leaves in G and $h=h_{1}+1$. Assign a vertex-coloring c to $G^{'}$ as follows: $c(v_{i})=1$ for $i=1,4,t$, $c(v_{i})=2$ for $2\le i\le 3$ and $c(v_{i})=i-4$ for $5\le i\le t-1$. We can check that $G^{'}$ is vertex-rainbow 3-tree connected with the vertex-coloring c, and thus $rvx_{3}(G^{'})\le t-5$. To the contrary, assume that $rvx_{3}(G^{'})\le t-6$. Then, there exists a 3-vertex-rainbow coloring c of $G^{'}$ using colors in $N_{t-6}$. Let $A_{1}$ be the set of colors assigned to the g vertices of the set $S_{1}=\{v_{1},v_{2},\ldots ,v_{g-1},v_{t}\}$ and $A_{2}$ be the set of colors assigned to the $t-g$ cut vertices of the set $S_{2}=\{v_{g},v_{g+1},\ldots ,v_{t-1}\}$. Then, $A_{1}\cup A_{2}=N_{t-6}$. Furthermore, $|A_{2}|=t-g$ by Observation 2.3. We may therefore assume that $A_{2}=N_{t-g}$.

If $g=6$, then $A_{2}=N_{t-6}=A_{1}\cup A_{2}$, and so $A_{1}\subseteq A_{2}$. Obviously, any tree connecting $\{v_{2},v_{4},v_{t}\}$ is not vertex-rainbow. If $g\ge 7$, then there are $g-6$ colors in $A_{1}$ different from $A_{2}$. Let $S_{3}=\{v_{1},v_{2},\ldots ,v_{g-1}\}$ and $A_{3}$ be the set of colors assigned to $S_{3}$. We consider the following two cases.

$\mathbf {Case~1}$ $c(v_{i})\ne c(v_{t})$, where $1\le i\le g-1$. Then, there are $g-7$ colors in $A_{3}$ different from $A_{2}$, and $A_{3}=A_{1}\setminus c(v_{t})$. Let $S_{3}^{'}\subseteq S_{3}$ and $|S_{3}^{'}|=g-7$. Then, we assign $g-7$ colors in $A_{3}$ that are different from $A_{2}$ to the vertices set $S_{3}^{'}$. Suppose $A_{3}\cap A_{2}=\emptyset$. Then $A_{3}=g-7$, and so $g-6$ colors are assigned to $C_{g}$, which contradicts $rvx_{3}(C_{g})=g-4$; Suppose $A_{3}\cap A_{2}\ne \emptyset$. According to $rvx_{3}(C_{g})=g-4$, we have that at least two colors of $A_{3}$ are among the colors that are assigned to $\{v_{g+1},v_{g+2},\ldots ,v_{t-1}\}$. Then, $c(v_{p})=c(v_{j})$, where $1\le p\le g-1$ and $g+1\le j\le t-1$. Furthermore, there exist four vertices of $S_{3}\setminus S_{3}^{'}\cup \{v_{p}\}$ satisfying the colors that are assigned to them are among the colors that are assigned to the other vertices of $G^{'}$. If $p=1$, then there is no vertex-rainbow tree connecting $\{v_{2},v_{3},v_{t}\}$; If $2\le p\le g-1$, then any tree connecting $\{v_{p-1},v_{p+1},v_{t}\}$ is not vertex-rainbow.

$\mathbf {Case~2}$ $c(v_{i})=c(v_{t})$, where $1\le i\le g-1$. Then, there are $g-6$ colors of $A_{3}$ that are not contained in $A_{2}$ and $A_{3}=A_{1}$. Let $S_{3}^{'}\subseteq S_{3}$ and $|S_{3}^{'}|=g-6$. Then, we assign $g-6$ colors in $A_{3}$ that are different from $A_{2}$ to the vertices set $S_{3}^{'}$. Suppose $A_{3}\cap A_{2}=\emptyset$. Then, $|A_{3}|=g-6$, and so $g-5$ colors are assigned to $C_{g}$, which contradicts $rvx_{3}(C_{g})=g-4$. Suppose $A_{3}\cap A_{2}\ne \emptyset$. Since $rvx_{3}(C_{g})=g-4$, we have at least one color of $A_{3}$ is among the colors that are assigned to $\{v_{g+1},v_{g+2},\ldots ,v_{t-1}\}$. Then, $c(v_{p})=c(v_{j})$, where $1\le p\le g-1,g+1\le j\le t-1$. Moreover, an argument similar to the one used in the proof of Case 1 shows that if $p=1$, then any tree connecting $\{v_{2},v_{3},v_{t}\}$ is not vertex-rainbow, and if $2\le p\le g-1$, then there is no vertex-rainbow tree connecting $\{v_{p-1},v_{p+1},v_{t}\}$. Finally, $rvx_{3}(G^{'})\ge t-5$. Therefore, $rvx_{3}(G^{'})=t-5$.

Next, we assign the color 1 to the leaves of G, the colors $t-4,t-3,\ldots ,n-5-h_{1}$ to the cut vertices in G but not in $G^{'}$. Let $d(v_{i})=2$, where $1\le i\le 6$. Then, $rvx_{3}(G)=n-5-h_{1}=n-4-h$ by checking the given 3-vertex-rainbow coloring, where $h\ge 1$. Let $d(v_{i})=2$ and $d(v_{6})\ge 3$, where $1\le i\le 5$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{6})$. Note that we must assign a new color $n-4-h_{1}$ to $v_{3}$ or $v_{4}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{2},v_{4}\}$ or $\{v_{m},v_{3},v_{7}\}$, and so $rvx_{3}(G)=n-4-h_{1}=n-3-h$, where $h\ge 2$. Let $d(v_{i})=2$ and $d(v_{5})\ge 3$, where $1\le i\le 4$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{5})$. Note that we must assign a new color $n-4-h_{1}$ to $v_{1}$ or $v_{4}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{2},v_{7}\}$ or $\{v_{m},v_{3},v_{7}\}$, and so $rvx_{3}(G)=n-4-h_{1}=n-3-h$, where $h\ge 2$. Let $d(v_{i})=2$ and $d(v_{4})\ge 3$, where $1\le i\le 3$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{4})$. Note that we must assign a new color $n-4-h_{1}$ to $v_{4}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{2},v_{7}\}$. Suppose that there exists another leaf $v_{m_{1}}$ of G satisfying $d(v_{m_{1}},C)=d(v_{m_{1}},v_{6})$. We must assign a new color $n-3-h_{1}$ to $v_{6}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{2}\}$, and so $rvx_{3}(G)=n-3-h_{1}=n-2-h$, where $h\ge 3$. Let $d(v_{1})=d(v_{2})=2$ and $d(v_{3})\ge 3$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{3})$. Note that we must assign the new color $n-4-h_{1}$ to $v_{3}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{1},v_{5}\}$. Suppose that there exists another leaf $v_{m_{1}}$ of G satisfying $d(v_{m_{1}},C)=d(v_{m_{1}},v_{5})$. Then, assign a new color $n-3-h_{1}$ to $v_{5}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{1}\}$, and so $rvx_{3}(G)=n-3-h_{1}=n-2-h$, where $h\ge 3$. Let $d(v_{1})=2$ and $d(v_{2})\ge 3$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{2})$. If $d(v_{4})=d(v_{5})=d(v_{6})=2$, then $c(v_{2})=n-4-h_{1}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{1},v_{4}\}$, and so $rvx_{3}(G)=n-4-h_{1}=n-3-h$, where $h\ge 2$. If $d(v_{6})=2$ and $d(v_{i})\ge 3$, where $4\le i\le 5$, then $c(v_{2})=n-4-h_{1}$ and $c(v_{i})=n-3-h_{1}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{7}\}$, and so $rvx_{3}(G)=n-3-h_{1}=n-2-h$, where $d(v_{m_{1}},C)=d(v_{m_{1}},v_{i})$ and $h\ge 3$. If $d(v_{6})\ge 3$ and $d(v_{3})=d(v_{4})=d(v_{5})=2$, then $c(v_{2})=n-4-h_{1}$ and $c(v_{3})=n-3-h_{1}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{4}\}$, and so $rvx_{3}(G)=n-3-h_{1}=n-2-h$, where $d(v_{m_{1}},C)=d(v_{m_{1}},v_{6})$ and $h\ge 3$. If $d(v_{6})\ge 3$ and $d(v_{4})\ge 3$, then $c(v_{2})=n-4-h_{1},c(v_{3})=n-3-h_{1}$ and $c(v_{4})=n-2-h_{1}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{m_{1}},v_{m_{2}}\}$, and so $rvx_{3}(G)=n-2-h_{1}=n-1-h$, where $d(v_{m_{1}},C)=d(v_{m_{1}},v_{4}),d(v_{m_{2}},C)=d(v_{m_{2}},v_{6})$ and $h\ge 4$. Let $d(v_{1})\ge 3$. Then, there exists a leaf $v_{m}$ of G satisfying $d(v_{m},C)=d(v_{m},v_{1})$. Note that we must assign the color $n-4-h_{1}$ to $v_{4}$ or $v_{5}$; otherwise, there is no vertex-rainbow tree connecting $\{v_{m},v_{3},v_{5}\}$ or $\{v_{m},v_{4},v_{6}\}$, and so $rvx_{3}(G)=n-4-h_{1}=n-3-h$, where $h\ge 2$. Suppose that there exist other leaves $v_{m_{1}},v_{m_{2}},v_{m_{3}},v_{m_{4}}$ and $v_{m_{5}}$ satisfying $d(v_{m_{i}},C)=d(v_{m_{i}},v_{i+1})$, $1\le i\le 5$. In order to ensure that there exists a vertex-rainbow tree connecting any three vertices of $\{v_{m},v_{m_{1}},v_{m_{2}},v_{m_{3}},v_{m_{4}},v_{m_{5}}\}$, we assign some new colors $n-4-h_{1},n-3-h_{1},n-2-h_{1}$ and $n-1-h_{1}$ to $v_{3},v_{4},v_{5}$ and $v_{6}$, respectively. Therefore, $rvx_{3}(G)=n-1-h_{1}=n-h$, where $h\ge 7$. For $h=1$, we have $rvx_{3}(G)=rvx_{3}(G^{'})=n-5$. Finally, $rvx_{3}(G)\le n-5$, and $G=G^{'}$ is a tight example. $\square$

3 The 3-Vertex-Rainbow Index of Complementary Graphs

Let G be a simple graph with order n. The complement graph $\overline{G}$ of G is the simple graph whose vertex set is V(G) and whose edges are the pairs of nonadjacent vertices of G. If $\overline{G}$ is an disconnected graph with $t\ge 2$ connected components, then G contains a complete t-partite spanning subgraph. We immediately draw the following conclusion.

Proposition 3.1

Let $\overline{G}$ be a graph with $t\ge 2$ connected components $\overline{G_{i}}$ and $n_{i}'=n(\overline{G_{i}})$ $(1\le i\le t)$. Then, $rvx_{3}(G)\le rvx_{3}(K_{n_{1}'},\ldots ,_{n_{t}'})$.

Now we investigate the 3-vertex-rainbow index of a connected graph G by use of its complement graph $\overline{G}$ with diameter at least 3.

Theorem 3.2

Let G be a connected graph of order n.

• (i) If $\overline{G}$ is connected and $diam(\overline{G})\ge 4$, then $rvx_{3}(G)=1$;

• (ii) If $\overline{G}$ is connected and $diam(\overline{G})=3$, then $1\le rvx_{3}(G)\le 2$, and the bounds are tight;

• (iii) If $\overline{G}$ is disconnected, then $0\le rvx_{3}(G)\le 1$, and the bounds are tight.

Proof

Choose a vertex x in $\overline{G}$, where x satisfies $\mathrm{ecc}_{\overline{G}}(x)=\mathrm{diam}(\overline{G})=d$. Denote $N_{\overline{G}}^{i}(x)=\{v:d(x,v)=i\}$ for $0\le i\le d$, especially, $N_{\overline{G}}^{0}(x)=\{x\}$ and $N_{\overline{G}}^{1}(x)=N_{\overline{G}}(x)$. Then, $\cup _{0\le i\le d}N_{\overline{G}}^{i}(x)$ is a vertex partition of $V(\overline{G})$. Let $X=\cup _{i\equiv 0(\mathrm{mod}~2)}N_{\overline{G}}^{i}(x)$ and $Y=\cup _{i\equiv 1(\mathrm{mod}~2)} N_{\overline{G}}^{i}(x)$.

(i) $\overline{G}$ is connected and $d\ge 4$. Then, G[X] (G[Y]) contains a spanning complete $k_{1}$-partite subgraph (complete $k_{2}$-partite subgraph) by the definition of complement graphs, where $k_{1}=\lceil {\frac{d+1}{2}}\rceil$ ($k_{2}=\lceil {\frac{d}{2}}\rceil$). Now, we show a vertex-coloring c of G as follows: $c(z)=1$ for $z\in G$. Let $S=\{u,v,w\}$, where u, v and w are any three different vertices of G.

Suppose $u,v,w\in N_{\overline{G}}^{i}(x)$, where i is even. Then, T is a vertex-rainbow S-tree with $E(T)=\{ux,vx,wx\}$. Suppose $u,v\in N_{\overline{G}}^{i}(x)$ and $w\in N_{\overline{G}}^{j}(x)$, where i, j are even and $i\ne j$. Then, T is a vertex-rainbow S-tree with $E(T)=\{uw,vw\}$. Suppose $u\in N_{\overline{G}}^{i}(x),v\in N_{\overline{G}}^{j}(x)$ and $w\in N_{\overline{G}}^{r}(x)$, where i, j and r are even and $i\ne j\ne r$. Then, T is a vertex-rainbow S-tree with $E(T)=\{uv,uw\}$. Suppose $u,v\in N_{\overline{G}}^{i}(x)$ and $w\in Y$, where i is even. Then, one of the following two cases holds. (1) $uw,vw\in E(G)$; (2) $uy,vy,wy\in E(G)$, where $y\in N_{\overline{G}}^{j}(x)$, j is even and $i\ne j$. For (1), there is a vertex-rainbow S-tree T with $E(T)=\{uw,vw\}$. For (2), there is a vertex-rainbow S-tree T with $E(T)=\{uy,vy,wy\}$. Suppose $u\in N_{\overline{G}}^{i}(x),v\in N_{\overline{G}}^{j}(x)$ and $w\in N_{\overline{G}}^{r}(x)$, where i, j are even and r is odd and $i\ne j$. Then, either $uv,vw\in E(G)$ or $uy,vy,wy\in E(G)$, where $y\in N_{\overline{G}}^{q}(x)$, q is even and $i\ne j\ne q$. If $uv,vw\in E(G)$, then T is a vertex-rainbow S-tree with $E(T)=\{uv,vw\}$. If $uy,vy,wy\in E(G)$, then T is a vertex-rainbow S-tree with $E(T)=\{uy,vy,wy\}$. Suppose $u\in X$ and $v,w\in Y$ or $u,v,w\in Y$. Then, a similar argument as above shows that we can find a vertex-rainbow S-tree. Therefore, $rvx_{3}(G)\le 1$.

Next, we prove $rvx_{3}(G)\ge 1$. Let $u\in N_{\overline{G}}^{d-2}(x),v\in N_{\overline{G}}^{d-1}(x)$ and $w\in N_{\overline{G}}^{d}(x)$. Then, $uv,vw\in E(\overline{G})$ and $uw\not \in E(\overline{G})$. It follows that $uv,vw\not \in E(G)$ and $uw\in E(G)$, and so $rvx_{3}(G)\ge 1$. Hence, $rvx_{3}(G)=1$.

(ii) $\overline{G}$ is connected and $d=3$. According to the definition of complement graphs, we know that G[X] (G[Y]) contains a spanning complete 2-partite subgraph. Now, we give the graph G a vertex-coloring c as follows: $c(z_{1})=1$ for $z_{1}\in X$ and $c(z_{2})=2$ for $z_{2}\in Y$. Denote $S=\{u,v,w\}$, where u, v and w are any three different vertices of G.

Assume that $u,v,w\in N_{\overline{G}}^{2}(x)$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{ux,vx,wx\}$. Assume that $u,v\in N_{\overline{G}}^{2}(x)$ and $w=x\in N_{\overline{G}}^{0}(x)$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{uw,vw\}$. Assume that $u,v\in N_{\overline{G}}^{2}(x)$ and $w\in N_{\overline{G}}(x)$. Then, there are two vertices $x\in N_{\overline{G}}^{0}(x)$ and $y\in N_{\overline{G}}^{3}(x)$ such that $xu,xv,xy,yw\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{xu,xv,xy,yw\}$. Assume that $u,v\in N_{\overline{G}}^{2}(x)$ and $w\in N_{\overline{G}}^{3}(x)$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{ux,vx,wx\}$. Assume that $u\in N_{\overline{G}}^{2}(x),v \in N_{G}^{0}(x)$ and $w\in N_{\overline{G}}(x)$. Then, there is a vertex $y\in N_{\overline{G}}^{3}(x)$ such that $vu,yv,yw\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{vu,yv,yw\}$. Assume that $u\in N_{\overline{G}}^{2}(x),v \in N_{G}^{0}(x)$ and $w\in N_{\overline{G}}^{3}(x)$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{vu,vw\}$. Assume that $u,v\in Y$ and $w=x\in N_{\overline{G}}^{0}(x)$. If $u,v\in N_{\overline{G}}^{3}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{wu,wv\}$; If $u,v\in N_{\overline{G}}(x)$, then there is a vertex $y\in N_{\overline{G}}^{3}(x)$ such that $yu,yv,wy\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{uy,vy,wy\}$; If $u\in N_{\overline{G}}^{3}(x)$ and $v\in N_{\overline{G}}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{uw,uv\}$. Assume that $u,v\in Y$ and $w\in N_{\overline{G}}^{2}(x)$. If $u,v\in N_{\overline{G}}^{1}(x)$, then there are two vertices $y\in N_{\overline{G}}^{3}(x)$ and $x\in N_{\overline{G}}^{0}(x)$ satisfying $xw,xy,yu,yv\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{xw,xy,yu,yv\}$; If $u,v\in N_{\overline{G}}^{3}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xv,xu,xw\}$; If $u\in N_{\overline{G}}^{1}(x)$ and $v\in N_{\overline{G}}^{3}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xv,xw,uv\}$. Assume that $u,v,w\in Y$. If $u,v,w\in N_{\overline{G}}^{1}(x)$ ($u,v,w\in N_{\overline{G}}^{3}(x)$), then there is a vertex $y\in N_{\overline{G}}^{3}(x)$ ($y\in N_{\overline{G}}^{1}(x)$) satisfying $uy,vy,wy\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{uy,vy,wy\}$; If $u,v\in N_{\overline{G}}^{1}(x)$ ($u,v\in N_{\overline{G}}^{3}(x)$) and $w\in N_{\overline{G}}^{3}(x)$ ($w\in N_{\overline{G}}^{1}(x)$), then the tree T connecting S is vertex-rainbow, where $V(T)=\{{u,v,w}\}$ and $E(T)=\{uw,vw\}$. From what has been discussed above, we get that $rvx_{3}(G)\le 2$.

Next, we show $rvx_{3}(G)\ge 1$. Let $u\in N_{\overline{G}}(x),v\in N_{\overline{G}}^{2}(x)$ and $w\in N_{\overline{G}}^{3}(x)$. Then, $uv,vw\in E(\overline{G})$ and $uw\not \in E(\overline{G})$. It follows that $uv,vw\not \in E(G)$ and $uw\in E(\overline{G})$, and so $rvx_{3}(G)\ge 1$. Hence $1\le rvx_{3}(G)\le 2$.

$\mathbf {Tight~Example~1}$. Let $\overline{G}$ be a connected graph of order n with $\mathrm{diam}(\overline{G})=3$. We can prove that $rvx_{3}(G)=1$.

Pick a vertex x of $\overline{G}$ that satisfies $\mathrm{ecc}_{\overline{G}}(x)=\mathrm{diam}(\overline{G})=3$. Denote $N_{\overline{G}}^{0}(x)=\{x\},N_{\overline{G}}(x)=\{y_{1},y_{2}\}, N_{\overline{G}}^{2}(x)=\{u_{1},u_{2}\},N_{\overline{G}}^{3}(x)=\{v_{1},v_{2}, \ldots ,v_{n-5}\}$ and $E(\overline{G})=\{xy_{1},xy_{2},u_{1}y_{1},u_{2}y_{2},u_{1}u_{2}, u_{1}v_{i},u_{2}v_{i}|1\le i\le n-5\}$. Then, $V(G)=\{x,y_{1},y_{2},u_{1},u_{2},v_{1},v_{2},\ldots ,v_{n-5}\}$ and $E(G)=\{y_{1}y_{2},u_{1}y_{2},u_{2}y_{1},xu_{1},xu_{2}, xv_{i},y_{1}v_{i},y_{2}v_{i}, v_{i}v_{j}|1\le i,j\le n-5\}$. Since the tree connecting $\{u_{1},u_{2},y_{1}\}$ has at least three edges, we have $rvx_{3}(G)\ge 1$. Now we only need to prove $rvx_{3}(G)\le 1$.

Assign color 1 to all vertices of G. Suppose $S=\{x,u_{1},u_{2}\}$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{1},xu_{2}\}$. Suppose $S=\{u_{1},u_{2},v_{i}\}$, where $1\le i\le n-5$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{1},xu_{2},xv_{i}\}$. Suppose $S=\{u_{1},u_{2},y_{j}\}$, where $1\le j\le 2$. If $j=1$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{1},xu_{2},u_{2}y_{j}\}$; If $j=2$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{1},xu_{2},u_{1}y_{j}\}$. Suppose $S=\{x,u_{j},v_{i}\}$, where $1\le i\le n-5$, $1\le j\le 2$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{j},xv_{i}\}$. Suppose $S=\{x,u_{1},y_{j}\}$, where $1\le j\le 2$. If $j=1$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{1},xu_{2},u_{2}y_{j}\}$; If $j=2$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{1},u_{1}y_{j}\}$. Suppose $S=\{x,u_{2},y_{j}\}$, where $1\le j\le 2$. Then, we have a similar argument with $S=\{x,u_{1},y_{j}\}$. Suppose $S=\{x,u,v\}$, where $u,v\in N_{\overline{G}}(x)\cup N_{\overline{G}}^{3}(x)$. If $u,v\in N_{\overline{G}}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xv_{1},uv_{1},vv_{1}\}$. If $u,v\in N_{\overline{G}}^{3}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xu,xv\}$. If $u\in N_{\overline{G}}(x)$ and $v\in N_{\overline{G}}^{3}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xv,uv\}$. Suppose $S=\{u_{1},u,v\}$, where $u,v\in N_{\overline{G}}(x)\cup N_{\overline{G}}^{3}(x)$. If $u,v\in N_{\overline{G}}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{u_{1}u,uv\}$. If $u,v\in N_{\overline{G}}^{3}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{u_{1}y_{2},uv,uy_{2}\}$. If $u\in N_{\overline{G}}(x)$ and $v\in N_{\overline{G}}^{3}(x)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{xu_{1},xv,uv\}$. Suppose $S=\{u_{2},u,v\}$, where $u,v\in N_{\overline{G}}(x)\cup N_{\overline{G}}^{3}(x)$. Then, we have a similar argument with $S=\{u_{1},u,v\}$. Suppose $S=\{u,v,w\}$, where $u,v,w\in N_{\overline{G}}(x)\cup N_{\overline{G}}^{3}(x)$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{uv,wu\}$. Therefore, $rvx_{3}(G)\le 1$.

$\mathbf {Tight~Example~2}$ Let $\overline{G}$ be a connected graph of order n with $\mathrm{diam}(\overline{G})=3$. We can prove that $rvx_{3}(G)=2$.

Pick a vertex x of $\overline{G}$ such that $\mathrm{ecc}_{\overline{G}}(x)=\mathrm{diam}(\overline{G})=3$. Suppose that $N_{\overline{G}}^{0}(x)=\{x\},N_{\overline{G}}^{1}(x)=N_{\overline{G}}(x)=\{y_{1},y_{2}, \ldots ,y_{n-3}\},N_{\overline{G}}^{2}(x)=\{u_{1}\},N_{\overline{G}}^{3}(x)=\{v_{1}\}$ and $E(\overline{G})=\{xy_{i},u_{1}y_{i},u_{1}v_{1}|1\le i\le n-3\}$. Then, $V(G)=\{x,u_{1},v_{1},y_{i}|1\le i\le n-3\}$ and $E(G)=\{xu_{1},xv_{1},v_{1}y_{i},y_{i}y_{j}|1 \le i, j\le n-3\}$. Since the tree T connecting $S=\{u_{1},y_{1},y_{2}\}$ has at least four edges and $V(T)\setminus S=\{x,v_{1}\}$, we have $rvx_{3}(G)\ge 2$. Now we only need to prove $rvx_{3}(G)\le 2$.

Define a vertex-coloring c of G as follows: $c(x)=c(u_{1})=1,c(v_{1})=c(y_{i})=2$, where $1\le i\le n-3$. Let $S=\{x,u_{1},v_{1}\}$. Then, T satisfying $E(T)=\{xu_{1},xv_{1}\}$ is a vertex-rainbow S-tree. Let $S=\{x,u_{1},y_{i}\}$. Then, T satisfying $E(T)=\{xu_{1},xv_{1},v_{1}y_{i}\}$ is a vertex-rainbow S-tree. Let $S=\{x,v_{1},y_{i}\}$. Then, T satisfying $E(T)=\{xu_{1},xv_{1},v_{1}y_{i}\}$ is a vertex-rainbow S-tree. Let $S=\{x,y_{i},y_{j}\}$. Then, T satisfying $E(T)=\{xv_{1},v_{1}y_{i},y_{i}y_{j}\}$ is a vertex-rainbow S-tree. Let $S=\{u_{1},v_{1},y_{i}\}$. Then, T satisfying $E(T)=\{xu_{1},xv_{1},v_{1}y_{i}\}$ is a vertex-rainbow S-tree. Let $S=\{u_{1},y_{i},y_{j}\}$. Then, T satisfying $E(T)=\{xu_{1},xv_{1},v_{1}y_{i},y_{i}y_{j}\}$ is a vertex-rainbow S-tree. Let $S=\{u,v,w\}\in N_{\overline{G}}(x)\cup N_{\overline{G}}^{3}(x)$. Then, T satisfying $E(T)=\{uv,uw\}$ is a vertex-rainbow S-tree. Thus, $rvx_{3}(G)\le 2$.

(iii) If $\overline{G}$ is disconnected, then $\overline{G}$ has $t\ge 2$ connected components. Suppose that $\overline{G_{1}},\overline{G_{2}},\ldots ,\overline{G_{t}}$ are the connected components of $\overline{G}$. It results that G contains a complete t-partite spanning subgraph. Given a vertex-coloring c of G as follows: assign the color 1 to all the vertices of G. Next, we show that there exists a vertex-rainbow tree connecting any three different vertices u, v and w of G. Let $S=\{u,v,w\}$. Let $u,v,w\in V(\overline{G_{i}})$, where $1\le i\le t$. Then, there is a vertex $y\in V(\overline{G_{j}})$ such that $uy,vy,wy\in E(G)$, where $1\le j\le t$ and $i\ne j$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{uy,vy,wy\}$. Let $u,v\in V(\overline{G_{i}})$ and $w\in V(\overline{G_{j}})$, where $1\le i\ne j\le t$, or $u\in V(\overline{G_{i}}),v\in V(\overline{G_{j}})$ and $w\in V(\overline{G_{r}})$, where $1\le i\ne j\ne r\le t$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{uw,wv\}$. Therefore, $rvx_{3}(G)\le 1$. Finally, we have $0\le rvx_{3}(G)\le 1$ by Proposition 2.2.

$\mathbf {Tight~Example~3}$ Let $\overline{G}$ be a graph of order n with $V(\overline{G})=\{y_{1},y_{2},\ldots ,y_{n-1},y_{n}\}$ and $E(\overline{G})=\{y_{n-1}y_{n}\}$. Then, $V(G)=V(\overline{G})$ and $E(G)=\{y_{i}y_{j},y_{i}y_{n-1},y_{i}y_{n}|1\le i\ne j\le n-2\}$. We can find that $\mathrm{sdiam}_{3}(G)=2$. Therefore, $rvx_{3}(G)=0$.

$\mathbf {Tight~Example~4}$ Let G be a connected graph of order n and $\overline{G}$ be disconnected. We can prove that $rvx_{3}(G)=1$.

Suppose that $V(\overline{G})=\{y_{1},y_{2},\ldots ,y_{n-1}, y_{n}\}$ and $E(\overline{G})=\{y_{n-2}y_{n-1},y_{n-1}y_{n},y_{n-2}y_{n}\}$. Then, $V(G)=V(\overline{G})$ and $E(G)=\{y_{n-2}y_{i},y_{n-1}y_{i},y_{n}y_{i},y_{i}y_{j}|1\le i,j\le n-3\}$. Since the tree T connecting $\{y_{n-2},y_{n-1},y_{n}\}$ has at least three edges, we have $rvx_{3}(G)\ge 1$. Now we only need to prove $rvx_{3}(G)\le 1$. Assign one color to all vertices of G. Let $X=\{y_{1},y_{2},\ldots ,y_{n-3}\}$ and $Y=\{y_{n-2},y_{n-1},y_{n}\}$. Suppose that u, v and w are any distinct vertices of G, denote $S=\{u,v,w\}$. Assume that at least one vertex of S lies on the set X. Without loss of generality, assume that $u\in X$. Then, we obtain a vertex-rainbow S-tree T, where $E(T)=\{uw,uv\}$. Assume that all vertices of S lie on the set Y. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{uy_{1},vy_{1},wy_{1}\}$, and so $rvx_{3}(G)\le 1$. $\square$

A graph $\overline{G}$ is connected with $\mathrm{diam}(\overline{G})=2$. Let x be a vertex of $\overline{G}$ satisfying $\mathrm{ecc}_{\overline{G}}(x)=\mathrm{diam}(\overline{G})=2$. Suppose that $N_{\overline{G}}(x)=\{y_{1},y_{2},\ldots ,y_{n-2}\}, N_{\overline{G}}^{2}(x)=\{y_{n-1}\}$ such that $y_{n-1}$ and $y_{i}$ are adjacent in $\overline{G}$, where $1\le i\le n-3$. Then, $rvx_{3}(G)$ can be very large if the number of cut vertices in $G[N_{\overline{G}}(x)]$ is sufficiently large. Here, we add an additional constraint to study the 3-vertex-rainbow index of G.

Theorem 3.3

Let $\overline{G}$ be a triangle-free graph with $diam(\overline{G})=2$. If G is connected, then $rvx_{3}(G)=1$.

Proof

Select a vertex x of $\overline{G}$ satisfying $\mathrm{ecc}_{\overline{G}}(x)=\mathrm{diam}(\overline{G})=2$. Let $|N_{\overline{G}}^{i}(x)|=n_{i}$, where $1\le i\le 2$. We need to consider the following four cases: (1) $n_{1}=1,n_{2}=1$; (2) $n_{1}=1,n_{2}\ge 2$; (3) $n_{1}\ge 2,n_{2}=1$; (4) $n_{1}\ge 2,n_{2}\ge 2$. If (1), (2) or (3) occurs, then G is not connected. Thus, we only need to study (4). Let $N_{\overline{G}}^{0}(x)=\{x\}, N_{\overline{G}}(x)=\{y_{1},y_{2},\ldots ,y_{k}\}$ and $N_{\overline{G}}^{2}(x)=\{w_{1},w_{2},\ldots ,w_{t}\}$, where $k+t+1=n$. For every $w_{j}\in N_{\overline{G}}^{2}(x)$, where $1\le j\le t$, define $N_{\overline{G}}(w_{j})=\{y_{i}\in N_{\overline{G}}(x):y_{i}w_{j}\in E(\overline{G})|1\le i\le k\}$. Since $\overline{G}$ is a triangle-free graph and $\mathrm{diam}(\overline{G})=2$, we have $N_{\overline{G}}(w_{j})\ne \emptyset$. Without loss of generality, assume that $y_{1}\not \in \bigcup \limits _{j=1}^t N_{\overline{G}}(w_{j})$. For every $w_{j}\in N_{\overline{G}}^{2}(x)$, we have $y_{1}w_{j}\not \in E(\overline{G})$. Then, $d_{\overline{G}}(y_{1},w_{j})\ge 3$. Hence, $\bigcup \limits _{j=1}^t N_{\overline{G}}(w_{j})=N_{\overline{G}}(x)=\{y_{1},y_{2},\ldots ,y_{k}\}$. First, we verify the following claim.

$\mathbf {Claim~1}$ For every vertex $y_{i}$ of $N_{\overline{G}}(x)$, where $1\le i\le k$, define $N_{G}(y_{i})=\{w_{j}\in N_{\overline{G}}^{2}(x): y_{i}w_{j}\in E(G)|1\le j\le t\}$. Then $N_{G}(y_{i})\ne \emptyset$.

Proof Without loss of generality, we assume that $y_{1}\in N_{\overline{G}}(x)$ satisfying $N_{G}(y_{1})=\emptyset$. Then, for every vertex $w_{j}\in N_{\overline{G}}^{2}(x)$, we have $y_{1}w_{j}\not \in E(G)$, and so $y_{1}w_{j}\in E(\overline{G})$. For every $y_{i}\in N_{\overline{G}}^{2}(x)\backslash \{y_{1}\}$. Then, we consider the following two cases: (1) There exists a vertex $w_{j}\in N_{\overline{G}}^{2}(x)$ such that $y_{i}w_{j}\not \in E(\overline{G})$. (2) Every vertex $w_{j}\in N_{\overline{G}}^{2}(x)$ such that $y_{i}w_{j}\in E(\overline{G})$. If (1) occurs, then $d(y_{i},w_{j})\ge 3$. If (2) occurs, then G is not connected. Therefore, $N_{G}(y_{i})\ne \emptyset$. $\square$

Define a vertex-coloring to G as follows: assign one color to all vertices of G. We need to verify that G is vertex-rainbow 3-tree connected with the above vertex-coloring. Let u, v and w be any three distinct vertices of G and $S=\{u,v,w\}$.

Let $u,v,w\in N_{\overline{G}}(x)$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{uv,uw\}$. Let $u,v\in N_{\overline{G}}(x)$ and $w=x\in N_{\overline{G}}^{0}(x)$. Then, there exists a vertex $w_{j}\in N_{\overline{G}}^{2}(x)$ satisfying $ww_{j},uw_{j},uv\in E(G)$ by Claim 1, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{ww_{j},uw_{j},uv\}$. Let $u,v\in N_{\overline{G}}(x)$ and $w\in N_{\overline{G}}^{2}(x)$. Then, one of the following two cases holds: (1) $uw,uv\in E(G)$; (2) $uw,vw\not \in E(G)$ and $uw_{j}\in E(G)$, where $w_{j}\in N_{\overline{G}}^{2}(x)\setminus \{w\}$. For (1), then the tree T connecting S is vertex-rainbow, where $E(T)=\{uv,uw\}$. For (2), we further consider the following subcases. If $vw_{j}\not \in E(G)$, then $ww_{j}\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{uv,uw_{j},ww_{j}\}$. If $vw_{j},ww_{j}\in E(G)$, then the tree T connecting S is vertex-rainbow, where $E(T)=\{uv,uw_{j},ww_{j}\}$. If $vw_{j}\in E(G)$ and $ww_{j}\not \in E(G)$, then $ww_{j}\in E(\overline{G})$, since $\overline{G}$ is a triangle-free graph and $d=2$, we know that there exists a vertex $y_{i}\in N_{\overline{G}}(x)\setminus \{u,v\}$ such that $y_{i}w_{j}\in E(\overline{G}),wy_{i}\not \in E(\overline{G})$, it follows that $wy_{i}\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{wy_{i},uy_{i},uv\}$. Let $u\in N_{\overline{G}}(x)$ and $v,w\in N_{\overline{G}}^{2}(x)$. If $uv\in E(G)$, then T is a vertex-rainbow S-tree, where $E(T)=\{xv,xw,uv\}$. If $uv,uw\not \in E(G)$, then there exists a vertex $w_{j}\in N_{\overline{G}}^{2}(x)$ such that $uw_{j}\in E(G)$, and so we have the following two cases: (3) $ww_{j}\in E(G)$; (4) $ww_{j},vw_{j}\not \in E(G)$. When (3) occurs, the tree T connecting S is vertex-rainbow, where $E(T)=\{uw_{j},ww_{j},wv\}$. When (4) occurs, since $\overline{G}$ is a triangle-free graph and $d=2$, we know that there exists a vertex $y_{i}\in N_{\overline{G}}(x)\setminus \{u\}$ such that $y_{i}w_{j}\in E(\overline{G}),wy_{i},vy_{i}\not \in E(\overline{G})$, it follows that $wy_{i},vy_{i}\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{wy_{i},vy_{i},uy_{i}\}$. Let $u\in N_{\overline{G}}(x),v\in N_{\overline{G}}^{2}(x)$ and $w=x$. Then, there exists a vertex $w_{j}\in N_{\overline{G}}^{2}(x)$ such that $uw_{j}\in E(G)$, and so the tree T connecting S is vertex-rainbow, where $E(T)=\{wv,ww_{j},uw_{j}\}$. Let u, v and $w\in N_{\overline{G}}^{2}(x)$. Then, the tree T connecting S is vertex-rainbow, where $E(T)=\{ux,vx,wx\}$. Let $u,v\in N_{\overline{G}}^{2}(x)$ and $w=x$. Note that the tree T is vertex-rainbow, where $E(T)=\{uw,vw\}$. Thus, $rvx_{3}(G)\le 1$.

Obviously, we know that a tree connecting $\{x,y_{i},y_{j}\}$ has at least three edges in G. Then, $rvx_{3}(G)\ge 1$, and so $rvx_{3}(G)=1$. $\square$