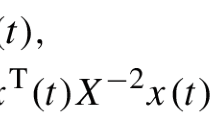1 Introduction

Impulsive effects exist widely in the world. As we know, the state of systems is often subject to instantaneous disturbances and experiences abrupt changes at certain instants, which might be caused by frequent changes or other suddenly noises. These systems are called impulsive systems, which are governed by impulsive differential equations. As known, the impulsive phenomenon is ubiquitous in the real world such as the mechanical systems with impacts [1], optimal control models in economics [2], orbital transfer of satellite [3], synchronization in chaotic secure communication systems [4], and so on.

Although impulses always appear as a form of disturbances in nature, they also can be used to control some special dynamical behaviors. As a representative example in dynamic portfolio management, we note that the dynamical behavior stock value of a particular investor can be described by an impulsive control system. More specifically, we see that when a certain amount of stock is purchased or sold, the stock value changes instantaneously to a new value. This situation is exactly like an impulsive control being applied to the dynamical system. The timings of the purchasing and selling of stock as well as the amount of the stock involved in each transaction can all be considered as decision variables to be determined by the investor.

The concept of impulsive control was firstly proposed by Yang Tao [5], and actually, it appears along with the opening of modern control theory. In this direction, many research work has been investigated. An impulsive controller was established to achieve the robust synchronization of uncertain dynamical networks [6], where the impulsive intervals have a finite upper bound. In [7], an impulsive-observer-based controller was designed to achieve an exponential stability result of linear impulsive systems. The consensus problem of second-order multi-agent systems (MASs) via impulsive control using position-only information with communication delays is studied in [8]. Also, using the concept of average impulsive gain, the synchronization of Lur’e networks was studied by designing a pinning impulsive controller in [9] and the synchronization problem for heterogenous impulsive complex networks was investigated in [10]. Lu et al. in [11] and Wang et al. in [12] proposed also the concept of average impulsive interval.

Impulsive control, as an important control means, may be in many cases more efficient than continuous control since the former is implemented only at impulsive instants, while the latter does so at every moment. Sometimes even only impulsive control can be used for control purpose. For example, a central bank cannot change its interest rate everyday in order to regulate the money supply in a financial market. The main idea of this method is to change the states of a system whenever some conditions are satisfied. Moreover, in networked systems, by using an impulsive control strategy, the driven network receives the signals from the driving system only in discrete times and the amount of conveyed information is decreased. This is predominant in practice due to reduced control cost.

As a class of infinite-dimensional systems, delay systems usually have complicated structures which lead to complex dynamics. The effects of time delay on system dynamics are bilateral; namely, it may not only cause the degradation of performance or some undesired dynamics of a system but also, inversely, make an unstable system stable or a system possess certain desired performance which is not possessed before. Furthermore, if control strategies are applied to the communication security systems or the networked dynamical systems [13, 14], then transmission delays and sampling delays are always inevitable in the process of information exchange. For example, these delays are induced by the networked environments, such as controller- to-actuator delays and sensor-to-controller delays. In this work, motivated by this point of view, it is not surprising but rather essential to consider a delayed control scheme to model many practical problems and in order to guarantee its effectiveness.

The main contribution of this paper lies in the following aspects. Firstly, a mixed control strategy which acts both in continuous and impulsive times is proposed by virtue of Dirac impulsive function to stabilize a class of uncertain nonlinear systems with multiple state delay. It is of great importance to point out that introducing a time-varying delay in the control scheme is more realistic and the chosen protocol can be easily implemented in practice since no instantaneous control input information is needed and this allows to improve performance. It is noted that the constructed impulsive function in this paper can be nonlinear which extend many existing results in which the linear impulsive function is required. Next, the same control strategy is adopted to practical stabilization of the perturbed system in which the origin is not necessarily an equilibrium point.

This paper is organized as follows: In Sect. 2, a model description and preliminaries are provided. In Sect. 3, some criteria on the robust stabilization for the model in consideration are stated and proved. In Sect. 4, the problem of robust practical stabilization of the perturbed system is studied. In Sect. 5, a numerical example is given to illustrate the effectiveness of Theorem 2.

2 Model Description and Preliminaries

Throughout this paper, we always use \(P^{T},\;\lambda _\mathrm{min}(P)\) and \(\lambda _\mathrm{max}(P)\) to denote the transpose, the smallest and the largest eigenvalues of a symmetrical real matrix P,  respectively. The notation \(P>0\) is that the matrix P is a positive definite matrix.

The vector (or matrix) norm is taken to be the Euclidean, denoted by \(\parallel . \parallel \)

Consider the class of nonlinear continuous systems with multiple time-varying delays described by

$$\begin{aligned} \displaystyle \dot{x}(t)= & {} [A+\varDelta A] x(t)+[B+\varDelta B] x(t-\tau _{0}(t))\nonumber \\&+\sum ^{m-1}_{i=1} g_{i}(x(t-\tau _{i}(t))) \end{aligned}$$
(1)

where

  • \(x(t)\in \mathbb {R}^{n}\) is the system state vector;

  • \(A,\;B\) are \(n \times n\) constant matrices;

  • \(\varDelta A\) and \(\varDelta B\) are the uncertain matrices, which vary within the range of

    $$\begin{aligned} \parallel \varDelta A\parallel \le \gamma , \parallel \varDelta B\parallel \le \beta , \end{aligned}$$
    (2)

    where \(\alpha ,\beta \) are known nonnegative constants.

  • \(g_{i}: \mathbb {R}^{n} \rightarrow \mathbb {R}^{n}, i \in \{1,2,\ldots ,m-1\}\) are continuous vector-valued functions;

  • the time delay functions \(\tau _{i}(.)\) may be unknown, time-varying, but they should be bounded by known positive constants \(\tau _{i},\;i \in \{0,1,\ldots ,m-1\}\), i.e., \(0 \le \tau _{i}(t) \le \tau _{i}.\)

Assume that system (1) satisfies the following initial condition: \(x(t)=\phi (t)\) for all \(t \in [-\tau _{M},0]\) where \(\tau _{M}=\max \{\tau _{0},\ldots ,\tau _{m-1} \}\) and \(\phi \in \mathcal C_{n,\tau _M}:=\mathcal C([-\tau _M,0],\mathbb R^n)\) which is the Banach space of all continuous functions mapping the interval \([-\tau _M,0]\) to \(\mathbb R^n\) equipped with the norm \(\displaystyle \Vert \phi (t) \Vert _{\tau _M}= \sup _{-\tau _M\le s\le t}\mid \phi (s)\mid .\)

In the remainder of this paper, we introduce the following assumptions: \((\mathcal {H}_{1})\) For \(i\in \{1,2,\ldots ,m-1\},\;g_{i}(0)=0 \) and there exist \(n\times n\) positive definite matrices \(M_{i},\;i\in \{1,2,\ldots ,m-1\}\) such that for all \(x,y \in \mathbb R^n\)

$$\begin{aligned} \parallel g_{i}(x)-g_{i}(y) \parallel ^{2}\le (x-y)^{T}M_{i}(x-y), \end{aligned}$$
(3)

In order to study the robust exponential stabilization problem of the uncertain delay system (1), we introduce a control input u(t, x(t)) into system (1) and further establish the following control system:

$$\begin{aligned} \displaystyle \dot{x}(t)= & {} [A+\varDelta A] x(t)+[B+\varDelta B]x(t-\tau _{0}(t))\nonumber \\&+\sum ^{m-1}_{i=1} g_{i}(x(t-\tau _{i}(t)))+u(t,x(t)), \end{aligned}$$
(4)

where \(u(t,x(t))= u_{1}(t,x(t))+u_{2}(t,x(t))\) and

$$\begin{aligned} u_{1}(t,x(t))= & {} \sum _{k=1}^{\infty }I_{k}(t)[F x(t)+G x(t-\tau _{m}(t))],\nonumber \\ u_{2}(t,x(t))= & {} \sum _{k=1}^{\infty }\delta (t-t_{k})[P_{k}(x(t))-x(t)], \end{aligned}$$
(5)

here F and G are two \(n \times n\) constant matrices, the time delay function \(\tau _{m}(.)\) satisfies \(0\le \tau _{m}(t)\le \tau _{m}\), \(P_{k}:\mathbb R^n \rightarrow \mathbb R^n\) is a vector-valued function for each \(k \in \mathbb Z^+=\{1,2,\ldots \},\; \delta (.)\) denotes the Dirac function, and \(I_{k}(t)\) is given by

$$\begin{aligned} I_{k}(t)=\left\{ \begin{array}{ll} 1, &{} t_{k-1}<t \le t_{k}; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

With \(0<t_{1}<t_{2}<\cdots<t_{k}<...\) and \(\displaystyle \lim _{k\rightarrow \infty }t_{k}= \infty .\) It is clear from (5) that for \(\forall k\in \mathbb Z^+,\) we have

$$\begin{aligned} u_{1}(t,x(t))=Fx(t)+G x(t-\tau _{m}(t)),\;\;t\in (t_{k-1},t_{k}]. \end{aligned}$$
(6)

From (4) and (5), we see that \(u_{2}(t,x(t))=0\) at \(t \ne t_{k}\) and for any small enough constant \(h>0\)

$$\begin{aligned} \displaystyle x(t_{k}+h)-x(t_{k})= & {} \int ^{t_{k}+h}_{t_{k}}[(A+\varDelta A) x(s)\nonumber \\&+(B+\varDelta B)x(s-\tau _{0}(s))\nonumber \\&+\sum ^{m-1}_{i=1} g_{i}(x(s-\tau _{i}(s)))+u(s,x(s))]\mathrm{d}s \nonumber \\= & {} \int ^{t_{k}+h}_{t_{k}}[(A+\varDelta A) x(s)\nonumber \\&+(B+\varDelta B)x(s-\tau _{0}(s))\nonumber \\&+\sum ^{m-1}_{i=1} g_{i}(x(s-\tau _{i}(s)))]\mathrm{d}s\nonumber \\&+\int ^{t_{k}+h}_{t_{k}}u_{1}(s,x(s))\mathrm{d}s+P_{k}(x(t_{k}))\nonumber \\&-x(t_{k}). \end{aligned}$$
(7)

Let \(h\rightarrow 0^{+},\) then we can obtain from (7)

$$\begin{aligned} x(t_{k}^{+})= & {} P_{k}(x(t_{k})) \end{aligned}$$
(8)

According to (6) and (8), system (4) can be rewritten as follows:

$$\begin{aligned} \displaystyle \dot{x}(t)= & {} [A+\varDelta A] x(t)+[B+\varDelta B]x(t-\tau _{0}(t))\nonumber \\&+ \sum ^{m-1}_{i=1} g_{i}(x(t-\tau _{i}(t)))+Fx(t)\nonumber \\&+Gx(t-\tau _{m}(t)),\quad t \ne t_{k}\nonumber \\ x(t_{k}^{+})= & {} P_{k}(x(t_{k})),\;\;\;\;k\in \mathbb Z^+\nonumber \\ x(t)= & {} \phi (t)\;\;\;\; \forall t \in [-\tau ,0]. \end{aligned}$$
(9)

where \(\tau =\max \{\tau _{M},\tau _{m} \}.\)

For each function \(P_{k}(.), \;k\in \mathbb Z^+,\) the following assumption is introduced \((\mathcal {H}_{2})\;\;P_{k}(0)=0\) and there is an \(n\times n\) positive definite matrix \(\overline{P}_{k}\) such that

$$\begin{aligned} P^{T}_{k}(x)P_{k}(x)\le x^{T}\overline{P}_{k}x,\;\forall x \in \mathbb R^n. \end{aligned}$$

Lemma 1

(Zhang et al.[15]) Let P be an \(n\times n\) positive definite matrix, Q be an \(n\times n\) symmetrical matrix, then for any \(x \in R^n\) we have

$$\begin{aligned} \lambda _\mathrm{min}(P^{-1}Q)x^{T}Px \le x^{T}Qx\le \lambda _\mathrm{max}(P^{-1}Q)x^{T}Px. \end{aligned}$$

3 Robust Stabilization Analysis

In this section, we prove that under the control scheme (5) the zero solution of the uncertain system (1) is globally exponentially stable for any \(\varDelta A, \varDelta B\) satisfying (2).

Theorem 1

Let \(\displaystyle \theta =\inf _{k\in \mathbb {N}}(t_{k}-t_{k-1})>0\). Under assumptions \((\mathcal {H}_{1})\) and \((\mathcal {H}_{2})\), if there exist \(n\times n\) matrix \(Q>0\), constants \(p>0,\;\lambda >0\) and \(\varepsilon _{i}>0, (i=1,\ldots ,m-1)\) such that the following conditions hold

  1. (a)

    \(\displaystyle QA+A^{T}Q+F^{T}Q+QF+ \sum _{i=1}^{m-1}\varepsilon _{i} Q^{2}+ \Big (p+4+\frac{\gamma ^{2}\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)}\Big )Q<0;\)

  2. (b)

    \(\displaystyle \lambda -p+\frac{\ln \delta }{\theta }+ \sum _{i=0}^{m}\alpha _{i}e^{\lambda \tau _{i}}<0,\) where

  • \(\displaystyle \delta =\sup _{k \in \mathbb {N}}\{\delta _{k}\},\; \delta _{k}=\max \{ 1, \lambda _\mathrm{max}(Q)\lambda _\mathrm{max}(Q^{-1}\overline{P}_{k})\}.\)

  • \(\displaystyle \alpha _{i}= \frac{\lambda _\mathrm{max}(Q^{-1}M_{i})}{\varepsilon _{i}};\forall 1\le i\le m-1, \alpha _{0}=\frac{\lambda _\mathrm{max}(B^{T}QB)}{\lambda _\mathrm{min}(Q)}+ \frac{\beta ^{2}\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)}\) and \(\displaystyle \alpha _{m}=\frac{\lambda _\mathrm{max}(G^{T}QG)}{\lambda _\mathrm{min}(Q)};\)

Then, the system (1) is robustly exponentially stable under the control strategy (5).

Proof

Consider the following auxiliary function:\(V(t)= x^{T}(t)Qx(t),\) which implies that \(\forall t\ne t_{k}\)

$$\begin{aligned} \lambda _\mathrm{min}(Q)\parallel x(t)\parallel ^{2}&\le V(t) \le&\lambda _\mathrm{max}(Q)\parallel x(t)\parallel ^{2}. \end{aligned}$$
(10)

Using condition (a) of Theorem 1, the Dini right derivative of V with respect to time t along the solution of system (9) is calculated and estimated as follows: \(\forall t\ne t_{k},\)

$$\begin{aligned} D^{+}V(t)\le & {} x^{T}(t)[A^{T}Q+QA+F^{T}Q+QF+\sum _{i=1}^{m-1}\varepsilon _{i}Q^{2}\nonumber \\&+(4+\frac{\gamma ^{2}\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)})Q]x(t)\end{aligned}$$
(11)
$$\begin{aligned}&+\sum _{i=0}^{m}\alpha _{i}V(t-\tau _{i}(t))\nonumber \\< & {} \displaystyle -pV(t)+\sum _{i=0}^{m}\alpha _{i}V(t-\tau _{i}(t)), \end{aligned}$$
(12)

When \(t=t_{k},\) from assumption \((\mathcal {H}_{2})\) and (10), we obtain

$$\begin{aligned} V(t_{k}^{+})\le & {} \lambda _\mathrm{max}(Q)x^{T}(t_{k})\overline{P}_{k}x(t_{k}) \nonumber \\\le & {} \lambda _\mathrm{max}(Q)\lambda _\mathrm{max}(Q^{-1}\overline{P}_{k})V(t_{k}) \nonumber \\\le & {} \delta _{k}V(t_{k}), \end{aligned}$$
(13)

where \(\delta _{k}=\max (1,\lambda _\mathrm{max}(Q)\lambda _\mathrm{max}(Q^{-1}\overline{P}_{k})).\) At this level, consider the following comparison system

$$\begin{aligned} \displaystyle \dot{W}(t)= & {} -pW(t)+\sum _{i=0}^{m}\alpha _{i}W(t-\tau _{i}(t)),t \ne t_{k}\nonumber \\ W(t_{k}^{+})= & {} \delta _{k}W(t_{k}),\;\;\;\;k\in \mathbb Z^+\nonumber \\ W(t)= & {} \lambda _\mathrm{max}(Q)\parallel x(t)\parallel ^{2}\;\;\;\; \forall t \in [-\tau ,0]. \end{aligned}$$
(14)

Let W(t) be the unique solution of the impulsive delay system (14).

It is clear that \(V(t)\le W(t), \;\;\;\; \forall t\ge 0.\) (see [16])

Clearly, when \(t \in [-\tau , 0]\) we have

$$\begin{aligned} \displaystyle W(t)\le & {} \lambda _\mathrm{max}(Q) \parallel x(t)\parallel ^{2}\nonumber \\\le & {} 2\delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}e^{-\lambda t}, \end{aligned}$$
(15)

Now, we shall prove that

$$\begin{aligned} \displaystyle W(t)\le & {} 2\delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}e^{-\lambda t},\forall t\ge 0. \end{aligned}$$
(16)

In fact, if the assertion (16) is not true, then from (15) and the continuity of the functions W with respect to \(t \ge 0,\) there exists a time \(t^{*}>0\) such that

$$\begin{aligned} W(t^{*})\ge & {} 2\delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}e^{-\lambda t^{*}} \end{aligned}$$
(17)

and

$$\begin{aligned} W(t)< & {} 2\delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}e^{-\lambda t}, \forall 0<t<t^{*}. \end{aligned}$$
(18)

According to the solution’s expression of W(t),  the conditions (b) of Theorem 1, \(t_{k}-t_{k-1}\ge \theta ,\forall k \in \mathbf {N}\) and using inequalities (1112), (17) and (18), we obtain the following estimate

$$\begin{aligned} \displaystyle W(t^{*})\le & {} \delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2} e^{-(p-\frac{\ln \delta }{\theta })t^{*}}\\&+\delta \int ^{t^{*}}_{0}e^{-(p-\frac{\ln \delta }{\theta })(t^{*}-s)}\big (\sum _{i=1}^{m}\alpha _{i}W(s-\tau _{i}(s))\big ) \mathrm{d}s\\< & {} \delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2} e^{-(p-\frac{\ln \delta }{\theta })t^{*}}\\&+\delta e^{-(p-\frac{\ln \delta }{\theta })t^{*}}\times \Big [\lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}\times \\&\left( \sum _{i=1}^{m}\alpha _{i}e^{\lambda \tau _{i}}\right) \times \int ^{t^{*}}_{0}e^{(p-\lambda -\frac{\ln \delta }{\theta })s}\mathrm{d}s\Big ]\\< & {} 2\delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}e^{-\lambda t^{*}}. \end{aligned}$$

which leads to a contradiction with (17) and so the estimate (16) holds. Finally, we have for all \(t\ge -\tau ,\)

$$\begin{aligned} \displaystyle \parallel x(t)\parallel\le & {} \sqrt{2\delta \frac{\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)}}\parallel x(0)\parallel _{\tau }e^{-\frac{\lambda }{2}t}. \end{aligned}$$

\(\square \)

Corollary 1

Let \(\displaystyle \theta =\inf _{k\in \mathbb {N}}(t_{k}-t_{k-1})>0\). Under assumptions \((\mathcal {H}_{1})\) and \((\mathcal {H}_{2})\), if there exist constants \(p>0,\;\lambda >0\) and \(\varepsilon _{i}>0, (i=1,\ldots ,m-1)\) such that the following conditions hold

  1. (a)

    \(\displaystyle A+A^{T}+F^{T}+F+\Big (\sum _{i=1}^{m-1}\varepsilon _{i}+p+4+\gamma ^{2}\Big )I<0;\)

  2. (b)

    \(\displaystyle \lambda -p+\frac{\ln \delta }{\theta }+ \sum _{i=0}^{m}\alpha _{i}e^{\lambda \tau _{i}}<0,\) where

  • \(\displaystyle \delta =\sup _{k \in \mathbb {N}}\{\delta _{k}\},\; \delta _{k}=\max \{ 1,\lambda _\mathrm{max}(\overline{P}_{k})\}.\)

  • \(\displaystyle \alpha _{i}= \frac{\lambda _\mathrm{max}(M_{i})}{\varepsilon _{i}};\forall 1\le i\le m-1,\) \(\displaystyle \alpha _{m}=\lambda _\mathrm{max}(G^{T}G),\) and \(\alpha _{0}=\lambda _\mathrm{max}(B^{T}B)+\beta ^{2}.\)

Then, the system (1) is robustly exponentially stable under the control scheme (5).

4 Robust Practical Stabilization Analysis

Consider the nonlinear uncertain time-varying delay system:

$$\begin{aligned} \displaystyle \dot{x}(t)= & {} [A+\varDelta A] x(t)+[B+\varDelta B]x(t-\tau _{0}(t))+f(t,x(t))\nonumber \\&+\sum ^{m-1}_{i=1} g_{i}(x(t-\tau _{i}(t)))+u(t,x(t)), \end{aligned}$$
(19)

in which we introduce the control input (5), where \(f: \mathbb {R}^{+}\times \mathbb {R}^{n}\longrightarrow \mathbb {R}^{n}\) is a continuous function satisfying

$$\begin{aligned} \parallel f(t,x(t))\parallel ^{2}\le \varrho , \; \varrho \ge 0. \end{aligned}$$
(20)

According to (6) and (8), system (19) can be rewritten as follows:

$$\begin{aligned} \displaystyle \dot{x}(t)= & {} [A+\varDelta A] x(t)+[B+\varDelta B]x(t-\tau _{0}(t))\nonumber \\&+\,f(t,x(t))+Fx(t)+\sum ^{m-1}_{i=1} g_{i}(x(t-\tau _{i}(t)))\nonumber \\&+\,Gx(t-\tau _{m}(t)), \quad t \ne t_{k}\nonumber \\ x(t_{k}^{+})= & {} P_{k}(x(t_{k})),\;\;\;\;k\in \mathbb Z^+\nonumber \\ x(t)= & {} \phi (t)\;\;\;\; \forall t \in [-\tau ,0]. \end{aligned}$$
(21)

Remark 1

The map f represent in many practical control systems, the perturbed term which could result from nonlinear systems modeling, disturbances, uncertainties, etc. Condition (20) leads us to study the robust practical exponential stability in the sense of the following definition.

Definition 1

Equation (21) is said to be robustly globally uniformly practically exponentially stable (or convergent to a ball with radius \(r\ge 0\)), if there exists a pair of positive constants \(\beta \) and \(\gamma \) such that the solution \(x(t;t_{0},\phi (0))\) of (21) satisfies \(\forall t \ge t_{0}\ge 0\)

$$\begin{aligned} \parallel x(t;t_{0},\phi (0)) \parallel \le r+ \beta \displaystyle \sup _{-\tau \le s \le 0} {\parallel \phi (s) \parallel } \; exp(- \gamma (t-t_{0})), \end{aligned}$$

for all initial function \(\phi \in \mathcal {PC}[[-\tau , 0],\mathbb {R}^{n}]\) and any uncertainties \(\varDelta A, \varDelta B\) satisfying (2).

In this case, the ball D(0, r) will be globally uniformly exponentially stable.

Theorem 2

Let \(\displaystyle \theta =\inf _{k\in \mathbb {N}}(t_{k}-t_{k-1})>0\). Under assumptions \((\mathcal {H}_{1})\) and \((\mathcal {H}_{2})\), if there exist \(n\times n\) matrix \(Q>0\), constants \(p>0,\;\lambda >0\) and \(\varepsilon _{i}>0, (i=0,\ldots ,m-1)\) such that the following conditions hold

  1. (a)

    \(\displaystyle QA+A^{T}Q+F^{T}Q+QF+ \sum _{i=0}^{m-1}\varepsilon _{i} Q^{2}+ \Big (p+4+\frac{\gamma ^{2}\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)}\Big )Q<0;\)

  2. (b)

    \(\displaystyle \lambda -p+\frac{\ln \delta }{\theta }+ \sum _{i=0}^{m}\alpha _{i}e^{\lambda \tau _{i}}<0,\) where

  • \(\displaystyle \delta =\sup _{k \in \mathbb {N}}\{\delta _{k}\},\; \delta _{k}=\max \{ 1, \lambda _\mathrm{max}(Q)\lambda _\mathrm{max}(Q^{-1}\overline{P}_{k})\}.\)

  • \(\displaystyle \alpha _{i}= \frac{\lambda _\mathrm{max}(Q^{-1}M_{i})}{\varepsilon _{i}};\forall 1\le i\le m-1\),

  • \(\alpha _{0}=\frac{\lambda _\mathrm{max}(B^{T}QB)}{\lambda _\mathrm{min}(Q)}+ \frac{\beta ^{2}\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)}\)

  • and \(\displaystyle \alpha _{m}=\frac{\lambda _\mathrm{max}(G^{T}QG)}{\lambda _\mathrm{min}(Q)};\)

Then, the system (19) is robustly practically exponentially stable under the control strategy (5) with radius \(\displaystyle r=\sqrt{\frac{\delta \varrho }{\lambda _\mathrm{min}(Q)\varepsilon _{0}\lambda }}.\)

Proof

Keeping the same function:\(V(t)= x^{T}(t)Qx(t),\) which satisfies (10), then from condition (a) of Theorem 2 and (20), the Dini right derivative of V with respect to time t along the solution of system (21) is estimated as follows: \(\forall t\ne t_{k},\)

$$\begin{aligned} D^{+}V(t)\le & {} x^{T}(t)[A^{T}Q+QA+F^{T}Q+QF+\sum _{i=0}^{m-1}\varepsilon _{i}Q^{2}\nonumber \\&+(4+\frac{\gamma ^{2}\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)})Q]x(t)\end{aligned}$$
(22)
$$\begin{aligned}&+\sum _{i=0}^{m}\alpha _{i}V(t-\tau _{i}(t))+\frac{\varrho }{\varepsilon _{0}}\nonumber \\< & {} \displaystyle -pV(t)+\sum _{i=0}^{m}\alpha _{i}V(t-\tau _{i}(t))+\frac{\varrho }{\varepsilon _{0}}, \end{aligned}$$
(23)

When \(t=t_{k},\) we have

$$\begin{aligned} V(t_{k}^{+})\le & {} \delta _{k}V(t_{k}), \end{aligned}$$
(24)

where \(\delta _{k}=\max (1,\lambda _\mathrm{max}(Q)\lambda _\mathrm{max}(Q^{-1}\overline{P}_{k})).\) As we proceeded in Theorem 1, consider the following comparison system

$$\begin{aligned} \displaystyle \dot{W}(t)= & {} -pW(t)+\sum _{i=0}^{m}\alpha _{i}W(t-\tau _{i}(t)) +\frac{\varrho }{\varepsilon _{0}} ,t \ne t_{k}\nonumber \\ W(t_{k}^{+})= & {} \delta _{k}W(t_{k}),\;\;\;\;k\in \mathbb Z^+\nonumber \\ W(t)= & {} \lambda _\mathrm{max}(Q)\parallel x(t)\parallel ^{2}\;\;\;\; \forall t \in [-\tau ,0]. \end{aligned}$$
(25)

Let W(t) be the unique solution of the impulsive delay system (25).

Recall that \(V(t)\le W(t), \;\;\;\; \forall t\ge 0.\) Clearly, when \(t \in [-\tau , 0]\) we have

$$\begin{aligned} \displaystyle W(t)\le & {} \le 2\delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}e^{-\lambda t}+\frac{\delta \varrho }{\varepsilon _{0}\lambda }, \end{aligned}$$

Using the same technique of reduction to absurdity, we prove that

$$\begin{aligned} \displaystyle W(t)\le & {} 2\delta \lambda _\mathrm{max}(Q) \parallel x(0)\parallel _{\tau }^{2}e^{-\lambda t}+\frac{\delta \varrho }{\varepsilon _{0}\lambda },\forall t\ge 0 \end{aligned}$$

Then, we have for all \(t\ge -\tau ,\)

$$\begin{aligned} \displaystyle \parallel x(t)\parallel\le & {} \sqrt{2\delta \frac{\lambda _\mathrm{max}(Q)}{\lambda _\mathrm{min}(Q)}}\parallel x(0)\parallel _{\tau }e^{-\frac{\lambda }{2}t} +\sqrt{\frac{\delta \varrho }{\lambda _\mathrm{min}(Q)\varepsilon _{0}\lambda }}. \end{aligned}$$

Corollary 2

Let \(\displaystyle \theta =\inf _{k\in \mathbb {N}}(t_{k}-t_{k-1})>0\). Under assumptions \((\mathcal {H}_{1})\) and \((\mathcal {H}_{2})\), if there exist constants \(p>0,\;\lambda >0\) and \(\varepsilon _{i}>0, (i=0,\ldots ,m-1)\) such that the following conditions hold

  1. (a)

    \(\displaystyle A+A^{T}+F^{T}+F+\Big (\sum _{i=0}^{m-1}\varepsilon _{i}+p+4+\gamma ^{2}\Big )I<0;\)

  2. (b)

    \(\displaystyle \lambda -p+\frac{\ln \delta }{\theta }+ \sum _{i=0}^{m}\alpha _{i}e^{\lambda \tau _{i}}<0,\) where

  • \(\displaystyle \delta =\sup _{k \in \mathbb {N}}\{\delta _{k}\},\; \delta _{k}=\max \{ 1,\lambda _\mathrm{max}(\overline{P}_{k})\}.\)

  • \(\displaystyle \alpha _{i}= \frac{\lambda _\mathrm{max}(M_{i})}{\varepsilon _{i}};\forall 1\le i\le m-1,\) \(\displaystyle \alpha _{m}=\lambda _\mathrm{max}(G^{T}G),\) and \(\alpha _{0}=\lambda _\mathrm{max}(B^{T}B)+\beta ^{2}.\)

Then, the system (19) is robustly practically exponentially stable under controller (5) with radius \(\displaystyle r=\sqrt{\frac{\delta \varrho }{\varepsilon _{0}\lambda }}.\)

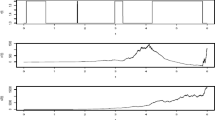
5 Numerical Example

To illustrate Theorem 2, we consider the system (19) with the following parameters: \(\displaystyle A=2, B=1, \gamma =1 , \beta =1, f(t,x(t))= \cos (x(t)), g_{1}(x(t-\tau _{1}(t)))=\sin (x(t-\tau _{1}(t))), g_{2}(x(t-\tau _{2}(t)))=\frac{1}{1+x(t-\tau _{2}(t))}, \tau _{0}(t)=\frac{\pi }{10}\frac{1}{1+t}, \tau _{1}(t)=\frac{e^{t}}{1+e^{t}}, \tau _{2}(t)=\frac{e^{t}}{1+2e^{t}},\) then \( M_{1}=M_{2}=1, \varrho =1,\tau =1.\) In controller (5), selecting \(P_{k}(x)=0,6x+0,1 \sin (x), F=-10,G=-1\) then \(\overline{P}_{k}=0,49.\) Finally, by choosing \(t_{k}-t_{k-1}=0.1\) for all \(k \in \mathbb {N}, Q=1, \varepsilon _{0}=\varepsilon _{1}=\varepsilon _{2}=1, p=7\), we take \(\lambda \simeq 0.3.\)

So, all conditions of Theorem 2 hold and then system (19) is robustly practically exponentially stable toward the ball of radius \(r=1.85\) under the control strategy (5) for every uncertainties in the range of (2).

6 Conclusion

In the present paper, an impulsive delayed-control strategy is established by virtue of Dirac impulsive function to robustly exponentially stabilize a class of continuous multiple time delays system and its perturbed one. A numerical example is given to demonstrate the synthesis procedure of the proposed control scheme. Since impulsive control is an efficient method to deal with the dynamical systems which cannot be controlled by continuous control method, the present result may be expected to have some applications to many practical control problems.