Trung’s Construction and the Charney–Davis Conjecture

Abstract

We consider a construction by which we obtain a simple graph ${\mathrm {Tr}}(H,v)$ from a simple graph H and a non-isolated vertex v of H. We call this construction “Trung’s construction.” We prove that ${\mathrm {Tr}}(H,v)$ is well covered, W$_2$ or Gorenstein if and only if H is so. Also, we present a formula for computing the independence polynomial of ${\mathrm {Tr}}(H,v)$ and investigate when the independence complex of ${\mathrm {Tr}}(H,v)$ satisfies the Charney–Davis conjecture. As a consequence of our results, we show that the independence complex of every Gorenstein planar graph with girth at least four satisfies the Charney–Davis conjecture.

1 Introduction

Throughout this paper, K is a field, $S=K[x_1,\ldots , x_n]$ and G denotes a simple undirected graph with vertex set $\mathrm {V}(G)=\{v_1,\ldots , v_n\}$ and edge set $\mathrm {E}(G)$. Recall that the edge ideal I(G) of G is the ideal of S generated by $\{x_ix_j|v_iv_j\in \mathrm {E}(G)\}$. Many researchers have studied how algebraic properties of S/I(G) relate to combinatorial properties of G (see [6, 7, 14, 17] and references therein). Recall that G is called a Gorenstein (resp. Cohen–Macaulay or CM for short) graph over K, if S/I(G) is a Gorenstein (resp. CM) ring. When G is Gorenstein (resp. CM) over every field, we say that G is Gorenstein (resp. CM). Finding combinatorial conditions on a graph equivalent to being Gorenstein has recently gained attention. For example, in [7] a characterization of planar Gorenstein graphs of girth at least four is presented. Also in [17], a condition on a planar graph equivalent to being Gorenstein is stated.

An importance of characterization of Gorenstein graphs comes from the Charney–Davis conjecture on the Euler characteristic of certain manifolds (see [3, 16]). This conjecture could be restated in terms of independence polynomials of Gorenstein graphs (see 2.1).

In this paper, first we recall some needed concepts and preliminary results. Then in Sect. 3, we show that planar Gorenstein graphs with girth at least four satisfy the Charney–Davis conjecture. All Gorenstein graphs with girth four are constructed using a recursive construction. We call a more general form of this recursive construction “Trung’s construction” and show that this construction preserves several properties related to independent sets such as being well covered, W$_2$ or Gorenstein. We also present a formula for computing the independence polynomial of graphs constructed using Trung’s construction and study when these graphs satisfy the Charney–Davis conjecture.

2 Preliminaries

Recall that a simplicial complex $\Delta$ on the vertex set $V=\{v_1,\ldots , v_n\}$ is a family of subsets of V (called faces) with the property that $\{v_i\}\in \Delta$ for each $i\in [n]=\{1,\ldots ,n\}$ and if $A\subseteq B\in \Delta$, then $A\in \Delta$. In the sequel, $\Delta$ always denotes simplicial complex. Thus, the family $\Delta (G)$ of all cliques of a graph G is a simplicial complex called the clique complex of G. Also, $\Delta ({\overline{G}})$ is called the independence complex of G, where ${\overline{G}}$ denotes the complement of G. Note that the elements of $\Delta ({\overline{G}})$ are independent sets of G. The ideal of S generated by $\{\prod _{v_i\in F} x_i|F\subseteq V$ is a non-face of $\Delta \}$ is called the Stanley–Reisner ideal of $\Delta$ and is denoted by $I_\Delta$, and $S/I_\Delta$ is called the Stanley–Reisner algebra of $\Delta$ over K. Therefore, we have $I_{\Delta ({\overline{G}})}= I(G)$. Many researchers have studied the relation between combinatorial properties of $\Delta$ and algebraic properties of $S/I_\Delta$, see, for example, [6, 10, 11, 14] and their references.

By the dimension of a face F of $\Delta$, we mean $|F|-1$ and the dimension of $\Delta$ is defined as $\max \{\dim (F)|F\in \Delta \}$. Let $f_i$ be the number of i-dimensional faces of $\Delta$ (if $\Delta \ne \emptyset$, then $f_{-1}=1$), then $(f_{-1}, \ldots , f_{d-1})$ is called the f-vector of $\Delta$, where $d-1=\dim (\Delta )$. Now, define $h_i$’s such that $h(t)= \sum _{i=0}^d h_it^i= \sum _{i=0}^d f_{i-1}t^i(1-t)^{d-i}$. Then, h(t) is called the h-polynomial of $\Delta$. It can be shown that the Hilbert series of $S/I_\Delta$ is $h(t)/(1-t)^ d$ (see [6, Proposition 6.2.1]). Denote by $\alpha (G)$ the independence number of G, that is, the maximum size of an independent set of G. Then, the polynomial $I(G,x)=\sum _{i=0}^{\alpha (G)} a_ix^i$, where $a_i$ is the number of independent sets of size i in G, is called the independence polynomial of G. Note that $a_i=f_{i-1}$ where $(f_{-1},\ldots , f_{\alpha (G)-1})$ is the f-vector of $\Delta ({\overline{G}})$. There are many papers related to this polynomial in the literature, see, for example, [9] and the references therein. It is easy to check that the h-polynomial h(t) of $\Delta ({\overline{G}})$ is $(1-t)^{\alpha (G)} I(G,t/(1-t))$.

A simplicial complex $\Delta$ is said to be Gorenstein* when $S/I_\Delta$ is Gorenstein over the field of rational numbers $\mathbb {Q}$ (for the definition of Gorenstein rings and other algebraic notions, the reader is referred to [2]), and there is no vertex v of $\Delta$ such that $\{v\}\cup F\in \Delta$ for every $F\in \Delta$. Note that if $\Delta =\Delta ({\overline{G}})$, then $\Delta$ is Gorenstein* if and only if G is Gorenstein over $\mathbb {Q}$ and has no isolated vertex.

The Charney–Davis conjecture states that if $\Delta$ is a Gorenstein* “flag” complex of dimension $2e-1$, then $(-1)^eh(-1) \ge 0$. Recall that $\Delta$ is called flag when every minimal non-face of $\Delta$ has two elements. This is equivalent to $\Delta =\Delta ({\overline{G}})$ where G is the graph whose edges are minimal non-faces of $\Delta$. This shows that the Charney–Davis conjecture can be stated in the language of graph theory (see below). In [16, Problem 4], Richard P. Stanley mentioned this conjecture as one of the “outstanding open problems in algebraic combinatorics” at the start of the twenty-first century. This conjecture was proved in dimension 3 in [4] and Stanley in [15] showed that this conjecture holds for barycentric subdivisions of shellable spheres. To see some other cases under which this conjecture is established, see [1, 5]. The following is a “more graph theoretical” restatement of the Charney–Davis conjecture.

Conjecture 2.1

(Charney & Davis) If G is a graph with no isolated vertices which is Gorenstein over $\mathbb {Q}$ and $\alpha (G)$ is even, then

$$\begin{aligned} (-1)^\frac{\alpha (G)}{2} I\left( G,-\frac{1}{2}\right) \ge 0. \end{aligned}$$

Next, we recall some properties of Gorenstein graphs. A graph G is called well covered, if all maximal independent sets of G have size $\alpha (G)$ and it is said to be a W$_2$ graph, if $|\mathrm {V}(G)|\ge 2$ and every pair of disjoint independent sets of G are contained in two disjoint maximum independent sets. In some texts, W$_2$ graphs are called 1-well-covered graphs. The following lemma states the relation of Gorenstein graphs and W$_2$ graphs.

Lemma 2.2

([7, Lemma 3.1]) Every Gorenstein graph without isolated vertices is a W$_2$ graph.

Recall that if $F\in \Delta$, then ${\mathrm {link}}_\Delta (F)=\{A\setminus F| F\subseteq A\in \Delta \}$. Suppose that $F\subseteq \mathrm {V}(G)$. By $\mathrm {N}[F]$, we mean $F\cup \{v\in \mathrm {V}(G)| uv\in \mathrm {E}(G)$ for some $u\in F\}$ and we set $G_F=G\setminus \mathrm {N}[F]$. We simply write $G_v$ instead of $G_{\{v\}}$.Thus if F is independent, then ${\mathrm {link}}_{\Delta ({\overline{G}})} F= \Delta ({\overline{G_F}})$. Another combinatorial property of a Gorenstein* graph G is that it has an Eulerian independence complex, that is, G is well covered and $I(G_F,-1)=(-1)^{\alpha (G_F)}$ for every independent set F of G. (One can readily check that this condition is equivalent to $\Delta ({\overline{G}})$ being an Euler complex as defined in [2, Definition 5.4.1].)

Lemma 2.3

• (i) A graph without isolated vertices is Gorenstein (over K) if and only if it has an Eulerian independence complex and is CM (over K).

• (ii) If G has an Eulerian independence complex and $\alpha (G)$ is odd, then $I(G,-1/2)=0$.

Proof

Part (i) is an especial case of [2, Theorem 5.5.2]. For part (i), note that if h(t) is the h-polynomial of $\Delta ({\overline{G}})$, then by the Dehn–Sommerville equation ([2, Theorem 5.4.2]), we have $h(-1)=0$. But $h(-1)=2^{\alpha (G)}I(G,-1/2)$ and the result follows. $\square$

Since every link of every CM simplicial complex is CM, one of the consequences of the above result is the following.

Corollary 2.4

Suppose that G is a Gorenstein graph (over K), then for every non-maximal independent set F of G, the graph $G_F$ is also Gorenstein (over K).

3 Trung’s Construction and the Charney–Davis Conjecture

In [12], a method for constructing a W$_2$ graph from another W$_2$ graph is presented and it is shown that all planar W$_2$ graphs with girth 4 are constructed by successively applying this method on a certain graph on eight vertices. In [7], it is proved that all such graphs are indeed Gorenstein. Recently, Trung generalized this construction, see [17, Proposition 3.9], and showed that this generalized construction preserves the Gorenstein property. Here, we recall this generalized construction and show that this construction preserves several properties related to independence complex of a graph.

Definition 3.1

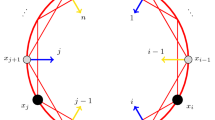
Suppose that H is a graph and v is a non-isolated vertex of H. Let a, b and c be three new vertices. Join c to b and to every neighbor of v; join b to a; and join a to v. We denote the obtained graph by ${\mathrm {Tr}}(H,v)$ and call this construction “Trung’s construction.”

This construction is illustrated in Fig. 1. Here, we show that many properties of the independence complex of a graph are preserved by Trung’s construction.

Fig. 1

a A graph H; b ${\mathrm {Tr}}(H,v)$

Theorem 3.2

Let H be a graph and v a non-isolated vertex of H. If $G={\mathrm {Tr}}(H,v)$, then

• (i) $\alpha (G)=\alpha (H)+1$;

• (ii) G is Gorenstein (over K) if and only if H is Gorenstein (over K).

Proof

(i) is clear. (ii): ($\Leftarrow$) [17, Proposition 3.9]; ($\Rightarrow$) Noting that $H=G_b$, this follows from (2.4). $\square$

Theorem 3.3

Let H be a graph and v a non-isolated vertex of H. Then, $G= {\mathrm {Tr}}(H,v)$ is well covered if and only if H is so.

Proof

Let F be a maximal independent set of G. We show that there is a maximal independent set of H with $|F|-1$ vertices. Note that $|F\cap \{a,b,c\}|$ equals 1 or 2. In the latter case, $F\cap \{a,b,c\}=\{a,c\}$ and $(F\cap \mathrm {V}(H)) \cup \{v\}$ is a maximal independent set of H. Now, suppose that $F\cap \{a,b,c\}=\{a\}$. If $F\setminus \{a\}$ is not a maximal independent set of H, then $\{x\}\cup F\setminus \{a\}$ is an independent set of H for some $x\in \mathrm {V}(H)$. Since $F\cup \{x\}$ is not independent in G, x is adjacent to a, that is, $x=v$. This means that $\mathrm {N}_H(v)\cap F=\emptyset$, where $\mathrm {N}_H(v)$ is the neighborhood of v in H. Thus, $F\cup \{c\}$ is an independent set of G larger than F, a contradiction. Thus, $F\setminus \{a\}$ is a maximal independent set of H. Similarly, in other cases that $|F\cap \{a,b,c\}|=1$, one can conclude that $F\cap \mathrm {V}(H)$ is a maximal independent set of H. Consequently, cardinality of each maximal independent sets of G is exactly one more than the cardinality of some maximal independent set of H. Conversely, each maximal independent set of H can be extended to a maximal independent set of G with exactly one more vertex. From this, the result follows. $\square$

Remark 3.4

The argument in the proof of (3.3) shows that maximal independent sets of ${\mathrm {Tr}}(H,v)$ are exactly the sets of the form $A\cup \{a\}$, $A\cup \{b\}$, $B\cup \{c\}$, $B\cup \{b\}$ or $B\cup \{a,c\}\setminus \{v\}$, where A, B are maximal independent sets of H with $v\in B\setminus A$.

Theorem 3.5

Let H be a graph and v a non-isolated vertex of H. Then, $G= {\mathrm {Tr}}(H,v)$ is W$_2$ if and only if H is so.

Proof

($\Rightarrow$): By [8, Lemma 3.3], for each independent set F of G with $|F|< \alpha (G)$, $G_F$ is W$_2$. Taking $F=\{b\}$, we deduce that $H=G_F$ is W$_2$.

($\Leftarrow$): Let A, B be disjoint independent sets of G. We must find disjoint maximum size independent sets $A', B'$ of G such that $A\subseteq A', B\subseteq B'$. We consider several cases:

Case 1: $c\notin A$ and $v\in B$. Then, $A_0=A\cap H$ and $B_0=B\cap H$ are disjoint independent sets of H and we can extend them to disjoint maximal independent sets $A'_0$ and $B'_0$ of H, respectively. If $A\cap \{a,b\}$ is nonempty, then let $E=A\cap \{a,b\}$ and if $A\cap \{a,b\}= \emptyset$, let $E=\{a\}$. Now, set $A'=A'_0\cup E$. If $b\in B$, let $B'=B'_0\cup \{b\}$; else, let $B'=B'_0\cup \{c\}$. One can readily check that $A'$ and $B'$ satisfy the required conditions.

Case 2: $c\in A$ and $v\in B$. Let $A_0=A \cap H_v$ and $B_0=B\cap H_v$. Note that by [13, Theorem 3], $H_v$ is W$_2$ with $\alpha (H_v)=\alpha (H)-1$. Suppose that $A'_0$ and $B'_0$ are disjoint maximal independent extensions of $A_0$ and $B_0$ in $H_v$. Now, $A'=A'_0\cup \{c,a\}$ and $B'=B'_0\cup \{v,b\}$ are disjoint maximum size independent sets of G. Since $c\in A$ and $v\in B$, we have $A\cap N_H(v)=\emptyset$ and $B\cap N_H(v)= \emptyset$. Therefore, $A\cap H=A_0$ and $B\cap H= B_0\cup \{v\}$ and it follows that $A\subseteq A'$ and $B\subseteq B'$, as required.

Note that if $v\in A$, then by changing the names of A and B, case 1 or 2 occurs. So we can assume that $v\notin A\cup B$.

Case 3: $v\notin A\cup B$ and $a,c\in A$. Let $A_0=(A \cap H)\cup \{v\}$ ($A_0$ is independent because $c\in A$ and hence $\mathrm {N}_H(v)\cap A=\emptyset$) and $B_0=B\cap H$ and extend them to disjoint maximum independent sets $A'_0$ and $B'_0$ of H. Now, $A'=(A'_0\setminus \{v\}) \cup \{a,c\}$ and $B'=B'_0 \cup \{b\}$ have the required properties.

Case 4: $v\notin A\cup B$, $c\in A$ and $a\notin A$. Let $A_0=(A \cap H)\cup \{v\}$ and $B_0=B\cap H$ and extend them to disjoint maximum independent sets $A'_0$ and $B'_0$ of H. Set $A'=A'_0\cup \{c\}$. If $b\in B$, set $B'=B'_0 \cup \{b\}$, and if $b\notin B$, set $B'=B'_0\cup \{a\}$.

Case 5: $v,c\notin A\cup B$ and $a\in A$. Let $A_0=A \cap H$ and $B_0=B\cap H$ and extend them to disjoint maximum independent sets $A'_0$ and $B'_0$ of H. Set $B'=B'_0\cup \{b\}$, and if $v\in A'_0$, set $A'=(A'_0\setminus \{v\})\cup \{a,c\}$; else, set $A'=A'_0\cup \{a\}$.

Case 6: $v,a,c\notin A\cup B$ and $b\in B$. Let $A_0=A$ and $B_0=B\cap H$ and extend them to disjoint maximum independent sets $A'_0$ and $B'_0$ of H. Set $B'=B'_0 \cup \{b\}$, and if $v\in A'_0$, let $A'=A'_0\cup \{c\}$, and if $v\notin A'_0$, set $A'= A'_0\cup \{a\}$.

Case 7: $v,a,b,c\notin A\cup B$. Let $A'_0$ and $B'_0$ be disjoint maximum size independent sets of H containing A and B, respectively. Then, v is not in at least one of $A'_0$ or $B'_0$, say $v\notin A'_0$. Then, $A'=A'_0\cup \{a\}$ and $B'= B'_0\cup \{b\}$ have the required properties.    $\square$

In the next theorem, we present a formula for computing the independence polynomial of ${\mathrm {Tr}}(H,v)$ in terms of independence polynomials of H and $H_v$.

Theorem 3.6

Let H be a graph and v be a non-isolated vertex of H. Then,

$$\begin{aligned} I({\mathrm {Tr}}(H,v),x)=(2x+1)I(H,x)+(x+x^2)I(H_v,x). \end{aligned}$$

Proof

Throughout the proof, F always denotes an independent set of $G={\mathrm {Tr}}(H,v)$ with $|F|=i$. We denote $F\cap \{a,b,c\}$ by $F_0$. Also for any graph $\Gamma$ by $a_i(\Gamma )$, we mean the number of independent sets of $\Gamma$ with cardinality i. If $i<0$, we set $a_i(\Gamma )=0$. Note that $F_0=\emptyset$ if and only if F is an independent set of H with size i. Thus, there are $a_i(H)$ such F’s. Also, $F_0=\{a\}$ if and only if $F=F_1\cup \{a\}$ for an independent set $F_1$ of $H-v$ with $|F_1|=i-1$. Thus, there are $a_{i-1}(H-v)$ choices of F with $F_0=\{a\}$. Similarly, there are $a_{i-1}(H)$ choices of F with $F_0=\{b\}$.

Now, assume that $F_0=\{c\}$. If $v\in F$, then $F\setminus \{v\}$ is an independent set of $H_v$ with cardinality $i-2$ and conversely by adding v and c to any such independent set of $H_v$, we get an F with $F_0=\{c\}$ and $v\in F$. Similarly, those F with $F_0=\{c\}$ and $v\notin F$ correspond to the independent sets of $H_v$ with size $i-1$. (Note that as $c\in F$, we have $N_H(v)\cap F=\emptyset$.) Therefore, there are totally $a_{i-1}(H_v)+a_{i-2}(H_v)$ choices for F with $F_0=\{c\}$.

Finally, if $F_0=\{a,c\}$, then $F\cap \mathrm {N}_{H}[v]=\emptyset$ ($N_H[v]$ means $\mathrm {N}[v]$ computed in the graph H) and hence $F\cap H\subseteq H_v$. Consequently, there is a one-to-one correspondence between those F with $F_0=\{a,c\}$ and independent sets of $H_v$ with size $i-2$. So there are $a_{i-2}(H_v)$ choices for F with $F_0=\{a,c\}$.

Totally, we get that $a_i(G)=a_i(H)+a_{i-1}(H-v)+a_{i-1}(H)+a_{i-1}(H_v)+2a_{i-2}(H_v)$. Note that $a_{i-1}(H-v)+a_{i-2}(H_v)= a_{i-1}(H)$, because $a_{i-1}(H-v)$ is number of independent sets of H with cardinality $i-1$ which do not contain v and $a_{i-2}(H_v)$ is the number of independent sets of H with size $i-1$ which contain v. We conclude that

$$\begin{aligned} a_i(G)=a_i(H)+ 2a_{i-1}(H) +a_{i-1}(H_v)+a_{i-2}(H_v). \end{aligned}$$

Multiplying by $x^i$ and taking summation over $i=0, \ldots , \alpha (G)$, we get the desired equation. $\square$

Corollary 3.7

Let H be a graph without isolated vertices which is Gorenstein over $\mathbb {Q}$ such that $\alpha (H)$ is odd and assume that $v \in \mathrm {V}(H)$. Then, $G={\mathrm {Tr}}(H,v)$ satisfies the Charney–Davis conjecture if and only if $H_v$ does so.

Proof

According to (3.6), $I(G,-1/2)= (-1/4)I(H_v,-1/2)$. Using the equality $\alpha (H_v)=\alpha (G)-2$, we conclude that $(-1)^{\alpha (G)/2}I(G,-1/2)\ge 0$ if and only if $(-1)^{\alpha (H_v)/2}I(H_v,-1/2)\ge 0$, as claimed. $\square$

If we start with a cycle of length 5 (which we denote by $C_5$) and apply the Trung’s construction repeatedly on vertices of degree 2, we get all planar Gorenstein graphs with girth 4 (see [7, Lemma 3.2]). Thus, we deduce the following application of Trung’s construction and Corollary 3.7. Recall that the Stanley–Reisner algebra of the disjoint union of two graphs is isomorphic to the tensor product of the Stanley–Reisner algebras of the two graphs. Hence, a graph is Gorenstein over K if and only if all of its connected components are Gorenstein over K.

Theorem 3.8

Suppose that G is a planar Gorenstein graph without isolated vertices with girth $\ge 4$ and assume that $\alpha (G)$ is even. Then, the Charney–Davis conjecture holds for G.

Proof

We prove the statement by induction on $|\mathrm {V}(G)|$. If G is not connected, say G is a disjoint union of $G_1$ and $G_2$, then both $G_1$ and $G_2$ are Gorenstein graphs without isolated vertices. If $\alpha (G_1)$ and $\alpha (G_2)$ are odd, then according to (2.3), $I(G_i,-1/2)=0$ for both i’s, and if $\alpha (G_1)$ and $\alpha (G_2)$ are even, then by the induction hypothesis, $(-1)^{\alpha (G_i)/2} I(G_i,-1/2)\ge 0$ for both $i=1,2$. Therefore, the result follows from the fact that $I(G,x)=I(G_1,x)I(G_2,x)$ (see, for example, [9, Section 2]).

Thus, we assume that G is connected. If G has girth $\ge 5$, then as G is W$_2$ and by [13, Theorem 7], $G \cong K_2$ or $G \cong C_5$, both of which satisfy the Charney–Davis conjecture. So we can suppose that girth$(G)=4$. Then according to [7, Lemma 3.2], G is constructed by several application of Trung’s construction on $C_5$, where in each application, the chosen vertex should be a vertex of degree 2. Thus, we can assume that $G={\mathrm {Tr}}(H,v)$, for a planar graph H of girth at least 4 which does not have any isolated vertex and $\deg _H(v)=2$. Clearly, $H_v$ is planar and has girth at least 4. Also, it is Gorenstein by (2.4). If $H_v$ has an isolated vertex, say y, then in H, y is adjacent to both neighbors of v (else $\deg _H(y)=1$, which contradicts (2.2)). Consequently, $\{y,v\}\cup N_H(v)$ is a 4-cycle in H. But this is against [12, Theorem 2], which says that every vertex on a 4-cycle in a W$_2$ graph has degree at least 3. Hence, $H_v$ has no isolated vertex and the Charney–Davis conjecture holds for $H_v$ by the induction hypothesis. Now, the result follows from (3.7). $\square$