1 Introduction

In this paper, we consider the following generalized pressureless Euler equations with dissipation

$$\begin{aligned} \left\{ \begin{array}{l} v_t+(v f(u))_x=0,\\ (vu)_t+(v uf(u))_x=-\alpha v u, \end{array}\right. \end{aligned}$$
(1.1)

with initial data

$$\begin{aligned} (v,u)(x,0)=(v_\pm ,u_\pm ),\ \ \ \ \pm x>0, \end{aligned}$$
(1.2)

where f(u) is given to be a smooth and strictly monotone function, the sign of v is assumed to be unchanging and \(\alpha >0\) is the constant dissipation coefficient. The dissipation term first appeared in [8] to reflect the clustering mechanism. If \(\alpha =0\), namely the dissipation vanishes, then system (1.1) becomes the so-called generalized pressureless Euler equations, whose Riemann problem was solved by Yang [25] in 1999. Then Yang and Sun solved the Riemann problem with delta initial data in [26] and obtained solutions with four kinds of different structures. Furthermore, Huang [9] solved the Cauchy problem by generalized potential. Mitrovic and Nedeljkov [14] studied its delta shock waves obtained as a limit of two shock waves. Recently, some research has been done on the generalized pressureless Euler equations with source term (see [29] for its Riemann problem with friction).

While if \(\alpha =0\), and \(f(u)=u,v\ge 0\), then (1.1) becomes the noted pressureless Euler equations, which are also called transport equations [1, 2]. It can be used to describe some important physical phenomena, such as the motion of free particles sticking together under collision and the formation of large scale structures in the universe [24]. The transport equations have been studied extensively since 1994. The existence of measure solutions of the Riemann problem was first proved by Bouchut [1], and the existence of the global weak solutions was obtained by Brenier and Grenier [2] and Weinan et al. [24]. Sheng and Zhang [19] discovered that the delta shock and vacuum states do occur in the Riemann solutions to the transport equation by the vanishing viscosity method. For more results about the Cauchy problem, one can refer to [10, 22, 23]. Recently, some research has been done on the pressureless Euler equations with source term. Ha et al. [8] first solved its Cauchy problem with dissipation by generalized potential in which the model is used to reflect the clustering mechanism of animals in nature. Shen solved its Riemann problem with friction which contained delta shocks and vacuum states in [15]. For more research on conservation laws with source term, one can refer to [6, 7, 16, 18] and the references cited therein.

Motivated by the research above, in this paper, we will focus on the generalized pressureless Euler equations with dissipation as presented in (1.1). Our main goal is to explore how the delta shock solution develops under the influence of the dissipation term. There are two difficulties lie in dealing with the Riemann problem for nonhomogeneous system (1.1). On one hand, under the influence of the dissipation term, the state variable u changes exponentially with respect to t, and the characteristics are curved, so the Riemann solutions of (1.1) and (1.2) are not self-similar anymore. To overcome this difficulty, by the generalized characteristic analysis and the similar derivation for generalized Rankine–Hugoniot conditions for the nonhomogeneous systems in [15, 16, 18], we obtain the generalized Rankine–Hugoniot conditions for (1.1). On the other hand, since the generality of the function f(u), the delta shock solution cannot be formulated concretely and explicitly. To overcome it, we will prove the existence and uniqueness of the delta shock solution qualitatively by skilled analysis. From this point of view, our result generalizes the result in [8] on Riemann problem aspects. In future, we will furthermore consider the Cauchy problem for (1.1). Moreover, with the obtained result for the Riemann problem (1.1) and (1.2), we can easily deal with the nonlinear geometric optic system with dissipation.

This paper is organized as follows. Section 2 solves the Riemann problem (1.1) and (1.2). The generalized Rankine–Hugoniot conditions are given, and the existence and uniqueness of the delta shock solution are established under the generalized Rankine–Hugoniot conditions and the generalized entropy condition. In Sect. 3, two typical examples are given to show the application of our results. Finally, discussions and conclusions are made in Sect. 4.

2 Riemann Problem for System (1.1)

In this section, we focus on solving the Riemann problem (1.1) and (1.2). Without loss of generality, we always assume that \(f'(u)>0, v\ge 0\) throughout this paper, since the rest cases can be discussed in a similar way.

For smooth solutions, (1.1) can be written as

$$\begin{aligned} \left\{ \begin{array}{l} v_t+(v f(u))_x=0,\\ u_t+f(u)u_x=-\alpha u, \end{array}\right. \end{aligned}$$
(2.1)

which is nonstrictly hyperbolic with a double eigenvalue \(\lambda _1=\lambda _2=f(u)\), and both \(\lambda _1,\lambda _2\) being linearly degenerate according to [17].

The characteristic equations of (2.1) are

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=f(u),\ \ \frac{\mathrm{d}u}{\mathrm{d}t}=-\alpha u,\ \ \frac{\mathrm{d}v}{\mathrm{d}t}=-v f(u)_x. \end{aligned}$$
(2.2)

So for the given initial point \((x_0,0)\), the characteristic curve of (1.1) through this point and the value of (v, u) along the characteristic curve before intersection can be expressed, respectively, as

$$\begin{aligned}&v=v_{-},\ \ u=u_-e^{-\alpha t},\ \ x=\int _0^tf(u_-e^{-\alpha t})\mathrm{d}t+x_0,\ \ x_{0}<0, \end{aligned}$$
(2.3)
$$\begin{aligned}&v=v_{+},\ \ u=u_+e^{-\alpha t},\ \ x=\int _0^tf(u_+e^{-\alpha t})\mathrm{d}t+x_0,\ \ x_{0}>0. \end{aligned}$$
(2.4)

Now we start to discuss the Riemann problem (1.1) and (1.2) in three cases.

Case 1 \(u_-=u_+\).

In this case, the left state \((v_-,u_-e^{-\alpha t})\) and the right state \((v_+,u_+e^{-\alpha t})\) are connected by a contact discontinuity \(J:x(t)=\int _0^tf(u_-e^{- \alpha t})\mathrm{d}t=\int _0^tf(u_+e^{-\alpha t})\mathrm{d}t.\) So the solution is

$$\begin{aligned} (v,u)(x,t)=\left\{ \begin{array}{ll} (v_-,u_-e^{-\alpha t}),&{}\quad x<\int _0^tf(u_-e^{- \alpha t})\mathrm{d}t,\\ (v_+,u_+e^{-\alpha t}),&{}\quad x>\int _0^tf(u_+e^{- \alpha t})\mathrm{d}t. \end{array}\right. \end{aligned}$$
(2.5)

Case 2 \(u_-<u_+\).

It is easy to see between the two characteristic curves \(x_1(t)=\int _0^tf(u_-e^{- \alpha t})\mathrm{d}t\) and \(x_2(t)=\int _0^tf(u_+e^{- \alpha t})\mathrm{d}t\) originated from (0,0); no point lies on characteristic curves originated from x-axis. So vacuum appears in the domain \(D=\{(x,t):x_1(t)<x<x_2(t)\}\). Then the solution can be expressed as

$$\begin{aligned} (v,u)(x,t)=\left\{ \begin{array}{ll} (v_-,u_-e^{-\alpha t}),&{}\quad x<x_1(t),\\ \mathrm{vacuum},&{}\quad x_1(t)<x<x_2(t),\\ (v_+,u_+e^{-\alpha t}),&{}\quad x>x_2(t). \end{array}\right. \end{aligned}$$
(2.6)

Case 3 \(u_->u_+\).

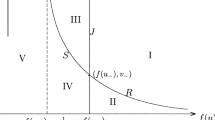
It is obvious that the characteristic curves for the Riemann problem (1.1) and (1.2) overlap in the domain \(\Omega =\{(x,t):x_2(t)<x<x_1(t)\}\) such that singularity will happen in \(\Omega \). Let us draw Fig. 1 to explain this phenomenon in detail.

Fig. 1
figure 1

The characteristic analysis of the delta shock wave for the Riemann problem (1.1) and (1.2) when \(u_{-} > u_{+}\)

Full size image

The formation of singularity for the solution to Riemann problem (1.1) and (1.2) is due to the overlap of linearly degenerate characteristics. Thus, the nonclassical situation appears for certain initial data where the Cauchy problem usually does not own a weak \(L^{\infty }\)-solution. In order to solve the Riemann problem (1.1) and (1.2) in the framework of nonclassical solutions, motivated by [3, 13, 19,20,21], a solution containing a weighted \(\delta \)-measure supported on a curve should be introduced.

Definition 2.1

To define the measure solution, a two-dimensional weighted \(\delta \)-measure \(p(s)\delta _S\) supported on a smooth curve \(S=\{(x(s),t(s)):a<s<b\}\) can be defined as

$$\begin{aligned} \langle p(s)\delta _S,\psi (x(s),t(s))\rangle =\int _a^bp(s)\psi (x(s),t(s))\sqrt{{x'(s)}^2+{t'(s)}^2}\mathrm{d}s, \end{aligned}$$
(2.7)

for any \(\psi \in C_0^\infty (R\times R_{+})\).

For convenience, we usually select the parameter \(s=t\) and use \(w(t)=\sqrt{1+{x'(t)}^2}p(t)\) to denote the strength of delta shock wave from now on. In what follows, let us provide the definition of delta shock wave solution to the Riemann problem (1.1) and (1.2) in the sense of distributions below. One can also refer to [4, 5, 11, 12] about the more exact definition of generalized delta shock wave solution for related systems with delta measure initial data.

Definition 2.2

Let (v, u) be a pair of distributions in which v has the form as follows:

$$\begin{aligned} v(x,t)={\hat{v}}(x,t)+w(x,t)\delta _{S}, \end{aligned}$$
(2.8)

in which \({\hat{v}},u\in L^{\infty }(R\times R_{+})\). Then it is called as the delta shock wave solution to the Riemann problem (1.1) and (1.2) if it satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \langle v,\psi _{t}\rangle +\langle v f(u),\psi _{x}\rangle =0,\\ \langle vu,\psi _{t}\rangle +\langle v uf(u),\psi _{x}\rangle =\langle \alpha vu,\psi \rangle , \end{array}\right. \end{aligned}$$
(2.9)

for any \(\psi \in C_0^\infty (R\times R^{+})\). Here we take

$$\begin{aligned} \langle v uf(u),\psi \rangle =\int _{0}^{\infty }\int _{-\infty }^{\infty }{\widehat{v}}uf(u)\psi \mathrm{d}x\mathrm{d}t+\langle w(t)u_{\delta }(t)f(u_{\delta }(t))\delta _{S},\psi \rangle , \end{aligned}$$

as an example to explain the inner product, in which we use the symbol S to express the smooth curve with the Dirac delta function supported on it; \(u_\delta (t)\) is the assignment of u on this delta shock wave S.

With the above definition, if \(u_->u_+\), a piecewise smooth solution of the Riemann problem (1.1) and (1.2) should be introduced in the form

$$\begin{aligned} (v,u)(x,t)=\left\{ \begin{array}{ll} (v_-,u_-e^{-\alpha t}),&{}\quad x<x(t),\\ (w(t)\delta (x-x(t)),u_{\delta }(t)),&{}\quad x=x(t),\\ (v_+,u_+e^{-\alpha t}),&{}\quad x>x(t), \end{array}\right. \end{aligned}$$
(2.10)

where x(t), w(t) and \(\sigma (t)=x'(t)\) denote, respectively, the location, weight and propagation speed of the delta shock and \(u_\delta (t)\) is the assignment of u on this delta shock wave curve such that \(u_\delta (t)e^{\alpha t}\) is assumed to be a constant. It is remarkable that the value of u should be given on the delta shock curve \(x=x(t)\) such that the product of v and u can be defined in the sense of distributions.

With the similar analysis and derivation as in [15, 16, 18, 29], by using Green’s formulas and integral by parts in (2.9), we can obtain the following generalized Rankine–Hugoniot condition

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}x}{\mathrm{d}t}=\sigma (t)=f(u_\delta (t)),\\ \frac{\mathrm{d}w(t)}{\mathrm{d}t}=[v] \sigma (t)-[vf(u)],\\ \frac{\mathrm{d}(w(t) u_ \delta (t))}{\mathrm{d}t}+\alpha {w(t) u_ \delta (t)}=[v u] \sigma (t)-[v uf(u)], \end{array}\right. \end{aligned}$$
(2.11)

where \([\rho ]=\rho (x(t)+0)-\rho (x(t)-0)\) denotes the jump across the discontinuity. Moreover, we supplement the so-called generalized entropy condition

$$\begin{aligned} f(u_+e^{-\alpha t})<\sigma (t)=f(u_\delta (t)))<f(u_+e^{-\alpha t}), \end{aligned}$$
(2.12)

which is equivalent to

$$\begin{aligned} u_+e^{-\alpha t}<u_\delta (t)<u_-e^{-\alpha t}. \end{aligned}$$
(2.13)

In this sense, the solution containing \(\delta \)-function is unique.

Now we solve (2.11) with initial condition

$$\begin{aligned} (x,w)|_{t=0}=(0,0). \end{aligned}$$
(2.14)

Moreover, we assume that \(v_-\) and \(v_+\) are not all zero. Otherwise the solution is trivial.

By virtue of the knowledge about delta shock waves in [15, 19,20,21, 25, 26], we find that the solution of (2.11) and (2.14) can be assumed to take the following form:

$$\begin{aligned} x(t)=\int _0^t\sigma (t)\mathrm{d}t=\int _0^tf(\widetilde{u_{\delta }} e^{- \alpha t})\mathrm{d}t,w(t)=w_0(1-e^{- \alpha t}), u_{\delta }(t)=\widetilde{u_{\delta }} e^{- \alpha t},\nonumber \\ \end{aligned}$$
(2.15)

where \(w_0, \widetilde{u_\delta }\) are constants to be determined, and furthermore, the entropy condition (2.13) is equivalent to

$$\begin{aligned} u_+<\widetilde{u_{\delta }}<u_-. \end{aligned}$$
(2.16)

Substituting (2.15) into (2.11), noting that the last equation of (2.11) is equivalent to

$$\begin{aligned} \frac{d(w(t) u_ \delta (t)e^{ \alpha t})}{\mathrm{d}t}=[v ue^{\alpha t}] \sigma (t)-[v ue^{ \alpha t}f(u)], \end{aligned}$$

so we have

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha w_0e^{- \alpha t}=[v]\sigma (t)-[vf(u)],\\ \alpha w_0e^{- \alpha t} \widetilde{u_ \delta } =[v ue^{\alpha t}] \sigma (t)-[v ue^{ \alpha t}f(u)], \end{array}\right. \end{aligned}$$
(2.17)

from which by eliminating \(w_0\), we have

$$\begin{aligned} ([v]f(\widetilde{u_{\delta }} e^{- \alpha t})-[vf(u)])\widetilde{u_ \delta }-[v ue^{\alpha t}]f(\widetilde{u_{\delta }} e^{- \alpha t})+[v ue^{ \alpha t}f(u)]=0. \end{aligned}$$
(2.18)

Let \(G(\widetilde{u_{\delta }})\) be the left side of (2.18), then we can calculate that

$$\begin{aligned} G(u)= & {} u(v_+-v_-)f(ue^{- \alpha t})-(v_+f(u_+e^{- \alpha t})-v_-f(u_-e^{- \alpha t})u\nonumber \\&-\,(v_+u_+-v_-u_-)f(ue^{- \alpha t})\nonumber \\&+\,v_+u_+f(u_+e^{- \alpha t})-v_-u_-f(u_-e^{- \alpha t}). \end{aligned}$$
(2.19)

By a simple computation, for \(u_->u_+\), we have

$$\begin{aligned} G(u_+)=-v_-(u_--u_+)(f(u_-e^{- \alpha t})-f(u_+e^{- \alpha t}))<0, \end{aligned}$$
(2.20)

and

$$\begin{aligned} G(u_-)=v_+(u_--u_+)(f(u_-e^{- \alpha t})-f(u_+e^{- \alpha t}))>0. \end{aligned}$$
(2.21)

So one can easily check that

$$\begin{aligned} G(u_+)G(u_-)=-v_-v_+(u_--u_+)^2(f(u_-e^{- \alpha t})-f(u_+e^{- \alpha t}))^2<0. \end{aligned}$$
(2.22)

Moreover, differentiating G(u) with respect to u yields that

$$\begin{aligned} G'(u)= & {} v_+(f(ue^{- \alpha t})-f(u_+e^{- \alpha t}))+v_-(f(u_-e^{- \alpha t})-f(ue^{- \alpha t}))\nonumber \\&+\,(v_+(u-u_+)+v_-(u_--u))f'(ue^{- \alpha t})e^{- \alpha t}>0, \end{aligned}$$
(2.23)

for \(u_+<u<u_-\). Hence, by using zero point theorem, we conclude that there exists one and only one zero point of function G(u) in the interval \((u_+,u_-)\). That is to say, Eq. (2.18) owns a unique solution, denoted by \(\widetilde{u_{\delta }}\), under the entropy condition (2.16). Returning to the relation (2.15), then x(t) and \(w_0\) will be solved uniquely. Therefore, by summarizing the above result, we have the following theorem.

Theorem 2.3

Assume that \(f'(u)>0, v\ge 0\), if \(u_{-}> u_{+}\), the Riemann problem (1.1) and (1.2) exists an unique delta shock wave solution of (2.10) where

$$\begin{aligned} x(t)=\int _0^t\sigma (t)\mathrm{d}t=\int _0^tf(\widetilde{u_{\delta }} e^{- \alpha t})\mathrm{d}t,w(t)=w_0(1-e^{- \alpha t}), u_{\delta }(t)=\widetilde{u_{\delta }} e^{- \alpha t},\nonumber \\ \end{aligned}$$
(2.24)

and the constants \(w_0\) and \(\widetilde{u_{\delta }}\) are uniquely determined by (2.16)–(2.18).

From the above discussions, it can be concluded that the Riemann problem (1.1) and (1.2) can be solved by contact discontinuities, vacuum or delta shock wave connecting two states \((v_\pm ,u_\pm e^{- \alpha t})\), where the characteristics, the contact discontinuities and the delta shock wave are curved. Precisely, if \(u_-<u_+\), then the Riemann solution of (1.1) and (1.2) can be expressed as (2.6), which consists of two contact discontinuities with the vacuum state between them (see Fig. 2). If \(u_->u_+\), then the Riemann solution of (1.1) and (1.2) can be expressed as (2.10) and (2.24), which is a delta shock wave connecting two states \((v_\pm ,u_\pm e^{- \alpha t})\) directly (see Fig. 3).

Fig. 2
figure 2

The Riemann solution of (1.1) and (1.2) when \(u_-<u_+<0\) and \(f(u_-)<0<f(u_+)\) for \(t>0\), the left is the (v, u) phase plane, and the right is the corresponding Riemann solution in the (x, t) plane

Full size image
Fig. 3
figure 3

The delta shock wave solution to the Riemann problem (1.1) and (1.2), in which the propagation speed of the delta shock wave is positive on the left and negative on the right at the initial time t=0

Full size image

Obviously, Theorem 2.3 is also true for the case \(f'(u)>0, v\le 0\). Moreover, similar results can be obtained for the cases \(f'(u)<0, v\ge 0\) and for the case \(f'(u)<0, v\le 0\). Thus, we have the following theorem.

Theorem 2.4

Assume that f(u) is a smooth and strictly monotone function and the sign of v is unchanging, then Riemann problem (1.1) and (1.2) exists a unique entropy solution of (2.10), which contains a vacuum state for the case \(u_{-}< u_{+}\) and a delta shock solution for the case \(u_{-}> u_{+}\).

Remark 2.1

It is clear to see that the dissipation term in system (1.1) takes the effect to curve the characteristics such that the discontinuity of the delta shock is also curved. The state variable u supported on the characteristics and the delta shock wave curve varies exponentially at the same rate \(\alpha \) with respect to the time t. What is more, the strength w(t) on the delta shock accumulates exponentially with the rate \(\alpha \) with respect to the time t. These are different from the homogenous case [25] and the nonhomogeneous case [15].

Remark 2.2

It is worthwhile to note from (2.5), (2.6), (2.10)–(2.13) that, when \(\alpha \rightarrow 0\), the solutions of the Riemann problem (1.1) and (1.2) converge to the corresponding ones for the homogenous generalized pressureless Euler equations with the same Riemann initial data [25].

3 Two Typical Examples

In this section, we present two typical examples to give the application of our results and proofs. In the following, we will focus on the delta shock waves for these two nonhomogeneous systems. These results will pave the way for the study of delta shocks for more general nonhomogeneous conservation laws.

Example 3.1

Consider the Riemann problem for the pressureless Euler equations with dissipation

$$\begin{aligned} \left\{ \begin{array}{ll} \rho _t+(\rho u)_x=0,\\ (\rho u)_t+(\rho u^2)_x=-\alpha \rho u, \end{array}\right. \end{aligned}$$
(3.1)

with initial data

$$\begin{aligned} (\rho ,u)(x,0)=(\rho _\pm ,u_\pm ),\ \ \ \ \pm x>0, \end{aligned}$$
(3.2)

with \(u_->u_+\), where \(\rho \) and u denote the density and velocity, respectively, and \(\rho _\pm ,u_\pm \) are given constants satisfying \(\rho _\pm >0\). In this case, \(f(u)=u,\ f'(u)=1>0\). The Cauchy problem for this model was first studied in [8].

When \(u_->u_+\), we look for the delta shock solution of the Riemann problem (3.1) and (3.2) of the form (2.10). Then we can obtain the following generalized Rankine–Hugoniot condition

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=\sigma (t)=u_\delta (t),\\ \frac{\mathrm{d}w(t)}{\mathrm{d}t}=[\rho ] \sigma (t)-[\rho u],\\ \frac{\mathrm{d}(w(t) u_ \delta (t))}{\mathrm{d}t}+{\alpha w(t) u_ \delta (t)}=[\rho u] \sigma (t)-[\rho u^2], \end{array}\right. \end{aligned}$$
(3.3)

and

$$\begin{aligned} u_\delta (t)=\widetilde{u_\delta }e^{-\alpha t},\ \ w(t)=w_0(1-e^{-\alpha t}), \end{aligned}$$
(3.4)

where \(\widetilde{u_\delta }\) and \(w_0\) are constants to be determined. So (3.3) is equivalent to

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha w_0e^{-\alpha t}=[\rho ] \sigma (t)-[\rho u],\\ \alpha w_0e^{-\alpha t} \widetilde{u_ \delta }=[\rho u] \sigma (t)e^{\alpha t}-[\rho u^2]e^{\alpha t}. \end{array}\right. \end{aligned}$$
(3.5)

Eliminating \(w_0\) in (3.5), we have

$$\begin{aligned} (\rho _+-\rho _-)(\widetilde{u_ \delta })^2-2(\rho _+u_+-\rho _-u_-)\widetilde{u_ \delta }+(\rho _+u_+^2-\rho _-u_-^2)=0. \end{aligned}$$
(3.6)

Let \(G(\widetilde{u_{\delta }})\) be the left side of (3.6), then under the entropy condition (2.13), i.e., \(u_+<\widetilde{u_ \delta }<u_-\), we have

$$\begin{aligned} G(u_+)G(u_-)=-\rho _-\rho _+(u_--u_+)^4<0, \end{aligned}$$
(3.7)

and

$$\begin{aligned} G'(u)=2\rho _+(u-u_+)+2\rho _-(u_--u)>0. \end{aligned}$$
(3.8)

Thus, Eq. (3.6) has a unique solution \(\widetilde{u_ \delta }\in (u_+,u_-)\). Of course, we can directly calculate from (3.6) to obtain that

$$\begin{aligned} \widetilde{u_\delta }=\frac{\sqrt{\rho _-}u_-+\sqrt{\rho _+}u_+}{\sqrt{\rho _-}+\sqrt{\rho _+}}, \end{aligned}$$
(3.9)

Then, we can obtain

$$\begin{aligned} x(t)=\frac{1}{\alpha }\frac{\sqrt{\rho _-}u_-+\sqrt{\rho _+}u_+}{\sqrt{\rho _-}+\sqrt{\rho _+}}(1-e^{-\alpha t}), \ \ w(t)=\frac{1}{\alpha }\sqrt{\rho _-\rho _+}(u_--u_+)(1-e^{-\alpha t}).\nonumber \\ \end{aligned}$$
(3.10)

Therefore, the unique delta shock solution of (3.1) and (3.2) is expressed as follows:

$$\begin{aligned} (\rho ,u)(x,t)=\left\{ \begin{array}{ll} (\rho _-,u_-e^{-\alpha t}),&{}\quad x<x(t),\\ (w(t)\delta (x-x(t)),\widetilde{u_\delta }e^{-\alpha t}),&{}\quad x=x(t),\\ (\rho _+,u_+e^{-\alpha t}),&{}\quad x>x(t), \end{array}\right. \end{aligned}$$
(3.11)

where \(x(t), \widetilde{u_\delta }\) and w(t) are expressed as (3.9) and (3.10), respectively.

Example 3.2

Consider the Riemann problem

$$\begin{aligned} \left\{ \begin{array}{ll} v_t+\left( \frac{vU}{\sqrt{1+U^2}}\right) _x=0,\\ (vU)_t+\left( \frac{vU^2}{\sqrt{1+U^2}}\right) _x=-\alpha vU, \end{array}\right. \end{aligned}$$
(3.12)

with initial data

$$\begin{aligned} (v,U)(x,0)=(v_\pm ,U_\pm ),\ \ \ \ \pm x>0, \end{aligned}$$
(3.13)

with \(U_->U_+\), \(v_-\cdot v_+>0\).

System (3.13) can be obtained by performing the transformation \(U=u/v\), i.e., \(u=vU\) from the nonlinear geometric optics system with a source term

$$\begin{aligned} \left\{ \begin{array}{ll} u_t+\left( \frac{u^2}{\sqrt{u^2+v^2}}\right) _x=-\alpha u,\\ v_t+\left( \frac{uv}{\sqrt{u^2+v^2}}\right) _x=0.\\ \end{array}\right. \end{aligned}$$
(3.14)

If \(\alpha =0\), then system (3.14) was systematically studied in [27, 28].

For system (3.12),

$$\begin{aligned} \lambda =f(U)= \frac{U}{\sqrt{1+U^2}},\ \ f'(U)= \frac{1}{(\sqrt{1+U^2})^3}>0. \end{aligned}$$
(3.15)

Let \((x(t),w(t),U_\delta (t))\) denote the delta shock solution of the Riemann problem (3.12) and (3.13) of the form (2.10). Then the following generalized Rankine–Hugoniot condition holds

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=\sigma (t)=f(U_\delta (t)),\\ \frac{\mathrm{d}w(t)}{\mathrm{d}t}=[v] \sigma (t)-\left[ \frac{vU}{\sqrt{1+U^2}}\right] ,\\ \frac{\mathrm{d}(w(t) U_\delta (t))}{\mathrm{d}t}+{\alpha w(t) U_\delta (t)}=[vU] \sigma (t)-\left[ \frac{vU^2}{\sqrt{1+U^2}}\right] , \end{array}\right. \end{aligned}$$
(3.16)

and

$$\begin{aligned} U_\delta (t)=\widetilde{U_\delta }e^{-\alpha t},\ \ w(t)=w_0(1-e^{-\alpha t}), \end{aligned}$$
(3.17)

where \(\widetilde{U_\delta }\) and \(w_0\) are constants to be determined. So (3.16) is equivalent to

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha w_0e^{-\alpha t}=[v] \sigma (t)-\left[ \frac{vU}{\sqrt{1+U^2}}\right] ,\\ \alpha w_0e^{-\alpha t} \widetilde{U_ \delta }=[vU] \sigma (t)e^{\alpha t}-\left[ \frac{vU^2}{\sqrt{1+U^2}}\right] e^{\alpha t}. \end{array}\right. \end{aligned}$$
(3.18)

Eliminating \(w_0\) in (3.18), we have

$$\begin{aligned} ([v]\widetilde{U_ \delta }-[vU]e^{\alpha t})\frac{ \widetilde{U_ \delta }e^{-\alpha t}}{\sqrt{1+( \widetilde{U_ \delta }e^{-\alpha t})^2}}-\left[ \frac{vU}{\sqrt{1+U^2}}\right] \widetilde{U_ \delta }+\left[ \frac{vU^2}{\sqrt{1+U^2}}\right] e^{\alpha t}=0.\nonumber \\ \end{aligned}$$
(3.19)

Let \(G(\widetilde{U_{\delta }})\) be the left side of (3.19), then under the entropy condition (2.13), i.e., \(U_+<\widetilde{U_ \delta }<U_-\), we have

$$\begin{aligned} G(U_+)G(U_-)=-v_-v_+(U_--U_+)^2\left( \frac{U_-e^{-\alpha t}}{\sqrt{1+(U_ -e^{-\alpha t})^2}}-\frac{U_+e^{-\alpha t}}{\sqrt{1+(U_ +e^{-\alpha t})^2}}\right) ^2<0,\nonumber \\ \end{aligned}$$
(3.20)

and

$$\begin{aligned} G'(u)= & {} v_+\left( \frac{Ue^{-\alpha t}}{\sqrt{1+(Ue^{-\alpha t})^2}}-\frac{U_+e^{-\alpha t}}{\sqrt{1+(U_ +e^{-\alpha t})^2}}\right) \nonumber \\&+\,v_-\left( \frac{U_-e^{-\alpha t}}{\sqrt{1+(U_ -e^{-\alpha t})^2}}-\frac{Ue^{-\alpha t}}{\sqrt{1+(Ue^{-\alpha t})^2}}\right) \nonumber \\&+\,(v_+(U-U_+)+v_-(U_--U))\frac{e^{-\alpha t}}{(\sqrt{1+(Ue^{-\alpha t})^2})^3}, \end{aligned}$$
(3.21)

which is positive for \(v_-,v_+>0\) and negative for \(v_-,v_+<0\) when \(U\in (U_+,U_-)\). Thus, Eq. (3.19) has a unique solution \(\widetilde{U_ \delta }\in (U_+,U_-)\). Owing to (3.16)–(3.18), we can solve x(t) and w(t) uniquely.

Therefore, the unique delta shock solution of (3.12) and (3.13) can be expressed as follows:

$$\begin{aligned} (v,U)(x,t)=\left\{ \begin{array}{ll} (v_-,U_-e^{-\alpha t}),&{}\quad x<x(t),\\ (w(t)\delta (x-x(t)),\widetilde{U_\delta }e^{-\alpha t}),&{}\quad x=x(t),\\ (v_+,U_+e^{-\alpha t}),&{}\quad x>x(t), \end{array}\right. \end{aligned}$$
(3.22)

where \(x(t)=\int _0^t\sigma (t)\mathrm{d}t=\int _0^tf(\widetilde{U_{\delta }} e^{- \alpha t})\mathrm{d}t\) and w(t) are uniquely determined by (3.17).

Formula (3.22) indicates that there is a weighted Dirac delta function only in the state variable v for system (3.12). By performing the transformation \(u=vU\), returning to system (3.14), we conjecture that weighted Dirac delta functions may appear simultaneously in the state variables u and v for system (3.14), which are consistent with the results obtained by Yang and Zhang in [27, 28] for a class of nonstrictly hyperbolic homogeneous conservation laws.

4 Conclusions and Discussions

In this work, we have constructed the Riemann solutions for the generalized pressureless Euler equations with a dissipation term in the fully explicit form. In particular, the delta shock wave solution has been discovered in some certain situations. We find that the dissipation term takes the effect to curve the characteristics such that the delta shock wave discontinuity is also curved. Compared with previous results on the generalized pressureless Euler equations, there are two new and interesting phenomena. On one hand, different from the homogeneous case in [26], the Riemann solutions of (1.1) and (1.2) are not self-similar any more. One the other hand, different from the nonhomogeneous case with friction in [29] where the state variable u changes linearly with respect to t, here the state variable u changes exponentially with respect to t under the influence of dissipation. Moreover, it is worthwhile to note that the Riemann solutions of (1.1) and (1.2) converge to the corresponding ones of the generalized pressureless Euler equations as \(\alpha \rightarrow 0\), namely the dissipation term vanishes.

It is shown that the Riemann solutions of the nonhomogeneous generalized pressureless Euler equations with a dissipation term share the same configurations with the homogeneous situation. In fact, for Example 3.1, it can be seen that the above-constructed Riemann solutions of (3.1) and (3.2) can be directly obtained from the ones of the Riemann problem for the homogeneous situation by the change of variables \(t\rightarrow 1-\frac{1}{\alpha }e^{-\alpha t}\) and \(u\rightarrow ue^{\alpha t}\). However, these solutions are drastically different from each other in that the characteristics are curves for the nonhomogeneous situation with dissipation, while the characteristics are straight lines for the homogeneous situation. Furthermore, the regions of constant flow are transformed into the regions of exponentially decelerated flow under the influence of dissipation.

It is worthwhile to point out that, compared with the method adopted in [15, 16, 18, 29] to take the state variable transformation to reformulate the nonhomogeneous conservation laws with friction into the homogeneous conservation laws, here we adopt the method to directly deal with the nonhomogeneous conservation laws with dissipation, which can be applied to conservation laws with much more general kind of source terms, such as discontinuous source terms. The (generalized) pressureless Euler equations with discontinuous source terms will be our next research focus.