Graphs with Large Italian Domination Number

Abstract

An Italian dominating function on a graph G with vertex set V(G) is a function $f :V(G) \rightarrow \{0,1,2\}$ having the property that for every vertex v with $f(v) = 0$, at least two neighbors of v are assigned 1 under f or at least one neighbor of v is assigned 2 under f. The weight of an Italian dominating function f is the sum of the values assigned to all the vertices under f. The Italian domination number of G, denoted by $\gamma _{I}(G)$, is the minimum weight of an Italian dominating of G. It is known that if G is a connected graph of order $n \ge 3$, then $\gamma _{I}(G) \le \frac{3}{4}n$. Further, if G has minimum degree at least 2, then $\gamma _{I}(G) \le \frac{2}{3}n$. In this paper, we characterize the connected graphs achieving equality in these bounds. In addition, we prove Nordhaus–Gaddum inequalities for the Italian domination number.

1 Introduction

Cockayne et al. [3] first introduced Roman domination as a graphical invariant in 2004, following a series of papers (see [13,14,15,16]) on defense strategies of the ancient Roman Empire. Since its introduction, over 100 papers have been published on Roman domination and its variants. We refer the reader to [1, 7, 9, 10] for some recent papers on Roman domination.

In this paper, we consider Italian domination, a variant of Roman domination. Italian domination was introduced as Roman $\{2\}$-domination in [2] and was renamed and studied further in [5]. See also [8, 12]. Let G be a graph with vertex set V(G) and edge set E(G). Two vertices v and w are neighbors in G if they are adjacent; that is, if $vw \in E(G)$. The open neighborhood of a vertex v in G is the set of neighbors of v, denoted by $N_G(v)$, and its closed neighborhood is $N_G[v] = N_G(v) \cup \{v\}$.

A function $f :V(G)\rightarrow \{0,1,2\}$ is a Roman dominating function, abbreviated RD-function, on G if every vertex $u \in V(G)$ for which $f(u)=0$ is adjacent to at least one vertex v for which $f(v)=2$. The weight of a RD-function is the value $\mathrm{w}(f) = f(V(G))=\sum _{u\in V(G)}f(u)$. The Roman domination number $\gamma _{R}(G)$ is the minimum weight of a RD-function on G, and a RD-function with weight $\gamma _R(G)$ is called a $\gamma _R$-function of G.

One may view Roman domination as graph labeling problem in which each vertex labeled 0 must be adjacent to at least one vertex labeled 2. An Italian dominating function, abbreviated an ID-function, of G is a function $f :V(G) \rightarrow \{0, 1, 2\}$ satisfying the condition that for every vertex $v \in V(G)$ with $f(v)=0$, $\sum _{u \in N(v)} f(u) \ge 2$. That is, either v is adjacent to at least one vertex u with $f(u) = 2$, or to at least two vertices x and y with $f(x) = f(y) = 1$. Viewed as a graph labeling problem, each vertex labeled 0 must have the labels of the vertices in its closed neighborhood sum to at least 2. The weight of a ID-function is the value $\mathrm{w}(f) = f(V(G))=\sum _{u\in V(G)}f(u)$. The Italian domination number, denoted by $\gamma _{I}(G)$, is the minimum weight of an ID-function in G, and an ID-function of G with weight $\gamma _{I}(G)$ is called a $\gamma _{I}$-function of G.

Our aim in this paper to continue the study of Italian dominating functions in graphs. We characterize connected graphs of order at least 3 with maximum possible Italian domination number. Further we characterize connected graphs with minimum degree at least two with maximum possible Italian domination number. We establish Nordhaus–Gaddum-type inequalities on the Italian domination number.

1.1 Terminology and Notation

For notation and graph theory terminology, we in general follow [4, 6]. Specifically, let $G = (V, E)$ be a graph with vertex set $V(G) = V$ of order $n(G) = |V|$ and edge set $E(G)=E$ of size $m(G) = |E|$, and let v be a vertex in V. The degree of v in G, denoted by $d_G(v)$, is the cardinality of its open neighborhood $N_G(v)$, where recall that $N_G(v) = \{u \in V \, | \, uv \in E\}$. The minimum and maximum degrees among the vertices of G are denoted by $\delta (G)$ and $\Delta (G)$, respectively. The open neighborhood of a set $S \subseteq V(G)$ is the set of all neighbors of vertices in S, denoted by $N_G(S)$, whereas the closed neighborhood of S is $N_G[S] = N_G(S) \cup S$. For a set $S \subseteq V(G)$, the subgraph induced by S in G is denoted by G[S]. Further, the graph obtained from G by deleting the vertices in S and all edges incident with S is denoted by $G - S$.

A set S of vertices in a graph G is a dominating set of G if every vertex in $V(G) \setminus S$ is adjacent to a vertex in S. The domination number $\gamma (G)$ is the minimum cardinality of a dominating set of G.

A vertex of degree one is a leaf, and its neighbor a support vertex. A graph G is r-regular if $\delta (G)=\Delta (G)=r$, and G is regular if it is r-regular for some r. We denote a path and cycle on n vertices by $P_n$ and $C_n$, respectively, and we denote a complete graph on n vertices by $K_n$. We denote a complete bipartite graph with partite sets X and Y, where $|X|=p$ and $|Y|=q$, by $K_{p,q}$. The graph $K_{1,q}$ is called a star. For $p,q \ge 1$, a double star $DS_{p,q}$ is the tree with exactly two vertices that are not leaves, one of which has p leaf neighbors and the other q leaf neighbors. A daisy with $k \ge 2$ petals is a connected graph that can be constructed from $k \ge 2$ disjoint cycles by identifying a set of k vertices, one from each cycle, into one vertex. If the k cycles have lengths $n_1, n_2, \ldots , n_k$, we denote the daisy by $D(n_1, n_2, \ldots , n_k)$. A linear forest is a forest in which every component is a path. We use the standard notation $[k] = \{1,\ldots ,k\}$.

The distance $d_G(u,v)$ between two vertices u and v in a connected graph G is the length of a shortest (u, v)-path in G. The maximum distance among all pairs of vertices of G is the diameter of G, denoted by $\mathrm{diam}(G)$. A diametral path of G is a shortest path whose length is equal to the diameter of G. A subdivision of an edge uv is obtained by removing the edge uv, adding a new vertex w, and adding the edges uw and vw. The complement of a graph G is denoted by $\overline{G}$.

A rooted tree T distinguishes one vertex r called the root. For each vertex $v \ne r$ of T, the parent of v is the neighbor of v on the unique (r, v)-path, while a child of v is any other neighbor of v in T. The set of children of v is denoted by C(v). A descendant of v is a vertex $u \ne v$ such that the unique (r, u)-path contains v. A grandchild of v is a descendant of v at distance 2 from v. We let D(v) denote the set of descendants of v, and we let $D[v] = D(v) \cup \{v\}$. The maximal subtree at v is the subtree of T induced by D[v] and is denoted by $T_v$.

2 Main Result

In this paper, we characterize the graphs with largest possible Italian domination number. For this purpose, we shall prove the following results, where ${{\mathcal {G}}}$ and ${{\mathcal {G}}}_{\ge 2}$ are families of graphs defined in Sect. 4. Proofs of Theorem 1 and 2 are given in Sects. 5 and 6.

Theorem 1

If G is a connected graph of order $n \ge 3$, then $\gamma _{I}(G) \le \frac{3}{4}n$ with equality if and only if $G \in {{\mathcal {G}}}$.

Theorem 2

If G is a connected graph of order n with $\delta (G) \ge 2$, then $\gamma _{I}(G) \le \frac{2}{3}n$ with equality if and only if $G \in {{\mathcal {G}}}_{\ge 2}$.

Next, we establish Nordhaus–Gaddum-type result for the Italian domination number. We shall prove the following result, a proof of which is given in Sect. 7.

Theorem 3

If G is a graph of order $n\ge 3$, then

$$\begin{aligned} 5 \le \gamma _{I}(G)+\gamma _{I}(\overline{G})\le n+2, \end{aligned}$$

and these bounds are tight. Further if $\gamma _{I}(G) \le \gamma _{I}(\overline{G})$, then $\gamma _{I}(G)+\gamma _{I}(\overline{G})=5$ if and only if there exists a vertex in G of degree $n-1$ with a neighbor of degree 1 in G or with two adjacent neighbors of degree 2 in G.

We following result shows that the upper bound in Theorem 3 can be improved slightly if the graph G has no small components. More precisely, we prove the following result, a proof of which is given in Sect. 7.

Theorem 4

If G is a graph of order $n \ge 16$ and having no component with fewer than three vertices, then $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le n-1$.

3 Known Results and Observations

The following theorem summarizes bounds relating domination and Roman domination-type parameters.

Theorem 5

([2]) For every graph G, $\gamma (G)\le \gamma _I(G) \le \gamma _{R}(G)\le 2\gamma (G)$.

If G is a graph of order n, then assigning to every vertex the weight 1 produces an ID-function of G, implying that $\gamma _{I}(G) \le n$. In addition, in [17] it was proved that $\gamma _{I}(G)=n$ if and only if $\Delta (G) \le 1$.

The Italian domination number of a path or a cycle is easy to compute (or see [8]). If $C :v_1,v_2 \ldots v_nv_1$ is a cycle of order $n \ge 3$, then the function that assigns weight 1 to the vertices of odd subscript and weight 0 to the vertices of even subscript is an example of a $\gamma _{I}$-function of the cycle.

Observation 1

([8]) For $n \ge 1$, $\gamma _{I}(P_n) = \lceil \frac{n+1}{2} \rceil$, while for $n \ge 3$, $\gamma _{I}(C_n) = \lfloor \frac{n+1}{2} \rfloor$.

The Italian domination number of a daisy is also easy to compute and follows readily from Observation 1 noting that there exists a $\gamma _{I}$-function of the cycle that assigns to any given selected vertex the weight 1.

Observation 2

If G is a daisy of order n, then $\gamma _{I}(G) \le \lfloor \frac{n+1}{2} \rfloor$.

Klostermeyer and MacGillivray [8] proved the following upper bounds on the Italian domination number in terms its order.

Theorem 6

([8]) If G is a graph of order $n \ge 3$, then

$$\begin{aligned} \gamma _{I}(G) \le \left\{ \begin{array}{cl} \frac{3}{4}n &{} \text {if } G \text { is connected} 3 \\ \frac{2}{3}n &{} \text {if } \ \delta (G) \ge 2 \\ \frac{1}{2}n &{} \text {if } \ \delta (G) \ge 3. \end{array} \right. \end{aligned}$$

Results of Nordhaus–Gaddum-type study the extreme values of the sum or product of a parameter on a graph and its complement. In their classical paper [11], Nordhaus and Gaddum discussed this problem for the chromatic number. We use the following Nordhaus–Gaddum results on the Roman domination of a graph and its complement.

Theorem 7

([1]) If G is a graph of order $n\ge 3$, then

$$\begin{aligned} 5\le \gamma _{R}(G)+\gamma _{R}(\overline{G})\le n+3. \end{aligned}$$

Furthermore, equality holds in the upper bound only when G or $\overline{G}$ is $C_5$ or $\frac{n}{2}K_2$.

Proposition 8

([17]) If G is a graph of order n, then $\gamma _{I}(G)=n$ if and only if $\Delta (G)\le 1$.

Proposition 9

([17]) If G is a graph of order $n\ge 2$, then $\gamma _{I}(G)=2$ if and only if $\Delta (G) = n-1$ or there exist two different vertices u and v such that $N(u)\cap N(v) = V(G)\setminus \{u,v\}$.

4 The Families ${{\mathcal {G}}}$, ${{\mathcal {T}}}$, ${{\mathcal {G}}}_{\ge 2}$ and ${{\mathcal {G}}}_{\ge 2}^{\min }$

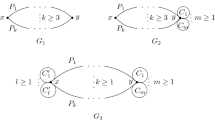
Let F be an arbitrary connected graph of order $n_{_F}\ge 1$, and let G be the graph of order $n = 4n_{_F}$ obtained from F by adding to each vertex v of F three new vertices u, w and x and the edges uv, vw and wx. Thus, uvwx is a path in G, where u is a leaf neighbor of v, w is a neighbor of v of degree 2 and x is a leaf neighbor of w. We call the graph F the underlying graph of the graph G. Let ${{\mathcal {G}}}$ be the family of all such graphs G. Further, let ${{\mathcal {T}}}$ be the family of all such graphs G whose underlying graph is a tree. We note that ${{\mathcal {T}}}$ is a subfamily of ${{\mathcal {G}}}$. When the underlying graph F is a cycle $C_4$ on four vertices, the graph G is illustrated in Fig. 1, where the assignment of weights is an example of a $\gamma _{I}$-function of G. We show that every graph in the family ${{\mathcal {G}}}$ has Italian domination number three-fourths its order.

Fig. 1

Graphs in the families ${{\mathcal {G}}}$ and ${{\mathcal {G}}}_{\ge 2}$

Proposition 10

If $G \in {{\mathcal {G}}}$ has order n, then $\gamma _{I}(G) = \frac{3}{4}n$.

Proof

Let G be an arbitrary graph in the family ${{\mathcal {G}}}$, and let G have order n. Let F be the underlying graph of G of order $n_{_F}$, and so $n = 4n_{_F}$. Adopting our earlier notation, let v be an arbitrary vertex of F, and let u, w and x be the three new vertices and uv, vw and wx the three new edges added to F when constructing G. Let f be a $\gamma _{I}$-function of G. We show that $f(u) + f(v) + f(w) + f(x) \ge 3$. If $f(v) = 0$, then $f(u) \ge 1$ and $f(w)+f(x) \ge 2$. If $f(v) = 1$, then $f(u) \ge 1$ and $f(w)+f(x) \ge 1$. If $f(v) = 2$, then $f(u) = 0$ and $f(w)+f(x) \ge 1$. In all three cases, $f(u) + f(v) + f(w) + f(x) \ge 3$, as claimed. Since this is true for every vertex v of F, we note that $\gamma _{I}(G) = \mathrm{w}(f) \ge 3n_{_F}$. The function $f^*$ that assigns the value 2 to every vertex of F, the value 1 to every vertex in $V(G) \setminus V(F)$ that has no neighbor in F, and the value 0 to all other vertices of G is an ID-function of G of weight $3n_{_F}$, implying that $\gamma _{I}(G) \le \mathrm{w}(f^*) = 3n_{_F}$. Consequently, $\gamma _{I}(G) = 3n_{_F}= \frac{3}{4}n$. $\square$

We next construct a class ${{\mathcal {G}}}_{\ge 2}$ of graphs with minimum degree two as follows. Let H be an arbitrary connected graph of order $n_{_H}\ge 1$, and let G be the graph of order $n = 3n_{_H}$ obtained from H by adding to each vertex v of H two new vertices u and w and the edges uv, vw and uw. Thus, $G[\{u,v,w\}] = K_3$, where both u and w have degree 2 in G. We call the graph H the underlying graph of the graph G. Further, we call a triangle of G that contains exactly one vertex of H a core triangle of G. For example, the above triangle $G[\{u,v,w\}]$ is a core triangle. Let ${{\mathcal {G}}}_{\ge 2}$ be the family of all such graphs G. Further, let ${{\mathcal {G}}}_{\ge 2}^{\min }$ be the family of all such graphs G whose underlying graph is a tree. We note that ${{\mathcal {G}}}_{\ge 2}^{\min }$ is a (proper) subfamily of ${{\mathcal {G}}}_{\ge 2}$. When the underlying graph H is a cycle $C_4$ on four vertices, the graph G is illustrated in Fig. 1b, where the assignment of weights is an example of a $\gamma _{I}$-function of G. We establish next properties of the graphs in the family ${{\mathcal {G}}}_{\ge 2}$.

Proposition 11

If $G \in {{\mathcal {G}}}_{\ge 2}$ has order n, and x and y are arbitrary vertices of G, then the following holds.

• (a) $\gamma _{I}(G) = \frac{2}{3}n$.

• (b) There exists a $\gamma _{I}$-function $f_i$ of G such that $f_i(x) = i$ for $i \in \{0,1,2\}$.

• (c) There exists a $\gamma _{I}$-function f of G such that $f(x) = f(y) = 1$.

Proof

(a) Let H be the underlying graph of $G \in {{\mathcal {G}}}_{\ge 2}$ of order $n_{_H}$, and so $n = 3n_{_H}$. Adopting our earlier notation, let v be an arbitrary vertex of H, and let u and w be the two new vertices and uv, vw and uw the three new edges added to H when constructing G. Let f be a $\gamma _{I}$-function of G. We show that $f(u) + f(v) + f(w) \ge 2$. If $f(v) = 0$, then $f(u) + f(w) \ge 2$. If $f(v) = 1$, then $f(u) + f(w) \ge 1$. If $f(v) = 2$, then $f(u) + f(w) \ge 0$. In all three cases, $f(u) + f(v) + f(w) \ge 2$, as claimed. Since this is true for every vertex v of H, we note that $\gamma _{I}(G) = \mathrm{w}(f) \ge 2n_{_H}$. The function $f^*$ that assigns the value 2 to every vertex of H and the value 0 to all vertices of $V(G) \setminus V(H)$ is an ID-function of G of weight $2n_{_H}$, implying that $\gamma _{I}(G) \le \mathrm{w}(f^*) = 2n_{_H}$. Consequently, $\gamma _{I}(G) = 2n_{_H}= \frac{2}{3}n$.

(b) Let x be an arbitrary vertex of G and let $G_x$ be the core triangle in $G \in {{\mathcal {G}}}_{\ge 2}$ that contains x. Let $f^*$ be the $\gamma _{I}$-function of G defined in Part (a). For $i \in \{0,1,2\}$, let $f_i$ be the $\gamma _{I}$-function of G defined as follows: let $f_i(v) = f^*(v)$ for all $v \in V(G) \setminus V(G_x)$. If $i = 0$, let $f_i$ assign the weight 0 to x and the weight 1 to the remaining two vertices of $G_x$. If $i = 1$, let $f_i$ assign the weight 1 to x and to exactly one other vertex of $G_x$, and the weight 0 to the remaining vertex of $G_x$. If $i = 2$, let $f_i$ assign the weight 2 to x and the weight 0 to the remaining two vertices of $G_x$. The resulting function $f_i$ is a $\gamma _{I}$-function of G such that $f_i(x) = i$ for $i \in \{0,1,2\}$.

(c) Let $f^*$ be the $\gamma _{I}$-function of G defined in Part (a). Let x and y be arbitrary vertices of G. Let $G_x$ and $G_y$ be the core triangles in $G \in {{\mathcal {G}}}_{\ge 2}$ that contains x and y, respectively. If $G_x = G_y$, let f be the $\gamma _{I}$-function of G defined as follows: let $f(v) = f^*(v)$ for all $v \in V(G) \setminus V(G_x)$, let $f(x) = f(y) = 1$ and let f assign the weight 0 to the remaining vertex of $G_x$. If $G_x \ne G_y$, let f be the $\gamma _{I}$-function of G defined as follows: let $f(v) = f^*(v)$ for all $v \in V(G) \setminus (V(G_x) \cup V(G_y)$, let f assign the weight 1 to x and one other vertex of $G_x$, the weight 1 to y and one other vertex of $G_y$, and the weight 0 to the remaining two vertices of $G_x \cup G_y$. The resulting function f is a $\gamma _{I}$-function of G such that $f(x) = f(y) = 1$. $\square$

5 Proof of Theorem 1

In this section, we present a proof of Theorem 1. We remark that although Theorem 6 gives that $\gamma _{I}(G) \le \frac{3}{4}n$ for connected graphs G of order $n\ge 3$, the extremal graphs are not characterized in [8]. Toward that end, we present a different proof of the $\frac{3}{4}$-bound here that leads to the characterizations of trees and connected graphs achieving equality in the bound. Since deleting an edge cannot decrease the Italian domination number, it suffices to first prove the bound for trees.

Theorem 12

If T is a tree of order $n \ge 3$, then $\gamma _{I}(T) \le \frac{3}{4}n$ with equality if and only if $T \in {{\mathcal {T}}}$.

Proof

If $T \in {{\mathcal {T}}}$ has order n, then by Proposition 10, $\gamma _{I}(T) = \frac{3}{4}n$. To prove the necessity, we proceed by induction on the order n of a tree T. Since $n \ge 3$, $\mathrm{diam}(T)\ge 2$. If $\mathrm{diam}(T) = 2$, then T is a star $K_{1,n-1}$ for $n\ge 3$ and $\gamma _{I}(T)=2<\frac{3}{4}n$. If $\mathrm{diam}(T) = 3$, then T is a double star $DS_{r,s}$ for $1 \le r \le s$. Hence, $n=r+s+2\ge 4$. If $r=1$, then $\gamma _{I}(T) = 3 \le \frac{3}{4}n$ with equality if and only if $s=1$ and thus $n=4$ and $T = P_4 \in {{\mathcal {T}}}$. If $r \ge 2$, then $n \ge 6$ and $\gamma _{I}(T)=4 <\frac{3}{4}n$. Hence, we may assume that $\mathrm{diam}(T) \ge 4$, for otherwise the desired result follows. Thus, $n \ge 5$. Given a subtree $T'$ with $n'$ vertices, where $3 \le n' < n$, the induction hypothesis yields a $\gamma _{I}$-function $f'$ of $T'$ with weight $\gamma _{I}(T') = \mathrm{w}(f') \le \frac{3}{4}n'$. Let $P :v_1v_2\ldots v_k$ ($k \ge 5$) be a diametral path of T such that $d_T(v_2)$ is as large as possible. We now root the tree T at the vertex $v_k$. We proceed further with the following two claims. $\square$

Claim 1

If $d_T(v_2) \ge 3$, then $\gamma _{I}(T) < \frac{3}{4}n$.

Proof

Suppose that $d_T(v_2)\ge 3$. Let $T'$ be obtained from T by deleting $v_2$ and its leaf neighbors. Since $\mathrm{diam}(T)\ge 4$, we have $n' \ge 3$. Applying the inductive hypothesis to $T'$, we have $\mathrm{w}(f') \le \frac{3}{4}n'$. Define f on V(T) by $f(x)=f'(x)$ for $x\in V(T')$, $f(v_2)=2$ and $f(x)=0$ for each leaf neighbor x of $v_2$. The resulting function f is an ID-function on T of weight $\mathrm{w}(f) = \mathrm{w}(f') + 2 \le \frac{3}{4}n' + 2 \le \frac{3}{4}(n-3)+2 < \frac{3}{4}n$. $\square$

Claim 2

If $d_T(v_2) = d_T(v_3) = 2$, then $\gamma _{I}(T) < \frac{3}{4}n$.

Proof

Suppose that $d_T(v_2) = d_T(v_3) = 2$. Let $T'$ be obtained from T by deleting $v_1$, $v_2$ and $v_3$. Since $\mathrm{diam}(T)\ge 4$, we have $n' \ge 2$. If $n'=2$, then T is the path $P_5$, and so $\gamma _{I}(T) = \gamma _{I}(P_5) = 3 < \frac{3}{4}n$. Hence, we may assume that $n' \ge 3$, for otherwise the desired result follows. Applying the inductive hypothesis to $T'$, we have $\mathrm{w}(f') \le \frac{3}{4}n'$. Define f on V(T) by $f(x)=f'(x)$ for $x\in V(T')$, $f(v_2)=2$ and $f(v_1)=f(v_3)=0$. The resulting function f is an ID-function on T of weight $\mathrm{w}(f) = \mathrm{w}(f') + 2 \le \frac{3}{4}n' + 2 \le \frac{3}{4}(n-3)+2 < \frac{3}{4}n$. $\square$

By Claim 1 and Claim 2, we may assume that $d_T(v_2) = 2$ and $d_T(v_3) \ge 3$, for otherwise the desired result follows. By the choice of $v_2$, every child of $v_3$ is either a leaf or a vertex similar to $v_2$, that is, a support vertex of degree 2 with exactly one leaf neighbor.

Claim 3

If the parent of $v_3$ is a support vertex of degree 2 in T, then $\gamma _{I}(T) < \frac{3}{4}n$.

Proof

Suppose that the parent, $v_4$, of $v_3$ is a support vertex of degree 2 in T. Thus, T is obtained from a star by subdividing t edges, where $t \ge 2$. If $v_3$ has no leaf neighbors, then the function f that assigns the weight 1 to $v_3$ and to every vertex at distance 2 from $v_3$ and the weight 0 to the remaining vertices of T is a ID-function of T of weight $t + 1$, implying that

$$\begin{aligned} \gamma _{I}(T) \le \mathrm{w}(f) = t + 1 < \frac{3}{4}(2t+1) = \frac{3}{4}n. \end{aligned}$$

If $v_3$ has at least one leaf neighbor, then the function f that assigns the weight 2 to $v_3$, the weight 1 to every vertex at distance 2 from $v_3$ and the weight 0 to the remaining vertices of T is a ID-function of T of weight $t + 2$, implying that

$$\begin{aligned} \gamma _{I}(T) \le \mathrm{w}(f) = t + 2 < \frac{3}{4}(2t+2) \le \frac{3}{4}n. \end{aligned}$$

This completes the proof of Claim 3. $\square$

By Claim 3, we may assume that the parent, $v_4$, of $v_3$ is not a support vertex of degree 2 in T. Let $T'$ be obtained from T by deleting $v_3$ and all its descendants. Thus, $T' = T - V(T_{v_3})$ and $n' \ge 3$. Applying the inductive hypothesis to $T'$, we have $\mathrm{w}(f') \le \frac{3}{4}n'$. As in the proof of Claim 3, we observe that $T_{v_3}$ is obtained from a star by subdividing $t \ge 1$ edges.

If $v_3$ has no leaf neighbors, then let f be the ID-function of T defined as follows: let $f(x) = f'(x)$ for all $x \in V(T')$, and let f assign the weight 1 to $v_3$ and to every grandchild of $v_3$ and the weight 0 to every child of $v_3$. The resulting ID-function of T has weight $\mathrm{w}(f) = \mathrm{w}(f') + t + 1$, implying that

$$\begin{aligned} \gamma _{I}(T) \le \mathrm{w}(f) = \mathrm{w}(f')+t+1 \le \frac{3}{4}n' +t+1 = \frac{3}{4}(n-2t-1)+t+1 < \frac{3}{4}n. \end{aligned}$$

Hence, we may assume that $v_3$ has $r \ge 1$ leaf neighbors. In this case, let f be the ID-function of T defined as follows: let $f(x) = f'(x)$ for all $x \in V(T')$, and let f assign the weight 2 to $v_3$, the weight 1 to every grandchild of $v_3$ and the weight 0 to every child of $v_3$. The resulting ID-function of T has weight $\mathrm{w}(f) = \mathrm{w}(f') + t + 2$, implying that

$$\begin{aligned} \gamma _{I}(T) \le \mathrm{w}(f) = \mathrm{w}(f')+t+2 \le \frac{3}{4}n' +t+2 = \frac{3}{4}(n-2t-1-r)+t+2 \le \frac{3}{4}n. \end{aligned}$$

(1)

This establishes the desired upper bound. Suppose that $\gamma _{I}(T) = \frac{3}{4}n$. Thus, we must have equality throughout the Inequality Chain (1). In particular, this implies that $\gamma _{I}(T) = \mathrm{w}(f)$ and $\mathrm{w}(f') = \frac{3}{4}n'$. Further, $t=1$ and $r=1$, and so $T_{v_3}$ is the path $v_1v_2v_3u_2$ where $u_2$ is the child of $v_3$ different from $v_2$. Applying the inductive hypothesis to $T'$, we have $T' \in {{\mathcal {T}}}$. We note that $n'$ is a multiple of 4.

Suppose that $n' = 4$, and so $n = 8$ and $T'$ is a path $P_4$. If $v_4$ is a leaf of $T'$, then by our choice of the diametral path P, the subtree $T'$ is the path $v_4v_5v_6v_7$. The function that assigns the weight 2 to $v_3$, the weight 1 to $v_1$, $v_5$ and $v_7$, and the weight 0 to the remaining vertices of T is a ID-function of T of weight $5 < \frac{3}{4}n = \gamma _{I}(T)$, a contradiction. Hence, $v_4$ is a vertex of degree 2 in $T'$, implying that $T \in {{\mathcal {T}}}$, as desired. Hence, we may assume that $n' \ge 8$.

Let $F'$ be the underlying tree of $T' \in {{\mathcal {T}}}$. By our earlier assumptions, $\gamma _{I}(T') = \mathrm{w}(f') = \frac{3}{4}n'$. By Proposition 10, we may choose $f'$ so that $f'(x) = 2$ for every vertex $x \in V(F')$, $f'(x) = 0$ for every vertex in $V(T') \setminus V(F')$ that has a neighbor in $F'$, and $f'(x) = 1$ for the remaining vertices of $T'$ that are not in $F'$ and have no neighbor in $F'$. Let $x_1x_2x_3x_4$ be the copy of $P_4$ in the construction of $T'$ that contains $v_4$, where $x_2 \in V(F')$. Thus, $x_1$ is a leaf neighbor of $x_2$, the vertex $x_3$ is a neighbor of $x_2$ of degree 2 in $T'$ and $x_4$ is a leaf neighbor of $x_3$ in $T'$. Since $n' \ge 8$, the vertex $x_2$ has at least one neighbor, say $y_2$, in $F'$. Let $X = \{x_1,x_2,x_3,x_4\}$ and let $W = \{v_1,v_2,v_3,u_2\}$.

We show that $x_2 = v_4$. Suppose, to the contrary, that $v_4 \in \{x_1,x_3,x_4\}$, and so $v_4 \notin V(F')$. Let $f^*$ be the ID-function of T defined as follows: let $f^*(x) = f'(x)$ for all $x \in V(T') \setminus X$. If $v_4 = x_1$, let $f^*$ assign the weight 2 to $v_3$ and $x_3$, the weight 1 to $v_1$, and the weight 0 to remaining vertices in $X \cup W$. If $v_4 = x_3$, let $f^*$ assign the weight 2 to $v_3$, the weight 1 to $v_1$, $x_1$ and $x_4$, and the weight 0 to remaining vertices in $X \cup W$. If $v_4 = x_4$, let $f^*$ assign the weight 2 to $v_3$ and $x_2$, the weight 1 to $v_1$, and the weight 0 to remaining vertices in $X \cup W$. In all three cases, we note that the resulting ID-function $f^*$ of T has weight

$$\begin{aligned} \mathrm{w}(f^*) = (\mathrm{w}(f') - 3) + 5 = \frac{3}{4}n' + 2 = \frac{3}{4}(n-4) + 2 < \frac{3}{4}n = \gamma _{I}(T), \end{aligned}$$

a contradiction. Hence, $x_2 = v_4$, implying that $T \in {{\mathcal {T}}}$. $\square$

We are now in a position to present a proof of Theorem 1. Recall its statement.

Theorem 1. If G is a connected graph of order $n \ge 3$, then $\gamma _{I}(G) \le \frac{3}{4}n$ with equality if and only if $G \in {{\mathcal {G}}}$.

Proof

If $G \in {{\mathcal {G}}}$ has order n, then by Proposition 10, $\gamma _{I}(G) = \frac{3}{4}n$. To prove the necessity, let G be a connected graph of order $n \ge 3$ and let T be an arbitrary spanning tree of G. Since deleting edges cannot decrease the Italian domination number, Theorem 12 implies that $\gamma _{I}(G) \le \gamma _{I}(T) \le \frac{3}{4}n$. It remains for us to show that if $\gamma _{I}(G) = \frac{3}{4}n$, then $G \in {{\mathcal {G}}}$. Suppose that $\gamma _{I}(G) = \frac{3}{4}n$, implying that $\gamma _{I}(T) = \frac{3}{4}n$. By Theorem 12, the spanning tree $T \in {{\mathcal {T}}}$. Let F be the underlying tree of T. We note that $n = 4k$ for some integer $k \ge 1$. Let $T_1, \ldots , T_k$ be the subtrees of T used to build the tree T, as described in Sect. 4, where each $T_i$ is isomorphic to a path $P_4$. Let $V_i = V(T_i)$ for $i \in [k]$. If $G[V_i]$ is not a path for some $i \in [k]$, then it is easy to see that there exists an ID-function of T of weight less than $\frac{3}{4}n$, a contradiction. Hence, $G[V_i] = T_i \cong P_4$ for all $i \in [k]$. If an edge uv of G joins vertices of $V_i$ and $V_j$ for $i \ne j$ such that $u \notin V(F)$ or $v \notin V(F)$, then an ID-function of weight less than $\frac{3}{4}n$ can be found analogously as in the last paragraph of the proof of Theorem 12, a contradiction. Hence, if uv is an edge of G that joins vertices of $V_i$ and $V_j$ for $i \ne j$, then both u and v belong to F, implying that $G \in {{\mathcal {G}}}$. $\square$

6 Proof of Theorem 2

We remark that although Theorem 6 gives that $\gamma _{I}(G) \le \frac{2}{3}n$ for connected graphs G of order n and minimum degree at least 2, the extremal graphs are not characterized in [8]. Toward that end, we present a different proof of the $\frac{2}{3}$-bound here that leads to the characterizations of the connected graphs achieving equality in the bound. For this purpose, we present a proof of Theorem 2. We refer to a graph G as an edge-minimal graph if G is edge minimal with respect to satisfying the conditions that $\delta (G) \ge 2$ and G is connected. Since deleting edges cannot decrease the Italian domination number, it suffices to first prove the following result for edge-minimal graphs. In what follows, we define a vertex of a graph G with minimum degree at least two as small if it has degree 2 in G, and large if it has degree more than 2 in G.

Theorem 13

If G is an edge-minimal graph of order n, then $\gamma _{I}(G) \le \frac{2}{3}n$ with equality if and only if $G \in {{\mathcal {G}}}_{\ge 2}^{\min }$.

Proof

If $G \in {{\mathcal {G}}}_{\ge 2}^{\min }$ has order n, then by Proposition 11, $\gamma _{I}(G) = \frac{2}{3}n$. To prove the necessity, we proceed by induction on the order n of an edge-minimal graph G of order n. If $n = 3$, then $G = C_3 \in {{\mathcal {G}}}_{\ge 2}^{\min }$. If $n = 4$, then $G = C_4$ and $\gamma _{I}(G) = 2 < \frac{2}{3}n$. If $n = 5$, then either $G = C_5$ or $G = K_{2,3}$ or G is the daisy D(3, 3). In all three cases, $\gamma _{I}(G) \le 3 < \frac{2}{3}n$. This establishes the base cases. Let $n \ge 6$ and suppose that if $G'$ is an edge-minimal graph of order $n'$ where $n' < n$, then $\gamma _{I}(G') \le \frac{2}{3}n'$ with equality if and only if $G' \in {{\mathcal {G}}}_{\ge 2}^{\min }$. Let G be an edge-minimal graph of order n.

If G is a cycle or a daisy, then by Observations 1 and 2, $\gamma _{I}(G) = \lfloor \frac{n+1}{2} \rfloor < \frac{2}{3}n$ noting that here $n \ge 6$. Hence, we may assume that G is neither a cycle nor a daisy, for otherwise the desired result follows. Thus, G contains at least two large vertices. Let ${{\mathcal {L}}}$ be set of all large vertices of G, i.e., ${{\mathcal {L}}}= \{ v \in V(G) \mid d_G(v) \ge 3 \}$. Let $|{{\mathcal {L}}}| = \ell$. By assumption, $\ell \ge 2$. We proceed further with the following series of claims. $\square$

Claim 4

If the set ${{\mathcal {L}}}$ is not an independent set, then $\gamma _{I}(G) \le \frac{2}{3}n$ with equality only if $G \in {{\mathcal {G}}}_{\ge 2}^{\min }$.

Proof

Suppose that $e=v_1v_2$ is an edge of G, where $v_1, v_2 \in {{\mathcal {L}}}$. By the edge minimality of G, the edge e is a bridge of G. Let $G_1 = (V_1,E_1)$ and $G_2 = (V_2,E_2)$ be the two components of $G-e$ where $v_i \in V_i$ for $i \in [2]$. For $i \in [2]$, let $|V_i| = n_i$, and so $n = n_1 + n_2$. We note that $\gamma _{I}(G) \le \gamma _{I}(G_1) + \gamma _{I}(G_2)$. For $i \in [2]$, the graph $G_i$ is an edge-minimal graph. Applying the inductive hypothesis to $G_i$, $\gamma _{I}(G_i) \le \frac{2}{3}n_i$ with equality if and only if $G_i \in {{\mathcal {G}}}_{\ge 2}^{\min }$. In particular, $\gamma _{I}(G) \le \frac{2}{3}n_1 + \frac{2}{3}n_2 = \frac{2}{3}n$. This establishes the desired upper bound on $\gamma _{I}(G)$.

Suppose, next, that $\gamma _{I}(G) = \frac{2}{3}n$. Thus, $\frac{2}{3}n = \gamma _{I}(G) \le \frac{2}{3}n_1 + \frac{2}{3}n_2 = \frac{2}{3}n$. Hence, we must have equality throughout this inequality chain. Thus, $\gamma _{I}(G_i) = \frac{2}{3}n_i$ for $i \in [2]$, and so $G_i \in {{\mathcal {G}}}_{\ge 2}^{\min }$. Let $T_i$ be the underlying tree of $G_i$ for $i \in [2]$. If $G_1 = C_3$ and $G_2 = C_3$, then $G \in {{\mathcal {G}}}_{\ge 2}^{\min }$, as desired. Hence, we may assume that $n_1 \ge 6$. If $v_1$ does not belong to the underlying tree $T_1$, then removing the edge joining $v_1$ to its neighbor in $T_1$ contradicts the edge minimality of G. Hence, $v_1 \in V(T_1)$. If $G_2 = C_3$, then $G \in {{\mathcal {G}}}_{\ge 2}^{\min }$. If $G_2 \ne C_3$, then $n_2 \ge 6$, implying by the edge minimality of G that $v_2 \in V(T_2)$, and therefore that $G \in {{\mathcal {G}}}_{\ge 2}^{\min }$. $\square$

By Claim 4, we may assume that the set ${{\mathcal {L}}}$ of large vertices is independent, for otherwise the desired result follows. By our earlier assumptions, $\ell \ge 2$. For $k \ge 3$, we define a k-handle of a graph G as a $(k+1)$-cycle with exactly one vertex of degree at least 3 in G. Further, we define a handle of G to be a k-handle for some $k \ge 3$. For $k \ge 1$, we define a k-linkage in G as a path on $k+2$ vertices that starts and ends at distinct large vertices and with k internal vertices of degree 2 in G.

Claim 5

If the graph G contains a k-linkage for some $k \ge 3$ or a k-handle for some $k \ge 5$, then $\gamma _{I}(G) < \frac{2}{3}n$.

Proof

Suppose that G contains a k-linkage $L :xv_1v_2 \ldots v_ky$ for some $k \ge 3$ that joins large vertices x and y. By definition, the k internal vertices of L all have degree 2 in G. Let $G^*$ be the graph of order $n' = n - 3 \ge 4$ obtained from G by deleting the set of vertices $\{v_1,v_2,v_3\}$. If $k \ge 4$, let $w = v_4$, while if $k = 3$, let $w = y$. If $k \ge 4$, let $G' = G^* + xw$. If $k = 3$ and $G^*$ is connected, let $G' = G^*$. If $k = 3$ and $G^*$ is disconnected, let $G' = G^* + xw$. In all cases, the resulting graph $G'$ is an edge-minimal graph. Applying the inductive hypothesis to $G'$, $\gamma _{I}(G') \le \frac{2}{3}n'$ with equality if and only if $G' \in {{\mathcal {G}}}_{\ge 2}^{\min }$. Let $f'$ be a $\gamma _{I}$-function of $G'$.

Let f be the ID-function of G defined as follows: let $f(v) = f'(v)$ for all $v \in V(G')$. If $f'(x) \ge 1$ and $f'(w) \ge 1$, let $f(v_2) = 1$ and $f(v_1) = f(v_3) = 0$. If $f'(x) = f'(w) = 0$, let $f(v_2) = 2$ and $f(v_1) = f(v_3) = 0$. If $f'(x) = 0$ and $f'(w) = 1$ or $f'(x) = 1$ and $f'(w) = 0$, let $f(v_1) = f(v_3) = 1$ and $f(v_2) = 0$. If $f'(x) = 0$ and $f'(w) = 2$, let $f(v_1) = 2$ and $f(v_2) = f(v_3) = 0$. If $f'(x) = 2$ and $f'(w) = 0$, let $f(v_3) = 2$ and $f(v_1) = f(v_2) = 0$. In all cases, the resulting ID-function f of G has weight

$$\begin{aligned} \mathrm{w}(f) \le \mathrm{w}(f') + 2 \le \frac{2}{3}n' + 2 = \frac{2}{3}n. \end{aligned}$$

(2)

Suppose that $\mathrm{w}(f) = \frac{2}{3}n$. Thus, we must have equality throughout the Inequality Chain (2). In particular, $\mathrm{w}(f') = \frac{2}{3}n'$, implying that $G' \in {{\mathcal {G}}}_{\ge 2}^{\min }$. By Proposition 11, the $\gamma _{I}$-function $f'$ of $G'$ can be chosen so that $f(x) = f(w) = 1$. In this case, $f(v_2) = 1$ and $f(v_1) = f(v_3) = 0$, implying that $\gamma _{I}(G) \le \mathrm{w}(f) = \mathrm{w}(f') + 1 = \frac{2}{3}n - 1$. Hence, if G contains a k-linkage for some $k \ge 3$, then $\gamma _{I}(G) < \frac{2}{3}n$. If G contains a k-handle $xv_1v_2 \ldots v_kx$ for some $k \ge 5$ and we let $w = v_4$ and let $G'$ be the graph obtained from G by deleting the set of vertices $\{v_1,v_2,v_3\}$ and adding the edge xw, then identical arguments as in the previous case when G contains a k-linkage show that $\gamma _{I}(G) < \frac{2}{3}n$. $\square$

By Claim 5, we may assume that the graph G contains no k-linkage where $k \ge 3$ and no k-handle where $k \ge 5$, for otherwise the desired result follows. We now consider the graph $F = G - {{\mathcal {L}}}$. By our earlier assumptions, F is a linear forest and every component of F is a path of order 1, 2, 3 or 4. Further, every component of F is joined by exactly two edges to vertices of ${{\mathcal {L}}}$ in G. Let ${{\mathcal {S}}}$ be a set of all small vertices (of degree 2) in G, and let $|{{\mathcal {S}}}| = s$. We note that $F = G[{{\mathcal {S}}}]$. Let $s_i$ be the number of components in F of order i for $i \in [4]$. Thus, $n = \ell + s = \ell + s_1 + 2s_2 + 3s_3 + 4s_4$. Let f be the ID-function of G defined as follows. Let f assign the weight 1 to every vertex of ${{\mathcal {L}}}$, the weight 1 to every vertex of ${{\mathcal {S}}}$ that has no neighbor in ${{\mathcal {L}}}$, the weight 1 to exactly one vertex from every component of F of order 2, and the weight 0 to the remaining vertices of G. Thus, $\gamma _{I}(G) < \frac{2}{3}n$ holds if the following is true:

$$\begin{aligned} \begin{array}{cccl} &{} \, \mathrm{w}(f) &{}< &{} \frac{2}{3}n \\ \Leftrightarrow &{} \, \ell + s_2 + s_3 + 2s_4 &{}< &{} \frac{2}{3}(\ell + s_1 + 2s_2 + 3s_3 + 4s_4) \\ \Leftrightarrow &{} \, \ell &{} < &{} 2s_1 + s_2 + 3s_3 + 2s_4. \end{array} \end{aligned}$$

Counting the edges $[{{\mathcal {L}}},{{\mathcal {S}}}]$ between ${{\mathcal {L}}}$ and ${{\mathcal {S}}}$, we note that $3\ell \le |[{{\mathcal {L}}},{{\mathcal {S}}}]| = 2(s_1 + s_2 + s_3 + s_4)$, and so

$$\begin{aligned} \ell \le \frac{2}{3}(s_1 + s_2 + s_3 + s_4) < 2s_1 + s_2 + 3s_3 + 2s_4. \end{aligned}$$

Therefore, $\gamma _{I}(G) < \frac{2}{3}n$ holds. This completes the proof of Theorem 13. $\square$

We are now in a position to present a proof of Theorem 2. Recall its statement.

Theorem 2. If G is a connected graph of order n with $\delta (G) \ge 2$, then $\gamma _{I}(G) \le \frac{2}{3}n$ with equality if and only if $G \in {{\mathcal {G}}}_{\ge 2}$.

Proof

If $G \in {{\mathcal {G}}}_{\ge 2}$ has order n, then by Proposition 11(a), $\gamma _{I}(G) = \frac{2}{3}n$. To prove the necessity, let G be a connected graph of order n with $\delta (G) \ge 2$. Let $G'$ be an arbitrary spanning graph of G obtained by deleting edges, if necessary, until the resulting graph is an edge-minimal graph (with respect to satisfying the conditions minimum degree at least 2 and the graph being connected). By Theorem 13, $\gamma _{I}(G') \le \frac{2}{3}n$ with equality if and only if $G' \in {{\mathcal {G}}}_{\ge 2}^{\min }$. Since deleting edges cannot decrease the Italian domination number, we note that $\gamma _{I}(G) \le \gamma _{I}(G') \le \frac{2}{3}n$. This establishes the desired upper bound. Suppose that $\gamma _{I}(G) = \frac{2}{3}n$, implying that $\gamma _{I}(G') = \frac{2}{3}n$ and $G' \in {{\mathcal {G}}}_{\ge 2}^{\min }$. If $G = G'$, then the desired result follows. Hence, we may assume that $G'$ is a proper subgraph of G, implying that $n = 3k$ for some $k \ge 2$. Thus, $G'$ has k core triangles, and so $kK_3$ is a spanning subgraph of $G'$. Let T be the underlying tree of $G'$.

Suppose that two core triangles of $G'$ are joined by two or more edges. Let H be the subgraph of G induced by the vertices of these two triangles. We note that H contains a vertex of degree 4 or 5 or H contains a 6-cycle as a subgraph. In both cases, $\gamma _{I}(H) \le 3$, implying that $\gamma _{I}(G) \le \gamma _{I}(H) + (k-2)\gamma _{I}(K_3) \le 3 + 2(k-2) < 2k = \frac{2}{3}n$, a contradiction. Hence, two (distinct) core triangles of $G'$ are joined by at most one edge in G.

Let $e = xy$ be an arbitrary edge in G that was deleted when constructing $G'$. We show that both x and y belong to the underlying tree T of $G'$. Suppose, to the contrary, that $x \notin V(T')$. Let $G_x$ and $G_y$ be the core triangles in $G'$ that contain x and y, respectively. By our earlier observations, the edge e is the only edge joining $G_x$ and $G_y$. Let $x'$ be the vertex of $G_x$ that belongs to T, and let w be a neighbor of $x'$ in T. Further, let $G_w$ be the core triangle in $G'$ that contains w. Let F be the subgraph of G induced by the vertices of these three core triangles, $G_w$, $G_x$ and $G_y$. We note that F contains a path $P_9$ as a subgraph, implying that $\gamma _{I}(G) \le \gamma _{I}(F) + (k-3)\gamma _{I}(K_3) \le 5 + 2(k-3) < 2k = \frac{2}{3}n$, a contradiction. Hence, both x and y belong to the underlying tree T of $G'$. Since $e = xy$ be an arbitrary edge in G, this implies that every edge of $E(G) \setminus E(G')$ joins two vertices of T and, therefore, $G \in {{\mathcal {G}}}_{\ge 2}$. $\square$

7 Nordhaus–Gaddum-Type Bounds

In this section, we establish Nordhaus–Gaddum-type results for the Italian domination number. Recall the statement of Theorem 3.

Theorem 3. If G is a graph of order $n\ge 3$, then

$$\begin{aligned} 5 \le \gamma _{I}(G)+\gamma _{I}(\overline{G})\le n+2, \end{aligned}$$

and these bounds are tight. Further if $\gamma _{I}(G) \le \gamma _{I}(\overline{G})$, then $\gamma _{I}(G)+\gamma _{I}(\overline{G})=5$ if and only if there exists a vertex in G of degree $n-1$ with a neighbor of degree 1 in G or with two adjacent neighbors of degree 2 in G.

Proof

If G is the cycle $C_5$ of order 5, then $\overline{G}$ is also the cycle $C_5$ of order 5, and we observe that $\gamma _{I}(G)+\gamma _{I}(\overline{G})=3+3=6=n+1$. If $G=\frac{n}{2}K_2$, then Propositions 8 and 9 imply $\gamma _{I}(G)+\gamma _{I}(\overline{G})=n+2$. Using these observations, the fact that $\gamma _{I}(G)\le \gamma _R(G)$ and Theorem 7, we obtain the desired upper bound. If G is a graph of order $n\ge 3$ with $\Delta (G)\le 1$, then we deduce from Propositions 8 and 9 that $\gamma _{I}(G)+\gamma _{I}(\overline{G})=n+2$. Therefore, the upper bound in Theorem 3 is sharp.

For the lower bound assume, without loss of generality, that $\gamma _{I}(G)\le \gamma _{I}(\overline{G})$. If $\gamma _{I}(G)\ge 3$, then $\gamma _{I}(G)+\gamma _{I}(\overline{G})\ge 6$. Thus, let now $\gamma _{I}(G)=2$. Then $\Delta (G)=n-1$ or there exist two different vertices u and v such that $N(u)\cap N(v)=V(G)\setminus \{u,v\}$ by Proposition 9. Therefore, $\overline{G}$ has a component of order 1 or a component of order 2. Since $n\ge 3$, this implies $\gamma _{I}(\overline{G})\ge 3$, and so $\gamma _{I}(G)+\gamma _{I}(\overline{G})\ge 5$.

Next, we characterize the graphs G of order $n\ge 3$ with $\gamma _{I}(G)+\gamma _{I}(\overline{G})=5$. Assume, without loss of generality, that $\gamma _{I}(G) \le \gamma _{I}(\overline{G})$. Suppose that there exists a vertex w in G of degree $n-1$. By Proposition 9, we note that $\gamma _{I}(G) = 2$. If the vertex w has a neighbor x of degree 1 in G, then let $\overline{f}$ be the ID-function of $\overline{G}$ that assigns the weight 1 to w, the weight 2 to x, and the weight 0 to the remaining vertices of $\overline{G}$. If the vertex w has two adjacent neighbors u and v of degree 2 in G, then let $\overline{f}$ be the ID-function of $\overline{G}$ that assigns the weight 1 to each of u, v and w, and the weight 0 to the remaining vertices of $\overline{G}$. In both cases, $\gamma _{I}(\overline{G}) \le \mathrm{w}(\overline{f}) = 3$, implying that $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le 5$. As shown earlier, $\gamma _{I}(G)+\gamma _{I}(\overline{G})\ge 5$. Consequently, $\gamma _{I}(G)+\gamma _{I}(\overline{G}) = 5$.

Conversely, suppose that $\gamma _{I}(G)+\gamma _{I}(\overline{G})=5$. Since $\gamma _{I}(G)\le \gamma _{I}(\overline{G})$, it follows that $\gamma _{I}(G)=2$ and $\gamma _{I}(\overline{G})=3$. Suppose that $\Delta (G) < n-1$. By Proposition 9, there exist two different vertices y and z such that $N(y) \cap N(z) = V(G) \setminus \{y,z\}$. By supposition, y and z are not adjacent. If $n = 3$, then the common neighbor of y and z has degree $n-1$, a contradiction. Hence, $n \ge 4$. Since the vertices y and z belong to a component of order 2 in $\overline{G}$, we note that $\gamma _{I}(\overline{G}) = 2 + \gamma _{I}(\overline{G}- \{y,z\}) \ge 2 + 2 = 4$, a contradiction. Hence, $\Delta (G) = n-1$. Let w be a vertex of degree $n-1$ in G. Let $\overline{f}$ be a $\gamma _{I}$-function of $\overline{G}$. Let $H = \overline{G}- w$ and note that H has order $n-1$. Since w is isolated in $\overline{G}$, we note that $\overline{f}(w) = 1$, implying that $\gamma _{I}(H) = 2$. If $\Delta (H) = n-2$, then there is a vertex x of degree $n-2$ in H. Such a vertex x is a neighbor of w of degree 1 in G. If $\Delta (H) < n-2$, then by Proposition 9, there exist two different vertices u and v such that $N_H(u) \cap N_H(v) = V(H) \setminus \{u,v\}$. Such vertices u and v are adjacent neighbors of degree 2 in G that have w as their common neighbor. $\square$

We prove next Theorem 4. Recall its statement.

Theorem 4. If G is a graph of order $n \ge 16$ and having no component with fewer than three vertices, then $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le n-1$.

Proof

Let G be a graph of order $n \ge 16$ and having no component with fewer than three vertices. First, assume that $\delta (G) = 1$, and let x be a vertex of degree 1 and y be its neighbor in G. The function $\overline{f}$ that assigns the weight 2 to x, the weight 1 to y, and the weight 0 to the remaining vertices of $\overline{G}$ is an ID-function of $\overline{G}$, implying that $\gamma _{I}(\overline{G}) \le \mathrm{w}(\overline{f}) = 3$. By Theorem 6, each component of G has Italian domination number at most three-fourths its order, and so $\gamma _{I}(G) \le \frac{3}{4}n$. Hence, $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le \frac{3}{4}n + 3 \le n-1$ since $n \ge 16$.

Thus, we may assume that $\delta (G) \ge 2$ and $\delta (\overline{G}) \ge 2$, for otherwise the desired result holds. By Theorem 6, $\gamma _{I}(G) \le \frac{2}{3}n$. If G is disconnected or $\mathrm{diam}(G) \ge 3$, then two vertices at distance 3 or more apart in G form a dominating set in $\overline{G}$. In this case, the function $\overline{f}$ that assigns the weight 2 to these two vertices and the weight 0 to the remaining vertices of $\overline{G}$ is an ID-function of $\overline{G}$, implying that $\gamma _{I}(\overline{G}) \le \mathrm{w}(\overline{f}) = 4$. Hence, $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le \frac{2}{3}n + 4 < n-1$ since $n \ge 16$. Thus, we may assume that $\mathrm{diam}(G) = \mathrm{diam}(\overline{G}) = 2$, for otherwise, the result holds. Let v be a vertex of minimum degree $\delta (G)$ in G. Since $\mathrm{diam}(G) = 2$, every vertex in $V(G) \setminus N[v]$ has at least one neighbor in N(v).

If $\delta (G) = 2$, then the function $\overline{f}$ that assigns the weight 2 to the vertex v, the weight 1 to the two neighbors of v in G, and the weight 0 to the remaining vertices of $\overline{G}$ is an ID-function of $\overline{G}$, implying that $\gamma _{I}(\overline{G}) \le \mathrm{w}(\overline{f}) = 4$ and again, $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le \frac{2}{3}n + 4 \le n-1$. Similarly, the result holds if $\delta (\overline{G}) = 2$.

Thus, we may assume that $\delta (G) \ge 3$ and $\delta (\overline{G}) \ge 3$. By Theorem 6, $\gamma _{I}(G) \le \frac{1}{2}n$ and $\gamma _{I}(\overline{G}) \le \frac{1}{2}n$. If some vertex $u \in V(G) \setminus N[v]$ has exactly one neighbor, say x, in N(v), then the function $\overline{f}$ that assigns the weight 2 to both u and v, the weight 1 to x, and the weight 0 to the remaining vertices of $\overline{G}$ is an ID-function of $\overline{G}$, implying that $\gamma _{I}(\overline{G}) \le \mathrm{w}(\overline{f}) = 5$. Hence, $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le \frac{1}{2}n + 5 < n-1$ since $n \ge 16$. The analogous result holds if such a vertex exists in $\overline{G}$.

Thus, we may assume that every vertex in $V(G) \setminus N[v]$ has at least two neighbors in N(v). The function f that assigns the weight 1 to every vertex in $N_G(v)$ and the weight 0 to the remaining vertices of G is an ID-function of G, implying that $\gamma _{I}(G) \le \mathrm{w}(f) = \delta (G)$. Similarly, $\gamma _{I}(\overline{G}) \le \delta (\overline{G})$. Hence, $\gamma _{I}(G) + \gamma _{I}(\overline{G}) \le \delta (G) + \delta (\overline{G}) = \delta (G) + n - \Delta (G) -1 \le n-1$. $\square$