On the Trace Norms of Orientations of Graphs

Abstract

The trace norm of the digraph is defined as the sum of the singular values of its adjacency matrix. We determine the orientations with, respectively, small and large trace norms among orientations of trees and unicyclic graphs, respectively.

1 Introduction

We consider digraphs without loops or multiple arcs. Let D be a digraph with vertex set V(D) and arc set E(D). Denote by uv the arc from vertex u to vertex v (i.e., the arc with tail u and head v). The outdegree (indegree, respectively) of a vertex u of D, denoted by $d_D^+(u)$ ($d_D^-(u)$, respectively), is the number of arcs of the form uv (vu, respectively) in D. A vertex u with $d_D^+(u)+d_D^-(u)=1$ is a leaf of D. A vertex u with $d_D^+(u)=0$ ($d_D^-(u)=0$, respectively) is called a sink (source, respectively) of D. The transpose $D^{\top }$ of a digraph D is obtained from D by reversing all arcs.

The adjacency matrix of an n-vertex digraph D is the $n\times n$ matrix $A(D)=(a_{uv})_{u,v\in V(G)}$, where $a_{uv}=1$ if $uv\in E(D)$ and 0 otherwise.

We mention that a (simple undirected) graph G corresponds naturally to a digraph D(G) with the same vertex set such that if there is an edge connecting vertices u and v in G, then there are arcs uv and vu in D(G). The adjacency matrix of G is $A(G)=A(D(G))$.

An orientation of a graph G is a digraph obtained by choosing a direction for each edge of G. A source-sink orientation (SS-orientation for short) of a graph G is an orientation such that each vertex is either a source or a sink.

For a real matrix M, its trace norm ${\mathcal {N}}(M)$ is the sum of singular values of M (i.e., the square roots of the eigenvalues of $MM^T$). For a (0, 1)-matrix M, bounds on ${\mathcal {N}}(M)$ may be found in [7, 12]. Agudelo et al. [3] studied the trace norm of a matrix related to the Laplacian matrix of a digraph.

For a digraph D, we call ${\mathcal {N}}(A(D))$ the trace norm of D. Let $\sigma _1, \dots , \sigma _n$ be the singular values of the A(D), arranged in a non-increasing order, where $n=|V(D)|$. Then, ${\mathcal {N}}(D)=\sum \limits _{i=1}^{n}\sigma _i$. If G is a graph, then $\varvec{\varepsilon }(G)={\mathcal {N}}(D(G))$ is just the energy of G, a graph invariant with many applications, being extensively studied [4, 8].

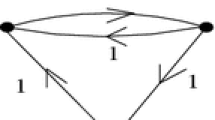
Let $P_n$ be a path on n vertices, and denote by $\overrightarrow{P_n}$ the directed path on n vertices. The vertices of $\overrightarrow{P_n}$ may be labeled as $v_1, \dots , v_n$ such that its arcs are $v_iv_{i+1}$ for $i=1, \dots , n-1$. Under this labeling, $v_1$ is the origin and $v_n$ is the end of $\overrightarrow{P_n}$. Let $C_n$ be a cycle on n vertices, where $n\ge 3$, and denote by $\overrightarrow{C_n}$ the directed cycle on n vertices. The vertices of $\overrightarrow{C_n}$ may be labeled as $v_1, \dots , v_n$ such that its arcs are $v_iv_{i+1}$ for $i=1, \dots , n$ with $v_{n+1}=v_1$. Let $S_n$ be the star on n vertices. Let $U_{n,3}$ with $n\ge 3$ be the graph obtained from $S_n$ by adding an edge (between two vertices of degree 1), and let $Y_n$ be the orientation of $U_{n,3}$ in Fig. 1.

Fig. 1

Digraph $Y_n$

Agudelo and Rada [2] gave lower bounds on the trace norm of digraphs. It is of interest to determine the orientations with minimum and maximum trace norms, respectively, among some classes of graphs. The classes of trees, unicyclic graphs, and bicyclic graphs have been considered by Agudelo et al. [1], Monsalve and Rada [9], and Monsalve, Rada, and Shi [10], respectively.

Theorem 1.1

[1] Let D be an orientation of a tree with n vertices. Then,

$$\begin{aligned} \sqrt{n-1}\le {\mathcal {N}}(D)\le n-1 \end{aligned}$$

with left equality if and only if D is isomorphic to an SS-orientation of $S_n$, and with right equality if and only if $D\cong \overrightarrow{P_n}$.

Theorem 1.2

[1] Let D be an orientation of a unicyclic graph with n vertices. Then,

$$\begin{aligned} {\mathcal {N}}(Y_n)\le {\mathcal {N}}(D)\le n \end{aligned}$$

with left equality if and only if D is isomorphic to $Y_n$ or $Y_n^{\top }$, and with right equality if and only if $D\cong \overrightarrow{C_n}$.

More results on the trace norms of digraphs may be found in [3, 11, 13].

We continue the study of the trace norms of orientations of trees and unicyclic graphs. We determine the orientations with small trace norms among all orientations of trees different from SS-orientations of $S_n$, the orientations with maximum trace norm among all orientations of trees different from $\overrightarrow{P_n}$, the orientations with minimum trace norm among all orientations of unicyclic graphs different from $Y_n$ and $Y_n^{\top }$, and the orientations with maximum trace norm among all orientations of unicyclic graphs different from $\overrightarrow{C_n}$. These results may help to understand graph energy in a broad sense.

2 Preliminaries

We need the following lemmas.

Lemma 2.1

[5] Let A be a $n\times n$ real matrix and B the submatrix of A obtained by deleting one row and one column of A. For $k=1,\dots , n-1$, we have

$$\begin{aligned} \sigma _k(A)\ge \sigma _k(B)\ge \sigma _{k+1}(A). \end{aligned}$$

Lemma 2.2

[5] Let A and C be $n\times n$ real matrices. Then,

$$\begin{aligned} \sum \limits _{i=1}^{n}|\sigma _i(A)-\sigma _i(C)|\le \sum \limits _{i=1}^{n}\sigma _i(A-C). \end{aligned}$$

Lemma 2.3

[1] Let D be a digraph and u a leaf of D. Then, ${\mathcal {N}}(D)-{\mathcal {N}}(D-u)\le 1$.

Let $D_i$ be a digraph with $v_i\in V(D_i)$ for $i=1,2$. The coalescence of the digraphs $D_1$ and $D_2$ with respect to the vertices $v_1$, $v_2$, denoted by $D_1\bullet _{v_1, v_2} D_2$, is the digraph obtained from $D_1$ and $D_2$ by identifying vertices $v_1$ and $v_2$. By similar argument as in the proof of Case 2 of Theorem 3.2 in [1], we have the following result.

Lemma 2.4

Let $D_i$ be a digraph with $v_i\in V(D_i)$ for $i=1,2$. Suppose that $v_1$ is a leaf of $D_1$ and $v_2$ is a leaf of $D_2$. Then, ${\mathcal {N}}(D_1\bullet _{v_1, v_2} D_2)\le {\mathcal {N}}(D_1)+{\mathcal {N}}(D_2)$.

Recall that the characteristic polynomial of a bipartite graph G with n vertices, denoted by $\phi (G, x)$, has the form

$$\begin{aligned} \phi (G, x)=\sum \limits _{k\ge 0}(-1)^kb_{2k}(G)x^{n-2k}, \end{aligned}$$

where $b_{2k}(G)\ge 0$ for all k. Let $G_1$ and $G_2$ be two bipartite graphs on n vertices. A quasi-order $\preceq$ is defined as $G_1\preceq G_2$ if $b_{2k}(G_1)\le b_{2k}(G_2)$ for all k. If $G_1\preceq G_2$ and $b_{2k}(G_1)<b_{2k}(G_2)$ for some k, then we write $G_1\prec G_2$. It turns out that $G_1\prec G_2\Rightarrow \varepsilon (G_1)< \varepsilon (G_2)$, see [8].

For integers a and b with $b\ge a\ge 1$, the tree obtained by adding an edge between the centers of two vertex-disjoint stars $S_{a+1}$ and $S_{b+1}$ is denoted by $B_{a+b+2}(a)$.

Lemma 2.5

[4] Let T be a tree with n vertices different from $S_n$, $B_n(1)$. Then,

$$\begin{aligned} \varepsilon (T)\ge \varepsilon (B_n(2))>\varepsilon (B_n(1))>\varepsilon (S_n) \end{aligned}$$

with equality if and only if $G\cong B_n(2)$.

For integer $n\ge 4$, the unicyclic graph obtained by attaching $n-4$ pendant edges at a vertex of a cycle of length 4 is denoted by $U_{n, 4}$.

Lemma 2.6

[6] Let G be a unicyclic graph with n vertices different from $U_{n,3}$. Then,

$$\begin{aligned} \varepsilon (G)\ge \varepsilon (U_{n,4})>\varepsilon (U_{n,3}). \end{aligned}$$

with equality if and only if $G\cong U_{n,4}$.

Lemma 2.7

[9] Let G be a graph and D an orientation of G. Then, $\varepsilon (G)\le 2{\mathcal {N}}(D)$ with equality if and only if D is an SS-orientation of G.

For vertex-disjoint graphs G and H, $G\cup H$ denotes the union of G and H, and kG denotes the union of k copies of G for integer $k\ge 2$.

3 Trace Norm of Orientations of Trees

First, we recall a result from [9].

Lemma 3.1

[9] Let D be a digraph. For $u\in V(D)$, let $N(u)=\{w\in V(D): wu\in E(D)\}$, and let D(u) be the digraph with vertex set $V(D)\cup \{u'\}$ and arc set $\left( E(D)\setminus \{wu: w\in N(u)\}\right) \cup \{wu': w\in N(u)\}$. For any $u\in V(D)$, we have ${\mathcal {N}}(D)={\mathcal {N}}(D(u))$.

Consider a digraph D. For a vertex u of D that is neither source nor sink, let $D'=D(u)$ as in Lemma 3.1. Then, u is a source and $u'$ is a sink in $D'$. If there exists a vertex in $D'$ that is neither a source nor a sink, then repeating this process, we may finally obtain a digraph ${\widetilde{D}}$, in which all vertices are either sources or sinks. The digraph ${\widetilde{D}}$ is called the SS-expansion of D. Let ${\widetilde{D}}=D$ if all vertices of D are either sources or sinks. Obviously, ${\widetilde{D}}$ consists of maximal vertex-disjoint digraphs whose vertices are either sources or sinks. In the sense of isomorphism, these maximal vertex-disjoint digraphs whose vertices are either sources or sinks of ${\widetilde{D}}$ may be viewed as maximal arc-disjoint subdigraphs whose vertices are either sources or sinks of D. Thus, we call these maximal vertex-disjoint digraphs whose vertices are either sources or sinks of ${\widetilde{D}}$ the maximal SS-subdigraphs of ${\widetilde{D}}$ or D. If D is an orientation of a tree, then the number of maximal SS-subdigraphs of D is one more than the number of vertices that are neither sources nor sinks.

Theorem 3.1

Let D be an orientation of a tree on n vertices, and $D_1, \dots , D_k$ be the maximal SS-subdigraphs of D. Then,

$$\begin{aligned} {\mathcal {N}}(D)=\sum _{i=1}^{k}{\mathcal {N}}(D_i). \end{aligned}$$

Proof

Note that $D_1, \dots , D_k$ are the maximal vertex-disjoint SS-subdigraphs of ${\widetilde{D}}$. By labeling the vertices of ${\widetilde{D}}$ properly, $A({\widetilde{D}})$ is a diagonal block matrix with diagonal blocks $A(D_1), \dots , A(D_k)$. Obviously, the singular values of $A({\widetilde{D}})$ consist of the singular values of $A(D_1), \dots , A(D_k)$. Thus, ${\mathcal {N}}({\widetilde{D}})=\sum _{i=1}^{k}{\mathcal {N}}(D_i)$. By Lemma 3.1, we have ${\mathcal {N}}(D)={\mathcal {N}}({\widetilde{D}})$. $\square$

Theorem 3.2

Let D be an orientation of a tree with n vertices, and $D\ncong \overrightarrow{P_n}$. Then, ${\mathcal {N}}(D)\le n-3+\sqrt{2}$ with equality if and only if D is obtainable by identifying the end (or origin) of some $\overrightarrow{P_s}$ and a vertex of some $\overrightarrow{P_t}$ except the origin (or end), where $s,t\ge 2$ and $s+t=n+1$.

Proof

Let T be the tree with orientation D. We only need to show that either ${\mathcal {N}}(D)<n-3+\sqrt{2}$ or ${\mathcal {N}}(D)=n-3+\sqrt{2}$ and D is obtainable by identifying the end (or origin) of some $\overrightarrow{P_s}$ and a vertex of some $\overrightarrow{P_t}$ except the origin (or end), where $s,t\ge 2$ and $s+t=n+1$.

Suppose first that the degree of u is at least 4 for some $u\in V(T)$. Then, T contains $S_5$ with center u. Let $D_1$ be the orientation of this $S_5$ in D. If $D_1$ contains an SS-orientation $D'$ of $S_4$, then by using Lemma 2.3 ($n-4$ times), we have

$$\begin{aligned} {\mathcal {N}}(D)\le n-4+{\mathcal {N}}(D')=n-4+\sqrt{3}<n-3+\sqrt{2}. \end{aligned}$$

Otherwise, $D_1$ consists of two arc-disjoint SS-orientations of $S_3$, ${\mathcal {N}}(D_1)=2\sqrt{2}$ by Theorem 3.1, and using Lemma 2.3 ($n-5$ times), we have

$$\begin{aligned} {\mathcal {N}}(D)\le n-5+{\mathcal {N}}(D_1)=n-5+2\sqrt{2}<n-3+\sqrt{2}. \end{aligned}$$

We assume that the maximum degree of T is at most 3. Suppose that there are two vertices with degree 3 in T. Then, D contains an SS-orientation of $S_4$, and as earlier, we have ${\mathcal {N}}(D)<n-3+\sqrt{2}$, or D contains two arc-disjoint SS-orientations of $S_3$. Assume that the latter case occurs. Let $D_1, \dots , D_k$ be the maximal SS-subdigraphs of D. We may assume that $D_i$ contains an SS-orientation of $S_3$ for $i=1,2$. Let $n_i=|V(D_i)|$ for $i=1,2,\dots ,k$. By considering the number of arcs in D, we have $\sum _{i=1}^k(n_1-1)=n-1$. For $i=1,2$, using Lemma 2.3 ($n_i-3$ times), we have ${\mathcal {N}}(D_i)\le {\mathcal {N}}(D^*)+n_i-3=n_i-3+\sqrt{2}$, where $D^*$ is an SS-orientation of $S_3$ in $D_i$. Now by Theorems 3.1 and 1.1,

$$\begin{aligned} \begin{array}{lll} {\mathcal {N}}(D) &{}=&{}{\mathcal {N}}(D_1)+{\mathcal {N}}(D_2)+\sum \limits _{i=3}^{k}{\mathcal {N}}(D_i)\\ &{}\le &{}n_1-3+\sqrt{2}+n_2-3+\sqrt{2}+\sum \limits _{i=3}^{k}(n_i-1)\\ &{}=&{} n-5+2\sqrt{2}\\ &{}<&{}n-3+\sqrt{2}, \end{array} \end{aligned}$$

Now we assume that the maximum degree of T is at most 3 and there is at most one vertex of degree 3. Let $V'$ be the set of vertices of T except leaves. If there are two vertices in $V'$ that are sources or sinks of D, then D contains two arc-disjoint SS-orientations of $S_3$, and as earlier, we have ${\mathcal {N}}(D)<n-3+\sqrt{2}$, or D contains an SS-orientation $D'$ of $P_4$, and thus we have by using Lemma 2.3 ($n-4$ times) that

$$\begin{aligned} {\mathcal {N}}(D)\le {\mathcal {N}}(D')+n-4=n-4+\sqrt{5}<n-3+\sqrt{2}. \end{aligned}$$

Now we assume that there is at most one vertex in $V'$ that is a source or a sink of D. There are two cases.

Suppose first that the maximum degree of T is 3, i.e., $T\not \cong P_n$. If v is a source or a sink of D for $v\in V'$, then D contains an SS-orientation of $S_4$ (if the degree of v in T is 3), or D contains two edge-disjoint SS-orientations of $S_3$ or an SS-orientation of $P_4$ (if the degree of v in T is 2), and in either case, we have ${\mathcal {N}}(D)<n-3+\sqrt{2}$, as earlier. We are left with the case that all vertices of degree 2 or 3 are neither sources nor sinks.

If $T\cong P_n$, then as $D\ncong \overrightarrow{P_n}$, there is exactly one vertex of degree 2 that is a source or a sink in D.

Therefore, D is obtainable by identifying the end (or origin) of some $\overrightarrow{P_s}$ and a vertex of some $\overrightarrow{P_t}$ except origin (or end), where $s,t\ge 2$ and $s+t=n+1$, for which we have by Theorem 3.1 that

$$\begin{aligned} {\mathcal {N}}(D)=(n-3){\mathcal {N}}(\overrightarrow{P_2})+{\mathcal {N}}(D')=n-3+\sqrt{2}, \end{aligned}$$

where $D'$ is an SS-orientation of $P_3$. $\square$

It follows from Theorems 1.1 and 3.2 that there is no orientation D of a tree on n vertices such that $n-3+\sqrt{2}<{\mathcal {N}}(D)<n-1$.

Recall that $\phi (nP_1,x)=x^n$ for $n\ge 1$, $\phi (S_{n},x) =x^n-(n-1)x^{n-2}$ for $n\ge 2$, and $\phi (B_n(a),x)=x^{n}-(n-1)x^{n-2}+a(n-2-a)x^{n-4}$ for $1\le a\le \lfloor \frac{n}{2}\rfloor -1$.

Lemma 3.2

$\varepsilon (S_2\cup S_{n-1})<\varepsilon (B_n(2))$ and $\varepsilon (S_{a+1}\cup S_{n-a})>\varepsilon (B_n(2))$ for $2\le a\le n-3$ and $n\ge 7$.

Proof

Obviously,

$$\begin{aligned} \phi (S_{a+1}\cup S_{n-a},x)= & {} \phi (S_{a+1},x)\phi (S_{n-a},x)\\= & {} (x^{a+1}-ax^{a-1})\left( x^{n-a}-(n-a-1)x^{n-a-2}\right) \\= & {} x^{n+1}-(n-1)x^{n-1}+a(n-a-1)x^{n-3} \end{aligned}$$

for $1\le a\le n-3$, and

$$\begin{aligned} \phi (B_n(2)\cup P_1,x)= & {} \phi (B_n(2),x)x\\= & {} x^{n+1}-(n-1)x^{n-1}+(2n-8)x^{n-3}. \end{aligned}$$

For $1\le a\le n-3$ and $n\ge 7$, we have

$$\begin{aligned} a(n-a-1){\left\{ \begin{array}{ll} =n-2<2n-8 &{} \text {if } a=1,\\ \ge 2n-6>2n-8 &{} \text {if } a\ge 2, \end{array}\right. } \end{aligned}$$

and thus $\varepsilon (S_2\cup S_{n-1})<\varepsilon (B_n(2))$ and $\varepsilon (S_{a+1}\cup S_{n-a})>\varepsilon (B_n(2))$ for $2\le a\le n-3$. $\square$

For $2\le a\le n-3$, we have

$$\begin{aligned}&\phi (S_{a+1}\cup B_{n-a}(1),x)\\= & {} \left( x^{a+1}-ax^{a-1}\right) \left( x^{n-a}-(n-a-1) x^{n-a-2}+(n-a-3)x^{n-a-4}\right) \\= & {} x^{n+1}-(n-1)x^{n-1}+(-a^2+(n-2)a+n-3)x^{n-3}-a(n-a-3)x^{n-5} \end{aligned}$$

and

$$\begin{aligned} \phi (S_2\cup B_{n-1}(1),x)=x^{n+1}-(n-1)x^{n-1}+(2n-6)x^{n-3}-(n-4)x^{n-5}. \end{aligned}$$

Thus, we have

Lemma 3.3

$\varepsilon (S_{a+1}\cup B_{n-a}(1))>\varepsilon (B_n(2))$ for $1\le a\le n-3$.

Lemma 3.4

$\varepsilon (S_2\cup S_{a+1}\cup S_{n-1-a})>\varepsilon (B_n(2))$ for $1\le a\le n-3$.

Proof

Note that

$$\begin{aligned} \begin{array}{lll} &{}&{}\phi (S_2\cup S_{a+1}\cup S_{n-1-a},x)\\ &{}=&{}(x^2-1)(x^{a+1}-ax^{a-1})\left( x^{n-1-a}-(n-a-2)x^{n-a-3}\right) \\ &{}=&{}x^{n+2}-(n-1)x^n+\left( -a^2+(n-2)a+(n-2)\right) x^{n-2}-a(n-2-a)x^{n-4} \end{array} \end{aligned}$$

and

$$\begin{aligned} \phi (B_n(2)\cup 2P_1,x)=x^{n+2}-(n-1)x^n+(2n-8)x^{n-2}. \end{aligned}$$

The result follows as $-a^2+(n-2)a+(n-2)\ge 2n-5>2n-8$. $\square$

Agudelo et al. [1] showed that among all orientations of trees of order n, the SS-orientations of $S_n$ achieve uniquely the minimum trace norm. For $0\le a\le \lfloor (n-1)/2\rfloor$, let ${\mathbb {S}}_{n,a}$ be the orientation of $S_n$ such that the outdegree of the center is a. For $0\le a\le n-3$, let ${\mathbb {B}}_{n,a}$ be the orientation of $B_n(1)$ containing $\overrightarrow{P_3}$ with end u such that the outdegree of u is a, where u is the vertex of $B_n(1)$ with degree $n-2$.

Theorem 3.3

Among the orientations of trees on n vertices with $n\ge 7$, the SS-orientations of $B_n(1)$ achieve uniquely the second smallest trace norm, ${\mathbb {S}}_{n,1}$, ${\mathbb {B}}_{n,0}$ and their transposes achieve uniquely the third smallest trace norm, and the SS-orientations of $B_n(2)$ achieve uniquely the fourth smallest trace norm.

Proof

Let T be a tree on n vertices and D an orientation of T, where D is not an SS-orientation of $S_n$.

Suppose first that $T\not \cong S_n, B_n(1)$. Then by Lemma 2.5, $\varepsilon (T)\ge \varepsilon (B_n(2))>\varepsilon (B_n(1))>\varepsilon (S_n)$ with equality if and only if $G\cong B_n(2)$. Let ${\mathbb {D}}$ be an SS-orientation of $B_n(2)$. By Lemma 2.7, we have

$$\begin{aligned} {\mathcal {N}}(D)\ge \frac{1}{2}\varepsilon (T)\ge \frac{1}{2}\varepsilon (B_n(2))={\mathcal {N}}({\mathbb {D}}) \end{aligned}$$

with equalities if and only if $T\cong B_n(2)$ and D is an SS-orientation of T, i.e., D is an SS-orientation of $B_n(2)$. Thus, if $T\not \cong S_n, B_n(1)$, then, among orientations of T, the SS-orientations of $B_n(2)$ achieve uniquely the smallest trace norm.

Suppose next that $T\cong S_n$. Then $D\cong {\mathbb {S}}_{n,a}$ or ${\mathbb {S}}_{n,a}^{\top }$ for some a with $1\le a\le \lfloor (n-1)/2\rfloor$ since D is not an SS-orientation of $S_n$. By Theorem 3.1 and by Lemma 2.7, we have

$$\begin{aligned} {\mathcal {N}}(D)={\mathcal {N}}(D_1)+{\mathcal {N}}(D_2)=\frac{1}{2}\varepsilon (S_{a+1}\cup S_{n-a}), \end{aligned}$$

where $D_1$ is an SS-orientation of $S_{a+1}$ and $D_2$ is an SS-orientation of $S_{n-a}$. By Lemmas 3.2 and 2.7 , we have

$$\begin{aligned} {\mathcal {N}}({\mathbb {S}}_{n,1})={\mathcal {N}} ({\mathbb {S}}_{n,1}^{\top })<{\mathcal {N}}({\mathbb {D}}) <{\mathcal {N}}({\mathbb {S}}_{n,a})={\mathcal {N}}({\mathbb {S}}_{n,a}^{\top }) \end{aligned}$$

for $2\le a\le \lfloor (n-1)/2\rfloor$.

Now suppose that $T\cong B_n(1)$. Let v be the vertex of degree 2 in $B_n(1)$.

Suppose that $d_D^+(v)d_D^-(v)=0$, say $d_D^-(v)=0$. If D is not an SS-orientation of $B_n(1)$, then $d_D^+(u)=a$ for some a with $1\le a\le n-3$, and by Lemma 3.3 and Theorem 3.1, we have

$$\begin{aligned} {\mathcal {N}}(D)={\mathcal {N}}(D_1)+ {\mathcal {N}}(D_2)=\frac{1}{2}\varepsilon (S_{a+1}\cup B_{n-a}(1))>\frac{1}{2}\varepsilon (B_n(2))={\mathcal {N}}({\mathbb {D}}), \end{aligned}$$

where $D_1$ is an SS-orientation of $S_{a+1}$ and $D_2$ is an SS-orientation of $B_{n-a}(1)$. If $d_D^+(v)d_D^-(v)\ne 0$, then $D, D^{\top }\cong {\mathbb {B}}_{n,b}$ for some b with $0\le b\le n-3$, and if $b\ge 1$, then by Theorem 3.1 and Lemmas 2.7 and 3.4 , we have

$$\begin{aligned} {\mathcal {N}}(D)={\mathcal {N}}(D_1)+{\mathcal {N}}(D_2)+{\mathcal {N}}(D_3)=\frac{1}{2}\varepsilon (S_2\cup S_{b+1}\cup S_{n-1-b})>\frac{1}{2}\varepsilon (B_n(2))={\mathcal {N}}({\mathbb {D}}), \end{aligned}$$

where $D_1$ is an SS-orientation of $S_2$, $D_2$ is an SS-orientation of $S_{b+1}$ and $D_3$ is an SS-orientation of $S_{n-1-b}$. Thus, if D is not an SS-orientation of $B_n(1)$, and $D, D^{\top }\not \cong {\mathbb {B}}_{n,0}$, we have

$$\begin{aligned} {\mathcal {N}}(D)>{\mathcal {N}}({\mathbb {D}}). \end{aligned}$$

Let ${\mathbb {B}}_n$ be an SS-orientation of $B_n(1)$. Note that $\varepsilon (S_2\cup S_{n-1})=x^{n+1}-(n-1)x^{n-1}+(n-2)x^{n-3}$ and $\varepsilon (B_n(1)\cup P_1)=x^{n+1}-(n-1)x^{n-1}+(n-3)x^{n-3}$. Thus, $\varepsilon (B_n(1))=\varepsilon (B_n(1)\cup P_1)<\varepsilon (S_2\cup S_{n-1})$. By Lemma 2.7, Theorem 3.1 and the fact that ${\mathcal {N}}({\mathbb {S}}_{n,1})<{\mathcal {N}}({\mathbb {D}})$, we have

$$\begin{aligned} {\mathcal {N}}({\mathbb {B}}_n)<{\mathcal {N}}({\mathbb {B}}_{n,0}) ={\mathcal {N}}(D_1)+{\mathcal {N}}(D_2)={\mathcal {N}}({\mathbb {S}}_{n,1}) <{\mathcal {N}}({\mathbb {D}}), \end{aligned}$$

where $D_1$ is an SS-orientation of $S_2$ and $D_2$ is an SS-orientation of $S_{n-1}$.

By Theorem 1.1 and combining the above three cases, the result follows. $\square$

4 Trace Norm of Orientations of Unicyclic Graphs

Lemma 4.1

Let D be an orientation of $C_n$ with u being a sink or source. Then, ${\mathcal {N}}(D)-{\mathcal {N}}(D-u)\le \sqrt{2}$.

Proof

Let $C_n=v_1v_2\dots v_nv_1$ with $u=v_1$. Assume that u is a source, i.e., $d_D^+(u)=2$ and $d_D^-(u)=0$. Consider the matrix A(D). The first row of A(D) is (0, 1, 0, ..., 0, 1) and the first column of A(D) is a zero vector. By deleting the first row and column from A(D), we obtain the adjacency matrix B of $D-u$. By Lemma 2.1,

$$\begin{aligned} \sigma _k(A)\ge \sigma _k(B)\ge \sigma _{k+1}(A) \end{aligned}$$

for $k=1,\dots , n-1$. Now consider the $n\times n$ matrix $C=\begin{pmatrix} 0 &{} 0\\ 0^T &{} B \end{pmatrix}$. Then $\sigma _k(C)=\sigma _k(B)$ for all $k=1,\dots , n-1$ and $\sigma _n(C)=0$. Furthermore, $\sigma _1(A-C)=\sqrt{2}$ and $\sigma _k(A-C)=0$ for all $k=2, \dots , n$. Since $|\sigma _i(A)-\sigma _i(C)|=\sigma _i(A)-\sigma _i(C)$ for all $i=1,\dots , n$, we have by Lemma 2.2 that

$$\begin{aligned} \begin{array}{lll} {\mathcal {N}}(D)-{\mathcal {N}}(D-u)&{}=&{}\sum \limits _{i=1}^{n}\sigma _i(A) -\sum \limits _{i=1}^{n-1}\sigma _i(B)\\ &{}=&{}\sum \limits _{i=1}^{n}\sigma _i(A)-\sum \limits _{i=1}^{n}\sigma _i(C)\\ &{}\le &{}\sum \limits _{i=1}^{n}\sigma _i(A-C)\\ &{}=&{}\sqrt{2}, \end{array} \end{aligned}$$

as desired. $\square$

Lemma 4.2

For $3\le k\le n-1$, let $D_{n,k}$ be the orientation of a graph on n-vertex oriented graphs shown in Fig. 2. Then, $\mathcal {N}(D_{n,k})=n-2+\sqrt{2}$.

Fig. 2

Digraph $D_{n,k}$

Proof

Let $D=D_{n,k}$. By Lemma 3.1 and Theorem 3.1, we have

$$\begin{aligned} {\mathcal {N}}(D)={\mathcal {N}}(D(v_1))=(n-2)\mathcal {\overrightarrow{P_2}}+{\mathcal {N}}(D')=n-2+\sqrt{2}, \end{aligned}$$

where $D'$ is an SS-orientation of $P_3$. $\square$

Lemma 4.3

Let D be an orientation of $C_n$ and $D\ne \overrightarrow{C_n}$. Then, ${\mathcal {N}}(D)\le n-3+\sqrt{5}$.

Proof

As $D\ne \overrightarrow{C_n}$, there is at least one sink or source in D. Suppose first that there is exactly one sink u in D, then there is exactly one source v in D. Let $w\in V(D)$ and $w\ne u,v$. By Lemma 3.1, ${\mathcal {N}}(D)={\mathcal {N}}(D(w))$. If $uv\in E(C_n)$, then by Theorem 3.1, ${\mathcal {N}}(D(w))=(n-3){\mathcal {N}}(\overrightarrow{P_2})+{\mathcal {N}}(D')=n-3+\sqrt{5}$, where $D'$ is an SS-orientation of $P_4$. If $uv\not \in E(C_n)$, then by Theorem 3.1, ${\mathcal {N}}(D(w))=(n-4){\mathcal {N}}(\overrightarrow{P_2})+2{\mathcal {N}}(D')=n-4+2\sqrt{2}<n-3+\sqrt{5}$, where $D'$ is an SS-orientation of $P_3$. Thus, ${\mathcal {N}}(D)={\mathcal {N}}(D(w))\le n-3+\sqrt{5}$.

Suppose now that D has at least two sinks. Let u be a sink of D. Then, $D-u$ is an oriented tree with $n-1$ vertices and $D-u\ne \overrightarrow{P_{n-1}}$. By Theorem 3.2, ${\mathcal {N}}(D-u)\le n-4+\sqrt{2}$. By Lemma 4.1, ${\mathcal {N}}(D)\le {\mathcal {N}}(D-u)+\sqrt{2}\le n-4+2\sqrt{2}<n-3+\sqrt{5}$. $\square$

Theorem 4.1

Let D be an oriented unicyclic graph with n vertices and $D\ne \overrightarrow{C_n}$. Then, ${\mathcal {N}}(D)\le n-2+\sqrt{2}$ with equality if and only if $D\cong D_{n,k}, D^{\top }_{n,k}$ for some k with $3\le k\le n-1$.

Proof

Let $G=G_D$. Assume that $C_k$ is the unique cycle of G. If $k=n$, then by Lemma 4.3, ${\mathcal {N}}(D)\le n-3+\sqrt{5}< n-2+\sqrt{2}$. Suppose that $k<n$. Let $D_1$ be the orientation of $C_k$ in D. If $D_1\ne \overrightarrow{C_k}$, then by Lemma 4.3, we have ${\mathcal {N}}(D_1)\le k-3+\sqrt{5}$, and thus by applying Lemma 2.3 ($n-k$ times), we have ${\mathcal {N}}(D)\le \mathcal {N}(D_1)+n-k\le k-3+\sqrt{5}+n-k=n-3+\sqrt{5}<n-2+\sqrt{2}$.

Assume that $D_1=\overrightarrow{C_k}$, $V(D_1)=\{v_1, \dots , v_k\}$ and $v_1v_2\in E(D_1)$.

If there is a vertex, say $v_1$, in $C_k$ with degree at least 4 in G, then this vertex has two neighbors outside $C_k$ in G, and thus D contains an induced subdigraph that is isomorphic to one of $U_1$ , $U^{\top }_1$ or $U_2$, where $U_1$ and $U_2$ are shown in Fig. 3. By Lemma 3.1 and Theorem 3.1, we have

$$\begin{aligned} {\mathcal {N}}(U_1)={\mathcal {N}}(U_1(v_1))=(k-1){\mathcal {N}}(\overrightarrow{P_2})+{\mathcal {N}}(D_1')=k-1+\sqrt{3}<k+\sqrt{2} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {N}}(U_2)={\mathcal {N}}(U_2(v_1))=(k-2){\mathcal {N}}(\overrightarrow{P_2})+2{\mathcal {N}}(D_2')=k-2+2\sqrt{2}<k+\sqrt{2}, \end{aligned}$$

where $D_1'$ is an SS-orientation of $S_4$ and $D_2'$ is an SS-orientation of $P_3$. Now with $i=1,2$, by applying Lemma 2.3 (repeatedly $n-(k+2)$ times), we have

$$\begin{aligned} {\mathcal {N}}(D)\le {\mathcal {N}}(U_i)+n-(k+2)<n-2+\sqrt{2}. \end{aligned}$$

Fig. 3

Digraphs $U_1$, $U_2$

If there are two vertices, say $v_1$ and $v_s$ with $s=2, \dots , k-1$, in $C_k$ with degree 3 in G, then each of them has a neighbor outside $C_k$ in G, and thus D contains an induced subdigraph $D^*$ that is isomorphic to one of the digraphs $W_{s,i}$, which are shown in Fig. 4 for $i=1,2,3,4$. By Lemma 3.1 and Theorem 3.1, if $(s,i)\ne (2,2)$, then

$$\begin{aligned} {\mathcal {N}}(W_{s,i})={\mathcal {N}}(W_{s,i}(v_1))=(k-2){\mathcal {N}}(\overrightarrow{P_2})+2{\mathcal {N}}(D_1')=k-2+2\sqrt{2} \end{aligned}$$

for $2\le s\le k-1$ and $1\le i\le 4$, and

$$\begin{aligned} {\mathcal {N}}(W_{2,2})={\mathcal {N}}(W_{2,2}(v_1))=(k-1){\mathcal {N}}(\overrightarrow{P_2})+{\mathcal {N}}(D_2')= k-1+\sqrt{5}, \end{aligned}$$

where $D_1'$ ($D_2'$, respectively) is an SS-orientation of $P_3$ ($P_4$, respectively). Thus, ${\mathcal {N}}(D^*)<k+\sqrt{2}$. In either case, by applying Lemma 2.3 (repeatedly $n-(k+2)$ times), we have

$$\begin{aligned} {\mathcal {N}}(D)\le {\mathcal {N}}(D^*)+n-(k+2)<n-2+\sqrt{2}. \end{aligned}$$

Fig. 4

Digraphs $W_{s,i}$ with $i=1,2,3,4$

Fig. 5

Digraphs $Q_1$, $Q_2$ and $Q_3$

Now we may assume that there is exactly one vertex, say $v_1$, in $C_k$ with degree 3 in G. Let $v_{k+1}$ be the unique neighbor of $v_1$ outside $C_k$. Suppose first that the degree of $v_{k+1}$ in G is at least 3. Then, D contains an induced subdigraph $D^*$ that is isomorphic to one of the digraphs $Q_i$ and $Q^{\top }_i$ for $i=1,2,3$, which are shown in Fig. 5. By Lemma 3.1 and Theorem 3.1, we have

$$\begin{aligned} {\mathcal {N}}(Q_1)= & {} {\mathcal {N}}(Q_1(v_1))=(k-1){\mathcal {N}}(\overrightarrow{P_2})+2{\mathcal {N}}(D_1')=k-1+2\sqrt{2}<k+1+\sqrt{2},\\ {\mathcal {N}}(Q_2)= & {} {\mathcal {N}}(Q_2(v_1))=k{\mathcal {N}}(\overrightarrow{P_2})+{\mathcal {N}}(D_2')=k+\sqrt{5} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {N}}(Q_3)={\mathcal {N}}(Q_3(v_1))\le k{\mathcal {N}}(\overrightarrow{P_2})+{\mathcal {N}}(D_2')=k+\sqrt{5}< k+1+\sqrt{2}, \end{aligned}$$

where $D_1'$ is an SS-orientation of $P_3$ and $D_2'$ is an SS-orientation of $P_4$. Thus, ${\mathcal {N}}(D^*)<k+1+\sqrt{2}$. Using Lemma 2.3 by $n-(k+3)$ times, we have

$$\begin{aligned} {\mathcal {N}}(D)\le {\mathcal {N}}(D^*)+n-(k+3)<n-2+\sqrt{2}. \end{aligned}$$

Assume that the degree of $v_{k+1}$ in G is 1 or 2. If the degree of $v_{k+1}$ in G is 1, then $D\cong D_{n,n-1}$, $D^{\top }_{n,n-1}$, and by Lemma 4.2, ${\mathcal {N}}(D)=n-2+\sqrt{2}$.

Assume that the degree of $v_{k+1}$ in G is 2. Then, $D=P\bullet _{v_{k+1},v} Q$, where $P=D_{k+1,k}$ or $D^{\top }_{k+1,k}$ and Q is an orientation of tree on $n-k$ vertices. Note that $v_{k+1}$ is a leaf of P and v is a leaf of Q. By Lemma 4.2, ${\mathcal {N}}(P)=(k+1)-2+\sqrt{2}$. If $Q\ne \overrightarrow{P_{n-k}}$, then by Theorem 3.2, ${\mathcal {N}}(Q)\le n-k-3+\sqrt{2}$, and by Lemma 2.4, we have

$$\begin{aligned} {\mathcal {N}}(D)\le & {} {\mathcal {N}}(P)+{\mathcal {N}}(Q)\le (k+1)-2+\sqrt{2}+n-k-3+\sqrt{2}\\= & {} n-4+2\sqrt{2}<n-2+\sqrt{2}. \end{aligned}$$

If $Q=\overrightarrow{P_{n-k}}$, then $D=D_{n,k}$, $D^{\top }_{n,k}$ with $3\le k\le n-2$ or D contains an induced subdigraph that is isomorphic to ${\hat{D}}$ or ${\hat{D}}^{\top }$, where ${\hat{D}}$ is shown in Fig. 6.

Fig. 6

Digraph ${\hat{D}}$

Suppose that $D\not \cong D_{n,k}$ or $D^{\top }_{n,k}$. By Lemma 3.1 and Theorem 3.1, we have

$$\begin{aligned} {\mathcal {N}}({\hat{D}})={\mathcal {N}}({\hat{D}}(v_1))=(k-1){\mathcal {N}}(\overrightarrow{P_2})+{\mathcal {N}}(D')=k-1+\sqrt{5}<k+\sqrt{2}, \end{aligned}$$

where $D'$ is an SS-orientation of $P_4$. Using Lemma 2.3 by $n-(k+2)$ times, we have

$$\begin{aligned} {\mathcal {N}}(D)\le {\mathcal {N}}({\hat{D}})+n-(k+2)<n-2+\sqrt{2}. \end{aligned}$$

If $D=D_{n,k}$ or $D^{\top }_{n,k}$, then by Lemma 4.2, ${\mathcal {N}}(D)=n-2+\sqrt{2}$. $\square$

In [9], Monsalve and Rada proved that $Y_n$ or $Y_n^{\top }$ achieves uniquely the minimum trace norm over the set of orientations of unicyclic graphs with $n\ge 7$ vertices.

Lemma 4.4

$\varepsilon (U_{n,4})<\varepsilon (B_{n-k+1}(1)\cup S_{k+1})$ for $1\le k\le n-3$.

Proof

It is obvious that $U_{n,4}$ and $U_{n,4}\cup 2P_1$ have equal energy. By Sachs theorem,

$$\begin{aligned} \begin{array}{lll} &{}&{}\phi (B_{n-k+1}(1)\cup S_{k+1},x)\\ &{}=&{}\left( x^{n-k+1}-(n-k)x^{n-k-1}+(n-k-2)x^{n-k-3}\right) (x^{k+1}-kx^{k-1})\\ &{}=&{}x^{n+2}-nx^n+\left( -k^2+(n-1)k+n-2\right) x^{n-2}-k(n-k-2)x^{n-4} \end{array} \end{aligned}$$

and

$$\begin{aligned} \phi (U_{n,4}\cup 2P_1,x)= x^{n+2}-nx^n+(2n-8)x^{n-2}. \end{aligned}$$

Let $f(k)=-k^2+(n-1)k+n-2$ with $1\le k\le n-3$. Then, $f(k)\ge \min \{f(1), f(n-3)\}=2n-4>2n-8$. The result follows from the increasing property of the energy. $\square$

Let $DS_n$ be the tree obtained from $P_4=v_1v_2v_3v_4$ by attaching k pendent vertices to $v_1$ and $n-4-k$ pendent vertices to $v_4$.

Lemma 4.5

$\varepsilon (U_{n,4})<\varepsilon (DS_{n+1})$ for $n\ge 4$.

Proof

By Sachs theorem,

$$\begin{aligned} \phi (DS_{n+1}, x)&=x^{n+1}-nx^{n-1}+\left( -k^2+(n-3)k+2n-5\right) x^{n-3}\\&\quad -k(n-k-3)x^{n-5} \end{aligned}$$

and

$$\begin{aligned} \phi (U_{n,4}\cup P_1, x)= x^{n+1}-nx^{n-1}+(2n-8)x^{n-3}. \end{aligned}$$

Let $g(k)=-k^2+(n-3)k+2n-5$ with $0\le k\le n-3$. Then, $g(k)\ge \min \{g(0), g(n-3)\}=2n-5>2n-8$. The result follows from the increasing property of the energy. $\square$

Let ${\mathbb {U}}_{n,4}$ be an SS-orientation of $U_{n,4}$.

Theorem 4.2

Let D be an orientation of a unicyclic graph with n vertices different from $Y_n$, $Y_n^{\top }$. Then,

$$\begin{aligned} {\mathcal {N}}(D)\ge {\mathcal {N}}({\mathbb {U}}_{n,4})>{\mathcal {N}}(Y_n)={\mathcal {N}}(Y_n^{\top }) \end{aligned}$$

with equality if and only if D is an SS-orientation of $U_{n,4}$.

Proof

Let $G=G_D$. If $G\not \cong U_{n,3}$, then by Lemmas 2.6 and 2.7, we have

$$\begin{aligned} {\mathcal {N}}(D)\ge \frac{1}{2}\varepsilon (G)\ge \frac{1}{2}\varepsilon (U_{n,4})={\mathcal {N}}({\mathbb {U}}_{n,4}) \end{aligned}$$

with equality if and only if $G\cong U_{n,4}$ and D is an SS-orientation of G. From [9], we have

$$\begin{aligned} {\mathcal {N}}({\mathbb {U}}_{n,4})>{\mathcal {N}}(Y_n)={\mathcal {N}}(Y_n^{\top }). \end{aligned}$$

Suppose that $G\cong U_{n,3}$ and $D\not \cong Y_n, Y_n^{\top }$. Then D is of the form ${\mathbb {U}}_{n,3; i}$, ${\mathbb {U}}_{n,3; i}^{\top }$ with $i=1,2,3$, which are displayed in Fig. 7, and in ${\mathbb {U}}_{n,3; 1}$ the indegree of v is k, $1\le k\le n-3$, and in ${\mathbb {U}}_{n,3; i}$ with $i=2,3$, the indegree of v is $k+1$, $0\le k\le n-3$.

Fig. 7

Digraphs ${\mathbb {U}}_{n,3;1}$, ${\mathbb {U}}_{n,3; 2}$, ${\mathbb {U}}_{n,3; 3}$

If $D,D^{\top }\cong {\mathbb {U}}_{n,3;1}, {\mathbb {U}}_{n,3;1}^{\top }$, then by Lemmas 2.7, 3.1 and  4.4 and Theorem 3.1,

$$\begin{aligned} {\mathcal {N}}(D)&={\mathcal {N}}(D(v))={\mathcal {N}}(D_1)+{\mathcal {N}}(D_2)\\&=\frac{1}{2}\varepsilon (B_{n-k+1}(1)\cup S_{k+1})>\frac{1}{2}\varepsilon (U_{n,4})={\mathcal {N}}({\mathbb {U}}_{n,4}), \end{aligned}$$

where $D_1$ is an SS-orientation of $B_{n-k+1}(1)$ and $D_2$ is an SS-orientation of $S_{k+1}$.

If $D,D^{\top }\cong {\mathbb {U}}_{n,3;i}, {\mathbb {U}}_{n,3;i}^{\top }$ with $i=2,3$, then by Lemmas 2.7, 3.1 and 4.5 ,

$$\begin{aligned} {\mathcal {N}}(D)={\mathcal {N}}(D(v))\ge \frac{1}{2}\varepsilon (DS_{n+1})> \frac{1}{2}\varepsilon (U_{n,4})={\mathcal {N}}({\mathbb {U}}_{n,4}). \end{aligned}$$

The result follows. $\square$