Strong Geodetic Number of Graphs and Connectivity

Abstract

A recent variation of the classical geodetic problem, the strong geodetic problem, is defined as follows. If G is a graph, then $\mathrm{sg}(G)$ is the cardinality of a smallest vertex subset S, such that one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these ${|S|\atopwithdelims ()2}$ geodesics cover all the vertices of G. In this paper, we first give some bounds for strong geodetic number in terms of diameter, connectivity, respectively. Next, we show that $2\le \mathrm{sg}(G)\le n$ for a connected graph G of order n, and graphs with $\mathrm{sg}(G)=2,n-1,n$ are characterized, respectively. In the end, we investigate the Nordhaus–Gaddum-type problem and extremal problems for strong geodetic number.

1 Introduction

Let V(G), E(G), e(G), $\overline{G}$, d(G) be the vertex set, edge set, size, complement, diameter of G, respectively. Covering vertices of a graph with shortest paths is a problem that naturally appears in different applications; modeling them as graphs, one arrives at different variations of the graph problem. Given a pair of vertices u and v in a graph G, the shortest path interval between u and v is the set of all vertices contained in shortest paths from u to v. The classical geodetic problem [7] is to determine a smallest set of vertices S of a given graph such that the (shortest path) intervals between them cover all the vertices. For more details on this subject, we refer to the survey [2] and the book [11] for a general framework on the geodesic convexity. Recent developments on the geodetic problem include the papers [3, 4, 12], for a detailed literature survey see [8, 9]. Another variation of the shortest path covering problem is the isometric path problem [5] where one is asked to determine the minimum number of geodesics required to cover the vertices; see [10]. Motivated by applications in social networks, very recently the so-called strong geodetic problem was introduced in [8] as follows.

Let $G=(V,E)$ be a graph. Given a set $S\subseteq V$, for each pair of vertices $\{x, y\}\subseteq S$, $x\ne y$, let $\widetilde{P}(x,y)$ be a selected fixed shortest path between x and y. Then we set

$$\begin{aligned}\widetilde{I}(S)=\{\widetilde{P}(x,y):x,y\in S\},\end{aligned}$$

and let $V(\widetilde{I}(S))=\bigcup _{\widetilde{P}\in \widetilde{I}(S)} V(\widetilde{P})$. If $V(\widetilde{I}(S))=V$ for some collection of paths $\widetilde{I}(S)$, then the set S is called a strong geodetic set. The strong geodetic problem is to find a minimum strong geodetic set S of G. Clearly, the collection $\widetilde{I}(S)$ of geodesics consists of exactly ${|S|\atopwithdelims ()2}$ paths. The cardinality of a minimum strong geodetic set is the strong geodetic number of G and denoted by $\mathrm{sg}(G)$. For the edge version of the strong geodetic problem, we refer the reader to [9].

In [8] it was proved that the problem of deciding whether the strong geodetic number equals a given value is NP-complete.

Let $\mathcal {G}(n)$ denote the class of simple graphs of order $n \ (n\ge 2)$ and $\mathcal {G}(n,m)$ the subclass of $\mathcal {G}(n)$ in which every graph has n vertices and m edges. Give a graph parameter f(G) and a positive integer n, the Nordhaus–Gaddum Problem is to determine sharp bounds for (1) $f(G)+f(\overline{G})$ and (2) $f(G)\cdot f(\overline{G})$, as G ranges over the class $\mathcal {G}(n)$, and characterize the extremal graphs, i.e., graphs that achieve the bounds. Nordhaus–Gaddum-type results in general have received wide attention; see a recent survey paper [1] by Aouchiche and Hansen.

In Sect. 2, we give some bounds for strong geodetic number in terms of diameter, connectivity, respectively, and give sharp upper and lower bounds for join and corona graphs. In Sects. 3 and 4, we show that $2\le \mathrm{sg}(G)\le n$ for a connected graph G of order n, and graphs with $\mathrm{sg}(G)=2,n-1,n$ are characterized, respectively. In Sects. 5 and 6, we investigate the Nordhaus–Gaddum-type problem and extremal problems for strong geodetic number, respectively.

In particular, in Sect. 6, we consider the following problems.

Problem 1

Given two positive integers n and k, compute the minimum integer

$$\begin{aligned} s(n,k)=\min \{|E(G)|:G\in \mathscr {G}(n,k)\}, \end{aligned}$$

where $\mathscr {G}(n,k)$ the set of all graphs of order n (that is, with n vertices) with strong geodetic number k, where $2\le k\le n$.

Problem 2

Given two positive integers n and k, compute the minimum integer f(n, k) such that for every connected graph G of order n, if $|E(G)|\ge f(n,k)$ then $\mathrm{sg}(G)\ge k$.

Problem 3

Given two positive integers n and k, compute the maximum integer g(n, k) such that for every graph G of order n, if $|E(G)|\le g(n,k)$ then $\mathrm{sg}(G)\le k$.

2 Bounds for Strong Geodetic Number

For trees, the following observation is immediate.

Observation 2.1

If T is any tree, then $\mathrm{sg}(T)$ equals the number of leaves in T.

Given a vertex x and a set U of vertices, an (x, U)-fan is a set of paths from x to U such that each pair of paths shares only the vertex x. The size of a (x, U)-fan is the number of internally disjoint paths from x to U.

Lemma 2.1

(Fan Lemma, [13], p. 170) A graph is k-connected if and only if it has at least $k+1$ vertices, and for every choice of a vertex x and a set U with $|U|\ge k$, the graph has an (x, U)-fan of size k.

By the Fan Lemma, we can derive the following result.

Theorem 2.1

Let G be a connected graph of order $n \ (n\ge 2)$, and let k be a positive integer. If $\mathrm{sg}(G)=n-k$, then $\kappa (G)\le k$ or $\kappa (G)\ge n-2k$.

Proof

If $n\le 3k+1$, then trivially $\kappa (G)\le k$ or $\kappa (G)\ge k+1\ge n-2k$, as desired. We may therefore assume that $n\ge 3k+2$ and assume, for a contradiction, that $k+1\le \kappa (G)\le n-2k-1$. Let $\kappa (G)=r$ so $k+1\le r\le n-2k-1$ and $n-r\ge 2k+1$. Let X be a minimum vertex cut set of G so $|X|=r\ge k+1$. Let $C_1,C_2,\ldots ,C_t$ be the components of $G-X$, of which $C_{t}$ is the smallest. Set $A=\bigcup _{i=1}^{t-1}V(C_i)$ and $x\in V(C_t)$. Clearly, $|A| \ge k + 1$. Choose $Y\subseteq A$ so that $|Y|=k+1$. Because G is $(k+1)$-connected, there is an (x, Y)-fan of size $k+1$ in G. Let $P_1,P_2,\ldots ,P_{k+1}$ be the $k+1$ internally disjoint paths in this fan. Let $Z=(\bigcup _{i=1}^{k+1}V(P_i))-Y-x$. Since $E_G[A,C_t]=\emptyset$, it follows that $|Z\cap X|\ge k+1$. Choose $k+1$ vertices in $Z\cap X$, say $v_1,v_2,\ldots ,v_{k+1}$, such that $v_i\in V(P_i)$. Let $S=V(G)-\{v_1,v_2,\ldots ,v_{k+1}\}$. For each $v_i \ (1\le i\le k+1)$, it has two nonadjacent neighbors in $P_i$, say $a_i,b_i$. Since $a_ib_i\notin E(G)$, it follows that a strong geodetic set connecting $a_i$ and $b_i$ can use the vertex $v_i$. So one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these geodesics cover all the vertices of G. So $\mathrm{sg}(G)\le |S|\le n-k-1$, a contradiction. Therefore, $\kappa (G)\le k$ or $\kappa (G)\ge n-2k$. $\square$

Iršič [6] obtained the upper and lower bounds of $\mathrm{sg}(G)$ in terms of diameter.

Theorem 2.2

[6] Let G be a connected graph of order $n \ (n\ge 2)$ with diameter d. Then

$$\begin{aligned} \left\lceil \frac{d(G)-3+\sqrt{(d(G)-3)^2+8n(d(G)-1)}}{2(d(G)-1)}\right\rceil \le \mathrm{sg}(G)\le n-d(G)+1. \end{aligned}$$

Similarly to the proof of Theorem 2.1, we can derive the following upper bound for strong geodetic number.

Proposition 2.1

Let G be a connected non-complete graph of order $n \ (n\ge 3)$. Then

$$\begin{aligned} \mathrm{sg}(G)\le \max \left\{ \left\lfloor \frac{n+\kappa (G)}{2}\right\rfloor ,n-\kappa (G)\right\} . \end{aligned}$$

Proof

Let X be a vertex cut set such that $|X|=\kappa (G)$. Let $C_1,C_2,\ldots ,C_r$ be the connected components of $G-X$. Note that $\sum _{i=1}^r|C_r|=n-\kappa (G)$. Let $C'=\bigcup _{i=1}^{r-1}C_i$. Then $|C_r|\ge \lceil \frac{n-\kappa (G)}{2}\rceil$ or $|C'|\ge \lceil \frac{n-\kappa (G)}{2}\rceil$. Without loss of generality, we suppose $|C'|\ge \lceil \frac{n-\kappa (G)}{2}\rceil$. Let $p=\min \left\{ \left\lceil \frac{n-\kappa (G)}{2}\right\rceil ,\kappa (G)\right\}$. Choose $v\in C_r$, $U\subseteq C'$ and $|U|=p$. From Lemma 2.1, there is an (v, U)-fan in G and this fan has p common vertices with X. Choose the other $n-p$ vertices as S. Then these geodesics cover all the vertices of G. So $\mathrm{sg}(G)\le \max \left\{ \left\lfloor \frac{n+\kappa (G)}{2}\right\rfloor ,n-\kappa (G)\right\}$. $\square$

To show the sharpness of the above upper bound, we consider the following example.

Example 1

For $n\ge 7$, we let G be a graph obtained from $K_{n-1}$ by adding a pendent edge. Then $\mathrm{sg}(G)=n-1=\max \left\{ \left\lfloor \frac{n+\kappa (G)}{2}\right\rfloor ,n-\kappa (G)\right\}$.

3 Results for Some Graph Classes

The graph join and corona operations are defined as follows.

• The join or complete product of two disjoint graphs G and H, denoted by $G\vee H$, is the graph with vertex set $V(G)\cup V(H)$ and edge set $E(G)\cup E(H)\cup \{uv\,|\, u\in V(G), v\in V(H)\}$.

• The corona$G*H$ is obtained by taking one copy of G and |V(G)| copies of H, and by joining each vertex of the ith copy of H with the ith vertex of G, where $i=1,2,\ldots ,|V(G)|$.

Proposition 3.1

Let G, H be two connected graphs such that G or H is not complete. Then

$$\begin{aligned} \mathrm{sg}(G\vee H)\le & {} \max \left\{ |V(G)|+\max \{|V(H)|-|E(\overline{G})|,0\},|V(H)|\right. \\&\left. +\max \{|V(G)|-|E(\overline{H})|,0\}\right\} , \end{aligned}$$

and

$$\begin{aligned} \mathrm{sg}(G\vee H)\ge \left\lceil \frac{-1+\sqrt{8(|V(G)|+|V(H)|)+1}}{2}\right\rceil . \end{aligned}$$

Proof

For each pair of nonadjacent vertices in G, the connecting path can cover a vertex of H. Observe that there are $|E(\overline{G})|$ such pairs. Choose $S=V(G)\cup X$ with $X\subseteq V(H)$ and $|X|=|V(H)|-|E(\overline{G})|$. Then the geodesics cover all the vertices of $G\vee H$, and hence $\mathrm{sg}(G\vee H)\le |V(G)|+\max \{|V(H)|-|E(\overline{G})|,0\}$. Similarly, $\mathrm{sg}(G\vee H)\le |V(H)|+\max \{|V(G)|-|E(\overline{H})|,0\}$. The result follows. The lower bound follows from Theorem 2.2. $\square$

To show the sharpness of upper and lower bounds, we consider the following examples.

Example 2

Let G, H be complete graphs of order n, m, respectively. Then $\mathrm{sg}(G\vee H)=n+m$ and $|V(G)|+\max \{|V(H)|-|E(\overline{G})|,0\}=|V(G)|+|V(H)|=n+m$ and $|V(H)|+\max \{|V(G)|-|E(\overline{H})|,0\}=|V(G)|+|V(H)|=n+m$. This implies that the upper bound is sharp.

Example 3

Let G be a graph obtained from a clique $K_n$ by adding x pendent edges $u_iv_i \ (1\le i\le x)$ such that $u_i\in V(K_n)$, and let H be a clique of order m, such that $n+m={x\atopwithdelims ()2}$. Then $|V(G)|=n+x$ and $|V(H)|=m$, and hence $\lceil \tfrac{-1+2\sqrt{2(|V(G)|+|V(H)|)+1}}{2}\rceil =x$. Clearly, $\mathrm{sg}(G\vee H)=x$. This implies that the lower bound is sharp.

Proposition 3.2

Let G, H be two connected graphs. Then

$$\begin{aligned} \mathrm{sg}(H)|V(G)|\le \mathrm{sg}(G*H)\le |V(G)|\left( |V(H)|-\left\lfloor \frac{\mathrm{d}(H)-1}{2}\right\rfloor \right) \end{aligned}$$

Proof

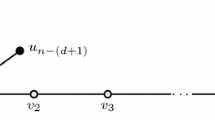
Let $V(G)=\{u_i\,|\,1\le i\le n\}$, and $H(u_i) \ (1\le i\le n)$ be the copies of H in $G*H$, and $V(H(u_i))=\{(u_i,v_j)\,|\,1\le j\le m\} \ (1\le i\le n)$, where $|V(H)|=m$. Let $v_1v_2\ldots v_{d+1}$ be a shortest path between $v_1$ and $v_{d+1}$ in H. For each $H(u_i) \ (1\le i\le n)$, let $(u_i,v_1),(u_i,v_{d+1})$ be the two vertices such their distance in $H(u_i)$ is $\mathrm{d}(H)$. Let $X_i=\{(u_i,v_{2j})\,|\,1\le j\le \lfloor \frac{d-1}{2}\rfloor \}$. Note that $|V(H(u_i))|-|X_i|=m-\lfloor \frac{d-1}{2}\rfloor =|V(H)|-\left\lfloor \frac{\mathrm{d}(H)-1}{2}\right\rfloor$. Choose $S=V(G*H)-\bigcup _{i=1}^nX_i=\bigcup _{i=1}^n(V(H(u_i))-X_i)$. For each $u_i \ (1\le i\le n)$, the geodesic from $(u_i,v_1)$ to $(u_i,v_{d+1})$ can cover it; for the vertex $(u_i,v_{2j}) \ (1\le j\le \lfloor \frac{d-1}{2}\rfloor )$, it can be covered by the geodesic from $(u_i,v_{2j-1})$ to $(u_i,v_{2j+1})$. It is clear that

$$\begin{aligned} \mathrm{sg}(H)|V(G)|\le \mathrm{sg}(G*H)\le |V(G)|\left( |V(H)|-\left\lfloor \frac{\mathrm{d}(H)-1}{2}\right\rfloor \right) . \end{aligned}$$

$\square$

To show the sharpness of upper and lower bounds, we consider the following example.

Example 4

Let H be a complete graph. Then $\mathrm{sg}(H)=|V(H)|$ and hence $\mathrm{sg}(G*H)=|V(G)||V(H)|$. This implies that the upper and lower bounds are sharp.

4 Graphs with Given Strong Geodetic Number

The following proposition is easily seen.

Proposition 4.1

Let G be a connected graph of order $n \ (n\ge 2)$. Then

$$\begin{aligned} 2\le \mathrm{sg}(G)\le n. \end{aligned}$$

We first classify those graphs with strong geodetic number equal to the lower bound of 2.

Proposition 4.2

Let G be a connected graph of order $n \ (n\ge 2)$. Then $\mathrm{sg}(G)=2$ if and only if G is a path.

Proof

If G is a path, then $\mathrm{sg}(G)=2$. Conversely, we suppose $\mathrm{sg}(G)=2$. From the definition, there exist an $S\subseteq V(G)$ with $|S|=2$ such that there is a shortest path connecting S that covers all vertices in $V(G)-S$. Let $S=\{x,y\}$. Then $d_G(x,y)=n-1$, and hence $\mathrm{diam}(G)\ge n-1$, so G is a path. $\square$

Next we classify those graphs with strong geodetic number at the opposite extreme from Proposition 4.1, equal to the order of the graph.

Proposition 4.3

Let G be a connected graph of order $n \ (n\ge 2)$. Then $\mathrm{sg}(G)=n$ if and only if G is a complete graph of order n.

Proof

Suppose $\mathrm{sg}(G)=n$. We claim that G is a complete graph of order n. Assume, to the contrary, that $G\ne K_n$. Then there exist two vertices $u,v\in V(G)$ such that $uv\notin E(G)$. Let $P=uw_1w_2\ldots w_rv$ be one of the shortest paths connecting u, v in G, where $r\ge 1$. Let $S=V(G)-\{w_1,w_2,\ldots ,w_{r}\}$. For each $\{x,y\}\subseteq S$, one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these geodesics cover all the vertices of G. So $\mathrm{sg}(G)\le |S|\le n-r\le n-1$, a contradiction. So G is a complete graph of order n.

Conversely, we suppose G is a complete graph of order n. Then for any pair of vertices (u, v), the unique geodesic between u and v is the edge uv. This means that no geodesic covers any vertices other than its endpoints, so all vertices must be in any strong geodetic set S, so $|S| = n$. $\square$

One step further, we classify those graphs with strong geodetic number equal to one less than the order of the graph.

Theorem 4.1

Let G be a connected graph of order $n \ (n\ge 6)$. Then $\mathrm{sg}(G)=n-1$ if and only if G satisfies one of the following.

• There is a cut vertex v of G such that each induced subgraph $G[V(C_i)\cup \{v\}] \ (1\le i\le t)$ is complete, where $C_1,C_2,\ldots ,C_t$ be the connected components of $G-v$.

• $G=K_n{\setminus } e$, where $e\in E(K_n)$.

Proof

Suppose $\mathrm{sg}(G)=n-1$. From Theorem 2.1, $\kappa (G)\le 1$ or $\kappa (G)\ge n-2$. Clearly, $\kappa (G)=1$ or $\kappa (G)=n-2$. If $\kappa (G)=1$, then there exist a cut vertex v. Let $C_1,C_2,\ldots ,C_t$ be the connected components of $G-v$. We have the following claim.

Claim 1

Each induced subgraph $G[V(C_i)\cup \{v\}] \ (1\le i\le t)$ is complete.

Proof of Claim 1

Assume, to the contrary, that $G[V(C_i)\cup \{v\}] \ (1\le i\le t)$ is not complete. Then there exist two vertices $w_1,w_2$ in some $C_j$ such that $w_1w_2\notin E(G)$, or there exists a vertex w in some $C_j$ such that $wv\notin E(G)$. For the latter case, we have $\mathrm{diam}(G)\ge 3$. From Theorem 2.2, we have $\mathrm{sg}(G)\le n-\mathrm{diam}(G)+1\le n-3+1=n-2$, a contradiction. For the former case, there is a shortest path $w_1v_1v_2\ldots v_rw_2$ connecting $w_1$ and $w_2$ in $C_j$, where $r\ge 1$. Let $S=V(G)-\{v_1,v_2,\ldots ,v_{r},v\}$. For the vertex pair $w_1,w_2$, geodesic set $\widetilde{P}(w_1,w_2)$ cover all the vertices in $\{v_1,v_2,\ldots ,v_{r}\}$. For the vertex pair $u_1\in C_i$ and $u_2\in C_j$, geodesic set $\widetilde{P}(u_1,u_2)$ cover the vertex v. So one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these geodesics cover all the vertices of G. So $\mathrm{sg}(G)\le |S|\le n-r-1\le n-2$, a contradiction. $\square$

From Claim 1, there is a cut vertex v of G such that each induced subgraph $G[V(C_i)\cup \{v\}] \ (1\le i\le t)$ is complete, where $C_1,C_2,\ldots ,C_t$ be the connected components of $G-v$.

If $\kappa (G)=n-2$, then $\delta (G)\ge n-2$ and hence G is a graph obtained from $K_n$ by deleting a matching M. Suppose $|M|\ge 2$. Let $u_1v_1,u_2v_2\in M\subseteq E(\overline{G})$. Since $n\ge 6$, it follows that there exist two vertices $w_1,w_2$ such that $u_1w_1v_1,u_2w_2v_2$ are two shortest paths connecting $\{u_1v_1\},\{u_2v_2\}$, respectively. Let $S=V(G)-\{w_1,w_2\}$. For the vertex pair $u_1,v_1$, geodesic set $\widetilde{P}(u_1,v_1)$ cover all the vertex $w_1$. For the vertex pair $u_2,v_2$, geodesic set $\widetilde{P}(u_2,v_2)$ cover all the vertex $w_2$. So one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these geodesics cover all the vertices of G. So $\mathrm{sg}(G)\le |S|\le n-2$, a contradiction. So $|M|=1$, that is, $G=K_n{\setminus } e$, where $e\in E(K_n)$.

Conversely, we suppose G satisfies the conditions of this theorem. From Proposition 4.1, we have $\mathrm{sg}(G)\le n-1$. It suffices to show that $\mathrm{sg}(G)\ge n-1$. Suppose $G=K_n{\setminus } e$, where $e\in E(K_n)$. For any $S\subseteq V(G)$ and $|S|\le n-2$, and for each pair $\{x,y\}\subseteq S$, these geodesics do not cover all the vertices of $V(G)-S$. So $\mathrm{sg}(G)\ge n-1$. Suppose that there is a cut vertex v of G such that each induced subgraph $G[V(C_i)\cup \{v\}] \ (1\le i\le t)$ is complete, where $C_1,C_2,\ldots ,C_t$ be the connected components of $G-v$. For any $S\subseteq V(G)$ and $|S|\le n-2$, and for each pair $\{x,y\}\subseteq S$, these geodesics do not cover the vertices of $V(G)-S$. So $\mathrm{sg}(G)\ge n-1$. $\square$

When the connectivity of the graph is used, we obtain the following.

Theorem 4.2

Let G be a connected graph of order $n \ (n\ge (2k+2)k+k+1)$, $\kappa (G)\ge k+1 \ (k\ge 2)$, and let k be a positive integer. Then $\mathrm{sg}(G)=n-k$ if and only if $G=K_n-\{e_1,e_2,\ldots ,e_k\}$, where $\{e_1,e_2,\ldots ,e_k\}$ is a subset of the edge set of $K_n$.

Proof

Suppose $\mathrm{sg}(G)=n-k$. From Theorem 2.1, we have $\kappa (G)\le k$ or $\kappa (G)\ge n-2k$. Since $\kappa (G)\ge k+1$ and $\delta (G)\ge \kappa (G)$, it follows that $\delta (G)\ge \kappa (G)\ge n-2k$. If $n-2k\le \delta (G)\le n-k-2$, there exist a vertex u, such that $d_G(u)=\delta (G)$, and there exist vertex set $\{w_1,w_2,\ldots ,w_k,w_{k+1}\}$, such that $\{w_1u,w_2u,\ldots ,w_ku,w_{k+1}u\}\notin E(G)$. Since $\delta (G)\ge n-2k$, it follows that there are at most $2k-1$ vertices does not adjacent to $w_i \ (1\le i\le k+1)$ for each i, so there are at most $(2k-2)(k+1)+1$ vertices does not adjacent to $\{w_1,w_2,\ldots ,w_k,w_{k+1}\}$. Since $n\ge 2k(k+1)+1$, it follows that there are at least $(2k+2)k+k+1-(2k-2)(k+1)-(k+1)-1\ge k+1$ vertices all adjacent to $\{w_1,w_2,\ldots ,w_k,w_{k+1}\}$ vertex set, say $u_1,u_2,\ldots ,u_k,u_{k+1}$. We choose $S=G-\{u_1,u_2,\ldots ,u_k,u_{k+1}\}$, for each $\{x,y\}\subseteq S$, one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these geodesic cover all the vertices of G. So $\mathrm{sg}(G)\le |S|\le n-k-1$, a contradict. Next we consider $n-k-1\le \delta (G)$. If $G\ne K_n-\{e_1,e_2,\ldots ,e_k\}$, then $|E(\overline{G})|\ge k+1$ or $|E(\overline{G})|\le k-1$. First, we consider $|E(\overline{G})|\ge k+1$. We can choose $k+1$ edges, say $e_1,e_2,\ldots ,e_{k+1}$. Since $n-k-1\le \delta (G)$, it follows that there are at lease $(2k+2)k+k+1-(2k+2)(k-1)-2(k+1)\ge k+1$ vertices all adjacent to $e_1,e_2,\ldots ,e_{k+1}$, say $v_1,v_2,\ldots ,v_k,v_{k+1}$. We choose $S=G-\{v_1,v_2,\ldots ,v_k,v_{k+1}\}$, for each $\{x,y\}\subseteq S$, one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these geodesic cover all the vertices of G. So $\mathrm{sg}(G)\le |S|\le n-k-1$, a contradict. Next we consider $|E(\overline{G})|\le k-1$. This case we can found that G is a graph obtain from $K_n$ by delete r edges, say $x_1y_1,x_2y_2,\ldots ,x_ry_r$. Since $n\ge 2k(k+1)$, it follows that diameter is 2. So each edge in $\{x_1y_1,x_2y_2,\ldots ,x_ry_r\}$ covers at most one vertex. Since any vertex set $|S|=n-k$ does not cover all vertex of G, this is the desired contradiction.

Conversely, we suppose $G=K_n-\{e_1,e_2,\ldots ,e_k\}$, where $\{e_1,e_2,\ldots ,e_k\}$ is the edge set of $K_n$. Let $e_i=u_iv_i \ (1\le i\le k)$, where the vertices in $\{u_i\,|\, 1\le i\le k\}\cup \{v_i\,|\, 1\le i\le k\}$ are not necessarily different. Since $n\ge (2k+2)k+k+1$, we can find the vertex set $\{w_1,w_2,\ldots ,w_k\}$ of G and edge induce subgraph $E_{\{w_1,w_2,\ldots ,w_k\},\{u_1,u_2,\ldots ,u_k,v_1,v_2,\ldots ,v_k\}}$ is complete bipartite graph. Let $S=G-\{w_1,w_2,\ldots ,w_k\}$. For each $\{x,y\}\subseteq S$, one can assign a fixed geodesic to each pair $\{x,y\}\subseteq S$ so that these geodesic cover all the vertices of G. So $\mathrm{sg}(G)\le |S|\le n-k$. Since any vertex set $|S|\le n-k-1$ does not cover all the vertices of G, we get $|S|=n-k$. $\square$

5 Nordhaus–Gaddum-Type Results

In this section, we study upper and lower bounds on the quantities $\mathrm{sg}(G)+\mathrm{sg}(\overline{G})$ and $\mathrm{sg}(G)\cdot \mathrm{sg}(\overline{G})$.

Theorem 5.1

Let $G\in \mathcal {G}(n) \ (n\ge 4)$ be a connected graph with a connected complement. Then

• (1) $2+\lceil \sqrt{n}\rceil \le \mathrm{sg}(G)+\mathrm{sg}(\overline{G})\le 2n-4$;

• (2) $2\lceil \sqrt{n}\rceil \le \mathrm{sg}(G)\cdot \mathrm{sg}(\overline{G})\le (n-2)^2$.

Moreover, the two upper bounds are sharp.

Proof

From Theorem 4.1 and Proposition 4.2, we have $\mathrm{sg}(G)+\mathrm{sg}(\overline{G})\le 2n-4$ and $\mathrm{sg}(G)\cdot \mathrm{sg}(\overline{G})\le (n-2)^2$. Since $\mathrm{diam}(G)\le 3$ or $\mathrm{diam}(\overline{G})\le 3$, it follows from Theorem 2.2 that $\mathrm{sg}(G)+\mathrm{sg}(\overline{G})\ge 2+\lceil \sqrt{n}\rceil$ and $\mathrm{sg}(G)\cdot \mathrm{sg}(\overline{G})\ge 2\lceil \sqrt{n}\rceil$. $\square$

To show the sharpness of the above bounds, we have the following examples.

Lemma 5.1

Let F be a graph obtained from a $K_{n-2}$ and a path $P_3$ by identifying a vertex of $K_{n-2}$ and an endpoint of $P_3$. Then $\mathrm{sg}(F)=n-2$.

Proof

From Theorem 2.2, we have $\mathrm{sg}(F)\le n-2$. We need to prove that $\mathrm{sg}(F)\ge n-2$. Let $P_3=uvw$ and u be the identifying vertex in F. For any $S\subseteq V(F)$ with $|S|=n-3$, there exists a vertex $x\in V(F)-S$ such that $x\notin \{u,v\}$. If $x=w$, then no geodesic covers w, a contradiction, meaning that $x\in V(F)-\{u,v,w\}$. Clearly, no geodesic covers x, also a contradiction, so $\mathrm{sg}(F)\le n-2$. $\square$

Lemma 5.2

Let H be a graph obtained from a complete bipartite graph $K_{2,n-3}$ by adding a pendant edge on one vertex of the small part. Then $\mathrm{sg}(H)=n-2$.

Proof

From Theorem 2.2, we have $\mathrm{sg}(H)\le n-2$. We need to prove that $\mathrm{sg}(H)\ge n-2$. Let $X=\{v_1,v_2,\ldots ,v_{n-3}\}$ be the vertex set of the large part, and $\{u,w\}$ be the vertex set of the small part, and v be the pendent vertex. For any $S\subseteq V(H)$ with $|S|=n-3$, we have $v\in S$. Let $\overline{S}=V(H)-S$. Then $0\le |\overline{S}\cap X|\le 3$. If $|\overline{S}\cap X|=0$, then $\overline{S}=\{u,v,w\}$, which contradicts the fact that $v\in S$. If $|\overline{S}\cap X|=1$, then we suppose that $\overline{S}\cap X=\{v_1\}$. Since $v\in S$, it follows that $\overline{S}=\{u,v_1,w\}$. Clearly, no geodesic covers $v_1$, a contradiction. If $|\overline{S}\cap X|=2$, then we suppose that $\overline{S}\cap X=\{v_1,v_2\}$. Then $u\in \overline{S}$ or $w\in \overline{S}$. Clearly, no geodesic covers $v_1$ or $v_2$, a contradiction. If $|\overline{S}\cap X|=3$, then we suppose that $\overline{S}\cap X=\{v_1,v_2,v_3\}$. Then no geodesic covers one of $v_1,v_2,v_3$, a contradiction. So $\mathrm{sg}(H)=n-2$. $\square$

Example 5

Let G be a graph obtained from a $K_{n-2}$ and a path $P_3$ by identifying a vertex of $K_{n-2}$ and an endpoint of $P_3$. Then $\overline{G}$ is a graph obtained from a complete bipartite graph $K_{2,n-3}$ by adding an pendent edge on one vertex of the small part. Clearly, $\mathrm{diam}(G)=\mathrm{diam}(\overline{G})=3$. From Theorem 2.2 and Lemmas 5.1 and 5.2, we have $\mathrm{sg}(G)=n-2$ and $\mathrm{sg}(\overline{G})=n-2$.

6 Extremal Problems

In this section, we give some results on extremal problems regarding the strong geodetic number. Recall that s(n, k) is the minimum size of all graphs of order n with strong geodetic number k, where $2\le k\le n$. Our first result concerns the quantity s(n, k).

Proposition 6.1

Let n, k be two integers with $2\le k\le n$. Then

$$\begin{aligned} s(n,k)= {\left\{ \begin{array}{ll} {n\atopwithdelims ()2}, &{} {\mathrm{if}}~k=n;\\ n-1, &{} {\mathrm{if}}~2\le k\le n-1. \end{array}\right. } \end{aligned}$$

Proof

From Proposition 4.3, we have $s(n,n)={n\atopwithdelims ()2}$. Let T be a tree with exactly k leaves. Clearly, $s(n,k)\le n-1$. Since we only consider connected graphs, we have $s(n,k)=n-1$ for $2\le k\le n-1$. $\square$

Recall that f(n, k) is the minimum integer such that for every connected graph G of order n, if $|E(G)|\ge f(n,k)$ then $\mathrm{sg}(G)\ge k$. Our next result is about g(n, k).

Proposition 6.2

Let n, k be two integers with $2\le k\le n$. Then

$$\begin{aligned} g(n,k)= {\left\{ \begin{array}{ll} {n\atopwithdelims ()2}, &{} {\mathrm{if}}~k=n;\\ {n\atopwithdelims ()2}-1, &{} {\mathrm{if}}~k=n-1. \end{array}\right. } \end{aligned}$$

For $2\le k\le n-2$, g(n, k) does not exist.

Proof

From Proposition 4.3, we have $g(n,n)={n\atopwithdelims ()2}$ and $g(n,n-1)={n\atopwithdelims ()2}-1$. For a star $K_{1,n-1}$, we have $\mathrm{sg}(K_{1,n-1})=n-1$ and $g(n,k)\le n-2$. This means that g(n, k) does not exist. $\square$

Recall that g(n, k) is the maximum integer such that for every graph G of order n, if $|E(G)|\le g(n,k)$ then $\mathrm{sg}(G)\le k$. Finally we consider f(n, k).

Proposition 6.3

Let n, k be two integers with $2\le k\le n$ and $n\ge 8$.

• (1) If $\lceil \frac{2n}{3}\rceil \le k\le n$, then $f(n,k)={n\atopwithdelims ()2}-n+k$;

• (2) If $\lceil \frac{1+\sqrt{1+8n}}{2}\rceil \le k\le \lceil \frac{2n}{3}\rceil -1$, then

  $$\begin{aligned} {n\atopwithdelims ()2}-n+k\le f(n,k)\le {n\atopwithdelims ()2}-\left\lfloor \frac{n}{3}\right\rfloor . \end{aligned}$$

• (3) If $3\le k\le \lceil \frac{1+\sqrt{1+8n}}{2}\rceil -1$, then

  $$\begin{aligned} {k-1\atopwithdelims ()2}+n-k+2\le f(n,k)\le {n\atopwithdelims ()2}-n+\left\lceil \frac{1+\sqrt{1+8n}}{2}\right\rceil . \end{aligned}$$

Proof

Suppose $\lceil \frac{1+\sqrt{1+8n}}{2}\rceil \le k\le n$. Let $K_n$ be a complete graph of order n and $K_k$ be a clique of order k in $K_n$. Let G be a graph obtained from $K_n$ by deleting $n-k+1$ edges in $K_k$. Clearly, $\mathrm{sg}(G)\le k-1$ and $e(G)={n\atopwithdelims ()2}-n+k-1$, and hence $f(n,k)\ge {n\atopwithdelims ()2}-n+k$.

(1) For $\lceil \frac{2n}{3}\rceil \le k\le n$, we suppose that G is a connected graph with $e(G)\ge {n\atopwithdelims ()2}-n+k$. Since $\lceil \frac{2n}{3}\rceil \le k\le n$, it follows that $e(\overline{G})\le n-k$. We claim that $\mathrm{sg}(G)\ge k$. If $\mathrm{sg}(G)\le k-1$, then there exists a vertex set S with $|S|\le k-1$ such that the geodesics from the vertex pairs of S can cover all the vertices of G. Since $|\overline{G}[S]|\le n-k$, it follows that the geodesics from S cover $n-k$ vertices in $V(G)-S$, which contradicts the fact that the geodesics from the vertex pairs of S can cover all the vertices of G. So $f(n,k)={n\atopwithdelims ()2}-n+k$.

(2) For $\lceil \frac{1+\sqrt{1+8n}}{2}\rceil \le k\le \lceil \frac{2n}{3}\rceil -1$, we suppose that G is a connected graph with $e(G)\ge {n\atopwithdelims ()2}-\left\lfloor \frac{n}{3}\right\rfloor$. From (1), we have $f(n,\lceil \frac{2n}{3}\rceil )={n\atopwithdelims ()2}-n+\lceil \frac{2n}{3}\rceil ={n\atopwithdelims ()2}-\left\lfloor \frac{n}{3}\right\rfloor$. That is to say, for any graph of $G'$, if $|E(G')|\ge {n\atopwithdelims ()2}-\left\lfloor \frac{n}{3}\right\rfloor$, then $\mathrm{sg}(G')\ge \lceil \frac{2n}{3}\rceil$. Since $\lceil \frac{1+\sqrt{1+8n}}{2}\rceil \le k\le \lceil \frac{2n}{3}\rceil -1$, it follows that $\mathrm{sg}(G)\ge k$. So ${n\atopwithdelims ()2}-n+k\le f(n,k)\le {n\atopwithdelims ()2}-\left\lfloor \frac{n}{3}\right\rfloor$.

(3) Let G be a graph obtained from a clique $K_{k-1}$ and a path $P_{n-k+2}$ by identifying a vertex of $K_{k-1}$ and an endpoint of $P_{n-k+2}$. Clearly, $\mathrm{sg}(G)=k-1$ and $e(G)={k-1\atopwithdelims ()2}+n-k+1$, and hence $f\dfrac{(}{n},k)\ge {k-1\atopwithdelims ()2}+n-k+2$.

For upper bound, we suppose that G is a connected graph with $e(G)\ge {n\atopwithdelims ()2}-n+\lceil \frac{1+\sqrt{1+8n}}{2}\rceil$. From (2), we have $f\dfrac{(}{n},\lceil \frac{1+\sqrt{1+8n}}{2}\rceil )={n\atopwithdelims ()2}-n+\lceil \frac{1+\sqrt{1+8n}}{2}\rceil$. That is to say, for any graph of $G'$, if $|E(G')|\ge {n\atopwithdelims ()2}-n+\lceil \frac{1+\sqrt{1+8n}}{2}\rceil$, then $\mathrm{sg}(G')\ge \lceil \frac{1+\sqrt{1+8n}}{2}\rceil$. Since $3\le k\le \lceil \frac{1+\sqrt{1+8n}}{2}\rceil -1$, it follows that $\mathrm{sg}(G)\ge k$. So ${k-1\atopwithdelims ()2}+n-k+2\le f(n,k)\le {n\atopwithdelims ()2}-n+\lceil \frac{1+\sqrt{1+8n}}{2}\rceil$. $\square$