1 Introduction

In many engineering contexts, there are many inverse problems for heat equation. The inverse problem for heat diffusion equation can be roughly divided into five principal classes. The first one is backward heat conduction problem. The problem of this kind is also known as reversed-time problem for determination of the initial temperature distribution from the known distribution at the final moment of time. The second one is the identification of the temperature or the flux of temperature at one of the inaccessible boundaries from the over-posed data at the other one which is accessible. This problem is also known as inverse heat conduction problem. The third one is the coefficient identification from over-posed data at the boundaries. The fourth one is the determination of the shape of the unknown boundaries or the crack inside the heat conduction body. The last one is the identification of the heat source, e.g., [1, 7].

In this paper, we focus on the problem of identifying the heat source from measured data for heat equation. This model has many important applications in practice, e.g., in finding a pollution source intensity and also for designing the final state in melting and freezing processes. The problem is ill-posed and any small change in the input data may result in a dramatic change in the solution. Numerical computation is very difficult. To obtain a stable numerical solution for these kinds of ill-posed problems, some regularization strategies should be applied.

The problem of identification of space-wise-dependent heat source has been discussed by many authors. For theoretical papers, we can refer to the references [2,3,4, 10, 12, 20,21,22]. For computational papers, we can refer to the references [5, 6, 11, 13,14,15,16,17,18,19] and the references therein.

Recently, Johansson and Lesnic proposed an iterative method [8] and a variational method [9] for solving the problem of this kind numerically. However, these methods need to solve a direct problem at each iterative step. The computational cost is very high. In this paper, we present a Tikhonov regularization method for solving this problem. Following the idea of [23] where the authors deal with the problem of identifying coefficient, we give some theoretical results. Being different from the work of numerical parts in [23], we give a new computational method for solving inverse heat source problem. The method is simple and effective. The main aim of this paper is to provide a new method for solving the problem of unknown heat source. Furthermore, our method can be extend to the case of higher dimensions easily.

This paper is organized as follows. In Sect. 2, we present the formulation of the inverse problem; in Sects. 3 and 4, some theoretical results are obtained; in Sect. 5, some numerical results are shown. Finally, we give a conclusion in Sect. 6.

2 Inverse Heat Source Problem

We consider the following inverse problem: find the temperature u and the heat source f which satisfy the heat conduction equation, namely

Problem I

$$\begin{aligned} u_t(x,t)=u_{xx}(x,t)+f(x), \quad 0<x<1,\quad 0<t<T, \end{aligned}$$
(2.1)

with the initial data and boundary conditions

$$\begin{aligned} u(x,0)=\varphi (x),\quad 0<x<1, \end{aligned}$$
(2.2)
$$\begin{aligned} u_x(0,t)=u_x(1,t)=0,\quad 0<t<T, \end{aligned}$$
(2.3)

here we need to reconstruct f(x) from the measured data \(g_\epsilon (x)\). Assume the measured data \(g_\epsilon (x)\) and exact data \(u(x,T):=g(x)\) satisfy

$$\begin{aligned} \Vert g(\cdot )-g_\epsilon (\cdot )\Vert \le \epsilon , \end{aligned}$$
(2.4)

where \(\Vert \cdot \Vert \) denotes the \(L^2\)-norm and \(\epsilon \) is the known noise level.

Assume that the given functions satisfy the compatibility conditions

$$\begin{aligned} \begin{array}{ll} \varphi _x(0)=\varphi _x(1)=0,\\ g_x(0)=g_x(1)=0.\\ \end{array} \end{aligned}$$
(2.5)

We know that the Problem I is ill-posed and the degree of the Problem I is equivalent to that of second-order numerical differentiation.

For the direct problem (2.1)–(2.3), using the results of [Lions, Chapter 3], we have

Lemma 1

Suppose that \(\varphi \) and f belong to \(L^2(0,1)\). Then the problem (2.1)–(2.3) has a unique solution \(u\in L^2(0,T;H_0^1(0,1))\cap C([0,T];H_0^1(0,1))\) in the distributional sense and

$$\begin{aligned} \Vert u\Vert _{L^2(0,T;H_0^1(0,1))}\le C(\Vert f\Vert _{L^2(0,1)}+\Vert \varphi \Vert _{L^2(0,1)}), \end{aligned}$$
(2.6)

where C is a constant.

3 Tikhonov Regularization Method

Consider the following optimal control problem

Problem P Find \({\overline{f}} \in F\) such that

$$\begin{aligned} J({\overline{f}})=\min _{f \in F}J(f), \end{aligned}$$
(3.1)

where

$$\begin{aligned} J(f)=\frac{1}{2}\int _{0}^{1}(u(x,T;f)-g_\epsilon )^2 \mathrm{d}x+\frac{\alpha }{2}\int _0^1 |\nabla f|^2 \mathrm{d}x, \end{aligned}$$
(3.2)
$$\begin{aligned} F=\left\{ f(x)| 0<f_{\min }\le f \le f_{\max }, \nabla f \in L^2(0,1)\right\} , \end{aligned}$$
(3.3)

u(x, t; f) is the solution of Eqs. (2.1)–(2.3) for a given heat source \(f(x)\in F\) and \(\alpha \) is the regularization parameter.

By using standard method, we can obtain existence of the minimizer of Problem P.

Theorem 1

There exists a minimizer \({\overline{f}}\in F\) of J(f), i.e.,

$$\begin{aligned} J({\overline{f}})=\min _{f\in F}J(f). \end{aligned}$$
(3.4)

The following theorem shows the necessary condition of existence of the minimizer \({\overline{f}}\):

Theorem 2

Let \({\overline{f}}\) be the solution of the Problem P. Then there exists a triple of functions \((u,v;{\overline{f}})\) satisfying the following system:

$$\begin{aligned}&\left\{ \begin{array}{ll} u_t=u_{xx}+{\overline{f}},&{} \quad 0<x<1,\quad 0<t<T,\\ u(x,0)=\varphi (x),&{}\quad 0 \le x \le 1,\\ u_x(0,t)=u_x(1,t)=0,&{}\quad 0<t<T, \end{array}\right. \end{aligned}$$
(3.5)
$$\begin{aligned}&\left\{ \begin{array}{ll} v_t+v_{xx}=0,&{}\quad 0<x<1,\quad 0<t<T,\\ v(x,T)=u(x,T;{\overline{f}})-g_\epsilon (x),&{}\quad 0 \le x \le 1,\\ v_x(0,t)=v_x(1,t)=0,&{}\quad 0<t<T, \end{array}\right. \end{aligned}$$
(3.6)

and

$$\begin{aligned} \int _0^T\int _0^1 v (h-{\overline{f}}) \mathrm{d}x \mathrm{d}t-\alpha \int _0^1 \nabla {\overline{f}} \cdot \nabla ({\overline{f}}-h)\mathrm{d}x \ge 0, \end{aligned}$$
(3.7)

for all \(h \in F\).

Proof

For any \(h\in F\), \(0\le \delta \le 1\), we have

$$\begin{aligned} f_\delta :=(1-\delta ){\overline{f}}+\delta h \in F. \end{aligned}$$
(3.8)

Then

$$\begin{aligned} J_\delta :=J(f_\delta )=\frac{1}{2}\int _0^1 (u(x,T;f_\delta )-g_\epsilon (x))^2 \mathrm{d}x +\frac{\alpha }{2}\int _0^1|\nabla f_\delta |^2 \mathrm{d}x. \end{aligned}$$
(3.9)

Let \(u_\delta \) be the solution of Eq. (2.1) with \(f=f_\delta \). Since \({\overline{f}}\) is an optimal solution, we have

$$\begin{aligned} \frac{d J_\delta }{d \delta }\big |_{\delta =0}=\int _0^1 (u(x,T;{\overline{f}})-g_\epsilon (x))\frac{\partial u_\delta }{\partial \delta }\big |_{\delta =0} \mathrm{d}x +\alpha \int _0^1\nabla {\overline{f}} \cdot \nabla (h-{\overline{f}}) \mathrm{d}x \ge 0.\nonumber \\ \end{aligned}$$
(3.10)

Denote \(\widetilde{u_\delta }:=\frac{\partial u_\delta }{\partial \delta }\), direct calculations lead to the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial }{\partial t}\widetilde{u_\delta }=\frac{\partial ^2}{\partial x^2}\widetilde{u_\delta }+(h-{\overline{f}}),\\ \widetilde{u_\delta }(x,0)=0,\\ \frac{\partial \widetilde{u_\delta }}{\partial x}(0,t)=\frac{\partial \widetilde{u_\delta }}{\partial x}(1,t)=0. \end{array}\right. \end{aligned}$$
(3.11)

Denote \(\eta =\widetilde{u_\delta }|_{\delta =0}\), then \(\eta \) satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \eta _t=\eta _{xx}+(h-{\overline{f}}),\\ \eta (x,0)=0,\\ \eta _x(0,t)=\eta _x(1,t)=0. \end{array}\right. \end{aligned}$$
(3.12)

From (3.10), we have

$$\begin{aligned} \int _0^1 (u(x,T;{\overline{f}})-g_\epsilon (x))\eta (x,T) \mathrm{d}x +\alpha \int _0^1\nabla {\overline{f}} \cdot \nabla (h-{\overline{f}}) \mathrm{d}x \ge 0. \end{aligned}$$
(3.13)

Let \({\mathfrak {L}}\eta :=\eta _t-\eta _{xx}\), and suppose v is the solution of the following problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathfrak {L^*}v=-v_t-v_{xx}=0,\\ v(x,T)=u(x,T;{\overline{f}})-g_\epsilon (x),\\ v_x(0,t)=v_x(1,t)=0, \end{array}\right. \end{aligned}$$
(3.14)

where \(\mathfrak {L^*}\) is the adjoint operator of the operator \({\mathfrak {L}}\). From (3.12) and (3.14), we have

$$\begin{aligned}&0=\int _0^T\int _0^1\eta \mathfrak {L^*}v\mathrm{d}x\mathrm{d}t=-\int _0^1 \eta (x,T)(u(x,T;{\overline{f}})-g_\epsilon (x))\mathrm{d}x+\int _0^T\int _0^1 v {\mathfrak {L}}\eta \mathrm{d}x \mathrm{d}t \nonumber \\&\quad =-\int _0^1 \eta (x,T)(u(x,T;{\overline{f}})-g_\epsilon (x))\mathrm{d}x+\int _0^T\int _0^1 v (h-{\overline{f}})\mathrm{d}x \mathrm{d}t. \end{aligned}$$
(3.15)

Combining (3.13) and (3.15), we can obtain

$$\begin{aligned} \int _0^T\int _0^1 v (h-{\overline{f}}) \mathrm{d}x \mathrm{d}t-\alpha \int _0^1 \nabla {\overline{f}} \cdot \nabla ({\overline{f}}-h)\mathrm{d}x \ge 0. \end{aligned}$$

Thus, we completed the proof of Theorem 2. \(\square \)

4 Uniqueness of the Minimizer \({\overline{f}}\)

Suppose that \(\overline{f_1}\) and \(\overline{f_2}\) are two minimizers of the optimal problem P, and \(\{u_i,\eta _i\}\), \((i=1,2)\) are the solutions of system (3.5) and (3.12) in which \({\overline{f}}=\overline{f_i}\), \((i=1,2)\), respectively.

To establish the result of uniqueness, we need the following lemmas. Since this result is obvious, here we omit the proof for them.

Lemma 2

For each bounded continuous function \(l(x)\in C(0,1)\), we have

$$\begin{aligned} \max _{x\in (0,1)}|l(x)|\le |l(x_0)|+\left( \int _0^1 |\nabla l(x)|^2\mathrm{d}x\right) ^{\frac{1}{2}}, \end{aligned}$$
(4.1)

where \(x_0\) is a fixed point in the interval (0, 1).

Now the following theorem is the main result of this section.

Theorem 3

Suppose \(\overline{f_1}\) and \(\overline{f_2}\) are two minimizers of the optimal control problem P corresponding to \(g_{\epsilon ,1}\) and \(g_{\epsilon ,2}\), respectively. If there exists a fixed point \(x_0\) such that

$$\begin{aligned} \overline{f_1}(x_0)=\overline{f_2}(x_0), \end{aligned}$$

and assume

$$\begin{aligned} g_{\epsilon ,1}(x)=g_{\epsilon ,2}(x), \end{aligned}$$

we have

$$\begin{aligned} \overline{f_1}(x)=\overline{f_2}(x), \quad \forall \, x \in (0,1). \end{aligned}$$

Proof

By taking \(h=\overline{f_2}\) when \({\overline{f}}=\overline{f_1}\) and taking \(h=\overline{f_1}\) when \({\overline{f}}=\overline{f_2}\) in (3.13), we get

$$\begin{aligned}&\int _0^1 (u_{1}(x,T;{\overline{f}})-g_{\epsilon ,1}(x))\eta _{1}(x,T) \mathrm{d}x +\alpha \int _0^1 \nabla \overline{f_1} \cdot \nabla (\overline{f_1}-\overline{f_2})\mathrm{d}x \ge 0,\end{aligned}$$
(4.2)
$$\begin{aligned}&\int _0^1 (u_{2}(x,T;{\overline{f}})-g_{\epsilon ,2}(x))\eta _{2}(x,T) \mathrm{d}x +\alpha \int _0^1 \nabla \overline{f_2} \cdot \nabla (\overline{f_2}-\overline{f_1})\mathrm{d}x \ge 0, \end{aligned}$$
(4.3)

where \(\overline{f_1}\) and \(\overline{f_2}\) are two minimizers of the optimal problem P corresponding to \(g_{\epsilon ,1}\) and \(g_{\epsilon ,2}\), respectively. And \(\{u_i,\eta _i\}\), \((i=1,2)\) are the solutions of system (3.5) and (3.12) in which \({\overline{f}}=\overline{f_i}\), \((i=1,2)\), respectively. Setting

$$\begin{aligned} u_{1}-u_{2}=W,\quad \eta _{1}+\eta _{2}=H, \end{aligned}$$

then W and H satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} W_t=W_{xx}+({\overline{f}}_{1}-{\overline{f}}_{2}), \\ W(x,0)=\varphi (x), \\ W_x(0,t)=W_x(1,t)=0, \end{array}\right. \end{aligned}$$
(4.4)
$$\begin{aligned} \left\{ \begin{array}{ll} H_t=H_{xx},\\ H(x,0)=0,\\ H_x(0,t)=H_x(1,t)=0. \end{array}\right. \end{aligned}$$
(4.5)

By the extremum principle, we know that Eq. (4.5) only has zero solution , thus we have

$$\begin{aligned} \eta _{1}(x,t)=-\eta _{2}(x,t). \end{aligned}$$
(4.6)

Further, \(\eta _{1}\) satisfies the following equation

$$\begin{aligned} \left\{ \begin{array}{ll} \eta _{1t}=\eta _{1xx}+({\overline{f}}_{2}-{\overline{f}}_{1}),\\ \eta _{1}(x,0)=0,\\ \eta _{1x}(0,t)=\eta _{1x}(1,t)=0. \end{array}\right. \end{aligned}$$
(4.7)

From (4.4) and (4.7), we get

$$\begin{aligned} W(x,t)=-\eta _{1}(x,t). \end{aligned}$$
(4.8)

Using Lemma 2 , we obtain

$$\begin{aligned} \max _{x\in (0,1)}|{\overline{f}}_{1}-{\overline{f}}_{2}|\le |({\overline{f}}_{1}-{\overline{f}}_{2})(x_0)| +(\int _0^1 |\nabla \left( {\overline{f}}_{1}-{\overline{f}}_{2}\right) |^2\mathrm{d}x)^{\frac{1}{2}}. \end{aligned}$$
(4.9)

By the assumption of Theorem 3, we have

$$\begin{aligned} \max _{x\in (0,1)}|{\overline{f}}_{1}-{\overline{f}}_{2}|\le \left( \int _0^1 |\nabla ({\overline{f}}_{1}-{\overline{f}}_{2})|^2\mathrm{d}x)^{\frac{1}{2}}=\Vert \nabla ({\overline{f}}_{1}-{\overline{f}}_{2}\right) \Vert _{L^{2}(0,1)}.\qquad \end{aligned}$$
(4.10)

On the other hand, combining (4.2), (4.3), (4.6) and (4.8), we obtain

$$\begin{aligned} \alpha \int _0^1 |\nabla ({\overline{f}}_{1}-{\overline{f}}_{2})|^2\mathrm{d}x&\le \int _0^1 (u_{1}(x,T;{\overline{f}})\\&\quad -g_{\epsilon ,1}(x))\eta _{1}(x,T) \mathrm{d}x+ \int _0^1 (u_{2}(x,T;{\overline{f}})-g_{\epsilon ,2}(x))\eta _{2}(x,T) \mathrm{d}x\\&=\int _0^1 W(x,T;{\overline{f}})\eta _{1}(x,T) \mathrm{d}x+ \int _0^1 (g_{\epsilon ,1}(x)-g_{\epsilon ,2}(x))\eta _{1}(x,T) \mathrm{d}x\\&\le -\int _0^1 |\eta _{1}(x,T)|^{2} \mathrm{d}x\\&\quad + \frac{1}{2}\int _0^1 |g_{\epsilon ,1}(x)-g_{\epsilon ,2}(x)|^{2} \mathrm{d}x+ \frac{1}{2}\int _0^1 |\eta _{1}(x,T)|^{2} \mathrm{d}x\\&\le \frac{1}{2}\int _0^1 |g_{\epsilon ,1}(x)-g_{\epsilon ,2}(x)|^{2} \mathrm{d}x- \frac{1}{2}\int _0^1 |\eta _{1}(x,T)|^{2} \mathrm{d}x\\&\le \frac{1}{2}\int _0^1 |g_{\epsilon ,1}(x)-g_{\epsilon ,2}(x)|^{2} \mathrm{d}x\\&=\frac{1}{2}\Vert g_{\epsilon ,1}(x)-g_{\epsilon ,2}(x)\Vert _{L^{2}(0,1)}^{2}. \end{aligned}$$

Combining (4.10), this yields

$$\begin{aligned} \max _{x\in (0,1)}|{\overline{f}}_{1}-{\overline{f}}_{2}|\le \left( \frac{1}{2\alpha }\right) ^{\frac{1}{2}}\Vert g_{\epsilon ,1}-g_{\epsilon ,2}\Vert _{L^{2}(0,1)}. \end{aligned}$$
(4.11)

When

$$\begin{aligned} g_{\epsilon ,1}(x)=g_{\epsilon ,2}(x), \end{aligned}$$

we have

$$\begin{aligned} \overline{f_1}(x)=\overline{f_2}(x),\,\,\,\,x\in (0,1).\\ \end{aligned}$$

This ends the proof. \(\square \)

Remark 1

Theorem 3 can be generalized to the following problem:

Problem P1. Find the heat source f(x, t) from extra data \(u(x,t)=g(x,t)\) which satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} u_t-u_{xx}=f(x,t), &{}\quad (x,t)\in (0,1)\times (0,T),\\ u(x,0)=\varphi (x), &{}\quad x\in (0,1),\\ u_x(0,t)=u_x(1,t)=0, &{}\quad t\in (0,T). \end{array}\right. \end{aligned}$$
(4.12)

We want to reconstruct f(x, t), first find \(f(x,t_n)\) where \(t_n=nh\) and \(h=T/n\), \(n=0,1,\ldots ,N\) such that \(J(f(\cdot ,t_n))=\inf _{f\in F}J_n(f)\). Thus we can obtain the solutions \(f(x,t_n)\) for \(n=0,1,\ldots ,N\). Then the \(f(x,t_n)\) can be taken as an approximate solution to f(x, t).

5 Numerical Results

In this section, in order to demonstrate the effectiveness of Tikhonov regularization, we do the numerical experiment by using MATLAB in IEEE double precision with unit round off \(1.1\cdot 10^{-16}\). We consider an example. We try to reconstruct the heat source defined by

$$\begin{aligned} f(x)=\pi ^2\cos (\pi x),\quad x\in (0,1). \end{aligned}$$
(5.1)

If we consider homogeneous boundary conditions [see (2.1)–(2.3)]

$$\begin{aligned} u_{x}(0,t)=0\quad \text{ and } \quad u_{x}(1,t)=0\quad \text{ for } \quad t\in [0,1]. \end{aligned}$$
(5.2)

The initial condition is given by

$$\begin{aligned} u(x,0)=0\quad \text{ for } \quad x\in [0,1]. \end{aligned}$$
(5.3)

Then in this case the forward problem given by (2.1)–(2.3) with f given by (5.1) has the analytical solution

$$\begin{aligned} u(x,t)=\sum _{n=1}^{\infty }\frac{1-e^{-(n\pi )^{2}t}}{(n\pi )^{2}}f_{n}\cos (n\pi x), \end{aligned}$$
(5.4)

where

$$\begin{aligned} f_{n}=2\int _{0}^{1}f(x)\cos (n\pi x)\mathrm{d}x, \end{aligned}$$

is the Fourier coefficient of f(x). From (5.4), we get

$$\begin{aligned} g(x)=u(x,1)=\sum _{n=1}^{\infty }\frac{1-e^{-(n\pi )^{2}}}{(n\pi )^{2}}f_{n}\cos (n\pi x). \end{aligned}$$
(5.5)

Define a linear operator \(A:f\rightarrow g\), then the inverse source problem can be rewritten as the following operator equation:

$$\begin{aligned} Af(x)=g(x),\quad 0<x<1. \end{aligned}$$
(5.6)

Using (5.5), it holds

$$\begin{aligned} Af(x)=\sum _{n=1}^{\infty }\frac{1-e^{-(n\pi )^{2}}}{(n\pi )^{2}}f_{n}\cos (n\pi x). \end{aligned}$$
(5.7)

Consequently, A is a linear self-adjoint compact operator, i.e., \(A^{*}=A\). For noisy data \(g_\epsilon (x)\), the Tikhonov regularization is to seek a function \(f^{\epsilon ,\alpha }\) which minimizes the Tikhonov function

$$\begin{aligned} J_\alpha (f)&=\int _0^1 (u(x,T)-g_\epsilon (x))^2\mathrm{d}x +\alpha \int _0^1(f^{\prime }(x))^2\mathrm{d}x \end{aligned}$$
(5.8)
$$\begin{aligned}&=\Vert Af-g_\epsilon \Vert _{L^{2}(0,1)}^{2}+\alpha \Vert f'\Vert _{L^{2}(0,1)}^{2}, \end{aligned}$$
(5.9)

where \( \alpha >0\) is known as the regularization parameter.

It follows from simple calculation we know its minimizer \(f^{\epsilon ,\alpha }\) satisfies

$$\begin{aligned} A^{*}Af-\alpha f''=A^{*}g_{\epsilon }. \end{aligned}$$
(5.10)

From (5.7), we know that

$$\begin{aligned} A^{*}Af=\sum _{n=1}^{\infty }\left( \frac{1-e^{-(n\pi )^{2}}}{(n\pi )^{2}}\right) ^{2}f_{n}\cos (n\pi x). \end{aligned}$$
(5.11)

On the other hand

$$\begin{aligned} f(x)=\sum _{n=1}^{\infty }f_{n}\cos (n\pi x). \end{aligned}$$
(5.12)

further

$$\begin{aligned} f''(x)=-\sum _{n=1}^{\infty }f_{n}(n\pi )^{2}\cos (n\pi x). \end{aligned}$$
(5.13)

From (5.7), we have

$$\begin{aligned} A^{*}g_{\epsilon }(x)=\sum _{n=1}^{\infty }\frac{1-e^{-(n\pi )^{2}}}{(n\pi )^{2}}g_{\epsilon ,n}\cos (n\pi x), \end{aligned}$$
(5.14)

where \(g_{\epsilon ,n}\) is the Fourier coefficient of \(g_{\epsilon }(x)\). Applying (5.10), (5.11), (5.13) and (5.14), we obtain

$$\begin{aligned} f^{\epsilon ,\alpha }(x)=\sum _{n=1}^{\infty }\frac{(n\pi )^{2}(1-e^{-(n\pi )^{2}})}{(1-e^{-(n\pi )^{2}})^{2}+\alpha (n\pi )^{6}} g_{\epsilon ,n}\cos (n\pi x). \end{aligned}$$
(5.15)

We use the function randn given in MATLAB to generate the noisy data, then its discrete noisy version is

$$\begin{aligned} g_{\epsilon }=g+\delta \cdot randn(size(g)). \end{aligned}$$
$$\begin{aligned} x_{i}=\frac{i-1}{M-1},\quad i=1,2,3,\ldots ,M. \end{aligned}$$
$$\begin{aligned} \epsilon =\Vert g_{\epsilon }-g\Vert _{l^{2}}=\left( \frac{1}{N}\sum _{j=1}^{N}|g_{\epsilon }-g|^{2}\right) ^{\frac{1}{2}}. \end{aligned}$$
(5.16)

Using this noisy data, we compute the regularizing solution

$$\begin{aligned} f^{\epsilon ,\alpha }(x)\approx \sum _{n=1}^{N}\frac{(n\pi )^{2}(1-e^{-(n\pi )^{2}})}{(1-e^{-(n\pi )^{2}})^{2}+\alpha (n\pi )^{6}} g_{\epsilon ,n}\cos (n\pi x). \end{aligned}$$
(5.17)

To show the accuracy of numerical solution, we compute the approximate \(l^{2}\) error denoted by

$$\begin{aligned} e(f,\epsilon )=\Vert f^{\epsilon ,\alpha }-f\Vert _{l^{2}}. \end{aligned}$$
(5.18)

and the approximate relative error in \(l^{2}\) norm denoted by

$$\begin{aligned} e_{r}(f,\epsilon )=\frac{\Vert f^{\epsilon ,\alpha }-f\Vert _{l^{2}}}{\Vert f\Vert _{l^{2}}}. \end{aligned}$$
(5.19)

we take the regularization parameter as \(\alpha =\epsilon ^{2}\) to observe the convergence of our regularizing solutions. we choose \(N = 50, M=100 \).

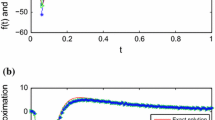
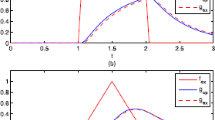
In the numerical experiment, Fig. 1a shows the numerical approximations to f(x) without regularization have a little large amplitude oscillation, this means the problem is unstable and ill-posed. From Fig. 1b and Table 1, we can find that the smaller the \(\epsilon \) is, the better the computed approximation is. This indicates that when using the proposed regularization method, the numerical results are recovered stable.

Fig. 1
figure 1

The exact solution and the regularized solutions for example. a No regularization and b Tikhonov regularization

Full size image
Table 1 Numerical results of the example
Full size table

Remark 2

In our numerical experiments, we take the regularization parameter as \(\alpha =\epsilon ^{2}\) to observe the convergence of our regularizing solutions. We can also choose the regularizing parameter \(\alpha \) using the a priori choice strategy based on the regularity of f(x) and the a posterior scheme by Morozov’s discrepancy principle to obtain the convergence rates and better numerical results. This should be future work.

6 Conclusion

In this paper, we investigate an inverse space-dependent source problem for a heat equation. We regularize it by the Tikhonov regularization method for overcoming its ill-posedness. The existence and uniqueness of the minimizer of the Tikhonov regularization functional are obtained. An optimal control method is used to get a stable solution. Numerical examples show that our proposed regularization methods are effective and stable.