1 Introduction

It is well known that nonlinear evolution equation (NLEEs) and their solutions play some important roles in mathematics, physics, chemistry, biology and other processes. In nonlinear science, Lie symmetry [1, 2] and Painlevé analysis [3, 4] are two kinds of effective methods for constructing exact solutions. However, due to the presence of nonlocal terms, the nonlocal symmetries cannot be determined completely in an algorithmic way. In latter studies, different from the traditional way to construct symmetries, one can start from the group transformation, such as the Darboux transformation (DT) [5], Bäcklund transformation (BT) [6], Möbious (conformal) invariant form [7], and potential system [8, 9]. Recently, Lou [10, 11] proposed the consistent Riccati expansion (CRE) method, which is used to identify CRE solvable systems (if the system has a CRE, then the system is defined to CRE solvable), and find the various interaction solutions between different types of excitations. Moreover, Lou also finds that the nonlocal symmetry from the truncated Painlevé expansion is just the residual of the expansion with respect to the singular manifold which is called residual symmetry [12, 13]. This method has been extended to many nonlinear differential equations [14,15,16,17,18,19,20,21].

In 1872, Boussinesq derived an equation describing the propagation of small amplitude, long waves in shallow water. This equation named by Boussinesq equation has traveling wave solutions called solitary waves, and their existence scientifically is proved. It is precisely because of Boussinesq’s scientific explanation that the study of the generalized Boussinesq water equation has been attracted the attention of many mathematicians, physicists and engineers. The classical Boussinesq water equation can be written by

$$\begin{aligned} u_{tt}=-\alpha u_{xxxx}+u_{xx}+\beta (u^{2})_{xx}, \end{aligned}$$
(1)

where u(x, t) is the elevation of the free surface of the fluid, the subscripts denote partial derivatives, and the constant coefficients \(\alpha \) and \(\beta \) depend on the depth of the fluid and the characteristic speed of the long waves. The equation is used to analyze the long waves in shallow water. It is also used in the analysis of many other physical applications such as the percolation of water in the porous subsurface of a horizontal layer of material.

The two-dimensional Boussinesq equation describes the propagation of gravity waves on the surface of water, in particular the head-on collision of oblique waves. The generalized (2 + 1)-dimensional Boussinesq equation [22] is usually written as

$$\begin{aligned} u_{tt}-\alpha u_{xx}-\beta u_{yy}-\gamma (u^{2})_{xx}-\delta u_{xxxx}=0, \end{aligned}$$
(2)

where \(\alpha , \beta , \gamma \) and \(\delta \) are arbitrary constants with \(\gamma \delta \ne 0 \). The two-dimensional equation combines the two-way propagation of the classical Boussinesq equation with the (weak) dependence on a second spatial variable, as occurs in the two-dimensional Korteweg–de Vries equation [23]. If \(\alpha =\beta =\gamma =\delta =1\), Eq. (2) is reduced to the following equation

$$\begin{aligned} u_{tt}-u_{xx}-u_{yy}-(u^{2})_{xx}-u_{xxxx}=0, \end{aligned}$$
(3)

where the suffices refer to differentiation with respect to time t and the two space variables x and y. Recently, Chen et al. [24] have studied the (2 + 1)-dimensional Boussinesq equation by using the new generalized transformation in homogeneous balance method (HBM). As a result, many explicit exact solutions, which contain new solitary wave solutions, periodic wave solutions and the combined formal solitary wave solutions and periodic wave solutions, are obtained. Tian et al. [25] have studied the Bäcklund transformation, infinite conservation laws and periodic wave solutions to a generalized (2 + 1)-dimensional Boussinesq equation. In this paper, we will study its soliton–cnoidal wave interaction solutions by using nonlocal symmetries of the equation.

In this paper, we concentrate on investigating the residual symmetries and CRE integrability of Eq. (3), which have not yet been discovered before. Besides we also study the soliton–cnoidal wave interaction solution of Eq. (3).

The paper is organized as follows. In Sect. 2, by use of the truncated Painlevé method, we obtain the nonlocal symmetries of the (2 + 1)-dimensional Boussinesq equation, and by means of localization process, we derive a new type of finite symmetry transformations. In Sect. 3, the (2 + 1)-dimensional Boussinesq equation is verified CRE solvable. Based on the CTE method, the interaction solution between a soliton and a cnoidal periodic wave of the equation is given. The last section is provided for a short summary and discussion.

2 Nonlocal Symmetry and Its Localization

2.1 Nonlocal Symmetry via the Truncated Painlevé Expansion

It is well known that the truncated Painlevé is one of the most effective methods to find traveling and nontraveling for NLEEs. By use of the Painlevé analysis, various integrate properties can be easily found if the studied model has Painlevé property , i.e., it is Painlevé integrable.

For Eq. (3), the truncated Painlevé expansion takes the general form [26]

$$\begin{aligned} u=\frac{u_{2}}{\phi ^{2}}+\frac{u_{1}}{\phi }+u_{0}, \end{aligned}$$
(4)

where \(\phi \) is the singular manifold, and \(u_{0}, u_{1}\) and \(u_{2}\) are the functions of (x, y, t) to be determined later.

Substituting Eq. (4) into Eq. (3) yields

$$\begin{aligned}&\left( -2u_{0,x}^{2}-u_{0,xxxx}-u_{0,yy}+u_{0,tt}-u_{0,xx}-2u_{0}u_{0,xx}\right) +\left( u_{1,tt}-u_{1,xx}-u_{1,yy}-u_{1,xxxx}\right. \nonumber \\&\quad \left. -\,2u_{1}u_{0,xx}-2u_{0}u_{1,xx}-4u_{1,x}u_{0,x}\right) \phi ^{-1} +\left( 2u_{0}u_{1}\phi _{xx}+4u_{1}u_{0,x}\phi _{x}+4u_{0}u_{1,x}\phi _{x}-2u_{1,x}^{2}\right. \nonumber \\&\quad \left. +\,u_{2,tt}-u_{2,xx}-u_{2,yy}-u_{2,xxxx}+u_{1}\phi _{yy}+u_{1}\phi _{xxxx} +u_{1}\phi _{xx}+4u_{1,xxx}\phi _{x}+6u_{1,xx}\phi _{xx}\right. \nonumber \\&\quad \left. +\,4u_{1,x}\phi _{xxx}-u_{1}\phi _{tt}-2u_{2}u_{0,xx}-2u_{1}u_{1,xx}-2u_{0} u_{2,xx}+2u_{1,x}\phi _{x}+2u_{1,y}\phi _{y}-2u_{1,t}\phi _{t}\right. \nonumber \\&\quad \left. -\,4u_{2,x}u_{0,x}\right) \phi ^{-2}+\left( 4u_{0}u_{2}\phi _{xx}-24u_{1,x} \phi _{x}\phi _{xx}-8u_{1}\phi _{x}\phi _{xxx}+8u_{2}u_{0,x}\phi _{x}+8u_{1,x}u_{1} \phi _{x}\right. \nonumber \\&\quad \left. +\,8u_{0}u_{2,x}\phi _{x}-4u_{0}u_{1}\phi _{x}^{2}-12u_{1,xx} \phi _{x}^{2}-6u_{1}\phi _{xx}^{2}+2u_{2}\phi _{xx}+2u_{2}\phi _{yy}+8u_{2,xxx} \phi _{x}\right. \nonumber \\&\quad \left. +\,12u_{2,xx}\phi _{xx}+8u_{2,x}\phi _{xxx}+2u_{2}\phi _{xxxx}-2u_{2} \phi _{tt}-2u_{2}u_{1,xx}-2u_{1}u_{2,xx}+2u_{1}^{2}\phi _{xx}\right. \nonumber \\&\quad \left. +\,2u_{1}\phi _{t}^{2}-2u_{1}\phi _{x}^{2}-2u_{1}\phi _{y}^{2}+4u_{2,x} \phi _{x}-4u_{2,t}\phi _{t}+4u_{2,y}\phi _{y}-4u_{2,x}u_{1,x}\right) \phi ^{-3}\nonumber \\&\quad +\,\left( 6u_{2}u_{1}\phi _{xx}-72u_{2,x}\phi _{x}\phi _{xx}-24u_{2}\phi _{x} \phi _{xxx}+36u_{1}\phi _{x}^{2}\phi _{xx}+12u_{2,x}u_{1}\phi _{x}+12u_{2} \phi _{x}u_{1,x}\right. \nonumber \\&\quad \left. -\,12u_{0}u_{2}\phi _{x}^{2}-2u_{2,x}^{2}-36u_{2,xx}\phi _{x}^{2}-18u_{2} \phi _{xx}^{2}-2u_{2}u_{2,xx}+6u_{2}\phi _{t}^{2}-6u_{2}\phi _{x}^{2}-6u_{2} \phi _{y}^{2}\right. \nonumber \\&\quad \left. +\,24u_{1,x}\phi _{x}^{3}-6u_{1}^{2}\phi _{x}^{2}\right) \phi ^{-4} +\left( 144u_{2}\phi _{x}^{2}\phi _{xx}+16u_{2,x}u_{2}\phi _{x}-24u_{2}\phi _{x}^{2} u_{1}+4u_{2}^{2}\phi _{xx}\right. \nonumber \\&\quad \left. +\,96u_{2,x}\phi _{x}^{3}-24u_{1}\phi _{x}^{4}\right) \phi ^{-5} +\left( -20u_{2}^{2}\phi _{x}^{2}-120u_{2}\phi _{x}^{4}\right) \phi ^{-6}=0. \end{aligned}$$
(5)

Vanishing all the coefficients of each powers of \(\phi \), we obtain

$$\begin{aligned} \begin{aligned} u_{2}&=-6\phi _{x}^{2}, ~~~~~~~~~~u_{1}=6\phi _{xx},\\ u_{0}&=-\frac{1}{2\phi _{x}^{2}}\left[ -3\phi _{xx}^{2}+4\phi _{x}\phi _{xxx} -\phi _{t}^{2}+\phi _{x}^{2}+\phi _{y}^{2}\right] . \end{aligned} \end{aligned}$$
(6)

Therefore, we have the solution of Eq. (3) as follows

$$\begin{aligned} u=-\frac{6\phi _{x}^{2}}{\phi ^{2}}+\frac{6\phi _{xx}}{\phi }-\frac{1}{2\phi _{x}^{2}} \left[ -3\phi _{xx}^{2}+4\phi _{x}\phi _{xxx}-\phi _{t}^{2} +\phi _{x}^{2}+\phi _{y}^{2}\right] , \end{aligned}$$
(7)

and Eq. (3) successfully satisfies the following Schwarzian form

$$\begin{aligned} S_{x}-CC_{x}-C_{t}+KK_{x}+K_{y}=0, \end{aligned}$$
(8)

where the notations C , K and S are defined as

$$\begin{aligned} C=\frac{\phi _{t}}{\phi _{x}}, ~~~~~~~~~~ K=\frac{\phi _{y}}{\phi _{x}},~~~~~~~~~~S=\frac{\phi _{xxx}}{\phi _{x}} -\frac{3}{2}\frac{\phi _{xx}^{2}}{\phi _{x}^{2}}. \end{aligned}$$
(9)

Hence, from the standard truncated Painlevé expansion, we get the Bäcklund transformation theorem as follows:

Theorem 2.1

(Bäcklund transformation theorem) Let \(\phi \) satisfy (8), then Eq. (7) is a Bäcklund transformation between \(\phi \) and the solution u of Eq. (3).

On the basis of the truncated Painlevé expansion(4), we can construct a series of exact solutions by employing Theorem 2.1. But here we are mainly focusing on constructing the nonlocal symmetry of Eq. (3), which is related to the expression (4).

As everyone knows, under the Möbious transformation

$$\begin{aligned} \phi \longrightarrow \frac{a+b \phi }{c+d \phi },(ad\ne bc), \end{aligned}$$
(10)

the Schwarzian equation (8) is invariant.

Due to above Möbious transformation, the Lie point symmetries of (8) have the following form

$$\begin{aligned} \sigma ^{\phi }=a_{1}+b_{1}\phi +c_{1}\phi ^{2}, \end{aligned}$$
(11)

where \(a_{1}, b_{1}\) and \(c_{1}\) are arbitrary constants.

From the truncated Painlevé expansion (4) and Theorem 2.1, a new nonlocal symmetry of Eq. (3) is presented and studied as follows.

Theorem 2.2

(nonlocal symmetry theorem) Eq. (3) admits the following nonlocal symmetry

$$\begin{aligned} \sigma ^{u}=6\phi _{xx}, \end{aligned}$$
(12)

where u and \(\phi \) satisfy the Bäcklund transformation (7).

Proof

Under the invariant property

$$\begin{aligned} u\rightarrow u+\epsilon \sigma ^{u}, \end{aligned}$$
(13)

we know that the symmetry equation for Eq. (3) reads

$$\begin{aligned} \sigma ^{u}_{tt}-\sigma ^{u}_{xx}-\sigma ^{u}_{yy}-4u_{x}\sigma ^{u}_{x}-2\sigma ^{u}u_{xx}-2u\sigma ^{u}_{xx}-\sigma ^{u}_{xxx}=0. \end{aligned}$$
(14)

By direct calculation, one can show that symmetry equations (14) with the help of (8) and BT (7) yield the nonlocal symmetry (12). \(\square \)

2.2 Localization Residual Symmetry

In order to look for the finite symmetry transformation of the nonlocal residual symmetry, we have to solve the following initial value problem:

$$\begin{aligned} \frac{\hbox {d} \hat{u}(\varepsilon )}{\hbox {d} \varepsilon }=\hat{\phi }_{x}(\varepsilon ),~~~~\hat{u}(0)=u, \end{aligned}$$
(15)

where \(\varepsilon \) is the group parameter.

Nevertheless, since the intervene of the function \(\hat{\phi }_{x}\) and its differentiation, it is very difficult to solve the infinite problem (15). So, we need to prolong the original system such that nonlocal residual symmetry becomes the local Lie point symmetry for a closed system. To this end, we introduce new variables to eliminate the space derivatives of \(\phi \)

$$\begin{aligned} \begin{aligned} f&=\phi _{x},\\ g&=\phi _{y},\\ h&=f_{x}. \end{aligned} \end{aligned}$$
(16)

It is easy to find nonlocal residual symmetry of (3) can be localized to the Lie point symmetry

$$\begin{aligned} \sigma ^{u}=-6h,~~\sigma ^{f}=2\phi f,~~\sigma ^{g}=2\phi g,~~\sigma ^{h}=2f^{2}+2\phi f h ,~~ \sigma ^{\phi }=\phi ^{2}, \end{aligned}$$
(17)

for the prolonged system

$$\begin{aligned} \begin{aligned}&u_{tt}-u_{xx}-u_{yy}-(u^{2})_{xx}-u_{xxxx}=0,\\&u=-\frac{1}{2\phi _{x}^{2}}\left[ -3\phi _{xx}^{2}+4\phi _{x}\phi _{xxx}-\phi _{t}^{2}+\phi _{x}^{2}+\phi _{y}^{2}\right] ,\\&f=\phi _{x},\\&g=\phi _{y},\\&h=f_{x}. \end{aligned} \end{aligned}$$
(18)

With the Lie point symmetry vector, the results (17) show that the residual symmetries (12) are localized in the properly prolonged system (18)

$$\begin{aligned} V=-6h \frac{\partial }{\partial u}+2\phi f \frac{\partial }{\partial f}+2\phi g \frac{\partial }{\partial g}+(2f^{2}+2\phi f h)\frac{\partial }{\partial h}+\phi ^{2} \frac{\partial }{\partial \phi }. \end{aligned}$$
(19)

Relatively, the initial value problem (15) becomes

$$\begin{aligned} \begin{aligned}&\frac{\hbox {d} \hat{u}(\varepsilon )}{\hbox {d} \varepsilon }=-6h,~~~~~~~~~~~~~~~~~~\hat{u}|_{\varepsilon =0}=u,\\&\frac{\hbox {d} \hat{f}(\varepsilon )}{\hbox {d} \varepsilon }=2\phi f ,~~~~~~~~~~~~~~~~~~\hat{f}|_{\varepsilon =0}=f,\\&\frac{\hbox {d} \hat{g}(\varepsilon )}{\hbox {d} \varepsilon }=2\phi g ,~~~~~~~~~~~~~~~~~~\hat{g}|_{\varepsilon =0}=g,\\&\frac{\hbox {d} \hat{h}(\varepsilon )}{\hbox {d} \varepsilon }=2f^{2}+2\phi f h,~~~~~~\hat{h}|_{\varepsilon =0}=h,\\&\frac{\hbox {d} \hat{\phi }(\varepsilon )}{\hbox {d} \varepsilon }=\phi ^{2} ,~~~~~~~~~~~~~~~~~~~~~\hat{\phi }|_{\varepsilon =0}=\phi .\\ \end{aligned} \end{aligned}$$
(20)

That is to say, the symmetries referred to the truncated Painlevé expansion are just a special Lie point symmetry of the extended system.

Then, by solving the corresponding initial value problem, it is not difficult to obtain the transformation group related to the symmetry (20) of the prolonged system as follows:

Theorem 2.3

If \(\{u, f, g, h, \phi \}\) is a solution of the prolonged system (18), so is \(\{\hat{u}, \hat{f}, \hat{g}, \hat{h}, \hat{\phi }\}\) given by

$$\begin{aligned} \begin{aligned} \hat{u}(\varepsilon )&=u+\frac{6\varepsilon h}{\varepsilon \phi -1}-\frac{6 \varepsilon ^{2} f^{2}}{(\varepsilon \phi -1)^2},\\ \hat{f}(\varepsilon )&=\frac{f}{(\varepsilon \phi -1)^{2}},\\ \hat{g}(\varepsilon )&=\frac{f}{(\varepsilon \phi -1)^{2}},\\ \hat{h}(\varepsilon )&=\frac{h}{(\varepsilon \phi -1)^{2}}-\frac{2f^{2} \varepsilon }{(\varepsilon \phi -1)^{3}},\\ \hat{\phi }(\varepsilon )&=-\frac{\phi }{\varepsilon \phi -1}, \end{aligned} \end{aligned}$$
(21)

with arbitrary group parameter \(\varepsilon \).

3 CRE Solvability and Soliton–Cnoidal Waves Solutions

In this section, we mainly introduce the CRE , and based on the CRE, we obtain the CTE. Besides, we also study the interactions between a soliton and a cnoidal wave for Eq. (3).

3.1 Preliminary

In this section, we mainly introduce the conceptions of CRE and CRE solvability for a given derivative nonlinear polynomial system

$$\begin{aligned} \begin{aligned}&\mathbf P (\mathbf x ,t,\mathbf u )=0, ~~~~~~~~~~~~~~~\mathbf P =\{P_{1},P_{2},\ldots ,P_{m}\},\\&\mathbf x =\{x_{1},x_{2},\ldots ,x_{n}\}, ~~~~\mathbf u =\{u_{1},u_{2},\ldots ,u_{n}\}. \end{aligned} \end{aligned}$$
(22)

We are committed to find the following possible truncated Painlevé expansion solution

$$\begin{aligned} u=\sum _{i=0}^{n}u_{i}R(w)^{i}, \end{aligned}$$
(23)

where R(w) is a solution of the Riccati equation

$$\begin{aligned} R_{w}=a_{0}+a_{1}R+a_{2}R^{2}, \end{aligned}$$
(24)

It includes tanh(w) as a special case, and w is an arbitrary function of \(\{x_{1},x_{2},\ldots ,x_{n},t\}\) and \(a_{0}\), \(a_{1}\), \(a_{2}\) are arbitrary constants. By using the leading order analysis of (22), we obtain n and m, meanwhile, by substituting (23) with (24) into (22) and by vanishing all the coefficients of the power of R(w), then we get all the expansion coefficient functions \(u_{i}\).

Based on the above analysis and Ref. [10], we have the following theorem:

Theorem 3.1

The expansion (23) is a consistent Riccati expansion (CRE) and the nonlinear system (22) is CRE solvable provided that the system for \(u_{i} (i=1,2,\ldots ,n)\) and w obtained by vanishing all the coefficients of the powers of R(w) after substituting (23) with (24) into (22) are consistent, or not over-determined.

3.2 CRE Solvability

In this section, we apply CRE method to Eq. (3). From the above analysis, the possible truncated expansion of Eq. (3) has the following form

$$\begin{aligned} u=u_{2}R(w)^{2}+u_{1}R(w)+u_{0}, \end{aligned}$$
(25)

where \(u_{0}, u_{1},u_{2}\) are the undetermined functions of (x, y, t).

Substituting (24) and (25) into (3), and vanishing coefficients of all the same powers of R(w), we have nine over-determined equations for the only six undetermined functions \(u_{0}, u_{1}, u_{2}\) and w. Fortunately, the over-determined is consistent and the final result reads

$$\begin{aligned} \begin{aligned} u_{2}&=-6a_{2}^{2}w_{x}^{2},~~~~~~~~~~~~~~u_{1}=-6a_{2}w_{xx}-6a_{1}a_{2}w_{x}^{2},\\ u_{0}&=-\frac{1}{2w_{x}^{2}}\left[ 4w_{x}w_{xxx}+6a_{1}w_{x}^{2}w_{xx}-3 w_{xx}^{2}+a_{1}^{2}w_{x}^{4}+w_{y}^{2}\right. \\&\quad \left. -w_{t}^{2}+8a_{0}a_{2}w_{x}^{4}+w_{x}^{2}\right] , \end{aligned} \end{aligned}$$
(26)

and the function w satisfies a generalization of the Schwarzian form of (3)

$$\begin{aligned} S_{1x}-C_{1}C_{1x}-C_{1t}+K_{1}K_{1x}+K_{1y}-\delta (w_{x}w_{xx})=0, \end{aligned}$$
(27)

where the notations \(C_{1}\) , \(K_{1}\), \(S_{1}\) and \(\delta \) are defined by

$$\begin{aligned} C_{1}=\frac{w_{t}}{w_{x}}, ~~~~~~~ K_{1}=\frac{w_{y}}{w_{x}},~~~~~~S_{1}=\frac{w_{xxx}}{w_{x}}-\frac{3}{2}\frac{w_{xx}^{2}}{w_{x}^{2}}, ~~~~~~~ \delta \equiv a_{1}^{2}-4a_{0}a_{2}. \end{aligned}$$
(28)

From above discussion, we find that all the coefficients of R(w) are zero. Apparently, because the over-determined system is consistent, we call Eq. (3) CRE solvable. Then, we have the following theorem:

Theorem 3.2

If w is a solution of

$$\begin{aligned} S_{1x}-C_{1}C_{1x}-C_{1t}+K_{1}K_{1x}+K_{1y}-\delta (w_{x}w_{xx})=0, \end{aligned}$$
(29)

then

$$\begin{aligned} u=u_{2}R(w)^{2}+u_{1}R(w)+u_{0}, \end{aligned}$$
(30)

is the solution of Eq. (3) with \(R_{w}\) being the solution of the Riccati equation (24).

3.3 CTE Solvability

Apparently, the Riccati equation (24) has a special solution

$$\begin{aligned} R(W)=\text{ tanh }(w). \end{aligned}$$
(31)

Hence, the truncated expansion expression (25) can be changed into the following form:

$$\begin{aligned} u=u_{2}\text{ tanh }(w)^{2}+u_{1}\text{ tanh }(w)+u_{0}, \end{aligned}$$
(32)

where \(u_{0}, u_{1}, u_{2}\) and w are determined by (24) , (26) and (27).

We know that the solution (32) is just consistent with Theorem 3.2. The simplified CRE can be termed as consistent tanh expansion (CTE). Clearly, a CRE solvable system must be CTE solvable, and vice versa. If the system is CTE solvable, some important solitary wave solutions can be constructed directly. In order to clarify this relation, we give the following Bäcklund transformation which comes from the aforementioned CTE theorem and use it to find exact solutions.

Theorem 3.3

(Bäcklund transformation Theorem ) If w is a solution of Eq. (27) with \(\delta =4, a_{0}=1, a_{1}=0, a_{2}=-1\), then

$$\begin{aligned} \begin{aligned} u&=-6w_{x}^{2}\text{ tanh }(w)^{2}+6w_{xx}\text{ tanh }(w)\\&\quad -\frac{1}{2w_{x}^{2}}\left[ 4w_{x}w_{xxx}-3w_{xx}^{2}+w_{y}^{2}-w_{t}^{2}-8w_{x}^{4}+w_{x}^{2}\right] , \end{aligned} \end{aligned}$$
(33)

is a Bäcklund transformation between w and the solution u of Eq. (3) with R(W) satisfying the Riccati equation (24).

3.4 Soliton–Cnoidal Wave Interaction Solution of Eq. (3)

It is well known that the interaction solutions between soliton and cnoidal periodic waves can display many more interesting physical phenomena, such as the Fermionic quantum plasma [27]. In what follows, based on the symbolic computations [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58], we mainly seek the interaction wave solution of Eq. (27) with respect to w.

To obtain the solution of Eq. (3), we consider w in the form

$$\begin{aligned} w=k_{0}x+l_{0}y+\omega _{0}t+g, \end{aligned}$$
(34)

where g is a function of x, y and t. It will result in the interaction solutions between a soliton and other waves. By using Theorem 3.3, some nontrivial solutions of Eq. (3) can be obtained from some quite trivial of Eq. (27).

Soliton Solution For Eq. (27), we take the following trivial solution

$$\begin{aligned} w=kx+ly+\omega t+g, \end{aligned}$$
(35)

where \(k, l, \omega \) and g are the arbitrary constants. Substituting (36) into Eq. (32) yields the following single soliton solution

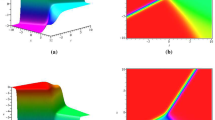
$$\begin{aligned} u=-6k^{2}\text{ tanh }(w)^{2}-\frac{1}{2k^{2}}\left[ l^{2}-\omega ^{2}-8k^{4}+k^{2}\right] , \end{aligned}$$
(36)

Figure 1 displays single soliton solution for u shown by (36) at \(t=1\) with the parameter selected as

$$\begin{aligned} \{k, l, w, g\}=\{1, 1, 1, 0\}. \end{aligned}$$
(37)

Figure 1a represents a three-dimensional space graph of single soliton solution with small excited state. Figure 1b represents a three-dimensional density graph of single soliton solution. Figure 1c represents the wave propagation of the wave along x axis.

Fig. 1
figure 1

(Color online) The single soliton solution of Eq. 3 shown by (36) at \(t=1\) with the parameter selections (37). a Perspective view of the real part of the wave; b overhead view of the wave; c wave propagation pattern of the x axis at \(y = 0\), \(t=1\)

Full size image

Soliton–cnoidal wave solutions From Ref. [10], it is easy to find that the solution w characters the interactions between a soliton and a cnoidal wave for Eq. (3), which is of the form

$$\begin{aligned} w=k_{0}x+l_{0}y+\omega _{0}t+W(X),~~~~ X=k_{1}x+l_{1}y+\omega _{1}t, \end{aligned}$$
(38)

where

$$\begin{aligned} W_{1}=W_{1}(X)=W_{X}, \end{aligned}$$
(39)

satisfies

$$\begin{aligned} W_{1X}^{2}=C_{0}+C_{1}W_{1}+C_{2}W_{1}^{2}+C_{3}W_{1}^{3}+C_{4}W_{1}^{4}, \end{aligned}$$
(40)

with

$$\begin{aligned} \begin{aligned} C_{0}&=\frac{k_{0}^{2}C_{2}}{k_{1}^{2}}-\frac{4k_{0}\omega _{0} \omega _{1}}{3k_{1}^{5}}-\frac{2k_{0}^{3}C_{3}}{k_{1}^{3}}+\frac{12 k_{0}^{4}}{k_{1}^{4}}\\&\quad +\frac{4k_{0}l_{0}l_{1}}{3k_{1}^{5}}-\frac{5k_{0}^{2} l_{1}^{2}}{3k_{1}^{6}}+\frac{5k_{0}^{2}\omega _{1}^{2}}{3k_{1}^{6}} +\frac{l_{0}^{2}}{3k_{1}^{4}}-\frac{\omega _{0}^{2}}{3k_{1}^{4}},\\ C_{1}&=-\frac{2\omega _{0}\omega _{1}}{k_{1}^{4}}+\frac{2k_{0}C_{2}}{k_{1}} -\frac{3k_{0}^{2}C_{3}}{k_{1}^{2}}+\frac{16k_{0}^{3}}{k_{1}^{3}}\\&\quad +\frac{2l_{0}l_{1}}{k_{1}^{4}}-\frac{2k_{0}l_{1}^{2}}{k_{1}^{5}} +\frac{2k_{0}\omega _{1}^{2}}{k_{1}^{5}},\\ C_{4}&=4, \end{aligned} \end{aligned}$$
(41)

which lead to the following explicit solution of Eq. (3)

$$\begin{aligned} \begin{aligned} u&=-6(k_{0}+k_{1}W_{1})^{2}\text{ tanh }(k_{0}x+l_{0}y+\omega _{0}t+W)^{2}\\&\quad +6k_{1}^{2}W_{1X}\text{ tanh }(k_{0}x+l_{0}y+\omega _{0}t+W)\\&\quad -\frac{1}{2k_{1}^{2}}\left[ 12k_{1}^{4}W_{1}^{2}+3W_{1}k_{1}^{4} C_{3}-24k_{1}^{3}k_{0}W_{1}+k_{1}^{4}C_{2}+k_{1}^{2} -12k_{0}^{2}k_{1}^{2}-\omega _{1}^{2}+l_{1}^{2}\right] . \end{aligned} \end{aligned}$$
(42)

Obviously, the explicit solution of (40) can be expressed in terms of different types of the Jacobi elliptic functions. Therefore, the solution (42) indicates the interactions between a soliton and cnoidal periodic waves. In the following, only one type of the special soliton–cnoidal wave is expressed to see the interaction property more intuitively.

A simple solution of (40) is given by

$$\begin{aligned} W_{1}=\mu _{0}+\mu _{1}\text{ sn }(mX,n). \end{aligned}$$
(43)

where \(\text{ sn }(mX,n)\) is the usual Jacobi elliptic sine function. The modulus n of the Jacobi elliptic function satisfies: \(0\le n\le 1\) . When \(n\rightarrow 1\), \(\text{ sn }(\xi )\) degenerates as hyperbolic function \(\tanh (\xi )\), and when \(n\rightarrow 0\), \(\text{ sn }(\xi )\) degenerates as a trigonometric function \(\sin (\xi )\).

Then, substituting Eq. (43) with Eq. (41) into Eq. (40) and setting the coefficients of \(\text{ sn }(\xi )\), \(\text{ cn }(\xi )\), \(\text{ dn }(\xi )\) equal to zero yields the following soliton–cnoidal wave interaction solution of (3)

$$\begin{aligned} \begin{aligned}&C_{2}=-\frac{1}{3k_{1}^{4}m^{2}}\left[ 3k_{1}^{4}m^{4}-72m^{2}k_{1}^{4}\mu _{0}^{2}-4\mu _{0}\omega _{0}\omega _{1}+4\mu _{0}l_{0}l_{1}-4\omega _{0}^{2}+4l_{0}^{2}\right] ,\\&\omega _{1}=\frac{1}{2}\left[ \frac{-\omega _{0}+\sqrt{\omega _{0}^{2}+4\mu _{0}l_{0}l_{1}+4l_{1}^{2}\mu _{0}^{2}}}{\mu _{0}}\right] ,\\&\mu _{1}=\frac{\sqrt{3l_{0}^{2}-3\mu _{0}\omega _{0}\omega _{1}+3\mu _{0}l_{0}l_{1}-3\omega _{0}^{2}}}{3mk_{1}^{2}},\\&n=\frac{2\mu _{1}}{m},~~~~~~~~~C_{3}=-16\mu _{0},~~~~~~~~~k_{0}=-k_{1}\mu _{0}.\\ \end{aligned} \end{aligned}$$
(44)

Hence, one kind of soliton–cnoidal wave solutions is obtained by taking Eq. (43) and

$$\begin{aligned} W=\mu _{0}X+\mu _{1}\int _{X_{0}}^{X}\text{ sn }(mY,n)\hbox {d} Y, \end{aligned}$$
(45)

with the parameter requirement (44) into the general solution (42).

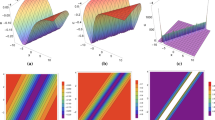
Figures 2 and 3 display this kind of soliton–cnoidal wave solutions. This kind of solution describing solitons moving on a cnoidal wave background instead of on the plane continuous wave background is very important in the real world and can be easily applicable to the analysis of physically interesting processes.

Fig. 2
figure 2

(Color online) The kink soliton+cnoidal periodic wave solutions for u by choosing suitable parameters: \(m=1.5, k_{1}=1, \omega _{0}=-1.6, l_{1}=1, \mu _{0}=\sqrt{3}, l_{0}=-1\). a evolution of the soliton–cnoidal structure; b the profile of the special structure at \(y = 0\), \(t=0\); c the profile of the special structure at \(x = 0\), \(t=0\)

Full size image
Fig. 3
figure 3

(Color online) The kink soliton+cnoidal periodic wave solutions for u by choosing suitable parameters: \(m=4, k_{1}=1, \omega _{0}=-1.6, l_{1}=1, \mu _{0}=\sqrt{3}, l_{0}=-1\). a evolution of the soliton–cnoidal structure; b the profile of the special structure at \(y = 0\), \(t=0\); c the profile of the special structure at \(x = 0\), \(t=0\)

Full size image

4 Conclusion and Discussions

In this work, we mainly have studied the Bäcklund transformations, nonlocal symmetry and soliton–cnoidal interaction solutions of the (2 + 1)-dimensional Boussinesq equation. Firstly, by use of the truncated Painlevé expansion method, the nonlocal symmetry and BT have been obtained, respectively. Then, with the help of the arbitrary parameter in the Schwarzian form of the system, many infinitely nonlocal symmetries have also been derived. The symmetry group transformation of the prolonged symmetry has been derived by using Lie’s first theorem. Furthermore, under the CRE, the system has been proved integrable. Based on a special form of CRE, that’s CTE method, we have obtained a BT. Finally, by means of CRE method, we have derived the interaction solution between a soliton and a cnoidal periodic wave.

It is worthwhile to further study the other types of effective methods which can also be extended to study the relationship between different types of nonlinearity. The discussed method is much meaningful for us to do further study nonlinear problems in mathematical physics.