The Augmented Zagreb Indices of Fluoranthene-Type Benzenoid Systems

Abstract

The augmented Zagreb index (AZI index) of a graph $G=(V,E)$, which is a valuable predictive index in the study of the heat of formation in octanes and heptanes, is defined as

$$\begin{aligned} \hbox {AZI}(G)=\sum _{uv\in E(G)}\left( \frac{d_{u}d_{v}}{d_{u}+d_{v}-2}\right) ^{3}{,} \end{aligned}$$

where $d_{u}$ and $d_{v}$ are the degrees of the terminal vertices u and v of edge uv, respectively. In this paper, we give the expressions for computing the augmented Zagreb indices of fluoranthene-type benzenoid systems, and we determine the extremal values of augmented Zagreb index in f-benzenoid systems with h hexagons. Especially, we give the extremal values of augmented Zagreb index in cata-catacondensed fluoranthene-type benzenoid systems with h hexagons.

1 Introduction

Molecular descriptors play a significant role in chemistry, pharmacology, etc. Among them, topological indices have a prominent place (see [16, 55]). Topological indices are numbers associated with chemical structures derived from their hydrogen-depleted graphs as a tool for compact and effective description of structural formulas which are used to study and predict the structure–property correlations of organic compounds.

Let G be a simple connected graph with vertex set V(G) and edge set E(G). The augmented Zagreb index (AZI index for short) was firstly introduced by Furtula et al. [21], which is defined to be

$$\begin{aligned} \hbox {AZI}(G)=\sum _{uv\in E(G)}\left( \frac{d_{u}d_{v}}{d_{u}+d_{v}-2}\right) ^{3}, \end{aligned}$$

where $d_{u}$ and $d_{v}$ are the degrees of the terminal vertices u and v of edge uv, respectively.

This graph invariant has proven to be a valuable predictive index in the study of the heat of formation in octanes and heptanes (see [21]), whose prediction power is better than atom–bond connectivity index (please refer to [11, 17, 18, 20, 22, 59] for its research background). Moreover, Gutman and Tošovič [31] tested the correlation abilities of 20 vertex-degree-based topological indices for the case of standard heats of formation and normal boiling points of octane isomers, and they found that the augmented Zagreb index yields the best results.

Furtula et al. [21] have studied extremal properties of augmented Zagreb index of trees and chemical trees, and they proved that among all trees the star has the minimum augmented Zagreb index value. Huang et al. [34] and Wang et al. [57] gave sharp lower and upper bounds for various classes of connected graphs (e.g., trees, unicyclic graphs, bicyclic graphs, etc.) and characterized corresponding extremal graphs. Zhan et al. [60] determined the minimal and the second minimal augmented Zagreb indices of the n-vertex unicyclic graphs. Additionally, they obtained the n-vertex bicyclic graphs in which the augmented Zagreb index attains its minimal value.

Fig. 1

Examples of fluoranthene-type benzenoid systems. 1 and 2 are cata-catacondensed, 3 is peri-catacondensed, 4 is cata-pericondensed, and 5 is peri-pericondensed

Our main concern is the class of the fluoranthene-type benzenoid systems. Fluoranthene is a well-known tetracyclic conjugated hydrocarbon, present in large amounts in coal tar [7]. It consists of a benzene and a naphthalene unit, joined through a five-membered ring. Other polycyclic conjugated hydrocarbon, consisting of two benzenoid units joined through a five-membered ring are referred as fluoranthene-type benzenoid system (or fluoranthenes) [28, 29]. A few examples of fluoranthene-type benzenoid systems are presented in Fig. 1.

In what follows we will represent the fluoranthene-type benzenoid system by means of their molecular graphs [26]. This, in particular, means that the carbon atoms are represented by vertices, and the carbon–carbon bonds by edges. The molecular graphs of fluoranthene-type benzenoid system are then defined in the following manner. Let X be a benzenoid system [28]. Let u and v be two vertices of X whose degree is two, and which both are adjacent to a vertex w of degree 3. Let Y be another benzenoid system. Let a and b be two adjacent vertices of Y whose degree is two. The fluoranthene-type benzenoid system F is obtained by joining (with a new edge) the vertices u and a , and by joining (with a new edge) the vertices v and b (see Fig. 2).

Fig. 2

The general form of an f-benzenoid system (F) and its construction from two benzenoid systems X and Y

What first needs to be noticed is that the vertices a, b, v, w, u of F form a five-membered cycle. Each fluoranthene-type benzenoid system possesses (by definition) exactly one five-membered cycle.

Although the structures of fluoranthene-type benzenoid systems and benzenoid hydrocarbons are evidently similar, fluoranthene-type benzenoid systems were excluded from the chemical graph theoretical consideration of benzenoid systems because of the presence of a five-membered ring. As a result, while the topological theory of benzenoid molecules is nowadays one of the most thoroughly elaborated aspect of chemical graph theory, the first attempts to develop an analogous theory of fluoranthene-type benzenoid systems started only very recently [28].

The fluoranthene-type benzenoid systems considered by us must pertain to plane graphs composed of regular hexagonals and a regular pentagon, all having the same edge lengths. Non-adjacent hexagon and hexagon–pentagon pairs must neither tough nor overlap (we exclude the helicenic and other geometrically non-plane species from the class of fluoranthene-type benzenoid systems). Fluoranthene-type benzenoid systems are compounds which, in view of their chemical and physical properties, belong among benzenoid hydrocarbons. For more about fluoranthene-type benzenoid system, one can see [28].

In what follows, instead of “fluoranthene-type benzenoid system” we shall say “f-benzenoid system”.

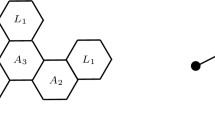
Throughout this paper, the notation and terminology are mainly taken from [9, 10, 24, 38,39,40,41]. A benzenoid system is said to be catacondensed if it has no internal vertices; otherwise, it is pericondensed [28]. In view of this, we propose the following classification of f-benzenoid system. If the f-benzenoid system F has just a single internal vertex, then it is said to be cata-catacondensed. This happens when both fragments X and Y (as shown in Fig. 2) are catacondensed benzenoid systems. A hexagon H of F is called a kink [15], denoted as $A_{2}$, if H has exactly two consecutive 2 vertices in F. If H has no 2 vertex, then H is called a branched hexagon [15], denoted as $A_{3}$. If a hexagon H has only one vertex of degree 2, we call it a $P_{3}$ hexagon. If a hexagon H has just two consecutive 3 vertices, we call it a $L_{1}$ hexagon. A hexagon H is called a $L_{2}$ hexagon if it has just two non-adjacent vertices of degree 2 (as shown in Fig. 3).

Fig. 3

Five modes of hexagons in F

Let $L_{h}$ denote the linear chain with h hexagons(as shown in Fig. 4a). A cata-catacondensed f-benzenoid system is called an f-linear chain when fragment X is $L_{2}$ and Y is $L_{h-2}$, and which is denoted as $FL_{h}$, $h\ge 3$ (as shown in Fig. 4b).

Fig. 4

Linear chain and f-linear chain. a Linear chain. b f-Linear chain

The extremal hexagonal systems with respect to some useful topological indices such as connectivity index, general connectivity index, second Zagreb index, atom–bond connectivity index, sum-connectivity index, geometric–arithmetic index, augmented Zagreb index, harmonic index in chemical applications have been extensively studied, and many results concerning this topic can be found in [3, 8, 14, 19, 27, 33, 36, 45, 46, 50,51,52,53,54, 58].

In [40, 41], we gave the expression of the second-order Randić and the general connectivity indices of fluoranthene-type benzenoid systems in terms of their inlet features. And they find the minimal and maximal value of the second-order Randić index and the general connectivity indices over the set of cata-catacondensed fluoranthene-type benzenoid systems and characterize their corresponding graphs.

In this paper, we give the expression of the augmented Zagreb index of f-benzenoid systems (not only cata-catacondensed f-benzenoid systems) in terms of their inlet features. The minimal and maximal values of the augmented Zagreb index over the set of cata-catacondensed fluoranthene-type benzenoid systems were given. In the final, we also discuss the minimal values of the augmented Zagreb indices of f-benzenoid systems with h hexagons.

2 The Augmented Zagreb Index of f-Benzenoid Systems

The following definitions were introduced in [28, 30]. If one goes along the perimeter of an f-benzenoid system F, then a fissure (resp. a bay, cove, fjord, or lagoon) corresponds to a sequence of three (resp. four, five, six, or seven) consecutive vertices on the perimeter, of which the first and the last are vertices of degree 2 and the rest are vertices of degree 3. (For examples see Fig. 5). The number of fissures, bays, coves, fjords and lagoons are denoted, respectively, by f, B, C, $F_{j}$ and L.

Fig. 5

Structural features occurring on the boundary of f-benzenoid systems

Fissures, bays, coves, fjords and lagoons are called various types of inlets. The total number of inlets on the perimeter of F, $f+B+C+F_{j}+L$, will be denoted by r. There is another parameter $b=B+2C+3F_{j}+4L$, called the number of bay regions, will be useful later. It is easy to see that $b\ge 2$ for all f-benzenoid systems, and b is just the number of (3, 3)-type edges on the perimeter. Evidently, $f+2B+3C+4F_{j}+5L$ is the number of vertices of degree 3 on the perimeter.

First of all, all vertices in an f-benzenoid system have degrees equal to 2 or 3, so, in further text, a j-vertex denotes a vertex of degree j, and a (j, k)-edge stands for an edge connecting a j-vertex with a k-vertex. The number of j-vertices and (j, k)-edges in the graph considered will be denoted by $n_{j}$ and $m_{jk}$, respectively. So it follows that

$$\begin{aligned} \hbox {AZI}(F)=8m_{22}+8m_{23}+\left( \frac{3}{2}\right) ^{6}m_{33}. \end{aligned}$$

(1)

If F is an f-benzenoid system with n vertices, m edges and h hexagons, then F possesses $h+1$ face cycles (h hexagons and a pentagon), so, $m=n+h$, and $n_{2}+n_{3}=n$, $2n_{2}+3n_{3}=2m$, it can be shown that $n_{2}=n-2h$, $n_{3}=2h$.

Some vertices and edges of F lie on its perimeter. These will be referred to as external vertices and external edges, and their numbers are denoted by $n_\mathrm{ex}$ and $m_\mathrm{ex}$, respectively. Evidently, $n_\mathrm{ex}=m_\mathrm{ex}$.

The vertices and edges that are not external are said to be internal, and their numbers are denoted by $n_{i}$ and $m_{i}$. Clearly, $n_\mathrm{ex}+n_{i}=n$ and $m_\mathrm{ex}+m_{i}=m$.

An f-benzenoid system with h hexagons and $n_{i}$ internal vertices represents a benzenoid hydrocarbon of the formula $C_{4h+5-n_{i}}H_{2h+5-n_{i}}$. For this reason, f-benzenoid systems with equal number of hexagons and equal number of internal vertices will be said to be isomeric. Isomeric f-benzenoid systems have also equal number of vertices and equal number of edges. The formula of all cata-catacondensed f-benzenoids with h six-membered rings is then $C_{4h+4}H_{2h+4}$ and, consequently, all these hydrocarbons are isomers.

Lemma 2.1

[28] Let F be an f-benzenoid system with n vertices, m edges h hexagons and $n_{i}$ internal vertices, then

• (a) The number of internal edges $m_{i}=h+n_{i}$;

• (b) $n=4h+5-n_{i}$;

• (c) $m=5h+5-n_{i}$.

Lemma 2.2

[28] Let F be an f-benzenoid system with n vertices and h hexagons $(h\ge 3)$. Then

• (a) $m_{22}+m_{23}+m_{33}=m$;

• (b) $6m_{22}+5m_{23}+4m_{33}=6n$,

where $m_{ij}$ represents the number of (i, j)-type edges in F.

Theorem 2.1

Let F be an f-benzenoid system with n vertices, h hexagons and r inlets. Then

$$\begin{aligned} \hbox {AZI}(F)=8n+\left( 3\left( \frac{3}{2}\right) ^{6}-16\right) h-\left( \left( \frac{3}{2}\right) ^{6}-8\right) r. \end{aligned}$$

(2)

Proof

First, we have

$$\begin{aligned} m_{33} =3h-r, \end{aligned}$$

since by Lemma 2.1, we know that the number of (3, 3)-type edges that do not lie on the perimeter is $h+n_{i}$, and the others (3, 3)-type edges are along the perimeter, so, we have

$$\begin{aligned} m_{33} =h+n_{i}+b, \end{aligned}$$

for $n=4h+5-n_{i}$, then, $n_{i}=4h+5-n$, so,

$$\begin{aligned} m_{33} =5h+5-n+b. \end{aligned}$$

We note that the number of external vertices of degree 3 is given by the expression $f+2B+3C+4F_{j}+5L$, so, we have

$$\begin{aligned} f+2B+3C+4F_{j}+5L=n_{3}-n_{i}. \end{aligned}$$

For $n_{3}=2h$, $n_{i}=4h+5-n$, then,

$$\begin{aligned} f+2B+3C+4F_{j}+5L=n-5-2h. \end{aligned}$$

On the other hand,

$$\begin{aligned} f+B+C+F_{j}+L=r. \end{aligned}$$

So, the number of bay regions is

$$\begin{aligned} b=B+2C+3F_{j}+4L=n-5-2h-r. \end{aligned}$$

Thus,

$$\begin{aligned} m_{33} =5h+5-n+b=5h+5-n+n-5-2h-r=3h-r. \end{aligned}$$

Second, it is clear that every inlet have two (2, 3)-type edges, thus, $m_{23}=2r$.

Furthermore, by Lemmas 2.1 and 2.2, we know that

$$\begin{aligned} m_{22}+m_{23}+m_{33}=h+n, \end{aligned}$$

hence, we have

$$\begin{aligned} m_{22}=h+n-m_{23}-m_{33}=n-2h-r. \end{aligned}$$

Now, Theorem 2.1 follows by substituting the values of $m_{ij}$ obtained above in Eq. (1).

This completes the proof.$\square$

From Eq. (2), we can see that the augmented Zagreb index of an f-benzenoid system is completely determined by the numbers of vertices, hexagons and inlets.

3 The Extremal Values of Augmented Zagreb Index in Cata-catacondensed f-Benzenoid Systems

In this section, we will try to find the minimal and maximal value of augmented Zagreb index over all cata-catacondensed f-benzenoid systems and characterize their corresponding graphs. For convenience, we let $\mathbb {FC}_{h}$ denote the set of all cata-catacondensed f-benzenoid systems with h hexagons.

Theorem 3.1

Let $F\in \mathbb {FC}_{h}$ be a cata-catacondensed f-benzenoid system with n vertices, h hexagons, and r inlets. Then, the augmented Zagreb index of F is

$$\begin{aligned} \mathrm{AZI}(F)=\left( 3\left( \frac{3}{2}\right) ^{6}+16\right) h-\left( \left( \frac{3}{2}\right) ^{6}-8\right) r+32. \end{aligned}$$

(3)

Proof

First, we know that a cata-catacondensed f-benzenoid system has just one internal vertex, so, by Lemma 2.1, we have $n=4h+4$. Hence, by Theorem 2.1, we get

$$\begin{aligned} \hbox {AZI}(F)=\left( 3\left( \frac{3}{2}\right) ^{6}+16\right) h-\left( \left( \frac{3}{2}\right) ^{6}-8\right) r+32. \end{aligned}$$

This completes the proof.$\square$

From Eq. (3), we can see that:

• (i) The augmented Zagreb index of a cata-catacondensed f-benzenoid system is completely determined only by the numbers of hexagons and inlets;

• (ii) Among all cata-catacondensed f-benzenoid systems with an equal number of hexagons (or vertices, since $n =4h+4$ for a cata-catacondensed f-benzenoid system with n vertices and h hexagons), the augmented Zagreb index is monotone decreasing over the number of inlets.

Our next result classifies all cata-catacondensed f-benzenoid systems with an equal number of vertices that have an equal augmented Zagreb index.

Corollary 3.1

Let $F', F''\in \mathbb {FC}_{h}$, then, $\mathrm{AZI}(F')=\mathrm{AZI}(F'')$ if and only if $r(F')=r(F'')$. Moreover, $\mathrm{AZI}(F')<\mathrm{AZI}(F'')$ if and only if $r(F')>r(F'')$.

From above analysis, we know that the augmented Zagreb indices of $F\in \mathbb {FC}_{h}$ are monotone decreasing over the number of inlets. So, it is interesting for us to find the extremal values of r in $\mathbb {FC}_{h}$.

Lemma 3.1

[40] For any $F\in \mathbb {CF}_{h}$, $h\ge 3$, we have

$$\begin{aligned} r(F)\ge \left\{ \begin{array}{ll} \frac{h+4}{2}, &{}\quad \mathrm{if}\ h\ \mathrm{is}\ \mathrm{even}\\ \frac{h+3}{2}, &{}\quad \mathrm{if}\ h\ \mathrm{is}\ \mathrm{odd}. \\ \end{array} \right. \end{aligned}$$

In [40], Li and Ye gave the following Lemma 3.3 which offers an upper bound for the inlets over f-benzenoid system with h hexagons and we now give a short proof of Lemma 3.3 by using the Lemma 3.2.

Lemma 3.2

[28] If an f-benzenoid system has h hexagons, $n_{i}$ internal vertices, and b bay regions, then the counts of edges of type (2,2) and (2,3) are $m_{22}=b+5, m_{23}=4h-2n_{i}-2b$.

Lemma 3.3

For any f-benzenoid system F with h hexagons, $r(F)\le 2h-3$.

Proof

By Lemma 3.2, we have

$$\begin{aligned} m_{23}=4h-2n_{i}-2b, \end{aligned}$$

on the other hand, we know that $m_{23}=2r$. So, we get

$$\begin{aligned} r=2h-3-(n_{i}+b-3). \end{aligned}$$

Since $n_{i}+b-3\ge 0$, Lemma 3.3 immediately follows.

This completes the proof.$\square$

Fig. 6

Catacondensed ladders $\Theta (m_{1},m_{2}, k)$ and $\Theta (2, 2, k)$

The catacondensed ladder is a type of branched catacondensed hexagonal system shown in Fig. 6 and denoted by $\Theta (m_{1}, m_{2}, k)$; k is a positive integer. This class of catacondensed systems has appeared frequently in the study of Kekulé structure of benzenoid systems [15].

We can use $\Theta (2, 2, k)$ as the basic structure to construct cata-catacondensed f-benzenoid systems $E_{h}$ with minimal number of inlets as follows:

Fig. 7

Cata-catacondensed f-benzenoid systems $E_{3}$, $E_{5}$, $E_{6}$ and a fluoranthenoid $F_{1}$

• (i) If h is even, then $E_{4}$ and $E_{6}$ be as shown in Fig. 7. When $h\ge 8$, we distinguish two cases:

  Case 1 :

  If $h\ \mathrm{mod}\ 4=0$, we first construct the catacondensed ladder $\Theta \left( 2, 2, \frac{h}{4}\right)$, then we delete the $L_{1}$ hexagon on the top of $\Theta \left( 2, 2, \frac{h}{4}\right)$, and then we attach an $E_{3}$ (as shown in Fig. 7) to the bottom kink of $\Theta \left( 2, 2, \frac{h}{4}\right)$ (as shown in Fig. 8).

  Case 2 :

  If $h\ \mathrm{mod}\ 4\ne 0$, we first construct the catacondensed ladder $\Theta \left( 2, 2, \frac{h-2}{4}\right)$, then we attach a hexagon to the top kink of $\Theta \left( 2, 2, \frac{h-2}{4}\right)$, and then we attach an $E_{3}$ to the bottom kink of it (as shown in Fig. 8).

• (ii) If h is odd, then $E_{3}$ and $E_{5}$ be as shown in Fig. 7. When $h\ge 7$, we distinguish two cases:

  Case 1 :

  If $(h-1)\ \mathrm{mod}\ 4=0$, we first construct the catacondensed ladder $\Theta \left( 2, 2, \frac{h-1}{4}\right)$, then attach a hexagon to the top kink of $\Theta \left( 2, 2, \frac{h-1}{4}\right)$, and then we attach an $F_{1}$ (as shown in Fig. 7) to the bottom kink (as shown in Fig. 9).

  Case 2 :

  If $(h-1)\ \mathrm{mod}\ 4\ne 0$, we first construct the catacondensed ladder $\Theta \left( 2, 2, \frac{h+1}{4}\right)$, then we delete the $L_{1}$ type hexagon on the top of $\Theta \left( 2, 2, \frac{h+1}{4}\right)$, and then we attach an $F_{1}$ to the bottom kink (as shown in Fig. 9).

Fig. 8

Two types of $E_{h}$ when h is even

Fig. 9

Two types of $E_{h}$ when h is odd

Now we give the minimal and maximal value of the augmented Zagreb indices over the set of cata-catacondensed f-benzenoid systems and characterize their corresponding graphs.

Theorem 3.2

For any $F\in \mathbb {CF}_{h}$, $h\ge 3$, we have

• (a) $\mathrm{AZI}(F)\le \mathrm{AZI}(E_{h})$

  $$\begin{aligned} =\left\{ \begin{array}{ll} \left( \frac{5}{2}\left( \frac{3}{2}\right) ^{6}+20\right) h+48-2\left( \frac{3}{2}\right) ^{6}, &{}\quad \mathrm{if}\ h\ \mathrm{is}\ \mathrm{even}\\ \left( \frac{5}{2}\left( \frac{3}{2}\right) ^{6}+20\right) h+44-\left( \frac{3}{2}\right) ^{7}, &{}\quad \mathrm{if}\ h\ \mathrm{is}\ \mathrm{odd}. \\ \end{array} \right. \end{aligned}$$

• (b) $\mathrm{AZI}(F)\ge \mathrm{AZI}(\mathrm{FL}_{h})=\left( \left( \frac{3}{2}\right) ^{6}+32\right) h+8+3\left( \frac{3}{2}\right) ^{6}$.

Proof

By the structure of $E_{h}$, $h\ge 3$ (as shown in Figs. 7, 8, 9), we have

$$\begin{aligned} r(E_{h})=\left\{ \begin{array}{ll} \frac{h+4}{2}, &{} \hbox {if}\ h\ \hbox {is}\ \hbox {even}\\ \frac{h+3}{2}, &{} \hbox {if}\ h\ \hbox {is}\ \hbox {odd}, \\ \end{array} \right. \end{aligned}$$

and for f-linear chain $FL_{h}$, $h\ge 3$, we have $r(FL_{h})=2h-3$, and then by Theorem 3.1, Lemmas 3.1 and 3.3, we deduce the result.

This completes the proof.$\square$

4 The Extremal Values of Augmented Zagreb Indices in f-Benzenoid Systems

In this section, we determine the extremal values of augmented Zagreb indices in f-benzenoid systems with h hexagons.

By the proof of Theorem 2.1, we have

$$\begin{aligned} r=n-5-2h-b, \quad n=4h+5-n_{i}, \end{aligned}$$

and so by Eq. (2) in Theorem 2.1, we deduce that

$$\begin{aligned} \hbox {AZI}(F)=\left( \left( \frac{3}{2}\right) ^{6}+32\right) h-\left( 16-\left( \frac{3}{2}\right) ^{6}\right) n_{i}+\left( \left( \frac{3}{2}\right) ^{6}-8\right) b+40 \end{aligned}$$

(4)

From Eq. (4), we know that in f-benzenoid systems with h hexagons, the smaller n (the greater $n_{i}$) and b are, the smaller augmented Zagreb index is.

So, in the next section, we try to find f-benzenoid systems with the greater $n_{i}$ and the smaller b.

By analogy with an extremal benzenoid system [9, 32], an f-benzenoid system possessing the maximum number of internal vertices $n_{i}=(n_{i})_\mathrm{max}$ for a given number of hexagons is defined to be an extremal f-benzenoid system. Firstly, we determine the expression for $(n_{i})_\mathrm{max}$.

Our result will rely on a result of Harary and Harborth [32]: Among the benzenoid systems with h hexagons, the spiral hexagon system $T_{h}$ has the maximum number of internal vertices, i.e., for any benzenoid system S with h hexagons,

$$\begin{aligned} n_{i}(S)\le n_{i}(T_{h})=2h+1-\left\lceil \sqrt{12h-3} \ \right\rceil , \end{aligned}$$

(5)

here the ceiling function is employed, $\lceil x\rceil$ is the smallest integer not smaller than x.

The spiral hexagon system$T_{h}$ is a hexagonal system with maximal number of internal vertices which are constructed by the spiral method illustrated in Fig. 10.

Fig. 10

The Harary–Harborth construction of hexagonal systems with maximal number of internal vertices [32]. Hexagons have to be added one-by-one, going along the indicated spiral line

For convenience, we let $\hbox {SH}_{h}(h\ge 3)$ denote the set of all f-benzenoid systems whose two fragments X and Y are both spiral hexagon systems. Especially, an f-benzenoid system $F^{*}\in \hbox {SH}_{h}$ with two fragments $X=T_{h-1}$ and $Y=T_{1}$ is called an f-spiral hexagon system (as shown in Fig. 11). It is obvious that

$$\begin{aligned} n_{i}(F^{*})=2h-\lceil \sqrt{12(h-1)-3} \ \rceil . \end{aligned}$$

Fig. 11

An f-benzenoid system $F'\in \hbox {SH}_{h}$ whose two fragments X and Y are both spiral hexagon systems, and an f-spiral hexagon system $F^{*}\in \hbox {SH}_{h}$ with two fragments $X=T_{h-1}$ and $Y=T_{1}$

Lemma 4.1

[41] For any f-benzenoid system $F'\in \hbox {SH}_{h}$, $h\ge 3$, we have

$$\begin{aligned} n_{i}(F')\le n_{i}(F^{*})=2h-\left\lceil \sqrt{12(h-1)-3} \ \right\rceil . \end{aligned}$$

In [41], we introduce a graph operation and a corresponding result which will be used later.

Operation 1

As shown in Fig. 12, for any f-benzenoid system F with fragments X and Y, let $h_{1}$ and $h_{2}$ denote the number of hexagons in X and Y, respectively. We can get a new f-benzenoid system $F'\in \hbox {SH}_{h}$ from F by replacing X and Y with spiral hexagon systems $T_{h_{1}}$ and $T_{h_{2}}$, respectively.

Fig. 12

$F'$ is obtained from F by applying Operation 1 to it

Lemma 4.2

[41] For any f-benzenoid system F with $h\ge 3$ hexagons, we have

$$\begin{aligned} n_{i}(F)\le 2h-\left\lceil \sqrt{12(h-1)-3} \ \right\rceil . \end{aligned}$$

Theorem 4.1

If $F_{0}$ is an f-benzenoid system with $h (h\ge 3)$ hexagons such that

$$\begin{aligned} \left. \begin{matrix} n_{i}(F_{0})=2h-u&{}\\ b(F_{0})=2&{}\\ \end{matrix}\right\} \end{aligned}$$

(6)

then $F_{0}$ has the smallest augmented Zagreb index in the f-benzenoid systems with h hexagons, and

$$\begin{aligned} \hbox {AZI}(F_{0})=3\left( \frac{3}{2}\right) ^{6}h+\left( 16-\left( \frac{3}{2}\right) ^{6}\right) u+2\left( \left( \frac{3}{2}\right) ^{6}+12\right) , \end{aligned}$$

where $u=\left\lceil \sqrt{12(h-1)-3} \ \right\rceil$.

By the structure of the f-spiral hexagon system $F^{*}$ with h hexagons, we know that $n_{i}(F^{*})=2h-u$. But, $b(F^{*})$ may not always equal to 2. It is obvious that if fragment X of $F^{*}$ satisfies that $b(X)=0$, i.e., X is a convex benzenoid system, we can get an f-benzenoid system $F^{*}$ such that $b(F^{*})=2$ or 3.

But, we know that the fragment X constructed by the “spiral” method is not necessarily convex (and may have a single bay, i.e., $B=1$). So, it is naturally for us to find a method to transform a spiral benzenoid system into a convex benzenoid system with equal number of internal vertices.

Fig. 13

The general form of a convex hexagonal system (CHS). The parameters $a_{i}\ge 1, i=1,2,\ldots , 6,$ count the hexagons on the respective side of CHS

The convex benzenoid systems is a special class of hexagonal systems [8] in which there are no bay regions. The structure of a convex benzenoid system W can be specified as $W=H(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6})$ for positive integers $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}$. Their general form is depicted in Fig. 13. It has been demonstrated [8] that W is completely determined by the parameters $a_{1}, a_{2}, a_{3}, a_{4}$, since it must be

$$\begin{aligned} a_{5}=a_{1}+a_{2}-a_{4}, \quad a_{6}=a_{3}+a_{4}-a_{1}. \end{aligned}$$

Fortunately, the authors in [53] precisely determined necessary and sufficient conditions for the existence of convex benzenoid systems with maximal number of internal vertices.

Lemma 4.3

[53] Let h be a positive integer. The following conditions are equivalent:

• (a) There exists a convex benzenoid system W with h hexagons satisfying

  $$\begin{aligned} n_{i}(W)=2h+1-\left\lceil \sqrt{12h-3} \ \right\rceil ; \end{aligned}$$

• (b) There exist a set of positive integers $a_{1}, a_{2}, a_{3}, a_{4}$ which are solutions of the system of equation

  $$\begin{aligned} \left. \begin{matrix} h=a_{1}a_{3}+a_{1}a_{4}+a_{2}a_{3}+a_{2}a_{4}-a_{2}-a_{3}\\ -\frac{1}{2}a_{1}(a_{1}+1)-\frac{1}{2}a_{4}(a_{4}+1)+1&{}\\ \left\lceil \sqrt{12h-3} \ \right\rceil =a_{1}+2a_{2}+2a_{3}+a_{4}-3&{}\\ \end{matrix}\right\} \end{aligned}$$

  (7)

If the system of equation (7) has a solution for a positive integer h, then there exists a convex benzenoid system W such that $n_{i}(W)=n_{i}(T_{h})$. But, Rada et al. [53] show that not for every positive integer h there is a solution for the system of equation (7). As a byproduct, they show that given a positive integer h, the existence of convex benzenoid systems with maximal number of internal vertices implies the existence of a solution to the following Diophantine equation

$$\begin{aligned} 21x^{2}+3y^{2}+z^{2}=28\left( \left\lceil \sqrt{12h-3} \ \right\rceil ^{2}-(12h-3)\right) . \end{aligned}$$

This gives a method to find values of h for which there are no convex benzenoid systems which satisfy $n_{i}(W)=n_{i}(T_{h})$.

We now return to the study of augmented Zagreb indices of f-benzenoid systems. If the following system

$$\begin{aligned} \left. \begin{matrix} h-1=a_{1}a_{3}+a_{1}a_{4}+a_{2}a_{3}+a_{2}a_{4}-a_{2}-a_{3}\\ \quad -\frac{1}{2}a_{1}(a_{1}+1)-\frac{1}{2}a_{4}(a_{4}+1)+1&{}\\ \left\lceil \sqrt{12(h-1)-3} \ \right\rceil =a_{1}+2a_{2}+2a_{3}+a_{4}-3&{}\\ \end{matrix}\right\} \end{aligned}$$

(8)

has a solution $\{a_{1}, a_{2}, a_{3}, a_{4}\}$ for a positive integer $h-1$, then there exists a convex benzenoid system $W_{h-1}$ such that

$$\begin{aligned} n_{i}(W_{h-1})=2(h-1)+1-\left\lceil \sqrt{12(h-1)-3} \ \right\rceil . \end{aligned}$$

If at least one element $a_{i}$ in the set $\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\}$ is equal to 2, we let $W_{h-1}$ be the X fragment, and it is obvious that $W_{h-1}$ possess only one fissure on the side of $a_{i}$. Let the three vertices of this fissure be u, w, v in Fig. 2, and let Y be a single hexagon, then we get an f-benzenoid system $F^{\star }_{1}$ with h hexagons such that $n_{i}(F^{\star }_{1})=2h-\left\lceil \sqrt{12(h-1)-3} \ \right\rceil$ and $b(F^{\star }_{1})=2$. (as shown in Fig. 14)

From above analysis, we can see that the set of relation in Eq. (6) is equivalent to the system

$$\begin{aligned} \left. \begin{matrix} h-1=a_{1}a_{3}+a_{1}a_{4}+a_{2}a_{3}+a_{2}a_{4}-a_{2}-a_{3}\\ \quad -\frac{1}{2}a_{1}(a_{1}+1)-\frac{1}{2}a_{4}(a_{4}+1)+1 &{}\\ \left\lceil \sqrt{12(h-1)-3} \ \right\rceil =a_{1}+2a_{2}+2a_{3}+a_{4}-3 &{} \\ \exists \ a_{i}\in \{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\}, \ a_{i}=2&{}\\ \end{matrix}\right\} \end{aligned}$$

(9)

Combining Theorem 4.1 and Lemma 4.2, we can get the following Theorem.

Theorem 4.2

Let $h-1$ be a positive integer such that the system of equation (9) has a solution. Then, $F^{\star }_{1}$ (as shown in Fig. 14) has the minimal augmented Zagreb index in the f-benzenoid systems with h hexagons, and

$$\begin{aligned} \hbox {AZI}\left( F^{\star }_{1}\right) =3\left( \frac{3}{2}\right) ^{6}h+\left( 16-\left( \frac{3}{2}\right) ^{6}\right) u+2\left( \left( \frac{3}{2}\right) ^{6}+12\right) , \end{aligned}$$

where $u=\left\lceil \sqrt{12(h-1)-3} \ \right\rceil$.

If for any solution $\{a_{1}, a_{2}, a_{3}, a_{4}\}$ of Eq. (8), there exist no elements in the set $\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\}$ which is equal to 2, without loss of generality, we assume that $a_{i}>2$, i.e., there exist at least two fissures on the side of $a_{i}$, then, we let $W_{h-1}$ be the X fragment and let the three vertices of the first fissure be the vertices u, w, v in Fig. 2, and let Y be a single hexagon, then we get an f-benzenoid system $F_{2}^{\star }$ such that $n_{i}(F^{\star }_{2})=2h-\lceil \sqrt{12(h-1)-3} \ \rceil$ and $b(F_{2}^{\star })=3$. (as shown in Fig. 14)

We have the following result.

Fig. 14

Two f-benzenoid systems $F^{\star }_{1}$ and $F^{\star }_{2}$ whose fragments X are convex hexagon systems $W_{h-1}$

Theorem 4.3

Let $h-1$ be a positive integer such that for any solution $\{a_{1}, a_{2}, a_{3}, a_{4}\}$ of the system of equation (8), no element in $\{a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6}\}$ is equal to 2. Then $F^{\star }_{2}$ (as shown in Fig. 13) has the minimal augmented Zagreb index in the f-benzenoid systems with h hexagons, and

$$\begin{aligned} \mathrm{AZI}\left( F^{\star }_{2}\right) =3\left( \frac{3}{2}\right) ^{6}h+\left( 16-\left( \frac{3}{2}\right) ^{6}\right) u+3\left( \frac{3}{2}\right) ^{6}+16, \end{aligned}$$

where $u=\left\lceil \sqrt{12(h-1)-3} \ \right\rceil$.

Proof

It is easy to see that $b(F^{\star }_{2})=3$. Let F be an f-benzenoid system with h hexagons. From Eq. (4), we have

$$\begin{aligned} \begin{aligned}&\hbox {AZI}(F)-\hbox {AZI}\left( F^{\star }_{2}\right) \\&\quad =-\left( \left( \frac{3}{2}\right) ^{6}-8\right) \left( b\left( F^{\star }_{2}\right) -b(F)\right) +\left( 16-\left( \frac{3}{2}\right) ^{6}\right) \left( n_{i}\left( F^{\star }_{2}\right) -n_{i}(F)\right) \;\; \end{aligned} \end{aligned}$$

(10)

We consider two cases.

Case 1 :

If $b(F)=2$, since $n_{i}(F)<n_{i}(F^{\star }_{2})$, i.e., $n_{i}(F^{\star }_{2})-n_{i}(F)\ge 1$, consequently from Eq. (10) we deduce

$$\begin{aligned} \hbox {AZI}(F)-\hbox {AZI}(F^{\star }_{2})\ge 24-2\left( \frac{3}{2}\right) ^{6}>0. \end{aligned}$$

Case 2 :

If $b(F)\ge 3$, which implies $3-b(F)\le 0$. Since $n_{i}(F^{\star }_{2})-n_{i}(F)\ge 0$ by Eq. (10) it follows that

$$\begin{aligned} \hbox {AZI}(F)-\hbox {AZI}\left( F^{\star }_{2}\right) \ge 0. \end{aligned}$$

This completes the proof.$\square$

Fig. 15

Two kinds of f-spiral hexagon systems $F^{*}_{1}$ and $F^{*}_{2}$

Theorems 4.2 and 4.3 imply that $F^{\star }_{1}$ or $F^{\star }_{2}$ has the minimal augmented Zagreb index when Eq. (8) has a solution for certain $h-1$. So a question arises naturally: if the system of equation (8) has no solution for certain $h-1$, which is the minimal augmented Zagreb index in the set of all f-benzenoid systems with h hexagons?

From Lemma 4.3 we know that, if Eq. (8) has no solution for certain $h-1$, there exists no convex benzenoid system $W_{h-1}$ such that

$$\begin{aligned} n_{i}(W_{h-1})=2(h-1)+1-\left\lceil \sqrt{12(h-1)-3} \ \right\rceil . \end{aligned}$$

In this case, we consider the f-spiral benzenoid system $F^{*}$ such that $b(T_{h-1})=1$. If there exists at least one side in $X=T_{h-1}$ being equal to 2, then we denote this f-spiral benzenoid system $F^{*}$ as $F^{*}_{1}$ what is formed by letting the three vertices of the single fissure at the side of $X=T_{h-1}$ equal to 2 be u, w, v in Fig. 2, and letting Y be a single hexagon (as shown in Fig. 14). If there exists no side in $X=T_{h-1}$ equal to 2, then we denote this f-spiral benzenoid system $F^{*}$ as $F^{*}_{2}$ which is formed by arbitrarily selecting one side which is larger than 2, and letting the three vertices of the first fissure at the chosen side of $X=T_{h-1}$ be u, w, v, and letting Y be a single hexagon (as shown in Fig. 15).

Theorem 4.4

Let $h-1$ be a positive integer such that the system of equation (8) has no solution. If there exists at least one side in $X=T_{h-1}$ equal to 2, then the f-spiral benzenoid system $F^{*}_{1}$ has minimal augmented Zagreb index over the set of all f-benzenoid systems with h hexagons, and

$$\begin{aligned} \hbox {AZI}\left( F^{*}_{1}\right) =3\left( \frac{3}{2}\right) ^{6}h+\left( 16-\left( \frac{3}{2}\right) ^{6}\right) u+3\left( \frac{3}{2}\right) ^{6}+16, \end{aligned}$$

where $u=\left\lceil \sqrt{12(h-1)-3} \ \right\rceil$.

Proof

It is easy to see that on this condition, $b(F^{*}_{1})=3$. Let F be a f-benzenoid system with h hexagons. From Eq. (4), we have

$$\begin{aligned} \begin{aligned}&\hbox {AZI}(F)-\hbox {AZI}\left( F^{*}_{1}\right) \\&\quad =-\left( \left( \frac{3}{2}\right) ^{6}-8\right) \left( b\left( F^{*}_{1}\right) -b(F)\right) +\left( 16-\left( \frac{3}{2}\right) ^{6}\right) \left( n_{i}\left( F^{*}_{1}\right) -n_{i}(F)\right) \end{aligned} \end{aligned}$$

(11)

We consider two cases.

Case 1 :

If $b(F)=2$, since $n_{i}(F)<n_{i}(F^{*}_{1})$, i.e., $n_{i}(F^{*}_{1})-n_{i}(F)\ge 1$, consequently from equation (11) we deduce

$$\begin{aligned} \hbox {AZI}(F)-\hbox {AZI}(F^{\star }_{1})\ge 24-2\left( \frac{3}{2}\right) ^{6}>0. \end{aligned}$$

Case 2 :

If $b(F)\ge 3$, which implies $3-b(F)\le 0$. Since $n_{i}(F^{*}_{1})-n_{i}(F)\ge 0$ by Eq. (11) it follows that

$$\begin{aligned} \hbox {AZI}(F)-\hbox {AZI}(F^{*}_{1})\ge 0. \end{aligned}$$

This completes the proof.$\square$

Theorem 4.5

Let $h-1$ be a positive integer such that the system of equation (8) has no solution. If there exists no side in $X=T_{h-1}$ equal to 2, then the f-spiral benzenoid system $F^{*}_{2}$ has minimal augmented Zagreb index over the set of all f-benzenoid systems with h hexagons and $b\ge 3$, and

$$\begin{aligned} \hbox {AZI}\left( F^{*}_{1}\right) =3\left( \frac{3}{2}\right) ^{6}h+\left( 16-\left( \frac{3}{2}\right) ^{6}\right) u+4\left( \left( \frac{3}{2}\right) ^{6}+2\right) , \end{aligned}$$

where $u=\left\lceil \sqrt{12(h-1)-3} \ \right\rceil$.

Proof

It is easy to see that on this condition, the fragment X in $F^{*}_{2}$ satisfies that $b(X)=1$, then $b(F^{*}_{2})=4$. Let F be a f-benzenoid system with h hexagons. From Eq. (4), we know that

$$\begin{aligned} \begin{aligned}&\hbox {AZI}(F)-\hbox {AZI}\left( F^{*}_{2}\right) =\\&-\left( \left( \frac{3}{2}\right) ^{6}-8\right) \left( b\left( F^{*}_{2}\right) -b(F)\right) +\left( 16-\left( \frac{3}{2}\right) ^{6}\right) \left( n_{i}\left( F^{*}_{2}\right) -n_{i}(F)\right) \end{aligned} \end{aligned}$$

(12)

We consider two cases.

Case 1 :

If $b(F)=3$, since $n_{i}(F)<n_{i}(F^{*}_{2})$, i.e., $n_{i}(F^{*}_{2})-n_{i}(F)\ge 1$, consequently from (12) we deduce

$$\begin{aligned} \hbox {AZI}(F)-\hbox {AZI}(F^{*}_{2})\ge 24-2\left( \frac{3}{2}\right) ^{6}>0. \end{aligned}$$

Case 2 :

If $b(F)\ge 4$, which implies $4-b(F)\le 0$. Since $n_{i}(F_{0})-n_{i}(F)\ge 0$ by (5) then again by (12) it follows that

$$\begin{aligned} \hbox {AZI}(F)-\hbox {AZI}(F^{*}_{2})\ge 0. \end{aligned}$$

This completes the proof.$\square$

We end this section by the following problem.

Problem 1

Let $h-1$ be a positive integer such that the system of equation (8) has no solution. If there exists no side in $X=T_{h-1}$ equal to 2, what is the minimal augmented Zagreb index over the set of all f-benzenoid systems with h hexagons and $b=2$.

5 Conclusions

In this paper, we give the expression for the augmented Zagreb indices of f-benzenoid systems in terms of their inlet features. And we find the minimal and maximal values of the augmented Zagreb indices over the set of cata-catacondensed f-benzenoid systems and characterize their corresponding graphs.

As future work, it would be interesting to consider the values of other topological indices of f-benzenoid systems, such as Wiener index [37] and Wiener polarity index [49], the Zagreb index  [1, 25, 48, 56, 57], ABC index [33, 50], the Harary index [2], graph energy [35, 43, 44], Randić energy [12], incidence energy [4], matching energy [47], energy of matrix [23], HOMO-LUMO index [42], entropy measures [5, 6], molecular identification numbers [13].