1 Introduction

Infectious diseases have had a profound impact on the evolution of human and cultural development. Understanding the transmission mechanism of infectious diseases can lead the public heath workers design better policies to prevent the spread of these diseases. Recently, various epidemic models have been proposed and investigated to get insight into the transmission mechanism of infectious diseases (see, for example, [5, 15] and the references cited therein). These models can contribute to the design and analysis of epidemiological surveys, suggest crucial data should be collected, identify trends, make general forecasts and estimate the uncertainty in forecasts [5].

There are many literatures focused on the effect of prevention and control measures, such as vaccination, antiviral use, quarantine and isolation (see, for example, [2,3,4, 6, 8, 10, 11] and the references cited therein). Obviously, these models provided useful information in comparing, planing, implementing, evaluating, and optimizing various detection, prevention, therapy and control programs. However, most of these studies concentrated on the influence of either vaccination or antiviral or isolation. Recently, there exist several studies including both vaccination and antiviral used, for example, the model studied by Qiu et al. in [11]. The results showed that higher levels of treatment may lead to an increase in epidemic size, so they suggested that antiviral treatment should be implemented appropriately. In this paper, we extent their model by including an insolation class. The new model allows us to investigate the optimal control strategy under the influence of vaccination, treatment and isolation.

Fig. 1
figure 1

Diagram of transitions between epidemiological classes

Full size image

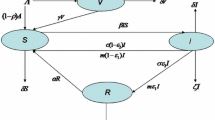
Therefore, based on the transfer diagram as shown in Fig. 1, the epidemic model with vaccination, treatment and isolation can be demonstrated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d}S}{\hbox {d}t}=\Lambda -\lambda (t) S-(\mu +d)S+\varepsilon R+\alpha V,\\ \displaystyle \frac{\hbox {d}V}{\hbox {d}t}=\mu S-(\alpha +d)V,\\ \displaystyle \frac{\hbox {d}I_\mathrm{u}}{\hbox {d}t}=(1-f)\lambda (t)S-(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)I_\mathrm{u},\\ \displaystyle \frac{\hbox {d}I_\mathrm{t}}{\hbox {d}t}=f\lambda (t)S-(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)I_\mathrm{t},\\ \displaystyle \frac{\hbox {d}Q}{\hbox {d}t}=\delta _\mathrm{u} I_\mathrm{u}+\delta _\mathrm{t}I_\mathrm{t}-(\gamma _\mathrm{q}+d)Q,\\ \displaystyle \frac{\hbox {d}R}{\hbox {d}t}=\gamma _\mathrm{u}I_\mathrm{u}+\gamma _\mathrm{t}I_\mathrm{t}+\gamma _\mathrm{q} Q-(\varepsilon +d)R,\\ \end{array} \right. \end{aligned}$$
(1.1)

where \(S(t),V(t),I_\mathrm{u}(t),I_\mathrm{t}(t),Q(t)\) and R(t) denote susceptible, vaccinated, untreated infectious, treatment infectious, isolation and recovered population at time \(t\ge 0\), respectively. The function \(\lambda (t)=\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N}\) represents the rate at which a susceptible individual becomes infected, and the total population number \(N=S+V+I_\mathrm{u}+I_\mathrm{t}+Q+R\); parameters \(\Lambda \) is a constant recruitment rate into the susceptible class; d is natural death rate; \(\mu \) is vaccinated rate; \(\alpha \) is immunity wanes rate; \(\varepsilon \) is the lose immunity rate; \(f\ (0\le f\le 1)\) is the fraction of infected receives treatment; \(\sigma \) is reduced factor of transmission rate by an individual who received treatment; \(\delta _\mathrm{u}\) and \(\delta _\mathrm{t}\) are, respectively, isolation rate of untreated and treated infectious; \(\gamma _\mathrm{u}\), \(\gamma _\mathrm{t}\) and \(\gamma _\mathrm{q}\) are recovery rate of untreated infectious, treated infectious and isolation, respectively.

Our paper focuses on investigating the global dynamics of model (1.1) that incorporates vaccination, treatment and isolation. By constructing suitable Lyapunov function, we derive sufficient conditions ensuring existence and uniqueness of a globally asymptotically stable steady state. To evaluate the optimal control strategies, we also discuss the sensitivity and uncertainty analysis of model parameters. The organization of this paper is as follows. We derive the equilibria and the basic reproduction number in Sect. 2 and perform global stability of equilibria in Sect. 3. Numerical simulations and sensitivity analysis are stated in Sect. 4. The final section has a summary of our observations and conclusions.

2 Equilibria and Basic Reproduction Number

Notice that the total population number N satisfies the equation \(\frac{\hbox {d}N}{\hbox {d}t}=\Lambda -\hbox {d}N,\) which implies that \(N(t)\rightarrow \frac{\Lambda }{d}\) as \(t\rightarrow \infty \). Therefore, the biologically feasible region

$$\begin{aligned} \Gamma =\left\{ (S,V,I_\mathrm{u},I_\mathrm{t},Q,R)\in {\mathbb {R}}_+^6|~0\le S+V+I_\mathrm{u}+I_\mathrm{t}+Q+R\le \frac{\Lambda }{d}\right\} \end{aligned}$$

is a positively invariant with respect to model (1.1).

Following the approach of van den Driessche and Watmough [1], the basic reproduction number can be expressed as

$$\begin{aligned} {\mathcal {R}}_0=(1-f){\mathcal {R}}_\mathrm{u}+f{\mathcal {R}}_\mathrm{t}, \end{aligned}$$
(2.1)

where

$$\begin{aligned} {\mathcal {R}}_\mathrm{u}=\frac{\beta (\alpha +d)}{(\mu +\alpha +d)(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)}\quad \text{ and }\quad {\mathcal {R}}_\mathrm{t}=\frac{\sigma \beta (\alpha +d)}{(\mu +\alpha +d)(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)}. \end{aligned}$$

Biologically, \({\mathcal {R}}_\mathrm{u}\) and \({\mathcal {R}}_\mathrm{t}\) represent the numbers of secondary infectious produced by untreated and treated cases, respectively, during the period of infection in a susceptible population. Fractions \(\frac{1}{\delta _\mathrm{u}+\gamma _\mathrm{u}+d}\) and \(\frac{1}{\delta _\mathrm{t}+\gamma _\mathrm{t}+d}\) represent the mean duration of untreated and treatment infection, respectively, and \(\frac{\alpha +d}{\mu +\alpha +d}\) is the fraction of the population that is susceptible. Note that each infected individual may either receive treatment with probability f or remain untreated with probability \(1-f\). Thus, \({\mathcal {R}}_0\) represents the number of secondary cases during the period of infection in a population where control measures (vaccination, treatment and isolation) are implemented.

The equilibria of model (1.1) satisfies the following equations

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \Lambda -\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N} S-(\mu +d)S+\varepsilon R+\alpha V=0,\\ \displaystyle \mu S-(\alpha +d)V=0,\\ \displaystyle (1-f)\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N}S-(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)I_\mathrm{u}=0,\\ \displaystyle f\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N}S-(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)I_\mathrm{t}=0,\\ \displaystyle \delta _\mathrm{u} I_\mathrm{u}+\delta _\mathrm{t}I_\mathrm{t}-(\gamma _\mathrm{q}+d)Q=0,\\ \displaystyle \gamma _\mathrm{u}I_\mathrm{u}+\gamma _\mathrm{t}I_\mathrm{t}+\gamma _\mathrm{q} Q-(\varepsilon +d)R=0,\\ \displaystyle N=S+V+I_\mathrm{u}+I_\mathrm{t}+Q+R. \end{array} \right. \end{aligned}$$
(2.2)

Following (2.2), one can verify that model (1.1) always admit a disease-free equilibrium \(E_0=(S_0,V_0,0,0,0,0)\) in the absence of infectious disease, where

$$\begin{aligned} S_0=\frac{\alpha +d}{\mu +\alpha +d}N_0,~V_0=\frac{\mu }{\mu +\alpha +d}N_0,~N_0 =\frac{\Lambda }{d}. \end{aligned}$$

If \(I_\mathrm{u}>0\) or \(I_\mathrm{t}>0\), it follows from the third and fourth equations of (2.2) that

$$\begin{aligned} \left| \begin{array}{cc} (1-f)\beta \frac{d}{\Lambda }S-(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)&{}(1-f )\sigma \beta \frac{d}{\Lambda }S\\ f\beta \frac{d}{\Lambda }S &{} f\sigma \beta \frac{d}{\Lambda }S-(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)\\ \end{array}\right| =0. \end{aligned}$$
(2.3)

Direct calculation implies that

$$\begin{aligned} S=\frac{(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)}{(1-f)\beta \frac{d}{\Lambda } (\delta _\mathrm{t} +\gamma _\mathrm{t}+d)+f\sigma \beta \frac{d}{\Lambda }(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)}\triangleq S^*. \end{aligned}$$

Then, substitute \(S^*\) back into (2.2), and the expressions for \(V,I_\mathrm{u},I_\mathrm{t},Q\) and R will be derived, that is, apart from the disease-free equilibrium \(E_0\), the model also has a unique positive endemic equilibrium. For ease of notations, denote

$$\begin{aligned} a=\frac{f(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)}{(1-f)(\delta _\mathrm{t} +\gamma _\mathrm{t}+d)},\ b=\frac{\delta _\mathrm{u}+a\delta _\mathrm{t}}{\gamma _\mathrm{q}+d}. \end{aligned}$$

Thus, we have the following result for model (1.1).

Theorem 1

There always exists disease-free equilibrium \(E_0=(S_0,V_0,0,0,0,0)\), where

$$\begin{aligned} S_0=\frac{\alpha +d}{\mu +\alpha +d}N_0,~V_0=\frac{\mu }{\mu +\alpha +d}N_0,~N_0 =\frac{\Lambda }{d}, \end{aligned}$$

whereas if \({\mathcal {R}}_0>1\), there exists a unique endemic equilibrium \(E^*=(S^*,V^*,I_\mathrm{u}^*,I_\mathrm{t}^*,Q^*,R^*)\), where

$$\begin{aligned} \begin{array}{l} S^*= \displaystyle \frac{(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)N_0}{(1-f)\beta (\delta _\mathrm{t} +\gamma _\mathrm{t}+d)+f\sigma \beta (\delta _\mathrm{u}+\gamma _\mathrm{u}+d)},\\ \displaystyle V^*=\frac{\mu }{\alpha +d}S^*,\quad I_\mathrm{u}^*= \displaystyle \frac{(\varepsilon +d)({\mathcal {R}}_0-1)N_0}{\frac{\alpha +d}{\mu +\alpha +d}(\beta +a\sigma \beta ) +\varepsilon (1+a+b){\mathcal {R}}_0},\\ \displaystyle I_\mathrm{t}^*=aI_\mathrm{u}^*,\quad \ Q^*=bI_\mathrm{u}^*,\quad R^*=N_0-S^*-V^*-I_\mathrm{u}^*-I_\mathrm{t}^*-Q^*.\\ \end{array} \end{aligned}$$

3 Dynamical Behaviors

Since the total population number N(t) satisfies \(N(t)\rightarrow \Lambda /d\triangleq N_0\) as \(t\rightarrow \infty \), based on the results of Mischaikow et al. in [9] and Tieme in [13], the dynamical behaviors of model (1.1) can be transferred to consider the following limit system

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d}S}{\hbox {d}t}=\Lambda -\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N_0} S-(\mu +d)S+\varepsilon R +\alpha V,\\ \displaystyle \frac{\hbox {d}V}{\hbox {d}t}=\mu S-(\alpha +d)V,\\ \displaystyle \frac{\hbox {d}I_\mathrm{u}}{\hbox {d}t}=(1-f)\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N_0}S-(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)I_\mathrm{u},\\ \displaystyle \frac{\hbox {d}I_\mathrm{t}}{\hbox {d}t}=f\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N_0}S-(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)I_\mathrm{t},\\ \displaystyle \frac{\hbox {d}Q}{\hbox {d}t}=\delta _\mathrm{u} I_\mathrm{u}+\delta _\mathrm{t}I_\mathrm{t}-(\gamma _\mathrm{q}+d)Q,\\ \displaystyle \frac{\hbox {d}R}{\hbox {d}t}=\gamma _\mathrm{u}I_\mathrm{u}+\gamma _\mathrm{t}I_\mathrm{t}+\gamma _\mathrm{q} Q-(\varepsilon +d)R.\\ \end{array} \right. \end{aligned}$$
(3.1)

In what following, we first consider the global dynamics of disease-free equilibrium \(E_0\) for model (3.1).

Theorem 2

If \({\mathcal {R}}_0<1\) and \(\alpha \ge \varepsilon \), the disease-free equilibrium \(E_0\) is globally asymptotically stable.

Proof

From Theorem 2 in van den Driessche and Watmough [1], \(E_0\) is locally asymptotically stable if \({\mathcal {R}}_0<1\), but unstable if \({\mathcal {R}}_0>1\). It is left to show that all solutions converge to the disease-free equilibrium when \({\mathcal {R}}_0<1\).

Notice that the variable V in the S equation of (3.1) can be replaced by \(N_0-S-I_\mathrm{u}-I_\mathrm{t}-Q-R\), and we can rewrite \(\frac{\hbox {d}S}{\hbox {d}t}\) as follows

$$\begin{aligned} \frac{\hbox {d}S}{\hbox {d}t}=\Lambda -\beta \frac{I_\mathrm{u}+\sigma I_\mathrm{t}}{N_0} S-(\mu +d)S+\varepsilon R +\alpha (N_0-S-I_\mathrm{u}-I_\mathrm{t}-Q-R). \end{aligned}$$
(3.2)

It then follows from Eq. (3.2) and \(\alpha \ge \varepsilon \) that

$$\begin{aligned} S'\le (\alpha +d)N_0-(\mu +\alpha +d)S. \end{aligned}$$
(3.3)

Define an auxiliary system

$$\begin{aligned} u'= (\alpha +d)N_0-(\mu +\alpha +d)u. \end{aligned}$$
(3.4)

It is easily to show that (3.4) has a globally asymptotically stable equilibrium \(u^*=S_0\), that is, \(\lim \nolimits _{t\rightarrow \infty }u(t)=S_0\). By standard comparison theorem, for sufficiently small \(\epsilon >0\), there exists a \(t_0>0\) such that \(S(t)<S_0+\epsilon \) for all \(t\ge t_0\). If \({\mathcal {R}}_0<1\), Eq. (2.1) implies \({\mathcal {R}}_\mathrm{u}<1\) and \({\mathcal {R}}_\mathrm{t}<1\). Therefore, we can choose arbitrary constant \(\epsilon \) such that

$$\begin{aligned} \beta \frac{S_0+\epsilon }{N_0}<\delta _\mathrm{u}+\gamma _\mathrm{u}+d,\ \ \ \beta \sigma \frac{S_0+\epsilon }{N_0}<\delta _\mathrm{t}+\gamma _\mathrm{t}+d. \end{aligned}$$
(3.5)

Considering the Lyapunov function \(W=I_\mathrm{u}+I_\mathrm{t}\) and differentiating W along the model (3.1) yield

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\hbox {d}W}{\hbox {d}t}=&{}\displaystyle \beta \frac{I_\mathrm{u}}{N_0}S-(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)I_\mathrm{u}+\beta \frac{\sigma I_\mathrm{t}}{N_0}S-(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)I_\mathrm{t}\\ \displaystyle \le &{}\left( \beta \frac{S_0+\epsilon }{N_0}-(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)\right) I_\mathrm{u}+ \left( \beta \sigma \frac{S_0+\epsilon }{N_0}-(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)\right) I_\mathrm{t}.\\ \end{array} \end{aligned}$$
(3.6)

It follows from (3.6) that \({\mathcal {R}}_0<1\) implies \(\hbox {d}W/\hbox {d}t\le 0\) with \(\hbox {d}W/\hbox {d}t=0\) if and only if \(I_\mathrm{u}=I_\mathrm{t}=0\). Then, the only invariant set where \(\hbox {d}W/\hbox {d}t=0\) is the singleton \(E_0\). Therefore, by LaSalle’s invariance principle Theorem [7], \(E_0\) is globally asymptotically stable in \(\Gamma \). This completes this proof. \(\square \)

In order to obtain the global stability of endemic equilibrium \(E^*\), we first give the following analytic result regarding the persistence of model (3.1).

Theorem 3

If \({\mathcal {R}}_0>1\), then the model (3.1) is uniformly persistent, i.e., there exists a constant \(\eta >0\) which is independent of the initial value in \(\Gamma \), such that

$$\begin{aligned} \begin{array}{l} \liminf \limits _{t\rightarrow \infty }S(t)>\eta ,\quad \liminf \limits _{t\rightarrow \infty }V(t)>\eta ,\quad \liminf \limits _{t\rightarrow \infty }I_\mathrm{u}(t)>\eta ,\\ \liminf \limits _{t\rightarrow \infty }I_\mathrm{t}(t)>\eta ,\quad \liminf \limits _{t\rightarrow \infty }Q(t)>\eta ,\quad \liminf \limits _{t\rightarrow \infty }R(t)>\eta . \end{array} \end{aligned}$$

We omit the proof of Theorem 3, as it can be easily verified by applying the Theorem 4.6 in [14] and using a similar argument as in the proof of Theorem 2.3 in [15]. This theorem illustrates that the basic reproduction number \({\mathcal {R}}_0\) is a threshold parameter of the disease dynamics.

Theorem 4

If \({\mathcal {R}}_0>1\), then the endemic equilibrium \(E^*\) is globally asymptotically stable under the conditions \(\varepsilon =0\) and \(a\sigma =1\).

Proof

For model (3.1), let us consider the following Lyapunov function

$$\begin{aligned} W(t)=2S_1^*g\left( \frac{S}{S^*}\right) +2V^*g\left( \frac{V}{V^*}\right) +\frac{ I_\mathrm{u}^*}{(1-f)}g\left( \frac{I_\mathrm{u}}{I_\mathrm{u}^*}\right) +\frac{I_\mathrm{t}^*}{f}g\left( \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) . \end{aligned}$$
(3.7)

Here, \(g(x)=x-1-\ln x\) for \(x\in (0,+\infty )\) and \(g(x)\ge 0\) with \(g(x)=0\) if and only if \(x=1\).

For ease of presentation, let

$$\begin{aligned} \begin{array}{ll} \displaystyle W_1=S^*g\left( \frac{S}{S^*}\right) ,\ W_2=V^*g\left( \frac{V}{V^*}\right) ,\ W_3=I_\mathrm{u}^*g\left( \frac{I_\mathrm{u}}{I_\mathrm{u}^*}\right) \ \text{ and }\ \displaystyle W_4=I_\mathrm{t}^*g\left( \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) .\end{array} \end{aligned}$$

For clarity, we first derivative \(W_i,\,i=1,2,3,4\) along the solution of (3.1) and then combined together to derive \(\frac{\hbox {d}W}{\hbox {d}t}\).

Since the endemic equilibrium \(E^*\) satisfies Eqs. (2.2), differentiating \(W_1\) along model (3.1) drives

$$\begin{aligned} \displaystyle \frac{\hbox {d}W_1}{\hbox {d}t}= & {} \displaystyle \left( 1-\frac{S^*}{S}\right) \left( -\beta \frac{d}{\Lambda }(SI_\mathrm{u}-S^*I_\mathrm{u}^*+\sigma SI_\mathrm{t}-\sigma S^*I_\mathrm{t}^*)\right) \nonumber \\&\displaystyle +\,\left( 1-\frac{S^*}{S}\right) \left( -(\mu +d)(S-S^*)+\alpha (V-V^*)\right) \nonumber \\= & {} \displaystyle -\,\beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( \frac{SI_\mathrm{u}}{S^*I_\mathrm{u}^*}-\frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\frac{S^*}{S}-1\right) -\,\beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( \frac{SI_\mathrm{t}}{S^*I_\mathrm{t}^*}-\frac{I_\mathrm{t}}{I_\mathrm{t}^*}+\frac{S^*}{S}-1\right) \nonumber \\&\displaystyle -\,(\mu +d)S^*\left( \frac{S^*}{S}+\frac{S}{S^*}-2\right) +\alpha V^*\left( \frac{V}{V^*}-\frac{S^*V}{SV^*}+\frac{S^*}{S}-1\right) \nonumber \\= & {} \displaystyle -\,\beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( \frac{SI_\mathrm{u}}{S^*I_\mathrm{u}^*}-\frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\ln \frac{S^*}{S}\right) -\beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( \frac{SI_\mathrm{t}}{S^*I_\mathrm{t}^*}-\frac{I_\mathrm{t}}{I_\mathrm{t}^*}+\ln \frac{S^*}{S}\right) \nonumber \\&\displaystyle -\,\Lambda g\left( \frac{S^*}{S}\right) -(\mu +d)S^*g\left( \frac{S}{S^*}\right) +\alpha V^*g\left( \frac{V}{V^*}\right) -\alpha V^*g\left( \frac{S^*V}{SV^*}\right) . \end{aligned}$$
(3.8)

Similar computations for \(W_2, W_3\) and \(W_4\) yield that

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\hbox {d}W_2}{\hbox {d}t} =&{}\displaystyle \left( 1-\frac{V^*}{V}\right) \left( \mu S-(\alpha +d)V\right) \\ =&{}\displaystyle \mu S^*g\left( \frac{S}{S^*}\right) -\mu S^*g\left( \frac{SV^*}{S^*V}\right) -(\alpha +d) V^*g\left( \frac{V}{V^*}\right) , \end{array} \end{aligned}$$
(3.9)
$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\hbox {d}W_3}{\hbox {d}t} =&{}\displaystyle \left( 1-\frac{I_\mathrm{u}^*}{I_\mathrm{u}}\right) \left( (1-f)\beta \frac{d}{\Lambda }(SI_\mathrm{u}-S^*I_\mathrm{u}^*+\sigma SI_\mathrm{t}\right. \\ &{}\displaystyle \left. -\,\sigma S^*I_\mathrm{t}^*)-(\delta _\mathrm{u}+\gamma _\mathrm{u}+d)(I_\mathrm{u}-I_\mathrm{u}^*)\right) \\ =&{}\displaystyle (1-f)\beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( \frac{SI_\mathrm{u}}{S^*I_\mathrm{u}^*}-\frac{S}{S^*}-\frac{I_\mathrm{u}}{I_\mathrm{u}^*}+1\right) \\ &{}\displaystyle +\,(1-f)\beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( \frac{SI_\mathrm{t}}{S^*I_\mathrm{t}^*}-\frac{SI_\mathrm{u}^*I_\mathrm{t}}{S^*I_\mathrm{u}I_\mathrm{t}^*}-\frac{I_\mathrm{u}}{I_\mathrm{u}^*}+1\right) \end{array} \end{aligned}$$
(3.10)

and

$$\begin{aligned} \begin{array}{rl} \displaystyle \frac{\hbox {d}W_4}{\hbox {d}t} =&{}\displaystyle \left( 1-\frac{I_\mathrm{t}^*}{I_\mathrm{t}}\right) \left( f\beta \frac{d}{\Lambda }(SI_\mathrm{u}-S^*I_\mathrm{u}^*+\sigma SI_\mathrm{t}-\sigma S^*I_\mathrm{t}^*)\right. \\ &{}\displaystyle \left. -\,(\delta _\mathrm{t}+\gamma _\mathrm{t}+d)(I_\mathrm{t}-I_\mathrm{t}^*)\right) \\ =&{}\displaystyle f\beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( \frac{SI_\mathrm{u}}{S^*I_\mathrm{u}^*}-\frac{SI_\mathrm{u}I_\mathrm{t}^*}{S^*I_\mathrm{u}^*I_\mathrm{t}}-\frac{I_\mathrm{t}}{I_\mathrm{t}^*}+1\right) \\ &{}\displaystyle +\,f\beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( \frac{SI_\mathrm{t}}{S^*I_\mathrm{t}^*}-\frac{S}{S^*}-\frac{I_\mathrm{t}}{I_\mathrm{t}^*}+1\right) . \end{array} \end{aligned}$$
(3.11)

Combing Eqs. (3.8)–(3.11) together and then rearranging the terms, we have

$$\begin{aligned} \displaystyle \frac{\hbox {d}W}{\hbox {d}t}= & {} \displaystyle -\,2\Lambda g\left( \frac{S^*}{S}\right) -2dS^*g\left( \frac{S}{S^*}\right) -2dV^*g\left( \frac{V}{V^*}\right) -2\mu S^*g\left( \frac{SV^*}{S^*V}\right) \nonumber \\&\displaystyle -\,2\alpha V^*g\left( \frac{S^*V}{SV^*}\right) + \beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( 2-\frac{S}{S^*}-\frac{SI_\mathrm{u}I_\mathrm{t}^*}{S^*I_\mathrm{u}^*I_\mathrm{t}} +\frac{I_\mathrm{u}}{I_\mathrm{u}^*}-\frac{I_\mathrm{t}}{I_\mathrm{t}^*}-2\ln \frac{S}{S^*}\right) \nonumber \\&\displaystyle +\, \beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( 2-\frac{S}{S^*}-\frac{SI_\mathrm{u}^*I_\mathrm{t}}{S^*I_\mathrm{u}I_\mathrm{t}^*} -\frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\frac{I_\mathrm{t}}{I_\mathrm{t}^*}-2\ln \frac{S}{S^*}\right) \nonumber \\\le & {} \displaystyle \beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( -g\left( \frac{S}{S^*}\right) -g\left( \frac{SI_\mathrm{u}I_\mathrm{t}^*}{S^*I_\mathrm{u}^*I_\mathrm{t}}\right) +\frac{I_\mathrm{u}}{I_\mathrm{u}^*}-\frac{I_\mathrm{t}}{I_\mathrm{t}^*}-\ln \frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\ln \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) \nonumber \\&\displaystyle +\, \beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( -g\left( \frac{S}{S^*}\right) -g\left( \frac{SI_\mathrm{u}^*I_\mathrm{t}}{S^*I_\mathrm{u}I_\mathrm{t}^*}\right) -\frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\frac{I_\mathrm{t}}{I_\mathrm{t}^*}+\ln \frac{I_\mathrm{u}}{I_\mathrm{u}^*}-\ln \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) \nonumber \\\le & {} \displaystyle \beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( \frac{I_\mathrm{u}}{I_\mathrm{u}^*}-\frac{I_\mathrm{t}}{I_\mathrm{t}^*}-\ln \frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\ln \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) + \beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( \frac{I_\mathrm{t}}{I_\mathrm{t}^*}-\frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\ln \frac{I_\mathrm{u}}{I_\mathrm{u}^*}-\ln \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) .\nonumber \\ \end{aligned}$$
(3.12)

It follows from the expressions of \(I_\mathrm{u}^*\) and \(I_\mathrm{t}^*\) and the condition \(a\sigma =1\) that

$$\begin{aligned} \beta \frac{d}{\Lambda }S^*I_\mathrm{u}^*\left( \frac{I_\mathrm{u}}{I_\mathrm{u}^*}{-}\frac{I_\mathrm{t}}{I_\mathrm{t}^*}-\ln \frac{I_\mathrm{u}}{I_\mathrm{u}^*}+\ln \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) {+} \beta \frac{d}{\Lambda }S^*\sigma I_\mathrm{t}^*\left( \frac{I_\mathrm{t}}{I_\mathrm{t}^*}-\frac{I_\mathrm{u}}{I_\mathrm{u}^*}{+}\ln \frac{I_\mathrm{u}}{I_\mathrm{u}^*}-\ln \frac{I_\mathrm{t}}{I_\mathrm{t}^*}\right) {=}0. \end{aligned}$$

Therefore, \(\hbox {d}W/\hbox {d}t\le 0\) for all \((S,V,I_\mathrm{u},I_\mathrm{t},Q,R)\in \mathrm{int}\Gamma \) (\(\mathrm{int} \Gamma \) be the interior of \(\Gamma \)) and \(\hbox {d}W/\hbox {d}t=0\) if and only if \(S=S^*,V=V^*,I_\mathrm{u}=I_\mathrm{u}^*,I_\mathrm{t}=I_\mathrm{t}^*\). Substituting these relations into the last two equations of (3.1) yields that the only invariant set of this case is the singleton \(\{E^*\}\). Based on the LaSalle’s invariance principle [7], then \(E^*\) is globally asymptotically stable in \(\mathrm{int}\Gamma \). This completes this proof. \(\square \)

4 Numerical Simulations and Sensitivity Analysis

To complement the mathematical analysis carried out in the previous section, we now investigate some of the numerical properties of model (3.1). We take the parameter values in the simulation as: \(\beta =0.5, \sigma =0.3, d=1/70, f=0.72, \gamma _\mathrm{u}=0.05, \gamma _\mathrm{t}=0.07, \gamma _\mathrm{q}=0.1, \delta _\mathrm{u}=0.05, \delta _\mathrm{t}=0.09\) and \(\Lambda /d=10000\). We change the vaccination coverage \(\mu \) and other three parameter values to study the dynamical behaviors for model (1.1).

Fig. 2
figure 2

Time plots of the model (1.1) with different initial values under the conditions \(\alpha \ge \varepsilon \) and \(a\sigma =1\). Here, \(\alpha =0.01,\varepsilon =0\), \(\sigma =0.59\), \(\beta =0.5, d=1/70, f=0.72, \gamma _\mathrm{u}=0.05, \gamma _\mathrm{t}=0.07, \gamma _\mathrm{q}=0.1, \delta _\mathrm{u}=0.05, \delta _\mathrm{t}=0.09\) and \(\Lambda /d=10000\). a\(u=0.04\), b\(u=0.01\)

Full size image

If we choose \(\alpha =0.01,\ \varepsilon =0\) and \(\sigma =0.59\), one can easily verify that these parameter values satisfy the conditions given in Theorems 2 and 4. The time plots of this case are shown in Fig. 2. As proved in Theorem 2, Fig. 2a illustrates that all the trajectories of model (1.1) converge to the disease-free equilibrium \(E_0=(3778, 6222, 0, 0, 0, 0)\) if \({\mathcal {R}}_0=0.923<1\). While if \({\mathcal {R}}_0=1.731>1\), Fig. 2b shows that all the trajectories converge to the unique endemic equilibrium \(E^*=(4092, 1685, 148, 249, 261, 3565)\), which testifies the validity of Theorem 4.

Notice that the main theoretical results in this paper are derived by suitable Lyapunov functions. As we all know, Lyapunov function (also called the Lyapunov’s second method for stability) is an important method to study the stability of dynamical systems. For most epidemic models, this method can only provide sufficient conditions for the stability due to the complexity of models. Generally, we can conjecture that the equilibria may be global asymptotically stability and numerical simulations are usually used to verify the rationality of this conjecture. For model (1.1), if numerical simulations show that the equilibria is global asymptotically stability for any parameter values, then this conjecture may be true. Without loss of generality, we choose \(\alpha =0.01,\varepsilon =0.02\) and \(\sigma =0.36\) which do not meet the conditions listed in Theorems 2 and 4. The corresponding time plots are shown in Fig. 3. We can observe from this figure that all the trajectories trend to the disease-free equilibrium \(E_0=(3778, 6222, 0, 0, 0, 0)\) if \({\mathcal {R}}_0=0.744<1\) and trend to the unique endemic equilibrium \(E^*=(5080, 2092, 195, 329, 344, 1960)\) if \({\mathcal {R}}_0=1.394>1\). Hence, the disease-free equilibrium of model (1.1) may be global asymptotically stability if \({\mathcal {R}}_0<1\) and the endemic equilibrium may be global asymptotically stability if \({\mathcal {R}}_0>1\).

Fig. 3
figure 3

Time plots of the model (1.1) with different initial values if the conditions \(\alpha \ge \varepsilon \) and \(a\sigma =1\) are not satisfied. Here, \(\alpha =0.01,\varepsilon =0.02\), \(\sigma =0.36\) and other parameter values are same as shown in Fig.2. a\(u=0.04\), b\(u=0.01\)

Full size image

Because the basic reproduction number \({\mathcal {R}}_0\) is the threshold quantity that determines when an infection invades and persists in a population, in what following, we focus on the sensitivity analysis and uncertainty analysis [12] of the basic reproduction number \({\mathcal {R}}_0\). The sensitivity analysis helps identify the important parameters in controlling the disease spreading while uncertainty analysis helps evaluate the robustness of the system under the parameter uncertainty of different levels.

For uncertainty analysis, we use the Latin hypercube sampling method in this paper. If a parameter is given a range and a center, we assume that this parameter satisfies triangular distribution, while if only a range is given to a parameter, we assume that this parameter follows the uniform distribution in that range. In this paper, we assume that parameters \(\beta \in (0,5)\) with center 0.5, \(\sigma \in (0,1)\) with center 0.003 and \(d\in (60,100)\) year with center 70 year, \(\mu \in (0,0.3)\) and other parameters all assumed in the range (0, 0.5). With each parameter’s distribution, 1000 values are chosen randomly using Latin hypercube sampling method. Histogram of the distribution of \({\mathcal {R}}_0\) is shown in Fig. 4b, which is generated from (2.1) using Latin hypercube sampling with 1000 samples. We observe from this histogram that 85.5% of the distribution of \({\mathcal {R}}_0\) is greater than 1. We also obtain that the mean and the standard deviation of the basic reproduction number \({\mathcal {R}}_0\) are 3.75 and 4.12, respectively.

To identify the relationship between the parameters and the basic reproduction number, we used the partial rank correlation (PRCCs) method in this paper to find statistical influence of \({\mathcal {R}}_0\). Partial rank correlation is computed to identify and measure the statistical influence of parameters \(\beta ,\sigma ,\alpha ,\mu ,f,\gamma _\mathrm{u},\gamma _\mathrm{t},\delta _\mathrm{u},\delta _\mathrm{t},d\) and \({\mathcal {R}}_0\). As shown in Fig.4a, when random sampling is considered, the transmission rate \(\beta \) is highly positively correlated with \({\mathcal {R}}_0\) and the corresponding value is +0.700003 and the fraction of infected receives treatment f is highly negatively correlated with \({\mathcal {R}}_0\) and the corresponding value is \(-0.589121\). Moderate positive correlation has been observed between \(\alpha \) and \({\mathcal {R}}_0\) and the corresponding value is \(+0.478532\) and moderate negative correlation has been observed among \(\mu ,\gamma _\mathrm{u},\delta _\mathrm{u}\) and \({\mathcal {R}}_0\) and the corresponding values are \(-0.370877,-0.499092,-0.502705\), respectively. Weak correlation exists among \(\gamma _\mathrm{t},\delta _\mathrm{t}\) and \({\mathcal {R}}_0\), and the corresponding values are, respectively, \(-0.236385 and -0.272603\). Hence, the transmission rate \(\beta \) and the treatment probability f are the most influential parameters in determining the value of basic reproduction number \({\mathcal {R}}_0\).

Fig. 4
figure 4

Sensitivity analysis and uncertainty analysis of the basic reproduction number \({\mathcal {R}}_0\). Figure a shows the sensitivity indices of \({\mathcal {R}}_0\) and b shows histogram obtained from Latin hypercube sampling using a sample size of 1000 for \({\mathcal {R}}_0\)

Full size image

5 Conclusions

In this paper, we study the global stability of an epidemic model with vaccination, treatment and isolation. By constructing suitable Lyapunov function, we obtain that if \({\mathcal {R}}_0<1\) and \(\alpha \ge \varepsilon \), then the disease-free equilibrium \(E_0\) is globally asymptotically stable. If \({\mathcal {R}}_0>1\), there exists a unique endemic equilibrium \(E^*\) which is globally asymptotically stable in the interior of the feasible region \(\Gamma \) under conditions \(\varepsilon =0\) and \(a\sigma =1\). Numerical simulations shown in Figs.2(c-d) extend these results to disease-free equilibrium \(E_0\) is globally asymptotically stable as \({\mathcal {R}}_0<1\) and \(E^*\) is globally asymptotically stable as \({\mathcal {R}}_0>1\).

Through partial rank correlation (PRCCs) and the Latin hypercube sampling method, the sensitivity and uncertainty analysis of \({\mathcal {R}}_0\) based on variation parameters \(\beta ,\sigma ,\alpha ,\mu ,f,\gamma _\mathrm{u},\gamma _\mathrm{t},\delta _\mathrm{u},\delta _\mathrm{t}\) and d have been obtained. The result presented in Fig.4 shows that transmission rate \(\beta \) and treatment probability f are crucial to stop the spread of diseases. It also shows the basic reproduction number \({\mathcal {R}}_0\) is more sensitive to the isolation rate (\(\delta _\mathrm{u}\)) and the recovery rate (\(\gamma _\mathrm{u}\)) of untreated infectious individuals than the isolation rate (\(\delta _\mathrm{t}\)) and the recovery rate (\(\gamma _\mathrm{t}\)) of treated infectious individuals; meanwhile, \({\mathcal {R}}_0\) is also sensitive to vaccination rate \(\mu \). These results imply that the vaccination, treatment and isolation are all play an important role in preventing the spread of an infectious disease.