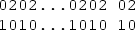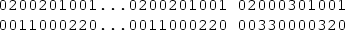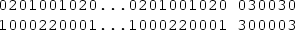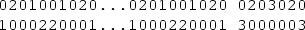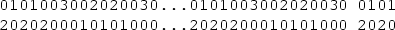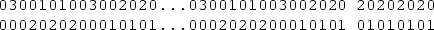Independent Rainbow Domination of Graphs

Abstract

Given a positive integer t and a graph F, the goal is to assign a subset of the color set $\{1,2,\ldots ,t\}$ to every vertex of F such that every vertex with the empty set assigned has all t colors in its neighborhood. Such an assignment is called the t-rainbow dominating function ($t\mathrm{RDF}$) of the graph F. A $t\mathrm{RDF}$ is independent ($It\mathrm{RDF}$) if vertices assigned with non-empty sets are pairwise non-adjacent. The weight of a $t\mathrm{RDF}$g of a graph F is the value $w(g) =\sum _{v \in V(F)}|g(v)|$. The independent t-rainbow domination number $i_{rt}(F)$ is the minimum weight over all $It\mathrm{RDF}$s of F. In this article, it is proved that the independent t-rainbow domination problem is NP-complete even if the input graph is restricted to a bipartite graph or a planar graph, and the results of the study provide some bounds for the independent t-rainbow domination number of any graph for a positive integer t. Moreover, the exact values and bounds of the independent t-rainbow domination numbers of some Petersen graphs and torus graphs are given.

1 Introduction

As a combinatorial optimization issue, ordinary domination consists of determining the minimum number of places in which to keep a resource such that every place either is adjacent to the place in which a resource exists or has a resource. In practical applications, some additional constraints or desires must be taken into account. For example [12], if we are given a large computer network which consists of some clients and servers with t distinct resources $s_1, s_2, \ldots , s_t$, we need to seek the minimum number of servers each one possessing a non-empty subset of these resources in order that any client can be connected directly to a subset of servers that together have each resource $s_i$ ($1 \le i \le t$). On the assumption that all resources have an identical cost, the goal is to seek the minimum value of the number of copies of such t resources. This application naturally can be modeled by the concept of t-rainbow domination. In addition, if a constraint prevents any pair of servers from occupying adjacent locations, then we have the independent t-rainbow domination problem.

For a graph F, $S \subseteq V(F)$ and $w \in V(F)$, let $N_S(w)$ denote the open neighborhood of w in S, i.e., $\{u| uw \in E(F), u \in S\}$, and let $N_S[w]$ denote the closed neighborhood of w, i.e., $N_S[w]=\{w\} \cup N_S(w)$. If $S=V(F)$ and no confusion can occur, $N_S(w)$ and $N_S[w]$ will be denoted shortly by N(w) and N[w], respectively. If $S^\prime \subseteq V(F)$, then the definition $N(S^\prime )= \cup _{x \in S^\prime }N(x)$ is applied. The degree of a vertex w is the total number of edges incident to w, and in this paper, $\Delta (F)$ denotes the maximum degree of a vertex in the graph F.

Inspired by several facility location problems, Brešar, Henning and Rall [1,2,3] initiated the study of the k-rainbow domination problem, and such a problem is proved to be NP-complete even if the input graph is a chordal graph or a bipartite graph (see Chang [4]). This problem has attracted considerable attention (see [19, 21, 25]), and many other types of domination are widely applied to real-world scenarios, see, for example, [5, 7, 9, 10, 13, 14, 22, 24, 26].

An independent set S of a graph F is a subset of V(F) for which vertices are pairwise non-adjacent. The independence number of F, denoted as $\alpha (F)$, is the maximum size of an independent set in F. Given a positive integer t and a graph F, the goal is to assign a subset of the color set $\{1,2,\ldots ,t\}$ to every vertex of F such that every vertex with the empty set assigned has all t colors in its neighborhood. Such an assignment is called the t-rainbow dominating function ($t\mathrm{RDF}$) of the graph F. A $t\mathrm{RDF}$ is independent ($It\mathrm{RDF}$) if vertices assigned non-empty sets are pairwise non-adjacent. The weight of a $t\mathrm{RDF}$g of a graph F is the value $w(g) =\sum _{v \in V(F)}|g(v)|$. If H is a vertex-induced subgraph of V(F), the weight restricted to H is $w_H(g) =\sum _{v \in H}|g(v)|$. The independent t-rainbow domination number$i_{rt}(F)$ is the minimum weight of an $It\mathrm{RDF}$s in F. The upper t-rainbow domination number of F, denoted by $I_{rt}(F)$, is the maximum weight of a minimal t-rainbow dominating function. (In other words, there is a dominating function f of weight $I_{rt}(F)$ on F such that no proper restriction of f is dominating.) We use i(F) to denote the independent domination number, i.e., the size of a smallest independent dominating set, of a graph F.

The rest of the paper is organized as follows: In Sect. 2, the independent k-rainbow domination problem is proved to be NP-complete. Section 3 provides some general bounds for the independent t-rainbow domination number. In Sect. 4, the independent 2-rainbow domination problem is studied on generalized Petersen graphs and tori. Closed expressions for infinite families are provided on the basis of constructions for which we conjecture that they are optimal. In Sect. 5, the independent 3-rainbow domination of trees is considered and a tight upper bound for $i_{r3}(T)$ of a tree T is given. Conclusions are summarized in the last section.

2 Complexity of Independent Rainbow Domination

It is well known that determining whether F has an independent dominating set with at most k vertices (where k is a positive integer) is NP-complete for a graph F even when F is a bipartite graph or a planar graph, or belong to some other classes of graphs; see [8]. In this section, we will prove that it is NP-complete to determine whether F has an independent t-rainbow dominating function of weight at most k for a positive integer k and a given graph F even if F is bipartite or planar.

Formally, the problem can be stated as

PROBLEM: INDEPENDENT t-RAINBOW DOMINATION

INSTANCE: Graph $G=\left( V,E\right)$. A natural number B.

QUESTION: Decide whether the independent t-rainbow domination number $i_{rt}(G)$ is at most B.

Theorem 1

Given a positive integer t, the independent t-rainbow domination problem is NP-complete for general graphs.

Proof

Theorem 1 can be proved via reducing to the independent t-rainbow domination problem from the independent domination problem. With a graph F on n vertices, the graph $F^\prime$ with the vertex set $V(F^\prime ) = V(F) \cup \{v_2, v_3, \ldots , v_t: v \in V(F)\} \cup \{v_x, v_y: v \in V(F)\}$ and edge set $E(F^\prime ) = E(F) \cup \{vv_i, v_iv_x: v \in V(F), 2 \le i \le t\} \cup \{v_xv_y: v \in V(F)\}$ is considered (see Fig. 1). We claim that F has an independent dominating set $I_D$ with $|I_D| \le s$ if and only if $F^\prime$ has an ItRDF f of weight $w(f) \le s+nt$.

Assume F contains an independent dominating set $I_D$ of cardinality at most s. Consider the following function f from $V(F^\prime )$ to ${\mathcal {P}}(\{1,2, \ldots , t\})$ by setting

$$\begin{aligned} f(u)= \left\{ \begin{array}{cl} \{1\},&{}\quad \text {if } u \in I_D \text { or } \\ &{}\quad u = v_y \text { for some }v \in V(F){\setminus } I_D, \\ \emptyset ,&{}\quad \text {if } u \in V(G) {\setminus } I_D \\ &{}\quad u = v_i \text { for some }v \in I_D \text { and } 2 \le i \le t \text { or } \\ &{}\quad u = v_y \text { for some }v \in I_D \text { or } \\ &{}\quad u = v_x \text { for some }v \in V(F){\setminus } I_D,\\ \{i\},&{} \quad \text {if } u = v_i \text { for some }v \in V(F){\setminus } I_D \text { and } 2 \le i \le t, \\ \{1,2,\ldots ,t\},&{}\quad \text {if } u = v_x \text { for some }v \in I_D. \\ \end{array} \right. \end{aligned}$$

If $f(u)=\emptyset$, the following four cases are considered:

Case 1$u \in V(F) {\setminus } I_D$.

Fig. 1

The graphs F and $F^\prime$ from the proof of Theorem 1, an example

From the definition of f, we obtain $f(u_i)=i$ for $2 \le i \le t$. Moreover, u has a neighbor $v \in I_D$. Hence, $f(v)=\{1\}$, and therefore, $f(N_{F^\prime }(u))=\{1,2,\ldots ,t\}$.

Case 2$u = v_i \text { for some }v \in I_D \text { and } 2 \le i \le t$.

From the definition of f, we obtain $f(v_x)=\{1,2,\ldots ,t\}$. Since $v_x$ is a neighbor of $v_i$, we have $f(N_{F^\prime }(u))=\{1,2,\ldots ,t\}$.

Case 3$u=v_y \text { for some }v \in I_D$ .

From the definition of f, we obtain $f(v_x)=\{1,2,\ldots ,t\}$. Since $v_x$ is a neighbor of $v_y$, we have $f(N_{F^\prime }(u))=\{1,2,\ldots ,t\}$.

Case 4$u=v_x \text { for some }v \in V(F){\setminus } I_D$.

From the definition of f, we obtain $f(v_i)=\{i\}$ for any $2 \le i \le t$ and $f(v_y)=\{1\}$. Since $v_i (2 \le i \le t)$ and $v_y$ are the neighborhood of $v_x$, we have $f(N_{F^\prime }(u))=\{1,2,\ldots ,t\}$.

Since any two vertices $u_1, u_2 \in V(F^\prime )$ (with $f(u_i)\ne \emptyset$ for $i=1,2$) are not adjacent in $F^\prime$, it follows that f is an ItRDF of $F^\prime$. Also the weight of f is $|I_D|+nt \le s+nt$.

Suppose $F^\prime$ has an ItRDF f of weight at most $s+nt$. Since $v_xv_y \in E(F^\prime )$ for some $v \in V(F)$, together with the definition of independent rainbow dominating function, we have $f(v_x)=\emptyset$ or $f(v_y)=\emptyset$. Therefore, $|f(v_y)| + |f(v_x)| + \sum _{i=2}^t |f(v_i)| \ge t$. Let $I_D = \{v \in V(F){:}\,f(v) \ne \emptyset \}$. Then we obtain $\sum _{v \in V(F^\prime )}=|I_D|+ \sum _{v \in V(F)}(|f(v_y)| + |f(v_x)| + \sum _{i=2}^t |f(v_i)|) \le s+nt$. Therefore, $|I_D| \le s$, as needed. $\square$

Noting that $F^\prime$ is bipartite or planar if F is a bipartite or planar graph, together with the fact that the independent domination problem is NP-complete for bipartite or planar graphs, we have

Corollary 1

The independent t-rainbow domination problem is NP-complete for bipartite graphs or planar graphs for any positive integer t.

3 Bounds for the Independent t-Rainbow Domination Number

Theorem 2

For any graph F with maximum degree $\varDelta$, we have $\lceil \frac{|V(F)|t}{\varDelta +t} \rceil \le \gamma _{rt}(F) \le i_{rt}(F) \le t \alpha (F) \le I_{rt}(F).$

Proof

The result $\lceil \frac{|V(F)|t}{\varDelta +t} \rceil \le \gamma _{rt}(F)$ is proved in [19]. Since any $It\mathrm{RDF}$ of a graph F is a $t\mathrm{RDF}$ of F, we have $\gamma _{rt}(F) \le i_{rt}(F)$. Let I be a maximal independent set of F with $|I|=\alpha (F)$. Let f be a function from V(F) to ${\mathcal {P}}(\{1,2, \ldots , t\})$ defined by $f(v)= \emptyset$ if $v \notin I$ and $f(v)= \{1,2,\ldots ,t\}$ if $v \in I$. Then f is an $It\mathrm{RDF}$ of F with weight $w(f)=t|I|=t\alpha (F)$. Therefore, $i_{rt}(F) \le t \alpha (F)$. By the definition of the upper t-rainbow domination number, we have $t\alpha (F)= w(f) \le I_{rt}(F)$. $\square$

Similarly to [19, Theorem 1 and Corollary 1], we have the following two results. The proof of Theorem 3 is left to the reader.

Theorem 3

For positive integers $t' \ge t$ and a connected graph F, we have

• i) $i_{rt^\prime }(F) \le i_{rt}(F) + (t'-t) \left\lfloor \frac{i_{rt}(F)}{t} \right\rfloor$;

• ii) $i_{rt^\prime }(F) \le {t^\prime } \frac{i_{rt}(F)}{t}$.

Theorem 4

Let F be a non-trivial graph. Then $\max \{i(F),t\}\le i_{rt}(F)\le ti(F)$, and these bounds are sharp.

Proof

On the assumption that f is an ItRDF of F, and $D=\{u\in V(F): f(u)\ne \emptyset \}$. Then D is an independent dominating set of F. So $i(F)\le |D|\le i_{rt}(F)$. Note that F is a non-trivial graph, so F has at least one vertex v for which $f(v)=\emptyset$. Hence, $t\le i_{rt}(F)$ and the inequality $\max \{i(F),t\}\le i_{rt}(F)$ holds. Moreover, for any independent domination set $D'$ of F, we can obtain an ItRDF $f'$ of F with $f'(u)=\{1,2,\ldots ,t\}$ if $u \in D'$ and $f'(u)=\emptyset$ otherwise. Hence, the inequality $i_{rt}(F)\le ti(F)$ holds.

Furthermore, it can be seen that $\max \{i(F),t\}= i_{rt}(F)$ for any complete bipartite graph F and $i_{rt}(F)= ti(F)$ for any star. Therefore, these bounds are sharp. $\square$

4 The Independent 2-Rainbow Domination Numbers of Some Classes of Graphs

Let $n>0, b \ge 0$, $0 \le k <n$ be integers, we denote by ${\mathbb {Z}}_n^{k,b}= \{x| x \in {\mathbb {Z}}, x \ge b, x \equiv k \text { (mod }n) \}$

4.1 Generalized Petersen Graphs

For positive integers $n\ge 3$ and $k \in \{1,2,\ldots ,n-1\}$, the generalized Petersen graph P(n, k) is defined to be a graph with the vertex set $\{h^1_i, h^2_i ~|~ i \in \{0,1,\ldots ,n-1\}\}$ and the edge set $\{h^1_ih^2_i, h^1_ih^1_{i+k}, h^2_ih^2_{i+1} ~|~ i \in \{0,1,\ldots ,n-1\}\}$, in which the subscripts are computed modulo n (see [6, 23]).

An ItRDF f is given by a pattern of two lines, where the values of the upper line are values of $\{f(h^2_0), f(h^2_1), \ldots , f(h^2_{n-1})\}$, and the values of the bottom line are values of $\{f(h^1_0), f(h^1_1), \ldots , f(h^1_{n-1})\}$, i.e., $h^2_i$ lies exactly above $h^1_i$ for each i. Moreover, the sets $\emptyset$, $\{1\}$, $\{2\}$ and $\{1,2\}$ are encoded with 0, 1, 2 and 3, respectively.

Let f be an I2RDF of P(n, k), we define the weight sequence$S_f=s_1s_2\ldots s_n$ of P(n, k) under f the following way: $s_i = |f(h^1_i)|+ |f(h^2_i)|$ for each i. For example, let $f\left( \left[ \begin{array}{ccccc} h^2_0&{}h^2_1&{}h^2_2&{}h^2_3&{}h^2_4 \\ h^1_0&{}h^1_1&{}h^1_2&{}h^1_3&{}h^1_4 \end{array}\right] \right) =\left[ \begin{array}{ccccc} 0&{}0&{}3&{}0&{}1 \\ 3&{}0&{}0&{}1&{}0 \end{array}\right]$ be an I2RDF of P(5, 1), then $S_f=20211$.

Theorem 5

Let $n \ge 4$.

$$\begin{aligned} i_{r2}(P(n, 1)) = \left\{ \begin{array}{ll} n, &{} \; \text { if } n \equiv 0 \; (\bmod 2)\\ &{} \\ n+1,&{} \; \text { if } n \equiv 1 \; (\bmod 2)\\ \end{array} \right. \end{aligned}$$

Proof

First the upper bounds are proved by giving constructions of I2RDF of P(n, 1) with the weight n if $n \equiv 0 \; (\bmod 2)$ and $n+1$ if $n \equiv 1 \;(\bmod 2)$ as follows.

• 1. $n \in {\mathbb {Z}}_4^{0,4}$:

  

• 2. $n \in {\mathbb {Z}}_4^{1,9}$:

  

• 3. $n \in {\mathbb {Z}}_4^{2,6}$:

  

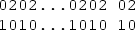
• 4. $n \in {\mathbb {Z}}_4^{3,7}$:

  

The pattern $\left[ \begin{array}{ccccc} 0&{}0&{}3&{}0&{}1 \\ 3&{}0&{}0&{}1&{}0 \end{array}\right]$ yields an I2RDF of P(5, 1) of the weight 6. Thus, $i_{r2}(P(5, 1)) \le 6$ and so all the upper bounds are established. Note that P(n, 1) is the ladder graph, which is the Cartesian product $P_2\Box P_n$.

Now, we will show the lower bounds. Let f be an I2RDF of P(n, 1) with minimum weight. For $i = 0, 1, 2, 3, 4$, let $L_i$ denote a set of columns of weight i and let $|L_i| = n_i$. Since f is independent, we have $n_3=n_4=0$. We have

$$\begin{aligned} w(f ) = n_1 + 2n_2 , \text { and } n = n_0 + n_1 + n_2 . \end{aligned}$$

$\square$

Claim 1

If $f(h^1_i)=f(h^2_i)=\emptyset$, then $|f(h^1_{i-1})|+|f(h^2_{i-1})|=2$ and $|f(h^1_{i+1})|+|f(h^2_{i+1})| = 2$.

From Claim 1, we have $n_2 \ge n_0$. Hence,

$$\begin{aligned} w(f )-n = n_2-n_0 \ge 0. \end{aligned}$$

Therefore, the theorem holds for $n \equiv 0 \;(\bmod 2)$.

We now consider $n \equiv 1 \;(\bmod \,2)$. Let S be a segment of a weight sequence of P(n, 1). We define three types of subsequences (segments) in the following way:

Type 1::

$S=a_1,a_2,\ldots , a_{2\ell +1}$ with $a_i=2$ for odd i, and $a_i=0$ for even i.

Type 2::

$S=a_1,a_2,\ldots , a_{\ell }$ with $a_i=1$ for each i.

Type 3::

$S=a_1,a_2,\cdots , a_{\ell }$ with $a_i=2$ for each i.

From Claim 1, it can be seen that the weight sequence $S_f$ of P(n, 1) under f can be decomposed into disjoint segments of Type 1, Type 2 and Type 3. Let $p_i$ be the number of maximal segments of Type i for $i \in \{1,2,3\}$. Then

$$\begin{aligned} w(f )-n = n_2-n_0 = p_1+p_3. \end{aligned}$$

Since n is odd and f is independent, then there exists an i such that $a_i=0$. So we have $p_1 > 0$ and $w(f )>n$, and so the proof is completed.

Theorem 6

Let $n \ge 7$.

$$\begin{aligned} i_{r2}(P(n, 2)) \le \left\{ \begin{array}{ll} \left\lceil \frac{4n}{5} \right\rceil , &{} \quad n \equiv 0 \bmod 10\\ &{} \\ \left\lceil \frac{4n}{5} \right\rceil +1,&{}\quad n \equiv 9 \bmod 10\\ &{} \\ \left\lceil \frac{4n}{5} \right\rceil +2,&{}\quad n \equiv 2,3,4,5,7,8 \bmod 10\\ &{} \\ \left\lceil \frac{4n}{5} \right\rceil +3,&{}\quad n \equiv 1, 6 \bmod 10\\ \end{array} \right. \end{aligned}$$

Proof

First the upper bounds are proved by giving constructions of I2RDF of P(n, 2) of the desired weight as follows.

• 1. $n \in {\mathbb {Z}}_{10}^{0,10}$:

  

• 2. $n \in {\mathbb {Z}}_{10}^{1,21}$:

  

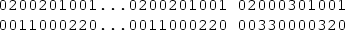
• 3. $n \in {\mathbb {Z}}_{10}^{2,22}$:

  

• 4. $n \in {\mathbb {Z}}_{10}^{3,23}$:

  

• 5. $n \in {\mathbb {Z}}_{10}^{4,14}$:

  

• 6. $n \in {\mathbb {Z}}_{10}^{5,15}$:

  

• 7. $n \in {\mathbb {Z}}_{10}^{6,16}$:

  

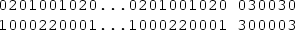
• 8. $n \in {\mathbb {Z}}_{10}^{7,17}$:

  

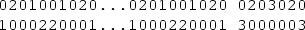
• 9. $n \in {\mathbb {Z}}_{10}^{8,18}$:

  

• 10. $n \in {\mathbb {Z}}_{10}^{9,19}$:

  

Let $P_7=\left[ \begin{array}{ccccccc} 0&{}3&{} 0&{} 1&{} 0&{} 0&{} 2\\ 0&{} 0&{} 0&{} 0&{}3&{}3&{} 0 \end{array}\right]$, $P_8=\left[ \begin{array}{cccccccc} 3&{} 0&{}3&{} 0&{} 0&{} 0&{} 2&{} 0 \\ 0&{} 2&{} 0&{} 0&{}3&{} 1&{} 0&{} 0 \end{array}\right]$, $P_{13}=\left[ \begin{array}{ccccccccccccc} 0&{} 0&{} 1&{} 0&{} 2&{} 0&{} 0&{} 2&{} 0&{}3&{} 0&{} 0&{}3 \\ 3&{} 2&{} 0&{} 0&{} 0&{} 1&{} 1&{} 0&{} 0&{} 0&{} 2&{} 0&{} 0 \end{array}\right]$,

$P_9=\left[ \begin{array}{ccccccccc} 1&{}0 &{} 3&{}0 &{}3&{}0&{}1&{}0&{}0 \\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}2&{}2 \end{array}\right]$, $P_{11}=\left[ \begin{array}{ccccccccccc} 0&{} 0&{}3&{} 0&{} 0&{} 1&{} 0&{} 2&{} 0&{} 0&{}3\\ 0&{} 0&{} 0&{}3&{} 2&{} 0&{} 0&{} 0&{} 1&{}3&{} 0 \end{array}\right]$, $P_{12}=\left[ \begin{array}{cccccccccccc} 3&{} 0&{} 1&{} 0&{} 0&{} 1&{} 0&{} 2&{} 0&{} 0&{} 2&{} 0\\ 0&{} 0&{} 0&{}3&{} 2&{} 0&{} 0&{} 0&{} 1&{}3&{} 0&{} 0 \end{array}\right]$. Then the pattern $P_n$ yields an I2RDF of P(n, 2) with the desired weight for each $n \in \{7,8,9,11,12,13\}$, and so all the upper bounds are established. $\square$

Theorem 7

Let $n \ge 7$.

$$\begin{aligned} i_{r2}(P(n, 3)) \le \left\{ \begin{array}{ll} \left\lceil \frac{7n}{8} \right\rceil , &{} \quad n \equiv 0,2,4,14 \bmod 16\\ &{} \\ \left\lceil \frac{7n}{8} \right\rceil +1,&{} \quad n \equiv 5,7,8,10,12,13,15 \bmod 16\\ &{} \\ \left\lceil \frac{7n}{8} \right\rceil +2,&{} \quad n \equiv 1,3,6,9,11 \bmod 16\\ \end{array} \right. \end{aligned}$$

Proof

First the upper bounds are proved by giving constructions of I2RDF of P(n, 3) of the desired weight.

• 1. $n \in {\mathbb {Z}}_{16}^{0,16}$:

  

• 2. $n \in {\mathbb {Z}}_{16}^{1,33}$:

  

• 3. $n \in {\mathbb {Z}}_{16}^{2,18}$:

  

• 4. $n \in {\mathbb {Z}}_{16}^{3,35}$:

  

• 5. $n \in {\mathbb {Z}}_{16}^{4,20}$:

  

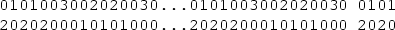
• 6. $n \in {\mathbb {Z}}_{16}^{5,37}$:

  

• 7. $n \in {\mathbb {Z}}_{16}^{6,22}$:

  

• 8. $n \in {\mathbb {Z}}_{16}^{7,39}$:

  

• 9. $n \in {\mathbb {Z}}_{16}^{8,24}$:

  

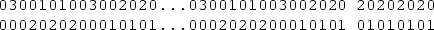
• 10. $n \in {\mathbb {Z}}_{16}^{9,25}$:

  

• 11. $n \in {\mathbb {Z}}_{16}^{10,26}$:

  

• 12. $n \in {\mathbb {Z}}_{16}^{11,27}$:

  

• 13. $n \in {\mathbb {Z}}_{16}^{12,28}$:

  

• 14. $n \in {\mathbb {Z}}_{16}^{13,29}$:

  

• 15. $n \in {\mathbb {Z}}_{16}^{14,30}$:

  

• 16. $n \in {\mathbb {Z}}_{16}^{15,31}$:

  

Let $P_7=\left[ \begin{array}{ccccccc} 3&{}0&{}0&{}3&{}0&{}0&{}0 \\ 0&{}0&{}0&{}0&{}2&{}3&{}2 \end{array}\right]$, $P_8=\left[ \begin{array}{cccccccc} 0&{}0&{}1&{}0&{}1&{}0&{}0&{}3\\ 0&{}2&{}0&{}3&{}0&{}2&{}0&{}0 \end{array}\right]$, $P_9=\left[ \begin{array}{ccccccccc} 0&{}0&{}3&{}0&{}0&{}3&{}0&{}0&{}3\\ 0&{}0&{}0&{}0&{}0&{}0&{}3&{}3&{}0 \end{array}\right]$,

$P_{11}=\left[ \begin{array}{ccccccccccc} 3&{}0&{}0&{}0&{}3&{}0&{}0&{}0&{}3&{}0&{}0\\ 0&{}1&{}3&{}0&{}0&{}0&{}3&{}2&{}0&{}0&{}0 \end{array}\right]$, $P_{12}=\left[ \begin{array}{cccccccccccc} 0&{}0&{}1&{}0&{}2&{}0&{}3&{}0&{}1&{}0&{}0&{}3\\ 0&{}2&{}0&{}1&{}0&{}2&{}0&{}1&{}0&{}2&{}0&{}0 \end{array}\right]$,

$P_{13}=\left[ \begin{array}{ccccccccccccc} 0&{}2&{}0&{}1&{}0&{}0&{}1&{}0&{}2&{}0&{}1&{}0&{}1\\ 2&{}0&{}0&{}0&{}3&{}3&{}0&{}0&{}0&{}2&{}0&{}2&{}0 \end{array}\right]$, $P_{14}=\left[ \begin{array}{cccccccccccccc} 2&{}0&{}1&{}0&{}2&{}0&{}2&{}0&{}0&{}3&{}0&{}0&{}1&{}0\\ 0&{}2&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}0&{}2&{}0&{}2 \end{array}\right]$,

$P_{15}=\left[ \begin{array}{ccccccccccccccc} 0&{}3&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}2&{}0&{}2&{}0&{}2&{}0\\ 0&{}0&{}0&{}0&{}2&{}3&{}2&{}0&{}0&{}0&{}1&{}0&{}3&{}0&{}1 \end{array}\right]$, $P_{17}=\left[ \begin{array}{ccccccccccccccccc} 0&{}3&{}0&{}0&{}2&{}0&{}2&{}0&{}1&{}0&{}2&{}0&{}1&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}1&{}0&{}3&{}0&{}1&{}0&{}2&{}0&{}0&{}0&{}2&{}3&{}2&{}0 \end{array}\right]$,

$P_{19}=\left[ \begin{array}{ccccccccccccccccccc} 0&{}2&{}0&{}2&{}0&{}0&{}3&{}0&{}1&{}0&{}0&{}0&{}1&{}0&{}2&{}0&{}2&{}0&{}2\\ 1&{}0&{}3&{}0&{}1&{}0&{}0&{}0&{}0&{}2&{}3&{}2&{}0&{}0&{}0&{}1&{}0&{}1&{}0 \end{array}\right]$,

$P_{21}=\left[ \begin{array}{ccccccccccccccccccccc} 0&{}1&{}0&{}1&{}0&{}0&{}3&{}0&{}0&{}2&{}0&{}2&{}0&{}1&{}0&{}2&{}0&{}0&{}1&{}0&{}2\\ 2&{}0&{}2&{}0&{}2&{}0&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}0&{}3&{}3&{}0&{}0&{}0 \end{array}\right]$,

$P_{23}=\left[ \begin{array}{ccccccccccccccccccccccc} 0&{}2&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}3&{}0&{}0&{}2&{}0&{}2&{}0&{}1&{}0&{}2&{}0&{}0&{}1\\ 0&{}0&{}2&{}0&{}2&{}0&{}2&{}0&{}2&{}0&{}0&{}0&{}1&{}0&{}1&{}0&{}1&{}0&{}0&{}0&{}3&{}3&{}0 \end{array}\right]$. Then the pattern $P_n$ yields an I2RDF of P(n, 3) with the desired weight for each $n \in \{7$, 8, 9, 11, 12, 13, 14, 15, 17, 19, $21, 23\}$, and this completes the proof. $\square$

Remark

We believe that the bounds given in Theorems 6 and 7 are the exact values. A method for the proofs may follow the path algebra approach [11, 15,16,17, 27]. As the corresponding matrices are rather large already for P(n, 2) and P(n, 3), we do not go in more detail here and leave it for future work.

In [20], it was shown that

Theorem 8

Let $m > 3$ and $k, \ell$ relatively prime to m with $\ell k \equiv 1$ mod m. Then P(m, k) is isomorphic to $P(m, \ell )$.

By Theorem 8, we have $P(2k+1, k+1) \cong P(2k+1, 2)$ and $P(3k+2, k+1) \cong P(3k+2, 3)$ for any $k \ge 2$. Therefore, we have

Corollary 2

Let $k \ge 2$.

$$\begin{aligned} i_{r2}(P(2k+1, {k+1})) \le \left\{ \begin{array}{ll} \left\lceil \frac{8k+4}{5} \right\rceil +1, &{} \quad k \equiv 4 \bmod 5\\ &{} \\ \left\lceil \frac{8k+4}{5} \right\rceil +2,&{} \quad k \equiv 1,2,3 \bmod 5\\ &{} \\ \left\lceil \frac{8k+4}{5} \right\rceil +3,&{} \quad k \equiv 0 \bmod 5\\ \end{array} \right. \end{aligned}$$

Corollary 3

Let $k \ge 2$.

$$\begin{aligned} i_{r2}(P(3k+2, k+1)) \le \left\{ \begin{array}{ll} \left\lceil \frac{21k+14}{8} \right\rceil , &{} \quad 3k \equiv 0,2,12,14 \bmod 16\\ &{} \\ \left\lceil \frac{21k+14}{8} \right\rceil +1,&{} \quad 3k \equiv 1,3,4,6,8,9,11 \bmod 16\\ &{} \\ \left\lceil \frac{21k+14}{8} \right\rceil +2,&{} \quad 3k \equiv 5,7,10,13,15 \bmod 16\\ \end{array} \right. \end{aligned}$$

4.2 Torus

The Cartesian product of graphs $F_1$ and $F_2$ is defined to be the graph $F_1 \Box F_2$ with vertex set $F_1 \times F_2=\{xy| x\in V(F_1) \text { and } y \in V(F_2)\}$ such that $(x_1,y_1)(x_2,y_2) \in E(F_1 \Box F_2)$ if $x_1x_2 \in E(F_1)$ and $y_1=y_2$, or $y_1y_2 \in E(F_2)$ and $x_1=x_2$ (see [15]). The torus is the graph $T_{m,n} = C_m \Box C_n$, which can be viewed as a kind of grid graph with n columns and m rows.

Theorem 9

Let $n \ge 3$.

$$\begin{aligned} i_{r2}(T_{3,n})) = \left\{ \begin{array}{ll} n, &{} \quad n \equiv \;(0 \bmod 6)\\ &{} \\ n+1,&{} \quad n \equiv \;(3 \bmod 6)\\ &{} \\ n+2,&{} \quad n \equiv 1,2,4,5 \;(\bmod 6)\\ \end{array} \right. \end{aligned}$$

Proof

First the upper bounds are proved by giving constructions of I2RDF of $T_{3,n}$ of the desired weight.

• 1. $n \in {\mathbb {Z}}_{6}^{0,6}$:

  

• 2. $n \in {\mathbb {Z}}_{6}^{1,13}$:

  

• 3. $n \in {\mathbb {Z}}_{6}^{2,14}$:

  

• 4. $n \in {\mathbb {Z}}_{6}^{3,15}$:

  

• 5. $n \in {\mathbb {Z}}_{6}^{4,10}$:

  

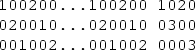
• 6. $n \in {\mathbb {Z}}_{6}^{5,11}$:

  

Let $P_3=\left[ \begin{array}{ccc} 0&{}0&{}3\\ 0&{}1&{}0\\ 2&{}0&{}0 \end{array}\right]$, $P_4=\left[ \begin{array}{cccc} 0&{}0&{}0&{}3\\ 0&{}3&{}0&{}0\\ 1&{}0&{}1&{}0 \end{array}\right]$, $P_5=\left[ \begin{array}{ccccc} 2&{}0&{}3&{}0&{}0\\ 0&{}3&{}0&{}2&{}0\\ 0&{}0&{}0&{}0&{}1 \end{array}\right]$, $P_7=\left[ \begin{array}{ccccccc} 0&{}1&{}0&{}0&{}2&{}0&{}1\\ 3&{}0&{}0&{}1&{}0&{}0&{}0\\ 0&{}0&{}2&{}0&{}0&{}3&{}0 \end{array}\right]$,

$P_8=\left[ \begin{array}{cccccccc} 0&{}0&{}2&{}0&{}0&{}0&{}0&{}1\\ 0&{}1&{}0&{}0&{}3&{}0&{}2&{}0\\ 2&{}0&{}0&{}1&{}0&{}3&{}0&{}0 \end{array}\right]$, $P_9=\left[ \begin{array}{ccccccccc} 0&{}2&{}0&{}0&{}3&{}0&{}0&{}1&{}0\\ 1&{}0&{}0&{}2&{}0&{}0&{}2&{}0&{}0\\ 0&{}0&{}1&{}0&{}0&{}1&{}0&{}0&{}2 \end{array}\right]$. Then the pattern $P_n$ yields an I2RDF of $T_{3,n}$ with the desired weight for each $n \in \{3$,4,5,7, $8, 9\}$, and all the upper bounds are established. The lower bounds can be determined by the dynamic algorithm used in [18], and the implementation is left to the reader. $\square$

Theorem 10

If m and n are positive integers, then $i_{r2}(T_{3m, 6n})=6mn$.

Proof

By Theorem 2, we have $i_{r2}(T_{3m, 6n}) \ge 6mn$. Let

$$\begin{aligned} P=\left[ \begin{array}{cccccc} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 2&{}\quad 0\\ 2&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 2&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}\right] , Q=[\overbrace{P,\dots ,P}^{n \text{ times }}], \text { and } R=\left[ \begin{array}{c} Q\\ \vdots \\ Q \end{array}\right] , \end{aligned}$$

where Q is repeated m times in R. Then R yields an I2RDF of $T_{3m,6n}$ with weight 6mn, which completes the proof. $\square$

5 The Independent 3-Rainbow Domination Numbers of Trees

The following result for paths and stars is easily proved:

Proposition 1

If $n \ge 3$, then

• 1) $i_{r3}(P_n)= \left\{ \begin{array}{ll} \lfloor \frac{3n}{4} \rfloor +1 ,&{}\quad \text { n=2 (mod 4)}\\ &{} \\ \lfloor \frac{3n}{4} \rfloor +2,&{}\quad \text { n=0,1,3 (mod 4)}\\ \end{array} \right.$

• 2) $i_{r3}(S_n)= 3$.

We first define the spider graph as follows. A spider $S = S(a_1, \ldots , a_r )$ is a tree formed by joining $r \ge 1$ vertex-disjoint paths of orders $a_1, \ldots , a_r$ as pendent paths to a single vertex b, which is called the anchor of S, e.g., Fig. 2 is the spider S(2, 2, 2). We denote by $H(k)=S(2,2,\ldots ,2)$ with a total of k 2s.

Fig. 2

The spider S(2, 2, 2)

Lemma 1

Let integers $t,k\ge 1$ and T belong to one of the following trees with n vertices:

• (i) a vertex u connected to every anchor of t spiders H(k).

• (ii) a vertex u connected to another vertex and each anchor of t spiders H(k).

• (iii) a vertex u connected to a pendent $P_2=v_1v_2$ and each anchor of t spiders H(k).

  Then T has an I3RDF g with $w_T(g) \le n$ such that $g(u)=\emptyset$ .

Proof

i) Assume T is a tree which is a vertex z connected to each anchor $y_i$ ($1 \le i \le s$) of s spiders H(k). Define a function $g: V(T) \rightarrow {\mathcal {P}}(\{3,2,1\})$ as follows. If $k \ge 2$, let $g(z)= \emptyset$, $g(y_1)=\{1,2\}$. The vertices of $P_2$ attached to $y_1$ is assigned with $\emptyset$ and $\{3\}$, respectively. For $i \ge 2$, $g(y_i)=\{2,3\}$. The vertices of $P_2$ attached to $y_i$ are assigned with $\emptyset$ and $\{1\}$, respectively. Then it is easy to see that $w_T(g) \le n$. If $k = 1$, let $g(z)= \emptyset$, $g(y_1)=\{3,2,1\}$. The vertices of $P_2$ attached to $y_1$ are assigned with $\emptyset$ and $\{3\}$, respectively. Then $w_T(g) \le n$.

ii) Consider a function $g: V(T) \rightarrow {\mathcal {P}}(\{3,2,1\})$ by letting the same color to the vertices as case i except v and let $g(v)=1$. Then we obtain $w_T(g) \le n$.

iii) Consider a function $g: V(T) \rightarrow {\mathcal {P}}(\{3,2,1\})$ by letting the same color to the vertices as case i except $v_1, v_2$. Assume $v_2$ be the leaf, and let $g(v_1)=\{3,2,1\}$ and $g(v_2)=\emptyset$. Then we obtain $w_T(g) \le n$. $\square$

Fig. 3

A tree in case i

Fig. 4

A tree in case ii

Fig. 5

A tree in case iii

Remark Figures 3, 4 and 5 show examples of I3RDFs of graphs of such three cases, where we use 0 to denote the empty set $\emptyset$.

Theorem 11

If T is an n-vertex tree with at least three vertices, then $i_{r3}(T) \le n$.

Proof

Assume that there exists an n-vertex tree T with minimum n such that $i_{r3}(T) > n$, i.e., $i_{r3}(T^R) \le n^\prime$ for each $n^\prime$-vertex tree $T^R$ if $n^\prime <n$. Then we have $\square$

Claim 2

T has no vertex which is adjacent to at least two leaves.

Proof of Claim 1

Assume that $u \in V(T)$ and $u_1$ and $u_2$ are two leaves adjacent to u. Let $T^R = T - u_1$ and $f^\prime$ be an optimal I3RDF of $T^R$. Then we have $w(f^\prime ) = i_{r3}(T^R) \le n-1$. If $f^\prime (u)=\emptyset$, then $f^\prime (N_{T^R}(u))=\{1,2,3\}$. Extend $f^\prime$ to g by putting $g(u_1)=\{1\}$ and $g(x)=f^\prime (x)$ for $x \in V(T){\setminus } \{u_1\}$. Then g is an I3RDF of T with $w(g) \le n$, a contradiction. If $f^\prime (u)\ne \emptyset$, then $f^\prime (u_2)=\emptyset$ and so $f^\prime (u)=\{1,2,3\}$. Extend $f^\prime$ to g by putting $g(u_1)=\emptyset$ and $g(x)=f^\prime (x)$ for $x \in V(T){\setminus } \{u_1\}$. Then g is an I3RDF of T with $w(g) \le n-1$, a contradiction.$\square$

Claim 3

T has no vertex u which is adjacent to both a leaf and a pendent $P_2$.

Proof of Claim 2

Suppose to the contrary that $u \in V(T)$ and there exist vertices $u_1, u_2, u_3 \in V(T)$ such that $\{uu_1, uu_2, u_2u_3\} \in E(T)$, $u_1, u_3$ are leaves and $d_T(u_2)=2$. Let $T^R = T - u_1$ and $f^\prime$ be an optimal I3RDF of $T^R$. Then we have $w(f^\prime ) = i_{r3}(T^R) \le n-1$. If $f^\prime (u)=\emptyset$, then $f^\prime (N_{T^R}(u))=\{1,2,3\}$. Extend $f^\prime$ to g by putting $g(u_1)=\{1\}$ and $g(x)=f^\prime (x)$ for $x \in V(T){\setminus } \{u_1\}$. Then g is an I3RDF of T with $w(g) \le n$, a contradiction. If $f^\prime (u)\ne \emptyset$, then $f^\prime (u_1)=f^\prime (u_2)=\emptyset$ and $f^\prime (\{u,u_3\})=\{1,2,3\}$. We may w.l.o.g assume that $f^\prime (u)=\{1,2\}$. Extend $f^\prime$ to g by putting $g(u_1)=\emptyset$, $g(u)=\{1,2,3\}$ and $g(x)=f^\prime (x)$ for $x \in V(T){\setminus } \{u_1,u\}$. Then we have $w(g) \le n$, a contradiction. $\square$

Claim 4

T has no vertex u which is adjacent to a pendent $P_3$.

Proof of Claim 3

Suppose to the contrary that $u \in V(T)$ and u is adjacent to a pendent $P_3=u_1u_2u_3$, say $uu_1, u_1u_2, u_2u_3 \in E(T)$. Let $T^R = T - \{u_1,u_2,u_3\}$ and $f^\prime$ be an optimal I3RDF of $T^R$. Then we have $w(f^\prime ) = i_{r3}(T^R) \le n-3$. Extend $f^\prime$ to g by putting $g(u_1)=g(u_3)=\emptyset$, $g(2)=\{1,2,3\}$ and $g(x)=f^\prime (x)$ for $x \in V(T){\setminus } \{u_1,u_2,u_3\}$. Then g is an I3RDF of T with $w(g) \le n$, a contradiction. $\square$

Let $P=x_1, x_2,\ldots , x_m$ be a longest path in T. By Claims 2, 3 and 4 , we have that $x_1$ is a leaf and $d(x_2)=2$, $x_3$ is adjacent to at least two pendent $P_2s$ and $x_4$ is adjacent to some anchors of pendent spiders H(k). Let $T_1$ and $T_2$ be two trees obtained by deleting the edge $x_4x_5$ from T and $T_1$ be the tree rooted at $x_4$. Let $f^\prime$ be an optimal I3RDF of $T_2$.

We now consider the following possible cases:

Case 1 There exists no leaf or pendent $P_2$ adjacent to $x_4$ in $T_1$ (see, e.g., Fig. 6).

Fig. 6

$x_4$ adjacent to no leaf or pendent $P_2$

Let $f^{\prime \prime }$ be an I3RDF of $T_1$ described in case i of Lemma 1. Then we obtain an I3RDF of T by putting $g(x)=f^{\prime \prime }(x)$ if $x \in V(T_1)$ and $g(x)=f^{\prime }(x)$ if $x \in V(T_2)$. By Lemma 1, $g(x_4)=\emptyset$ and so g is independent. Therefore, $w_T(g) \le w_{T_1}(g)+w_{T_2}(g) \le n$, a contradiction.

Case 2 There exists exactly one leaf z adjacent to $x_4$ in $T_1$ (see, e.g., Fig. 7).

Fig. 7

$x_4$ adjacent to one pendent vertex z

Let $f^{\prime \prime }$ be an I3RDF of $T_1$ described in case ii of Lemma 1. Then we obtain an I3RDF of T by putting $g(x)=f^{\prime \prime }(x)$ if $x \in V(T_1)$ and $g(x)=f^{\prime }(x)$ if $x \in V(T_2)$. By Lemma 1, $g(x_4)=\emptyset$ and so g is independent. Therefore, $w_T(g) \le w_{T_1}(g)+w_{T_2}(g) \le n$, a contradiction.

Case 3 There exists exactly one pendent $P_2=w_1w_2$ adjacent to $x_4$ (see, e.g., Fig. 8).

Fig. 8

$x_4$ adjacent to one pendent vertex z

Let $f^{\prime \prime }$ be an I3RDF of $T_1$ described in case iii of Lemma 1. Then we obtain an I3RDF of T by putting $g(x)=f^{\prime \prime }(x)$ if $x \in V(T_1)$ and $g(x)=f^{\prime }(x)$ if $x \in V(T_2)$. By Lemma 1, $g(x_4)=\emptyset$ and so g is independent. Therefore, $w_T(g) \le w_{T_1}(g)+w_{T_2}(g) \le n$, a contradiction.

Case 4 There exist at least two pendent $P_2s$ adjacent to $x_4$ (see, e.g., Fig. 9).

Fig. 9

$x_4$ adjacent to at least two pendent $P_2s$

Fig. 10

A tree T in ${\mathcal {L}}_5$ with $i_{r3}(T)=n$

Let $u_1u_2$ be a $P_2$ adjacent to $x_3$, $w_1w_2$ be a $P_2$ adjacent to $x_4$ and $T^R=T-\{u_1,u_2,w_1,w_2\}$. Let $f_1$ be an optimal I3RDF of $T^R$. Then it is impossible that $f_1(x_3)=f_1(x_4)=\emptyset$ (otherwise, recolor $x_3$ and the pendent $P_2s$ adjacent to $x_3$ as described in Lemma 1 to obtain an I3RDF with smaller weight). Assume that $f_1(x_3)=\emptyset$ and $f_1(x_4) \ne \emptyset$. If $|f_1(x_4)|=1$, we can adjust the coloring of $T_1$ as described in Lemma 1 such that $|f_1(x_4)|=2$. Let $u_2$ and $w_2$ be leaves. We can assume w.l.o.g. that $f_1(x_4)=\{2,3\}$. Extending $f_1$ to g by putting $g(u_1)=\{1,2,3\}$, $g(u_2)=g(w_1)=\emptyset$, $g(w_2)=\{1\}$ and $g(x)=f_1(x)$ for $x \in V(T)\backslash \{u_1, u_2, w_1, w_2\}$. Therefore, $w_T(g) \le w_{T^R}(g)+4 \le n$, a contradiction. The case when $f_1(x_3)\ne \emptyset$ and $f_1(x_4) = \emptyset$ is similar.

Case 5$d(x_4)=2$.

In this case, we have that $x_3$ is adjacent to at least two pendent $P_2s$ by Claim 4. We define a function $f^{\prime \prime }{:}\,V(T_1) \rightarrow {\mathcal {P}}(\{1,2,3\})$ as follows. $f^{\prime \prime }(x_4)=\emptyset$, $f^{\prime \prime }(x_3)=\{1,2,3\}$. For each pendent $P_2=v_1v_2$ ($v_2$ is a leaf) adjacent to $x_3$, let $f^{\prime \prime }(v_2)=\{1\}$ and $f^{\prime \prime }(v_1)=\emptyset$. Then we obtain an I3RDF of T by putting $g(x)=f^{\prime \prime }(x)$ if $x \in V(T_1)$ and $g(x)=f^{\prime }(x)$ if $x \in V(T_2)$. Therefore, $w_T(g) \le w_{T_1}(g)+w_{T_2}(g) \le n$, a contradiction.

Theorem 12

If $n\ge 6$, there exists an n-vertex tree T for which $i_{r3}(T) = n$.

Proof

Let $P_4$ be a path with $V(P_4)=\{v_1,x,v_3,v_4\}$ and $E(P_4)=\{v_1x, xv_3, v_3v_4\}$, and $P_3$ be a path with $V(P_3)=\{x,v_2,v_3\}$ and $E(P_3)=\{xv_2, v_2v_3\}$. Let ${\mathcal {L}}_k$ be the set of graphs each of which consists of the disjoint union of k copies of $P_4$ or $P_3$ plus a path through the vertex x of these copies. Figure 10 shows a graph in ${\mathcal {L}}_5$.

It can be seen that each tree T in ${\mathcal {L}}_k$ satisfies that $i_{r3}(T) = n$. By adding some $P_3s$ or $P_4s$ to a path, we can obtain such a tree of any order n for $n \ge 6$. $\square$

6 Conclusion

In this paper, we investigate the complexity of the independent t-rainbow domination problem. More precisely, we prove that the independent t-rainbow domination problem is NP-complete if the input is a bipartite graph or planar graph. Moreover, considering generalized Petersen graphs and tori, the exact values of $i_{r2}(P(n,1))$ and $i_{r2}(T_{3,n}))$ are determined, and upper bounds for $i_{r2}(P(n,2))$ and $i_{r2}(P(n,3))$ are given. Proving closed expressions of independent t-rainbow domination of the torus $T_{n,m}$ and the Petersen graph P(n, k) for larger t, n and k remain a challenge for further work.