Simultaneous Resolvability in Families of Corona Product Graphs

Abstract

Let $\mathcal{G}$ be a graph family defined on a common vertex set V and let d be a distance defined on every graph $G\in \mathcal{G}$. A set $S\subset V$ is said to be a simultaneous metric generator for $\mathcal{G}$ if for every $G\in \mathcal{G}$ and every pair of different vertices $u,v\in V$ there exists $s\in S$ such that $d(s,u)\ne d(s,v)$. The simultaneous metric dimension of $\mathcal{G}$ is the smallest integer k such that there is a simultaneous metric generator for $\mathcal{G}$ of cardinality k. We study the simultaneous metric dimension of families composed by corona product graphs. Specifically, we focus on the case of two particular distances defined on every $G\in \mathcal{G}$, namely the geodesic distance $d_G$ and the distance $d_{G,2}:V\times V\rightarrow \mathbb {N}\cup \{0\}$ defined as $d_{G,2}(x,y)=\min \{d_{G}(x,y),2\}$.

1 Introduction

A generator of a metric space (X, d) is a set $S\subset X$ of points in the space with the property that every point of X is uniquely determined by the distances from the elements of S. Given a simple and connected graph $G=(V,E)$, we consider the function $d_G:V\times V\rightarrow \mathbb {N}\cup \{0\}$, where $d_G(x,y)$ is the length of a shortest path between u and v and $\mathbb {N}$ is the set of positive integers. Then $(V,d_G)$ is a metric space since $d_G$ satisfies (i) $d_G(x,x)=0$ for all $x\in V$,(ii) $d_G(x,y)=d_G(y,x)$ for all $x,y \in V$ and (iii) $d_G(x,y)\le d_G(x,z)+d_G(z,y)$ for all $x,y,z\in V$. A vertex $v\in V$ is said to distinguish two vertices x and y if $d_G(v,x)\ne d_G(v,y)$. A set $S\subset V$ is said to be a metric generator for G if any pair of vertices of G is distinguished by some element of S. A minimum cardinality metric generator is called a metric basis, and its cardinality the metric dimension of G, denoted by $\dim (G)$.

The notion of metric dimension of a graph was introduced by Slater in [23], where metric generators were called locating sets. Harary and Melter independently introduced the same concept in [14], where metric generators were called resolving sets.

The concept of adjacency generator¹ was introduced by Jannesari and Omoomi in [16] as a tool to study the metric dimension of lexicographic product graphs. A set $S\subset V$ of vertices in a graph $G=(V,E)$ is said to be an adjacency generator for G if for every two vertices $x,y\in V-S$ there exists $s\in S$ such that s is adjacent to exactly one of x and y. A minimum cardinality adjacency generator is called an adjacency basis of G, and its cardinality the adjacency dimension of G, denoted by $\dim _A(G)$. Since any adjacency basis is a metric generator, $\dim (G)\le \dim _A(G)$. Besides, for any connected graph G of diameter at most two, $\dim _A(G)=\dim (G)$. Moreover, S is an adjacency generator for G if and only if S is an adjacency generator for its complement $\overline{G}$. This is justified by the fact that given an adjacency generator S for G, it holds that for every $x,y\in V- S$ there exists $s\in S$ such that s is adjacent to exactly one of x and y, and this property holds in $\overline{G}$. Thus, $\dim _A(G)=\dim _A(\overline{G}).$

This concept has been studied further by Fernau and Rodríguez-Velázquez in [9, 10] where they showed that the metric dimension of the corona product of a connected non-trivial graph G of order n and some non-trivial graph H equals n times the adjacency dimension of H. As a consequence of this strong relation, they showed that the problem of computing the adjacency dimension is NP-hard. Moreover, they pointed out some relations between adjacency generators and dominating sets. Notably, they described a number of cases where the adjacency dimension of the corona product of G and H depends on the order of G, the adjacency dimension of H and the domination number of G or that of a third graph obtained from it. Other relations between adjacency generators and dominating sets may be easily verified, for instance the fact that an adjacency generator for a graph dominates all its vertices, except for at most one. Furthermore, some strongly related concepts have been proposed, for instance identifying codes [17] and locating-dominating sets [24]. For a vertex v of a graph G, $N_G(v)$ will denote the set of neighbours or open neighbourhood of v in G, i.e. $N_G(v)=\{u \in V(G):\; u \sim v\}$. The closed neighbourhood, denoted by $N_G[v]$, equals $N_G(v) \cup \{v\}$. If there is no ambiguity, we will simple write N(v) or N[v]. An identifying code (locating-dominating set) of a graph G is a subset $S\subseteq V(G)$ such that every pair of vertices $x,y\in V(G)$ $\left( x,y\in V(G)-S\right)$ satisfy $\emptyset \ne S\cap N[x]\ne S\cap N[y]\ne \emptyset$. Clearly, all identifying codes and locating-dominating sets are also adjacency generators and dominating sets. In general, an adjacency generator is not necessarily a dominating set, nor an identifying code, nor a locating-dominating set. Likewise, a dominating set is not necessarily an adjacency generator, nor an identifying code, nor a locating-dominating set. Following an analogous idea, resolving dominating sets are defined in [3] as metric generators that are also dominating sets.

As pointed out in [9, 10], any adjacency generator for a graph $G=(V,E)$ is also a metric generator in a suitably chosen metric space. Given a positive integer t, we define the distance function $d_{G,t}:V\times V\rightarrow \mathbb {N}\cup \{0\}$, where

$$\begin{aligned} d_{G,t}(x,y)=\min \{d_G(x,y),t\}. \end{aligned}$$

Then any metric generator for $(V,d_{G,t})$ is a metric generator for $(V,d_{G,t+1})$ and, as a consequence, the metric dimension of $(V,d_{G,t+1})$ is less than or equal to the metric dimension of $(V,d_{G,t})$. In particular, the metric dimension of $(V,d_{G,1})$ equals $|V|-1$, the metric dimension of $(V,d_{G,2})$ equals $\dim _A(G)$ and, if G has diameter D(G), then $d_{G,D(G)}=d_G$ and so the metric dimension of $(V,d_{G,D(G)})$ equals $\dim (G)$. Notice that when using the metric $d_{G,t}$ the concept of metric generator needs not be restricted to the case of connected graphs.²

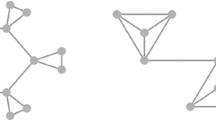
Let ${\mathcal G}=\{G_1,G_2,...,G_k\}$ be a family of (not necessarily edge-disjoint) connected graphs $G_i=(V,E_i)$ with common vertex set V (the union of whose edge sets is not necessarily the complete graph). Ramírez-Cruz, Oellermann and Rodríguez-Velázquez defined in [21, 22] a simultaneous metric generator for ${\mathcal {G}}$ as a set $S\subset V$ such that S is simultaneously a metric generator for each $G_i$. A minimum cardinality simultaneous metric generator for ${\mathcal {G}}$ is a simultaneous metric basis of ${\mathcal {G}}$, and its cardinality, the simultaneous metric dimension of ${\mathcal {G}}$, is denoted by $\hbox {Sd}({\mathcal {G}})$ or explicitly by $\hbox {Sd}( G_1,G_2,...,G_k )$. By analogy, we defined in [20] the concept of simultaneous adjacency generator for $\mathcal{G}$, simultaneous adjacency basis of $\mathcal{G}$ and the simultaneous adjacency dimension of $\mathcal{G}$, denoted by $\hbox {Sd}_A(\mathcal{G})$ or explicitly by $\hbox {Sd}_A(G_1,G_2,...,G_k)$. For instance, the set $\{1,3,6,7,8\}$ is a simultaneous adjacency basis of the family $\mathcal{G}=\{G_1,G_2,G_3\}$ shown in Fig. 1, while the set $\{1,6,7,8\}$ is a simultaneous metric basis, so $\hbox {Sd}_A(\mathcal{G})=5$ and $\hbox {Sd}(\mathcal{G})=4$.

Fig. 1

The set $\{1,3,6,7,8\}$ is a simultaneous adjacency basis of $\{G_1,G_2,G_3\}$, whereas $\{1,6,7,8\}$ is a simultaneous metric basis

The study of simultaneous parameters in graphs was introduced by Brigham and Dutton in [4], where they studied simultaneous domination. This should not be confused with studies on families sharing a constant value on a parameter, for instance the study presented in [15], where several graph families such that all members have a constant metric dimension are studied, enforcing no constraints regarding whether all members share a metric basis or not. As we mentioned previously, the study of the simultaneous metric dimension was introduced in [21, 22], where the authors obtained sharp bounds for this invariant for general families of graphs and gave closed formulae or tight bounds for the simultaneous metric dimension of several specific graph families. For a given graph G they described a process for obtaining a lower bound on the maximum number of graphs in a family containing G that has simultaneous metric dimension equal to $\dim (G)$. Moreover, it was shown that the problem of finding the simultaneous metric dimension of families of trees is NP-hard, even though the metric dimension of individual trees can be efficiently computed. This suggests the usefulness of finding the simultaneous metric dimension for special classes of graphs or obtaining good bounds on this invariant. In this paper, we obtain closed formulae for the simultaneous metric and adjacency dimensions of families composed by corona product graphs. In particular, we show that the simultaneous adjacency dimension is an important tool for the study of the simultaneous metric dimension of such families.

Throughout the paper, we will use the notation $K_n$, $C_n$, $N_n$ and $P_n$ for complete graphs, cycle graphs, empty graphs and path graphs of order n, respectively. We use the notation $u \sim v$ if u and v are adjacent and $G \cong H$ if G and H are isomorphic graphs. Two vertices $x,y\in V(G)$ are twins in G if $N_G[x]=N_G[y]$ or $N_G(x)=N_G(y)$. If $N_G[x]=N_G[y]$, they are said to be true twins, whereas if $N_G(x)=N_G(y)$ they are said to be false twins. We also define $\delta (v)=|N(v)|$ as the degree of vertex v, as well as $\delta (G)=\min _{v \in V(G)}\{\delta (v)\}$ and $\Delta (G)=\max _{v \in V(G)}\{\delta (v)\}$. The subgraph induced by a set S of vertices will be denoted by $\langle S\rangle$, the diameter of a graph will be denoted by D(G) and its girth by $\mathtt {g}(G)$. Any other definitions will be introduced whenever a concept is needed.

The remainder of this paper is structured as follows: Sect. 2 will briefly cover the most important, previously existing, general results concerning the simultaneous adjacency dimension. Then, Sect. 3 introduces the main results of this work, the consequences of which are discussed further in Sect. 4. Finally, our conclusions are presented in Sect. 5.

2 The Simultaneous Adjacency Dimension: Basic Bounds and Tools

We start by stating the general bounds on $\hbox {Sd}_A(\mathcal{G})$.

Remark 1

For any family $\mathcal{G}=\{G_1,G_2,...,G_k\}$ of connected graphs on a common vertex set V and any subfamily $\mathcal {H} \subseteq \mathcal {G}$, the following results hold:

• (i) $\underset{i\in \{1,...,k\}}{\max }\{\dim _A(G_i)\} \le \hbox {Sd}_A(\mathcal{H}) \le \hbox {Sd}_A(\mathcal{G}) \le \min \left\{ |V|-1,\displaystyle \sum _{i=1}^{k}\dim _A(G_i)\right\}$.

• (ii) $\hbox {Sd}_A(\mathcal{G})\ge \hbox {Sd}(\mathcal{G})$.

Proof

The bound in (ii) was stated in [20], as well as $\underset{i\in \{1,...,k\}}{\max }\{\dim _A(G_i)\} \le \hbox {Sd}_A(\mathcal{H}) \le \hbox {Sd}_A(\mathcal{G}) \le |V|-1$. Moreover, the upper bound $\hbox {Sd}_A(\mathcal{G}) \le \displaystyle \sum _{i=1}^{k}\dim _A(G_i)$ is a direct consequence of the fact that the set $S=\displaystyle \bigcup _{i=1}^kB_i$, where $B_i$ is an adjacency basis of $G_i$, is a simultaneous adjacency generator for $\mathcal {G}$. $\square$

It was also shown in [20] that if $\mathcal{G}$ is graph family defined on a common vertex set V, such that for every pair of different vertices $u,v \in V$ there exists a graph $G \in \mathcal{G}$ where u and v are twins, then $\hbox {Sd}_A(\mathcal{G})=\vert V \vert - 1$. In particular, any family $\mathcal{G}$ containing a complete graph or an empty graph satisfies $\hbox {Sd}_A(\mathcal{G})=\vert V \vert - 1$. Moreover, since a graph and its complement have the same adjacency generators, we have that $\hbox {Sd}_A(\mathcal{G})=\hbox {Sd}_A(\overline{\mathcal{G}})=\hbox {Sd}_A(\mathcal{G}\cup \overline{\mathcal{G}})$, where $\overline{\mathcal{G}}=\{\overline{G} :\; G \in \mathcal{G}\}$.

We now describe an approach, presented in [20], for constructing large graph families whose simultaneous adjacency dimension is bounded by the adjacency dimension of a single graph. Let $G=(V,E)$ be a graph and let $\hbox {Perm}(V)$ be the set of all permutations of V. Given a subset $X\subseteq V$, the stabilizer of X is the set of permutations

$$\begin{aligned} \mathcal{S}(X)=\{f\in \hbox {Perm}(V): f(x)=x, \; \text{ for } \text{ every } x\in X\} . \end{aligned}$$

As usual, we denote by f(X) the image of a subset X under f, i.e., $f(X)=\{f(x):\; x\in X\}$. Let $G=(V,E)$ be a graph and let $B\subset V$ be a non-empty set. For any permutation $f\in \mathcal{S}(B)$ of V we say that a graph $G'=(V,E')$ belongs to the family $\mathcal{G}_{B,f}(G)$ if and only if $N_{G'}(x)=f(N_G(x))$ for every $x\in B$. We define the subgraph $\langle B_G\rangle _{w}=(N_G[B],E_{w})$ of G, weakly induced by B, where $N_G[B]=\cup _{x\in B}N_G[x]$ and $E_{w}$ is the set of all edges having at least one vertex in B. It was shown in [20] that $\langle B_G \rangle _w \cong \langle B_{G'} \rangle _w$ for any $f\in \mathcal{{S}}(B)$ and any graph $G'\in \mathcal{{G}}_{B,f}(G)$. We define the graph family $\mathcal{G}_B(G)$, associated to B, as

$$\begin{aligned} \mathcal{G}_B(G)=\displaystyle \bigcup _{f\in \mathcal{S}(B)}\mathcal{G}_{B,f}(G). \end{aligned}$$

Fig. 2

A subfamily $\mathcal{H}$ of $\mathcal{G}_B(C_8)$, where $B=\{1,3,7\}$. For every $H_i \in \mathcal{H}$, $\dim _A(H_i)=\dim _A(C_8)=3$. Moreover, B is a simultaneous adjacency basis of $\mathcal{H}$, so $\hbox {Sd}_A(\mathcal{H})=3$

The following result shows that, given a graph G and an adjacency basis B of G, it is possible to obtain large families of graphs having B as a simultaneous adjacency generator.

Theorem 2

[20] Any adjacency basis B of a graph G is a simultaneous adjacency generator for any family of graphs $\mathcal{H} \subseteq \mathcal{G}_B(G)$. Moreover, if $G\in \mathcal{H}$, then

$$\begin{aligned} \hbox {Sd}_A(\mathcal{H})=\dim _A(G). \end{aligned}$$

To illustrate this, Fig. 2 shows a graph family $\mathcal{H}=\{H_1,H_2,H_3,H_4\} \subseteq \mathcal{G}_B(C_8)$, where $B=\{1,3,7\}$ and $\hbox {Sd}_A(\mathcal{H})=\dim _A(C_8)$. In general, for a graph G of order n and an adjacency basis B of G,

$$\begin{aligned} |\mathcal{G}_B(G)|=(n-\dim _A(G))!\cdot 2^{n-\dim _A(G) \atopwithdelims ()2}. \end{aligned}$$

(1)

3 Main Results

Let G be a graph of order n and let H be a graph. The corona product of G and H, denoted by $G\odot H$, was defined in [11] as the graph obtained from G and H by taking one copy of G and n copies of H and joining by an edge each vertex of the i-th copy of H with the i-th vertex of G. The reader is referred to [1, 2, 5–13, 18, 19, 25–28] for some known results on corona product graphs.

In order to present our results on the simultaneous metric and adjacency dimensions of families composed by corona product graphs, we need to introduce some additional notation. We denote by $\mathcal{G}_{nt}(V)$ $\left( \mathcal{G}_{nt}^{con}(V)\right)$ the set of all (connected) non-trivial graphs defined on a vertex set V. For two graph families $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$, we define the family

$$\begin{aligned} \mathcal{G}\odot \mathcal{H}=\{G \odot H :\; G\in \mathcal{G}\; \mathrm{and }\; H\in \mathcal{H}\}. \end{aligned}$$

In particular, if $\mathcal{G}=\{G\}$, we will use the notation $G \odot \mathcal{H}$, whereas if $\mathcal{H}=\{H\}$ we will use the notation $\mathcal{G} \odot H$.

Given $G\in \mathcal {G}$ and $H\in \mathcal {H}$, we denote by $H_i=(V_i',E_i)$ the subgraph of $G\odot H$ corresponding to the i-th copy of H. Notice that for any $i\in V$ the graph $H_i$, which is isomorphic to H, does not depend on G. Hence, the graphs in $\mathcal{G}\odot \mathcal{H}$ are defined on the vertex set $V\cup \left( \displaystyle \bigcup _{i\in V}V_i'\right)$. Analogously, for every $i\in V$ we define the graph family

$$\begin{aligned} \mathcal{H}_i=\{H_i=(V_i',E_i): \; H\in \mathcal{H}\}. \end{aligned}$$

Also, given a set $W\subset V'$ and $i\in V$, we denote by $W_i$ the subset of $V_i'$ corresponding to W. To clarify this notation, Fig. 3 shows the graph $C_4 \odot (K_1 \cup K_2)$. In the figure, $V=\{1,2,3,4\}$ and $V'=\{a,b,c\}$, whereas $V'_i=\{a_i,b_i,c_i\}$ for $i \in \{1,2,3,4\}$.

Fig. 3

The graph $G \odot H$, where $G \cong C_4$ and $H \cong K_1 \cup K_2$

3.1 The Simultaneous Metric Dimension of $\mathcal{G}\odot \mathcal{H}$

We first introduce a useful relation between the metric generators of two corona product graphs with a common second factor, which allows to determine the simultaneous metric dimension of numerous families of corona product graphs through the study of the metric dimension of a specific corona product graph.

Theorem 3

Let $G_1,G_2\in \mathcal{G}_{nt}^{con}(V)$ and $H\in \mathcal{G}_{nt}(V')$. Then, any metric generator for $G_1 \odot H$ is a metric generator for $G_2 \odot H$.

Proof

We claim that any metric generator B for $G_1\odot H$ is a metric generator for $G_2\odot H$. To see this, we differentiate the following three cases for two different vertices $x,y \in V(G_2\odot H)-B$.

• 1. $x,y\in V_i'$. Since no vertex belonging to $B-V_i'$ distinguishes the pair x, y in $G_1 \odot H$, there must exist $u\in V_i'\cap B$ which distinguishes them. This vertex u also distinguishes x and y in $G_2 \odot H$.

• 2. Either $x\in V_i'$ and $y\in V_j'$ or $x=i$ and $y\in V_j'$, where $i\ne j$. For these two possibilities we take $u\in B\cap V_i'$ and we conclude that $d_{G_2\odot H}(x,u)\le 2 \ne 3\le d_{G_2\odot H}(y,u)$.

• 3. $x=i$ and $y\in V'_i$. In this case, we take $u\in B\cap V'_j$, for any $j\ne i$, and we have that $d_{G_2\odot H}(x,u)<d_{G_2\odot H}(y,u)$.

• 4. $x=i$ and $y=j$. In this case, for $u\in B\cap V_i'$ we have $d_{G_2\odot H}(x,u)=1 \ne 2\le d_{G_2\odot H}(y,u)$.

In conclusion, B is a metric generator for $G_2\odot H$. $\square$

The following result is a direct consequence of Theorem 3.

Corollary 4

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$. Then, for any $G\in \mathcal {G}$,

$$\begin{aligned} \hbox {Sd}(\mathcal{G} \odot \mathcal{H})=\hbox {Sd}(G \odot \mathcal{H}). \end{aligned}$$

A strong link between the metric dimension of the corona product of two graphs and the adjacency dimension of the second graph involved in the product operation was shown in [9], as any connected graph G of order $n\ge 2$ and any non-trivial graph H satisfy $\dim (G\odot H)=n \cdot \dim _A(H)$. An analogous behaviour may be observed for families of the form $\mathcal{G}\odot \mathcal{H}$.

Theorem 5

For any $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and any $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$,

$$\begin{aligned} \hbox {Sd}(\mathcal{G} \odot \mathcal{H}) = \vert V \vert \cdot \hbox {Sd}_A(\mathcal{H}). \end{aligned}$$

Proof

Throughout the proof we consider two arbitrary graphs $G \in \mathcal{G}$ and $H \in \mathcal{H}$. Let B be a simultaneous metric basis of $\mathcal{G} \odot \mathcal{H}$ and let $B_i=B \cap V'_i$. Clearly, $B_i \cap B_j=\emptyset$ for every $i \ne j$. Since no pair of vertices $x,y \in H_i$ is distinguished by any vertex $v \in B_j$, $i \ne j$, we have that $B_i$ is an adjacency generator for $H_i$. Hence, the set $B'\subset V'$ corresponding to $B_i\subset V'_i$ is an adjacency generator for H and, since $B'$ does not depend on the choice of H, it is a simultaneous adjacency generator for $\mathcal {H}$ and, as a result,

$$\begin{aligned} \hbox {Sd}(\mathcal{G} \odot \mathcal{H})=|B|\ge \displaystyle \sum _{i\in V}|B_i| =|V|\cdot |B'|\ge |V|\cdot \hbox {Sd}_A(\mathcal{H}). \end{aligned}$$

It was proven in [9] that, given an adjacency generator W for H, the set $S=\displaystyle \bigcup _{i\in V} W_i$, where $W_i=W \cap V'_i$, is a metric generator for $G \odot H$. Now, let $W'$ be a simultaneous adjacency basis of $\mathcal{H}$ and let $W'_i=W' \cap V'_i$. Clearly, the set $S'=\displaystyle \bigcup _{i\in V} W'_i$ is a metric generator for any $G \odot H \in \mathcal{G}\odot \mathcal{H}$, so it is a simultaneous metric generator for $\mathcal{G}\odot \mathcal{H}$ and so

$$\begin{aligned} \hbox {Sd}(\mathcal{G} \odot \mathcal{H}) \le |S'| = \displaystyle \sum _{i\in V} |W'_i| = |V| \cdot \hbox {Sd}_A(\mathcal{H}). \end{aligned}$$

Therefore, the equality holds. $\square$

3.2 The Simultaneous Adjacency Dimension of $\mathcal{G}\odot \mathcal{H}$

Given two graph families $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$, Remark 1 and Theorem 5 lead to

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})\ge \hbox {Sd}(\mathcal{G} \odot \mathcal{H})=|V|\cdot \hbox {Sd}_A(\mathcal{H}). \end{aligned}$$

(2)

Therefore, there exists an integer $f(\mathcal{G},\mathcal{H})\ge 0$ such that

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})=|V|\cdot \hbox {Sd}_A(\mathcal{H})+f(\mathcal{G},\mathcal{H}). \end{aligned}$$

(3)

We will use the notation $f(G,\mathcal{H})$ for the cases where $\mathcal{G}=\{G\}$. It is easy to check that for any simultaneous adjacency basis W of $\mathcal {H}$ and any $i\in V$, the set $(V-\{i\})\cup \left( \displaystyle \bigcup _{j\in V}W_j\right)$ is a simultaneous adjacency generator for $\mathcal{G} \odot \mathcal{H}$, where $W_j$ is the subset of $V'_j$ corresponding to $W\subset V'$. Hence,

$$\begin{aligned} 0\le f(\mathcal{G},\mathcal{H}) \le |V|-1. \end{aligned}$$

(4)

From now on, our goal will be to determine the value of $f(\mathcal{G},\mathcal{H})$ under different sets of conditions. We begin by pointing out a useful fact which we will use throughout the remainder of this section. Let B be a simultaneous adjacency basis of $\mathcal{G}\odot \mathcal{H}$, and let $B_i=B \cap V'_i$. The following observation is a consequence of the fact that for any graph $G \odot H \in \mathcal{G}\odot \mathcal{H}$ and $i \in V$, no vertex in $B-B_i$ is able to distinguish two vertices in $V_i'$.

Remark 6

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$. Let B be a simultaneous adjacency basis of $\mathcal{G}\odot \mathcal{H}$ and let $B_i=B\cap V'_i$ for every $i \in V$. Then, $B_i$ is a simultaneous adjacency generator for $\mathcal{H}_i$.

We will first characterize cases where $f(\mathcal{G},\mathcal{H})=0$. To that end, recall the notion of simultaneous domination which, as we mentioned previously, was introduced in [4]. On a graph family $\mathcal{G}$, defined on a common vertex set V, a set $M \subseteq V$ is a simultaneous dominating set if it is a dominating set of every graph $G \in \mathcal{G}$.

Theorem 7

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$. If there exists a simultaneous adjacency basis B of $\mathcal{H}$ which is also a simultaneous dominating set and satisfies $B \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'$, then

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})=|V|\cdot \hbox {Sd}_A(\mathcal{H}). \end{aligned}$$

Proof

By Eq. (2), we only need to show that $\hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})\le |V|\cdot \hbox {Sd}_A(\mathcal{H})$. To this end, assume that B is a simultaneous adjacency basis of $\mathcal{H}$ which is a simultaneous dominating set of $\mathcal{H}$ and satisfies $B \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'$. Consider an arbitrary graph $G \odot H \in \mathcal{G}\odot \mathcal{H}$ and let $B_i=B \cap V'_i$, for every $i\in V$. It was proven in [9] that, given an adjacency generator W for H that is also a dominating set, the set $S=\displaystyle {\bigcup _{i\in V}}W_i$, where $W_i=W \cap V'_i$, is an adjacency generator for $G \odot H$. In consequence, we have that the set $S'=\displaystyle {\bigcup _{i\in V}}B_i$ is an adjacency generator for $G \odot H$ and, since $S'$ does not depend on the choice of G and H, it is a simultaneous adjacency generator for $\mathcal{G} \odot \mathcal{H}$. Thus, $\hbox {Sd}_A(\mathcal{G} \odot \mathcal{H}) \le |S'|= |V|\cdot \hbox {Sd}_A(\mathcal{H})$, and the equality holds.

We now address cases where $f(\mathcal {G},\mathcal {H})=|V|-1$.

Theorem 8

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$. If for every simultaneous adjacency basis B of $\mathcal{H}$ there exists $H \in \mathcal{H}$ of which B is not a dominating set, then

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})=|V| \cdot \hbox {Sd}_A(\mathcal{H})+|V|-1. \end{aligned}$$

Proof

By Eqs. (3) and (4), we have that $\hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})\le |V| \cdot \hbox {Sd}_A(\mathcal{H})+|V|-1.$ It remains to prove that $\hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})\ge |V| \cdot \hbox {Sd}_A(\mathcal{H})+|V|-1.$

Let U be a simultaneous adjacency basis of $\mathcal{G} \odot \mathcal{H}$, let $U_i=U \cap V'_i$ and let $U_0=U \cap V$. By Remark 6, $U_i$ is a simultaneous adjacency generator for $\mathcal{H}_i$ for every $i \in V$. Consider the partition $\{V_1,V_2\}$ of V defined as

$$\begin{aligned} V_1=\{i \in V:\; |U_i|=\hbox {Sd}_A(\mathcal{H})\}\ \text {and}\ V_2=\{i \in V:\; |U_i|\ge \hbox {Sd}_A(\mathcal{H})+1\}. \end{aligned}$$

For any $i,j \in V_1$, $i\ne j$, we have that there exist a graph $H \in \mathcal{H}$ and two vertices $x \in V'_i-U_i$ and $y \in V'_j-U_j$ such that $U_i \cap N_{H}(x)=\emptyset$ and $U_j \cap N_{H}(y)=\emptyset$. Thus, $i \in U$ or $j \in U$ and so $|U_0| \ge |V_1|-1$. In conclusion,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})&=|U_0|+\displaystyle {\sum _{i\in V_1}}|U_i|+ \sum _{i\in V_2}|U_i|\\&\ge (|V_1|-1)+|V_1|\cdot \hbox {Sd}_A(\mathcal{H})+|V_2|\cdot (\hbox {Sd}_A(\mathcal{H})+1)\\&=|V|\cdot \hbox {Sd}_A(\mathcal{H})+|V|-1. \end{aligned}$$

Therefore, the result follows. $\square$

As usual, given a graph G, we denote its domination number as $\gamma (G)$. By analogy, we will denote as $\hbox {S}\gamma (\mathcal{G})$ the simultaneous domination number of a family $\mathcal{G}$, that is, the minimum cardinality of a simultaneous dominating set. With this notation in mind, we present our next result.

Theorem 9

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$. If there exists a simultaneous adjacency basis of $\mathcal{H}$ which is also a simultaneous dominating set, and for every simultaneous adjacency basis B of $\mathcal{H}$ there exist $H \in \mathcal{H}$ and $v \in V'-B$ such that $B \subseteq N_H(v)$, then

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})=|V|\cdot \hbox {Sd}_A(\mathcal{H}) + S\gamma (\mathcal{G}). \end{aligned}$$

Proof

We first address the proof of $\hbox {Sd}_A(\mathcal{G} \odot \mathcal{H}) \ge |V|\cdot \hbox {Sd}_A(\mathcal{H})+\hbox {S}\gamma (\mathcal{G})$. Let U be a simultaneous adjacency basis of $\mathcal{G} \odot \mathcal{H}$, let $U_i=U \cap V'_i$, and let $U_0 = U \cap V$. By Remark 6, $U_i$ is a simultaneous adjacency generator for $\mathcal{H}_i$ for every $i \in V$. Consider the partition $\{V_1,V_2\}$ of V defined as

$$\begin{aligned} V_1=\{i \in V:\;|U_i|=\hbox {Sd}_A(\mathcal{H})\}\ \text {and}\ V_2=\{i \in V:\;|U_i| \ge \hbox {Sd}_A(\mathcal{H})+1\}. \end{aligned}$$

For every $i \in V_1$, the set $U_i$ is a simultaneous adjacency basis of $\mathcal{H}_i$, so there exist $H \in \mathcal{H}$ and $x \in V'_i$ such that $U_i \subseteq N_H(x)$, causing i and x not to be distinguished by any $y \in U_i$ in any graph belonging to $\mathcal{G}\odot H$. Thus, either $i \in U_0$ or for every $G \in \mathcal{G}$ there exists $z \in U_0$ such that $d_{G \odot H,2}(i,z)=1 \ne 2=d_{G \odot H,2}(x,z)$. In consequence, $V_2 \cup U_0$ must be a simultaneous dominating set of $\mathcal{G}$, so $|V_2 \cup U_0| \ge \hbox {S}\gamma (\mathcal{G})$. Finally,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})&=\displaystyle {\sum _{i \in V_1}}|U_i|+\displaystyle {\sum _{i \in V_2}}|U_i|+|U_0|\\&\ge \displaystyle {\sum _{i \in V_1}}\hbox {Sd}_A(\mathcal{H})+\displaystyle {\sum _{i \in V_2}}\left( \hbox {Sd}_A(\mathcal{H})+1\right) +|U_0|\\&=|V|\cdot \hbox {Sd}_A(\mathcal{H})+|V_2|+|U_0|\\&\ge |V|\cdot \hbox {Sd}_A(\mathcal{H})+|V_2 \cup U_0|\\&\ge |V|\cdot \hbox {Sd}_A(\mathcal{H})+\hbox {S}\gamma (\mathcal{G}). \end{aligned}$$

Let B be a simultaneous adjacency basis of $\mathcal{H}$ which is also a simultaneous dominating set of $\mathcal{H}$ and let $B_i=B \cap V'_i$. Moreover, let M be a minimum simultaneous dominating set of $\mathcal{G}$. Consider an arbitrary $G \odot H \in \mathcal{G}\odot \mathcal{H}$. It was shown in [9] that, given a dominating set $M'$ of G and an adjacency generator W for H that is also a dominating set of H, the set $S=M'\bigcup \left( \displaystyle {\bigcup _{i\in V}}W_i\right)$, where $W_i=W \cap V'_i$, is an adjacency generator for $G \odot H$. In consequence, the set $S'=M\bigcup \left( \displaystyle {\bigcup _{i\in V}}B_i\right)$ is a simultaneous adjacency generator for $\mathcal{G} \odot \mathcal{H}$. Thus, $\hbox {Sd}_A(\mathcal{G} \odot \mathcal{H}) \le \vert S' \vert = |V|\cdot \hbox {Sd}_A(\mathcal{H})+\hbox {S}\gamma (\mathcal{G})$, so the equality holds. $\square$

To give our next result, we need some additional definitions. For a graph G and a vertex $v \in V(G)$, let $G-v$ be the graph obtained by removing from G the vertex v and all its incident edges. Consider the following auxiliary domination parameter, which was defined in [9]:

$$\begin{aligned} \gamma '(G)=\underset{v \in V(G)}{\min }\{\gamma (G-v)\}. \end{aligned}$$

Theorem 10

Let G be a connected graph of order $n \ge 2$ and let $\mathcal{H}\subseteq \mathcal{G}_{nt}(V')$ such that some of its simultaneous adjacency bases are also simultaneous dominating sets, and some are not. If there exists a simultaneous adjacency basis $B'$ of $\mathcal{H}$ such that $B' \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'-B'$, and for every simultaneous adjacency basis B of $\mathcal{H}$ which is also a simultaneous dominating set there exist $H' \in \mathcal{H}$ and $w \in V'-B$ such that $B \subseteq N_{H'}(w)$, then

$$\begin{aligned} \hbox {Sd}_A(G \odot \mathcal{H})=n\cdot \hbox {Sd}_A(\mathcal{H})+\gamma '(G). \end{aligned}$$

Proof

In the family $G\odot \mathcal{H}$, we have that $V=V(G)$. We first address the proof of $\hbox {Sd}_A(G \odot \mathcal{H}) \ge n\cdot \hbox {Sd}_A(\mathcal{H})+\gamma '(G)$. Let U be a simultaneous adjacency basis of $G \odot \mathcal{H}$, let $U_i=U \cap V'_i$, and let $U_0 = U \cap V$. By Remark 6, $U_i$ is a simultaneous adjacency generator for $\mathcal{H}_i$ for every $i \in V$. Consider the partition $\{V_1,V_2,V_3\}$ of V, where $V_1$ contains the vertices $i \in V$ such that $U_i$ is a simultaneous adjacency basis of $\mathcal{H}_i$ but is not a simultaneous dominating set, $V_2$ contains the vertices $i \in V$ such that $U_i$ is a simultaneous adjacency basis and a simultaneous dominating set of $\mathcal{H}_i$, and $V_3$ is composed by the vertices $i \in V$ such that $U_i$ is not a simultaneous adjacency basis of $\mathcal{H}_i$.

If $i,j \in V_1$, then there exist a graph $H \in \mathcal{H}$ and two vertices $v_i \in V'_i-U_i$ and $v_j \in V'_j-U_j$ such that $U_i \cap N_H(v_i)=\emptyset$ and $U_j \cap N_H(v_j)=\emptyset$. Thus, $i \in U_0$ or $j \in U_0$, so $|U_0 \cap V_1| \ge |V_1|-1$. If $i \in V_2$, then there exist $H \in \mathcal{H}$ and $x \in V'_i$ such that $U_i \subseteq N_H(x)$. In consequence, the pair i, x is not distinguished by any $y \in U_i$, so either $i \in U_0$ or there exists $z \in U_0$ such that $d_{G \odot H,2}(i,z)=1 \ne 2=d_{G \odot H,2}(x,z)$. Therefore, at most one vertex of G is not dominated by $U_0 \cup V_3$, so $|U_0 \cup V_3| \ge \gamma '(G)$. Finally,

$$\begin{aligned} \hbox {Sd}_A(G \odot \mathcal{H})&=\displaystyle {\sum _{i \in V_1 \cup V_2}}|U_i| + \displaystyle {\sum _{i \in V_3}}|U_i| + |U_0|\\&\ge \displaystyle {\sum _{i \in V_1 \cup V_2}}\hbox {Sd}_A(\mathcal{H}) + \displaystyle {\sum _{i \in V_3}}(\hbox {Sd}_A(\mathcal{H})+1) + |U_0|\\&=n \cdot \hbox {Sd}_A(\mathcal{H})+|V_3|+|U_0|\\&\ge n \cdot \hbox {Sd}_A(\mathcal{H})+|V_3 \cup U_0|\\&\ge n \cdot \hbox {Sd}_A(\mathcal{H})+\gamma '(G). \end{aligned}$$

Now, let $B'$ be a simultaneous adjacency basis of $\mathcal{H}$ such that $B' \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'-B'$, and assume that for any simultaneous adjacency basis B of $\mathcal{H}$ which is also a simultaneous dominating set there exist $H' \in \mathcal{H}$ and $w \in V'-B$ such that $B \subseteq N_{H'}(w)$. Let $B''$ be one of such simultaneous adjacency bases of $\mathcal{H}$. Let $B'_i=B' \cap V'_i$ and $B''_i=B'' \cap V'_i$. Additionally, let M be a minimum dominating set of $G-x$, where x is a vertex such that $\gamma '(G)=\gamma (G-x)$. Consider an arbitrary graph $G \odot H \in G \odot \mathcal{H}$. It was proven in [9] that, given a minimum dominating set $M'$ of $G-x$, an adjacency generator $W'$ for H satisfying $W' \nsubseteq N_H(v)$ for every $v \in V'-W'$, and an adjacency generator $W''$ for H that is also dominating, the set $S=M'\bigcup W'_x\bigcup \left( \displaystyle {\bigcup _{i\in V-\{x\}}}W''_i\right)$ is an adjacency generator for $G\odot H$. In consequence, we have that the set $S'=M\bigcup B'_x\bigcup \left( \displaystyle {\bigcup _{i\in V-\{x\}}}B''_i\right)$ is a simultaneous adjacency generator for $G \odot \mathcal{H}$. Thus, $\hbox {Sd}_A(G \odot \mathcal{H}) \le \vert S' \vert = n\cdot \hbox {Sd}_A(\mathcal{H})+\gamma '(G)$, so the equality holds. $\square$

4 Consequences of Theorems 5, 7, 8, 9 and 10

The following result is a direct consequence of Theorems 2 and 5.

Proposition 11

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$. Let H be a non-trivial graph and let B be an adjacency basis of H. Then, for every $\mathcal{H} \subseteq \mathcal{G}_B(H)$ such that $H \in \mathcal{H}$,

$$\begin{aligned} \hbox {Sd}(\mathcal{G}\odot \mathcal{H})=|V|\cdot \dim _A(H). \end{aligned}$$

Proposition 11 allows us to construct large graph families of the form $\mathcal{G}\odot \mathcal{H}$ for which the exact value of $\hbox {Sd}(\mathcal{G}\odot \mathcal{H})$ can be determined in terms of the adjacency dimension of a single graph. For instance, consider the families $\mathcal{G}=\{G_1,G_2,\ldots ,G_k\}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}=\mathcal{G}_B(C_8)$.³ Applying Eq. (1), we have that $\mathcal{G}\odot \mathcal{H}$ contains $122880\cdot k$ graphs, yet the fact that $\dim _A(C_8)=3$ is sufficient to compute $\hbox {Sd}(\mathcal{G}\odot \mathcal{H})=|V|\cdot \dim _A(C_8)=3\cdot |V|$.

In order to analyse special cases of Theorems 7,  8,  9 and  10, we will first introduce the following classes of graph families:

• $\mathfrak {G}_B(P_n)$: For an integer $n\ge 7$, let $P_n$ be a path graph of order n and let $C(P_n)$ be the cycle graph obtained from $P_n$ by joining its leaves by an edge. We say that a graph family $\mathcal{G}$ belongs to $\mathfrak {G}_B(P_n)$ if and only if $\mathcal{G}\subseteq \mathcal{G}_B(P_n)\cup \mathcal{G}_B(C(P_n))$, for some simultaneous adjacency basis B of $\{P_n,C(P_n)\}$, and $P_n\in \mathcal{G}$ or $C(P_n)\in \mathcal{G}$.

• $\mathfrak {H}$: We say that a graph family $\mathcal{G}\subseteq \mathcal{G}_{nt}^ {con}(V)$ belongs to $\mathfrak {H}$ if and only if $|V|\ge 7$ and every $G \in \mathcal{G}$ is a cycle graph, or $D(G)\ge 6$, or $\mathtt {g}(G) \ge 5$ and $\delta (G) \ge 3$.

We now state some useful properties of (the graphs composing) such families.

Lemma 12

[16] For any integer $n\ge 4$, $\dim _A(C_n)=\dim _A( P_n)= \left\lfloor \frac{2n+2}{5}\right\rfloor$.

Lemma 13

Let $P_n$ and $C_n$ be a path and a cycle graph of order $n \ge 7$. If $n \equiv 1,3 \pmod 5$, then no adjacency basis of $P_n$ or $C_n$ is a dominating set. Otherwise, there exist adjacency bases of $P_n$ and $C_n$ that are dominating sets.

Proof

The proof for the cases where $n\equiv 0,2,4\pmod 5$ is given in [20]. We now address the remaining cases. In $C_n$, consider an adjacency basis B and a path $v_iv_{i+1}v_{i+2}v_{i+3}v_{i+4}$, where the subscripts are taken modulo n. If $v_i,v_{i+2} \in B$ and $v_{i+1} \notin B$, then $\{v_{i+1}\}$ is said to be a 1-gap of B. Likewise, if $v_i,v_{i+3} \in B$ and $v_{i+1},v_{i+2} \notin B$, then $\{v_{i+1},v_{i+2}\}$ is said to be a 2-gap of B and if $v_i,v_{i+4} \in B$ and $v_{i+1},v_{i+2},v_{i+3} \notin B$, then $\{v_{i+1},v_{i+2},v_{i+3}\}$ is said to be a 3-gap of B. Since B is an adjacency basis of $C_n$, it has no gaps of size 4 or larger and it has at most one 3-gap. Moreover, every 2- or 3-gap must be neighboured by two 1-gaps and the number of gaps of either size is at most $\dim _A(C_n)$. We now differentiate the following cases for $C_n$:

• 1. $n=5k+1$, $k\ge 2$. In this case, $\dim _A(C_n)=2k$, and thus $n-\dim _A(C_n)=3k+1$. Since any 2-gap must be neighboured by two 1-gaps, any adjacency basis B of $C_n$ has at most k 2-gaps. Now, assume that B has no 3-gaps. Then $|V(C_n)-B|=3k<3k+1=n-|B|$, which is a contradiction. Thus, any adjacency basis of $C_n$ has a 3-gap, i.e. it is not a dominating set.

• 2. $n=5k+3$, $k\ge 1$. In this case, $\dim _A(C_n)=2k+1$, and thus $n-\dim _A(C_n)=3k+2$. As in the previous case, any adjacency basis B of $C_n$ has at most k 2-gaps. Now assume that B has no 3-gaps. Then $|V(C_n)-B|=3k+1<3k+2=n-|B|$, which is a contradiction. Thus, any adjacency basis of $C_n$ has a 3-gap, i.e. it is not a dominating set.

By the set of cases above, the result holds for $C_n$.

Now, let $C'_n$ be the cycle obtained from $P_n$ by joining its leaves $v_1$ and $v_n$ by an edge. Let $V=V(P_n)=V(C'_n)$ and let B be an adjacency basis of $P_n$. Since for two different vertices $x,y\in V$, $d_{C'_n,2}(x,y)\ne d_{P_n,2}(x,y)$ if and only if $x,y\in \{ v_1,v_n\}$, if $v_1,v_n \in B$ or $v_1,v_n \notin B$, then B is an adjacency basis of $C_n$. Moreover, some vertex $w \in V-B$ satisfies $B \cap N_{P_n}(w)=B \cap N_{C'_n}(w)=\emptyset$, so B is not a dominating set of $P_n$. We now treat the case where $v_1 \in B$ and $v_n \notin B$. If $v_{n-1} \notin B$ then B is not a dominating set of $P_n$. If $v_{n-1} \in B$ and $v_2 \notin B$, we have that $d_{C'_n,2}(v_2,v_{n-1})=d_{P_n,2}(v_2,v_{n-1})=2 \ne 1=d_{P_n,2}(v_n,v_{n-1})=d_{C'_n,2}(v_n,v_{n-1})$, whereas for any other pair of different vertices $x,y \in V-B$ there exists $z \in B$ such that $d_{C'_n,2}(x,z)=d_{P_n,2}(x,z) \ne d_{P_n,2}(y,z)=d_{C'_n,2}(y,z)$, so B is an adjacency basis of $C'_n$ where $\{v_n\}$ is a 1-gap. In consequence, some vertex $w \in V-(B\cup \{v_n\})$ satisfies $B \cap N_{P_n}(w)=B \cap N_{C'_n}(w)=\emptyset$, so B is not a dominating set of $P_n$. Finally, if $v_2,v_{n-1} \in B$, then for any pair of different vertices $x,y \in V-B$ there exists $z \in B-\{v_1\}$ such that $d_{C'_n,2}(x,z)=d_{P_n,2}(x,z) \ne d_{P_n,2}(y,z)=d_{C'_n,2}(y,z)$, so B is an adjacency basis of $C'_n$ where $\{v_n\}$ is a 1-gap. As in the previous case, some vertex $w \in V-(B\cup \{v_n\})$ satisfies $B \cap N_{P_n}(w)=B \cap N_{C'_n}(w)=\emptyset$, so B is not a dominating set of $P_n$. The proof is complete. $\square$

Lemma 14

[20] Let G be a connected graph. If $D(G)\ge 6$, or $G \cong C_n$ with $n\ge 7$, or G is a graph of girth $\mathtt {g}(G) {\ge }{5}$ and minimum degree $\delta (G){\ge } {3}$, then for every adjacency generator B for G and every $v\in V(G)$, $B\not \subseteq N_G(v).$

Given two vertex-disjoint graphs $G=(V_{1},E_{1})$ and $H=(V_{2},E_{2})$, the join of G and H, denoted by $G+H$, is the graph with vertex set $V(G+H)=V_{1}\cup V_{2}$ and edge set $E(G+H)=E_{1}\cup E_{2}\cup \{uv\,:\,u\in V_{1},v\in V_{2}\}$. For two graph families $\mathcal{G}$ and $\mathcal{H}$, defined on common vertex sets $V_1$ and $V_2$, respectively, such that $V_1 \cap V_2 = \emptyset$, we define the family

$$\begin{aligned} \mathcal{G}+\mathcal{H}=\{G+H:\;G\in \mathcal{G},H\in \mathcal{H}\}. \end{aligned}$$

In particular, if $\mathcal{G}=\{G\}$ we will use the notation $G+\mathcal{H}$.

Lemma 15

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}(V_1)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V_2)$. Then, every simultaneous adjacency basis of $\mathcal{G}+\mathcal{H}$ is a simultaneous dominating set of $\mathcal{G}+\mathcal{H}$.

Proof

Let B be a simultaneous adjacency basis of $\mathcal{G}+\mathcal{H}$, let $W_1=B\cap V_1$ and $W_2=B\cap V_2$. Since no pair of different vertices $u,v \in V_2-W_2$ is distinguished in any $G+H\in \mathcal{G}+\mathcal{H}$ by any vertex from $W_1$, we have that $W_2$ is a simultaneous adjacency generator for $\mathcal{H}$ and, in consequence, $W_2 \ne \emptyset$. By an analogous reasoning we can see that $W_1$ is a simultaneous adjacency generator for $\mathcal{G}$ and, in consequence, $W_1 \ne \emptyset$. Moreover, every vertex in $V_1$ is dominated by every vertex in $W_2$, whereas every vertex in $V_2$ is dominated by every vertex in $W_1$, so B is a dominating set for every $G+H \in \mathcal{G}+\mathcal{H}$. $\square$

The following result, presented in [20], characterizes a large number of families of the form $\mathcal{G}+\mathcal{H}$ whose simultaneous adjacency bases are formed by the union of simultaneous adjacency bases of $\mathcal{G}$ and $\mathcal{H}$.

Lemma 16

[20] Let $\mathcal{G}\subseteq \mathcal{G}_{nt}(V_1)$ and $\mathcal{H}\subseteq \mathcal{G}_{nt}(V_2)$. If there exists a simultaneous adjacency basis B of $\mathcal{G}$ such that for every $G \in \mathcal{G}$ and every $v\in V_1$, $B\not \subseteq N_G(v)$, then

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G}+\mathcal{H})=\hbox {Sd}_A(\mathcal{G})+\hbox {Sd}_A(\mathcal{H}). \end{aligned}$$

Using Lemmas 12,  13,  14,  15 and  16, we will give several results obtained as particular cases of Theorems 7,  8,  9 and  10. First, we will show particular cases of Theorem 7.

Proposition 17

For every $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and every $\mathcal{H}\in \mathfrak {G}_B(P_n)$ such that $n \equiv 0,2,4 \pmod 5$ and B is a dominating set of $P_n$,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})=|V|\cdot \left\lfloor \frac{2n+2}{5}\right\rfloor . \end{aligned}$$

Proof

The existence of B is a consequence of Lemma 13. Since $P_n \in \mathcal{H}$ or $C(P_n) \in \mathcal{H}$, by Theorem 2 we deduce that B is a simultaneous adjacency basis of $\mathcal{H}$. Let $V'=V(P_n)=V(C(P_n))$. By the definition of $\mathcal{G}_B$, we have that $\displaystyle {\bigcup _{v \in B}}N_{H}(v)=\displaystyle {\bigcup _{v \in B}}N_{P_n}(v)=V'$ or $\displaystyle {\bigcup _{v \in B}}N_{H}(v)=\displaystyle {\bigcup _{v \in B}}N_{C(P_n)}(v)=V'$ for every $H \in \mathcal{H}$, so B is a dominating set of every $H \in \mathcal{H}$. Moreover, by Lemma 14, we have that $B \nsubseteq N_{P_n}(v)$ and $B \nsubseteq N_{C(P_n)}(v)$ for every $v \in V'$. Furthermore, by the definition of $\mathcal{G}_B$, we have that $B \cap N_{H}(v)=B \cap N_{P_n}(v)$ or $B \cap N_{H}(v)=B \cap N_{C(P_n)}(v)$ for every $H \in \mathcal{H}$ and every $v\in V'$, so $B \nsubseteq N_{H}(v)$ for every $H \in \mathcal{H}$ and every $v\in V'$. In consequence, the result follows from Theorems 2 and 7, as well as Lemma 12. $\square$

It was shown in [20] that every simultaneous adjacency basis of a family $\mathcal{G}+\mathcal{H}$ satisfying the assumptions of Lemma 16 is the union of a simultaneous adjacency basis of $\mathcal{H}$ and a simultaneous adjacency basis B of $\mathcal{G}$ such that $B \nsubseteq N_G(v)$ for every $G \in \mathcal{G}$ and every $v \in V_1$.

Proposition 18

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$, $\mathcal{H}\subseteq \mathcal{G}_{nt}(V'_1)$ and $\mathcal{H}'\subseteq \mathcal{G}_{nt}(V'_2)$. If there exist a simultaneous adjacency basis B of $\mathcal{H}$ that satisfies $B \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'_1$, and a simultaneous adjacency basis $B'$ of $\mathcal{H}'$ that satisfies $B' \nsubseteq N_{H'}(v')$ for every $H' \in \mathcal{H}'$ and every $v' \in V'_2$, then

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot (\mathcal{H}+\mathcal{H}'))=|V| \cdot \hbox {Sd}_A(\mathcal{H})+|V| \cdot \hbox {Sd}_A(\mathcal{H}'). \end{aligned}$$

Proof

Let B and $B'$ be simultaneous adjacency bases of $\mathcal{H}$ and $\mathcal{H}'$, respectively, that satisfy the premises of the theorem, and let $S=B\cup B'$. As shown in [20], S is a simultaneous adjacency basis of $\mathcal{H}+\mathcal{H}'$. Moreover, since $B \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'_1$, and $B' \nsubseteq N_{H'}(v')$ for every $H' \in \mathcal{H}'$ and every $v' \in V'_2$, we have that $S \nsubseteq N_{H+H'}(x)$ for every $H+H' \in \mathcal{H}+\mathcal{H}'$ and every $x \in V'_1 \cup V'_2$. Finally, by Lemma 15, we have that S is a simultaneous dominating set of $\mathcal{H}+\mathcal{H}'$, so $\hbox {Sd}_A(\mathcal{G} \odot (\mathcal{H}+\mathcal{H}'))=|V| \cdot \hbox {Sd}_A(\mathcal{H}+\mathcal{H}')=|V| \cdot \hbox {Sd}_A(\mathcal{H})+|V| \cdot \hbox {Sd}_A(\mathcal{H}')$ by Theorem 7 and Lemma 16. $\square$

The following result is a direct consequence of Lemma 14 and Proposition 18.

Proposition 19

For every $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H},\mathcal{H}'\in \mathfrak {H}$,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot (\mathcal{H}+\mathcal{H}'))=|V| \cdot \hbox {Sd}_A(\mathcal{H})+|V| \cdot \hbox {Sd}_A(\mathcal{H}'). \end{aligned}$$

In addition, following a reasoning analogous to that of the proof of Proposition 17, we obtain the following result as a consequence of Theorem 2, Lemma 14 and Proposition 18.

Proposition 20

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and let $\{H\},\{H'\}\in \mathfrak {H}$. Let B and $B'$ be adjacency bases of H and $H'$, respectively. Then, for any pair of families $\mathcal{H} \subseteq \mathcal{G}_B(H)$ and $\mathcal{H}' \subseteq \mathcal{G}_{B'}(H')$ such that $H \in \mathcal{H}$ and $H' \in \mathcal{H}'$,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot (\mathcal{H}+\mathcal{H}'))=|V| \cdot \dim _A(H)+|V| \cdot \dim _A(H'). \end{aligned}$$

In what follows, we give particular cases of Theorem 8.

Proposition 21

For every $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and every $\mathcal{H}\in \mathfrak {G}_B(P_n)$ such that $n \equiv 1,3 \pmod 5$,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})=|V|\cdot \left( \left\lfloor \frac{2n+2}{5}\right\rfloor +1\right) -1. \end{aligned}$$

Proof

Note that B is an adjacency basis of both $P_n$ and $C(P_n)$, so by Lemma 13 it is not a dominating set of neither. Let x be the vertex not dominated by B in $P_n$ and $C(P_n)$. Then, by the definition of $\mathcal{G}_B$, in any $H\in \mathcal{H}$, there exists $y=f(x)$, $f\in \mathcal{S}(B)$, that is not dominated by B, so the result follows from Theorems 2 and 8, as well as Lemma 12. $\square$

Proposition 22

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and let $\mathcal{H}=\{N_t \cup H_1,N_t \cup H_2,\ldots ,N_t \cup H_k\}$, where $N_t$ is an empty graph of order $t \ge 1$ and $\{H_1,H_2,\ldots ,H_k\}\subseteq \mathcal{G}_{nt}^{con}(V'')$. Then,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot \mathcal{H})=|V|\cdot \hbox {Sd}_A(\mathcal{H})+|V|-1. \end{aligned}$$

Proof

Consider that the common vertex set of $\mathcal{H}$ has the form $V'=V(N_t) \cup V''$, where $V(N_t)$ and $V''$ are disjoint. Let B be a simultaneous adjacency basis of $\mathcal{H}$, and let $B''=B \cap V''$. Consider an arbitrary graph $N_t \cup H \in \mathcal{H}$. Either $|V(N_t)|=1$ or every pair of different vertices $u,v \in V(N_t)$ are false twins, so $V(N_t) \subseteq B$ if and only if there exists $v \in V''$ such that $B \cap N_{H}(v)=\emptyset$. If such v exists, it is not dominated by B; otherwise, $V(N_t)-B=\{v'\}$ and $B \cap N_{H}(v')=\emptyset$. In either case, the result follows from Theorem 8. $\square$

We now discuss particular cases of Theorem 9.

Proposition 23

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$, $\mathcal{H}\subseteq \mathcal{G}_{nt}(V'_1)$ and $\mathcal{H}'\subseteq \mathcal{G}_{nt}(V'_2)$. If there exists a simultaneous adjacency basis B of $\mathcal{H}$ that satisfies $B \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'_1$, and for every simultaneous adjacency basis $B'$ of $\mathcal{H}'$ there exist $H' \in \mathcal{H}$ and $v' \in V'_2$ such that $B' \subseteq N_{H'}(v')$, then

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot (\mathcal{H}+\mathcal{H}'))=|V| \cdot \hbox {Sd}_A(\mathcal{H})+|V| \cdot \hbox {Sd}_A(\mathcal{H}')+\hbox {S}\gamma (\mathcal{G}). \end{aligned}$$

Proof

Let S be a simultaneous adjacency basis of $\mathcal{H}+\mathcal{H}'$, let $W=S \cap V'_1$ and let $W'=S \cap V'_2$. As discussed in [20], W and $W'$ are simultaneous adjacency bases of $\mathcal{H}$ and $\mathcal{H}'$, respectively. Since there exist $H' \in \mathcal{H}$ and $v' \in V'_2$ such that $W' \subseteq N_{H'}(v')$, we have that $S \subseteq N_{H+H'}(v')$ for any $H \in \mathcal{H}$ by the definition of the join operation. Moreover, by Lemma 15, S is a simultaneous dominating set of $\mathcal{H}+\mathcal{H}'$, so $\hbox {Sd}_A(\mathcal{G} \odot (\mathcal{H}+\mathcal{H}'))=|V| \cdot \hbox {Sd}_A(\mathcal{H}+\mathcal{H}')+\hbox {S}\gamma (\mathcal{G})=|V| \cdot \hbox {Sd}_A(\mathcal{H})+|V| \cdot \hbox {Sd}_A(\mathcal{H}')+\hbox {S}\gamma (\mathcal{G})$ by Theorem 9 and Lemma 16. $\square$

The following results are particular cases of Proposition 23.

Proposition 24

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$, $\mathcal{H}\in \mathfrak {H}$ and $K_t$ a complete graph of order $t \ge 2$. Then,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot (K_t+\mathcal{H}))=|V| \cdot \hbox {Sd}_A(\mathcal{H})+|V|\cdot (t-1)+\hbox {S}\gamma (\mathcal{G}). \end{aligned}$$

Proof

By Lemma 16, $\hbox {Sd}_A(K_t+\mathcal{H})=\hbox {Sd}_A(\mathcal{H})+t-1$. Let $V'$ be the common vertex set of $\mathcal{H}$. By Lemma 14, every simultaneous adjacency basis B of $\mathcal{H}$ satisfies $B \nsubseteq N_H(v)$ for every $H \in \mathcal{H}$ and every $v \in V'$. Furthermore, every adjacency basis of $K_t$ has the form $B'=V(K_t)-\{v\}$, where v is an arbitrary vertex of $K_t$. Clearly, $B' \subseteq N_{K_t}(v)$, so the result follows from Proposition 23. $\square$

Following a reasoning analogous to that of the proofs of Propositions 17, 21 and 24, we obtain the following result as a consequence of Theorem 2, Lemmas 14 and 16, and Proposition 23.

Proposition 25

Let $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$, $\{H\}\in \mathfrak {H}$, B an adjacency basis of H and $K_t$ a complete graph of order $t\ge 2$. Then, for any family $\mathcal{H} \subseteq \mathcal{G}_B(H)$ such that $H \in \mathcal{H}$,

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot (K_t+\mathcal{H}))=|V| \cdot \dim _A(H)+|V|\cdot (t-1)+\hbox {S}\gamma (\mathcal{G}). \end{aligned}$$

As an example of the previous result, consider two families $\mathcal{G}\subseteq \mathcal{G}_{nt}^{con}(V)$ and $\mathcal{H}\in \mathfrak {G}_B(P_n)$, and a complete graph $K_t$ of order $t \ge 2$. We have that

$$\begin{aligned} \hbox {Sd}_A(\mathcal{G} \odot (K_t+\mathcal{H}))=|V|\cdot \left( \left\lfloor \frac{2n+2}{5}\right\rfloor +t-1\right) +\hbox {S}\gamma (\mathcal{G}). \end{aligned}$$

To conclude our exposition, we will give some examples which are particular cases of Theorem 10. Consider the family $\{P_5,C_5\}$, where $V(P_5)=V(C_5)=\{v_1,v_2,v_3,v_4,$ $v_5\}$, $E(P_5)=\{v_1v_2, v_2v_3,$ $v_3v_4, v_4v_5\}$ and $E(C_5)=E(P_5) \cup \{v_1v_5\}$. We have that the set $\{v_2,v_4\}$ is the sole simultaneous adjacency basis which is also a simultaneous dominating set and $v_3$ satisfies $\{v_2,v_4\} \subseteq N_{P_5}(v_3)$ and $\{v_2,v_4\} \subseteq N_{C_5}(v_3)$. Moreover, the set $\{v_1,v_5\}$ (as well as $\{v_2,v_3\}$ and $\{v_3,v_4\}$) is a simultaneous adjacency basis such that every vertex $v_x$ satisfies $N_{P_5}(v_x) \nsubseteq \{v_1,v_5\}$ and $N_{C_5}(v_x) \nsubseteq \{v_1,v_5\}$. Now, consider any connected graph G of order $n \ge 2$. We have that $\hbox {Sd}_A(G \odot \{P_5,C_5\})=2n+\gamma '(G)$.

5 Concluding Remarks

In this paper, we have studied the behaviour of the simultaneous metric and adjacency dimensions in families composed by corona product graphs. The most important conclusion we extract from this study is the possibility of expressing both parameters for families composed by product graphs in terms of the simultaneous adjacency dimension of the family composed by the second factors, which is a smaller family and is defined on a smaller vertex set. Furthermore, we were able to verify that in some cases, both parameters may even be defined in terms of the adjacency dimension of a single graph. These results are particularly relevant in light of the circumstance that the computation of these parameters is in general NP-hard.

This sort of “interchangeability” of the first factors observed in several cases, as well as the possibility of characterizing one family using one adjacency basis of one graph, may be interpreted as a “fault-tolerant” behaviour. In this sense, it may be interesting to explore to what extent this may be expanded. For instance, under some circumstances, the metric and adjacency dimensions of a relaxed corona product $G \odot ' H$, where each vertex of G is joined by an edge only to a subset of the vertices of its corresponding copy of H, still behave in the same manner as in $G\odot H$, and this behaviour extends to the simultaneous scenario.⁴ Likewise, for a graph G and an adjacency basis B of G, it is interesting to explore the construction of families having a set $B'$, slightly different from B, as a simultaneous adjacency generator, and the degree of variability on G that such families would allow.