On Choosability with Separation of Planar Graphs Without Adjacent Short Cycles

Abstract

A (k, d)-list assignment L of a graph is a function that assigns to each vertex v a list L(v) of at least k colors satisfying $|L(x)\cap L(y)|\le d$ for each edge xy. An L-coloring is a vertex coloring $\pi$ such that $\pi (v) \in L(v)$ for each vertex v and $\pi (x) \ne \pi (y)$ for each edge xy. A graph G is (k, d)-choosable if there exists an L-coloring of G for every (k, d)-list assignment L. This concept is known as choosability with separation. In this paper, we prove that planar graphs without 4-cycles adjacent to $4^-$-cycles are (3, 1)-choosable. This is a strengthening of a result which says that planar graphs without 4-cycles are (3, 1)-choosable.

1 Introduction

A graph G is an ordered pair (V(G), E(G)) consisting of a set V(G) of vertices and a set E(G), disjoint from V(G), of edges, together with an incidence function $\psi _G$ that associates with each edge of G an unordered pair of (not necessarily distinct) vertices of G. All graphs considered in this paper are finite, loopless, and without multiple edges, unless otherwise stated. A graph G is planar if it can be drawn on the plane so that its edges meet only at the vertices of the graph. Given a graph G, a list assignment L is a mapping that assigns to each vertex $v \in V (G)$ a list L(v) of colors. An L-coloring is a vertex coloring $\pi$ such that $\pi (v) \in L(v)$ for each vertex v and $\pi (x) \ne \pi (y)$ for each edge xy. If there is an L-coloring for each list assignment L with $|L(v)| \ge k$ for each vertex v, then we say G is k-choosable and the minimum such integer k is the list chromatic number of G, denoted by $\chi _l(G)$.

Motivated by forcing the lists of the adjacent vertices to be somewhat separated, the concept known as choosability with separation was raised. A graph G is said to be (k, d)-choosable if there is an L-coloring for each list assignment L with $|L(v)| \ge k$ for each vertex v such that $|L(x) \cap L(y)| \le d$ for each edge xy. Obviously, G is (k, k)-choosable if and only if it is k-choosable. Moreover, if G is (k, d)-choosable, then it is $(k',d')$-choosable for all $k'\ge k$ and $d'\le d$. This concept was introduced by Kratochvíl, Tuza, and Voigt [4]. They investigated this concept for complete graphs and sparse graphs. Recently, Füredi, Kostochka, and Kumbhat [2, 3] have extended the study of dense graphs to complete bipartite graphs and multipartite graphs.

One significant theorem established in a paper by Thomassen [7] is that every planar graph is 5-choosable. The upper bound 5 is best possible since it cannot be lowered to 4 by an example given in [8]. It follows that every planar graph is (5, d)-choosable for all non-negative integers d and there exists a non-(4, 4)-choosable planar graph. Moreover, there exist non-(4, 3)-choosable planar graphs given by Mirzakhani [5]. On the other hand, Kratochvíl, Tuza, and Voigt [4] positively confirmed the (4, 1)-choosability of planar graphs. The question of whether every planar graph is (4, 2)-choosable seems to be a difficult open problem.

Now we turn our attention to (3, d)-choosability of planar graphs. It is proved in [1] that every triangle-free planar graph is (3, 1)-choosable. This result is sharp since non-(3, d)-choosable triangle-free planar graphs with $d=2$ and $d=3$ were constructed by Škrekovski [6] and Voigt [9], respectively. In addition, Choi, Lidický, and Stolee [1] proved that planar graphs without 4-cycles are (3, 1)-choosable and planar graphs without 5- and 6-cycles are (3, 1)-choosable.

In this paper, we aim to study (3, 1)-choosability of planar graphs in which certain 4-cycles can be allowed. More precisely, we will prove the following theorem that is a strengthening of a result in [1].

Theorem 1

Every planar graph without 4-cycles adjacent to $4^-$-cycles is (3, 1)-choosable.

Before proving our main result, we need to introduce some notation and terminology. Suppose that G is a planar graph embedded on the plane. We denote its vertex set, edge set, order, and size by V(G), E(G), |G|, and |E|, respectively. Suppose that C is a cycle in G. C is called a $k^-$-cycle if the length of C is at most k. A triangle is the same as a 3-cycle. Two cycles are called adjacent if they share at least one edge. A walk of G is a non-empty alternating sequence of vertices and edges denoted by $W=v_0e_1v_1e_2\ldots e_kv_k$, where $e_i=v_{i-1}v_i$ for each $i\in \{1, 2, \ldots , k\}$. If all the vertices of a walk $v_0e_1v_1e_2\ldots e_kv_k$ are mutually distinct, then we call such a walk a path, simply denoted by $P=v_0v_1\ldots v_{k-1}v_k$. If $S\subset V(G)$, then $G-S$ represents the subgraph obtained from G by deleting the vertices in S and all the edges incident with some vertices in S.

Let $\mathcal {G}$ denote the class of planar graphs without 4-cycles adjacent to $4^-$-cycles. If $G\in \mathcal {G}$, then the following three configurations will be excluded from G:

• (A1) two 3-cycles sharing an edge;

• (A2) two 4-cycles sharing an edge;

• (A3) a 3-cycle and a 4-cycle sharing an edge.

2 Proof of Theorem 1

In what follows, let L be a list assignment on V(G). A $(*,1)$ -list assignment is a list assignment L such that $|L(v)|\ge 1$ for each vertex v and $|L(x)\cap L(y)|\le 1$ for each edge xy. For $i\in \{1,2,3\}$, a vertex v is called an $L_i$ -vertex if $|L(v)|=i$, denoted by $v\in L_i$.

Instead of showing Theorem 1, we prove Theorem 2 which is a stronger result inspired by the proof with clever ideas in [1]. Since any (3, 1)-list assignment for $G\in \mathcal {G}$ satisfies all conditions of Theorem 2, we may easily derive Theorem 1 from Theorem 2.

Theorem 2

Let $G\in \mathcal {G}$ with an outer face F and let P be a subpath of F with order at most 3. If L is a $(*,1)$-list assignment satisfying the following six conditions, then G is L-colorable.

• (C1) $|L(v)|\ge 3$ for $v\in V(G)\setminus V(F)$;

• (C2) $|L(v)|\ge 2$ for $v\in V(F)\setminus V(P)$;

• (C3) $|L(v)|=1$ for $v\in V(P)$;

• (C4) the subgraph induced by V(P) in G is L-colorable;

• (C5) no $L_2$-vertices are adjacent in G;

• (C6) no $L_2$-vertex is adjacent to at least two vertices in P.

Proof

Suppose the theorem is not true. Among counterexamples with minimum $|G|+|E|$, we choose G to possess the smallest $\sum _{v\in V(G)} |L(v)|$, that is, the sum of list sizes is the smallest. Note that G is connected.

In the following, for $v\in V(G)$, we use $N_G(v)$ to denote the neighborhood of v in G. For simplicity, we use N(v) instead of $N_G(v)$ when G is clear. If $v\in V(P)$, then v is called a P-vertex. A middle P-vertex is a P-vertex which has exactly two neighbors in P. The following claim will be used often. $\square$

Claim 1

For each edge $xy\in E(G)\setminus E(P)$, $|L(x)\cap L(y)|=1$.

Proof

By definition, $|L(x)\cap L(y)|\le 1$. If $|L(x)\cap L(y)|=0$, then it suffices to L-color $G-xy$ and extend this coloring to G , which is a contradiction. $\square$

For our convenience, in what follows, we will use the notation (G; P, L) to denote by a graph G with respect to the path P under the list assignment L.

Claim 2

G is 2-connected. In particular, F is a cycle.

Proof

Suppose to the contrary that there exists a cut vertex $v\in V(G)$, and let $G_1$ and $G_2$ be two connected subgraphs such that $V(G_1)\cap V(G_2)=\{v\}$ and $G_1\cup G_2=G$. Clearly, both $G_1$ and $G_2$ have at least two vertices. If P is fully contained in some $G_i$, say $G_1$, then $G_1$ admits an L-coloring $\pi _1$ by the minimality of G. Let $L'$ be a list assignment on $V(G_2)$ such that $L'(u)=\{\pi _1(u)\}$ if $u=v$, and $L'(u)=L(u)$ otherwise. Consider $P'=v$ as a subpath of the outer face of $G_2$. Since $(G_2; P',L')$ satisfies all conditions (C1)-(C6) of Theorem 2, there is an $L'$-coloring $\pi _2$ of $G_2$. Combining $\pi _1$ and $\pi _2$, we get an L-coloring of G, a contradiction. Now suppose that $P=xvy$ with $xv\in E(G_1)$ and $vy\in E(G_2)$. Let $P_1=xv$ and $P_2=yv$. Let $L^{i*}$ be the list assignment L restricted to $G_i$. Then $(G_i;P_i,L^{i*})$ satisfies (C1)-(C6). By the minimality of G, there exists an $L^{i*}$-coloring $\pi _i$ of $G_i$ for each $i\in \{1,2\}$. Taking $\pi _1(v)=\pi _2(v)$, we get an L-coloring $\pi _1\cup \pi _2$ of G, a contradiction. $\square$

An edge $v_0v_1$ is called a chord of C if $v_0, v_1\in V(C)$ but $v_0v_1\notin E(C)$. A 2-chord of C is defined to be a path $Q=v_0v_1v_2$ such that $v_0, v_2\in V(C)$ and $v_1\notin V(C)$. Further, if $v_0v_2\notin E(C)$, then we call Q a nice 2-chord. Let $V_\mathrm{int}(C)$ and $V_\mathrm{ext}(C)$ denote the sets of vertices located inside and outside C, respectively.

Claim 3

G contains no triangle T with $V_\mathrm{int}(T)\ne \emptyset$.

Proof

Assume to the contrary that G contains a triangle $T=xyzx$ such that int$(T)\ne \emptyset .$ Let $G_1=G[V_\mathrm{ext}(T)\cup T]$ and $G_2=G[V_\mathrm{int}(T)\cup T]$. Clearly, $P\subseteq G_1$. Since $|G_1|<|G|$, $G_1$ has an L-coloring $\pi$. So x, y, z are colored. Let $G'=G_2-xy$, and $P'=xzy$. Let $L'$ be a list assignment on $V(G')$ such that $L'(u)=\{\pi (u)\}$ if $u\in \{x,y,z\}$, and $L'(u)=L(u)$ otherwise. It is easy to check that (C1)-(C6) hold for $(G';P',L')$. Thus, by the minimality of G, $G'$ has an $L'$-coloring $\pi '$. Consequently, the coloring $\pi \cup \pi '$ is an L-coloring of G, a contradiction. $\square$

Claim 4

$|F|\ne 3$.

Proof

Suppose to the contrary that $|F|=3$. Then $V_\mathrm{int}(F)=\emptyset$ by Claim 3, and thus $G=F$. Let $F=v_1v_2v_3v_1$. If $|P|=3$, then G is L-colorable by (C4). If $|P|=2$, say $P=v_1v_2$, then $v_3\in L_{3}$ by (C6). It suffices to color $v_3$ with a color in $L(v_3)\setminus (L(v_1)\cup L(v_2))$ after $v_1$ and $v_2$ have been colored. If $|P|=1$, say $P=v_1$, then by (C5), we may assume that $v_2\in L_{2}\cup L_{3}$ and $v_3\in L_{3}$. We color $v_1$ with $a\in L(v_1)$, $v_2$ with $b\in L(v_2)\setminus \{a\}$, and $v_3$ with $c\in L(v_3)\setminus \{a,b\}$. In all cases, we reach a contradiction. $\square$

A chord xy is called bad if there exists an $L_2$-vertex $z\in V(F)$ such that $zx,zy\in E(F)$. Note that xyzx is a 3-cycle. Otherwise, xy is called good.

For our convenience, in the proofs of Claims 5 and  6, we always use $F_1$ and $F_2$ to denote the two cycles in $F\cup \{xy\}$ that contain the chord xy. Let $G_i=G[ V_\mathrm{int}(F_i)\cup V(F_i) ]$ for $i\in \{1,2\}$. For two vertices $u,v\in V(F_i)$, let $F_i(u,v)$ denote the path in $F_i$ from u to v along the boundary of F (except u and v).

Claim 5

If xy is a good chord of F, then either x or y is a middle P-vertex.

Proof

Assume that neither x nor y is a middle P-vertex. Without loss of generality, assume that P is fully contained in $F_1-xy$. Moreover, xy is chosen as a good chord such that $|V(G_2)|$ is as small as possible. It means that xy is the unique good chord located in $G_2$.

Clearly, $G_1$ admits an L-coloring $\pi$ by the minimality of G. Let $P'=xy$. Let $L'$ be a list assignment on $V(G_2)$ such that $L'(u)=\{\pi (u)\}$ if $u\in \{x,y\}$, and $L'(u)=L(u)$ otherwise. One may inspect that (C1)-(C4) are valid for $(G_2;P',L')$. Since every $L_2'$-vertex in $G_2$ is just an $L_2$-vertex in G, (C5) holds for $(G_2;P',L')$. If (C6) is also true, then $G_2$ has an $L'$-coloring $\pi '$, and therefore $\pi \cup \pi '$ is an L-coloring of G, a contradiction. Otherwise, suppose that there exists an $L_2'$-vertex $z\in F_2(x,y)$ such that $zx, zy\in E(G_2)$. Note that $z\in L_2$ and xyzx is a triangle. Since xy is good, we see that at least one of xz and yz is a chord, say zx. Then $|F_2(x,z)|\ge 3$ due to $G\in \mathcal {G}$, implying that zx is a good chord of $F_2$ (also a good chord of F), contradicting the choice of xy. $\square$

Claim 6

Each chord of F is bad.

Proof

Suppose to the contrary that F has a good chord xy. By Claim 5, we may assume that $P=wxv$ such that $w\in V(F_1)$ and $v\in V(F_2)$. Without loss of generality, assume that $|F_1(w,y)|\le |F_2(v, y)|$. Let $P_1=wx$. By the minimality of G, $G_1$ admits an L-coloring $\pi$ with respect to $P_1$. Let $L'$ be a list assignment on $V(G_2)$ such that $L'(u)=\{\pi (u)\}$ if $u\in \{x,y\}$, and $L'(u)=L(u)$ otherwise. Let $P_2=vxy$. One may easily check that (C1), (C2), (C3), and (C5) are valid for $(G_2; P_2,L')$ since $L_2$-vertices remain $L_2'$-vertices. Next, we will show that (C4) and (C6) are also satisfied for $(G_2; P_2,L')$, implying that $G_2$ has an $L'$-coloring $\pi '$ and therefore $\pi \cup \pi '$ is an L-coloring of G, a contradiction.

The proof splits into the following two cases.

Case 1. $0\le |F_1(w,y)|\le 1$.

Note that $F_1$ is a 3-cycle or a 4-cycle. Since $G\in \mathcal {G}$, we derive that $vy\notin E(G)$ and therefore $|F_2(v, y)|\ge 2$. This implies immediately that (C4) holds for $(G_2; P_2, L')$. If (C6) is not true for $(G_2; P_2,L')$, then there exists an $L_2'$-vertex $z\in F_2(v,y)$ adjacent to at least two vertices of $P_2$. Since $z\in L_2$, $x, v\in V(P)$, and (G; P, L) satisfies (C6), we see that $zy\in E(G)$ and exactly one of x and v is adjacent to z. If $zx\in E(G)$, then xyzx is a 3-cycle. If $zv\in E(G)$, then xyzvx is a 4-cycle. Both cases contradict the assumption that $G\in \mathcal {G}$.

Case 2. $|F_1(w,y)|\ge 2$.

Then $|F_2(v,y)|\ge 2$. Moreover, xy is chose as a chord that minimizes $|V(G_2)|$ under the assumption $|F_2(v,y)|\ge 2$. It means that if there is $t\in F_2(v,y)$ such that xt is a chord of F and $|F_2(v,t)|\ge 2$, then we select xt instead of xy.

If $yv\in E(G)$, then $yv\notin E(F_2)$ and thus yv is a chord of $F_2$ (also a good chord of F). Further, yv is a good chord of F since $G\in \mathcal {G}$. However, neither v nor y is a middle P-vertex, which contradicts Claim 5. Thus, $yv\notin E(G)$, implying that (C4) holds for $(G_2; P_2, L')$. Also if (C6) is false for $(G_2; P_2, L')$, then there exists an $L_2'$-vertex $z\in F_2(v,y)$ such that $zy\in E(G)$ and exactly one of x and v is adjacent to z. If $zx\in E(G)$, then $|F_2(v,z)|\ge 2$, hence zx is a good chord of $F_2$ as $G\in \mathcal {G}$. This contradicts the choice of xy. So $zv\in E(G)$, and this implies that xyzvx is a 4-cycle. Since $|F_2(v,y)|\ge 2$, at least one of zv and zy is a chord of $F_2$. If zy is a chord of $F_2$, then $|F_2(y,z)|\ge 3$. Thus, either zv or zy is a good chord of F since no $L_2$-vertex can be adjacent to both endpoints. However, none of v, y, and z is a middle P-vertex, contradicting Claim 5. $\square$

Claim 7

If xy is a chord of F, then x and y are either $L_{2}$-vertices or $L_3$-vertices.

Proof

By Claim 6, xy is bad, so there is an $L_2$-vertex $z\in V(F)$ such that $zx,zy\in E(F)$ and xyzx forms a 3-cycle. By Claim 3, $V_\mathrm{int}(xyzx)=\emptyset$. By symmetry, it suffices to show that $x\in L_{3}$. By (C5), $x\notin L_2$. Let $x\in L_1$, that is, $x\in V(P)$. Since $|P|\le 3$ and there are no adjacent triangles in G, we deduce that $y\notin L_1$, and thus $y\in L_{3}$ by (C5). Without loss of generality, assume that $L(x)=\{a\}$, $L(z)=\{a, b\}$, and $L(y)=\{a, c, d\}$ such that $b\notin \{c,d\}$ by Claim 1. By the minimality of G, $G-yz$ admits an L-coloring $\pi$. In fact, $\pi$ is also an L-coloring of G since no conflict is caused by adding the edge yz back to $G-yz$, a contradiction. $\square$

Recall that a nice 2-chord of a cycle C is a path $Q=v_0v_1v_2$ such that $v_0, v_2\in V(C)$, $v_1\notin V(C)$, and $v_0v_2\notin E(C)$. In the proofs of Claims 8–10, we shall define $F_1$ and $F_2$ to be the two cycles in $F\cup Q$ that contain Q. For $i\in \{1,2\}$, let $G_i=G[ V_\mathrm{int}(F_i)\cup V(F_i) ]$, and for $u, v\in V(F_i)$, let $F_i(u,v)$ denote the path in $F_i$ from u to v along the boundary of F (except u and v). A nice 2-chord $Q=v_0v_1v_2$ of F is called worse if $v_0\in V(P)$, $v_2\in L_{3}$ and there is an $L_2$-vertex $v^*\in V(F)$ such that $v^*v_0,v^*v_2\in E(F)$. Note that $v^*v_0v_1v_2v^*$ is a 4-cycle.

Claim 8

Let $Q=v_0v_1v_2$ be a nice 2-chord of F. If $v_2\in L_2$, then $v_0$ is a middle P-vertex.

Proof

Suppose to the contrary that $v_0$ is not a middle P-vertex. Without loss of generality, assume that $P\subseteq F_1\cap F$. Furthermore, choose Q so that $|V(G_2)|$ is as small as possible. By the minimality of G, $G_1$ has an L-coloring $\pi$. Let $L'$ be a list assignment on $V(G_2)$ such that $L'(u)=\{\pi (u)\}$ if $u\in \{v_0, v_1, v_2\}$, and $L'(u)=L(u)$ otherwise. Let $P'=v_0v_1v_2$. It is not difficult to see that (C1)–(C3) and (C5) hold for $(G_2;P',L')$. If (C4) fails, implying $v_0v_2\in E(G_2)$, then the definition of a nice 2-chord asserts that $|F_2(v_0, v_2)|\ge 1$ and hence $v_0v_2$ is a chord of F. By Claim 6, $v_0v_2$ is bad. However, $v_2$ is an $L_2$-vertex, which contradicts Claim 7.

If (C6) is true, then an $L'$-coloring $\pi '$ of $G_2$ can be established. Consequently, combining $\pi$ and $\pi '$ constructs an L-coloring of G, a contradiction. Now assume that (C6) is not true for $(G_2;P',L')$. Then there exists an $L_2'$-vertex $z\in F_2(v_0, v_2)$ adjacent to at least two of $v_0, v_1, v_2$. Note that $z\in L_2$ and $v_2\in L_2$. Since (C5) holds for (G; P, L), we know that $zv_2\notin E(G)$ and thus $|F_2(z, v_2)|\ge 1$. So $zv_0,zv_1\in E(G)$. It follows that $zv_1v_2$ is a nice 2-chord where $|V(G_2)|$ is smaller, which contradicts the choice of $v_0v_1v_2$. $\square$

Claim 9

Let $Q=v_0v_1v_2$ be a nice 2-chord of F. If $v_2\in L_{3}$ and $v_0$ is a non-middle P-vertex, then Q is worse.

Proof

First we note that $|F_i(v_0, v_2)|\ge 1$ for $i\in \{1, 2\}$. Since $v_0$ is not a middle vertex, without loss of generality, we may assume that $P\subseteq F_1\cap F$. Then $G_1$ has an L-coloring $\pi$ by the minimality of G. Let $L'$ be a list assignment on $V(G_2)$ such that $L'(u)=\{\pi (u)\}$ if $u\in \{v_0, v_1, v_2\}$, and $L'(u)=L(u)$ otherwise. Let $P'=v_0v_1v_2$.

Using an argument similar to Claim 8, we can show that all conditions (C1)–(C5) are satisfied for $(G_2;P',L')$. Thus, it remains to check that (C6) holds for $(G_2;P',L')$. Let $z\in F_2(v_0, v_2)$ be an $L_2'$-vertex adjacent to at least two of $v_0, v_1, v_2$. If $v_1z\notin E(G_2)$, then z is adjacent to both $v_0$ and $v_2$. Moreover, by Claim 7, we see that $zv_0$ and $zv_2$ are both edges of $F_2$, and thus Q is worse. So now assume that $v_1z\in E(G_2)$. That is, $v_0v_1z$ is a 2-chord. If $|F_2(z, v_0)|\ge 1$, then $v_0$ is a middle P-vertex by Claim  8, a contradiction. So $|F_2(z, v_0)|=0$. Similarly, $|F_2(z, v_2)|=0$ since $v_2$ cannot be a middle P-vertex due to $v_2\in L_{3+}$. So $v_0z\in E(F_2)$ and $v_2z\in E(F_2)$. However, adjacent triangles $zv_0v_1z$ and $zv_1v_2z$ are established, which is a contradiction to the assumption that $G\in \mathcal {G}$. $\square$

Claim 10

Let $Q=v_0v_1v_2$ be a nice 2-chord of F with $v_0\in V(P)$ and $v_2\in L_{2}\cup L_{3}$. Then $v_1$ is not adjacent to any vertex in $V(P)\setminus \{v_0\}$.

Proof

Assume to the contrary that there is $u\in V(P)\setminus \{v_0\}$ such that $v_1u\in E(G)$. Without loss of generality, assume that $u\in V(F_1\cap F)$. Then $v_0v_1u\ldots v_0$ is a $4^-$-cycle since $|P|\le 3$. Since $G\in \mathcal {G}$, we have that $|F_1(u, v_2)|\ge 2$ and $|F_2(v_0, v_2)|\ge 2$. This implies that $uv_1v_2$ and $v_0v_1v_2$ are both nice 2-chords that are not worse. If $v_2\in L_2$, then both $v_0$ and u are middle P-vertices by Claim 8, which is impossible since there is at most one middle P-vertex. So assume that $v_2\in L_{3}$. Then at least one of $v_0$ and u, say u, is not a middle P-vertex. By Claim 9, $uv_1v_2$ is worse, a contradiction. $\square$

In the rest of the paper, we let $N^*(v)=N(v)\cap V_\mathrm{int}(F)$ for any $v\in V(F)$.

Claim 11

If xyz is a subpath of F with $|L(y)|=2$, then $L(x)\cap L(y)\ne L(y)\cap L(z)$.

Proof

Suppose to the contrary that $L(y)=\{a,b\}$ and $a\in L(x)\cap L(y)$ and $a\in L(y)\cap L(z)$. By (C5), $x, z\in L_1\cup L_{3}$. By Claim 6, there does not exist $t\in V(F)\setminus \{x,z\}$ adjacent to y. Namely, $N^*(y)=N(y)\setminus \{x,z\}$.

Let $L'$ be a list assignment on the vertices of $G-y$ such that $L'(u)=L(u)\setminus \{b\}$ for $u\in N^*(y)$, and $L'(u)=L(u)$ otherwise. Let $G'$ be the graph obtained from $G-y$ by removing the edges between $L_2'$-vertices with disjoint lists. Let $P'=P$. Now we are going to verify that (C1)–(C6) are all valid for $(G';P',L')$.

Let $u\in V(G')$. Note that $|L'(u)|\ge 2$ if $u\in N^*(y)$, and $L'(u)=L(u)$ if $u\in V(G')\setminus N^*(y)$. So (C1)–(C4) hold automatically for $(G';P',L')$. By the definition of $G'$, there are no adjacent $L_2'$-vertices in $N^*(y)$. So if (C5) is false for $(G';P',L')$, then the only possibility is that there is an edge $ty^*\in E(G)$ such that $y^*\in N^*(y)$, $t\in L_2\cap (V(F)\setminus \{x, y, z\})$. However, $yy^*t$ forms a nice 2-chord such that neither of its ends is a middle P-vertex, contradicting Claim 8. Hence (C5) holds for $(G';P',L')$.

If (C6) is false for $(G';P',L')$, then there must exist an $L'_2$-vertex $y^*\in N^*(y)$ adjacent to at least two vertices in $P'$, say $w_1$ and $w_2$. If $w_i\in V(F)\setminus \{x,y,z\}$ for some $i\in \{1,2\}$, then $yy^*w_i$ is a nice 2-chord. By Claim 10, $y^*$ is not adjacent to any P-vertex except $w_i$, a contradiction. So assume that $\{w_1, w_2\}=\{x, z\}$. That is, $y^*x, y^*z\in E(G)$, so $xyy^*x$ and $zyy^*z$ are two adjacent triangles, also a contradiction. Therefore (C6) holds for $(G';P',L')$.

Now, by the minimality of G, $G'$ admits an $L'$-coloring $\pi$. Extend $\pi$ to G by coloring y with b to get an L-coloring of G, a contradiction. $\square$

Claim 12

If $F=xyzwx$ is a 4-cycle with $x\in V(P)$ and $y, w\in L_1\cup L_2$, then $z\in L_1\cup L_2$.

Proof

Suppose to the contrary that $z\in L_{3}$. Obviously, there is a color $c\in L(z)\setminus (L(y)\cup L(w))$. Since $xz,yw\notin E(G)$ by $G\in \mathcal{{G}}$, we see that $N^*(z)=N(z)\setminus \{y,w\}$. Let $L'$ be a list assignment on $V(G)\setminus \{z\}$ such that $L'(u)=L(u)\setminus \{c\}$ for $u\in N^*(z)$, and $L'(u)=L(u)$ otherwise. Let $G'$ be the graph obtained from $G-z$ by removing edges between $L_2'$-vertices with disjoint lists. Let $P'=P$. It is easy to check that (C1)–(C4) hold for $(G';P',L')$. By the definition of $G'$, no two $L'_2$-vertices in $N^*(z)$ are adjacent in $G'$. Since $G\in \mathcal {G}$, none of $z^*\in N^*(z)$ is adjacent to a vertex in $\{x, y, w\}$. So (C5) and (C6) both hold for $(G';P',L')$. Hence, by the minimality of G, $G'$ is $L'$-colorable and we may easily obtain an L-coloring of G by further coloring z with c, a contradiction. $\square$

Claim 13

If $|F|=4$, then $|P|\le 2$.

Proof

Let $F=xyzwx$. Suppose to the contrary that $|P|=3$, say $P=wxy$. Then $x, y, w\in L_1$. By (C6), we know that $z\in L_{3}$, contradicting Claim 12. $\square$

Claim 14

If xyz is a subpath of F with $y\in L_{3}$, then $x,z\in L_2$.

Proof

Assume that the claim is not true. By Claim 4, $|F|\ge 4$. So the proof can be divided into the following two cases by symmetry.

Case 1. $x,z\in L_1\cup L_{3}$.

Choose $a\in L(y)$. Let $L'$ be the list assignment on V(G) such that $L'(y)=L(y)\setminus \{a\}$, and $L'(u)=L(u)$ for $u\in V(G)\setminus \{y\}$. This will change y into an $L_2'$-vertex, whereas all other vertices keep their color lists unaltered. Then (C1)–(C4) hold obviously for $(G;P,L')$. If there is an $L_2$-vertex $t\in V(F)\setminus \{x,y,z\}$ adjacent to y, that is, ty is a chord, then we see that t should be an $L_3$-vertex by Claim 7. This shows that (C5) holds for $(G;P,L')$. Moreover, if (C6) fails for $(G;P,L')$, then x and z are both P-vertices. This leads to $|F|=4$ and $|P|=3$, contradicting Claim 13. Thus, (C6) holds for $(G;P,L')$. By the choice of L, G has an $L'$-coloring, which is also an L-coloring of G.

Case 2. $x\in L_2$ and $z\in L_1\cup L_{3}$.

In this case, we select $c\in L(x)\cap L(y)$. Let $G'=G-xy$. Let $L'$ be the list assignment on the vertices of $G'$ such that $L'(y)=L(y)\setminus \{c\}$, and $L'(u)=L(u)$ for $u\in V(G')\setminus \{y\}$. Let $P'=P$. Similarly, as only the vertex y has changed its color list, (C1)–(C4) hold for $(G';P',L')$. F has at most one bad chord with one end y, and it must be bad by Claim 6. Let $yy'$ be the chord, if any, so that $yy'xy$ forms a 3-cycle. This implies that $N(y)= N^*(y)\cup \{x, z\}$ or $N(y)= N^*(y)\cup \{x, z, y'\}$. This fact, together with Claim 7, shows that (C6) holds for $(G';P',L')$. If (C5) fails for $(G';P',L')$, then the only possible case is that $yy'\in E(G')$ with $y,y'\in L'_2$. Since $y'\in L_2$, we get a contradiction to Claim 7. Thus, (C5) holds for $(G';P',L')$. By the minimality of G, $G'$ is $L'$-colorable, and hence G is L-colorable which is also an L-coloring for G, a contradiction. $\square$

Claim 15

If $u\in V(F)\cap L_{3}$, then u is adjacent to exactly two $L_2$-vertices in V(F).

Proof

We know $|F|\ge 4$ and let xuy be a subpath of F. By Claim 14, x and y are $L_2$-vertices. If $u'\in V(F)\setminus \{x,u,y\}$, then $u'\in L_{3}$ by Claim 7. $\square$

Claim 16

$|F|\ge 5$.

Proof

Suppose to the contrary that $|F|\le 4$. By Claim 4, $|F|=4$, say $F=xyzwx$. Then $|P|\le 2$ by Claim 13. If $|P|=2$, say $P=xy$, then at least one of z and w, say w, belongs to $L_{3}$ by (C5). However, this contradicts Claim 14. Now assume $|P|=1$, say $P=x$. Again, by Claim 14, we deduce that $y,w\in L_2$ and thus $z\in L_{3}$ by (C5). However, this is impossible by Claim 12. $\square$

In what follows, we assume that $F=v_1v_2\ldots v_mv_{m+1}\ldots v_tv_1$ such that $v_i\in V(F)\setminus V(P)$ for $i=1,\ldots , m$ and $v_{j}\in V(P)$ for $j=m+1, \ldots , t$. By Claim 16, $t\ge 5$. Since $|P|\le 3$, we have that $m\ge 2$ and $t\le m+3$. Moreover, by Claim 14, $v_i\in L_2$ for odd i and $v_j\in L_{3}$ for even j, where $i, j\in \{1,\ldots , m\}$. It follows from $v_m\in L_2$ that m is odd and thus at least 3.

The proof of Theorem 2 splits into Cases I and II. In each case, we first pick a special subset X of vertices in G, and then color the vertices in X with distinct colors from their corresponding color lists. Let $\pi$ denote the L-coloring of X. Second, we define $L'$ to be a list assignment on the vertices of $G-X$ such that $L'(u)=L(u)\setminus \{\pi (x)\mid x\in X$ and $xu\in E(G)\}$, and $L'(u)=L(u)$ otherwise. Let $G'$ be the graph obtained from $G-X$ by removing all edges among the vertices with disjoint $L'$-lists that are not in E(P). Let $P'=P$. If (C1)–(C6) hold for $(G';P',L')$, then $G'$ admits an $L'$-coloring $\pi '$. Combining $\pi$ and $\pi '$, we get an L-coloring of G, a contradiction.

Since $v_1,v_3\in L_2$, and $v_2\in L_{3}$, any chord with $v_2$ as an end is bad and both ends are $L_{3}$-vertices by Claim 6. This consequence gives us the following important observation.

Observation 1

$N(v_2)=N^*(v_2)\cup \{v_1, v_3\}$ or $N(v_2)=N^*(v_2)\cup \{v_1, v_3, v_4\}$.

From now on, there are no more claims and the proof of our main theorem is starting.

Case I $v_2v_4\notin E(G)$.

Then $N(v_2)=N^*(v_2)\cup \{v_1, v_3\}$ by Observation 1. We select a color $c\in L(v_2)\setminus (L(v_1)\cup L(v_3))$. Since $G\in \mathcal{G}$, we know that $|N^*(v_2)\cap N^*(v_3)|\le 1$. So we have two subcases to consider.

Subcase I $_1$ There is no vertex $w\in N^*(v_2)\cap N^*(v_3)$ such that $c\in L(w)$.

Let $X=\{v_2\}$. Set $\pi (v_2)=c$. Observe that only vertices in $N^*(v_2)$ have changed their color lists to $L'$ lists, while other vertices in $V(G')\setminus N^*(v_2)$ have kept their color lists unaltered. Since $|L'(u)|\ge 2$ for each $u\in N^*(v_2)$, (C1)–(C4) hold automatically for $(G';P',L')$. If (C6) fails for $(G';P',L')$, then there must exist $x\in N^*(v_2)$ adjacent to at least two $P'$-vertices. This contradicts Claim 10 since $P'=P$. Now we are going to show that (C5) holds for $(G';P',L')$.

Let $Y_1$ and $Y_2$ denote the set of $L_2'$-vertices in $N^*(v_2)$ and in $\{v_5, \ldots , v_{m}\}$, respectively. Let $Y_3=\{v_1, v_3\}$. So $Y_1\cup Y_2\cup Y_3$ forms the set of $L'_2$-vertices in $V(G')$. The definition of $G'$ implies that $E(G'[Y_1])=\emptyset$. Since each vertex in $Y_2\cup Y_3$ is also an $L_2$-vertex in G and (C5) is valid for (G; P, L), we conclude that $E(G'[Y_2\cup Y_3])=\emptyset$. So, if (C5) is not true for $(G';P',L')$, then there must exist a vertex $u\in Y_1$ adjacent to some vertex $u'\in Y_2\cup Y_3$. By Claim 8, $u'\notin Y_2$ since $v_2$ is not the middle P-vertex. Thus, $u'\in Y_3$, that is, $u'=v_1$ or $u'=v_3$. If $u'=v_3$, then $u\in N^*(v_2)\cap N^*(v_3)$. This contradicts the assumption on the current subcase.

So now we assume that $uv_1\in E(G)$, see Fig. 1. Note that $c\in L(u)$. Without loss of generality, assume that $L(v_1)=\{a,b\}$, $L(v_2)=\{c, d_1, d_2\}$, and $L(u)=\{c, c_1, c_2\}$. By Claim 1, we may assume that $L(v_t)=\{a\}$. By Claim 11, $a\notin L(v_2)$, and thus $b\in L(v_2)$ by Claim 1. Since $c\notin L(v_1)$, we may assume that $b=d_1$. Since $b\ne c$, Claim 1 implies that $b\notin L(u)$. By the minimality of G, $G'-uv_1$ admits an L-coloring $\pi '$ and thus $G-uv_1$ is L-colorable by combining $\pi$ and $\pi '$. Therefore, G is L-colorable after replacing the edge $uv_1$ back since the color b is not in L(u), a contradiction.

Fig. 1

One possible case that $uv_1\in E(G')$ of Subcase I$_1$

Subcase I $_2$ There exists a vertex $w\in N^*(v_2)\cap N^*(v_3)$ such that $c\in L(w)$.

Let $X=\{v_2, v_3\}$. Set $\pi (v_2)=c$ and $\pi (v_3)=d\in L(v_3)\setminus L(v_4)$. Note that $d\ne c$. Moreover, we claim that $d\notin L(w)$. Otherwise, we assume that $L(v_3)=\{d, d_1\}$, $L(w)=\{c, d, f\}$ and $L(v_2)=\{c, c_1, c_2\}$. Observe that $L(v_2)\cap L(w)=\{c\}$ and thus $d\notin \{c_1, c_2\}$ by Claim 1. It follows that $d_1\in \{c_1, c_2\}$ by $c\ne d$. By Claim 11, $d_1\notin L(v_4)$, hence $L(v_3)\cap L(v_4)=\emptyset$, contradicting Claim 1.

Since $v_3\in L_2$, we have $N(v_3)=N^*(v_3)\cup \{v_2, v_4\}$. Note that only vertices in $N^*(v_2)\cup N^*(v_3)$ have changed their color lists, whereas other vertices in $V(G')\setminus (N^*(v_2)\cup N^*(v_3))$ have kept their color lists to $L'$ lists unchanged. The fact that $d\notin L(w)$ guarantees that $|L'(u)|\ge 2$ for each $u\in N^*(v_2)\cup N^*(v_3)$. So (C1)–(C4) hold for $(G';P',L')$. By Claim 10, it is easy to check that (C6) holds for $(G';P',L')$. Now we are about to verify (C5) for $(G';P',L')$.

Denote by $Y_1$, $Y_2$, and $Y_3$ the sets of $L_2'$-vertices in $N^*(v_2)$, $N^*(v_3)$, and $\{v_5, \ldots , v_{m}\}$, respectively. Let $Y_4=\{v_1\}$. Then $Y_1\cup Y_2\cup Y_3\cup Y_4$ forms the set of $L'_2$-vertices in $V(G')$. By the definition of $G'$ and that $G'$ is in $\mathcal {G}$, $E(G'[Y_1\cup Y_2])=\emptyset$. Since each vertex in $Y_3\cup Y_4$ is also an $L_2$-vertex in G and (C5) is true for (G; P, L), we deduce that $E(G'[Y_3\cup Y_4])=\emptyset$. Moreover, $E(G'[Y_2\cup Y_4])=\emptyset$ by the absence of adjacent triangles, and $E(G'[Y_3\cup Y_i])=\emptyset$ for $i\in \{1,2\}$ since there does not exist $u\in Y_3$ adjacent to $u'\in Y_1\cup Y_2$ by Claim 8. So if (C5) fails for $(G';P',L')$, then $E(G'[Y_1\cup Y_4])\ne \emptyset$. Similarly, we may let $L(v_1)=\{a\}$, $L(v_1)=\{a,b\}$, $L(v_2)=\{c, d_1, d_2\}$, and $L(u)=\{c, c_1, c_2\}$. By a similar discussion as the previous Case I$_1$, we deduce that $b\notin L(u)$ and thus we may obtain an L-coloring of G after replacing the edge $uv_1$ back, a contradiction.

Case II $v_2v_4\in E(G)$.

In this case, $N(v_2)=N^*(v_2)\cup \{v_1, v_3, v_4\}$. Note that $v_2v_4$ is a bad chord of F. By Claim 7, $v_4\in L_{3}$, and hence $v_5\in L_2$ and $v_5\ne v_t$. It is easy to see that $N(v_4)=N^*(v_4)\cup \{v_2, v_3, v_5\}$ or $N(v_4)=N^*(v_4)\cup \{v_2, v_3, v_5,v_6\}$, as shown in Fig. 2.

Fig. 2

Two possible cases in Subcase II$_1$

Subcase II $_1$ There is a vertex $y\in N^*(v_5)\cup \{v_6\}$ such that $yv_4\in E(G)$.

Since G contains no adjacent triangles, the existence of y is unique. Let $X=\{v_2, v_3, v_4\}$. Set $\pi (v_4)=a\in L(v_4)\setminus (L(y)\cup L(v_5))$ and $\pi (v_2)=b\in L(v_2)\setminus (L(v_1)\cup \{a\})$. If $L(v_3)\ne \{a,b\}$, we set $\pi (v_3)=c\in L(v_3)\setminus \{a,b\}$. Otherwise, $L(v_3)=\{a,b\}$ and thus $a\notin L(v_2)$. We color $v_3$ with b and recolor $v_2$ with a color $b'\in L(v_2)\setminus (L(v_1)\cup \{b\})$. Thus, $v_2,v_3,v_4$ can always be precolored with different colors.

It is easy to see that $y\in L_{3}$ by Claim 7 and (C1), and $yv_2,yv_3\notin E(G)$ by $G\in \mathcal{{G}}$. Further, since $a\notin L(y)$, we have $y\in L_{3}'$. Since $N(v_2)=N^*(v_2)\cup \{v_1, v_3, v_4\}$, there is no other chord starting from $v_2$ except $v_2v_4$. Hence, (C1)–(C4) all hold for $(G';P',L')$. By Claim 10, one may easily verify that (C6) is true for $(G';P',L')$. It suffices to check that (C5) holds for $(G';P',L')$.

Let $Y_1,Y_2,$ and $Y_3$ denote the set of $L_2'$-vertices in $N^*(v_2)$, $N^*(v_4)$, and $\{v_7, \ldots , v_{m}\}$, respectively. Let $Y_4=\{v_1,v_5\}.$ Similar to the discussion for Subcase I$_2$, we know that $E(G'[Y_1\cup Y_2])=\emptyset$ and $E(G'[Y_3\cup Y_4])=\emptyset$. If $E(G'[Y_2\cup Y_4])\ne \emptyset$, in other words, there exists $t\in Y_2$ such that $tv_1\in E(G)$ or $tv_5\in E(G)$, then since $t\ne y$, we can find a 3-cycle adjacent to a 4-cycle, a contradiction. Thus, $E(G'[Y_2\cup Y_4])=\emptyset$. Moreover, by Claim 8, we confirm that there does not exist a vertex $u\in Y_3$ adjacent to some vertex $u'\in Y_1\cup Y_2$, and thus $E(G'[Y_3\cup Y_i])=\emptyset$ for $i\in \{1,2\}$. So if (C5) fails for $(G';P',L')$, then $E(G'[Y_1\cup Y_4])\ne \emptyset$. It implies that there exists $u\in Y_1$ such that $uv_1\in E(G)$ or $uv_5\in E(G)$. Obviously, it must be the case that $uv_1\in E(G)$ since $G\in \mathcal {G}$. The following discussion is the same as previous Case I$_1$.

Subcase II $_2$ No vertex $y\in N^*(v_5)\cup \{v_6\}$ is adjacent to $v_4$.

It follows that $N(v_4)=N^*(v_4)\cup \{v_2, v_3, v_5\}$. Let $X=\{v_2, v_3, v_4\}$. Define $\pi (v_4)=a\in L(v_4)\setminus L(v_5)$, $\pi (v_2)=b\in L(v_2)\setminus (L(v_1)\cup \{a\})$, and $\pi (v_3)=c\in L(v_3)\setminus \{b\}$ such that $c\ne a$. Reasoning as for Subcase II$_1$, one can verify that a, b, c exist. It remains us to check that all (C1)–(C6) hold for $(G';P',L')$. Though its proof is very similar to that of above Case II$_1$, we like to write, for completeness, its details.

Clearly, (C1)–(C4) all hold for $(G';P',L')$. Again, by Claim 10, we see that (C6) is valid for $(G';P',L')$. We only need to check that (C5) holds for $(G';P',L')$.

Let $Y_1, Y_2,$ and $Y_3$ denote the set of $L_2'$-vertices in $N^*(v_2)$, $N^*(v_4)$, and $\{v_7, \ldots , v_{m}\}$, respectively. Let $Y_4=\{v_1,v_5\}.$ Similarly, we know that $E(G'[Y_1\cup Y_2])=\emptyset$ and $E(G'[Y_3\cup Y_4])=\emptyset$. If $E(G'[Y_2\cup Y_4])\ne \emptyset$, then there exists $t\in Y_2$ such that $tv_1\in E(G)$ or $tv_5\in E(G)$. By the assumption on the current subcase, $tv_5\notin E(G)$ and so $tv_1\in E(G)$. However, we can find a 3-cycle $v_2v_3v_4v_2$ adjacent to a 4-cycle $v_1v_2v_4tv_1$, a contradiction. Thus, $E(G'[Y_2\cup Y_4])=\emptyset$. Moreover, by Claim 8, we confirm that there does not exist a vertex $u\in Y_3$ adjacent to some vertex $u'\in Y_1\cup Y_2$, and thus $E(G'[Y_3\cup Y_i])=\emptyset$ for $i\in \{1,2\}$. So if (C5) fails for $(G';P',L')$, then $E(G'[Y_1\cup Y_4])\ne \emptyset$. It follows that there is $u\in Y_1$ such that $uv_1\in E(G)$ or $uv_5\in E(G)$. If $uv_5\in E(G)$, then a 3-cycle $v_2v_3v_4v_2$ is adjacent to a 4-cycle $v_2v_4v_5uv_2$, a contradiction. So $uv_1\in E(G)$. By applying a similar argument as Case I$_1$, we may obtain an L-coloring of G. $\square$

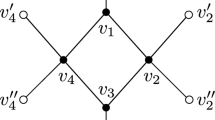
In Fig. 3, let thick edges denote the selected subpath P. Clearly, all conditions (C1)–(C6) are satisfied for each of these three configurations with respect to the given $(*, 1)$-list assignment L. However, none of them are L-colorable. These examples show that Theorem 2 is best possible in the sense that none of the forbidden configurations (A1), (A2), and (A3), stated in Sect. 2, can be allowed.

Fig. 3

Three structures with given $(*,1)$-list assignment