Correctors for the Nonlinear Wave Equations in Perforated Domains

Abstract

In this paper, we are concerned with a nonlinear hyperbolic problem in periodically perforated domains with a homogeneous Neumann condition on the holes. By the periodic unfolding method, we derive the corrector results for the homogenization of this problem.

1 Introduction

In this paper, we study the correctors for the homogenization of a nonlinear wave equation in a perforated domain $\varOmega _\varepsilon ^*=\varOmega {\backslash } S_\varepsilon$, where $\varOmega \subset {\mathbb {R}}^n$ is an open and bounded set with Lipschitz continuous boundary and $S_\varepsilon$ is a set of $\varepsilon$-periodic holes of size $\varepsilon$.

Let A be a periodic, symmetric, bounded and elliptic matrix. The problem under consideration is

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_{\varepsilon }''-\text {div}(A^{\varepsilon }\nabla u_{\varepsilon })+g(u_{\varepsilon }')=f_{\varepsilon }\ \ \ \ \ &{}\text {in}\ \varOmega _{\varepsilon }^*\times (0,T),\\ \displaystyle u_{\varepsilon }=0 &{}\text {on}\ \partial \varOmega \times (0,T),\\ \displaystyle A^{\varepsilon }\nabla u_{\varepsilon }\cdot n_{\varepsilon }=0 &{}\text {on}\ \partial S_{\varepsilon }\times (0,T),\\ \displaystyle u_{\varepsilon }(x,0)=u_{\varepsilon }^0,\ u'_{\varepsilon }(x,0)=u^1_{\varepsilon } &{} \text {in}\ \varOmega _{\varepsilon }^*, \end{array}\right. } \end{aligned}$$

(1.1)

where $A^\varepsilon (x):=A(\frac{x}{\varepsilon })$ and $n_\varepsilon$ is the outward unit normal vector field defined on $\partial S_\varepsilon$. The function g is nonlinear and satisfies some suitable growth assumptions [see (3.4)]. The data $\{u_{\varepsilon }^0, u^1_{\varepsilon },f_\varepsilon \}$ are given in $V^\varepsilon \times V^\varepsilon \times H^1(0,T;L^2(\varOmega _\varepsilon ^*))$.

The study of this problem can at least date back to the work of Lions [22], in which Lions studied the optimal control for nonlinear hyperbolic systems. It is also closely related to nonlinear relativistic damped problems. In [3], Cavalcanti, Domingos Cavalcanti, Andrade and Ma studied a similar problem with a Dirichlet condition on the boundary of the holes (the size of the holes is smaller than the period). For other nonlinear problems, just to name a few, we here mention the work in [4, 24–26] and the references therein.

For problem (1.1), Gaveau [19] proved the existence and uniqueness of the solution, as well as the homogenization result. In this paper, we consider the correctors for this homogenization. The proofs mainly rely on the periodic unfolding method, which was originally introduced in Cioranescu et al. [6] (see also [7]) and extended to perforated domains in Cioranescu et al. [12] (see Cioranescu et al. [8] for more general situations and a comprehensive presentation). Next we state our main results, in which we will use some notations to be defined in the next section.

The first part of the paper is devoted to the homogenization of problem (1.1) in terms of the unfolding operators. This form contains more information than that of Gaveau [19] (see Remark 3.3). Moreover, it can be used to obtain the corrector results for problem (1.1).

In fact, under suitable assumptions on the initial data [see (3.2)–(3.4) and (3.8)], there exist $u\in L^{\infty }(0,T;H_0^1(\varOmega ))$ with $u'\in L^{\infty }(0,T;H_0^1(\varOmega ))$ and $u''\in L^{\infty }(0,T;L^2(\varOmega )) ,\,\widehat{u}\in L^{\infty }(0,T;L^2(\varOmega ,$ $H_\mathrm{per}^1(Y^*)))$ with ${\mathcal {M}}_{Y^*}(\widehat{u})=0$, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {T}}_{\varepsilon }^*(u_{\varepsilon })\rightarrow u\ \ \ \mathrm{strongly \ in} \ L^q\left( 0,T;L^2(\varOmega ,H^1(Y^*))\right) ,\\ {\mathcal {T}}_{\varepsilon }^*(\nabla u_{\varepsilon })\rightharpoonup \nabla u+\nabla _y\widehat{u}\ \ \ \mathrm{weakly}^*\ in\ L^\infty (0,T;L^2(\varOmega \times Y^*)),\\ {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\rightarrow u'\ \ \ \mathrm{strongly \ in} \ L^q\left( 0,T;L^2(\varOmega ,H^1(Y^*))\right) ,\\ \Vert u'_\varepsilon -u'\Vert _{L^q\left( 0,T; L^2(\varOmega ^*_\varepsilon )\right) }\rightarrow 0, \end{array}\right. } \end{aligned}$$

where q is any number in $(1,+\infty )$ and ${\mathcal {T}}_{\varepsilon }^*$ is the unfolding operator. Moreover,

$$\begin{aligned} {\left\{ \begin{array}{ll} \widetilde{u}_{\varepsilon }\rightharpoonup \theta u \ \ \ \mathrm{weakly}^*\ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega )),\\ A^{\varepsilon }\widetilde{\nabla u_{\varepsilon }}\rightharpoonup \theta A^0\nabla u \ \ \ \mathrm{weakly}^*\ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega )),\\ \widetilde{g(u'_{\varepsilon })}\rightharpoonup \theta g(u')\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega )). \end{array}\right. } \end{aligned}$$

We also get the following homogenized wave equation

$$\begin{aligned} {\left\{ \begin{array}{ll} u''-\mathrm{{div}}(A^{0}\nabla u)+g(u')=f\ \ \ \ \ &{}\text {in}\ \varOmega \times (0,T),\\ u=0 &{}\text {on}\ \partial \varOmega \times (0,T),\\ u(x,0)=u^0,\ u'(x,0)=u^1 &{} \text {in}\ \varOmega , \end{array}\right. } \end{aligned}$$

(1.2)

where the homogenized matrix $A^0$ is the classical constant positive-definite one in Cioranescu and Saint Jean Paulin [13] (see also [9]).

The second part of the paper deals with the corrector results of problem (1.1), which is completely new. To investigate the corrector results, some additional assumptions are needed, as already evidenced in classical works (see for instance [1, 11]).

Indeed, under the assumptions (4.1)–(4.3), we get the following corrector results:

$$\begin{aligned}&\Vert u'_\varepsilon -u'\Vert _{\mathcal {C}^0(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0, \ \ \ \\&\Vert \nabla u_\varepsilon -C^\varepsilon \nabla u\Vert _{\mathcal {C}^0(0,T; L^1(\varOmega ^*_\varepsilon ))}\rightarrow 0, \end{aligned}$$

where the corrector matrix $C^\varepsilon =(C^\varepsilon _{ij})_{1\le i,j\le n}$ is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} C^\varepsilon _{ij}(x)=C_{ij}\big (\frac{x}{\varepsilon }\big )\ \ &{}\text {a.e. on} \ \varOmega ^*_\varepsilon ,\\ C_{ij}(y)=\delta _{ij}(y)+\frac{\partial \chi _j}{\partial y_i}(y) \ \ &{}\text {a.e. on} \ Y^*. \end{array}\right. } \end{aligned}$$

Observe that $C^\varepsilon$ is exactly the corrector matrix of the linear problem studied in [16, 23].

For the homogenization and corrector results in the linear case, we refer to [10] for a fixed domain and [16] (see also [9, 23]) for a perforated domain. We also refer to Cioranescu et al. [11] for a perforated domain with $\varepsilon$-periodic holes of size $r_\varepsilon \ll \varepsilon$. For the semilinear case, Brahim-Otsman et al. [1] gave the homogenization and corrector results for a fixed domain. Our study is also related to that for the parabolic case in [14, 15, 17, 18, 20, 27].

This paper is organized as follows. In Sect. 2, we briefly recall the unfolding method in perforated domains. Section 3 is devoted to the homogenization result. In Sect. 4, we give some additional assumptions on the initial data and prove the corrector results.

2 Preliminaries

2.1 Some Notations

Let $b=(b_1,\ldots ,b_n)$ be a basis in ${\mathbb {R}}^n$. Set

$$\begin{aligned} {\mathcal {G}}=&\left\{ \xi \in {\mathbb {R}}^n{:}\ \xi =\sum \limits _{i=1}^{n}k_ib_i,\ (k_1,\ldots ,k_n)\in {\mathbb {Z}}^n\right\} ,\\ Y=&\left\{ \xi \in {\mathbb {R}}^n{:}\ \xi =\sum \limits _{i=1}^{n}y_ib_i,\ (y_1,\cdots ,y_n)\in (0,1)^n\right\} . \end{aligned}$$

Suppose that $\varOmega \subset {\mathbb {R}}^n$ is an open and bounded set with Lipschitz continuous boundary $\partial \varOmega$, and S is a closed proper subset of $\overline{Y}$ with Lipschitz continuous boundary. Denote $\varepsilon$ by the general term of a sequence of positive real numbers which converge to zero. Set

$$\begin{aligned} \tau _{\varepsilon }(\varepsilon S)=\bigcup _{\xi \in {\mathcal {G}}}\varepsilon (\xi +S). \end{aligned}$$

Throughout the paper, we make the following assumption:

$$\begin{aligned} \tau _{\varepsilon }(\varepsilon S)\cap \partial \varOmega =\emptyset . \end{aligned}$$

(2.1)

Define the perforated domain

$$\begin{aligned} \varOmega _{\varepsilon }^*=\varOmega {\setminus } \tau _{\varepsilon }(\varepsilon S). \end{aligned}$$

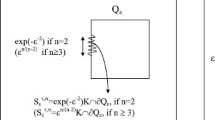
Assumption (2.1) implies that $\partial \varOmega _{\varepsilon }^*=\partial \varOmega \cup \partial S_{\varepsilon },$ where $S_{\varepsilon }$ is the subset of $\tau _{\varepsilon }(\varepsilon S)$ contained in $\varOmega$. See Fig. 1 for the perforated domain.

Fig. 1

The perforated domain

Next, we recall some notations related to the unfolding method introduced in [7, 8], which are displayed in Fig. 2.

Fig. 2

The sets $\widehat{\varOmega }_{\varepsilon }^{*}, \ {\varOmega }_{\varepsilon }^{*},\ \widehat{\varLambda }^*_\varepsilon \ \text {and}\ {\varLambda }^*_\varepsilon$

Set

$$\begin{aligned} \widehat{\varOmega }_{\varepsilon }=\text {interior}\left\{ \bigcup _{\xi \in \varXi _\varepsilon }\varepsilon (\xi +\overline{Y})\right\} \ \text {and} \ \varLambda _\varepsilon =\varOmega {\setminus } {\widehat{\varOmega }_\varepsilon }, \end{aligned}$$

where $\varXi _\varepsilon =\{\xi \in {\mathcal {G}}\mid \varepsilon (\xi +Y)\subset \varOmega \}.$ Let

$$\begin{aligned} \widehat{\varOmega }_{\varepsilon }^{*}=\widehat{\varOmega }_{\varepsilon }{{\setminus }} S_{\varepsilon } \ \ \text {and} \ \ {\varLambda }^*_\varepsilon =\varOmega _{\varepsilon }^{*}{{\setminus }} {\widehat{\varOmega }^*_\varepsilon }. \end{aligned}$$

Define $V^\varepsilon$ by

$$\begin{aligned} V^\varepsilon :=\left\{ v\in H^1(\varOmega ^*_{\varepsilon })\mid v=0 \ \text {on} \ \partial \varOmega \right\} , \end{aligned}$$

endowed with the norm

$$\begin{aligned} \Vert v\Vert _{V^\varepsilon }=\Vert \nabla v\Vert _{L^2(\varOmega ^*_{\varepsilon })}. \end{aligned}$$

Remark 2.1

[5]

• (i) Let $\{v_\varepsilon \}$ be a sequence in $V^\varepsilon$. For $v\in H_0^1(\varOmega )$, the following two assertions are equivalent:

  • (a) $\Vert v_{\varepsilon }\Vert _{V^\varepsilon }\le C \ \text {and} \ \widetilde{v_\varepsilon } \rightharpoonup \theta v\ \text {weakly in} \ L^2(\varOmega ),$

  • (b) $Q_\varepsilon v_{\varepsilon } \rightharpoonup v\ \text {weakly in} \ H_0^1(\varOmega ).$ Here $Q_\varepsilon$ is the linear extension operator introduced in [13].

• (ii) As stated in [Remark 2.2, 5], we have the following Poincar$\acute{e}$-Sobolev inequality with a constant independent of $\varepsilon$. Namely, for any $v\in V_\varepsilon$,

  $$\begin{aligned} \Vert v\Vert _{L^k(\varOmega ^*_{\varepsilon })}\le C\Vert \nabla v\Vert _{L^2(\varOmega ^*_{\varepsilon })}, \end{aligned}$$

  for every $k\in [2,+\infty )$, if $n=2$ and for every $k\in [2,2^*]$ (where $2^*=\frac{2n}{n-2}$), if $n>2$.

For $\alpha ,\beta \in {\mathbb {R}}$ with $0<\alpha <\beta$, we denote $M(\alpha ,\beta ,\mathcal {O})$ the set of the $n\times n$ matrix fields $A=(a_{ij})_{n\times n}\in (L^\infty (\mathcal {O}))^{n^2}$ such that

$$\begin{aligned} (A(x)\lambda ,\lambda )\ge \alpha |\lambda |^2, \quad |A(x)\lambda |\le \beta |\lambda | \end{aligned}$$

for any $\lambda \in {\mathbb {R}}^n$ and a.e. on $\mathcal {O}$.

In what follows, we will use the following notations:

• $Y^*=Y{\setminus } \bar{S}$;

• |D| denotes the Lebesgue measure of a measurable set D in ${\mathbb {R}}^n$;

• $\theta =\frac{|Y^*|}{|Y|}$;

• ${\mathcal {M}}_{{\mathcal {O}}}(v)=\frac{1}{|{\mathcal {O}}|}\int _{{\mathcal {O}}}v\mathrm{d}x;$

• $\widetilde{g}$ is the zero extension to $\varOmega$ of any function g defined on a subset of $\varOmega$;

• $\varOmega _T=\varOmega \times (0,T)$.

• C denotes a generic constant which does not depend upon $\varepsilon$.

• $\delta _{ij}$ denotes the usual Kronecker symbol.

• The notation $L^p(\mathcal {O})$ will be used both for scalar and vector-valued functions defined on the set $\mathcal {O}$, since no ambiguity will arise.

2.2 A Brief Review of the Unfolding Method

In this subsection, we briefly recall the definition and properties of the unfolding operators in perforated domains. We refer the reader to [8, 16] for further properties and related comments.

For any $x\in {\mathbb {R}}^n$, we use $[x]_Y$ to denote the unique integer combination $\sum _{j=1}^{n}k_jb_j$ of the period such that $x-[x]_Y\in Y$. Set $\{x\}_Y=x-[x]_Y\in Y$. Then, we have

$$\begin{aligned} x=\varepsilon \Big (\Big [\frac{x}{\varepsilon }\Big ]_Y+\Big \{\frac{x}{\varepsilon }\Big \}_Y\Big ) \ \ \text {for} \ \ x\in {\mathbb {R}}^n. \end{aligned}$$

Definition 2.2

For $p\in [1,+\infty )$ and $q\in [1, \infty ]$, let $\phi$ be in $L^q(0,T;L^p({\varOmega }^*_{\varepsilon }))$. The unfolding operator ${\mathcal {T}}_\varepsilon ^*: L^q(0,T;L^p({\varOmega }^*_{\varepsilon })) \mapsto L^q(0,T;L^p({\varOmega }\times Y^*))$ is defined as follows:

$$\begin{aligned} {\mathcal {T}}_\varepsilon ^*(\phi )(x,y,t)={\left\{ \begin{array}{ll}\displaystyle \phi \Big (\varepsilon \Big [\frac{x}{\varepsilon }\Big ]_Y+\varepsilon y,t\Big )\ \ \ \ &{}\text {a.e. for}\ (x,y,t)\in \widehat{\varOmega }_\varepsilon \times Y^*\times (0,T),\\ \displaystyle 0 &{} \text {a.e. for}\ (x,y,t)\in {\varLambda }_\varepsilon \times Y^*\times (0,T). \end{array}\right. } \end{aligned}$$

Proposition 2.3

Let $p\in [1,+\infty )$ and $q\in [1, \infty ]$.

• (i) ${\mathcal {T}}^*_\varepsilon$ is linear and continuous from $L^q(0,T;L^p(\varOmega ^*_\varepsilon ))$ to $L^q(0,T;L^p(\varOmega \times Y^*))$.

• (ii) Let $w\in L^q(0,T;L^p(\varOmega ^*_\varepsilon ))$. For a.e. $t\in (0,T)$, we have

  $$\begin{aligned}\Vert {\mathcal {T}}^*_{\varepsilon }(w)\Vert _{L^p(\varOmega \times Y^*)}=|Y|^{1/p}\Vert w\Vert _{L^p(\widehat{\varOmega }^*_\varepsilon )}\le |Y|^{1/p}\Vert w\Vert _{L^p({\varOmega }^*_\varepsilon )}. \end{aligned}$$

• (iii) For $w,v\in L^q(0,T;L^p(\varOmega ^*_\varepsilon )),\,{\mathcal {T}}_\varepsilon ^*(vw)={\mathcal {T}}_\varepsilon ^*(v){\mathcal {T}}_\varepsilon ^*(w)$.

• (iv) For $q\in [1,+\infty ]$, let $\phi _\varepsilon$ be in $L^q(0,T;L^1(\varOmega ^*_{\varepsilon }))$ and satisfy

  $$\begin{aligned} \int _{0}^{T}\int _{\varLambda ^*_{\varepsilon }}|\phi _\varepsilon | \,\mathrm{d}x\,\mathrm{d}t\rightarrow 0, \end{aligned}$$

  then

  $$\begin{aligned} \int _0^T\int _{\varOmega ^*_\varepsilon }\phi _{\varepsilon }\,\mathrm{d}x\,\mathrm{d}t-\frac{1}{|Y|}\int _0^T\int _{\varOmega \times Y^*}{\mathcal {T}}^*_{\varepsilon }(\phi _{\varepsilon })\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}t \rightarrow 0. \end{aligned}$$

• (v) For $p,q\in [1,\infty )$, let $\{\omega _\varepsilon \}$ be a sequence in $L^q(0,T;L^p(\varOmega ))$ such that

  $$\begin{aligned} \omega _\varepsilon \rightarrow \omega \ \text {strongly in}\ L^q(0,T;L^p(\varOmega )). \end{aligned}$$

  Then

  $$\begin{aligned} {\mathcal {T}}^*_\varepsilon (\omega _\varepsilon )\rightarrow \omega \ \text { strongly in}\ L^q(0,T;L^p(\varOmega \times Y^*)). \end{aligned}$$

• (vi) For $p\in (1,\infty )$ and $q\in (1,\infty ]$, let $\{\omega _\varepsilon \}$ be a sequence in $L^q(0,T;L^p(\varOmega ^*_\varepsilon ))$ such that

  $$\begin{aligned} \Vert \omega _\varepsilon \Vert _{L^q(0,T;L^p(\varOmega ^*_\varepsilon ))}\le C. \end{aligned}$$

  If

  $$\begin{aligned} {\mathcal {T}}^*_\varepsilon (\omega _\varepsilon )\rightharpoonup \widehat{\omega } \ \text {weakly in}\ L^q\left( 0,T;L^p(\varOmega \times Y^*)\right) , \end{aligned}$$

  then we have

  $$\begin{aligned} \widetilde{\omega }_\varepsilon \rightharpoonup \theta {\mathcal {M}}_{Y^*}(\widehat{\omega })\ \text {weakly in}\ L^q(0,T;L^p(\varOmega )). \end{aligned}$$

  For $q=\infty$, the weak convergences above are replaced by the weak$^*$ convergences, respectively.

• (vii) Let $p,q\in [1,+\infty )$. If $\omega _\varepsilon \in L^q(0,T;L^p(\varOmega ^*_\varepsilon ))$ and $\omega \in L^q(0,T;L^p(\varOmega ))$, then the following two assertions are equivalent:

  • (a) ${\mathcal {T}}^*_{\varepsilon }(\omega _\varepsilon )\rightarrow \omega$ strongly in $L^q(0,T;L^p(\varOmega \times Y^*))$ and $\Vert \omega _{\varepsilon }\Vert _{L^q(0,T;L^p(\varLambda ^*_\varepsilon ))}\rightarrow 0$

  • (b) $\Vert \omega _{\varepsilon }-\omega \Vert _{L^q(0,T;L^p({\varOmega }^*_{\varepsilon }))}\rightarrow 0.$

Finally, we state an important convergence theorem which is crucial to achieving our homogenization result. We refer the interested reader to [16] for the detailed proof.

Theorem 2.4

Let $\{w_\varepsilon \}$ be a sequence in $L^\infty (0,T; V^\varepsilon )$ such that

$$\begin{aligned} \Vert \nabla w_\varepsilon \Vert _{L^\infty (0,T;L^2(\varOmega ^*_{\varepsilon }))}\le C \ \ \text {and} \ \ \Big \Vert \frac{\partial w_\varepsilon }{\partial t}\Big \Vert _{ L^\infty \left( 0,T;L^2(\varOmega ^*_{\varepsilon })\right) }\le C. \end{aligned}$$

Then, there exist $w\in L^\infty (0,T;H_0^1(\varOmega ))$ with $\frac{\partial w}{\partial t}\in L^\infty (0,T;L^2(\varOmega ))$ and $\widehat{w}\in L^\infty (0,T;L^2(\varOmega ;H_\mathrm{per}^{1}(Y^*)))$ with $M_{Y^*}(\widehat{w})\equiv 0$, such that, up to a subsequence,

$$\begin{aligned}&\mathrm{(i)}\ \ {\mathcal {T}}_\varepsilon ^*(w_\varepsilon )\rightharpoonup w \ \ \text {weakly}^* \ \text {in}\ L^\infty (0,T; L^2(\varOmega ;H^1(Y^*))),\nonumber \\&\mathrm{(ii)}\ \ {\mathcal {T}}_\varepsilon ^*(\nabla w_\varepsilon )\rightharpoonup \nabla w +\nabla _y \widehat{w}\ \ \text {weakly}^* \ \text {in}\ L^\infty (0,T;L^2(\varOmega \times Y^*)),\nonumber \\&\mathrm{(iii)}\ \ {\mathcal {T}}_\varepsilon ^*\Big (\frac{\partial w_\varepsilon }{\partial t}\Big )\rightharpoonup \frac{\partial w}{\partial t}\ \ \text {weakly}^* \ \text {in}\ L^\infty (0,T;L^2(\varOmega \times Y^*)),\nonumber \\&\mathrm{(iv)}\ \ {\mathcal {T}}_\varepsilon ^*(w_\varepsilon )\rightarrow w \ \ \text {strongly in}\ L^q(0,T; L^2(\varOmega ; H^1(Y^*))),\nonumber \\&\mathrm{(v)}\ \ \Vert w_\varepsilon -w\Vert _{L^q(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0, \end{aligned}$$

(2.2)

where q is any number in $(1,+\infty )$.

3 Homogenization Result

In this section, we study the asymptotic behavior, as $\varepsilon \rightarrow 0$, of the problem (1.1). The study was done in [19] by the Tartar’s oscillating test functions method. Here we use the unfolding method to study the homogenization, which will be used for getting the corrector results. We first state the precise assumptions on the problem (1.1).

• For any $\varepsilon$, let $A^\varepsilon$ be a matrix such that

  $$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle A^\varepsilon (x)=A(x/\varepsilon )\ \text {a.e. on} \ \varOmega ,\\ \displaystyle A\in M(\alpha ,\beta ,Y),\\ \displaystyle A \ \ \text {is symmetric and} \ Y\text {-periodic}. \end{array}\right. } \end{aligned}$$

  (3.1)

• We suppose that

  $$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle u^0_{\varepsilon }\in V^\varepsilon ,\\ \displaystyle u^1_\varepsilon \in V^\varepsilon ,\\ \displaystyle f_\varepsilon \in H^1(0,T;L^2(\varOmega _{\varepsilon }^*)), \end{array}\right. } \end{aligned}$$

  (3.2)

  where $H^1(0,T;L^2(\varOmega _{\varepsilon }^*))=\left\{ v_{\varepsilon }\mid v_{\varepsilon }\in L^2\big (0,T;L^2(\varOmega _{\varepsilon }^*),\ v'_{\varepsilon }\in L^2\big (0,T;L^2\right. \left. (\varOmega _{\varepsilon }^*)\big )\right\}$.

• We also assume that $u^0_{\varepsilon }$ is solution of the problem

  $$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle -\text {div}(A^{\varepsilon }\nabla u^0_{\varepsilon })=h^0_{\varepsilon }\ \ \ \ \ &{}\text {in}\ \varOmega _{\varepsilon }^*,\\ \displaystyle u^0_{\varepsilon }=0 &{}\text {on}\ \partial \varOmega ,\\ \displaystyle A^{\varepsilon }\nabla u^0_{\varepsilon }\cdot n_{\varepsilon }=0 &{}\text {on}\ \partial S_{\varepsilon } \end{array}\right. } \end{aligned}$$

  (3.3)

  for some $h^0_{\varepsilon }\in L^2(\varOmega _{\varepsilon }^*)$.

• Let $g\in C^1({\mathbb {R}})$ be such that

  $$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{(i)} \ g \ \mathrm{is \ a \ non}\text {-}\mathrm{decreasing \ function \ satisfying} \ g(0)=0,\\ \mathrm{(ii)} \ \mathrm{there \ exist \ a \ constant} \ C_1 \ \mathrm{and \ an \ exponent} \ \rho \ \mathrm{with}\\ \qquad 1\le \rho<\infty , \ \mathrm{if} \ n=2 \ \mathrm{and} \ 1\le \rho <\frac{n}{n-2}, \ \mathrm{if} \ n>2,\\ \qquad \mathrm{such \ that} \ |g'(s)|\le C(1+|s|^{\rho -1}) \ \mathrm{for \ all} \ s\in {\mathbb {R}}. \end{array}\right. } \end{aligned}$$

  (3.4)

Note that this assumption implies that

$$\begin{aligned} |g(s)|\le C_2(1+|s|^\rho ) \ \ \text {for all} \ s\in {\mathbb {R}}, \end{aligned}$$

(3.5)

where $C_2$ is some positive constant.

Remark 3.1

For a measurable function v defined on $\varOmega _{\varepsilon }^*\times (0,T)$, we can get

$$\begin{aligned} {\mathcal {T}}_{\varepsilon }^*(g(v))(x,y,t)=g({\mathcal {T}}_{\varepsilon }^*(v))(x,y,t) \ \ \text {in} \ \varOmega \times Y^*\times (0,T), \end{aligned}$$

by Definition 2.2 and $g(0)=0$.

Set

$$\begin{aligned} {\mathcal {W}}_{\varepsilon }=\Big \{v_{\varepsilon }\mid v_{\varepsilon }\in L^2\big (0,T;V^\varepsilon \big ),\ v'_{\varepsilon }\in L^2\big (0,T;L^2(\varOmega _{\varepsilon }^*)\big )\Big \} \end{aligned}$$

with the norm defined by

$$\begin{aligned} \Vert v_{\varepsilon }\Vert _{{\mathcal {W}}_{\varepsilon }}=\Vert v_{\varepsilon }\Vert _{L^2(0,T;V^\varepsilon )} +\Vert v'_{\varepsilon }\Vert _{L^2(0,T;L^2(\varOmega _{\varepsilon }^*))}. \end{aligned}$$

The variational formulation of problem (1.1) is to find a $u_{\varepsilon }\in {\mathcal {W}}_{\varepsilon }$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \langle u_{\varepsilon }'',v\rangle _{(V^\varepsilon )',V^\varepsilon } +\int _{\varOmega _{\varepsilon }^*}A^{\varepsilon }\nabla u_{\varepsilon }\cdot \nabla v \,\mathrm{d}x +\int _{\varOmega _{\varepsilon }^*}g(u'_\varepsilon )v\,\mathrm{d}x=\int _{\varOmega _{\varepsilon }^*}f_{\varepsilon }v\,\mathrm{d}x\\ \displaystyle \text {in}\ \mathcal {D}'(0,T) \ \ \text {for all}\ v\in V^\varepsilon ,\\ \displaystyle u_{\varepsilon }(x,0)=u^0_{\varepsilon },\ u'_{\varepsilon }(x,0)=u^1_{\varepsilon } \ \ \ \ \text {in}\ \varOmega _{\varepsilon }^*. \end{array}\right. } \end{aligned}$$

(3.6)

For every fixed $\varepsilon$, Gaveau [19] proved that problem (1.1) has a unique solution $u_\varepsilon$ satisfying the following estimate:

$$\begin{aligned}&\Vert u_{\varepsilon }\Vert _{L^{\infty }(0,T;V_\varepsilon )} +\Vert u'_{\varepsilon }\Vert _{L^\infty (0,T;V_\varepsilon )}+\Vert u''_{\varepsilon }\Vert _{L^\infty (0,T;L^2(\varOmega ^*_\varepsilon ))}\nonumber \\&\quad \le C\left( 1+\Vert u^0_\varepsilon \Vert _{V^\varepsilon }+\Vert u^1_\varepsilon \Vert ^\rho _{V^\varepsilon }+\Vert h^0_\varepsilon \Vert _{L^2(\varOmega ^*_\varepsilon )} +\Vert f_\varepsilon (0)\Vert _{L^2(\varOmega ^*_\varepsilon )}\right. \nonumber \\&\qquad \left. +\,\Vert f_\varepsilon \Vert _{L^2(\varOmega ^*_\varepsilon \times (0,T))} +\Vert f'_\varepsilon \Vert _{L^2(\varOmega ^*_\varepsilon \times (0,T))}\right) , \end{aligned}$$

(3.7)

where the constant C does not depend on $\varepsilon$. Observe that the term $f_\varepsilon (0)$ is well defined due to the embedding

$$\begin{aligned} H^1(0,T;L^2(\varOmega _{\varepsilon }^*))\subset {\mathcal {C}}(0,T; L^2(\varOmega ^*_\varepsilon )). \end{aligned}$$

In order to study the homogenization, we further suppose that

$$\begin{aligned} {\left\{ \begin{array}{ll} (i) \ \widetilde{h^0_\varepsilon }\rightharpoonup h \ \text {weakly in }L^2(\varOmega ),\\ (ii) \ \Vert u_{\varepsilon }^0\Vert _{V^\varepsilon }\le C \ \text {and} \ \Vert u_{\varepsilon }^1\Vert _{V^\varepsilon }\le C,\\ (iii) \ \widetilde{u^0_\varepsilon } \rightharpoonup \theta u^0\ \text {weakly in }L^2(\varOmega ),\\ (iv) \ \widetilde{u^1_\varepsilon }\rightharpoonup \theta u^1\ \text {weakly in }L^2(\varOmega ),\\ (v) \ \widetilde{f_\varepsilon }\rightharpoonup \theta f\ \text {weakly in }\ L^2(0,T;L^2(\varOmega )),\\ (vi) \ \Vert f'_{\varepsilon }\Vert _{L^2(0,T;L^2(\varOmega ^*_\varepsilon ))}\le C, \end{array}\right. } \end{aligned}$$

(3.8)

where C is a constant independent of $\varepsilon$. Notice that these assumptions are equivalent to those in [19] due to Remark 2.1(i).

Theorem 3.2

Under the assumptions (3.1)–(3.4), let $u_{\varepsilon }$ be the solution of problem (1.1) with (3.8). Then, there exist $u\in L^{\infty }(0,T;H_0^1(\varOmega ))$ with $u'\in L^{\infty }(0,T;H_0^1(\varOmega ))$ and $u''\in L^{\infty }(0,T;L^2(\varOmega )) ,\,\widehat{u}\in L^{\infty }(0,T;L^2(\varOmega ,H_\mathrm{per}^1(Y^*)))$ with ${\mathcal {M}}_{Y^*}(\widehat{u})=0$, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} (i) \ {\mathcal {T}}_{\varepsilon }^*(u_{\varepsilon })\rightharpoonup u\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega ,H^1(Y^*))),\\ (ii) \ {\mathcal {T}}_{\varepsilon }^*(u_{\varepsilon })\rightarrow u\ \ \ \mathrm{strongly} \ \mathrm{in} \ L^q(0,T;L^2(\varOmega ,H^1(Y^*))),\\ (iii) \ {\mathcal {T}}_{\varepsilon }^*(\nabla u_{\varepsilon })\rightharpoonup \nabla u+\nabla _y\widehat{u}\ \ \ \mathrm{weakly}^*\ \mathrm{in}\ L^\infty (0,T;L^2(\varOmega \times Y^*)),\\ (iv) \ {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\rightharpoonup u'\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega ,H^1(Y^*))),\\ (v) \ {\mathcal {T}}_{\varepsilon }^*(u''_{\varepsilon })\rightharpoonup u''\ \ \ \mathrm{weakly}^*\ \mathrm{in}\ L^\infty (0,T;L^2(\varOmega \times Y^*)),\\ (vi) \ {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\rightarrow u'\ \ \ \mathrm{strongly \ in} \ L^q(0,T;L^2(\varOmega ,H^1(Y^*))),\\ (vii) \ \Vert u'_\varepsilon -u'\Vert _{L^q(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0, \end{array}\right. } \end{aligned}$$

(3.9)

where q is any number in $(1,+\infty )$. Moreover, we have the following convergences:

$$\begin{aligned}&(i) \ \widetilde{u}_{\varepsilon }\rightharpoonup \theta u \ \ \ \mathrm{weakly}^*\ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega )),\nonumber \\&(ii) \ A^{\varepsilon }\widetilde{\nabla u_{\varepsilon }}\rightharpoonup \theta A^0\nabla u \ \ \ \mathrm{weakly}^*\ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega )),\nonumber \\&(iii) \ \widetilde{g(u'_{\varepsilon })}\rightharpoonup \theta g(u')\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega )). \end{aligned}$$

(3.10)

The pair $(u,\widehat{u})$ with ${\mathcal {M}}_{Y^*}(\widehat{u})=0$ is the unique solution of the following problem:

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \theta \int _0^T\int _{\varOmega }u\varPsi \varphi '' \mathrm{d}x\,\mathrm{d}t+\frac{1}{|Y|}\int _0^T\int _{\varOmega \times Y^*}A(\nabla u+\nabla _y \widehat{u})(\nabla \varPsi +\nabla _y \varPhi )\varphi \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}t\\ \displaystyle + \ \theta \int _0^T\int _{\varOmega }g(u')\varPsi \varphi \,\mathrm{d}x\,\mathrm{d}t=\theta \int _0^T\int _{\varOmega }f\varPsi \varphi \,\mathrm{d}x\,\mathrm{d}t\\ \displaystyle \text {for any}\ \ \varPsi \in H_0^1(\varOmega ),\ \varPhi \in L^2(\varOmega ;H^1_\mathrm{per}(Y^*)) \ \text {and} \ \varphi \in {\mathcal {D}}(0,T),\\ \displaystyle u=0 \ \ \ \ \text {on} \ \ \varOmega \times (0,T),\\ \displaystyle u(x,0)=u^0,\ \ u'(x,0)=u^1 \ \ \text {in} \ \ \varOmega . \end{array}\right. } \end{aligned}$$

(3.11)

We also have

$$\begin{aligned} \widehat{u}=\sum \limits _{j=1}^{n}\frac{\partial u}{\partial x_j}{\chi }_j \end{aligned}$$

with $\chi _j\in H^1_\mathrm{per}(Y^*)$ ($j=1,\ldots ,n$) being the solution of the cell problem:

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle -\mathrm{div}_y\big (A\nabla _y(\chi _j+y_j)\big )=0 &{}\ \ \text {in } Y^*,\\ \displaystyle A\nabla _y(\chi _j+y_j)\cdot n_1=0 &{}\ \ \text {on}\ \partial S,\\ \displaystyle {\mathcal {M}}_{Y^*}(\chi _j)=0,\ \ \ &{}\ \, \chi _j \ \ Y\text {-periodic}. \end{array}\right. } \end{aligned}$$

(3.12)

Further, we get that u is the unique solution of the following homogenized wave equation

$$\begin{aligned} {\left\{ \begin{array}{ll} u''-\mathrm{{div}}(A^{0}\nabla u)+g(u')=f\ \ \ \ \ &{}\text {in}\ \varOmega \times (0,T),\\ u=0 &{}\text {on}\ \partial \varOmega \times (0,T),\\ u(x,0)=u^0,\ u'(x,0)=u^1 &{} \text {in}\ \varOmega , \end{array}\right. } \end{aligned}$$

(3.13)

where the homogenized matrix $A^0=(a_{ij}^0)_{1\le i,j\le n}$ is defined by

$$\begin{aligned} a^0_{ij}= {\mathcal {M}}_{Y^*}\Big (a_{ij}+\sum \limits _{k=1}^{n}a_{ik}\frac{\partial \chi _j}{\partial y_k}\Big ). \end{aligned}$$

(3.14)

Proof

By (3.8), we deduce from (3.7) that

$$\begin{aligned} \Vert u_{\varepsilon }\Vert _{L^{\infty }(0,T;V_\varepsilon )} +\Vert u'_{\varepsilon }\Vert _{L^\infty (0,T;V_\varepsilon )}+\Vert u''_{\varepsilon }\Vert _{L^\infty (0,T;L^2(\varOmega ^*_\varepsilon ))} \le C, \end{aligned}$$

(3.15)

where C is a constant independent of $\varepsilon$. From Theorem 2.4, there exist $u\in L^{\infty }(0,T;H_0^1(\varOmega ))$ with $u'\in L^{\infty }(0,T;L^2(\varOmega ))$ and $\widehat{u}\in L^{\infty }(0,T;L^2(\varOmega ,H_\mathrm{per}^1(Y^*)))$ with ${\mathcal {M}}_{Y^*}(\widehat{u})=0$, such that (3.9)(i)–(iii) hold, at least for a subsequence (still denoted by $\varepsilon$). Also, we have

$$\begin{aligned} {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\rightharpoonup u'\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty \left( 0,T;L^2(\varOmega \times Y^*)\right) . \end{aligned}$$

(3.16)

On the other hand, using again Theorem 2.4, we get that there exists $a\in L^{\infty }(0,T;H_0^1(\varOmega ))$ with $a'\in L^{\infty }(0,T;L^2(\varOmega ))$, such that, up to a subsequence (still denoted by $\varepsilon$),

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\rightharpoonup a\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty \left( 0,T;L^2(\varOmega ,H^1(Y^*))\right) ,\\ {\mathcal {T}}_{\varepsilon }^*(u''_{\varepsilon })\rightharpoonup a'\ \ \ \mathrm{weakly}^*\ \mathrm{in}\ L^\infty \left( 0,T;L^2(\varOmega \times Y^*)\right) ,\\ {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\rightarrow a\ \ \ \mathrm{strongly} \ \mathrm{in} \ L^q\left( 0,T;L^2(\varOmega ,H^1(Y^*))\right) ,\\ \Vert u'_\varepsilon -a\Vert _{L^q\left( 0,T; L^2(\varOmega ^*_\varepsilon )\right) }\rightarrow 0. \end{array}\right. } \end{aligned}$$

This, together with (3.16), implies $a=u'$. Hence, we obtain (iv)–(vii) of (3.9).

In the following, we consider the convergence of $g(u'_\varepsilon )$. Let

$$\begin{aligned} {\left\{ \begin{array}{ll} s=2^*,\ \ \ \ \ &{}\text {if} \ n>2,\\ s\in (2,+\infty ), &{}\text {if} \ n=2. \end{array}\right. } \end{aligned}$$

(3.17)

We first prove that ${\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })$ is bounded in $L^\infty (0,T;L^s(\varOmega \times Y^*))$. In fact, using Proposition 2.3(ii) and the Poincaré–Sobolev inequality in Remark 2.1, we derive

$$\begin{aligned} \Vert {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\Vert _{L^\infty (0,T;L^s(\varOmega \times Y^*))} \le C\Vert u'_{\varepsilon }\Vert _{L^\infty (0,T;L^s(\varOmega ^*_\varepsilon ))} \le C\Vert u'_{\varepsilon }\Vert _{L^\infty (0,T;V_\varepsilon )}. \end{aligned}$$

(3.18)

Combining this with (3.15), we get

$$\begin{aligned} \Vert {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\Vert _{L^\infty \left( 0,T;L^s(\varOmega \times Y^*)\right) } \le C. \end{aligned}$$

Together with (3.9)(ii), we obtain

$$\begin{aligned} {\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon })\rightarrow u'\ \ \ \mathrm{strongly \ in} \ L^r(\varOmega _T\times Y^*), \ \ \ \forall r\in [2,s), \end{aligned}$$

(3.19)

where we have used the interpolation theorem.

Let $r=\rho$ if $n=2$ and $\frac{2^*}{2}\le r<2^*$ if $n>2$. Then, we have $r\ge \rho$. As done in the proof of [2, Theorem 5.2], from (3.4) and the classical results in [21], we get

$$\begin{aligned} {\mathcal {T}}_{\varepsilon }^*(g(u'_{\varepsilon }))=g({\mathcal {T}}_{\varepsilon }^*(u'_{\varepsilon }))\rightarrow g(u')\ \ \ \mathrm{strongly \ in} \ L^{\frac{r}{\rho }}(\varOmega _T\times Y^*). \end{aligned}$$

(3.20)

On the other hand, from (3.5), we deduce

$$\begin{aligned} \int _{\varOmega ^*_\varepsilon }|g(u'_\varepsilon )|^2\mathrm{d}x\le C\left( |\varOmega |+\Vert u'_\varepsilon \Vert _{L^{2\rho }(\varOmega ^*_\varepsilon )}^{2\rho }\right) \le C\left( 1+\Vert u'_\varepsilon \Vert _{V^\varepsilon }^{2\rho }\right) . \end{aligned}$$

Moreover, from (3.7), it follows that

$$\begin{aligned} \Vert g(u'_\varepsilon )\Vert _{L^\infty (0,T;L^2(\varOmega ^*_\varepsilon ))}\le C. \end{aligned}$$

Combining this with (3.20), we obtain

$$\begin{aligned} {\mathcal {T}}_{\varepsilon }^*(g(u'_{\varepsilon }))\rightharpoonup g(u')\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty \left( 0,T;L^2(\varOmega \times Y^*)\right) . \end{aligned}$$

(3.21)

Thus, Proposition 2.3(vi) allows us to get

$$\begin{aligned} \widetilde{g(u'_{\varepsilon })}\rightharpoonup \theta g(u')\ \ \ \mathrm{weakly}^* \ \mathrm{in} \ L^\infty (0,T;L^2(\varOmega )). \end{aligned}$$

(3.22)

Arguing as done in the proof of [Theorem 3.1, 16], we can obtain the homogenized problem (3.10). Since the solution of (3.10) is unique, each convergence in this theorem holds for the whole sequence. $\square$

Remark 3.3

In addition to the homogenization result in Gaveau [19], we derived the unfolded formulation (3.11), as well as the convergence on $u'_\varepsilon$ [see (3.9)(vii)].

4 Corrector Results

This section is devoted to the correctors for the homogenization in Sect. 3. It is known (see for instance [1, 10]) that some additional assumptions on the initial data are necessary to obtain the corrector results. Motivated by the assumptions in [16], we make the following assumptions:

• For $u^1_\varepsilon \in V_\varepsilon$ and $f_\varepsilon \in L^2(0,T;L^2(\varOmega ^*_\varepsilon ))$, we suppose that

  $$\begin{aligned}&\mathrm{(i)} \ \Vert u_{\varepsilon }^1\Vert _{V^\varepsilon }\le C, \nonumber \\&\mathrm{(ii)} \ \Vert u^1_\varepsilon -u^1\Vert _{L^2(\varOmega ^*_\varepsilon )}\rightarrow 0,\nonumber \\&\mathrm{(iii)} \ \Vert f_\varepsilon -f\Vert _{L^2(0,T;L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0, \nonumber \\&\mathrm{(iv)} \ \Vert f'_{\varepsilon }\Vert _{L^2(0,T;L^2(\varOmega ^*_\varepsilon ))}\le C, \end{aligned}$$

  (4.1)

  where $u^1\in L^2(\varOmega )$ and $f\in L^2(0,T;L^2(\varOmega ))$.

Remark 4.1

As for the assumptions on $u^1_\varepsilon$ and $f_\varepsilon$, by Proposition 2.3(vii), we know (4.1) implies (3.8).

• For $g\in C^1({\mathbb {R}})$, suppose that it satisfies (3.4)(i) and

  $$\begin{aligned} |g'(s)|\le C_0, \ \ \forall s\in {\mathbb {R}}, \end{aligned}$$

  (4.2)

  where $C_0$ is a constant independent of s.

• For $u_\varepsilon ^0$, we assume that it is the solution of the problem (3.3) with

  $$\begin{aligned} \Vert h^0_\varepsilon -h\Vert _{L^2(\varOmega ^*_\varepsilon )}\rightarrow 0, \ \ h=-\mathrm{div}(A^0\nabla u^0)\in L^2(\varOmega ), \end{aligned}$$

  (4.3)

  for some $u^0\in H_0^1(\varOmega )$.

Remark 4.2

For any $h\in L^2(\varOmega )$, the classical arguments (see also [10]) provide that there exists $u^0\in H_0^1(\varOmega )$ such that $h=-\mathrm{div}(A^0\nabla u^0)$ due to the ellipticity of the matrix $A^0$.

Proposition 4.3

Let $A^\varepsilon$ be a coefficient matrix satisfying (3.1). Suppose that $u^0_{\varepsilon }$ is the solution of the problem (3.3) with (4.3). Then, we have

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle \mathrm{(i)} \;\; \Vert u^0_\varepsilon \Vert _{V^\varepsilon }\le C,\\ \displaystyle \mathrm{(ii)} \;\; \widetilde{u^0_\varepsilon } \rightharpoonup \theta u^0\ \text {weakly in }L^2(\varOmega ),\\ \displaystyle \mathrm{(iii)} \;\; \int _{\varOmega ^*_\varepsilon }A^\varepsilon \nabla u^0_\varepsilon \nabla u^0_\varepsilon \,\mathrm{d}x\rightarrow \theta \int _{\varOmega }A^0 \nabla u^0 \nabla u^0\,\mathrm{d}x, \end{array}\right. } \end{aligned}$$

(4.4)

where C is a constant independent of $\varepsilon$.

Proof

The variational formulation of problem (3.3) is to find a $u^0_{\varepsilon }\in V^{\varepsilon }$ such that

$$\begin{aligned} \int _{\varOmega ^*_\varepsilon }A^\varepsilon \nabla u_\varepsilon ^0\nabla v \,\mathrm{d}x= \int _{\varOmega ^*_\varepsilon }h^0_\varepsilon v \,\mathrm{d}x \ \ \ \text {for all } v\in V^\varepsilon . \end{aligned}$$

(4.5)

For each $\varepsilon >0$, the Lax–Milgram theorem provides the existence and uniqueness of the solution of problem (3.3). Moreover, the norm $\Vert u^0_\varepsilon \Vert _{V^\varepsilon }$ is bounded by a constant C which is independent of $\varepsilon$.

Let $\varPsi ,\phi \in {\mathcal {D}}({\varOmega })$ and $\psi \in H_\mathrm{per}^1(Y^*)$. Set

$$\begin{aligned} v_{\varepsilon }(x)=\varPsi (x)+\varepsilon \phi (x) \psi ^{\varepsilon }(x) \ \ \text {with}\ \ \psi ^{\varepsilon }(x)=\psi \Big (\frac{x}{\varepsilon }\Big ), \end{aligned}$$

(4.6)

then

$$\begin{aligned} \nabla v_{\varepsilon }=\nabla \varPsi +\varepsilon \psi ^{\varepsilon }\nabla \phi +\phi (\nabla _y \psi )\Big (\frac{\cdot }{\varepsilon }\Big ). \end{aligned}$$

From Proposition 2.3, we have

$$\begin{aligned}&{\mathcal {T}}_{\varepsilon }^*(v_{\varepsilon })\rightarrow \varPsi \ \ \ \text {strongly in}\ L^2(\varOmega \times Y^*),\\&{\mathcal {T}}_{\varepsilon }^*(\phi \psi ^{\varepsilon })\rightarrow \varPhi \ \ \ \text {strongly in}\ L^2(\varOmega \times Y^*)\ \text {with}\ \varPhi =\phi (x)\psi (y),\\&{\mathcal {T}}_{\varepsilon }^*(\nabla v_{\varepsilon })\rightarrow \nabla \varPsi +\nabla _y\varPhi \ \ \ \text {strongly in}\ L^2(\varOmega \times Y^*). \end{aligned}$$

On the other hand, as for $h^0_\varepsilon$, the assumption (4.3) yields

$$\begin{aligned} \mathcal {T}_\varepsilon ^*(h^0_\varepsilon )\rightarrow h \ \ \text {strongly in} \ L^2(0,T;L^2(\varOmega \times Y^*)) \end{aligned}$$

(4.7)

due to Proposition 2.3(vii). Moreover, we use Proposition 2.3(iv) to get

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\int _{\varOmega ^*_\varepsilon }h^0_\varepsilon v_\varepsilon \,\mathrm{d}x =\lim _{\varepsilon \rightarrow 0}\frac{1}{|Y|}\int _{\varOmega \times Y^*}\mathcal {T}_\varepsilon ^*(h^0_\varepsilon )\mathcal {T}_\varepsilon ^*(v_\varepsilon )\,\mathrm{d}x =\theta \int _{\varOmega }h\varPsi \,\mathrm{d}x. \end{aligned}$$

(4.8)

Then, arguing as in [8], we deduce that

$$\begin{aligned}&{\mathcal {T}}^*_\varepsilon (u^0_\varepsilon ) \rightharpoonup U^0\ \text {weakly in}\ L^2(\varOmega ,H^1(Y^*)),\nonumber \\&\widetilde{u^0_\varepsilon } \rightharpoonup \theta U^0\ \text {weakly in }L^2(\varOmega ), \end{aligned}$$

(4.9)

where $U^0\in H_0^1(\varOmega )$ is the unique solution of

$$\begin{aligned} -\mathrm{div}(A^0\nabla U^0)=h. \end{aligned}$$

Together with $h=-\mathrm{div}(A^0\nabla u^0)$, by uniqueness, this implies $U^0=u^0$ which gives (4.4)(ii).

Finally, choosing $u^0_\varepsilon$ as test function in (4.5), in view of (4.7) and (4.9), we have

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\int _{\varOmega ^*_\varepsilon }A^\varepsilon \nabla u_\varepsilon ^0 \nabla u_\varepsilon ^0\,\mathrm{d}x =\lim _{\varepsilon \rightarrow 0}\int _{\varOmega ^*_\varepsilon }h^0_\varepsilon u_\varepsilon ^0 \,\mathrm{d}x =\theta \int _{\varOmega }h u^0\,\mathrm{d}x=\theta \int _{\varOmega }A^0 \nabla u^0 \nabla u^0\,\mathrm{d}x, \end{aligned}$$

where we used the same argument as that in (4.8). $\square$

Now we are in a position to state the corrector results for the homogenization of problem (1.1).

Theorem 4.4

Let $A^\varepsilon$ be a coefficient matrix satisfying (3.1). Suppose that $u_\varepsilon$ is the solution of problem (1.1) with (4.1)–(4.3). Let u be the solution of the homogenized problem (1.2), then we have

$$\begin{aligned}&\Vert u'_\varepsilon -u'\Vert _{\mathcal {C}^0(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0, \ \ \ \nonumber \\&\Vert \nabla u_\varepsilon -C^\varepsilon \nabla u\Vert _{\mathcal {C}^0(0,T; L^1(\varOmega ^*_\varepsilon ))}\rightarrow 0. \end{aligned}$$

(4.10)

The corrector matrix $C^\varepsilon =(C^\varepsilon _{ij})_{1\le i,j\le n}$ is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} C^\varepsilon _{ij}(x)=C_{ij}\big (\frac{x}{\varepsilon }\big )\ \ &{}\text {a.e. on} \ \varOmega ^*_\varepsilon ,\\ C_{ij}(y)=\delta _{ij}(y)+\frac{\partial \chi _j}{\partial y_i}(y) \ \ &{}\text {a.e. on} \ Y^*, \end{array}\right. } \end{aligned}$$

(4.11)

where $\chi _j$ $(j=1,2,\ldots ,n)$ is the solution of the cell problem (3.12).

To prove the corrector results, we are going to use a result proved for the linear case by Donato and the present author in [16]. Here we state it below for the reader’s convenience.

Theorem 4.5

Let $A^\varepsilon$ be a coefficient matrix satisfying (3.1). Suppose that $u_\varepsilon$ is the solution of the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll}\displaystyle u_{\varepsilon }''-\text {div}(A^{\varepsilon }\nabla u_{\varepsilon })=F_{\varepsilon }\ \ \ \ \ &{}\text {in}\ \varOmega _{\varepsilon }^*\times (0,T),\\ \displaystyle u_{\varepsilon }=0 &{}\text {on}\ \partial \varOmega \times (0,T),\\ \displaystyle A^{\varepsilon }\nabla u_{\varepsilon }\cdot n_{\varepsilon }=0 &{}\text {on}\ \partial S_{\varepsilon }\times (0,T),\\ \displaystyle u_{\varepsilon }(x,0)=u_{\varepsilon }^0,\ u'_{\varepsilon }(x,0)=u^1_{\varepsilon } &{} \text {in}\ \varOmega _{\varepsilon }^*, \end{array}\right. } \end{aligned}$$

(4.12)

where the initial data satisfy (4.4) and the following two assumptions:

$$\begin{aligned}&\mathrm{(i)} \ \Vert u^1_\varepsilon -u^1\Vert _{L^2(\varOmega ^*_\varepsilon )}\rightarrow 0,\nonumber \\&\mathrm{(ii)} \ \Vert F_\varepsilon -F\Vert _{L^2(0,T;L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0, \end{aligned}$$

(4.13)

with $u^1\in L^2(\varOmega )$ and $F\in L^2(0,T;L^2(\varOmega ))$. Let u be the solution of the homogenized problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u''-\mathrm{{div}}(A^{0}\nabla u)=F\ \ \ \ \ &{}\text {in}\ \varOmega \times (0,T),\\ u=0 &{}\text {on}\ \partial \varOmega \times (0,T),\\ u(x,0)=u^0,\ u'(x,0)=u^1 &{} \text {in}\ \varOmega , \end{array}\right. } \end{aligned}$$

where the homogenized matrix $A^0$ is defined by (3.14). Then, we have the following corrector results:

$$\begin{aligned}&\Vert u'_\varepsilon -u'\Vert _{\mathcal {C}^0(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0, \ \ \ \\&\Vert \nabla u_\varepsilon -C^\varepsilon \nabla u\Vert _{\mathcal {C}^0(0,T; L^1(\varOmega ^*_\varepsilon ))}\rightarrow 0. \end{aligned}$$

Here the corrector matrix $C^\varepsilon$ is defined by (4.11).

Proof of Theorem 4.4

By the last convergence in (3.9), we have

$$\begin{aligned} \Vert u'_\varepsilon -u'\Vert _{L^2(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0. \end{aligned}$$

For the function g, the assumption (4.2) implies that

$$\begin{aligned} |g(s_1)-g(s_2)|\le C_0|s_1-s_2|, \ \ \forall s_1,s_2\in {\mathbb {R}}. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \Vert g(u'_\varepsilon )-g(u')\Vert _{L^2(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0. \end{aligned}$$

(4.14)

Let $F_\varepsilon =f_\varepsilon -g(u'_\varepsilon )$ and $F=f-g(u')$. From (4.1)(iii) and (4.14), we have

$$\begin{aligned} \Vert F_\varepsilon -F\Vert _{L^2(0,T; L^2(\varOmega ^*_\varepsilon ))}\rightarrow 0. \end{aligned}$$

Together with Proposition 4.3 and (4.1), we directly get (4.10) from Theorem 4.5. $\square$