Homomorphic Images of Circuits in $\hbox {PSL}(2,{\mathbb {Z}})$-Space

Abstract

Each conjugacy class of actions of $PGL\left( {2,{\mathbb {Z}}} \right)$ on the projective line over a finite field $F_q$ denoted by $PL\left( {F_q } \right)$, can be represented by a coset diagram $D\left( {\theta ,q} \right)$, where $\theta \in F_q$ and q is a prime power. The coset diagrams are composed of fragments, and the fragments are further composed of two or more circuits at a certain common point. Professor Graham Higman raised a question: for what values of q and $\theta$, can a fragment $\gamma$ be found in $D\left( {\theta ,q} \right) ?$ Mushtaq in 1983 found that the condition for the existence of a fragment in $D\left( {\theta ,q} \right)$ is a polynomial f in ${\mathbb {Z}}\left[ z \right]$. In this paper, we answer the question: how many polynomials are obtained from the fragments, composed by joining the circuits $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, where $n_2 <n_1 <m_2 <m_1$, at all points of connection.

1 Introduction

It is well known that the modular group $PSL\left( {2,{\mathbb {Z}}} \right)$ [1, 3, 4] is generated by the linear fractional transformations $x:z\rightarrow {-1}/z$ and $y:z\rightarrow {z-1}/z$ which satisfy the relations $x^{2}=y^{3}=1$.

If t is $z\rightarrow 1/z$ which does not belong to $PSL\left( {2,{\mathbb {Z}}} \right)$, then x, y, t generate the extended modular group $PGL\left( {2,{\mathbb {Z}}} \right)$ and satisfy the relations $x^{2}=y^{3}=t^{2}=\left( {xt} \right) ^{2}=\left( {yt} \right) ^{2}=1$.

Let q be a power of a prime p. Let $PL\left( {F_q } \right)$ denote the projective line over the finite field $F_q$. Then $PL\left( {F_q } \right) =F_q \cup \left\{ \infty \right\}$. The group $PGL\left( {2,q} \right)$ has its customary meaning, as the group of all linear fractional transformations $z\rightarrow {az+b}/{cz+d}$ such that a, b, c, d are in $F_q$ and $ad-bc$ is non-zero, while $PSL\left( {2,q} \right)$ is its subgroup consisting of those where $ad-bc$ is a quadratic residue in $F_q$.

In 1978, G. Higman introduced a new type of graph called a coset diagram for $PGL\left( {2,{\mathbb {Z}}} \right)$. In 1983, Mushtaq [6] laid its foundation. The three cycles of y are denoted by small triangles whose vertices are permuted counter-clockwise by y and any two vertices which are interchanged by x are joined by an edge. The fixed points of x and y are denoted by heavy dots. Notice $\left( {yt} \right) ^{2}=1$ is equivalent to $tyt=y^{-1}$, which means that t reverses the orientation of the triangles representing the three cycles of y (as reflection does); because of this, there is no need to make the diagram more complicated by introducing t-edges. For details about coset diagrams, one can refer to [2, 8–10].

Two homomorphisms $\alpha$ and $\beta$ from $PGL\left( {2,{\mathbb {Z}}} \right)$ to $PGL\left( {2,q} \right)$ are called conjugate if $\beta =\alpha \rho$ for some inner automorphism $\rho$ on $PGL\left( {2,q} \right)$. We call $\alpha$ to be non-degenerate if neither of x, y lies in the kernel of $\alpha$. In [7] it has been shown that there is a one-to-one correspondence between the conjugacy classes of non-degenerate homomorphisms from $PGL\left( {2,{\mathbb {Z}}} \right)$ to $PGL\left( {2,q} \right)$ and the elements $\theta \ne 0,3$ of $F_q$ under the correspondence which maps each class to its parameter $\theta$. When $\theta =0,3$ we get degenerate homomorphisms [7]. In other words, it has been shown that for each $\theta$ in $F_q$, there exists a conjugacy class determined by the pair $\left( {\overline{x} ,\overline{y} } \right)$ via $\alpha$. Thus each $\theta$ of $F_q$ determines a pair $\left( {\overline{x} ,\overline{y} } \right)$ which further gives a coset diagram. This implies that for each such conjugacy class, we get a unique coset diagram. It is unique in the sense that for all pairs $\left( {\overline{x} ,\overline{y} } \right)$ in the same conjugacy class, we get the same coset diagram except that the labeling of the vertices vary from pair to pair. Thus the elements, which are conjugate over the field $F_q$, will give essentially the same coset diagram. Let $D\left( {\theta ,q} \right)$ denote the coset diagram corresponding to the action of $PGL\left( {2,{\mathbb {Z}}} \right)$ on $PL\left( {F_q } \right)$ via a homomorphism with parameter $\theta$.

2 Occurrence of Fragments in $D\left( {\theta ,q} \right)$

By a circuit in a coset diagram for an action of $PGL\left( {2,{\mathbb {Z}}} \right)$ on $PL\left( {F_q } \right)$, we mean a closed path of triangles and edges. Coset diagrams for the action of $PGL\left( {2,{\mathbb {Z}}} \right)$on $PL\left( {F_q } \right)$ are composed of fragments, whereas the fragments themselves are composed of circuits. For a sequence of positive integers $n_1,n_2,...,n_{2k}$, the circuit which contains a fixed point of an element $w=\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{n_2 }...\left( {xy^{-1}} \right) ^{n_{2k} }\in PSL\left( {2,{\mathbb {Z}}} \right)$ for some $k\ge 1$, we mean the circuit in which $n_1$ triangles have one vertex inside the circuit and $n_2$ triangles have one vertex outside the circuit and so on. Since it is a cycle $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$, so it does not make any difference if $n_1$ triangles have one vertex outside the circuit $n_1 ,n_2 ,...,n_{2k}$ and $n_2$ triangles have one vertex inside the circuit and so on.

For a given sequence of positive integers, the circuit of the type $\left( n_1,n_2,...,n_{2k^{{\prime }}},n_1,n_2,...,n_{2k^{{\prime }}},...,n_1,n_2,...,n_{2k^{{\prime }}}\right)$, where $k^{{\prime }}$ divides k, is said to have a period of length $2k^{{\prime }}$. A circuit which is not of this type is called a non-periodic circuit. A circuit is called simple, if each vertex of the circuit is fixed by a unique word w or its inverse $w^{-1}$. Two circuits $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$ are connected circuits, if any two vertices in the circuits $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$ are joined by a path.

Consider two non-periodic and simple circuits $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $\left( m_1 ,m_2 ,...,m_{2k^{{\prime }}} \right)$. Let $v_i$ be any vertex in $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ fixed by a word $w_i$ and $v_j$ be any vertex in $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$ fixed by a word $w_j$. In order to connect these two circuits at $v_i$ and $v_j$, we choose, without any loss of generality $\left( {n_1,n_2,...,n_{2k}}\right)$ and apply $w_j$ on $v_i$ in such a way that $w_j$ ends at $v_i$. Consequently, we get a fragment $\gamma$, containing a vertex $v=v_i =v_j$ fixed by the pair $w_i,w_j$.

The action of $PGL\left( {2,{\mathbb {Z}}} \right)$ on $PL\left( {F_{q^{2}} } \right)$ yields two components, namely $PL\left( {F_q } \right)$ and $PL\left( {F_{q^{2}} } \right) -PL\left( {F_q } \right)$. For sake of simplicity, let $\overline{PL\left( {F_q } \right) }$ denote the complement $PL\left( {F_{q^{2}} } \right) -PL\left( {F_q } \right)$. If a fragment occurs in the coset diagram $D\left( {\theta ,q} \right)$ corresponding to an action of $PGL\left( {2,{\mathbb {Z}}} \right)$ on a projective line, then the projective line in which it occurs may be $PL\left( {F_q } \right)$ or $\overline{PL\left( {F_q } \right) } \hbox { .}$ Since $D\left( {\theta ,q} \right)$ is made of fragments, it is therefore necessary to ask, when a fragment exists in $D\left( {\theta ,q} \right)$. In [5], this question is answered in the following way.

Theorem 1

Given a fragment, there is a polynomial f in ${\mathbb {Z}}\left[ z\right]$ such that

• (i) if the fragment occurs in $D\left( {\theta ,q}\right)$, then $f\left( \theta \right) =0$,

• (ii) if $f\left( \theta \right) =0$, then the fragment, or a homomorphic image of it occurs in $D\left( {\theta ,q}\right)$ or in $\overline{PL\left( {F_q}\right) }$.

In [5], the method of calculating a polynomial from a fragment is given. Here we describe this method briefly. Let $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$ be two non-periodic circuits, and a fragment $\gamma$ is composed by joining a vertex $v_i$, fixed by $w_i =\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{n_2 }...\left( {xy^{-1}} \right) ^{n_{2k} }$ in $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ with the vertex $v_j$ fixed by $w_j =\left( {xy} \right) ^{m_1 }\left( {xy^{-1}} \right) ^{m_2 }...\left( {xy^{-1}} \right) ^{m_{2k^{{\prime }}} }$ in $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$. Then $\lambda$ contains a vertex $v_i =v_j$, fixed by the pair $w_i ,w_j$. Let X and Y be the matrices corresponding to x and y of $PGL\left( {2,q} \right)$. Then $w_i$ and $w_j$ can be expressed as

$$\begin{aligned} W_i= & {} \left( {XY}\right) ^{n_1}\left( {XY^{-1}}\right) ^{n_2}...\left( {XY^{-1}}\right) ^{n_{2k} }\\ W_j= & {} \left( {XY}\right) ^{m_1}\left( {XY^{-1}}\right) ^{m_2}...\left( {XY^{-1}}\right) ^{m_{2k^{{\prime }}}} \end{aligned}$$

where $k,k^{{\prime }}>0$. By making use of Eqs. (3.1)–(3.7) of [5], the matrices $W_i,W_j$ and $W_i W_j$ can be expressed linearly as

$$\begin{aligned} W_i= & {} \lambda _0 I+\lambda _1 X+\lambda _2 Y+\lambda _3 XY \\ W_j= & {} \mu _0 I+\mu _1 X+\mu _2 Y+\mu _3 XY \end{aligned}$$

such that $\lambda _i$ and $\mu _i$, for $i=0,1,2,3$ are expressions in r and $\Delta$, where r is the trace of XY and $\Delta$ is its determinant. Since $\left( v\right) w_i =v$ and $\left( v \right) w_j =v$, the $2\times 2$ matrices $W_i$ and $W_j$ have an eigenvector in common. This by Lemma 3.1 of [5] means that the algebra generated by $W_i$ and $W_j$ has dimension 3. The algebra contains $I,W_i,W_j,W_i W_j$ and so these must be linearly dependent. Using Eqs. (3.1)–(3.7) of [5], the matrix $W_i W_j$ can be expressed as

$$\begin{aligned} W_i W_j =\nu _0 I+\nu _1 X+\nu _2 Y+\nu _3 XY, \end{aligned}$$

where $\nu _i$, for $i=0,1,2,3$ can be calculated in terms of the $\lambda _i$ and $\mu _i$, using Eqs. (3.1)–(3.7) of [5]. The condition that $I,W_i ,W_j$ and $W_i W_j$ are linearly dependent, can be expressed as

$$\begin{aligned} \left| {{\begin{array}{ccc} {\lambda _1 } &{} {\lambda _2 } &{} {\lambda _3 } \\ {\mu _1 } &{} {\mu _2 } &{} {\mu _3 } \\ {\nu _1 } &{} {\nu _2 } &{} {\nu _3 } \\ \end{array} }} \right| =0. \end{aligned}$$

If we carry out the calculation of $\nu _1 ,\nu _2 ,\nu _3$ in terms of $\lambda _i$ and $\mu _i$, we find that this is equivalent to

$$\begin{aligned}&\left( {\lambda _2 \mu _3 -\mu _2 \lambda _3 } \right) ^{2}+\Delta \left( {\lambda _3 \mu _1 -\mu _3 \lambda _1 } \right) ^{2}+\left( {\lambda _1 \mu _2 -\mu _1 \lambda _2 } \right) ^{2}\\&\quad +\,r\left( {\lambda _2 \mu _3 -\mu _2 \lambda _3 } \right) \left( {\lambda _3 \mu _1 -\mu _3 \lambda _1 } \right) +\left( {\lambda _2 \mu _3 -\mu _2 \lambda _3 } \right) \left( {\lambda _1 \mu _2 -\mu _1 \lambda _2 } \right) =0. \end{aligned}$$

This gives a homogeneous equation in $\Delta$ and r. In [7], $\theta$ is defined as ${r^{2}}/\Delta$, so we can substitute $\Delta \theta$ for $r^{2}$ to get a polynomial in $\theta$.

Let $v_i$ and $v_k$ be any two vertices in a fragment $\lambda$, such that $v_i$ is fixed by the pair $w_i,w_j$ and $v_k$ is fixed by the pair $w_k,w_l$. Suppose $f\left( \theta \right)$ is a polynomial obtained by choosing the vertex $v_i$ in $\lambda$, that is, $f\left( \theta \right)$ is obtained from the words $w_i$ and $w_j$. Suppose $g\left( \theta \right)$ is a polynomial obtained by choosing the vertex $v_k$ in $\lambda$, that is, $g\left( \theta \right)$ is obtained from the words $w_k$ and $w_l$. If $f\left( \theta \right) =0$, then by Theorem 1, the fragment $\lambda$, or its homomorphic image occurs in $D\left( {\theta ,q}\right)$ or in $\overline{PL\left( {F_q}\right) }$. So there exists a vertex in $D\left( {\theta ,q}\right)$ or in $\overline{PL\left( {F_q}\right) }$ which is fixed by $w_k$ and $w_l$. Again, by Theorem 1, we have $g\left( \theta \right) =0$. Similarly, if $g\left( \theta \right) =0$, then $f\left( \theta \right) =0$. This shows that a unique polynomial is obtained from a fragment. Also there does not exist two distinct fragments $\gamma$ and $\delta$ such that if $\gamma$ exists in $D\left( {\theta ,q}\right)$, then also $\delta$ and vice versa. This shows that two distinct fragments do not have the same condition for the existence in $D\left( {\theta ,q}\right)$, that is, they have distinct polynomials.

Let the homomorphic image of the fragment $\gamma$ occur in the coset diagram $D\left( {\theta ,q} \right)$. Since $D\left( {\theta ,q} \right)$ admits an axis of symmetry, the mirror image of $\gamma$ under the permutation t will also occur.

By $\gamma ^{*}$ we shall mean, the mirror image of $\gamma$. If $w=xy^{\eta _1 }xy^{\eta _2 }...xy^{\eta _n } \quad (\eta =1$or $-1)$ is a word, then let $w^{*}=xy^{-\eta _1}xy^{-\eta _2}...xy^{-\eta _n }$. If a vertex v is fixed by w, then the vertex fixed by $w^{*}$ is denoted by $v^{*}$.

Remark 1

Since t reverses the orientation of the triangles representing the three cycles of y (as reflection does), so if y contains a vertex v fixed by the pair $w_i,w_j$, then obviously its mirror image $\gamma ^{*}$ contains a vertex $v^{*}$ fixed by the pair $w_i ^{*},w_j ^{*}$. Since $D\left( {\theta ,q} \right)$ has a vertical symmetry, therefore if $\gamma$ exists in $D\left( {\theta ,q} \right)$, then its mirror image $\gamma ^{*}$ also exists in $D\left( {\theta ,q} \right)$. So condition for the existence of $\gamma$ and $\gamma ^{*}$ in $D\left( {\theta ,q} \right)$ is the same, that is, a unique polynomial is obtained from $\gamma$ and $\gamma ^{*}$. The mirror image of $\gamma$ is formed by flipping it horizontally. There are certain fragments which remain exactly the same, if we flip them horizontally, that is, they have the same orientations as those of their mirror images. These kinds of fragments have vertical symmetry and may have fixed points of t. A fragment $\gamma$ containing a vertex v fixed by the pair $w_i ,w_j$, has the same orientation as that of its mirror image if and only if it contains a vertex $v^{*}$ fixed by the pair $w_i ^{*},w_j ^{*}$. For example, the fragment formed by joining a vertex $v_i$, fixed by $\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{n_2 }$ in $\left( {n_1 ,n_2 } \right)$ with the vertex $v_j$, fixed by $\left( {xy} \right) ^{{m_1 +n_1 }/2}\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{{m_1 -n_1 }/2}$ in $\left( {m_1 ,m_2 } \right)$ has the same orientation as that of its mirror image. Diagrammatically, it means

Since $\gamma$ and $\gamma ^{*}$ are the same fragments except their orientations, so we have the following Theorem.

Theorem 2

Let $\gamma$ and $\delta$ be two fragments, such that $\gamma$ contains a vertex fixed by the pair $w_i,w_j$. Then $\gamma$ and $\delta$ are the same if and only if $\delta$ contains a vertex fixed by the pair $w_i,w_j$ or the pair $w_i^{*},w_j^{*}$.

3 Points of Connection

If a fragment $\gamma$ is created by joining a vertex $v_i$ in $\left( {n_1,n_2,...,n_{2k}}\right)$ with the vertex $v_j$ in $\left( {m_1,m_2,...,m_{2k^{{\prime }}}}\right)$, then $v_i$ and $v_j$ are not the only vertices, that are joined. But there are many (depends upon $v_i$ and $v_j$) vertices in $\left( {n_1,n_2,...,n_{2k}}\right)$ and $\left( {m_1,m_2,...,m_{2k^{{\prime }}}}\right)$ that are joined. That is, a fragment has finitely many vertices of connection in $\left( {n_1,n_2,...,n_{2k}}\right)$ and $\left( {m_1,m_2,...,m_{2k^{{\prime }}}}\right)$.

Remark 2

If v is fixed by $w_i \in PSL\left( {2,{\mathbb {Z}}} \right)$, then $\left( v \right) w$ is fixed by the conjugate $w^{-1}w_i w$ of $w_i$.

Definition 1

Let $v_i,v_k$ and $v_j,v_l$ be the vertices in $\left( {n_1,n_2,...,n_{2k}}\right)$ and $\left( m_1,m_2,...,m_{2k^{{\prime }}}\right)$, respectively, such that $v_i,v_k,v_j$ and $v_l$ are fixed by $w_i,w_k,w_j$ and $w_l$, respectively. Let $\gamma$ be the fragment formed by joining $v_i$ with $v_j$. Then a pair of vertices $V\left( {v_k,v_l}\right)$ is equivalent to the pair of vertices $V\left( {v_i,v_j}\right)$ if and only if by joining $v_i$ and $v_j$ to create $\gamma ,\,v_k$, and $v_l$ also get connected with each other. If two pairs of vertices $V\left( {v_k,v_l}\right)$ and $V\left( {v_i,v_j} \right)$ are equivalent, then we write $V\left( {v_k,v_l} \right) \sim V\left( {v_i,v_j}\right)$.

Let $\gamma$ be the fragment formed by joining the vertex $v_i$, fixed by $w_i$, in $\left( {n_1,n_2,...,n_{2k}}\right)$ with the vertex $v_j$, fixed by $w_j$, in $\left( {m_1,m_2,...,m_{2k^{{\prime }}}}\right)$ and R be the set of pairs of vertices that are equivalent to $V\left( {v_i,v_j}\right)$. Suppose P is the set of words such that for any $w\in P$, both vertices $\left( {v_i } \right) w$ and $\left( {v_j } \right) w$ lie on $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $\left( {m_1,m_2,...,m_{2k^{{\prime }}}}\right)$, respectively.

Theorem 3

For any $w\in P$, there is a pair of vertices in R.

Proof

Let $w\in P$, then $\left( {v_i } \right) w$ and $\left( {v_j } \right) w$ lie on $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $( m_1 ,m_2 ,...,m_{2k^{{\prime }}})$, respectively. We join $\left( {v_i } \right) w$ with $\left( {v_j } \right) w$ and create a fragment $\delta$. Then by Remark 2, the vertex $\left( {v_i } \right) w=\left( {v_j } \right) w$ of $\delta$ is fixed by the pair $w^{-1}w_i w,w^{-1}w_j w$, whereas the vertex $\left( {\left( {v_i } \right) w} \right) w^{-1}=\left( {\left( {v_j } \right) w} \right) w^{-1}$ of $\delta$ is fixed by the pair $w\left( {w^{-1}w_i w} \right) w^{-1}=w_i ,w\left( {w^{-1}w_j w} \right) w^{-1}=w_j$. This show that $\delta$ and $\gamma$ are the same fragments. Therefore, by joining $v_i$ and $v_j$ to create $\gamma ,\quad \left( {v_i } \right) w$ and $\left( {v_j } \right) w$ also get connected. Hence $V\left( {\left( {v_i } \right) w,\left( {v_j } \right) w} \right) \sim V\left( {v_i ,v_j } \right)$. $\square$

Remark 3

Let $v_i$ and $v_j$ be any vertices in a circuit such that $v_i$ is fixed by $w_i$, and $\left( {v_i}\right) w=v_j$. Then in addition to w, there is another path $w_i^{-1}w$ from $v_i$ to $v_j$. Moreover, $w_i$ and $w_i^{-1}w$ are the only two paths from $v_i$ to $v_j$.

Theorem 4

Corresponding to each pair of vertices $V\left( {v_k,v_l}\right) \in R$, there is a unique word $w\in P$ such that $\left( {v_i } \right) w=v_k ,\left( {v_j } \right) w=v_l$.

Proof

Let $V\left( {v_k ,v_l } \right) \in R$, so $V\left( {v_k ,v_l } \right) \sim V\left( {v_i ,v_j } \right)$. Therefore, by joining $v_i$ and $v_j$ to create $\gamma , \quad v_k$ and $v_l$ also get connected with each other. This implies that there is a same path from $v_i$ to $v_k$ in $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and from $v_j$ to $v_l$ in $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$ that is, $\left( {v_i } \right) w=v_k$ and $\left( {v_j } \right) w=v_l$. Since $v_k$ and $v_l$ lie on $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$, respectively, therefore $\left( {v_i } \right) w$ and $\left( {v_j } \right) w$ lie on $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$ and $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$, respectively. This shows that $w\in P$. By Remark 3, there is another path $w_i ^{-1}w$, from $v_i$ to $v_k$ in $\left( {n_1 ,n_2 ,...,n_{2k} } \right)$, that is, $\left( {v_i } \right) w_i ^{-1}w=v_k$. But $\left( {v_j } \right) w_i ^{-1}w\ne v_l$, therefore $w_i ^{-1}w\notin P$. Similarly for the second path $w_j ^{-1}w$, from $v_j$ to $v_l$ in $\left( {m_1 ,m_2 ,...,m_{2k^{{\prime }}} } \right)$, we have $\left( {v_i } \right) w_j ^{-1}w\ne v_k$. Hence w is a unique word in P.    

$\square$

Theorem 5

There is a one-to-one correspondence between R and P.

The Proof is an immediate consequence of Theorems 3 and 4.

4 Counting of the Number of Vertices of Connection for a Fragment

Each point of connection gives a pair of words, which further gives a polynomial. Since a unique polynomial is obtained from a fragment $\gamma$, so a unique polynomial is evolved for all the vertices of connection for $\gamma$. Therefore, it is important to know all the vertices of connection for $\gamma$.

Let $\gamma$ be created by joining the vertex $v_i$ fixed by $w_i$ in $\left( {n_1 ,n_2 } \right)$ with the vertex $v_j$ fixed by $w_j$ in $\left( {m_1 ,m_2 } \right)$, and $s=\left| R \right|$. Then there are at least s vertices of connection in $\left( {n_1,n_2}\right)$ and $\left( {m_1 ,m_2 } \right)$ to obtain $\gamma$. Note that s is not the total number of vertices of connection in $\left( {n_1,n_2}\right)$ and $\left( {m_1,m_2}\right)$ to compose $\gamma$. To find the total number of vertices of connection, one has to be extra careful.

If $\gamma$ has different orientations from its mirror image, then by Remark 1, $\gamma$ does not contain a vertex fixed by the pair $w_i^{*},w_j ^{*}$. That is, by joining $v_i$ with $v_j$ to create $\gamma$, $v_i ^{*}$ and $v_j ^{*}$ are not connected. So there are s vertices of connection for the mirror image of $\gamma$.

But if $\gamma$ has the same orientation as that of its mirror image, then by Remark 1, $\gamma$ contains a vertex fixed by the pair $w_i ^{*},w_j ^{*}$. That is, by joining $v_i$ with $v_j$, the vertices $v_i ^{*}$ and $v_j ^{*}$ also get connected. Hence total number of vertices of connection for $\gamma$ are $\left\{ {\begin{array}{ll} 2s&{} \hbox {if}\,\gamma \,\hbox {has different orientations from its mirror image} \\ s&{} \hbox {if}\,\gamma \,\hbox {has the same orientation as that of its mirror image} \\ \end{array}}\right. .$

5 Joining of Circuits

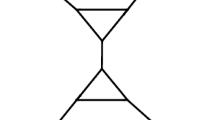
Consider two circuits $\left( {n_1,n_2}\right)$ and $\left( {m_1,m_2}\right)$.

In above figures, one can see that

$$\begin{aligned}&e_{3i_1 +1}\,\hbox {is fixed by}\,\left( {xy} \right) ^{i_1 }\left( {xy^{-1}} \right) ^{n_2 }\left( {xy} \right) ^{n_1 -i_1 },\\&f_{3j_1 +1}\,\hbox {is fixed by}\,\left( {xy} \right) ^{j_1 }\left( {xy^{-1}} \right) ^{n_1 }\left( {xy} \right) ^{n_2 -j_1 },\\&e_{3\left( {i_1+1}\right) }\,\hbox {is fixed by}\,\left( {xy^{-1}} \right) ^{n_1 -\left( {i_1 +1} \right) }\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{i_1 +1},\\&f_{3\left( {j_1+1}\right) }\,\hbox {is fixed by}\,\left( {xy^{-1}} \right) ^{n_2 -\left( {j_1 +1} \right) }\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{j_1 +1},\\&u_{3i_2+1}\,\hbox {is fixed by}\,\left( {xy} \right) ^{i_2 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -i_2 },\\&v_{3j_2+1}\,\hbox {is fixed by}\,\left( {xy} \right) ^{j_2 }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -j_2 },\\&u_{3\left( {i_2+1}\right) }\,\hbox {is fixed by}\,\left( {xy^{-1}} \right) ^{m_1 -\left( {i_2 +1} \right) }\left( {xy} \right) ^{m_2 }\left( {xy^{-1}} \right) ^{i_2 +1},\\&v_{3\left( {j_2+1}\right) }\,\hbox {is fixed by}\,\left( {xy^{-1}} \right) ^{m_2 -\left( {j_2 +1} \right) }\left( {xy} \right) ^{m_1 }\left( {xy^{-1}} \right) ^{j_2 +1}, \end{aligned}$$

where

$$\begin{aligned} i_1= & {} 0,1,2...,n_1 -1,j_1 =0,1,2...,n_2 -1,\\ i_2= & {} 0,1,2...,m_1 -1,j_2 =0,1,2...,m_2 -1. \end{aligned}$$

The number of vertices in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$ are $3\left( {n_1 +n_2 } \right)$ and $3\left( {m_1 +m_2 } \right)$, respectively. So there are $9\left( {n_1 +n_2 } \right) \left( {m_1 +m_2 } \right)$ vertices of connection in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$. For convenience, let $n_1 \ge n_2$ and $m_1$ cannot be less than $n_1 ,n_2$ and $m_2$. For example, consider two circuits $\left( {3,5} \right)$ and $\left( {7,8} \right)$, then we take $m_1 =8,m_2 =7,n_1 =5$ and $n_2 =3$ that is, $\left( {m_1 ,m_2 } \right) =\left( {8,7} \right) , \quad \left( {n_1 ,n_2 } \right) =\left( {5,3} \right)$.

Professor Graham Higman raised a question: for what values of q and $\theta$, can a fragment $\gamma$ be found in $D\left( {\theta ,q} \right) ?$ Mushtaq in 1983 found that the condition for the existence of a fragment in $D\left( {\theta ,q} \right)$ is a polynomial f in ${\mathbb {Z}}\left[ z \right]$. Let us join $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$ at a certain point, and form a fragment $\gamma$. As, a fragment has so many vertices of connection in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$. So if we change the point of connection in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, it is not necessary that we get a fragment different from $\gamma$. It is therefore necessary to ask, how many distinct fragments (polynomials) are formed, if we join the circuits $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$ at all vertices of connection? In this section, we answer this question for $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, where $n_2 <n_1 <m_2 <m_1$. We also mention those vertices of connection in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, which are important. There is no need to join $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$ at the points, which are not mentioned as important. Because if we join $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$ at such a point u, we obtain a fragment, which we have already been obtained by joining at important points.

First we prove some lemmas, which are used in our main results.

Let $i_1 =0,1,2,...,n_1 -1$.

Lemma 1

If the vertex $f_{3n_2}$, fixed by $\left( {xy}\right) ^{n_1}\left( {xy^{-1}} \right) ^{n_2 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3i_1 +1}$, fixed by $\left( {xy} \right) ^{i_1 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -i_1 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $n_1$ distinct fragments, and there are $6\,\sum _{i_1 =0}^{n_1 -1} {\left( {i_1 +2} \right) }$ vertices of connection of these fragments.

Proof

Let $\gamma _{i_1}$ be the fragments formed by joining the vertex $f_{3n_2}$ with the vertices $u_{3i_1+1}$. Then

$$\begin{aligned} P_1= & {} \left\{ x,xy^{-1},xy,xyx,xyxy^{-1},\left( {xy} \right) ^{2},\right. \\&\left. ...,\left( {xy} \right) ^{i_1 }x,\left( {xy} \right) ^{i_1 }xy^{-1},\left( {xy} \right) ^{i_1 +1},e,y,y^{-1}\right\} \end{aligned}$$

is the set of words such that for any $w\in P_1$, both the vertices $\left( {f_{3n_2}}\right) w$ and $\left( {u_{3i_1 +1} } \right) w$ lie on $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, respectively. By Theorem 5, each fragment in $\left\{ {\gamma _{i_1 } } \right\}$ has at least $\left| {P_1 } \right| =3\left( {i_1 +2} \right)$ vertices of connection in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$. $\square$

Now we show that none of the fragments in $\left\{ {\gamma _{i_1}}\right\}$ has the same orientation as that of its mirror image. Let $\gamma _k\in \left\{ {\gamma _{i_1}}\right\}$, then $\gamma _k$ is formed by joining the vertex $f_{3n_2}$ fixed by $\left( {xy}\right) ^{n_1}\left( {xy^{-1}}\right) ^{n_2}$, with the vertex $u_{3k+1}$ fixed by $\left( {xy}\right) ^{k}\left( {xy^{-1}}\right) ^{m_2 }\left( {xy}\right) ^{m_1-k}$. By Theorems 3 and 4, $V\left( {f^{*}_{3n_2 } ,u^{*}_{3k+1} } \right) \sim V\left( {f_{3n_2 } ,u_{3k+1} } \right)$ if and only if there exists a word $w\in P_1$ such that $\left( {f_{3n_2 } } \right) w=f^{*}_{3n_2 },\quad \left( {u_{3k+1} } \right) w=u^{*}_{3k+1}$. But there does not exist such a word in $P_1$. This implies that $V\left( {f^{*}_{3n_2},u^{*}_{3k+1}}\right)$ is not equivalent to $V\left( {f_{3n_2},u_{3k+1} } \right)$, that is, by joining $f_{3n_2}$ with $u_{3k+1}$ to create $\gamma _k,\quad f^{*}_{3n_2}$ is not connected with $u^{*}_{3k+1}$. Therefore, $\gamma _k$ has different orientations from its mirror image. So each fragment in $\left\{ {\gamma _{i_1}}\right\}$ has at least $6\left( {i_1 +3} \right)$ vertices of connection in $\left( {n_1,n_2}\right)$ and $\left( {m_1,m_2}\right)$.

Now we show that any two fragments $\gamma _k,\gamma _l\in \left\{ {\gamma _{i_1}}\right\}$ where $k\ne l$, are distinct. Since $\gamma _k$ is formed by joining the vertex $f_{3n_2}$ fixed by $\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{n_2}$, with the vertex $u_{3k+1}$ fixed by $\left( {xy} \right) ^{k}\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -k}$ and $\gamma _l$ is formed by joining the vertex $f_{3n_2 }$ fixed by $\left( {xy}\right) ^{n_1}\left( {xy^{-1}}\right) ^{n_2}$, with the vertex $u_{3l+1}$ fixed by $\left( {xy}\right) ^{l}\left( {xy^{-1}} \right) ^{m_2}\left( {xy}\right) ^{m_1-l}$. Therefore, by Theorem 4, if $V\left( {f_{3n_2},u_{3l+1}}\right) \sim V\left( {f_{3n_2},u_{3k+1}}\right)$, then there exists a word $w\in P_1$ such that $\left( {f_{3n_2}}\right) w=f_{3n_2},\quad \left( {u_{3k+1}}\right) w=u_{3l+1}$. There is only one word $e\in P_1$ for which $\left( {f_{3n_2}}\right) e=f_{3n_2}$, but $\left( {u_{3k+1}}\right) e\ne u_{3l+1}$. This implies that $V\left( {f_{3n_2},u_{3l+1}}\right)$ is not equivalent to $V\left( {f_{3n_2 } ,u_{3k+1}}\right)$, that is, by joining $f_{3n_2}$ with $u_{3k+1}$ to create $\gamma _k,\quad f_{3n_2}$ is not connected with $u_{3l+1}$. Therefore, $\gamma _k$ does not contain a vertex fixed by $\left( {xy}\right) ^{n_1}\left( {xy^{-1}}\right) ^{n_2}$ and $\left( {xy} \right) ^{l}\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -l}$. Also by Theorem 4, if $V\left( {f^{*}_{3n_2 } ,u^{*}_{3l+1} } \right) \sim V\left( {f_{3n_2 } ,u_{3k+1} } \right)$, then there exists a word $w\in P_1$ such that $\left( {f_{3n_2 } } \right) w=f^{*}_{3n_2}, \quad \left( {u_{3k+1} } \right) w=u^{*}_{3l+1}$. But $P_1$ does not contain such a word. This implies that $V\left( {f^{*}_{3n_2},u^{*}_{3l+1}}\right)$ is not equivalent to $V\left( {f_{3n_2 } ,u_{3k+1} } \right)$, that is, by joining $f_{3n_2}$ with $u_{3k+1}$ to create $\gamma _k, \quad f^{*}_{3n_2}$ is not connected with $u^{*}_{3l+1}$. Therefore, $\gamma _k$ does not contain a vertex fixed by $\left( {xy^{-1}}\right) ^{n_1}\left( {xy}\right) ^{n_2}$ and $\left( {xy^{-1}}\right) ^{l}\left( {xy}\right) ^{m_2}\left( {xy^{-1}} \right) ^{m_1 -l}$. Hence by Theorem 2, all the fragments in $\left\{ {\gamma _{i_1}}\right\}$ are distinct. Therefore, $\left| {\gamma _{i_1}}\right| =n_1$ and there are $6\sum _{i_1=0}^{n_1-1}{\left( {i_1 +2} \right) }$ vertices of connection for all these fragments.

Let

$$\begin{aligned} j_1 =\frac{m_1 +n_1 +r_1}{2},\frac{m_1 +n_1 +2+r_1}{2},...,m_1 -1, \end{aligned}$$

where $r_1 =\left\{ {\begin{array}{l} 0\hbox { if }m_1 +n_1 \hbox { is even integer} \\ 1\hbox { if }m_1 +n_1 \hbox { is odd integer} \\ \end{array}}\right. .$ It is clear that $j_1 >i_1$.

Lemma 2

If the vertex $f_{3n_2}$, fixed by $\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{n_2 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3j_1 +1}$, fixed by $\left( {xy} \right) ^{j_1 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -j_1 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $1/2\left( {m_1 -n_1 -r_1 } \right)$ distinct fragments, and there are $3\left( {n_1 +2} \right) \left( {m_1 -n_1 -1} \right)$ vertices of connection of these fragments.

Proof

Let $\mu _{j_1}$ be the fragments formed by joining the vertex $f_{3n_2}$ with the vertices $u_{3j_1+1}$. Then

$$\begin{aligned} P_2 =\left\{ {\begin{array}{l} x,xy^{-1},xy,xyx,xyxy^{-1},\left( {xy} \right) ^{2},...,\left( {xy} \right) ^{n_1 -1}x,\left( {xy} \right) ^{n_1 -1}xy^{-1},\left( {xy} \right) ^{n_1 }, \\ \left( {xy} \right) ^{n_1 }x,\left( {xy} \right) ^{n_1 }xy^{-1},\left( {xy} \right) ^{n_1 +1},e,y^{-1},y \\ \end{array}} \right\} \end{aligned}$$

is the set of words such that for any $w\in P_2$, both the vertices $\left( {f_{3n_2 } } \right) w$ and $\left( {u_{3j_1 +1}}\right) w$ lie on $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1,m_2}\right)$, respectively. By Theorem 5, each fragment in $\left\{ {\mu _{j_1}}\right\}$ has at least $\left| {P_2 } \right| =3\left( {n_1 +2} \right)$ vertices of connection. $\square$

Now we show that all fragments in $\left\{ {\mu _{j_1}}\right\}$ are distinct, and only $\mu _{{m_1 +n_1 }/2} \in \left\{ {\mu _{j_1}}\right\}$ has the same orientation as that of its mirror image. Let $\mu _k ,\mu _l \in \left\{ {\mu _{j_1}}\right\}$, then $\mu _k$ is formed by joining the vertices, $f_{3n_2}$ and $u_{3k+1}$ and $\mu _l$ is formed by joining $f_{3n_2 }$ with $u_{3l+1}$. By Theorem 3 and 4, $V\left( {f_{3n_2},u_{3l+1}}\right) \sim V\left( {f_{3n_2 } ,u_{3k+1} } \right)$, if and only if there exists a word $w\in P_2$ such that $\left( {f_{3n_2}}\right) w=f_{3n_2},\quad \left( {u_{3k+1}}\right) w=u_{3l+1}$. There is only one word $e\in P_2$ for which $\left( {f_{3n_2}} \right) e=f_{3n_2}$, but $\left( {u_{3k+1}}\right) e\ne u_{3l+1}$. This implies that $V\left( {f_{3n_2},u_{3l+1}}\right)$ is not equivalent to $V\left( {f_{3n_2},u_{3k+1}}\right)$, that is, by joining $f_{3n_2}$ with $u_{3k+1}$ to create $\mu _k,\quad f_{3n_2}$ is not connected with $u_{3l+1}$. Therefore, $\mu _k$ does not contain a vertex fixed by $\left( {xy}\right) ^{n_1}\left( {xy^{-1}}\right) ^{n_2}$ and $\left( {xy}\right) ^{l}\left( {xy^{-1}}\right) ^{m_2}\left( {xy}\right) ^{m_1-l}$. Also by Theorem 3 and 4, $V\left( {f^{*}_{3n_2},u^{*}_{3l+1}}\right) \sim V\left( {f_{3n_2},u_{3k+1}}\right)$, if and only if there exists a word $w\in P_2$ such that $\left( {f_{3n_2}}\right) w=f^{*}_{3n_2}, \quad \left( {u_{3k+1} } \right) w=u^{*}_{3l+1}$. There is only one word $\left( {xy} \right) ^{n_1}x\in P_2$ for which $\left( {f_{3n_2}} \right) \left( {xy} \right) ^{n_1}x=f^{*}_{3n_2}$ and $\left( {u_{3k+1}}\right) \left( {xy}\right) ^{n_1 }x=u^{*}_{3\left( {m_1+n_1-k}\right) +1}$. This implies that for $l=m_1+n_1 -k$, $V\left( {f^{*}_{3n_2},u^{*}_{3l+1} } \right) \sim V\left( {f_{3n_2},u_{3k+1}}\right)$, that is, by joining $f_{3n_2}$ with $u_{3k+1}$ to create $\mu _k,\quad f^{*}_{3n_2}$ and $u^{*}_{3l+1}$ also get connected. Therefore, $\mu _k$ contains a vertex fixed by $\left( {xy^{-1}} \right) ^{n_1 }\left( {xy}\right) ^{n_2}$ and $\left( {xy^{-1}} \right) ^{l}\left( {xy} \right) ^{m_2}\left( {xy^{-1}}\right) ^{m_1 -l}$. Hence by Theorem 2, the fragments $\mu _k$ and $\mu _l$ are the mirror images of each other if and only if $l=m_1+n_1-k$. Now for all $k\in \left\{ {{m_1 +n_1 +r_1 }/2,{m_1 +n_1 +2+r_1 }/2,...,m_1 -1} \right\} -{m_1 +n_1 }/2$, we have $m_1 +n_1 -k<{m_1 +n_1 +r_1 }/2$, implying that $\mu _{m_1 +n_1 -k} \notin \left\{ {\mu _{j_1 } } \right\}$. But for $k={m_1 +n_1 }/2$, we get $m_1 +n_1 -k={m_1 +n_1 }/2$. Therefore, $\mu _{{m_1 +n_1 }/2}$ has the same orientation as that of its mirror image. Hence any two fragments $\mu _k ,\mu _l \in \left\{ {\mu _{j_1 } } \right\}$ are distinct. Since $j_1 ={m_1 +n_1 +r_1 }/2,{m_1 +n_1 +2+r_1 }/2,...,m_1 -1$, therefore $\left| {\mu _{j_1 } } \right| =1/2\left( {m_1 -n_1 -r_1 } \right)$.

Let $m_1 +n_1$ be an even integer, then there is only one fragment $\mu _{{m_1 +n_1 }/2}\in \left\{ {\mu _{j_1 } } \right\}$ having the same orientation as that of its mirror image, and all other $1/2\left( {m_1 -n_1 -2} \right)$ fragments have different orientations from their mirror images. Hence there are

$$\begin{aligned} 2\left| {P_2 } \right| \left( {\frac{m_1 -n_1 -2}{2}} \right) +\left| {P_2 } \right|= & {} 6\left( {n_1 +2} \right) \left( {\frac{m_1 -n_1 -2}{2}} \right) +3\left( {n_1 +2} \right) \\= & {} 3\left( {n_1 +2} \right) \left( {m_1-n_1 -1} \right) \end{aligned}$$

vertices of connection for the fragments in $\left\{ {\mu _{j_1 } } \right\}$.

Let $m_1 +n_1$ be an odd integer, then all fragments in $\left\{ {\mu _{j_1 } } \right\}$ have different orientations from their mirror images. Hence there are $2\left| {P_2 } \right| \left( {{m_1 -n_1 -1}/2} \right) =6\left( {n_1 +2} \right) \left( {{m_1 -n_1 -1}/2} \right) =3\left( {n_1 +2} \right) \left( {m_1 -n_1 -1} \right)$ vertices of connection for the fragments in $\left\{ {\mu _{j_1 } } \right\}$.

Lemma 3

If the vertex $f_{3n_2}$, fixed by $\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{n_2 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3i_1+1}$, fixed by $\left( {xy} \right) ^{i_1 }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -i_1 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $n_1$ distinct fragments, and there are $6\,\sum _{i_1 =0}^{n_1 -1} {\left( {i_1 +2} \right) }$ vertices of connection of these fragments.

The proof is obtained by interchanging $m_1 ,m_2 ,P_1$ and $\gamma _{i_1 }$ by $m_2 ,m_1 ,P_3$ and $\gamma ^{{\prime }}_{i_1 }$, respectively, in the proof of Lemma 1.

Let

$$\begin{aligned} j_2 =\frac{m_2 +n_1 +r_2}{2},\frac{m_2 +n_1 +2+r_2}{2},...,m_2 -1, \end{aligned}$$

where $r_2 =\left\{ {\begin{array}{l} 0\hbox { if }m_2 +n_1 \hbox { is even integer} \\ 1\hbox { if }m_2 +n_1 \hbox { is odd integer} \\ \end{array}} \right. .$

Lemma 4

If the vertex $f_{3n_2}$, fixed by $\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{n_2 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3j_2 +1}$, fixed by $\left( {xy} \right) ^{j_2 }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -j_2 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $1/2\left( {m_2 -n_1 -r_2 } \right)$ distinct fragments, and there are $3\left( {n_1 +2} \right) \left( {m_2 -n_1 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $m_1 ,m_2 ,j_1 ,P_2$ and $\mu _{j_1 }$ by $m_1 ,m_1 ,j_2 ,P_4$ and $\mu ^{{\prime }}_{j_2 }$, respectively, in the proof of Lemma 2.

Let $i_2 =1,2,...,n_2 -1$.

Lemma 5

If the vertex $e_{3n_1 }$, fixed by $\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{n_1 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3i_2 +1}$, fixed by $\left( {xy} \right) ^{i_2 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -i_2 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $\left( {n_2 -1} \right)$ distinct fragments, and there are $6\hbox { }\sum _{i_2 =1}^{n_2 -1} {\left( {i_2 +2} \right) }$ vertices of connection of these fragments.

The proof is obtained by interchanging $n_1 ,n_2 ,i_1 ,P_1$ and $\gamma _{i_1 }$ by $n_2 ,n_1 ,i_2 ,P_5$ and $\lambda _{i_2 }$, respectively, in the proof of Lemma 1.

Let

$$\begin{aligned} j_3 =\frac{m_1 +n_2 +r_3}{2},\frac{m_1 +n_2 +2+r_3}{2},...,m_1 -1, \end{aligned}$$

where $r_3 =\left\{ {\begin{array}{l} 0\hbox { if }m_1 +n_2 \hbox { is even integer} \\ 1\hbox { if }m_1 +n_2 \hbox { is odd integer} \\ \end{array}} \right. .$

Lemma 6

If the vertex $e_{3n_1}$, fixed by $\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{n_1 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3j_3 +1}$, fixed by $\left( {xy} \right) ^{j_3 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -j_3 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $1/2\left( {m_1 -n_2 -r_3 } \right)$ distinct fragments, and there are $3\left( {n_2 +2} \right) \left( {m_1 -n_2 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $n_1 ,n_2 ,j_1 ,P_2$ and $\mu _{j_1 }$ by $n_2 ,n_1 ,j_3 ,P_6$ and $\nu _{j_3 }$, respectively, in the proof of Lemma 2.

Lemma 7

If the vertex $e_{3n_1}$, fixed by $\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{n_1 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3i_2 +1}$, fixed by $\left( {xy} \right) ^{i_2 }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -i_2 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $\left( {n_2 -1} \right)$ distinct fragments, and there are $6\,\sum _{i_2 =1}^{n_2 -1} {\left( {i_2 +2} \right) }$ vertices of connection of these fragments.

The proof is obtained by interchanging $n_1 ,n_2 ,m_1 ,m_2 ,i_1 ,P_1$ and $\gamma _{i_1 }$ by $n_2 ,n_1 ,m_2, m_1, i_2 ,P_7$ and $\lambda ^{{\prime }}_{i_2 }$, respectively, in the proof of Lemma 1.

Let

$$\begin{aligned} j_4 =\frac{m_2 +n_2 +r_4}{2},\frac{m_2 +n_2 +2+r_4}{2},...,m_2 -1, \end{aligned}$$

where $r_4 =\left\{ {\begin{array}{l} 0\hbox { if }m_2 +n_2 \hbox { is even integer} \\ 1\hbox { if }m_2 +n_2 \hbox { is odd integer} \\ \end{array}} \right. .$

Lemma 8

If the vertex $e_{3n_1}$, fixed by $\left( {xy} \right) ^{n_2}\left( {xy^{-1}} \right) ^{n_1 }$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3j_4 +1}$, fixed by $\left( {xy} \right) ^{j_4 }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -j_4 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $1/2\left( {m_2 -n_2 -r_4 } \right)$ distinct fragments, and there are $3\left( {n_2 +2} \right) \left( {m_2 -n_2 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $n_1 ,n_2 ,m_1 ,m_2 ,j_1 ,P_2$ and $\mu _{j_1 }$ by $n_2 ,n_1 ,m_2, m_1 ,j_4 ,P_8$ and $\nu _{j_4 }^{\prime }$, respectively, in the proof of Lemma 2.

Let

$$\begin{aligned}&p_1=1,2,...,m_1-1,\,p_2 =1,2,...,m_2 -1,\,q_1 =1,2,...,\frac{n_1 -\left( {r_5 +2} \right) }{2}\quad \hbox {and}\\&\quad q_2=1,2,...,\frac{n_2 -\left( {r_6 +2} \right) }{2} \end{aligned}$$

where $r_5 =\left\{ {\begin{array}{l} 0\hbox { if }n_1 \hbox { is even integer} \\ 1\hbox { if }n_1 \hbox { is odd integer} \\ \end{array}} \right.$ and $r_6 =\left\{ {\begin{array}{l} 0\hbox { if }n_2 \hbox { is even integer} \\ 1\hbox { if }n_2 \hbox { is odd integer} \\ \end{array}} \right. .$

Lemma 9

If the vertices $e_{3q_1}$, fixed by $\left( {xy^{-1}} \right) ^{n_1 -q_1 }\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{q_1 }$ in $\left( {n_1 ,n_2 } \right)$ are connected with the vertices $u_{3p_1 +1,}$ fixed by $\left( {xy} \right) ^{p_1 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $1/2\left( {n_1 -\left( {r_5 +2} \right) } \right) \left( {m_1 -1} \right)$ distinct fragments, and there are $6\left( {n_1 -\left( {r_5 +2} \right) } \right) \left( {m_1 -1} \right)$ vertices of connection of these fragments.

Proof

Let $\phi _{\left( {q_1,p_1}\right) }$ be the fragments formed by joining the vertices $e_{3q_1}$, fixed by $\left( {xy^{-1}} \right) ^{n_1 -q_1 }\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{q_1 }$ in $\left( {n_1 ,n_2 } \right)$ with the vertices $u_{3p_1 +1}$, fixed by $\left( {xy} \right) ^{p_1 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1 }$ in $\left( {m_1 ,m_2}\right)$. Then $P_9 =\left\{ {e,y^{-1},y,x,xy^{-1},xy} \right\}$ is the set of words such that for any $w\in P_9$, both the vertices $\left( {e_{3q_1 } } \right) w$ and $\left( {u_{3p_1 +1}}\right) w$ lie on $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1,m_2}\right)$, respectively. By Theorem 5, each fragment in $\left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$ has at least $\left| {P_9 } \right| =6$ vertices of connection. $\square$

Now we show that all fragments in $\left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$ are distinct. Let $\phi _{\left( {k_1 ,l_1 } \right) } ,\phi _{\left( {k_2 ,l_2 } \right) } \in \left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$, then $\phi _{\left( {k_1 ,l_1 } \right) }$ is formed by joining the vertex $e_{3k_1 }$ with $u_{3l_1 +1}$ and $\phi _{\left( {k_2 ,l_2 } \right) }$ is formed by joining the vertex $e_{3k_2 }$ with $u_{3l_2 +1}$. By Theorems 3 and 4, $V\left( {e_{3k_2 } ,u_{3l_2 +1} } \right) \sim V\left( {e_{3k_1 } ,u_{3l_1 +1} } \right)$, if and only if there exists a word $w\in P_9$ such that $\left( {e_{3k_1 } } \right) w=e_{3k_2 } , \quad \left( {u_{3l_1 +1} } \right) w=u_{3l_2 +1}$. There is only one word $xy^{-1}\in P_9$ for which $\left( {e_{3k_1 } } \right) xy^{-1}=e_{3\left( {k_1 +1} \right) }$, but $\left( {u_{3l_1 +1} } \right) xy^{-1}\ne \left( {u_{3l_2 +1} } \right)$. This implies that $V\left( {e_{3k_2 } ,u_{3l_2 +1} } \right)$ is not equivalent to $V\left( {e_{3k_1 } ,u_{3l_1 +1} } \right)$, that is, by joining $e_{3k_1 }$with $u_{3l_1 +1}$ to create $\phi _{\left( {k_1 ,l_1 } \right) } , \quad e_{3k_2 }$ is not connected with $u_{3l_2 +1}$. Therefore, $\phi _{\left( {k_1 ,l_1 } \right) }$ does not contain a vertex fixed by $\left( {xy^{-1}} \right) ^{n_1 -k_2 }\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{k_2 }$ and $\left( {xy} \right) ^{l_2 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -l_2 }$. Also by Theorem 3 and 4, $V\left( {e^{*}_{3k_2 } ,u^{*}_{3l_2 +1} } \right) \sim V\left( {e_{3k_1 } ,u_{3l_1 +1} } \right)$, if and only if there exists a word $w\in P_9$ such that $\left( {e_{3k_1 } } \right) w=e^{*}_{3k_2 } , \quad \left( {u_{3l_1 +1} } \right) w=u^{*}_{3l_2 +1}$. There is only one word $x\in P_9$ for which $\left( {e_{3k_1 } } \right) x=e^{*}_{3\left( {n_1 -k_1 } \right) } , \quad \left( {u_{3l_1 +1} } \right) x=u^{*}_{3\left( {m_1 -l_1 } \right) +1}$, this implies that for $k_2 =n_1 -k_1 ,l_2 =m_1 -l_1 , \quad V\left( {e^{*}_{3k_2 } ,u^{*}_{3l_2 +1} } \right) \sim V\left( {e_{3k_1 } ,u_{3l_1 +1} } \right)$, that is, by joining $e_{3k_1 }$ with $u_{3l_1 +1}$ to create $\phi _{\left( {k_1 ,l_1 } \right) } , \quad e^{*}_{3k_2 }$ and $u^{*}_{3l_2 +1}$ also get connected. Therefore, $\phi _{\left( {k_1 ,l_1 } \right) }$ contains a vertex fixed by $\left( {xy} \right) ^{n_1 -k_2 }\left( {xy^{-1}} \right) ^{n_2 }\left( {xy} \right) ^{k_2 }$ and $\left( {xy^{-1}} \right) ^{l_2 }\left( {xy} \right) ^{m_2 }\left( {xy^{-1}} \right) ^{m_1 -l_2 }$. Hence by Theorem 2, the fragments $\phi _{\left( {k_1 ,l_1 } \right) }$ and $\phi _{\left( {k_2 ,l_2 } \right) }$ are mirror images of each other if and only if $k_2 =n_1 -k_1 ,l_2 =m_1 -l_1$. Now for all $k_1 \in \left\{ {1,2,...,{n_1 -\left( {r_5 +2} \right) }/2} \right\}$, we have $n_1 -k_1 >{n_1 -\left( {r_5 +2} \right) }/2$, implies $\phi _{\left( {n_1 -k_1 ,m_1 -l_1 } \right) } \notin \left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$. Hence all fragments in $\left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$ are distinct. Therefore, $\left| {\phi _{\left( {q_1 ,p_1 } \right) } } \right| =1/2\left( {n_1 -\left( {r_5 +2} \right) } \right) \left( {m_1 -1} \right)$.

Now we prove none of the fragments in $\left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$ has the same orientation as that of its mirror image. Let $\phi _{\left( {k_1 ,l_1 } \right) } \in \left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$ has the same orientation as that of its mirror image, that is, $\phi _{\left( {k_1 ,l_1 } \right) }$ is the mirror image of itself. But as proved earlier, $\phi _{\left( {k_1 ,l_1 } \right) }$ is the mirror image of $\phi _{\left( {n_1 -k_1 ,m_1 -l_1 } \right) }$. This shows that $k_1 =n_1 -k_1 ,l_1 =m_1 -l_1$, that is, $k_1 ={n_1 }/2,l_1 ={m_1 }/2$. Hence $\phi _{\left( {k_1 ,l_1 } \right) }$ is the mirror image of itself, if $k_1 ={n_1 }/2, l_1 ={m_1 }/2$. But $\phi _{\left( {{n_1 }/2,{m_1 }/2} \right) } \notin \left\{ {\phi _{\left( {q_1 ,p_1 } \right) } } \right\}$, as ${n_1 }/2>{n_1 -\left( {r_5 +2} \right) }/2$. Hence none of the fragments in $\left\{ {\phi _{\left( {q_1 , p_1 } \right) } } \right\}$ has the same orientation as that of its mirror image. This shows that each fragment in $\left\{ {\phi _{\left( {q_1 , p_1 } \right) } } \right\}$ has $2|P_9 |=12$ vertices of connection. Since $\left| {\phi _{\left( {q_1 ,p_1 } \right) } } \right| =1/2\left( {n_1 -\left( {r_5 +2} \right) } \right) \left( {m_1 -1} \right)$, therefore there are $6\left( {n_1 -\left( {r_5 +2} \right) } \right) \left( {m_1 -1} \right)$ vertices of connection for all fragments in $\left\{ {\phi _{\left( {q_1 , p_1 } \right) } } \right\}$.

Lemma 10

If the vertices $e_{3q_1}$, fixed by $\left( {xy^{-1}} \right) ^{n_1 -q_1 }\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{q_1 }$ in $\left( {n_1 ,n_2 } \right)$ are connected with the vertices $v_{3p_2 +1}$, fixed by $\left( {xy}\right) ^{p_2}\left( {xy}\right) ^{-1m_{1}}\left( {xy} \right) ^{m_2 -p_2 }$ in $\left( {m_1 , m_2 } \right) ,$ then there are $1/2\left( {n_1 -\left( {r_5 +2} \right) } \right) \left( {m_2 -1} \right)$ distinct fragments, and there are $6\left( {n_1 -\left( {r_5 +2} \right) } \right) \left( {m_2 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $m_1,m_2,p_1,P_9$ and $\varphi _{\left( {q_1,p_1}\right) }$ by $m_2,m_1,p_2, P_{10}$ and $\varphi _{\left( {q_1 , p_2 } \right) }^{^{\prime }}$, respectively, in the proof of Lemma 9.

Lemma 11

If the vertices $f_{3q_2}$, fixed by $\left( {xy^{-1}} \right) ^{n_2 -q_2 }\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{q_2 }$ in $\left( {n_1 ,n_2 } \right)$ are connected with the vertices $u_{3p_1 +1}$, fixed by $\left( {xy} \right) ^{p_1 }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $1/2\left( {n_2 -\left( {r_6 +2} \right) } \right) \left( {m_1 -1} \right)$ distinct fragments, and there are $6\left( {n_2 -\left( {r_6 +2} \right) } \right) \left( {m_1 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $n_1 ,n_2 ,q_1 ,P_9$ and $\varphi _{\left( {q_1 , p_1 } \right) }$ by $n_2 ,n_1 ,q_2 ,P_{11}$ and $\psi _{\left( {q_2 , p_1 } \right) }$, respectively, in the proof of Lemma 9.

Lemma 12

If the vertices $f_{3q_2}$, fixed by $\left( {xy^{-1}} \right) ^{n_2 -q_2 }\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{q_2 }$ in $\left( {n_1 ,n_2 } \right)$ are connected with the vertices $v_{3p_2 +1}$, fixed by $\left( {xy} \right) ^{p_2 }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -p_2 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $1/2\left( {n_2 -\left( {r_6 +2} \right) } \right) \left( {m_2 -1} \right)$ distinct fragments, and there are $6\left( {n_2 -\left( {r_6 +2} \right) } \right) \left( {m_2 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $n_1 ,n_2 ,m_1 ,m_2 ,q_1 ,p_1 ,P_9$ and $\varphi _{\left( {q_1 , p_1 } \right) }$ by $n_2 , n_1 , m_2 , m_1 ,q_2 , p_2 , P_{12}$ and $\psi _{\left( {q_2 , p_2 } \right) }^{\prime }$, respectively, in the proof of Lemma 9.

Let

$$\begin{aligned} p_1^{^{\prime }} =\left\{ {{\begin{array}{ll} 1,...,m_1-1&{}\quad \hbox {if}\,n_1\,\hbox {is odd} \\ 1,2,...,\frac{m_1-r_7}{2}&{}\quad \hbox {if}\,n_1\,\hbox {is even} \\ \end{array} }} \right. ,\,p_2^{^{\prime }} =\left\{ {{\begin{array}{ll} 1,...,m_2-1 &{}\quad \hbox {if}\,n_1\,\hbox {is odd} \\ 1, 2,...,\frac{m_2-r_8}{2}&{} \quad \hbox {if}\,n_1\,\hbox {is even} \\ \end{array} }} \right. , \end{aligned}$$

where $r_7 =\left\{ {{\begin{array}{ll} 0 &{} {\hbox {if }{m_1 }\hbox { is even}} \\ 1 &{} {\hbox {if }{m_1 }\hbox { is odd}} \\ \end{array} }} \right.$, $r_8 =\left\{ {{\begin{array}{ll} 0 &{} {\hbox {if }{m_2 }\hbox { is even}} \\ 1 &{} {\hbox {if }{m_2 }\hbox { is odd}} \\ \end{array} }} \right. .$

Lemma 13

• (i) If $n_1 \in 2{\mathbb {Z}}^{+}-1$, and the vertex $e_{{3\left( {n_1 -1} \right) }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_1 +1}/2}\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{{n_1 -1}/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3p_1^{\prime } +1}$, fixed by $\left( {xy} \right) ^{p_1^{^{\prime }} }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1^{^{\prime }} }$ in $\left( {m_1 , m_2 } \right)$, then there are $\left( {m_1 -1} \right)$ distinct fragments, and there are $12\left( {m_1 -1} \right)$ vertices of connection of these fragments.

• (ii) If $n_1 \in 2{\mathbb {Z}}^{+}$, and the vertex $e_{{3n_1 }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_1 }/2}\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{{n_1 }/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3p_1^{\prime } +1}$, fixed by $\left( {xy} \right) ^{p_1^{^{\prime }} }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1^{^{\prime }} }$ in $\left( {m_1 , m_2 } \right)$, then there are $1/2\left( {m_1 -r_7 } \right)$ distinct fragments, and there are $6\left( {m_1 -1} \right)$ vertices of connection of these fragments.

Proof

$\left( i\right)$ Let $\phi _{\left( {{n_1 -1}/2,p_1^{\prime } } \right) }$ be the fragments formed by joining the vertex $e_{{3\left( {n_1 -1} \right) }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_1 +1}/2}\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{{n_1 -1}/2}$ in $\left( {n_1 ,n_2 } \right)$ with the vertices $u_{3p_1^{\prime } +1}$, fixed by $\left( {xy} \right) ^{p_1^{\prime } }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1^{\prime } }$ in $\left( {m_1 , m_2 } \right)$. Then $P_{13} =\left\{ {e,y^{-1},y,x,xy^{-1},xy} \right\}$ is the set of words such that for any $w\in P_{13}$, both the vertices $\left( {e_{{3\left( {n_1 -1} \right) }/2} } \right) w$ and $\left( {u_{3p_1^{\prime } +1} } \right) w$ lie on $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, respectively. By Theorem 5, each fragment in $\left\{ {\phi _{\left( {{n_1 -1}/2,p_1^{\prime }} \right) } } \right\}$ has at least $|\;P_{13} \;|=6$ vertices of connection. Since in Lemma 9, it is proved that any two fragments $\phi _{\left( {k_1 , l_1 } \right) } ,\phi _{\left( {k_2 , l_2 } \right) }$ are distinct, this implies that all fragments in $\left\{ {\phi _{\left( {{n_1 -1}/2,p_1^{\prime } } \right) } } \right\}$ are distinct. Since $p_1^{^{\prime }} =\left\{ {{\begin{array}{ll} {1,..., m_1 -1} &{} {\hbox {if }{n_1 \;}\hbox {is odd}} \\ {1, 2,..., {m_1 -r_7 }/2} &{} {\hbox {if }{n_1 \;}\hbox {is even}} \\ \end{array} }} \right.$, therefore $\left| {\phi _{{n_1 -1}/2, p_1^{\prime } } } \right| =m_1 -1$. Also in Lemma 9, it is proved that $\phi _{\left( {{n_1 }/2,{m_1 }/2} \right) }$ has the same orientation as that of its mirror images. But $\phi _{\left( {{n_1 }/2, {m_1 }/2} \right) } \notin \left\{ {\phi _{\left( {{n_1 -1}/2,p_1^{\prime } } \right) } } \right\}$, implying that none of the fragments in $\left\{ {\phi _{\left( {{n_1 -1}/2,p_1^{\prime } } \right) } } \right\}$ has the same orientation as that of its mirror image. Hence there are $2|P_{13}|\left| {\phi _{{n_1 -1}/2, p_1^{\prime } } } \right| =12\left( {m_1 -1} \right)$ vertices of connection for all fragments in $\left\{ {\phi _{\left( {{n_1 -1}/2,p_1^{\prime } } \right) } } \right\}$.

$\left( {ii}\right)$ Let $\phi _{({n_1 }/2, p_1^{\prime } )}$ be the fragments formed by joining the vertex $e_{{3n_1 }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_1 }/2}\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{{n_1 }/2}$ in $\left( {n_1 ,n_2 } \right)$ with the vertices $u_{3p_1^{\prime } +1}$, fixed by $\left( {xy} \right) ^{p_1^{^{\prime }} }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1^{^{\prime }} }$ in $\left( {m_1 , m_2 } \right)$. Then $P_{13} =\left\{ {e,y^{-1},y,x,xy^{-1},xy} \right\}$ is the set of words such that for any $w\in P_{13}$, both the vertices $\left( {e_{{3n_1 }/2} } \right) w$ and $\left( {u_{3p_1^{\prime } +1} } \right) w$ lie on $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, respectively. By Theorem 5, each fragment in $\left\{ {\phi _{({n_1 }/2, p_1^{\prime } )} } \right\}$ has at least $\left| {P_{13} } \right| =6$ vertices of connection. Since in Lemma 9, it is proved that any two fragments $\phi _{\left( {k_1 , l_1 } \right) } , \quad \phi _{\left( {k_2 , l_2 } \right) }$ are distinct, this implies that all fragments in $\left\{ {\phi _{({n_1 }/2, p_1^{\prime } )} } \right\}$ are distinct. Since $p_1^{^{\prime }} =\left\{ {{\begin{array}{ll} {1,..., m_1 -1} &{} {\hbox {if }{n_1 \;}\hbox {is odd}} \\ {1, 2,..., {m_1 -r_7 }/2} &{} {\hbox {if }{n_1 \;}\hbox {is even}} \\ \end{array} }} \right.$, therefore $\left| {\phi _{\left( {{n_1 }/2,p_1^{\prime } } \right) } } \right| ={m_1 -r_7 }/2$. Also in Lemma 9, it is proved that $\phi _{\left( {{n_1 }/2, {m_1 }/2} \right) }$ has the same orientation as that of its mirror images. $\square$

Now if $m_1$ is an even integer, then all fragments in $\left\{ {\phi _{({n_1 }/2, p_1^{\prime } )} } \right\}$ are distinct and only one fragment $\phi _{\left( {{n_1 }/2, {m_1 }/2} \right) }$ in $\left\{ {\phi _{({n_1 }/2, p_1^{\prime } )} } \right\}$ has the same orientation as that of its mirror image. Hence there are $2\;\left| {P_{13} } \right| \;\left( {\left| {\phi _{(\frac{n_1 }{2}, p_1^{\prime } )} } \right| -1} \right) +\left| {P_{13} } \right| =12\left( {{m_1 -2}/2} \right) +6=6\left( {m_1 -1} \right)$ vertices of connection for all fragments in $\left\{ {\phi _{({n_1}/2, p_1^{\prime })}}\right\}$.

If $m_1$ is an odd integer, then all fragments in $\left\{ {\phi _{({n_1}/2, p_1^{\prime } )} } \right\}$ are distinct and none of them has the same orientation as that of its mirror image. Hence there are $2|P_{13}|\left| {\phi _{(\frac{n_1}{2}, p_1^{\prime } )} } \right| =6\left( {m_1 -1} \right)$ vertices of connection for all fragments in $\left\{ {\phi _{({n_1 }/2, p_1^{\prime } )} } \right\}$.

Lemma 14

• (i) If $n_1 \in 2{\mathbb {Z}}^{+}-1$, and the vertex $e_{{3\left( {n_1 -1} \right) }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_1 +1}/2}\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{{n_1 -1}/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3p_2^{\prime } +1}$, fixed by $\left( {xy} \right) ^{p_2^{\prime } }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -p_2^{\prime } }$ in $\left( {m_1 , m_2 } \right)$, then there are $\left( {m_2 -1} \right)$ distinct fragments, and there are $12\left( {m_2 -1} \right)$ vertices of connection of these fragments.

• (ii) If $n_1 \in 2{\mathbb {Z}}^{+}$, and the vertex $e_{{3n_1 }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_1 }/2}\left( {xy} \right) ^{n_2 }\left( {xy^{-1}} \right) ^{{n_1 }/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3p_2^{\prime } +1}$, fixed by $\left( {xy} \right) ^{p_2^{\prime } }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -p_2^{\prime } }$ in $\left( {m_1 , m_2 } \right)$, then there are $1/2\left( {m_2 -r_8 } \right)$ distinct fragments, and there are $6\left( {m_2 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $p_1^{\prime } , m_1 , m_2 , P_{13}$ and $\phi _{\left( {{n_1 -r_5 }/2, p_1^{\prime } } \right) }$ by $p_2^{\prime } ,m_2 ,m_1 ,P_{14}$ and $\phi _{\left( {{n_1 -r_5 }/2,p_2^{\prime } } \right) }^{\prime }$, respectively, in the proof of Lemma 13.

Let

$$\begin{aligned} p_1^{\prime \prime } =\left\{ {{\begin{array}{ll} 1,...,m_1 -1 &{} \hbox {if}\,n_2\,\hbox {is odd} \\ 1,2,...,\frac{m_1-r_7}{2}&{} \hbox {if}\,n_2\,\hbox {is even} \\ \end{array} }} \right. , \quad p_2^{\prime \prime }=\left\{ \begin{array}{ll} 1,...,m_2 -1&{}\hbox {if}\,n_2\,\hbox {is odd} \\ 1,2,...,\frac{m_2-r_8}{2} &{} \hbox {if}\,n_2\,\hbox {is even}\\ \end{array}.\right. \end{aligned}$$

Lemma 15

• (i) If $n_2 \in 2{\mathbb {Z}}^{+}-1$, and the vertex $f_{{3\left( {n_2 -1} \right) }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_2 +1}/2}\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{{n_2 -1}/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3p_1^{{\prime }{\prime }} +1}$, fixed by $\left( {xy} \right) ^{p_1^{{\prime }{\prime }} }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1^{{\prime }{\prime }} }$ in $\left( {m_1 ,m_2 } \right)$, then there are $\left( {m_1 -1} \right)$ distinct fragments, and there are $12\left( {m_1 -1} \right)$ vertices of connection of these fragments.

• (ii) If $n_2 \in 2{\mathbb {Z}}^{+}$, and the vertex $f_{{3n_2 }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_2 }/2}\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{{n_2 }/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $u_{3p_1^{{\prime }{\prime }} +1}$, fixed by $\left( {xy} \right) ^{p_1^{{\prime }{\prime }} }\left( {xy^{-1}} \right) ^{m_2 }\left( {xy} \right) ^{m_1 -p_1^{{\prime }{\prime }} }$ in $\left( {m_1 , m_2 } \right)$, then there are $1/2\left( {m_1 -r_7 } \right)$ distinct fragments, and there are $6\left( {m_1 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $p_1^{\prime } , n_1 , n_2 , P_{13}$ and $\phi _{\left( {{n_1 -r_5 }/2, p_1^{\prime } } \right) }$ by $p_1^{^{\prime \prime }} , n_2 ,n_1 , P_{15}$ and $\psi _{\left( {{n_2 -r_6 }/2,p_1^{{\prime }{\prime }} } \right) }$, respectively, in the proof of Lemma 13.

Lemma 16

• (i) If $n_2 \in 2{\mathbb {Z}}^{+}-1$, and the vertex $f_{{3\left( {n_2 -1} \right) }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_2 +1}/2}\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{{n_2 -1}/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3p_2^{{\prime }{\prime }} +1}$, fixed by $\left( {xy} \right) ^{p_2^{{\prime }{\prime }} }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -p_2^{{\prime }{\prime }} }$ in $\left( {m_1 , m_2 } \right)$, then there are $\left( {m_2 -1} \right)$ distinct fragments, and there are $12\left( {m_2 -1} \right)$ vertices of connection of these fragments.

• (ii) If $n_2 \in 2{\mathbb {Z}}^{+}$, and the vertex $f_{{3n_2 }/2}$, fixed by $\left( {xy^{-1}} \right) ^{{n_2 }/2}\left( {xy} \right) ^{n_1 }\left( {xy^{-1}} \right) ^{{n_2 }/2}$ in $\left( {n_1 ,n_2 } \right)$ is connected with the vertices $v_{3p_2^{{\prime }{\prime }} +1}$, fixed by $\left( {xy} \right) ^{p_2^{{\prime }{\prime }} }\left( {xy^{-1}} \right) ^{m_1 }\left( {xy} \right) ^{m_2 -p_2^{{\prime }{\prime }} }$ in $\left( {m_1 , m_2 } \right)$, then there are $1/2\left( {m_2 -r_7 } \right)$ distinct fragments, and there are $6\left( {m_2 -1} \right)$ vertices of connection of these fragments.

The proof is obtained by interchanging $n_1 , n_2 , m_1 , m_2 , p_1^{\prime } , P_{13}$ and $\phi _{\left( {{n_1 -r_5 }/2, p_1^{\prime } } \right) }$ by $n_2 ,n_1 , m_2 , m_1 , p_2^{^{\prime \prime }} ,P_{16}$ and $\psi _{\left( {{n_2 -r_6 }/2,p_2^{{\prime }{\prime }} } \right) }^{\prime }$, respectively, in the proof of Lemma 13.

Lemma 17

Let $\beta$ be the fragment formed by joining the vertex $f_{3n_2}$, fixed by $\left( {xy} \right) ^{n_1 }\left( {xy} \right) ^{n_2 }$ in $\left( {n_1 ,n_2 } \right)$ with the vertex $v_{3m_2}$, fixed by $\left( {xy} \right) ^{m_1 }\left( {xy} \right) ^{m_2 }$ in $\left( {m_1 ,m_2 } \right)$, then there are $6\left( {n_1 +n_2 +2} \right)$ vertices of connection for $\beta$.

Proof

Let us join the vertex $f_{3n_2}$, fixed by $\left( {xy}\right) ^{n_1}\left( {xy}\right) ^{n_2}$ in $\left( {n_1,n_2}\right)$ with the vertex $v_{3m_2}$, fixed by $\left( {xy}\right) ^{m_1}\left( {xy} \right) ^{m_2}$ in $\left( {m_1,m_2}\right)$, and create a fragment $\beta$. Then

$$\begin{aligned}&P_{17} \\&\quad =\left\{ {\begin{array}{l} x, xy^{-1}, xy, xyx, xyxy^{-1},\left( {xy} \right) ^{2},..., \left( {xy} \right) ^{n_1 -1}x, \left( {xy} \right) ^{n_1 -1}xy^{-1}, \left( {xy} \right) ^{n_1 },\left( {xy} \right) ^{n_1 }x, \left( {xy} \right) ^{n_1 }xy^{-1},\left( {xy} \right) ^{n_1 +1}, \\ y^{-1}, y, yx, yxy^{-1},yxy,\left( {yx} \right) ^{2},\left( {yx} \right) ^{2}y^{-1}, \left( {yx} \right) ^{2}y, \left( {yx} \right) ^{3},...,\left( {yx} \right) ^{n_2 -1}y^{-1}, \left( {yx} \right) ^{n_2 -1}y, \left( {yx} \right) ^{n_2 }, \\ \left( {yx} \right) ^{n_2 }y^{-1}, \left( {yx} \right) ^{n_2 }y, e \\ \end{array}} \right\} \end{aligned}$$

is the set of words such that for any $w\in P_{17}$, both the vertices $\left( {f_{3n_2 } } \right) w$ and $\left( {v_{3m_2}} \right) w$ lie on $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 , m_2 } \right)$, respectively. By Theorem 5, each fragment in $\beta$ has at least $\left| {P_{17} } \right| \;=3\left( {n_1 +n_2 +2} \right)$ vertices of connection in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 , m_2 } \right)$. $\square$

Now we show that $\beta$ has different orientations from its mirror image. By Theorem 4, if $V\left( {f_{3n_2 }^*, v_{3m_2 }^*} \right) \sim V\left( {f_{3n_2 } ,v_{3m_2 } } \right)$, then there exists a word $w\in P_{17}$ such that $\left( {f_{3n_2 } } \right) w=f_{3n_2 }^{*} , \quad \left( {v_{3m_2 } } \right) w=v_{3m_2 }^*$. There are two words $\left( {xy} \right) ^{n_1 }x, \left( {yx} \right) ^{n_2 -1}y\in P_{17}$, for which $\left( {f_{3n_2 } } \right) \left( {xy} \right) ^{n_1 }x=f_{3n_2 }^*$ and $\left( {f_{3n_2 } } \right) \left( {yx} \right) ^{n_2 -1}y=f_{3n_2 }^*$. But neither $\left( {v_{3m_2 } } \right) \left( {xy} \right) ^{n_1 }x=v_{3m_2 }^{*}$ nor $\left( {v_{3m_2 } } \right) \left( {yx} \right) ^{n_2 -1}y=v_{3m_2 }^{*}$. This implies that $V\left( {f_{3n_2 }^*, v_{3m_2 }^*} \right)$ is not equivalent to $V\left( {f_{3n_2 } , v_{3m_2 } } \right)$, that is, by joining $f_{3n_2 }$ with $v_{3m_2 }$ to create $\beta , \quad f_{3n_2 }^*$ is not connected with $v_{3m_2 }^*$. Therefore, $\beta$ has different orientations from its mirror image. So $\beta$ has $2\;\left| {P_{17} } \right| \;=6\left( {n_1 +n_2 +2} \right)$ vertices of connection in $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 , m_2 } \right)$.

Lemma 18

Let $\beta ^{{\prime }}$ be the fragment formed by joining the vertex $e_{3n_1}$, fixed by $\left( {xy} \right) ^{n_2 }\left( {xy} \right) ^{n_1 }$ in $\left( {n_1 ,n_2 } \right)$ with the vertex $v_{3m_2 }$, fixed by $\left( {xy} \right) ^{m_1 }\left( {xy} \right) ^{m_2 }$ in $\left( {m_1 , m_2 } \right)$, then there are $6\left( {n_1 +n_2 +2} \right)$ vertices of connection for $\beta ^{^{\prime }}$.

The proof is obtained by interchanging $n_1 , n_2 ,P_{17}$ and $\beta$ by $n_2 , n_1 ,P_{18}$ and $\beta ^{^{\prime }}$, respectively, in the proof of Lemma 17.

We define $\rho$ as

$$\begin{aligned} {\begin{array}{|l|l|l|} \hline {\left( {n_1 , n_2 } \right) } &{} {\left( {m_1 , m_2 } \right) } &{} \rho \\ \hline {\left( {\hbox {even,even}} \right) } &{} {\left( {\hbox {odd,odd}} \right) } &{} 0 \\ \hline {\left( {\hbox {even,odd}} \right) } &{} {\left( {\hbox {odd,odd}} \right) \hbox { }} &{} 2 \\ \hline {\left( {\hbox {odd,odd}} \right) } &{} {\left( {\hbox {odd,odd}} \right) } &{} 4 \\ \hline {\left( {\hbox {even,even}} \right) } &{} {\left( {\hbox {even,odd}} \right) } &{} 4 \\ \hline {\left( {\hbox {even,even}} \right) } &{} {\left( {\hbox {even,even}} \right) } &{} 8 \\ \hline {\left( {\hbox {even,odd}} \right) } &{} {\left( {\hbox {even,odd}} \right) } &{} 3 \\ \hline \end{array}}. \end{aligned}$$

Now we are in a position, to prove our main results.

Theorem 6

There are $1/2\left\{ {\left( {n_1 +n_2 } \right) \left( {m_1 +m_2 } \right) +\rho } \right\}$ polynomials obtained by joining the circuits $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 , m_2 } \right)$, where $n_2 <n_1 <m_2 <m_1$, at all vertices of connection.

Proof

Let us connect the following vertices

• (i) $f_{3n_2}$ with $u_{3i_1 +1} , u_{3j_1 +1} , v_{3i_1 +1} , v_{3j_2 +1}$.

• (ii) $e_{3n_1}$ with $u_{3i_2 +1} , u_{3j_3 +1} , v_{3i_2 +1} , v_{3j_4 +1}$.

• (iii) $e_{3q_1}$ with $u_{3p_1 +1} , v_{3p_2 +1}$.

• (iv) $f_{3q_2}$ with $u_{3p_1 +1} , v_{3p_2 +1}$.

• (v) $e_{{3\left( {n_1-r_5}\right) }/2}$ with $u_{3p_1^{\prime }+1},v_{3p_2^{\prime }+1}$.

• (vi) $f_{{3\left( {n_2 -r_6 } \right) }/2}$ with $u_{3p_1^{{\prime }{\prime }} +1} , v_{3p_2^{{\prime }{\prime }} +1}$.

• (vii) $v_{3m_2}$ with $f_{3n_2},e_{3n_1}$.

$\square$

Then by using Lemmas 1–18, we obtain the set of fragments

$$\begin{aligned} F=\left\{ {{\begin{array}{l} \gamma _{i_1},\mu _{j_1},\gamma _{i_1}^{\prime },\mu _{j_2}^{\prime },\lambda _{i_2},\nu _{j_3},\lambda _{i_2}^{\prime },\nu _{j_4}^{\prime },\phi _{\left( {q_1,p_1}\right) },\phi _{\left( {q_1,p_2}\right) }^{\prime },\psi _{\left( {q_2,p_1}\right) },\psi _{\left( {q_2,p_2}\right) }^{\prime }, \\ \phi _{\left( \frac{n_1-r_5}{2},p_1^{\prime }\right) },\phi _{\left( {\frac{n_1-r_5}{2},p_2^{\prime }}\right) }^{\prime },\psi _{\left( {\frac{n_2-r_6}{2},p_1^{{\prime }{\prime }}}\right) },\psi _{\left( {\frac{n_2-r_6}{2},p_1^{{\prime }{\prime }}}\right) }^{\prime },\beta ,\beta ^{^{\prime }} \\ \end{array}}}\right\} \end{aligned}$$

and there are

$$\begin{aligned} S= & {} 12\sum _{i_1=0}^{n_1 -1}\left( {i_1+2}\right) +12\left( {n_1+n_2+2}\right) +3\left( n_1+2 \right) \left( m_1+m_2-2n_1-2\right) \\&+\,12\sum _{i_2=1}^{n_2-1}\left( i_2+2\right) +3\left( n_2+2\right) \left( m_1+m_2-2n_2-2\right) \\&+\,6(n_1+n_2-2)(m_1+m_2-2) \end{aligned}$$

vertices of connection of these fragments. For $n_2 <n_1 <m_2 <m_1 , \quad S=9\left( {n_1 +n_2 } \right) \left( {m_1 +m_2 } \right)$, and so $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$ are connected at all points. Since $\left| F \right| =\frac{1}{2}\left\{ {\left( {n_1 +n_2 } \right) \left( {m_1 +m_2 } \right) +\rho } \right\}$, hence there are $1/2\left\{ {\left( {n_1 +n_2 } \right) \left( {m_1 +m_2 } \right) +\rho } \right\}$ distinct fragments, formed by joining the circuits $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 , m_2 } \right)$, where $n_2 <n_1 <m_2 <m_1$, at all vertices of connection. Since a unique polynomial is obtained from a fragment, hence there are $1/2\left\{ {\left( {n_1 +n_2 } \right) \left( {m_1 +m_2 } \right) +\rho } \right\}$ polynomials, obtained by joining the circuits $\left( {n_1 ,n_2 } \right)$ and $\left( {m_1 ,m_2 } \right)$, where $n_2 <n_1 <m_2 <m_1$, at all vertices of connection.

6 Conclusion

The total number of points of connection of $\left( {n_1,n_2}\right)$ and $\left( {m_1,m_2}\right)$ are $9\left( {n_1+n_2}\right) \left( {m_1+m_2}\right)$. Theorem 6, assures us, in order to create all the fragments, by joining $\left( {n_1,n_2}\right)$ and $\left( {m_1,m_2}\right)$, we just have to connect $1/2\left\{ {\left( {n_1+n_2}\right) \left( {m_1+m_2}\right) +\rho }\right\}$ vertices of these circuits. There is no need to connect these circuits at the remaining points. So, for each pair of circuits, we find a class of $1/2\left\{ {\left( {n_1+n_2}\right) \left( {m_1 +m_2 } \right) +\rho }\right\}$ number of fragments and corresponding to each such class, we get a class of polynomials. Each polynomial in this class splits linearly in a suitable Galois field [5] and corresponding to each zero, we get a triplet $\left( {\overline{x}, \overline{y},\overline{t}}\right)$ [7], which is a group. Hence each pair of circuits gives us a class of groups.