Non-isolating Bondage in Graphs

Abstract

A dominating set of a graph $G = (V,E)$ is a set D of vertices of G such that every vertex of $V(G){\setminus }D$ has a neighbor in D. The domination number of a graph G, denoted by $\gamma (G)$, is the minimum cardinality of a dominating set of G. The non-isolating bondage number of G, denoted by $b'(G)$, is the minimum cardinality among all sets of edges $E' \subseteq E$ such that $\delta (G-E') \ge 1$ and $\gamma (G-E') > \gamma (G)$. If for every $E' \subseteq E$ we have $\gamma (G-E') = \gamma (G)$ or $\delta (G-E') = 0$, then we define $b'(G) = 0$, and we say that G is a $\gamma$-non-isolatingly strongly stable graph. First we discuss various properties of non-isolating bondage in graphs. We find the non-isolating bondage numbers for several classes of graphs. Next we show that for every non-negative integer, there exists a tree having such non-isolating bondage number. Finally, we characterize all $\gamma$-non-isolatingly strongly stable trees.

1 Introduction

Let $G = (V,E)$ be a graph. By the neighborhood of a vertex v of G, we mean the set $N_G(v) = \{u \in V(G) :uv \in E(G)\}$. The degree of a vertex v, denoted by $d_G(v)$, is the cardinality of its neighborhood. Let $\delta (G)$ mean the minimum degree among all vertices of G. By a leaf we mean a vertex of degree one, while a support vertex is a vertex adjacent to a leaf. We say that a support vertex is strong (weak, respectively) if it is adjacent to at least two leaves (exactly one leaf, respectively). The distance between two vertices of a graph is the number of edges in a shortest path connecting them. The eccentricity of a vertex is the greatest distance between it and any other vertex. The diameter of a graph G, denoted by ${\mathrm{diam}}(G)$, is the maximum eccentricity among all vertices of G. We denote the path (cycle, respectively) on n vertices by $P_n$ ($C_n$, respectively). A wheel $W_n$, where $n \ge 4$, is a graph with n vertices, formed by connecting a vertex to all vertices of a cycle $C_{n-1}$. Let T be a tree, and let v be a vertex of T. We say that v is adjacent to a path $P_n$ if there is a neighbor of v, say x, of degree two such that the tree resulting from T by removing the edge vx, and which contains the vertex x, is a path $P_n$. Let $K_{p,q}$ denote a complete bipartite graph the partite sets of which have cardinalities p and q. By a star we mean a connected graph in which exactly one vertex has degree greater than one.

A subset $D \subseteq V(G)$ is a dominating set, abbreviated DS, of G if every vertex of $V(G){\setminus }D$ has a neighbor in D. The domination number of a graph G, denoted by $\gamma (G)$, is the minimum cardinality of a dominating set of G. For a comprehensive survey of domination in graphs, see for example [5].

The bondage number b(G) of a graph G is the minimum cardinality among all sets of edges $E' \subseteq E$ such that $\gamma (G-E') > \gamma (G)$. The concept of bondage in graphs was introduced in [2] and further studied for example in [1, 3, 4, 6–9].

We define the non-isolating bondage number of a graph G, denoted by $b'(G)$, to be the minimum cardinality among all sets of edges $E' \subseteq E$ such that $\delta (G-E')$ $\ge 1$ and $\gamma (G-E') > \gamma (G)$. Thus $b'(G)$ is the minimum number of edges of G that have to be removed in order to obtain a graph with no isolated vertices, and with the domination number greater than that of G. If for every $E' \subseteq E$ we have $\gamma (G-E') = \gamma (G)$ or $\delta (G-E') = 0$, then we define $b'(G) = 0$, and we say that G is a $\gamma$-non-isolatingly strongly stable graph.

First we discuss various properties of non-isolating bondage in graphs. We find the non-isolating bondage numbers for several classes of graphs. Next we show that for every non-negative integer, there exists a tree having such non-isolating bondage number. Finally, we characterize all $\gamma$-non-isolatingly strongly stable trees.

2 Results

We begin with the following well known observations.

For every graph G of diameter at least two there exists a $\gamma (G)$-set that contains all support vertices.

If H is a subgraph of G such that $V(H) = V(G)$, then $\gamma (H) \ge \gamma (G)$.

If n is a positive integer, then $\gamma (P_n) = \lfloor (n+2)/3 \rfloor$.

For every integer $n \ge 3$ we have $\gamma (C_n) = \lfloor (n+2)/3 \rfloor$.

Observation 1

If n is a positive integer, then $\gamma (K_n) = 1$.

Observation 2

For every integer $n \ge 4$ we have $\gamma (W_n) = 1$.

Observation 3

Let p and q be positive integers such that $p \le q$. Then

$$\begin{aligned} \gamma (K_{p,q}) = \left\{ \begin{array}{ll} 1 &{}\quad {\mathrm{if} }\, p = 1; \\ 2 &{}\quad {\mathrm{otherwise}.} \end{array} \right. \end{aligned}$$

First we calculate the non-isolating bondage numbers of paths.

Lemma 4

For any positive integer n we have

$$\begin{aligned} b'(P_n) = \left\{ \begin{array}{ll} 0 &{} \quad {{\mathrm{if}}}\, n = 1,2,3,4,5,7; \\ 1 &{} \quad {{\mathrm{if}}}\, n \ge 6 \;\,{ {\mathrm{and}} }\;\, n \ne 3k+1; \\ 2 &{} \quad {{\mathrm{if}}}\, n \ge 10\;\, {{\mathrm{and}} }\;\, n = 3k+1. \end{array} \right. \end{aligned}$$

Proof

Let us observe that if a path has at most five or exactly seven vertices, then removing any edges does not increase the domination number, or gives an isolated vertex. Assume that $n = 6$ or $n \ge 8$. First assume that $n = 3k$. We have $\gamma (P_n) = \lfloor (n+2)/3 \rfloor = \lfloor (3k+2)/3 \rfloor = k$. We also have $\gamma (P_{n-2})+\gamma (P_2)$ $= \lfloor n/3 \rfloor +1 = k+1 > \gamma (P_n)$. Thus $b'(P_n) = 1$ if $n = 3k$ and $n \ge 6$. Now assume that $n = 3k+2$. We have $\gamma (P_n) = \lfloor (n+2)/3 \rfloor = \lfloor (3k+4)/3 \rfloor = k+1$. We also have $\gamma (P_{n-4})+\gamma (P_4) = \lfloor n/3 \rfloor +2 = k+2 > \gamma (P_n)$. Thus $b'(P_n) = 1$ if $n = 3k+2$ and $n \ge 8$. Now assume that $n = 3k+1$. We have $\gamma (P_n) = \lfloor (n+2)/3 \rfloor$ $= \lfloor (3k+3)/3 \rfloor = k+1$. Let us observe that removing any edge does not increase the domination number. We have $\gamma (P_{n-6})+\gamma (P_4)+\gamma (P_2) = \lfloor (n-4)/3 \rfloor +3$ $= \lfloor (3k-3)/3 \rfloor +3 = k+2 > \gamma (P_n)$. Therefore $b'(P_n) = 2$ if $n = 3k+1$ and $n \ge 10$. $\square$

We now investigate the non-isolating bondage in cycles.

Lemma 5

For every integer $n \ge 3$ we have

$$\begin{aligned} b'(C_n) = \left\{ \begin{array}{ll} 0 &{}\quad {\mathrm{if} }\, b'(P_n) = 0; \\ b'(P_n)+1 &{}\quad {\mathrm{if} }\, b'(P_n) \ne 0. \end{array} \right. \end{aligned}$$

Proof

We have $\gamma (P_n) = \gamma (C_n)$. Clearly, $C_n-e = P_n$. This implies that $b'(C_n) = 0$ if $b'(P_n) = 0$, while $b'(C_n) = b'(P_n)+1$ if $b'(P_n) \ne 0$. $\square$

We now find the non-isolating bondage numbers of complete graphs.

Proposition 6

If n is a positive integer, then

$$\begin{aligned} b'(K_n) = \left\{ \begin{array}{ll} 0 &{}\quad {\mathrm{for} }\, n = 1,2,3; \\ \lfloor (n+1)/2 \rfloor &{}\quad {\mathrm{for} }\, n \ge 4. \end{array} \right. \end{aligned}$$

Proof

Obviously, $b'(K_1) = 0$ and $b'(K_2) = 0$. We have $K_3-e = C_3$ and $b'(C_3) = 0$. This implies that $b'(K_3) = 0$. Now assume that $n \ge 4$. By Observation 1 we have $\gamma (K_n) = 1$. Let us observe that the domination number of a graph equals one if and only if the graph has a universal vertex. Given a complete graph, we increase the domination number if and only if for every vertex we remove at least one incident edge. If n is even, then we remove $n/2 = \lfloor (n+1)/2 \rfloor$ edges. If n is odd, then we remove $(n-1)/2+1 = (n+1)/2 = \lfloor (n+1)/2 \rfloor$ edges. $\square$

We now calculate the non-isolating bondage numbers of wheels.

Proposition 7

For integers $n \ge 4$ we have

$$\begin{aligned} b'(W_n) = \left\{ \begin{array}{ll} 2 &{} \quad {\mathrm{if} }\, n = 4; \\ 1 &{} \quad {\mathrm{if} }\, n \ge 5. \end{array} \right. \end{aligned}$$

Proof

Since $W_4 = K_4$, using Proposition 6 we get $b'(W_4) = b'(K_4) = \lfloor 5/2 \rfloor = 2$. Now assume that $n \ge 5$. By Observation 2 we have $\gamma (W_n) = 1$. The domination number of a graph equals one if and only if it has a universal vertex. Removing an edge of $W_n$ incident to the vertex of maximum degree gives a graph without universal vertices. Therefore $b'(W_n) = 1$ for $n \ge 5$. $\square$

We now investigate the non-isolating bondage in complete bipartite graphs.

Proposition 8

Let p and q be positive integers such that $p \le q$. Then

$$\begin{aligned} b'(K_{p,q}) = \left\{ \begin{array}{ll} 0 &{}\quad {\mathrm{if} }\, p = 1,2; \\ 4 &{}\quad {\mathrm{if} }\, p = 3; \\ p &{}\quad {\mathrm{otherwise}.} \end{array} \right. \end{aligned}$$

Proof

Let $E(K_{p,q}) = \{a_ib_j :1 \le i \le p \ {\mathrm{and} } \ 1 \le j \le q\}$. If $p = 1$, then obviously $b'(K_{p,q}) = 0$ as removing any edge produces an isolated vertex. Now assume that $p \ge 2$. By Observation 3 we have $\gamma (K_{p,q}) = 2$. Let $E'$ be a subset of the set of edges of $K_{2,q}$ such that $\delta (K_{2,q}-E') \ge 1$. Each vertex $b_i$ is adjacent to $a_1$ or $a_2$ in the graph $K_{2,q}-E'$. Observe that the vertices $a_1$ and $a_2$ form a dominating set of $K_{2,q}-E'$. Therefore $b'(K_{2,q}) = 0$. Now assume that $p = 3$. It is not very difficult to verify that removing any three edges does not increase the domination number while not producing an isolated vertex. We have $\gamma (K_{3,q}-a_1b_2-a_1b_3$ $-a_2b_1-a_3b_1) = 3 > 2 = \gamma (K_{3,q})$. Therefore $b'(K_{3,q}) = 4$. Now assume that $p \ge 4$. If we remove at most $p-1$ edges, then there are vertices $a_i$ and $b_j$ which have degrees q and p, respectively. It is easy to observe that the vertices $a_i$ and $b_j$ still form a dominating set. Let us observe that $\gamma (K_{p,q}-a_1b_1-a_2b_1-a_3b_2$ $-a_4b_2-a_5b_2-\cdots -a_pb_2) = 3 > 2 = \gamma (K_{p,q})$. Therefore $b'(K_{p,q}) = p$ if $p \ge 4$. $\square$

The authors of [2] proved that the bondage number of any tree is either one or two.

Theorem 9

([2]) For every tree T we have $b(T) \in \{1,2\}$.

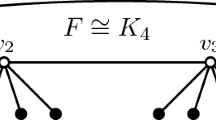
Let us observe that for every non-negative integer there exists a tree with such non-isolating bondage number. We have $b'(P_4) = 0$. For positive integers k, consider trees $T_k$ of the form presented in Fig. 1. It is not difficult to verify that $b'(T_k) = k$.

Fig. 1

A tree $T_k$ having $4k+2$ vertices, where both central vertices are of degree $k+1$

Hartnell and Rall [3] characterized all trees with bondage number equal to two. We characterize all trees with the non-isolating bondage number equal to zero, that is, all $\gamma$-non-isolatingly strongly stable trees.

We now show that joining two $\gamma$-non-isolatingly strongly stable trees gives us also a $\gamma$-non-isolatingly strongly stable tree.

Lemma 10

Let $T_1$ and $T_2$ be vertex-disjoint $\gamma$-non-isolatingly strongly stable trees. Let x be a support vertex of $T_1$ and let y be a leaf of $T_2$. Let T be a tree obtained by joining the vertices x and y. If $\gamma (T) = \gamma (T_1)+\gamma (T_2)$, then the tree T is also $\gamma$-non-isolatingly strongly stable.

Proof

Let $E_1$ be a subset of the set of edges of T such that $\delta (T-E_1) \ge 1$. If $xy \in E_1$, then we get $\gamma (T-E_1) = \gamma (T_1-E_1 \cap E(T_1))+\gamma (T_2-E_1 \cap E(T_2)) = \gamma (T_1)+\gamma (T_2) = \gamma (T)$. Now assume that $xy \notin E_1$. Let z be the neighbor of y other than x. If $yz \notin E_1$, then let $E_2 = E_1 \cup \{xy\}$. Similarly as earlier we get $\gamma (T-E_2) = \gamma (T)$. We have $\gamma (T-E_1) \le \gamma (T-E_2)$, and consequently, $\gamma (T-E_1) = \gamma (T)$. Now assume that $yz \in E_1$. Let $E_3 = E_1 \cup \{xy\}{\setminus }\{yz\}$. Similarly as earlier we get $\gamma (T-E_3) = \gamma (T)$. Let $D_2$ be a $\gamma (T-E_3)$-set that contains the vertices x and z. It is easy to observe that $D_2$ is also a DS of the graph $T-E_1$. Therefore $\gamma (T-E_1) \le \gamma (T-E_3)$. This implies that $\gamma (T-E_1) = \gamma (T)$. We now conclude that $b'(T) = 0$. $\square$

We next show that a subtree of a $\gamma$-non-isolatingly strongly stable tree is also $\gamma$-non-isolatingly strongly stable.

Lemma 11

Let T be a $\gamma$-non-isolatingly strongly stable tree. Assume that $T'$ is a subtree of T such that $T-T'$ has no isolated vertices. Then $b'(T') = 0$.

Proof

If $T'$ consists of a single vertex, then obviously $b'(T') = 0$. Thus assume that $T' \ne K_1$. Let $E_1$ be the minimum subset of E(T) such that $T'$ is a component of $T-E_1$. Now let $E'$ be a subset of $E(T')$ such that $\delta (T'-E') \ge 1$. Notice that $\delta (T-E_1-E') \ge 1$. The assumption $b'(T) = 0$ implies that $\gamma (T-E_1) = \gamma (T)$ and $\gamma (T-E_1-E') = \gamma (T)$. We have $T-E_1-E' = T'-E' \cup (T-T')$ and $T-E_1 = T' \cup (T-T')$. We now get $\gamma (T'-E') = \gamma (T-E_1-E')-\gamma (T-T')$ $= \gamma (T)-\gamma (T-E_1)+\gamma (T') = \gamma (T')$. This implies that $b'(T') = 0$. $\square$

For the purpose of characterizing all $\gamma$-non-isolatingly strongly stable trees, we introduce a family $\mathcal {T}$ of trees $T = T_k$ that can be obtained as follows. Let $T_1 \in \{P_1,P_2\}$. If k is a positive integer, then $T_{k+1}$ can be obtained recursively from $T_k$ by one of the following operations.

• Operation $\mathcal {O}_1$: Attach a vertex by joining it to any support vertex of $T_k$.

• Operation $\mathcal {O}_2$: Attach a path $P_2$ by joining one of its vertices to a vertex of $T_k$, which is adjacent to a path $P_1$ or $P_4$, or is not a leaf and is adjacent to a support vertex.

• Operation $\mathcal {O}_3$: Attach a path $P_3$ by joining one of its leaves to a vertex of $T_k$ adjacent to a path $P_1$ or $P_3$.

• Operation $\mathcal {O}_4$: Attach a path $P_5$ by joining one of its leaves to any support vertex of $T_k$.

We now prove that every tree of the family $\mathcal {T}$ is $\gamma$-non-isolatingly strongly stable.

Lemma 12

If $T \in \mathcal {T}$, then $b'(T) = 0$.

Proof

We use induction on the number k of operations performed to construct the tree T. If $T = P_1$, then obviously $b'(T) = 0$. If $T = P_2$, then $b'(T) = 0$ as removing the edge gives isolated vertices. Let k be a positive integer. Assume that the result is true for every tree $T' = T_k$ of the family $\mathcal {T}$ constructed by $k-1$ operations. Let $T = T_{k+1}$ be a tree of the family $\mathcal {T}$ constructed by k operations.

First assume that T is obtained from $T'$ by Operation $\mathcal {O}_1$. Let x be the attached vertex, and let y be its neighbor. Let z be a leaf adjacent to y and different from x. Let D be a $\gamma (T)$-set that contains all support vertices. The set D is minimal, thus $x \notin D$. Obviously, D is a DS of the tree $T'$. Therefore $\gamma (T')$ $\le \gamma (T)$. Now let $E'$ be a subset of the set of edges of T such that $\delta (T-E') \ge 1$. Since both x and z are leaves of T, we have $xy \notin E'$ and $yz \notin E'$. The assumption $b'(T') = 0$ implies that $\gamma (T'-E') = \gamma (T')$. Let us observe that there exists a $\gamma (T'-E')$-set that contains the vertex y. Let $D'$ be such a set. It is easy to see that $D'$ is a DS of the graph $T-E'$. Thus $\gamma (T-E') \le \gamma (T'-E')$. We now get $\gamma (T-E') \le \gamma (T'-E') = \gamma (T') \le \gamma (T)$. On the other hand, we have $\gamma (T-E') \ge \gamma (T)$. This implies that $\gamma (T-E') = \gamma (T)$, and consequently, $b'(T) = 0$.

Now assume that T is obtained from $T'$ by Operation $\mathcal {O}_2$. The vertex to which is attached $P_2$ we denote by x. Let $v_1v_2$ be the attached path. Let $v_1$ be joined to x. If x is adjacent to a leaf or a support vertex, say a, then let D be a $\gamma (T)$-set that contains all support vertices. We have $v_2 \notin D$ as the set D is minimal. It is easy to observe that $D{\setminus }\{v_1\}$ is a DS of the tree $T'$. If x is adjacent to a path $P_4$, then we denote it by abcd. Let a and x be adjacent. Let us observe that there exists a $\gamma (T)$-set that contains the vertices $v_1$, c, and x. Let D be such a set. It is easy to observe that $D{\setminus }\{v_1\}$ is a DS of the tree $T'$. We conclude that $\gamma (T') \le \gamma (T)-1$. Now let $E'$ be a subset of the set of edges of T such that $\delta (T-E') \ge 1$. Since $v_2$ is a leaf of T, we have $v_1v_2 \notin E'$. If $xv_1 \in E'$, then $\delta (T'-(E' \cap E(T'))) \ge 1$. We get $\gamma (T-E') = \gamma (P_2 \cup T'-(E'{\setminus }\{xv_1\}))$ $= \gamma (T'-(E' \cap E(T')))+\gamma (P_2) = \gamma (T')+1 \le \gamma (T)$. Now assume that $xv_1 \notin E'$. By $T_x$ ($T_x'$, respectively), we denote the component of $T-E'$ ($T'-E'$, respectively) which contains the vertex x. If $\delta (T'-(E' \cap E(T'))) \ge 1$, then let $D_x'$ be any $\gamma (T_x')$-set. It is easy to see that $D_x' \cup \{v_1\}$ is a DS of the tree $T_x$. Thus $\gamma (T_x) \le \gamma (T_x')+1$. We now get $\gamma (T-E') = \gamma (T-E'-T_x)+\gamma (T_x) \le \gamma (T-E'-T_x)+\gamma (T_x')+1$ $= \gamma (T'-E'-T_x')+\gamma (T_x')+1 = \gamma (T'-E')+1 = \gamma (T')+1 \le \gamma (T)$. Now assume that $\delta (T'-(E' \cap E(T'))) = 0$. This implies that x is the only isolated vertex of $T'-(E' \cap E(T'))$, and so x is not adjacent to any leaf in the trees $T'$ and T. Consequently, $T_x'$ consists only of the vertex x, and $T_x$ is a path $P_3$. Let us observe that $\delta (T'-(E'{\setminus }\{xa\})) \ge 1$. Let $T_a'$ be the component of $T'-E'$, which contains the vertex a. Now let $T_a''$ be a tree obtained from $T_a'$ by attaching a vertex to the vertex a. We now get $\gamma (T-E') = \gamma (T-E'-T_x)+\gamma (P_3) = \gamma (T'-E'-T_x')+1$ $= \gamma (T'-E'-T_x'-T_a')+\gamma (T_a')+1 \le \gamma (T'-E'-T_x'-T_a')+\gamma (T_a'')+1 = \gamma ((T'-E'$ $-T_x'-T_a') \cup T_a'')+1 = \gamma (T'-(E'{\setminus }\{xa\}))+1 = \gamma (T'-E')+1 = \gamma (T')+1 \le \gamma (T)$. We conclude that $\gamma (T-E') = \gamma (T)$, and consequently, $b'(T) = 0$.

Now assume that T is obtained from $T'$ by Operation $\mathcal {O}_3$. The vertex to which is attached $P_3$ we denote by x. If x is a support vertex, then using Lemma 10, for $T_1 = T'$ and $T_2 = P_3$, we get $b'(T) = 0$. Now assume that x is adjacent to a path $P_3$, say abc. Let a and x be adjacent. The attached path we denote by $v_1v_2v_3$. Let $v_1$ be joined to x. Let us observe that there exists a $\gamma (T)$-set that contains all support vertices and does not contain the vertex $v_1$. Let D be such a set. We have $v_3 \notin D$ as the set D is minimal. Observe that $D{\setminus }\{v_2\}$ is a DS of the tree $T'$. Therefore $\gamma (T') \le \gamma (T)-1$. Now let $E'$ be a subset of the set of edges of T such that $\delta (T-E') \ge 1$. We have $v_2v_3$ $\notin E'$ as the vertex $v_3$ is a leaf. If $xv_1 \in E'$, then $v_1v_2 \notin E'$; otherwise we get an isolated vertex. Let us observe that $\delta (T'-(E' \cap E(T'))) \ge 1$. We get $\gamma (T-E')$ $=~\gamma (P_3 \cup T-(E'{\setminus }\{xv_1\})) = \gamma (T'-(E' \cap E(T')))+\gamma (P_3) = \gamma (T')+1 \le \gamma (T)$. Now assume that $xv_1 \notin E'$. Because of the similarity between the paths abc and $v_1v_2v_3$ adjacent to the vertex x, it suffices to consider only the possibility when $xa \notin E'$. Let us observe that $\delta (T'-(E' \cap E(T'))) \ge 1$. By $T_x$ ($T_x'$, respectively), we denote the component of $T-E'$ ($T'-(E' \cap E(T'))$, respectively) which contains the vertex x. If $v_1v_2 \notin E'$, then let $D_x'$ be any $\gamma (T_x')$-set. It is easy to see that $D_x' \cup \{v_2\}$ is a DS of the tree $T_x$. Thus $\gamma (T_x) \le \gamma (T_x')+1$. We now get $\gamma (T-E') = \gamma (T-E'-T_x)+\gamma (T_x) \le \gamma (T-E'-T_x)+\gamma (T_x')+1$ $= \gamma (T'-E'-T_x')+\gamma (T_x')+1 = \gamma (T'-E')+1 = \gamma (T')+1 \le \gamma (T)$. Now assume that $v_1v_2 \in E'$. Because of the similarity between the paths abc and $v_1v_2v_3$, it suffices to consider only the possibility when $ab \in E'$. Let $D_x'$ be a $\gamma (T_x')$-set that contains all support vertices (so $x \in D_x'$). It is easy to see that $D_x'$ is a DS of the tree $T_x$. Thus $\gamma (T_x) \le \gamma (T_x')$. We get $\gamma (T-E') = \gamma (T-E'-T_x)+\gamma (T_x)$ $\le \gamma (T-E'-T_x)+\gamma (T_x') = \gamma (T'-E'-T_x')+\gamma (T_x') = \gamma (T'-E') = \gamma (T') \le \gamma (T)$. We now conclude that $\gamma (T-E') = \gamma (T)$, and consequently, $b'(T) = 0$.

Now assume that T is obtained from $T'$ by Operation $\mathcal {O}_4$. By Lemma 4 we have $b'(P_5) = 0$. Using Lemma 10, for $T_1 = T'$ and $T_2 = P_5$, we get $b'(T) = 0$. $\square$

We now prove that if a tree is $\gamma$-non-isolatingly strongly stable, then it belongs to the family $\mathcal {T}$.

Lemma 13

Let T be a tree. If $b'(T) = 0$, then $T \in \mathcal {T}$.

Proof

If ${\mathrm{diam}}(T) \in \{0,1\}$, then $T \in \{P_1,P_2\} \subseteq \mathcal {T}$. If ${\mathrm{diam}}(T) = 2$, then T is a star. The tree T can be obtained from $P_2$ by an appropriate number of Operations $\mathcal {O}_1$. Thus $T \in \mathcal {T}$. Now assume that ${\mathrm{diam}}(T) \ge 3$. Thus the order n of the tree T is at least four. We obtain the result by the induction on the number n. Assume that the lemma is true for every tree $T'$ of order $n' < n$.

First assume that some support vertex of T, say x, is strong. Let y be a leaf adjacent to x. Let $T' = T-y$. Let $D'$ be a $\gamma (T')$-set that contains all support vertices. It is easy to see that $D'$ is a DS of the tree T. Thus $\gamma (T) \le \gamma (T')$. Now let $E'$ be a subset of the set of edges of $T'$ such that $\delta (T'-E') \ge 1$. Since $b'(T) = 0$, we have $\gamma (T-E') = \gamma (T)$. Let us observe that there exists a $\gamma (T-E')$-set that contains the vertex x. Let D be such a set. The set D is minimal, thus $y \notin D$. Obviously, D is a DS of the graph $T'-E'$. Therefore $\gamma (T'-E') \le \gamma (T-E')$. We now get $\gamma (T'-E') \le \gamma (T-E') = \gamma (T) \le \gamma (T')$. On the other hand, we have $\gamma (T'-E') \ge \gamma (T')$. This implies that $\gamma (T'-E') = \gamma (T')$, and consequently, $b'(T') = 0$. By the inductive hypothesis, we have $T' \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_1$. Thus $T \in \mathcal {T}$. Henceforth, we assume that every support vertex of T is weak.

We now root T at a vertex r of maximum eccentricity ${\mathrm{diam}}(T)$. Let t be a leaf at maximum distance from r, v be the parent of t, and u be the parent of v in the rooted tree. If ${\mathrm{diam}}(T) \ge 4$, then let w be the parent of u. If ${\mathrm{diam}}(T) \ge 5$, then let d be the parent of w. If ${\mathrm{diam}}(T) \ge 6$, then let e be the parent of d. By $T_x$ we denote the subtree induced by a vertex x and its descendants in the rooted tree T.

Assume that $d_T(u) \ge 3$. Thus some child of u is a leaf or a support vertex other than v. Let $T' = T-T_v$. By Lemma 11 we have $b'(T') = 0$. By the inductive hypothesis, we have $T' \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_2$. Thus $T \in \mathcal {T}$.

Now assume that $d_T(u) = 2$. Assume that $d_T(w) \ge 3$. First assume that there is a child of w other than u, say k, such that the distance of w to the most distant vertex of $T_k$ is three. It suffices to consider only the possibility when $T_k$ is a path $P_3$, say klm. Let $T' = T-T_u$. By Lemma 11 we have $b'(T') = 0$. By the inductive hypothesis, we have $T' \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_3$. Thus $T \in \mathcal {T}$.

Now assume that some child of w is a leaf. Let $T' = T-T_u$. By Lemma 11 we have $b'(T') = 0$. By the inductive hypothesis, we have $T' \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_3$. Thus $T \in \mathcal {T}$.

Thus there is a child of w, say k, such that the distance of w to the most distant vertex of $T_k$ is two. Consequently, k is a support vertex of degree two. Due to the earlier analysis of the children of the vertex u, it suffices to consider only the possibility when $d_T(w) = 3$. Let $T' = T-T_w$. It is easy to observe that $D' \cup \{v,k\}$ is a DS of the tree T. Thus $\gamma (T) \le \gamma (T')+2$. We have $\delta (T-dw-uv-wk) \ge 1$. We now get $\gamma (T-dw-uv-wk) = \gamma (T' \cup P_2 \cup P_2 \cup P_2) = \gamma (T')+3\gamma (P_2)$ $= \gamma (T')+3 \ge \gamma (T)+1 > \gamma (T)$. This implies that $b'(T) \ne 0$, a contradiction.

If $d_T(w) = 1$, then $T = P_4$. Let $T' = P_2 \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_2$. Thus $T \in \mathcal {T}$. Now assume that $d_T(w) = 2$. First assume that there is a child of d other than w, say k, such that the distance of d to the most distant vertex of $T_k$ is four or one. It suffices to consider only the possibilities when $T_k$ is a path $P_4$, or k is a leaf. Let $T' = T-T_w$. Let us observe that there exists a $\gamma (T')$-set that contains the vertex d. Let $D'$ be such a set. It is easy to observe that $D' \cup \{v\}$ is a DS of the tree T. Thus $\gamma (T) \le \gamma (T')+1$. We have $\delta (T-dw-uv) \ge 1$. We now get $\gamma (T-dw-uv) = \gamma (T' \cup P_2 \cup P_2)$ $= \gamma (T')+2\gamma (P_2) = \gamma (T')+2 \ge \gamma (T)+1 > \gamma (T)$. This implies that $b'(T) \ne 0$, a contradiction.

Now assume that there is a child of d, say k, such that the distance of d to the most distant vertex of $T_k$ is three. It suffices to consider only the possibility when $T_k$ is a path $P_3$, say klm. Let $T' = T-T_l$. Due to the similarity of $T'$ to the tree T from the previous case when d is adjacent to a leaf, we conclude that $b'(T') \ne 0$. On the other hand, by Lemma 11 we have $b'(T') = 0$, a contradiction.

Now assume that there is a child of d, say k, such that the distance of d to the most distant vertex of $T_k$ is two. Thus k is a support vertex of degree two. Let $T' = T-T_k$. By Lemma 11 we have $b'(T') = 0$. By the inductive hypothesis, we have $T' \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_2$. Thus $T \in \mathcal {T}$.

If $d_T(d) = 1$, then $T = P_5$. Let $T' = P_2 \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_3$. Thus $T \in \mathcal {T}$.

Now assume that $d_T(d) = 2$. First assume that e is adjacent to a leaf, say k. Let $T' = T-T_d$. By Lemma 11 we have $b'(T') = 0$. By the inductive hypothesis, we have $T' \in \mathcal {T}$. The tree T can be obtained from $T'$ by Operation $\mathcal {O}_4$. Thus $T \in \mathcal {T}$.

Now assume that e is not adjacent to any leaf. Let $E'$ be the set of edges incident with e excluding ed. Let $G' = T-T_d-e$. Let $D'$ be any $\gamma (G')$-set. It is easy to observe that $D' \cup \{d,v\}$ is a DS of the tree T. Thus $\gamma (T)\, \le \gamma (G')+2$. We have $\delta (T-(E' \cup \{dw,uv\})) \ge 1$. We now get $\gamma (T-(E' \cup \{dw,uv\})) = \gamma (G'$ $\cup P_2 \cup P_2 \cup P_2) = \gamma (G')+3\gamma (P_2) = \gamma (G')+3 \ge \gamma (T)+1 > \gamma (T)$. This implies that $b'(T) \ne 0$, a contradiction. $\square$

As an immediate consequence of Lemmas 12 and 13, we have the following characterization of all $\gamma$-non-isolatingly strongly stable trees.

Theorem 14

Let T be a tree. Then $b'(T) = 0$ if and only if $T \in \mathcal {T}$.