The Harmonic Index of Some Graphs

Abstract

The harmonic index of a graph G is defined as the sum of weights $\frac{2}{d(u)+d(v)}$ over all edges uv of G, where d(u) and d(v) are the degrees of the vertices u and v in G, respectively. Let $\mathscr {T}(n,\gamma )$ and $\mathscr {C}_n^\pi$ be the sets of trees of order n with domination number $\gamma$ and connected graphs of order n with degree sequence $\pi$, respectively. In this paper, the tree with minimum harmonic index among trees in $\mathscr {T}(n,\gamma )$ is determined, as well as the trees with maximum harmonic index among trees in $\mathscr {T}(n,\gamma )$ when $\gamma =2,\lceil \frac{n}{3}\rceil$. Moreover, we show that among graphs in $\mathscr {C}_n^\pi$, the maximum harmonic index is attained by a BFS graph.

1 Introduction

Let G be a simple connected graph with vertex set V(G) and edge set E(G). Its order is |V(G)|, denoted by n. For $v\in V(G)$, let $N_G(v)$ be the set of neighbors of v in G. $d_G(v) = |N_G(v)|$ is called the degree of v in G or written as d(v) for short. A pendent vertex of G is a vertex of degree 1. Let $\triangle =\triangle (G)$ denote the maximum degree of G. The distance of u and v (in G) is the length of the shortest path between u and v, denoted by d(u, v). We use $G-uv$ to denote the graph obtained from G by deleting the edge $uv\in E(G)$ from G. Similarly, $G+uv$ is the graph obtained by adding an edge $uv\notin E(G)$ to G. As usual, we denote by $P_n$ the path of order n.

The Randić index and the second Zagreb index of G are defined in [14] and [6] as the sums of the weights $\left( d(u)d(v)\right) ^{-\frac{1}{2}}$ and the weights d(u)d(v) over all edges uv of G, respectively. Those indices are two of the most successful molecular descriptors in structure–property and structure–activity relationship studies. The mathematical properties of those graph invariants have been studied extensively (see recent book [5], survey [8] and papers [6, 7]). Another variant of the Randić index (or the Zagreb index), named the harmonic index H(G), which is defined in [3] as

$$\begin{aligned} H(G)=\sum _{uv\in E(G)}\frac{2}{d(u)+d(v)}, \end{aligned}$$

where the summation goes over all edges uv of G. Estimating bounds for H(G) is of great interest, and there are many results that have been obtained. For example, Zhong [19–21] gave the minimum and maximum values of the harmonic index for simple connected graphs, trees, unicyclic graphs and bicyclic graphs and characterized the corresponding extremal graphs, respectively. Favaron et al. [4], Deng et al. [2], Lv and Li [11, 12] established the relationships between the harmonic index of a graph and its the eigenvalues, its chromatic number, its matching number, respectively; More results on the harmonic index of a graph can been found in [9, 16].

Recall that a matching of a graph G is a set of independent edges of G, and the matching number $\beta (G)$ is the cardinality of a maximum matching of G. A subset S of V(G) is called a dominating set of G if for every vertex $v\in V\backslash S$, there exists a vertex $u\in S$ such that v is adjacent to u. A vertex in the dominating set is called dominating vertex. For a dominating set S of G and $u\in S$ and $v\in V(G)\backslash S$, if $uv\in E(G)$, then v is said to be dominated by u. The domination number of graph G, denoted by $\gamma (G)$, is defined as the minimum cardinality of dominating sets of G. Let $\mathscr {T}(n,\gamma )$ be the set of trees of order n with domination number $\gamma$.

A non-increasing sequence $\pi (G)=(d_0, d_1,\ldots ,d_{n-1})$ of non-negative integers is called a degree sequence (or graphic) if there exists a graph G of order n for which $d_0, d_1,\;dots,d_{n-1}$ are the degrees of its vertices. Given a degree sequence $\pi (G)=(d_0, d_1,\ldots ,d_{n-1})$ , let $\mathscr {T}_n^\pi$ and $\mathscr {C}_n^\pi$ be the sets of trees and connected graphs of order n with degree sequence $\pi$, respectively.

In this paper, the tree with minimum harmonic index among trees in $\mathscr {T}(n,\gamma )$ is determined, as well as the trees with maximum harmonic index among trees in $\mathscr {T}(n,\gamma )$ when $\gamma =2,\lceil \frac{n}{3}\rceil$. Moreover, we show that among graphs in $\mathscr {C}_n^\pi$, the maximum harmonic index is attained by a BFS graph.

2 Preliminaries

In this section, we present some of the preliminaries to be used in our argument.

Let $\pi =(d_0,d_1,\ldots ,d_{n-1})$ be a non-increasing degree sequence, and $G\in \mathscr {C}_n^\pi$. We introduce an ordering of the vertices of G induced by breadth-first search (BFS for short): Create a sorted list of vertices beginning with $v_0$, a vertex of degree $d(v_0)=d_0=\triangle (G)$; append all neighbors $v_1,v_2, \ldots , v_{d_0}$ of $v_0$ sorted by decreasing degrees; then append all neighbors of $v_1$ that are not already in the list, also sorted by decreasing degrees; continue recursively with $v_2,v_3,\ldots$, until all vertices of G are processed. In this way, we get a rooted graph $G^\prime \in \mathscr {C}_n^\pi$ with root $v_0$. For a graph G with root $v_0$, the distance $d(v,v_0)$ is called the height h(v) of a vertex v, and $h(G)=\max \{h(v)|v\in V\}$ the height of G. Note that $h(G)\ge 1$ for any non-trivial graph G. Let $V_i=\{v\in V|d(v,v_0)=i\}$, $i=0,1,\ldots ,h(G)$. Then obviously, $V_0=\{v_0\}$, $V_1=N(v_0)$, $N(u)\subseteq V_{h(u)-1}\cup V_{h(u)}\cup V_{h(u)+1}$ if $1\le h(u)\le h(G)-1$, and $N(u)\subseteq V_{h(G)-1}\cup V_{h(G)}$ if $h(u)=h(G)$. Moreover, for a vertex $v_i\in V_i$, $i\ge 1$, $N(v_i)\cap V_{i-1}\ne \emptyset$. We call the least one in $N(v_i)\cap V_{i-1}$ in the ordering the parent of $v_i$.

Definition 2.1

([1, 18]) Let G be a connected rooted graph with root $v_0$. A well ordering $\prec$ of the vertices is called breadth-first searching ordering with non-increasing degrees (BFS ordering for short) if the following conditions holds for all vertices u, $v\in V$:

• (i) $u\prec v$ implies $h(u)\le h(v)$;

• (ii) $u\prec v$ implies $d(u)\ge d(v)$;

• (iii) let uv, $xy\in E$ and uy, $xv\notin E$ with $h(u)=h(x)=h(v)-1=h(y)-1$. If $u\prec x$ , then $v\prec y$.

A graph having a BFS ordering of its vertices is called a BFS graph. If a BFS graphs is a tree, then it is also called a BFS tree.

Fact 2.2

• (a) Every graph has an ordering of its vertices which satisfies the conditions (i) and (iii) by using breadth-first search.

• (b) Not all connected graphs have an ordering that satisfies the condition (ii). Hence not all connected graphs are BFS graphs.

• (c) Given a degree sequence $\pi$ , there may exist more than one BFS graphs in $\mathscr {C}_n^\pi$. If $\pi$ is a tree degree sequence, then there exist a unique BFS tree in $\mathscr {C}_n^\pi$ (under isomorphism).

• (d) If $\pi$ is a tree degree sequence, then T is a greedy tree (see Definition 2.3) in $\mathscr {T}_n^\pi$ if and only if T is a BFS tree in $\mathscr {T}_n^\pi$.

Definition 2.3

([15]) Suppose that the degrees of the non-leaf vertices are given. The greedy tree is achieved by the following ”greedy algorithm”:

• (1) Label the vertex with the largest degree as v (the root).

• (2) Label the neighbors of v as $v_1, v_2,\ldots ,$ assign the largest degrees available to them such that $d(v_1)\ge d(v_2)\ge \cdots$.

• (3) Label the neighbors of $v_1$ (except v) as $v_{11}, v_{12},\cdots$, such that they take all the largest degrees available and that $d(v_{11})\ge d(v_{12})\ge \ldots$ then do the same for $v_2, v_3, \ldots$.

• (4) Repeat (3) for all the newly labeled vertices, always start with the neighbors of the labeled vertex with largest degree whose neighbors are not labeled yet.

Let n and $\beta$ be positive integers and $n\ge 2\beta$. Let $T^0(n,\beta )$ be a tree of order n, which is obtained from a star $S_{n-\beta +1}$ by attaching a pendant edge to each of certain $\beta -1$ non-central vertices of $S_{n-\beta +1}$. Obviously, $T^0(n,\beta )$ is a tree of order n with an $\beta$-matching, where $T^0(n,\beta )$ is shown in Fig. 1.

Fig. 1

The tree $T^0(n,\beta )$

The following lemmas are useful for our argument.

Lemma 2.4

([11]) Let T be a tree of order n with an $\beta$-matching, where $n\ge 2\beta$. Then $H(T)\ge H(T^0(n,\beta ))$. The equality holds if and only if $T\cong T^0(n,\beta )$.

Lemma 2.5

([10]) Let G be a graph and D be a subset of V(G). If D is covered by some matching of G, then is also covered by a maximum matching of G.

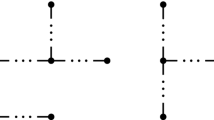
Let $e = uv$ be an edge of a graph G. Let $G'$ be the graph obtained from G by contracting the edge e into a new vertex u(v) and adding a new pendent edge to u(v). We say that $G'$ is obtained from G bys.e.p an edge uv (see Fig. 2).

Fig. 2

Two graphs G and $G^\prime$ for s.e.p.

Lemma 2.6

([9]) Let $e=uv$ be a cut edge of a connected graph G and suppose that $G-uv = G_1\cup G_2$ $(|V(G_1)|, |V(G_2)|\ge 2)$, where $G_1$ and $G_2$ are two components of $G-uv$, $u\in V(G_1)$ and $v\in V(G_2)$. Let $G^\prime$ be the graph obtained from G by running s.e.p on the edge uv. Then $H(G)>H(G^\prime )$.

The following lemma is an easy exercise of calculus.

Lemma 2.7

Let $g(x)=\frac{2}{(a+x)^2}-\frac{2}{(b+x)^2}$, where a, b, and x are the positive integers. Then g(x) is increasing on x when $a\ge b$; g(x) is decreasing on x when $a<b$.

Lemma 2.8

Let $P_k(a, b)(a+b=l,l\ge 2)$ be a tree obtained by attaching a and b pendent vertices to the two pendent vertices u and v of $P_k(k\ge 2)$, respectively. Then we have

$$\begin{aligned} H(P_k(0,l))<H(P_k(1,{l-1}))<\cdots < H\left( P_k\left( {\left\lfloor \frac{l}{2}\right\rfloor }, {\left\lceil \frac{l}{2}\right\rceil }\right) \right) . \end{aligned}$$

Proof

We consider the following two cases.

Case 1 :

$k\ge 3$. That is $uv\notin E(P_k(a, b))$.

Note that $H(P_k(a,b))=\frac{2a}{a+1+1}+\frac{2}{a+1+2} +\frac{2(k-3)}{2+2}+\frac{2b}{b+1+1} +\frac{2}{b+1+2}$ and $a+b=l$.

Let

$$\begin{aligned} f(x)=H(P_k(x,{l-x}))= & {} \frac{2(l-x)}{l-x+1+1}+\frac{2}{l-x+1+2}+\frac{2(k-3)}{2+2}\\&+\frac{2x}{x+1+1}+\frac{2}{x+1+2}. \end{aligned}$$

Then for $0\le x\le \frac{l}{2}$, we have

$$\begin{aligned} f^\prime (x)= & {} \frac{-4}{(l-x+2)^2}+\frac{4}{(x+2)^2}+\frac{2}{(l-x+3)^2}+\frac{-2}{(x+3)^2}\\= & {} 2\left( \frac{2}{(x+2)^2}-\frac{2}{(l-x+2)^2}\right) -\left( \frac{2}{(x+3)^2}-\frac{2}{(l-x+3)^2}\right) \\= & {} \left( \frac{2}{(x+2)^2}-\frac{2}{(l-x+2)^2}\right) +\left[ \left( \frac{2}{(x+2)^2}-\frac{2}{(l-x+2)^2}\right) \right. \\&-\left. \left( \frac{2}{(x+3)^2}-\frac{2}{(l-x+3)^2}\right) \right] . \end{aligned}$$

Note that $\frac{2}{(x+2)^2}-\frac{2}{(l-x+2)^2}>0$ for $0\le x<\lfloor \frac{l}{2}\rfloor$. Thus Lemma 2.7 implies $\left( \frac{2}{(x+2)^2}-\frac{2}{(l-x+2)^2}\right) - \left( \frac{2}{(x+3)^2}-\frac{2}{(l-x+3)^2}\right) >0$. That is $f^\prime (x)>0$ for $0\le x<\lfloor \frac{l}{2}\rfloor$. Moreover, $f^\prime (\frac{l}{2})=0$. Therefore, f(x) is monotonously increasing on $[0,\frac{l}{2}]$.

Case 2 :

$k=2$. That is $uv\in E(P_k(a,b))$.

By the similar argument as Case 1, the result follows.

The proof is completed. $\square$

Lemma 2.9

(Switching transformation) Let $G\in \mathscr {C}_n^\pi$ with uv, $xy\in E(G)$ and uy, $xv\notin E(G)$. Let $G_0=G-uv-xy+uy+vx$. If $d(u)\ge d(x)$ and $d(v)\le d(y)$, then $H(G_0)\ge H(G)$. Moreover, the equality holds if and only if $d(u)=d(x)$ or $d(v)=d(y)$.

Proof

Note that $d(u)\ge d(x)$ and $d(v)\le d(y)$. Then we have

$$\begin{aligned} H(G)-H(G_0)= & {} \frac{2}{d(y)+d(x)}+\frac{2}{d(v)+d(u)}-\frac{2}{d(v)+d(x)}-\frac{2}{d(y)+d(u)}\\= & {} \left( \frac{2}{d(y)\!+\!d(x)}\!-\!\frac{2}{d(v)\!+\!d(x)}\right) \!-\! \left( \frac{2}{d(y)\!+\!d(u)}\!-\!\frac{2}{d(v)\!+\!d(u)}\right) \\= & {} \left( d(v)-d(y)\right) \left( \frac{2}{(d(y)+d(x))(d(v)+d(x))}\right. \\&\qquad \left. -\,\frac{2}{(d(y)+d(u))(d(v)+d(u))}\right) \\\le & {} 0. \end{aligned}$$

Hence, $H(G_0)\ge H(G)$. Moreover, the equality holds if and only if $d(u)=d(x)$ or $d(v)=d(y)$. $\square$

3 The Main Results

In this section, the tree with minimum harmonic index among trees in $\mathscr {T}(n,\gamma )$ is determined, as well as the trees with maximum harmonic index among trees in $\mathscr {T}(n,\gamma )$ when $\gamma =2,\lceil \frac{n}{3}\rceil$. Moreover, we show that among graphs in $\mathscr {C}_n^\pi$, the maximum harmonic index is attained by a BFS graph.

3.1 Trees with Given Domination Number

In this subsection, we consider the problem of determining the tree with maximum(or minimum) harmonic index among trees in $\mathscr {T}(n,\gamma )$. The tree with minimum harmonic index among trees in $\mathscr {T}(n,\gamma )$ is determined, as well as the trees with maximum harmonic index among trees in $\mathscr {T}(n,\gamma )$ when $\gamma =2,\lceil \frac{n}{3}\rceil$.

The following lemmas are needed.

Lemma 3.1

([17]) For a connected graph G, we have $\gamma (G)\le \beta (G)$.

Lemma 3.2

Let $T_0$ be a tree with minimum harmonic index among trees in $\mathscr {T}(n,\gamma )$. Then $\gamma (T_0)=\beta (T_0)=\gamma$.

Proof

By Lemma 3.1, it suffices to prove that $\gamma (T_0)\ge \beta (T_0)$.

Otherwise, assume to the contrary that $\beta (T_0)>\gamma (T_0)=\gamma$. Let $S=\{v_1,v_2,\cdots ,v_\gamma \}$ be a dominating set of $T_0$. Then there exist $\gamma$ independent edges $v_1v^0_1$, $v_2v^0_2$, $\ldots$, $v_\gamma v^0_\gamma$ in $T_0$. Clearly, those $\gamma$ independent edges form a matching of $T_0$ and cover S. Hence, by Lemma 2.5, there exist a maximum matching $M=\{e_1, e_2, \ldots , e_{\beta (T_0)}\}$ in $T_0$ such that M covers S. Note that $|M|=\beta (T_0)>\gamma$. Then we may choose $\gamma$ edges from M. Without loss of generality, we assume that $e_1, e_2, \ldots , e_{\gamma }$ such that $\{e_1, e_2, \ldots , e_{\gamma }\}$ covers S. Let $e_{\gamma +1}=w_1w_2$. Note that if $w_1$, $w_2$ are dominated by the same vertex $v_i\in S$, then there is a triangle $C_3=w_1w_2v_i$ in $T_0$. This is impossible since $T_0\in \mathscr {T}(n,\gamma )$. Thus we conclude that $w_1$, $w_2$ are dominated by two different vertices from S. Without loss of generality, we assume that $w_1$ and $w_2$ are dominated by the vertex $v_1$ and $v_2$, respectively. Clearly, $v_1v_2 \notin E(T_0)$ (otherwise, $T_0$ contains a $C_4=v_1v_2w_2w_1$, which is impossible since $T_0\in \mathscr {T}(n,\gamma )$). Now we construct a new tree $T^\prime _0$ from $T_0$ by running s.e.p on the edges $v_1w_1$ and $v_2w_2$, respectively. Clearly, $S=\{v_1,v_2,\ldots ,v_\gamma \}$ is also a minimum dominating set of $T^\prime _0$. That is $T^\prime _0 \in \mathscr {T}(n,\gamma )$, where $T_0$ and $T^\prime _0$ are shown in Fig. 3, respectively. Then Lemma 2.6 implies that $H(T_0)>H(T^\prime _0)$. This contradicts to the choice of $T_0$. The proof is completed. $\square$

Fig. 3

The structures of $T_0$ and $T^\prime _0$ in Lemma 3.2

From Lemmas 2.4 and 3.2, the following result is immediate.

Theorem 3.3

For any tree $T\in \mathscr {T}(n,\gamma )$, we have

$$\begin{aligned} H(T)\ge \frac{2(n-2\gamma +1)}{n-\gamma +1}+\frac{2(\gamma -1)}{n-\gamma +2}+\frac{2(\gamma -1)}{3}. \end{aligned}$$

Moreover, the equality holds if and only if $T\cong T^0(n,\gamma )$.

Note that if $\gamma =1$, then there is a single tree, i.e., the star $S_n$, in $\mathscr {T}(n,\gamma )$. We now turn to determine the trees with maximum harmonic index among trees in $\mathscr {T}(n,\gamma )$ when $\gamma =2,\lceil \frac{n}{3}\rceil$.

Theorem 3.4

Among trees in $\mathscr {T}(n,\lceil \frac{n}{3}\rceil )$ with $n>4$, the path $P_n$ has the maximal harmonic index.

Proof

It is well known that the path $P_n$ has the maximal harmonic index among trees of order n [19]. Assume that $n=3k+r$ where $0\le r\le 2$ and $S_0=\{v_2,v_5,\cdots ,v_{3k-1}\}$. Note that the vertex subset $S_0$ is dominating set of $P_n$ for $n=3k$, and $S_0\cup \{v_{3k+1}\}$ for $n=3k+1$ or $3k+2$. By the definition of domination number, we have $\gamma (P_n)\le \lceil \frac{n}{3}\rceil$. If $\gamma (P_n)<\lceil \frac{n}{3}\rceil$, that is $\gamma (P_n)\le \lceil \frac{n}{3}\rceil -1$, then we claim that at least three vertex are dominated by one vertex from a dominating set. By the structure of $P_n$, this is impossible. Then we have $\gamma (P_n)=\lceil \frac{n}{3}\rceil$. This completes the proof. $\square$

Theorem 3.5

Among trees in $\mathscr {T}(n,2)$ with $n\ge 4$, the tree $P_4({\lfloor \frac{n-4}{2}\rfloor },{\lceil \frac{n-4}{2}\rceil })$ has the maximal harmonic index.

Proof

If $n=4,5,6$, the result follows in view of Theorem 3.4. In what follows, we consider the case when $n\ge 7$. Assume that $T_1\in \mathscr {T}(n,2)$ has the maximal harmonic index and $S=\{w_1,w_2\}$ is a dominating set of $T_1$. We have the following two claims. $\square$

Claim 1

$w_1$ is not adjacent to $w_2$.

Proof of Claim 1

If not, then $w_1$ and $w_2$ are adjacent. Therefore $T_1$ must be of the form $P_2(a, b)$ with $a+b=n-2$ and $a\le b$. Since by Lemma 2.8, we have $b-a\le 1$. That is $T_1\cong P_2({\lfloor \frac{n-2}{2}\rfloor },{\lceil \frac{n-2}{2}\rceil })$. Note that $\frac{n-2}{2}>2$ for $n>4$ and $P_3({\lfloor \frac{n-2}{2}\rfloor },{\lceil \frac{n-2}{2}\rceil -1})\in \mathscr {T}(n,2)$. It is known that $T_1$ can be obtained from $P_3({\lfloor \frac{n-2}{2}\rfloor },{\lceil \frac{n-2}{2}\rceil -1})$ by s.e.p an cut edge. Thus Lemma 2.6 implies that $H(P_3({\lfloor \frac{n-2}{2}\rfloor },{\lceil \frac{n-2}{2}\rceil -1}))>H(T_1)$, which contradicts the choice of $T_1$. Completing the proof of Claim 1. $\square$

Claim 2

$d(w_1,w_2)=3$.

Proof of Claim 2

From Claim 1, we have $d(w_1,w_2)\ge 2$. If $d(w_1,w_2)\ge 4$, then there exists at least one vertex x on the shortest path between $w_1$ and $w_2$ such that x can not be dominated by the two vertices $w_1$ and $w_2$. This contradicts the fact that $T_1\in \mathscr {T}(n,2)$. Thus, we have $2\le d(w_1,w_2)\le 3$. If $d(w_1,w_2)=2$, then Lemma 2.8 implies that $T_1\cong P_3({\lfloor \frac{n-3}{2}\rfloor },{\lceil \frac{n-3}{2}\rceil })$. Assume that the common neighbor of $w_1$ and $w_2$ is $w_0$. Note that $\frac{n-3}{2}\ge 2$ and $P_4({\lfloor \frac{n-3}{2}\rfloor },{\lceil \frac{n-3}{2}\rceil }-1)\in \mathscr {T}(n,2)$. It is known that $T_1$ can be obtained from $P_4({\lfloor \frac{n-3}{2}\rfloor },{\lceil \frac{n-3}{2}\rceil }-1)$ by s.e.p an cut edge. Thus Lemma 2.6 implies that $H(P_4({\lfloor \frac{n-3}{2}\rfloor },{\lceil \frac{n-3}{2}\rceil }-1))> H(T_1)$, which contradicts the choice of $T_1$. Completing the proof of Claim 2.

From the proof of Claim 2, we find that $T_1$ must be of the form $P_4(a,b)$ with $a+b=n-4$. This together with Lemma 2.8 imply that the result follows. $\square$

3.2 Connected Graphs with Given Degree Sequence

In this section, we show that, there is a BFS graph with maximal harmonic index among graphs in $\mathscr {C}_n^\pi$.

Theorem 3.6

Let $\pi$ be a degree sequence. Then among all graphs in $\mathscr {C}_n^\pi$, there exists a BFS graphs $G^*$ with maximal harmonic index.

Proof

Let G be a graph with maximal harmonic index among all graphs in $\mathscr {C}_n^\pi$. Choose a vertex $v_0$ of degree $\triangle =\triangle (G)$ as its root. Let $v_0\prec v_1\prec \cdots \prec v_{n-1}$ be the well ordering of the vertices of G induced by BFS beginning with $v_0$. Notice that, conditions (i) and (iii) of Definition 2.1 hold for this ordering. If this ordering is not a BFS ordering, then there exist $i<j$ such that $d(v_i)<d(v_j)$. Choose i and j such that $d(v_0)\ge d(v_1)\ge \cdots \ge d(v_{i-1})\ge d(v_j)\ge d(v_k)$ and $d(v_j)>d(v_i)$, where $k\ge i$. Then $i\ge 1$ and $h(v_j)\ge h(v_i)\ge 1$ since $d(v_0)=\triangle$. We consider the following two cases.

Case 1 :

$h(v_i)=h(v_j)$.

Note that $d(v_0)\ge d(v_1)\ge \cdots \ge d(v_{\triangle })$, $v_j\notin V_0\cup V_1$ and hence $h(v_i)=h(v_j)\ge 2$. Let $u_i$ and $u_j$ be the parent of $v_i$ and $v_j$ , respectively. Then $u_i\prec u_j\prec v_i$ and $d(u_i)\ge d(u_j)$, and $u_iv_j$, $u_jv_i\notin E(G)$. Let $G_1=G-u_iv_i-u_jv_j+u_iv_j+u_jv_i$.

Case 2 :

$h(v_i)<h(v_j)$.

Let $u_i$ be the parent of $v_i$ and $u_j\in N(v_j)-N(v_i)-\{v_i\}$. $u_j$ is available since $d(v_j)>d(v_i)$ and $u_i\notin N(v_j)$. Obviously, $u_i\in \{v_0,v_1,\ldots ,v_{i-1}\}$ and $d(u_i)\ge d(u_j)$, and $u_iv_j$, $u_jv_i\notin E(G)$. Let $G_1=G-u_iv_i-u_jv_j+u_iv_j+u_jv_i$.

In both cases we have $G_1\in \mathscr {C}_n^\pi$, and $H(G_1)= H(G)$ from Lemma 2.9. Let $w_0\prec w_1\prec \cdots w_{n-1}$ be the well ordering of the vertices of $G_1$ induced by BFS beginning with $w_0=v_0$. Then we have $d(w_0)\ge d(w_1)\ge \cdots \ge d(w_{i})\ge d(v_k)$ where $k\ge i+1$.

If $G_1$ is not a BFS graph yet, we can repeat the switching transformation $G\longrightarrow G_1$, and finally arrive at a BFS graph $G^*\in \mathscr {C}_n^\pi$ with $H(G^*)= H(G)$. The proof is thus completed. $\square$

Note that Fact 2.2.(d) tells that $T\in \mathscr {T}_n^\pi$ is a greedy tree if and only if T is a BFS tree. Hence, the following result is immediate from Theorem 3.6.

Corollary 3.7

([13]) Given a degree sequence $\pi$, among trees in $\mathscr {T}_n^\pi$, the maximal harmonic index is attained by a greedy tree $T^*$.

Remark 3.8

In fact, a graph with maximal harmonic index in $\mathscr {C}_n^\pi$ need not be a BFS graph, even in the case of trees. For example, let $\pi =(3,3,2,2,1,1,1,1)$, and $T_1$, $T_2\in \mathscr {T}_n^\pi$ be two trees which are shown in Fig. 4, respectively. Clearly, $T_1$ is not a BFS tree and $T_2$ is a BFS tree, but both $T_1$ and $T_2$ are two trees with maximal harmonic index in $\mathscr {T}_n^\pi$, respectively.

Moreover, a BFS graph in $\mathscr {C}_n^\pi$ may not be a graph with maximal harmonic index in $\mathscr {C}_n^\pi$. For example, let $\pi =(4,4,3,3,2,1,1)$, and $G_1$, $G_2\in \mathscr {C}_n^\pi$ be two graphs which are shown in Fig. 5, respectively. Clearly, both $G_1$ and $G_2$ are BFS graphs, and $H(G_1)<H(G_2)$. That is, $G_1$ is a BFS graph but not a graph with maximal harmonic index in $\mathscr {C}_n^\pi$.

Fig. 4

Two trees with degree sequence $\pi =(3,3,2,2,1,1,1,1)$

Fig. 5

Two BFS graphs with degree sequence $\pi =(4,4,3,3,2,1,1)$