Maximum Induced Matching of Hexagonal Graphs

Abstract

A matching in a graph is a set of edges no two of which share a common vertex. A matching is an induced matching if no two edges in the matching have a third edge in the graph connecting them. The problem of finding a maximum induced matching or shortly MIM is known to be NP-hard in general, and it remains so even when the input graph is bipartite. The decision problem of MIM is NP-complete in general, and it remains NP-complete even if restricted to several classes of graphs. On the other hand, the problem has been shown to be polynomial for some special sets of graphs. In this paper, we give tight upper and lower bounds on maximum induced matching in special subset of planar graphs, called hexagonal graphs.

1 Introduction

Let $G=(V,E)$ be a simple connected graph. A set of edges $M\subseteq E(G)$ is a matching or an independent edge set if no two edges of M share a common vertex. Matchings have been researched extensively for many years. In this paper, we consider induced matching, which is a matching in which no two edges in the matching have a third edge in the graph connecting them. In other words, the set of edges in the subgraph of G induced by V(M) coincides with M. Finding a maximum induced matching of a given graph G (or shortly MIM) is a well-known problem. Stockmeyer and Vazirani [16] introduced MIM as a variant of the maximum matching problem and motivated MIM as the “risk-free” marriage problem: find the maximum number of married couples such that each married person is compatible with no married person other than his/her spouse.

Induced matchings have stimulated a great deal of interest in the discrete mathematics community, since finding large induced matchings is a subtask of finding a strong edge colouring (i.e. a proper colouring of the edges such that no edge is adjacent to two edges of the same colour) using a small number of colours. For a brief survey of applications of this type of colouring and some open questions, we refer the reader to [12, 19]. There is an immediate connection between the size of an induced matching and the irredundancy number of a graph [7]. Besides, Golumbic and Lewenstein [8] introduced induced matching as an application for secure communication channels. Similar applications exist for VLSI and network flow problems.

In [5], Edmonds proved that the largest matching in a graph can be computed in polynomial time. On the other hand, Stockmeyer and Vazirani [16] and Cameron in [2] showed that MIM is NP-hard in general and it remains NP-hard even when the input graph is bipartite. Determining whether a graph has an induced matching of size at least k is NP-complete and remains so even if restricted, for example, to bipartite graphs of maximum degree 4, planar bipartite graphs, 3-regular planar graphs and Hamiltonian graphs, see [4] for a detailed history.

On the other hand, MIM has been shown to be solvable in polynomial time for several graph classes, including, for example, chordal graphs, circular arc graphs, weakly chordal graphs and outerplanar graphs (see [4, 14] for a survey and [13] for hhd-free graphs). Recently, authors in [11] showed that planar twinless graphs always contain an induced matching of size at least n / 40, while there are planar twinless graphs that do not contain an induced matching of size $(n+10)/ 27$. They derive similar results for outerplanar graphs and graphs of bounded genus. For trees linear time algorithm for MIM was given by Fricke and Laskar [6]. Independently simpler linear time algorithms were constructed in [8, 20]. Since the problem is NP-hard, several results regarding the approximability of MIM can be found in the literature, see for example [4, 9] and references there. Very recently, the existence of $O(1.4786^n)$-time algorithm for the MIM problem was proved in [3].

In this paper, we discuss MIM for special subset of planar graphs, called hexagonal graphs, which are induced subgraphs of triangular lattice and arise in frequency assignment problem of cellular networks. We take a combinatorial approach to the problem, establishing tight lower and upper bounds on the size of maximum induced matching in an arbitrary hexagonal graph. More precisely, in Sect. 2 we give formal definitions, notions and derive some partial results. In Sect. 3, we give a procedure for a special vertex colouring of hexagonal graphs and some of its consequences. Our main result is given in Sect. 4, where tight bounds on the size of maximum induced matching in an arbitrary hexagonal graph are computed. In the last section, some open problems are presented.

2 Preliminaries

A simple graph is determined by $G=(V,E)$, where $V=V(G)$ is the vertex set and $E=E(G)$ is the set of (unordered) pairs of vertices, called edges. For an edge $\{u,v\}$, we are using a short notation uv and call vertices u and v endpoints of the edge uv. A path on n vertices is denoted by $P_n$. We say that a graph is connected if there is a path between each pair of vertices and is disconnected otherwise.

Let us recall that a set of edges $M\subseteq E(G)$ is called a matching of G if no two edges of M share a common vertex. A matching $M\subseteq E(G)$ of a graph $G=(V,E)$ is said to be an induced matching of G if no two edges in M are joined by an edge of $E(G){\setminus }M$. An induced matching M is a maximum induced matching if M has the maximum size among all induced matchings of the graph. The size of a maximum induced matching of G is denoted by $\nu (G)=\max \{\left| M \right| \mid M \subseteq E(G) {\text { is an induced matching of }} G\}$. For the problem of finding a maximum induced matching of a given graph G, we are using the short abbreviation MIM(G).

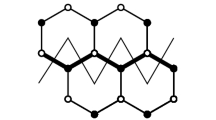
As we already mentioned, we will discuss the MIM problem in a special subclass of planar graphs, called hexagonal graphs. Graph G is called a hexagonal graph if it is induced on the subset of vertices of the triangular lattice. Hexagonal graphs arise within the problem of frequency assignment in cellular networks. For a more detailed explanation of the problem and a survey of existing results on the topic, we refer the reader to [15, 17, 18] and references there. An example of a hexagonal graph is presented in Fig. 1.

Fig. 1

An example of a hexagonal graph

More precisely, we will derive tight bounds for the size of maximum induced matching of a connected hexagonal graph G with respect to the number of vertices of G.

In the continuation of this section, some notations, definitions and some partial results are given. For an arbitrary vertex $v\in V(G)$, the following notations are used:

$\begin{array}{ll} N_{G}(v) &{}{\text {for the }}{} open neighborhood {\text { of vertex }} v\in V(G) \text { in graph } G{:} \\ &{} N_{G}(v)=\{u\in V(G)\mid uv\in E(G)\}; \\ N_{G}\left[ v\right] &{} \text {for the }{} closed neighborhood \text { of vertex } v\in V(G) \text { in graph } G{:}\\ &{} N_{G}\left[ v\right] =\{v\} \cup N_{G}(v); \\ d_{G}(v) &{} \text {for the }{} vertex degree \text { of vertex } v\in V(G) \text { in graph } G{:} \\ &{} d_{G}(v) =\left| N_G(v)\right| ; \\ \delta _{V(G)} &{} \text {for the }{} minimal vertex degree \text { in graph } G. \\ \end{array}$

For an arbitrary edge $e=uv\in E(G)$, the following notations are used:

$\begin{array}{ll} N_{G}(e) &{}\text {for the }{} open neighborhood \text { of edge } e\in E(G) \text { in graph } G{:} \\ &{} N_G(e)=N_G(uv)=(N_G(u)\cup N_G(v)){\setminus }\{u,v\}; \\ N_{G}\left[ e\right] &{} \text {for the }{} closed neighborhood \text { of edge } e\in E(G) \text { in graph } G{:}\\ &{} N_G\left[ e\right] =N_G\left[ uv\right] =N_{G}(u)\cup N_{G}(v); \\ d_{G}(e) &{} \text {for the }{} edge degree \text { of edge } e\in E(G) \text { in graph } G{:} \\ &{} d_G(e)=\left| N_G(uv)\right| =\left| N_G(u)\cup N_G(v)\right| -2; \\ \delta _{E(G)} &{} \text {for the }{} minimal edge degree \text { in graph } G; \\ G(e) &{} \text {for the subgraph of } G \text { induced on vertices } V(G){\setminus }N_G\left[ e\right] {:} \\ &{} G(e)=G{\setminus }N_G\left[ e\right] ; \\ I_G(e) &{} \text {for isolated vertices in } G(e), \\ &{} I_G(e)=\{w\in V(G(e))\mid d_{G(e)}(w)=0\}.\\ \end{array}$

Let G be a connected hexagonal graph. We want to find an induced matching M of G. Note that an induced matching of a graph G actually divides the set of vertices V(G) into two subsets such that endpoints of edges in M are in the first set, say S, and all the other vertices are in the second set, let us say $P=V(G){\setminus }S$, called the set of protectors. Therefore, the induced matching can also be discussed as a special bicolouring $c:V(G)\rightarrow \left\{ \text {white, black} \right\}$, which assigns white colour to vertices of S and black colour to protectors, i.e. vertices of P.

Suppose that edge $e=uv \in E(G)$ belongs to the induced matching M of G, which means that vertices u and v belong to S and are assigned white colour. Note that in this case all vertices in the open neighbourhood of the edge e must be protectors and therefore coloured black. Moreover, all isolated vertices in G(e) are assigned black colours too. Therefore, the inclusion of an edge e to the induced matching M of G contributes $d_G(e)+\left| I_G(e)\right|$ black vertices to the set of protectors P.

The three connected hexagonal graphs $H_1$, $H_2$ and $H_3$ depicted in Figs. 2 and 3 satisfy the following equation:

$$\begin{aligned} \min \{d_{H_{i}}(e)+\left| I_{H_{i}}(e)\right| \mid e\in E(H_{i})\}=5,{\quad } i=1,2,3. \end{aligned}$$

(1)

Fig. 2

Graphs $H_1$ and $H_2$: $\left| V(H_1)\right| =\left| V(H_2)\right| =7$, $\nu (H_1)=\nu (H_2)=1$

Fig. 3

Graph $H_3$: $\left| V(H_3)\right| =13$, $\nu (H_3)=3$

For all the other hexagonal graphs, the result is given in the following lemma. Note that the lemma is very technical and its proof strongly relies on properties of hexagonal graphs. Let us recall that a hexagonal graph G is an induced subgraph of triangular lattice, which means that if $u,v \in V(G)$ are adjacent in underlying triangular lattice, then uv must be an edge in G. Moreover, for every vertex $u \in V(G)$, $d_G(v)\le 6$ and for every edge $e \in E(G)$, $d_G(e)\le 8$.

Lemma 1

Let G be a connected hexagonal graph with $n \ge 2$ vertices which is not isomorphic to graphs $H_1$, $H_2$ or $H_3$. Then

$$\begin{aligned} \min \{d_G(e)+\left| I_G(e)\right| \mid e\in E(G)\}\le 4. \end{aligned}$$

Proof

Let G be a connected hexagonal graph such that $\left| V(G)\right| =n\ge 2$ and $G \ncong H_1,H_2,H_3$. Clearly, for each edge $e\in E(G)$, $d_G(e)+\left| I_G(e)\right| \le n-2$, and thus for $2\le n\le 6$, the statement of the lemma is true.

Suppose that $n\ge 7$. We claim that there exists an edge $e^{\prime }\in E(G)$ such that $d_G(e^{\prime })+\left| I_G(e^{\prime })\right| \le 4$. To prove the claim, we will use the following observation. If for an edge $e=uv\in E(G)$, there is an isolated vertex $w\in I_G(e)$ in G(e), and then for the vertex w, we have $N_{G}(w)\subseteq N_{G}(e)$. Namely, such vertex $w\in I_G(e)$ has just one or at most two (adjacent) neighbours in a connected hexagonal graph G, i.e. either $d_{G}(w)=1$ or $d_{G}(w)=2$, and the neighbourhood $N_{G}(w)$ of the vertex $w\in I_G(e)$ consists either of one vertex or it consists of two adjacent vertices in the set $N_{G}(e)$. Therefore, $\left| I_G(e)\right| >0$ only if $1\le \delta _{V(G)} \le 2$.

It is not difficult to see that for any connected hexagonal graph G, $\delta _{V(G)}\le 3$ and $\delta _{E(G)}\le 4$. If $\delta _{V(G)}=3$, then for an edge e with $d_G(e)=\delta _{E(G)}$ there are no isolated vertices in G(e), and thus, $d_G(e)+\left| I_G(e)\right| =d_G(e)\le 4$.

Furthermore, each vertex of $N_{G}(e)$ can be connected to at most two vertices of $I_G(e)$, and thus, $\left| I_G(e)\right| \le 2d_G(e)$. If $\delta _{E(G)}=1$, then for the edge $e\in E(G)$ such that $d_{G}(e)=\delta _{E(G)}$, $d_{G}(e)+\left| I_G(e)\right| \le 3d_{G}(e) = 3$.

Therefore, it remains to show that there exists an edge $e^{\prime }\in E(G)$ such that $d_{G}(e^{\prime })+\left| I_G(e^{\prime } )\right| \le 4$ only for the cases when $1\le \delta _{V(G)}\le 2$ and $2\le \delta _{E(G)}\le 4$.

• (1) Let $\delta _{V(G)}=1$ and $\delta _{E(G)}\ge 2$. Then for every edge $e=uv \in E(G)$ such that $d_G(u)=1$, $2\le d_G(e)\le 3$.

• (a) Suppose first that there exists the edge $e=uv$ such that $d_G(u)=1$, $d_G(e)=2$ and let $N_{G}(e)=\{v_{1},v_{2}\}$. If $\left| I_G(e)\right| \le 2$, then $d_{G}(e)+\left| I_G(e)\right| \le 4$. Suppose that $\left| I_G(e)\right| \ge 3$. If $v_{1}v_{2} \in E(G)$, then edge $v_1v_2$ can have at most five additional neighbours in G besides v and at most three of them can be non-adjacent. Since vertices of $I_G(e)$ must be non-adjacent, in this case the set $I_G(e)$ contains exactly three vertices, say $I_G(e)=\{w_1,w_2,w_3\}$. According to geometric properties of hexagonal graphs in this case $G\cong H_1$, a contradiction. Suppose $v_{1}v_{2} \notin E(G)$. Then at least one vertex of $N_{G}(e)$, let us say $v_{1}$, has two neighbours in $I_G(e)$, denote them by $w_{1},w_{2}$, and both of them are of degree one, $d_{G}(w_{1})=d_{G}(w_{2})=1$. For the edge $e^{\prime }=w_{1}v_{1}$, we have $N_G(e^{\prime })=\{v,w_{2}\}$ and the subgraph $G(e^{\prime })$ has two components, one of them is isolated vertex u and the other component contains vertex $v_{2}$ and at least one adjacent vertex $w_3 \in I_G(e)$ such that $v_{2}w_{3}\in E(G)$, because $\left| I_G(e)\right| \ge 3$. Thus, $I_G(e^{\prime })=\{u\}$ and $d_G(e^{\prime })+\left| I_G(e^{\prime })\right| =3$.

• (b) Assume now that each edge in E(G) with one endpoint of degree one is of degree three in G. Let $e=uv \in E(G)$, $d_G(u)=1$, $N_{G}(e)=\{v_{1},v_{2},v_{3}\}$ and $v_{1}v_{2}, v_{2}v_{3}\in E(G)$. If $\left| I_G(e)\right| \le 1$, then $d_{G}(e)+\left| I_G(e)\right| \le 4$. Suppose that $\left| I_G(e)\right| \ge 2$ and let $w_{1},w_{2}\in I_G(e)$. Then there are two possibilities, either $d_G(w_1)=d_G(w_2)=1$ or $d_G(w_i)=2$ for at least one vertex $w_i$, $i=1,2$.

  • Let us suppose first there exists a vertex $w_i \in I_G(e)$ with $d_G(w_i)=2$. Without loss of generality, let $d_G(w_1)=2$ and $w_1v_1,w_1v_2\in E(G)$. Then the edge $e^{\prime }=v_{1}w_{1}$ can have only one additional neighbour besides v and $v_2$ in G, and thus, $2\le d_G(e^{\prime }) \le 3$. If $d_{G}(e^{\prime }) =2$, then $N_{G}(e^{\prime }) =\{v,v_2\}$ and the subgraph $G(e^{\prime })$ has two components, one of them is isolated vertex u and the other component contains adjacent vertices $v_{3}$ and $w_2$, and thus, $d_{G}(e^{\prime })+\left| I_G(e^{\prime })\right| =3$. If $d_{G}(e^{\prime }) =3$, then there exists the vertex $z \in N_{G}(v_1)$ such that $N(e^{\prime }) =\{v,v_2,z\}$. If $d_{G}(z)=1$, then $z \in I_G(e)$ and for the edge $zv_1$, we have $N_{G}(zv_1) =\{v,v_2,w_1\}$. Since $G \ncong H_2$, vertex $v_{3}$ must have at least one additional neighbour besides v and $v_{2}$ in G. Therefore, we have $I_G(zv_1)=\{u\}$ and $d_{G}(zv_1)+\left| I_G(zv_1)\right| =4$. If $d_{G}(z)\ge 2$, then the subgraph $G(e^{\prime })$ has three or four components. In both cases, one of the components is isolated vertex u and the other component contains at least two adjacent vertices ($v_{3}$ and $w_2$). Suppose there is a vertex $a\ne u \in I_G(e^{\prime })$. Then $az \in E(G)$, $d_G(a)=1$ and $d_G(az)\le 2$, a contradiction. Therefore $I_G(e^{\prime }) =\{u\}$ and $d_G(e^{\prime })+\left| I_G(e^{\prime })\right| =4$.

  • Suppose now $d_G(w_1)=d_G(w_2)=1$. Since each edge with the endpoint $w_i$ is of degree three, vertices $w_1$ and $w_2$ are neighbours of vertices $v_1$ and $v_3$, let us say $v_1w_1,v_3w_2 \in E(G)$, and there are vertices $z_1, z_3 \in V(G)$ such that $z_1v_1, z_1v_2,z_3v_2, z_3v_3 \in E(G)$. For the edge $e^{\prime }=w_1v_1$, we have $N_G(w_1v_1) =\{v,v_2,z_1\}$ and $u\in I_G(w_1v_1)$. If $\left| I_G(w_1v_1)\right| =1$, then $d_G(e^{\prime })+\left| I_G(e^{\prime })\right| =4$. If $\left| I_G(w_1v_1)\right| \ge 2$, then there exists a neighbour a of $z_1$ such that $a\in I_G(w_1v_1)$, and consequently, there exists a vertex $z_2\in V(G)$ such that $z_2z_1,z_2v_2, z_2z_3 \in E(G)$, since $d_G(az_1)=3$. Note that for the edge $az_1$ we have $1\le \left| I_G(az_1)\right| \le 2$. If $\left| I_G(az_1)\right| =1$, then $d_G(az_1)+\left| I_G(az_1)\right| =4$. If $\left| I_G(az_1)\right| =2$, then for the edge $w_2v_3$ we have $d_G(w_2v_3)+\left| I_G(w_2v_3)\right| =4$, since $G \ncong H_3$.

• (2) Suppose now $\delta _{V(G)}=2$ and let $e=uv\in E(G)$ be an edge with minimal edge degree, i.e. $d_G(e)=\delta _{E(G)}\ge 2$. If there exists vertex $w\in I_G(e)$, then $d_G(w)=2$ and vertex w is a neighbour of two adjacent vertices from $N_G(e)$.

• (a) If $d_G(e)=\delta _{E(G)}=2$, then $\left| I_G(e)\right| \le 1$ and $d_G(e)+\left| I_G(e)\right| \le 3$.

• (b) If $d_G(e)=\delta _{E(G)}=3$, then $\left| I_G(e)\right| \le 2$. If $\left| I_G(e)\right| \le 1$, then $d_G(e)+\left| I_G(e)\right| \le 4$. Let us suppose that $\left| I_G(e)\right| =2$ and let us denote $N_G(e)=\{v_{1},v_{2},v_{3}\}$. As $\delta _{V(G)}=2$, vertices $v_{1}$, $v_{2}$ and $v_{3}$ must be consecutive in triangular lattice such that $uv_1,vv_1,vv_2,vv_3,v_{1}v_{2},v_{2}v_{3}\in E(G)$ and $I_G(e)=\{w_{1},w_{2}\}$, where $w_1v_1,w_1v_2,w_2v_2,w_{2}v_{3}\in E(G)$. Then for the edge $e^{\prime }=v_{1}w_1$, we have $d_G(e^{\prime })=3$, $\left| I_G(e^{\prime })\right| =0$ and $d_G(e^{\prime })+\left| I_G(e^{\prime })\right| =3$.

• (c) If $d_G(e)=\delta _{E(G)}=4$ and $\left| I_G(e)\right| =0$, then $d_G(e)+\left| I_G(e)\right| =4$. Suppose now $N_G(e)=\left\{ v_0,v_1,v_2,v_3\right\}$ and $w\in I_G(e)$ is a neighbour of adjacent vertices $v_{1},v_{2}$. Since $d_G(w)=2$ and $\delta _{E(G)}=4$, we have $d_G(v_1)=d_G(v_2)=5$ and $d_G(wv_1)=d_G(wv_2)=4$. There are only two non-isomorphic cases for position of vertices $v_1$ and $v_2$ regarding vertices u, v. Either one of the vertices $v_1$ and $v_2$ is a common neighbour of u and v (say $v_1$), or both vertices $v_1$ and $v_2$ are common neighbours of just one of the vertices u and v, say v. In both cases, vertices $v_0,v_1,v_2$ and $v_3$ must be consecutive in triangular lattice, and without loss of generality, let $v_0v_1,v_2v_3 \in E(G)$. In the first case, $N_G(wv_1)=\left\{ v_0,u,v,v_2\right\}$ and subgraph $G(wv_1)$ has at most two components. One component contains vertex $v_3$ and at least one additional vertex as $d_G(v_2)=5$. Suppose that the other component is isolated vertex $v^{\prime }$. But then $N_G(v^{\prime })=\left\{ v_0\right\}$, a contradiction as $\delta _{V(G)}=2$. Therefore, $\left| I_G(wv_1)\right| =0$ and $d_G(wv_1)+\left| I_G(wv_1)\right| =4$. Without loss of generality, let $uv_0,vv_0,vv_1,vv_2,vv_3 \in E(G)$ in the second case. As $d_G(v_2)=5$, there exists a vertex a such that $av_2,av_3 \in E(G)$. Then $N_G(wv_2)=\left\{ v_1,v,v_3,a\right\}$, and one component of subgraph $G(wv_2)$ contains at least three consecutive vertices where two of them are u and $v_0$. Suppose there exists vertex $v^{\prime } \in I_G(wv_2)$. But then $N_G(v^{\prime } )=\left\{ a,v_3\right\}$ and $N_G(v^{\prime }v_3)=\left\{ a,v_2,v\right\}$, a contradiction as $\delta _{E(G)}=4$. Therefore $\left| I_G(wv_2)\right| =0$ and $d_G(wv_2)+\left| I_G(wv_2)\right| =4$. $\square$

3 A Procedure for Vertex Colouring of Hexagonal Graphs

In this section, a procedure for a special vertex colouring of hexagonal graphs and some consequences are given.

Let G be an arbitrary connected hexagonal graph with $\left| V(G)\right| \ge 2$. The following procedure presents a bicolouring $c:V(G) \rightarrow \left\{ \text {white, black} \right\}$, which assigns white colours to vertices of S and black colours to vertices of P, called protectors, such that $V(G)=S\cup P$.

Procedure 2

Let G be a connected hexagonal graph such that $\left| V(G)\right| \ge 2$, and let $H_1$, $H_2$ and $H_3$ be graphs depicted in Figs. 2 and 3, respectively.

• Step 1 If graph G is isomorphic to graph $H_1$ or to graph $H_2$, then colour two adjacent vertices white and other five vertices black. If graph G is isomorphic to graph $H_3$, then colour six vertices white and seven vertices black such that each white vertex is a neighbour of exactly one white vertex.

• Step 2 If graph G is not isomorphic to any of the graphs $H_1$, $H_2$ and $H_3$, then do what follows.

  • Step 2a If there exists one, choose an edge $e\in E(G)$ with minimal possible number $d_G(e)+\left| I_G(e)\right| \le 4$ so that the subgraph $G(e){\setminus }I_G(e)$ is either a connected or an empty graph.

  • Step 2b Otherwise, choose an edge $e\in E(G)$ with minimal possible number $d_G(e)+\left| I_G(e)\right| \le 4$ so that the subgraph $G(e){\setminus }I_G(e)$ is not a connected graph.

  Colour the endpoints of the edge e white and vertices of $N_{G}(e)\cup I_G(e)$ black.

While there exists one, for every connected uncoloured component $G_i$ of the subgraph $G(e){\setminus }I_G(e)$ go to the Step 1 $(G\rightarrow G_i)$.

Note that Step 2 of the procedure is divided into substeps (2a) and (2b). At first it looks like that every connected hexagonal graph G such that $G \ncong H_1, H_2, H_3$ belongs to Step 2a, but actually this is not the case. Namely, Fig. 4 represents an example of a hexagonal graph $G_1$ that belongs to Step 2b. More precisely, for every edge e such that $d_{G_1}(e)+\left| I_{G_1}(e)\right| \le 4$, the subgraph $G_{1}(e){\setminus }I_{G_{1}}(e)$ is disconnected.

Proposition 3

Let G be a connected hexagonal graph coloured by Procedure 2, and let S be the set of vertices that were assigned white colour. Then, vertices of the set S correspond to endpoints of edges of an induced matching of G and $\nu (G) \ge \frac{\left| S\right| }{2}$.

Proof

Statement of Proposition 3 is clear for the graphs $H_1, H_2$ and $H_3$. If $G \ncong H_1, H_2, H_3$, then by Lemma 1 there exists an edge $e\in E(G)$ with $d_G(e)+\left| I_G(e)\right| \le 4$, and $G(e){\setminus }I_G(e)$ is either a connected graph or a disconnected graph or an empty graph. For the edge $e=uv$, chosen by the Procedure 2, vertices in its open neighbourhood $N_G(e)$ and isolated vertices in $G(e)=G{\setminus }N_G\left[ e \right]$ were coloured black. Therefore, a particular colouring within the procedure is independent of all colourings of the previous loops in the procedure. It follows that at the end of the procedure each white vertex is a neighbour of exactly one white vertex. Thus, vertices coloured white by the Procedure 2 correspond to endpoints of the edges of an induced matching M in G, and $\left| M \right| =\left| S\right| / 2$, where S is a set of white vertices. Therefore, $\nu (G)=\max \{\left| M \right| \mid M \subseteq E(G) {\text { is an induced matching of }} G\}\ge \left| S\right| / 2$. $\square$

Fig. 4

Graph $G_1$: $\left| V(G_1)\right| =10$, $\nu (G_1)=3$

In the sequel, we will determine the number of protectors needed for a given number of white vertices representing edge endpoints of an induced matching in an arbitrary hexagonal graph, which will be used in the next section. Note that edges with both endpoints coloured white are called white edges. The set of white edges corresponds to induced matching.

Lemma 4

For each connected hexagonal graph, which is not isomorphic to any of graphs $H_1$, $H_2$ and $H_3$, at most one connected component, obtained during the realization of Procedure 2, can be isomorphic either to $H_1$ or to $H_2$.

Proof

Let G be a connected hexagonal graph such that $G \ncong H_1, H_2, H_3$. Suppose that at each step of the Procedure 2 there exists an edge $e\in E(G_{i})\subseteq E(G)$ with $d_{G_i}(e)+\left| I_{G_{i}}(e)\right| \le 4$ (where $G_i$ represents the uncoloured connected component after previous colourings) such that the subgraph $G_i(e){\setminus }I_{G_{i}}(e)$ is a connected (or an empty) graph. In this case, according to Eq. (1), graphs $H_1$ or $H_2$ can be isomorphic only to the last component.

Suppose now that during the realization of Procedure 2 we have to choose an edge $e\in E(G_{i})\subseteq E(G)$ with $d_{G_{i}}(e)+\left| I_{G_{i}}(e)\right| \le 4$ such that $G_i(e){\setminus }I_{G_{i}}(e)$ is a disconnected graph and one of the components is isomorphic either to $H_1$ or to $H_2$. Because we got this component by removing the edge e together with its neighbourhood from graph $G_i$, vertices of the component may have been adjacent only to the vertices in $N_{G_i}(e)$. Without loss of generality, suppose that the component is isomorphic to $H_1$. Note that $H_1$ has four vertices of degree at most two. Let us denote them by $v_1,v_2,v_3$ and $v_4$ in the clockwise direction in triangular lattice. Because of the structure of the graph $H_1$, at least one of its vertices of degree at most two, say $v_k$, where $k \in \left\{ 1,2,3,4\right\}$, must have been adjacent to at least one of the vertices in $N_{G_i}(e)$. Then the vertex $v_l \in \left\{ v_1,v_2,v_3,v_4 \right\} {\setminus }\left\{ v_k \right\}$ such that $l \equiv k+2$ (mod 5) could not be adjacent to the vertices in $N_{G_i}(e)$. Therefore, there exists an edge $e^{\prime }\in E(G_{i})$ with one endpoint $v_l$ such that $d_{G_{i}}(e^{\prime })+\left| I_{G_{i}}(e^{\prime })\right| \le 4$ and $G_{i}(e^{\prime }){\setminus }I_{G_{i}}(e^{\prime })$ is a connected graph, a contradiction. The same can be shown for the graph $H_2$. It follows that if we choose Step 2b of Procedure 2, then components in the graph $G_i(e){\setminus }I_{G_{i}}(e)$ cannot be isomorphic neither to $H_1$ nor to $H_2$.

Finally, suppose that during the realization of Procedure 2 we have to choose an edge $e\in E(G_{i})\subseteq E(G)$ with $d_{G_{i}}(e)+\left| I_{G_{i}}(e)\right| \le 4$ such that $G_i(e){\setminus }I_{G_{i}}(e)$ is a disconnected graph and one of the components has more then seven vertices. Suppose that during the continuation of the Procedure 2 on this component, the last subgraph is isomorphic either to $H_1$ or to $H_2$. In this case, there would exist an edge $e^{\prime }$ (in the last subgraph isomorphic either to $H_1$ or to $H_2$) such that $G_i(e^{\prime }){\setminus }I_{G_{i}}(e^{\prime })$ is a connected graph. $\square$

Lemma 5

Let G be a connected hexagonal graph and M an induced matching of G. Further, let S be the set of endpoints of edges of M. For the set of protectors $P=V(G)\backslash S$, we have

$$\begin{aligned} \frac{\left| S \right| -2}{4} \le \left| P \right| \le 2 \left| S \right| +1. \end{aligned}$$

Proof

Let M be an induced matching of a connected hexagonal graph G and $P=V(G)\backslash S$, where S is the set of endpoints of edges of M.

To prove the upper bound, we take into account the following facts. For graphs $H_1$ and $H_2$ from Fig. 2, five protectors are needed for only one white edge, i.e. for two white vertices. On the other hand, for graph $H_3$ only seven protectors are needed for three white edges, which means that less than three protectors are needed per one white edge. Thus, by Lemmas 1 and 4, it follows that for colouring by Procedure 2 at most four protectors are needed for every white edge, except maybe for one (the last) white edge, where five black protectors are needed. Therefore, for an arbitrary connected hexagonal graph G, at most $4(\left| S \right| / 2-1)+5=2 \left| S \right| +1$ protectors are needed for $\left| S \right| / 2$ white edges.

For the lower bound, note that each black vertex of P can have at most three white neighbours which are endpoints of white edges (see graph $G_3$ depicted in Fig. 6). A connected hexagonal graph, where each black vertex is a neighbour of exactly three white edges, can be obtained by gluing graph $G_3$ and several copies of $\hat{P}_5$ depicted in Fig. 7 (for details see the next section). Note that in the graph obtained by $G_3$ and $k-1$ copies of $\hat{P}_5$ we have k black vertices and $3+(k-1) \cdot 2=2k+1$ white edges. Therefore, for $\left| P \right|$ black vertices, there are at most $3\left| P \right| -(\left| P \right| -1)=2\left| P \right| +1$ white edges in M, and thus, $\left| M \right| = \left| S\right| / 2 \le 2\left| P \right| +1$, and we have $(\left| S\right| -2) / 4 \le \left| P \right|$. $\square$

Both inequalities of Lemma 5 are tight. Namely, the example of the connected hexagonal graph $G_2$ depicted on Fig. 5 attains the maximal possible number of protectors depending on the number of white edges, $\left| P(G_2)\right| =17=2 \cdot 8+1=2 \left| S(G_2) \right| +1$. On the other hand, the example of hexagonal graph $G_3$ in Fig. 6 attains the lower bound for the number of protectors, $\left| P(G_3)\right| =1=(6-2) / 4$.

Fig. 5

Graph $G_2$: $\left| V(G_2)\right| =25$, $\nu (G_2)=4$

Fig. 6

Graph $G_3$: $\left| V(G_3)\right| =7$, $\nu (G_3)=3$

4 The Main Result

In this section, the lower and the upper bounds for $\nu (G)$ in an arbitrary connected hexagonal graph G are given. First, we will prove the lower bound.

Proposition 6

Let G be a connected hexagonal graph with $n\ge 2$ vertices. Then

$$\begin{aligned} \nu (G)\ge \left\lceil \frac{n-1}{6}\right\rceil . \end{aligned}$$

Proof

Let G be a connected hexagonal graph with $n= \left| V(G)\right| \ge 2$. For hexagonal graphs $H_i$, $i=1,2,3$ from Figs. 2 and 3, we have $\nu (H_1)= \nu (H_2)=1=(7-1) / 6$, and $\nu (H_3)=3 > (13-1) / 6$.

Suppose now that $G \ncong H_1, H_2, H_3$. Let us apply Procedure 2 on graph G. By Proposition 3, the colouring with Procedure 2 corresponds to an induced matching M and $\nu (G) \ge \left| S\right| / 2=\left| M \right|$, where S is a set of white vertices (i.e. endpoints of edges of M). Considering $\left| P \right| =n- \left| S \right|$ and Lemma 5, we get $n-\left| S \right| \le 2\left| S \right| +1$ or $\left| S \right| \ge (n-1) / 3$. Therefore, $\nu (G)\ge \left| S \right| / 2 \ge (n-1) / 6$ and as $\nu (G)$ is an integer; the inequality $\nu (G) \ge \left\lceil (n-1) / 6\right\rceil$ actually holds. $\square$

Note that bound of Proposition 6 is tight. Namely, for each $n\ge 2$ there exists a hexagonal graph G, obtained by connecting several components of graph $H_1$, with $\nu (G)$ equal to the bound of Proposition 6. For example, Fig. 5 represents graph $G_2$, obtained by connecting four components of graph $H_1$ such that $n=25$ and $\nu (G)=\left\lceil (n-1) / 6\right\rceil =4$.

For obtaining the upper bound of $\nu (G)$ in an arbitrary connected hexagonal graph G, we will try to construct a connected hexagonal graph on $n \ge 2$ vertices such that the cardinality of the maximum induced matching set M of G is as large as possible among all hexagonal graphs with n vertices. In other words, we will construct a connected hexagonal graph with maximum possible number of white edges regarding the number of vertices.

For $n=2$, we get a path $P_2$ with $\nu (G)=1$. It is obvious that we have to add at least three additional vertices to the graph $P_2$ to obtain another white edge. One of the possible graphs with $n=5$ and $\nu (G)=2$ is a path $P_5$. The third white edge can be obtained if we add another two vertices such that we obtain a special hexagonal graph on seven vertices, depicted on Fig. 6. Note that in every other connected hexagonal graph on seven vertices, including path $P_7$, we can obtain at most two white edges. Therefore, by adding every additional five vertices to the existent connected hexagonal graph, we can contribute at most two additional white edges in the following way. We add a special path on five vertices $\hat{P}_5$ with the following geometric properties: the inner two edges of the path form a $120^{\circ }$ angle between each other and a $180^{\circ }$ angle with the other neighbouring edge (see Fig. 7), such that the middle vertex of the path is connected to one of the endpoints of white edges in the existent graph.

Fig. 7

Path $\hat{P}_5$ with $\nu (\hat{P}_5)=2$

Using this construction, we obtain a special tree on n vertices, which is denoted by $\hat{T}_n$. More precisely, a construction of a hexagonal graph $\hat{T}_n$ is the following. We start with a path $P_2$ and then continue with connecting several (say k) copies of a path $\hat{P}_5$ such that the middle vertex of the particular path $\hat{P}_5$ is connected to one of the endpoints of the starting edge or to one of the endpoints of previously connected paths $\hat{P}_5$. At the end, we can add at most four additional vertices. Therefore, $n=\left| V(\hat{T}_n) \right| =2+5k+l$, where $k= \left\lfloor (n-2) / 5\right\rfloor$ and l is an integer such that $0 \le l \le 4$. Figure 8 shows one of the possible examples of such a tree with 15 vertices denoted by $\hat{T}_{15}$. This tree is composed of the starting path $P_2$, two copies of path $\hat{P}_5$ and three additional vertices.

Fig. 8

Tree $\hat{T}_{15}$ with $\nu (\hat{T}_{15})=6$

Lemma 7

For a graph $\hat{T}_n$ with $n=2+5k+l$ and $l\in \{0,1,2,3,4\}$, we have:

$$\begin{aligned} \nu (\hat{T}_n)= \left\{ \begin{array}{ll} 2 \left\lfloor \frac{n-2}{5}\right\rfloor +1 &{}\quad \hbox {if}{\quad } l\in \{0,1,2\}\\ 2 \left\lfloor \frac{n-2}{5}\right\rfloor +2&{}\quad \hbox {if}{\quad }l\in \{3,4\} \\ \end{array} \right. . \end{aligned}$$

Proof

Let $0\le l \le 2$. Then, the maximum induced matching set M (set of white edges) of $\hat{T}_n$ consists of one edge from the starting path $P_2$ and of two edges from every path $\hat{P}_5$. Therefore, there are $1+2k$ white edges in this case. Using $k= \left\lfloor (n-2) / 5\right\rfloor$, the equality is proved.

In the case $3\le l \le 4$, there is one additional white edge in comparison with the previous case, so we have $2k+2$ white edges. $\square$

Proposition 8

Let G be a connected hexagonal graph with $n\ge 2$ vertices and let $n=2+5k+l$ where $l\in \{0,1,2,3,4\}$. Then

$$\begin{aligned} \nu (G)\le \left\{ \begin{array}{ll} 2 \left\lfloor \frac{n-2}{5}\right\rfloor +1 &{}\quad \hbox {if}{\quad }l\in \{0,1,2\}\\ 2 \left\lfloor \frac{n-2}{5}\right\rfloor +2&{}\quad \hbox {if}{\quad }l\in \{3,4\} \\ \end{array} \right. . \end{aligned}$$

Proof

According to Lemma 7, for a given $n \ge 2$ the bound is attained by a graph $\hat{T}_n$. Suppose there exists a hexagonal graph G with $n\ge 2$ such that $\nu (G) > \nu (\hat{T}_n)$. Let M be a maximum induced matching of G, and let S be the set of endpoints of edges of M. Further let $n=2+5k+l$, where $l\in \{0,1,2,3,4\}$. Then $k= \left\lfloor (n-2) / 5\right\rfloor$.

For $0\le l \le 2$, we have $\nu (G)\ge 2 \left\lfloor (n-2) / 5\right\rfloor +1+1=2k+2$. Therefore, $\left| S\right| =2\nu (G) \ge 4k+4$ and $\left| P\right| =n- \left| S\right| \le 2+5k+l-(4k+4)=k+l-2 \le k$. Using Lemma 5, we have $\nu (G)=\left| M\right| =\left| S\right| / 2 \le 2 \left| P\right| -1 \le 2k-1$, a contradiction.

Similarly, for $3\le l \le 4$ we have $\nu (G)\ge 2 \left\lfloor (n-2) / 5\right\rfloor +2+1=2k+3$. Therefore, $\left| S\right| =2\nu (G) \ge 4k+6$ and $\left| P\right| =n- \left| S\right| \le 2+5k+l-(4k+6)=k+l-4 \le k$. Using Lemma 5, we again have $\nu (G) \le 2k-1$, a contradiction. $\square$

Using Propositions 6 and 8, we obtain the following theorem.

Theorem 9

Let G be a connected hexagonal graph with $n\ge 2$ vertices and let $n=2+5k+l$ where $l\in \{0,1,2,3,4\}$. Then

$$\begin{aligned} \left\lceil \frac{n-1}{6}\right\rceil \le \nu (G)\le \left\{ \begin{array}{ll} 2 \left\lfloor \frac{n-2}{5}\right\rfloor +1 &{}\quad \hbox {if}{\quad }l\in \{0,1,2\}\\ 2 \left\lfloor \frac{n-2}{5}\right\rfloor +2&{}\quad \hbox {if}{\quad }l\in \{3,4\} \\ \end{array} \right. . \end{aligned}$$

Proof

Straightforward by Propositions 6 and 8. $\square$

5 Conclusions

If we are interested in the number of vertices in the set P, i.e. the number of protectors, the problem is very similar to the problem of finding a graph invariant $\psi _3$, which is a special case of so-called k-path vertex problem defined recently in [1]. The problem is to find the minimum number of vertices needed to destroy every path of order k in G, denoted by $\psi _{k}(G)$. For the case $k=3$, we are looking for the minimal cardinality set of protectors P needed to destroy every path of order 3. In this case, vertices of the set $S=V(G)\backslash P$ induce a subgraph with maximum degree 1 and thus correspond to the so-called dissociation set of G. Therefore, for $\psi _{3}(G)$ problem, a graph induced by vertices in the set S is composed of paths $P_2$ and isolated vertices, while in our problem the set S induces a graph composed only of paths $P_2$. Determining $\psi _{k}(G)$ for $k\ge 2$ was shown to be NP-hard problem in general and polynomial only for some special sets of graphs (for details we refer to [1, 10] and references there). Therefore, it would be interesting to examine $\psi _3(G)$ or even $\psi _k(G)$ for hexagonal graphs.